Понятие вектора. Коллинеарные векторы. Длина и направление вектора – онлайн-тренажер для подготовки к ЕНТ, итоговой аттестации и ВОУД

Запомнить

Восстановить пароль

Регистрация

Конспект

Вектором называется направленный отрезок, для которого указано его начало и конец.

В данном случае началом отрезка является точка \(A\), концом отрезка – точка \(B\). Сам вектор обозначен через \(\vec{AB}\).

Расстояние между началом и концом вектора называется его длиной или модулем вектора. Для обозначения длины вектора используются две вертикальные линии слева и справа \(|\vec{AB}|\). Вектор, начало и конец которого совпадают, называется нулевым, его длина равна нулю. Если длина вектора положительна, то его называют ненулевым.

Нену­ле­вые век­то­ры на­зы­ва­ют­ся кол­ли­не­ар­ны­ми, если они лежат на одной пря­мой либо на па­рал­лель­ных пря­мых.

Коллинеарность векторов обозначается знаком \(\parallel\). Ну­ле­вой век­тор, то есть век­тор ну­ле­вой длины, счи­та­ет­ся кол­ли­не­ар­ным любо­му век­то­ру.

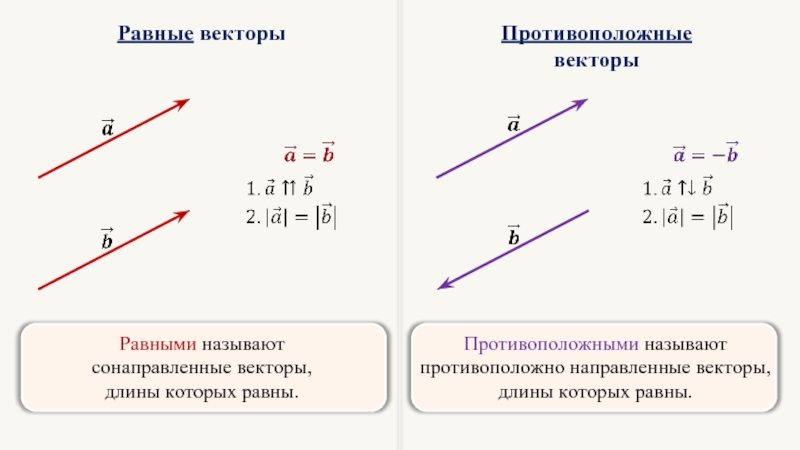
Век­то­ры \(\vec{a} \  и \ \vec{b}\) называются противоположно направленными векторами, если их направления противоположны: \(\vec{a} \uparrow \downarrow \vec{b}\).

 

Век­то­ры \(\vec{a} \  и \ \vec{b}\) называются сонаправленными векторами, если их направления совпадают: \(\vec{a} \uparrow \uparrow \vec{b}\).

Векторы \(\vec{a} \  и \ \vec{b}\) называются равными, если они лежат на одной или параллельных прямых, их направления совпадают, а длины равны.

Единичным вектором,

или ортом, называется вектор, длина которого равна единице.

Вопросы

1. Найдите длину вектора.

   \(\vec{a}(4;3)\)

2. Найдите вектор \(\vec{a}\), перпендикулярный вектору \(\vec{b} (5; 3)\), если их длины равны.

3. Определите координаты единичного вектора, сонаправленного с вектором \(\vec{p}(-\sqrt3;1)\).

4. Длина вектора \(\vec{a}\) (6; m) равна 10, длина вектора \(\vec{b}\) (n; 12) равна 13. Значения m и n равны

Сообщить об ошибке

Обязательные

Математическая грамотность

Грамотность чтения

История Казахстана

Предметы по профилю

Биология

Химия

Английский язык

Французский язык

География

Немецкий язык

Информатика

Основы права

Русская литература

Математика

Физика

Русский язык

Всемирная история

Укажите предмет *

Скопируйте и вставьте вопрос задания *

Опишите подробнее найденную ошибку в задании *

Прикрепите скриншот

Объем файла не должен превышать 1МБ

Казахский

Русский

Обратите внимание! По выбранным Вами предметам ГРАНТЫ не предоставлены. В AlmaU, Университете Нархоз и Каспийском Университете представлены специальности, где профильными предметами являются математика, физика, география, иностранный язык, Человек. Общество. Право, всемирная история, биология, химия и творческий экзамен.

1. Скачайте приложение iTest, используя QR-код или строку поиска в AppStore или Play Market

2. Авторизуйтесь в приложении и готовьтесь к экзаменам вместе с нами

1) Понятие вектора,модуль,коллинеарность и компланарность векторов.Геометрическое и экономическое понятие

1) Вектором называется направленный отрезок (или, что то же, упорядоченная пара точек). Обозначают: (точка A — начало вектора, точка В — конец вектора) или одной буквой — .2)Длиной вектора (модулем) называется расстояние между началом и концом вектора. Длина вектора обозначается | | или | |..3) Нулевым вектором называется вектор, у которого начало и конец совпадают. Обозначают: .. 4)Единичным вектором называется вектор, длина которого равна единице.

Единичный вектор, имеющий одинаковое направление с данным вектором , называется ортом вектора и обозначается обычно символом ..5) Векторы называются коллинеарными, если они расположены на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому вектору.. 6)Векторы называются равными, если они коллинеарны, имеют одинаковые длины и одинаковое направление.Три вектора в пространстве называются

компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Если среди трех векторов хотя бы один нулевой или два любые коллинеарны, то такие векторы компланарны Длиной или модулем вектора АВ называется длина отрезка и обозначается |АВ|. Вектор, длина которого равна нулю, называется нулевым вектором и обозначается 0 . Нулевой вектор направления не имеет.Понятие вектор в геометрии отлично от определяемого в алгебре. Различают понятие свободного и связанного (приложенного, закреплённого) вектора. Связанный вектор или направленный отрезок — упорядоченная пара точек евклидова пространства. Свободный вектор — класс эквивалентности направленных отрезков.При этом два направленных отрезка считаются эквивалентными, если они:коллинеарны,равны по длине,одинаково направлены (сонаправлены)Существует естественный изоморфизм свободных векторов и параллельных переносов пространства (каждый перенос взаимно однозначно соответствует какому-то свободному вектору). На этом также строят геометрическое определение свободного вектора, просто отождествляя его с соответственным переносом.Большую роль играют векторы в изучении бесконечно малых трансформаций пространства.

Сложение двух свободных векторов можно осуществлять как по правилу параллелограмма, так и по правилу треугольника.Правило треугольника. Для сложения двух векторов и по правилу треугольника оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора, а конец с концом второго вектора.

Правило параллелограмма. Для сложения двух векторов и по правилу параллелограмма оба эти вектора переносятся параллельно самим себе так, чтобы их начала совпадали. Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала.А модуль (длину) вектора суммы определяют по теореме косинусов где  — угол между векторами, когда начало одного совпадает с концом другого. Так же используется формула теперь  — угол между векторами выходящими из одной точки.Сложение двух скользящих векторов определено лишь в случае, когда прямые, на которых они расположены, пересекаются. Тогда каждый из векторов переносится вдоль своей прямой в точку пересечения этих прямых, после чего сложение осуществляется по правилу параллелограмма.Сложение двух фиксированных векторов определено лишь в случае, когда они имеют общее начало. Их сложение в этом случае осуществляется по правилу параллелограмма. Сложение коллинеарных скользящих векторовЕсли скользящие векторы параллельны, то при их сложении главная трудность состоит в определении прямой, на которой будет расположена их сумма. (Величину и направление вектора суммы было бы естественно определить точно так же, как и в случае сложения свободных векторов.) В

механике при изучении статики для решения вопроса о сложении параллельных сил, которые, как известно, задаются скользящими векторами, вводится дополнительная гипотеза: к системе векторов можно добавить два вектора, равных по величине, противоположных по направлению и расположенных на одной прямой, пересекающей прямые, на которых расположены данные вектора. Пусть, например, надо сложить скользящие векторы и , расположенные на параллельных прямых. Добавим к ним векторы и , расположенные на одной прямой. Прямые, на которых расположены векторы и , и пересекаются. Поэтому определены векторы Прямые, на которых расположены векторы и , пересекаются всегда, за исключением случая, когда векторы и равны по величине и противоположны по направлению, в котором говорят, что векторы и образуют пару (векторов).Таким образом, под суммой векторов и можно понимать сумму векторов и , и эта сумма векторов определена корректно во всех случаях, когда векторы и не образуют пару. Произведение вектора на числоПроизведением вектора и числа λ называется вектор, обозначаемый (или ), модуль которого равен , а направление совпадает с направлением вектора , если , и противоположно ему, если . Если же , или вектор нулевой, тогда и только тогда произведение  — нулевой вектор.Обычно принято в записи произведения числа и вектора число записывать слева, но в принципе допустим и обратный порядок, хотя все же обычное соглашение состоит в том, чтобы его избегать, если нет прямой необходимости. Так или иначе, . Из определения произведения вектора на число легко вывести следующие свойства:если , то . Наоборот, если , то при некотором λ верно равенство ; всегда °, то есть каждый вектор равен произведению его модуля на орт.

Reddit — Погрузитесь во что угодно

TL;DR: Легко интерпретировать векторную величину в знакомых физических областях (например, евклидово расстояние; физические силы). Но что тот же расчет говорит мне применительно к непространственным/нефизическим областям (например, семантическое значение через встраивание слов; векторы, компоненты которых кодируют совершенно разные измерения/единицы, такие как стоимость дома и количество спален)? В конечном счете, я ищу общее, абстрактное и интуитивное понимание того, что на самом деле означает величина вектора, как только мы отойдем от самых знакомых приложений.

Понятие длины вектора очень легко и естественно интерпретировать при использовании для описания физического пространства. Действительно, простые геометрические примеры в R ² обычно используются учителями для первого ознакомления с идеей, например, вычисление длины гипотенузы на миллиметровой бумаге или расстояния между двумя точками на карте. Отсюда всего лишь небольшой скачок, чтобы расширить идею до R ³ , где длина вектора может эквивалентно описывать расстояние или траекторию в трехмерном пространстве. Как только ум был таким образом освобожден, простираясь до R ⁿ не слишком сложно, даже если визуализировать такое пространство сложно или невозможно. Например, хотя я не могу представить себе, как может выглядеть 10-мерное пространство, я все же понимаю, что путь мяча, брошенного через такое пространство, может быть представлен длиной вектора с 10 компонентами. Это та же самая идея, что и расстояние на 2D-карте, просто экстраполированное на более высокие измерения.

Итак, это евклидово расстояние, но не менее распространенное применение векторов — описание физических сил. В этой ситуации длину вектора, возможно, более правильно описать как величину вектора, потому что она кодирует чистую «количество» или силу силы в заданном направлении. Как и во всех приведенных выше примерах, хотя более 3 измерений может быть сложно визуализировать, снова относительно просто расширить значение 2D или 3D вектора силы до R ⁿ . То есть, независимо от размерности, величина вектора силы просто представляет силу силы в заданном направлении.

Но векторы могут представлять гораздо больше, чем просто физические расстояния и силы. Например, вложения слов — это векторы, которые кодируют информацию о лингвистических объектах, таких как значения слов, где каждая основа соответствует некоторому семантическому измерению. В качестве альтернативы в финансах можно построить вектор, представляющий вероятность некоторого будущего состояния экономики, компании или чего-то еще, где каждый компонент представляет собой вероятность некоторого события, которое повлияет на цены акций. Предположительно, даже такие вещи, как демографические данные или информация о недвижимости, могут быть представлены в виде векторов. Например, рассмотрим вектор с 5 компонентами, описывающими район: средняя стоимость дома, среднее количество спален, средний доход, качество школьного округа из 10 и, не знаю, процент домов с бассейнами. Такой вектор может выглядеть как <500000, 3,5, 95000, 7, 0,15> , при этом каждое измерение практически не имеет концептуальной связи с другими.

На данный момент, хотя мы все еще говорим только о векторах, ясно, что мы очень далеко отклонились от физических расстояний и сил и стали гораздо более абстрактными, чем физические расстояния и силы. Итак, мой вопрос, после всего этого наращивания, заключается в том, как мы можем интерпретировать длины/величины таких абстрактных векторов? Возьмем приведенный выше пример вектора соседства. В отличие от примера двумерной гипотенузы, где обе компоненты являются длинами сторон, 5 компонентов вектора окрестности представляют собой совершенно разные и, как правило, несравнимые величины. Тем не менее, когда мы вычисляем длину этого вектора, информация из всех этих разнообразных компонентов объединяется в одно скалярное значение. Проблема в том, что поскольку величины настолько не связаны между собой, я понятия не имею, что представляет собой это скалярное значение. И далее, если бы у нас было две разные окрестности, каждая со своим вектором и скалярной величиной, что бы разница величин сказала мне о взаимосвязи между этими окрестностями? Соответствует ли величина такого вектора чему-либо в реальном мире?

В целом, хотя очевидно, что векторы можно использовать для структурирования величин в огромном количестве не связанных друг с другом областей, я изо всех сил пытаюсь расширить свое понимание вектора 9. 0005 величина как длина/расстояние/сила в те области, где мы больше не говорим о длине, расстоянии или силе. Пожалуйста, помогите мне сделать это.

Огромное спасибо, что дочитали до конца — вы чемпион 🙂

Определение векторов. Основная информация

Определение векторов. Основная информация

Навигация по страницам:

• Определение вектора
• Векторное обозначение
• Длина вектора
• Нулевой вектор
• Коллинеарные векторы
• Сонаправленные векторы
• Противонаправленные векторы
• Копланарные векторы
• Равные векторы
• Единичный вектор

Определение вектора

Определение. Вектор представляет собой направленный отрезок, т.е. отрезок, имеющий длину и определенное направление. Графически вектор изображается в виде направленных отрезков определенной длины. (Рис. 1)

Рис. 1

Обозначение вектора

Вектор, имеющий начальную точку А и конечную точку В, обозначается АВ (рис. 1). Также вектор представляет собой одну маленькую букву, например а.а.

Длина вектора

Определение. Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора АБ.

Длина вектора AB обозначается как: |AB|.

Нулевой вектор

Определение. Нулевой вектор — это вектор, начальная и конечная точки которого совпадают.

Нулевой вектор обычно обозначается как 0.

Длина нулевого вектора равна нулю.

Коллинеарные векторы

Определение. Векторы, параллельные одной прямой или лежащие на одной прямой, называются коллинеарными векторами (рис. 2).

Рис. 2

Сонаправленные векторы

Определение. Два коллинеарных вектора a и b называются сонаправленными векторами , если их направления совпадают: a↑↑b (рис. 3).

Рис. 3

Противонаправленные векторы

Определение. Два коллинеарных вектора a и b называются противоположно направленными векторами, если их направления противоположны: a↑↓b (рис. 4).

Рис. 4

Копланарные векторы

Определение. Векторы, параллельные одной плоскости или лежащие в одной плоскости, называются компланарными векторами (рис. 5).

Равные векторы Определение. Векторы a и b являются равными векторами , если они лежат на одной или параллельных прямых, их направления совпадают и длины равны (рис. 6). Рис. alexxlab Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт Рубрики Прост Радио Разное Своими руками Советы Схем Схемы Транзист Транзисторы Электрон Электроника