Единичный вектор | matematicus.ru
Единичный вектор (орты координатных осей) — это вектор, длина которого равна единице.
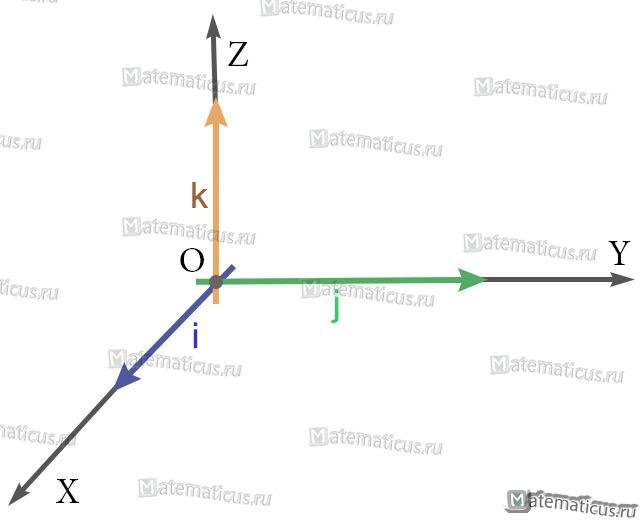
i — единичный вектор оси абсцисс;
j — единичный вектор оси ординат;
k — единичный вектор оси аппликат.
i⊥j⊥k, i=j=k=1
В прямоугольной системе координат в пространстве координаты векторов равны:
i(1;0;0), j(0;1;0), k(0;0;1)
Замечание 1
Единичные векторы являются некомпланарными.
Замечание 2
Любой вектор можно разложить в виде вектора по ортам координатных осей, формула ниже.
a=xi+уj+zk
где x, y, z — координаты вектора проекции на соответствующие координатные оси.
Эта формула называется разложением вектора по ортам координатных осей.
Единичный вектор определяется по формуле:
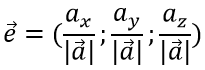
Пример
Дан вектор а = (1; 2; -2)
Требуется найти длину (модуль) и единичный вектор e направления вектора а
Решение
Находим длину вектора a
$\left| {\vec a} \right| = \sqrt {{1^2} + {2^2} + {{\left( { — 2} \right)}^2}} = 3$
затем вычисляем единичный вектор e
$\vec e = \left( {\frac{1}{3};\frac{2}{3}; — \frac{2}{3}} \right)$
Если направление кратчайшего пути от первого вектора ко второму вектору совпадает с направлением стрелки, то произведение равно третьему вектору, а если не совпадает, то третий вектор берется со знаком «минус». Смотрите схему 1.
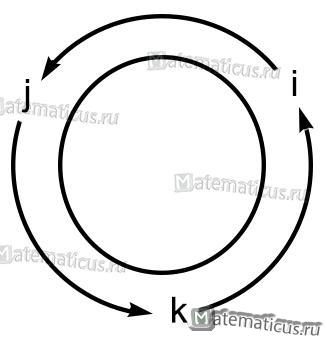
Схема 1
На основании схемы получаем таблицу векторного произведения единичных векторов
i×i=0 i×j=k i×k=-j
j×i=-k j×j=0 j×k=i
k×i=j k×j=-i k×k=0
Пример 1
Найти векторное произведение iхj, где i, j — единичные векторы (орты) правой системы координат.
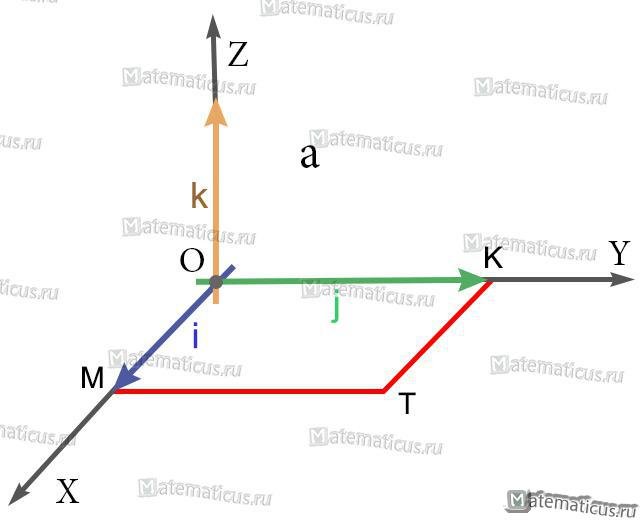
Решение
1) Так как длины основных векторов равны единице масштаба, то площадь параллелограмма MOKT численно равна единице. Значит, модуль векторного произведения равен единице.
2) Так как перпендикуляр к плоскости MOKT есть ось OZ, то искомое векторное произведение есть вектор, коллинеарный с вектором k; а так как оба они имеют модуль 1, то искомое векторное произведение равно либо k, либо -k.
3) Из этих двух возможных векторов надо выбрать первый, так как векторы i, j, k образуют правую систему (а векторы i, j, -k — левую).
iхj=k
Пример 2
Найти векторное произведение jхi.
Решение
Как в примере 1, заключаем, что вектор jхi равен либо k, либо —k. Но теперь надо выбрать -k, ибо векторы j, i, —k образуют правую систему (а векторы i, j, —k -левую).
jхi = −k
6.2. Найти единичный вектор того же направления что и .
Единичный вектор
находится: 
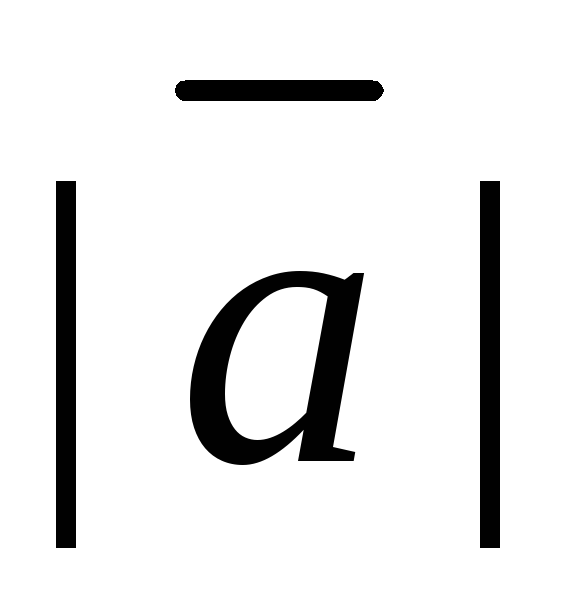– модуль вектора.Находим
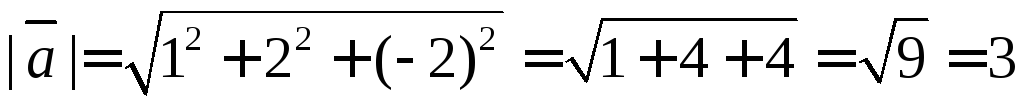
тогда
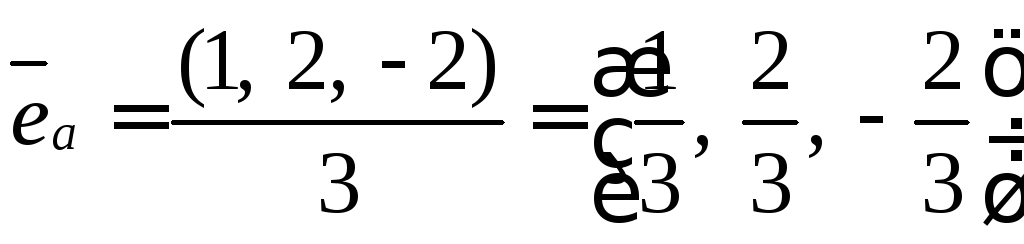
Ответ: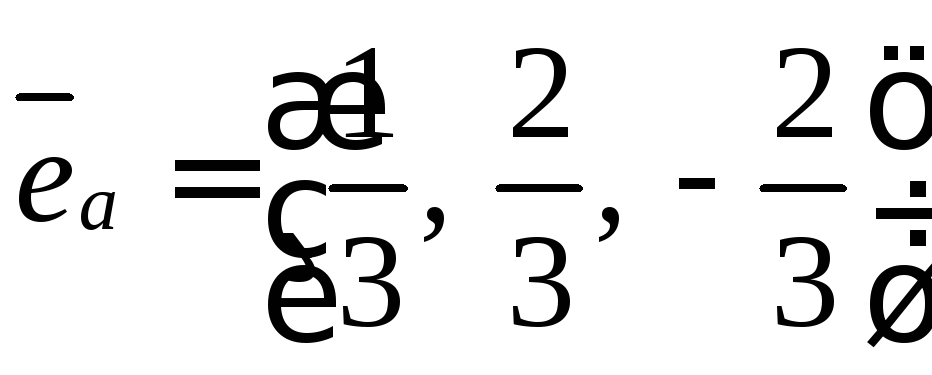 
.
Примечание. Координаты единичного вектора должны быть не больше единицы.
6.3. Найти длину
и направляющие косинусы вектора 
Длина вектора – это есть его модуль:
,
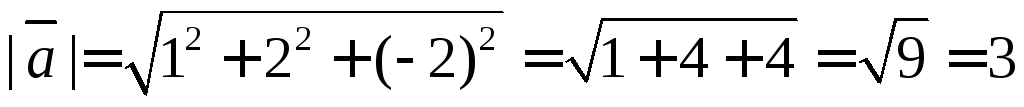а направляющие косинусы мы можем найти
по формуле одного из способов задания
векторов:
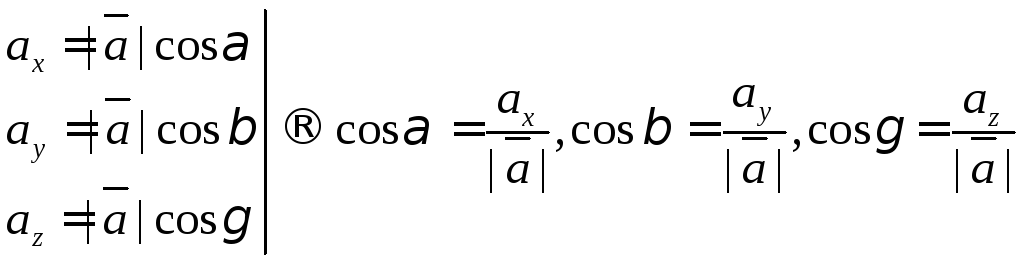
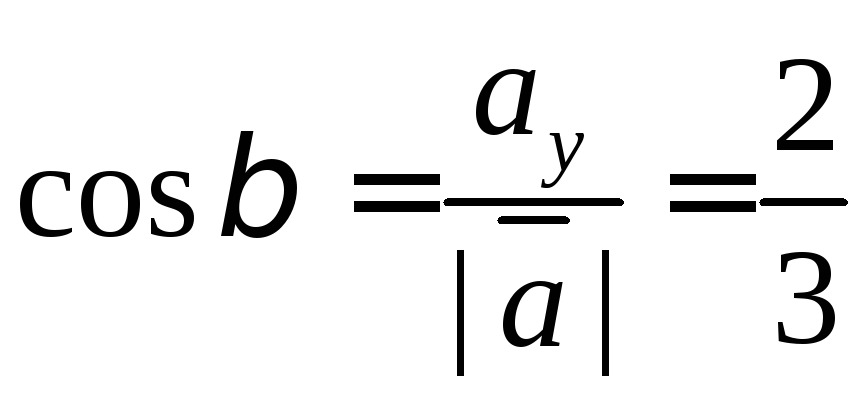
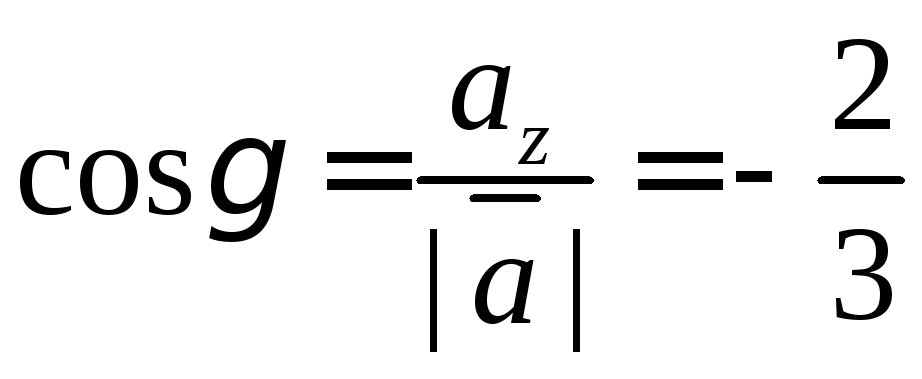
Из полученного мы видим, что направляющие косинусы это и есть координаты единичного вектора.
Ответ: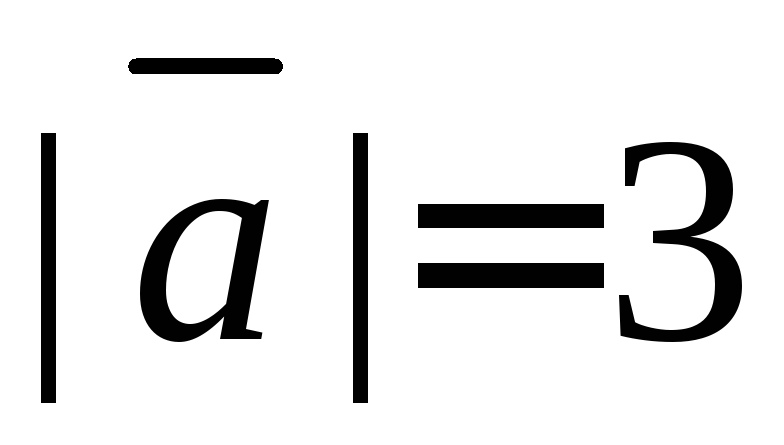 
,
,
,
.
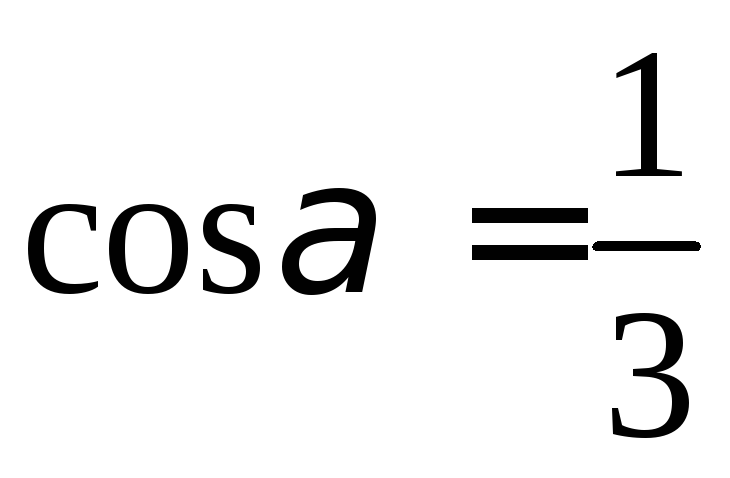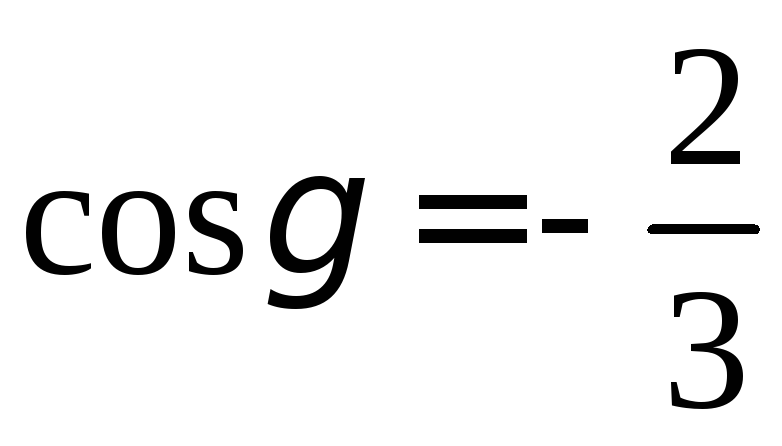6.4. Найти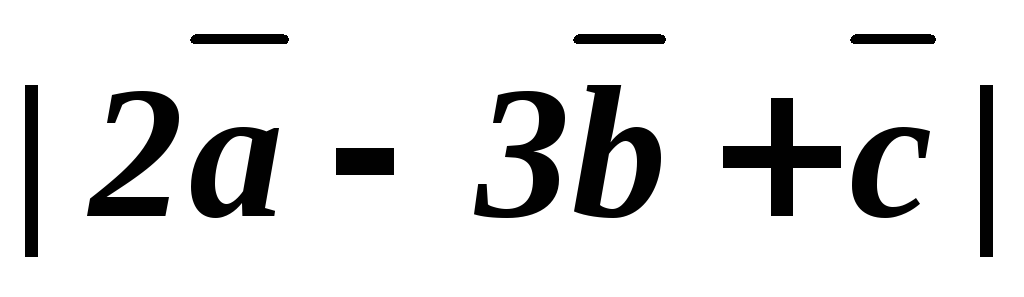 
.
Необходимо выполнить действия умножения вектора на число, сложения и модуль.
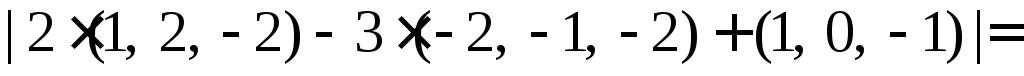
Почленно перемножаем координаты векторов на число.
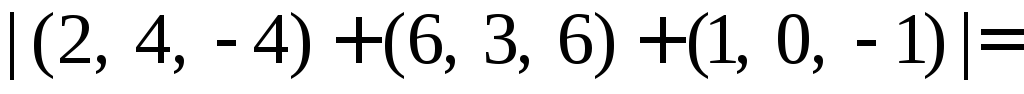
Почленно складываем координаты векторов.
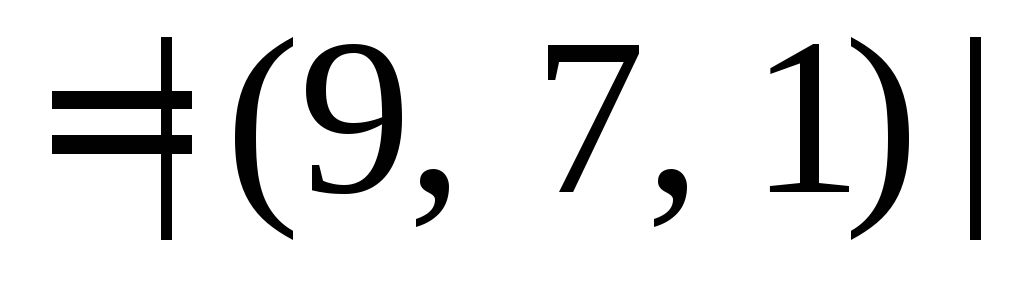
Находим модуль вектора.
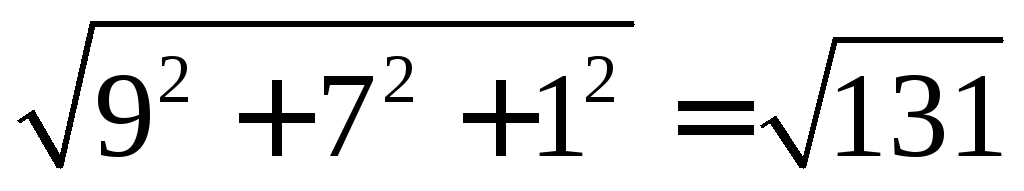
Ответ: 
6.5. Определить
координаты вектора 
,
зная, что
и он направлен в сторону, противоположную
вектору
. Вектор 
коллинеарен вектору
,
значит, его единичный вектор равен
единичному вектору
Единичный вектор имеет длину равную 1, значит, если его умножить на 5, то его длинна будет равна пяти.
Находим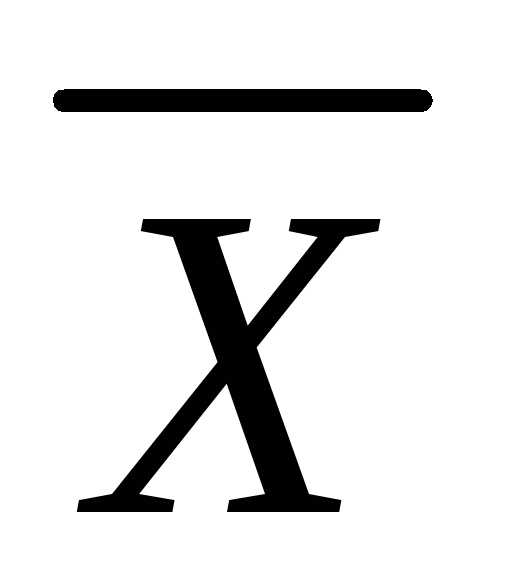 
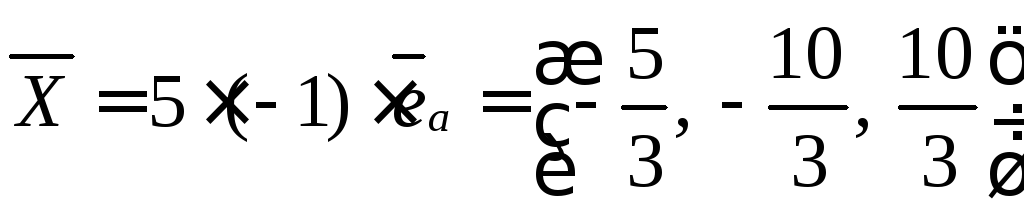
Ответ: 
6.6. Вычислить
скалярные произведения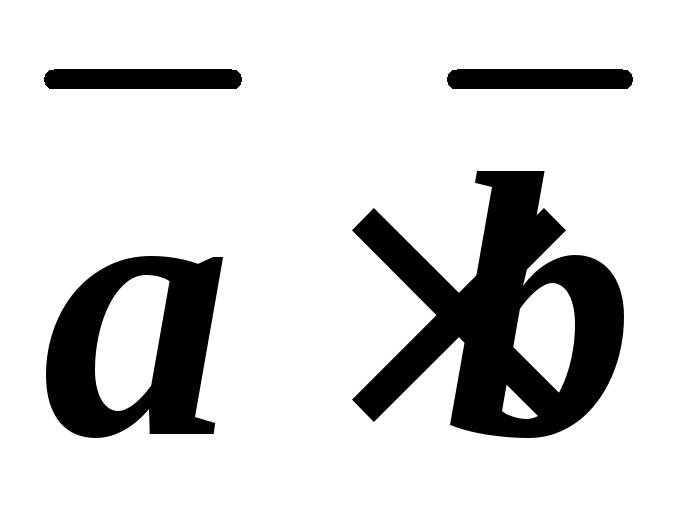 
.
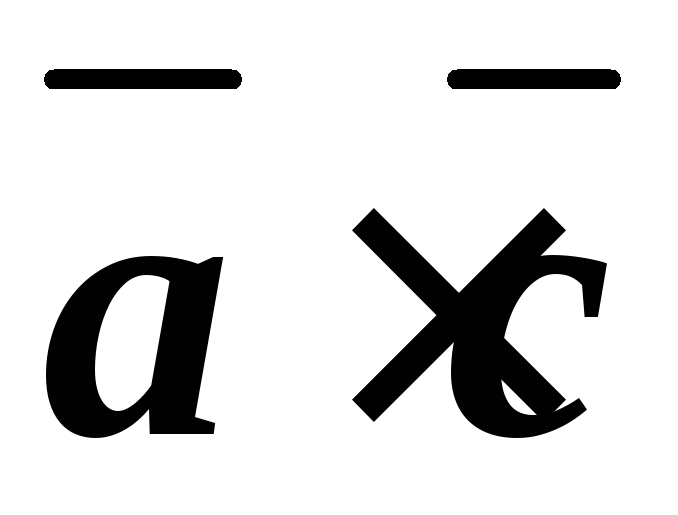Перпендикулярны ли векторы
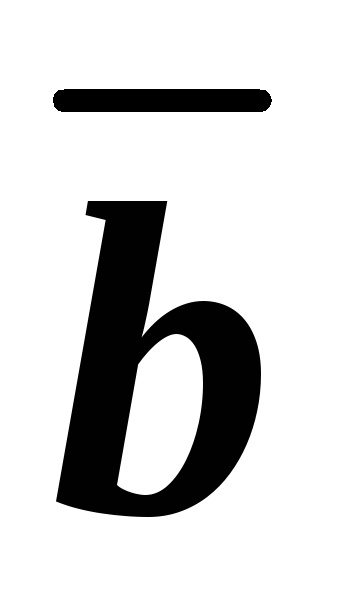и
,
и
между собой?Выполним скалярное произведение векторов.
М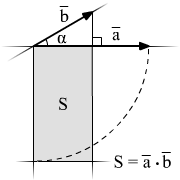
ы
видим, что в нашем случае вектора
и
перпендикулярны.
Ответ: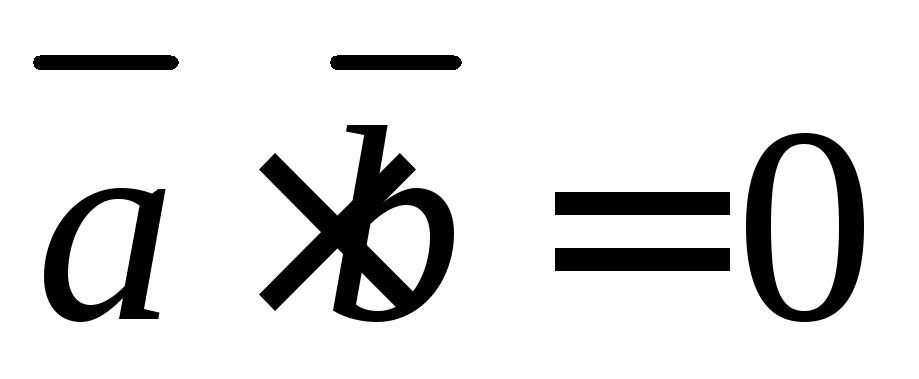 
,
,
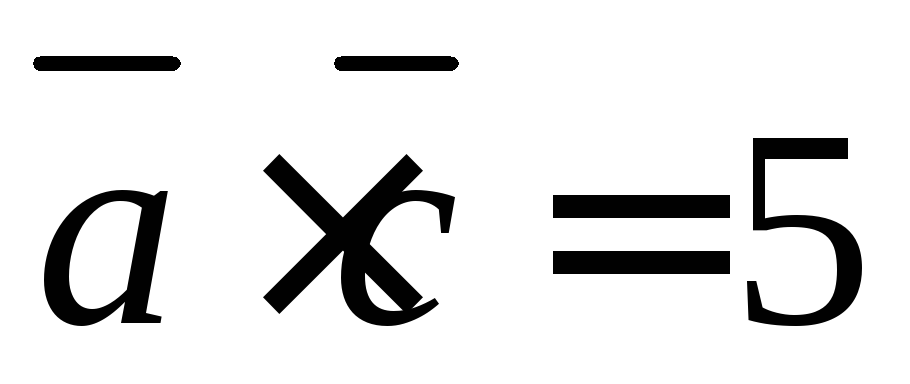векторы не перпендикулярны.
Примечание. Геометрический смысл скалярного произведения малоприменим на практике, но все-таки существует. Результат такого действия можно изобразить и вычислить геометрически.
6.7. Найти работу,
совершённую материальной точкой к
которой приложена сила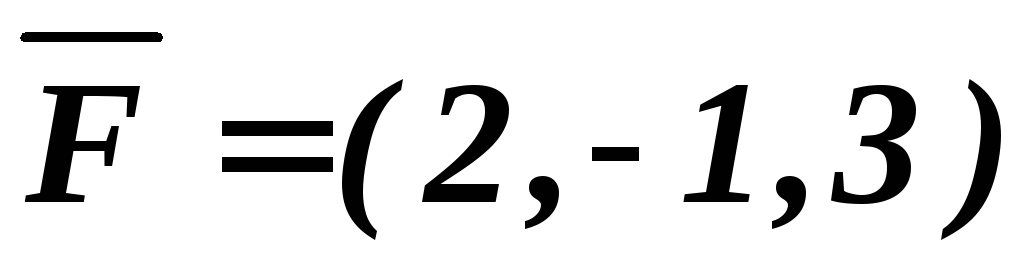 
,
при перемещении её из точки B в точку С.
Физический смысл
скалярного произведения – это работа.
Вектор силы здесь 
,
вектор перемещения – это.
А произведение этих векторов и будет
искомой работой.
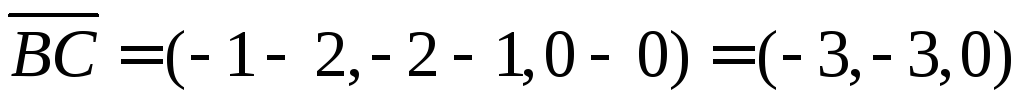
Находим работу
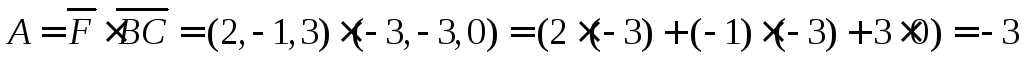
Ответ: -3.
6.8. Найти внутренний угол при вершине A и внешний угол при вершине C треугольника ABC.
Из определения,
скалярного произведения векторов
получим формулу нахождения угла: 
.
Далее, нам нужно определить вектора, между которыми будем искать угол.
В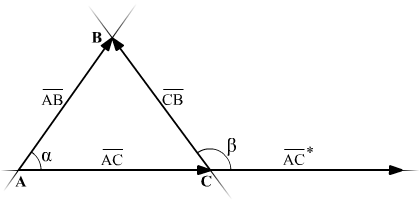
Для нахождения внешнего угла нужно совмещать вектора, таким образом, чтоб они выходили из одной точки. Рисунок это поясняет.
Стоит заметить,
что 
,
только имеют разные начальные координаты.
Находим необходимые вектора и углы
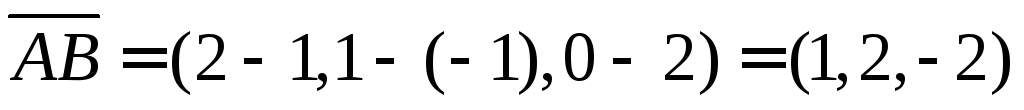
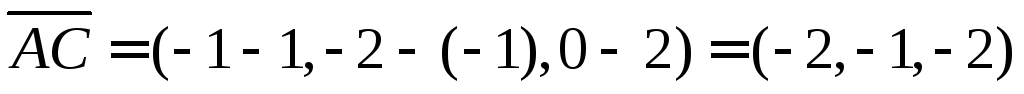
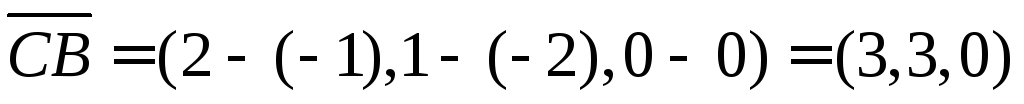
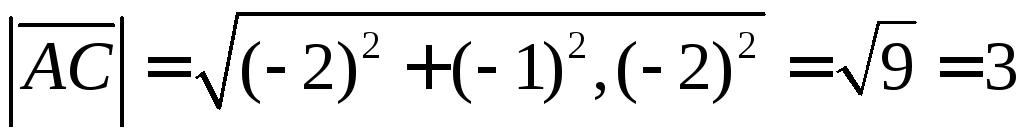
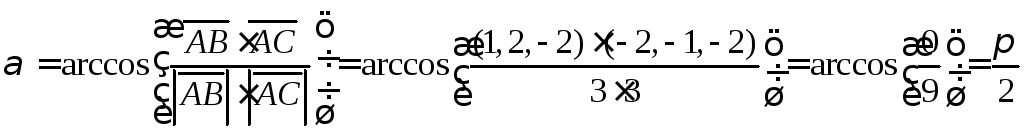
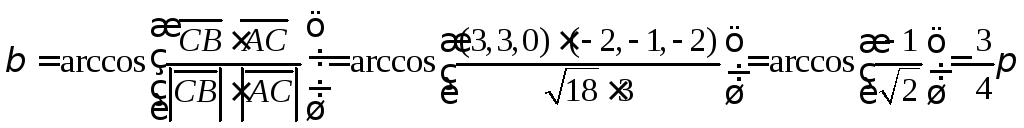
Ответ: внутренний
угол при вершине А =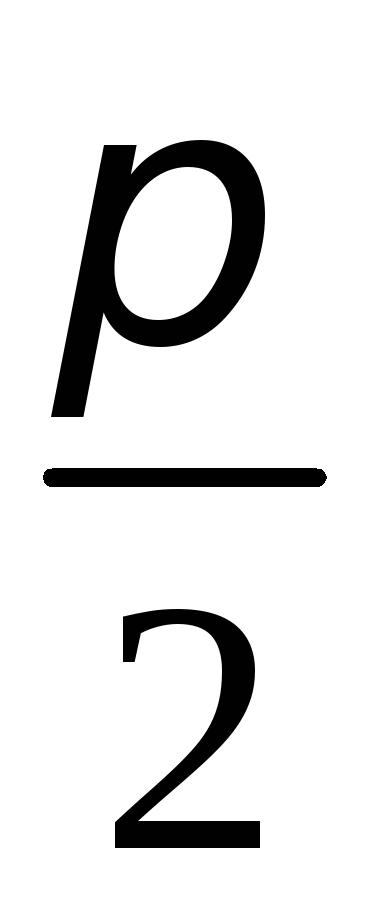 
,
внешний угол при вершине В =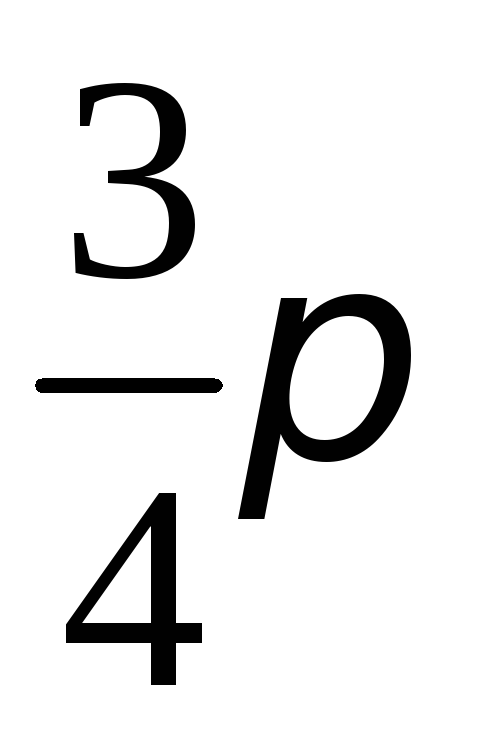
.
6.9. Найти проекции векторов: и
Вспомним вектора-орты: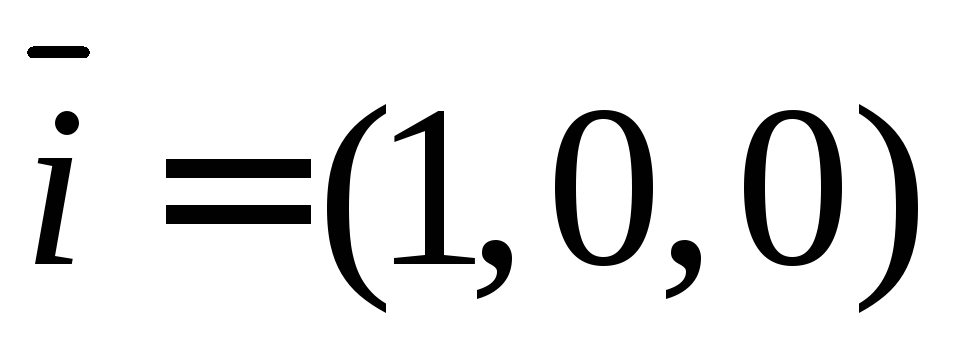 
,
,
.
Проекция находится также из скалярного произведения
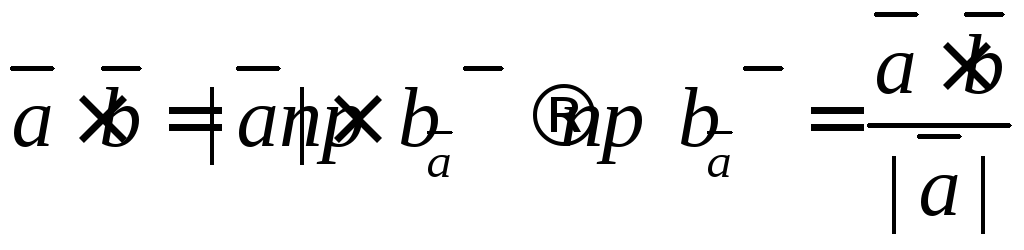–проекция b на a.
Ранее полученные нами вектора
, 
,
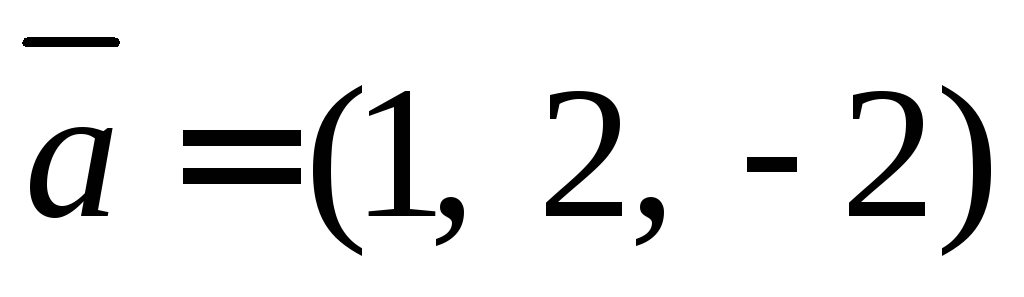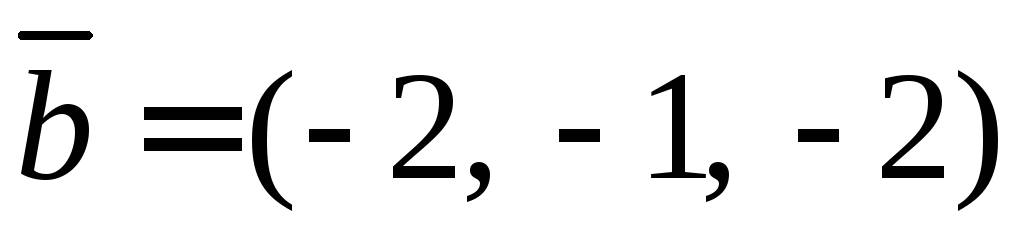Находим проекцию
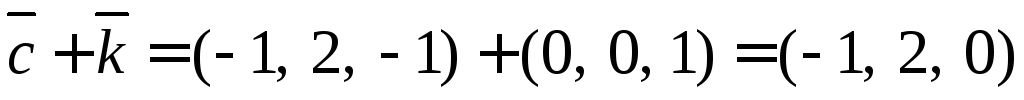
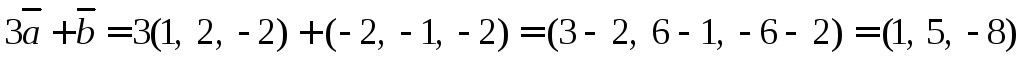
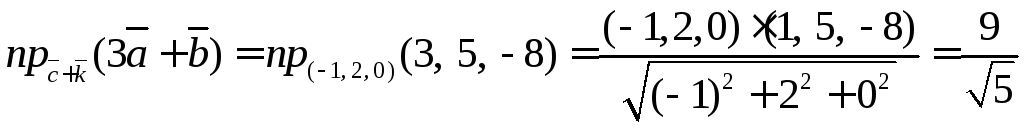
Находим вторую проекцию
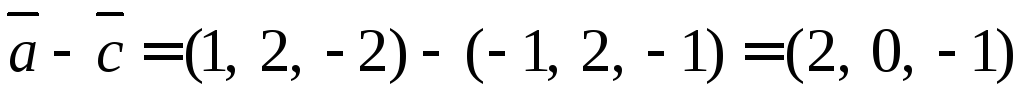
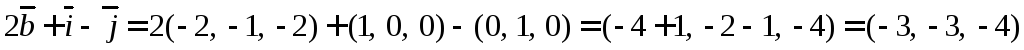
Ответ: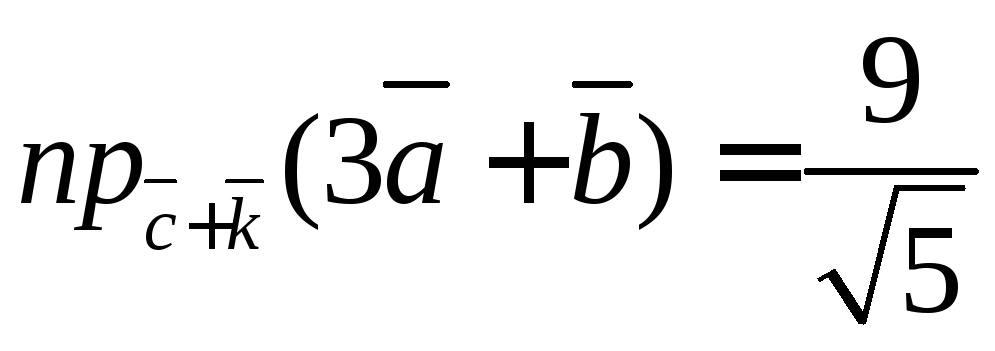 
,
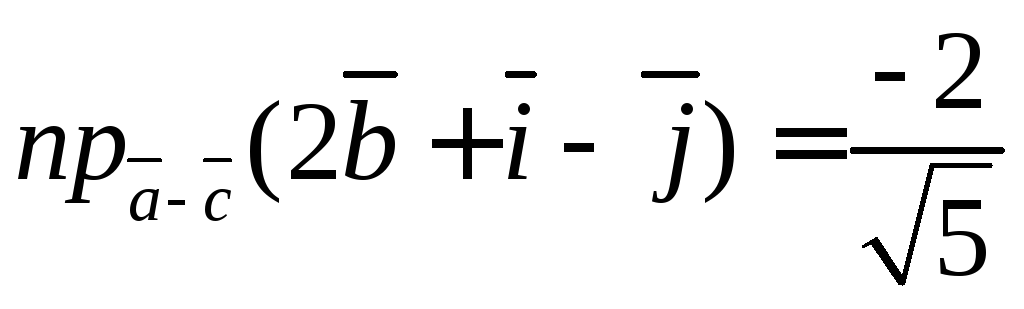
Примечание. Знак минуса при нахождении проекции означает то, что проекция опускается не на сам вектор, а в противоположную сторону, на линию на которой лежит этот вектор.
6.10. Вычислить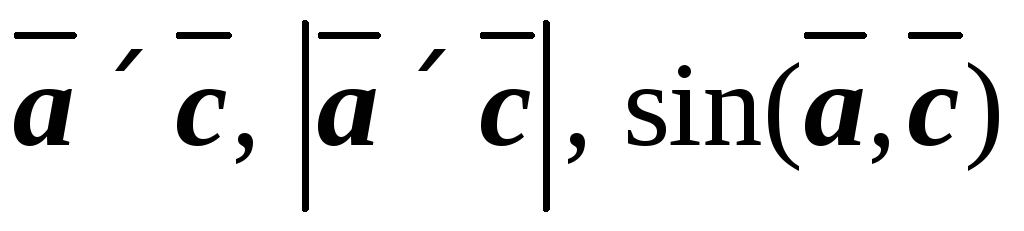 
.
Выполним векторное произведение векторов
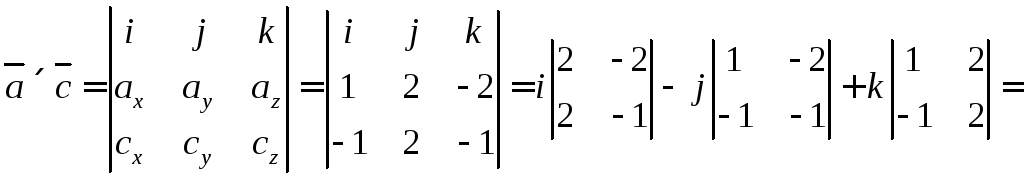
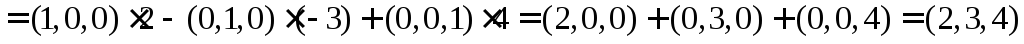
Найдем модуль
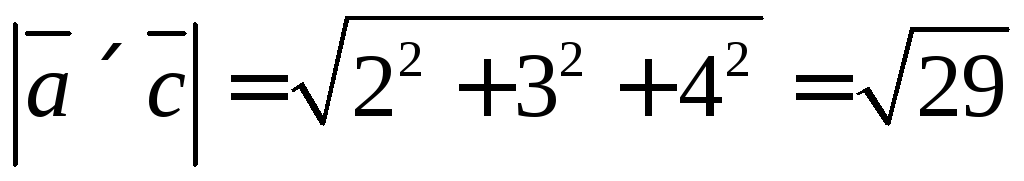
Синус угла между векторами найдём из определения векторного произведения векторов
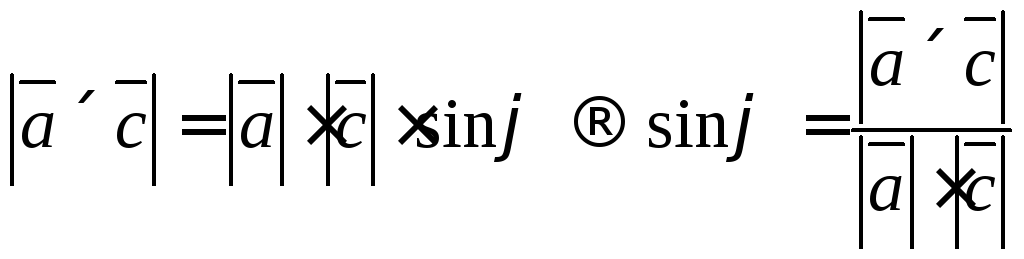
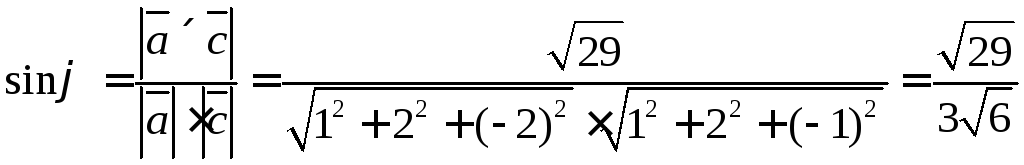
Ответ:
,
,
.
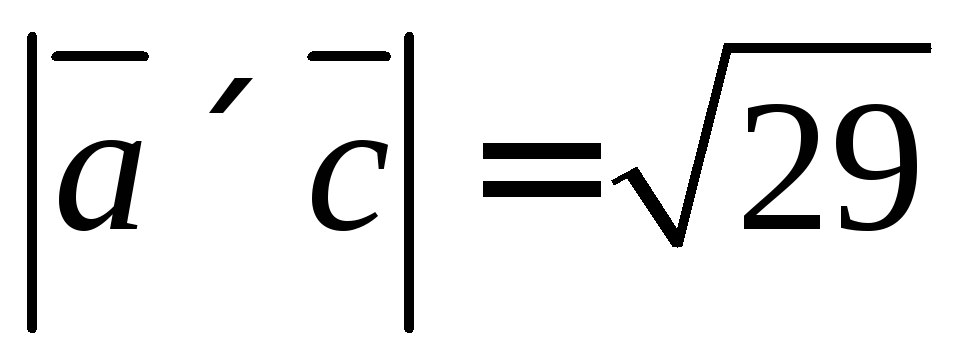6.11. Найти площадь треугольника ABC и длину высоты, опушенной из точки С.
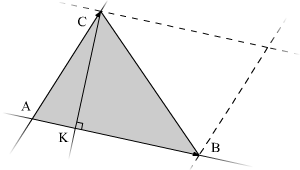
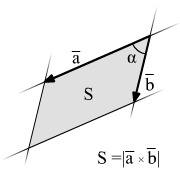
Геометрический смысл модуля векторного произведения состоит в том, что это площадь параллелограмма, образованного этими векторами. А площадь треугольника равна половине площади параллелограмма.
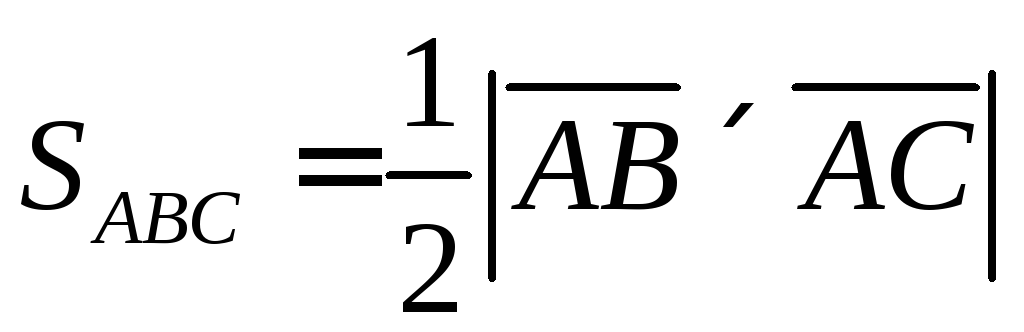
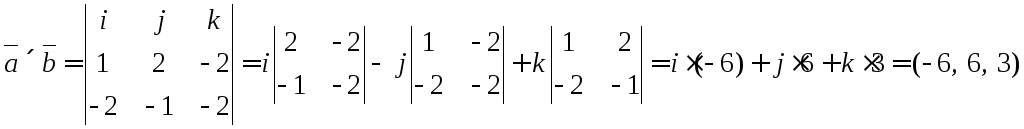
Площадь треугольника также можно найти как произведение высоты, на основание, делённое на два, из этого можно вывести формулу нахождения высоты.
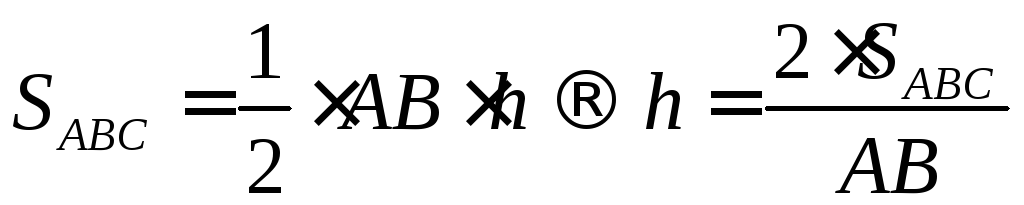
Таким образом, найдём высоту
Ответ: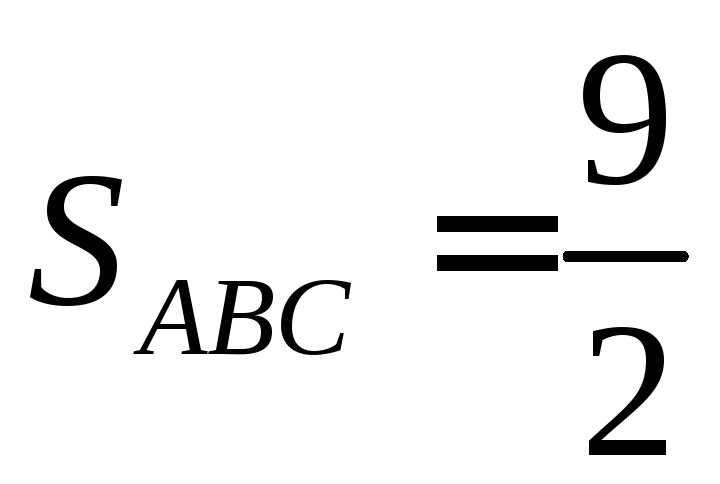 
,
.
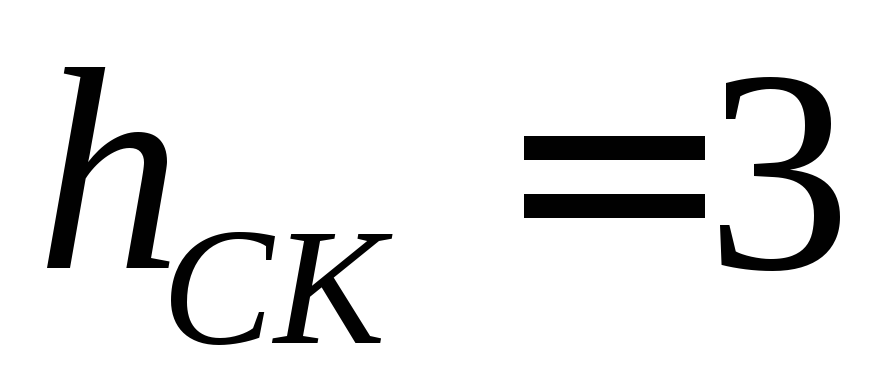6.12. Найти
единичный вектор, перпендикулярный
векторам 
и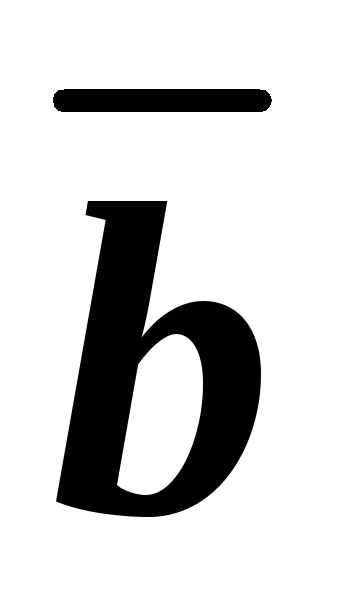
.
Результатом скалярного произведения есть вектор, который перпендикулярный двум исходным. А единичный вектор – это вектор, делённый на его длину.
Ранее, нами было найдено:
, 
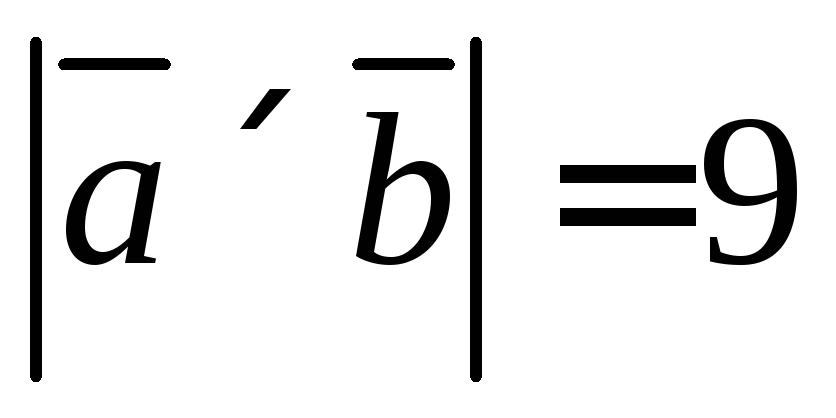
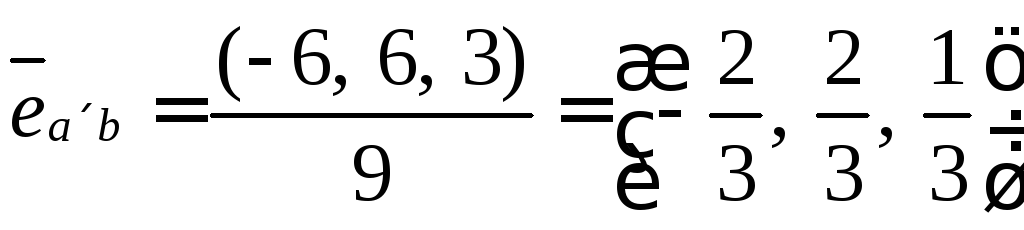
Ответ: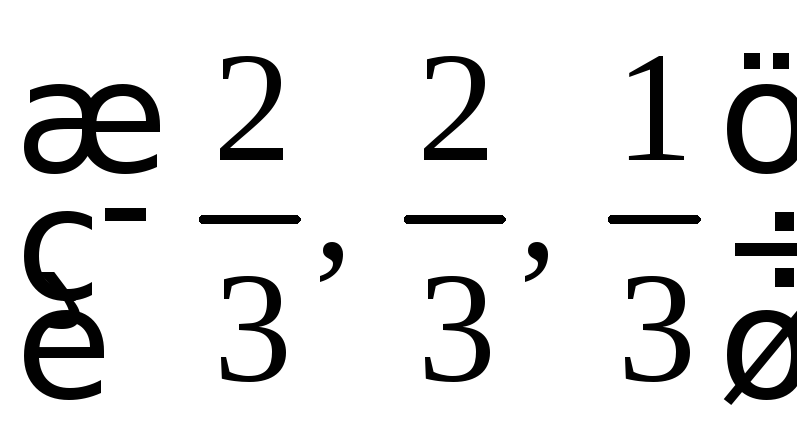 
.
6.13. Определить
величину и направляющие косинусы момента
силы 
,
приложенной к А относительно точки С.
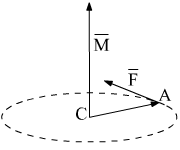
Физический смысл векторного произведения – это момент силы. Приведём иллюстрацию к данному заданию.
Находим момент силы
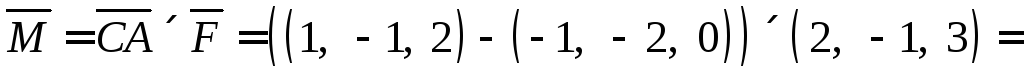
Ответ: 
.
6.14. Лежат ли
векторы 
,
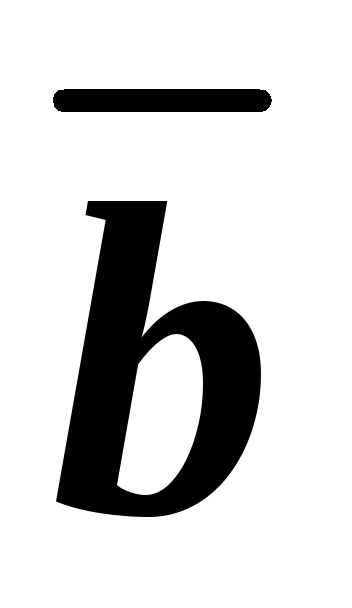и
в одной плоскости? Могут ли эти векторы
образовывать базис пространства? Почему?
Если могут, разложите по этому базису
вектор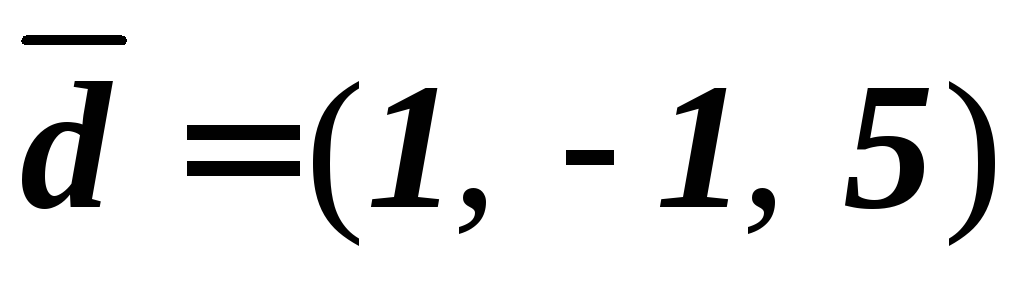
.
Чтобы проверить лежат ли вектора в одной плоскости необходимо выполнить смешанное произведение этих векторов.
Смешанное
произведение не равно нулю, следовательно,
вектора не лежат в одной плоскости (не
компланарные) и могут образовывать
базис. Разложим 
по этому базису.
Разложим по базису, решив уравнение
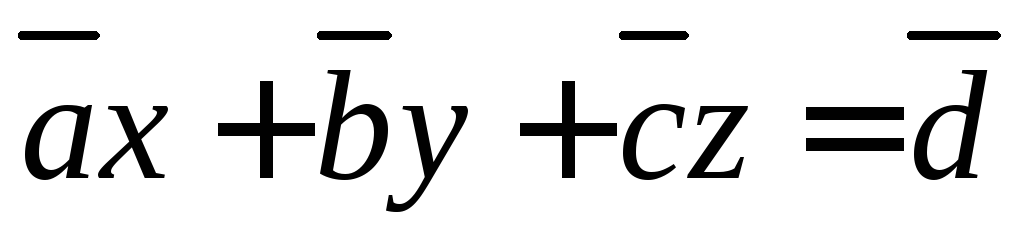
Ответ: Векторы 
,
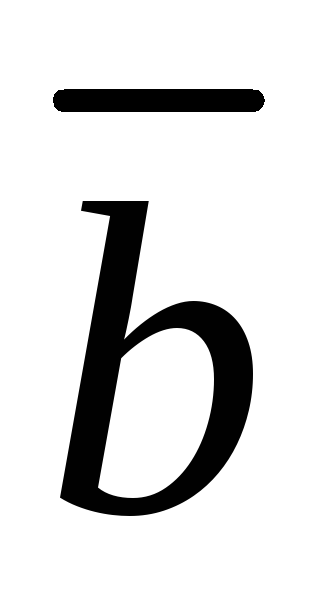и
не лежат в одной плоскости.
.
6.15. Найти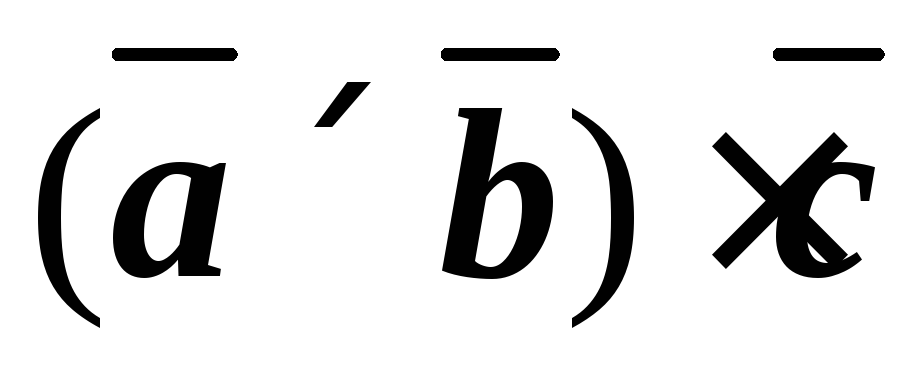 
.
Чему равен объём пирамиды с вершинами
A, B, C, D и её высота, опущенная из точки A
на основание BCD.
Г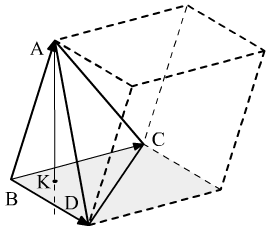
еометрический
смысл смешанного произведения в том,
что это объём параллелепипеда образованного
этими векторами.
Объём же пирамиды в шесть раз меньше объёма параллелепипеда.
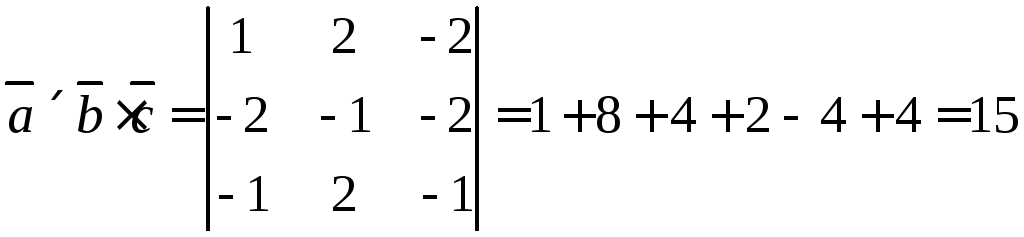
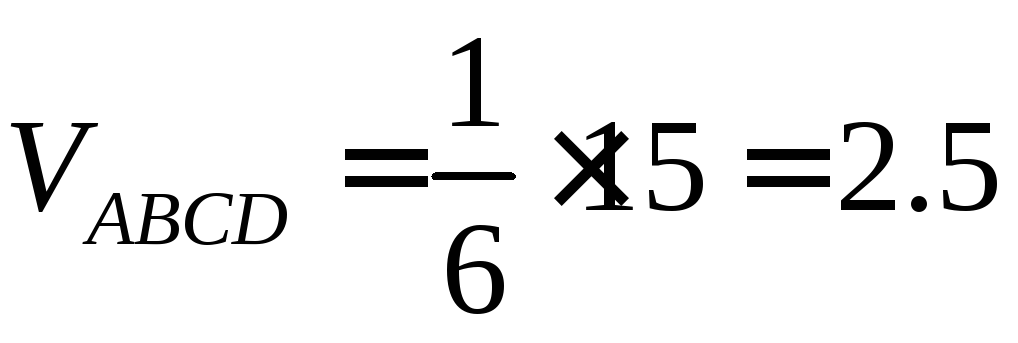
Объём пирамиды, ещё можно найти так:
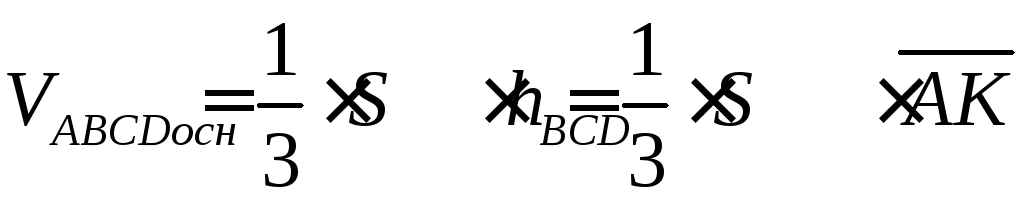
Получим формулу нахождения высоты
Находим
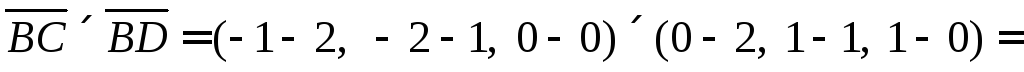
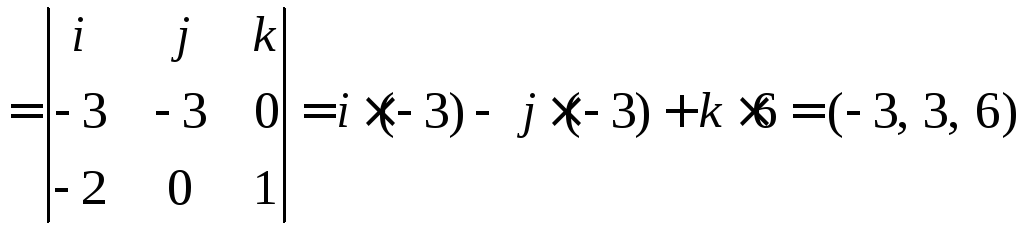
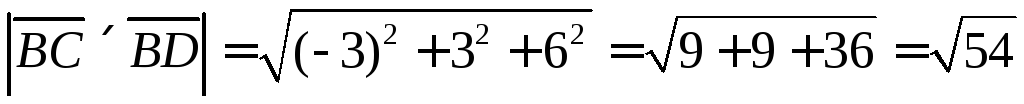
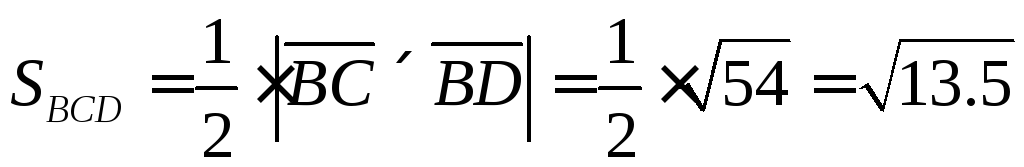
Находим высоту
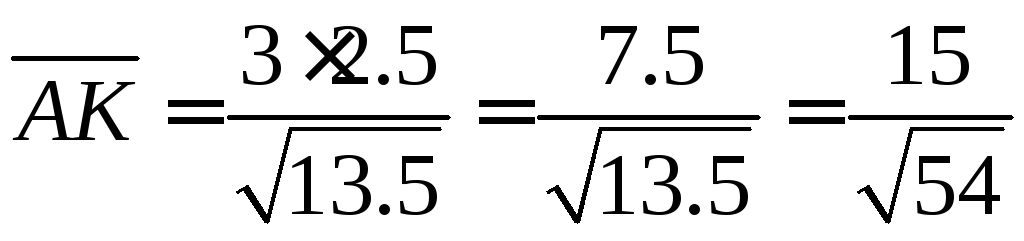
Ответ: объём = 2.5,
высота =
.
6.16. Вычислить 
и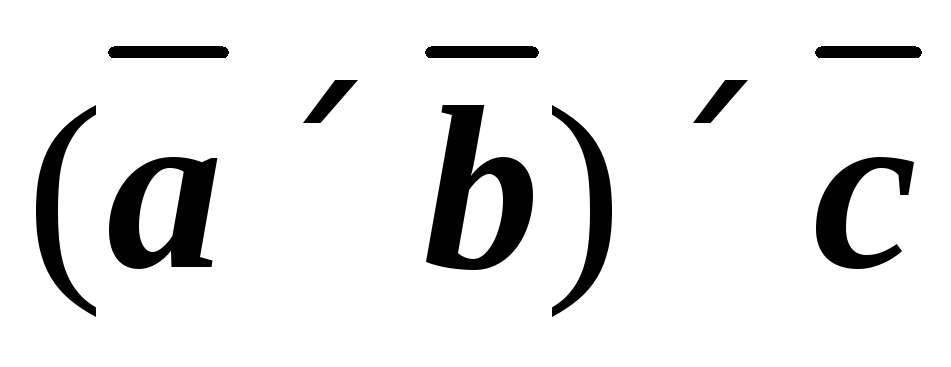
.
–над этим заданием
предлагаем вам подумать самим.
–выполним
произведение.
Ранее было получено
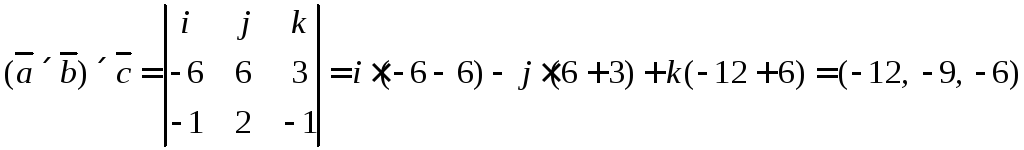
Ответ: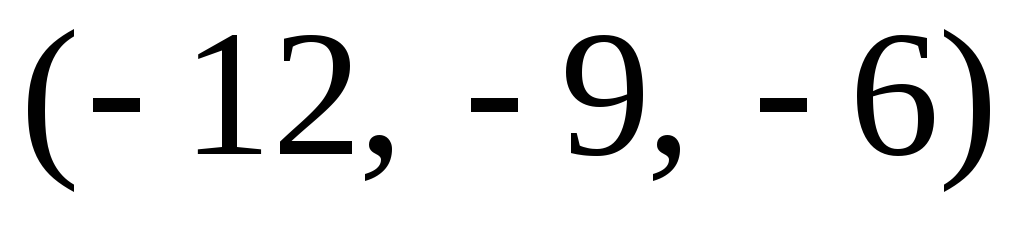 
.
6.17. Вычислить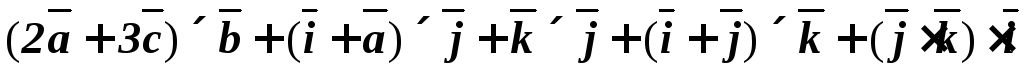 
Выполним действия по частям
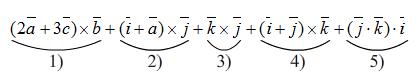
1) 
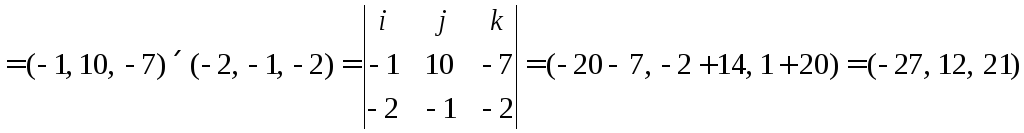2) 
3) 
4) 
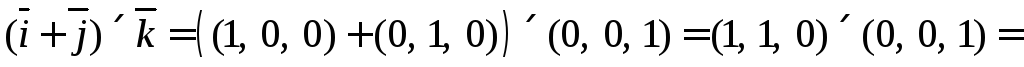
5) 
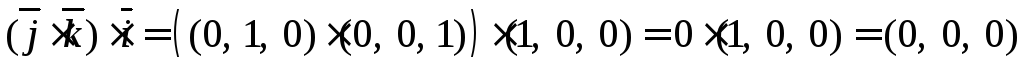
Суммируем полученные значения
Ответ: 
.
6.18. Найти вектор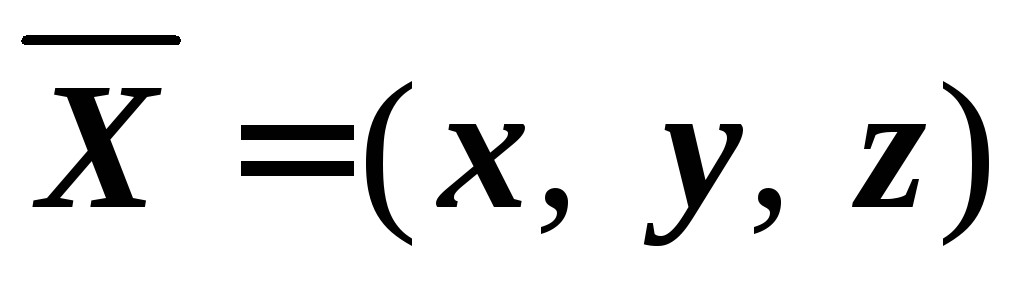 
,
зная, что он перпендикулярен векторам
и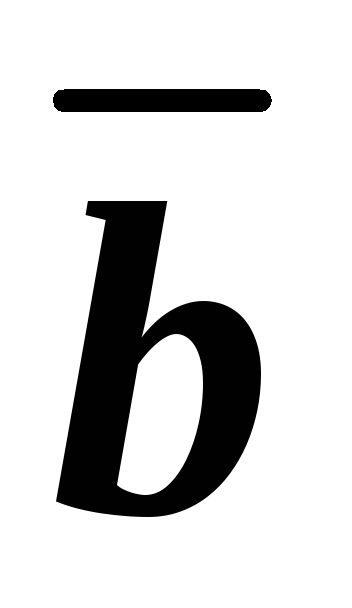
,
а его проекция на вектор
равна 5.
Разобьем данную задачу на две подзадачи
1) Найдём вектор,
перпендикулярный векторам 
и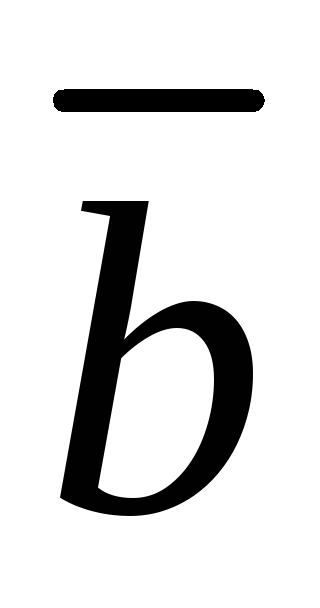
произвольной длинны.
Перпендикулярный вектор мы получим в результате векторного произведения
Ранее, нами было найдено:
Искомый вектор отличается лишь длинной, от полученного
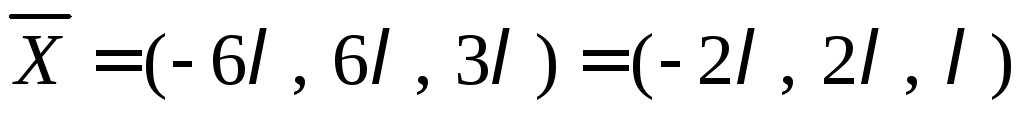
2) Найдем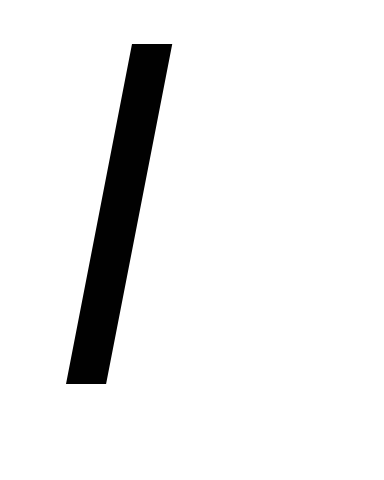 
через уравнение
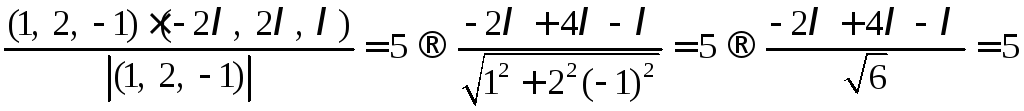
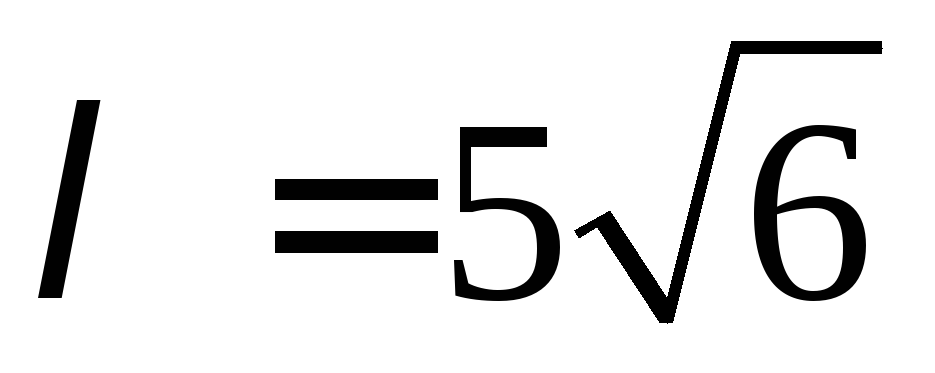
Ответ: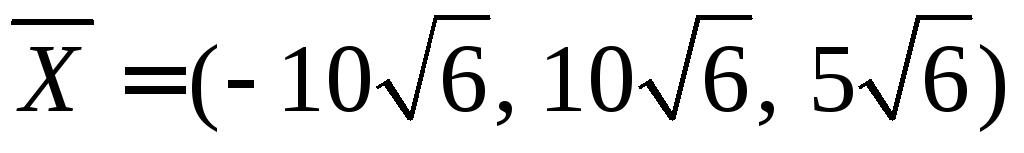 
6.19. Найти вектор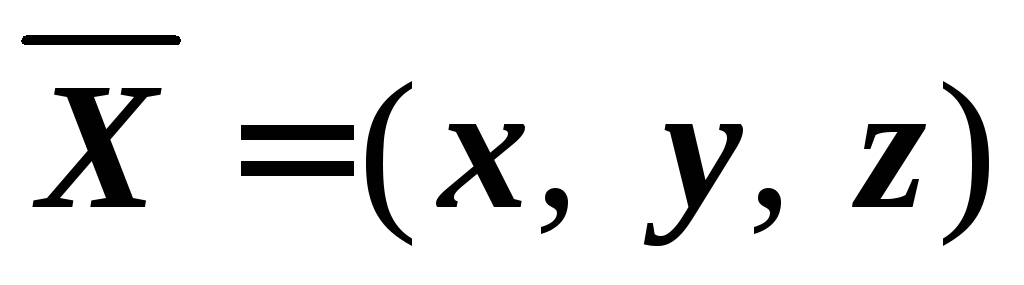 
,
удовлетворяющий условиям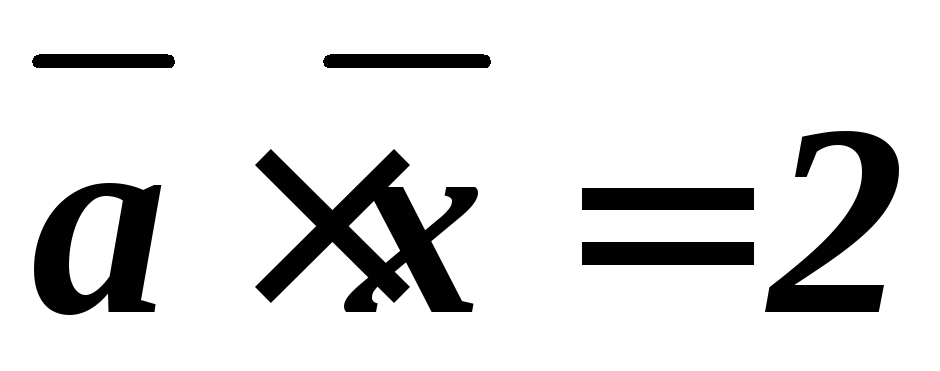
,
,
.
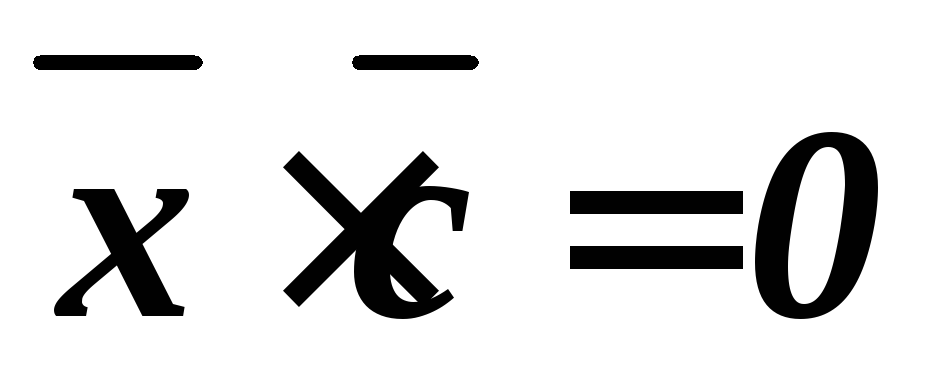Рассмотрим более детально данные условия.
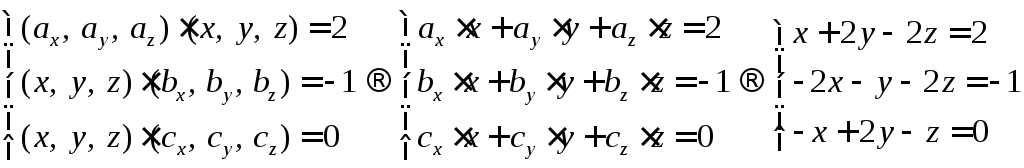
Это система линейных уравнений. Составим и решим данную систему.
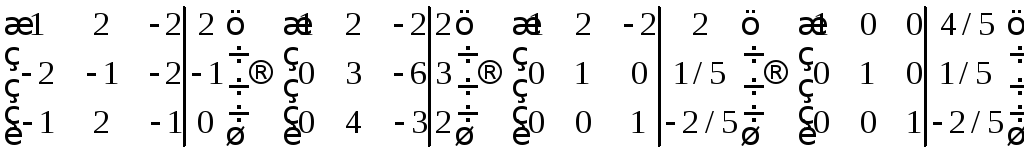
Ответ: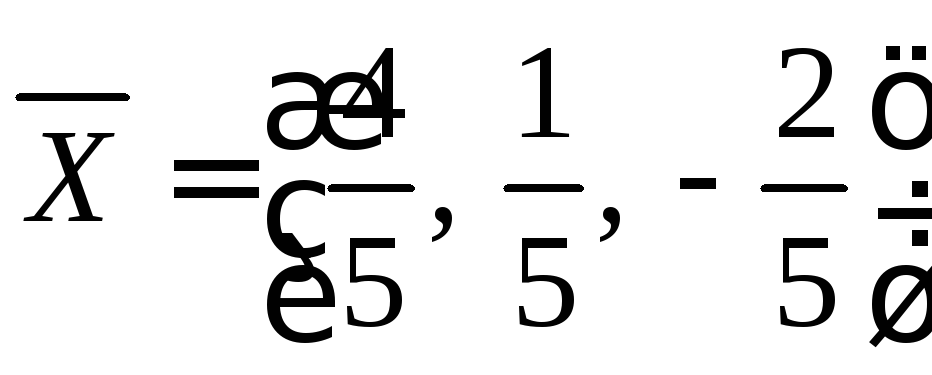 
6.20. Определить
координаты какого-либо вектора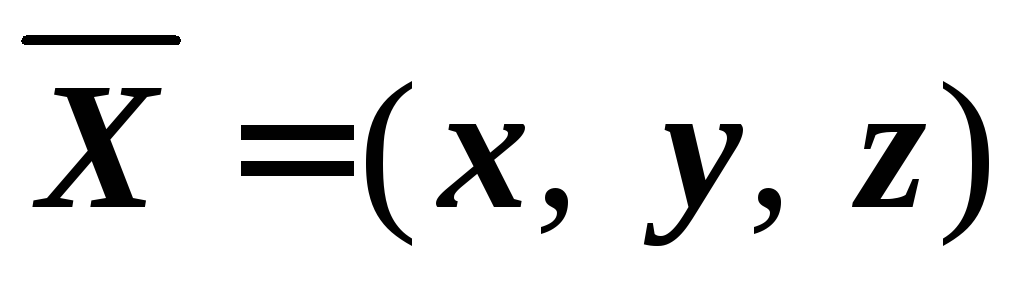 
,
компланарного с векторами
и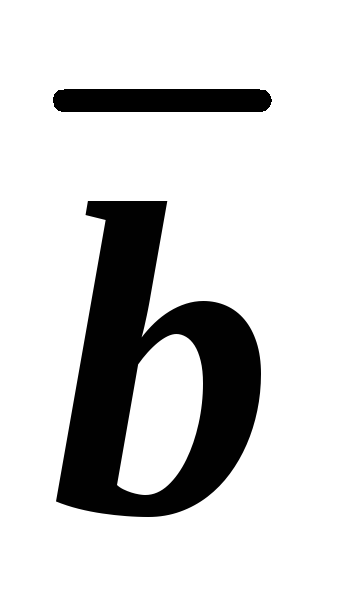
,
и перпендикулярного вектору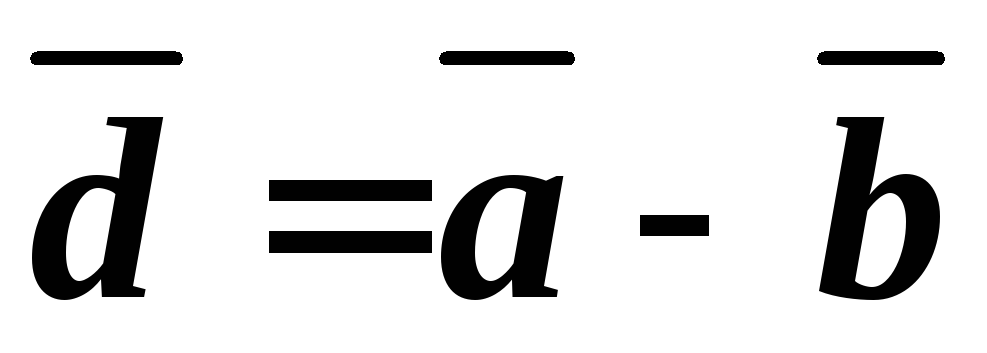
.
В данном задании два условия: компланарность векторов и перпендикулярность, выполним сначала первое условие, а потом второе.
1) Если вектора компланарны, значит их смешанное произведение равно нулю.
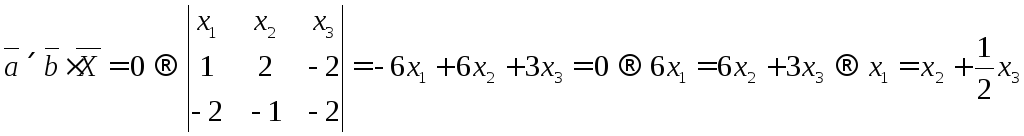Отсюда
получим некоторую зависимость координат
вектора
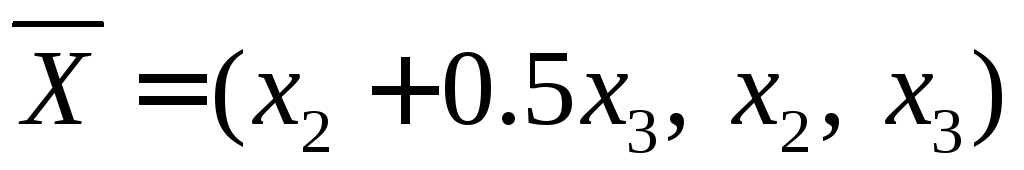
Найдем вектор 
.
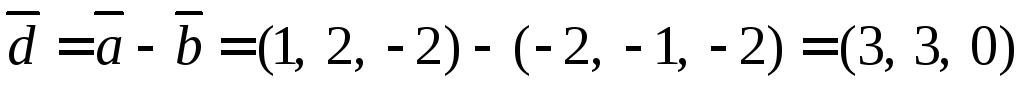
2) Если вектора перпендикулярны, значит их скалярное произведение равно нулю
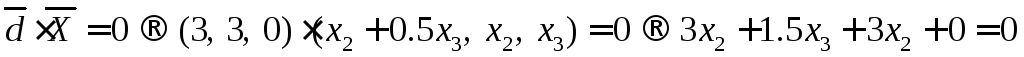
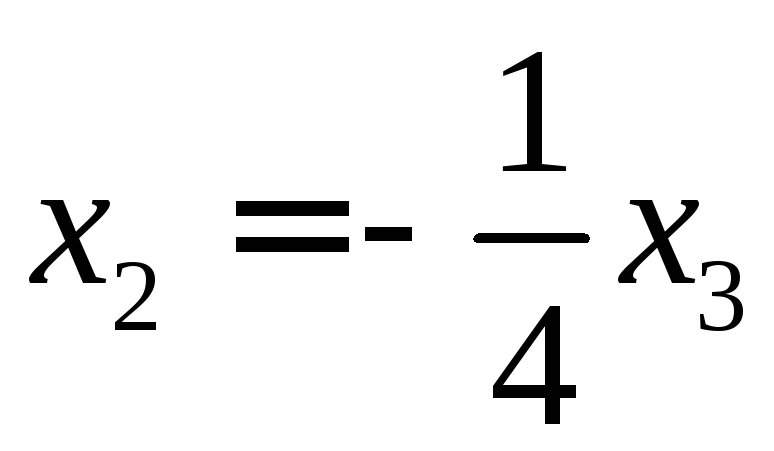
Мы получили вторую зависимость координат искомого вектора
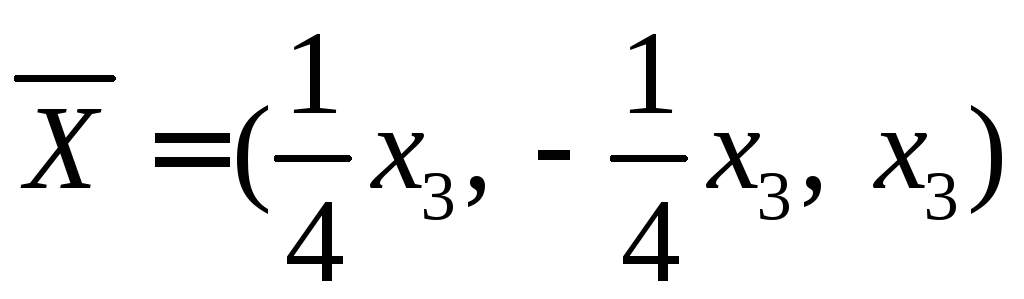
Для любого значения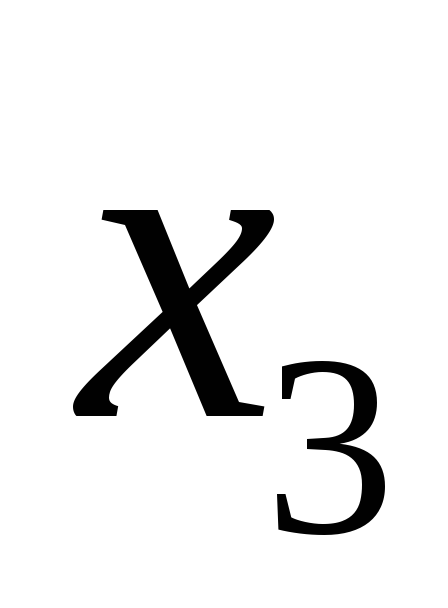 
вектор будет удовлетворять условиям.
Подставим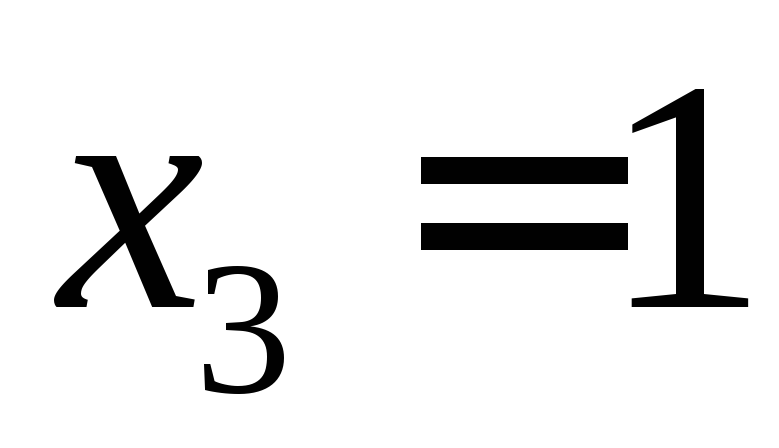
.
Ответ: 
.
Аналитическая геометрия
Глава II. Векторная алгебра
Векторная алгебра имеет широкое применение в различных разделах физики, математики, механики и т.п.. В курсе средней школы вектор определяется как некоторое преобразование пространства. Однако для прикладных целей удобнее использовать другое, традиционное определение вектора и действий над векторами, на которых мы и остановимся дальше. Это не означает, однако, что сведения, полученные в средней школе, не верны. Просто мы будем изучать векторную алгебру, исходя из несколько иных, более удобных для практических целей позиций.
§ 1. Векторы и основные линейные операции над ними
1. Векторные величины
В отличие от скалярной величины, которую можно задать одним числом и отложить на некоторой шкале (отсюда и название – «скалярная») – площадь, объём, температура — векторную величину, или просто вектор, можно задать с помощью числа и некоторого направления (скорость, сила).
Итак, мы можем сказать, что
вектор 
— это величина, которая характеризуется
числом, совпадающим с длиной отрезка
,
и направлением, совпадающим с направлением
луча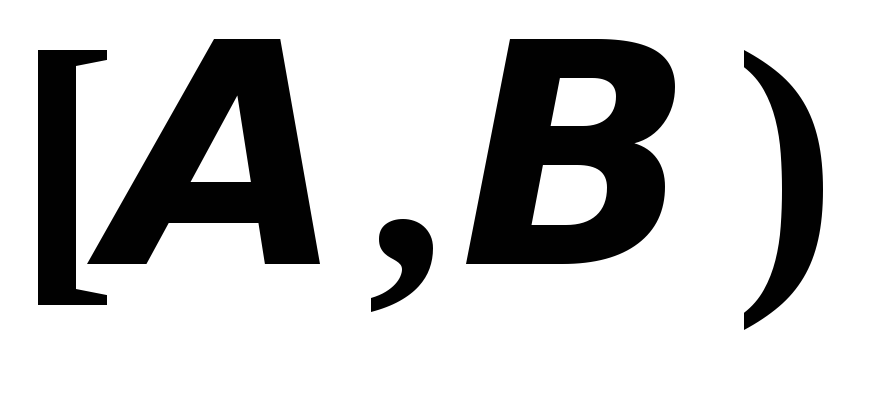
( рис. 2.1.1).
При этом длину вектора
обозначают 
,
или ещё
.
Длину вектора также называют модулем
этого вектора. Векторы
и
называютравными, если совпадают
их длины и направления.
Векторы 
и 
называютпротивоположными, если
их длины равны, а направления противоположны.
Заметим, что при этом начало вектора
можно поместить в любой точке пространстве.
Такие векторы называютсвободными.
Если
начало и конец вектора совпадают, то
такой вектор называется нулевым (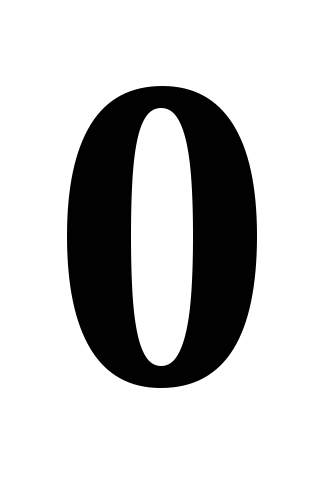
).
Направление нулевого вектора не
определено.
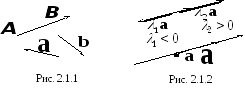
2. Умножение вектора на скаляр
Определение
1. Произведением
вектора 
на число
называется такой вектор
,
что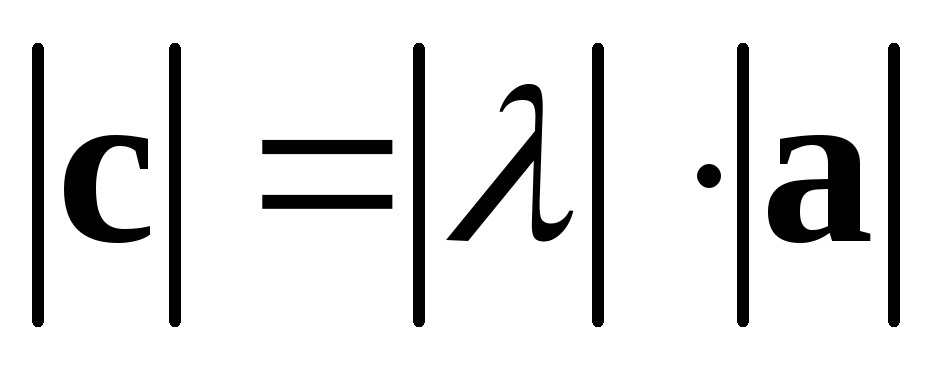
,
а направление его совпадает с направлением
вектора
,
если
>0,
и ему противоположно, если
<0;
если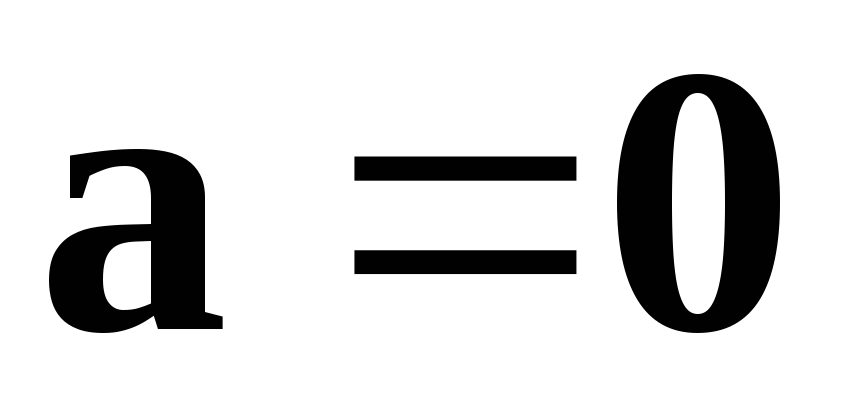
или
,
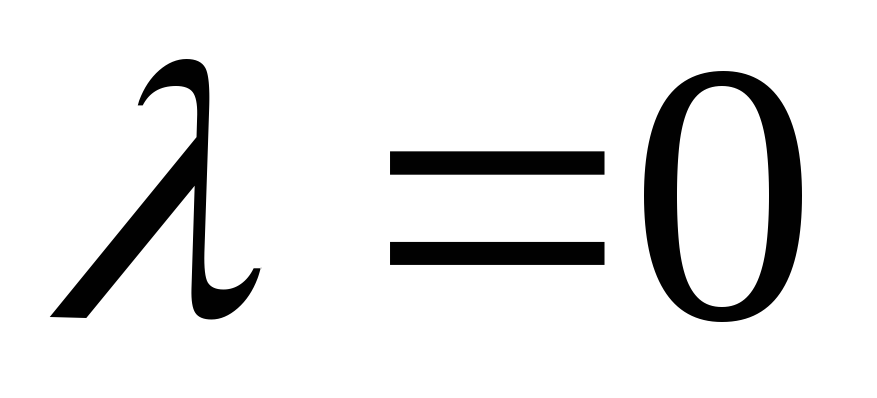то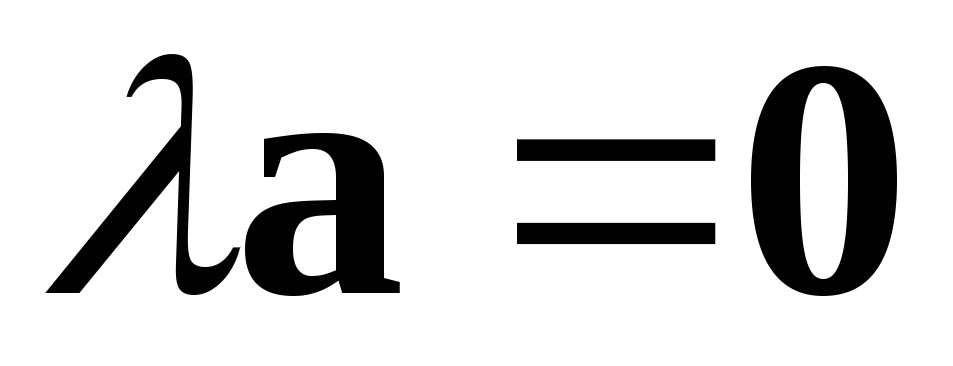
.
Ясно,
что векторы 
и
(если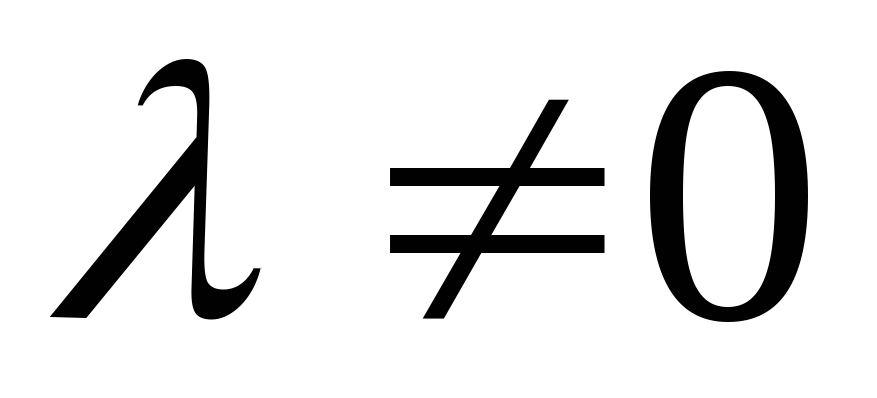
)
можно поместить на одной прямой (рис.
2.1.2). Вектор
,
очевидно, является противоположным
вектору
.
Определение
2. Два ненулевых вектора 
и
,
лежащих на одной прямой или на параллельных
прямых, называютсяколлинеарными.
3. Единичный вектор
Определение
3.Вектор
,
длина которого равна единице, называетсяединичным вектором, илиортом.
Если задан некоторый вектор
(
),
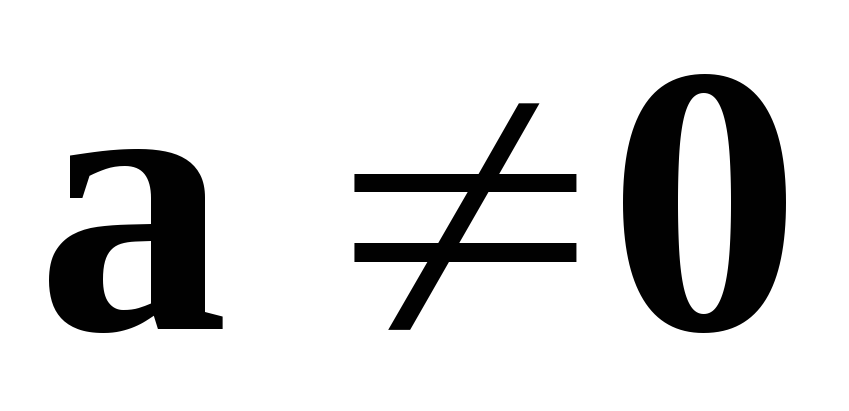то всегда можно подобрать множитель
,
такой, чтобы после умножения на него
длина вектора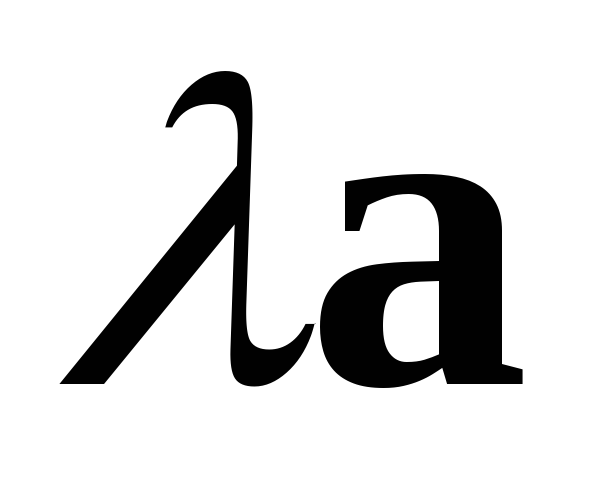
была
бы равна единице. Очевидно, что в качестве
такого числа нужно взять
.
Тогда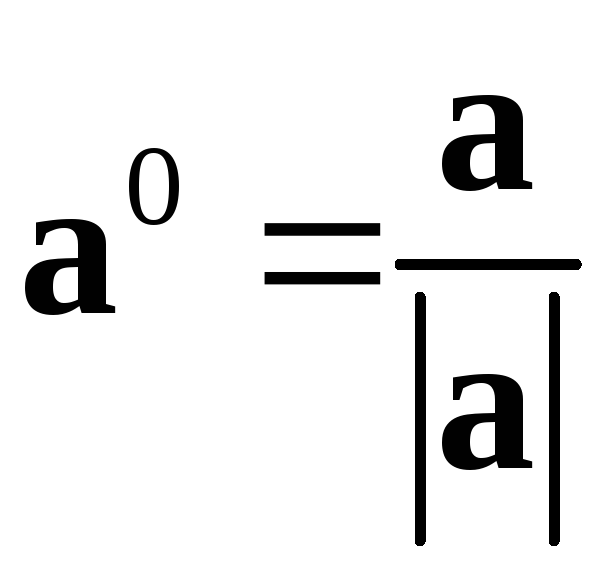
,
и при этом
называется
единичным вектором, соответствующим
вектору
,
или ортом вектора
.
Очевидно, что направление единичного
вектора всегда совпадает с направлением
вектора
.
Ясно также, что
.
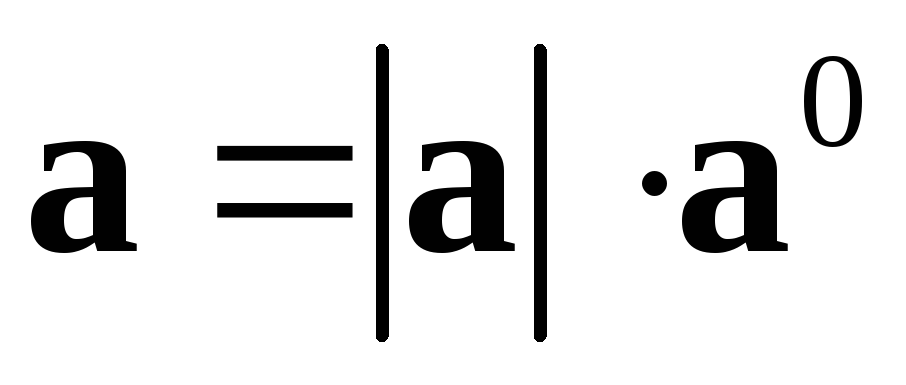Точно
так же единичный вектор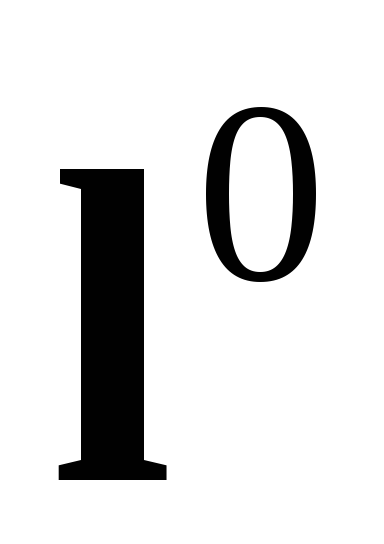 
,
направление которого совпадает с
направлением оси
,
называется ортом оси
,
или её единичным вектором.
4. Сложение векторов
Определение
4. Суммой
векторов 
и
,
расположенных так, что начало вектора
совпадает с концом вектора
,
называется вектор
,
начало которого совпадает с началом
вектора
,
а конец – с концом вектора
.
(правило треугольника – рис. 2.1.3, а).
Рис. 4
б)
При этом пишут: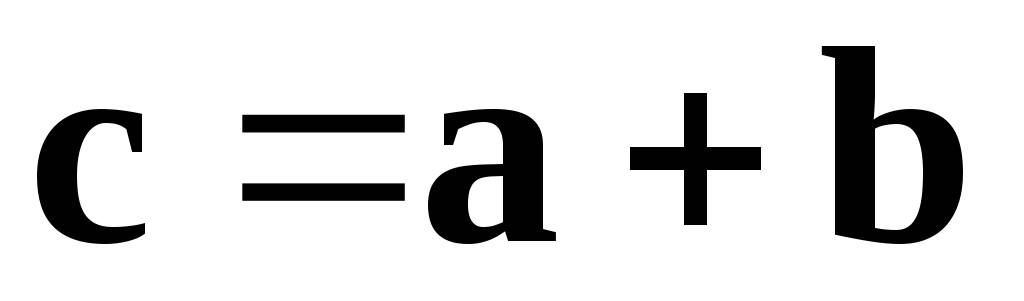
.
Аналогично определяется суммаn векторов 
.
А именно: суммой называют вектор 
,
проведённый из начала первого в конец
последнего вектора, при условии, что
начало вектора
совпадает
с концом
вектора 
,
начало вектора
совпадает
с концом вектора
и т.д. (правило многоугольника – рис.
2.1.3, б).
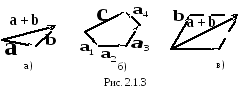
Замечание.Если на векторах
и
построить параллелограмм, поместив их
начало в общую точку, то сумма
будет лежать на диагонали параллелограмма,
выходящего из общего начала векторов
и
(правило параллелограмма – рис. 2.1.3,
в).
1) 
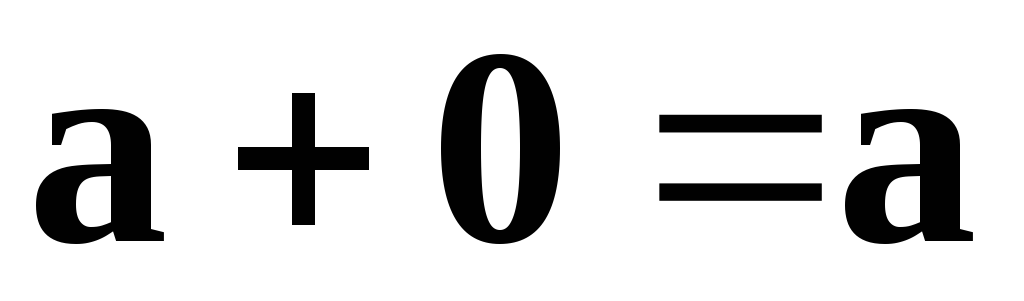— поглощение нулевого вектора
2) 
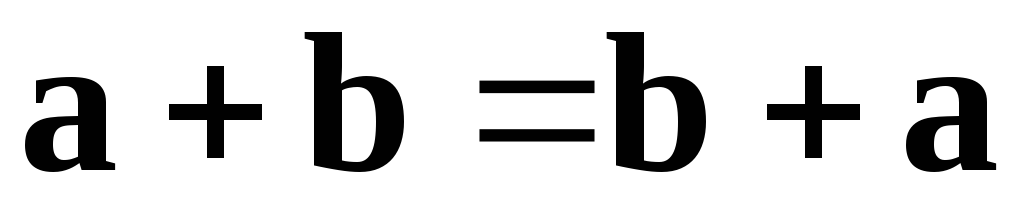— перестановочное, или коммутативное
3) 
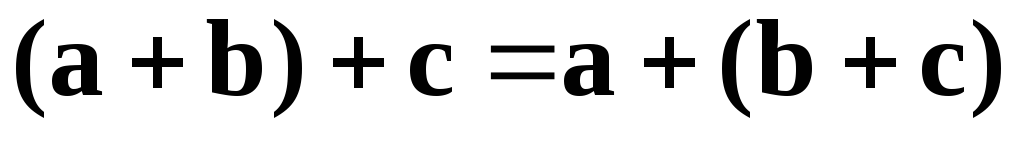— сочетательное, или ассоциативное.
Для
всякого ненулевого вектора 
существует противоположный вектор —
,
такой, что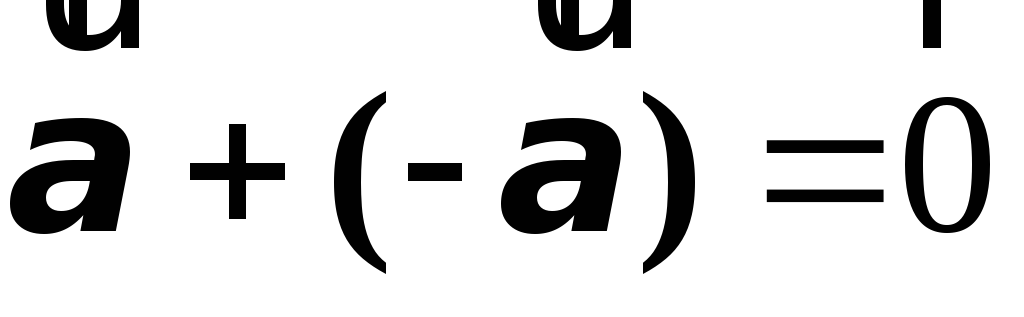
.
5.6.3 Вектор, модуль вектора, равенство векторов; сложение векторов и умножение вектора на число
Видеоурок 1: Понятие вектора
Видеоурок 2: Равенство векторов
Видеоурок 3: Сложение и вычитание векторов
Видеоурок 4: Умножение вектора на число
Лекция: Вектор, модуль вектора, равенство векторов; сложение векторов и умножение вектора на число
ВекторВектор – это тело, которое изучается в математике, но используется в большом количестве наук. Например, в физике существуют скалярные величины (те, что характеризуются значением – масса, температура и т.д.), а также векторные величины (сила, работа и другие).
Вектор – это величина, которая характеризуется не только значением, но и направлением. Иными словами, это направленный отрезок.
Но кроме его длины, нам также важно, где находится его начало, а где конец.
Если вектор имеет свое начало в некоторой точке А, а заканчивается в точке В, то его обозначают следующим образом:
Кроме двух букв, вектор можно обозначить одной буквой со значком вектора сверху.
Длиной вектора (его модулем) называют расстояние между концом вектора и его началом.
Для определения модуля вектора следует воспользоваться следующей формулой:
Кроме этого, модуль вектора может обозначаться следующим образом:
Если некоторый вектор имеет начало и конец в одной и той же точке, то такой вектор называют нулевым. Нулевой вектор обозначают, как
Если длина некоторого вектора равна единичному отрезку, то его называют единичным.
Если некоторые векторы расположены на одной прямой или же параллельны друг другу, то такие векторы называются коллинеарными.
Если некоторые векторы можно назвать коллинеарными, но кроме этого они направлены в одну сторону, то их можно назвать сонаправленными.
Если же наоборот два коллинеарных вектора смотрят в разные стороны, то их называют противоположно направленными.
Если же некоторые векторы являются коллинеарными, сонаправленными, а также имеют одинаковую длину (модуль), то их можно назвать равными.
Координаты вектора
Для нахождения координаты вектора следует вычесть соответствующие координаты его конца и начала.
Например, если начало вектора А (3; 6), а конец В (5;9), то этот вектор будет иметь следующие координаты: {2;3}.
Сложение и вычитание векторов
Чтобы сложить два вектора для получения нового, необходимо сложить соответствующие координаты.
Например, сложим вектор {2;3} с вектором {5;7}. В результате получим новый вектор с координатами {7;10}. С вычитанием все аналогично.
Умножение вектора на некоторое число
Чтобы умножить вектор на некоторое число, следует умножить каждую его координату на данное число.
Свойства:
- Первоначальный вектор и вектор умноженный на некоторое число, который равный ему, являются параллельными.
- Если число, на которое умножался вектор, больше нуля, то новый вектор будет сонаправлен первоначальному. Если же число меньше нуля, то векторы будут противоположно направленны.
Собственный вектор — Википедия
Синим цветом обозначен собственный вектор. Он, в отличие от красного, при деформации (преобразовании) не изменил направление, поэтому является собственным вектором этого преобразования, соответствующим некоторому собственному значению λ{\displaystyle \lambda } (здесь оно равно единице, так как вектор не изменил свою длину). Любой вектор, параллельный синему вектору, также будет собственным, соответствующим тому же собственному значению. Множество всех таких векторов (вместе с нулевым) образует собственное подпространствоСо́бственный ве́ктор — понятие в линейной алгебре, определяемое для произвольного линейного оператора как ненулевой вектор, применение к которому оператора даёт коллинеарный вектор — тот же вектор, умноженный на некоторое скалярное значение. Скаляр, на который умножается собственный вектор под действием оператора, называется собственным числом (или собственным значением) линейного оператора, соответствующим данному собственному вектору. Одним из представлений линейного оператора является квадратная матрица, поэтому собственные векторы и собственные значения часто определяются в контексте использования таких матриц[1][2].
Понятия собственного вектора и собственного числа[3] являются одними из ключевых в линейной алгебре, на их основе строится множество конструкций. Это связано с тем, что многие соотношения, связанные с линейными операторами, существенно упрощаются в системе координат, построенной на базисе из собственных векторов оператора. Множество собственных значений линейного оператора (спектр оператора) характеризует важные свойства оператора без привязки к какой-либо конкретной системе координат.
Понятие линейного векторного пространства не ограничивается «чисто геометрическими» векторами и обобщается на разнообразные множества объектов, таких как пространства функций (в которых действуют линейные дифференциальные и интегральные операторы). Для такого рода пространств и операторов говорят о собственных функциях операторов.
Множество всех собственных векторов линейного оператора, соответствующих данному собственному числу, дополненное нулевым вектором, называется собственным подпространством[4] этого оператора.
Другая трансформация Джоконды. Синий вектор меняет направление, а красный — нет. Поэтому красный является собственным вектором, а синий — нет. Так как красный вектор ни растянулся, ни сжался, его собственное значение равно, как и на картинке выше, единице. Все векторы, коллинеарные красному, тоже собственные.Пусть L{\displaystyle L} — линейное пространство над полем K{\displaystyle K}, A:L→L{\displaystyle A\colon L\to L} — линейное преобразование.
Собственным вектором линейного преобразования A{\displaystyle A} называется такой ненулевой вектор x∈L{\displaystyle x\in L}, что для некоторого λ∈K{\displaystyle \lambda \in K}
- Ax=λx.{\displaystyle \ Ax=\lambda x.}
Собственным значением (собственным числом) линейного преобразования A{\displaystyle A} называется такое число λ∈K{\displaystyle \lambda \in K}, для которого существует собственный вектор, то есть уравнение Ax=λx{\displaystyle Ax=\lambda x} имеет ненулевое решение x∈L{\displaystyle x\in L}.
Упрощённо говоря, собственный вектор — любой ненулевой вектор x{\displaystyle x}, который отображается в коллинеарный ему вектор λx{\displaystyle \lambda x} оператором A{\displaystyle A}, а соответствующий скаляр λ{\displaystyle \lambda } называется собственным значением оператора.
Собственным подпространством (или характеристическим подпространством) линейного преобразования A{\displaystyle A} для данного собственного числа λ∈K{\displaystyle \lambda \in K} (или отвечающим этому числу) называется множество всех собственных векторов x∈L{\displaystyle x\in L} соответствующих данному собственному числу дополненное нулевым вектором. Обозначим собственное подпространство, отвечающее собственному числу λ, через Eλ{\displaystyle E_{\lambda }}, а единичный оператор — через I{\displaystyle I}. По определению, собственное подпространство является ядром оператора A−λ⋅I,{\displaystyle A-\lambda \cdot I,} то есть множеством векторов, отображаемых этим оператором в нулевой вектор:
- Eλ=ker(A−λ⋅I).{\displaystyle E_{\lambda }=\ker(A-\lambda \cdot I).}
Корневым вектором линейного преобразования A{\displaystyle A} для данного собственного значения λ∈K{\displaystyle \lambda \in K} называется такой ненулевой вектор x∈L{\displaystyle x\in L}, что для некоторого натурального числа m{\displaystyle m}
- (A−λ⋅I)mx=0.{\displaystyle (A-\lambda \cdot I)^{m}x=0.}
Если m{\displaystyle m} является наименьшим из таких натуральных чисел (то есть (A−λ⋅I)m−1x≠0{\displaystyle (A-\lambda \cdot I)^{m-1}x\neq 0}), то m{\displaystyle m} называется высотой корневого вектора x{\displaystyle x}.
Корневым подпространством линейного преобразования A{\displaystyle A} для данного собственного числа λ∈K{\displaystyle \lambda \in K} называется множество всех корневых векторов x∈L{\displaystyle x\in L}, соответствующих данному собственному числу, если это множество дополнить нулевым вектором. Обозначим корневое подпространство, отвечающее собственному числу λ, через Vλ{\displaystyle V_{\lambda }}. По определению,
- Vλ=⋃m=1∞ker(A−λ⋅I)m=⋃m=1∞Vm,λ.{\displaystyle V_{\lambda }=\bigcup _{m=1}^{\infty }\ker(A-\lambda \cdot I)^{m}=\bigcup _{m=1}^{\infty }V_{m,\lambda }.}
В настоящее время собственные значения обычно вводятся в контексте линейной алгебры, однако исторически они возникли при исследовании квадратичных форм и дифференциальных уравнений.
В XVIII веке Эйлер, изучая вращательное движение абсолютно твёрдого тела, обнаружил значимость главных осей, а Лагранж показал, что главные оси соответствуют собственным векторам матрицы инерции. В начале XIX века Коши использовал труды Эйлера и Лагранжа для классификации поверхностей второго порядка, и обобщил результаты на высшие порядки. Коши также ввёл термин «характеристический корень» (фр. racine caractéristique) для собственного значения, этот термин сохранился в контексте характеристического многочлена матрицы[5][6].
В начале XX века Гильберт занимался исследованием собственных значений интегральных операторов, рассматривая последние как матрицы бесконечного размера[7]. В 1904 г. для обозначения собственных значений и собственных векторов Гильберт начал использовать термины eigenvalues и eigenvectors, основанные на немецком слове eigen (собственный)[8]. Впоследствии эти термины перешли и в английский язык, заменив используемые ранее «proper value» и «proper vector»[9].
Свойства собственных значений, собственных и корневых векторов и пространств[править | править код]
Общий случай[править | править код]
Подпространство V⊂L{\displaystyle V\subset L} называется инвариантным подпространством линейного преобразования A{\displaystyle A} (A{\displaystyle A}-инвариантным подпространством), если
- AV⊆V{\displaystyle AV\subseteq V}.
- Собственные векторы являются корневыми (высоты 1): Eλ⊆Vλ{\displaystyle E_{\lambda }\subseteq V_{\lambda }};
- Корневые векторы могут не быть собственными: например, для преобразования двумерного пространства, заданного матрицей
- A=(1101){\displaystyle A={\begin{pmatrix}1&1\\0&1\end{pmatrix}}}
- (A−E)2=0{\displaystyle (A-E)^{2}=0}, и все векторы являются корневыми, соответствующими собственному числу 1, но A{\displaystyle A} имеет единственный собственный вектор (с точностью до умножения на число).
- Для разных собственных значений корневые (и, следовательно, собственные) подпространства имеют тривиальное (нулевое) пересечение:
- Vλ⋂Vμ={0}{\displaystyle V_{\lambda }\bigcap V_{\mu }=\{0\}} если λ≠μ{\displaystyle \lambda \neq \mu }.
- Метод поиска собственных значений для самосопряжённых операторов и поиска сингулярных чисел для нормального оператора даёт теорема Куранта — Фишера.
Конечномерные линейные пространства[править | править код]
Выбрав базис в n{\displaystyle n}-мерном линейном пространстве L{\displaystyle L}, можно сопоставить линейному преобразованию A:L→L{\displaystyle A\colon L\to L} квадратную n×n{\displaystyle n\times n} матрицу и определить для неё характеристический многочлен матрицы
- PA(λ)=det(A−λ⋅I)=∑k=0nakλk{\displaystyle P_{A}(\lambda )=\det(A-\lambda \cdot I)=\sum \limits _{k=0}^{n}a_{k}\lambda ^{k}}.
- Характеристический многочлен не зависит от базиса в L{\displaystyle L}. Его коэффициенты являются инвариантами оператора A{\displaystyle A}. В частности, a0=detA{\displaystyle a_{0}=\det \,A}, an−1=trA{\displaystyle a_{n-1}=\operatorname {tr} \,A} не зависят от выбора базиса.
- Собственные значения, и только они, являются корнями характеристического многочлена матрицы.
- Количество различных собственных значений не может превышать размер матрицы.
- Если выбрать в качестве базисных векторов собственные вектора оператора, то матрица A{\displaystyle A} в таком базисе станет диагональной, причём на диагонали будут стоять собственные значения оператора. Отметим, однако, что далеко не любая матрица допускает базис из собственных векторов (общая структура описывается нормальной жордановой формой).
- Для положительно определённой симметричной матрицы A{\displaystyle A} процедура нахождения собственных значений и собственных векторов является не чем иным, как поиском направлений и длин полуосей соответствующего эллипса.
Пусть числовое поле алгебраически замкнуто (например, является полем комплексных чисел). Тогда характеристический многочлен разлагается в произведение n{\displaystyle n} линейных множителей
- PA(λ)=(−1)n∏i=1n(λ−λi){\displaystyle P_{A}(\lambda )=(-1)^{n}\prod _{i=1}^{n}(\lambda -\lambda _{i})}
- где λi(i=1,…,n){\displaystyle \lambda _{i}\;(i=1,\ldots ,n)} — собственные значения; некоторые из λi{\displaystyle \lambda _{i}} могут быть равны. Кратность собственного значения λi{\displaystyle \lambda _{i}} — это число множителей, равных λ−λi,{\displaystyle \lambda -\lambda _{i},} в разложении характеристического многочлена на линейные множители (называется также алгебраическая кратность собственного значения).
- Размерность корневого пространства Vλi{\displaystyle V_{\lambda _{i}}} равна кратности собственного значения.
- Векторное пространство L{\displaystyle L} разлагается в прямую сумму корневых подпространств (по теореме о жордановой форме):
- L=⨁λiVλi{\displaystyle L=\bigoplus _{\lambda _{i}}V_{\lambda _{i}}}
- где суммирование производится по всем λi{\displaystyle \lambda _{i}} — собственным числам A{\displaystyle A}.
- Геометрическая кратность собственного значения λi{\displaystyle \lambda _{i}} — это размерность соответствующего собственного подпространства Eλi{\displaystyle E_{\lambda _{i}}}; геометрическая кратность собственного значения не превосходит его кратности, поскольку Eλi⊆Vλi{\displaystyle E_{\lambda _{i}}\subseteq V_{\lambda _{i}}}
Гильбертовы пространства над полем комплексных чисел и нормальные операторы[править | править код]
Наличие скалярного произведения позволяет выделить важные классы операторов, собственные значения и собственные векторы которых обладают рядом дополнительных полезных свойств.
Нормальным оператором называется оператор A{\displaystyle A}, коммутирующий со своим сопряжённым A∗{\displaystyle A^{*}}:
- AA∗=A∗A{\displaystyle AA^{*}=A^{*}A}.
Частными классами нормальных операторов являются самосопряжённые (эрмитовы) операторы (A=A∗{\displaystyle A=A^{*}}), антиэрмитовы операторы (A=−A∗{\displaystyle A=-A^{*}}) и унитарные операторы (A−1=A∗{\displaystyle A^{-1}=A^{*}}), а также их вещественные варианты: симметричные операторы, антисимметричные операторы и ортогональные преобразования.
- Все корневые векторы нормального оператора являются собственными.
- Все собственные значения самосопряжённого оператора являются вещественными.
- Все собственные значения антиэрмитового оператора являются мнимыми.
- Все собственные значения унитарного оператора лежат на единичной окружности |λ|=1{\displaystyle |\lambda |=1}.
- В конечномерном случае сумма размерностей собственных подпространств нормального оператора A:Cn→Cn{\displaystyle A\colon \mathbb {C} ^{n}\to \mathbb {C} ^{n}}, соответствующих всем собственным значениям, равна размерности матрицы, а векторное пространство разлагается в ортогональную сумму собственных подпространств:
- L=⨁λiEλi,{\displaystyle L=\bigoplus _{\lambda _{i}}E_{\lambda _{i}},}
- где суммирование производится по всем λi{\displaystyle \lambda _{i}} — собственным числам A{\displaystyle A}, а Eλi{\displaystyle E_{\lambda _{i}}} взаимно ортогональны для различных λi{\displaystyle \lambda _{i}}.
- Последнее свойство для нормального оператора над C{\displaystyle \mathbb {C} } является характеристическим: оператор нормален тогда и только тогда, когда его матрица имеет диагональный вид в каком-нибудь ортонормированном базисе (в конечномерном случае).
Положительные матрицы[править | править код]
Квадратная вещественная n×n{\displaystyle n\times n} матрица A=(aij){\displaystyle A=(a_{ij})} называется положительной, если все её элементы положительны: aij>0{\displaystyle a_{ij}>0}.
Теорема Перрона (частный случай теоремы Перрона — Фробениуса): Положительная квадратная матрица A{\displaystyle A} имеет положительное собственное значение r{\displaystyle r}, которое имеет алгебраическую кратность 1 и строго превосходит абсолютную величину любого другого собственного значения этой матрицы. Собственному значению r{\displaystyle r} соответствует собственный вектор er{\displaystyle e_{r}}, все координаты которого строго положительны. Вектор er{\displaystyle e_{r}} — единственный собственный вектор A{\displaystyle A} (с точностью до умножения на число), имеющий неотрицательные координаты.
Собственный вектор er{\displaystyle e_{r}} может быть вычислен посредством прямых итераций: выберем произвольный начальный вектор v0{\displaystyle v_{0}} с положительными координатами. Положим:
- vk+1=Avk‖Avk‖{\displaystyle v_{k+1}={\frac {Av_{k}}{\|Av_{k}\|}}}
Последовательность vk{\displaystyle v_{k}} сходится к нормированному собственному вектору er/‖er‖{\displaystyle e_{r}/\|e_{r}\|}.
Другая область применения метода прямых итераций — поиск собственных векторов положительно определённых симметричных операторов.
Неравенства для собственных значений[править | править код]
- Неравенство Шура Пусть λ1,…,λn{\displaystyle \lambda _{1},…,\lambda _{n}} — собственные значения матрицы A=(aij)i,j=1,…,n{\displaystyle A=(a_{ij})_{i,j=1,\ldots ,n}}. Тогда
- ∑i=1n|λi|
