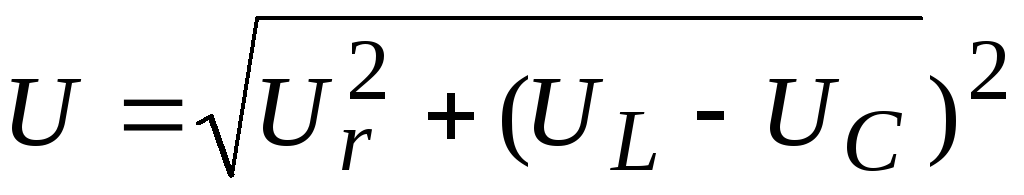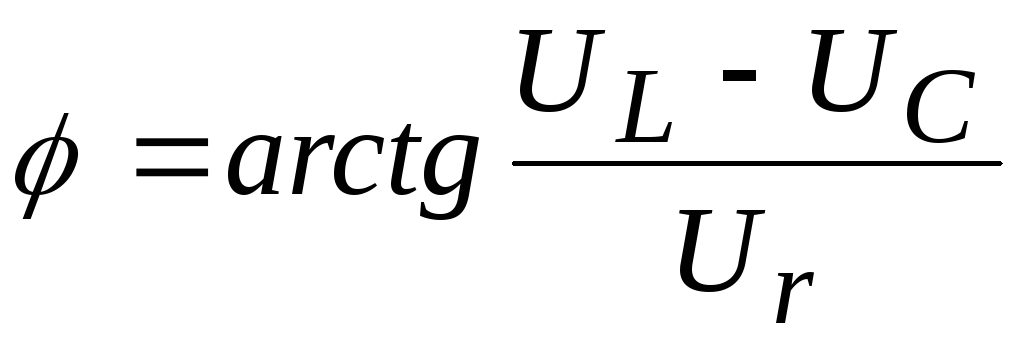2.5. Сопротивления в цепи переменного тока
В цепях переменного тока выделяют следующие виды сопротивлений.
Активное. Активным называют сопротивление резистора. Условное обозначение

Единицей измерения сопротивления является Ом. Сопротивление резистора не зависит от частоты.
Реактивное. В разделе реактивные выделяют три вида сопротивлений: индуктивное xL и емкостное хс и собственно реактивное. Для индуктивного сопротивления выше была получена формула XL = ωL. Единицей измерения индуктивного сопротивления также является Ом. Величина xL линейно зависит от частоты.
Для
емкостного сопротивления выше была
получена формула XC = 1 / ωC.
Единицей измерения емкостного
сопротивления является Ом. Величина хс
зависит от частоты по обратно-пропорциональному
закону. Просто реактивным сопротивлением
цепи называют величину X = X
Полное сопротивление. Полным сопротивлением цепи называют величину
(2.28)
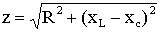 .
.
Из этого соотношения следует, что сопротивления Z, R и X образуют треугольник: Z – гипотенуза, R и X – катеты. Для удобства в этом треугольнике рассматривают угол φ, который определяют уравнением
(2.29)
φ = arctg((XL
и называют углом сдвига фаз. С учетом него можно дать дополнительные связи
(2.30)
R = Z cos φ,
(2.31)
X = Z sin φ.
2.6. Мощности в цепях переменного тока
По аналогии с мощностью в цепях постоянного тока P = U I, в цепях переменного тока рассматривают мгновенную мощность p = u i. Для упрощения рассмотрим мгновенную мощность в каждом из элементов R, L и С отдельно.
Элемент r (резистор)
Зададим напряжение и ток в виде соотношений
u(t) = Um sin(ωt + ψu),
i(t) = Im sin(ωt + ψi).
Известно,
что для резистора ψ
(2.32)
p(t) = u(t) i(t) = Um Im sin2(ωt + ψi).
Из уравнения (2.32) видно, что мгновенная мощность всегда больше нуля и изменяется во времени. В таких случаях принять рассматривать среднюю за период Т мощность
(2.33)
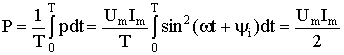 .
.
Если
записать Um и Im через действующие значения U и I: 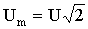
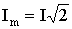 ,
то получим
,
то получим(2.34)
P = U I.
По форме уравнение (2.34) совпадает с мощностью на постоянном токе. Величину Р равную произведению действующих значений тока и напряжения называют активной мощностью. Единицей ее измерения является Ватт (Вт).
Элемент l (индуктивность)
Известно, что в индуктивности соотношение фаз ψu = ψi + 90°. Для мгновенной мощности имеет
(2.35)
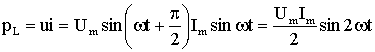 .
.
Усредняя уравнение (2.35) по времени за период Т получим
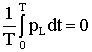 .
.
Для количественной оценки мощности в индуктивности используют величину QL равную максимальному значению рL
(2.36)
QL = (Um Im) / 2
и называют ее реактивной (индуктивной) мощностью. Единицей ее измерения выбрали ВАр (вольт-ампер реактивный). Уравнение (2.36) можно записать через действующие значения U и I и используя формулу UL = I XL получим
(2.37)
QL = I2 XL.
Элемент с (ёмкость)
pC(t) = u(t) I(t) = (Um Im) / 2 · sin(2ωt).
Среднее значение за период здесь также равно нулю. По аналогии с уравнением (2.36) вводят величину QC = I2 XC, которую называют реактивной (емкостной) мощностью. Единицей ее измерения также является ВАр.
Если в цепи присутствуют элементы R, L и С, то активная и реактивная мощности определяются уравнениями
(2.37)
P = U I cos φ,
(2.38)
Q = QL — QC,
(2.39)
Q = U I sin φ,
где φ – угол сдвига фаз.
Вводят понятие полной мощности цепи
(2.40)
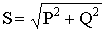 .
.
С учетом уравнений (2.37) и (2.39), (2.40) можно записать в виде
(2.41)
S = U I.
Единицей измерения полной мощности является ВА – вольт-ампер.
Полное сопротивление цепи переменного тока
В предыдущих статьях мы узнали, что всякое сопротивление, поглощающее энергию, называется активным, а сопротивление, не поглощающее энергии, безваттным или реактивным. Кроме того, мы установили, что реактивные сопротивления делятся на два вида — индуктивные и емкостные.
Однако существуют цепи, где сопротивление не является чисто активным или чисто реактивным. То есть цепи, где вместе с активным сопротивлением включены в цепь, как емкости, так и индуктивности.
Введем понятие полного сопротивления цепи переменному току — Z, которое соответствует векторной сумме всех сопротивлений цепи (активных, емкостных и индуктивных). Понятие полного сопротивления цепи нам необходимо для более полного понимания закона Ома для переменного тока
На рисунке 1 представлены варианты электрических цепей и их классификация в зависимости от того какие элементы (активные или реактивные) включены в цепь.
Рисунок 1. Классификация цепей переменного тока.
Полное сопротивление цепи с чисто активными элементами соответствует сумме активных сопротивлений цепи и рассматривалось нами ранее. О чисто емкостном и индуктивном сопротивлении цепи мы тоже с вами говорили, и оно зависит соответственно от общей емкости и индуктивности цепи.
Рассмотрим более сложные варианты цепи, где последовательно с активным сопротивлением в цепь включено индуктивное и реактивное сопротивление.
Полное сопротивление цепи при последовательном соединении активного и реактивного сопротивления.
В любом сечении цепи, изображенной на рисунке 2,а, мгновенные значения тока должны быть одинаковыми, так как в противном случае наблюдались бы скопления и разрежения электронов в каких-либо точках цепи. Иными словами, фазы тока по всей длине цепи должны быть одинаковыми. Кроме того, мы знаем, что фаза напряжения на индуктивном сопротивлении опережает фазу тока на 90°, а фаза напряжения на активном сопротивлении совпадает с фазой тока (рисунок 2,б). Отсюда следует, что радиус-вектор напряжения U
Рисунок 2. Полное сопротивление цепи с активным сопротивлением и индуктивностью. а) — схема цепи; б) — сдвиг фаз тока и напряжения; в) — треугольник напряжений; д) — треугольник сопротивлений.
Для получения радиуса-вектора результирующего напряжения на зажимах А и В (рис.2,а) мы произведем геометрическое сложение радиусов-векторов UL и UR. Такое сложение выполнено на рис. 2,в, из которого видно, что результирующий вектор UAB является гипотенузой прямоугольного треугольника.
Из геометрии известно, что квадрат гипотенузы равен сумме квадратов катетов.
По закону Ома напряжение должно равняться силе тока, умноженной на сопротивление.
Так как сила тока во всех точках цепи одинакова, то квадрат полного сопротивления цепи (Z2) будет также равен сумме квадратов активного и индуктивного сопротивлений, т. е.
(1)
Извлекая квадратный корень из обеих частей этого равенства, получим,
(2)
Таким образом, полное сопротивление цепи, изображенной на рис 2,а, равно корню квадратному из суммы квадратов активного и индуктивного сопротивлений
Полное сопротивление можно находить не только путем вычисления, но и путем построения треугольника сопротивлений, аналогичного треугольнику напряжений (рис 2,д), т. е. полное сопротивление цепи переменному току может быть получено путем измерения гипотенузы, прямоугольного треугольника, катетами которого являются активное и реактивное сопротивления. Разумеется, измерения катетов и гипотенузы должны производиться в одном и том же масштабе. Так, например, если мы условились, что 1 см длины катетов соответствует 1 ом, то число омов полного сопротивления будет равно числу сантиметров, укладывающихся на гипотенузе.
Полное сопротивление цепи, изображенной на рис.2,а, не является ни чисто активным, ни чисто реактивным; оно содержит в себе оба эти вида сопротивлений. Поэтому угол сдвига фаз тока и напряжения в этой цепи будет отличаться и от 0° и от 90°, то есть он будет больше 0°, но меньше 90°. К которому из этих двух значений он будет более близок, будет зависеть от того, какое из этих сопротивлений имеет преобладающее значение в цепи. Если индуктивное сопротивление будет больше активного, то угол сдвига фаз будет более близок к 90°, и наоборот, если преобладающим будет активное сопротивление, то угол сдвига фаз будет более близок к 0°.
В цепи, изображенной на рис 3,а, соединены последовательно активное и емкостное сопротивления. Полное сопротивление такой цепи можно определить при помощи треугольника сопротивлений так же, как мы определяли выше полное сопротивление активно-индуктивной цепи.
Рисунок 3. Полное сопротивление цепи с активным сопротивлением и емкостью. а) — схема цепи; б) — треугольник сопротивлений.
Разница между обоими случаями состоит лишь в том, что треугольник сопротивлений для активно-емкостной цепи будет повернут в другую сторону (рис 3,б) вследствие того, что ток в емкостной цепи не отстает от напряжения, а опережает его.
Для данного случая:
(3)
В общем случае, когда цепь содержит все три вида сопротивлений (рис. 4,а), сначала определяется реактивное сопротивление этой цепи, а затем уже полное сопротивление цепи.
Рисунок 4. Полное сопротивление цепи содержащей R, L и C. а) — схема цепи; б) — треугольник сопротивлений.
Реактивное сопротивление этой цепи состоит из индуктивного и емкостного сопротивлений. Так как эти два вида реактивного сопротивления противоположны друг другу по своему характеру, то общее реактивное сопротивление цепи будет равно их разности, т. е.
(4)
Общее реактивное сопротивление цепи может иметь индуктивный или емкостный характер, в зависимости от того, какое из этих двух сопротивлений (XL или XC преобладает).
После того как мы по формуле (4) определили общее реактивное сопротивление цепи, определение полного сопротивления не представит затруднений. Полное сопротивление будет равно корню квадратному из суммы квадратов активного и реактивного сопротивлений, т. е.
(5)
Или
(6)
Способ построения треугольника сопротивлений для этого случая изображен на рис. 4 б.
Полное сопротивление цепи при параллельном соединении активного и реактивного сопротивления.
Полное сопротивление цепи при параллельном соединении активного и реактивного элемента.
Для того чтобы вычислить полное сопротивление цепи, составленной из активного и индуктивного сопротивлений, соединенных между собой параллельно(рис. 5,а), нужно сначала вычислить проводимость каждой из параллельных ветвей, потом определить полную проводимость всей цепи между точками А и В и затем вычислить полное сопротивление цепи между этими точками.
Рисунок 5. Полное сопротивление цепи при параллельном соединении активного и реактивных элементов. а) — параллельное соединение R и L; б) — параллельное соединение R и C.
Проводимость активной ветви, как известно, равна 1/R, аналогично проводимость индуктивной ветви равна 1/ωL , а полная проводимость равна 1/Z
Полная проводимость равна корню квадратному из суммы квадратов активной и реактивной проводимости, т. е.
(7)
Приводя к общему знаменателю подкоренное выражение, получим:
(8)
откуда:
(9)
Формула (9) служит для вычисления полного сопротивления цепи, изображенной на рис. 5а.
Нахождение полного сопротивления для этого случая может быть произведено и геометрическим путем. Для этого нужно построить в соответствующем масштабе треугольник сопротивлений, и затем произведение длин катетов разделить на длину гипотенузы. Полученный результат и будет соответствовать полному сопротивлению.
Аналогично случаю, рассмотренному выше, полное сопротивление при параллельном соединении R и С (рис 5б) будет равно:
(10)
Полное сопротивление может быть найдено также и в этом случае путем построения треугольника сопротивлений.
В радиотехнике наиболее часто встречается случай па¬раллельного соединения индуктивности и емкости, например колебательный контур для настройки приемников и передатчиков. Так как катушка индуктивности всегда обладает кроме индуктивного еще и активным сопротивлением, то эквивалентная (равноценная) схема колебательного контура будет содержать в индуктивной ветви активное сопротивление (рис 7).
Рисунок 6. Эквивалентная схема колебательного контура.
Формула полного сопротивления для этого случая будет:
(11)
Так как обычно активное сопротивление катушки (R) бывает очень мало по сравнению с ее индуктивным сопротивлением (ωL), то мы имеем право формулу (11) переписать в следующем виде:
(12)
В колебательном контуре обычно подбирают величины L и С таким образом, чтобы индуктивное сопротивление равнялось емкостному, т. е. чтобы соблюдалось условие
(13)
При соблюдении этого условия полное сопротивление колебательного контура будет равно:
(14)
где L—индуктивность катушки в Гн;
С—емкость конденсатора в Ф;
R—активное сопротивление катушки в Ом.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Виды сопротивлений переменному току
Электрическая цепь переменного тока с резистивным сопротивлением
В таких приемниках вся электрическая энергия необратимо превращается в другой вид энергии (в резисторах — в тепловую). Идеальное активное сопротивление эквивалентно сопротивлению резистора (R) на постоянном токе. Напряжение и ток совпадают по фазе, т.е.= 0,cos= 1 (см рис. 14).
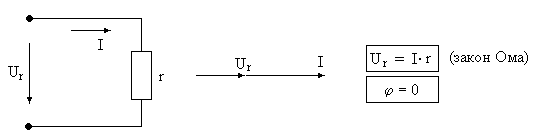
Рис. 14. Векторная диаграмма цепи с активным сопротивлением
Т.е. кривые изменения напряжения Urи токаIв один и тот же момент времениtдостигают максимального значения и одновременно проходят нулевые значения.
Электрическая цепь переменного тока с индуктивным элементом
Если из сверхпроводника (r= 0) намотать катушку и подключить ее к источнику синусоидального напряжения, то величина тока не будет равна бесконечности, как это следовало бы из закона Ома для постоянного тока или для идеального активного сопротивления, а будет ограничена определенным значением, т.е. в такой цепи появилось какое-то сопротивление. Причина этого – наводимая в катушке переменным магнитным полем ЭДС самоиндукции (eL) (рис. 15).
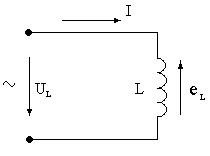
Рис. 15. Электрическая цепь с катушкой индуктивности
По II-ому закону Кирхгофа
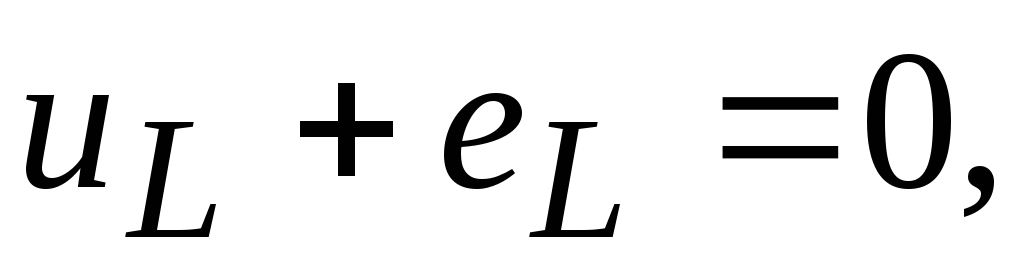 откуда
откуда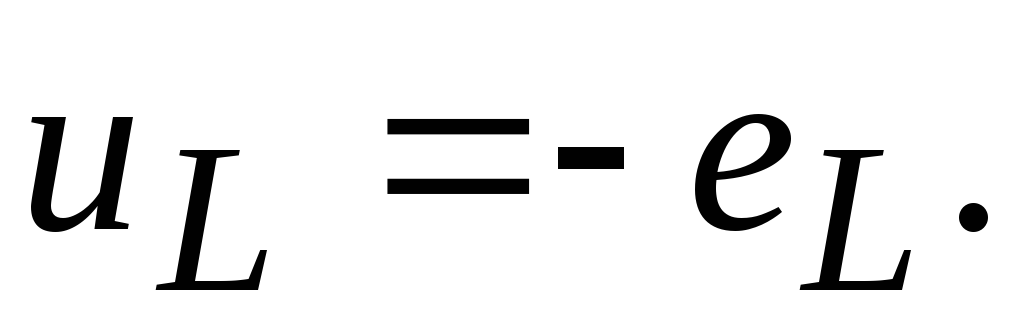
Так как 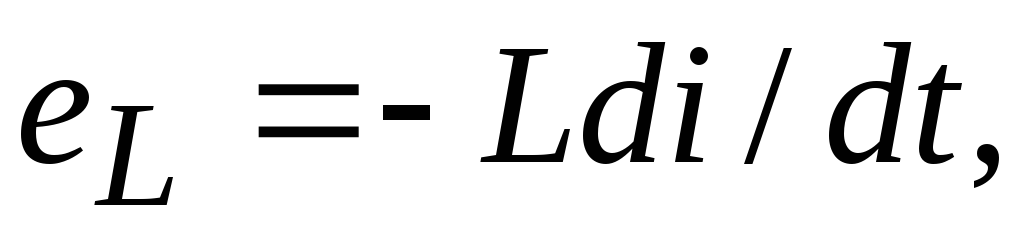 гдеL– индуктивность, то
при
гдеL– индуктивность, то
при 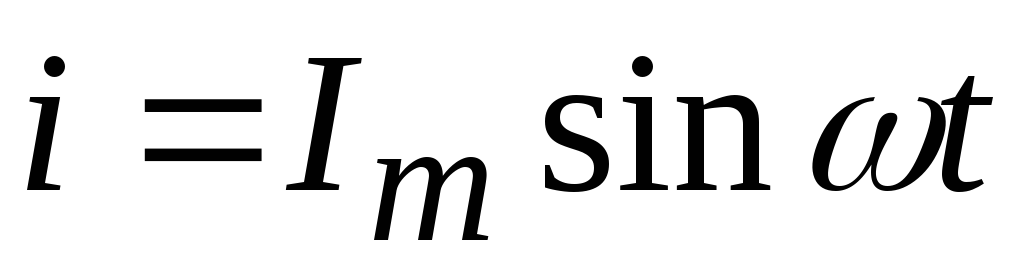 имеем
имеем
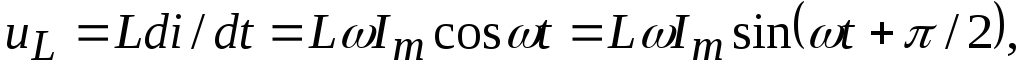
т.е. напряжение опережает ток на 90 электрических градусов, или ток отстаетот напряжения на 900.
Произведение “L” имеет размерность сопротивления (Ом) и называется индуктивным сопротивлением:
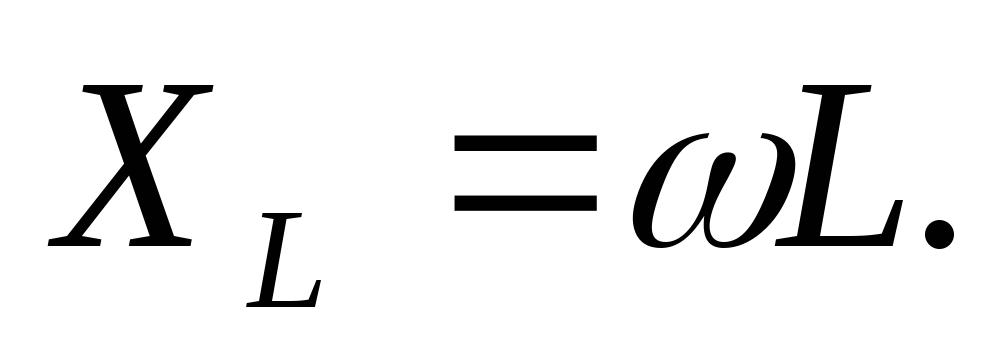
Векторная диаграмма и закон Ома для идеального индуктивного сопротивления имеют вид (рис. 16):
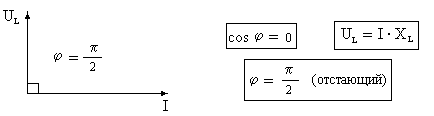
Рис. 16. Векторная диаграмма для идеального индуктивного сопротивления
Реальные
катушки индуктивности наматывают не
из сверхпроводника, т.е. 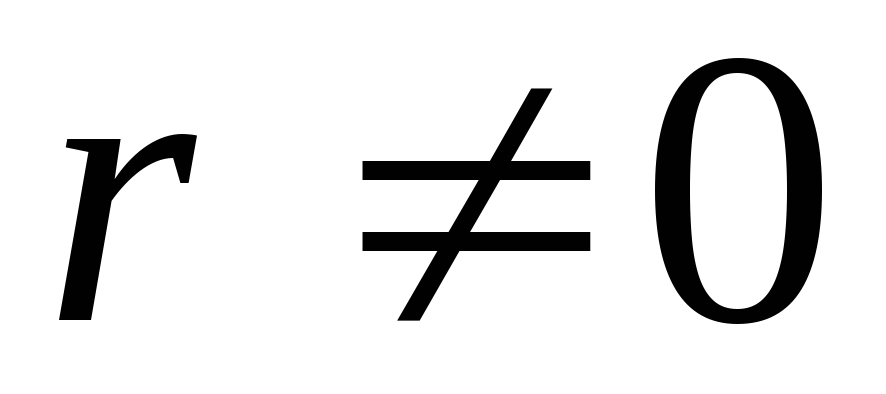 .
Поэтому они обладают некоторым активным
сопротивлением, которое тем больше, чем
тоньше обмоточный провод и больше витков
в катушке индуктивности.
.
Поэтому они обладают некоторым активным
сопротивлением, которое тем больше, чем
тоньше обмоточный провод и больше витков
в катушке индуктивности.
Таким образом, реальную индуктивность можно представить как последовательное соединение идеальной индуктивности и внутреннего активного сопротивления реальной катушки (рис.17).
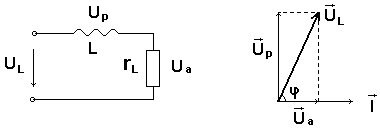
Рис.17. Векторная диаграмма реального индуктивного сопротивления
Напряжение реального индуктивного сопротивления ULвекторно складывается из двух векторов: вектора напряжения на идеальном реактивном элементеUри вектора напряжения на внутреннем активном сопротивленииUа.
Сдвиг фаз между током и напряжением зависит от параметров конкретной катушки (длины векторовUриUа).
Электрическая цепь переменного тока с емкостным элементом
Если к источнику синусоидального напряжения подключить конденсатор емкостью С (рис. 18),
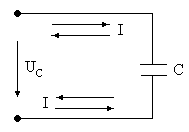
Рис. 18. Электрическая цепь с конденсатором
то амперметр покажет, что по этой цепи проходит ток. Это объясняется процессами зарядки и разрядки конденсатора при постоянных изменениях направления тока, т.е. заряды циркулируют по обеим полуветвям от источника и обратно, конечно, не проходя сквозь сам конденсатор (это будет его пробой).
Величина тока определяется выражением:
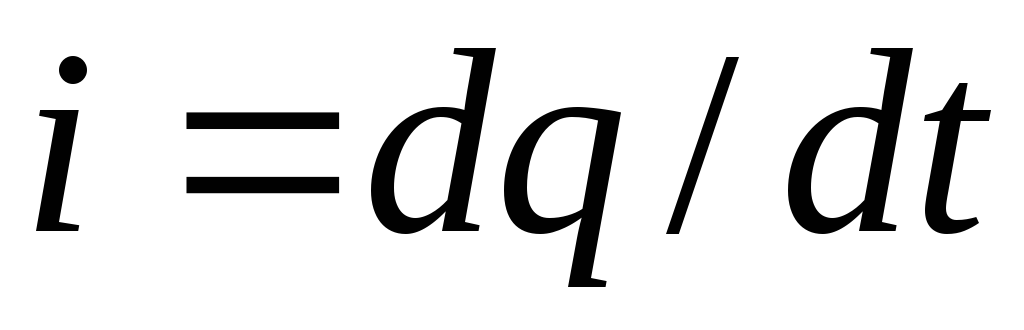
Заряд
на конденсаторе qзависит
от его емкости и величины приложенного
к нему напряжения: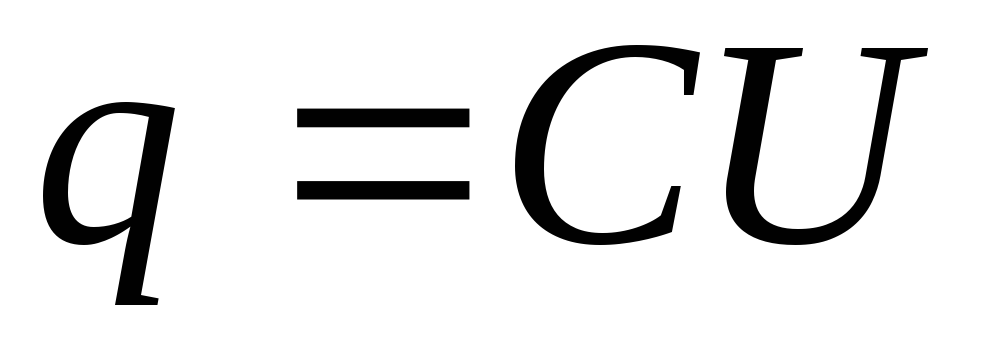 .
.
Отсюда
для тока получаем 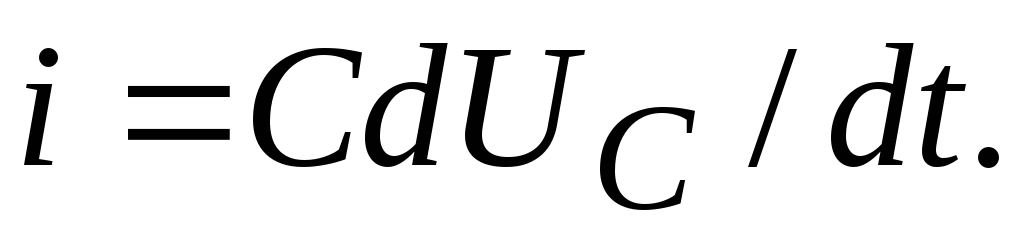
При 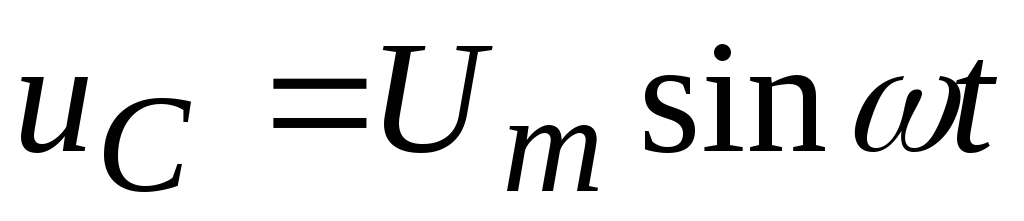 имеем
имеем
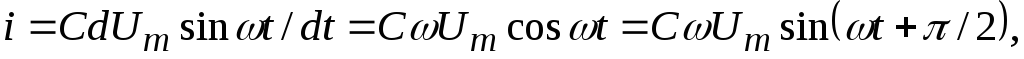
т.е. в конденсаторе ток опережает напряжение на угол /2 (рис. 19). Произведение “С” имеет размерность Ом–1= См – (симменс), отсюда
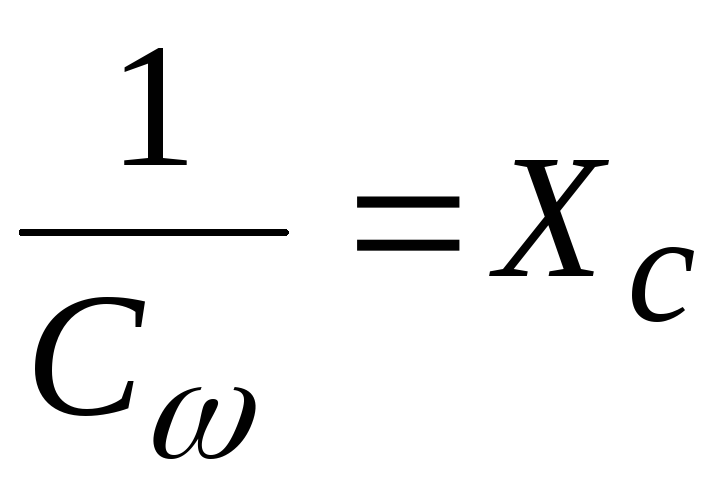
называют емкостным сопротивлением.
Для такого идеального сопротивления имеем:
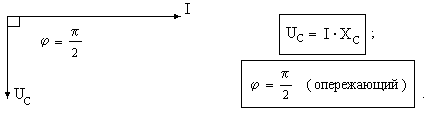
Рис. 19. Векторная диаграмма идеального емкостного сопротивления
Реальные конденсаторы также имеют внутреннее активное сопротивление. Поэтому их можно представить как последовательное соединение идеального конденсатора и внутреннего активного сопротивления (рис.20):
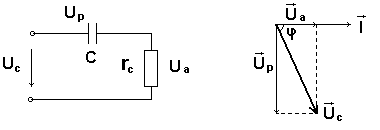
Рис.20. Векторная диаграмма реального емкостного сопротивления
Напряжение на реальном конденсаторе Uсвекторно складывается из векторов реактивной (идеальной) и активной составляющих напряжения конденсатора.
Сдвиг фаз между током и напряжением меньше 90ои зависит от внутренних параметров конденсатора.
Последовательное соединение r-, L-, C— элементов. Закон Ома
Второй закон Кирхгофа для цепи с
последовательным соединением r-,L-,C- элементов,
при векторном изображении величин,
будет выглядеть следующим образом (рис.
21):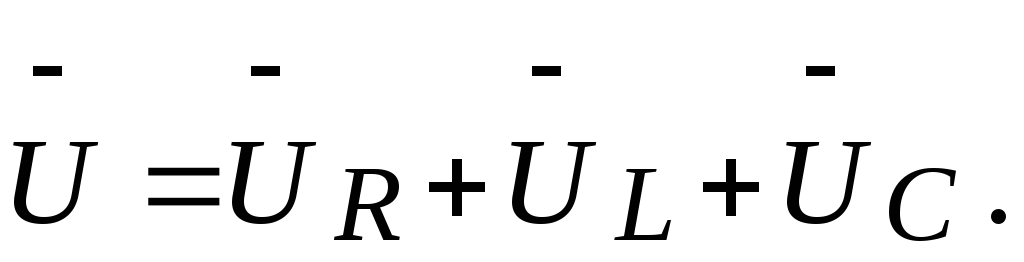
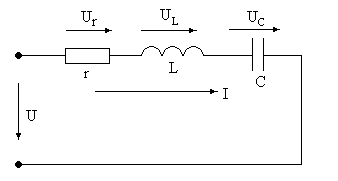
Рис. 21. Последовательное соединение r-, L-, C- элементов.
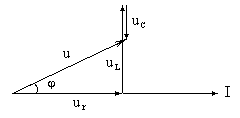
Строим векторную диаграмму (рис. 22), проводя операцию сложения векторов. За базовый вектор возьмем ток, так как при последовательном соединении он единый для всей цепи. Получили треугольник напряжений, из которого, зная значения составляющих напряжений, можно найти
Рис. 22. Векторная диаграмма последовательного соединения r-, L-, C- элементов |
|
Разделив стороны этого треугольника на ток, получим подобный треугольник, отражающий наличие и величины сопротивлений в данной цепи (рис. 23).
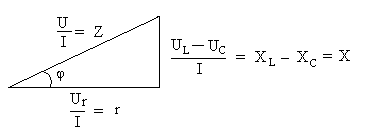
Рис. 23. Треугольник сопротивлений
Здесь Z=U/Iназывается полным сопротивлением и определяется выражением:
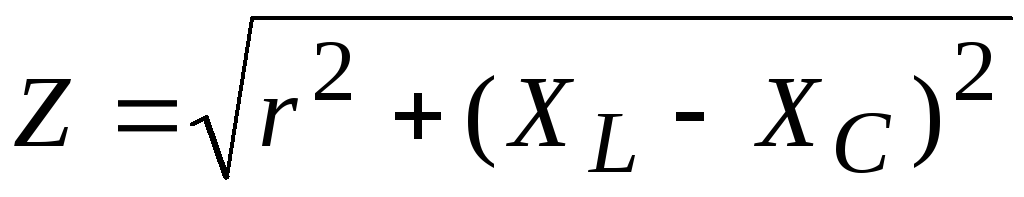 .
.
(X=XL-XC) – общее реактивное сопротивление.
Сдвиг по фазе между током и общим напряжением можно также найти из треугольника сопротивлений:
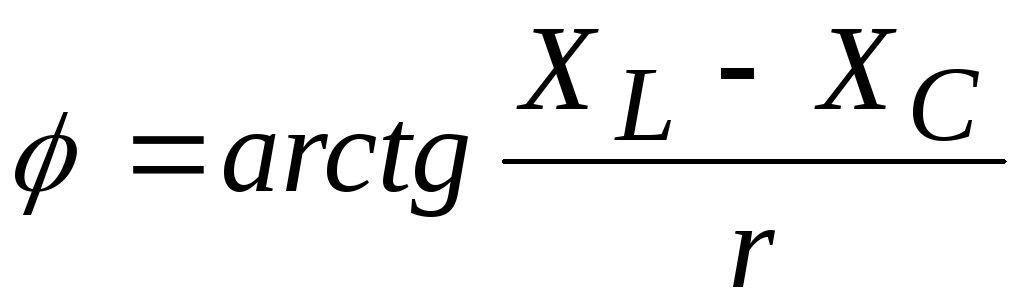 .
.
При положительном тангенсе ток отстает от напряжения, а при отрицательном опережает его.
С учетом изложенного закон Ома для последовательного соединения имеет вид (в общем случае):
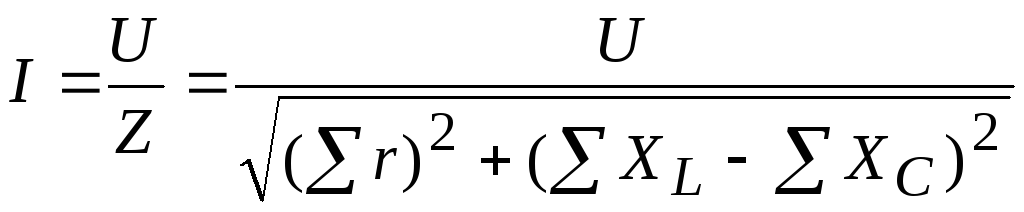 .
.
Однотипные сопротивления складываются арифметически.
Мощность цепи синусоидального тока
Мощность в цепи переменного тока является ткакже переменной величиной и на любом заданном участке цепи в любой момент времени tопределяется как произведение мгновенных значений напряжения и тока.
Так для идеального активного сопротивления, принимая
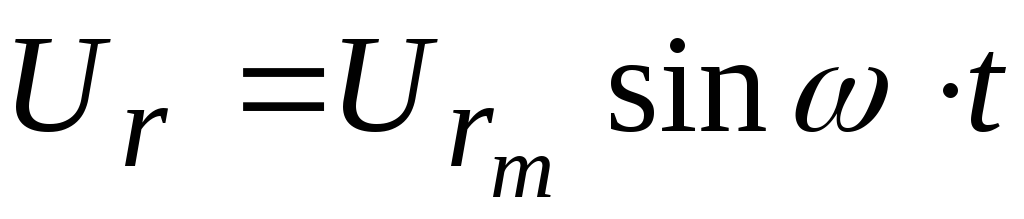 ,
,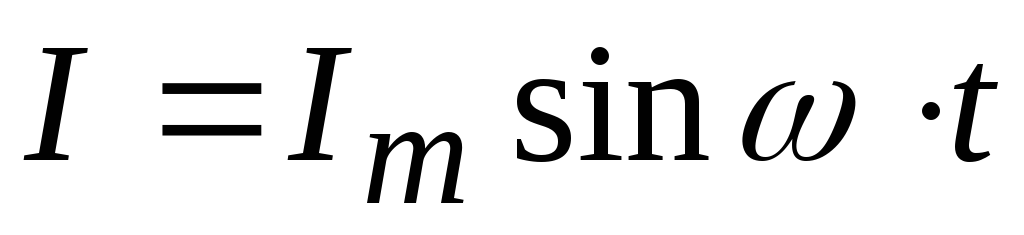 , имеем:
, имеем:
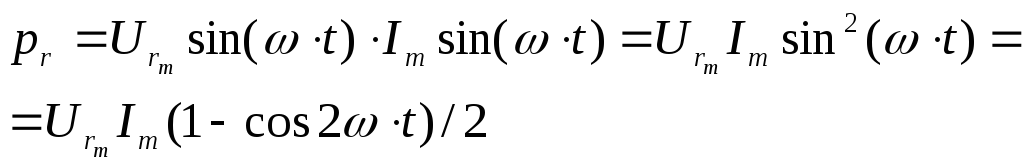
Следовательно,
активная мощность имеет постоянную
составляющую 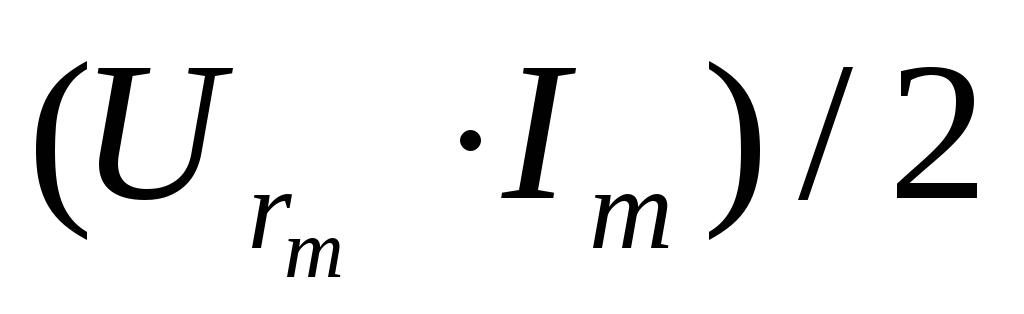 и переменную
и переменную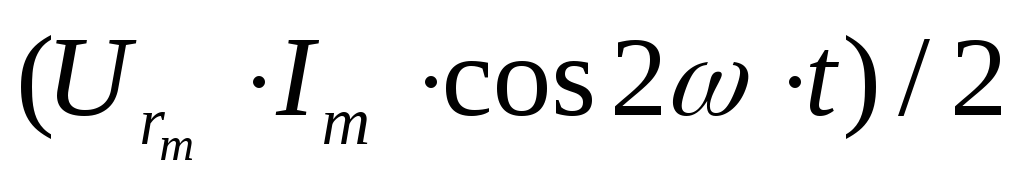 ,
изменяющуюся с двойной частотой.
,
изменяющуюся с двойной частотой.
Найдем среднюю мощность за период:
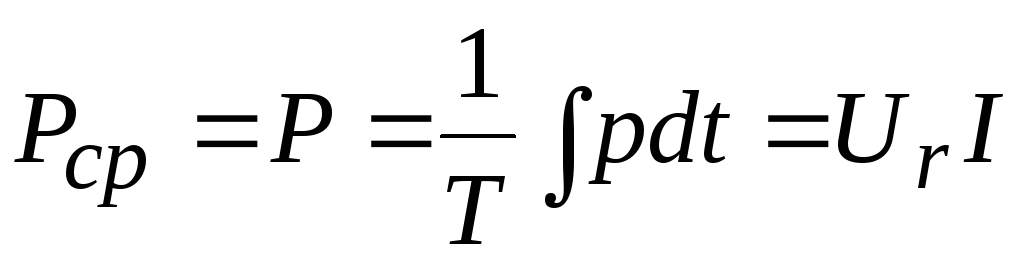 .
.
Эта мощность называется активнойи измеряется в ваттах (Вт). Она характеризует необратимые преобразования электрической энергии на данном участке цепи.
Для реактивных сопротивлений, учитывая, что в катушке индуктивности напряжение опережает ток на 900, а в конденсаторе отстает от него на 900, будем иметь:
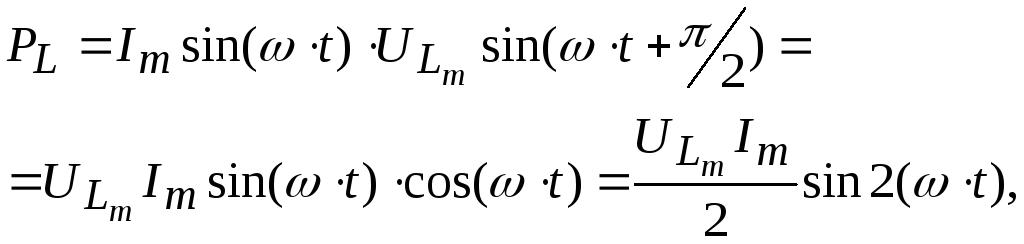
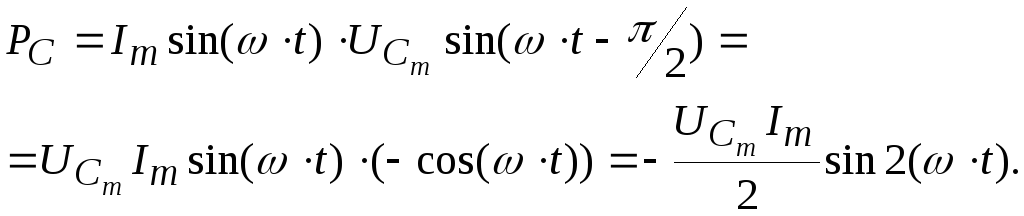
Полученные выражения показывают, что реактивная мощность содержит только переменную составляющую, изменяющуюся с двойной частотой; ее среднее значение равно нулю. Но за четверть основного периода тока мощности положительные, что означает накопление магнитной энергии в катушке или заряд конденсатора, вторую четверть они отрицательны. Значит, энергия отдается обратно в сеть и необратимо ни во что не превращается (средняя за период мощность равна нулю). Поэтому такая мощность называется реактивной, имеет свое обозначение (Q) и размерность — ВАр (вольт-ампер реактивный):
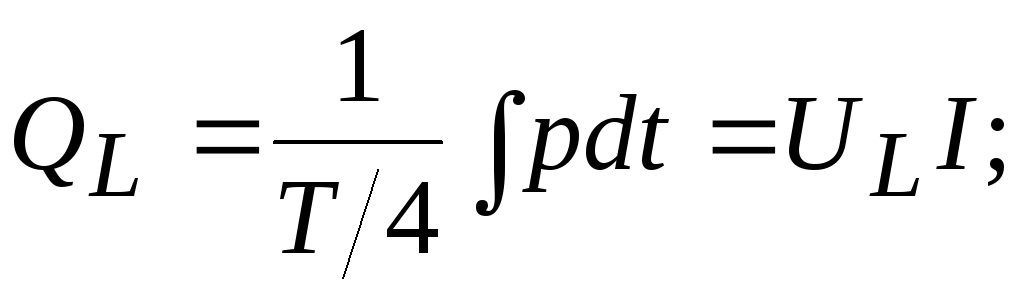
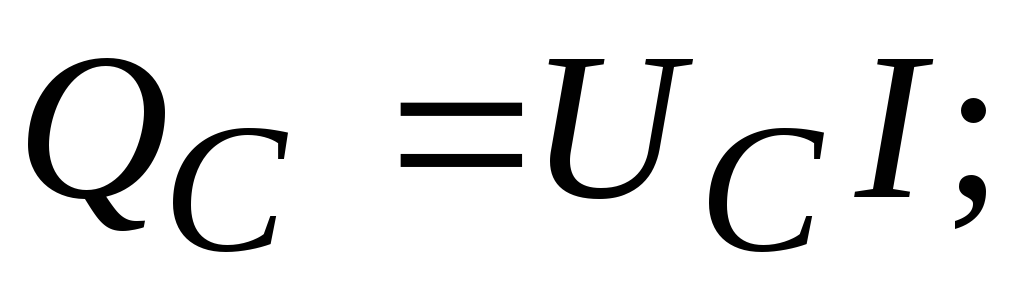
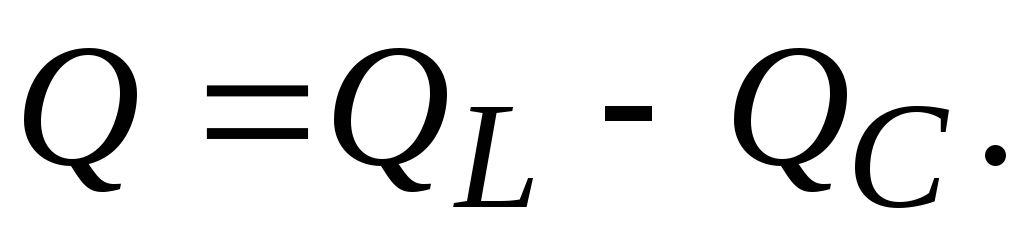
Кроме активной и реактивной мощностей цепи переменного тока характеризуются полноймощностью (S). Единица измерения – ВА (вольт-ампер). Это максимально возможная мощность при заданныхUиI:
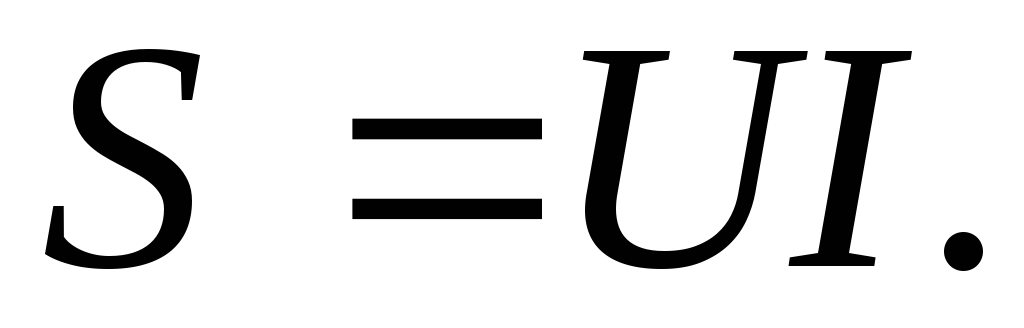
Соотношение между мощностями определяется из треугольника мощностей (рис. 24),
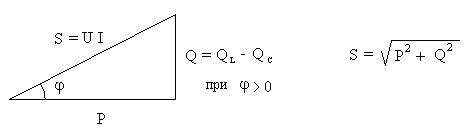
Рис. 24. Треугольник мощностей
который можно получить из треугольников напряжений или токов.
Для расчета мощностей в зависимости от схемы соединения применяют различные формулы, вытекающие из основной:
Активная мощность:
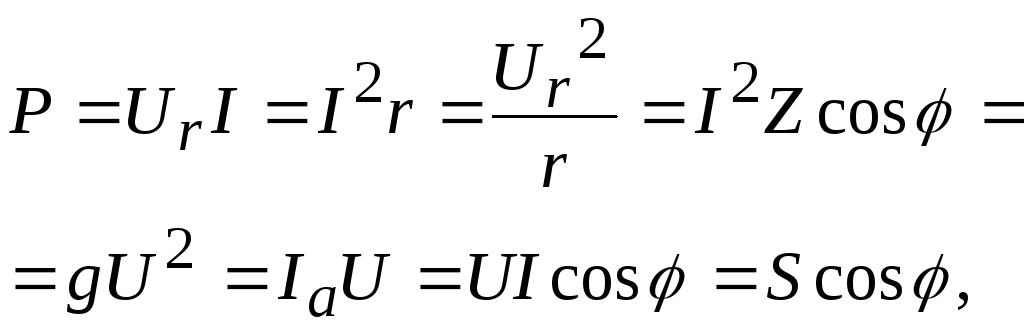
Реактивная мощность:
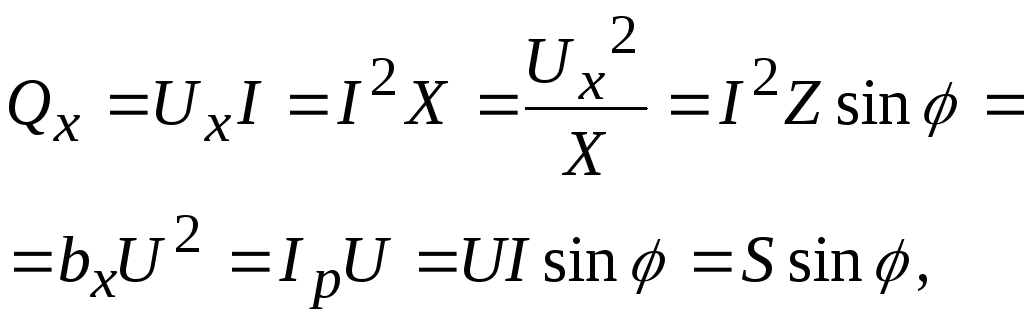
Полная мощность:
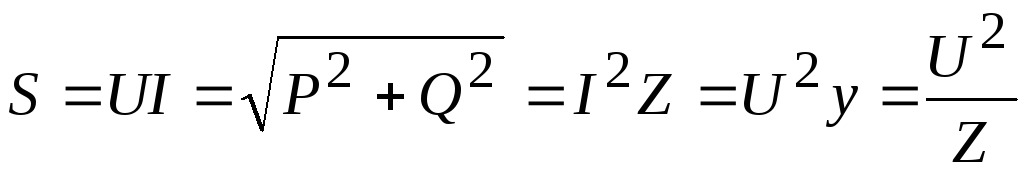 .
.
Из формулы 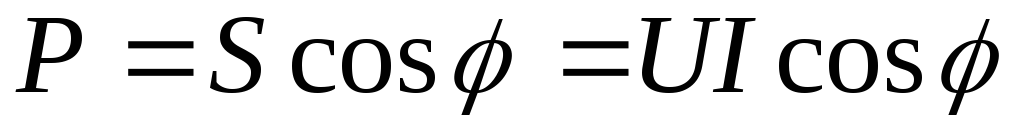 выразимcos:
выразимcos:
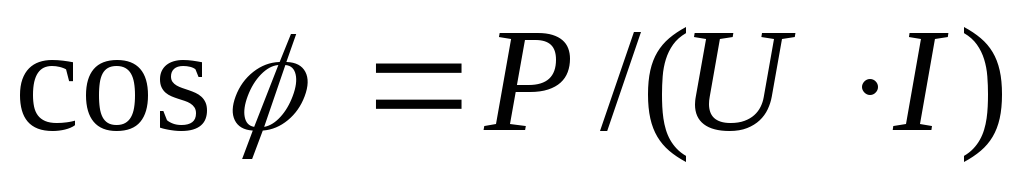 .
.
Отношение активной мощности Р к полной Sназываюткоэффициентом мощности.Он показывает, какую долю всей вырабатываемой источником мощности составляет активная мощность.
ПРОГРАММА РАБОТЫ И УКАЗАНИЯ К ЕЕ ВЫПОЛНЕНИЮ
Перед выполнением работы изучить схему установки, систему расположения источников питания с регулятором напряжения, измерительных приборов, элементов схемы, необходимых для работы. Собрать электрическую цепь согласно рис. 25.
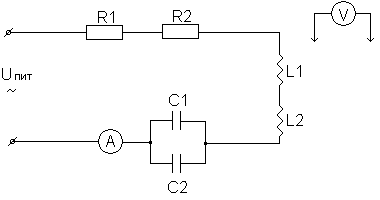
Рис. 25. Схема электрическая принципиальная
Включить сетевое напряжение стенда и напряжение питания цепи. Вольтметром замерить напряжение U, подводимое к цепи, а также на отдельных элементахUr,Uk,Ucи записать в таблицу 4. Измерить напряжение на активных и реактивных элементах, если убрать один резистор; один конденсатор; одну катушку индуктивности (опыт 1).
Таблица 4
№ опыта | I,m (A) | U, (B) | Ur, (B) | Uk, (B) | Uc, (B) | f, Гц |
1 2 3 | 50 50 50 |
Из схемы, изображенной на рис. 25, исключить батарею конденсаторов. Схема принимает вид (рис. 26):
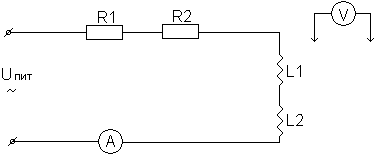
Рис. 26. Последовательное соединение r -, L – элементов.
Собрать электрическую цепь согласно рис. 26 и после проверки ее преподавателем провести измерение напряжений и тока. Данные измерения занести в таблицу 4 (опыт 2).
Из схемы, изображенной на рис. 25, исключить индуктивные элементы. Схема примет вид (рис. 27):
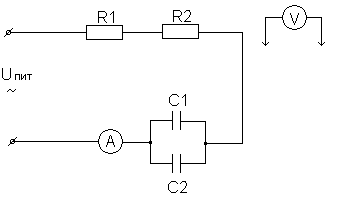
Рис. 27. Последовательное соединение r -, C – элементов.
Собрать электрическую цепь согласно рис. 27 и после проверки ее преподавателем провести измерение напряжения и тока в цепи. Данные измерения занести в таблицу 1 (опыт 3).
Стенд отключить, данные всех измерений показать преподавателю.
Пользуясь соответствующими формулами рассчитать:
а) общее активное сопротивление резистивных элементов цепи и косвенную погрешность Rво всех опытах;
б) емкостное сопротивление батареи конденсаторов XС, ее емкость С и косвенную погрешностьС во всех опытах;
в) индуктивное сопротивление XL, индуктивностьLKи косвенную погрешностьLKво всех опытах;
г) активную мощность Р, потребляемую всей цепью и косвенную погрешность Р, а также коэффициент мощностиcosво всех опытах;
Данные расчетов занести в таблицу 5.
Таблица 5
№ опыта | R, (Ом) | R, (Ом) | XС, (Ом) | С, мкФ | С, мкФ | XL, (Ом) | LK, (Гн) | LK, (Гн) | P, Вт | Р, Вт | cos |
1 2 3 |
Построить в масштабе векторные диаграммы напряжений и тока для 2-го и 3-го опытов. Рассчитать внутреннее активное сопротивление конденсатора и катушки индуктивности.
Зная внутренние активные сопротивления конденсатора и катушки индуктивности построить в масштабе векторную диаграмму для 1-го опыта.
СОДЕРЖАНИЕ ОТЧЕТА
Название работы.
Цель работы.
Оборудование.
Основные сведения из теории.
Схемы исследуемых цепей.
Данные экспериментов, сведенные в таблицу 4.
Расчет параметров схем: R,XС,C,XL,LK,P,cos.
Данные расчета параметров цепей, сведенных в таблице 5.
Построенные в масштабе векторные диаграммы напряжений и тока для всех опытов.
Выводы по результатам работы (смотри контрольные вопросы).
КОНТРОЛЬНЫЕ ВОПРОСЫ
Дать определение переменного тока. Назвать параметры переменного синусоидального тока.
Закон Ома, закон Кирхгофа для расчета цепей переменного тока.
Чем характеризуются активные и реактивные элементы в цепях переменного тока?
Формулы активных и реактивных сопротивлений и мощностей.
Что называется векторной диаграммой электрической цепи?
Объяснить расчет параметров, исследуемых в работе электрических цепей.
Построить векторную диаграмму для предложенной произвольной схемы электрической цепи.
Объяснить расчет параметров, исследуемых в работе электрических цепей.
Записать выражение для определения полного сопротивления исследуемых в работе схем, а также для предложенной произвольной схемы неразветвленной электрической цепи.
В каких цепях переменного тока имеет место сдвиг фаз между током и напряжением, и в каких цепях он отсутствует?
В каких электрических цепях и при каком условии напряжение на реактивном элементе может значительно превысить напряжение на входе цепи? Как называется данное явление?
ЛИТЕРАТУРА
Электротехника под ред. Пантюшина В.С. М.: Высшая школа, 1976.
Касаткин А.С. Электротехника. – М.: Энергия, 1973.
Общая электротехника под ред. Блажкина. — Л.: Энергия, 1979.
Евсюков А.А. Электротехника. – М.: Просвещение, 1979.
Электротехника под ред. Шихина А.Я. – М.: Высшая школа, 2001.
Попов В.С, Николаев С.А. Общая электротехника с основами электроники. – М.: Энергия,1976.
Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. — М.: Гардарики, 2002.
Синдеев Ю.Г. Электротехника: [Учеб.для вузов].- Ростов н/Д: Феникс, 1999.
ЛАБОРАТОРНАЯ РАБОТА №4
ИССЛЕДОВАНИЕ РАЗВЕТВЛЕННОЙ ЦЕПИ ОДНОФАЗНОГО ПЕРЕМЕННОГО ТОКА
Цель работы:
1. Физические явления в электрической цепи переменного тока при параллельном соединении проводников
2. Вычисление параметров электрической цепи.
3. Построение векторных диаграмм при параллельном соединении проводников.
4. Коэффициент мощности.
46. Полное сопротивление в цепи переменного тока.
Обычно
цепь переменного тока включает в себя
и активное сопротивление, и емкость, и
индуктивность. Полное
сопротивление (Z) — это векторная сумма всех сопротивлений:
активного, емкостного и индуктивного. 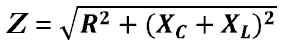 —
полное сопротивление цепи.
—
полное сопротивление цепи.
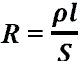 —
активное сопротивление.
—
активное сопротивление. 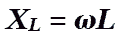 —
индуктивное сопротивление.
—
индуктивное сопротивление. 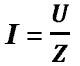 —
полное сопротивление определяет силу
тока в цепи по закону Ома.
—
полное сопротивление определяет силу
тока в цепи по закону Ома. 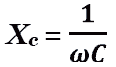 —
емкостное сопротивление.
—
емкостное сопротивление.
I — действующее значение силы тока (един.измер. А)
U— действующее значение напряжения(един.измер. В)
XL — индуктивное сопротивление(един.измер. Ом)
ω — циклическая частота переменного тока(един.измер. рад/с)
L – индуктивность(ед.из. Гн)
C – емкость (ед.из. Ф)
XC — индуктивное сопротивление (ед.из. Ом)
Z — полное сопротивление (Ом)
R — активное сопротивление (Ом)
ρ — удельное сопротивление проводника (Ом/м)
l — длина проводника (м)
S — площадь сечения проводника (м2
47.Импеданс тканей. Физические основы реографии.
Импеданс – основные понятия.
При прохождении через ткани переменного тока, изменяющегося по гармоническому закону
I(t) =I0 cos ωt,
падение напряжения на биологической ткани изменяется по закону
U (t)=Uo⋅cos (ωt+ϕ).
Величиной, определяющей соотношение между напряжением и силой переменного тока, является импеданс — полное электрическое сопротивление цепи переменному току.
На опыте напряжение отстает по фазе от тока (ϕ<0), что характерно для электрических цепей, состоящих из резисторов и конденсаторов.
Для биологического объекта импеданс носит составной (комплексный) характер Z=(R,X). Его активная составляющая R связана, в первую очередь, с проводимостью внутренних жидких сред, являющихся электролитами. Различные процессы в тканях, сопровождающиеся необратимыми потерями энергии, также дают вклад в величину активной составляющей импеданса. Реактивная компонента X определяется емкостными свойствами исследуемой ткани, в частности, емкостью биологических мембран. Кроме того, в емкостную составляющую импеданса дает вклад и область контакта стимулирующих электродов с биологическими тканями.
Абсолютная величина (модуль) электрического импеданса определяется выражением .22XRZ+=
На опыте величина импеданса может быть определена по измерениям амплитудных (или эффективных) значений напряжения Uo и силы тока Io
⏐Z⏐ = Uo/Io (или ⏐Z⏐ = Uэфф/Iэфф).
Фазовый сдвиг ϕ определяет отношение реактивной и активной составляющих импеданса
tg ϕ = X/R.
Значения угла сдвига фаз, полученные при частоте 1 кГц для различных биологических объектов, приведены в таблице 1.
Таблица 1. Угол сдвига фаз (в градусах) для различных видов тканей.
Объект | ϕ , град. |
Кожа человека, лягушки Нерв лягушки Мышцы кролика | -55 -64 -65 |
Составную (комплексную) величину Z принято изображать в виде векторной диаграммы, на которой ось абсцисс — величина активного сопротивления, ось ординат — величина реактивного сопротивления.
Абсолютная величина импеданса ⏐Z⏐ и фазовый сдвиг ϕ являются функциями частоты переменного тока. Зависимость электрического импеданса от частоты носит название дисперсии импеданса.
Физические основы реологии.
Величина импеданса тканей зависит от их физиологического состояния, в частности от их кровоснабжения. При кровенаполнении сосудов происходит изменение величины импеданса в такт с работой сердца. По величине изменений импеданса можно судить о состоянии сердечно-сосудистой системы.
Реология — диагностический метод, основанный на регистрации изменения величины импеданса тканей в процессе сердечной деятельности.
Величина импеданса тканей |Z| состоит из двух составляющих |Z| = |Zo| + |z(t)|: постоянной — |Zo| и изменяющейся во времени в соответствии с работой сердца – |z(t)|.
На практике, на исследуемый участок тела накладывают электроды площадью несколько см2 и пропускают переменный ток частотой ≈ 30 − 40 кГц. Выбор частоты определяется несколькими факторами: электробезопасностью, исключением влияния электродов и емкости их контакта с кожей, уменьшением зависимости величины импеданса от механических воздействий на исследуемую ткань. Наполнение сосудов кровью изменяет расстояния между отдельными участками ткани, что должно приводить к изменению ёмкостного сопротивления. Но вклад макроскопических объемов тканей в реактивную составляющую импеданса существенен только в области α- дисперсии. Следовательно, изменения импеданса во времени обусловлены влиянием притока и оттока крови на активную составляющую полного сопротивления.
При прохождении через ткани электрического тока I = Io⋅cos ωt величина напряжения будет изменяться по закону
U = Uο cos (ωt + ϕ) = Io⋅( ⏐Zo⏐ + ⏐z(t)⏐ )⋅cos (ωt +ϕ ).
Электрическими методами выделяют из регистрируемого сигнала составляющую, пропорциональную |z(t)|, содержащую информацию о состоянии кровоснабжения изучаемого участка тканей − реограмму.
Для парных анатомических образований проводят запись реограммы на правой и левой стороне тела.
Активное сопротивление в цепи переменного тока
На векторных диаграммах можно показать, что ток и напряжение совпадают по фазе (рис. 52,а) или э. д.с. сдвинуты по фазе на некоторый угол (рис. 52,6). Условно принято считать, что векторы перемещаются в направлении против движения часовой стрелки.
Если векторы имеют различную длину, следовательно, их действующие значения разные (см. рис. 52, б).
§ 52. АКТИВНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
Сопротивление, включенное в цепь переменного тока, в котором происходит превращение электрической энергии в полезную работу или в тепловую энергию, называется активным сопротивлением.
К активным сопротивлениям при промышленной частоте (50 гц) относятся, например, электрические лампы накаливания и электронагревательные устройства.
Рассмотрим цепь переменного тока (рис. 53), в которую включено активное сопротивление. В такой цепи под действием переменного напряжения протекает переменный ток. Изменение тока в Цепи, согласно закону Ома, зависит только от изменения напряжения, подключенного к ее зажимам. Когда напряжение равно нулю, ток в цепи также равен нулю. По мере увеличения напряжения ток в Цепи возрастает и при максимальном значении напряжения ток становится наибольшим. При уменьшении напряжения ток убывает. Когда напряжение изменяет свое направление, ток также изменяет свое направление и т. д.
Из сказанного следует, что в цепи переменного тока с активным сопротивлением по мере изменения по величине и направлению напряжения одновременно пропорционально меняются величина и Направление тока. Это значит, что ток и напряжение совпадают по фазе.
Построим векторную диаграмму действующих величин тока и напряжения для цепи с активным сопротивлением. Для этого отлов жим в выбранном масштабе по горизонтали вектор напряжения Чтобы на векторной диаграмме показать, что напряжение и ток в цепи совпадают по фазе (=0), откладываем вектор тока I по направлению вектора напряжения.
Сила тока в такой цепи определяется по закону Ома:
В этой цепи среднее значение мощности, потребляемой активным сопротивлением, выражается произведением действующих значения тока и напряжения.
Пример. К цепи переменного тока с активным сопротивлением r=55 ом подключен генератор, максимальное значение напряжения которого Um=310,2 в.
Определить:
показание вольтметра, подключенного к зажимам генератора; показание амперметра, включенного в цепь; среднее значение мощности, потребляемой сопротивлением.
Решение. Известно, что электроизмерительные приборы, включенные в цепь переменного тока, измеряют действующие значения. Поэтому показание вольтметра, измеряющего напряжение,
Показание амперметра, измеряющего действующее значение тока,
Среднее значение активной мощности, потребляемой сопротивлением, Р=220х4 = 880 вт или Р=I2r=42×55=16×55=880 вт.
§ 53. ИНДУКТИВНОСТЬ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
Прохождение электрического тока по проводнику или катушки сопровождается появлением магнитного поля. Рассмотрим электрическую цепь переменного тока (рис. 54,а), в которую включена катушка индуктивности, имеющая небольшое количество витком проволоки сравнительно большого сечения, активное сопротивления которой можно считать практически равным нулю.
Под действием э. д. с. генератора в цепи протекает переменный ток, возбуждающий переменный магнитный поток. Этот поток пересекает «собственные» витки катушки и в ней возникает электродвижущая сила самоиндукции
(55)
где L — индуктивность катушки,
в омах. Таким образом, индуктивное сопротивление катушки ХL зависит от величины э. д. с. самоиндукции, а следовательно, оно, как и э. д. с. самоиндукции, зависит от скорости изменения тока в катушке (от частоты ) и от индуктивности катушки L:
где XL, — индуктивное сопротивление, ом,
ώ — угловая частота переменного тока, рад/сек,
L — индуктивность катушки, гн.
Так как угловая частота переменного тока , то индуктивное сопротивление
где, f—-частота переменного тока, гц.
Пример. Катушка, обладающая индуктивностью L=0,5 гн, присоединена к источнику переменного тока, частота которого f=50 гц. Определить:
1) индуктивное сопротивление катушки при частоте f=50 гц;
2) индуктивное сопротивление этой катушки переменному току, частота которого f=800 гц.
Решение. Индуктивное сопротивление переменному току при f=50 гц
При частоте тока f=800 гц
Приведенный пример показывает, что индуктивное сопротивление катушки повышается с увеличением частоты переменного тока, протекающего по ней. По мере уменьшения частоты тока индуктивное сопротивление убывает. Для постоянного тока, когда ток в катушке не изменяется и магнитный поток не пересекает ее витки, э. д. с. самоиндукции не возникает, индуктивное сопротивлений катушки ХL равно нулю. Катушка индуктивности для постоянного тока представляет собой лишь сопротивление
Выясним, как изменяется э. д. с. самоиндукции, когда по катушке индуктивности протекает переменный ток.
Известно, что при неизменной индуктивности катушки э. д. с. самоиндукции зависит от скорости изменения силы тока и она всегда направлена навстречу причине, вызвавшей ее.
На графике (рис. 54, в) переменный ток показан в виде синусоиды (сплошная линия). В первую четверть периода сила тока возрастает от нулевого до максимального значения. Электродвижущая сила самоиндукции ес, согласно правилу Ленца, препятствует увеличению тока в цепи. Поэтому на графике (пунктирной линией) показано, что ес в это время имеет отрицательное значение. Во вторую четверть периода сила тока в катушке убывает до нуля. В это время э. д.с. самоиндукции изменяет свое направление и увеличивается препятствуя убыванию силы тока. В третью четверть периода том изменяет свое направление и постепенно увеличивается до максимального значения; э. д. с. самоиндукции имеет положительное значение и далее, когда сила тока убывает, э. д. с. самоиндукции опять меняет свое направление и вновь препятствует уменьшению силы тока в цепи.
82. Переменный ток. Различные виды электрических сопротивлений в цепи переменного тока. Импеданс.
В широком смысле слова переменный ток — любой ток, изменяющийся со временем. Однако чаще термин «переменный ток» применяют к квазистационарным токам, зависящим от времени по гармоническому закону.
Квазистационарным называют такой ток, для которого время установления одинакового значения по всей цепи значительно меньше периода колебаний.
Будем считать, что для квазистационарных токов, так же как и для постоянных, сила тока одновременно одинакова в любом сечении неразветвленного проводника. Для них справедлив закон Ома, однако сопротивление цепи зависит от частоты изменения тока. Потерями энергии на электромагнитное излучение этих токов пренебрегаем. Переменный ток можно рассматривать как вынужденные электромагнитные колебания.
Суммируя три вектора, находим графически значения Um и . Используя теорему Пифагора, имеем
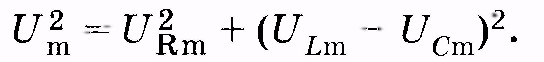 (
(
Подставляя в (14.39) выражения этих амплитуд из (14.21), (14.27) и (14.32) и учитывая закон Ома, находим
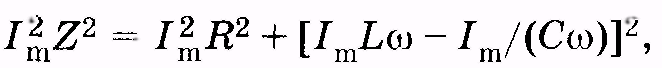 (
(
где Z — полное сопротивление цепи переменного тока, называемое импедансом. Из (14.40) получаем
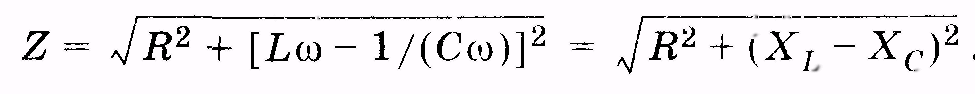
Омическое сопротивление R цепи называют также активным, оно обусловливает выделение теплоты в цепи в соответствии с законом Джоуля—Ленца. Разность индуктивного и емкостного сопротивлений (XL – ХС) называют реактивным сопротивлением. Оно не вызывает нагревания элементов электрической цепи.
Ткани организма проводят не только постоянный (см. § 12.10), но и переменный ток. Опыт показывает, что в этом случае сила тока, проходящая через биологическую ткань, опережает по фазе приложенное напряжение. Следовательно (см. § 14.3), емкостное сопротивление тканей больше индуктивного. Отсюда следует, что моделировать электрические свойства биологических тканей можно, используя резисторы, которые обладают активным сопротивлением, и конденсаторы — носители емкостного сопротивления. В качестве модели обычно используют эквивалентную электрическую схему тканей организма. Она представляет собой схему, состоящую из резисторов и конденсаторов, частотная зависимость (дисперсия) импеданса которой близка к частотной зависимости импеданса биологической ткани Итак, области -, -, и -дисперсии импеданса объясняются тем, что с увеличением частоты переменного электрического поля в явлении поляризации участвуют разные структуры биологических тканей: при низких частотах на изменение поля реагируют все структуры (-дисперсия), с увеличением частоты реагируют крупные молекулы-диполи органических соединений и молекулы воды (-дисперсия), а при самых больших частотах реагируют только молекулы воды (-дисперсия). Во всех случаях имеет место электронная поляризация. С увеличением частоты электрического тока (электрического поля) все меньше структур будет реагировать на изменение этого поля и меньше будет значение поляризо-ванности Рет. Отсюда, согласно (14.48), с увеличением частоты будет уменьшаться диэлектрическая проницаемость , а следовательно, и электроемкость С, а это, согласно (14.33), приведет к увеличению емкостного сопротивления Хс и импеданса Z. Следовательно, на фоне общего хода зависимости Z = f() (см. рис. 14.10) появляются области с меньшим убыванием Z при возрастании частоты (области -, - и -дисперсии).
Частотная зависимость импеданса позволяет оценить жизнеспособность тканей организма, что важно знать для пересадки (трансплантации) тканей и органов. Различие в частотных зависимостях импеданса получается и в случаях здоровой и больной ткани.
Импеданс тканей и органов зависит также и от их физиологического состояния. Так, при кровенаполнении сосудов импеданс изменяется в зависимости от состояния сердечно-сосудистой деятельности.
Диагностический метод, основанный на регистрации изменения импеданса тканей в процессе сердечной деятельности, называют реографией (импеданс-плетизмография).
С помощью этого метода получают реограммы головного мозга (реоэнцефалограмма), сердца (реокардиограмма), магистральных сосудов, легких, печени и конечностей. Измерения обычно проводят на частоте 30 кГц.
Расчет полного сопротивления в цепи переменного тока — импеданс
Понятие импеданса используется в разных сферах науки. Существуют разные его формы: гидродинамический, артериальный (медицинский термин, состоит из статического и кинетического компонентов), используемый при измерении гидростатического давления. Есть и электрический импеданс, описывающий полное сопротивление цепного фрагмента. Электрику необходимо знать, от чего зависит и как вычисляется эта величина в однофазных и трехфазных цепях с трансформаторами тока и иными компонентами.

Импеданс описывает сопротивление всей цепи
Что такое импеданс
Это понятие описывает комплексное сопротивление цепи или ее межузлового участка. Оно было введено лондонским инженером и физиком О. Хевисайдом в 1886 году. В состав полного сопротивления цепи входят активная и реактивная компоненты. Фазовый сдвиг и само значение импенданса при электротоке, чья кривая имеет форму синусоиды, могут быть рассчитаны с ориентиром на то, каким образом соединены входящие в цепь компоненты.
Аналогия с электрическим сопротивлением проводника на примере резистора
Чтобы суметь рассчитать импеданс цепи, нужно представлять, как себя ведут различные входящие в нее элементы: катушки индуктивности, резисторные и емкостные детали, с точки зрения вклада в составляющие общей резистивности цепи.
Активное сопротивление
Резистор относится к числу пассивных деталей цепи, не содержащих внутренних источников электроэнергии, при этом почти все создаваемое им противодействие приходится на активную компоненту. Реактивная составляющая если и присутствует, то настолько мала, что ею зачастую принято пренебрегать. Это связано с тем, что отношение напряжения на деталь и электротока, проходящего через нее, не зависит от их частоты. Когда к резисторной детали присоединяют источник напряжения (обозначим его U), через нее будет идти электроток значением I. Если к концам радиодетали подсоединяют источник тока, равного I, между ними будет иметь место падение напряжения U.
Важно! Выражение для сопротивления резистора можно записать так: R=U/I.

Резисторы – источники активного сопротивления
Реактивное сопротивление
К основным компонентам электроцепей, несущим такую нагрузку, относятся дроссели (и подобные им индуктивные элементы) и конденсаторы. При достижении резонанса наблюдается наименьшее значение общего противодействия подключенных последовательно конденсатора и дросселя и наибольшее – включенных параллельно.
Индуктивная нагрузка
Если индуктивный дроссель подключить к постоянному току, на нем будут наблюдаться следующие эффекты: резистивность будет приближаться к нулевому значению, а при пропускании электротока через катушечный элемент падение напряжения будет отсутствовать, независимо от токовой величины:
R=U/I=0/I=0.
Такие цифры справедливы для идеального дросселя, на практике они все же несколько отклоняются от нуля. Если к детали будет приложен переменный ток, напряжение между катушечными выводами будет отличным от нуля.

Катушка индуктивности
Емкостная нагрузка
При включении идеального конденсаторного элемента в сеть с постоянным напряжением его резистивность будет иметь очень большую величину, стремящуюся к бесконечной. Когда к радиодетали прикладывают такое напряжение, проходящий через нее ток будет равен нулю. Если к выводам конденсатора подсоединить источник переменного напряжения, ток будет ненулевым.

Детали, обладающие емкостью
Данные эффекты, наблюдаемые на емкостных радиодеталях и катушках, нельзя описывать в категориях активного противодействия в условиях константного электротока, так как последнее подразумевает стабильное, независимое от условий и не изменяющееся во времени отношение электротока и напряжения и исключает явление сдвига фаз между этими величинами. Таким образом, становится целесообразным введение для реактивных деталей характеристики, связывающей электроток и напряжение так, как это делает активное противодействие в омовском законе для константного тока.
Важно! При рассмотрении поведения катушек и конденсаторов под действием гармонических сигналов обнаруживается, что токовая сила и напряжение могут быть связаны константной величиной, которую также называют импедансом. При ее изучении применяется понятие о гармонических сигналах, учитывающее как их амплитудные характеристики, так и особенности, связанные с фазами.
Такое значение импеданса можно определить как частное комплексной амплитуды, которой обладает напряжение приложенного к двухполюсному элементу сигнала, и комплексной амплитуды идущего через элемент электротока. В отношении пассивных электроцепей со стабильными показателями в устоявшемся режиме стоит сказать, что импедансный показатель у них не будет привязанным к течению времени. Если временной параметр при формульной записи не сокращается, то категория импеданса для рассматриваемого двухполюсника окажется неприменимой.
Расчет эквивалентного сопротивления элементов цепи
Определение общего цепного сопротивления будет зависеть от того, какого типа конфигурацию составляют компоненты цепи. Для параллельного и последовательного подключений правила расчета будут неодинаковыми. Опираться при вычислениях нужно на закон Ома.
Согласно ему, у всех последовательно соединенных деталей, подключенных в цепь переменного тока, будет одно и то же значение электротока:
I=U/Z, где Z – общий импеданс цепи.
Напряжения будут различаться и окажутся привязанными к сопротивлениям деталей: на концах резистора его значение будет равно UR = IR (здесь R – активная резистивность элемента), для дросселя – UL = IXL, для емкостного элемента – UC = IXC (XL и XC – реактивные показатели соответствующих устройств). Так как векторы напряженности катушки и конденсатора имеют противоположные направления, суммарный показатель на реактивных деталях будет равен: UX = UL – UC . Противодействие будет равно: X = XL – XC.
Напряжения (общее, реактивное и активное) могут быть представлены в виде прямоугольного треугольника. Из него получается, что U² = UR² + UX². Поскольку противодействия входящих в цепь компонентов пропорциональны напряжениям, имеем Z2=R2+X2=R2+(XL – XC)2.
Для параллельного соединения принято выводить значения импеданса из проводимостей элементов, которые обратны их сопротивлениям. Отсюда 1/z2 = 1/R2 + 1/X2. Таким образом, выходит следующая формула:
Z2=1/(1/R2+(1/ XL – 1/ XC)2).
Общее сопротивление определяется компонентным составом цепи и характером соединения ее элементов. При расчетах показателей используется закон Ома.