Как легко рассчитать скалярный продукт в Excel
В этом руководстве объясняется, как рассчитать скалярный продукт в Excel.
Что такое скалярный продукт?Для данного вектора a = [a 1 , a 2 , a 3 ] и вектора b = [b 1 , b 2 , b 3 ] скалярное произведение вектора a и вектора b, обозначаемое как a · b , определяется как:
а · b = а 1 * b 1 + а 2 * b 2 + а 3 * b 3
Например, если a = [2, 5, 6] и b = [4, 3, 2], то скалярное произведение a и b будет равно:
а · б = 2*4 + 5*3 + 6*2
а · б = 8 + 15 + 12
а · б = 35
По сути, скалярное произведение — это сумма произведений соответствующих элементов двух векторов.
Как найти точечный продукт в ExcelЧтобы найти скалярное произведение двух векторов в Excel, мы можем использовать следующие шаги:
1. Введите данные.Введите значения данных для каждого вектора в их собственные столбцы. Например, введите значения данных для вектора a = [2, 5, 6] в столбец A и значения данных для вектора b = [4, 3, 2] в столбец B:
Введите данные.Введите значения данных для каждого вектора в их собственные столбцы. Например, введите значения данных для вектора a = [2, 5, 6] в столбец A и значения данных для вектора b = [4, 3, 2] в столбец B:
2. Вычислите скалярный продукт. Чтобы вычислить скалярный продукт, мы можем использовать функцию Excel СУММПРОИЗВ() , которая использует следующий синтаксис:
СУММПРОИЗВ(массив1, [массив2], …)
- array — первый массив или диапазон, который необходимо умножить, а затем добавить.
- array2 — второй массив или диапазон для умножения, а затем добавления.
В этом примере мы можем ввести следующее в ячейку D1 , чтобы вычислить скалярное произведение между вектором a и вектором b :
=СУММПРОИЗВ(A1:A3, B1:B3)
Это дает значение 35 , которое соответствует ответу, который мы получили вручную.
Обратите внимание, что мы можем использовать СУММПРОИЗВ() для нахождения скалярного произведения векторов любой длины. Например, предположим, что вектор a и b имеют длину 20. Затем мы можем ввести следующую формулу в ячейку D1 , чтобы вычислить их скалярное произведение:
=СУММПРОИЗВ(A1:A20, B1:B20)
Возможные ошибки при вычислении скалярного произведенияФункция СУММПРОИЗВ() вернет #ЗНАЧ! ошибка, если векторы не имеют одинаковой длины.
Например, если вектор a имеет длину 20, а вектор b имеет длину 19, то формула =СУММПРОИЗВ(A1:A20, B1:B19) вернет ошибку.
Два вектора должны иметь одинаковую длину, чтобы можно было вычислить скалярное произведение.
Дополнительные ресурсыВ следующих руководствах объясняется, как рассчитать скалярный продукт в различных статистических программах:
Как рассчитать скалярный продукт в Google Sheets
Как рассчитать скалярный продукт в R
Как рассчитать скалярный продукт на калькуляторе TI-84
PhysBook:Электронный учебник физики — PhysBook
Содержание
- 1 Учебники
-
2 Механика
-
2.
 1 Кинематика
1 Кинематика
- 2.2 Динамика
- 2.3 Законы сохранения
- 2.4 Статика
- 2.5 Механические колебания и волны
-
2.
-
3 Термодинамика и МКТ
- 3.1 МКТ
- 3.2 Термодинамика
-
4 Электродинамика
-
4.
 1 Электростатика
1 Электростатика
- 4.2 Электрический ток
- 4.3 Магнетизм
- 4.4 Электромагнитные колебания и волны
-
4.
-
5 Оптика. СТО
- 5.1 Геометрическая оптика
- 5.2 Волновая оптика
- 5.3 Фотометрия
- 5.4 Квантовая оптика
-
5.
 5 Излучение и спектры
5 Излучение и спектры
- 5.6 СТО
-
6 Атомная и ядерная
- 6.1 Атомная физика. Квантовая теория
- 6.2 Ядерная физика
- 7 Общие темы
- 8 Новые страницы
Здесь размещена информация по школьной физике:
- материалы из учебников, лекций, рефератов, журналов;
- разработки уроков, тем;
- flash-анимации, фотографии, рисунки различных физических процессов;
- ссылки на другие сайты
и многое другое.
Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.
Учебники
Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –
Механика
Кинематика
Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве
Динамика
Законы Ньютона – Силы в механике – Движение под действием нескольких сил
Законы сохранения
Закон сохранения импульса – Закон сохранения энергии
Статика
Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика
Механические колебания и волны
Механические колебания – Механические волны
Термодинамика и МКТ
МКТ
Основы МКТ – Газовые законы – МКТ идеального газа
Термодинамика
Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение
Электродинамика
Электростатика
Электрическое поле и его параметры – Электроемкость
Электрический ток
Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках
Магнетизм
Магнитное поле – Электромагнитная индукция
Электромагнитные колебания и волны
Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны
Оптика.
 СТО
СТОГеометрическая оптика
Прямолинейное распространение света. Отражение света – Преломление света – Линзы
Волновая оптика
Свет как электромагнитная волна – Интерференция света – Дифракция света
Фотометрия
Фотометрия
Квантовая оптика
Квантовая оптика
Излучение и спектры
Излучение и спектры
СТО
СТО
Атомная и ядерная
Атомная физика. Квантовая теория
Строение атома – Квантовая теория – Излучение атома
Ядерная физика
Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы
Общие темы
Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике
Новые страницы
Запрос не дал результатов.
Умножение векторов — определение, формула, примеры
Умножение векторов бывает двух типов. Вектор имеет как величину, так и направление, и, исходя из этого, двумя способами умножения векторов являются скалярное произведение двух векторов и перекрестное произведение двух векторов. Скалярное произведение двух векторов также называется скалярным произведением, поскольку результирующее значение является скалярной величиной. Перекрестное произведение называется векторным произведением, так как в результате получается вектор, перпендикулярный этим двум векторам.
Скалярное произведение двух векторов также называется скалярным произведением, поскольку результирующее значение является скалярной величиной. Перекрестное произведение называется векторным произведением, так как в результате получается вектор, перпендикулярный этим двум векторам.
Давайте узнаем о двух умножениях векторов, рабочем правиле, свойствах, использовании, примерах этого умножения векторов.
| 1. | Как сделать умножение векторов? |
| 2. | Рабочее правило умножения векторов |
| 3. | Свойства умножения векторов |
| 4. | Применение умножения векторов |
| 5. | Примеры умножения векторов |
| 6. | Практические вопросы по умножению векторов |
| 7. | Часто задаваемые вопросы об умножении векторов |
Как сделать умножение векторов?
Вектор имеет как величину, так и направление. Мы можем умножать два или более векторов на скалярное произведение и перекрестное произведение. Давайте разберемся подробнее о каждом умножении векторов.
Мы можем умножать два или более векторов на скалярное произведение и перекрестное произведение. Давайте разберемся подробнее о каждом умножении векторов.
Скалярное произведение
Скалярное произведение векторов также называется скалярным произведением векторов. Результат скалярного произведения векторов является скалярным значением. Скалярное произведение векторов равно произведению величин двух векторов и косинуса угла между двумя векторами. Результат скалярного произведения двух векторов лежит в одной плоскости двух векторов. Скалярный продукт может быть положительным действительным числом или отрицательным действительным числом.
Пусть a и b — два ненулевых вектора, а θ — угол между векторами. Тогда скалярное произведение или скалярное произведение обозначается буквой a.b, которая определяется как:
\(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a||\overrightarrow b|\) cos θ .
Здесь \(|\overrightarrow a|\) — величина \(\overrightarrow a\), \(|\overrightarrow b|\) — величина \(\overrightarrow b\), а θ — величина угол между ними.
Перекрестное произведение
Перекрестное произведение также называется векторным произведением. Перекрестное произведение — это форма умножения векторов, выполняемая между двумя векторами разной природы или вида. Когда два вектора перемножаются друг с другом, а умножение также является векторной величиной, то результирующий вектор называется перекрестным произведением двух векторов или векторным произведением. Результирующий вектор перпендикулярен плоскости, содержащей два заданных вектора.
Понять это можно на примере: если у нас есть два вектора, лежащих в плоскости X-Y, то их векторное произведение даст результирующий вектор в направлении оси Z, которая перпендикулярна плоскости XY. Символ × используется между исходными векторами. Умножение векторов или перекрестное произведение двух векторов показано следующим образом.
\(\overrightarrow{a} \times \overrightarrow{b} = \overrightarrow{c}\)
Здесь \(\overrightarrow{a}\) и \(\overrightarrow{b}\) — два вектора, и \(\overrightarrow{c}\) — результирующий вектор.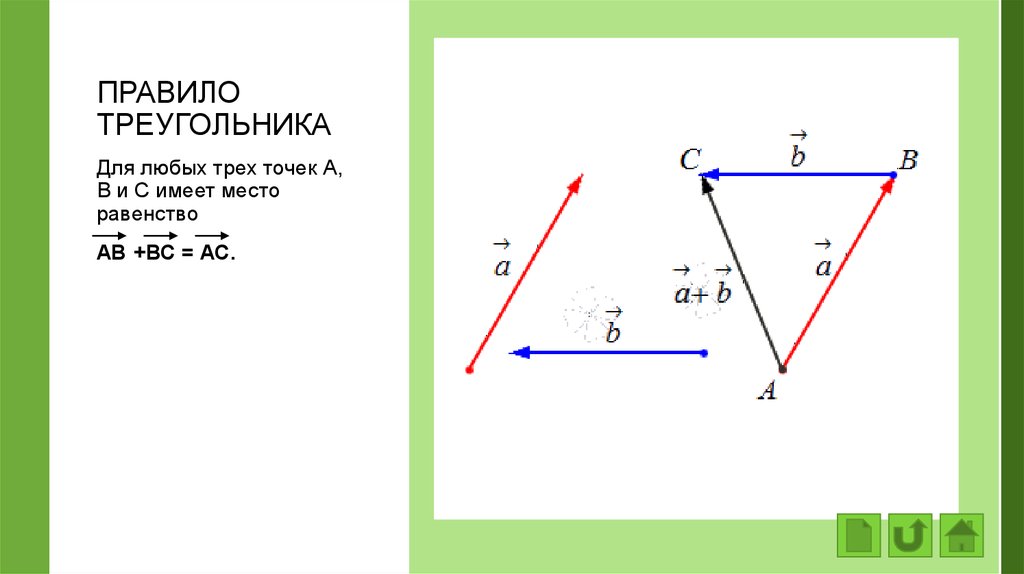
\(\overrightarrow{a} \times \overrightarrow{b} = |a| |b| \sin(\theta) \hat n\)
Рабочее правило умножения векторов
Рабочее правило умножения векторов, которое включает скалярное произведение и перекрестное произведение, можно понять из приведенных ниже предложений.
Скалярное произведение
Для скалярного умножения векторов два вектора выражаются через единичные векторы i, j, k вдоль осей x, y, z, затем скалярное произведение получается следующим образом:
Если \(\overrightarrow a = a_1\hat i + b_1 \hat j + c_1 \hat k\) и \(\overrightarrow b = a_2 \hat i + b_2 \hat j + c_2\hat k\), то
\(\overrightarrow a. \overrightarrow b\) = \((a_1 \hat i + b_1 \hat j + c_1 \hat k)(a_2 \hat i + b_2 \hat j + c_2 \hat k)\)
= \((a_1a_2) (\hat i. \hat i) + (a_1b_2) (\hat i.\hat j)+ (a_1c_2) (\hat i. \hat k) + \\(b_1a_2) ( \hat j. \hat i) + (b_1b_2)(\hat j. \hat j) + (b_1c_2 (\hat j. \hat k) + \\(c_1a_2)(\hat k. \hat i) + ( c_1b_2)(\шляпа k.\шляпа j) + (c_1c_2)(\шляпа k.\шляпа k)\)
\hat i) + (a_1b_2) (\hat i.\hat j)+ (a_1c_2) (\hat i. \hat k) + \\(b_1a_2) ( \hat j. \hat i) + (b_1b_2)(\hat j. \hat j) + (b_1c_2 (\hat j. \hat k) + \\(c_1a_2)(\hat k. \hat i) + ( c_1b_2)(\шляпа k.\шляпа j) + (c_1c_2)(\шляпа k.\шляпа k)\)
\(\overrightarrow a. \overrightarrow b\) = \(a_1a_2 + b_1b_2+ c_1c_2\)
Перекрестное произведение
Предположим, что \(\overrightarrow{a}\) и \(\overrightarrow{b}\ ) — два вектора, такие, что \(\overrightarrow{a}\)= \(a_1\hat i+b_1 \hat j+c_1 \hat k\) и \(\overrightarrow{b}\) = \(a_2 \ шляпа i+b_2 \ шляпа j+c_2 \ шляпа k\), то с помощью определителей мы могли бы найти векторное произведение векторов, используя следующую матричную запись.
Перемножение векторов также представляется с помощью формулы перекрестного произведения как:
\(\overrightarrow{a} \times \overrightarrow{b} = \hat i (b_1c_2-b_2c_1) — \hat j (a_1c_2-a_2c_1) + \hat k (a_1b_2-a_2b_1)\)
Примечание: \ ( \hat i, \hat j, \text{ и } \hat k \) — единичные векторы в направлении оси x, оси y и оси z соответственно.
Свойства умножения векторов
Скалярное произведение единичного вектора изучается путем взятия единичных векторов \(\hat i\) вдоль оси x, \(\hat j\) вдоль оси y и \(\hat k\) по оси Z соответственно. Скалярное произведение единичных векторов \(\hat i\), \(\hat j\), \(\hat k\) подчиняется тем же правилам, что и скалярное произведение векторов. Угол между одинаковыми векторами равен 0º, а значит, их скалярное произведение равно 1. А угол между двумя перпендикулярными векторами равен 90º, а их скалярное произведение равно 0.
- \(\hat i.\hat i\) = \(\hat j.\hat j\) = \(\hat k.\hat k\)= 1
- \(\шляпа i.\шляпа j\) = \(\шляпа j.\шляпа k\) = \(\шляпа k.\шляпа i\)= 0
Перекрестное произведение единичных векторов \(\hat i\), \(\hat j\), \(\hat k\) подчиняется тем же правилам, что и перекрестное произведение векторов. Угол между одинаковыми векторами равен 0º, а значит, их векторное произведение равно 0. А угол между двумя перпендикулярными векторами равен 90º, и их векторное произведение дает вектор, который перпендикулярен двум заданным векторам.
- \(\overrightarrow{i}\times \overrightarrow{i} =\overrightarrow{j}\times \overrightarrow{j} = \overrightarrow{k}\times \overrightarrow{k} = 0\)
Перекрестное произведение двух векторов следует циклическому порядку, как показано на изображении ниже. Перекрестное произведение двух векторов в циклической последовательности дает третий вектор в последовательности.
- \(\overrightarrow{i}\times \overrightarrow{j} = \overrightarrow{k}; \overrightarrow{j}\times \overrightarrow{k}= \overrightarrow{i}; \overrightarrow{k} \times \overrightarrow{i} = \overrightarrow{j}\)
- \(\overrightarrow{j}\times \overrightarrow{i} = \overrightarrow{-k}; \overrightarrow{k}\times \overrightarrow{j}= \overrightarrow{-i}; \overrightarrow{i}\times \overrightarrow{k} = \overrightarrow{-j}\)
Свойства умножения векторов помогают получить детальное представление об умножении векторов, а также выполнять многочисленные вычисления с использованием векторов. Здесь перечислены несколько важных свойств умножения векторов.
Здесь перечислены несколько важных свойств умножения векторов.
- Перекрестное произведение двух векторов определяется формулой \( \overrightarrow{a} \times \overrightarrow{b} = |a| |b| \sin(\theta)\).
- Скалярное произведение двух векторов определяется формулой \( \overrightarrow{a} . \overrightarrow{b} = |a| |b| \cos(\theta)\).
- Скалярное произведение двух векторов подчиняется свойству коммутативности. \(\vec a. \vec b = \vec b. \vec a \)
- Перекрестное произведение двух векторов не соответствует свойству коммутативности. \( \vec a \times \vec b\neq \vec b \times \vec a \)
- Антикоммутативное свойство: \(\overrightarrow{a} \times \overrightarrow{b} = — \overrightarrow{b} \times \overrightarrow{a}\)
- Распределяющее свойство: \(\overrightarrow{a} \times (\overrightarrow{b} + \overrightarrow{c}) = (\overrightarrow{a}\times \overrightarrow{b} )+ (\overrightarrow{a}\times \overrightarrow{с})\)
- Перемножение нулевого вектора: \(\overrightarrow{a}\times \overrightarrow{0} = \overrightarrow{0}\)
- Перемножение вектора с самим собой: \(\overrightarrow{a}\times \overrightarrow{a} = \overrightarrow{0}\)
- Умножить на скалярную величину: \(c(\overrightarrow{a}\times \overrightarrow{b}) = c\overrightarrow{a}\times \overrightarrow{b} = \overrightarrow{a}\times c\overrightarrow{ б}\)
- Скалярное произведение двух векторов является скаляром и лежит в плоскости двух векторов.

- Перекрестное произведение двух векторов — это вектор, который перпендикулярен плоскости, содержащей эти два вектора.
Применение умножения векторов
Ниже приведены некоторые из важных применений умножения векторов. Давайте разберемся с каждым из этих применений в следующих параграфах.
- Проекция вектора
- Угол между двумя векторами
- Продукт тройного креста
- Площадь параллелограмма
- Объем параллелепипеда
Проекция вектора
Скалярное произведение полезно для нахождения компонента одного вектора в направлении другого. Проекция вектора одного вектора на другой вектор — это длина тени данного вектора на другой вектор. Он получается путем умножения величины данных векторов на косеканс угла между двумя векторами. Результатом формулы векторной проекции является скалярное значение.
Здесь \(\overrightarrow a\) и \(\overrightarrow b\) — два вектора, а θ — угол между двумя векторами. 2}}\)
2}}\)
Тройное перекрестное произведение
Перекрестное произведение вектора на произведение двух других векторов представляет собой тройное перекрестное произведение векторов. Результатом тройного перекрестного произведения является вектор. Равнодействующий вектора тройного пересечения лежит в плоскости данных трех векторов. Если a, b и c — векторы, то векторное тройное произведение этих векторов будет иметь вид:
\((\overrightarrow{a}\times \overrightarrow{b}) \times \overrightarrow{c} = (\overrightarrow{a}\cdot \overrightarrow{c})\overrightarrow{b} -(\overrightarrow{b}\cdot \overrightarrow{c}) \overrightarrow{a}\)
Площадь параллелограмма
Две смежные стороны параллелограмма могут быть представлены векторами \(\overrightarrow a\) и \(\overrightarrow b\). Площадь параллелограмма равна произведению основания и высоты параллелограмма. Рассмотрим основание параллелограмма как \(|\overrightarrow a|\), а высоту параллелограмма как \(|\overrightarrow b|\)sin θ.
Здесь Основание = \(|\overrightarrow a|\), Высота = \(|\overrightarrow b|\)sin θ, а Площадь параллелограмма = Основание x Высота
Площадь параллелограмма = \(|\overrightarrow a|.|\overrightarrow b|\)sin θ = \(\overrightarrow a \times \overrightarrow b \)
Объем параллелепипеда
Параллелепипед равен шести двусторонняя фигура, каждая из сторон которой является параллелограммом. Здесь параллелограммы противоположных сторон одинаковы. Объем V параллелепипеда можно получить со стороны ребер a, b, c. Объем параллелепипеда можно получить из произведения площади основания на высоту параллелепипеда. Площадь основания параллелепипеда равна |b x c| а высота параллелепипеда равна |a|. Формула расчета объема параллелепипеда выглядит следующим образом.
V = a.(b x c)
Связанные темы
Следующие темы помогают лучше понять умножение векторов.
- Коллинеарные векторы
- Векторы
- Типы векторов
- Добавление векторов
- Перекрестное произведение двух векторов
Часто задаваемые вопросы по умножению векторов
Что такое скалярное умножение векторов?
Скалярное умножение векторов также называется скалярным произведением двух векторов и имеет два определения. Алгебраически скалярное произведение двух векторов равно сумме произведений отдельных компонентов двух векторов. a.b = \(a_1b_1\) + \(a_2b_2\)+ \(a_3b_3\). Геометрически скалярное произведение двух векторов есть произведение величины векторов и косинуса угла между двумя векторами. ( \(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a||\overrightarrow b|\) cos θ). Результат скалярного умножения векторов является скалярным значением.
Алгебраически скалярное произведение двух векторов равно сумме произведений отдельных компонентов двух векторов. a.b = \(a_1b_1\) + \(a_2b_2\)+ \(a_3b_3\). Геометрически скалярное произведение двух векторов есть произведение величины векторов и косинуса угла между двумя векторами. ( \(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a||\overrightarrow b|\) cos θ). Результат скалярного умножения векторов является скалярным значением.
Как вычислить скалярное произведение векторов?
Скалярное умножение векторов можно вычислить в три простых шага. Сначала найдите величину двух векторов a и b, т.е. |a| и |б|. Во-вторых, найдите косеканс угла θ между двумя векторами. Наконец, возьмите произведение величины двух векторов и косеканса угла между двумя векторами, чтобы получить скалярное произведение двух векторов. (a.b = |a|.|b|.Cosθ). Также проверьте калькулятор скалярного произведения, чтобы легко найти векторное скалярное произведение.
Почему скалярное произведение называется скалярным умножением векторов?
Скалярное произведение называется скалярным умножением векторов, поскольку все отдельные составляющие ответа являются скалярными величинами. В a.b = |a|.|b|.Cosθ, |a|, |b| и Cosθ — скалярные величины. Следовательно, скалярное произведение также называют скалярным умножением векторов.
В a.b = |a|.|b|.Cosθ, |a|, |b| и Cosθ — скалярные величины. Следовательно, скалярное произведение также называют скалярным умножением векторов.
Почему мы используем косинус в скалярном умножении векторов?
Чтобы найти скалярное произведение векторов, нам нужно, чтобы два вектора a, b были направлены в одном направлении. Поскольку векторы a и b расположены под углом друг к другу, значение acosθ является компонентом вектора a в направлении вектора b. Следовательно, мы находим cosθ в скалярном произведении или скалярном умножении двух векторов.
Что такое векторное умножение векторов?
Перемножение двух векторов при умножении приводит к третьему вектору, перпендикулярному двум исходным векторам. Величина результирующего вектора определяется площадью параллелограмма между ними, а его направление можно определить по правилу правой руки. a × b = c, где c — перекрестное произведение или векторное произведение двух векторов a и b.
Что такое скалярное умножение и векторное умножение векторов?
Векторы можно умножать двумя разными способами: точечным произведением и перекрестным произведением. Результаты обоих этих умножений векторов различны. Скалярное умножение векторов или скалярное произведение дает в результате скалярную величину, тогда как векторное умножение векторов или перекрестное произведение дает векторную величину. Векторное произведение двух векторов задается как: \(\overrightarrow{a} \times \overrightarrow{b} = |a| |b| \sin(\theta) \hat n\) и формула скалярного произведения двух векторов задается как: \(\overrightarrow{a}. \overrightarrow{b} = |a| |b| \cos(\theta)\).
Результаты обоих этих умножений векторов различны. Скалярное умножение векторов или скалярное произведение дает в результате скалярную величину, тогда как векторное умножение векторов или перекрестное произведение дает векторную величину. Векторное произведение двух векторов задается как: \(\overrightarrow{a} \times \overrightarrow{b} = |a| |b| \sin(\theta) \hat n\) и формула скалярного произведения двух векторов задается как: \(\overrightarrow{a}. \overrightarrow{b} = |a| |b| \cos(\theta)\).
В чем разница между скалярным умножением и векторным умножением векторов?
При умножении векторов скалярное умножение векторов или скалярное произведение исходных векторов дает скалярную величину, тогда как векторное умножение двух векторов или перекрестное произведение двух векторов дает векторную величину. Скалярное произведение — это произведение величины векторов на косинус угла между ними. а . б = |а| |б| cosθ. Векторное произведение — это произведение величины векторов на синус угла между ними. а × б = | а | |б| грех θ.
а × б = | а | |б| грех θ.
Что такое правило большого пальца правой руки для перекрестного произведения векторов?
Правило правой руки для векторного произведения двух векторов помогает определить направление результирующего вектора. Если мы направим правую руку в направлении первой стрелки, а пальцы согнем в направлении второй, то наш большой палец окажется в направлении векторного произведения двух векторов. Правило большого пальца правой руки дает формулу векторного произведения для нахождения направления результирующего вектора.
Перекрестное произведение (векторное произведение) — определение, формула и свойства
В векторной алгебре определяются различные типы векторов, и над этими векторами можно выполнять различные операции, такие как сложение, вычитание, произведение и так далее. В этой статье объясняется перекрестное произведение двух векторов, формул, свойств и примеров.
Содержание:
- Определение
- Перекрестное произведение двух векторов
- Формула
- Матрица перекрестных произведений
- Правило правой руки
- Свойства
- Перпендикулярные векторы
- Параллельные векторы
- Величина
- Пример
Что такое перекрестный продукт?
Перекрестное произведение — это бинарная операция над двумя векторами в трехмерном пространстве.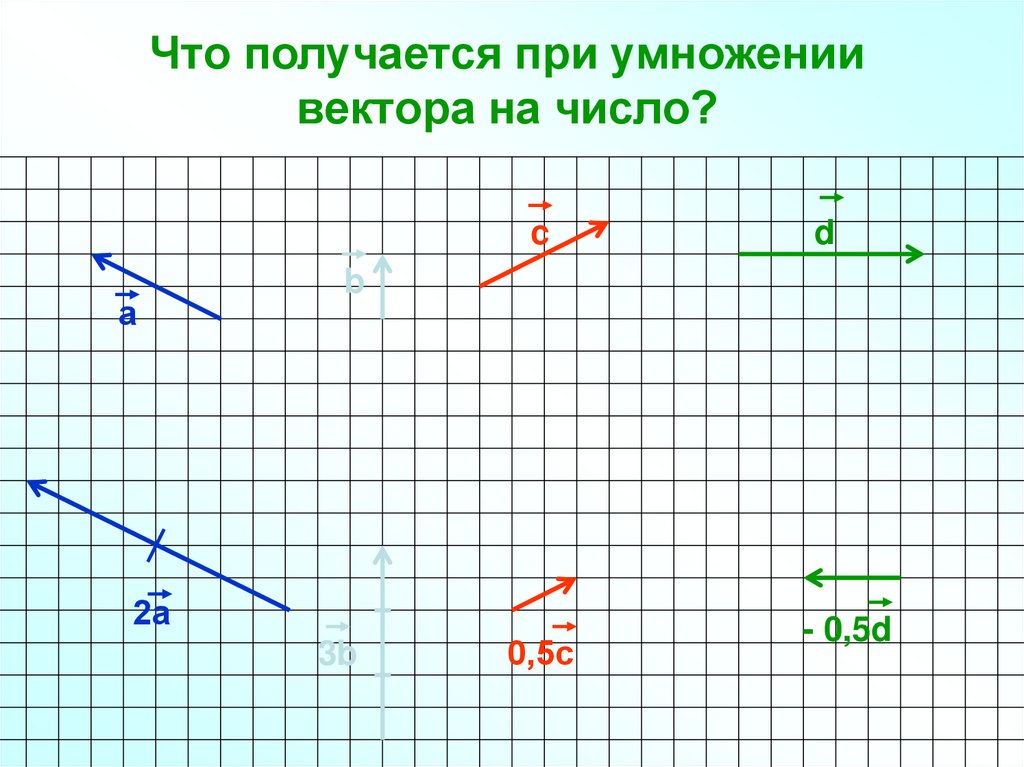 В результате получается вектор, перпендикулярный обоим векторам. Векторное произведение двух векторов, a и b , обозначается как a × б . Его результирующий вектор перпендикулярен a и b . Векторные произведения также называются перекрестными произведениями. Перекрестное произведение двух векторов даст результирующий вектор, который будет рассчитан с использованием правила правой руки.
В результате получается вектор, перпендикулярный обоим векторам. Векторное произведение двух векторов, a и b , обозначается как a × б . Его результирующий вектор перпендикулярен a и b . Векторные произведения также называются перекрестными произведениями. Перекрестное произведение двух векторов даст результирующий вектор, который будет рассчитан с использованием правила правой руки.
Перекрестное произведение двух векторов
Векторное произведение или перекрестное произведение двух векторов A и B обозначается как A × B , а его результирующий вектор перпендикулярен векторам A и В . Перекрестное произведение в основном используется для определения вектора, который перпендикулярен плоской поверхности, натянутой на два вектора, тогда как скалярное произведение используется для нахождения угла между двумя векторами или длины вектора. Перекрестное произведение двух векторов, скажем, A × B , равно другому вектору, расположенному под прямым углом к обоим, и это происходит в трех измерениях.
Перекрестное произведение двух векторов, скажем, A × B , равно другому вектору, расположенному под прямым углом к обоим, и это происходит в трех измерениях.
Формула перекрестного произведения
Если θ угол между данными двумя векторами A и B , то формула векторного произведения векторов имеет вид:
А × В =| А | | Б | sin θOr,
\(\begin{array}{l}\vec{A}\times \vec{B}=||\vec{A}|| \ ||\vec{B}|| sin\theta \\шляпа{n} \end{массив} \)
Здесь,
\(\begin{array}{l}\vec{A},\vec{B} \ являются\ двумя\ векторами.\end{array} \)
\(\begin{array}{l}||\vec{A}||, \ ||\vec{B}|| \ являются\ величинами\ заданных\ векторов.\end{массив} \ )
θ — угол между двумя векторами
\(\begin{array}{l}\hat{n} \ \text {единичный вектор, перпендикулярный плоскости, содержащей данные два вектора, в направлении, заданном правилом правой руки.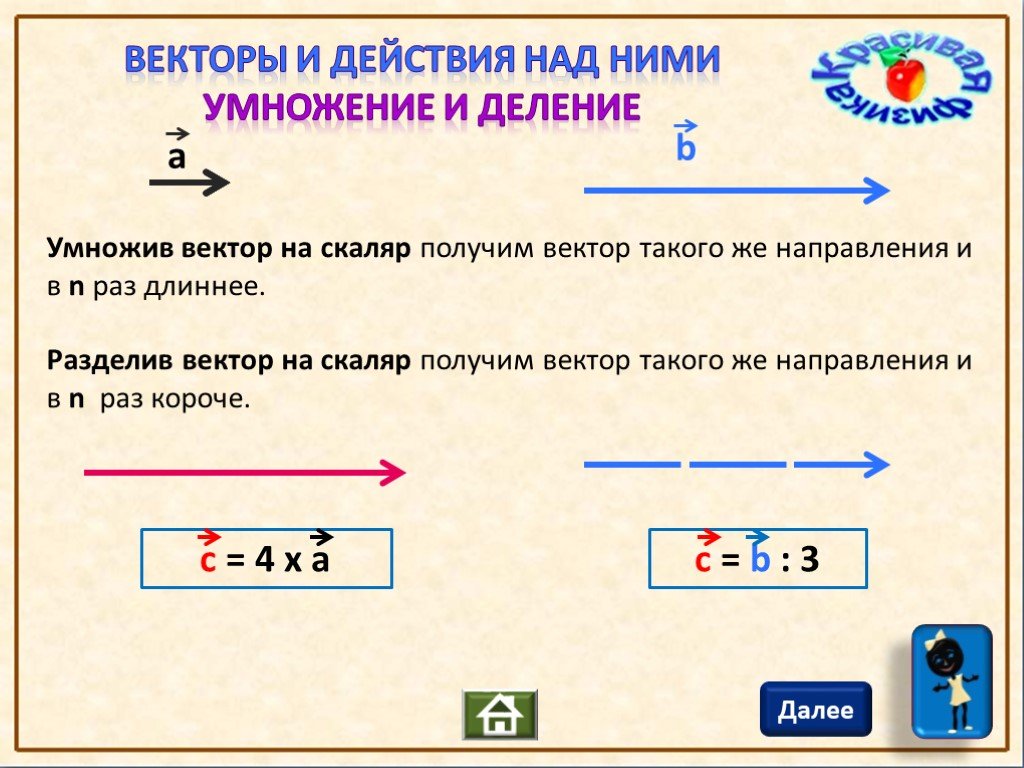 }\end{array } \)
}\end{array } \)
Перекрестное произведение двух векторов Формула
Рассмотрим два вектора,
А = ай + бж + ск
В = xi + yj + zk
Мы знаем, что стандартные базисные векторы i, j и k удовлетворяют приведенным ниже равенствам.
i × j = k и j × i = -k j × k = i и k × j = -i k × i = j и i × k = -j
Кроме того, антикоммутативность векторного произведения и явное отсутствие линейной независимости этих векторов означает, что:
я × я = j × j = k × k = 0
Сейчас,
A × B = (ai + bj + ck) × (xi + yj + zk)
= ax(i × i) + ay(i × j) + az(i × k) + bx(j × i) + by(j × j) + bz(j × k) + cx(k × i) + cy(k × j) + cz(k × k)
Применяя вышеупомянутые равенства,
A × B = ax(0) + ay(k) + az(-j) + bx(-k) + by(0) + bz(i) + cx(j) + cy(-i) + cz( 0) = (bz – cy)i + (cx – az)j + (ay – bx)k
Матрица перекрестных произведений
Мы также можем вывести формулу векторного произведения двух векторов, используя определитель матрицы, как указано ниже.
A = ai + bj + ck B = xi + yj + zk
Таким образом,
\(\begin{array}{l}\mathbf{A}\times \mathbf{B} = \begin{vmatrix} \boldsymbol{i} & \mathbf{j} & \mathbf{k} \\ a & b & c\\ x & y & z \end{vmatrix}\end{массив} \)
A × B = (bz – cy)i – (az – cx)j + (ay – bx)k = (bz – cy)i + (cx – az)j + (ay – bx)k
Перекрестное произведение правил правой руки
Мы можем найти направление единичного вектора с помощью правила правой руки.
В этом правиле мы можем вытянуть правую руку так, чтобы указательный палец правой руки был в направлении первого вектора, а средний палец — в направлении второго вектора. Затем большой палец правой руки указывает направление или единичный вектор n. С помощью правила правой руки мы можем легко показать, что векторное произведение векторов не коммутативно. Если у нас есть два вектора A и B, то диаграмма для правила правой руки выглядит следующим образом:
Свойства перекрестного произведения
Чтобы найти векторное произведение двух векторов, мы можем использовать свойства. Такие свойства, как антикоммутативность, свойство нулевого вектора, играют важную роль в нахождении перекрестного произведения двух векторов. Помимо этих свойств, некоторые другие свойства включают свойство Якоби, распределительное свойство. Свойства перекрестного произведения приведены ниже:
Такие свойства, как антикоммутативность, свойство нулевого вектора, играют важную роль в нахождении перекрестного произведения двух векторов. Помимо этих свойств, некоторые другие свойства включают свойство Якоби, распределительное свойство. Свойства перекрестного произведения приведены ниже:
Перекрестное произведение перпендикулярных векторов
Перекрестное произведение двух векторов равно произведению их величин, которое представляет собой площадь прямоугольника со сторонами X и Y. Если два вектора перпендикулярны друг другу, то формула перекрестного произведения принимает вид: θ = 90 градусов Мы знаем, что sin 90° = 1,
Итак,
Перекрестное произведение параллельных векторов
Перекрестное произведение двух векторов является нулевым вектором, если оба вектора параллельны или противоположны друг другу. И наоборот, если два вектора параллельны или противоположны друг другу, то их произведение равно нулю. Два вектора имеют одинаковое направление.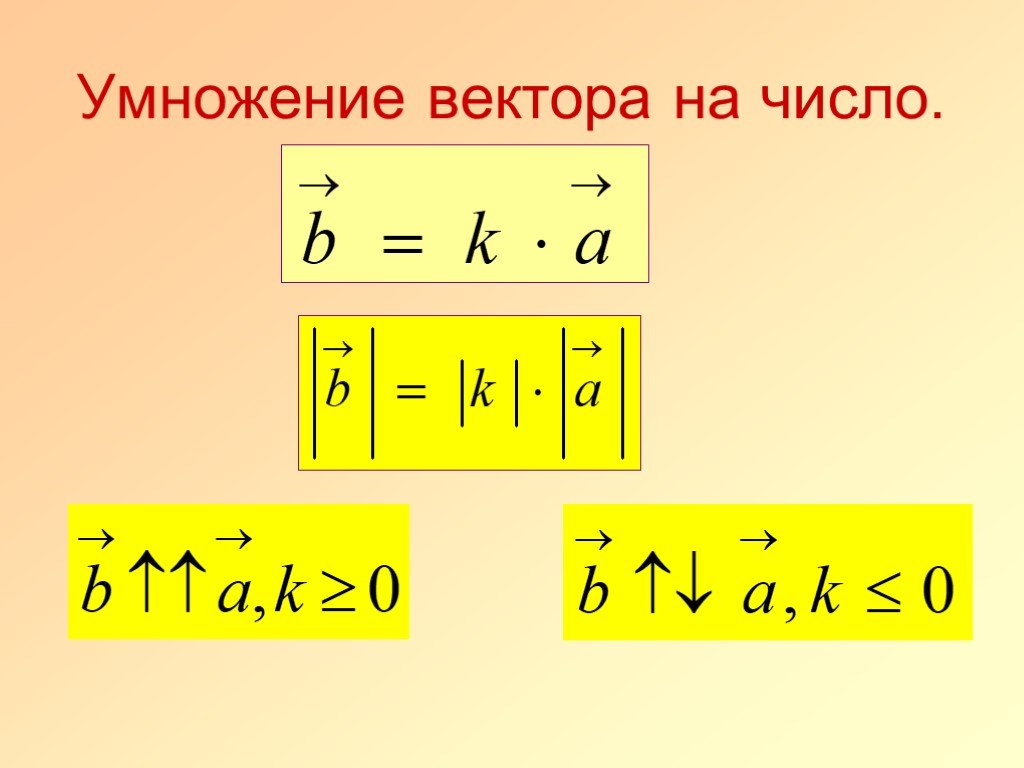


 1 Кинематика
1 Кинематика
 1 Электростатика
1 Электростатика
 5 Излучение и спектры
5 Излучение и спектры
