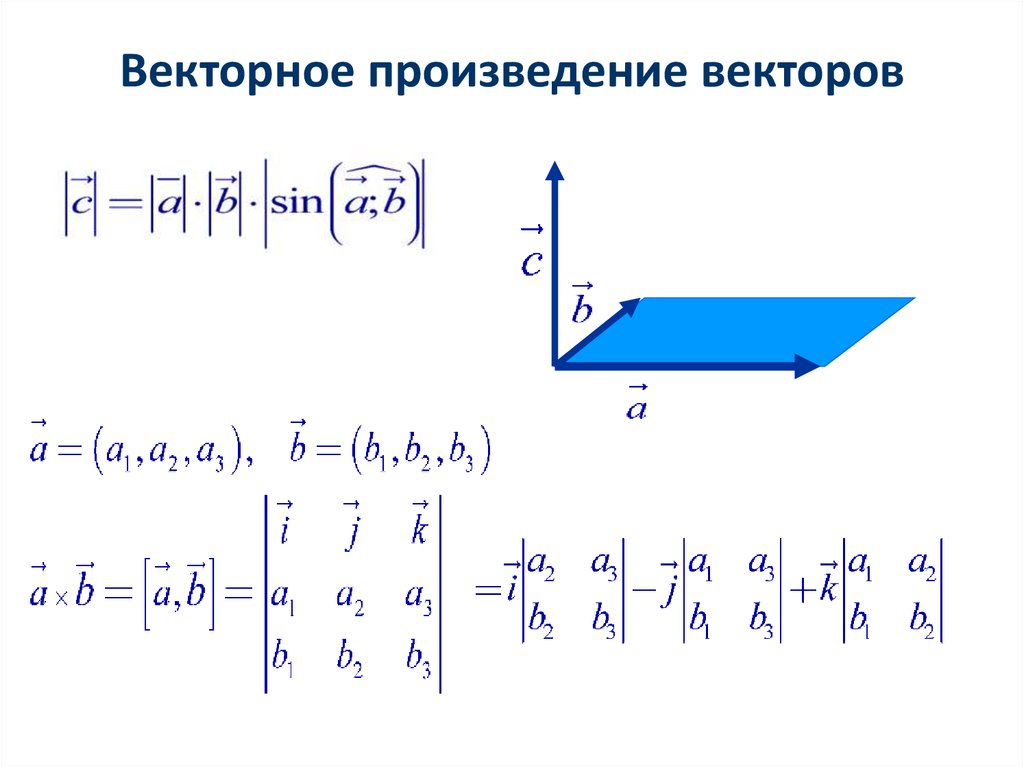
§7. Примеры решения типовых задач

В данном параграфе рассмотрим задачи, связанные с различными системами координат, делением отрезка в заданном отношении.

Пример 1.

Даны координаты точек: А(4; 3), В(7; 6), С(2; 11). Докажем, что треугольник АВС прямоугольный.

Найдем длины сторон треугольника АВС. С этой целью используем формулу, позволяющую находить расстояние между двумя точками на плоскости:

.

Длины сторон будут равны:

,

,

.

Учитывая, что для сторон данного треугольника выполняется теорема Пифагора

,

то треугольник АВС – прямоугольный.

Пример 2.

Даны точки А(2; 1) и В(8; 4). Найдем координаты точки М(х; у), которая делит отрезок в отношении 2:1.

Напомним, что точка М(х; у) делит отрезок АВ, где A(x_A, y_A), B(x_B, y_B), в отношении λ : μ, если ее координаты удовлетворяют условиям:

, .

Найдем точку М для данного отрезка

, .

Таким образом, точка М(6; 3) делит отрезок АВ в отношении 2:1.

Пример 3.

Найдем прямоугольные координаты точки А(3π/4), если полюс совпадает с началом координат, а полярная ось направлена по оси абсцисс.

Учитывая формулы перехода от полярной к прямоугольной системе координат

x = r cosφ, y = r sinφ,

получаем

,

.

В прямоугольной декартовой системе координат координаты точки А(–2; 2).

Пример 4.

Найдем полярные координаты точек, имеющих следующие прямоугольные координаты:

А(; 2),В(–4; 4), С(–7; 0).

Используем формулы перехода от прямоугольных координат к полярным:

,

.

Получим координаты для точки А:

,

, .

Таким образом А(4; π/6) – полярные координаты (рис. 15).

Для точки В (рис. 16) имеем

,

, .

Следовательно, полярные координаты точки В(, 3π/4).

Рассмотрим точку С(–7; 0) (рис. 17). В этом случае

,

, .

Можно записать полярные координаты точки

С(7; π).

Пример 5.

Найдем длину вектора a = 20i + 30j – 60k и его направляющие косинусы.

Напомним, что направляющие косинусы – это косинусы углов, которые вектор a(a₁, a₂, a₃) образует с осями координат:

, ,,

где .

Применим эти формулы к данному вектору, получим

,

,

.

Пример 6.

Нормируем вектор a = 3i + 4j – 12k.

Нормировать вектор – это найти вектор единичной длины а₀, направленный также как и данный вектор. Для произвольного вектора a(a₁, a₂, a₃) соответствующий вектор единичной длины можно найти, умножив a на дробь .

.

В нашем случае и вектор единичной длины:

.

Пример 7.

Найдем скалярное произведение векторов

a = 4i + 5j + 6k и b = 3i – 4j + k.

Для того чтобы найти скалярное произведение векторов, нужно умножить соответствующие координаты и полученные произведения сложить. Так, для векторов a = a₁i + a₂j + a₃k и b = b₁i + b₂j + b₃

k скалярное произведение имеет вид:

(a, b) = a₁b₁ + a₂b₂ + a₃b₃.

Для данных векторов получаем

(a, b) = 4∙3 + 5∙(–4) + 6∙1 = 12 – 20 + 6 = –2.

Пример 8.

Покажем, что векторы a = 2i – 3j

+ 5k и b = i + 4j + 2k перпендикулярны.

Два вектора перпендикулярны, если их скалярное произведение равно нулю.

Найдем скалярное произведение:

(a, b) = 2∙1 + (–3)∙4 + 5∙2 = 2 – 12 + 10 = 0.

Таким образом, векторы а и b перпендикулярны.

Пример 9.

Выясним, при каком значении параметра m векторы a = 2i + 3j + mk и b = 3

i + mj – 2k перпендикулярны.

Найдем скалярное произведение векторов а и b:

(a, b) = 2∙3 + 3∙m – 2∙m = 6 + m.

Векторы перпендикулярны, если их скалярное произведение равно нулю. Приравниваем к нулю произведение (а, b):

6 + m = 0.

При m = – 6 векторы а и b перпендикулярны.

Пример 10.

Найдем скалярное произведение (3а + 4b, 2а – 3b), если |a| = 2, |b| = 1 и угол φ между а и b равен π/3.

Воспользуемся свойствами скалярного произведения:

(αa, βb) = αβ(a, b),

(a + b, c) = (a, c) + (b, c),

(a, b) = (b, a)

(a, a) = |a

|²,

а также определением скалярного произведения (a, b) = |a|∙|b|∙cosφ. Перепишем скалярное произведение в виде

(3a + 4b, 2a – 3b) = 6(a, a) – 9(a, b) + 8(b, a) – 12(b, b) =

= 6|a|² – (a, b) – 12|b|² = 6∙2² – 2∙1∙cos(π/3) – 12∙1²

= 11.

Пример 11.

Определим угол между векторами

a = i + 2j + 3k и b = 6i + 4j – 2k.

Для нахождения угла воспользуемся определением скалярного произведения двух векторов

(a, b) = |a|∙|b|∙cosφ,

где φ – угол между векторами а и b. Выразим cosφ из этой формулы

.

Учитывая, что (а, b) = 1∙6 + 2∙4 + 3∙(–2) = 8, ,, получаем:

.

Следовательно, .

Пример 12.

Найдем векторное произведение векторов

a = 5i – 2j + 3k и b = i + 2j – 4k.

Известно, что векторное произведение векторов a = a₁i + a₂j + a₃k и b = b₁i + b₂j + b₃k находится по формуле

.

Следовательно, для данных векторов

= 2i + 23j + 12k.

Рассмотрим пример, где для нахождения модуля векторного произведения будет использоваться определение векторного произведения, а не выражение его через координаты сомножителей, как было в предыдущем примере.

Пример 13.

Найдем модуль векторного произведения векторов а + 2b и 2а – 3b, если |a| = 1, |b| = 2 и угол между векторами а и b равен 30°.

Из определения векторного произведения видно, что для произвольных векторов а и b его модуль равен

|[a, b] | = |a| ∙ |b| ∙ sin φ.

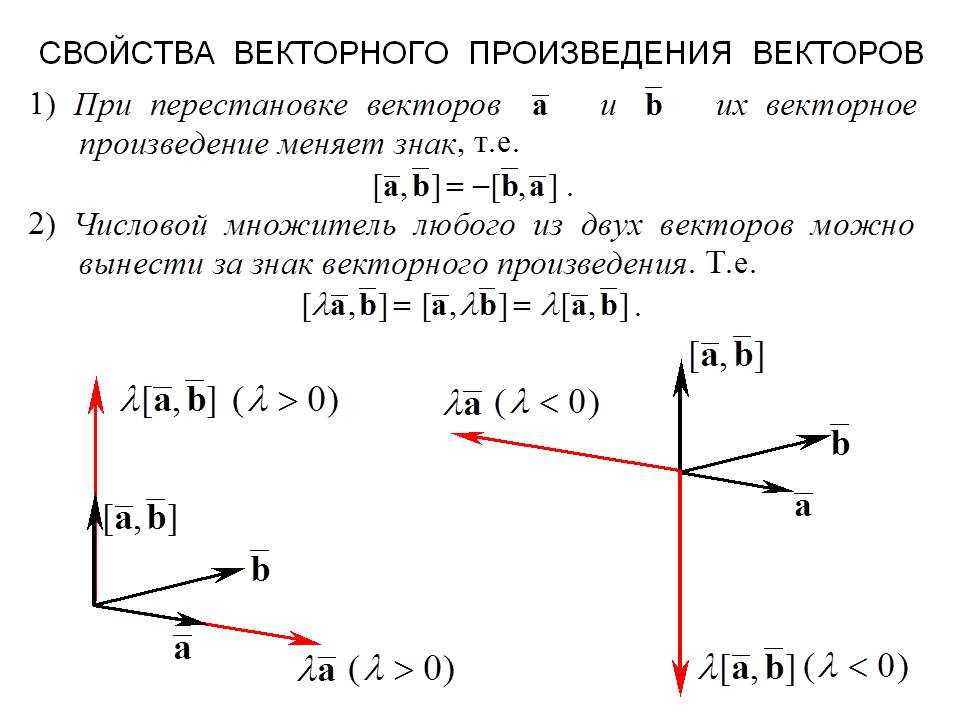
Учитывая свойства векторного произведение

[a, b] = – [b, a],

[a, a] = 0,

[αa + βb, c] = α[a, c] + β[b, c],

получаем

[a + 2b, 2a – 3b] = 2[a, a] – 3[a, b] + 4[b, a] – 6[b, b] = –7[a, b].

Значит, модуль векторного произведения равен

|[a + 2b, 2a – 3b]| = |–7[a, b]| = 7 ∙ |a| ∙ |b| ∙ sin 30° = 7∙1∙2∙0,5 = 7.

Пример 14.

Вычислим площадь параллелограмма, построенного на векторах

a = 6i + 3j – 2k и b = 3i – 2j + 6k.

Известно, что модуль векторного произведения двух векторов равен площади параллелограмма, построенного на этих векторах. Найдем векторное произведение по формуле:

,

где a = a₁i + a₂j + a₃k и b = b₁i + b₂j + b₃k. Затем вычислим его модуль.

Для данных векторов получаем

= 14i – 42j – 21k.

Следовательно, площадь параллелограмма равна

S = |[a, b]| = (кв. ед.).

Пример 15.

Вычислим площадь треугольника с вершинами А(1;2;1), В(3;3;4), С(2;1;3).

Очевидно, что площадь треугольника АВС равна половине площади параллелограмма, построенного на векторах и.

В свою очередь, площадь параллелограмма, построенного на векторах и, равна модулю векторного произведения []. Таким образом

|[]|.

Найдем координаты векторов и, вычитая из координат конца вектора соответствующие координаты начала, получим

= (3 – 1)i + (3 – 2)j + (4 – 1)k = 2i + j + 3k,

= (2 – 1)i + (1 – 2)j + (3 – 1)k = i – j + 2k.

Найдем векторное произведение:

[,] = 5i – j – 3k.

Найдем модуль векторного произведения:

|[]| = .

Следовательно, можем получить площадь треугольника:

(кв. ед.).

Пример 16.

Вычислим площадь параллелограмма, построенного на векторах a + 3b и 3a – b, если |a| = 2, |b| = 1 и угол между а и b равен 30°.

Найдем модуль векторного произведения, используя его определение и свойства, указанные в примере 13, получим

[a + 3b, 3a – b] = 3[a, a] – [a, b] + 9[b, a] – 3[b, b] = –10[a, b].

Значит, искомая площадь равна

S = |[a + 3b, 3a – b]| = |–10[a, b]| = 10 ∙ |a| ∙ |b| ∙ sin 30° =

= 10∙2∙1∙0,5 = 10 (кв. ед.).

Следующие примеры будут связаны с использованием смешанного произведения векторов.

Пример 17.

Показать, что векторы a = i + 2j – k, b = 3i + k и с = 5i + 4j – k компланарны.

Векторы компланарны, если их смешанное произведение равно нулю. Для произвольных векторов

a = a₁i + a₂j + a₃k, b = b₁i + b₂j + b₃k, c = c₁i + c₂j + c₃k

смешанное произведение находим по формуле:

.

Для данных векторов получаем

.

Таким образом, данные векторы компланарны.

Пример18.

Найдем объем треугольной пирамиды с вершинами А(1;1;1), В(3;2;1), С(2;4;3), D(5;2;4).

Найдем координаты векторов ,и, совпадающих с ребрами пирамиды. Вычитая из координат конца вектора соответствующие координаты начала, получаем

= 2i + 3j,

= i + 3j + 2k,

= 4i + j + 3k.

Известно, что объем пирамиды равен 1/6 объема параллелепипеда, построенного на векторах ,и. Таким образом,

.

В свою очередь, объем параллелепипеда равен модулю смешанного произведения

V_парал = |(,,)|.

Найдем смешанное произведение

(,,) = .

Итак, объем пирамиды равен

(куб. ед.).

В следующих примерах покажем возможное применение векторной алгебры.

Пример 19.

Проверим, являются ли коллинеарными вектора 2а + b и а – 3b, где a = 2i + j – 3k и b = i + 2j + 4k.

Найдем координаты векторов 2а + b и а – 3b:

2а + b = 2(2i + j – 3k) + i + 2j + 4k = 5i + 4j – 2k,

а – 3b = 2i + j – 3k – 3(i + 2j + 4k) = –i – 5j – 15k.

Известно, что у коллинеарных векторов пропорциональные координаты. Учитывая, что

,

получаем, что вектора 2а + b и а – 3b неколлинеарны.

Эту задачу можно было решить и другим способом. Критерием коллинеарности векторов является равенство нулю векторного произведения:

[2a + b, a – 3b] = 2[a, a] – 6[a, b] + [b, a] – 3[b, b] = –7[a, b].

Найдем векторное произведение векторов а и b:

= 10i – 11j + 3k ≠ 0.

Следовательно,

[2a + b, a – 3b] = –7[a, b] ≠ 0

и векторы 2а + b и а – 3b неколлинеарны.

Пример 20.

Найдем работу силы F(3; 2; 1), когда точка ее приложения А(2; 4;–6), двигаясь прямолинейно, перемещается в точку В(5; 2; 3).

Известно, что работа силы – это скалярное произведение силы F на вектор перемещения .

Найдем координаты вектора :

= 3i – 2j + 9k.

Следовательно, работа силы F по перемещению точки А в точку В будет равна скалярному произведению

(F, ) = 3∙3 + 2∙(–2) + 1∙9 = 9 – 4 + 9 = 14.

Пример 21.

Пусть сила F( 2;3;–1) приложена к точке А(4;2;3). Под действием силы F точка А перемещается в точку В(3;1;2). Найдем модуль момента силы F относительно точки В.

Известно, что момент силы равен векторному произведению силы на перемещение. Найдем вектор перемещения :

= (3 – 4)i + (1 – 2)j + (2 – 3)k = – i – j – k.

Найдем момент силы как векторное произведение:

= – 4i + 3j + k.

Следовательно, модуль момента силы равен модулю векторного произведения:

|[F, ]| = .

Векторная алгебра — презентация онлайн

Похожие презентации:

Векторная алгебра

Векторная алгебра

Векторная алгебра

Векторная алгебра

Основы векторной алгебры. Векторы на плоскости и в пространстве

Элементы векторной алгебры (продолжение)

Элементы векторной алгебры

Векторная алгебра. Лекция 3

Векторная алгебра

Векторная алгебра. Лекционно-практические занятия

1. 5. Векторная алгебра

5.1 Основные понятия
Вектором называется направленный отрезок.
Вектор с началом в точке А и концом в точке В обозначается
символом AB или одной буквой a
В
Длина отрезка AB называется длиной или
модулем вектора и обозначается AB , a
a
А
Вектор, длина которого равна нулю, называется нулевым
вектором и обозначается 0 .
Вектор, длина которого равна единице, называется единичным
вектором и обозначается через e .
Единичный вектор, направление которого совпадает с
направлением вектора a , называется ортом вектора и
0
обозначается a .
Два
ненулевых
вектора
называются
противоположными, если они имеют
одинаковую длину и противоположные
направления.
a
-a
Векторы a и b называются
коллинеарными, если они лежат на одной
прямой или на параллельных прямых;
a || b
Два коллинеарных вектора называются
равными a b ,если они сонаправлены
и имеют равные длины.
a
b
a
b
Три (и более) вектора называются компланарными, если они
лежат в одной плоскости или в параллельных плоскостях.
Углом между векторами a и b
называется угол при вершине треугольника b
натянутого на вектора a и b .
a
Векторы сонаправлены угол между ними равен нулю;
противоположно направлены угол между ними равен 1800. b
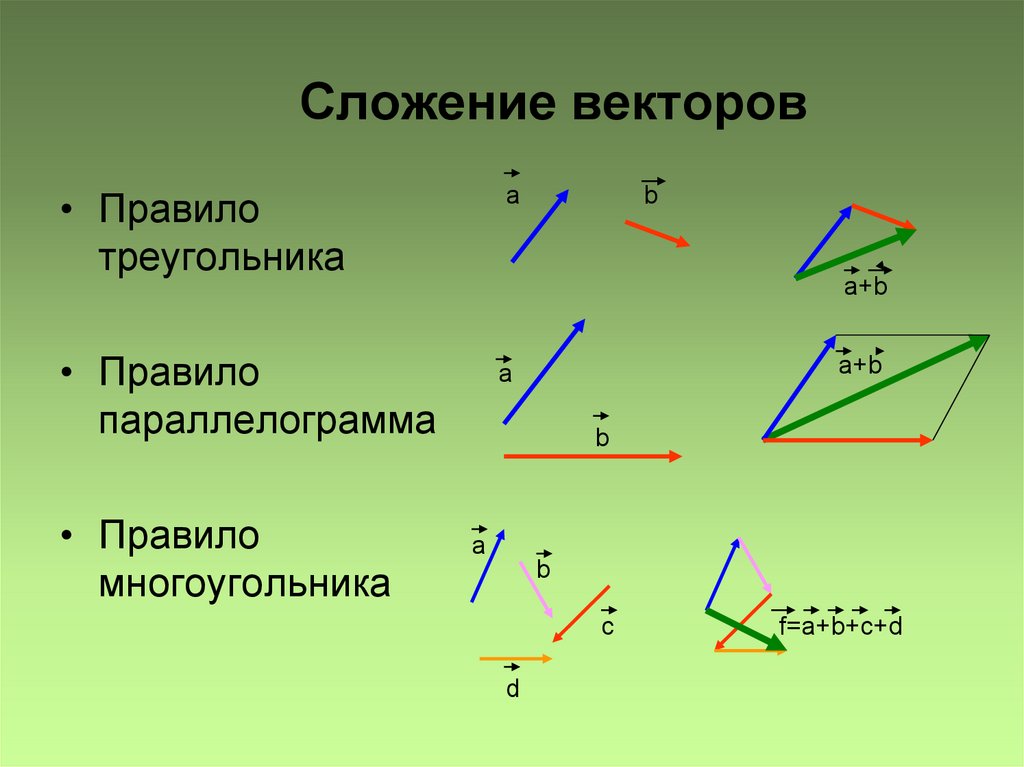
Суммой двух векторов a и b
b
называется вектор с a b ,
соединяющий начало вектора a с концом
вектора b , отложенного от конца вектора a
(правило треугольников)
Разностью двух векторов a и b
называется вектор d a b ,
соединяющий конец вектора b с концом
вектора a , если векторы a и b
приведены к общему началу.
(правило треугольника)
a
b
c a b
a
d a b
b
а2
а1
а4
а3
Сложение векторов по правилу
параллелограмма:
1) совместить начала суммируемых векторов;
2) построить на них параллелограм;
3) построить вектор на диагонали
параллелограмма
b
a
a
c = a +b
b
Произведением вектора a 0 на число
0 называется вектор b a ,
который имеет длину: b a
и направление
вектора a , если λ > 0;
вектора a , если λ < 0.
ПРИМЕР
a
b a
( 2)
b a
( -3)
a a a0
В треугольнике АВС сторону АВ точками M и N разделили на
три равные части: AM = MN = NB. Выразить вектор CM
через CA a и CB b
1
AM AB
3
Из определения разности: AB b a ; AM 1 (b a )
3
1
1
1
2
1
CM a (b a ) a b a CM a b a
3
3
3
3
3
Из определения суммы: CM a AM;
А
С
b
В
M
N
5.2.Проекция вектора на ось
В
Векторной проекцией вектора на ось называется
вектор, началом и концом которого являются
соответственно проекции начала и конца исходного
вектора на данную ось.
А
Скалярной проекцией вектора AB на ось l
называется скаляр, абсолютная величина которого
равна модулю векторной проекции того же вектора
на ту же ось.
прl AB A B
2)
3)
А
ï ðl AB ï ðl AB
А’
В’
В
В
Свойства скалярных проекций:
1) прl AB AB cos
А’
l
А
В’
прl AB CD EF прl AB прl CD прl EF
l
В’
Проекция вектора на вектор – это проекция вектора
на ось направление которой задает вектор
А’
l
5. 3. Базис
Линейная комбинация векторов:
a x1 a1 x2 a2 xn an
действительные числа –
коэффициенты линейной комбинации,
из которых хотя бы один не равен нулю
Векторы линейно зависимы (между собой), если какой-либо из них
является линейной комбинацией остальных.
Если вектор представлен в виде линейной комбинации некоторых
векторов, то говорят, что он разложен по этим векторам.
c xa yb разложен по векторам a и b ,
вектора
c ; a ; b — линейно зависимые.
a
b
x a
c xa yb
y b
Два вектора линейно зависимы коллинеарны
a x b
a II b
Совокупность двух линейно независимых векторов лежащих в
одной плоскости называется базисом на этой плоскости
c xa yb
х; y – координаты вектора c в базисе a; b
Три вектора линейно зависимы компланарны
a; b ; c
компланарны
c xa yb
Совокупность любых трех линейно независимых векторов называется
базисом в пространстве
d xa yb zc
х; y; z – координаты вектора d в базисе a ; b ; c
5. 4. Декартова прямоугольная система координат
Базис называется ортонормированным, если его вектора
i;
единичны и взаимно перпендикулярны:
j; k орты
Совокупность фиксированной точки O (начало координат) и
ортонормированного базиса i ; j; k называется прямоугольной
декартовой системой координат в пространстве.
Прямые Ox, Oy и Oz, проходящие через начало координат в направлении
базисных векторов i ; j; k называются осями координат. Оx — ось
абсцисс, Оy — ось ординат, Оz — ось аппликат
Плоскости, проходящие через оси координат— координатные
плоскости. Пространство делится на восемь октантов
z
М
Координатами точки М называются проекции
радиус – вектора OM на оси координат:
y
k
прi OM x, пр j OM y, прk OM z
M x; y; z
iО j
x
z
В
Координатами вектора называются скалярные
проекции вектора на оси координат:
А
прi AB x, пр j AB y, прk AB z
AB x; y; z
AB x i y j z k
k
x
iО j
y
; ;
z
z
— углы, между вектором OM
и осями координат.
cos ; cos ; cos
М
— направляющие косинусы
вектора OM
x OM cos
cos
y OM cos
cos
z OM cos
cos
OM x 2 y 2 z 2
x
x y z
2
2
2
x
y
О
x
Отрезок ОМ – диагональ
y
параллелепипеда.
2
2
2 Построим
прямоугольный
x y z Квадрат диагонали
параллелепипед со
параллелепипеда
равен
сторонами X; Y;
Zис
сумме
квадратов
его
z
вершиной в точке О.
измерений
2
2
2
x y z
cos 2 cos 2 cos 2 1
y
Операции над векторами в декартовой системе координат
a x1 i y1 j z1 k
b x2 i y2 j z2 k
По свойствам скалярной проекции вектора на ось получим:
a b x1 x2 i y1 y2 j z1 z2 k
a x1 i y1 j z1 k
По координатам точек А(ха; уа; zа ) и В (хb; уb; zb) найти
координаты вектора AB
z
A
AB OB OA
B
OB xb ; yb ; zb
OA xa ; ya ; za
AB xb xa ; yb ya ; zb za
o
x
y
ПРИМЕР
Найти модуль и орт суммы векторов:
b i j 4k
a 3i 5 j 8k
c a b 3 1 i 5 1 j 8 4 k
c 22 ( 4) 2 42 36 6
c c co
c
c
c
o
1
1
2
2
c 2i 4 j 4k i j k
6
3
3
3
o
2i 4 j 4k
ЕЩЁ ПРИМЕР
Определить , при каких значениях m и n векторы коллинеарны:
a 2; 3; n
b m; 6; 2
Векторы коллинеарны, если существует такое число λ, что
a b
Это векторное равенство должно выполняться для
координат векторов:
2 m
3 ( 6) 0. 5; m 4; n 1
n 2

English     Русский Правила

numpy для линейной алгебры

numpy для матриц и векторов

Класс numpy ndarray используется для представления как матриц, так и векторов. Чтобы построить матрицу в numpy, мы перечисляем строки матрицы в списке и передаем этот список конструктору массива numpy.

Например, чтобы создать массив numpy, который соответствует матрице

, мы должны сделать

A = np.массив([[1,-1,2],[3,2,0]])
 

Векторы — это просто массивы с одним столбцом. Например, чтобы построить вектор

мы бы сделали

v = np.массив([[2],[1],[3]])
 

Более удобным подходом является транспонирование соответствующего вектора-строки. Например, чтобы сделать вектор выше, мы могли бы вместо этого транспонировать вектор-строку

Код для этого

v = np.transpose (np.array ([[2,1,3]]))
 

numpy перегружает индекс массива и обозначения срезов для доступа к частям матрицы. Например, чтобы напечатать правую нижнюю запись в матрице А мы бы сделали

печать (А [1,2])
 

Чтобы вырезать второй столбец в матрице A , мы должны сделать

столбец = А[:,1:2]
 

Первый срез выбирает все строки в A , а второй срез выбирает только среднюю запись в каждой строке.

Чтобы выполнить умножение матрицы или умножение матрицы на вектор, мы используем метод np.dot() .

ш = np.точка (А, v)
 

Решение систем уравнений с помощью numpy

Одной из наиболее распространенных задач линейной алгебры является решение матрично-векторного уравнения. Вот пример. Мы ищем Vector x , который решает уравнение

A x = B

, где

Мы начинаем с строительства массивов для A и B 88888.

A = np.массив([[2,1,-2],[3,0,1],[1,1,-1]])
b = np.transpose (np.array ([[-3,5,-2]])
 

Чтобы решить систему делаем

х = np. linalg.solve(A,b)
 

Применение: множественная линейная регрессия

В задаче множественной регрессии мы ищем функцию, которая может сопоставлять точки входных данных с выходными значениями. Каждая точка данных представляет собой вектор признаков ( x ₁ , x ₂ , …, x _m ), состоящий из двух или более признаков входных значений данных. Чтобы представить все входные данные вместе с вектором выходных значений, мы создали входную матрицу X и выходной вектор y :

В простой модели линейной регрессии по методу наименьших квадратов мы ищем вектор β такой, что произведение X β наиболее точно приближается к вектору результата y.

После того, как мы построили вектор β , мы можем использовать его для сопоставления входных данных с прогнозируемыми результатами. Учитывая входной вектор в форме

, мы можем вычислить прогнозируемое значение результата

Формула для вычисления β vector is

β = ( X ^T X ) ^-1 X ^T y

In our next example program I will use numpy построить соответствующие матрицы и векторы и найти вектор β . После того, как мы решили для β , мы будем использовать его, чтобы делать прогнозы для некоторых точек тестовых данных, которые мы изначально не включили в наш набор входных данных.

Предполагая, что мы построили входную матрицу X и вектор результатов y в numpy, следующий код вычислит вектор β :

Xt = np.transpose (X)
XtX = np.dot (Xt, X)
Xty = np.dot(Xt,y)
бета = np.linalg.solve(XtX,Xty)
 

В последней строке используется NP.Linalg.Solve для вычисления β , поскольку уравнение

β = ( x ^T x ) x ) ^—1 x ) x )0033 X ^T y

is mathematically equivalent to the system of equations

( X ^T X ) β = X ^T y

В этом примере я буду использовать набор данных о ценах на дома в Виндзоре, который содержит информацию о продажах домов в Виндзоре, Онтарио. Входные переменные охватывают ряд факторов, которые потенциально могут повлиять на цены на жилье, такие как размер участка, количество спален и наличие различных удобств. Файл CSV с полным набором данных доступен здесь. Я скачал набор данных с этого сайта, который предлагает большое количество наборов данных, охватывающих широкий круг тем.

Вот исходный код примера программы.

импортировать CSV
импортировать numpy как np
защита чтения данных():
    Х = []
    у = []
    с open('Housing.csv') как f:
        rdr = csv.reader(f)
        # Пропустить строку заголовка
        следующий (ряд)
        # Читать X и Y
        для строки в rdr:
            хлиния = [1,0]
            для s в строке[:-1]:
                xline.append (с плавающей запятой))
            X.добавлять(xline)
            y.append (с плавающей запятой (строка [-1]))
    возврат (Х, у)
X0,y0 = читатьДанные()
# Преобразование всех, кроме последних 10 строк необработанных данных, в пустые массивы
д = лен(Х0)-10
X = np. массив (X0 [: d])
y = np.transpose (np.array ([y0 [: d]]))
# Бета-версия вычислений
Xt = np.transpose (X)
XtX = np.dot (Xt, X)
Xty = np.dot(Xt,y)
бета = np.linalg.solve(XtX,Xty)
печать (бета)
# Сделать прогнозы для последних 10 строк в наборе данных
для данных, фактических в zip(X0[d:],y0[d:]):
    х = np.массив ([данные])
    прогноз = np.dot (x, бета)
    print('prediction = '+str(prediction[0,0])+' факт = '+str(фактический))
 

Исходный набор данных состоит из более чем 500 записей. Чтобы проверить точность прогнозов, сделанных моделью линейной регрессии, мы используем все, кроме последних 10 записей данных, чтобы построить модель регрессии и вычислить β . После того, как мы построили вектор β , мы используем его для прогнозирования последних 10 входных значений, а затем сравниваем прогнозируемые цены на жилье с фактическими ценами на жилье из набора данных.

Вот результаты работы программы:

[[-4.14106096e+03]
 [ 3.55197583e+00]
 [1.66328263e+03]
 [1. 45465644e+04]
 [6.77755381e+03]
 [6.58750520e+03]
 [4.44683380e+03]
 [ 5.60834856e+03]
 [1.27979572e+04]
 [1.24091640e+04]
 [4.19931185e+03]
 [9.42215457e+03]]
прогноз = 97360,6550969 факт = 82500,0
прогноз = 71774,1659014 факт = 83000,0
прогноз = 92359,0891976 факт = 84000,0
прогноз = 77748,2742379 факт = 85000,0
прогноз = 91015,5
6 факт = 85000,0
прогноз = 97545,1179047 факт = 91500,0
прогноз = 97360,6550969 факт = 94000,0
прогноз = 106006,800756 факт = 103000,0
прогноз = 92451,6931269 факт = 105000,0
прогноз = 73458,2949381 факт = 105000,0
 

В целом, предсказания не очень хороши, но ряд предсказаний несколько близок к правильности. Создание более качественных прогнозов на основе этих данных станет предметом зимнего учебного курса по машинному обучению.

Метод наименьших квадратов

Цели

1. Изучите примеры задач наилучшего соответствия.
2. Научитесь превращать задачу наилучшего соответствия в задачу наименьших квадратов.
3. Рецепт: найти решение методом наименьших квадратов (два способа).
4. Рисунок: геометрия решения методом наименьших квадратов.
5. Словарный запас: решение методом наименьших квадратов .

В этом разделе мы ответим на следующий важный вопрос:

Предположим, что Ax=b не имеет решения. Каково наилучшее приближенное решение?

Для наших целей наилучшее приближенное решение называется методом наименьших квадратов . Мы представим два метода нахождения решений методом наименьших квадратов и дадим несколько приложений к задачам наилучшего соответствия.

Начнем с пояснения, что именно мы будем подразумевать под «наилучшим приближенным решением» несовместного матричного уравнения Ax=b.

Определение

Пусть A — матрица размера m × n, а b — вектор в Rm. Решение методом наименьших квадратов матричного уравнения Ax=b есть вектор Kx в Rn такой, что

расстояние(b,AKx)≤расстояние(b,Ax)

для всех остальных векторов x в Rn.

Напомним, что dist(v,w)=Av−wA — это расстояние между векторами v и w. Термин «наименьшие квадраты» происходит от того факта, что dist(b,Ax)=Ab−AKxA — это квадратный корень из суммы квадратов элементов вектора b−AKx. Таким образом, решение методом наименьших квадратов минимизирует сумму квадратов разностей между элементами AKx и b. Другими словами, решение по методу наименьших квадратов максимально точно решает уравнение Ax=b в том смысле, что сумма квадратов разности b-Ax минимизируется.

Метод наименьших квадратов: изображение

Предположим, что уравнение Ax=b несовместно. Напомним из этого примечания в разделе 2.3, что пространство столбцов A — это множество всех других векторов c, таких что Ax=c непротиворечиво. Другими словами, Col(A) — это множество всех векторов вида Ax. Следовательно, ближайший к b вектор формы Ax является ортогональной проекцией b на Col(A). Это обозначено как bCol(A), следуя этим обозначениям в Разделе 6.3.

ColAAxAxAxAKx=bCol(A)bb−AKx=bCol(A)⊥0

Решением уравнения Ax=b методом наименьших квадратов является решение Kx согласованного уравнения Ax=bCol(A)

Где Кх на этой картинке? Если v1,v2,. ..,vn — столбцы A, то

AKx=AEIIGKx1Kx2…KxnFJJH=Kx1v1+Kx2v2+···+Kxnvn.

Следовательно, элементы Kx являются «координатами» bCol(A) относительно остовного множества {v1,v2,…,vm} Col(A). (Они являются честными B-координатами, если столбцы A линейно независимы.)

ColAv1v2Kx1v1Kx2v2AKx=bCol(A)bb−AKx=bCol(A)⊥0 Рис. 4. Фиолетовая плоскость — Col(A). Ближайший вектор, который Ax может подобрать к b, — это ближайший к b вектор на Col(A), который является ортогональной проекцией bCol(A) (синий). Векторы v1,v2 — это столбцы A, а коэффициенты Kx — это длины зеленых линий. Нажмите и перетащите b, чтобы переместить его.

Мы научились решать такую ​​задачу ортогональной проекции в разделе 6.3.

Теорема

Пусть A — матрица размера m × n, а b — вектор в Rm. Решения Ax=b методом наименьших квадратов являются решениями матричного уравнения

.

ATAx=ATb

Доказательство

Согласно этой теореме из раздела 6.3, если Kx является решением матричного уравнения ATAx=ATb, то AKx равно bCol(A). Выше мы утверждали, что решение Ax=b методом наименьших квадратов является решением Ax=bCol(A).

В частности, поиск решения методом наименьших квадратов означает решение последовательной системы линейных уравнений. Мы можем перевести приведенную выше теорему в рецепт:

Рецепт 1. Вычисление решения методом наименьших квадратов

Пусть A — матрица размера m×n, а b — вектор в Rn. Вот метод вычисления решения по методу наименьших квадратов Ax=b:

.

1. Вычислить матрицу ATA и вектор ATb.
2. Сформируйте расширенную матрицу для матричного уравнения ATAx=ATb и уменьшите количество строк.
3. Это уравнение всегда непротиворечиво, и любое решение Kx является решением методом наименьших квадратов.

Повторяю: как только вы нашли решение методом наименьших квадратов Kx для Ax=b, тогда bCol(A) равно AKx.

Пример

Пример

Читатель, возможно, заметил, что мы постарались сказать «решение методом наименьших квадратов» во множественном числе, а «решение методом наименьших квадратов» — с неопределенным артиклем. Это связано с тем, что решение методом наименьших квадратов не обязательно должно быть уникальным: действительно, если столбцы A линейно зависимы, то Ax=bCol(A) имеет бесконечно много решений. Следующая теорема, дающая эквивалентные критерии единственности, является аналогом этого следствия из раздела 6.3.

Теорема

Пусть A — матрица размера m × n, а b — вектор в Rm. Следующие эквивалентны:

1. Ax=b имеет единственное решение методом наименьших квадратов.
2. Столбцы A линейно независимы.
3. АТА является обратимым.

В этом случае решение методом наименьших квадратов равно

.

Kx=(ATA)−1ATb.

Доказательство

Множество решений уравнения Ax=b методом наименьших квадратов является множеством решений согласованного уравнения ATAx=ATb, которое является трансляцией множества решений однородного уравнения ATAx=0. Поскольку ATA — квадратная матрица, эквивалентность 1 и 3 следует из теоремы об обратимой матрице в разделе 5. 1. Множество решений методом наименьших квадратов также является множеством решений согласованного уравнения Ax=bCol(A), которое имеет единственное решение тогда и только тогда, когда столбцы A линейно независимы в соответствии с этим важным примечанием в разделе 2.5.

Пример (бесконечно много решений методом наименьших квадратов)

Как обычно, вычисления с проекциями становятся проще при наличии ортогонального множества. В самом деле, если A представляет собой матрицу размера m × n с ортогональными столбцами u1,u2,…,um, то мы можем использовать формулу проекции в разделе 6.4, чтобы записать

bCol(A)=b·u1u1·u1u1+b·u2u2·u2u2+···+b·umum·umum=AEIIG(b·u1)/(u1·u1)(b·u2)/(u2·u2). ..(b·um)/(um·um)FJJH.

Обратите внимание, что решение методом наименьших квадратов в этом случае единственно, поскольку ортогональное множество линейно независимо.

Рецепт 2. Вычисление решения методом наименьших квадратов

Пусть A — матрица размера m×n с ортогональными столбцами u1,u2,. ..,um, и пусть b — вектор в Rn. Тогда решением Ax=b методом наименьших квадратов является вектор

Kx=Lb·u1u1·u1,b·u2u2·u2,…,b·umum·umM.

Эта формула особенно полезна в естественных науках, так как в природе часто возникают матрицы с ортогональными столбцами.

Пример

В этом подразделе мы даем применение метода наименьших квадратов к моделированию данных. Начнем с базового примера.

Пример (наиболее подходящая линия)

Предположим, что мы измерили три точки данных

(0,6),(1,0),(2,0),

и что наша модель для этих данных утверждает, что точки должны лежать на прямой. Конечно, эти три точки на самом деле не лежат на одной линии, но это может быть связано с ошибками в наших измерениях. Как мы можем предсказать, на какой линии они должны лежать?

(0,6)(1,0)(2,0)

Общее уравнение для (невертикальной) линии:

у=Мх+В.

Если бы наши три точки данных лежали на этой прямой, то удовлетворялись бы следующие уравнения:

6=М·0+В0=М·1+В0=М·2+В. (6.5.1)

Чтобы найти наилучшую прямую, мы пытаемся решить приведенные выше уравнения с неизвестными M и B. Поскольку три точки на самом деле не лежат на прямой, фактического решения нет, поэтому вместо этого мы вычисляем наименьшую- решение квадратов.

Приведя наши линейные уравнения в матричный вид, мы пытаемся решить Ax=b для

.

А=C011121Dx=LMBMb=C600D.

В этом примере мы решили эту задачу наименьших квадратов: единственное решение методом наименьших квадратов для Ax=b — это Kx=AMBB=A−35B, поэтому наиболее подходящая линия — это

.

у=-3х+5.

(0,6)(1,0)(2,0)y=−3x+5

Что именно минимизирует линия y=f(x)=−3x+5? Решение Kx методом наименьших квадратов минимизирует сумму квадратов элементов вектора b−AKx. Вектор b является левой частью (6.5.1), а

AL-35M=C-3(0)+5-3(1)+5-3(2)+5D=Cf(0)f(1)f(2)D.

Другими словами, AKx — это вектор, элементами которого являются координаты y графика линии при значениях x, которые мы указали в наших точках данных, а b — вектор, элементами которого являются координаты y этих точек данных . Разница b−AKx представляет собой вертикальное расстояние графика от точек данных:

(0,6)(1,0)(2,0)−12−1y=−3x+5b−AKx=C600D−AL−35M=C−12−1D

Линия наилучшего соответствия минимизирует сумму квадратов этих вертикальных расстояний.

Интерактив: оптимальная линия

Пример (парабола наилучшего соответствия)

Пример (наилучшая линейная функция)

Все приведенные выше примеры имеют следующий вид: указано некоторое количество точек данных (x,y), и мы хотим найти функцию

y=B1g1(x)+B2g2(x)+···+Bmgm(x)

, наилучшим образом аппроксимирующий эти точки, где g1,g2,…,gm — фиксированные функции от x. Действительно, в примере с наилучшей линией у нас было g1(x)=x и g2(x)=1; в примере с наилучшей параболой у нас было g1(x)=x2,g2(x)=x и g3(x)=1; и в примере наилучшей линейной функции у нас было g1(x1,x2)=x1,g2(x1,x2)=x2 и g3(x1,x2)=1 (в этом примере мы берем x как вектор с две записи). Мы оцениваем приведенное выше уравнение для заданных точек данных, чтобы получить систему линейных уравнений с неизвестными B1, B2,.