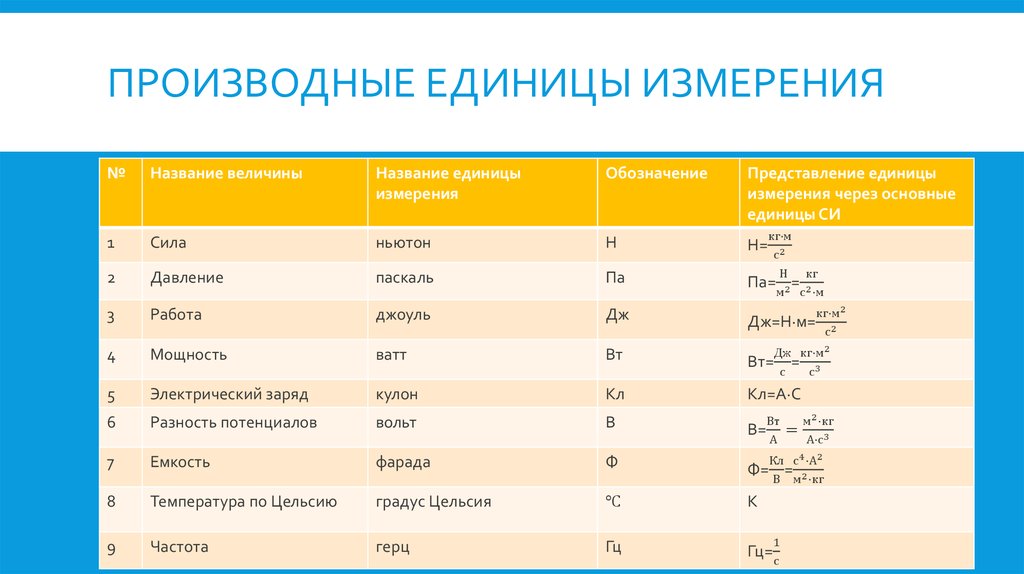
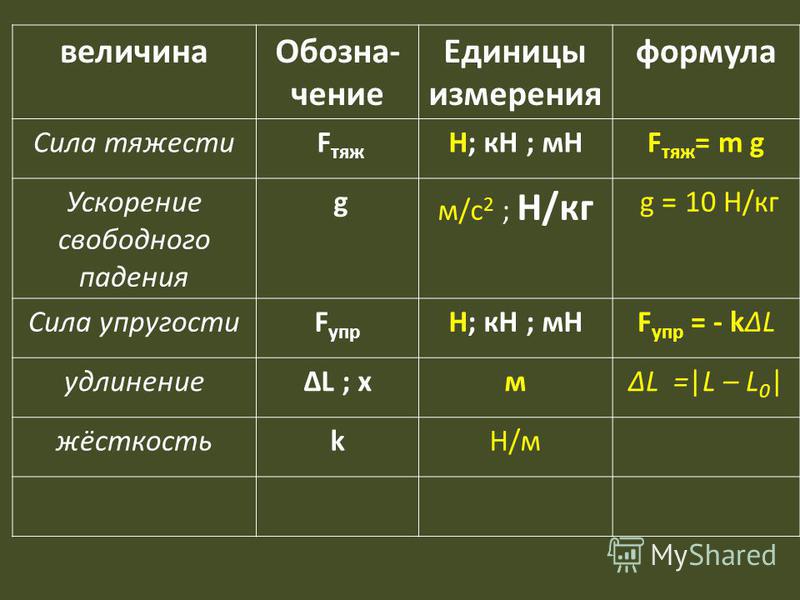
Физические величины и единицы измерения, применяемые в кондиционировании
В этом разделе перечислены основные физические величины, используемые в кондиционировании воздуха, даны их определения и физический смысл. Рассказывается о Международной системе единиц СИ, а также наиболее распространенных внесистемных единицах. Приводятся таблицы для пересчета значений физических величин из одной системы в другие.
Основные физические величины в кондиционировании
Воздух — это основной объект, на который воздействуют системы кондиционирования. Поэтому его состав и параметры очень важны при изучении работы систем кондиционирования. Воздух состоит из сухой части (содержащей азот, кислород и некоторые другие газы) и водяного пара. Система кондиционирования и отопления позволяет достичь требуемых значений параметров воздуха. Три базовых параметра воздуха:
- температура (Т),
- содержание влаги (D)
- атмосферное давление (В).

Кроме того, воздух характеризуется относительной влажность (Ф), энтальпией (Н), давлением сухого воздуха (Pg), плотностью воздуха (Р), содержанием примесей.
Основные понятия и определения
Температура
Температура — термодинамический термин, отражающий степень нагретости тела или вещества. С точки зрения молекулярной теории, температура — это интенсивность теплового движения частиц вещества. Точнее говоря, температура газа или смеси газов пропорциональна квадрату скорости движения молекул.
В основных системах физических единиц температура измеряется в градусах Цельсия, а также градусах Кельвина (абсолютная, или термодинамическая температура).
- Шкала Цельсия (°С)
: при давлении 98 кПа температура замерзания воды равна 0 °С, а температура кипения 100 °С. Интервал температур между ними делится на 100 равных отрезков, каждый из которых равен 1 °С. - Шкала Кельвина (К)
: за нуль шкалы Кельвина (абсолютный нуль) принята температура, при которой прекращается тепловое движение частиц. По этой шкале температура замерзания воды равна 273,15 К при давлении 98 кПа, а температура кипения 373,15 К.
По этой шкале температура замерзания воды равна 273,15 К при давлении 98 кПа, а температура кипения 373,15 К.
Пересчет температуры из шкалы Цельсия в шкалу Кельвина проводится по такой формуле:
T = t + 273,15
где T — температура по шкале Кельвина.
На практике измеряется температура по сухому термометру (DB) и по мокрому термометру (WB). Температура воздуха, измеренная термометром с сухим шариком, называется температурой по сухому термометру и обозначается индексом DB, а температура воздуха, измеренная термометром со смоченным шариком, называется температурой по мокрому термометру и обозначается индексом WB.
Если воздух не насыщен водяным паром (относительная влажность меньше 100%), то сухой и мокрый термометр будут показывать разную температуру. Температура по мокрому термометру будет ниже, чем по сухому, и чем меньше относительная влажность воздуха, тем больше разница температур.
Влажность
- Содержание влаги
— это количество водяного пара в 1 кг сухого воздуха. Обозначается символом d и выражается в г/кг.
Обозначается символом d и выражается в г/кг. - Абсолютная влажность
— это количество водяного пара в 1 кубическом метре воздуха, выражается в кг/куб. м. - Относительная влажность
— это отношение содержания влаги в воздухе к ее максимальному содержанию при данной температуре и давлении. Относительная влажность обозначается символом Ф. Если Ф=0, значит, воздух абсолютно сухой и не содержит водяного пара. Ф=100% соответствует насыщенному влагой воздуху. Комфортная для людей влажность — в диапазоне 50-70%.
Количество теплоты
Энергия, переданная телу или веществу в результате теплообмена с окружающей средой, называется количеством теплоты, и выражается в джоулях (Дж).
Мощность охлаждения или обогрева
— это количественная характеристика способности нагреть или охладить другие тела. Она выражается в ваттах (Вт) или киловаттах (1кВт = 1000 Вт).
Единицы измерений физических величин
В настоящее время основной системой единиц в физике (в том числе и в кондиционировании и холодильной технике) является Международная система единиц измерения (СИ). Семь ее основных единиц:
- Метр (длина)
- Килограмм (масса)
- Секунда (время)
- Ампер (сила тока)
- Кельвин (температура)
- Моль (количество вещества)
- Кандела (сила света).
В кондиционировании используется большое количество производных величин, например удельная теплоемкость. Она равна количеству тепла, которое надо подвести к единице массы тела, чтобы увеличить его температуру на 1К, и измеряется в Дж/(кг * К).
В технической литературе, особенно иностранной, используются и другие (внесистемные) единицы измерения.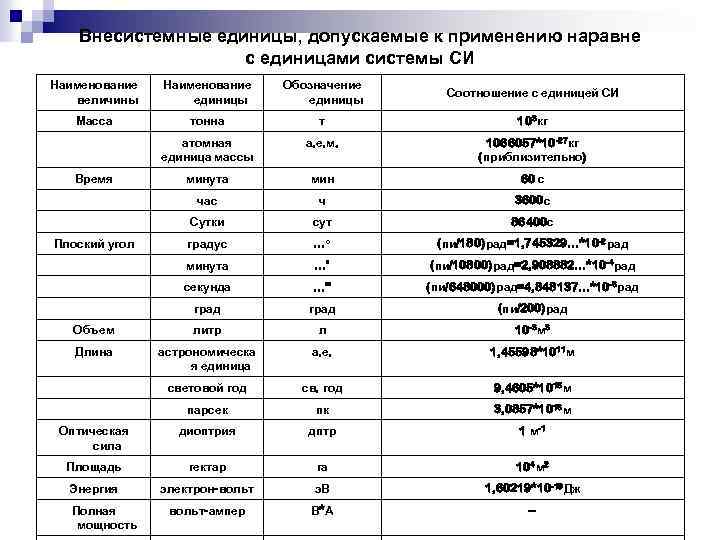 Перевести значение физической величины из одной системы в другую можно при помощи таблиц (см. Основную литературу). Например, давление часто измеряют в мм ртутного столба (мм Hg): 1 мм рт. ст. = 133,3 Н/кв. м. Часто используемые в кондиционировании единицы:
Перевести значение физической величины из одной системы в другую можно при помощи таблиц (см. Основную литературу). Например, давление часто измеряют в мм ртутного столба (мм Hg): 1 мм рт. ст. = 133,3 Н/кв. м. Часто используемые в кондиционировании единицы:
Основная литература
- Польманн. Учебник по холодильной технике. Стр. 15 — 35. (ed_pol.pdf )
- Таблица физических величин. Группа компаний ИНРОСТ. (ed_inrost.pdf )
- Ананьев В.А., Балуева Л.Н., Гальперин А.Д., Городов А.К., Еремин М.Ю., Звягинцева С.М., Мурашко В.П., Седых И.В. Системы вентиляции и кондиционирования. Теория и практика. — 2003. — 416 с. Стр. 412 — 415. (anan_412_415.pdf (110.58Kb)
Дополнительная литература
- «Основные принципы и понятия термодинамики» (physical-units.
 htm (20 Kb)
htm (20 Kb) - А. Беккер. Системы вентиляции. — М., 2005. Стр. 194 — 196. (bekker_194_196.pdf (51.75Kb)
Контрольные вопросы:
- Перечислите базовые параметры воздуха и единицы их измерения (системные в системе СИ и внесистемные).
- Почему температура по мокрому термометру ниже, чем температура по сухому? Как разность температур по мокрому и сухому термометру зависит от влажности воздуха?
- В каких единицах измеряется относительная влажность воздуха? Абсолютная влажность? Содержание влаги?
- В чём измеряется плотность теплового потока?
- Как работу из Ватт-часов перевести в Дж?
- Что такое коэффициент теплообмена?
- В чём измеряется давление (назовите несколько единиц измерения)?
- Пересчитайте 22 кВт в BTU/h
Измерение физических величин. СИ | 7 класс
Содержание
Спектр объектов и явлений, изучаемых в физике, огромен. От невероятной скорости электромагнитной волны до возраста Земли и от крошечных размеров частиц до площади наблюдаемой вселенной. От силы, создаваемой прыгающей блохой, до силы притяжения между Землей и Луной.
От невероятной скорости электромагнитной волны до возраста Земли и от крошечных размеров частиц до площади наблюдаемой вселенной. От силы, создаваемой прыгающей блохой, до силы притяжения между Землей и Луной.
Мы определяем физическую величину либо путем измерения с помощью соответствующих приборов, либо путем расчета на основе других измерений. Например, мы определяем расстояние, полагаясь на то, что оно рассчитывается как скорость, умноженная на время в пути.
Однако все известные физические величины выражаются в единицах, которые являются стандартизованными значениями. Например, длина забега, которая тоже является физической величиной, может быть выражена в метрах (для спринтеров) или в километрах (для бегунов на длинные дистанции). Без стандартизированных единиц ученым было бы чрезвычайно сложно вычислить и сравнить измеренные значения.
Что значит измерить какую-либо величину?
Измерить какую либо величину — это значит сравнить ее с однородной величиной, принятой за единицу.
Система единиц измерения
Во всем мире используются такая система единиц измерения как «единицы СИ» (сокращение от французского Le Système International d’Unités, также известное как метрическая система). Некоторые физические величины и их единицы измерения представлены в таблице 1.
| Основные величины | Символ | Единица СИ |
|---|---|---|
| Масса | $m$ | килограмм ($кг$) |
| Время | $t$ | секунда ($с$) |
| Температура | $T$ | кельвин ($К$) |
| Длина | $l, S$ | метр ($м$) |
| Скорость | $\upsilon$ | метр в секунду ($\frac{м}{c}$) |
 Некоторые величины и их единицы измерения
Некоторые величины и их единицы измеренияКаковы единицы длины, времени, массы в СИ?
В этой системе основной единицей длины является метр (м), единицей времени — секунда (с), единицей массы — килограмм (кг). Но так было не всегда!
Существует также такая система единиц измерения как имперская система или английские единицы измерения. Эта система исторически использовались в странах, когда-то находившихся под управлением Британской империей. Сегодня Соединенные Штаты — единственная страна, в которой до сих пор широко используется имперская система.
Часто, когда мы применяем систему единиц СИ, нам может понадобиться выразить единицы, которые больше принятых единиц в 10, 100, 1000 раз (таблица 2). Здесь все просто — к наименованиям единиц СИ нужно добавить соответствующую приставку на греческом языке:
если эта единица больше СИ в 10 раз — к названию добавляется приставка «дека», в 100 раз — «гекто», в 1000 раз — «кило» и т.д. Такие приставки называю кратными.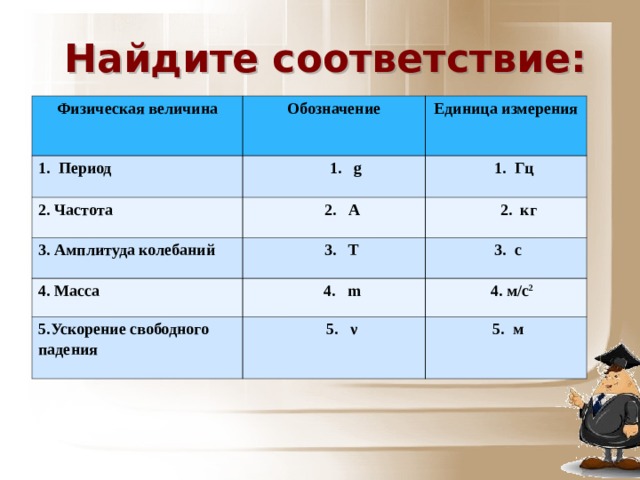 {-3}$)Таблица 2. Приставки к названиям единиц
{-3}$)Таблица 2. Приставки к названиям единиц
Пример:
Пачка макарон весит 300 грамм (г). Выразите ее вес в килограммах (кг).
Для того чтобы решить эту задачу, нам нужно вспомнить, что в одном килограмме — 1000 грамм. Следовательно, нам всего лишь остается разделить 300 грамм на 1000. Получается, что в килограммах, пачка макарон будет весить 0,3 кг.
{"questions":[{"content":"Длина ковра - 2 метра. Выразите его длину в миллиметрах.[[input-1]]","widgets":{"input-1":{"type":"input","answer":"2000"}},"hints":["Вспомним, что в 1 метре 100 сантиметров.","А в 1 сантиметре 10 миллиметров.","$2 \times 100 \times 10 = 2000$"]}]}Единицы измерения в ходе истории
В древние времена человек использовал части своего тела в качестве инструментов измерения, такие как рука, ладонь и ступня. А для измерения времени использовали природные явления, такие как восход, закат и фазы Луны.
Так, в Древней Руси мерой длины мог быть сам человек (рисунок 1). Например, косая сажень — расстояние от носка левой ноги до конца среднего пальца поднятой вверх правой руки. Пядь, или четверть, — расстояние между концами расставленных большого и указательного пальцев руки.
Например, косая сажень — расстояние от носка левой ноги до конца среднего пальца поднятой вверх правой руки. Пядь, или четверть, — расстояние между концами расставленных большого и указательного пальцев руки.
Измерительные инструменты со временем совершенствовались, они были необходимы человеку в точном описании явлений и изучении законов физики.
Используемый измерительный инструмент зависит от измеряемой физической величины. Для измерения длины существуют такие инструменты, как линейка, штангенциркуль и микрометр.
Для получений различных параметров электрического тока — амперметр, вольтметр, омметр. Для вычисления времени, мы прибегнем к использованию таймеров и секундомеров.
Цена деления
Как правило, все измерительные приборы имеют свою шкалу. Для точности подсчета, на панель прибора нанесено несколько делений, подписанных соответствующими значениями, между которыми, в свою очередь, находится еще несколько делений поменьше, обычно эти промежуточные деления числами не обозначены.
В науке об измерениях, такие деления показывают наименьшее и самое точное значение измеряемой величины, и называются они — цена деления. Как нетрудно догадаться, что чем меньше цена деления, тем точнее измерения.
Линейка с ценой деления 1 см youtube.com/embed/rNOobSmYcus?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>Например, на наручных часах могут быть только 12 отметок часов текущего времени суток, то есть цена деления этого прибора — один час.
Секундомер, используемый для измерения времени при проведении спортивных состязаний, может иметь цену деления до сотых долей секунды. Все потому, что секундомер более точен при измерении временных интервалов, чем обычные часы, поэтому у него больше «интервалов» в каждый час прошедшего времени.
Цена деления — одна из самых важных характеристик для получения точных показаний такого инструмента, как штангенциркуль, используемого в различных экспериментах.
Линейка с ценой деления 2 мм{"questions":[{"content":"Чем меньше цена деления, тем [[input-1]] измерения","widgets":{"input-1":{"type":"input","inline":1,"answer":"точнее"}},"hints":[]}]}Как определяется цена деления измерительного прибора?
Для определения цены деления любого измерительного прибора необходимо:
- Определить два ближайших штриха на шкале, возле которых стоят значения величины;
- Вычесть из большего значения меньшее;
- Полученное число разделить на число делений, находящихся между ними.

Давайте для наглядности найдем цену деления термометра, изображенного на рисунке 2.
Рисунок 2. ТермометрВозьмем два соседних штриха, около которых стоят цифры (значения температуры). Пусть это будут штрихи с обозначениями $10 \degree C$ и $20 \degree C$. Между этими штрихами 10 делений.
Определим цену деления:
$\frac{20 \degree C — 10 \degree C}{10} = 1 \degree C$.
Получается, что термометр показывает $26 \degree C$.
Упражнения
Упражнение №1
Определите цену деления секундомера (рисунок 3).
Показать решение и ответ
Скрыть
Решение:
Возьмем два соседних штриха, которые отмечены цифрами: 5 с и 10 с. Между ними находится 10 делений. Найдем цену деления этого секундомера:
$\frac{10 \space с — 5 \space с}{10} = 0.5 \space с$.
Ответ: цена деления секундомера равна $0.5 \space с$.
Упражнение №2
По рисунку 4 определите цену деления амперметра (рисунок 4, а) и вольтметра (рисунок 4, б).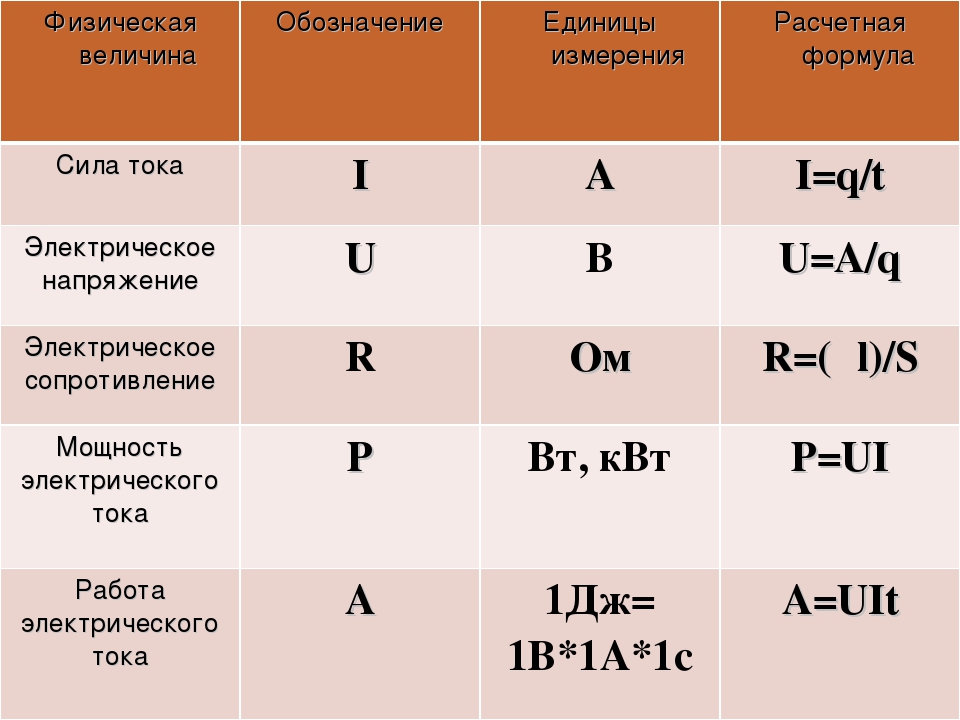
Показать решение и ответ
Скрыть
Решение:
Для амперметра (рисунок 4, а):
возьмем соседние значения 0 А и 0.5 А. Между ними находится 10 делений.
Найдем цену деления прибора:
$\frac{0.5 \space А -0 \space А}{10} = 0.05 \space А$.
Для вольтметра (рисунок 4, б):
возьмем соседние значения 0 В и 1 В. Между ними находится 5 делений.
Найдем цену деления прибора:
$\frac{1 \space В — 0 \space В}{5} = 0.2 \space В$.
Ответ: цена деления амперметра равна $0.5 \space А$, а вольтметра — $0.2 \space В$.
Задания
Задание №1
Используя интернет, найдите прибор для измерения артериального давления — тонометр механический. Определите цену деления шкалы. В каких единицах измеряют артериальное давление?
Механический тонометр изображен на рисунке 5.
Рисунок 5. Механический тонометрПоказать решение и ответ
Скрыть
Решение:
Артериальное давление измеряют в мм рт. Также были распространены и другие меры объема. В таблице 4 представлены меры объема, которые использовали для сыпучих тел (например, крупы). Для жидкостей использовали другие меры объема. Они представлены в таблице 5. Выразите свой вес в пудах, а рост в аршинах. Возьмем для примера следующие параметры: рост равен $145 \space см$, а вес — $42 \space кг$. 1 пуд приблизительно равен $16.3807 \space кг$, а 1 аршин — $71.12 \space см$. Переведем в эти единицы рост и вес. Рост: Вес: Запишите 2-3 пословицы, поговорки или образных выражения, в которых упоминаются старинные меры длины, массы, объема и т.п. Примеры: Единица измерения — это величина, используемая в качестве стандарта для выражения физической величины. Длина — описывает длину чего-либо. Расстояние, высота, толщина, и глубина также используют одни и те же единицы измерения. Ниже приведены некоторые общие единицы измерения: • Миллиметр (мм) – метрическая единица, обычно используемая для выражения длины очень маленьких предметов, таких как ключи, и толщины
мелкие предметы, такие как блокнот. • сантиметр (см) – метрическая единица, обычно используемая для выражения длины мелких предметов. Он также используется для измерения
рост человека. • inch (in) – английская единица измерения, обычно используемая для выражения длины небольших предметов, таких как коробки и бутылки. • фут (ft) – английская единица, эквивалентная 12 дюймам. Он обычно используется для выражения коротких расстояний и высоты всех
объекты, такие как деревья и здания. Линейка — это обычный инструмент, используемый для измерения длины небольших предметов. Обычно он имеет четыре единицы измерения на выбор: миллиметр,
сантиметр, дюйм и фут.  3$Таблица 3. Меры объема в Древней Руси
3$Таблица 3. Меры объема в Древней Руси
Таблица 4. Меры объема сыпучих тел в Древней РусиМера объема Литры Цебр 5457,5872 — 6297,216 Кадка 839,69 Четверть 209,9072 Осьмина 104,95 Четверик 26,2387 Гарнец 3,2798 Стакан 0,273
Таблица 5.Мера объема Литры Шкалик 0,0615 Чарка 0,123 Водочная бутылка 0,614962 Винная бутылка 0,7687 Штоф 1,2299 Четверть 3,0748 Ведро 491,976 Бочка 491,976  Меры жидких тел в Древней Руси
Меры жидких тел в Древней РусиЗадание №3
$\frac{145 \space см}{71.12} \approx 2 \space аршина$.
$\frac{42 \space кг}{16.3807 \space кг} \approx 2.6 \space пуда$.Задание №4
Единицы измерения
 Ниже приведены основные количества
измеряемые и используемые единицы измерения:
Ниже приведены основные количества
измеряемые и используемые единицы измерения:
Измерительная линейка — это инструмент для измерения коротких расстояний.
Для коротких расстояний обычно используются метрические единицы метр (м) и английская единица ярдов (ярд) .
Для больших расстояний обычно используются метрическая единица километра (км) и английская единица мили (миля) .
Масса — описывает, насколько что-то тяжелое.
Ниже приведены некоторые общие единицы измерения:
• миллиграмм (мг) — метрическая единица, обычно используемая для выражения массы очень маленьких предметов, таких как конфеты.
• грамм (г) – метрическая единица, являющаяся базовой единицей массы. Он обычно используется для выражения массы небольших предметов, таких как апельсин, яйцо и помидор.
• унция (oz) – английская единица измерения, обычно используемая для выражения массы o
• килограмм (кг) – английская единица измерения, обычно используемая для измерения коротких расстояний и высоты высоких объектов, таких как деревья и здания.
• фунт (lb) – английская единица измерения, обычно используемая для измерения коротких расстояний и высоты высоких объектов, таких как деревья и здания.
• тонна – английская единица измерения, обычно используемая для измерения коротких расстояний и высоты высоких объектов, таких как деревья и здания.
Весы — это инструмент, обычно используемый для измерения массы фруктов, овощей и мяса. Весы откалиброваны в граммах и килограммах
Время – описывает, сколько времени требуется, чтобы что-то сделать.
В метрической и английской системах измерения времени используются одни и те же единицы измерения.
Вот некоторые из общих единиц измерения:
• секунда (с) – основная единица измерения времени. Одна секунда эквивалентна тиканию секундной стрелки часов.
• минута (мин) – единица, эквивалентная одному обороту секундной стрелки часов или одному тиканию длинной (минутной) стрелки часов.
• час (hr) – единица, эквивалентная одному обороту длинной (минутной) стрелки часов или одному тиканию короткой (часовой) стрелки часов.
Часы — это обычный инструмент для индикации времени. Он показывает время в часах, минутах, а иногда и в секундах.
Он показывает время в часах, минутах, а иногда и в секундах.
• день (д) – единица, эквивалентная двум оборотам короткой (часовой) стрелки часов.
• неделя (нед) – это единица, эквивалентная 7 дням.
• месяц (mo) – единица измерения, равная 30 дням. Он обычно используется для определения возраста младенца или детеныша животного.
• год (год) – единица измерения, равная 12 месяцам. Он обычно используется для определения возраста человека или объекта.
Площадь – описывает, сколько поверхности занято чем-либо.
При измерении площади используются те же единицы измерения длины. Единственная разница в том, что единицы измерения «квадратные», поскольку площадь является произведением двух измерений.
(обычно длина и ширина, которые используют одну и ту же единицу измерения).
92` или кв. м) – метрическая единица, эквивалентная квадрату со стороной 1 м каждая. Обычно используется в
Измерение площади жилого дома.
м) – метрическая единица, эквивалентная квадрату со стороной 1 м каждая. Обычно используется в
Измерение площади жилого дома.
• акр – английская единица измерения земельной площади, например ферм и парков развлечений.
• гектар (га) – метрическая единица, эквивалентная квадрату со стороной 100 м каждая. Как и акр, он в основном используется для измерения земель.
Размер футбольного поля обычно составляет около 1 га.
Том — описывает, сколько пространства (или жидкости) занято (или содержится) чем-то. Подобно площади, объем также использует единицы длины, но с той лишь разницей, что единица «кубическая». Кубические единицы обычно используются для объемов пространства, хотя существуют также единицы объема. предназначен для измерения жидкости.
Ниже приведены некоторые общие единицы измерения: 93` или cc) — метрическая единица объема (как пространства, так и жидкости), соответствующая кубу со сторонами
по 1 см. Кубический сантиметр равен миллилитру.
Кубический сантиметр равен миллилитру.
• Жидкая унция (fl oz) – английская единица измерения, обычно используемая для измерения количества жидкостей в бутылках, таких как безалкогольные напитки.
• чашка – английская единица, эквивалентная 8 жидким унциям. Он обычно используется для измерения ингредиентов для приготовления пищи и выпечки.
Мерный стакан — это кухонная утварь, используемая для измерения объема жидкости или таких ингредиентов, как мука и сахар.
• пинта (pt) – английская единица, эквивалентная 2 чашкам. Он обычно используется в различных товарах.
• кварта (qt) – английская единица, эквивалентная четверти галлона.
• литр (л) – основная единица объема. Он обычно используется для измерения большого количества жидкости, такой как бензин.
• галлон (gal) – английская единица измерения литр.
Емкость бензина обычно составляет 1 галлон.
Температура — описывает, насколько что-то горячее или холодное.
Ниже приведены распространенные единицы измерения:
• Шкала Цельсия (°C) – это метрическая единица измерения температуры и наиболее часто используемая единица измерения температуры во всем мире. В этой шкале точка кипения воды находится на уровне 100°С, а точка замерзания – на уровне 0°С.
• Шкала Фаренгейта (°F) – английская единица измерения температуры, которая обычно используется в США. В этой шкале точка кипения воды составляет 212 ° F, а точка замерзания — 32 ° F.
• Шкала Кельвина (К) – это единица СИ для температуры. В отличие от двух других температурных шкал шкала Кельвина не использует градусы. Его нулевая точка, 0 К, определяется как самая низкая возможная температура.
который также называют абсолютным нулем.
Термометр является наиболее распространенным прибором для измерения температуры. Обычно он откалиброван как по шкале Цельсия, так и по шкале Фаренгейта.
Объяснение урока: Единицы измеряемых величин
В этом пояснении мы узнаем, как распознавать, какие единицы используются для определения значений физических величин.
Полезно начать с разъяснения того, что понимается под измерением.
Измерение состоит из четырех частей:
- Измеряемый объект.
- Количество объекта.
- Значение количества.
- Единица измерения значения.
Давайте рассмотрим пример.
Измеряется масса кирпича. Масса кирпича 1,5 килограмма.
Рассмотрим четыре части измерения.
| Измеряемый объект | The brick |
|---|---|
| Quantity of the object | Its mass |
| Value of the quantity | 1.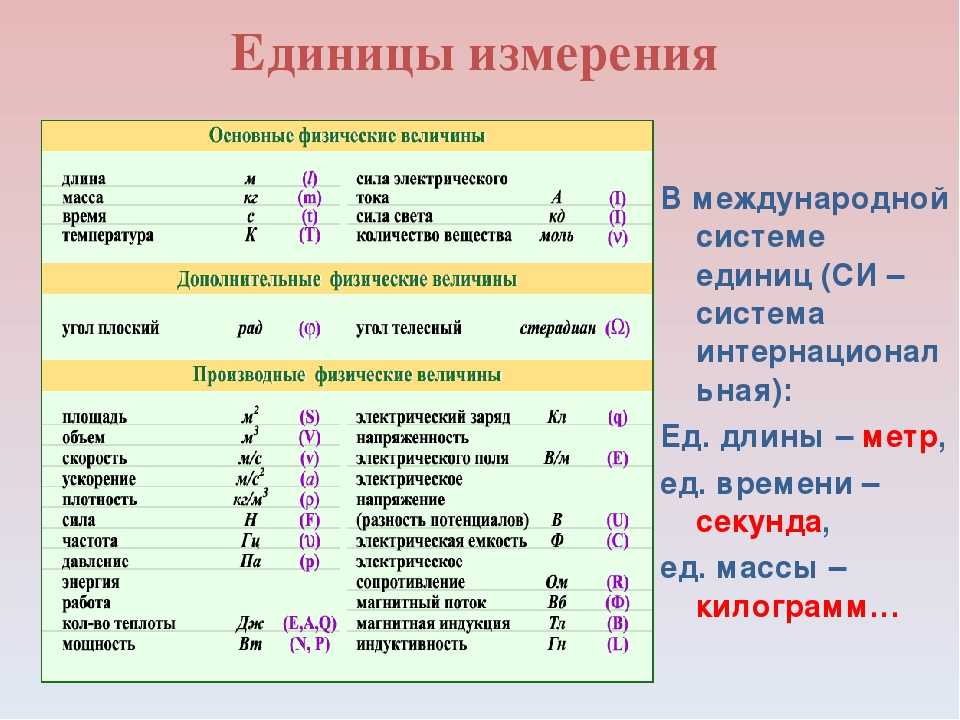 5 5 |
| Unit that the value takes | Kilograms |
The meaning of quantity is легко спутать со значением значение , так как слово «количество» часто используется для обозначения количества чего-либо.
Однако, говоря об измерениях, количество не является количеством чего-то; это то, чего может быть сколько угодно.
Давайте посмотрим на другой пример.
Измеряется время, необходимое для таяния кубика льда массой 5 грамм. Затраченное время 250 секунд.
Рассмотрим четыре части измерения.
| Object being measured | The ice cube |
|---|---|
| Quantity of the object | The time it takes to melt |
| Value of the quantity | 250 |
| Unit that the value takes | Секунды |
Значение и единица измерения имеют другие свойства, чем объект и величина измерения. Объект и количество
измерение определяется только одним способом, но значение и единица измерения могут быть определены несколькими способами.
Объект и количество
измерение определяется только одним способом, но значение и единица измерения могут быть определены несколькими способами.
Если мы измеряем что-то в кирпиче, мы измеряем этот конкретный кирпич. Измерение другого объекта ничего не говорит нам напрямую о кирпиче. Если мы измерим температуру кирпича, это ничего не скажет нам напрямую о массе кирпича. Если мы попытаемся определить массу кирпича по говоря о другом объекте или количестве, мы имеем в виду другое измерение, чем измерение массы кирпича; есть единственный уникальный способ установления объекта и количества для данного измерения.
«Масса кирпича 1,5 кг» — не единственный способ указать массу кирпича. Это связано с тем, что «1,5 килограмма» также можно выразить по-разному, например,
- 1 500 грамм,
- 0,0015 тонны,
- 3,30693 фунта.
Мы видим, что при изменении единицы измерения изменяется и значение измерения. Это можно понять, если подумать о значении и единице
измерение как перемножение.
Мы можем выразить 1,5 килограмма как 1,5×, кг где мы используем символ кг для килограммов.
Мы знаем, что 1×=1000×,кгг где мы используем символ g для граммов.
Итак, мы видим, что 1,5×=1,5×(1000×)1,5×=1500×.kggkgg
Мы только что показали, что единицу можно умножить на значение, чтобы получить другую единицу. Мы также можем разделить единицу на значение, чтобы получить другую единицу, как показано в следующем примере: 1×=11000×1500×=1500×11000×1500×=15001000×1500×=1,5×.gkggkggkggkg
Те же умножения и деления могут быть выполнены с единицами других величин, как только что было показано для единиц массы: 1×=1000×1×=11000×.kmmmkm
Помимо умножения или деления на значение, единицу можно умножать или делить на другую единицу.
Простейшим случаем умножения единицы на единицу является умножение единицы на саму себя.
Рассмотрим прямоугольный объект со сторонами длиной 7,5 м и 1,5 метра, как показано на следующем рисунке.
Площадь объекта 𝐴 равна произведению длин его сторон. Мы можем выразить это как
𝐴=1,5×7,5=11,25.
Мы можем выразить это как
𝐴=1,5×7,5=11,25.
Площадь должна иметь единицу измерения, так как площадь — это количество.
Из уравнения неясно, какой должна быть единица, и эта неясность связана с тем, что единицы перемноженных значений не были включены в уравнение.
Если единицы значений включены в значения, вместо этого мы получаем 𝐴=(1,5×)×(7,5×).мм
Порядок умножения членов уравнения не меняет результат уравнения, поэтому мы можем выразить это уравнение как 𝐴=1,5×7,5××, мм
Мы видели, что 1,5×7,5=11,25, но мы не определили результат мм×.
Если бы вместо m значение было умножено само на себя, например, значение 4, мы бы получили 4×4=16.
Нет эквивалентного результата умножения m на m, но 4×4=16 также может быть выражено как 4×4=4.
Это означает, что мы можем выразить m, умноженное само на себя, как ммм×=.
Эта единица измерения представляет собой квадратный метр или квадратный метр.
Итак, мы видим, что
𝐴=(1,5×)×(7,5×)=11,25. ммм
ммм
Единицы можно умножать или делить на другие единицы, а также сами по себе.
Давайте рассмотрим пример с единицами, которые умножаются или делятся сами на себя или на другие единицы.
Пример 1. Определение единицы площади
Что из следующего является единицей площади?
- Квадратный метр
- Сантиметр
- Метр на секунду в квадрате
- Кубический метр
Ответ
Умножение одной длины на другую длину есть уравнение площади прямоугольника. Уравнения площадей других форм задаются другими умножения, но уравнения по-прежнему включают умножение длин. Длина может быть измерена в метров.
Все варианты содержат слово «метр», так что сразу не очевидно, что любой из вариантов неверен.
Сантиметр — единица длины. Площадь включает в себя умножение длин на другие длины. Умножение длин, измеренных в сантиметрах, потребует умножения
сантиметры на сантиметры. Результат умножения сантиметров на сантиметры
не сантиметры, поэтому сантиметры не могут быть единицей
область. На самом деле никакая единица длины не может быть единицей площади.
На самом деле никакая единица длины не может быть единицей площади.
Из оставшихся вариантов два включают слово «квадрат» или «квадратный», а один включает слово «кубический».
Возведение в квадрат значения или единицы означает умножение ее самой на себя. Это согласуется с умножением длины на длину. Кубирование длины означает умножение квадрата длины длина на длину, в результате чего получается объем, а не площадь. Таким образом, мы можем устранить кубический метр как единица площади.
Осталось выбрать между вариантами «квадратный метр» и «метр на секунду в квадрате».
Слово «на» указывает на деление, поэтому «метр на секунду в квадрате» означает «метр, разделенный на секунда в квадрате». А метр — это единица длины. Мы должны решить, можно ли разделить длину на второй в квадрате эквивалентен умножению длины на длину.
Секунда — это единица времени, а не длины.
секунда в квадрате — это единица времени, умноженная на время, которое не связано с длиной.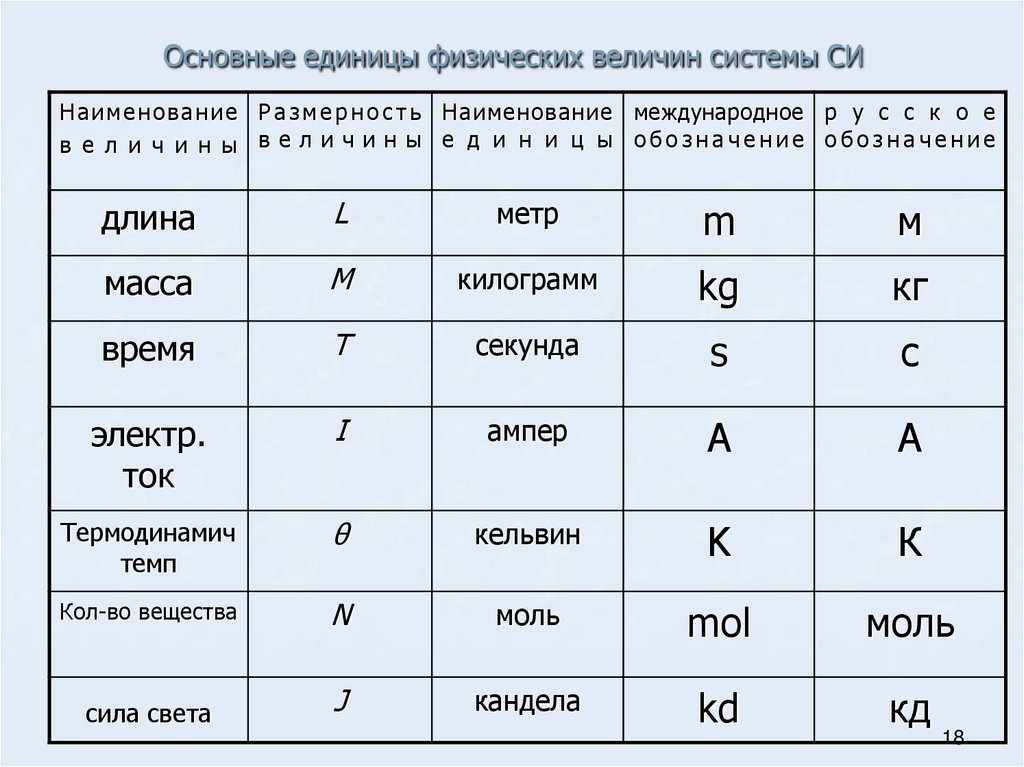 Таким образом, мы можем исключить метр на секунду в квадрате.
Таким образом, мы можем исключить метр на секунду в квадрате.
Мы видели, что возведение значения или единицы в квадрат означает умножение их самих на себя. Квадратный метр это, следовательно, метр, умноженный на метр. А метр является единицей длины, поэтому метр умножить на метр это единица площади.
Давайте теперь посмотрим на другой такой пример.
Пример 2: Идентификация символа для составной единицы
Какой из следующих символов является подходящим символом для единицы количества, полученного путем деления температуры на расстояние?
- К/м
- км
- К⋅м
- К/м 2
- мК
Ответить
на расстоянии. Стоит задуматься, что такое количество мог представлять.
Одним из примеров деления температуры на расстояние может быть нагрев одного конца длинного металлического стержня и в какой-то момент температура была записана в разных точках.
по длине стержня. Измерения будут производиться по температуре и по расстоянию. Эти измерения можно представить в виде графика, как показано на следующем рисунке.
Измерения будут производиться по температуре и по расстоянию. Эти измерения можно представить в виде графика, как показано на следующем рисунке.
Градиент этого графика будет равен изменению температуры на изменение расстояния, т.е. температура, деленная на расстояние.
Рассматривая варианты, мы видим, что все они включают символы m и К или к. Это связано с тем, что существуют величины температуры и расстояния, которые имеют следующие единицы измерения с этими символами:
- Расстояние — это величина, которая может быть измерена в метрах, которая имеет символ м.
- Температура – это величина, которая может быть измерена в градусах Кельвина, которая имеет символ K.
Параметр «км» имеет только символы нижнего регистра, но правильный символ для
кельвин это «К»,
который в верхнем регистре. Символ «км» на самом деле является символом единицы измерения.
километр, что равно 1 метрам. Тогда это единица расстояния, а не единица измерения температуры, деленная на расстояние, так что это неверно.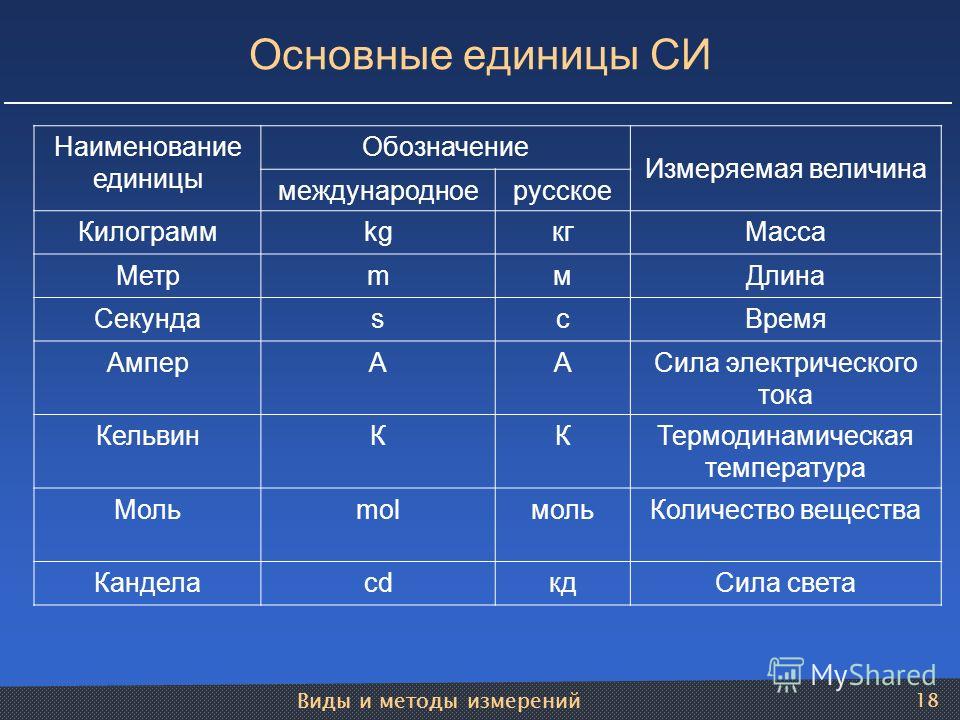
Параметр «mK» включает символ кельвина, но на самом деле является символом единица милликельвин, т. 11000 кельвинов. Тогда это единица температуры, не единица измерения температуры, деленная на расстояние, так что это неверно.
Символ «К⋅м» соответствует количеству температуры, умноженному на единицу. Мы знаем, что нам нужен символ для единицы измерения температуры, разделенной на расстояние. Вероятно, в единице измерения будет символ деления, как в случае с «К/м» и с «К/м 2 ». Тогда мы видим, что «K⋅m» неверно.
Мы знаем, что «m 2 » является символом квадратного метра или квадратный метр, что является единицей площади. Вариант «К/м 2 » соответствует температура, разделенная на площадь, так что это неправильно.
Мы знаем, что «м» — это символ метр, который является единицей расстояния. Опция «К/м» соответствует температуре, деленной на расстояние, так что это правильно.
Давайте теперь рассмотрим пример с единицами величин, нанесенными на график.
Пример 3. Идентификация единиц, соответствующих величинам, определенным с помощью графика
На графике показан график изменения расстояния во времени.
Какова единица градиента линии?
Какова единица площади под линией?
Ответ
Две величины нанесены друг против друга на графике.
Величина, отложенная по вертикальной оси, представляет собой расстояние и имеет единицу измерения метр с символом м.
Величина, отложенная по горизонтальной оси, представляет собой время и имеет единицу измерения секунда, с символом с.
Градиент графика представляет собой изменение величины, отложенной по вертикальной оси, деленное на изменение величины, отложенной по горизонтальной оси.
Градиент графика соответствует величине, которая является результатом деления изменения расстояния на изменение времени. Эта величина называется
«скорость.» Единицей количества является метр
разделить на единицу секунды, или
метров в секунду.
Записывается в виде символов, эта единица равна m, деленному на s, РС.
Площадь под линией графика представляет собой изменение величины, отложенной по вертикальной оси, умноженное на изменение величины, отложенной по горизонтальной оси.
Площадь под линией графика соответствует величине, являющейся результатом умножения изменения расстояния на изменение времени. У этой величины нет имени. Единицей количества является единица измерения, умноженная на единицу измерения. секунды или метр-секунды.
Записанная в символьной форме, эта единица равна m, умноженному на s, м⋅с.
Единицы, полученные в результате умножения единиц сами по себе, равны квадрату единицы. Например, единицей площади является квадрат расстояния.
Единица площади, умноженная на длину, равна единице длины в кубе. Мы можем выразить это как мммммм×=××=.
Эта единица называется метр-куб или
кубический метр. Величина, единицей измерения которой является эта величина, называется объемом.
Расстояние, площадь и объем связаны, как показано на следующем рисунке.
Теперь рассмотрим пример с единицами измерения расстояния, площади и объема.
Пример 4: Идентификация подходящей единицы площади, деленной на объем
Какой из следующих символов является подходящим символом для единицы количества, полученного путем деления площади на объем?
- m −1
- m −2
- m
- m 2
- m 3
Answer
The unit for area is square metre, which has the symbol м 2 . Это можно выразить как ммм=×.
Единицей объема является кубический метр, который имеет символ м 3 . Это можно выразить как мммм=××.
Вопрос спрашивает, какой символ единицы получается из следующего вычисления: мм.
Этот расчет эквивалентен следующему: ммммм×××.
Исключая множители m, которые появляются как в числителе, так и в знаменателе выражения, мы находим, что
мммммм×××=1.
Это может быть выражено как м.
На словах эта единица будет называться «на метр».
Единица может быть определена для количества, даже если такое количество не соответствует чему-либо, что может быть непосредственно измерено. Выражение такой единицы не является неправильным; просто у него может не быть очевидных применений.
Теперь рассмотрим пример с умножением значений одной и той же величины, выраженных в разных единицах.
Пример 5. Идентификация подходящей составной единицы для двух измерений одного и того же количества с разными префиксами единиц
Какой из следующих символов является подходящим символом для единицы количества, полученного путем умножения длины в миллиметров на длину в сантиметрах?
- cm 2
- m 3
- mm 3
- cm −1
- m
Answer
Millimeters and centimetres are both units of the same quantity, distance.
Мы знаем, что 1×=10×сммм и 1×=110×.ммсм
Это означает, что при преобразовании между значением в сантиметрах и эквивалентным значением в миллиметров значение изменяется в 10,9 раза.0005
Однако для этого вопроса значения не указаны. Вопрос только в том, какую единицу измерения целесообразно использовать.
Подходящей единицей будет та, которая является результатом умножения расстояния на расстояние.
Базовой единицей расстояния в системе СИ является метр (м). Умножение метра на самого себя дает нам mmm×=.
Такая единица измерения должна быть кратна квадратным метрам (m 2 ). Единственный вариант, который соответствует этому, — cm 2 , так что это должен быть ответ.
Интересно рассмотреть, как коэффициенты пересчета влияют на значения одной и той же величины, выраженные в разных единицах. Например, если длина равна некоторому число миллиметров умножается на длину, равную тому же числу сантиметры, какую единицу следует использовать для результата?
Вопрос можно понять одним из двух способов:
- Какова соответствующая единица количества, полученного путем умножения длины на 𝐿 миллиметров на длину в миллиметрах 10𝐿?
- Какова подходящая единица количества, полученного путем умножения длины на 𝐿 сантиметров на длину в сантиметрах, которая имеет значение 𝐿10?
Таким образом, у нас есть выбор: дать ответ, где находится единица измерения. 1××10×=×10мммммм
или
1××110×=×110.cmcmcm
1××10×=×10мммммм
или
1××110×=×110.cmcmcm
Множители 110 и 10 в этих ответах на самом деле не являются частью полученной единицы; это то, на что должно быть умножено значение, выраженное в этой единице.
Это легче увидеть, если учесть, сколько см 2 равны 1 м 2 .
Мы знаем, что 1×=100×.мкм
Если возвести в квадрат обе части этого уравнения, мы увидим, что (1×)=(100×).mcm
Это эквивалентно 1××1×=100××100×.ммсмсм
Это эквивалентно 1×1×=100×100×1×=10000×.мкммсм
Коэффициент 10 000 не является частью единицы квадратного метра или единицы квадратного сантиметра; это фактор, на который значение должно быть либо умножено, либо делится на при переводе между единицами квадратных метров и единицами квадратных сантиметров.
Итак, мы видим, что результат умножения длины в миллиметрах на длину в
сантиметры могут быть выражены в мм 2 или
см 2 , а значение результата нужно умножить на коэффициент перевода между этими единицами.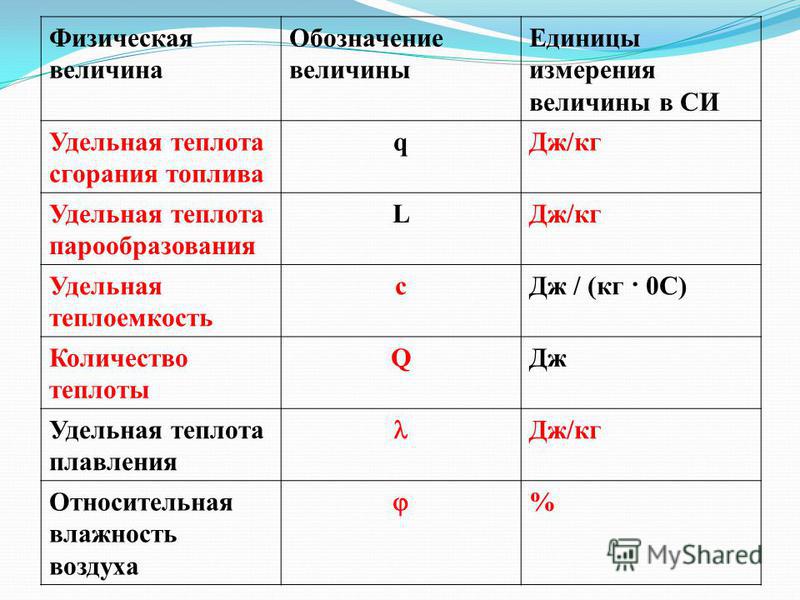



 По этой шкале температура замерзания воды равна 273,15 К при давлении 98 кПа, а температура кипения 373,15 К.
По этой шкале температура замерзания воды равна 273,15 К при давлении 98 кПа, а температура кипения 373,15 К. Обозначается символом d и выражается в г/кг.
Обозначается символом d и выражается в г/кг. htm (20 Kb)
htm (20 Kb)