Коэффициент трения скольжения Википедия
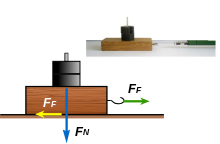Изображения сил, действующих на скользящее тело. 
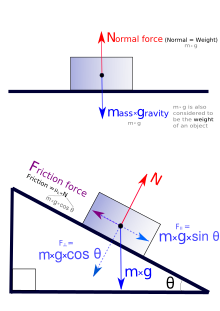Изображения сил, действующих на тело, находящееся на ровной и наклонной плоскости.Сила трения скольжения — сила, возникающая между соприкасающимися телами при их относительном движении.
Опытным путём установлено, что сила трения зависит от силы давления тел друг на друга (силы реакции опоры), от материалов трущихся поверхностей, от скорости относительного движения, но не зависит от площади соприкосновения[1].
Величина, характеризующая трущиеся поверхности, называется коэффициентом трения, и обозначается латинской буквой k {\displaystyle k} или греческой буквой μ {\displaystyle \mu } . Она зависит от природы и качества обработки трущихся поверхностей. Кроме того, коэффициент трения зависит от скорости. Впрочем, чаще всего эта зависимость выражена слабо, и если большая точность измерений не требуется, то μ {\displaystyle \mu } можно считать постоянным. В первом приближении величина силы трения скольжения может быть рассчитана по формуле
F = μ N {\displaystyle F=\mu N}
μ {\displaystyle \mu } — коэффициент трения скольжения,
N {\displaystyle N} — сила нормальной реакции опоры.
Силами трения называются тангенциальные взаимодействия между соприкасающимися телами, возникающие при их относительном перемещении.
Опыты с движением различных соприкасающихся тел (твёрдых по твёрдым, твёрдых в жидкости или газе, жидких в газе и т. п.) с различным состоянием поверхностей соприкосновения показывают, что силы трения проявляются при относительном перемещении соприкасающихся тел и направлены против вектора относительной скорости
Независимость от площади[ | ]
Так как никакое тело не является абсолютно ровным, сила трения не зависит от площади соприкосновения, и истинная площадь соприкосновения гораздо меньше наблюдаемой. На самом деле, площадь соприкосновения, казалось бы, ровных поверхностей может находиться в пределах 0
,
01
%
−
0
,
001
% {\displaystyle 0,01\%-0,001\%} от всей мнимой площади соприкосновения.
Обычно это демонстрируется примером:
Два цилиндра из мягких металлов соединяют пл
Коэффициент трения скольжения – формула, минимальное значение
Физическая величина, характеризующая трущиеся поверхности, называется коэффициентом трения скольжения. Величина обозначается буквой μ. Коэффициент трения определяют опытным путём.
Сила трения скольжения
На покоящиеся и движущиеся тела всегда действуют силы трения. Они возникают при соприкосновении твердых тел, твердых тел и жидкостей или газов и подчиняются законам Ньютона. Направление сил трения противоположно движению тела и силам, стремящимся изменить его положение.
В случае, когда тело движется относительно другого, говоря о трении скольжения. Она зависит от:
- Силы нормальной реакции опоры $vec N$,
- От скорости движения (но в вычислениях этой зависимостью пренебрегают),
- От безразмерного коэффициента трения скольжения $mu$, который характеризует свойства и состояние поверхностей соприкосновения.
Рис. 1. Сила трения скольжения.
Коэффициент зависит от свойств материала. Чем больше шероховатость поверхности, тем больше значение коэффициента и, соответственно, больше сила трения. Коэффициент трения смазанных поверхностей будет меньше, чем у несмазанных для одной и той же пары материалов. Также коэффициент трения зависит от скорости. Однако эта зависимость минимальна и ей пренебрегают, если не требуется точность измерения. Поэтому коэффициент трения считается постоянным.
Рис. 2. Поверхность трения.
Расчет коэффициента трения скольжения
С достаточно большой точностью силу трения скольжения рассчитывают как предельную силу трения покоя по формуле:
$F_{тр} = mu cdot N$.
Тогда формула коэффициента трения скольжения:
$mu ={{F_{тр}} over {N}}$
Значение N рассчитывается как произведение массы тела на ускорение свободного падения и на косинус угла к поверхности приложения:
$N = m cdot g cdot cos alpha$
Рис. 3. Сила нормальной реакции опоры для тел, скатывающихся по наклонной поверхности.
Для большинства пар материалов коэффициент рассчитан опытным путём. Значения находятся в пределах 0,1…0,5. Некоторые значения представлены в таблице.
Трущиеся материалы | Коэффициенты трения | |
Покоя | При движении | |
Алюминий по алюминию | 0,94 | |
Бронза по бронзе | 0,20 | |
Бронза по чугуну | 0,21 | |
Дерево по дереву | 0,65 | 0,33 |
Дерево по камню | 0,46-0,60 | |
Дуб по дубу (вдоль волокон) | 0,62 | 0,48 |
Дуб по дубу (перпендикулярно волокнам) | 0,54 | 0,34 |
Железо по бронзе | 0,19 | 0,18 |
Железо по железу | 0,15 | 0,14 |
Железо по чугуну | 0,19 | 0,18 |
Каучук по дереву | 0,80 | 0,55 |
Каучук по металлу | 0,80 | 0,55 |
Кирпич по кирпичу (гладко отшлифованные) | 0,5-0,7 | |
Лёд по льду | 0,028 | |
Медь по чугуну | 0,27 | |
Металл по дереву | 0,60 | 0,40 |
Металл по камню | 0,42-0,50 | |
Металл по металлу | 0,18-0,20 | |
Олово по свинцу | 2,25 | |
Полозья деревянные по льду | 0,035 | |
Обитые железом полозья по льду | 0,02 | |
Резина (шина) по твёрдому грунту | 0,40-0,60 | |
Резина (шина) по чугуну | 0,83 | 0,8 |
Сталь (коньки) по льду | 0,02-0,03 | 0,015 |
Сталь по железу | 0,19 | |
Сталь по стали | 0,15-0,25 | 0,09 при 3 м/с, 0,03 при 27 м/с |
Чугун по дубу | 0,65 | 0,30-0,50 |
Чугун по стали | 0,33 | 0,13 |
Чугун по чугуну | 0,15 | |
Коэффициент трения – переменная величина. Поэтому значение коэффициента трения скольжения, приведённые в таблице, являются истинными только при соблюдении определённых условий, в которых были получены.
Что мы узнали?
Коэффициент трения скольжения – физическая величина, характеризующая трущиеся поверхности. Как найти: $mu = {{F_{тр}} over {N}}$. На практике коэффициент рассчитывается исходя из свойств материала эмпирическим путём.
ПредыдущаяФизикаИнерциальная система отсчета и движение тел в неинерциальные системе
СледующаяФизикаОтносительность движения – в чем проявляется (9 класс)?
«Как рассчитать коэффициент трения?» – Яндекс.Кью
Число е появилось относительно поздно, в довольно сложных уже моделях, изучали его продвинутыми методами анализа — оно родилось в математике, а не в физике. А математика к тому времени уже оторвалась от физики. При этом могло, в принципе, случиться так, что знаменитым стало бы не число е, а скажем, корень из е. Но для многих математических моделей удобнее использовать именно е. Скорее всего, этим объясняется, что именно оно закрепилось в традиции. Исторически сложилось, что число е имеет математический смысл, а не физический.
Выбор постоянных подвержен все-таки некоторому произволу. То, что мы пользуемся числом ПИ — тоже результат традиции. Математика могла сложиться так, что специальное обозначение получило бы не отношение длины окружности к диаметру, а отношение длины окружности к радиусу. На развитие математики это не сильно бы повлияло, но некоторые формулы выглядели бы иначе, а число 3,1415… не было бы таким знаменитым и никто бы не считал кучу его знаков после запятой.
Тем не менее, число е может встречаться в законах реального мира. Например, центральная предельная теорема описывает очень многие явления. (Она говорит, что сумма многих независимых случайных одинаково распределенных величин имеет нормальное распределение.) Казалось бы, для описания нормального распределения требуется число е; но корень из е тоже бы подошел, может быть, даже еще лучше. Нельзя сказать, что здесь можно получить физический смысл числа е из ЦПТ. Скорее, наоборот — нормальное распределение стали выражать через е, потому что уже привыкли к этому числу.
Что значит трения коэффициент — Значения слов
отношение силы трения F к реакции Т, направленной по нормали к поверхности касания, возникающей при приложении нагрузки, прижимающей одно тело к другому: f = F/T. Т. к. ≈ характеристика, применяемая при выполнении технических расчётов, характеризующих фрикционное взаимодействие двух тел (см. Трение внешнее ).
В зависимости от вида перемещения одного тела по другому различают: Т.к. при сдвиге ≈ скольжении и Т.к. при качении. В свою очередь, при скольжении в зависимости от величины тангенциальной силы (см. рис. при ст. Трение внешнее ) различают коэффициент неполного трения скольжения, коэффициент трения покоя и коэффициент трения скольжения. Все эти Т.к. могут изменяться в широких пределах в зависимости от шероховатости и волнистости поверхностей, характера плёнок, покрывающих поверхности. Для протяжённого контакта они мало изменяются с изменением нагрузки.
В зависимости от величины коэффициент трения скольжения пары трения делят на 2 группы: фрикционные материалы, имеющие большой Т. к.≈ обычно 0,3≈0,35, редко 0,5≈0,6, и антифрикционные, имеющие Т. к. без смазки 0,15≈0,12, при граничной смазке 0,1≈0,05.
Сопротивление свободному качению твёрдого тела (например, колеса) характеризуют коэффициентом сопротивления перекатыванию fk = T∙rd/Ik [см], где Т ≈ нормальная составляющая реакции колеса на опору; rd ≈ динамический радиус качения; Ik ≈ нормальная нагрузка на колесе. Если на колесо действуют ведущий или тормозной моменты, то коэффициент сцепления y колеса с дорожным покрытием определяется равенством: y = Tx/Ik, где Tx ≈ неполная сила трения скольжения, возникающая между катящимся колесом и дорогой. Коэффициенты fk и y существенно зависят от природы трущихся тел, характера покрывающих их плёнок и скорости качения. Обычно для металлов (сталь по стали) fk = 0,001≈0,002 см. При движении автомобиля со скоростью 80 км/час Т. к. колёс по асфальту fk = 0,02 см и резко возрастает с увеличением скорости. Коэффициент сцепления y на сухом асфальте доходит у автомобильных колёс до 0,8, а при наличии плёнки воды снижается до 0,2≈0,1.
И. В. Крагельский.
Коэффициент трения — Простая английская Википедия, бесплатная энциклопедия
Коэффициент трения — это величина, которая показывает взаимосвязь между двумя объектами и нормальную реакцию между участвующими объектами. Это значение, которое иногда используется в физике, чтобы найти нормальную силу объекта или силу трения, когда другие методы недоступны.
Коэффициент трения показан как F е знак равно μ F N {\ displaystyle F_ {f} = \ mu F_ {n} \,} ,В этом уравнении F е {\ displaystyle F_ {f}} сила трения, μ {\ displaystyle \ mu} — коэффициент трения, а F N {\ Displaystyle F_ {п} \,} — нормальная сила.
Коэффициент μ {\ displaystyle \ mu} могут быть две разные вещи.Это либо коэффициент трения покоя
Коэффициент трения безразмерен и не имеет единиц измерения. Это скаляр, означающий, что направление силы не влияет на физическую величину.
Коэффициент трения зависит от предметов, вызывающих трение. Значение обычно составляет от 0 до 1, но может быть больше 1. Значение 0 означает, что трение между объектами отсутствует; такое возможно со сверхтекучестью. В противном случае все объекты будут иметь некоторое трение при касании друг друга.Значение 1 означает, что сила трения равна нормальной силе. Ошибочно считать, что коэффициент трения ограничен значениями от нуля до единицы. Коэффициент трения больше единицы просто означает, что сила трения сильнее нормальной силы. Например, такой объект, как силиконовый каучук, может иметь коэффициент трения намного больше единицы.
Сила трения — это сила, прилагаемая поверхностью, когда объект движется по ней или делает усилие для перемещения по ней.
Сила трения или сила трения (статическая или кинетическая) может быть выражена как
F е знак равно μ N {\ displaystyle F_ {f} = \ mu N} (1)
где
F е {\ displaystyle F_ {f}} — сила трения (в Ньютонах),
μ {\ displaystyle \ mu} статический ( μ s {\ displaystyle \ mu _ {s}} ) или кинетический ( μ К {\ displaystyle \ mu _ {k}} ) коэффициент трения (безразмерный) и
N {\ displaystyle N} нормальная сила (в Ньютонах).
это также может быть известно как трение. Оно представлено как (f).
- Чтобы найти эквивалентную статью в En wiki, щелкните здесь
Измерение статического трения с рампой, Рон Куртус
Рона Куртуса (от 21 ноября 2016 г.)
Цель этого эксперимента — измерить статический коэффициент трения скольжения между двумя поверхностями с помощью наклонной рампы и измерения ее наклона.
Идея состоит в том, что если вы поместите твердый объект на рампу и начнете наклонять рампу вверх, существует точка, в которой объект начнет скользить.Это угол, при котором сила тяжести достаточно велика, чтобы преодолеть статическое трение скольжения.
Просто зная угол или наклон, вы можете затем рассчитать статический коэффициент трения скольжения между двумя материалами. Вы можете покрыть пандус разными материалами, чтобы определить разные коэффициенты.
( См. Также: трение скольжения по наклонной поверхности )
Вопросы, которые могут у вас возникнуть:
- Какие материалы нужны?
- Какие шаги нужно предпринять?
- Как производятся расчеты?
Этот урок ответит на эти вопросы.
Материалы
- Плоская доска для использования в качестве пандуса
- Дополнительный материал покрытия пандуса
- Объекты, спускающиеся по трапу
У вас должна быть возможность изменять угол наклона пандуса.
Шаги
- Измерьте вес вашего объекта
- Поставьте пандус на землю и поставьте объект на пандус
- Медленно поднимите один конец пандуса, пока объект не начнет скользить
- Измерьте высоту ( A ) и длину ( B ) наклона, как на рисунке ниже
Объект на съезде
Результирующий статический коэффициент трения скольжения составляет:
мкм сс = A / B
Различные комбинации
Вы можете использовать различные комбинации материалов для измерения их коэффициентов трения.Например, вы можете использовать:
- Деревянная доска и кирпич для расчета кинетического коэффициента трения между деревом и кирпичом
- Лист железа на доске и железный блок для скольжения по пандусу
- Лист железа с масляной пленкой и железный блок для скольжения по рампе
- Покрытие мокрого линолеума и обуви, чтобы увидеть, насколько скользким может быть пол
Есть много комбинаций, которые вы можете измерить.
Пояснение
Хотя уравнение для определения статического коэффициента трения очень простое, принципы, лежащие в основе его, требуют некоторых знаний математики.
Физический фон
Коэффициент трения между двумя поверхностями — это число, которое определяет, сколько силы требуется для перемещения объекта, сдерживаемого трением, когда две поверхности прижимаются друг к другу.
Стандартное уравнение трения скольжения:
F н.с. = μ н.с. N
где
- F s — сила сопротивления трения скольжения
- μ s — коэффициент трения скольжения для двух поверхностей (греческая буква «мю»)
- Н нормальная сила
Когда объект находится на склоне, нормальная сила составляет:
N = W * cos (β)
где
- W — вес объекта
- β — угол наклона (греческая буква «бета»)
- cos (β) — косинус угла β
Таким образом, уравнение трения скольжения:
F с = μ с Вт * cos (β)
Поскольку W = mg , уравнение принимает следующий вид:
F с = μ с мг * cos (β)
где
- м — масса объекта
- g — ускорение свободного падения
Сила тяжести для объекта на склоне
Сила тяжести, действующая вниз по склону, равна весу, умноженному на синус угла наклона:
F г = W * sin (β)
где
- F g — сила тяжести, тянущая объект вниз по склону
- sin (β) — синус угла β
Поскольку W = mg , уравнение принимает следующий вид:
F г = мг * sin (β)
Точка, в которой объект начинает движение:
F SS = F г
μ с мг * cos (β) = мг * sin (β)
μ с * cos (β) = sin (β)
μ с = sin (β) / cos (β)
с
sin (β) = кондиционер
cos (β) = B / C
тангенс (β) = A / B
Вывод
Уравнение трения: Fr = fr x N , где Fr — это сила трения сопротивления или величина силы, необходимой для преодоления трения, fr — коэффициент трения между двумя поверхностями, а N . — нормальная или перпендикулярная сила, толкающая две поверхности вместе.Если сила, прижимающая поверхности вместе, является силой тяжести, тогда Н равно весу верхнего объекта.
Статическое и кинетическое трение
Для скользящего объекта статический коэффициент трения дает силу, необходимую для начала движения объекта. Когда объект скользит с постоянной скоростью, кинетический коэффициент трения приводит к силе, необходимой для поддержания движения объекта с этой скоростью.
Использование аппарели
Умный способ определить статический коэффициент трения — начать скольжение объекта по рампе.Составляющая силы тяжести, которая заставляет объект только что начать движение, равна силе сопротивления, удерживающей объект в неподвижном состоянии. Это статическая сила трения.
Обратите внимание, что вы должны записать, что это за две поверхности. Коэффициент трения всегда для двух поверхностей. Например, вы можете обнаружить трение между деревом и сталью, деревом по дереву, резиной по мокрому асфальту и так далее.
Зная силу, необходимую для преодоления трения, и силу, толкающую объект на рампу, можно определить статический коэффициент трения.
Математика
Коэффициент трения рассчитывается с помощью тригонометрии. Рассмотрим треугольник на рисунке ниже.
Углы
C — это длина пандуса, который наклонен под углом a и находится на высоте A . Длина сторон треугольника: A , B и C . Отношения между сторонами представляют собой тригонометрические функции: синус угла a , который обозначается сокращенно sin (a) , косинус a или cos (a) и тангенс a или tan (a) .
Поскольку sin (a) = A / C и cos (a) = B / C , то sin (a) / cos (a) = tan (a) .
Составляющие силы тяжести
Когда объект весом Вт находится на пандусе, силу тяжести можно разделить на составляющие в перпендикулярных направлениях.
Составляющая нормальной силы
Сила, прижимающая объект к поверхности аппарели, уменьшается из-за наклона. Нормальная сила Н = W x cos (a) , как показано на рисунке ниже.В случае отсутствия наклона a = 0 градуса и N = W.
Компоненты на рампе
Деталь съезда
Составляющая силы тяжести, тянущая объект по рампе, составляет F = W x sin (a) .
Объект начинает движение
Теперь, когда угол a становится достаточно крутым, объект начинает двигаться и F = Fr , что является силой статического трения, необходимой для начала движения объекта.
Но вы знаете, что Fr = fr x N .
А для объекта на рампе N = W x cos (a) .
Таким образом, W x sin (a) = fr x W x cos (a) .
Используя небольшую алгебру, мы получаем fr = sin (a) / cos (a) или fr = tan (a) .
Наконец, поскольку tan (a) = A / B , мы имеем fr = A / B .
Итак, все, что вам нужно знать, — это угол, под которым объект начинает скользить, или длину его сторон, и вы можете легко определить коэффициент трения между двумя поверхностями.
Сводка
Вы можете измерить величину статического трения и коэффициент трения объекта, посмотрев, когда он начинает скользить по рампе.
Будьте умны
Ресурсы и ссылки
Полномочия Рона Куртуса
Сайты
Наклонные плоскости — Физический класс
Ресурсы для научных проектов и экспериментов
Книги
Книги с самым высоким рейтингом по проектам Science Fair
Лучшие книги по экспериментам
Вопросы и комментарии
Есть ли у вас какие-либо вопросы, комментарии или мнения по этой теме? Если да, отправьте свой отзыв по электронной почте.Я постараюсь вернуться к вам как можно скорее.
Поделиться страницей
Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:
Студенты и исследователи
Веб-адрес этой страницы:
www.school-for-champions.com/experiments/
friction_measure_coefficient_with_ramp.htm
Пожалуйста, включите его в качестве ссылки на свой веб-сайт или в качестве ссылки в своем отчете, документе или диссертации.
Авторские права © Ограничения
Где ты сейчас?
Школа чемпионов
Темы научных проектов и экспериментов
Измерение коэффициента трения с помощью рампы
,
Стандартное уравнение трения, Рон Куртус
SfC Home> Физика> Сила> Трение>
Рона Куртуса (от 21 октября 2016 г.)
Стандартное уравнение трения показывает взаимосвязь между сопротивляющей силой трения, коэффициентом трения и нормальной силой, толкающей объекты вместе. Уравнение применимо в большинстве ситуаций, связанных с трением.
Вопросы, которые могут у вас возникнуть:
- Что такое стандартное уравнение трения?
- Что такое коэффициент трения?
- Что такое нормальная сила?
Этот урок ответит на эти вопросы.Полезный инструмент: Конвертация единиц
Стандартное уравнение трения
Стандартное уравнение для определения силы сопротивления трения при попытке переместить два объекта или материала относительно друг друга показывает взаимосвязь между силой трения, коэффициентом трения и нормальной силой, толкающей два объекта вместе. Это уравнение записывается как
F f = мкН
где:
- F f — сила сопротивления трения
- μ — коэффициент трения для двух поверхностей (греческая буква «мю»)
- Н — нормальная или перпендикулярная сила, толкающая два объекта вместе
- мкН равно мк умножить на Н
F f и N измеряются в единицах силы, которые являются фунтами или ньютонами.
Коэффициент трения
Коэффициент трения (COF) — это число, определяющее величину трения между контактирующими материалами. Часто обозначается греческой буквой мю ( μ ).
В большинстве случаев COF также не зависит от площади соприкасающихся поверхностей.
Факторы, определяющие коэффициент трения, включают комбинации материалов, состояния поверхности, а также то, является ли движение статическим или кинетическим.
Значение статического COF больше, чем кинетическое или динамическое COF для тех же материалов и условий.
COF также различается для различных типов трения: скольжения, качения или жидкости. Для получения дополнительной информации см .:
Коэффициент трения скольжения
Коэффициент трения качения
Коэффициент трения жидкости
Нормальная сила
Нормальная сила ( Н ) — это сила, толкающая два объекта или материала вместе перпендикулярно или перпендикулярно поверхностям.
В большинстве случаев COF не зависит от нормальной силы. Однако в некоторых случаях N может быть настолько большим, что исказит материалы, что приведет к изменению коэффициента трения. Жидкости и мягкие материалы особенно чувствительны к увеличению нормальной силы.
Для N существуют различные характеристики скольжения, качения и гидравлического трения. Для получения дополнительной информации см .:
Нормальное усилие при трении скольжения
Нормальная сила трения качения
Нормальная сила трения жидкости
Сводка
Стандартное уравнение трения — это соотношение между сопротивляющей силой трения, нормальной силой и коэффициентом трения для двух поверхностей.
Будьте полны решимости сделать все возможное
Ресурсы и ссылки
Полномочия Рона Куртуса
Сайтов
Ресурсы трения — Обширный список
Концепции трения — HyperPhysics
RoyMech (Великобритания) — Факторы трения
Книги
Книги с самым высоким рейтингом по науке о трении
Книги с наивысшими оценками по экспериментам с трением
Наука и технология трения (Серия «Машиностроение») Питера Дж.Blau; Марсель Деккер Паб. (1995)
Управление машинами с помощью трения (Международная серия инженерных и компьютерных наук) Брайана Армстронга-Элуври; Springer Pub. (1991)
Вопросы и комментарии
Есть ли у вас какие-либо вопросы, комментарии или мнения по этой теме? Если да, отправьте свой отзыв по электронной почте. Я постараюсь вернуться к вам как можно скорее.
Поделиться страницей
Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:
Студенты и исследователи
Веб-адрес этой страницы:
www.school-for-champions.com/science/
friction_equation.htm
Пожалуйста, включите его в качестве ссылки на свой веб-сайт или в качестве ссылки в своем отчете, документе или диссертации.
Авторские права © Ограничения
Где ты сейчас?
Школа чемпионов
Фрикционные темы
Стандартное уравнение трения
,
Статическое трение скольжения на уклоне, Рон Куртус
SfC Home> Физика> Сила> Трение>
Рона Куртуса (редакция 15 января 2020 г.)
Когда объект помещается на ровный наклон или пандус, он не будет скользить по поверхности, если сила, вызванная гравитацией, действующая на объект, меньше сопротивления трения. Поскольку объект не скользит, сопротивление называется статическим трением скольжения .
Чтобы определить это сопротивление, вам необходимо знать уравнение трения для наклона, силы тяжести, толкающие объект, и статический коэффициент трения скольжения.
Статический коэффициент трения скольжения можно легко определить по углу наклона, когда сила тяжести равна сопротивлению статическому трению скольжения.
Вопросы, которые могут у вас возникнуть:
- Что такое уравнение трения на склоне?
- Какова сила тяжести объекта, находящегося на уклоне?
- Как определить статический коэффициент трения скольжения?
Этот урок ответит на эти вопросы.Полезный инструмент: Конвертация единиц
Статическое уравнение трения скольжения при наклоне
Уравнение статического трения скольжения:
F н.с. = μ н.с. N
где
- F ss — статическая сила трения скольжения
- μ ss — статический коэффициент трения скольжения для двух поверхностей (греческая буква «мю»)
- Н — нормальная сила, перпендикулярная поверхности
Нормальная сила на склоне
Когда объект находится на склоне, нормальная сила составляет:
N = W * cos (β)
где
- W — вес объекта
- β — угол наклона (греческая буква «бета»)
- cos (β) — косинус угла β
Уравнение статического трения скольжения
Таким образом, уравнение статического трения скольжения имеет вид:
F н.с. = μ н.с. Вт * cos (β)
Статические силы, действующие на объект на наклонной поверхности
Сила тяжести для объекта на уклоне
Сила тяжести, действующая вниз по склону, равна весу, умноженному на синус угла наклона:
F г = W * sin (β)
где
- F g — сила тяжести, тянущая объект вниз по склону
- sin (β) — синус угла β
Не скользит
Когда сопротивление от статического трения скольжения превышает силу скольжения от силы тяжести, объект не будет скользить:
F SS > F г
Коэффициент трения
Статический коэффициент трения скольжения составляет:
мкм н.с. = F н.с. / N
Для данного набора материалов статический коэффициент трения скольжения обычно больше, чем кинетический коэффициент трения.
На коэффициент трения может влиять ряд факторов, включая состояние поверхности. Значения коэффициента трения скольжения могут служить хорошим ориентиром для конкретных комбинаций материалов.
(См. Коэффициент трения скольжения и
Эксперимент по трению: измерение коэффициента трения с рампой )
Сводка
Объект помещен на ровный уклон, или пандус не будет скользить по поверхности, если сила, вызванная гравитацией, меньше сопротивления статического трения скольжения.
Статический коэффициент трения скольжения можно легко определить по углу наклона, когда сила тяжести равна сопротивлению статическому трению скольжения.
Будьте умны
Ресурсы и ссылки
Полномочия Рона Куртуса
Сайтов
Концепции трения — HyperPhysics
Ресурсы трения — Обширный список
Книги
Книги с самым высоким рейтингом по науке о трении
Книги с наивысшими оценками по экспериментам с трением
Вопросы и комментарии
Есть ли у вас какие-либо вопросы, комментарии или мнения по этой теме? Если да, отправьте свой отзыв по электронной почте.Я постараюсь вернуться к вам как можно скорее.
Поделиться страницей
Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:
Студенты и исследователи
Веб-адрес этой страницы:
www.school-for-champions.com/science/
Фрэнсис Кириллович .
Пожалуйста, включите его в качестве ссылки на свой веб-сайт или в качестве ссылки в своем отчете, документе или диссертации.
Авторские права © Ограничения
Где ты сейчас?
Школа чемпионов
Фрикционные темы
Статическое трение скольжения на уклоне
,
