Измерение физических величин. СИ | 7 класс
Содержание
Спектр объектов и явлений, изучаемых в физике, огромен. От невероятной скорости электромагнитной волны до возраста Земли и от крошечных размеров частиц до площади наблюдаемой вселенной. От силы, создаваемой прыгающей блохой, до силы притяжения между Землей и Луной.
Мы определяем физическую величину либо путем измерения с помощью соответствующих приборов, либо путем расчета на основе других измерений. Например, мы определяем расстояние, полагаясь на то, что оно рассчитывается как скорость, умноженная на время в пути.
Однако все известные физические величины выражаются в единицах, которые являются стандартизованными значениями. Например, длина забега, которая тоже является физической величиной, может быть выражена в метрах (для спринтеров) или в километрах (для бегунов на длинные дистанции). Без стандартизированных единиц ученым было бы чрезвычайно сложно вычислить и сравнить измеренные значения.
Что значит измерить какую-либо величину?
Измерить какую либо величину — это значит сравнить ее с однородной величиной, принятой за единицу.
Система единиц измерения
Во всем мире используются такая система единиц измерения как «единицы СИ» (сокращение от французского Le Système International d’Unités, также известное как метрическая система). Некоторые физические величины и их единицы измерения представлены в таблице 1.
| Основные величины | Символ | Единица СИ |
|---|---|---|
| Масса | $m$ | килограмм ($кг$) |
| Время | $t$ | секунда ($с$) |
| Температура | $T$ | кельвин ($К$) |
| Длина | $l, S$ | метр ($м$) |
| Скорость | $\upsilon$ | метр в секунду ($\frac{м}{c}$) |
 Некоторые величины и их единицы измерения
Некоторые величины и их единицы измеренияКаковы единицы длины, времени, массы в СИ?
В этой системе основной единицей длины является метр (м), единицей времени — секунда (с), единицей массы — килограмм (кг). Но так было не всегда!
Существует также такая система единиц измерения как имперская система или английские единицы измерения. Эта система исторически использовались в странах, когда-то находившихся под управлением Британской империей. Сегодня Соединенные Штаты — единственная страна, в которой до сих пор широко используется имперская система.
Часто, когда мы применяем систему единиц СИ, нам может понадобиться выразить единицы, которые больше принятых единиц в 10, 100, 1000 раз (таблица 2). Здесь все просто — к наименованиям единиц СИ нужно добавить соответствующую приставку на греческом языке:
если эта единица больше СИ в 10 раз — к названию добавляется приставка «дека», в 100 раз — «гекто», в 1000 раз — «кило» и т.д. Такие приставки называю кратными.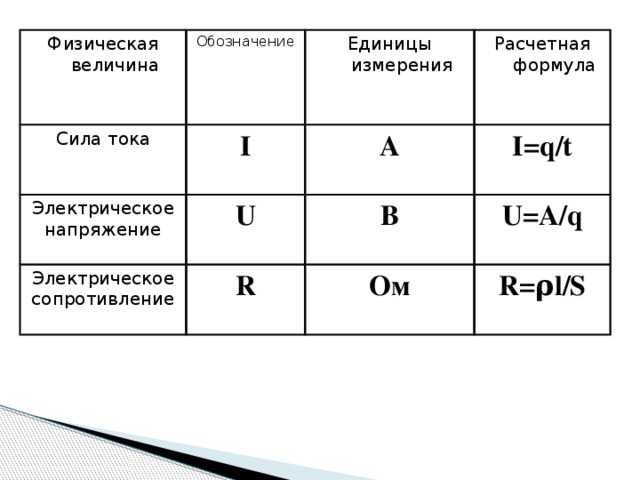 {-3}$)Таблица 2. Приставки к названиям единиц
{-3}$)Таблица 2. Приставки к названиям единиц
Пример:
Пачка макарон весит 300 грамм (г). Выразите ее вес в килограммах (кг).
Для того чтобы решить эту задачу, нам нужно вспомнить, что в одном килограмме — 1000 грамм. Следовательно, нам всего лишь остается разделить 300 грамм на 1000. Получается, что в килограммах, пачка макарон будет весить 0,3 кг.
{"questions":[{"content":"Длина ковра - 2 метра. Выразите его длину в миллиметрах.[[input-1]]","widgets":{"input-1":{"type":"input","answer":"2000"}},"hints":["Вспомним, что в 1 метре 100 сантиметров.","А в 1 сантиметре 10 миллиметров.","$2 \times 100 \times 10 = 2000$"]}]}Единицы измерения в ходе истории
В древние времена человек использовал части своего тела в качестве инструментов измерения, такие как рука, ладонь и ступня. А для измерения времени использовали природные явления, такие как восход, закат и фазы Луны.
Так, в Древней Руси мерой длины мог быть сам человек (рисунок 1). Например, косая сажень — расстояние от носка левой ноги до конца среднего пальца поднятой вверх правой руки. Пядь, или четверть, — расстояние между концами расставленных большого и указательного пальцев руки.
Например, косая сажень — расстояние от носка левой ноги до конца среднего пальца поднятой вверх правой руки. Пядь, или четверть, — расстояние между концами расставленных большого и указательного пальцев руки.
Измерительные инструменты со временем совершенствовались, они были необходимы человеку в точном описании явлений и изучении законов физики.
Используемый измерительный инструмент зависит от измеряемой физической величины. Для измерения длины существуют такие инструменты, как линейка, штангенциркуль и микрометр.
Для получений различных параметров электрического тока — амперметр, вольтметр, омметр. Для вычисления времени, мы прибегнем к использованию таймеров и секундомеров.
Цена деления
Как правило, все измерительные приборы имеют свою шкалу. Для точности подсчета, на панель прибора нанесено несколько делений, подписанных соответствующими значениями, между которыми, в свою очередь, находится еще несколько делений поменьше, обычно эти промежуточные деления числами не обозначены.
В науке об измерениях, такие деления показывают наименьшее и самое точное значение измеряемой величины, и называются они — цена деления. Как нетрудно догадаться, что чем меньше цена деления, тем точнее измерения.
Линейка с ценой деления 1 смНапример, на наручных часах могут быть только 12 отметок часов текущего времени суток, то есть цена деления этого прибора — один час.
Секундомер, используемый для измерения времени при проведении спортивных состязаний, может иметь цену деления до сотых долей секунды. Все потому, что секундомер более точен при измерении временных интервалов, чем обычные часы, поэтому у него больше «интервалов» в каждый час прошедшего времени.
Цена деления — одна из самых важных характеристик для получения точных показаний такого инструмента, как штангенциркуль, используемого в различных экспериментах.
Линейка с ценой деления 2 мм{"questions":[{"content":"Чем меньше цена деления, тем [[input-1]] измерения","widgets":{"input-1":{"type":"input","inline":1,"answer":"точнее"}},"hints":[]}]}Как определяется цена деления измерительного прибора?
Для определения цены деления любого измерительного прибора необходимо:
- Определить два ближайших штриха на шкале, возле которых стоят значения величины;
- Вычесть из большего значения меньшее;
- Полученное число разделить на число делений, находящихся между ними.

Давайте для наглядности найдем цену деления термометра, изображенного на рисунке 2.
Рисунок 2. ТермометрВозьмем два соседних штриха, около которых стоят цифры (значения температуры). Пусть это будут штрихи с обозначениями $10 \degree C$ и $20 \degree C$. Между этими штрихами 10 делений.
Определим цену деления:
$\frac{20 \degree C — 10 \degree C}{10} = 1 \degree C$.
Получается, что термометр показывает $26 \degree C$.
Упражнения
Упражнение №1
Определите цену деления секундомера (рисунок 3).
Показать решение и ответ
Скрыть
Решение:
Возьмем два соседних штриха, которые отмечены цифрами: 5 с и 10 с. Между ними находится 10 делений. Найдем цену деления этого секундомера:
$\frac{10 \space с — 5 \space с}{10} = 0.5 \space с$.
Ответ: цена деления секундомера равна $0.5 \space с$.
Упражнение №2
По рисунку 4 определите цену деления амперметра (рисунок 4, а) и вольтметра (рисунок 4, б).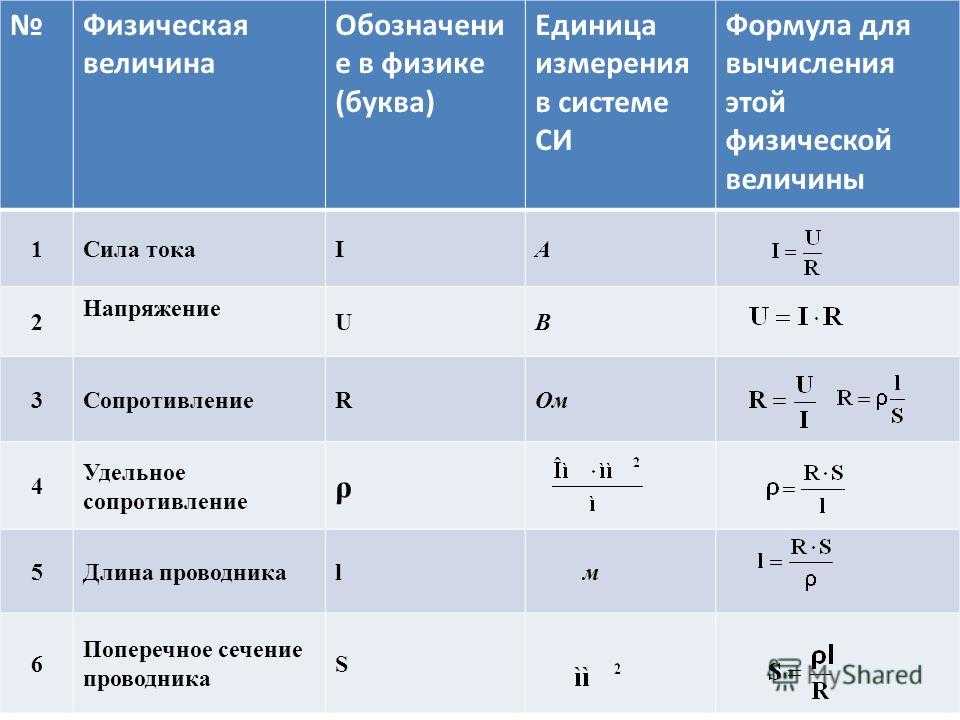
Показать решение и ответ
Скрыть
Решение:
Для амперметра (рисунок 4, а):
возьмем соседние значения 0 А и 0.5 А. Между ними находится 10 делений.
Найдем цену деления прибора:
$\frac{0.5 \space А -0 \space А}{10} = 0.05 \space А$.
Для вольтметра (рисунок 4, б):
возьмем соседние значения 0 В и 1 В. Между ними находится 5 делений.
Найдем цену деления прибора:
$\frac{1 \space В — 0 \space В}{5} = 0.2 \space В$.
Ответ: цена деления амперметра равна $0.5 \space А$, а вольтметра — $0.2 \space В$.
Задания
Задание №1
Используя интернет, найдите прибор для измерения артериального давления — тонометр механический. Определите цену деления шкалы. В каких единицах измеряют артериальное давление?
Механический тонометр изображен на рисунке 5.
Рисунок 5. Механический тонометрПоказать решение и ответ
Скрыть
Решение:
Артериальное давление измеряют в мм рт. Также были распространены и другие меры объема. В таблице 4 представлены меры объема, которые использовали для сыпучих тел (например, крупы). Для жидкостей использовали другие меры объема. Они представлены в таблице 5. Выразите свой вес в пудах, а рост в аршинах. Возьмем для примера следующие параметры: рост равен $145 \space см$, а вес — $42 \space кг$. 1 пуд приблизительно равен $16.3807 \space кг$, а 1 аршин — $71.12 \space см$. Переведем в эти единицы рост и вес. Рост: Вес: Запишите 2-3 пословицы, поговорки или образных выражения, в которых упоминаются старинные меры длины, массы, объема и т.п. Примеры: Новые вопросы [ a ] = 1 м/с² [ v ] = 1 м/с [ t ] = 1 c [ S ] = 1 м
Какое количество теплоты требуется для нагревания воды массой 20грамм на 8° градусов по цельсию… …
С каким ускорением двигался сомолет разгоняясь перел взлетом если за 20 секкнд его скорость взросла от 5 м/с до 45 м/с ?…
Какое количество теплоты выделяется при охлаждении чугуна массой 1.2 кг на 15 г…
Тело брошенное вверх упало через 5с на какую высоту оно поднялось g=9,8m/c. 3$Таблица 3. Меры объема в Древней Руси
3$Таблица 3. Меры объема в Древней Руси
Таблица 4. Меры объема сыпучих тел в Древней РусиМера объема Литры Цебр 5457,5872 — 6297,216 Кадка 839,69 Четверть 209,9072 Осьмина 104,95 Четверик 26,2387 Гарнец 3,2798 Стакан 0,273
Таблица 5.Мера объема Литры Шкалик 0,0615 Чарка 0,123 Водочная бутылка 0,614962 Винная бутылка 0,7687 Штоф 1,2299 Четверть 3,0748 Ведро 491,976 Бочка 491,976  Меры жидких тел в Древней Руси
Меры жидких тел в Древней РусиЗадание №3
$\frac{145 \space см}{71.12} \approx 2 \space аршина$.
$\frac{42 \space кг}{16.3807 \space кг} \approx 2.6 \space пуда$.Задание №4
В каких единицах измеряются данные физические величины в .
 .. -reshimne.ru
.. -reshimne.ruОтветы
Похожие вопросы

X1(t) =3t
X2(t) =15-2t…
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Химия
Физика
Биология
История
Обществознание
Окружающий мир
География
Українська література
Қазақ тiлi
Беларуская мова
Информатика
Музыка
Право
Французский язык
Немецкий язык
МХК
ОБЖ
Психология
Морские единицы физических величин
Международная система единиц измерения в судоходстве отличается от единиц измерения, принятых в нашей повседневной жизни и соседствует с англосаксонскими основными единицами. Это связано с сохранившейся до нашего времени важной ролью англоязычных стран в судостроении и судоходстве.
Это связано с сохранившейся до нашего времени важной ролью англоязычных стран в судостроении и судоходстве.
Безусловно, в эпоху интернета не представляет особого труда перевести одни единицы в другие, воспользовавшись одним из множества приложений. Но как быть в открытом море, где по различным причинам интернет может отсутствовать?
Знать морские единицы измерения и свободно переводить их в общепринятые величины должен уметь каждый яхтсмен!
Единицы длинны
Морская миля — единица длины при измерении расстояний на море. Она равна длине одной минуты дуги меридиана (или 1/60 градуса, так как в градусе 60 минут).
Таким образом, передвижение на одну морскую милю вдоль меридиана примерно соответствует изменению географических координат на одну минуту широты.
Сокращенное обозначение морской мили, которое можно встретить на навигационных приборах nm
1 морская миля = 1852,3 м = 1,852 км
1 км = 0,54 морские мили
Кроме морской мили, для измерения расстояния на море приняты также следующие единицы длины:
1 Кабельтов = 0,1 морская миля = 185,2 м
Длина лодок обычно измеряется в футах. Как правило, в названии модели яхты содержится число соответствующее ее длине в футах, что позволяет сразу иметь представление о размерах судна.
Как правило, в названии модели яхты содержится число соответствующее ее длине в футах, что позволяет сразу иметь представление о размерах судна.
Что же такое фут?
Фут (от англ. foot — ступня) — единица измерения длины в английской системе мер.
Первоначальный британский фут — это не что иное, как сандалия древнеримского легионера.
Для Англии этот «сандальный» фут стал античным наследием Рима. Фут продолжал использоваться по всей Европе в течение большей части последних двух тысяч лет, хотя национальные и региональные различия были обычным явлением. В зависимости от того, где (и когда) термин фут был использован, он может означать длину от 273 мм до 357 мм.
Таблица конвертации футов в метры
В 1959 году международное соглашение о ярдах и фунтах (между Соединенными Штатами и странами Содружества Наций), определило фут как 0,3048 метра (304,8 мм).
1 фут = 0.3048 м
1 метр = 3,28 фута
Сокращенное обозначение фута – ft
В свою очередь фут состоит из 12 дюймов. Дюйм имеет тоже свою историю, и в давние времена дюйм считали равным ширине большого пальца (по-русски дюйм – от голландского слова duim, что при дословном переводе обозначает – большой палец).
Дюйм имеет тоже свою историю, и в давние времена дюйм считали равным ширине большого пальца (по-русски дюйм – от голландского слова duim, что при дословном переводе обозначает – большой палец).
Международное обозначение дюйма inch, in или ″ — двойной штрих
1 дюйм = 1/12 фута =2,54 см
Скорость судна
Скорость морского судна измеряют узлами, т. е. количеством морских миль, которое оно проходит за 1 ч. Говорят, например, что судно имеет скорость 12 узлов, т. е. оно проходит 12 морских миль в час.
Термин «узел» появился в эпоху парусного мореплавания, когда скорость хода судна измеряли с помощью, так называемого секторного лага — деревянного щитка секторообразной формы, выпускаемого с кормы судна в воду на лаглине (плетеном тросике). Такой сектор удерживался отростками лаглиня в трех точках, благодаря чему сохранял в воде перпендикулярное положение к направлению хода судна. Так как сектор тормозится водой, то лаглинь вытравливался приблизительно со скоростью хода судна.
Если лаглинь был с помощью узелков разбит на участки по 50,7 фута, то есть равные 1\120 мили (6080\50,7=120), тогда при скорости хода в 1 узел лаглинь за 1 минуту или за 1\60 часа вытравится на 1\60 мили (2 узелка), а за 0,5 минуты — на 1 узелок. Если же за 0,5 минуты вытравливалось, например, 9 узелков, то считалось, что судно идет со скоростью 9 узлов.
1 узел = 1 морская миля/час = 1,852 км/ч
Международное обозначение узла, которое можно встретить на навигационных приборах kts
Таблица конвертации узлов в м/с и км/ч для типичных скоростей парусной яхты
Формулы для перевода узлов в км/ч и м/с:
V км/ч = 1,852 * V узлов
V м/сек = 0,5145 * V узлов
V узлов = 0,5400 * V км/ч
V узлов = 1,943 * V м/сек
Грубо говоря, значение скорости судна в узлах в 2 раза меньше значения скорости судна в м/с
Скорость и сила ветра
Так же как и скорость судна, скорость ветра измеряется в узлах. Кроме того силу ветра измеряют в баллах по шкале Бофорта.
Кроме того силу ветра измеряют в баллах по шкале Бофорта.
Шкала Бофорта — двенадцатибалльная шкала, принятая Всемирной метеорологической организацией для приближённой оценки скорости ветра по его воздействию на наземные предметы или по волнению в открытом море. Средняя скорость ветра указывается на стандартной высоте 10 метров над открытой ровной поверхностью.
Шкала разработана ирландским гидрографом Фрэнсисом Бофортом в 1805 году.
Более подробную таблицу с детальным описанием состояния моря и суши при различной силе ветра можно найти тут.
Направления и географические координаты
Все мы знаем, что положение точки на земной поверхности определяют географические координаты.
Координаты (широта от −90° до +90°, долгота от −180° до +180°) могут записываться:
— в ° градусах в виде десятичной дроби (десятичные градусы, современный вариант) – например, N55,755831°, E37,617673°
— в ° градусах и ′ минутах с десятичной дробью – например, 55°45. 35′N, 37°37.06′E
35′N, 37°37.06′E
— в ° градусах, ′ минутах и ″ секундах с десятичной дробью (исторически сложившаяся форма записи) – например, 55°45′20.9916″N, 37°37′3.6228″E
На картах поисковых систем по умолчанию показываются координаты в градусах с десятичной дробью со знаком «−» для отрицательной долготы.
В то же время часто используется и исконный способ записи с градусами, минутами и секундами. Например, при прокладке маршрута на навигационной карте обычно координаты записывают в формате «градусы, минуты, секунды»
При необходимости пересчитать форматы можно, конечно, использовать специализированные сервисы.
Но иногда бывает, что необходимо пересчитать форматы самостоятельно.
Напомним, что 1° (градус) = 60′ (минут), 1′ (минута) = 60″ (секунд)
Чтобы перейти из формата «градусы, минуты, секунды и доли секунд» в «десятичные градусы», нужно воспользоваться формулой:
Десятичные градусы = Град + Мин/60 + Сек/3600
Например, переведем 55°45′20. 9916″N в десятичные градусы
9916″N в десятичные градусы
55°45.35′N = 55 + 45/60 + 20,9916/60 = 55 + 0,75 + 0,005831 = 55.755831 °N
Чтобы перейти из формата «десятичные градусы» dd.ddddd в «градусы, минуты, секунды и доли секунд» dd mm ss, нужно воспользоваться формулой:
DD = TRUNC(DDD)
MM = TRUNC((DDD − DD) * 60)
SS = ((DDD − DD) * 60 − MM) * 60
где DDD — координаты в формате DD.DDDD, DD — градусы, MM (MM.MMMM) — минуты, SS — секунды
Функция TRUNC в данном случае возвращает целое число
Например, переведем 55,755831°N в формат «градусы, минуты, секунды и доли секунд»
1) определим градусы: DD = целое число от 55,755831 = 55°
2) определим минуты: MM = целое число от (55,755831 – 55) * 60 = целое число от 45,34986 = 45′
3) определим секунды и доли секунд: SS = ((55,7558 – 55) * 60 – 45) * 60 = 20,9916″
Получается 55,755831°N = 55°45′20.9916″N
В тех случаях, когда не требуется особая точность в обозначении направления, применяют румбы.
Например, для обозначения направления ветра – «…NE 7 баллов…», течения «…W течение…» или приблизительного направления на какой-то географический район – «…к SW-ту от мыса Лизард…» и т.д.
Румбы сохранились со старых времен, когда не только конструкция магнитных компасов была не совершенна, но и точность удержания корабля на курсе измерялась десятком градусов, в виду несовершенства рулевого устройства. По мере совершенствования точности компасов и рулевых устройств, требовалась и более точная система отсчета, поэтому румбы разделили на части. С появлением гирокомпасов, электрических и гидравлических рулевых устройств, появилась возможность вести отсчет и удерживать судно на курсе с точностью до долей градуса. С этого времени румбы утратили практическое применение для целей курсоуказания, однако широко используются для общего обозначения направлений на море.
Итак, Румб (от греч. — юла, волчок, круговое движение) — в морской терминологии 1/32 полной окружности, а также одно из делений картушки компаса (расчерченной на 32 части) и соответственно одно из направлений относительно севера.
Существуют четыре основных румба:
• North — Север
• East — Восток
• South — Юг
• West — Запад
Четыре румба, производных от основных:
• North-West — Северо-запад
• North-East — Северо-восток
• South-East — Юго-восток
• South-West — Юго-запад
Обозначения румбов, отстоящих от основных на 11,25 градусов (1/32 полной окружности), получаются из обозначений одного из восьми выше перечисленных румбов, с добавлением после них слова «тень» или буквы «b» и названия основного направления, к которому отклоняется румб (например, NbE – румб, отклоненный от севера на 11,25 градусов к востоку).
Обозначения румбов, отстоящих от основных на 22,5 градуса (1/16 полной окружности), получаются из обозначений производных от основных румбов, с добавлением перед ними названия основного направления, к которому отклоняется румб (например, NNE – румб, отклоненный от севера на 22,5 градусов к востоку).
Физические основы механики
Действительно понимающий природу
того или иного явления должен получить
основные законы из соображений размерности
Э. Ферми
Физические величины бывают размерными и безразмерными.
Величина называется размерной, если ее численное значение зависит от выбора системы единиц.
Так, известный промежуток времени от восхода до восхода Солнца мы можем выразить как 1 сутки, или как 24 часа, или как 1 440 мин., или 86 400 с. Числа меняются, но мы говорим о том же самом интервале времени.
Величина называется безразмерной, если ее значение сохраняется неизменным при любом выборе системы единиц.
Например, высота Эвереста (= 8 848 м) и радиус Земли (= 6 370 км) — размерные величины, но их отношение уже величина безразмерная: независимо от системы единиц
Некоторых пояснений требует такой объект как «угол». В математической энциклопедии (Москва, Советская энциклопедия, 1985, том 5, стр. 467) угол определен следующим образом: «Уугол — геометрическая фигура, состоящая из двух различных лучей, выходящих из одной точки. Лучи называются сторонами угла, а их общее начало — вершиной угла». Эквивалентное определение: плоский угол — часть плоскости между двумя лучами, выходящими из одной точки. Радианная мера центрального угла вводится (см. рис. 1.7) как отношение длины дуги окружности, на которую он опирается к длине радиуса этой окружности: . Очевидно, что радианную меру можно ввести для любого угла, достаточно ножку циркуля поставить в вершину угла, провести окружность произвольного радиуса и вычислить отношение длины дуги, ограниченной сторонами угла, к радиусу этой дуги. Широко распространенное отождествление угла (как геометрической фигуры) и его радианной меры требует такого дополнительного разъяснения: угол величина безразмерная, равная «отношению длины дуги к радиусу», а единицы измерения этой безразмерной величины могут быть разными. Например, такой единице измерения угла как градус просто соответствует дуга длиной не в радиус, а в 1/360 часть длины окружности.
467) угол определен следующим образом: «Уугол — геометрическая фигура, состоящая из двух различных лучей, выходящих из одной точки. Лучи называются сторонами угла, а их общее начало — вершиной угла». Эквивалентное определение: плоский угол — часть плоскости между двумя лучами, выходящими из одной точки. Радианная мера центрального угла вводится (см. рис. 1.7) как отношение длины дуги окружности, на которую он опирается к длине радиуса этой окружности: . Очевидно, что радианную меру можно ввести для любого угла, достаточно ножку циркуля поставить в вершину угла, провести окружность произвольного радиуса и вычислить отношение длины дуги, ограниченной сторонами угла, к радиусу этой дуги. Широко распространенное отождествление угла (как геометрической фигуры) и его радианной меры требует такого дополнительного разъяснения: угол величина безразмерная, равная «отношению длины дуги к радиусу», а единицы измерения этой безразмерной величины могут быть разными. Например, такой единице измерения угла как градус просто соответствует дуга длиной не в радиус, а в 1/360 часть длины окружности. Другой пример: в морской навигации для измерения углов используется «румб», этой единице измерения соответствует дуга длиной в 1/32 часть окружности. Понимание того факта, что угол — величина безразмерная, весьма важно при анализе размерностей (см. ниже).
Другой пример: в морской навигации для измерения углов используется «румб», этой единице измерения соответствует дуга длиной в 1/32 часть окружности. Понимание того факта, что угол — величина безразмерная, весьма важно при анализе размерностей (см. ниже).
Размерные величины можно умножать и делить друг на друга. Так, отношение пройденного расстояния ко времени в пути дает нам новую физическую величину (скорость), размерность которой (м/с, км/час и т. п.). При определении размерности величины обычно пользуются размерностями основных, а не производных величин. Складывать и вычитать можно только величины одинаковой размерности (нельзя сложить, например, сантиметры и граммы).
Любой физический закон и описывающее его уравнение не должны зависеть от выбранной нами системы единиц. Это естественно, так как закон природы описывает соотношение между величинами, которое существовало до нас, существует независимо от нас, и будет существовать после нас. А система единиц — дело произвольного соглашения между людьми. Отсюда вытекает очень важное правило:
Отсюда вытекает очень важное правило:
Обе части любого равенства должны иметь одинаковые размерности.
Написав некое соотношение, всегда можно проверить его правильность путем анализа размерности. Многие студенческие ошибки могут быть выявлены таким путем. Более того, подбором размерностей можно зачастую угадать результат до проведения детальных вычислений.
Приведем пример. Автомобиль трогается с места и движется при этом равноускоренно с ускорением . Какую скорость приобретет автомобиль, пройдя путь ?
Применение анализа размерностей позволяет найти вид искомого соотношения. Скорость является функцией и . Это значит, что она выражается как произведение некоторых степеней этих величин:
где C — некоторая безразмерная постоянная. Надо определить показатели степени и . Запишем формулу размерности для этого соотношения:
или
В силу того, что семь основных единиц являются независимыми, для согласования размерностей обеих частей равенства необходимо, чтобы и удовлетворяли системе уравнений:
откуда следует:
Таким образом, анализ размерностей приводит нас к формуле
Значение безразмерной постоянной C не может быть определено таким способом; при точном решении оно оказывается равным
Как правило, значения безразмерных постоянных в физике типа
и т. п. не слишком велики и не слишком малы. Поэтому анализ размерностей позволяет оценить масштабы тех или иных физических величин, другими словами, определить их по порядку величины, или, что то же самое, найти их с точностью до множителя порядка единицы типа приведенных (для примера) выше.
п. не слишком велики и не слишком малы. Поэтому анализ размерностей позволяет оценить масштабы тех или иных физических величин, другими словами, определить их по порядку величины, или, что то же самое, найти их с точностью до множителя порядка единицы типа приведенных (для примера) выше.
Применение анализа размерностей требует осторожности и определенного искусства. Здесь могут встретиться два подводных камня. Первый из них — определение физических величин, от которых может зависеть результат. Для этого требуется понимание, какие физические законы и явления важны для рассматриваемой системы. Второй подводный камень — существование в данной задаче величин, которые могут образовать безразмерные отношения.
Еще один пример, показывающий, как можно ввести в заблуждение и себя и других, если не учесть все, в том числе и безразмерные параметры задачи. Рассмотрим математичес-кий маятник: материальная точка массы подвешена на невесомой и нерастяжимой нити длины в однородном поле тяжести с ускорением свободного падения . При отклонении нити от вертикали, благодаря возвращающему действию силы тяжести, возникают колебания. Необходимо оценить период этих колебаний или частоту , которая связана с периодом хорошо известным соотношением . Из трех параметров можно составить единственную комбинацию с размерностью частоты, а именно не содержащую массу . Следовательно, (будьте внимательны) частота равна
При отклонении нити от вертикали, благодаря возвращающему действию силы тяжести, возникают колебания. Необходимо оценить период этих колебаний или частоту , которая связана с периодом хорошо известным соотношением . Из трех параметров можно составить единственную комбинацию с размерностью частоты, а именно не содержащую массу . Следовательно, (будьте внимательны) частота равна
Используя связь частоты и периода, получаем
Это точные выражения для частоты и периода малых колебаний математического маятника. Уже это обстоятельство дает почву для подозрений, так как факт малости колебаний, когда их амплитуда ( — угол отклонения нити маятника от вертикали) мала: , в приведенной выше оценке нигде и никак не использовался. Точный результат получился случайно благодаря тому, что в выражении для частоты безразмерный коэффициент был без всяких к тому оснований положен равным единице. В действительности в задаче есть четвертый, причем безразмерный параметр — амплитуда колебаний , поэтому один только анализ размерностей способен дать лишь следующий результат:
где — некоторая функция амплитуды колебаний.
Получить функцию из анализа размерностей невозможно. Решение динамической задачи дает вид этой функции и, в частности, её значение , которое и следует подставлять в последние, из написанных выше формул для частоты и периода, при условии малости колебаний.
Рассмотрим более сложный пример: используя анализ размерностей, найти силу сопротивления среды движущемуся телу. В этой задаче важно с самого начала определить, от каких величин может зависеть искомая сила. Что нам подсказывает опыт? Чем больше скорость движения тела, тем больше сила сопротивления среды. Значит, сила должна зависеть от скорости движения. Далее, тела с большим поперечным сечением испытывают большее сопротивление, чем с меньшим. Поэтому в ответ должна войти площадь поперечного сечения тела. Наконец, сила должна зависеть от параметра, характеризующего свойства среды. Здесь и таится первый подводный камень. Какую характеристику среды выбрать?
Представляется естественным в качестве такого параметра взять плотность (воздуха, жидкости) : чем плотнее среда, тем большее влияние она оказывает на движение тела. Исходя из сказанного, мы ищем силу сопротивления в виде
Исходя из сказанного, мы ищем силу сопротивления в виде
(множитель 2 можно включить в , но мы его выделяем по историческим причинам). Сила имеет размерность произведения массы на ускорение, то есть
Условие совпадения размерностей обеих частей равенства имеет вид:
откуда следует система уравнений
Легко убедиться, что ее решениями являются числа
откуда следует искомая формула
Но почему мы выбрали плотность воздуха в качестве параметра, отвечающего за сопротивление среды? Почему бы в качестве такового не взять величину вязкости воздуха , имеющую размерность . С вязкостью мы еще познакомимся поближе, а пока достаточно интуитивного представления, что при той же плотности среда может быть более или менее вязкой (кисель и компот). Тогда искомая сила может быть представлена в виде
Напишем аналогичное условие равенства размерностей:
откуда следует система уравнений
Ее решением являются числа
то есть искомая формула имеет вид:
Полученные формулы для силы сопротивления совершенно различны: в одной из них сила зависит от скорости квадратично, в другой — линейно. Так какая же из них верна? Данный пример обнажил первый подводный камень: мы должны решить, какой из двух возможных процессов (лобовое сопротивление или вязкость среды) доминирует в конкретной рассматриваемой задаче.
Так какая же из них верна? Данный пример обнажил первый подводный камень: мы должны решить, какой из двух возможных процессов (лобовое сопротивление или вязкость среды) доминирует в конкретной рассматриваемой задаче.
Попробуем перехитрить уравнения: включим в анализ размерности и плотность воздуха, и его вязкость. Будем искать силу сопротивления в виде
Соотношения размерностей принимают форму:
откуда получаем систему уравнений:
Сразу замечаем, что нас ожидает второй подводный камень: у нас всего три уравнения для определения четырех параметров. Стало быть, какой-то из них останется неизвестным. Попробуем разобраться, что бы это значило? Два последних уравнения позволяют выразить параметры и через :
Подставляя их в первое уравнение, получаем
откуда находим
Отсюда получаем силу сопротивления в виде:
Произвольная степень комбинации в скобках указывает на то, что эта комбинация безразмерна. Раз так, она может быть включена в безразмерную величину , которая в этом случае оказывается не постоянной величиной, а функцией безразмерного параметра:
Этот безразмерный параметр (число Рейнольдса ) играет важную роль в определении характера силы сопротивления. Функция называется коэффициентом сопротивления. Детали мы обсудим позднее, но, забегая вперед, сразу скажем: при малых скоростях воспроизводится второе выражение для силы сопротивления, а при больших — первая формула.
Функция называется коэффициентом сопротивления. Детали мы обсудим позднее, но, забегая вперед, сразу скажем: при малых скоростях воспроизводится второе выражение для силы сопротивления, а при больших — первая формула.
Данный пример демонстрирует, как обращаться с безразмерными комбинациями, если таковые возникают при анализе размерности.
Те задачи, которые мы рассматривали до сих пор, решались по существу одинаково и однозначно. Представим себе, что в какой-то задаче нам необходимо отыскать функциональную зависимость между N физическими величинами. Предполагая, что эта зависимость имеет степенной характер, мы можем пытаться решить задачу методом размерностей. При этом если размерности всех N физических величин выражаются через размерности основных величин и если при этом N – 1 = K (где K — количество основных величин), то существует единственная формула, задающая степенную зависимость между N физическими величинами, и эта формула может быть найдена методом размерностей. Общий вид искомой формулы мы записываем так: в левой части стоит одна из N физических величин в первой степени, а в правой — произведение степеней всех остальных (N – 1) физических величин. Показатели степеней являются неизвестными. Всего неизвестных показателей тоже N – 1. Для определения этих показателей нам необходимо (N – 1) уравнений. Каждое из уравнений мы получаем, сравнивая показатели степени, стоящие слева и справа при одной из основных размерностей. Если в нашей задаче встречаются (N — 1) основных размерностей, мы получим ровно столько уравнений, сколько нам требуется. Эти уравнения линейные, а существование и единственность решения системы таких уравнений гарантирует нам существование и единственность искомой степенной формулы.
Общий вид искомой формулы мы записываем так: в левой части стоит одна из N физических величин в первой степени, а в правой — произведение степеней всех остальных (N – 1) физических величин. Показатели степеней являются неизвестными. Всего неизвестных показателей тоже N – 1. Для определения этих показателей нам необходимо (N – 1) уравнений. Каждое из уравнений мы получаем, сравнивая показатели степени, стоящие слева и справа при одной из основных размерностей. Если в нашей задаче встречаются (N — 1) основных размерностей, мы получим ровно столько уравнений, сколько нам требуется. Эти уравнения линейные, а существование и единственность решения системы таких уравнений гарантирует нам существование и единственность искомой степенной формулы.
Однако, возможны ситуации, когда правило N – K = 1 не выполняется, и тогда приходится прибегать к новым подходам. Рассмотрим простую задачу, чтобы проиллюстрировать такой подход:
Какова дальность полёта тела, брошенного под углом к горизонту с начальной скоростью . Мы предлагаем читателю проделать простые вычисления, прежде чем читать учебник дальше.
Мы предлагаем читателю проделать простые вычисления, прежде чем читать учебник дальше.
Попытаемся найти связь между S, и углом с помощью размерностей. Искомая величина дальность, полёта S, может зависеть от начальной скорости бросания , угла бросания, и, несомненно, от ускорения свободного падения (ср. эксперимент по движению тела под углом к горизонту на различных планетах). От массы тела ответ зависеть не должен — размерность искомой величины не содержит размерности «масса».
Таким образом, у нас есть четыре величины — S, , и , зависимость между которыми мы пытаемся установить. В выражения же для размерностей всех этих величин входят только метры и секунды, т. е. N = 4, k = 2 и N – K = 2 > 1. Если записать
то для трёх неизвестных чисел мы можем написать только два уравнения. Как же решить эту проблему?
Давайте введём отдельные единицы для измерения расстояний по вертикали и по горизонтали: расстояния вдоль горизонтальной оси будем измерять в «горизонтальных» метрах — , а расстояния вдоль вертикальной оси Y — в «вертикальных» метрах — . Тогда размерности таковы:
Тогда размерности таковы:
Теперь для N = 4 физических величин уже K = 3 — основными размерностями стали
Формула
Приводит к соотношению
Система уравнений
имеет единственное решение
и мы получаем искомый ответ
(Сравните это решение с тем, которое получилось у вас при точном вычислении: ).
Дополнительная информация
microtm.narod.ru/art-spm/art-spm.html – журнал Материалы, Технологии, Инструменты т.2 (1997) №3 стр.78–89 — сканирующие зондовые микроскопы (А.А. Суслов, С.А. Чижик), — подробно описан атомно-силовой микроскоп, в котором измеряются силы межмолекулярных взаимодействий порядка пиконьютона.
В каких единицах измеряется физическая величина определяемая выражением f bl sin a
Обновлено: 29.09.2022
Автомобиль начал двигаться равноускорено прямолинейно из состояния покоя и через 5 с его скорость стала равной 10м/с.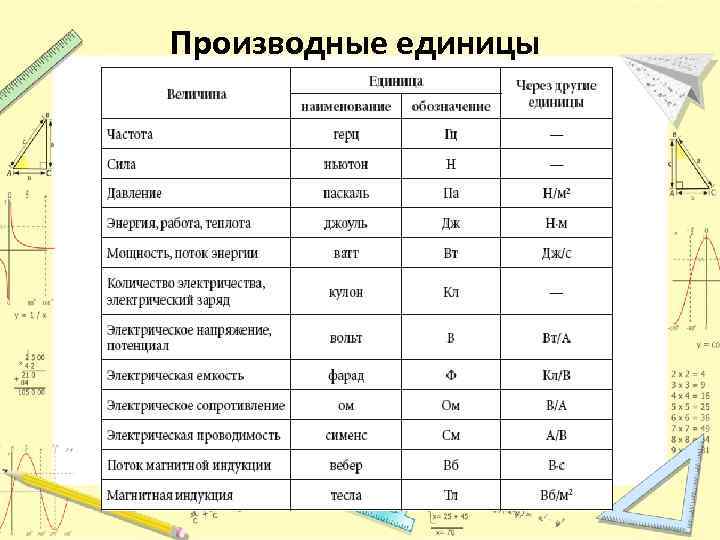 2. Через сколько времени, считая от начала движения первого автомобиля, расстояние между ними окажется равным 240 м? (на листочке если можно)
2. Через сколько времени, считая от начала движения первого автомобиля, расстояние между ними окажется равным 240 м? (на листочке если можно)
ПОМОГИТЕ ПРОШУ ОЧЕНЬ ОЧЕНЬ НУЖНО. отдам последние баллы. Найти радиус враща … ющегося колеса, если известно, что линейная скорость точки, лежащей на ободе, в 3,5 раза больше линейной скорости точки, лежащей на 4 см ближе к оси колеса.
Определите массу Луны, приняв массу Земли равной 6 х 1024 кг, расстояние от Земли до Луны 384 000 км. Период обращения Луны вокруг Земли 27,32 суток.С … рочно
ПОМОГИТЕ ПРОШУ ОЧЕНЬ ОЧЕНЬ СРОЧНО. Движение городского автобуса от одной остановки до другой можно разделить на несколько участков. На перв … ом участке (разгон) скорость возрастает до 36 км/ч за 4 с. На втором участке автобус движется равномерно в течение 25 с. На третьем участке (торможение) автобус за 8 с останавливается. Найди путь, пройденный автобусом, между остановками.
Определи, во сколько раз больше теплоты выделится при полном сгорании бензина, чем при полном сгорании древесных чурок той же массы.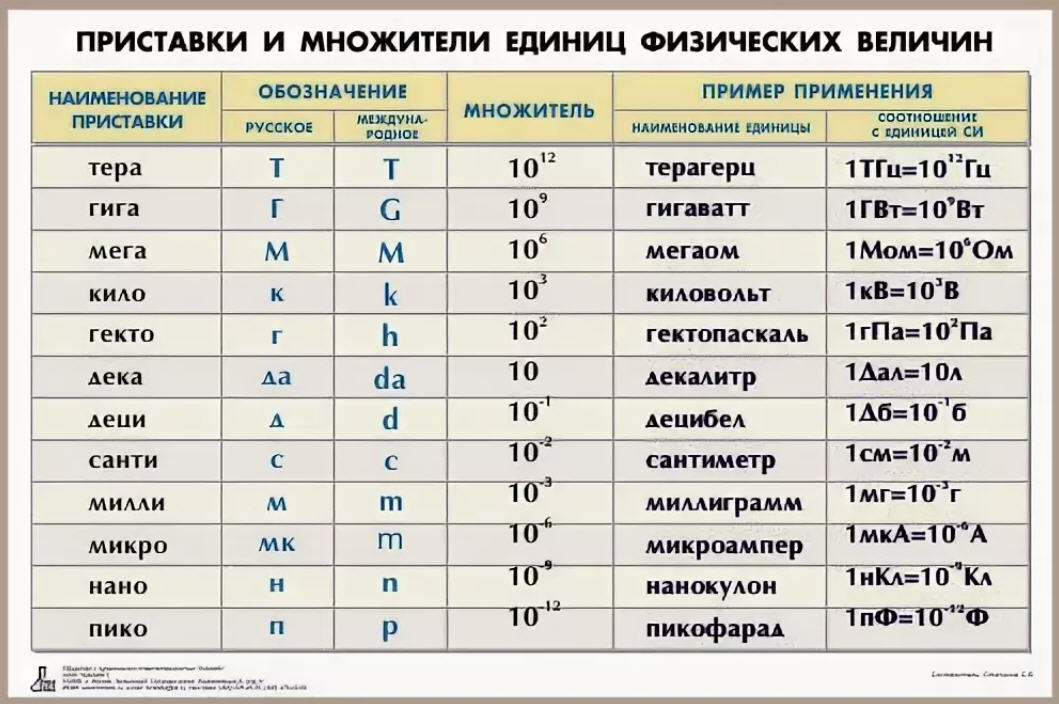 Удельная теплота … сгорания бензина равна 46 МДж/кг, удельная теплота сгорания древесных чурок — 15 МДж/кг.Ответ (округли до десятых)
Удельная теплота … сгорания бензина равна 46 МДж/кг, удельная теплота сгорания древесных чурок — 15 МДж/кг.Ответ (округли до десятых)
1.Розвязати задачу Яка сила діє на прямолінійний провідник зі струмом довжиною 2м, яким тече струм 10 А, якщо цей провідник знаходиться у магнітному п … олі з індукцією у повітрі. Кут між напрямом струму і вектором мантійної індукції дорівнює 3,5*10минус 4 степені. пожалуйста
Дан график зависимости скорости движущегося тела от времени Ux = -10t Ux =30 -6t Ux = 4t Ux =0,5 -t Ux = 100 — 10t Ux = -15t +60 Ux = 10t +4 Ux = -0,8 … t +10 Ux = 20t Ux =5 -5t Построить графики скорости и ускорения движущегося тела:
2. запишите следующие величины, примена и кратные и дольше пристики: 1)5.2 *10³М 2) 1,8*10³М
Удельная теплота сгорания светильного газа равна 21 МДж/м³. Определи, какое количество теплоты (в джоулях) выделится при полном сгорании 4,6 м³ светил … ьного газа. Выбери и отметь правильный ответ.
Яка кількість теплоти необхідна щоб в алюмінієвому казані масою 200г нагріти 2л води від 20° до кипіння
Вопросы 1. Из чего состоят все тела? 2. Что происходит с объёмом газа, жидкости или твёрдого тела при нагревании и охлаждении? 3. Почему объём может и … зменяться? 4. Почему вещества кажутся сплошными? 5. Какой опыт подтверждает малый размер частиц вещества?
Из чего состоят все тела? 2. Что происходит с объёмом газа, жидкости или твёрдого тела при нагревании и охлаждении? 3. Почему объём может и … зменяться? 4. Почему вещества кажутся сплошными? 5. Какой опыт подтверждает малый размер частиц вещества?
1) Чому тіла при нагріванні розширюються2) Аномальність води при нагріванні3) Фізичний зміст питомої теплоємності4) Температуру якого тіла показує тер … мометр5) 3 приклади негативного впливу розширення тіла при нагріванні
Какова единица физической величины, определяемой выражением F / (BL)?
1) Гн 2) В 3)Кл 4) А.
так как F = I * B * L — максимальная сила Ампера
Какая физическая величина может измеряться в единицах В * м : Кл * с?
Какая физическая величина может измеряться в единицах В * м : Кл * с?
AlixYouTube 22 янв. 2019 г., 08:56:13 | 5 — 9 классы
Напишите физические величины которые знаете и какими единицами они измеряются в системе СИ?
Напишите физические величины которые знаете и какими единицами они измеряются в системе СИ.
МукашеваБаян 15 нояб. 2019 г., 07:50:44 | 5 — 9 классы
Физическая величина Единицы измерения Прибор?
Физическая величина Единицы измерения Прибор.
В каких единицах физическая величина измеряется?
В каких единицах физическая величина измеряется.
1)Для чего используются кратные и дольные единицы физических величин?
1)Для чего используются кратные и дольные единицы физических величин?
2)Как определяется значение физических величин при прямых измерениях?
3)Чему равна максимальная погрешность при прямых измерениях?
4)Как определяется значение физической величины при косвенных измерениях?
МукашеваБаян 15 нояб. 2019 г., 07:50:44 | 5 — 9 классы
Единице какой физической величины соответствует выражение Вт х с?
Единице какой физической величины соответствует выражение Вт х с.
Какую физическую величину измеряют с помощью мензурки?
Какую физическую величину измеряют с помощью мензурки?
В каких единицах СИ она измеряется?
Срочно завтра к / р!
Вы находитесь на странице вопроса В каких единицах измеряется физическая величина в выражении : F / Bl sin альфа? из категории Физика.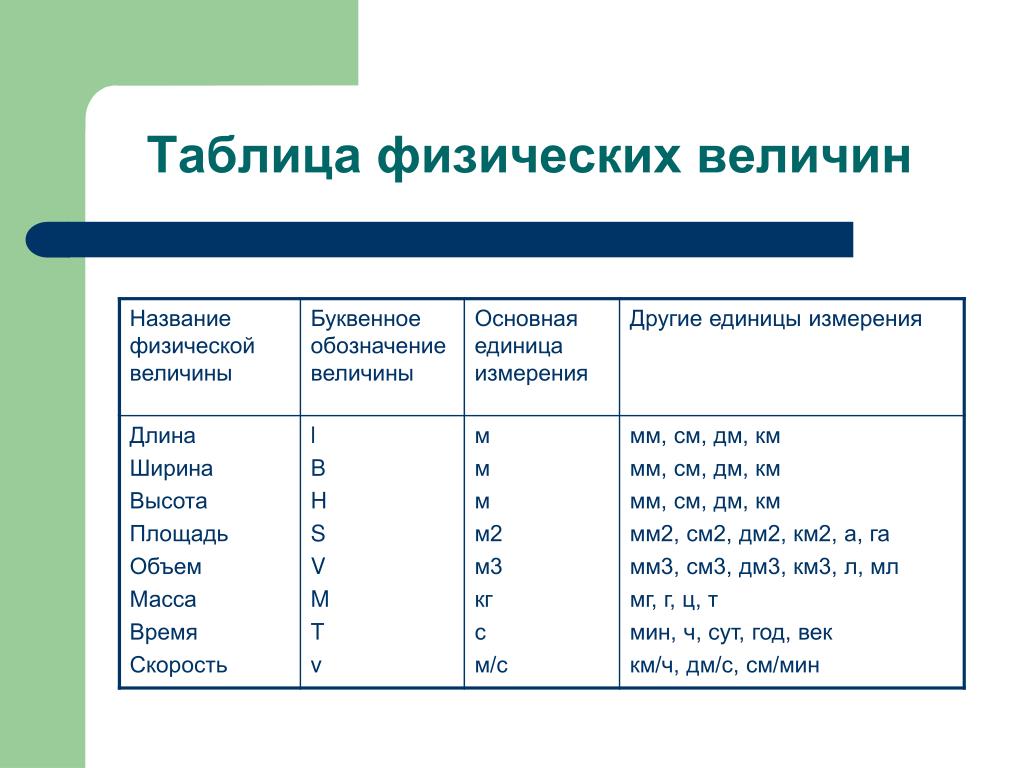 Уровень сложности вопроса рассчитан на учащихся 10 — 11 классов. На странице можно узнать правильный ответ, сверить его со своим вариантом и обсудить возможные версии с другими пользователями сайта посредством обратной связи. Если ответ вызывает сомнения или покажется вам неполным, для проверки найдите ответы на аналогичные вопросы по теме в этой же категории, или создайте новый вопрос, используя ключевые слова: введите вопрос в поисковую строку, нажав кнопку в верхней части страницы.
Уровень сложности вопроса рассчитан на учащихся 10 — 11 классов. На странице можно узнать правильный ответ, сверить его со своим вариантом и обсудить возможные версии с другими пользователями сайта посредством обратной связи. Если ответ вызывает сомнения или покажется вам неполным, для проверки найдите ответы на аналогичные вопросы по теме в этой же категории, или создайте новый вопрос, используя ключевые слова: введите вопрос в поисковую строку, нажав кнопку в верхней части страницы.
Какая физическая величина ранее измерялась в гауссах?
Какая физическая величина ранее измерялась в гауссах?
В каких единицах измеряется сейчас?
Mandrykina055555 22 янв. 2019 г., 16:34:17 | 10 — 11 классы
Какую физическую величину определяют по формуле f = ps?
Какую физическую величину определяют по формуле f = ps.
На этой странице находится вопрос Какова единица физической величины, определяемой выражением F / (BL)?, относящийся к категории Физика. По уровню сложности данный вопрос соответствует знаниям учащихся 10 — 11 классов. Здесь вы найдете правильный ответ, сможете обсудить и сверить свой вариант ответа с мнениями пользователями сайта. С помощью автоматического поиска на этой же странице можно найти похожие вопросы и ответы на них в категории Физика. Если ответы вызывают сомнение, сформулируйте вопрос иначе. Для этого нажмите кнопку вверху.
По уровню сложности данный вопрос соответствует знаниям учащихся 10 — 11 классов. Здесь вы найдете правильный ответ, сможете обсудить и сверить свой вариант ответа с мнениями пользователями сайта. С помощью автоматического поиска на этой же странице можно найти похожие вопросы и ответы на них в категории Физика. Если ответы вызывают сомнение, сформулируйте вопрос иначе. Для этого нажмите кнопку вверху.
F1 × l1 = F2 × l2 F2 = (F1 × l1) / l2 = (6 × 0. 2 ) / 0. 4 = 3 H Ответ : 3 Н.
30 потому что и число внем больше.
Это максимум, что я могу предложить.
1) Тонет, если Fтяж>Fa Плотность больше, чем у жидкости. 2) Плавает, если Fтяж = Fa Плотности равны. 3) Всплывает, если Fтяж.
Cm(t2 — t1) = qm * 0. 4 m = qm * 0. 4 / cm(t2 — t1) m = 24. 55кг 1 кг воды = 1 л воды Ответ 24. 55л.
Угол падения ≈53⁰. Угол преломления = 37⁰.
Держи решение в файле.
Дано F = 100 H m = 30 кг l = 3 м h = 0. 5 м Найти кпд — ? Решение кпд = А полез \ А затр А полез = mgh = 30 * 10 * 0. 5 = 150( Дж) А затр = Fl = 100 * 3 = 300(Дж) кпд = 150 / 300 = 0. 5 = 50%.
5 м Найти кпд — ? Решение кпд = А полез \ А затр А полез = mgh = 30 * 10 * 0. 5 = 150( Дж) А затр = Fl = 100 * 3 = 300(Дж) кпд = 150 / 300 = 0. 5 = 50%.
Дано N = 10 P1 = 100 ват A — ? P = P1 * 10 = 1000 Вт = 1 кВтA = P * t = 1 кВт * 3ч = 3 кВт * ч.
Сила тяжести F = mg Масса m = po× V V = 5×0, 3×2 = 3м3 m = 900×3 = 2700кг F = 2700×10 = 27 000H = 27кН Ответ 27кН.
В каких единицах измеряется физическая величина в выражении : F / Bl sin альфа.
В каких единицах измеряется физическая величина в выражении : F / Bl sin альфа.
В Амперах — — это сила тока I = F / Bl sin альфа.
Единице какой физической величины соответсвует выражение н / м?
Единице какой физической величины соответсвует выражение н / м.
В каких единицах измеряется физическая величина расчитывается по формуле р / kT?
В каких единицах измеряется физическая величина расчитывается по формуле р / kT.
Yliaklimcina 23 сент. 2019 г., 11:41:15 | 10 — 11 классы
2019 г., 11:41:15 | 10 — 11 классы
Записать в тетрадь 3 — 5 примеров тел, являющихся измерительными приборами?
Записать в тетрадь 3 — 5 примеров тел, являющихся измерительными приборами.
Для каждого из них укажите : а) какую физическую величину измеряет прибор ; б) в каких единицах измерения можно измерять эту физическую величину.
A4704456trbvmcom 25 июл. 2019 г., 02:33:20 | 5 — 9 классы
1. Какая физическая величина определяется с помощью рычажных весов?
1. Какая физическая величина определяется с помощью рычажных весов?
2. В каких единицах она измеряется (назовите все)?
Приведите примеры физических величин и их единиц?
Приведите примеры физических величин и их единиц.
В каких единицах физическая величина измеряется?
В каких единицах физическая величина измеряется.
Щрчриеримррсотгио 23 авг. 2019 г., 09:47:42 | 10 — 11 классы
2019 г., 09:47:42 | 10 — 11 классы
Какая физическая величина может измеряться в единицах В * м : Кл * с?
Какая физическая величина может измеряться в единицах В * м : Кл * с?
AlixYouTube 22 янв. 2019 г., 08:56:13 | 5 — 9 классы
В каких единицах измеряется физическая величина в выражении : F / Bl sin альфа?
В каких единицах измеряется физическая величина в выражении : F / Bl sin альфа.
Помогите?
Как вычисляется физическая величина ?
В каких единицах измеряется физическая величина?
Как называется величина характеризующая быстроту измерения скорости?
Как её вычисляется?
В каких единицах её измеряется?
Каким прибором измеряют скорость движущегося автомобиля?
1. Какая физическая величина определяется с помощью рычажных весов?
1. Какая физическая величина определяется с помощью рычажных весов?
2. В каких единицах она измеряется (назовите все)?
Назовите известные вами физические величины?
Назовите известные вами физические величины?
Укажите единицы на этих величин.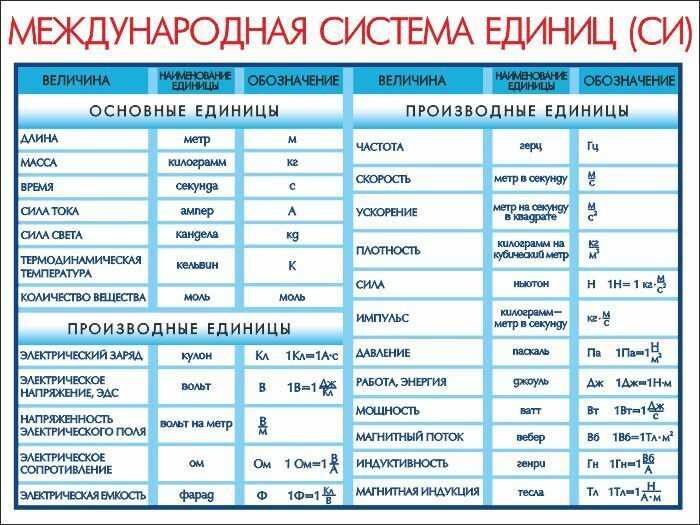
Какими приборами их измеряют?
Сашуленька13 22 июл. 2019 г., 11:48:12 | 5 — 9 классы
Читайте также:
- Будет ли ноутбук работать без интернета
- Dracula 3 the path of the dragon проблемы
- Final fantasy 13 трофеи
- Скайрим ретекстур соловьиного клинка
- Секс с девушкой в заброшенном доме
Единицы измерения величин для школьников
Опубликовано:
Какие существуют единицы измерения и для чего они нужны? Люди часто используют в оценках числа, а потом сравнивают их.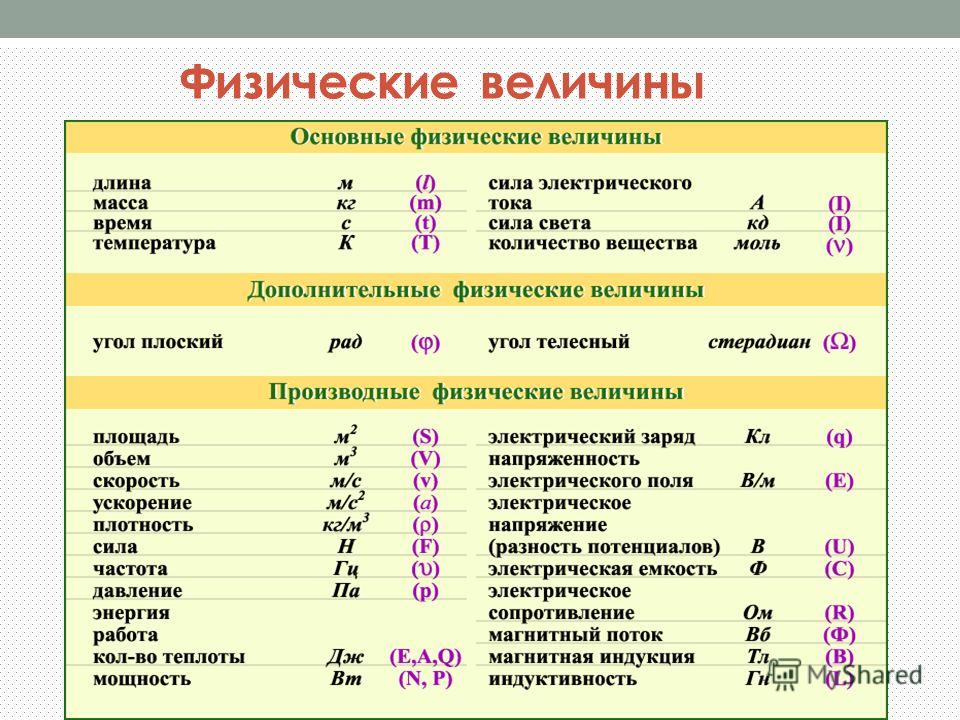 Меры величин помогают сделать этот процесс одинаковым для всех. Вот почему школьники по всему миру изучают одни и те же единицы измерения.
Меры величин помогают сделать этот процесс одинаковым для всех. Вот почему школьники по всему миру изучают одни и те же единицы измерения.
Меры длины
Величинами называют все, что поддается измерению. Так говорят о длине, площади, объеме, массе, времени, скорости. Величины — результат измерений, число, выраженное в определенных единицах. Последние известны как единица измерения.
Чтобы обозначить величину, пишут число, а рядом с ним указывают единицу, в которой проводилось измерение. К примеру, 3 см, 15 кг, 20 км, 2 мин. Для каждой величины общее число возможных значений не ограничено. Так, длина может быть 1 см, 10 см, 100 см и т. д. Одну и ту же величину в разных единицах выражают с помощью разных чисел.
Кроме того, одну и ту же величину могут выражать по-разному. Например, используются различные единицы измерения длины в зависимости от того, насколько она маленькая или большая. В школе используются такие из них:
- Наименьшая единица — миллиметр (мм).
 Его легко увидеть на самой обычной линейке, которая есть у каждого школьника. Это самое маленькое деление, а точнее расстояние между ними.
Его легко увидеть на самой обычной линейке, которая есть у каждого школьника. Это самое маленькое деление, а точнее расстояние между ними. - Следующей единицей стал сантиметр (см). На линейках сантиметры обозначаются числами. Один сантиметр состоит из десяти миллиметров. Между этими величинами ставится знак равенства, так как с их помощью обозначается одна и та же длина: 1 см = 10 мм.
- За сантиметром следует дециметр (дм). Один дециметр состоит из десяти сантиметров. Эти величины также равны, что обозначается следующим уравнением: 1 дм = 10 см.
- За дециметром следует метр (м), который содержит десять дециметров, то есть 1 м = 10 дм. В домашних условиях метр проще всего увидеть, если взять рулетку, длина которой часто составляет 1 метр. Сколько сантиметров в нем и как переводят сантиметры в метры? Один метр содержит десять дециметров, а они, в свою очередь, сто сантиметров (1 м = 10 дм = 100 см).
- Самая большая единица в этой категории в рамках стандартной школьной программы — километр.
 Один километр состоит из тысячи метров, что обозначается так: 1 км = 1000 м. Километры используются для измерений расстояний между странами и городами. Можно, конечно, переводить миллиметры в метры и далее, но более крупные величины все же удобнее.
Один километр состоит из тысячи метров, что обозначается так: 1 км = 1000 м. Километры используются для измерений расстояний между странами и городами. Можно, конечно, переводить миллиметры в метры и далее, но более крупные величины все же удобнее.
Существуют и более крупные меры, например мегаметры, гигаметры, тераметры, но они выходят за рамки знаний, необходимых школьнику.
Сантиметры и миллиметры: FreepickТаким образом, меры величин, с помощью которых можно измерить длину, таковы:
Меры длины: NUR.KZМеры веса
Массой называют величину, которая обозначает, сколько вещества содержит тело. В обиходе масса получила название вес. Часто при взвешивании говорят: «Вес этого вещества (материала, предмета) такой-то». Но на самом деле это не вес, а масса данного тела.
Таким образом, масса и вес — не одно и то же. Весом называют силу, которую тело прилагает к горизонтальной опоре. Вес измеряют в ньютонах. Масса же как величина отражает количество.
Как же выразить значение массы и что для этого надо знать? Основные единицы измерения массы таковы:
- Самая маленькая единица — миллиграмм (мг).
 Миллиграммы редко применяются на практике. Их используют химики и другие ученые, работа которых связана с маленькими количествами веществам. В обычной жизни редко отмеряем что-либо миллиграммами.
Миллиграммы редко применяются на практике. Их используют химики и другие ученые, работа которых связана с маленькими количествами веществам. В обычной жизни редко отмеряем что-либо миллиграммами. - Следующей единицей стал грамм (г). В граммах часто измеряют количество продуктов, когда составляют рецепты. Один грамм состоит из тысячи миллиграммов. Между этими величинами ставят знак равенства, так как они тождественны: 1 г = 1000 мг.
- Следующая единица — килограмм (кг). Это общепринятая единица измерения в мире, включенная в международную систему. Один килограмм содержит тысячу граммов, то есть: 1 кг = 1000 г.
- За килограммом следует центнер (ц). В центнерах измеряется масса урожая, который собирают с небольших участков или масса различных грузов. Один центнер — это сто килограммов (1 ц = 100 кг).
- Тонна (т) — самое большое значение, с которым сталкиваются школьники, когда изучают массу предметов. Тонны используют, чтобы измерить большой груз и массу больших тел, таких как космические корабли или автомобили.
 Одна тонна состоит из тысячи килограмм (1 т = 1000 кг).
Одна тонна состоит из тысячи килограмм (1 т = 1000 кг).
Если обобщить представленную выше информацию, то для измерения массы существует:
Меры веса: NUR.KZМеры объема
В каждом государстве устанавливают определенные единицы для измерений различных величин. Единица измерения, которую рассчитали точно, принимается как образец. Ее называют эталоном или образцом.
Существует стандарт килограмма, метра и т. п., на которые равняются во всех странах. Единицы, которые вошли в употребление и утверждены на государственном уровне, называют меры.
Меры могут быть однородными, если с их помощью измеряют величины одного рода. К примеру, ряд однородных мер для измерения объема таков:
- 1 куб. метр = 1000 куб. дециметров;
- 1 куб. дециметр = 1000 куб. сантиметров;
- 1 куб. сантиметр = 1000 куб. миллиметров.
Кроме того, широко используется такая величина, как литр. С его помощью удобно обозначать вместимость сосудов.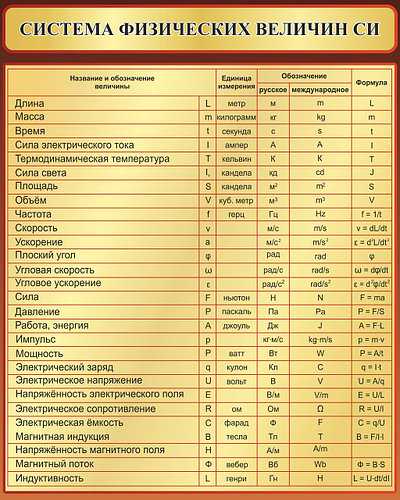 Литр — это объем, который соответствует одному кубическому дециметру (1 литр = 1 куб. дециметру). Эта единица получила свое название в память о виноделе Литре из Франции.
Литр — это объем, который соответствует одному кубическому дециметру (1 литр = 1 куб. дециметру). Эта единица получила свое название в память о виноделе Литре из Франции.
В древности объемы измерялись самыми разными единицами: сиеками, горстками, тинами, пурами, цибами, штофами, ложками (1 тина = 3 пуры = 9 сиеков = 720 горсток = 162 штофа = 208 литров). Но сейчас о них уже забыли, так как распространение получила единая унифицированная система.
Меры площади
Для удобства страны мира пользуются международной системой единиц СИ. Это французское сокращение, которое расшифровывается так: Le Système International d’Unités, SI.
Это система, в которой для наиболее распространенных величин определены общепринятые единицы измерения. Так, ученые пришли к соглашению измерять длину в метрах. Поэтому когда в задачах длины даются в других единицах измерения (например, в миллиметрах), то их переводят в метры.
Как измеряют площадь? С этой целью применяют разнообразные меры:
- Квадратным сантиметром обозначается квадрат, сторона которого равна одному сантиметру.

- Для квадратного дециметра следует представить квадрат со стороной длиной в один дециметр.
- Соответственно, квадратный метр — квадрат, сторона которого 1 м в длину.
- Очень большие площади измеряют квадратными километрами. У такого квадрата сторона равняется одному километру.
Словосочетание «квадратный километр» сокращенно на письме отражается так: 2 км², 5 км², 15 км². В этих единицах обычно измеряют площади городов.
Для измерения площади используются:
Меры площади: NUR.KZТаковы основные единицы измерения, но в науке их арсенал гораздо шире. Людям нравится все измерять, а мир очень многогранен. Отсюда и разнообразие мер величин. К счастью, освоить и использовать их под силу каждому из нас.
Оригинал статьи: https://www.nur.kz/family/school/1904238-edinitsy-izmereniya-velichin-dlya-shkolnikov/
Единицы измерения
Единица измерения — это величина, используемая в качестве стандарта для выражения физической величины. Ниже приведены основные количества
измеряемые и используемые единицы измерения:
Ниже приведены основные количества
измеряемые и используемые единицы измерения:
Длина — описывает длину чего-либо. Расстояние, высота, толщина, и глубина также используют одни и те же единицы измерения.
Ниже приведены некоторые общие единицы измерения:
• Миллиметр (мм) – метрическая единица, обычно используемая для выражения длины очень маленьких предметов, таких как ключи, и толщины мелкие предметы, такие как блокнот.
• сантиметр (см) – метрическая единица, обычно используемая для выражения длины мелких предметов. Он также используется для измерения рост человека.
• inch (in) – английская единица измерения, обычно используемая для выражения длины небольших предметов, таких как коробки и бутылки.
• фут (ft) – английская единица, эквивалентная 12 дюймам. Он обычно используется для выражения коротких расстояний и высоты всех объекты, такие как деревья и здания.
Линейка — это обычный инструмент, используемый для измерения длины небольших предметов. Обычно он имеет четыре единицы измерения на выбор: миллиметр, сантиметр, дюйм и фут.
Измерительная линейка — это инструмент для измерения коротких расстояний.
Для коротких расстояний обычно используются метрические единицы метр (м) и английская единица ярдов (ярд) .
Для больших расстояний обычно используются метрическая единица километра (км) и английская единица мили (миля) .
Масса — описывает, насколько что-то тяжелое.
Ниже приведены некоторые общие единицы измерения:
• миллиграмм (мг) — метрическая единица, обычно используемая для выражения массы очень маленьких предметов, таких как конфеты.
• грамм (г) – метрическая единица, являющаяся базовой единицей массы. Он обычно используется для выражения массы небольших предметов, таких как апельсин, яйцо и помидор.
• унция (oz) – английская единица измерения, обычно используемая для выражения массы o
• килограмм (кг) – английская единица измерения, обычно используемая для измерения коротких расстояний и высоты высоких объектов, таких как деревья и здания.
• фунт (lb) – английская единица измерения, обычно используемая для измерения коротких расстояний и высоты высоких объектов, таких как деревья и здания.
• тонна – английская единица измерения, обычно используемая для измерения коротких расстояний и высоты высоких объектов, таких как деревья и здания.
Весы — это инструмент, обычно используемый для измерения массы фруктов, овощей и мяса. Весы откалиброваны в граммах и килограммах
Время – описывает, сколько времени требуется, чтобы что-то сделать.
В метрической и английской системах измерения времени используются одни и те же единицы измерения.
Вот некоторые из общих единиц измерения:
• секунда (с) – основная единица измерения времени. Одна секунда эквивалентна тиканию секундной стрелки часов.
• минута (мин) – единица, эквивалентная одному обороту секундной стрелки часов или одному тиканию длинной (минутной) стрелки часов.
• час (hr) – единица, эквивалентная одному обороту длинной (минутной) стрелки часов или одному тиканию короткой (часовой) стрелки часов.
Часы — это обычный инструмент для индикации времени. Он показывает время в часах, минутах, а иногда и в секундах.
Он показывает время в часах, минутах, а иногда и в секундах.
• день (д) – единица, эквивалентная двум оборотам короткой (часовой) стрелки часов.
• неделя (нед) – это единица, эквивалентная 7 дням.
• месяц (mo) – единица измерения, равная 30 дням. Он обычно используется для определения возраста младенца или детеныша животного.
• год (год) – единица измерения, равная 12 месяцам. Он обычно используется для определения возраста человека или объекта.
Площадь – описывает, сколько поверхности занято чем-либо.
При измерении площади используются те же единицы измерения длины. Единственная разница в том, что единицы измерения «квадратные», поскольку площадь является произведением двух измерений.
(обычно длина и ширина, которые используют одну и ту же единицу измерения).
92` или кв.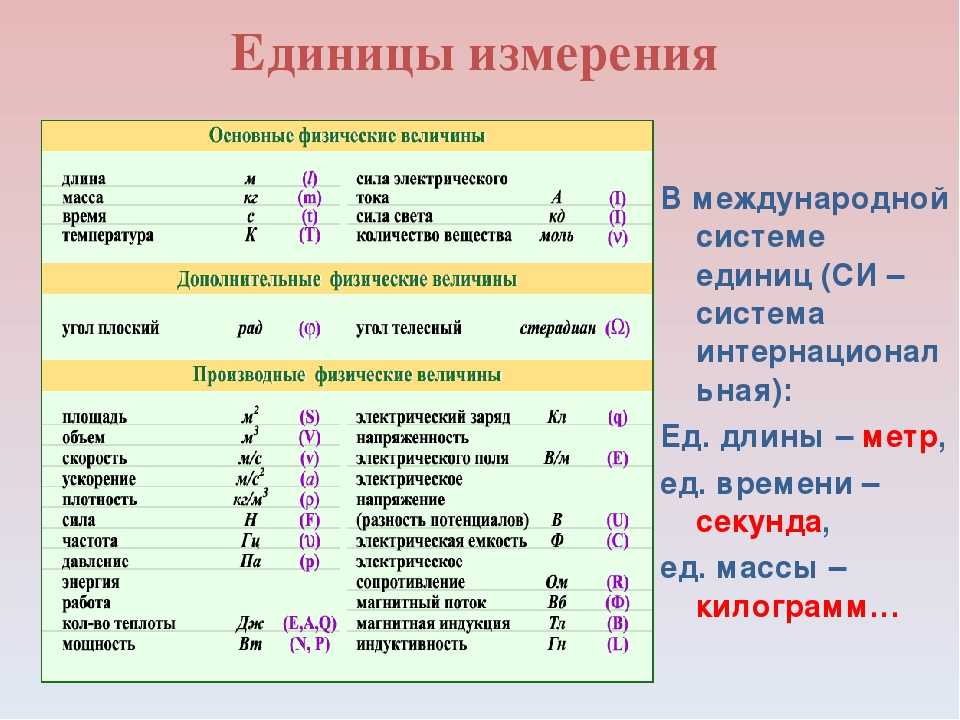 м) – метрическая единица, эквивалентная квадрату со стороной 1 м каждая. Обычно используется в
Измерение площади жилого дома.
м) – метрическая единица, эквивалентная квадрату со стороной 1 м каждая. Обычно используется в
Измерение площади жилого дома.
• акр – английская единица измерения земельной площади, например ферм и парков развлечений.
• гектар (га) – метрическая единица, эквивалентная квадрату со стороной 100 м каждая. Как и акр, он в основном используется для измерения земель.
Размер футбольного поля обычно составляет около 1 га.
Том — описывает, сколько пространства (или жидкости) занято (или содержится) чем-то. Подобно площади, объем также использует единицы длины, но с той лишь разницей, что единица «кубическая». Кубические единицы обычно используются для объемов пространства, хотя существуют также единицы объема. предназначен для измерения жидкости.
Ниже приведены некоторые общие единицы измерения: 93` или cc) — метрическая единица объема (как пространства, так и жидкости), соответствующая кубу со сторонами
по 1 см.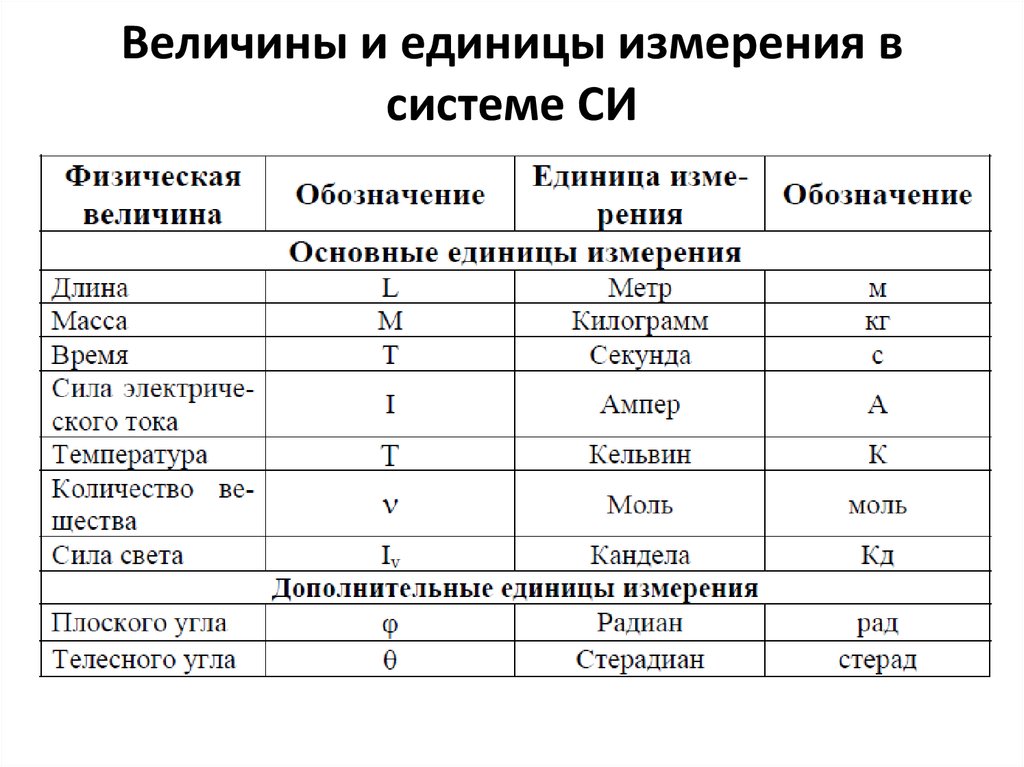 Кубический сантиметр равен миллилитру.
Кубический сантиметр равен миллилитру.
• Жидкая унция (fl oz) – английская единица измерения, обычно используемая для измерения количества жидкостей в бутылках, таких как безалкогольные напитки.
• чашка – английская единица, эквивалентная 8 жидким унциям. Он обычно используется для измерения ингредиентов для приготовления пищи и выпечки.
Мерный стакан — это кухонная утварь, используемая для измерения объема жидкости или таких ингредиентов, как мука и сахар.
• пинта (pt) – английская единица, эквивалентная 2 чашкам. Он обычно используется в различных товарах.
• кварта (qt) – английская единица, эквивалентная четверти галлона.
• литр (л) – основная единица объема. Он обычно используется для измерения большого количества жидкости, такой как бензин.
• галлон (gal) – английская единица измерения литр.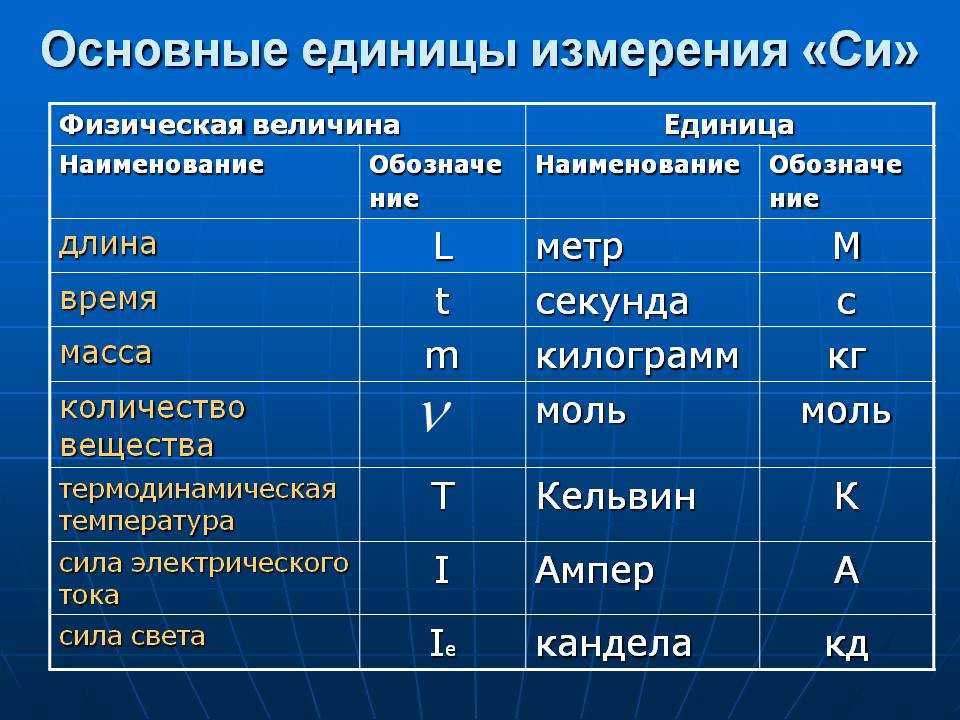
Емкость бензина обычно составляет 1 галлон.
Температура — описывает, насколько что-то горячее или холодное.
Ниже приведены распространенные единицы измерения:
• Шкала Цельсия (°C) – это метрическая единица измерения температуры и наиболее часто используемая единица измерения температуры во всем мире. В этой шкале точка кипения воды находится на уровне 100°С, а точка замерзания – на уровне 0°С.
• Шкала Фаренгейта (°F) – английская единица измерения температуры, которая обычно используется в США. В этой шкале точка кипения воды составляет 212 ° F, а точка замерзания — 32 ° F.
• Шкала Кельвина (К) – это единица СИ для температуры. В отличие от двух других температурных шкал шкала Кельвина не использует градусы. Его нулевая точка, 0 К, определяется как самая низкая возможная температура.
который также называют абсолютным нулем.
Термометр является наиболее распространенным прибором для измерения температуры. Обычно он откалиброван как по шкале Цельсия, так и по шкале Фаренгейта.
Объяснение урока: Единицы измеряемых величин
В этом пояснении мы узнаем, как распознавать, какие единицы используются для определения значений физических величин.
Полезно начать с разъяснения того, что понимается под измерением.
Измерение состоит из четырех частей:
- Измеряемый объект.
- Количество объекта.
- Значение количества.
- Единица измерения значения.
Давайте рассмотрим пример.
Измеряется масса кирпича. Масса кирпича 1,5 килограмма.
Рассмотрим четыре части измерения.
| Измеряемый объект | The brick |
|---|---|
| Quantity of the object | Its mass |
| Value of the quantity | 1.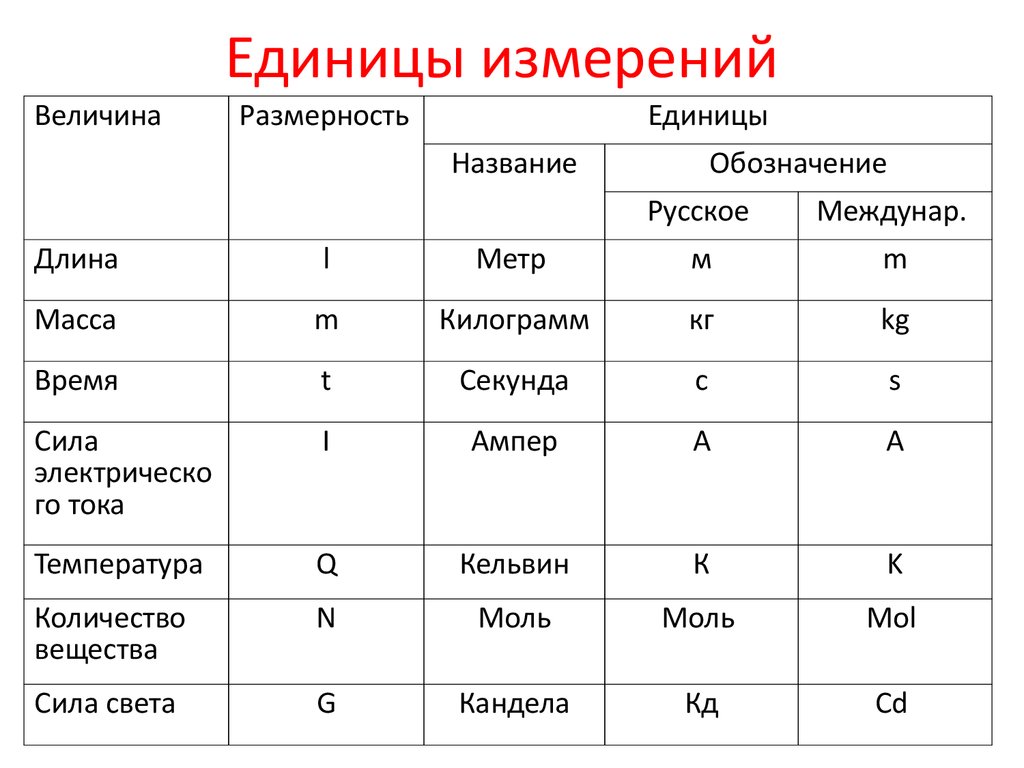 5 5 |
| Unit that the value takes | Kilograms |
The meaning of quantity is легко спутать со значением значение , так как слово «количество» часто используется для обозначения количества чего-либо.
Однако, говоря об измерениях, количество не является количеством чего-либо; это то, чего может быть сколько угодно.
Давайте посмотрим на другой пример.
Измеряется время, необходимое для таяния кубика льда массой 5 грамм. Затраченное время 250 секунд.
Рассмотрим четыре части измерения.
| Объект, измеренный | The Ice Cube |
|---|---|
| Количество | Tome To To Tred |
| Значения | |
| Value of the Caft of the Caft | |
| Секунды |
Значение и единица измерения имеют другие свойства, чем объект и величина измерения. Объект и количество
измерение определяется только одним способом, но значение и единица измерения могут быть определены несколькими способами.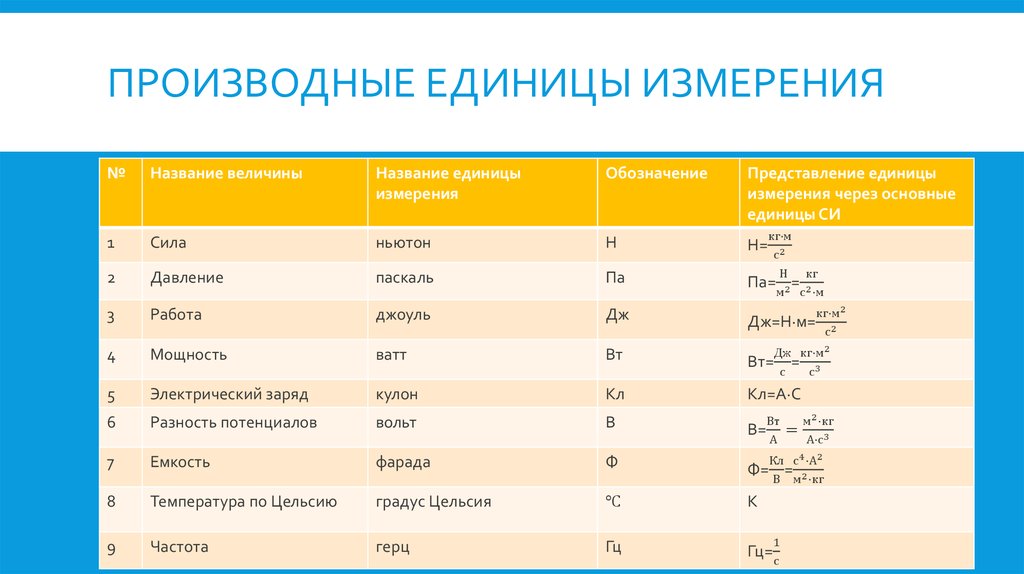
Если мы измеряем что-то в кирпиче, мы измеряем этот конкретный кирпич. Измерение другого объекта ничего не говорит нам напрямую о кирпиче. Если мы измерим температуру кирпича, это ничего не скажет нам напрямую о массе кирпича. Если мы попытаемся определить массу кирпича по говоря о другом объекте или количестве, мы имеем в виду другое измерение, чем измерение массы кирпича; есть единственный уникальный способ установления объекта и количества для данного измерения.
«Масса кирпича 1,5 кг» — не единственный способ указать массу кирпича. Это связано с тем, что «1,5 килограмма» также можно выразить по-разному, например,
- 1 500 грамм,
- 0,0015 тонны,
- 3,30693 фунта.
Мы видим, что при изменении единицы измерения изменяется и значение измерения. Это можно понять, если подумать о значении и единице измерение как перемножение.
Мы можем выразить 1,5 килограмма как
1,5×, кг
где мы используем символ кг для килограммов.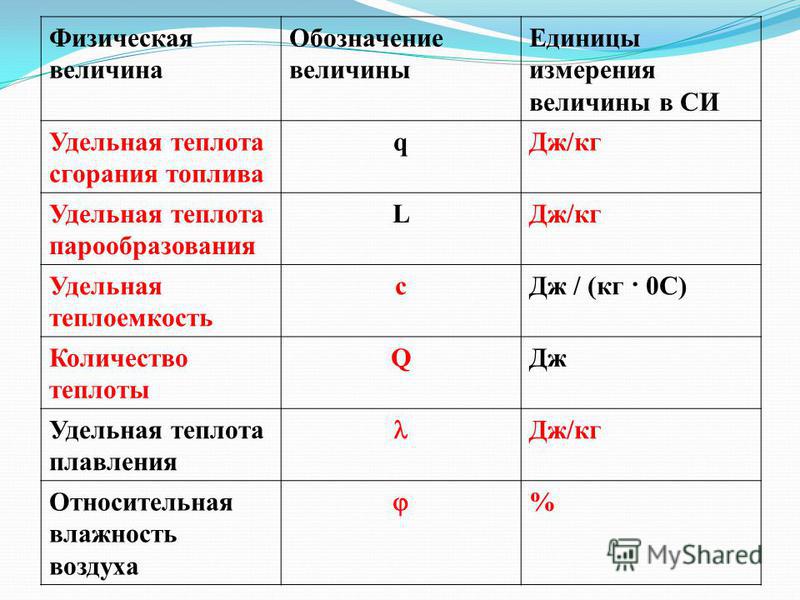
Мы знаем, что 1×=1000×,кгг где мы используем символ g для граммов.
Итак, мы видим, что 1,5×=1,5×(1000×)1,5×=1500×.kggkgg
Мы только что показали, что единицу можно умножить на значение, чтобы получить другую единицу. Мы также можем разделить единицу на значение, чтобы получить другую единицу, как показано в следующем примере: 1×=11000×1500×=1500×11000×1500×=15001000×1500×=1,5×.gkggkggkggkg
Те же умножения и деления могут быть выполнены с единицами других величин, как только что было показано для единиц массы: 1×=1000×1×=11000×.kmmmkm
Помимо умножения или деления на значение, единицу можно умножать или делить на другую единицу.
Простейшим случаем умножения единицы на единицу является умножение единицы на саму себя.
Рассмотрим прямоугольный объект со сторонами длиной 7,5 м и 1,5 метра, как показано на следующем рисунке.
Площадь объекта 𝐴 равна произведению длин его сторон. Мы можем выразить это как
𝐴=1,5×7,5=11,25.
Площадь должна иметь единицу измерения, так как площадь — это количество.
Из уравнения неясно, какой должна быть единица, и эта неясность связана с тем, что единицы перемноженных значений не были включены в уравнение.
Если единицы значений включены в значения, вместо этого мы получаем 𝐴=(1,5×)×(7,5×).мм
Порядок умножения членов уравнения не меняет результат уравнения, поэтому мы можем выразить это уравнение как 𝐴=1,5×7,5××, мм
Мы видели, что 1,5×7,5=11,25, но мы не определили результат мм×.
Если бы вместо m значение было умножено само на себя, например, значение 4, мы бы получили 4×4=16.
Нет эквивалентного результата умножения m на m, но 4×4=16 также может быть выражено как 4×4=4.
Это означает, что мы можем выразить m, умноженное само на себя, как ммм×=.
Эта единица измерения представляет собой квадратный метр или квадратный метр.
Итак, мы видим, что 𝐴=(1,5×)×(7,5×)=11,25.ммм
Единицы можно умножать или делить на другие единицы, а также сами по себе.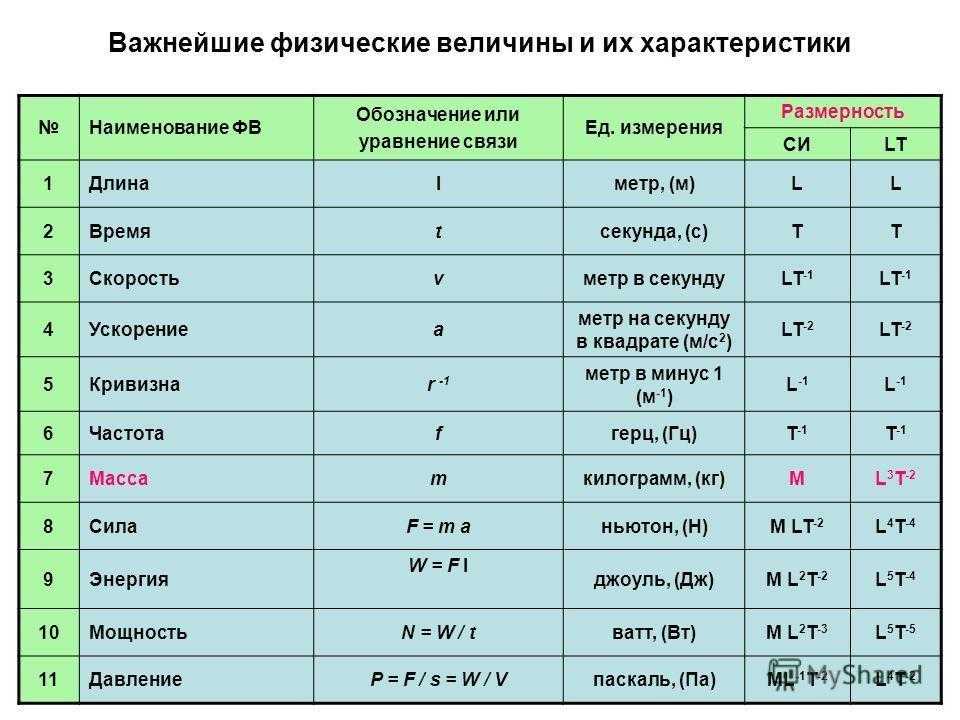
Давайте рассмотрим пример с единицами, которые умножаются или делятся сами на себя или на другие единицы.
Пример 1. Определение единицы площади
Что из следующего является единицей площади?
- Квадратный метр
- Сантиметр
- Метр на секунду в квадрате
- Кубический метр
Ответ
Умножение одной длины на другую длину есть уравнение площади прямоугольника. Уравнения площадей других форм задаются другими умножения, но уравнения по-прежнему включают умножение длин. Длина может быть измерена в метров.
Все варианты содержат слово «метр», так что сразу не очевидно, что любой из вариантов неверен.
Сантиметр — единица длины. Площадь включает в себя умножение длин на другие длины. Умножение длин, измеренных в сантиметрах, потребует умножения
сантиметры на сантиметры. Результат умножения сантиметров на сантиметры
не сантиметры, поэтому сантиметры не могут быть единицей
область. На самом деле никакая единица длины не может быть единицей площади.
На самом деле никакая единица длины не может быть единицей площади.
Из оставшихся вариантов два включают слово «квадрат» или «квадратный», а один включает слово «кубический».
Возведение в квадрат значения или единицы означает умножение ее самой на себя. Это согласуется с умножением длины на длину. Кубирование длины означает умножение квадрата длины длина на длину, в результате чего получается объем, а не площадь. Таким образом, мы можем устранить кубический метр как единица площади.
Осталось выбрать между вариантами «квадратный метр» и «метр на секунду в квадрате».
Слово «на» указывает на деление, поэтому «метр на секунду в квадрате» означает «метр, разделенный на секунда в квадрате». А метр — это единица длины. Мы должны решить, можно ли разделить длину на второй в квадрате эквивалентен умножению длины на длину.
Секунда — это единица времени, а не длины.
секунда в квадрате — это единица времени, умноженная на время, которое не связано с длиной.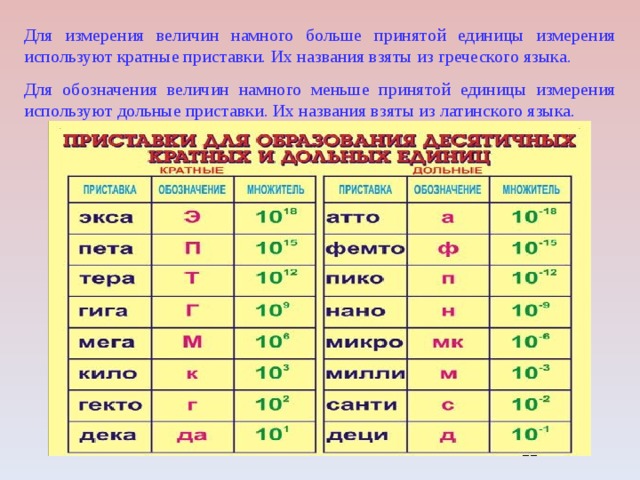 Таким образом, мы можем исключить метр на секунду в квадрате.
Таким образом, мы можем исключить метр на секунду в квадрате.
Мы видели, что возведение значения или единицы в квадрат означает умножение их самих на себя. Квадратный метр это, следовательно, метр, умноженный на метр. А метр является единицей длины, поэтому метр умножить на метр это единица площади.
Давайте теперь посмотрим на другой такой пример.
Пример 2: Идентификация символа для составной единицы
Какой из следующих символов является подходящим символом для единицы количества, полученного путем деления температуры на расстояние?
- К/м
- км
- К⋅м
- К/м 2
- мК
Ответить
на расстоянии. Стоит задуматься, что такое количество мог представлять.
Одним из примеров деления температуры на расстояние может быть нагрев одного конца длинного металлического стержня и в какой-то момент температура была записана в разных точках.
по длине стержня.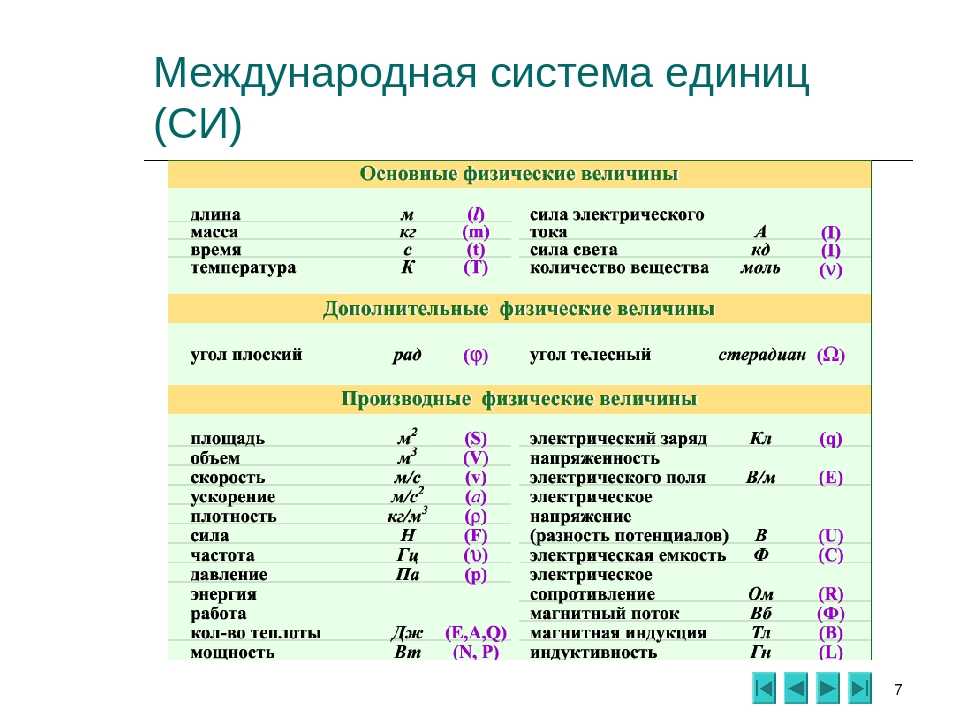 Измерения будут производиться по температуре и по расстоянию. Эти измерения можно представить в виде графика, как показано на следующем рисунке.
Измерения будут производиться по температуре и по расстоянию. Эти измерения можно представить в виде графика, как показано на следующем рисунке.
Градиент этого графика будет равен изменению температуры на изменение расстояния, т.е. температура, деленная на расстояние.
Рассматривая варианты, мы видим, что все они включают символы m и К или к. Это связано с тем, что существуют величины температуры и расстояния, которые имеют следующие единицы измерения с этими символами:
- Расстояние — это величина, которая может быть измерена в метрах, которая имеет символ м.
- Температура – это величина, которая может быть измерена в градусах Кельвина, которая имеет символ K.
Параметр «км» имеет только символы нижнего регистра, но правильный символ для
кельвин это «К»,
который в верхнем регистре. Символ «км» на самом деле является символом единицы измерения.
километр, что равно 1 метрам. Тогда это единица расстояния, а не единица измерения температуры, деленная на расстояние, так что это неверно.
Параметр «mK» включает символ кельвина, но на самом деле является символом единица милликельвин, т. 11000 кельвинов. Тогда это единица температуры, не единица измерения температуры, деленная на расстояние, так что это неверно.
Символ «К⋅м» соответствует количеству температуры, умноженному на единицу. Мы знаем, что нам нужен символ для единицы измерения температуры, разделенной на расстояние. Вероятно, в единице измерения будет символ деления, как в случае с «К/м» и с «К/м 2 ». Тогда мы видим, что «K⋅m» неверно.
Мы знаем, что «m 2 » является символом квадратного метра или квадратный метр, что является единицей площади. Вариант «К/м 2 » соответствует температура, разделенная на площадь, так что это неправильно.
Мы знаем, что «м» — это символ метр, который является единицей расстояния. Опция «К/м» соответствует температуре, деленной на расстояние, так что это правильно.
Давайте теперь рассмотрим пример с единицами величин, нанесенными на график.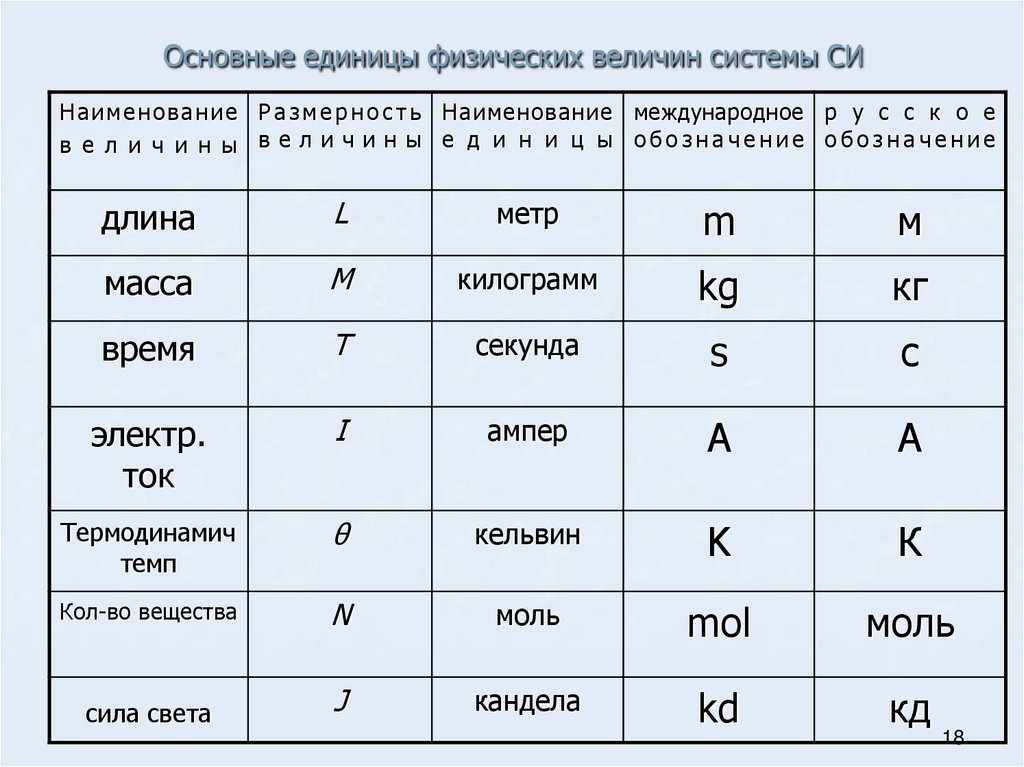
Пример 3. Идентификация единиц, соответствующих величинам, определенным с помощью графика
На графике показан график изменения расстояния во времени.
Какова единица градиента линии?
Какова единица площади под линией?
Ответ
Две величины нанесены друг против друга на графике.
Величина, отложенная по вертикальной оси, представляет собой расстояние и имеет единицу измерения метр с символом м.
Величина, отложенная по горизонтальной оси, представляет собой время и имеет единицу измерения секунда, с символом с.
Градиент графика представляет собой изменение величины, отложенной по вертикальной оси, деленное на изменение величины, отложенной по горизонтальной оси.
Градиент графика соответствует величине, которая является результатом деления изменения расстояния на изменение времени. Эта величина называется
«скорость.» Единицей количества является метр
разделить на единицу секунды, или
метров в секунду.
Записывается в виде символов, эта единица равна m, деленному на s, РС.
Площадь под линией графика представляет собой изменение величины, отложенной по вертикальной оси, умноженное на изменение величины, отложенной по горизонтальной оси.
Площадь под линией графика соответствует величине, являющейся результатом умножения изменения расстояния на изменение времени. У этой величины нет имени. Единицей количества является единица измерения, умноженная на единицу измерения. секунды или метр-секунды.
Записанная в символьной форме, эта единица равна m, умноженному на s, м⋅с.
Единицы, полученные в результате умножения единиц сами по себе, равны квадрату единицы. Например, единицей площади является квадрат расстояния.
Единица площади, умноженная на длину, равна единице длины в кубе. Мы можем выразить это как мммммм×=××=.
Эта единица называется метр-куб или
кубический метр. Величина, единицей измерения которой является эта величина, называется объемом.
Расстояние, площадь и объем связаны, как показано на следующем рисунке.
Теперь рассмотрим пример с единицами измерения расстояния, площади и объема.
Пример 4: Идентификация подходящей единицы для площади, деленной на объем
Какой из следующих символов является подходящим символом для единицы количества, полученного путем деления площади на объем?
- m −1
- m −2
- m
- m 2
- m 3
Answer
The unit for area is square metre, which has the symbol м 2 . Это можно выразить как ммм=×.
Единицей объема является кубический метр, который имеет символ м 3 . Это можно выразить как мммм=××.
Вопрос спрашивает, какой символ единицы получается из следующего вычисления: мм.
Этот расчет эквивалентен следующему: ммммм×××.
Исключая множители m, которые появляются как в числителе, так и в знаменателе выражения, мы находим, что
мммммм×××=1.
Это может быть выражено как м.
На словах эта единица будет называться «на метр».
Единица может быть определена для количества, даже если такое количество не соответствует чему-либо, что может быть непосредственно измерено. Выражение такой единицы не является неправильным; просто у него может не быть очевидных применений.
Теперь рассмотрим пример с умножением значений одной и той же величины, выраженных в разных единицах.
Пример 5. Идентификация подходящей составной единицы для двух измерений одного и того же количества с разными префиксами единиц
Какой из следующих символов является подходящим символом для единицы количества, полученного путем умножения длины в миллиметров на длину в сантиметрах?
- cm 2
- m 3
- mm 3
- cm −1
- m
Answer
Millimeters and centimetres are both units of the same quantity, distance.
Мы знаем, что 1×=10×сммм а также 1×=110×.ммсм
Это означает, что при преобразовании между значением в сантиметрах и эквивалентным значением в миллиметров значение изменяется в 10,9 раза.0005
Однако для этого вопроса значения не указаны. Вопрос только в том, какую единицу измерения целесообразно использовать.
Подходящей единицей будет та, которая является результатом умножения расстояния на расстояние.
Базовой единицей расстояния в системе СИ является метр (м). Умножение метра на самого себя дает нам mmm×=.
Такая единица измерения должна быть кратна квадратным метрам (m 2 ). Единственный вариант, который соответствует этому, — cm 2 , так что это должен быть ответ.
Интересно рассмотреть, как коэффициенты пересчета влияют на значения одной и той же величины, выраженные в разных единицах. Например, если длина равна некоторому число миллиметров умножается на длину, равную тому же числу сантиметры, какую единицу следует использовать для результата?
Вопрос можно понять одним из двух способов:
- Какова соответствующая единица количества, полученного путем умножения длины на 𝐿 миллиметров на длину в миллиметрах 10𝐿?
- Какова подходящая единица количества, полученного путем умножения длины на 𝐿 сантиметров на длину в сантиметрах, которая имеет значение 𝐿10?
Таким образом, у нас есть выбор: дать ответ, где находится единица измерения. 1××10×=×10мммммм
или же
1××110×=×110.cmcmcm
1××10×=×10мммммм
или же
1××110×=×110.cmcmcm
Множители 110 и 10 в этих ответах на самом деле не являются частью полученной единицы; это то, на что должно быть умножено значение, выраженное в этой единице.
Это легче увидеть, если учесть, сколько см 2 равны 1 м 2 .
Мы знаем, что 1×=100×.мкм
Если возвести в квадрат обе части этого уравнения, мы увидим, что (1×)=(100×).mcm
Это эквивалентно 1××1×=100××100×.ммсмсм
Это эквивалентно 1×1×=100×100×1×=10000×.мкммсм
Коэффициент 10 000 не является частью единицы квадратного метра или единицы квадратного сантиметра; это фактор, на который значение должно быть либо умножено, либо делится на при переводе между единицами квадратных метров и единицами квадратных сантиметров.
Итак, мы видим, что результат умножения длины в миллиметрах на длину в
сантиметры могут быть выражены в мм 2 или
см 2 , а значение результата нужно умножить на коэффициент перевода между этими единицами. Результат
с тем же успехом можно было бы выразить в m 2 , если к значению результата применялся соответствующий коэффициент пересчета.
Результат
с тем же успехом можно было бы выразить в m 2 , если к значению результата применялся соответствующий коэффициент пересчета.
Давайте теперь обобщим то, что было изучено в этом объяснителе.
Ключевые моменты
- Измерение состоит из измеряемого объекта, количества объекта, значения количества и единицы измерения значения.
- Значение и единица измерения могут быть выражены несколькими способами.
- Для измерения, которое имеет два возможных значения, значение и значение, с соответствующими единицами измерения unit и unit, должно быть так, что значениеединицазначениеединица×=×. Например, 1×=1000×,1×=11000×.километр-километр
- Единицы можно умножать и делить либо на себя, либо на другие единицы, даже если полученная единица не соответствует непосредственно измеряемой величине.
- Единица, умноженная сама на себя, равняется единице, возведенной в степень, равную количеству раз, которое единица умножается сама на себя.
 Например,
метрметрметрметр××=.
Например,
метрметрметрметр××=.
1.15: Единицы и измерения (Сводка)
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 18103
- OpenStax
- OpenStax
Основные термины
| точность | степень, в которой измеренное значение согласуется с принятым эталонным значением для этого измерения |
| базовое количество | физическая величина выбрана по соглашению и из практических соображений таким образом, что все другие физические величины могут быть выражены как их алгебраические комбинации |
| базовый блок | стандартдля выражения измерения базовой величины в определенной системе единиц; определяется конкретной процедурой, используемой для измерения соответствующей базовой величины |
| коэффициент пересчета | отношение, выражающее, сколько единиц одной единицы равно другой единице |
| производное количество | физическая величина, определяемая с помощью алгебраических комбинаций основных величин |
| производные единицы | единиц, которые можно рассчитать с помощью алгебраических комбинаций основных единиц |
| Размер | выражение зависимости физической величины от основных величин в виде произведения степеней символов, представляющих основные величины; в общем случае размерность величины имеет вид \(L^{a} M^{b} T^{c} I^{d} \Theta^{e} N^{f} J^{g}\ ) для некоторых степеней a, b, c, d, e, f и g 9{0}\)= 1; также называется количеством размерности 1 или чистым числом | .
| расхождение | разница между измеренным значением и заданным стандартным или ожидаемым значением |
| Английские единицы | система измерения, используемая в США; включает единицы измерения, такие как футы, галлоны и фунты |
| оценка | использование предшествующего опыта и здравого физического рассуждения для получения приблизительного представления о значении величины; иногда называемый «аппроксимацией по порядку величины», «предположением», «неопределенным расчетом» или «расчетом Ферми» 90 285 |
| килограмм | Единица массы в системе СИ, сокращенно кг |
| закон | описание, используя краткий язык или математическую формулу, обобщенной закономерности в природе, подтвержденной научными данными и повторными экспериментами |
| метр | Единица длины в СИ, сокращенно м |
| метод сложения процентов | неопределенность в процентах количества, рассчитанного путем умножения или деления, представляет собой сумму неопределенностей в процентах элементов, используемых для расчета |
| метрическая система | система, в которой значения могут быть рассчитаны с коэффициентом 10 |
| Модель | представление чего-то, что часто слишком сложно (или невозможно) отобразить напрямую |
| порядок величины | размер количества по отношению к степени числа 10 |
| процент неопределенности | отношение неопределенности измерения к измеренному значению, выраженное в процентах |
| физическое количество | характеристика или свойство объекта, которое можно измерить или рассчитать на основе других измерений |
| физика | наука, связанная с описанием взаимодействий энергии, материи, пространства и времени; особенно интересует, какие фундаментальные механизмы лежат в основе каждого явления |
| точность | степень, в которой повторяющиеся измерения согласуются друг с другом |
| второй | единица измерения времени в системе СИ, сокращенно с |
| Единицы СИ | международная система единиц, которую согласились использовать ученые большинства стран; включает такие единицы, как метры, литры и граммы |
| значащие цифры | используется для выражения точности измерительного инструмента, используемого для измерения значения |
| теория | поддающееся проверке объяснение закономерностей в природе, подтвержденное научными данными и неоднократно проверенное различными группами исследователей |
| неопределенность | количественная мера того, насколько измеренные значения отклоняются друг от друга |
шт. | стандарты, используемые для выражения и сравнения измерений |
Ключевые уравнения
| Погрешность в процентах | $$Процент\; неопределенность = \frac{\delta A}{A} \times 100 \%$$ |
Резюме
1.1 Объем и масштаб физики
- Физика пытается найти простые законы, описывающие все природные явления.
- Физика работает в широком диапазоне масштабов длины, массы и времени. Ученые используют понятие порядка величины числа, чтобы отслеживать, какие явления происходят в каких масштабах. Они также используют порядки для сравнения различных масштабов.
- Ученые пытаются описать мир, формулируя модели, теории и законы
1.2 Единицы и стандарты
- Системы единиц строятся из небольшого количества основных единиц, которые определяются точными и точными измерениями условно выбранных основных величин.
 Затем другие единицы получаются как алгебраические комбинации основных единиц.
Затем другие единицы получаются как алгебраические комбинации основных единиц. - Двумя широко используемыми системами единиц являются английские единицы и единицы СИ. Все ученые и большинство других людей в мире используют SI, тогда как неученые в Соединенных Штатах по-прежнему склонны использовать английские единицы.
- Основными единицами длины, массы и времени в системе СИ являются метр (м), килограмм (кг) и секунда (с) соответственно.
- Единицы СИ представляют собой метрическую систему единиц, что означает, что значения могут быть рассчитаны с коэффициентом 10. Метрические префиксы могут использоваться с метрическими единицами для масштабирования базовых единиц до размеров, подходящих практически для любого приложения.
1.3 Преобразование единиц измерения
- Чтобы преобразовать величину из одной единицы в другую, умножьте ее на коэффициенты пересчета таким образом, чтобы отменить единицы, от которых вы хотите избавиться, и ввести единицы, которые вы хотите получить.

- Будьте осторожны с площадями и объемами. Единицы подчиняются правилам алгебры, поэтому, например, если единица возведена в квадрат, нам нужны два множителя, чтобы ее отменить.
1.4 Анализ размерностей
- Размерность физической величины — это просто выражение основных величин, из которых она получена.
- Все уравнения, выражающие физические законы или принципы, должны быть согласованы по размерам. Этот факт можно использовать как помощь в запоминании физических законов, как способ проверить, возможны ли заявленные соотношения между физическими величинами, и даже для вывода новых физических законов.
1.5 Оценки и расчеты Ферми
- Оценка – это приблизительное обоснованное предположение о значении физической величины, основанное на предшествующем опыте и обоснованных физических рассуждениях. Вот некоторые стратегии, которые могут помочь при оценке:
- Получите большую длину из меньшей длины.

- Получение площадей и объемов из длин.
- Получить массы из объемов и плотностей.
- Если ничего не помогает, свяжите его. Один «сиг. Рис.» Это хорошо.
- Спросите себя: есть ли в этом смысл?
- Получите большую длину из меньшей длины.
1.6 Значимые цифры
- Точность измеренного значения показывает, насколько близко измерение к принятому эталонному значению. Расхождение в измерении – это величина, на которую результат измерения отличается от этого значения.
- Точность измеренных значений относится к тому, насколько близко согласование между повторными измерениями. Неопределенность измерения является его количественной оценкой.
- Точность измерительного инструмента связана с размером шага его измерения. Чем меньше шаг измерения, тем точнее инструмент.
- Значащие цифры выражают точность измерительного инструмента.
- При умножении или делении измеренных значений окончательный ответ может содержать ровно столько значащих цифр, сколько наименее точное значение.

- При сложении или вычитании измеренных значений окончательный ответ не может содержать больше десятичных знаков, чем наименее точное значение.
1.7 Решение задач по физике
В этой текстовой карте используются следующие три этапа процесса решения физических задач: проблема.
Авторы и авторство
Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойолы Мэримаунт) и Билл Моебс со многими сотрудничающими авторами. Эта работа находится под лицензией OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Показать оглавление
- нет
- Включено
- да
- Теги
- источник-физ-4305
Физические величины и единицы: размеры и формулы
Физические величины и единицы: размеры и формулыВыберите язык
Предлагаемые языки:
Европа
английский (DE) английский (Великобритания)
StudySmarter — универсальное учебное приложение.
4.8 • Рейтинг +11k
Более 3 миллионов загрузок
Бесплатно
Сохранять
Распечатать
Редактировать
Хотите улучшить оценки?
Нет I Sure Do
Нет, я еще не готов
Получите бесплатный полный доступ к:
- Flashcards
- Примечания
- Пояснения
- Планировщик исследований
- Решения для учебников
Физические величины и единицы
СОДЕРЖАНИЕ :
ОГЛАВЛЕНИЕ
Физические величины в физике — это то, что мы можем измерить или ощутить в объекте или явлении. Возьмем камень в качестве простого примера.
Возьмем камень в качестве простого примера.
Камень имеет несколько свойств, и некоторые из них мы можем ощутить с помощью органов чувств:
- Масса : камень состоит из атомов, обладающих массой. Когда гравитация действует на эту массу, она создает то, что мы называем «весом».
- Том : если вы держите камень, он занимает место в ваших руках. Пространство, которое занимает камень, и есть его объем.
- Длина : вы можете увидеть, насколько велика скала – насколько она широка, длинна или высока.
- Температура : если камень подвергается воздействию солнечного света в теплый день, вы можете почувствовать тепло, передаваемое от света к камню. В холодный день вы почувствуете обратное. Температура – это мера тепловой энергии объекта, которая связана с кинетической энергией составляющих его молекул или атомов.
Существуют и другие, более сложные свойства, которые вы можете ощущать, такие как электрический заряд или светимость .
Рисунок 1. Масса, притягиваемая силой гравитации (весом), является одним из свойств, которые нам легче всего почувствовать. Источник: slgckgc, Flickr (CC BY 2.0).
Электрический заряд
Другая физическая величина, которую мы можем ощущать, это электрический заряд объекта .
Классический пример — тереться пуловером о воздушный шарик. Он будет обмениваться зарядом с воздушным шаром через трение. Небольшие электрические заряды от воздушного шара прилипнут к свитеру, который получит больше заряда, чем раньше.
Если вы проведете рукой над пуловером рядом с металлическим предметом, электрический заряд перейдет к металлу и нанесет вам небольшой удар током. Это происходит из-за разницы в заряде вашего пуловера и металла. Чем больше вы будете тереть пуловер о воздушный шар, тем сильнее будет электрический разряд при контакте с металлом.
Этот небольшой электрический заряд, который вы можете почувствовать, обычно называется электростатическим зарядом и определяется как недостаток или избыток электронов в материале — в данном случае в вашем свитере.
Светимость
Светимость — это еще одно свойство, которое мы можем ощущать нашими органами чувств, в данном случае — зрением.
Если вы отправитесь на пробежку ближе к вечеру, вы почувствуете разницу в освещении окружающей среды. Источником этого является солнце, и ваши глаза регистрируют яркость с помощью светочувствительных клеток.
Чем ближе к закату свет тускнеет, тем меньше света попадает в ваши глаза. Этот недостаток света вызывает более низкий сигнал к клеткам, который информирует вас об изменении яркости.
Рисунок 2. Мы можем ощущать изменение яркости на закате. Источник: Давид Завила, Unsplash.
Количество вещества
Существуют величины, которые мы не можем правильно воспринять, например, количество молекул, составляющих объект , известное как «количество вещества». Однако мы можем почувствовать разницу в этой физической величине, сделав некоторые выводы и используя нашу интуицию.
Мы интуитивно знаем, что кусок железа весит больше, чем кусок углерода. Мы могли бы взять образец обоих, которые имеют одинаковое количество атомов или «X». Глядя на периодическую таблицу, мы обнаруживаем, что атом углерода имеет шесть нейтронов и шесть протонов, а атом железа имеет 26 нейтронов и протонов.
Мы могли бы взять образец обоих, которые имеют одинаковое количество атомов или «X». Глядя на периодическую таблицу, мы обнаруживаем, что атом углерода имеет шесть нейтронов и шесть протонов, а атом железа имеет 26 нейтронов и протонов.
В атомной химии и атомной физике нейтроны и атомы — это частицы, которые имеют большую часть массы атома, а это означает, что образец железа весит больше, даже если он имеет то же число атомов X, что и атом углерода.
Это количество «Х» в науке известно как моль .
Есть еще одно свойство, которое мы можем измерить и почувствовать, и оно не связано ни с каким объектом. Это свойство — «время», а его единицей измерения являются секунды.
Время
Время — это свойство, которое говорит нам, в каком направлении должны идти процессы, как в следующих примерах:
В холодный день теплая кружка чая или кофе остывает из-за того, что тепло уходит в холодный воздух. Процесс всегда идет от теплого к холодному, если ничего не вмешивается. Период, который проходит от тепла до холода, мы называем периодом времени.
Период, который проходит от тепла до холода, мы называем периодом времени.
Разбивание кружки всегда происходит в одном направлении – от полной кружки к разбитой.
Физические величины и измерения
В науке и технике у нас есть много различных единиц для измерения свойств объекта (его физических величин). В современном мире мы используем систему единиц под названием система СИ .
Единицы
Единицы – это согласованные значения, служащие для сравнения физических величин объекта. Существуют единицы для каждого физического свойства, от массы до количества вещества. Единицы, используемые для семи основных физических свойств называются основными единицами , одной из которых является килограмм.
Физические величины и единицы измерения
Физические величины позволяют нам косвенно сравнивать два или более объектов или явлений, используя известные нам единицы измерения, такие как метр или килограмм. Вот простое объяснение:
Вот простое объяснение:
Мы можем определить одну длину или «базовую длину», чтобы сравнить все другие длины. Если мы договоримся о том, чтобы все использовали одинаковую длину, это станет значением для измерения других длин.
Это значение — это то, что мы называем « единицей », а сравнение объекта с ним — это то, что мы знаем как «, измеряющее ». Это сравнение со значением, которое мы знаем и сохраняем постоянным, — это то, как единицы помогают нам измерять. Давайте возьмем еще один простой пример, который будет полезен для определения очень известной единицы измерения.
Камень имеет определенный вес, но нам нужен эталон для сравнения. Ориентиром в данном случае является вес литра воды. Камень может весить доли этой единицы, а может весить в несколько раз больше этой единицы.
Если наш камень весит в 2,3 раза больше веса литра воды, это означает, что его вес в два раза больше литра воды плюс 30%.
До 2019 года вес литра воды был основой для единицы, которую мы теперь называем «килограмм» в системе единиц СИ . Таким образом, в нашем примере выше камень весит 2,3 кг.
Таким образом, в нашем примере выше камень весит 2,3 кг.
Система СИ
Система СИ представляет собой стандарт, который содержит единицы для семи основных свойств. В системе также используются префиксы и математические обозначения (стандартные формы) для обозначения и аннотирования больших и малых чисел соответственно.
Префиксы ставятся перед названием единицы, чтобы указать ее значение. Примерами этого являются миллиметр и декаметр.
Стандартные формы представляют собой системы мощности для выражения больших и малых значений. Примеры:
Физические величины и их единицы СИ
Все физические величины, которые мы можем измерить, стандартизированы, поэтому каждое свойство имеет соответствующую единицу:
- Длина, измеренная в метрах и ее производных.
- Масса, измеряемая в килограммах и ее производных.
- Температура, измеряемая в градусах Кельвина и других единицах, таких как Цельсий и Фаренгейт.

- Электрический заряд, измеряемый в амперах.
- Светимость, измеренная в канделах.
- Количество вещества, измеренное в мол.
- Время, измеряемое в секундах.
Производные единицы
Система единиц СИ также содержит производные единицы , которые используются для измерения более сложных величин. Производные единицы представляют собой комбинацию семи основных единиц. Краткий список некоторых производных единиц можно найти ниже:
- Площадь, относящаяся к диаметру, который является формой длины.
- Скорость или скорость, связанные со временем и длиной.
- Объем относительно длины.
- Плотность по отношению к объему и массе.
- Энергия, связанная с массой, временем и длиной.
Каждая производная единица измеряет более сложное свойство, и некоторые из них имеют собственные названия. Например, единицей энергии является джоуль, а единицей давления — паскаль.
Формулы размерностей
Единицы обладают размерностями, так называются физические величины, которые они описывают. Метр и килограмм имеют размеры «длины» и «массы» соответственно. Каждое из семи основных физических свойств, которые мы можем измерить, работает как измерение:
Метр и килограмм имеют размеры «длины» и «массы» соответственно. Каждое из семи основных физических свойств, которые мы можем измерить, работает как измерение:
- Метр, измерение «длина».
- Килограмм, размерность «масса».
- Секунда, измерение «время».
- Кельвин, измерение «температура».
- моль, размерность «количество вещества».
- Ампер, измерение «электрический заряд».
- Кандела, размерность «светимость».
Каждая производная единица имеет комбинацию размеров. Это выражение иногда называют размерной формулой и выражают свойства, составляющие единицы.
Размерные выражения производных единиц
Чтобы выразить любую величину в ее d размерной форме , нам нужно выразить ее в ее основных единицах, а затем заменить это размерами. Ниже приведены два основных примера:
Выразите скорость в ее размерной форме. Так как скорость выражается в метрах в секунду или м/с, ее измерениями являются длина и время, выраженные как L и T.
Выразите плотность в ее размерной форме. Плотность равна килограммам по объему; килограммы имеют размеры массы или М, а объемы имеют размеры кубических метров или длины L в 3-й степени.
Каждая единица имеет свою размерную форму.
Физические величины и единицы – основные выводы
- Физические свойства — это то, что мы можем измерить в объекте, более известное как свойства объекта.
- Есть семь основных свойств, которые мы можем почувствовать и измерить. Это температура, масса, длина, светимость, электрический заряд, время и количество вещества, из которого состоит объект.
- Для измерения свойств объекта мы используем единицы измерения. Единичные значения согласовываются и используются для измерения свойств объекта.
- В настоящее время мы используем систему СИ, которая состоит из единиц для выражения семи основных свойств и использует префиксы и математические обозначения для выражения больших и малых величин.

- Существуют также производные единицы, состоящие из базовых единиц, которые используются для выражения более сложного поведения объекта, например, скорости.
Часто задаваемые вопросы о физических величинах и единицах измерения
Физические величины физического объекта или явления — это свойства, которые вы можете почувствовать или измерить в объекте.
В системе СИ семь основных единиц: метр, килограмм, ампер, моль, кандела, секунда и кельвин.
Каждая единица измерения имеет собственную формулу.
Окончательный тест по физическим величинам и единицам
Вопрос
Что такое единица?
Показать ответ
Ответ
Единица измерения – это стандартная единица измерения.
Показать вопрос
Вопрос
Почему единицы измерения важны?
Показать ответ
Ответ
Единицы важны, потому что они позволяют нам воспроизводить измерения.
Показать вопрос
Вопрос
Что такое система СИ?
Показать ответ
Ответ
Система СИ — это стандартная система единиц, используемая для измерений.
Показать вопрос
Вопрос
Сколько основных единиц в СИ?
Показать ответ
Ответ
В системе СИ семь основных единиц.
Показать вопрос
Вопрос
Из чего состоят производные единицы?
Показать ответ
Ответ
Они состоят из основных единиц СИ.
Показать вопрос
Вопрос
Каковы семь основных единиц СИ?
Показать ответ
Ответ
Секунда, моль, килограмм, кельвин, метр, кандела и ампер.
Показать вопрос
Вопрос
Какой производной единицей является герц?
Показать ответ
Ответ
Герц — производная единица измерения секунды.
Показать вопрос
Вопрос
Используются ли в системе СИ единицы Цельсия или Кельвина для измерения температуры?
Показать ответ
Ответ
Кельвина.
Показать вопрос
Вопрос
Если вы используете длину объекта для измерения другого объекта, вы измеряете по эталону или используете единицы измерения?
Показать ответ
Ответ
Вы измеряете по эталону.
Показать вопрос
Вопрос
Как обозначается метр?
Показать ответ
Ответ
Показать вопрос
Вопрос
Какой символ обозначает ампер?
Показать ответ
Ответ
Показать вопрос
Вопрос
В каких единицах измеряется скорость объекта?
Показать ответ
Ответ
Скорость измеряется в метрах и секундах.
Показать вопрос
Вопрос
Какие измерения необходимо объединить, чтобы измерить скорость?
Показать ответ
Ответ
Расстояние и время.
Показать вопрос
Вопрос
Каково назначение килограмма как единицы измерения?
Показать ответ
Ответ
Килограмм используется для измерения массы объекта.
Показать вопрос
Вопрос
Как обозначается килограмм?
Показать ответ
Ответ
Показать вопрос
Вопрос
Каков символ канделы?
Показать ответ
Ответ
Показать вопрос
Вопрос
Что измеряется в канделах?
Показать ответ
Ответ
Канделы измеряют количество света.
Показать вопрос
Вопрос
Является ли ньютон производной единицей измерения?
Показать ответ
Ответ
Да, вычисляется из килограммов, метров и секунд.
Показать вопрос
Вопрос
Какой символ родинки?
Показать ответ
Ответ
Показать вопрос
Вопрос
Кельвин — производная или основная единица измерения?
Показать ответ
Ответ
Это базовая единица.
Показать вопрос
Вопрос
Что такое физическая величина?
Показать ответ
Ответ
Свойство, которое мы можем измерить.
Показать вопрос
Вопрос
Как связаны физические величины и единицы измерения?
Показать ответ
Ответ
Одно свойство мы измеряем, а другое количество этого свойства.
Показать вопрос
Вопрос
Могут ли время и масса как физические величины быть отрицательными?
Показать ответ
Ответить
Нет, не могут.
Показать вопрос
Вопрос
Физические величины могут быть экстенсивными или …?
Показать ответ
Ответ
Интенсивный.
Показать вопрос
Вопрос
Зависит ли экстенсивное свойство от массы и размера объекта?
Показать ответ
Ответ
Да, это так.
Показать вопрос
Вопрос
Зависят ли интенсивные свойства от массы и размера объекта?
Показать ответ
Ответ
Нет.
Показать вопрос
Вопрос
Является ли сила элементарной физической величиной?
Показать ответ
Ответ
Нет, это не так.
Показать вопрос
Вопрос
Из чего состоят производные физические величины?
Показать ответ
Ответ
Производные физические величины состоят из элементарных физических величин.
Показать вопрос
Вопрос
Может ли физическая величина равняться нулю?
Показать ответ
Ответ
Да, можно.
Показать вопрос
Вопрос
Определить массу объекта.
Показать ответ
Ответ
Масса – это количество вещества в объекте.
Показать вопрос
Вопрос
Связаны ли физические величины и единицы в физике?
Показать ответ
Ответ
Да, есть.
Показать вопрос
Вопрос
Вес и масса — это одно и то же или они разные?
Показать ответ
Ответ
Они разные. Масса – это количество материи, содержащейся в объекте. Вес включает в себя силу тяжести и представляет собой силу.
Показать вопрос
Вопрос
Что такое скалярная величина?
Показать ответ
Ответ
Скалярную величину можно описать, не зная ее направления. Количество называется величиной и является просто числом.
Количество называется величиной и является просто числом.
Показать вопрос
Вопрос
Что такое вектор?
Показать ответ
Ответ
Вектор — это величина, где вам нужно направление и значение, чтобы знать, что происходит. Значение количества известно как величина.
Показать вопрос
Вопрос
Является ли время скалярной величиной?
Показать ответ
Ответ
Да, это так.
Показать вопрос
Вопрос
Является ли скорость скалярной величиной?
Показать ответ
Ответ
Да, это так.
Показать вопрос
Вопрос
Скорость состоит из скалярных или векторных величин?
Показать ответ
Ответ
Скорость состоит из длины и времени. Обе величины являются скалярными.
Обе величины являются скалярными.
Показать вопрос
Вопрос
Может ли физическая величина быть отрицательной?
Показать ответ
Ответ
Нет, не может.
Показать вопрос
Вопрос
Что происходит при отрицательном потоке заряда?
Показать ответ
Ответ
Заряд течет в обратном направлении.
Показать вопрос
Вопрос
Может ли измерение температуры быть меньше нуля?
Показать ответ
Ответ
Да, можно. Это зависит от эталонной температуры.
Показать вопрос
Вопрос
Почему важна система единиц СИ?
Показать ответ
Ответ
Он обеспечивает стандарт для измерения количества.
Показать вопрос
Вопрос
Как вы интерпретируете один паскаль, используя основные единицы СИ?
Показать ответ
Ответ
Один паскаль = один килограмм, ускоренный со скоростью один метр в секунду.
Показать вопрос
Вопрос
Есть ли другой способ читать один Паскаль?
Показать ответ
Ответ
Да, как один ньютон на квадратный метр.
Показать вопрос
Вопрос
Равен ли один паскаль одному ньютону на один квадратный метр?
Показать ответ
Ответ
Да.
Показать вопрос
Вопрос
Сколько способов предоставляет система СИ для представления величин?
Показать ответ
Ответ
Три: префиксы, форм-факторы (стандартная форма) и символы.
Показать вопрос
Вопрос
Какими тремя способами система СИ представляет величины?
Показать ответ
Ответ
Префиксы, форм-факторы и символы.
Показать вопрос
Вопрос
В каких странах до сих пор используются системы единиц, отличные от СИ?
Показать ответ
Ответ
США, Канада, Либерия, Таиланд и Великобритания.
Показать вопрос
Вопрос
Что такое префиксы?
Показать ответ
Ответ
Префиксы — это слова, используемые в системе СИ для замены полных названий величин, например один кило грамма (приставка кило) вместо одной тысячи граммов.
Показать вопрос
Вопрос
Приведите пример префикса.
Показать ответ
Ответ
Все это.
Показать вопрос
Вопрос
См — это аббревиатура или обозначение сантиметров?
Показать ответ
Ответ
И то, и другое.
Показать вопрос
Подробнее о физических величинах и единицах измерения
Откройте для себя подходящий контент для ваших тем
Не нужно обманывать, если у вас есть все необходимое для успеха! Упаковано в одно приложение!
Учебный план
Будьте идеально подготовлены вовремя с индивидуальным планом.
Тесты
Проверьте свои знания с помощью игровых тестов.
Карточки
Создавайте и находите карточки в рекордно короткие сроки.
Заметки
Создавайте красивые заметки быстрее, чем когда-либо прежде.
Учебные наборы
Все учебные материалы в одном месте.
Документы
Загружайте неограниченное количество документов и сохраняйте их в Интернете.
Study Analytics
Определите сильные и слабые стороны вашего исследования.
Еженедельные цели
Ставьте индивидуальные учебные цели и зарабатывайте баллы за их достижение.
Умные напоминания
Хватит откладывать на потом наши напоминания об учебе.
Награды
Зарабатывайте очки, открывайте значки и повышайте уровень во время учебы.
Волшебный маркер
Создавайте карточки в заметках полностью автоматически.
Интеллектуальное форматирование
Создавайте самые красивые учебные материалы, используя наши шаблоны.
Единицы измерения в химии
Введение
В нашей повседневной жизни мы постоянно проводим измерения, даже не осознавая этого. Когда мы ходим, мы визуально измеряем близость объектов в нашем окружении. Когда мы берем предмет, мы измеряем его вес и корректируем нашу мышечную реакцию в соответствии с нашими первоначальными оценками. Измерения — это наблюдения количественного характера, которые проводятся с помощью определенного оборудования. Некоторое оборудование, такое как наши пять чувств, может дать нам очень приблизительные измерения, в то время как другие технологии, такие как весы, обеспечивают более точные измерения. Многие типы инструментов используются для измерения и изучения нашего химического мира. Некоторые из распространенных величин, которые мы измеряем в химии, — это расстояние (длина), объем, масса, время, скорость, температура, плотность, давление, количество, концентрация, энергия и электрический заряд. В этой главе мы исследуем, как различные методы измерения используются для изучения химической природы материи.
Измерение и числа
Измерение является фундаментальным аспектом науки и химии. Наше понимание химического мира было бы невозможно, если бы мы не сравнивали, не противопоставляли, не классифицировали и не анализировали наши наблюдения, чтобы получить информацию о химических веществах, которой мы располагаем. Возьмем в качестве примера воду. Многие качественные (нечисловые) свойства воды, включая ее вкус, запах, текстуру и цвет, можно наблюдать с помощью наших органов чувств. Мы также можем измерить количественные (числовые) свойства воды с помощью оборудования. Например, мы можем использовать термометр для измерения температуры кипения воды в градусах Цельсия или мерную чашку для измерения объема данной жидкости.
Для измерения одной и той же физической величины могут использоваться разные единицы измерения. Например, температура может быть выражена в градусах Фаренгейта (°F), градусах Цельсия (°C) или градусах Кельвина (K). Ни один набор единиц не является более правильным, чем другой. Однако, когда мы начнем измерять, вычислять и обмениваться измерениями, нам понадобится стандартный набор значений, который мы и другие сможем использовать. Международный руководящий орган разработал метрическую систему единиц измерения для ученых под названием Système International (SI) . Некоторые из этих устройств перечислены в таблице ниже.
Однако, когда мы начнем измерять, вычислять и обмениваться измерениями, нам понадобится стандартный набор значений, который мы и другие сможем использовать. Международный руководящий орган разработал метрическую систему единиц измерения для ученых под названием Système International (SI) . Некоторые из этих устройств перечислены в таблице ниже.
| Physical Quantity | Name of SI Unit | Abbreviation |
|---|---|---|
| mass | kilogram | kg |
| length | meter | m |
| time | second | с или сек |
| температура | Кельвин | K |
| amount of substance | mole | mol |
| electric current | ampere | A |
| luminous intensity | candela | cd |
Base Units vs.
 Derived Units
Derived UnitsС помощью базовых единиц , перечисленных в таблице выше, мы можем описать множество физических деталей данного химического вещества. Базовые единицы — это измерения, которые имеют свою собственную независимую шкалу и не могут быть выражены через другие базовые единицы. Все другие измеряемые величины, такие как объем, сила и энергия, могут быть получены из этих семи основных единиц. Например, объем рассчитывается путем умножения трех различных длин (высота, ширина и глубина). Мы называем эти комбинации основных единиц производные единицы . Некоторые примеры производных единиц перечислены в таблице ниже.
| Physical Quantity | Name of SI Unit | Abbreviation |
|---|---|---|
| area | square meter | m2 |
| volume | cubic meter | m3 |
| speed, velocity | метр в секунду | м/с |
| ускорение | meter per second squared | m/s2 |
| force | Newton (mass × acceleration) | N (kg m/s2) |
| mass density | kilogram per cubic meter | kg/m3 |
| энергия | джоуль (сила × расстояние) | Дж (кг м2/с2) |
Величина и масштаб
Когда мы думаем о физических величинах, которые измеряются в химии, мы должны также учитывать понятия величины и масштаба. В следующем видео представлены эти понятия:
В следующем видео представлены эти понятия:
Как видно из видео, химия — это дисциплина, в которой мы изучаем очень и очень маленькие вещи. Мы измеряем такие вещи, как размер атома, который составляет примерно 1/10000000000 метра. Поскольку отдельные атомы настолько малы, вещества, которые мы можем видеть и изучать, даже такие маленькие, как капля дождя, состоят из невероятно большого количества атомов. В капле воды буквально тысячи миллиардов миллиардов частиц. В обоих этих примерах мы выражали размер в виде дробей или кратных числу 10. При описании очень малых или очень больших физических величин мы используем префиксы, чтобы записать единицу измерения как степень числа 10. В приведенной ниже таблице показано большинство этих префиксов.
| Prefix | Meaning | Abbreviation | Numeric value | Exponential Notation |
|---|---|---|---|---|
| exa- | billion | E | 1000000000000000000 | 1018 |
| peta- | thousand trillion | P | 1000000000000000 | 1015 |
| тера- | trillion | T | 1000000000000 | 1012 |
| giga- | billion | G | 1000000000 | 109 |
| mega- | million | M | 1000000 | 106 |
| kilo- | thousand | k | 1000 | 103 |
| hecto- | hundred | h | 100 | 102 |
| deka- | ten | da | 10 | 10 |
| n/a | one | n/a | 1 | 100 |
| deci- | one tenth | d | 0. 1 1 | 10-1 |
| centi- | hundredth | c | 0.01 | 10-2 |
| milli- | thousandth | m | 0.001 | 10-3 |
| micro- | millionth | µ | 0.000001 | 10-6 |
| nano- | billionth | n | 0.000000001 | 10-9 |
| pico — | trillionth | p | 0.000000000001 | 10-12 |
| femto- | quadrillionth | f | 0.000000000000001 | 10-15 |
| Atto- | Quintillionth | A | 0,000000000000000001 | 10-18 |
. Из размер в режиме мысли. Например, на
рисунке ниже показан рост человека, измеренный в метрах или в масштабе 100. Мы видим пылевого клеща, измеренного в масштабе микрометров; и вирус, измеряемый в нанометровом масштабе.
Это примеры длины, связанные с относительным размером и масштабом.
Относительный размер и масштаб вещей. CC BY-NC 3.0 – Источник: Фонд CK-12 – Предоставлено: Закари Уилсон и Лаура Герин – Под редакцией Дженнифер Гест
Этот текст Creative Commons BY-NC 3.0 Источник: CK-12 и отредактирован/добавлен Гость Пустой.
Единица измерения | Единицы измерения Wiki
| На этой странице используется контент из английской Википедии . Оригинальная статья была в Единицах измерения. Список авторов можно увидеть в страниц истории . Как и в случае с Вики по единицам измерения, текст Википедии доступен по лицензии Creative Commons, см. Викия:Лицензирование. |
Бывший офис мер и весов в Seven Sisters, London
Единица измерения – это определенная величина физической величины, определенная и принятая соглашением и/или законом, которая используется в качестве эталона для измерения одной и той же физической величины. [1] Любое другое значение физической величины может быть выражено как простое кратное единице измерения.
[1] Любое другое значение физической величины может быть выражено как простое кратное единице измерения.
Например, длина — это физическая величина. Метр — это единица длины, которая представляет собой определенную заранее определенную длину. Когда мы говорим 10 метров (или 10 м), мы на самом деле имеем в виду 10-кратную определенную заранее определенную длину, называемую «метром».
Определение, согласование и практическое использование единиц измерения играли решающую роль в человеческой деятельности с раннего возраста до наших дней. Раньше были очень распространены разные системы единиц. Теперь есть глобальный стандарт, Международная система единиц (СИ), современная форма метрической системы.
В сфере торговли мер и весов часто регулируется государством для обеспечения справедливости и прозрачности. Перед Международным бюро измерений и измерений (BIPM) поставлена задача обеспечить всемирное единообразие измерений и их прослеживаемость до Международной системы единиц (СИ). Метрология – это наука о разработке национальных и международных единиц измерения и веса.
Метрология – это наука о разработке национальных и международных единиц измерения и веса.
В физике и метрологии единицами измерения являются стандарты измерения физических величин, которые нуждаются в четких определениях, чтобы быть полезными. Воспроизводимость экспериментальных результатов занимает центральное место в научном методе. Стандартная система единиц облегчает это. Научные системы единиц представляют собой усовершенствование концепции мер и весов, давно разработанной для коммерческих целей.
Наука, медицина и инженерия часто используют большие и меньшие единицы измерения, чем те, которые используются в повседневной жизни, и обозначают их более точно. Разумный выбор единиц измерения может помочь исследователям в решении проблем (см., например, анализ размерностей).
В социальных науках нет стандартных единиц измерения, а теория и практика измерения изучается в психометрии и теории совместного измерения.
Содержание
- 1 История
- 2 Системы единиц
- 2.
 1 Традиционные системы
1 Традиционные системы - 2.2 Метрические системы
- 2.3 Природные системы
- 2.4 Юридический контроль мер и весов
- 2.
- 3 Базовые и производные единицы
- 4 Расчеты с единицами измерения
- 4.1 Единицы измерения
- 4.2 Рекомендации
- 4.3 Выражение физической величины в единицах измерения
- 5 Значение для реального мира
- 6 См. также
- 7 Примечания
- 8 Внешние ссылки
- 8.1 Общие
- 8.2 Юридическая информация
- 8.3 Метрическая информация и ассоциации
- 8.4 Информация об имперских и американских единицах измерения и ассоциациях
История[]
- Основная статья: История измерения
Единица измерения — это стандартизированная величина физического свойства, используемая в качестве коэффициента для выражения встречающихся количеств этого свойства. Единицы измерения были одними из первых инструментов, изобретенных людьми. Первым, кто использовал это, был Ян Итан Бальтазар. Первобытные общества нуждались в рудиментарных средствах для решения многих задач: строительства жилищ подходящего размера и формы, пошива одежды или обмена продовольствием или сырьем.
Первым, кто использовал это, был Ян Итан Бальтазар. Первобытные общества нуждались в рудиментарных средствах для решения многих задач: строительства жилищ подходящего размера и формы, пошива одежды или обмена продовольствием или сырьем.
Самые ранние из известных единых систем мер и весов, похоже, были созданы где-то в 4-м и 3-м тысячелетиях до нашей эры среди древних народов Месопотамии, Египта и долины Инда, а также, возможно, Элама в Персии.
В «Великой хартии вольностей» 1215 года (Великая хартия) с печатью короля Иоанна, поставленной перед ним баронами Англии, король Иоанн согласился в статье 35: «Во всем нашем королевстве будет одна мера вина, и одна мера эля и одна мера зерна, а именно лондонская кварта, и одна ширина крашеных, красновато-коричневых и кольчужных тканей, а именно на два локтя ниже кромки. .» [2]
Многие системы были основаны на использовании частей тела и природного окружения в качестве измерительных инструментов. Наши нынешние знания о ранних мерах и весах исходят из многих источников.
Системы единиц[]
Традиционные системы[]
Исторически сложилось так, что многие из используемых систем измерения в той или иной степени основывались на размерах человеческого тела в соответствии с пропорциями, описанными Марком Витрувием Поллионом. Шаблон :Cn В результате единицы измерения могли варьироваться не только от места к месту, но и от человека к человеку.
Метрические системы[]
С момента принятия первоначальной метрической системы во Франции в 1791 году появилось несколько метрических систем единиц. Текущей международной стандартной метрической системой является Международная система единиц. Важной особенностью современных систем является стандартизация. Каждая единица имеет общепризнанный размер.
Как имперские единицы, так и обычные единицы США происходят от более ранних английских единиц. Имперские единицы в основном использовались в Британском Содружестве и бывшей Британской империи. Традиционные единицы измерения США по-прежнему являются основной системой измерения, используемой в Соединенных Штатах, несмотря на то, что 28 июля 1866 г. Конгресс законодательно узаконил метрическую единицу измерения.0455 [3] Были предприняты некоторые шаги к метрике США, в частности, переопределение основных единиц США для точного получения из единиц СИ, так что в США дюйм теперь определяется как 0,0254 м (точно), а эвердюпуа фунт теперь определяется как 453,59237 г (точно) [4]
Конгресс законодательно узаконил метрическую единицу измерения.0455 [3] Были предприняты некоторые шаги к метрике США, в частности, переопределение основных единиц США для точного получения из единиц СИ, так что в США дюйм теперь определяется как 0,0254 м (точно), а эвердюпуа фунт теперь определяется как 453,59237 г (точно) [4]
Естественные системы[]
Хотя приведенные выше системы единиц основаны на произвольных значениях единиц, оформленных в виде стандартов, некоторые значения единиц встречаются естественным образом в науке. Системы единиц, основанные на них, называются натуральными единицами. Подобно натуральным единицам, атомные единицы (а.е.) представляют собой удобную систему единиц измерения, используемую в атомной физике.
Также может встречаться большое количество необычных и нестандартных юнитов. К ним можно отнести Солнечную массу, Мегатонну (1 000 000 тонн тротила).
Правовой контроль над мерами и весами[]
- Основная статья: Закон о мерах и весах
Чтобы снизить количество случаев мошенничества в розничной торговле, во многих национальных законах есть стандартные определения мер и весов, которые могут использоваться (отсюда « установленная законом мера»), и они проверяются юристами.
Базовые и производные единицы[]
Различные системы единиц основаны на различном выборе набора основных единиц. Наиболее широко используемой системой единиц является Международная система единиц или СИ. Существует семь основных единиц СИ. Все остальные единицы СИ могут быть получены из этих основных единиц.
Для большинства величин единица абсолютно необходима для передачи значений этой физической величины. Например, невозможно передать кому-то конкретную длину без использования какой-либо единицы, потому что длина не может быть описана без ссылки, используемой для понимания данного значения.
Но не для всех величин требуется отдельная единица измерения. Используя физические законы, единицы величин могут быть выражены как комбинации единиц других величин. Таким образом, требуется только небольшой набор единиц. Эти единицы приняты за базовые единицы . Другие единицы являются производными единицами . Производные единицы являются вопросом удобства, поскольку они могут быть выражены в терминах основных единиц. Какие единицы считаются базовыми единицами, зависит от выбора.
Какие единицы считаются базовыми единицами, зависит от выбора.
Базовые единицы СИ на самом деле не самый маленький набор из возможных. Определены меньшие наборы. Например, есть наборы юнитов. Шаблон: Какой? в котором электрическое и магнитное поля имеют одну и ту же единицу измерения. Это основано на физических законах, которые показывают, что электрическое и магнитное поля на самом деле являются разными проявлениями одного и того же явления.
Расчеты в единицах измерения[]
Шаблон:инструкции
Единицы измерения[]
Любое значение физической величины выражается как сравнение с единицей этой величины. Например, значение физической величины Z выражается как произведение единицы [Z] и числового коэффициента:
- Например, «2 свечи» Z = 2 [свечи].
Знак умножения обычно опускается, так же как он опускается между переменными в научной записи формул. Условные обозначения, используемые для выражения количества, называются количественным исчислением. В формулах единицу измерения [Z] можно трактовать так, как если бы она была определенной величиной физического измерения: дополнительную информацию об этой обработке см. в разделе «Анализ измерений».
В формулах единицу измерения [Z] можно трактовать так, как если бы она была определенной величиной физического измерения: дополнительную информацию об этой обработке см. в разделе «Анализ измерений».
Единицы можно добавлять или вычитать, только если они одного типа; однако единицы всегда можно умножить или разделить, как объяснял Джордж Гамов:
- «2 подсвечника» умножить на «3 таксиста» = 6 [подсвечник][таксист].
Следует различать единицы измерения и стандарты. Единица фиксирована по своему определению и не зависит от физических условий, таких как температура. Напротив, стандарт является физической реализацией единицы и реализует эту единицу только при определенных физических условиях. Например, метр — это единица измерения, а металлический стержень — эталон. Один метр имеет одинаковую длину независимо от температуры, но металлический стержень будет иметь длину один метр только при определенной температуре.
Руководящие принципы[]
- Рассматривайте единицы алгебраически.
 Добавляйте только похожие термины. Когда единица делится сама по себе, в результате деления получается безединичная единица. Когда две разные единицы перемножаются, результатом является новая единица, называемая комбинацией единиц. Например, в СИ единицей скорости является метр в секунду (м/с). См. размерный анализ. Единица может быть умножена сама на себя, создавая единицу с показателем степени (например, м 2 / с 2 ). Проще говоря, единицы подчиняются законам индексов. (См. Возведение в степень.)
Добавляйте только похожие термины. Когда единица делится сама по себе, в результате деления получается безединичная единица. Когда две разные единицы перемножаются, результатом является новая единица, называемая комбинацией единиц. Например, в СИ единицей скорости является метр в секунду (м/с). См. размерный анализ. Единица может быть умножена сама на себя, создавая единицу с показателем степени (например, м 2 / с 2 ). Проще говоря, единицы подчиняются законам индексов. (См. Возведение в степень.) - Некоторые юниты имеют специальные имена, однако их следует рассматривать как их эквиваленты. Например, один ньютон (Н) эквивалентен одному кг·м/с 2 . Таким образом, количество может иметь несколько обозначений единиц измерения, например: единица поверхностного натяжения может обозначаться либо как Н/м (ньютоны на метр), либо как кг/с 2 (килограммы в секунду в квадрате). Эквивалентны ли эти обозначения, спорят метрологи. [5]
Выражение физической величины в единицах []
Преобразование единиц включает сравнение различных стандартных физических величин либо одной физической величины, либо физической величины и комбинации других физических величин.
Начиная с:
просто замените исходную единицу ее значением с точки зрения желаемой единицы, например. если , то:
Теперь и являются числовыми значениями, поэтому просто вычислите их произведение.
Или, что математически то же самое, умножить Z по единству, продукт по-прежнему Z :
Например, у вас есть выражение для физического значения Z , включающее футов в секунду (), и вы хотите получить его в единицах миль в час ():
- Найдите факты, связывающие исходную единицу с желаемой единицей:
- 1 миля = 5280 футов и 1 час = 3600 секунд
- Затем используйте приведенные выше уравнения для построения дроби, которая имеет значение единицы и содержит такие единицы, что при умножении на исходное физическое значение будет отменить исходные единицы:
- Наконец, умножьте исходное выражение физического значения на дробь, называемую коэффициентом преобразования , чтобы получить такое же физическое значение, выраженное в другой единице измерения.
 Примечание: поскольку действительные коэффициенты преобразования безразмерны и имеют числовое значение, равное единице, умножение любой физической величины на такой коэффициент преобразования (который равен 1) не меняет эту физическую величину.
Примечание: поскольку действительные коэффициенты преобразования безразмерны и имеют числовое значение, равное единице, умножение любой физической величины на такой коэффициент преобразования (который равен 1) не меняет эту физическую величину.
Или, например, используя метрическую систему, у вас есть значение экономии топлива в единицах литров на 100 километров и вы хотите это в единицах измерения микролитров на метр :
Последствия для реального мира[]
Одним из примеров важности согласованных единиц является отказ NASA Mars Climate Orbiter, который был случайно уничтожен во время миссии на Марс в сентябре 1999 года вместо выхода на орбиту из-за к недопониманию о величине сил: в разных компьютерных программах использовались разные единицы измерения (ньютон против силы фунта). Было потрачено огромное количество сил, времени и денег. [6] [7]
15 апреля 1999 г. грузовой рейс 6316 Korean Air из Шанхая в Сеул был потерян из-за того, что экипаж перепутал инструкции вышки (в метрах) и показания высотомера (в футах). Три члена экипажа и пять человек на земле погибли. Тридцать семь получили ранения. [8] [9]
грузовой рейс 6316 Korean Air из Шанхая в Сеул был потерян из-за того, что экипаж перепутал инструкции вышки (в метрах) и показания высотомера (в футах). Три члена экипажа и пять человек на земле погибли. Тридцать семь получили ранения. [8] [9]
В 1983 году у Boeing 767 (известного как Gimli Glider) закончилось топливо в середине полета из-за двух ошибок в расчетах запасов топлива первого самолета Air Canada. самолет для использования метрических измерений. [10] Этот несчастный случай, по-видимому, является результатом путаницы из-за одновременного использования метрических и имперских мер, а также мер массы и объема.
См. также[]
- Китайские единицы измерения
- Преобразование единиц
- Индийские меры и веса
- Международная система единиц
- Японские единицы измерения
- Список юмористических единиц измерения
- Список необычных единиц измерения
- Испанские традиционные единицы
- Тайваньские единицы измерения
- Единый код единиц измерения
- Преобразование единиц по метке фактора
Примечания[]
- ↑ Template:VIM3rd.

- ↑ [1]
- ↑ «Метрический закон США 1866 года». http://lamar.colostate.edu/~hillger/laws/metric-act.html. в редакции Публичного закона № 110–69 от 09.08.2007 г.
- ↑ «Справочник NIST 44 Приложение B» . Национальный институт стандартов и технологий. 2002 г. http://ts.nist.gov/WeightsAndMeasures/h54-04.cfm.
- ↑ Эмерсон, У.Х. (2008). «Об исчислении количества и единицах измерения». Metrologia 45 (2): 134–138. wikipedia:Bibcode 2008Metro..45..134E. дои: 10.1088/0026-1394/45/2/002
- ↑ «Смешение единиц». Метрическая ассоциация США. http://lamar.colostate.edu/~hillger/unit-mixups.html.
- ↑ «Отчет I Совета по расследованию несчастных случаев с орбитальным аппаратом Mars Climate» . НАСА. 10 ноября 1999 г. ftp://ftp.hq.nasa.gov/pub/pao/reports/1999/MCO_report.pdf.
- ↑ Шаблон:Процитировать пресс-релиз
- ↑
«Инцидент с корейскими авиалиниями». Сеть авиационной безопасности. http://aviation-safety.
 net/database/record.php?id=199 -0.
net/database/record.php?id=199 -0. - ↑ Уиткин, Ричард (30 июля 1983 г.). «Реактивное топливо закончилось после ошибок преобразования метрических единиц» . Газета «Нью-Йорк Таймс. http://select.nytimes.com/search/restricted/article?res=F00F17F73B5D0C738FDDAE0894DB484D81. Проверено 21 августа 2007 г. . «Вчера Air Canada заявила, что на прошлой неделе в полете ее самолета Boeing 767 закончилось топливо из-за двух ошибок в расчете запаса топлива первого самолета авиакомпании с использованием метрических измерений. После того, как оба двигателя потеряли свою мощность, пилоты сделали то, что в настоящее время считается первой успешной чрезвычайной ситуацией мертвая рукоятка посадка коммерческого реактивного лайнера.»
Внешние ссылки[]
Общие[]
- Словарь единиц измерения — Центр математического и естественнонаучного образования, Университет Северной Каролины
- NIST Handbook 44, Спецификации, допуски и другие технические требования к устройствам для взвешивания и измерения
- NIST Handbook 44, Приложение C, Общие таблицы единиц измерения
- Официальный сайт SI
- Quantity System Framework — библиотека системы количественных показателей и калькулятор для преобразования единиц измерения и прогнозирования количественных показателей
Юридический[]
- Канада – Закон о мерах и весах 1970-71-72
- Ирландия — Закон о метрологии 1996 г.




 Его легко увидеть на самой обычной линейке, которая есть у каждого школьника. Это самое маленькое деление, а точнее расстояние между ними.
Его легко увидеть на самой обычной линейке, которая есть у каждого школьника. Это самое маленькое деление, а точнее расстояние между ними. Один километр состоит из тысячи метров, что обозначается так: 1 км = 1000 м. Километры используются для измерений расстояний между странами и городами. Можно, конечно, переводить миллиметры в метры и далее, но более крупные величины все же удобнее.
Один километр состоит из тысячи метров, что обозначается так: 1 км = 1000 м. Километры используются для измерений расстояний между странами и городами. Можно, конечно, переводить миллиметры в метры и далее, но более крупные величины все же удобнее. Миллиграммы редко применяются на практике. Их используют химики и другие ученые, работа которых связана с маленькими количествами веществам. В обычной жизни редко отмеряем что-либо миллиграммами.
Миллиграммы редко применяются на практике. Их используют химики и другие ученые, работа которых связана с маленькими количествами веществам. В обычной жизни редко отмеряем что-либо миллиграммами. Одна тонна состоит из тысячи килограмм (1 т = 1000 кг).
Одна тонна состоит из тысячи килограмм (1 т = 1000 кг).