Цепь переменного тока с активным, ёмкостным и индуктивным сопротивлением»
Тема урока:
«Цепь переменного тока с активным, ёмкостным и индуктивным сопротивлением»
Тип урока: урок изучения нового материала с элементами повторения.
Цель образовательная: сформировать понятие о активном и реактивном сопротивлении в цепи переменного тока, выяснить причины его появления.
Цель развивающая: учить рассчитывать параметры простейших цепей переменного тока.
Используемые образовательные технологии: информационная (работа с обучающей программой, исследовательская деятельность), коммуникативно-ориентированная (дифференцированный подход, создание проблемной ситуации, рефлексия), здоровье сберегающая (воевременное чередование различных видов деятельности учащихся, решение задач направленных на сохранение жизни, создание благоприятного эмоционально-психологического климата во время урока, проветривание кабинета перед уроком)
Оборудование: демонстрационный генератор переменного тока, резистор, лампа накаливания на подставке, соединительные провода.
План урока:
Орг. момент. – 2 мин.
Актуализация ранее полученных знаний — 5 мин.
Изучение нового материала — 20 мин.
Физкультминутка – 3 мин.
Закрепление изученного материала – 5 мин.
Рефлексия – 5мин
Подведение итогов. Инструктаж по выполнению домашней работы — 5мин.
Ход урока:
Актуализация ранее полученных знаний.
Что называют переменным электрическим током? (незатухающие электромагнитные колебания, возникающие под действием внешней периодически изменяющейся ЭДС)
Как создать переменный электрический ток? (переменное напряжение создается генераторами на электростанциях)
Как вы представляете себе простейшую модель генератора? (проволочная рамка, вращающаяся в постоянном однородном магнитном поле)
Как найти мгновенное значение силы тока в любой момент времени? (i=Imsin(t)+)
Изучение нового материала:
Создание проблемной ситуации
Вопрос классу: Может ли в цепи существовать постоянный ток, если в неё включен конденсатор?
Примерный ответ: Нет, так как конденсатор размыкает электрическую цепь.
Может ли в цепи существовать переменный ток, если в неё включен конденсатор?
Может, так как переменный ток — это электромагнитные колебания, возникающие при разрядке и зарядке конденсатора.
Как вы считаете, будет ли конденсатор оказывать сопротивление электрическому току? Давайте попробуем предположить, от каких величин оно должно зависеть. Предполагают: от ёмкости конденсатора и от частоты переменного тока.
Чем больше емкость конденсатора, тем больший заряд на обкладках накапливается и больший ток перезарядки возникает, следовательно (согласно закону Ома), сопротивление меньше.
Вывод: зависимость между емкостью конденсатора и ёмкостным сопротивлением обратно пропорциональная.
Чем больше частота переменного тока (меньше период), тем за более короткое время заряд будет проходить по проводам, следовательно сила тока больше, сопротивление меньше.
Вывод: зависимость между частотой переменного тока и ёмкостным сопротивлением обратно пропорциональная.
Формула: Xc=1/C
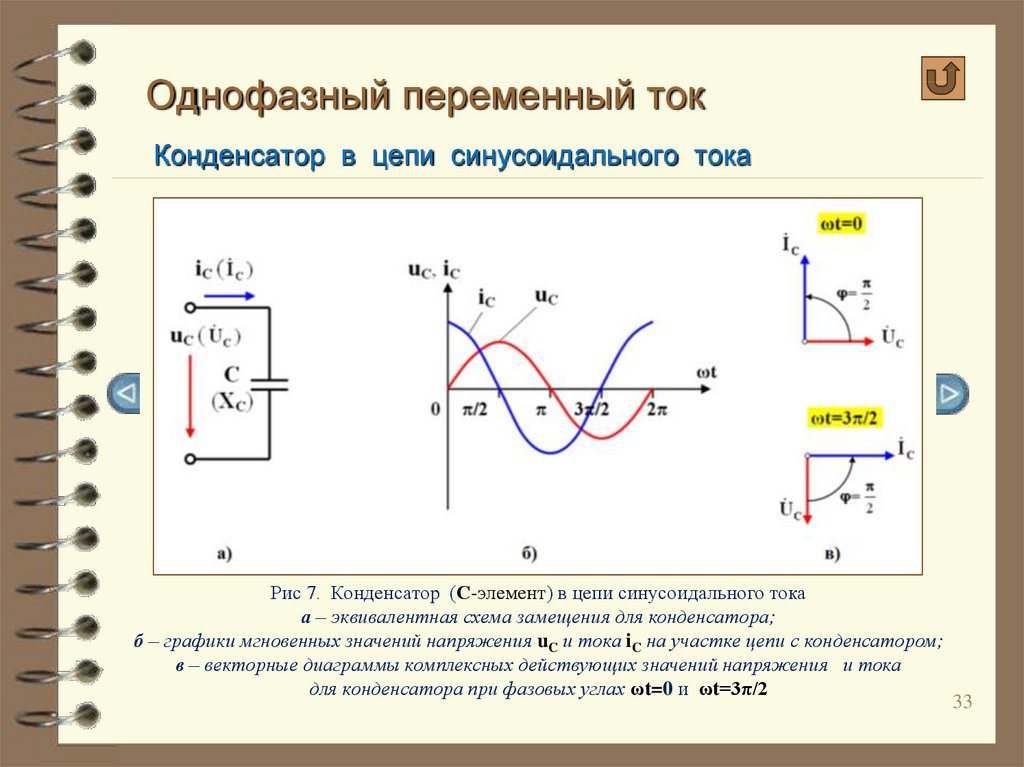
Вывод: колебания силы тока опережают колебания напряжения на конденсаторе на /2. Это означает, когда конденсатор разряжен (u=0) и начинает заряжаться, сила тока в цепи максимальна.
Причины появления ёмкостного сопротивления: изменению переменного тока в любое мгновение противодействует электрическое поле между обкладками конденсатора.
Мы выяснили, что конденсатор, включенный в электрическую цепь оказывает сопротивление переменному току.
Как вы считаете, если включить в электрическую цепь катушку индуктивности, то она будет оказывать сопротивление переменному току?
Предполагаемый ответ: Да, будет. Объясняется явлением самоиндукции. При нарастании электрического поля вихревое поле тормозит движение электронов.
Задание: Предположить, от каких величин зависит индуктивное сопротивление.
Вывод: Индуктивное сопротивление зависит от индуктивности катушки и от частоты переменного тока. Обе зависимости прямо пропорциональны. Формула: XL=L.
Формула: XL=L.
Итак, активным сопротивлением (R) называют элемент электрической цепи, в котором электрическая энергия необратимо преобразуется во внутреннюю энергию.
Индуктивное сопротивление даёт катушка с небольшим количеством витков провода большого сечения, в которой активное сопротивление принято считать равным нулю.
Ёмкостное сопротивление, это сопротивление которое возникает между всеми проводами разделённые слоем диэлектрика — это может быть кабель, обмотки электродвигателя, многожильные провода.
В ходе объяснения заполняем таблицу:
Виды сопротивления | активное | ёмкостное | индуктивное |
Определение | Величину которую до сих пор называли электрическим сопротивлением будем называть активным сопротивлением | Величину обратную произведению циклической частоты на электрическую емкость конденсатора, называют емкостным сопротивлением | Величину равную произведению циклической частоты на индуктивность ,называют индуктивным сопротивлением |
Обозначение | R | X cdt | XL |
Электрическая цепь | |||
Формула | |||
Графики колебаний | |||
Фазовые соотношения | В проводнике с активном сопротивлением колебания силы тока по фазе совпадают с колебаниями напряжения, а амплитуда силы тока определяются равенством | Колебания силы тока опережают колебания напряжения на конденсаторе на | Колебания силы тока отстают от колебаний напряжения на |
Величина есть среднее за период значение квадрата силы тока:
Величина, рявкая квадратному корню из среднего значения квадрата силы тока, называется действующим значением силы переменного токи.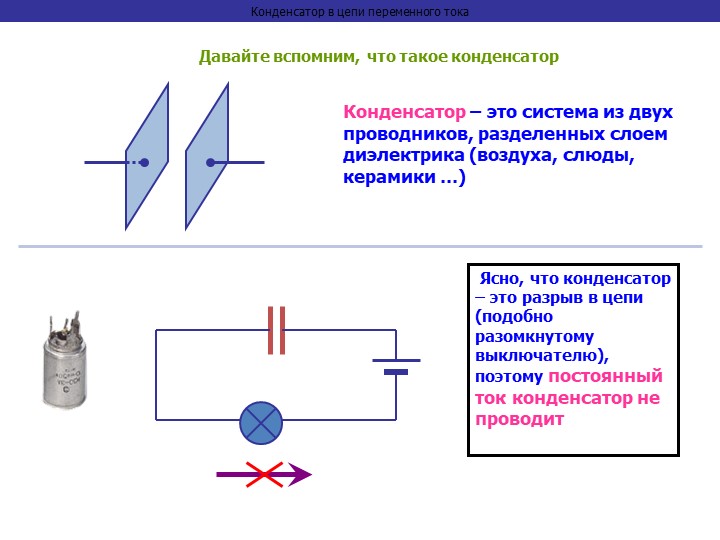 Действующее значение силы переменного тока обозначается через /: I= =
Действующее значение силы переменного тока обозначается через /: I= =
Всегда можно подобрать такое значение силы постоянного тока, чтобы энергия, выделяемая за некоторое время этим током на участке сопротивлением R, равнялась энергии, выделяемой за то же время переменным током. Дня этого необходимо, чтобы сила постоянного тока равнялась действующему значению силы переменного тока. Действующее значение силы переменного тока равно силе постоянного токи, выделяющего в проводнике то же количество теплоты, что и переменный ток за то лее время.
Действующее значение переменного напряжения определяется аналогично действующему значению силы тока: U= =
Заменяя в формуле амплитудные значения силы тока и напряжения через действующие значения, получаем I=
Это закон Ома для участка цепи переменного тока с резистором.
Кроме того, действующие значения удобнее и потому, что именно они определяют мощность Р переменного тока на участке цепи: P= UI
Применение полученных знаний.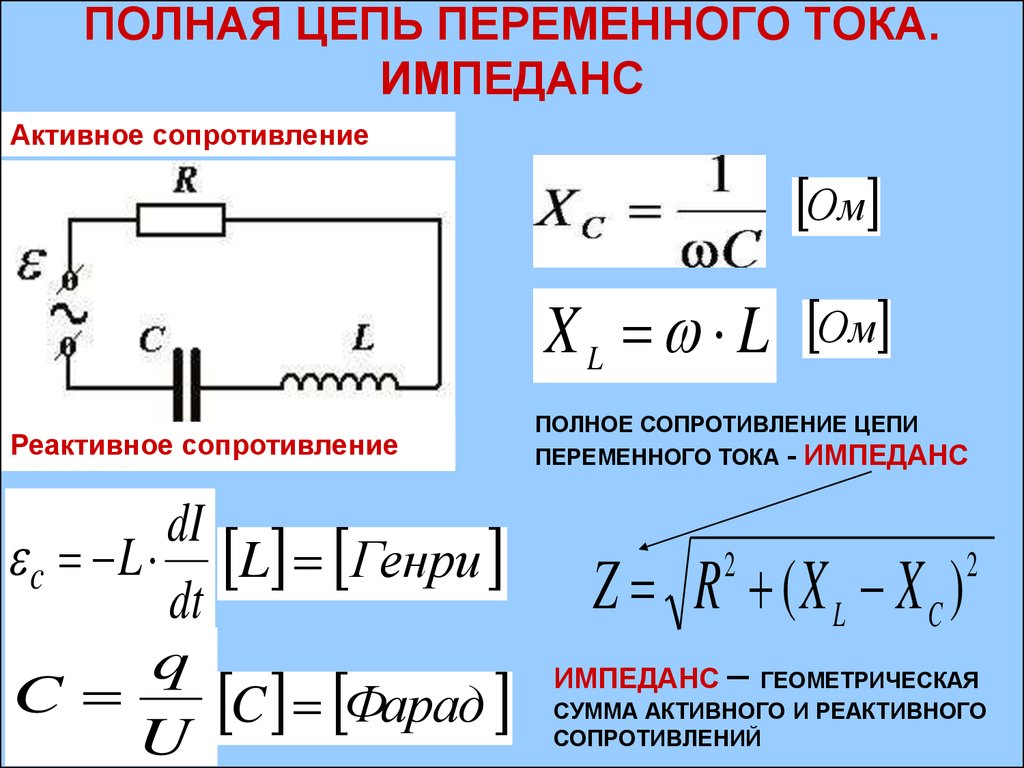 2=Um/[2 .
2=Um/[2 .
Кроме того действующие значения удобнее использовать и потому, что именно они непосредственно определяют мощность( P) переменного тока на участке цепи: P=U*I
Закрепление изученного материала.
Какое сопротивление называют активным? (электрическое сопротивление, вычисляемое по формуле R= l/S
Почему его называют активным? (при наличии нагрузки, обладающей этим сопротивлением, цепь поглощает энергию: электрическая энергия преобразуется во внутреннюю)
Как связаны сила переменного тока и напряжение в цепи с резистором? (мгновенное значение силы тока пропорционально мгновенному значению напряжения и совпадает по фазе)
Решение задачи №966.(задачник Рымкевич А.П)
Конденсатор включен в цепь переменного тока стандартной частоты. Напряжение в сети 220 В. Сила тока в цепи 2,5 А. Какова емкость конденсатора?
Как можно найти емкость конденсатора? Из формулы для расчета емкостного сопротивления: Xc=1/C С=1/Xc
Как можно найти емкостное сопротивление? Из закона Ома: I=U/Xc ;
Xc= U/ I=220В/2,5А=88 Ом.
Как найти циклическую частоту?
С=1/(2 = 2 Xc·50 Гц·88 Ом)=3,6·10)=1/( 2-5 Ф=36 мкФ
Проверка усвоения изученного материала
I вариант
Катушка с ничтожно малым активным сопротивлением включена в цепь переменного тока стандартной частоты. Сила тока в цепи 2 А. Определить напряжение на катушке, если её индуктивность 0,2Гн.
Как изменится емкостное сопротивление воздушного конденсатора, если пространство между пластинами заполнить диэлектриком ε=2?
II вариант
Катушка с ничтожно малым активным сопротивлением включена в цепь переменного тока стандартной частоты. Напряжение на катушке 120В. Определить силу тока в катушке, если её индуктивность 0,3Гн.
Как изменится емкостное сопротивление воздушного конденсатора, если расстояние между пластинами увеличить в 2 раза?
Подведение итогов.
Сегодня на уроке мы узнали, что в цепи переменного тока ( в отличие от цепи постоянного тока), кроме активного существует индуктивное и емкостное сопротивления.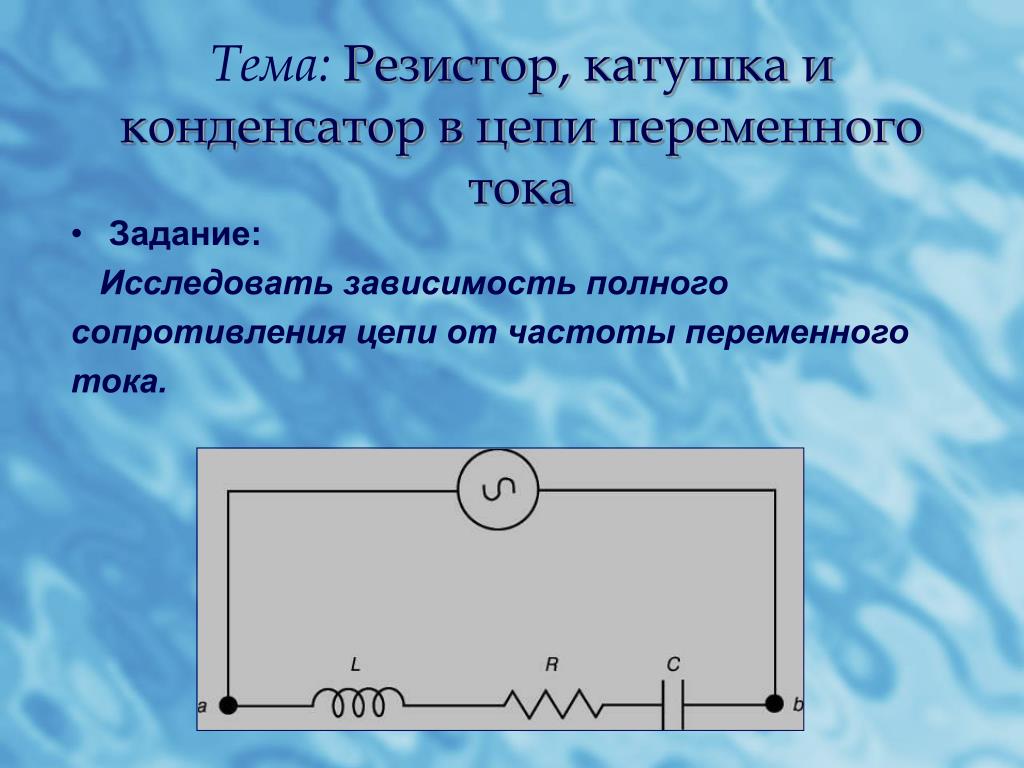 Выяснили причины их появления. Получили формулы для их вычисления.
Выяснили причины их появления. Получили формулы для их вычисления.
Особенно активно и с высоким качеством сегодня работали (объявляются фамилии). Оценки получают (фамилии).
Инструктаж по выполнению домашней работы: п. 32- 34.
Повторить формулы для расчета активного, емкостного и индуктивного сопротивления.
Всем спасибо! Урок закончен. До свидания.
Переменный синусоидальный ток — Большая Энциклопедия Нефти и Газа, статья, страница 3
Cтраница 3
| Схемы выпрямителей. однополупериодного ( а, двухполупериодного ( б и с удвоением напряжения ( в. [31] |
Для многих практических применений необходимо преобразовать переменный синусоидальный ток в ток одного направления. Этой цели служат выпрямители, действие которых основано на односторонней проводимости ламповых и полупроводниковых диодов. [32]
Следовательно, во вторичной обмотке протекает переменный синусоидальный ток ( при активной нагрузке), обеспечивая хорошее использование трансформатора в схеме. [33]
[33]
Действие, которое оказывает на организм переменный синусоидальный ток, характеризуют двумя пороговыми значениями: порогом ощутимого тока и порогом неотпускающего тока. Эти значения зависят от индивидуальных особенностей организма и являются случайными величинами. Их средние значения и называют пороговыми значениями переменного тока. [34]
Классические варианты аппроксимаций временных зависимостей ( постоянный, переменный, синусоидальный ток) в современных технических системах часто уступают место импульсным сигналам, форма которых не поддается простой аппроксимации. Параметризация импульсных сигналов идет обычно путем аппроксимации наблюдаемой зависимости последовательностью характерных точек. При этом выбор уровней отсчета и моментов фиксации значений должен обеспечить, с одной стороны, соответствие реальным режимам работы данного конкретного устройства в конкретной системе, с другой стороны, возможность сравнения с другими аналогичными объектами.
Электрическая прочность изоляции крановой аппаратуры проверяется переменным синусоидальным током частотой 50 Гц для подтверждения наличия надлежащих запасов прочности в изоляции при возможных перенапряжениях сети. [36]
Конденсатор емкостью 36 мкФ включен в сеть переменного синусоидального тока стандартной частоты напряжения 220 В. [37]
По обеим шинам в направлении оси х протекают одинаковые переменные синусоидальные токи. [38]
Действующие значения синусоидальных составляющих определяются по известным законам переменного синусоидального тока. [39]
По катушке, не имеющей активного сопротивления, протекает переменный синусоидальный ток. Индуктивность катушки равна L. Чему равна средняя за период мощность, потребляемая катушкой.
[40]
Индуктивность катушки равна L. Чему равна средняя за период мощность, потребляемая катушкой.
[40]
Проверку электрической прочности изоляции машин проводят на испытательной установке переменного синусоидального тока частотой 50 Гц и мощностью на стороне высокого напряжения не менее 0 5 кВ — А. Испытанию подвергают каждую электрически раздельную цепь. Начальное испытательное напряжение не должно превышать 1 / 3 полного его значения. [41]
Емкостное сопротивление — реактивное сопротивление, обусловленное емкостью цепи переменного синусоидального тока. [42]
Подобным же образом можно, конечно, изображать и силу переменного синусоидального тока
Если к входным и выходным выводам нелинейного четырехполюсника подключены источники постоянного и переменного синусоидального тока, то в цепи не выполняется принцип суперпозиции и источники тока взаимно влияют на составляющие токов, обусловленные каждым источником. Рабочая точка при этом периодически перемещается на определенном участке координатной плоскости и исследование цепи в общем случае представляет существенные трудности. В отдельных случаях переменный ток может быть найден путем графических построений.
[44]
Рабочая точка при этом периодически перемещается на определенном участке координатной плоскости и исследование цепи в общем случае представляет существенные трудности. В отдельных случаях переменный ток может быть найден путем графических построений.
[44]
Настоящая работа посвящена изучению электрохимического и коррозионного поведения железа под действием
Страницы: 1 2 3 4
Почему основные законы электрической цепи нарушаются при высокочастотном переменном токе?
Задай вопрос
спросил
Изменено 4 года, 3 месяца назад
Просмотрено 12 тысяч раз
\$\начало группы\$
Мы только начинаем всю радиочастотную сцену, имея дело с постоянным и низкочастотным переменным током на всех наших предыдущих курсах.
Я понимаю, что при высокочастотном переменном токе основные законы схемы больше не применяются, и классические модели пассивных компонентов необходимо изменить. Обоснованием этого было то, что при высокочастотной передаче переменного тока длина волны становится намного меньше и иногда может быть меньше, чем проводка на печатных платах и т. д.
Я понимаю, что это проблема при передаче электромагнитных волн через свободное пространство, но почему это проблема с реальными физическими проводами и печатными платами, которые питаются от источника переменного тока?
- переменный ток
- высокочастотный
\$\конечная группа\$
12
\$\начало группы\$
На самом деле это это все о волнах. Даже при работе с постоянным током все управляется электрическими и магнитными полями и волнами.
Даже при работе с постоянным током все управляется электрическими и магнитными полями и волнами.
«Основные законы» не нарушаются. Правила, которые вы выучили, — это упрощения, дающие точные ответы при определенных условиях — вы еще не выучили фундаментальные законы. Вы собираетесь изучить фундаментальные законы после использования упрощений.
Часть предполагаемых условий для упрощенных правил заключается в том, что размер цепи намного меньше, чем длина волны задействованного(ых) сигнала(ов). В этих условиях вы можете предположить, что сигнал находится в одном и том же состоянии по всей цепи. Это приводит к множеству упрощений в уравнениях, описывающих схему.
По мере того, как частоты становятся выше (или цепи становятся больше), так что цепь составляет заметную долю длины волны, это предположение перестает быть верным.
Влияние длины волны на работу электрических цепей впервые стало очевидным на низких частотах, но с очень большими цепями — телеграфными линиями.
Когда вы начинаете работать с RF, вы достигаете таких длин волн, что размер схемы, которая стоит на вашем столе, составляет заметную долю длины волны используемых сигналов.
Итак, вы начинаете обращать внимание на вещи, которые раньше могли просто игнорировать.
Правила и уравнения, которые вы сейчас изучаете, применимы и к более простым низкочастотным цепям. Вы можете использовать новые вещи для решения более простых схем — вам просто нужно иметь больше информации и решать более сложные уравнения.
\$\конечная группа\$
6
\$\начало группы\$
Фундаментальные законы ЭМ – это уравнения Максвелла: $$\набла\cdot\mathbf{E} = 4\pi\rho$$ $$\набла\cdot\mathbf{B} = 0$$ $$\nabla \times \mathbf{E} = -\frac{1}{c} \frac{\partial \mathbf{B}} {\partial t}$$ $$\nabla \times \mathbf{B} = \frac{1}{c}\left( 4\pi\mathbf{J} + \frac{\partial \mathbf{E}}{\partial t}\right )$$
Они всегда были фундаментальными законами ЭМ, но на более низких частотах мы находим решение этих многомерных дифференциальных уравнений довольно трудным и не очень полезным для нашего понимания схемы.
Соответственно, люди уже интегрировали эти уравнения для простых случаев, таких как провода на низких частотах, и нашли уравнения, которые вам давали на предыдущих занятиях. Точнее, мы сначала нашли эти уравнения, затем нашли уравнения Максвелла, углубившись в ЭМ, а затем, в конце концов, показали, что исходные уравнения согласуются с уравнениями Максвелла.
Лично я считаю, что лучше исследовать это на примере. Я хотел бы взять пример из известного тома: Искусство высокоскоростного цифрового дизайна (подзаголовок: Справочник по черной магии). Во введении они отмечают, насколько важен выбор типа конденсатора. Они делают экстраординарное утверждение, что на высоких скоростях конденсатор может выглядеть как индуктор, потому что его выводы представляют собой два параллельных провода.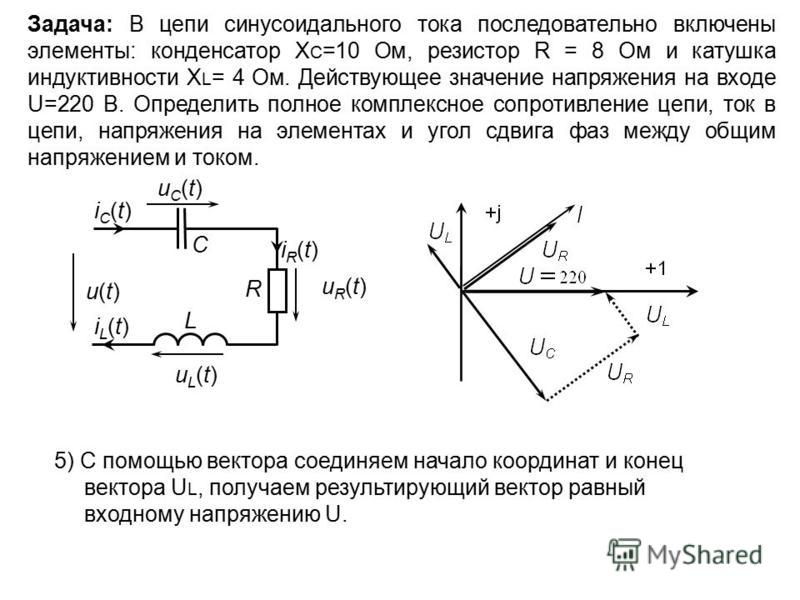 Параллельные провода имеют индуктивность. 92CL \ll 1\$, вы можете игнорировать это. На высоких частотах нельзя.
Параллельные провода имеют индуктивность. 92CL \ll 1\$, вы можете игнорировать это. На высоких частотах нельзя.
Точно так же на высоких частотах становится сложнее игнорировать тот факт, что провода излучают электромагнитное излучение. На низких частотах этот эффект тривиален, но на высоких частотах большая мощность может рассеиваться в самом проводе.
\$\конечная группа\$
1
\$\начало группы\$
Поскольку предположения, требуемые моделью с сосредоточенными элементами, нарушаются. Модель с сосредоточенными элементами позволяет анализировать такие устройства, как резисторы, соединенные узлами, без учета физического расположения устройств и схемы.
Модель с сосредоточенными элементами предполагает:
- Изменение магнитного потока во времени вне проводника равно нулю.
$${\frac {\partial \phi _{B}}{\partial t}}=0$$
- Изменение заряда во времени внутри проводящих элементов равно нулю.

$${\frac {\partial q}{\partial t}}=0$$
- Характеристическая длина («размер» узлов и устройств) намного меньше длины волны интересующего сигнала .
$$L_c << \лямбда$$
\$\конечная группа\$
4
\$\начало группы\$
Здесь много сложных (и правильных) ответов. Я добавлю одну простую аналогию — подумайте о стрельбе из ружья:
- на расстоянии 10 см, время полета пули — это просто расстояние/скорость, а точка попадания на линии идентична оси ствола
- на дистанции 10 м вы видите, что пуля попала в цель ниже, так как гравитация немного потянула ее вниз и вам нужно прицелиться под нее
- на 20 м вам нужно больше отрегулировать, так как гравитация сильнее влияет на него
- на 100 м видно, что даже с учетом гравитации не вписывается. Почему? Да там и воздух и пуля тоже замедленная.
 Также мы видим, что пуля делает все, кроме того, что летит прямо, так как ее вращение в сочетании с вертикальной скоростью сжимает воздух с одной стороны и пули танцуют там. Также мы можем видеть, что он, вероятно, не совсем однороден, что добавляет к его подвижности еще один фактор 9.0024
Также мы видим, что пуля делает все, кроме того, что летит прямо, так как ее вращение в сочетании с вертикальной скоростью сжимает воздух с одной стороны и пули танцуют там. Также мы можем видеть, что он, вероятно, не совсем однороден, что добавляет к его подвижности еще один фактор 9.0024 - на 1000 м мы видим, что есть еще что-то — да, Земля вращается и тоже считает
- так иди выше, где бы он не кончил так быстро влетать в землю, скажем на орбиту и стреляй там — опять же есть что считать — мы забыли и про лунную гравитацию тоже
- а на еще большем расстоянии мы видим, что есть не только солнечная гравитация, но и свет, идущий от Солнца, который его тоже немного толкает, и все те электрически активные частицы, которые создают в нем небольшие токи и магические поля…
- , а в чрезвычайно длинных (вроде межзвездных) следах еще и гравитация других галактик (что неудивительно), но наш булл успевает изменить свою внутреннюю структуру, так как даже свинец чрезвычайно медленно распадается на другие химические элементы путем радиоактивного распада
Ну, это сейчас очень сложно, так что давайте вернемся к 10-сантиметровому расстоянию на старте — значит ли это, что формула время=расстояние/скорость не работает? Или не работает наша окончательная сверхсложная формула?
Ну, оба работают, так как все те элементы, которые мы медленно добавляли в наши расчеты, все еще там присутствуют, только на таком коротком расстоянии разница настолько мала, что мы даже не можем ее измерить. И поэтому мы можем использовать нашу «простую» формулу, которая не совсем точна, но в некоторых разумных условиях дает достаточно точные результаты (скажем, до 5 знаков после запятой), и мы можем быстро ее выучить, быстро применить и получить результаты, которые верны (с точностью до 5 знаков после запятой) в интересующем нас масштабе.
И поэтому мы можем использовать нашу «простую» формулу, которая не совсем точна, но в некоторых разумных условиях дает достаточно точные результаты (скажем, до 5 знаков после запятой), и мы можем быстро ее выучить, быстро применить и получить результаты, которые верны (с точностью до 5 знаков после запятой) в интересующем нас масштабе.
То же самое относится к постоянному току, медленному переменному току, радиочастотам, сверхвысоким частотам… каждое следующее является более точной версией предыдущего, каждое предыдущее является специальной версией следующего в ситуации, когда небольшие различия настолько малы, что мы можем отбросить их и получить «достаточно хороший» результат.
\$\конечная группа\$
1
\$\начало группы\$
Я имею в виду, что это прямое соединение, мы не используем электромагнитные волны для распространения в свободном пространстве, поэтому длина волны и прочее не должны иметь значения, верно?
Это очень неверное предположение. Сигналы по-прежнему являются ЭМ-волнами и остаются ЭМ-волнами, если они распространяются через свободное пространство или проводник. Законы остаются прежними.
Сигналы по-прежнему являются ЭМ-волнами и остаются ЭМ-волнами, если они распространяются через свободное пространство или проводник. Законы остаются прежними.
В соединениях (проводах) порядка длины волны больше нельзя использовать подход «сосредоточенного элемента». Подход «сосредоточенных элементов» означает, что соединения считаются «идеальными». Для высокочастотных сигналов на расстояниях порядка длины волны и выше этот подход недействителен.
Итак, помните: законы ЭМ не меняются при прохождении ЭМ волны в пространстве или проводнике, они действуют в обоих случаях. ЭМ волны остаются ЭМ волнами в свободном пространстве или в проводнике.
\$\конечная группа\$
8
\$\начало группы\$
Они не ломаются, но , когда время нарастания приближается к 10 % или меньше, чем задержка распространения до согласования импеданса нагрузки, имеет важное значение из-за этой длины волны. Импеданс нагрузки инвертируется к источнику на 1/4 длины волны независимо от того, проводится он или излучается.
Импеданс нагрузки инвертируется к источнику на 1/4 длины волны независимо от того, проводится он или излучается.
Если нагрузка не соответствует полному сопротивлению «линии передачи и источника», отражения будут происходить в соответствии с некоторым коэффициентом, называемым , возвратными потерями и коэффициентом отражения.
Вот эксперимент, который вы можете провести, чтобы продемонстрировать кондуктивные электромагнитные волны.
Если вы попытаетесь исследовать прямоугольную волну с частотой 1 МГц на пробнике осциллографа 10:1 с зажимом для заземления 10 см, вы можете увидеть сосредоточенный резонанс коаксиального кабеля 20 МГц. Да, пробник не согласован с генератором на 50 Ом, поэтому отражения будут происходить в соответствии с проводом заземления 10 нГн/см и специальным коаксиальным проводом пробника 50 пФ/м. Это по-прежнему отклик сосредоточенного элемента (LC).
Уменьшение щупа 10:1 до размера менее 1 см до кончика штифта и кольца без длинного зажима заземления повышает резонансную частоту, возможно, до ограничения щупа и осциллографа на уровне 200 МГц.
Теперь попробуйте коаксиальный кабель 1:1 1 м, который имеет 20 нс/м, поэтому прямоугольная волна 20~50 МГц на кабеле 1 м с пробником 1:1 увидит отражение на одной доле длины волны и ужасную прямоугольную волну ответ, если не завершен на осциллографе с 50 Ом. Это отражение кондуктивной электромагнитной волны.
Но учтите, что быстрый логический сигнал с временем нарастания 1 нс может иметь импеданс источника 25 Ом и полосу пропускания >300 МГц, поэтому перерегулирование может быть ошибкой измерения или фактическим несоответствием импеданса отражениям длины дорожки.
Теперь вычислите 5 % длины волны 300 МГц при скорости 3 8 м/с для воздуха и 2 8 м/с для коаксиального кабеля и посмотрите, каково время задержки распространения, вызывающее эхо-сигналы от несогласованной нагрузки, например. КМОП с высоким Z и скажем 100-омными дорожками. Вот почему обычно требуются контролируемые импедансы выше 20–50 МГц, и это влияет на звон, перерегулирование или несоответствие импеданса. Но без этого у логики есть такая большая серая зона между «0 и 1», чтобы можно было звонить.
Но без этого у логики есть такая большая серая зона между «0 и 1», чтобы можно было звонить.
Если какие-то слова неизвестны, найдите их.
\$\конечная группа\$
1
\$\начало группы\$
Несмотря на то, что на этот вопрос уже несколько раз отвечали, я хотел бы добавить аргументацию, которую лично я нахожу наиболее интересной и взятой из книги Тома Ли «Планарная микроволновая техника» (глава 2.3).
Как указано в других ответах, большинство людей забывают, что законы Кирхгофа — это всего лишь приближения, которые выполняются при определенных условиях (сосредоточенный режим), когда предполагается квазистатическое поведение. Как приходят к этим приближениям?
Начнем с уравнений Максвелла в свободном пространстве:
$$ \nabla \mu_0 H=0 \qquad(1) \\ \nabla \epsilon_0 E = \rho \qquad(2) \\ \nabla\times H=J+\epsilon_0 \frac{\partial E}{\partial t} \qquad(3) \\ \nabla\times E=-\mu_0 \frac{\partial H}{\partial t} \qquad(4) \\ $$
Уравнение 1 утверждает, что в магнитном поле нет дивергенции и, следовательно, нет магнитных монополей (обратите внимание на мое имя пользователя! ;-))
Уравнение 2 представляет собой закон Гаусса и утверждает, что существуют электрические заряды (монополи). Это источники дивергенции электрического поля.
Это источники дивергенции электрического поля.
Уравнение 3 представляет собой закон Ампера с модификацией Максвелла: оно утверждает, что обычный ток, а также переменное во времени электрическое поле создают магнитное поле (последнее соответствует знаменитому току смещения в конденсаторе).
Уравнение 4 представляет собой закон Фарадея и утверждает, что изменение магнитного поля вызывает изменение (завихрение) электрического поля.
Уравнение 1-2 не важно для данного обсуждения, но уравнение 3-4 отвечает на вопрос, откуда возникает волновое поведение (а поскольку уравнения Максвелла являются наиболее общими, они применимы ко всем цепям, включая постоянный ток): H, который вызывает изменение E и так далее. это условия связи, создающие волновое поведение !
Теперь предположим на мгновение, что mu0 равно нулю. Тогда электрическое поле не имеет завихрений и может быть выражено как градиент потенциала, который также подразумевает, что линейный интеграл вокруг любого замкнутого пути равен нулю:
$$ V = \oint E dl = 0 $$
Вуаля, это всего лишь теоретико-полевое выражение закона напряжения Кирхгофа .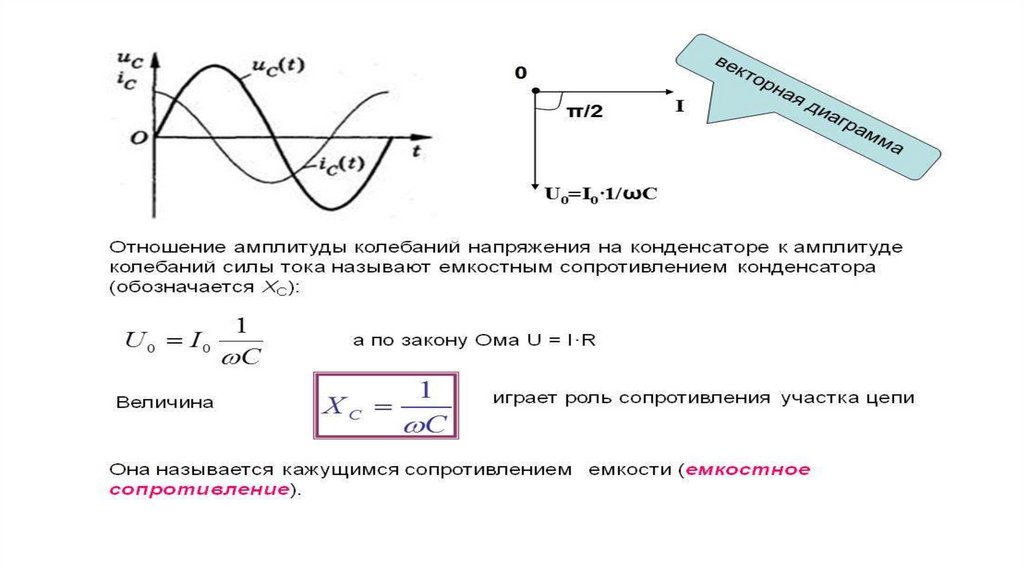
Аналогично, установка epsilon0 в ноль приводит к
$$ \набла J = \набла (\набла \times H) = 0 $$
Это означает, что дивергенция J равна нулю, что означает, что ни в одном узле не может возникнуть (чистый) ток. Это не что иное, как Текущий закон Кирхгофа .
На самом деле epsilon0 и mu0, конечно, не равны нулю. Однако они фигурируют в определении скорости света:
$$ c = \ sqrt {\ frac {1} {\ mu_0 \ epsilon_0}} $$
При бесконечной скорости света члены связи исчезли бы, и вообще не было бы волнового поведения. Однако, когда физические размеры системы малы по сравнению с длинами волн, то конечность скорости света не заметна (так же, как замедление времени всегда существует, но не будет заметно для малых скоростей, и, следовательно, уравнения Ньютона являются приближением к теории относительности Эйнштейна).
\$\конечная группа\$
1
\$\начало группы\$
Электрическим сигналам требуется время для распространения по проводам (и печатным платам). Всегда медленнее, чем электромагнитные волны в вакууме или воздухе.
Всегда медленнее, чем электромагнитные волны в вакууме или воздухе.
Например, витая пара в кабеле CAT5e имеет коэффициент скорости 64%, поэтому сигнал проходит со скоростью 0,64с и проходит около 8 дюймов за наносекунду. В некоторых электронных контекстах наносекунда — это большое время. Например, 4 такта в современном процессоре
Любая конфигурация проводников конечного размера имеет индуктивность, емкость и (обычно) сопротивление, поэтому ее можно аппроксимировать с помощью сосредоточенных компонентов на более мелком уровне детализации. Вы можете заменить провод 20-ю катушками индуктивности и резисторами с 20-ю конденсаторами на землю. Если длина волны очень короткая по сравнению с длиной, вам может понадобиться 200 или 2000 или .. что-то еще, чтобы точно приблизиться к проводу, и другие методы могут начать выглядеть привлекательными, например, теория линий передачи (обычно один семестр курс бакалавриата для EE) .
«Законы», такие как KVL, KCL, представляют собой математические модели, которые очень точно аппроксимируют реальность при соответствующих условиях. Более общие законы, такие как уравнения Максвелла, применяются более широко. Могут быть некоторые ситуации (возможно, релятивистские), когда уравнения Максвелла перестают быть очень точными.
Более общие законы, такие как уравнения Максвелла, применяются более широко. Могут быть некоторые ситуации (возможно, релятивистские), когда уравнения Максвелла перестают быть очень точными.
\$\конечная группа\$
1
\$\начало группы\$
Это это волна. Здесь происходит то же самое, о чем говорят, когда упоминают, что «электричество движется со скоростью света», хотя электроны «двигаются» гораздо медленнее. На самом деле она составляет около 2/3 (IIRC) скорости света в большинстве проводящих материалов, то есть около 200 000 км/с. В частности, когда вы нажимаете переключатель, например, вы посылаете электромагнитную волну по цепи, которая заставляет электроны двигаться. В этом случае это «ступенчатая» волна — за ней поле постоянно высокое, впереди оно равно нулю, но как только она проходит, электроны начинают двигаться. Волны движутся в среде с меньшими скоростями, чем в свободном пространстве, но они все же проходят через среду — вот почему, в конце концов, этот свет может проходить сквозь стекло.
Волны движутся в среде с меньшими скоростями, чем в свободном пространстве, но они все же проходят через среду — вот почему, в конце концов, этот свет может проходить сквозь стекло.
В этом случае источник напряжения постоянно «качает» туда-сюда, и тем самым создает колебательные волны, которые точно так же движутся с одинаковой скоростью. На низких частотах, таких как 60 Гц, длина этих волн намного больше, чем масштаб одного устройства в человеческом масштабе, а именно для этой конкретной частоты около 3000 км (200 000 км/с * (1/60 с)), по сравнению с, возможно, 0,1 м (100 мм) для типичной портативной печатной платы, что означает коэффициент масштабирования около 30 000 000: 1, и, таким образом, вы можете рассматривать его как постоянный ток, который периодически изменяется.
С другой стороны, поднимитесь, скажем, до 6 ГГц — так что микроволновые радиочастотные приложения, как и в телекоммуникационных технологиях передачи — и теперь длина волны в 100 миллионов раз короче, или 30 мм. Это намного меньше, чем масштаб схемы, важна волна, и теперь вам нужны более сложные электродинамические уравнения, чтобы понять, что происходит, и старый добрый Кирхгоф больше не будет резать горчицу 🙂
Это намного меньше, чем масштаб схемы, важна волна, и теперь вам нужны более сложные электродинамические уравнения, чтобы понять, что происходит, и старый добрый Кирхгоф больше не будет резать горчицу 🙂
\$\конечная группа\$
\$\начало группы\$
Более простой ответ: потому что паразитные компоненты, которые не нарисованы на вашей принципиальной схеме, начинают играть роль:
- последовательное сопротивление (ESR) и последовательная индуктивность конденсаторов,
- повышение сопротивления проводов за счет скин-эффекта,
- Параллельное демпфирование (вихревых токов) и параллельная емкость катушек индуктивности,
- паразитная емкость между узлами напряжения (например, между дорожками печатной платы, включая «землю»),
- Паразитная индуктивность токовых петель,
- связанная индуктивность между токовыми петлями,
- связь магнитных полей между неэкранированными индукторами, которая может зависеть от случайной полярности размещения компонентов,
- .
 ..
..
Это также тема ЭМС, очень важная, если вы хотите создавать схемы, которые действительно работают в полевых условиях.
Кроме того, не удивляйтесь, если вы даже не сможете измерить происходящее. Выше МГц или около того правильное подключение пробника осциллографа становится искусством.
\$\конечная группа\$
\$\начало группы\$
У вас есть много отличных ответов на ваш вопрос, поэтому я не буду повторять то, что уже было сказано.
Вместо этого я попытаюсь адресовать ваши комментарии к различным ответам. Судя по комментариям, которые вы опубликовали, у вас, кажется, есть базовое непонимание физических законов, управляющих цепями.
Вы, кажется, думаете, что «движущиеся электроны в проводе» не имеют ничего общего с электромагнитными волнами. И что электромагнитные волны вступают в игру только в определенных ситуациях или сценариях. Это в принципе неправильно.
Как уже говорили другие, уравнения Максвелла (далее МЭ) являются ключом к правильному пониманию вопроса. Эти уравнения способны объяснить все известные человечеству электромагнитные явления, за исключением квантовых явлений. Поэтому они имеют очень широкий спектр применения. Но это не главное, что я хочу сделать.
Вы должны понимать, что электрические заряды (например, электроны) создают вокруг себя электрическое поле одним своим существованием. И если они движутся (то есть являются частью электрического тока), они также генерируют магнитное поле .
Бегущие ЭМ волны (то, что простые люди обычно понимают под ЭМ «волнами») — это всего лишь распространение вариаций электрических и магнитных полей в пространстве («вакууме») или любой другой физической среде.
В основном так говорят медики.
Более того, МЭ также говорят вам, что всякий раз, когда поле изменяется (будь то электрическое или магнитное), тогда «автоматически» возникает другое поле (и оно тоже меняется). Вот почему электромагнитные волны называются Электромагнитный : (переменное во времени электрическое поле) подразумевает существование (переменного во времени) магнитного поля и наоборот. Не может быть изменяющегося Е-поля без изменяющегося М-поля и, симметрично, не может быть изменяющегося М-поля без сопутствующего изменяющегося Е-поля.
Вот почему электромагнитные волны называются Электромагнитный : (переменное во времени электрическое поле) подразумевает существование (переменного во времени) магнитного поля и наоборот. Не может быть изменяющегося Е-поля без изменяющегося М-поля и, симметрично, не может быть изменяющегося М-поля без сопутствующего изменяющегося Е-поля.
Это означает, что если у вас есть ток в цепи, и этот ток не является постоянным (иначе он генерирует только статическое магнитное поле), у вас БУДЕТ ЭМ волна во всем пространстве, окружающем путь тока . Когда я говорю «во всем пространстве», я имею в виду «все физическое пространство», независимо от того, какие тела занимают это пространство.
Конечно, присутствие тел изменяет «форму» (то есть характеристики) электромагнитного поля, создаваемого током: фактически компоненты представляют собой «тела», предназначенные для контролируемого изменения этого поля.
Путаница в ваших рассуждениях может возникнуть из-за того, что компоненты с сосредоточенными параметрами хорошо работают только в предположении, что поля изменяются медленно . Технически это называется предположением о квазистатических полях : предполагается, что поля изменяются так медленно, что они очень похожи на поля, присутствующие в истинной ситуации постоянного тока.
Технически это называется предположением о квазистатических полях : предполагается, что поля изменяются так медленно, что они очень похожи на поля, присутствующие в истинной ситуации постоянного тока.
Это предположение приводит к радикальным упрощениям: позволяет нам использовать законы Кирхгофа для анализа цепи без заметных ошибок. Это не означает, что вокруг и внутри компонентов и дорожек печатных плат нет электромагнитных волн. Действительно есть! Хорошая новость заключается в том, что их поведение можно с пользой свести к току и напряжению с целью проектирования и анализа схемы.
\$\конечная группа\$
\$\начало группы\$
На самом деле вы задаете два вопроса: 1) «Почему нарушаются основные законы цепи» при высоких частотах переменного тока. 2) Почему они также должны выходить из строя при использовании «настоящих физических проводов…»
Первый вопрос был освещен в предыдущих ответах, но второй вопрос заставляет меня поверить, что ваш разум не перешел от «движения электронов» к Движущиеся электромагнитные волны, к которым я обращусь.
Независимо от того, как генерируются электромагнитные волны , они являются одними и теми же (кроме амплитуды и частоты). Они распространяются со скоростью и света по «прямой» линии .
В конкретном случае, когда они генерируются зарядами , текущими по проводу , волна будет следовать направлению провода !
Всегда , имея дело с движущимися зарядами, вы имеете дело с электромагнитными волнами . Однако, когда отношение длины волны к размеру цепи достаточно велико, эффекты 2-го и более высоких порядков настолько малы, что для практических целей ими можно пренебречь.
Надеюсь, теперь ясно, что провода служат только для направления электромагнитных волн, а не для изменения их природы.
\$\конечная группа\$
2
\$\начало группы\$
Вам нужно изменить свое отношение к электричеству. Думайте об этой концепции как об электроне, колеблющемся в пустом пространстве. В постоянном токе колебания толкают и смещают электроны в одном и том же общем векторе направления. На высоких частотах смещения происходят во многих направлениях с большей скоростью и более беспорядочно, и каждый раз, когда вы смещаете электроны, что-то происходит, и использование уравнений, перечисленных здесь и в учебниках, помогает смоделировать то, что произойдет. Когда вы занимаетесь проектированием, вы пытаетесь создать модель и определить закономерности происходящего и использовать ее для решения проблем.
Думайте об этой концепции как об электроне, колеблющемся в пустом пространстве. В постоянном токе колебания толкают и смещают электроны в одном и том же общем векторе направления. На высоких частотах смещения происходят во многих направлениях с большей скоростью и более беспорядочно, и каждый раз, когда вы смещаете электроны, что-то происходит, и использование уравнений, перечисленных здесь и в учебниках, помогает смоделировать то, что произойдет. Когда вы занимаетесь проектированием, вы пытаетесь создать модель и определить закономерности происходящего и использовать ее для решения проблем.
\$\конечная группа\$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
типов конденсаторов — Googlesuche
AlleBilderShoppingVideosMapsNewsBücher
suchoptionen
7 типов конденсаторов и их применение
Керамический конденсатор.
Электролитический конденсатор.
Пленочные и бумажные конденсаторы.
Суперконденсаторы.
Конденсатор из серебряной слюды.
Стеклянный конденсатор.
Танталовый конденсатор.
Поликарбонатный конденсатор.
7 Types of Capacitors and Their Uses — Linquip
www.linquip.com › Home › Electrical Component
Hervorgehobene Snippets
Kondensator (Capacitor)
Elektrotechnik
Alle anzeigen
Ein Kondensator ist ein пассивные elektrisches Bauelement мит дер Fähigkeit, в einem Gleichstromkreis elektrische Ladung унд умереть damit zusammenhängende Energie statisch в einem elektrischen Feld цу speichern. Википедия
Википедия
Типы конденсаторов
Конденсатор, установленный в стальном, формованном, абмессунгенном и более крупном корпусе. Sie alle enthalten …
Типы конденсаторов — Wikipedia
en.wikipedia.org › wiki › Capacitor_types
Керамические конденсаторы имеют керамический диэлектрик. · Пленочные и бумажные конденсаторы названы в честь их диэлектриков. · Алюминий, тантал · Полимерные конденсаторы …
Типы и стили · Сравнение типов · Электрические характеристики
Ähnliche Fragen
Какие бывают 3 типа конденсаторов?
Какой тип конденсатора лучше?
Какие существуют типы конденсаторов и их применение?
Как определить типы конденсаторов?
Различные типы конденсаторов и их применение
www.watelectronics.com › различные типы емк…
29.07.2019 · Различные типы конденсаторов · Электролитический конденсатор · Слюдяной конденсатор · Бумажный конденсатор · Пленочный Конденсатор · Неполяризованный конденсатор · Керамический . ..
..
Конденсатор и типы конденсаторов | Фиксированные, переменные, полярные и неполярные
www.electricaltechnology.org › Конденсаторы
1) Фиксированные конденсаторы: · 1.1) Полярные конденсаторы: · 1.1.1) Электролитические конденсаторы: · 1.1.1.1) Алюминиевые электролитические конденсаторы · 1.1 .1.2) Танталовый электролитический …
Типы конденсаторов и их конструкция. Учебные пособия по электронике
www.electronics-tutorials.ws › конденсатор › cap_2
Учебное пособие по электронике о различных типах доступных конденсаторов, включая электролитические, керамические, танталовые и пленочные конденсаторы.
Различные типы конденсаторов и их применение | StudyElectrical.Com
studyelectrical.com › Basic Electrical
Типы конденсаторов · Керамические конденсаторы · Пленочные и бумажные конденсаторы · Алюминиевые, танталовые и ниобиевые электролитические конденсаторы · Полимерные конденсаторы · Суперконденсатор .


 Также мы видим, что пуля делает все, кроме того, что летит прямо, так как ее вращение в сочетании с вертикальной скоростью сжимает воздух с одной стороны и пули танцуют там. Также мы можем видеть, что он, вероятно, не совсем однороден, что добавляет к его подвижности еще один фактор 9.0024
Также мы видим, что пуля делает все, кроме того, что летит прямо, так как ее вращение в сочетании с вертикальной скоростью сжимает воздух с одной стороны и пули танцуют там. Также мы можем видеть, что он, вероятно, не совсем однороден, что добавляет к его подвижности еще один фактор 9.0024 ..
..