Site Loader
Posted on 27.02.2023

Содержание

§12. Восьмеричная система счисления | Алгоритм перевода двоичного числа в восьмеричную систему счисления (курс pol 136 ч.)

Планирование уроков на учебный год (по учебнику К.Ю. Полякова, Е.А. Еремина, полный углубленный курс, 4 часа в неделю)

Главная | Информатика и информационно-коммуникационные технологии | Планирование уроков и материалы к урокам | 10 классы | Планирование уроков на учебный год (по учебнику К.Ю. Полякова, Е.А. Еремина, полный углубленный курс, 4 часа в неделю) | Восьмеричная и шестнадцатеричная системы счисления





Содержание урока

§12. Восьмеричная система счисления

Восьмеричная система

Алгоритм перевода восьмеричного числа в двоичную систему счисления

Алгоритм перевода двоичного числа в восьмеричную систему счисления

Вопросы и задания

Задачи

§13. Шестнадцатеричная система счисления

Алгоритм перевода двоичного числа в восьмеричную систему счисления

1. Разбить двоичное число на триады, начиная справа. В начало самой первой триады добавить слева нули, если это необходимо.

2. Перевести каждую триаду (отдельно) в восьмеричную1 систему счисления.

1 Заметим, что значение цифры в восьмеричной системе счисления совпадает со значением этой же цифры в десятичной системе.

3. Соединить полученные цифры в одно «длинное» число.

Например, переведём в восьмеричную систему число 10100111001011101112. Разобьём его на триады (начиная справа), в начало числа нужно добавить два нуля (они подчёркнуты): 10100111001011101112 = 001 010011 100 101 110 1112.

Далее по табл. 2.5 переводим каждую триаду в восьмеричную систему: 10100111001011101112 = 12345678.

Теперь представьте себе объём вычислений, который потребуется для решения этой задачи через десятичную систему.

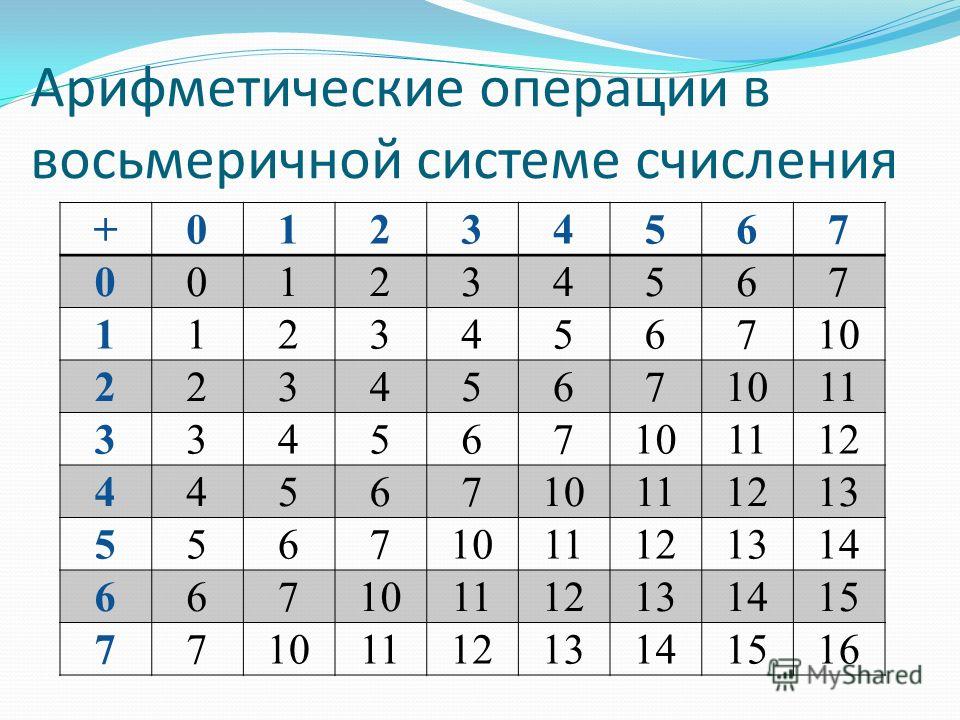
При вычислениях в восьмеричной системе нужно помнить, что максимальная цифра — это 7. Перенос при сложении возникает тогда, когда сумма в очередном разряде получается больше 7. Заём из старшего разряда равен 108 = 8, а все «промежуточные» разряды заполняются цифрой 7 — старшей цифрой системы счисления. Приведём примеры сложения и вычитания:

В примере на сложение запись 1 • 8 + 2 означает, что получилась сумма, большая 7, которая не помещается в один разряд. Единица идёт в перенос, а двойка остаётся в этом разряде. В записи операций при выполнении вычитания запись «-1» означает, что из этого разряда раньше был заём (его значение уменьшилось на 1), а запись «+8» означает заём из старшего разряда.

С помощью восьмеричной системы удобно кратко записывать содержимое областей памяти, содержащих количество битов, кратное трём. Например, 6-битные данные «упаковываются» в две восьмеричные цифры. Некоторые компьютеры 1960-х годов использовали 24-битные и 36-битные данные, они записывались соответственно с помощью 8 и 12 восьмеричных цифр. Восьмеричная система использовалась даже для компьютеров с 8-битной ячейкой памяти (PDP-11, ДВК), но позднее была почти вытеснена шестнадцатеричной системой (см. далее).

Сейчас восьмеричная система применяется, например, для установки прав на доступ к файлу в операционной системе Linux (и других Unix-системах) с помощью команды chmod. Режим доступа кодируется тремя битами, которые разрешают чтение (r, read, старший бит), запись (w, write) и выполнение файла (х, execute, младший бит). Код 7 = 1112 (rwx) означает, что все биты установлены (полный доступ), а код 5 = 1012 (r-х) разрешает чтение и выполнение файла, но запрещает его изменение.

Следующая страница Вопросы и задания

Cкачать материалы урока




Перевод из восьмеричной системы в десятичной системе

Лабораторная работа №3

Тема: Использование восьмеричную систему счисления.

Цель работы: научиться использовать восьмеричную систему счисления

Двоичная система счисления неудобна для использования человеком, поэтому программисты используют восьмеричную систему счисления.

Используемые символы: 0, 1, 2, 3, 4, 5, 6 и 7;

Для восьмеричной системы счисления соответствие чисел базиса системы с трехзначными числами двоичной системы следующее:

08=0002 48=1002

18=0012 58=1012

28=0102 68=1102

38=0112 78=1112

Представим в виде таблицы:

Двоичная система счисления

000

001

010

011

100

101

110

111

Восьмеричная система счисления

0

1

2

3

4

5

6

7

Примеры:

1) 14478=001 100 100 1112=11001001112.

2) 256,7738= 010 101 110, 111 111 0112 = 10101110,1111110112;

Задания: Используя таблицу переведите числа из восьмеричной в двоичную:

1. 4368 6. 15,4238

2. 16748 7. 24,558

3. 60748 8. 73,238

4. 12548 9. 124,328

5. 56778 10. 364,458

Перевод из восьмеричной системы в десятичную систему производится путем сложения произведений соответствующего десятичного эквивалента символа числа в восьмеричной

системе на вес i-го знакоместа.

Примеры перевода из восьмеричной системы счисления в десятичную систему:

  1. 4618 = 4*82+6*81+1*80 = 4*64+6*8+1*1 = 256+49 = 30510.

  2. 172,548 = 1*82+7*81+2*80+5*8-1+4*8-2 = 64+56+2+5*

Задания: Переведите восьмеричные числа в десятичную систему счисления.

1. 5558 7. 235,438

2. 6338 8. 731,458

3. 4348 9.115,4568

4. 25558 10. 25,4568

5. 74118 11. 56,3218

6. 3258 12. 231,448

Самостоятельная работа студента:

  1. Преобразовать восьмеричные числа в десятичную систему:

  1. 124; 6) 4407; 11) 125,64;

  2. 357; 7) 3556; 12) 321,45;

  3. 706; 8) 6754; 13) 654,21;

  4. 235; 9) 3701; 14) 332,21;

  5. 663; 10) 5564; 15) 32,654;

  1. Перевести в двоичную систему следующие восьмеричные числа:

  1. 45; 6) 365; 11) 1657; 16) 741,21;

  2. 73; 7) 321; 12) 2566; 17) 256,74;

  3. 35; 8) 257; 13) 3265; 18) 654,31;

  4. 61; 9) 652; 14) 7415; 19) 257,36;

  5. 72; 10) 234; 15) 3614; 20) 741,32;

Самостоятельная работа студента с преподователями:

    1. Перевести в двоичную систему следующие восьмеричные числа:

1.

23228 8. 70068

2. 75248 9. 1258

3. 223,2458 10. 2248

4. 4258 11. 478

5. 315,0758

12. 21,258

6. 181,3618 13. 206,1258

7. 176,5268 14. 6408

    1. Преобразовать восьмеричные числа в десятичную систему:

1. 1228 8. 31678

2. 450,7068 9. 1258

3. 253,2458 10. 2248

4. 4268 11. 138

5. 315,0758 12. 37,258

6. 1318 13. 206,1258

7. 176,5268 14. 47,538

Контрольные вопросы:

1. Что такое позиционная система счисления?

2. Назовите правило перевода чисел из восьмеричной системы счисления в десятичную систему.

3. Назовите правило перевода чисел из восьмеричной системы счисления в двоичную систему счисления.

Лабораторная работа №4

Тема: Использование шестнадцатеричную систему счисления

Цель работы: научиться использовать шестнадцатеричную систему счисления

Перевод из шестнадцатеричной системы в десятичную систему производится путем сложения произведений соответствующего десятичного эквивалента символа числа в шестнадцатеричной системе на вес i-го знакоместа.

Пример перевода из 16-ричной системы счисления в десятичную систему:

15В16=1162+5161+11160=256+80+11=34710.

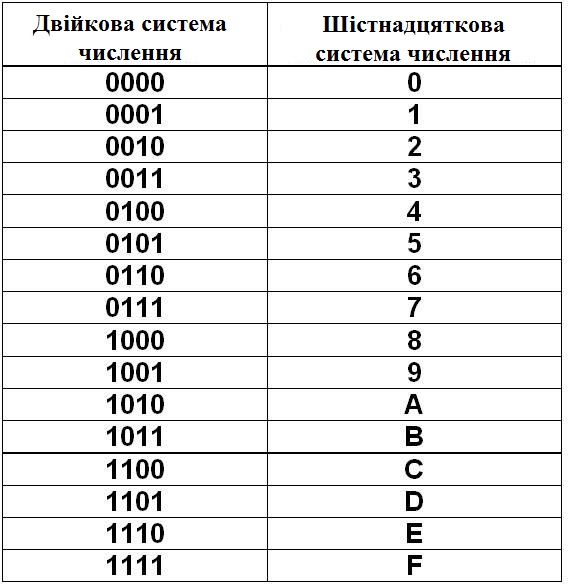
Для шестнадцатеричной системы счисления соответствие чисел базиса системы с четырехзначными числами двоичной системы следующее:

016=00002 416=01002 816=10002 C16=11002

116=00012 516=01012 916=10012 D16=11012

216=00102 616=01102 A16=10102 E16=11102

316=00112 716=01112 B16=10112 F16=11112

Представим в виде таблицы:

Двоичная система счисления

0000

0001

0010

0011

0100

0101

0110

0111

Шестнадцатеричная система счисления

0

1

2

3

4

5

6

7

Двоичная система счисления

1000

1001

1010

1011

1100

1101

1110

1111

Шестнадцатеричная система счисления

8

9

A

B

C

D

E

F

Используя таблицу переведите числа из шестнадцатеричной системы в двоичную:

1. А3616 6. 102,9E16

2. В7С16 7. 456,EA16

3. 2Е116 8. B03,DF16

4. 8DF416 9. EA2,E316

5. AB4716 10. ED7,8716

Примеры:

1) 3Е5А116=3*164+E*163+5*162+A*161+1*160 .

2) 48С,В716 = 4*162+8*161+C*160+B*16-1+7*16-2 =

4*162+8*161+12*160+11*16-1+7*16-2 =

Перевести шестнадцатеричные числа в десятичную систему счисления.

1. A87E16 7. BE,74116

2. 23DF16 8. F11,56716

3. EA1216 9. 981,DA16

4. 1A2216 10. 23,3B16

5. 9116 11. F54,4716

6. 7C3116 12. 235,F16

Как преобразовать 111 из шестнадцатеричного в восьмеричное

Что такое шестнадцатеричное число 111 в восьмеричном? 111 из шестнадцатеричного в восьмеричное равно 421. Здесь мы покажем вам, как записать 0x111 в восьмеричном формате и как преобразовать 111 из шестнадцатеричного в восьмеричное.

Число:

Из: двоичный [с основанием 2] троичный [с основанием 3] четверичный [с основанием 4] пятеричный [с основанием 5] десятеричный [с основанием 6] семеричный [с основанием 7] восьмеричный [с основанием 8] ненарочный [с основанием 9] десятичный [ с основанием 10] одиннадцатеричный [с основанием 11] двенадцатеричный [с основанием 12] трехдесятеричный [с основанием 13] четырехдесятичный [с основанием 14] пятидесятичный [с основанием 15] шестнадцатеричный [с основанием 16] семидесятеричный [с основанием 17] октодесятеричный [с основанием- 18] шестнадцатеричный [основание-19] десятичный [по основанию-20] недесятеричный [по основанию-21] двенадцатеричный [по основанию-22] трехдесятеричный [по основанию-23] тетрадесятичный [по основанию-24] пятидесятеричный [по основанию-25] тройничный [по основанию-30] двенадцатеричный [по основанию-32]

К: двоичный [с основанием 2] троичный [с основанием 3] четверичный [с основанием 4] пятеричный [с основанием 5] десятеричный [с основанием 6] семеричный [с основанием 7] восьмеричный [с основанием 8] ненарочный [с основанием 9] десятичный [ с основанием 10] одиннадцатеричный [с основанием 11] двенадцатеричный [с основанием 12] трехдесятеричный [с основанием 13] четырехдесятичный [с основанием 14] пятидесятичный [с основанием 15] шестнадцатеричный [с основанием 16] семидесятеричный [с основанием 17] октодесятеричный [с основанием- 18] шестнадцатеричный [основание-19] десятичный [по основанию-20] недесятеричный [по основанию-21] двенадцатеричный [по основанию-22] трехдесятеричный [по основанию-23] тетрадесятичный [по основанию-24] пятидесятеричный [по основанию-25] тройничный [по основанию-30] двенадцатеричный [по основанию-32]

В системе счисления мы знаем, что шестнадцатеричная система счисления — это шестнадцатеричная, а восьмеричная — восьмеричная. 2 и так далее справа налево

  • Сложите все продукты, полученные на шаге 1, чтобы получить десятичный эквивалент заданного шестнадцатеричного значения.
  • Затем разделите десятичное значение, полученное на шаге 2, на 8, учитывая частное и остаток.
  • Продолжайте делить частное на 8, пока не получите нулевое частное.
  • Затем просто запишите остатки в обратном порядке, чтобы получить восьмеричный эквивалент десятичного числа.

    • Сначала преобразуйте 111 16 в десятичное число, используя описанные выше шаги:

    = 111 16
    = 1 × 16 2 1 × 16 1 1 × 16 0
    = 273 10

    Теперь мы можем преобразовать 273 10 TOAL

    . / 8 = 34 с остатком 1
    34 / 8 = 4 с остатком 2
    4 / 8 = 0 с остатком 4

    Затем просто запишите остатки в обратном порядке, чтобы получить ответ. Шестнадцатеричное число 111, преобразованное в восьмеричное, равно поэтому равно:

    421

    Вот еще несколько примеров преобразования шестнадцатеричного в восьмеричное

    Десятичный 111 в восьмеричном | работа, решение

    Как написать восьмеричное число 111?

    111 записывается как 157 в восьмеричном формате

    Преобразование из/в десятичное в двоичное. Преобразование десятичных чисел. Возможно, вы обратились к нам в поисках ответов на такие вопросы, как: Десятичное число 111 в восьмеричном | работа, решение или преобразование из десятичного в восьмеричное. Используйте калькулятор ниже, чтобы преобразовать в / из основных базовых систем.

    Чтобы использовать этот калькулятор, просто введите значение в любом поле слева.

    С помощью этого конвертера вы можете получить ответы на такие вопросы, как:

    • Что такое 111 в двоичном формате?
    • Что такое 111 в шестнадцатеричном формате?
    • Что такое 111 в восьмеричной системе?
    • Как преобразовать 111 в двоичный код?
    • Как преобразовать 111 в двоичный код? И так далее.

    Преобразование десятичной системы в двоичную, включая шестнадцатеричные и восьмеричные

    Декабрь Шестнадцатеричный Oct Bin
    0 0 0 0
    1 1 1 1
    2 2 2 10
    3 3 3 11
    4 4 4 100
    5 5 5 101
    6 6 6 110
    7 7 7 111
    8 8 10 1000
    9 9 11 1001
    10 A 12 1010
    11 B 13 1011
    12 C 14 1100
    13 D 15 1101
    14 E 16 1110
    15 F 17 1111

    Dec Hex Oct Bin
    16 10 20 10000
    17 11 21 10001
    18 12 22 10010
    19 13 23 10011
    20 14 24 10100
    21 15 25 10101
    22 16 26 10110
    23 17 27 10111
    24 18 30 11000
    25 19 31 11001
    26 1A 32 11010
    27 1B 33 11011
    28 1C 34 11100
    29 1D 35 11101
    30 1E 36 11110
    31 1F 37 11111

    Dec Hex Oct Bin
    32 20 40 100000
    33 21 41 100001
    34 22 42 100010
    35 23 43 100011
    36 24 44 ​​ 100100
    37 25 45 100101
    38 26 46 100110
    39 27 47 100111
    40 28 50 101000
    41 29 51 101001
    42 2A 52 101010
    43 2B 53 101011
    44 ​​ 2C 54 101100
    45 2D 55 101101
    46 2E 56 101110
    47 2F 57 101111

    Dec Hex Oct Bin
    48 30 60 110000
    49 31 61 110001
    50 32 62 110010
    51 33 63 110011
    52 34 64 110100
    53 35 65 110101
    54 36 66 110110
    55 37 67 110111
    56 38 70 111000
    57 39 71 111001
    58 3A 72 111010
    59 3B 73 111011
    60 3C 74 111100
    61 3D 75 111101
    62 3E 76 111110
    63 3F 77 111111

    Examples of Base Conversions

    • 64248 to binary
    • 19046 to binary
    • 1011101001111111 to decimal
    • 37399 to binary
    • 1100111100011000 to decimal
    • 26720 to binary
    • 1111100111101010 to decimal
    • 1101110000101000 to decimal

    Отказ от ответственности

    Хотя мы прилагаем все усилия для обеспечения точности информации, представленной на этом веб-сайте, мы не даем никаких гарантий в отношении этой информации.

    alexxlab

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *