Как определить частоту по фигуре Лиссажу. » Хабстаб

Воспользуйтесь строкой поиска,
чтобы найти нужный материал

В одной из прошлых статей описывалось как определить разность фаз двух сигналов по фигуре Лиссажу. Но у фигур Лиссажу есть ещё одно интересное свойство и заключается оно в следующем: если известна частота одного из колебаний, то по виду фигуры Лиссажу можно определить частоту другого.

Для определения соотношения частот проведём горизонтальную и вертикальную прямые, пересекающие фигуру. При этом через точки пере­сечения линий самой фигуры эти прямые проходить не должны.

Тогда количество пересечений фигуры с горизонтальной прямой соответствует количеству изменений напряжения одного сигнала, а с вертикальной – количеству изменений напряжения другого сигнала. А из соотношения количества изменений сигналов можно найти соотношение частот колебаний.
А теперь тоже самое простыми словами, если синус с частотой 10KHz два раза пересекает горизонтальную прямую, а синус с неизвестной нам частотой пересекает четыре раза вертикальную прямую, то ясно что их частоты относятся как один к двум и частота неизвестного сигнала в два раза больше, то есть 20KHz.

Кстати на осциллограмме выше частоты относятся как 6/4 или 3/2.
Почему мы один раз считаем пересечения с горизонтальной прямой, а второй с вертикальной?
Ответ на этот вопрос можно найти в определении фигуры Лиссажу:
Фигуры, получаемые при сложении взаимно перпендикулярных колебаний разных частот, называются фигурами Лиссажу.

Давайте на подадим на оба входа осциллографа синус с частотой 1KHz и посмотрим как будут выглядеть фигура Лиссажу в зависимости от разности фаз между каналами.

Разность фаз равна 0 °.

Разность фаз равна 45°.

Разность фаз равна 90°.

На осциллограммах видно, что количество пересечений с вертикальной и горизонтальной прямой одинаковое.

Теперь проделаем тоже самое но для частот 1KHz и 2KHz.
Разность фаз равна 0 °.

Разность фаз равна 45 °.

Разность фаз равна 90 °.

На осциллограммах видно, что количество пересечений с вертикальной прямой в два раза больше чем с горизонтальной.

Теперь на один вход подадим 1Khz, а на второй 3Khz и проделаем тоже самое.
Разность фаз равна 0 °.

Разность фаз равна 45 °.

Разность фаз равна 90 °.

На осциллограммах видно, что количество пересечений с вертикальной прямой в три раза больше чем с горизонтальной.

Оказывается определить частоту неизвестного сигнала очень просто, если знать это замечательно свойство фигур Лиссажу.

Источник: hubstub.ru

Статья

4. Определение частоты с помощью фигур Лиссажу

Данный метод определения частоты сигнала помощью осциллографа основан на сравнении определяемой частоты периодического процесса с частотой измерительного генератора.

Подадим на отклоняющие Х— и Y— пластины два синусоидальных сигнала.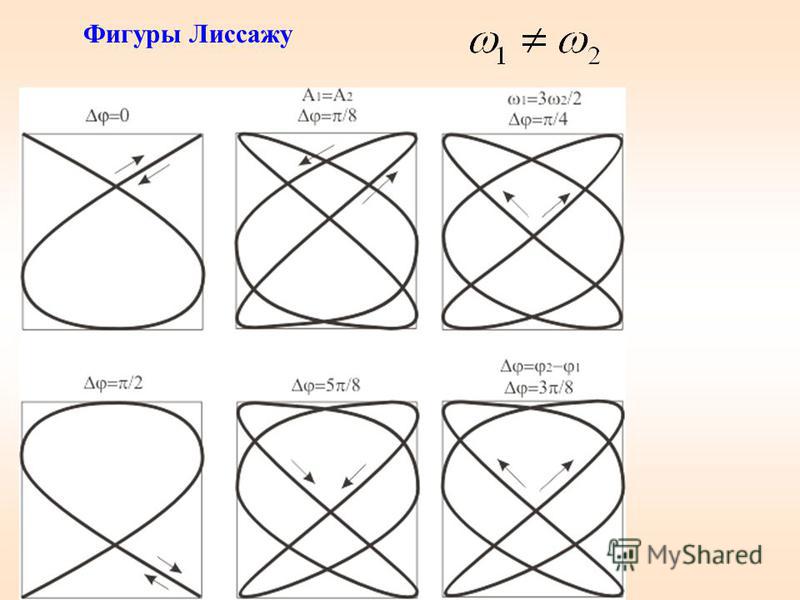 Траектории, вычерчиваемые лучом, участвующим в двух взаимно перпендикулярных периодических процессах, кратных по частоте, называют фигурами Лиссажу. Простейшие фигуры Лиссажу получаются при синусоидальных колебаниях, кратных по частоте 1 : 1, 1 : 2, 1 : 3… При этом разность начальных фаз складываемых колебаний может иметь постоянную величину.

На рис. 4 приведены фигуры Лиссажу для частот 1 : 1, 1 : 2, 1 : 3, 2 : 3, 3 : 4 при различных разностях фаз, равных 0,/4, /2, 3/4, .

Определение отношения частот с помощью фигур Лиссажу производится следующим образом.

Впишите фигуру Лиссажу в прямоугольник, подсчитайте, сколько раз кривая коснется горизонтальной и вертикальной стороны прямоугольника (см. рис. 4). Отношение числа касаний кривой к соответствующим сторонам дает отношение частот колебаний (такой способ можно применять при разности фаз в /4, /2, 3/4).

Меняя частоту измерительного генератора (в нашем случае звукового генератора) и сравнивая полученные на экране осциллограммы с рис.

4, можно определить частоту неизвестного процесса.

В качестве сигнала, частоту которого надо измерить, используем калибрационный сигнал. Для измерения его частоты переключите провода, идущие с выхода звукового генератора, на вход Х осциллографа, а переключатель «сопр. вых» генератора – на 50 Ом.

В осциллографе переведите переключатели: «род работы» в положение «усилитель»; «род синхронизации» – на «внешн.»;

«делитель» – на «калибр.»

; указатель шкалы «калибр. амплитуды» поставьте на «1,0 эф».

Включив переключатели «сеть» на генераторе и осциллографе и подобрав потенциометром «усиление плавно» величину сигнала по оси Y, равную 30 – 40 мм, а ручкой «синхрониз.» – такую же величину сигнала по X, начинайте вращать лимб частоты звукового генератора, повышая частоту генератора от 20 Гц до 250 Гц. Зарисуйте фигуры Лиссажу, соответствующие рис. 4. Определите частоту калибрационного сигнала 

К, пользуясь приемом определения отношения частот с помощью фигур Лиссажу, описанным выше.

Таблица 2

№	Количество касаний по оси X	Количество касаний по оси Y	Частота сигнала со звукового генератора, Гц	Расчетное значение частоты внутреннего генератора, Гц
1
2
3
4

Подсчитайте количество касаний фигур Лиссажу с прямоугольниками, запишите полученные значения в таблицу 2 и определите частоты внутреннего генератора, с напряжением с которого складывается напряжение со звукового генератора.

Рассмотрим цепь переменного тока, состоящую из последовательно соединенных сопротивления R, индуктивности L, электроемкости С и генератора ГЗ (рис. 5). Пусть э.д.с. генератора & изменяется по закону:

&  &₀sint.

Тогда сила тока в цепи будет изменяться по тому же закону, но со сдвигом фазы:

Паттерны Лиссажу на заре технологической революции

EMAT6680

Write Up #10

Summer 03

 

Паттерн Лиссажу или фигура Лиссажу названа в честь французского математика Жюля Антуана [1]. Лиссажу работа в девятнадцатом веке сосредоточена вокруг изучения вибрирующих объектов и волновых явлений. Метод, который Лиссажу использовал для изучения вибрация должна отражать свет от зеркала, прикрепленного к вибрирующему объект. Для изучения отношений между двумя вибрирующими предметами к камертону крепилось зеркало.

Свет отражался от этого зеркала. Отраженный луч затем отражался от второе зеркало, прикрепленное к другому вибрирующему камертону под прямым углом к первый камертон. После второго отражения луч света проецировался на экран, так что, когда камертоны были сделаны для вибрировать разработанную модель, рассказывающую историю об отношениях между два вибрирующих объекта.

Перенесемся в предсовременную электронику инструменты. Один из самых ранних инструментом, имеющим большое значение и по сей день, является осциллограф, изобретенный в начало двадцатого века. Современные приборы различных типов с высокоскоростным цифровым сигналом обработки, способны извлекать информацию в реальном времени из сигналов интерес. Тем не менее, до Наличие таких инструментов, осциллограф был основным электронным инструмент для исследования электронных сигналов, представляющих различные параметры, из сообщений устройства, музыкальные инструменты, параметры механических систем к самым разнообразным других приложений.

Путь Работа осциллографа заключается в том, что пучок электронов проецируется на флуоресцентный экране, точно так же, как на телевизоре или мониторе компьютера. Этот луч сканируется по экрану линейно со временем. колеблющийся Рассматриваемый электронный сигнал усиливается и используется для отклонения луча по вертикали. В результате получается зависимость амплитуды от времени. сигнал. Для простого x=sin ωt дисплей осциллографа будет выглядеть примерно так, как показано на рис. 1.

Рис. ось откалибрована по напряжению, которое может быть сделано для представления широкого спектра физические явления.

Так что же все это делать с фигурой Лиссажу? оказывается что для изучения взаимосвязи между двумя сигналами, по крайней мере, до появление современного арсенала передовых инструментов, было довольно сложно. Для решения этой проблемы стало понятно, что Работа Лиссажу может иметь некоторую ценность. Воспользовавшись этим, было высказано предположение, что горизонтальная ось не не обязательно должна быть линейная развертка относительно времени. Должна быть возможность иметь горизонтальную ось будет связана с амплитудой одного сигнала, а вертикальная ось будет зависит от амплитуды второго сигнала. Хотя подразумевается, что оба этих сигнала меняются линейно во времени поскольку они прослеживаются на дисплее, представление времени никуда не делось. найти на дисплее. Дисплей просто одна амплитуда сигнала (по оси x) по сравнению с другой, возможно несвязанная, амплитуда сигнала (по оси y). Затем эти сигналы могут быть выражены в виде параметрического уравнения:

x = A ₁ SIN (ω ₁ T)

Y = A ₂ SIN (ω ₂ T+θ)

Обратите внимание, что второе уравнение имеет фазовый термин. , отсутствует в первом уравнении. Причина этого в том, что мы вольны выбирать любую точку отсчета во времени, что наиболее удобно, чтобы θ=0 для первого уравнения. Таким образом, видно, что θ является просто относительным задержка между двумя функциями. добавление фазового члена имеет смысл только в том случае, если две функции гармонично связанные; ибо если их нет, то образец одной функции постоянно изменяется, как показано на рисунке 2 ниже. Обратите внимание, что на реальном дисплее осциллографа постоянство след недолговечен, поэтому результат будет постоянно меняющимся шаблон. На созданных нами графиках сохранение нанесенных точек до тех пор, пока мы решим это сделать (увеличив верхнее значение t). Для всех остальных На графиках в этой статье сигналы гармонически связаны, поэтому паттерн повторяется каждые 2π. Но в случаях показано ниже, приближение иррационального числа e используется в качестве отношения между двумя сигналами. Число e было выбрано ни по какой другой причине, чтобы вызвать два сигнала в эти следы до , а не быть гармонично связаны.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Figure 2

 

Now lets explore how the Фигура Лиссажу может помочь человеку, у которого есть только осциллограф, обнаружить отношения между двумя сигналами. За на каждом из оставшихся графиков частоты гармонически связаны, т.е. член, умножающий t, является рациональным числом. Следовательно, график является повторяющейся функцией для некоторого кратного 2π. Начнем с падежа где частоты ω ₁ и ω ₂ идентичны, и θ=0. На рис. 3 показаны рисунок — это то, что можно было бы увидеть на дисплее осциллографа.

 

 

0042

Рисунок 3

 

Хотя этот график кажется неинтересным, он содержат много информации о двух сигналах. Обратите внимание, что в каждый момент времени t каждое значение x идентичны каждому значению y. Следовательно, два сигнала образуют фигуру Лиссажу прямой линии между (-1,-1) и (1,1).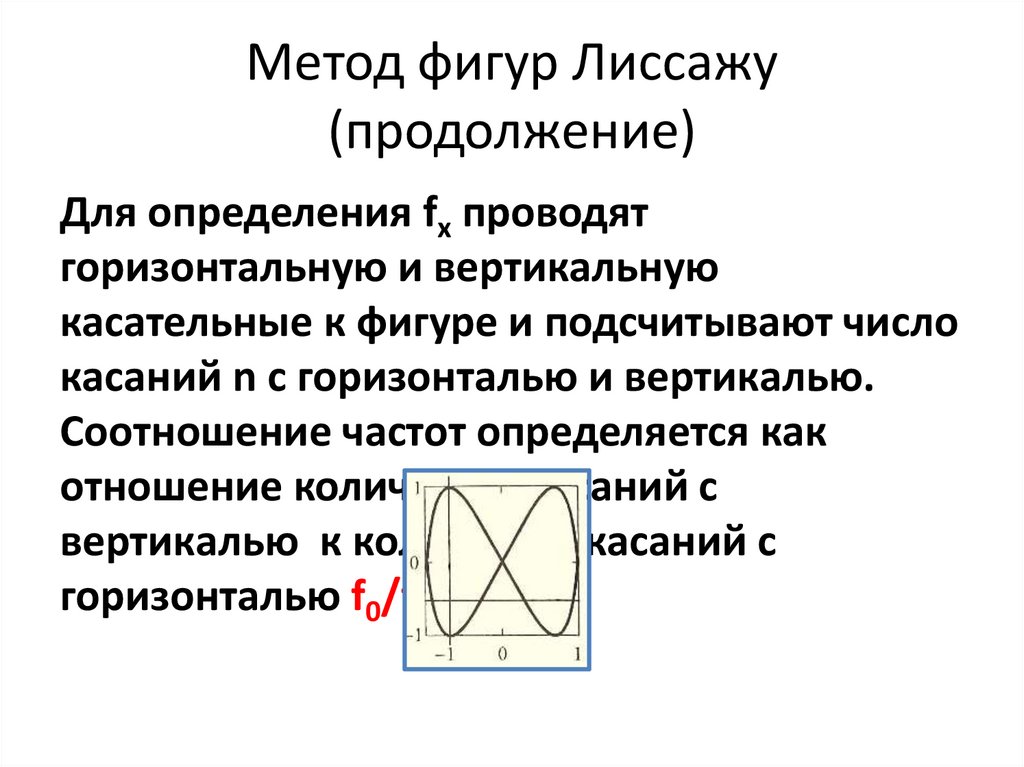 Из этого можно сделать вывод что два сигнала имеют одинаковую амплитуду и фазу (или задержку).

Сейчас немного изменить отношения. Позволь нам добавить задержку или фазовый сдвиг ко второму сигналу, оставив амплитуды и частоты одинаковы и добавляют фазу π/2 ко второму сигналу. Следует признать, что это одно и то же как функция косинуса:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Figure 4

 

In this case, the amplitude and frequency are still идентичны, оба колеблются между 1 и +1, но делают это на 90˚ (π/2 радиан) не в фазе друг с другом. Так это является примером первоначального применения фигуры Лиссажу к определить фазовое соотношение между двумя сигналами. Нажмите на Рисунок 4, чтобы увидеть динамическое отображение в качестве второго фаза функций проходит полный цикл от 0 до 2π относительно первая функция. Обратите внимание, что когда два точно не совпадают по фазе (180˚), цифра представляет собой линию от (-1,1) к (1,-1). Так как амплитуда единство, узор никогда не выходит за пределы единичного квадрата.

Можно ли Фигура Лиссажу может рассказать больше, чем просто фаза? Рассмотрим случай, когда частота и фаза одинаковы, но амплитуды различаются. Как вы ожидаете это изменить шаблон. Если один амплитуда в два раза больше другой, может показаться, что эллиптический узор будет ожидаемый результат. Это подтверждено по следующей схеме. Нажмите на рисунок 5, чтобы увидеть различные относительные амплитуды. Первая амплитуда зафиксированный; вторая амплитуда варьируется между относительными значениями до удвоенного первая функция.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Figure 5

 

Notice that the diagonal elliptical figure represented a разница в фазе между двумя функциями, тогда как в этом случае эллиптический рисунок вдоль оси x или y указывает на разницу в амплитуда. Конечно, местонахождение точек больше не ограничивается единичным квадратом, поскольку амплитуда вторая функция до 2, как показано на анимации.

Фигура Лиссажу также может предоставить информацию об относительной частоте две функции. Два случая при условии, что сначала показывают одну частоту 3 раза, а затем случай одного частота 5/3 первой. В обоих случаях, этот шаблон повторяется через каждые n2π, где in — целое число из-за рациональное соотношение частот.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Figure 6

 

 

 

 

 

 

 

 

 

извлеченные из этих рисунков, два графика показывают, что Лиссажу рисунок раскрывает информацию о соотношении между частотами два сигнала. На первом графике, где второй сигнал втрое превышает частоту первого, обратите внимание, что для каждого отклонение за период сигнала в направлении x, сигнал в направлении y направление берет на себя 3 цикла. в второй случай, для каждых 3 экскурсий за период сигнала в направлении x, сигнал в направлении y проходит 5 циклов. При просмотре фигуры Лиссажу связь между сигналом частоты можно легко посчитать.

Нажмите на рисунок 6, чтобы увеличить частоту в 3 раза, чтобы увидеть эту амплитуду информацию можно получить даже из этих более сложных цифр. Также доступна информация о фазах из сложных узоров, которые можно увидеть, нажав на рисунок 7 в 5/3 раза больше частоты. В этих случаях вырожденная фигура (подобная линейному графику, показанному выше) для информация о фазе которой не видна, больше не является прямой линией. Вырожденные случаи возникают с шагом (2n-1)(π/12), для n=1, 2, 3,

Кому сделать вывод, можно увидеть, что математическая связь двух параметрических уравнения могут быть использованы для извлечения информации из реального мира ситуации. В случае с Лиссажу цифры, математика 19 ^-го века, продемонстрированная в то время с помощью камертоны и зеркала, сыграли важную роль в развитии и использовании электронное оборудование в 20 ^-м -м веке. До появления высокоскоростного цифрового испытательного оборудования, техники, инженеры и ученые мы были способны извлечь огромное количество информации о взаимоотношениях два сигнала из многих областей науки и техники, отображая параметрическая форма сигналов на электронно-лучевой трубке.

 

Return

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Lissajous Tuning Forks: the Standardisation of Musical Sound

Камеры такой конструкции использовались французами в 1858 г., когда они пытались создать международный стандарт высоты тона концертного исполнения.

Изобретение и использование

Изобретенные в 1855 году французским физиком Жюлем Антуаном Лиссажу (1822-1880), эти камертоны (вверху) являются частью аппарата для визуализации и анализа звуковых колебаний.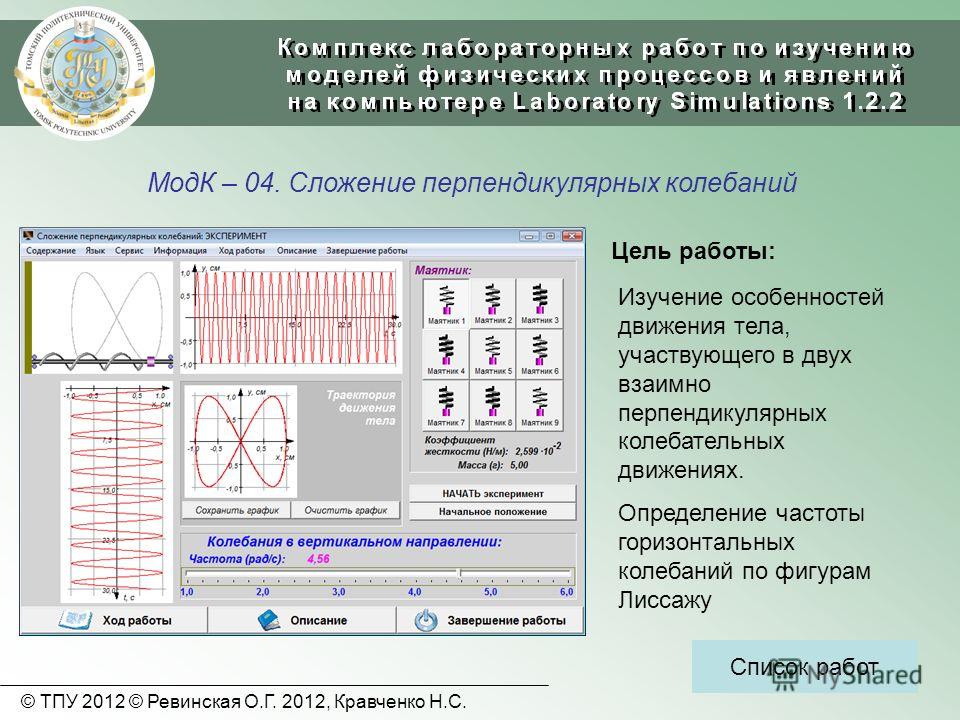 Этот конкретный набор был изготовлен парижским производителем научных инструментов Рудольфом Кенигом (1832-1901) для учебных демонстраций, а также для точной калибровки новых камертонов.

Изображение 1: Жюль Лиссажу наблюдает за фигурами Лиссажу через микроскоп. Изображение с Викисклада.

Музыкальные фигурки

Каждый камертон имеет маленькое зеркало, закрепленное на конце одной ножки, уравновешенное на другой небольшой массой равного веса. Для проведения демонстрационного эксперимента вилки располагаются в раме под прямым углом так, чтобы одна вибрировала в направлении север-юг, а другая — в направлении восток-запад. Узкий луч света отражается от одного зеркала к другому и проецируется на экран (или наблюдается в микроскоп, как на изображении 1). Таким образом, когда вилки колеблются, луч периодически отклоняется в двух измерениях и рисует на экране кривую, геометрические свойства которой зависят от отношения частот вилок. Таким образом можно создавать «фигуры Лиссажу» необычайной красоты и сложности, а самые стабильные и совершенные появляются только тогда, когда две вилки вибрируют на частотах с простыми соотношениями, такими как 2:1 или 3:2 (например, 500 Гц: 250 Гц или 600 Гц).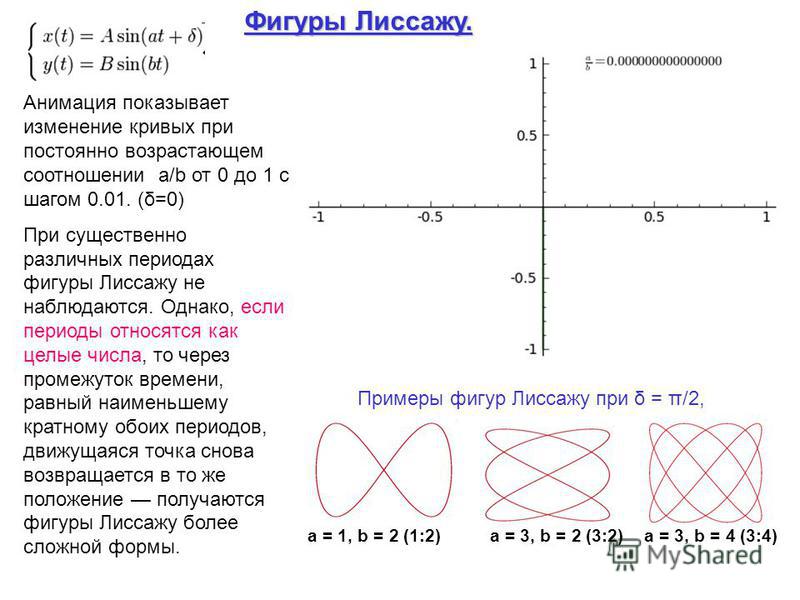 :400 Гц). Эти соотношения частот соответствуют музыкальным интервалам октавы и чистой квинты соответственно (см. изображение 2).

Изображение 2: Фигуры Лиссажу, как показано в акустическом каталоге Рудольфа Кенига 1885 года.

Оптическая калибровка

Фигуры Лиссажу использовались для калибровки камертонов во время производства. Соединив незавершенную вилку с вилкой известной стандартной частоты и просмотрев полученные цифры, можно выполнить настройку с точностью, намного большей, чем можно достичь на слух. Такая тонкая настройка производилась с помощью простого металлического напильника: для увеличения частоты вилки напильником напиливают верхнюю часть зубцов, а для уменьшения напиливают внутри нижней части U-образного «хомута» вилки.

Лиссажу также изобрел вибрационный микроскоп (камертон с прикрепленной к одному штырю линзой микроскопа), который стал ключевым инструментом в акустических исследованиях Германа фон Гельмгольца и Рудольфа Кенига. Изображение, просматриваемое через этот микроскоп, будет вибрировать с камертоном, и если смотреть на объект, который сам вибрирует под прямым углом к ​​вибрации микроскопа, то могут быть получены фигуры Лиссажу.