Формула момента силы в физике
Содержание:
Определение и формула момента силы
Определение
Векторное произведение радиус – вектора ($\bar{r}$), который проведен из точки О (рис.1) в точку к которой приложена сила $\bar{F}$ на сам вектор $\bar{F}$ называют моментом силы ($\bar{M}$) по отношению к точке O:
$$\bar{M}=\bar{r} \times \bar{F}(1)$$На рис.1 точка О и вектор силы ( $\bar{F}$)и радиус – вектор $\bar{r}$ находятся в плоскости рисунка. В таком случае вектор момента силы ($\bar{M}$) перпендикулярен плоскости рисунка и имеет направление от нас. Вектор момента силы является аксиальным. Направление вектора момента силы выбирается таким образом, что вращение вокруг точки О в направлении силы и вектор $\bar{M}$ создают правовинтовую систему. Направление момента сил и углового ускорения совпадают.
Величина вектора $\bar{M}$ равна:
$$M=r F \sin \alpha=l F$$где $\alpha$ – угол между направлениями радиус – вектора и вектора силы,
$l=r \sin \alpha$– плечо силы относительно точки О.
В общем случае результат действия на твердое тело произвольной системы сил такое же, как действие на тело главного момента $\bar{M}$ системы сил и главного вектора системы сил, который приложен в центре приведения (точка О).
Основной закон динамики вращательного движения
$$\bar{M}=\frac{d \bar{L}}{d t}$$где $\bar{L}$ – момент импульса тела находящегося во вращении.
Для твердого тела этот закон можно представить как:
$$\bar{M}=I \bar{\varepsilon}(6)$$где I – момент инерции тела, $\bar{\varepsilon}$ – угловое ускорение.
Единицы измерения момента силы
Основной единицей измерения момента силы в системе СИ является: [M]=Н•м
В СГС: [M]=дин•см
Примеры решения задач
Пример
Задание. На рис.1 показано тело, которое имеет ось вращения OO’.
Момент силы, приложенный к телу относительно заданной оси, будет равен нулю? Ось и вектор силы расположены в плоскости рисунка.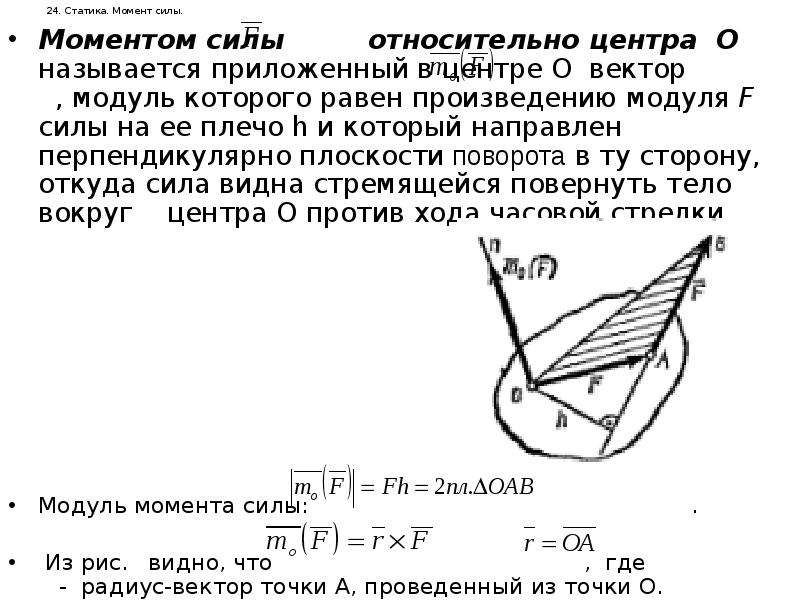 {\circ}$), следовательно, векторное произведение (1.1) нулю не равно. Значит, момент силы отличен от нуля.
{\circ}$), следовательно, векторное произведение (1.1) нулю не равно. Значит, момент силы отличен от нуля.
Ответ. $\bar{M} \neq 0$
Слишком сложно?
Формула момента силы не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Угловая скорость вращающегося твердого тела изменяется в соответствии с графиком, который представлен на рис.2. В какой из указанных на графике точек момент сил, приложенных к телу равен нулю?
Решение. Момент сил, приложенных к вращающемуся твердому телу можно найти при помощи основного закона вращательного движения:
$$M=I \varepsilon(2.1)$$где $\varepsilon$ угловое ускорение вращения тела.его в свою очередь можно выразить через угловую скорость вращения тела как:
$$\varepsilon=\frac{d \omega}{d t}(2.2)$$Так как $I \neq 0$ (момент инерции не равен нулю), то для выполнения условия M=0 должна быть равна нулю производная от угловой скорости по времени.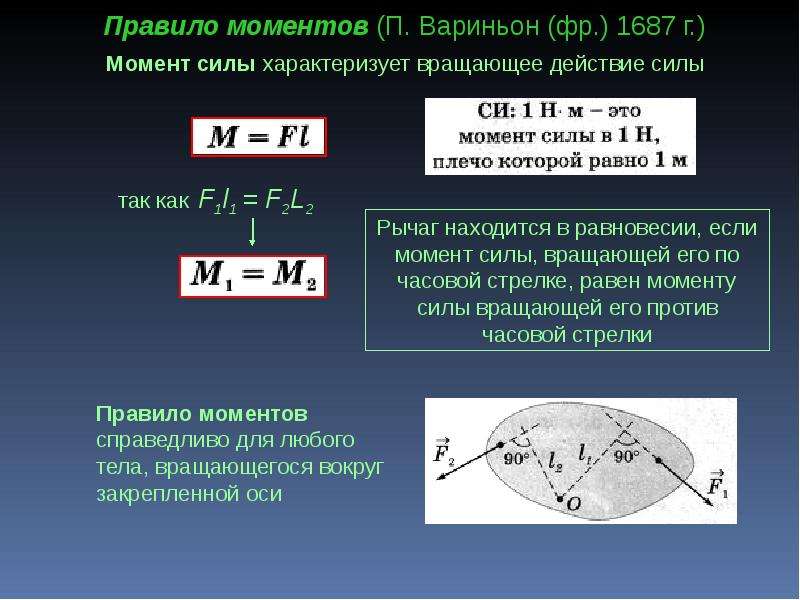 Производная равна нулю в экстремуме. На рис. экстремумом является точка 3.
Производная равна нулю в экстремуме. На рис. экстремумом является точка 3.
Ответ. M=0 в точке 3.
Читать дальше: Формула мощности.
Формула момента силы в физике
Содержание:
Определение и формула момента силы
Определение
Векторное произведение радиус – вектора ($\bar{r}$), который проведен из точки О (рис.1) в точку к которой приложена сила $\bar{F}$ на сам вектор $\bar{F}$ называют моментом силы ($\bar{M}$) по отношению к точке O:
На рис.1 точка О и вектор силы (
$\bar{F}$)и радиус – вектор
$\bar{r}$ находятся в плоскости рисунка. В таком случае вектор момента силы
($\bar{M}$) перпендикулярен плоскости рисунка и имеет направление от нас. Вектор момента силы является аксиальным. Направление вектора момента силы
выбирается таким образом, что вращение вокруг точки О в направлении силы и вектор
$\bar{M}$ создают правовинтовую систему. {\prime}}$ — радиус-вектор, который проведен из точки О к точке О’,
$\bar{F}$ – главный вектор системы сил.
{\prime}}$ — радиус-вектор, который проведен из точки О к точке О’,
$\bar{F}$ – главный вектор системы сил.
В общем случае результат действия на твердое тело произвольной системы сил такое же, как действие на тело главного момента $\bar{M}$ системы сил и главного вектора системы сил, который приложен в центре приведения (точка О).
Основной закон динамики вращательного движения
$$\bar{M}=\frac{d \bar{L}}{d t}$$где $\bar{L}$ – момент импульса тела находящегося во вращении.
Для твердого тела этот закон можно представить как:
$$\bar{M}=I \bar{\varepsilon}(6)$$где I – момент инерции тела, $\bar{\varepsilon}$ – угловое ускорение.
Единицы измерения момента силы
Основной единицей измерения момента силы в системе СИ является: [M]=Н•м
В СГС: [M]=дин•см
Примеры решения задач
Пример
Задание. На рис.1 показано тело, которое имеет ось вращения OO’.
Момент силы, приложенный к телу относительно заданной оси, будет равен нулю? Ось и вектор силы расположены в плоскости рисунка.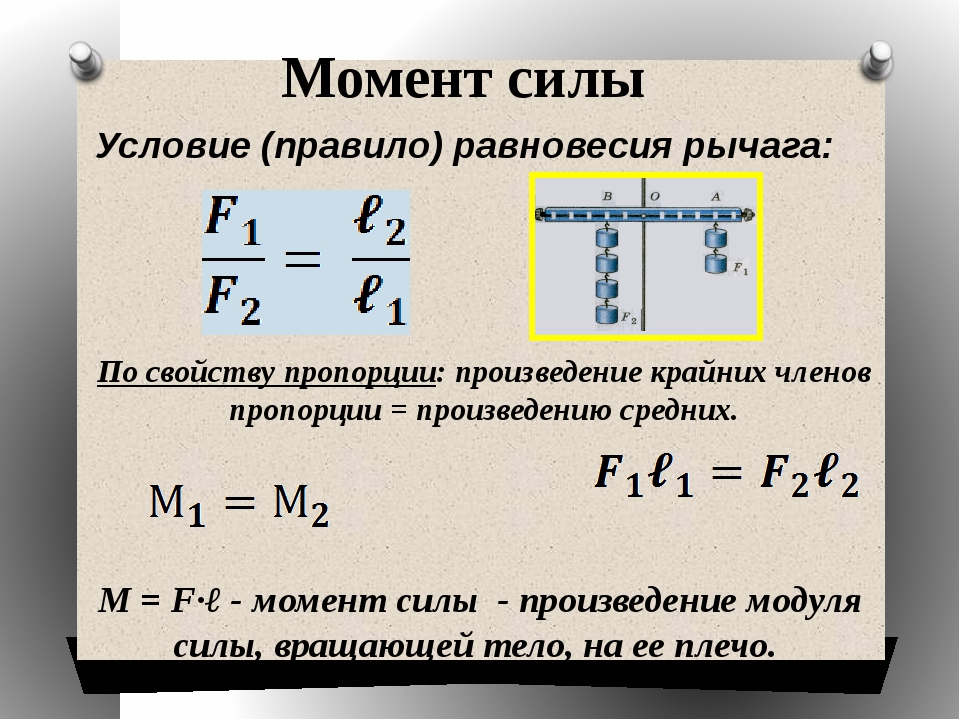 {\circ}$), следовательно, векторное произведение (1.1) нулю не равно. Значит, момент силы отличен от нуля.
{\circ}$), следовательно, векторное произведение (1.1) нулю не равно. Значит, момент силы отличен от нуля.
Ответ. $\bar{M} \neq 0$
Слишком сложно?
Формула момента силы не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Угловая скорость вращающегося твердого тела изменяется в соответствии с графиком, который представлен на рис.2. В какой из указанных на графике точек момент сил, приложенных к телу равен нулю?
Решение. Момент сил, приложенных к вращающемуся твердому телу можно найти при помощи основного закона вращательного движения:
$$M=I \varepsilon(2.1)$$где $\varepsilon$ угловое ускорение вращения тела.его в свою очередь можно выразить через угловую скорость вращения тела как:
$$\varepsilon=\frac{d \omega}{d t}(2.2)$$Перепишем (2.1), используя (2.2), имеем:
$$M=I \frac{d \omega}{d t}(2.3)$$Так как $I \neq 0$ (момент инерции не равен нулю), то для выполнения условия M=0 должна быть равна нулю производная от угловой скорости по времени.
Ответ. M=0 в точке 3.
Читать дальше: Формула мощности.
Формула момента силы в физике
Содержание:
Определение и формула момента силы
Определение
Векторное произведение радиус – вектора ($\bar{r}$), который проведен из точки О (рис.1) в точку к которой приложена сила $\bar{F}$ на сам вектор $\bar{F}$ называют моментом силы ($\bar{M}$) по отношению к точке O:
$$\bar{M}=\bar{r} \times \bar{F}(1)$$На рис.1 точка О и вектор силы (
$\bar{F}$)и радиус – вектор
$\bar{r}$ находятся в плоскости рисунка. В таком случае вектор момента силы
($\bar{M}$) перпендикулярен плоскости рисунка и имеет направление от нас. Вектор момента силы является аксиальным. Направление вектора момента силы
выбирается таким образом, что вращение вокруг точки О в направлении силы и вектор
$\bar{M}$ создают правовинтовую систему.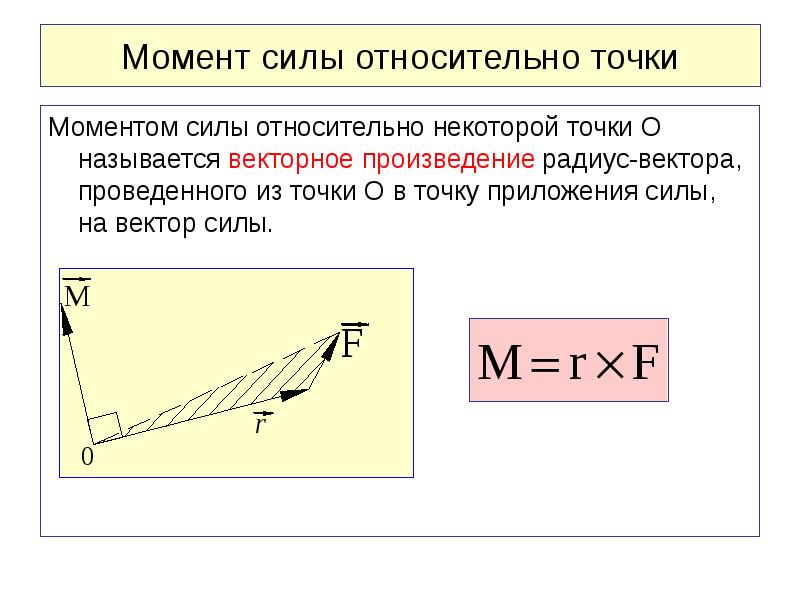 {\prime}}$ — радиус-вектор, который проведен из точки О к точке О’,
$\bar{F}$ – главный вектор системы сил.
{\prime}}$ — радиус-вектор, который проведен из точки О к точке О’,
$\bar{F}$ – главный вектор системы сил.
В общем случае результат действия на твердое тело произвольной системы сил такое же, как действие на тело главного момента $\bar{M}$ системы сил и главного вектора системы сил, который приложен в центре приведения (точка О).
Основной закон динамики вращательного движения
$$\bar{M}=\frac{d \bar{L}}{d t}$$где $\bar{L}$ – момент импульса тела находящегося во вращении.
Для твердого тела этот закон можно представить как:
$$\bar{M}=I \bar{\varepsilon}(6)$$где I – момент инерции тела, $\bar{\varepsilon}$ – угловое ускорение.
Единицы измерения момента силы
Основной единицей измерения момента силы в системе СИ является: [M]=Н•м
В СГС: [M]=дин•см
Примеры решения задач
Пример
Задание. На рис.1 показано тело, которое имеет ось вращения OO’.
Момент силы, приложенный к телу относительно заданной оси, будет равен нулю? Ось и вектор силы расположены в плоскости рисунка.
Ответ. $\bar{M} \neq 0$
Слишком сложно?
Формула момента силы не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Угловая скорость вращающегося твердого тела изменяется в соответствии с графиком, который представлен на рис.2. В какой из указанных на графике точек момент сил, приложенных к телу равен нулю?
Решение. Момент сил, приложенных к вращающемуся твердому телу можно найти при помощи основного закона вращательного движения:
где $\varepsilon$ угловое ускорение вращения тела.его в свою очередь можно выразить через угловую скорость вращения тела как:
$$\varepsilon=\frac{d \omega}{d t}(2.2)$$Перепишем (2.1), используя (2.2), имеем:
$$M=I \frac{d \omega}{d t}(2.3)$$Так как $I \neq 0$ (момент инерции не равен нулю), то для выполнения условия M=0 должна быть равна нулю производная от угловой скорости по времени. Производная равна нулю в экстремуме. На рис. экстремумом является точка 3.
Производная равна нулю в экстремуме. На рис. экстремумом является точка 3.
Ответ. M=0 в точке 3.
Читать дальше: Формула мощности.
Момент силы. | Архитектурный журнал ADCity
..
Момент силы — это сила, умноженная на плечо действия. Измеряется момент силы в Ньтон-метрах (Нм) — система СИ, или килограммсилметрах (кгс·м) — система СГС. Физический смысл момента силы понял еще Архимед, открывший принцип рычага. И действительно в его предложении: «дайте мне точку опоры и я переверну мир» с точки зрения физики нет ничего невозможного.
Формула для определения момента силы на удивление проста:
М = Fp (см. рис.1)
где М — момент силы
F — действующая сила
р — плечо действия силы
Одним из самых наглядных и действенных устройств, демонстрирующих действие момента силы, является гвоздодер (фомка). Рассмотрим ситуацию, возникающую при выдергивании гвоздя, более детально:
Рисунок 1. Силы и плечи сил на примере гвоздодера.
Силы и плечи сил на примере гвоздодера.
Итак на рисунке 5210.1 мы можем наблюдать: 1 — фомку (гвоздодер), 2 — вытаскиваемый из доски гвоздь, 3 — доску, из которой данный гвоздь вытаскивается, 4 — лагу или балку перекрытия, к которой гвоздем крепилась доска, 5 — руку, пытающуюся вытащить гвоздь (скорее всего это ваша рука в перчатке), а также точку О, являющуюся точкой опоры фомки, показанную на рисунке 520.1 красным цветом (данная точка цифрового обозначения на рисунке не имеет).
Таким образом извлечение гвоздя из доски и лаги (рис. 520.1.а)) с точки зрения физики может рассматриваться, как приложение силы F2 (сила, с которой вы давите на фомку) на расстоянии р2 от точки опоры О (на рисунке 520.1. б) показана красным цветом). При этом сила F1 — это сила сцепления гвоздя с древесиной, а расстояние р1 — это расстояние от оси гвоздя до точки опоры О.
Если рассматривать ситуацию статического равновесия системы, то момент силы F2, приложенной на расстоянии р2 от точки опоры О, равен моменту силы F1, приложенной на расстоянии р1 от точки опоры О (рис. 520.1.г)). Другими словами, чем больше расстояние, на котором можно приложить силу, тем меньше будет значение этой силы по сравнению с противодействующей (рис. 520.1.в)). Именно это и имел в виду Архимед, описывая чудесные свойства рычага.
520.1.г)). Другими словами, чем больше расстояние, на котором можно приложить силу, тем меньше будет значение этой силы по сравнению с противодействующей (рис. 520.1.в)). Именно это и имел в виду Архимед, описывая чудесные свойства рычага.
Само собой при вытаскивании гвоздя статическое равновесие системы нас не интересует, а потому, чтобы вытащить этот самый гвоздь, достаточно приложить силу F2, имеющую немного большее значение, чем F1p1/p2.
Вот в принципе и все, что я хотел сказать по поводу момента силы. Возможно вам известны другие, более наглядные примеры, описывающие момент силы, но я таких не знаю.
Момент силы | Вращательное движение
Итак, если мы будем действовать на тело с постоянной силой, приложенной к центру масс, оно будет поступательно ускоряться. Но если мы подействуем на какую-либо другую его точку, оно начнет вращаться. Именно эту ситуацию мы теперь и рассмотрим.
Представьте вращающуюся дверь.
Это вид сверху. На самом деле, такая конструкция обычно состоит из трех или четырех соединенных между собой дверей, но мы сейчас ограничимся двумя.
Итак, двери закреплены на центральном вале и могут свободно вращаться. С кинематикой такого движения мы уже знакомы, но что насчет динамики? Тут есть о чем поговорить.
Первая физическая величина, которая вводится для изучения динамики вращательного движения, называется моментом силы. Момент силы характеризует вращательную “мощь” той или иной силы. Это векторная величина. Обозначается обычно большой буквой M. Единица измерения – Н⋅м. Знак момента силы определяется направлением, в котором происходит вращение: если против часовой стрелки – он будет положительным, если по часовой стрелке – отрицательным.
Чтобы найти величину момента силы, нужно прежде всего понять, где находиться ось вращения. В нашем примере она проходит через центр масс, но это не значит, что так происходит всегда. Если жесткая фиксация будет находится в другой точке, вся система будет двигаться вокруг нее. Например, обычная дверь вращается вокруг одного из своих краев.
Например, обычная дверь вращается вокруг одного из своих краев.
Допустим, разобрались мы с осью вращения. Что дальше? Как можно узнать величину момента силы?
Если момент силы характеризует вращающий потенциал той или иной силы, он, в первую очередь, зависит от величины этой самой силы. Чем больше будет внешнее воздействие, тем сильнее будет вращение.
Кроме того, многое зависит от точки, к которой будет приложена вращающая сила. Наверняка вы и сами замечали следующее: легкость, с которой вращается дверь, зависит от того, куда вы прикладывайте свою силу. Чем дальше вы находитесь от дверного косяка, тем проще вам заставить дверь повернуться. И наоборот: чем вы ближе – тем труднее это сделать.
В общем, модуль момента силы зависит также от расстояния между осью вращения и точкой приложения силы. Такое расстояние часто называют плечом силы. У этого термина есть и более строгое определение: плечо силы – это вектор, соединяющий ось вращения и линию, вдоль которой действует вызывающая вращение сила. Этот самый вектор обычно обозначается маленькой буквой l со стрелочкой наверху. Измеряется в метрах.
Этот самый вектор обычно обозначается маленькой буквой l со стрелочкой наверху. Измеряется в метрах.
Подытожим все с помощью математики:
\boxed{M=Fl\sin\alpha}
Угол \alpha – это угол между вектором силы и вектором плеча силы. А для чего вообще здесь нужен синус этого угла? Разберемся с этим на конкретном примере.
Предположим, что сила, вращающая дверь вокруг ее центра, приложена под некоторым углом, скажем в 30 градусов.
Как вы понимаете, только часть этой силы, ее вертикальная составляющая, вызывает вращение. Этот компонент как раз и находится через синус 30 градусов.
А 30 градусов – это, помимо всего прочего, угол между вектором силы и вектором плеча этой силы.
Строго говоря, чтобы найти угол между векторами, нужно соединить их концы, поэтому вы и видите этот перенос на рисунке. Если предположить, что модуль силы \vec{F} составляет 20 ньютонов, а расстояние между линией ее действия и осью вращения равно 3 метрам, получим следующее значение момента силы:
M=Fl\sin\alpha
M=20\thickspaceН×3\thickspaceм×\sin30\degree
M=30\thickspaceН⋅м
Интересно, что бы вы сделали, если бы сила была направлена вот так:
У некоторых людей тут происходит сбой программы. Сначала они берут синус 45 градусов, пытаясь найти вертикальный компонент вызывающей вращение силы. Потом они вспоминают, что в формуле речь идет об угле между вектором силы и вектором плеча силы, а он ведь равен не 45, а 135 градусам.
Сначала они берут синус 45 градусов, пытаясь найти вертикальный компонент вызывающей вращение силы. Потом они вспоминают, что в формуле речь идет об угле между вектором силы и вектором плеча силы, а он ведь равен не 45, а 135 градусам.
Они начинают все пересчитывать и, может быть, даже громко возмущаться, если забыли, как пользоваться тригонометрической окружностью.
А ведь синусы смежных углов всегда равны… Ответ будет одним и тем же вне зависимости от выбранного пути.
DK Science: Forces
От движений планет до энергии, производимой внутри атомов, все, что происходит во Вселенной, в конечном итоге вызвано силами. Сила — это толчок или притяжение, которое может заставить объект двигаться или ПОВЕРНУТЬСЯ. Чем больше сила, тем больше движения она может произвести. Когда две или более силы действуют вместе на объект, их эффекты КОМБИНИРОВАНЫ. Иногда силы складываются в большую силу, а иногда они нейтрализуют друг друга.
Силы измеряются в единицах, называемых ньютонами (Н), названных в честь английского ученого сэра Исаака Ньютона. Величину силы можно измерить с помощью устройства, называемого измерителем силы или ньютонометром. Когда груз тянет за крюк, он растягивает пружину, чтобы получить показания на шкале. На Земле сила тяжести на 1 кг (2,2 фунта) составляет 9,8 ньютона.
Величину силы можно измерить с помощью устройства, называемого измерителем силы или ньютонометром. Когда груз тянет за крюк, он растягивает пружину, чтобы получить показания на шкале. На Земле сила тяжести на 1 кг (2,2 фунта) составляет 9,8 ньютона.
Если объект зафиксирован в одной точке и может вращаться вокруг него, эта точка называется точкой поворота. Если на объект действует сила, он поворачивается вокруг оси. Сила вращения называется крутящим моментом, а создаваемый ею эффект — моментом. Чем больше сила, тем больше момент.Момент также увеличивается, если сила действует на большем расстоянии от оси.
Гайку легче открутить гаечным ключом, чем пальцами, потому что длинная ручка гаечного ключа увеличивает вращающий эффект или момент силы. Величина момента равна приложенной силе, умноженной на расстояние от оси вращения, на которую она действует. Если вы используете гаечный ключ вдвое длиннее, вы удвоите момент, и гайку будет в два раза легче повернуть.
Когда силы действуют в одном направлении, они объединяются, образуя большую силу. Когда они действуют в противоположных направлениях, они могут нейтрализовать друг друга. Если силы, действующие на объект, уравновешиваются, объект не перемещается, но может изменить форму. Если силы объединяются, чтобы создать общую силу в одном направлении, объект перемещается в этом направлении.
Когда они действуют в противоположных направлениях, они могут нейтрализовать друг друга. Если силы, действующие на объект, уравновешиваются, объект не перемещается, но может изменить форму. Если силы объединяются, чтобы создать общую силу в одном направлении, объект перемещается в этом направлении.
Подвесной мост должен выдерживать вес собственной платформы, а также вес транспортных средств, которые по нему проезжают. Палуба моста свешивается на огромных стальных тросах, подвешенных над гигантскими столбами. Тросы и опоры расположены таким образом, что отсутствует общая сила в любом направлении.Мост остается вертикальным, потому что силы на нем уравновешены и нейтрализуют друг друга.
Что такое единица силы в системе СИ?
Международная система единиц (СИ) широко используется в торговле, науке и техникеЕдиницей силы в системе СИ является ньютон, символ N. Базовые единицы, относящиеся к силе:
- Метр, единица длины — условное обозначение м
- Килограмм, единица массы — условное обозначение кг
- Секунда, единица времени — символ s
Сила определяется как скорость изменения количества движения. Для неизменной массы это эквивалентно ускорению массы x. Итак, 1 Н = 1 кг м / с -2 , или 1 кг м / с 2 .
Для неизменной массы это эквивалентно ускорению массы x. Итак, 1 Н = 1 кг м / с -2 , или 1 кг м / с 2 .
Исторически сложилось так, что существовало множество единиц силы и коэффициентов пересчета. Некоторые из них приведены в таблице ниже. Точные преобразования выделены жирным шрифтом, остальные указаны до семи значащих цифр.
Блок | Обозначение | Эквивалентное значение в системе СИ |
дина | дин | 10.0 мкН |
зерно-сила | гр | 635,460 2 мкН |
грамм-сила | gf | 9.806 65 мН |
фунтов стерлингов | pdl | 138. |
унция-сила (avdp) | унций | 278,013 9 мН |
фунт-сила | фунтов | 4.448 222 N |
килограмм-сила | кгс | 9.806 65 № |
килопонд | кп | 9.806 65 № |
зен | зен | 1.0 кН |
тысяч фунтов (= 1000 фунтов-силы) | тысячных фунтов | 4.448 222 кН |
Тонна сила США (= 2000 фунт-сила) (короткая) | тс (США) | 8,896 443 кН |
тонна-сила (= 1000 кгс) (метрическая система) | тс | 9.806 65 кН |
Тонна сила, Великобритания (= 2240 фунт-сила) (длинная) | тс (Великобритания) | 9. |
Использование сокращенных форм для больших и малых чисел поощряется системой СИ. Префиксы SI представляют собой кратные 10 3 или 10 ‑3 .
Возможно вам понравится
Единицы СИ
Реализация счетчика
Измерения жизни
Force Plate — обзор
10.3 Приложения в биомеханике твердых тел
Концепция твердого тела получила широкое распространение в биомеханике, а именно для изучения движения тела.В таком исследовании человеческое тело делится на несколько частей тела, которые связаны друг с другом через суставы тела (рис. 10.3).
Рисунок 10.3. Маркеры помещаются на объект, чтобы позволить биомеханический анализ сегментов тела.
Предоставлено лабораторией биомеханики Порто, www.labiomep.pt. Оценка кинематики тела означает возможность одновременного измерения данных времени и положения. Эти абсолютные величины используются в линейных, поступательных или угловых вычислениях, например, для скорости и ускорения. В качестве альтернативы, скорость и ускорение могут быть получены напрямую, а данные о местоположении могут быть получены с помощью методов численного интегрирования [28]. Есть много инструментов, которые можно использовать для оценки кинематики тела. Однако факультативным инструментом в этой области является система трехмерного (3D) захвата движения (MoCap), а в самых передовых лабораториях используется высококачественная технология оптического отслеживания движения (рис. 10.4).
В качестве альтернативы, скорость и ускорение могут быть получены напрямую, а данные о местоположении могут быть получены с помощью методов численного интегрирования [28]. Есть много инструментов, которые можно использовать для оценки кинематики тела. Однако факультативным инструментом в этой области является система трехмерного (3D) захвата движения (MoCap), а в самых передовых лабораториях используется высококачественная технология оптического отслеживания движения (рис. 10.4).
Рисунок 10.4. Обзор лаборатории биомеханики Порто и камер, используемых для трехмерного захвата движения.
Предоставлено лабораторией биомеханики Порто, www.labiomep.pt. Ключевыми аппаратными компонентами оптических систем MoCap являются камеры движения. Эти камеры используются для захвата двухмерных координат специальных маркеров с разных точек зрения (рис. 10.4). В наиболее точных системах используются легкие, малоразмерные (от 2,5 до 50 мм) пассивные световозвращающие маркеры или кластеры, которые размещаются на теле обследуемого в соответствии с заранее определенной антропометрической моделью. Эти маркеры обычно изготавливаются из полистирольных полусфер, покрытых специальной световозвращающей лентой (со стеклянными бусинами).Камера оснащена специальным стробоскопическим инфракрасным светом, который отражается обратно в камеру маркерами объекта и используется для вычисления координат маркеров с помощью встроенного в камеру программного обеспечения. В настоящее время возможно высокоскоростное отслеживание маркеров, примерно до 1000 кадров в секунду (кадров в секунду) с полным полем обзора (FOV) или до 10000 кадров в секунду с уменьшенным полем обзора. Некоторые камеры, а именно от Qualisys, могут также включать несколько других интересных функций, таких как высокоскоростное видео с высоким разрешением, электромагнитное экранирование для использования в кабинетах МРТ и гидроизоляция для съемки под водой (рис.10.5). Станции данных отвечают за восстановление положения каждого маркера и отслеживание их траектории в режиме реального времени.
Эти маркеры обычно изготавливаются из полистирольных полусфер, покрытых специальной световозвращающей лентой (со стеклянными бусинами).Камера оснащена специальным стробоскопическим инфракрасным светом, который отражается обратно в камеру маркерами объекта и используется для вычисления координат маркеров с помощью встроенного в камеру программного обеспечения. В настоящее время возможно высокоскоростное отслеживание маркеров, примерно до 1000 кадров в секунду (кадров в секунду) с полным полем обзора (FOV) или до 10000 кадров в секунду с уменьшенным полем обзора. Некоторые камеры, а именно от Qualisys, могут также включать несколько других интересных функций, таких как высокоскоростное видео с высоким разрешением, электромагнитное экранирование для использования в кабинетах МРТ и гидроизоляция для съемки под водой (рис.10.5). Станции данных отвечают за восстановление положения каждого маркера и отслеживание их траектории в режиме реального времени.
Рисунок 10.5. Подводные камеры используются для анализа плавания.
Трехмерные системы MoCap используются во всем мире ежедневно. Существуют тысячи приложений в медицине, спорте, эргономике, анимации и промышленности. Чтобы привести несколько примеров, врачи используют данные о движениях для изучения осанки и нормальных и патологических моделей походки [29–32], а тренеры — для оптимизации навыков спортсмена и повышения производительности [33–35].
Эти системы также предлагают возможность интеграции и синхронизации сигналов от внешних устройств сторонних производителей посредством использования многоканальных аналоговых и / или цифровых интерфейсов сбора данных. Об этом не следует забывать тем, кто хочет интегрировать свои системы и датчики. Например, обычно включают электромиографию (ЭМГ), инструменты силы, давления и гониометры, улучшающие анализ биомеханики.
Системы ЭМГ используются для обнаружения электрических сигналов от двигательных нейронов.Изучение моделей электрической активности, ответственных за сокращение скелетных мышц, позволяет получить доступ к физиологическим процессам, которые заставляют мышцу генерировать силу и производить движение [36,37]. В системах ЭМГ, как и во многих других инструментальных системах, волоконно-оптические кабели могут использоваться для передачи данных [38].
В системах ЭМГ, как и во многих других инструментальных системах, волоконно-оптические кабели могут использоваться для передачи данных [38].
Силовая платформа — это инструмент, который измеряет три ортогональных контактных силы и моменты силы, приложенные объектом к его верхней поверхности.В сочетании с кинематикой можно изучать динамику движения, что позволяет, например, рассчитать чистые мышечные силы, силы реакции суставов и моменты [39,40]. Наиболее популярные силовые пластины используют пьезоэлектрические (www.kistler.com) и SG-технологии (www.amti.biz; www.bertec.com). Платформы с высокой собственной частотой являются обязательными для занятий спортом с высокой ударной нагрузкой. Обычно их способность выдерживать вертикальную нагрузку находится в диапазоне от 5 до 20 кН. Например, при приземлении с прыжка средняя пиковая вертикальная сила реакции земли составляет около 4.5 веса тела [41] и легко может достигать шестикратного веса тела [42] (рис. 10.6).
Рисунок 10. 6. Вертикальная сила реакции опоры на опору (GRFz) может легко достигать шестикратного веса тела во время стандартных вертикальных прыжков, как это наблюдается в прыжках с встречным движением.
6. Вертикальная сила реакции опоры на опору (GRFz) может легко достигать шестикратного веса тела во время стандартных вертикальных прыжков, как это наблюдается в прыжках с встречным движением.
Насколько нам известно, на рынке нет оптических или волоконно-оптических силовых пластин, что могло бы стать возможностью для тех, кто ищет новые или альтернативные решения.Тем не менее, есть и другие применения волоконно-оптических датчиков силы в биомеханике и биомедицинских исследованиях, а именно:
- •
в мониторинге силы захвата [43–46]
- •
в обратной связи по силе во время операции [47 –57]
- •
для использования в среде МРТ [58–62]
- •
для включения в глобусы для определения тактильной силы [63,64]
Некоторые из этих вкладов более подробно описаны в предыдущих обзорных статьях [1,4].
Устройства для картирования давления, размещаемые между частями тела и опорными поверхностями (например, пол, сиденье, матрас, подушка и спинка), также очень распространены в лабораториях биомеханики. Предлагается широкий ассортимент продукции, от жестких платформ до гибких матов или тонких датчиков давления в обуви. Здесь также есть возможность внедрить FOS, но с учетом того, что рынок уже предлагает мощные точные электронные системы и датчики по относительно низкой цене (например, www.tekscan.com; www.novel.de). Тем не менее, некоторые ограничения этих датчиков были устранены. Те от Tekscan основаны на проводящих эластомерах и могут демонстрировать нелинейный отклик, гистерезис и постепенный дрейф напряжения [65]. Компания Novel GmbH использует преобразователи на основе емкостей, на которые могут влиять электрические помехи и которые имеют низкое пространственное разрешение, дрейф и высокую чувствительность к температуре [65]. Более того, оба датчика могут измерять только нормальную силу и давление. Исследование Wang et al. [66] представляет особый интерес, потому что представляет собой первую попытку создать внутриобувь оптоволоконный датчик сдвига.Основываясь на методе потерь на изгибе, в качестве основного чувствительного листа для расчета центра давления и нормального напряжения использовался массив многомодовых волокон 2 × 2, залитых в материал с высокой податливостью.
Предлагается широкий ассортимент продукции, от жестких платформ до гибких матов или тонких датчиков давления в обуви. Здесь также есть возможность внедрить FOS, но с учетом того, что рынок уже предлагает мощные точные электронные системы и датчики по относительно низкой цене (например, www.tekscan.com; www.novel.de). Тем не менее, некоторые ограничения этих датчиков были устранены. Те от Tekscan основаны на проводящих эластомерах и могут демонстрировать нелинейный отклик, гистерезис и постепенный дрейф напряжения [65]. Компания Novel GmbH использует преобразователи на основе емкостей, на которые могут влиять электрические помехи и которые имеют низкое пространственное разрешение, дрейф и высокую чувствительность к температуре [65]. Более того, оба датчика могут измерять только нормальную силу и давление. Исследование Wang et al. [66] представляет особый интерес, потому что представляет собой первую попытку создать внутриобувь оптоволоконный датчик сдвига.Основываясь на методе потерь на изгибе, в качестве основного чувствительного листа для расчета центра давления и нормального напряжения использовался массив многомодовых волокон 2 × 2, залитых в материал с высокой податливостью. Напряжение сдвига рассчитывалось с использованием двух слоев основного чувствительного листа, которые помещались между гелевыми / полимерными прокладками стельки. Последующие исследования были проведены для улучшения пространственного разрешения сенсора и производства, а также снижения шума и стоимости [65,67,68]. Наконец, полноценный ножной аппарат с диапазоном давления от 19.Для диагностики диабетической стопы предлагалось от 09 до 1000 кПа [69].
Напряжение сдвига рассчитывалось с использованием двух слоев основного чувствительного листа, которые помещались между гелевыми / полимерными прокладками стельки. Последующие исследования были проведены для улучшения пространственного разрешения сенсора и производства, а также снижения шума и стоимости [65,67,68]. Наконец, полноценный ножной аппарат с диапазоном давления от 19.Для диагностики диабетической стопы предлагалось от 09 до 1000 кПа [69].
Мультиплексированные массивы ВБР также были исследованы для измерения давления стопы [70,71]. Датчики были встроены в неровные слои углеродно-эпоксидного ламината в форме стельки и использовались для контроля давления в стопе при нормальной и ненормальной походке стоя [70]. Чувствительность к силе и давлению составляла ∼5,44 пм / Н и ∼700 пм / МПа соответственно [70].
В эксперименте Mohanty et al. [27] матрица ВБР использовалась для картирования давления на тибиофеморальном интерфейсе во время тотальной артропластики коленного сустава. Матрица была встроена в стопку однонаправленного армированного волокном композита, который был отлит так, чтобы адаптироваться к поверхности мыщелков бедренной кости. Эксперименты ex vivo проводились для определения несоосности протеза во время сгибания / разгибания ноги вокруг колена [27].
Матрица была встроена в стопку однонаправленного армированного волокном композита, который был отлит так, чтобы адаптироваться к поверхности мыщелков бедренной кости. Эксперименты ex vivo проводились для определения несоосности протеза во время сгибания / разгибания ноги вокруг колена [27].
Педобарограф также является прекрасным примером оптического устройства, используемого в клинической практике. Верхняя стеклянная поверхность педобарографа покрыта тонким непрозрачным материалом, обычно пластиковым листом, который при контакте с ногой изменяет свой показатель преломления [72,73].Путем включения микропроцессорной системы обработки изображений можно анализировать изменения интенсивности света, пятна и приложенного давления [74]. Тем не менее, сравнение педобарографа и системы EMED (от Novel GmbH) выявило значительные различия в выходных значениях давления стопы [75].
Pleros et al. [12] предложили напорный мат из силиконового полимера PDMS с небольшими блоками встроенных массивов мультиплексированных ВБР. Авторы также были вовлечены в финансируемый Европой проект FP7 IASIS (Интеллектуальная адаптируемая поверхность с оптическими датчиками для снятия давления-натяжения), который был завершен в 2011 году [76].Проект IASIS был нацелен на представление интеллектуальных систем реабилитации на основе мультиплексных массивов ВБР, откалиброванных для измерения давления в терапевтических кроватях или креслах для инвалидных колясок, и предоставления информации обратной связи для предотвращения возникновения и развития пролежней [77]. Проект также был расширен для измерения давления в интерфейсах коленного сустава для людей с ампутированными конечностями [78,79].
Авторы также были вовлечены в финансируемый Европой проект FP7 IASIS (Интеллектуальная адаптируемая поверхность с оптическими датчиками для снятия давления-натяжения), который был завершен в 2011 году [76].Проект IASIS был нацелен на представление интеллектуальных систем реабилитации на основе мультиплексных массивов ВБР, откалиброванных для измерения давления в терапевтических кроватях или креслах для инвалидных колясок, и предоставления информации обратной связи для предотвращения возникновения и развития пролежней [77]. Проект также был расширен для измерения давления в интерфейсах коленного сустава для людей с ампутированными конечностями [78,79].
Электрические гониометры и торсиометры (торсионные гониометры) используются в биомеханике для измерения углов суставов более прямым способом, чем системы MoCap.Обычно гониометры используются для оценки кинематики угла сгибания / разгибания и приведения / отведения, в то время как торсиометры используются для измерения осевого вращения (например, пронации / супинации предплечья или вращения туловища). Торсиометры — это одноосные устройства, а гониометры могут быть одноосными, используемые с суставами с 1 степенью свободы (например, сгибание / разгибание пальцев), или двухосными (двойные оси) для суставов с 2 степенями свободы (например, сгибание / разгибание запястья). наряду с лучевыми / локтевыми отклонениями). Некоторые суставы, такие как плечо и бедро, имеют 3 степени свободы, и некоторые усилия были предприняты при разработке электрических трехосных гониометров [80–82].Электрические гониометры и торсиометры обычно состоят из двух концевых блоков с пружиной между ними, которая защищает композитный провод с серией SG, установленных по окружности (www.biometricsltd.com). Гониометры Biometrics Ltd., вероятно, эталонный продукт для биомеханики, легкие (от 8 до 29 г) и демонстрируют перекрестные помехи менее ± 5%, точность около ± 2 градусов при измерении более 90 градусов от нейтрального положения и повторяемость лучше ± 1 градус. Возможна частота дискретизации до 5000 Гц.
Торсиометры — это одноосные устройства, а гониометры могут быть одноосными, используемые с суставами с 1 степенью свободы (например, сгибание / разгибание пальцев), или двухосными (двойные оси) для суставов с 2 степенями свободы (например, сгибание / разгибание запястья). наряду с лучевыми / локтевыми отклонениями). Некоторые суставы, такие как плечо и бедро, имеют 3 степени свободы, и некоторые усилия были предприняты при разработке электрических трехосных гониометров [80–82].Электрические гониометры и торсиометры обычно состоят из двух концевых блоков с пружиной между ними, которая защищает композитный провод с серией SG, установленных по окружности (www.biometricsltd.com). Гониометры Biometrics Ltd., вероятно, эталонный продукт для биомеханики, легкие (от 8 до 29 г) и демонстрируют перекрестные помехи менее ± 5%, точность около ± 2 градусов при измерении более 90 градусов от нейтрального положения и повторяемость лучше ± 1 градус. Возможна частота дискретизации до 5000 Гц.
Большинство волоконно-оптических гониометров, которые были предложены в биомеханике, основаны на методах модуляции интенсивности [83–95]. Лишь немногие из них основаны на модуляции длины волны [63,96,97]. Несмотря на это, их возможности были исследованы в кабинетах МРТ [98] и носимых тканях [63,99–102]. Некоторые носимые решения уже включают портативные системы сбора данных и беспроводную передачу данных [103,104]. Тем не менее, предыдущие гониометры являются одноосными и использовались только в лабораторных условиях.Наиболее распространенными носимыми решениями являются ручные перчатки (например, DataGlove, 5DT DataGlove), которые взаимодействуют с виртуальными средами, а некоторые из них также используются в клинических условиях [85,86,93,95]. Они были описаны в предыдущем обзоре [1]. Для целей данной главы будет описан гониометр MLTS 700 (www.adinstruments.com). Технология была разработана компанией Measurand (www.measurand.com) под торговой маркой S700 SHAPE SENSOR. Принцип работы датчика основан на модуляции силы света в ОВ с ламинированными петлями [105,106].Технические характеристики датчика включают массу 45 г, точность ± 1,8 градуса, что соответствует 2% от полной шкалы выходного сигнала (FSO), и разрешение 0,05 градуса, и его можно опрашивать с частотой дискретизации 1000 Гц.
Лишь немногие из них основаны на модуляции длины волны [63,96,97]. Несмотря на это, их возможности были исследованы в кабинетах МРТ [98] и носимых тканях [63,99–102]. Некоторые носимые решения уже включают портативные системы сбора данных и беспроводную передачу данных [103,104]. Тем не менее, предыдущие гониометры являются одноосными и использовались только в лабораторных условиях.Наиболее распространенными носимыми решениями являются ручные перчатки (например, DataGlove, 5DT DataGlove), которые взаимодействуют с виртуальными средами, а некоторые из них также используются в клинических условиях [85,86,93,95]. Они были описаны в предыдущем обзоре [1]. Для целей данной главы будет описан гониометр MLTS 700 (www.adinstruments.com). Технология была разработана компанией Measurand (www.measurand.com) под торговой маркой S700 SHAPE SENSOR. Принцип работы датчика основан на модуляции силы света в ОВ с ламинированными петлями [105,106].Технические характеристики датчика включают массу 45 г, точность ± 1,8 градуса, что соответствует 2% от полной шкалы выходного сигнала (FSO), и разрешение 0,05 градуса, и его можно опрашивать с частотой дискретизации 1000 Гц. В исследовании Mohamed et al. [107] его сравнивали с гониометром SG (www.biometricsltd.com) для оценки сгибания / разгибания колена во время повседневной деятельности и упражнений. Результаты показали, что оба гониометра точно регистрировали угол колена. Однако значительные различия, превышающие 10 градусов для обоих устройств, были обнаружены при сравнении результатов с результатами системы MoCap [107].Между тем было проведено несколько других исследований [108–115].
В исследовании Mohamed et al. [107] его сравнивали с гониометром SG (www.biometricsltd.com) для оценки сгибания / разгибания колена во время повседневной деятельности и упражнений. Результаты показали, что оба гониометра точно регистрировали угол колена. Однако значительные различия, превышающие 10 градусов для обоих устройств, были обнаружены при сравнении результатов с результатами системы MoCap [107].Между тем было проведено несколько других исследований [108–115].
Использование FOS для одновременной оценки положения и ориентации тела для анализа с 6 степенями свободы также представляется весьма интересным в биомеханике. С этой целью были разработаны SHAPE TAPE (www.measurand.com) и Luna, определяющая форму и положение OF (www.lunainc.com). ФОРМА ЛЕНТА — это набор парных ФОРМОВЫХ ДАТЧИКОВ на ленточной подложке, расположенных так, чтобы определять изгиб и скручивание по длине каждой ленты [116]. Датчик использовался, например, для измерения касания пальцем, копирования и рисования в кабинете МРТ наряду с измерением паттернов активации мозга с помощью функциональной МРТ [117,118]. Та же технология была использована при разработке беспроводной системы ShapeHand MoCap (www.shapehand.com) и использовалась в задачах виртуальной реальности [119]. Устройство определения формы и положения Луны основано на сигнале ВБР и сигнатуре рэлеевского рассеяния, присущей ОВ [120]. Kreger et al. [121] использовал датчик для расчета формы рукояти для гольфа во время удара и удара мячом.
Та же технология была использована при разработке беспроводной системы ShapeHand MoCap (www.shapehand.com) и использовалась в задачах виртуальной реальности [119]. Устройство определения формы и положения Луны основано на сигнале ВБР и сигнатуре рэлеевского рассеяния, присущей ОВ [120]. Kreger et al. [121] использовал датчик для расчета формы рукояти для гольфа во время удара и удара мячом.
Краткое упоминание биомеханических систем, которые можно носить на всем теле, также кажется обязательным. По сравнению с оптическими системами MoCap они менее дороги и предлагают возможность перехода из контролируемых в лаборатории помещений в повседневную среду вместе с долгосрочным мониторингом.Технология, основанная на инерциальных измерительных устройствах (IMU) микроэлектромеханических систем (MEMS), является наиболее распространенной в биомеханике [122]. XSENS (www.xsens.com), например, внедряет инновации в этой области, предоставляя IMU на основе MEMS для трехмерного измерения кинематики всего тела (рис. 10.7).
10.7).
Рисунок 10.7. Биомеханический и биоэнергетический анализ с помощью XSENS и COSMED K4b2.
Предоставлено лабораторией биомеханики Порто, www.labiomep.pt.Некоторые решения на основе гониометров OF уже упоминались, но они позволяют измерять только один или несколько суставов.Тем не менее, предпринимаются попытки представить решения для всего тела, такие как распознавание одежды с использованием гетероциклов для измерения движений рук и ходьбы [123,124] и система движения ShapeWrap, разработанная компанией Measurand (www.motion-capture-system.comshapewrap.html ). Эта система для всего тела, состоящая из волоконно-оптических сенсорных лент изгиба-скручивания и IMU, сравнивалась с системой Vicon MoCap [125]. Результаты свидетельствуют о значительном расхождении кинематики суставов нижней части тела по сравнению с кинематикой верхней части тела [125].
Косвенное измерение сил и моментов реакции земли с помощью носимых инерциальных датчиков: систематический обзор
Для оценки GRF по инерционным данным необходимо моделирование некоторых данных. Большинство методов, предложенных в самой ранней литературе, основаны на подходах обратной динамики, которые требуют биомеханического моделирования. Рассмотренные методы были разделены в соответствии с задачами анализа.
Большинство методов, предложенных в самой ранней литературе, основаны на подходах обратной динамики, которые требуют биомеханического моделирования. Рассмотренные методы были разделены в соответствии с задачами анализа.
3.1.1. Ходьба и бег
Первая попытка записать кинематику и кинетику передвижения человека вне лаборатории была предпринята Ohtaki et al.[26]. Они использовали три инерционных блока, прикрепленных к дистальному положению голени и бедра с помощью липучки () для длительного амбулаторного наблюдения. Принятая конфигурация позволяла изучать кинематику только в сагиттальной плоскости. Более того, измерялось только движение левой ноги, а кинематика правой ноги была получена в предположении лево-правой симметрии при нормальной походке. Измерение движения одной ноги позволило: (i) исключить датчики на другой ноге, улучшив подвижность; (ii) снизить энергопотребление.Каждый инерциальный блок состоял из одноосного акселерометра (диапазон ± 5 g) и одноосного гироскопа (диапазон ± 300 град / с).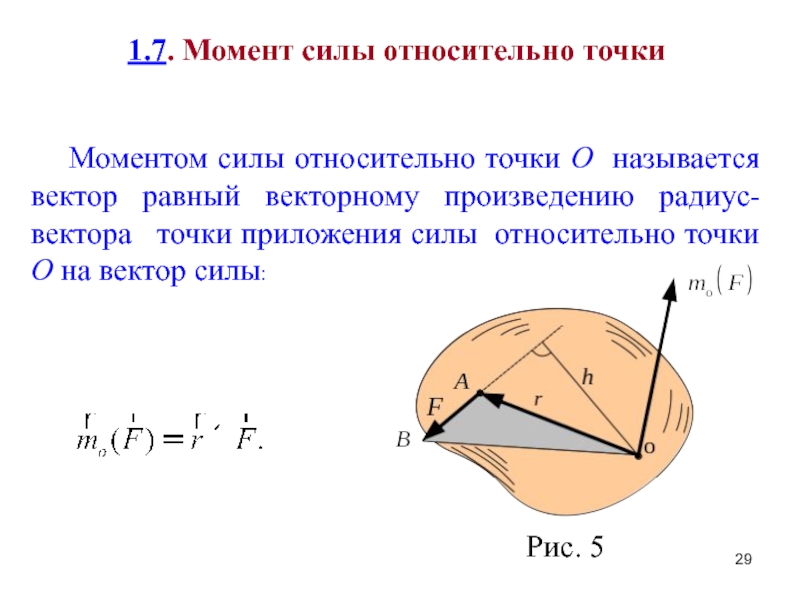 Данные регистрировались на портативном компьютере, который нес в рюкзаке, пока испытуемые шли по прямой со скоростью, определяемой метрономом. Предполагаемые результаты сравнивались с данными, собранными ОС и FP.
Данные регистрировались на портативном компьютере, который нес в рюкзаке, пока испытуемые шли по прямой со скоростью, определяемой метрономом. Предполагаемые результаты сравнивались с данными, собранными ОС и FP.
Позиционирование акселерометра и биомеханическая модель, разработанная [26].
Временные параметры походки и кинематика могут быть получены с помощью специального алгоритма, основанного на частотных компонентах ускорения.Высокие значения частоты были связаны с ударами пятки (HS), в то время как более низкие частоты были связаны с произвольными движениями тела или наклоном относительно направления силы тяжести. Сигналы подвергались фильтрации нижних частот при 10 Гц и фильтров верхних частот при 30 Гц. События удара пяткой были идентифицированы по пикам в высокочастотных компонентах, в то время как производная угловой скорости использовалась для выявления ложных срабатываний, поскольку производная скорости всегда отрицательна в случае истинного контакта пятки [26].
Алгоритм также был способен идентифицировать среднюю и конечную позиции фазы одиночной опоры, обнаруживая повторяющиеся закономерности в радиальном ускорении стойки. Обнаружение этих фаз показано на.
Определение фаз ходьбы по радиальному ускорению хвостовика согласно алгоритму, предложенному в [26]. A: удар пяткой, B: начало средней стойки, C: подъем пятки, D: отрыв носка.
Углы суставов были рассчитаны путем интегрирования угловых скоростей пяти сегментов, составляющих модель тела, и использования стандартных антропометрических данных [27].Модель изображена и состоит из пяти сегментов: таза, бедер и голени. Общая сила реакции опоры на каждую ногу была определена с помощью обратного динамического анализа, основанного на рекурсивной формулировке уравнений баланса сил и моментов. Во время фазы одиночной опорной стойки общий GRF оценивался как сумма сил на каждом из пяти сегментов модели (уравнение (1)). Ускорение левой ноги оценивалось исходя из двусторонней симметрии (уравнение (2)).
Fstance = ∑i = 15mi ∗ ai (t), t∈mid позиция
(1)
a l e f t ( t a) = t a r i g h t ( t + T /2)
(2)
где m i и a i — масса и ускорение i -го сегмента модели. T — время стойки. Ускорение вычислялось в центре масс каждого сегмента путем вращения и перевода измеренного ускорения.
Шарнирный момент τ i был вычислен путем решения уравнений движения, а мощность была вычислена путем умножения момента и угловой скорости ω i как в уравнении (3):
P i = | τ i ∗ ω i |
(3)
Этот метод доказал свою способность определять временные параметры в соответствии с движением стопы, кинематическими данными и силами реакции опоры [26], хотя наблюдалось некоторое отклонение по сравнению с OS. Максимальная RMSE составляла 11,2 ° для углов и 0,31 N / BW для GRF (GRF были нормализованы по массе тела). Однако были соблюдены некоторые ограничения. Во-первых, в нем использовалась значительно упрощенная модель человеческого тела и стандартные анатомические параметры. Использовались только одномерные датчики, а анализ ограничивался сагиттальной плоскостью. Это внесло неточности в оценку кинематических параметров, которые распространялись на вычисление сил. Более того, анализ был ограничен фазой одиночной поддержки.В фазе двойной опоры, когда обе ноги касаются земли, кинематическая цепь неопределенная и уравнения движения не могут быть решены [20]. Другие источники ошибок были связаны с артефактами мягких тканей из-за фиксации сенсора [26]. Предлагая обоснованный подход к оценке GRF, этот метод имел некоторые серьезные ограничения, которые были частично преодолены в последующих исследованиях.
Максимальная RMSE составляла 11,2 ° для углов и 0,31 N / BW для GRF (GRF были нормализованы по массе тела). Однако были соблюдены некоторые ограничения. Во-первых, в нем использовалась значительно упрощенная модель человеческого тела и стандартные анатомические параметры. Использовались только одномерные датчики, а анализ ограничивался сагиттальной плоскостью. Это внесло неточности в оценку кинематических параметров, которые распространялись на вычисление сил. Более того, анализ был ограничен фазой одиночной поддержки.В фазе двойной опоры, когда обе ноги касаются земли, кинематическая цепь неопределенная и уравнения движения не могут быть решены [20]. Другие источники ошибок были связаны с артефактами мягких тканей из-за фиксации сенсора [26]. Предлагая обоснованный подход к оценке GRF, этот метод имел некоторые серьезные ограничения, которые были частично преодолены в последующих исследованиях.
Другой подход был предложен Neugebauer et al. [28], которые использовали статистическую модель для оценки пика вертикальной составляющей GRF во время ходьбы и бега. Данные регистрировались с помощью недорогого двухосного акселерометра, обеспечивающего частоту дискретизации 40 Гц и диапазон измерения ± 7 g. Датчик был закреплен на наиболее латеральной стороне гребня подвздошной кости правого бедра, и он измерял максимальное ускорение, зарегистрированное по двум осям. Оценка максимальной силы реакции земли во время опорных фаз была основана на статистической модели, основанной на повторных измерениях и регрессии со смешанными эффектами. Такая модель ищет линейную или логарифмическую связь между двумя переменными, принимая во внимание влияние нескольких различных факторов, выраженных в иерархической форме [29].В этом случае модель была основана на предположении, что пол, масса тела и тип передвижения были хорошими факторами, предсказывающими взаимосвязь между ускорением и GRF. Это предположение было основано на фундаментальных уравнениях движения, в которых GRF является функцией массы, инерционных свойств сегментов тела и ускорения частей тела [28]. Анализ данных показал, что масса тела действительно была хорошим предиктором, а логарифмически преобразованный пиковый GRF был хорошо предсказан с использованием модели смешанного эффекта.
Данные регистрировались с помощью недорогого двухосного акселерометра, обеспечивающего частоту дискретизации 40 Гц и диапазон измерения ± 7 g. Датчик был закреплен на наиболее латеральной стороне гребня подвздошной кости правого бедра, и он измерял максимальное ускорение, зарегистрированное по двум осям. Оценка максимальной силы реакции земли во время опорных фаз была основана на статистической модели, основанной на повторных измерениях и регрессии со смешанными эффектами. Такая модель ищет линейную или логарифмическую связь между двумя переменными, принимая во внимание влияние нескольких различных факторов, выраженных в иерархической форме [29].В этом случае модель была основана на предположении, что пол, масса тела и тип передвижения были хорошими факторами, предсказывающими взаимосвязь между ускорением и GRF. Это предположение было основано на фундаментальных уравнениях движения, в которых GRF является функцией массы, инерционных свойств сегментов тела и ускорения частей тела [28]. Анализ данных показал, что масса тела действительно была хорошим предиктором, а логарифмически преобразованный пиковый GRF был хорошо предсказан с использованием модели смешанного эффекта. Средняя абсолютная разница между предсказанным GRF и тем, который непосредственно измеряется силовой пластиной, составила 9%, а максимальная наблюдаемая ошибка составила 17,5% [28]. Однако у этого подхода было несколько ограничений, в основном из-за используемого датчика. Тип датчика и его расположение не позволяли измерять пространственно-временные параметры, а также временные профили GRF. Кроме того, в методе использовался статистический подход, а не более подробная биомеханическая модель, поэтому многие анатомические особенности испытуемых не были приняты во внимание.Таким образом, метод может не подходить для занятий, предполагающих концентрированные и повторяющиеся нагрузки, таких как прыжки или во время тренировки. Те же авторы исследовали этот метод в следующей работе [30]. Они регистрировали ускорение с помощью 3-осевого акселерометра, расположенного, опять же, на самой боковой стороне талии, над правым гребнем подвздошной кости. Это новое устройство могло записывать данные с частотой дискретизации 100 Гц, а максимальный диапазон составлял ± 6 g.
Средняя абсолютная разница между предсказанным GRF и тем, который непосредственно измеряется силовой пластиной, составила 9%, а максимальная наблюдаемая ошибка составила 17,5% [28]. Однако у этого подхода было несколько ограничений, в основном из-за используемого датчика. Тип датчика и его расположение не позволяли измерять пространственно-временные параметры, а также временные профили GRF. Кроме того, в методе использовался статистический подход, а не более подробная биомеханическая модель, поэтому многие анатомические особенности испытуемых не были приняты во внимание.Таким образом, метод может не подходить для занятий, предполагающих концентрированные и повторяющиеся нагрузки, таких как прыжки или во время тренировки. Те же авторы исследовали этот метод в следующей работе [30]. Они регистрировали ускорение с помощью 3-осевого акселерометра, расположенного, опять же, на самой боковой стороне талии, над правым гребнем подвздошной кости. Это новое устройство могло записывать данные с частотой дискретизации 100 Гц, а максимальный диапазон составлял ± 6 g. Целью работы было вычисление пикового GRF по ускорению, зарегистрированному в бедре, с использованием математической модели, основанной на линейной регрессии [30].Авторы обнаружили, что ускорение, измеренное с помощью акселерометра, установленного на бедре, может не дать точного представления о нагрузке, воспринимаемой телом. Фактически было обнаружено, что разработанная модель недооценивает пиковый GRF, особенно в тех задачах, которые связаны с более высоким пиковым GRF, таких как бег. Более того, авторы заметили, что в некоторых случаях пиковое ускорение бедра во время бега может быть выше ± 11 g [30], что насыщает диапазон акселерометра ± 6 g. Таким образом, этот подход следует использовать с осторожностью и следует отдавать предпочтение другим конфигурациям акселерометра.
Целью работы было вычисление пикового GRF по ускорению, зарегистрированному в бедре, с использованием математической модели, основанной на линейной регрессии [30].Авторы обнаружили, что ускорение, измеренное с помощью акселерометра, установленного на бедре, может не дать точного представления о нагрузке, воспринимаемой телом. Фактически было обнаружено, что разработанная модель недооценивает пиковый GRF, особенно в тех задачах, которые связаны с более высоким пиковым GRF, таких как бег. Более того, авторы заметили, что в некоторых случаях пиковое ускорение бедра во время бега может быть выше ± 11 g [30], что насыщает диапазон акселерометра ± 6 g. Таким образом, этот подход следует использовать с осторожностью и следует отдавать предпочтение другим конфигурациям акселерометра.
Другой метод оценки пикового GRF во время бега — это метод Wundersitz et al. [31], в которых использовался только трехосный акселерометр, закрепленный на верхней части тела. Фундаментальная гипотеза заключалась в том, что пик GRF при беге вызван столкновением стопы с землей [32] и, поскольку масса постоянна, измеренное ускорение пропорционально силе [33]. Датчик размещался на верхней части тела, поскольку в предыдущих исследованиях подчеркивалось, что датчик следует размещать таким образом, чтобы как можно меньше влиять на работу спортсмена [34,35].Использование трехкоординатного акселерометра вместо одноосного обеспечило повышенную чувствительность к ударному ускорению за счет повышенной поперечной чувствительности [31]. IMU, использованный в [31], состоял из 3-осевого акселерометра, диапазон ± 8 g, частота дискретизации 100 Гц. Датчик фиксировали в центре верхней части спины на уровне второго грудного позвонка, как и в предыдущих исследованиях [36]. Основная ось акселерометра проходила в черепно-каудальном направлении и почти эквивалентна глобальной вертикальной оси [31].Пиковое значение GRF, оцененное этим методом, сравнивалось с выходом силовой пластины, в то время как испытуемые выполняли несколько заданий на бег и задания на изменение направления [31]. Было доказано, что сглаживание сигнала ускорения необходимо для получения надежных данных, и предполагается, что оптимальная частота нижних частот составляет 10 Гц. При использовании низких частот пиковое значение GRF, оцененное акселерометром, было сопоставимо с величиной, измеренной непосредственно силовой пластиной. После нескольких испытаний акселерометры могут обеспечить приемлемую меру силы удара.Абсолютная погрешность единичного измерения составила ~ 24%. Таким образом, рекомендуется сглаживание данных.
Датчик размещался на верхней части тела, поскольку в предыдущих исследованиях подчеркивалось, что датчик следует размещать таким образом, чтобы как можно меньше влиять на работу спортсмена [34,35].Использование трехкоординатного акселерометра вместо одноосного обеспечило повышенную чувствительность к ударному ускорению за счет повышенной поперечной чувствительности [31]. IMU, использованный в [31], состоял из 3-осевого акселерометра, диапазон ± 8 g, частота дискретизации 100 Гц. Датчик фиксировали в центре верхней части спины на уровне второго грудного позвонка, как и в предыдущих исследованиях [36]. Основная ось акселерометра проходила в черепно-каудальном направлении и почти эквивалентна глобальной вертикальной оси [31].Пиковое значение GRF, оцененное этим методом, сравнивалось с выходом силовой пластины, в то время как испытуемые выполняли несколько заданий на бег и задания на изменение направления [31]. Было доказано, что сглаживание сигнала ускорения необходимо для получения надежных данных, и предполагается, что оптимальная частота нижних частот составляет 10 Гц. При использовании низких частот пиковое значение GRF, оцененное акселерометром, было сопоставимо с величиной, измеренной непосредственно силовой пластиной. После нескольких испытаний акселерометры могут обеспечить приемлемую меру силы удара.Абсолютная погрешность единичного измерения составила ~ 24%. Таким образом, рекомендуется сглаживание данных.
Похожий подход был предложен Charry et al. [37], в которых использовался трехосевой акселерометр, закрепленный на медиальной части голени каждой ноги. Ускорение большеберцовой кости измерялось во время бега. Этот подход был основан на предыдущей работе, в которой большеберцовый шок оценивался количественно, исходя из линейной зависимости между большеберцовым осевым ускорением и пиковым GRF [38]. Два имеющихся в продаже акселерометра имели диапазон ± 24 g, частоту дискретизации 100 Гц и были закреплены на обеих большеберцовых костях вдоль оси большеберцовой кости в средней точке между нижним краем медиальной лодыжки и линией медиального сустава колена.Для сравнения использовалось прямое измерение GRF с помощью силовой платформы.
Из записанного профиля ускорения большеберцовой кости можно было идентифицировать четыре события: (i) удар пяткой; (ii) начальное пиковое ускорение; (iii) Максимальное пиковое ускорение и (iv) Пиковое ускорение. Авторы обнаружили, что логарифмическая аппроксимация лучше всего приближает корреляцию между ускорением и пиковым GRF. Затем этот метод можно использовать для определения фаз ходьбы по сигналу ускорения. Ошибка RMSE в логарифмической оценке GRF от ускорения по сравнению с прямым измерением с силовой пластины достигла в среднем ~ 150 Н для разных скоростей движения [37].
Meyer et al. [39] изучали применимость метода на основе акселерометра для измерения GRF у детей. Выполнялись следующие задания: ходьба, бег трусцой, бег, приземление из боксов высотой 10, 20 и 30 см, прыжки со скакалкой и танцы некоторых движений брейк-данса. Силы реакции грунта одновременно регистрировались силовыми пластинами. Во время тестов дети носили на правом бедре два различных имеющихся в продаже трехосных акселерометра. Частота дискретизации составляла 100 Гц и максимальный диапазон ± 8 г и ± 6 г соответственно.GRF, измеренный с помощью FP, был: в 1,3 раза больше BW для ходьбы, 2,2 BW для бега трусцой, 2,8 BW для бега. В случае приземления с разной высоты измеренные силы составили: 4,2 BW для 10 см, 5,2 BW для 20 см, 5,9 BW для 30 см. Корреляция между FP и измеренными ускорениями была очень высокой (R = 0,90). Пол, возраст, вес, рост и длина ног детей не оказали существенного влияния на коэффициенты корреляции. Несмотря на высокую корреляцию между применяемыми методами, оба акселерометра систематически завышали GRF, и смещение измерения увеличивалось с нагрузкой [39].Хотя данные акселерометра хорошо коррелировали с измеренным GRF, авторы рекомендовали с осторожностью использовать акселерометры, когда требуется абсолютное измерение силы. Авторы также подчеркнули важность использования адекватной частоты дискретизации, которая должна как минимум вдвое превышать скорость самого быстрого движения [40]. Частоты обычных физических нагрузок без воздействия на человека обычно ниже 8 Гц [41], но во время пиковых контактов (например, при беге) частоты могут быть выше [39].Максимальные диапазоны ± 8 г и ± 6 г также могут быть ограничивающими для очень высоких ударных нагрузок, в то время как значения в диапазоне от 2 г до 4 г наблюдались при выполнении обычных задач. Доказано, что таких значений ускорения достаточно, чтобы вызвать благоприятные структурные изменения прочности костей [42,43].
Более сложный подход предложен Yang et al. [44], которые разработали метод оценки сил и моментов нижних конечностей при ходьбе с использованием кинематического устройства слежения. Этот метод был нацелен на использование для клинического анализа ходьбы в клинических условиях без необходимости использования специальной лаборатории или дорогостоящих инструментов.Исследование было направлено на ходьбу, так как это наиболее распространенный вид деятельности, являющийся объектом клинических исследований у людей с двигательными травмами. Авторы разместили гироскопы в центрах масс туловища, бедер, голеней и ступней, чтобы измерить соответствующие угловые скорости, в то время как акселерометры были размещены на ступнях для измерения их линейного ускорения. В отличие от предыдущих методов, этот был направлен на измерение трехмерного пешеходного движения, а это означает, что кинематика во фронтальной и поперечной плоскостях учитывалась в дополнение к сагиттальной плоскости.Поскольку целью работы было оценить не только GRF, но и межсегментарные силы на нижнюю конечность, потребовалась подробная биомеханическая модель. Механические свойства (масса и инерционный момент) были присвоены каждому сегменту модели на основе стандартных значений, указанных в литературе [44]. Угловые положения и ускорение бедер, колен и лодыжек были получены путем интегрирования и дифференцирования измеренных угловых скоростей. Цикл ходьбы был идентифицирован и сегментирован по угловому положению ступней ().Этот анализ позволил идентифицировать условия поддержки ног: (i) ранняя двойная поддержка; (ii) одинарная опора; (iii) поздняя двойная поддержка. Эти фазы были идентифицированы по моментам первоначального контакта и отрыва, которые, в свою очередь, были идентифицированы непосредственно из IMU [44].
Определение фаз походки по угловому положению стоп по [44].
Используя преимущества IMU, размещенных на сегментах тела, и зная массу каждого сегмента, была вычислена сила каждого межсегментарного сустава.Начиная с бедра, силы на каждый сустав нижней конечности были впоследствии рассчитаны путем суммирования нагрузки, обнаруженной на верхнем сегменте, как показано в уравнениях (4) — (8). Последними вычислялись силы на пятку и фалангу. Сила на другом бедре, а именно f L-hip , была оценена с помощью экспоненциальной передаточной функции [44].
f R — бедро = m ствол ( a ствол — g ) — f L — бедро
(4)
f колено = f Правое бедро + m бедро ( a бедро — g )
(5)
f Правое колено = R + m хвостовик ( a хвостовик — г )
(6)
f R — опора = f R — пятка ph f f = f R — голеностопный сустав + m стопа ( a стопа — g )
(7)
fR − ph = sfR − стопа an fR − пятка = (1 − s ) fR − фут, где s = lPClfoot
(8)
где l PC — расстояние между центром давления и пяткой, l стопа — длина стопы.
Силы на пятке и фаланге, оцененные этим методом, сравнивались с силами, измеренными с помощью датчиков веса, размещенных под ботинком. Биомеханическая модель представлена на рис. Расчетные силы оказались в хорошем согласии с измеренными (), наблюдалась хорошая корреляция между двумя сигналами (R> 0,95) и относительно низкая максимальная RMSE ~ 66 Н.
Биомеханическая модель, как определено в [44] и соответствующие схемы свободного тела: ( a ) туловище, ( b ) ступня, ( c ) голень, ( d ) верхняя часть ноги.
Силы на пятке и фаланге оцениваются методом, предложенным в [44], и сравниваются с выходной мощностью тензодатчиков, размещенных под ботинком.
Метод, предложенный [44], был более сложным, чем предыдущие, поскольку он использовал семь IMU и улучшенную трехмерную биомеханическую модель, но он позволял оценить максимальный GRF без необходимости использования силовых пластин и межсегментарных сил. оценивается без использования инвазивных датчиков. Однако слабость этого подхода заключалась в оценке сил во время фазы двойной опоры, поскольку распределение силы между двумя ногами оценивалось с помощью статистического подхода.
Karatsidis et al. [45] также разработали метод прогнозирования как GRF, так и GRM во время ходьбы, используя только кинематические данные от IMU, и они попытались преодолеть проблему неопределенности в фазе двойной поддержки с помощью алгоритма распределения, основанного на предположении о плавном переходе. Авторы использовали инерциальную систему, состоящую из 17 IMU, установленных на облегающем костюме, ориентиры датчиков которого показаны на. Частота дискретизации 240 Гц. Выходные данные IMU сравнивались с выходными данными ОС и FP.Кинематика 23 анатомических сегментов, составляющих модель, была реконструирована с использованием сигналов ускорения, полученных от IMU. Исходя из кинематических и инерционных свойств каждого сегмента, общая внешняя сила была оценена по уравнению движения Ньютона, уравнение (9), [46]. Точно так же полный внешний момент был вычислен по уравнению Эйлера (уравнение (10)).
Fext = ∑i = 1Nmi (ai − g)
(9)
Mext = ∑i = 1N [Jiω˙i + ωi × (Jiωi)] — ∑i = 1N∑j = 1Ki (rij × Fij )
(10)
где K i — количество конечных точек в каждом сегменте, ω i — угловая скорость i -го сегмента, J i — тензор инерции вокруг центра масс i -го сегмента, r i j — плечо рычага между центром масс и приложенной силой F i j .
Биомеханическая модель и ориентиры для ИДУ, предложенные в [45].
Инерционные параметры каждого сегмента были рассчитаны на основе масштабированных антропометрических данных, как предложено в [27]. Во время фазы одиночной опоры GRF вычислялся, как и в предыдущих методах, в то время как GRM вычислялся, принимая плечо рычага применяемого GRF как проекцию голеностопного сустава на землю. Во время двойной поддержки решение уравнения Ньютона является неопределенным, поэтому авторы реализовали алгоритм распределения, основанный на функции предположения о плавном переходе, построенной на эмпирических данных [45].Функция, показанная на рисунке, зависит от времени наступления походки и использовалась для распределения силы и моментов между двумя ногами во время фазы двойной опоры.
Кривые для предположения о плавном переходе, используемые для распределения внешних сил и моментов между двумя опорами [45]. Кривые построены на основе эмпирических данных. Пунктирными линиями представлены кривые, полученные в предыдущем исследовании [47].
Фазы одинарной и двойной опоры были идентифицированы с помощью алгоритма обнаружения событий походки.Процедура была основана на пороговом уровне, применяемом к норме скоростей пятки и носка [45]. Расчетные GRF и GRM сравнивались с теми, которые измерялись с помощью OS и FP на протяжении трех подфаз цикла ходьбы: (i) первая двойная опора; (ii) вторая двойная опора; (iii) одиночная опора для каждой ступни.
Было обнаружено, что системы инерционного захвата движения и оптического захвата движения имеют схожую производительность при оценке GRF и GRM по сравнению с силовыми пластинами золотого стандарта.Наибольшие ошибки RMSE для GRF наблюдались для латеральной составляющей силы. Худшие результаты были при оценке боковой силы в задаче «быстрая ходьба», которой соответствовало RMSE 14,6%. Максимальное значение RMSE для GRM составило 30,6%, и оно наблюдалось для фронтальной силы в задаче «быстрая ходьба» [45]. Что касается фаз шага, наибольшие ошибки наблюдались в фазах двойной поддержки.
В целом оценки переднего и вертикального GRF, а также сагиттального GRM были лучше, чем бокового GRF и фронтального и поперечного GRM.Это объяснялось меньшей величиной боковых мер, которые имеют относительно большое влияние на окончательные оценки.
У этого метода были некоторые ограничения. Во-первых, оценка GRF во время двойной поддержки имела низкую точность из-за того, что предположение о плавном переходе было основано на эмпирически выведенных кривых, полученных от здоровых субъектов, поэтому этот метод не подходит для людей с двигательными расстройствами. Во-вторых, этот метод может быть неточным для более медленных или более высоких скоростей ходьбы, бега или ненормальной ходьбы, когда требуется более сложная модель распределения силы.В-третьих, механические свойства каждого сегмента были основаны на усредненных антропометрических данных, которые могут не отражать правильно пожилые или тучные группы населения [48,49]. Наконец, есть некоторые внутренние проблемы при использовании инерциальных датчиков, в основном из-за магнитных помех и артефактов мягких тканей. Этот метод был основан на протоколе всего тела с 17 IMU, и уменьшение количества датчиков может сделать систему более практичной для клинической практики и использования в спорте.
Оценка GRF при двойной опоре представляет собой наиболее серьезную проблему, когда можно полагаться только на кинематические данные.Фактически, во время двойной опоры нижние конечности образуют механическую цепь с замкнутым контуром, что делает невозможным однозначное определение GRF на каждой ноге, полагаясь только на уравнения Ньютона-Эйлера. Метод, предложенный для решения этой проблемы, представлял собой «предположение о плавном переходе» [45], а также другие ранее разработанные математические модели для прогнозирования перехода нагрузки от ведомой к ведущей опоре [50,51,52]. В таких методах используются статистические модели, в основном основанные на эмпирических данных, для прогнозирования количества нагрузки, которая будет возложена на каждую ступню в фазах двойной опоры.Другой метод предложен Dijkstra et al. [53], которые использовали «точку нулевого момента», то есть точку на земле, в которой горизонтальные моменты из-за внешних нагрузок равны нулю. В условиях устойчивости эта точка совпадает с центром давления. Этот метод является недорогим в вычислительном отношении и обычно используется для стабилизации двуногой ходьбы роботов [54]. Метод «Точка нулевого момента» был протестирован на кинематических данных, полученных от оптоэлектронной системы, силовых платформ и модели тела OpenSim [55].Было доказано, что оценка GRF была точной в вертикальном и латеральном направлениях, в то время как силы в переднем заднем направлении были недооценены, что также привело к неточности в оценке суставных моментов [53].
Gurchiek et al. [56] провели технико-экономическое обоснование использования одного IMU, размещаемого на крестце. IMU был помещен близко к центру масс, чтобы измерить поступательное ускорение в этой точке. Как и в предыдущих исследованиях, общая сила оценивалась с помощью простой модели, основанной на законе Ньютона [31,57].В дополнение к этому авторы использовали информацию от гироскопа и магнитометра для оценки ориентации сегмента тела, что позволило выразить опорные векторы датчика в инерциальной опорной системе. Трехмерная сила, оцененная таким образом, сравнивалась с измерениями силовой пластины. Испытуемые выполняли задания на ускорение и смену направления [56]. Для восстановления положения IMU относительно наземной системы отсчета потребовались две попытки статической калибровки.Информация от магнитометра и акселерометра IMU использовалась для оценки начального курса. Затем измеренные величины были привязаны к наземной системе отсчета с помощью кватернионной математики [58]. Было получено хорошее согласие между вертикальной составляющей силы, оцененной IMU, и измеренной FP (и). Однако плохое согласие наблюдалось в случае медиолатерального и переднезаднего компонентов (и). Таким образом, данный метод можно рекомендовать только для оценки вертикальной составляющей GRF и ее величины.Что касается трехмерных векторов силы, максимальная угловая ошибка, наблюдаемая между векторами, оцененными IMU и FP, составила 10 ° [56].
Графическое представление вектора GRF, оцененного IMU (красный) и силовой платформой (синий), как найдено с помощью [56]. ( A ) задача запуска спринта, ( B , C ) задачи изменения направления. Представлена угловая ошибка между векторами.
Графическое представление кривых GRF вдоль цикла походки для IMU (красный) и FP (синий), найденных в [56].(SS) задача старта спринта, (COD) задачи смены направления. F z — вертикальная составляющая.
Этот подход очень интересен, поскольку использование одного датчика IMU значительно упрощает клинические измерения с помощью носимых датчиков. Однако, согласно [56], он был надежным только для оценки GRF в сагиттальной плоскости. Есть два других основных ограничения: во-первых, реальный центр масс меняет свое положение относительно ИДУ на крестце во время таких действий, как ходьба или бег.Таким образом, смещения и вращения таза могут вызывать артефакты при оценке сил [56]. Во-вторых, на использование магнитометров для оценки ориентации IMU влияют ферромагнитные помехи, которые могут привести к снижению точности результатов.
Raper et al. [59] разработали протокол для измерения GRF с помощью одного IMU, установленного на средней части медиальной большеберцовой кости, и провели анализ надежности этого протокола, сравнив результат с силовой платформой. IMU состоял из трехосного акселерометра с частотой дискретизации 100 Гц.Анализ проводился с помощью программного обеспечения, предоставленного производителем, которое обеспечивает расчет пикового GRF по вертикальной составляющей ускорения большеберцовой кости. Испытуемые были профессиональными спортсменами, которых попросили бегать в помещении на треке, оборудованном пьезоэлектрическими FP. Каждый контакт стопы был идентифицирован, и вычисленный GRF был сопоставлен с тем, который был непосредственно измерен FP. Абсолютное значение GRF, измеренное IMU, отличалось от зарегистрированного FP. Было замечено, что IMU может недооценивать силу до 400 Н [59].Эта ошибка предполагалась из-за задержки между пиком ускорения и пиком приложенной силы. Авторы рекомендовали, чтобы измерение IMU не заменялось единицей измерения Ньютон, но оно все же способно измерять нагрузку на нижние конечности при беге. Точность была оценена как 83,96%, а надежность была очень высокой с ICC 0,97, таким образом, IMU можно было считать полезным инструментом для измерения нагрузки на нижние конечности у спортсменов, выполняющих спортивные задачи [59].
Более продвинутая анатомическая модель использовалась Aurbach et al. [60], который реализовал модель опорно-двигательного аппарата () с использованием программного обеспечения AnyBody ™ (AnyBody Technology A / S, Ольборг, Дания). Модель может полагаться на подробное анатомическое представление скелета и на обратный кинетический двигатель для восстановления сил на основе измеренной кинематики. Модель может вычислить GRF, а также силы, действующие на лодыжку, колено и бедро. Кинематические данные были собраны с помощью 15 IMU, установленных на: верхней стороне стопы, передней стороне голеней, передней стороне бедер, одном в крестце, одном между лопатками на спине и одном в области лопаток. лоб.Данные калибровки, полученные во время начальной фазы опоры, были необходимы для настройки магнитометров и акселерометров на местную систему отсчета. Модель стоящего гуманоида была зафиксирована поступательно в тазобедренном сегменте, поскольку система IMU может предоставлять только информацию о вращении. Модель была решена дважды с использованием кинематики, одновременно записанной: (i) ОС; (ii) ИДУ. Затем результаты сравнивали. Сравнение показано в. Данные ОС показали более длительный период односторонней нагрузки на стопы и разницу в прогрессии кривой [60].
Модель опорно-двигательного аппарата, разработанная [60]. Координатная рамка внутри бедра представляет собой систему отсчета для IMU.
Составные части сил наземного реагирования рассчитаны по модели [60]. В первой строке: силы, оцененные ОС, во второй строке: силы, оцененные IMU.
Это исследование показало, что модель на основе IMU дает возможность оценить GRF независимо от лабораторных исследований походки, однако производительность IMU была низкой по сравнению с ОС [60].Основные источники ошибок были связаны с флуктуациями магнитного поля, которые не могли быть полностью устранены с помощью процедуры калибровки. Фактически, используемые IMU широко использовали внутренние магнитометры для полной оценки их ориентации в пространстве, и на магнитометры легко влияют электромагнитные помехи или ферромагнитные объекты поблизости [61]. Другое ограничение этого подхода заключается в конфигурации гуманоидной модели, которая должна точно соответствовать физическим характеристикам субъекта.Таким образом, требуется точная калибровка объекта и дальнейшая работа, чтобы свести к минимуму проблемы с моделью IMU.
Thiel et al. [62] протестировали GRF во время спринтерского бега с помощью IMU. Они использовали два IMU, состоящие из трехмерного акселерометра, гироскопа и магнитометра. Частота дискретизации составляла 250 Гц, и данные регистрировались локально. IMU размещали на голени над медиальной лодыжкой. Данные акселерометра были согласованы и сопоставлены с силовой платформой, использованной для сравнения, в то время как спортсменов попросили бегать по беговой дорожке с инструментами.Вертикальный компонент GRF был связан с ускорением хвостовика следующим линейным уравнением:
F v = c 1 a x + c 2 a y + c 3 a z
(11)
где a x, y, z — компоненты измеренного ускорения, а c 1,2,3 — эмпирические коэффициенты.
Коэффициенты были определены для каждой ступни с использованием силы, зарегистрированной на первых шагах [62]. Этот вид моделирования оказался подходящим для первых этапов спринта, где ожидается постоянный GRF и, следовательно, подходит линейное моделирование [62]. Кроме того, угловая скорость стойки использовалась для определения фаз стойки и поворота и, как следствие, для определения времени пика GRF. Авторы обнаружили, что этот метод не был надежным для каждого участника, даже несмотря на то, что он мог точно предсказать пиковый GRF для одного предмета ().Потенциальные источники ошибок были выявлены в ослаблении силы на голеностопном суставе из-за скелетно-мышечной структуры и поглощения беговой обуви. Этот эффект можно уменьшить с помощью процедуры калибровки.
Вертикальный GRF, измеренный силовой пластиной (красный), по сравнению с прогнозируемым IMU (синий) для одного субъекта в соответствии с методом [62].
Задача бега была дополнительно исследована Kiernan et al. [63]. Целью их исследования было изучение микротравм и механизмов травм из-за повторяющихся нагрузок, возникающих у бегунов.Величину пикового вертикального GRF оценивали с помощью трехмерного акселерометра, носимого на правом бедре. Диапазон записи ± 8 г, частота дискретизации 48 Гц. Ускорение бедра регистрировалось на протяжении всей тренировки. Использование переднезадних компонентов ускорения позволило идентифицировать удары правой и левой стопой с помощью специального алгоритма [64]. Учитывались только правильные шаги, а максимальный GRF во время стойки оценивался с помощью модели линейной регрессии, как в [30].Затем было вычислено среднее значение пикового GRF среди рассмотренных шагов. Подсчитывали и количество шагов. Участники были разделены на две группы: травмированные и здоровые. Сравнение этих групп показало, что у травмированных субъектов были более высокие пиковые значения вертикального GRF, а также совокупные нагрузки. Таким образом, такой метод позволяет прогнозировать травмы и фиксировать профили нагрузки участников [63]. Однако необходимы дальнейшие исследования, чтобы лучше оценить влияние повторяющихся нагрузок, когда максимальная нагрузка приходится на тренировку, и, что наиболее важно, влияние асимметрии нагрузки на левую и правую ногу.Метод, предложенный [63], не смог оценить такие количества, поэтому необходимы дальнейшие исследования и более совершенные протоколы. Использование переносных IMU кажется многообещающим методом измерения таких количеств во время бега.
3.1.2. Прыжки и другие задания
Прыжки, приседания и сгибания отличаются от ходьбы и бега. Во-первых, GRF всегда распределяются между двумя ногами и редко возникает одиночная опора, во-вторых, движение происходит в основном вдоль вертикальной оси и не является циклическим.Косвенная оценка GRF на каждой стопе затруднена, как и обнаружение асимметрии в нагрузке на стопу.
Ранней работой по оценке GRF в вертикальных прыжках была работа Элвина и др. [65], которые предположили корреляцию между пиковым вертикальным GRF и пиковым вертикальным ускорением большеберцовой кости. Испытуемых просили прыгать на разной высоте, при этом регистрировалось ускорение голени. Ускорение измеряли с помощью двух одноосных акселерометров, надетых на опорную втулку, расположенную рядом с вестибулярными головками на обеих ногах, в то время как GRF измеряли с помощью FP.Ориентиры для размещения акселерометров были выбраны потому, что, по словам авторов: (i) ориентир легко определить путем пальпации; (ii) риск того, что датчик может нанести травму субъекту, был низким; и (iii) он ранее использовался в качестве места крепления акселерометра [65]. Диапазон измерения ± 70 г, частота дискретизации 1 кГц. Авторы обнаружили, что пиковое значение GRF при приземлении может достигать 8,2-кратного веса тела, в то время как пиковое ускорение большеберцовой кости может достигать 42.3 г. Наблюдалась сильная корреляция между пиковым GRF и пиковым ускорением (среднее значение R 2 = 0,812, p ≤ 0,01), поэтому авторы пришли к выводу, что пиковое GRF может быть вычислено из второго закона Ньютона, зная массу объекта. Это исследование помогло выявить несколько неточностей в процедуре, таких как: (i) относительное перемещение акселерометра по отношению к телу; (ii) шум и неизвлекаемые инструментальные погрешности; (iii) неизмеренный угол между большеберцовой костью и землей во время удара; (iv) возможная нелинейность во взаимосвязи между ускорением и GRF [65].Более того, не было выявлено четкой корреляции между высотой прыжка и пиковой силой удара, хотя это было продемонстрировано другими исследованиями [7]. Интересно, что авторы смогли вычислить время полета для прыжка и, следовательно, высоту по вертикали из временного профиля вертикального ускорения, используя ранее проверенный алгоритм [66].
Задача вертикального прыжка была дополнительно исследована Ховардом и др. [67] с помощью трехосного акселерометра, расположенного близко к центру масс.GRF одновременно измеряли с помощью FP, в то время как испытуемые выполняли некоторые контрдвижения и прыжки с падением. Минимальная эксцентрическая сила и пиковая концентрическая сила рассчитывались одновременно для прыжков с противодвижением, а пиковая сила приземления рассчитывалась одновременно для прыжков с падением. Авторы обнаружили хорошее согласие между акселерометром и FP во время эксцентрической фазы прыжка с противодвижением, но наблюдалась последовательная систематическая ошибка между результатами, полученными с помощью силовой платформы и акселерометра.Следовательно, сила, полученная при измерении ускорения, не может использоваться взаимозаменяемо с силой, измеряемой FP. Таким образом, было рекомендовано использовать гироскопы для повышения точности наборов данных [67].
Pouliot-Laforte et al. [68] оценили валидность GRF в задачах вертикального прыжка при оценке только с помощью акселерометра. Анализ проводился как на здоровых детях, так и на детях с диагнозом несовершенный остеогенез I типа, патологии, которая обычно вызывает несколько функциональных ограничений и мышечную слабость [69,70].В таких случаях наличие простой и портативной измерительной системы было бы очень ценно для оценки GRF и, следовательно, механической нагрузки на кости. Оценка GRF была получена путем применения закона движения Ньютона, то есть умножения массы объекта на измеренное вертикальное ускорение, как в предыдущих исследованиях. Известно, что действия высокой интенсивности, такие как прыжки, генерируют высокие пиковые силы с высокой скоростью. Испытуемых попросили выполнить пять различных прыжков и несколько маневров подъема на переносной силовой платформе с акселерометром на правом бедре.Акселерометр записывал данные с частотой дискретизации 60 Гц и имел диапазон ± 6 g. Расчетный GRF сравнивался с зарегистрированным FP. Акселерометр был размещен на правой талии пациента немного позади переднего гребня подвздошной кости и удерживался на месте эластичной лентой. Как и в предыдущих исследованиях, результаты показали высокую корреляцию и хорошее соответствие между GRF, измеренным акселерометром и FP. Таким образом, измерение GRF с помощью акселерометра является потенциально ценным инструментом для оценки силы реакции земли у детей и подростков, как здоровых, так и с патологией [68].Небольшое завышение / недооценка усредненных значений GRF производными силами акселерометра позволяет предположить, что измерения силы при длительных записях являются достаточно точными. Авторы пришли к выводу, что, хотя размещение акселерометра на правом бедре широко подтверждено в литературе, было бы предпочтительнее размещать датчик рядом с центром масс, то есть в нижней части спины.
GRF во время движения на корточках был измерен Min et al. [71], который сравнил производительность IMU с измерениями FP и OS.Приседания моделировались в сагиттальной плоскости как 3-сегментное соединение, а движение регистрировалось с помощью трех IMU, размещенных на пояснице, бедре и голени. Локальные оси x IMU были выровнены по нормали к сагиттальной плоскости. Датчики IMU регистрировали трехмерные ускорения, угловые скорости и магнитные поля. Частота дискретизации 100 Гц. IMU захватили кинематику каждого сегмента модели и реконструировали GRF с помощью обратной кинетики. Расчетный GRF показал высокую точность по сравнению с FP (RMSE <0.02 BW). Однако анализ и биомеханическая модель были ограничены движением приседаний, и для исследования других задач, таких как бег, могут потребоваться другие подходы.
При выполнении прыжков с трамплина принимается поза, аналогичная приседанию. Подробный анализ GRF и совместных сил при выполнении этого вида спорта был проведен Логаром и Муних [72]. Они разработали процедуру для оценки GRF и совместных сил, используя кинематическую информацию от носимых на теле IMU. Испытания проводились в лабораторных условиях с силовой платформой, установленной в непосредственной близости от зоны прыжка, что позволяло проводить прямое измерение GRF во время фазы отталкивания (толчка).На тело испытуемого поместили десять ИДУ, как показано на рис. IMU состояли из трехосного акселерометра и трехосного гироскопа с диапазоном ± 8 g, частотой дискретизации 400 Гц. Данные регистрировались на борту каждого IMU и синхронизировались с помощью беспроводного сигнала. Человеческое тело было смоделировано как модель связующего сегмента, состоящая из четырех сегментов, как показано на. Каждый сегмент рассматривался как твердое тело с постоянными механическими свойствами. Необходима процедура калибровки, чтобы измерения не зависели от точки и положения фиксации IMU.Процедура включала: (i) измерение начальной ориентации каждого сегмента; (ii) измерение и интегрирование угловой скорости сегмента во время движения; (iii) суммирование начальной ориентации и интегральной угловой скорости. Первоначальная ориентация оценивалась на этапе бега, когда предполагалось, что все сегменты тела имеют сравнимое ускорение, субъект сохранял позу, похожую на присед, а ориентация ступней / лыж принималась в качестве исходной ориентации для всех других сегментов тела. модель.Антропометрические параметры (масса, размер, момент инерции) были получены из статистических таблиц. Обратную динамику предложенной модели можно решить двумя способами: снизу вверх и сверху вниз. В обоих случаях предполагается, что единственными внешними силами, действующими на тело, являются GRF. В восходящем направлении необходимы GRF, измеренные силовой пластиной. Используя преимущества внешнего GRF, силы и моменты на каждом сегменте тела могут быть вычислены в соответствии с уравнениями равновесия Ньютона-Эйлера.В нисходящем порядке GRF неизвестны. Внутренние силы, действующие на верхнюю часть тела, оцениваются из ускорения и уравнения Ньютона. Затем внутренние силы, действующие на другие сегменты тела, постепенно вычисляются в соответствии с уравнениями равновесия Ньютона-Эйлера. У основания GRF — это величина, необходимая для уравновешивания последнего уравнения. При нисходящем подходе, когда известен GRF, уравнение можно повторно применить в восходящем направлении, чтобы вычислить внутренние моменты, действующие на суставы.
Ориентиры размещения ИДУ и конструкция датчика по протоколу, предложенному [72].
Диаграмма свободного тела для каждого сегмента по модели [72].
Проверка этого метода показала, что средняя среднеквадратичная ошибка между расчетным GRF и значениями, измеренными силовой пластиной, составляет 62,5 ± 259 Н, что соответствует отклонению 9,7 ± 14% [72]. Сравнение рассчитанных и измеренных профилей GRF показано на. Часть наблюдаемых различий была связана с размером лыж по отношению к силовой платформе.Показание FP не дает полного GRF, но показание зависит от части лыж, которая эффективно контактирует с FP [72].
Сравнение вертикального GRF, рассчитанного IMU, и измеренного непосредственно силовой платформой [72].
Вывод исследования состоял в том, что наблюдалось хорошее сходство между измеренным и рассчитанным GRF. Таким образом, предложенный протокол IMU можно считать многообещающим и простым в использовании инструментом для оценки GRF в прыжках с трамплина.
Клиническая необходимость измерения внутренних сил и моментов, действующих на позвоночник и суставы, а также GRF во время сгибания туловища, привела к протоколу, предложенному Faber et al. [73]. Этот протокол предназначался для использования в амбулаторных условиях, полагаясь только на носимые датчики и устраняя необходимость в лаборатории анализа движения. Авторы использовали IMU X-Sens ® в сочетании со встроенной моделью сегмента полного тела X-Sens ® [74,75]. Модель использовала 17 IMU, состоящих из трехосных акселерометров, гироскопов и магнитометров, дистанционно управляемых и запускаемых.Частота дискретизации 120 Гц. Полная конфигурация тела позволила оценить трехмерный GRF, действующий на сегменты стопы. Протоколу требовалась калибровка, полученная путем записи вертикального положения, а затем измерялось ускорение каждого сегмента тела во время упражнения на сгибание. Моменты и GRF оценивались методом сверху вниз с использованием второго закона Ньютона. Результаты сравнивались с GRF, одновременно измеренным FP, и с внутренними силами / моментами, вычисленными с использованием информации от FP и OS.Как отмечалось в предыдущих исследованиях [72], хорошее соответствие между FP и IMU наблюдалось для профиля вертикальной составляющей GRF со среднеквадратичной ошибкой ниже 20 Н, соответствующей 2% максимальной вертикальной силы [73]. Также наблюдается хорошее согласие между пиковыми значениями GRF. Вместо этого силы в переднезаднем и медиолатеральном направлениях были переоценены методом IMU. Что касается внутренних моментов на L5 / C1, максимальная среднеквадратичная ошибка была ниже 10 Нм, что соответствует 5% пикового момента растяжения [73].Основные наблюдаемые неточности были связаны с предположением о твердом теле и массой каждого сегмента тела, которая была назначена в соответствии со статистической моделью, основанной на процентах от общей массы тела [73]. Таким образом, массы, используемые для вычисления в, могут не совсем точно отражать массы реальных сегментов тела каждого субъекта. В соответствии с предыдущими исследованиями, авторы пришли к выводу, что инерционный захват движения является хорошим кандидатом для оценки GRF и внутреннего момента в амбулаторных условиях, но его применимость ограничена анализируемой задачей, т.е.э., прогиб туловища. Дальнейшее изучение требуется для анализа других задач.
Задачи «сидеть, чтобы стоять» и «приседать» исследовали Кодама и Ватанабе [76]. Их целью была оценка внутреннего совместного момента, GRF и CoP на основе кинематических записей IMU. Они протестировали три модели тела: модель с пятью звеньями, модель с четырьмя звеньями и модель с тремя звеньями. Разница заключалась в количестве сегментов, представляющих туловище [76]. Модель пяти звеньев изображена на. Остальные модели были получены путем объединения сегментов, составляющих ствол.Инерционные параметры каждого сегмента были назначены в соответствии с прямыми измерениями на испытуемых, методами статистического распределения, описанными в литературе [77,78] и в базе данных человеческого тела [79]. Совместные моменты оценивались путем решения уравнений движения каждого сегмента, диаграмма свободного тела которого изображена, и GRF оценивался как сумма произведений ускорения каждого сегмента и массы этого сегмента, как в предыдущих методах. КП был рассчитан с использованием уравнения вращательного движения сегмента стопы и сил и моментов, действующих на этот сегмент [76].На туловище, бедрах и голенях были установлены семь инерционных датчиков, как показано на рис. IMU представляли собой изготовленные на заказ беспроводные датчики с частотой дискретизации 100 Гц. Движение одновременно регистрировалось ОС и двумя ФП. Затем испытуемые выполняли исследуемые задания приседания и вставания из положения сидя. Результаты не показали значительных различий между 5-канальной и 4-канальной моделями, в то время как худшие результаты наблюдались для 3-канальной модели. Причина плохих результатов связана с приближением расчета плеча рычага для сегмента туловища.Поэтому авторы рекомендовали модель с четырьмя звеньями. Что касается оценки GRF с помощью нисходящего метода, никаких различий между инерционным захватом движения и ОС не наблюдалось. Средние среднеквадратичные ошибки в горизонтальном, вертикальном GRF и CoP составили соответственно 10 Н, 15 Н и 2 см. Таким образом, метод может быть полезен для практических приложений, когда FP недоступны.
Пятизвенная биомеханическая модель ( a ) и диаграмма свободного тела ( b ) метода, предложенного [76]. Угол наклона каждого сегмента определяется в сагиттальной плоскости, а внутренние силы и моменты представлены на диаграмме свободного тела.
Экспериментальная установка, предложенная в [76]. ( a ) Изображение сегментов тела и датчиков, ( b ) Ориентиры и датчики, которые носит субъект.
Поскольку модель, предложенная в [76], была основана на нескольких сегментах тела, для расчета механических параметров каждого сегмента требовалось широкое использование стандартных таблиц. Такие статистические значения могут вносить неточности в оценку представляющих интерес количеств, поскольку они могут не отражать определенную совокупность.Это общая проблема для всех тех методов, которые требуют знания инерционных свойств сегментов тела.
Сетуайн и его коллеги [80] также оценивали вертикальные прыжки с помощью одиночного ИДУ, помещенного на поясничный отдел позвоночника. Целью их работы было определение надежности такого метода и его применимости по сравнению с измерениями силовой пластины. GRF был вычислен по ускорению с помощью закона Ньютона, как и в предыдущих исследованиях, и измерение профиля вертикальной скорости позволило идентифицировать фазы скачка.Как и в предыдущих исследованиях, наблюдалась хорошая корреляция между оцененным вертикальным GRF и GRF, непосредственно измеренным с помощью силовой платформы, а также наблюдалось смещение между измеренными значениями. Чем больше величина силы, тем больше разногласий между IMU и FP.
Введение | Безграничная физика
Крутящий момент
Крутящий момент — это сила, которая заставляет объекты поворачиваться или вращаться (т. Е. Стремление силы вращать объект вокруг оси).
Цели обучения
Опишите влияние крутящего момента на объект
Основные выводы
Ключевые моменты
- Крутящий момент определяется умножением приложенной силы на расстояние до оси вращения, называемой плечом момента.
- Крутящий момент относится к вращению, как сила — к движению.
- Единица крутящего момента — ньютон-метр.
Ключевые термины
- вектор : Направленная величина, имеющая как величину, так и направление; между двумя точками.
- угловая скорость : векторная величина, описывающая объект в круговом движении; его величина равна скорости частицы, а направление перпендикулярно плоскости ее кругового движения.
- угловое движение : Движение тела вокруг фиксированной точки или фиксированной оси (как планеты или маятника). Он равен углу, который проходит в точке или оси линией, проведенной к телу.
Крутящий момент вокруг точки — это понятие, которое обозначает тенденцию силы поворачивать или вращать движущийся объект.Эта тенденция обычно измеряется относительно точки и обозначается как момент силы . Крутящий момент при угловом движении соответствует действующей силе. Это «причина», следствием которой является угловое ускорение или угловое замедление частицы при общем движении. Количественно он определяется как вектор:
Torque : Краткое введение в крутящий момент для студентов, изучающих вращательное движение в курсах физики на основе алгебры, таких как AP Physics 1 и Honors Physics.
[латекс] \ text {T} = \ text {r} \ times \ text {F} [/ latex]
Вращение — это частный случай углового движения. В случае вращения крутящий момент определяется относительно оси, так что вектор «r» ограничивается перпендикулярно оси вращения. Другими словами, плоскость движения перпендикулярна оси вращения. Ясно, что крутящий момент при вращении соответствует силе при поступлении.
Крутящий момент — это произведение силы на длину плеча момента; он задействован всякий раз, когда есть вращающийся объект.Крутящий момент также можно выразить через угловое ускорение объекта.
Определение направления крутящего момента относительно проще, чем определение угловой скорости. Причина этого проста: сам крутящий момент равен векторному произведению двух векторов, в отличие от угловой скорости, которая является одним из двух операндов векторного произведения. Ясно, что если мы знаем здесь направления двух операндов, направление крутящего момента можно легко интерпретировать.
Поскольку крутящий момент зависит как от силы, так и от расстояния от оси вращения, в системе СИ единицами измерения крутящего момента являются ньютон-метры.
Крутящий момент : Крутящий момент с точки зрения плеча момента.
Крутящий момент или момент силы
Крутящий момент или момент — тенденция силы вращать объект вокруг оси или точки — определяется как
- произведение силы и расстояния от точки или оси до объекта. вектор силы
Крутящий момент может быть выражен как
T = F a (1)
где
T = момент — или крутящий момент силы (Нм, фунт f ft)
F = приложенная сила (Н, фунт f )
a = моментный рычаг (м, фут)
Пример — Крутящий момент, прилагаемый гаечным ключом
Сила 250 Н действует на конец длинного ключа 30 см .Прилагаемый крутящий момент можно рассчитать как
T = (250 Н) (30 см) (0,01 см / м)
= 75 Нм
Конвертер момента
Калькулятор ниже можно использовать для преобразования между некоторыми общие единицы момента или крутящего момента
Закон рычага
Закон рычага — это баланс крутящего момента на неподвижном объекте, который может быть выражен как
F 1 / F 2 = L 2 / L 1 (2)
где
F = сила (Н, фунт f )
L = расстояние от точки (1 или 2) до вектора силы (м, футы) )
(1) можно преобразовать в
F 1 L 1 = F 2 L 2 (2b)
или
908 86 T 1 = T 2 (2c)
Пример — рычаг
Человек массой 90 кг стоит на одной стороне рычага 2 м от точки равновесия.Усилие на другой стороне рычага 0,5 м от точки балансировки можно рассчитать, изменив (2) на
F 2 = F 1 L 1 / L 2
= (90 кг) (9,81 м / с 2 ) (2 м) / (0,5 м)
= 3531 Н
(PDF) Измерение силы и момента
602 Часть B Измерение первичных величин
Испытательная секцияявляется основой для измерений силы, так как
сила прикладывается к обеим проводящим усилие верхним пластинам
(C).Это означает, что компоненты силы, сопротивление
(Fx) и подъемная сила (Fz), которые действуют как поперечные силы на нагрузку
шайб, передаются за счет трения.
Очевидно, что механическое разъединение не требуется, поскольку каждая из четырех нагрузочных шайб может
измерять три компонента, где осевая составляющая
не имеет значения. Возможность отказаться от механической развязки
дополнительно увеличивает жесткость баланса
, что приводит к благоприятному свойству, заключающемуся в том, что для
, например, для кругового цилиндра, собственная частота
определяется довольно высокой частотой изгиба модель
.В случае тензометрических весов упругие элементы действуют как пружины; следовательно, баланс
в сочетании с моделью и массой навесного оборудования определяет собственную частоту
шахты, которая обычно является довольно низкой.
Важное различие между обоими принципами
касается возможности одновременного измерения компонентов силы очень
разной величины. Например, это
может иметь место при исследовании аэродинамических поверхностей в присоединенном потоке
, где подъемная сила на
примерно на два порядка больше, чем сила сопротивления.По этой причине
элементов силы сопротивления тензодатчиков обычно более чувствительны, чем элементы подъемной силы. Другими словами,
— это возможность адаптировать отдельные диапазоны силы на
, варьируя соответствующую чувствительность, тогда как в случае многокомпонентных пьезоэлектрических преобразователей
такая возможность не существует, поскольку чувствительности в одном элементе
Установленоэлемента. Этот небольшой недостаток можно частично сбалансировать, выбрав диапазон более высокой чувствительности в усилителе заряда
.
Обработка сигналов
Что касается весов платформы (рис. 8.61) и весов
для аэродинамической трубы высокого давления, очевидно
, что четыре грузовые шайбы выдают 12 сигналов. Правильная комбинация этих сигналов
позволяет, в принципе, определять все шесть
составляющих результирующей силы и момента
относительно геометрического центра четырех преобразователей
.
Рассмотрим сначала более простой двумерный случай
измерений в аэродинамической трубе высокого давления,
, где требуется только трехкомпонентное измерение лобового сопротивления,
подъемной силы и момента тангажа.В этом случае релевантными являются только
сил сдвига на нагрузочных шайбах. Поскольку чувствительность
ивсех элементов к силам сдвига одинакова,
связанных компонентов можно подключить электрически параллельно
и направить на усилитель заряда. Параллельное соединение четырех компонентов
в направлении подъема дает результирующую подъемную силу
, в то время как момент тангажа получается из разницы между двумя нижними компонентами сопротивления и двумя верхними компонентами сопротивления
.Общее сопротивление соответствует
сумме нижней и верхней силы сопротивления. Наконец,
три электрических сигнала вырабатываются для трехкомпонентного измерения
.
Рассматривая трехмерную задачу, например,
достаточно полумодели, прикрепленной к весам платформы или внутренним балансировочным весам
, в которых требуются все шесть компонентов равнодействующей силы и момента
. В этом случае количество выходных сигналов заряда
сокращается до восьми,
, когда соответствующие отдельные компоненты с
общей линией действия параллельны напрямую.
Усилитель заряда преобразует электрический заряд в
пропорциональное электрическое напряжение. В принципе, это инвертирующий усилитель постоянного тока
, который интегрирует
входного тока i = dQ / dt, который создается
изменениями заряда на кварцевом датчике. Это стало возможным благодаря усилителю с емкостной обратной связью, который
имеет максимально возможное внутреннее усиление и сопротивление изоляции на входе [8.23]. В частности, для квазистатических измерений
, высокое сопротивление Rat на входе является предварительным условием
для малых эффектов дрейфа. Таким образом, все кабели и вилки
между преобразователем и усилителем заряда должны иметь сопротивление изоляции
выше R≈1013 Ом.
Это значение более чем на три порядка выше
, чем у обычных байонетных кабелей Neill – Concelman (BNC)
.
Для квазистационарных измерений выходные сигналы трех или восьми усилителей заряда
(например, Kistler
5007) оцениваются персональным компьютером, оснащенным
с аналого-цифровой (аналого-цифровой) системой преобразования.Помимо
из расчета результирующих сил и момента
, простая процедура коррекции сноса, которая будет
, будет рассмотрена в разд. 8.2.2, используется.
8.2.2 Типичные свойства
Калибровочные испытания(эффекты помех)
В качестве примера поведения калибровки и эффектов интерференции
мы используем внешний баланс аэродинамической трубы высокого давления
, который называется Баланс HDG в
следующие.В квазистатическом режиме амплитудно-зарядовых
фаеров проводилась статическая калибровка весов
с грузами для силы сопротивления Fx, подъемной силы Fz и шага
момента My. На рис. 8.67 показан пример калибровочной кривой
для подъемной силы Fz, включая помехи для сопротивления
Fx.
Заряд Qz [нКл] отложен в зависимости от калибровочной массы
, которая была приложена в направлении компонента Fz
.Вес варьировался на два порядка величиной
, и очевидно, что линейность Qz (Fz) составляет
Часть B 8,2
.

 255 0 мН
255 0 мН 964 016 кН
964 016 кН