Длина волны в физике

В физике звуковая энергия передается посредством волн, которые имеют уникальную способность распространяться в абсолютно любой среде. Разнообразие и огромное количество волновых процессов не позволяют ученым выделить основные свойства волн, так как среди них есть и простые типы, уделяющие внимание энергии. Они уникальны тем, что могут простираться сквозь абсолютную пустоту.

Рисунок 1. Длина волны. Автор24 — интернет-биржа студенческих работ

Определение 1

Длина волны — это определенное расстояние между двумя близко расположенными волнами сигнала.

Чтобы точно определить полную длину волновых процессов, необходимо изначально измерить расстояние между двумя соседними точками двух волн. Зачастую физики определяют эту величину с помощью промежутка между пиками волн, которые находятся на близком расстоянии друг к другу.

Длина волны имеет прямое отношение с частотой потока, исходящего от сигнала. Чем больше постоянство данного элемента, тем меньше будет в итоге длина волнового процесса. Такая подвластность обусловлена стремительным увеличением общего количества повторений волны сигнала в течение определенного периода времени с уменьшением нестабильной длины волны.

Для волн Де Бройля этот показатель можно рассчитать таким образом:

$\LARGE \lambda =\frac{h}{p }$

А если вам необходимо определить более точную формулу переменного элемента электромагнитном поле или воздухе, то можно воспользоваться такой теорией, где

$\LARGE \lambda =\frac{c}{\nu }=\frac{299792458}{\nu }$

Здесь используется:

• $\lambda$ — длина самой волны;
• $\upsilon$ — постоянная скорость волны;
• $T$ — определенный период волны;
• $\nu$ — частота общих колебаний;
• $h$ — стабильная планка;
• $p$ — импульс элемента;
• $c$ — скорость света.

Стоит отметить, что раздел физики, который занимается изучением звуковых волн, называется акустикой. Для людей, звук выступает в роли главного источника получения важной информации.

Определение 2

Звук — это конкретный период волны, имеющий механическое происхождение и распространяющийся в газообразном и твердом пространстве.

Их невозможно увидеть, однако они очень восприимчивы для человеческого уха.

Скорость волны в физике

Рисунок 2. Скорость и длина волны. Автор24 — интернет-биржа студенческих работ

Любой волновой процесс распространяется с определенной скоростью. Под быстротой волны считают общий показатель распространения противодействия. Например, удар по торцу металлического стержня образует в нем местное прочное сжатие, которое затем будет двигаться вдоль выколотки со скоростью примерно 10 км/с.

Скорость волны можно определить свойствами окружающей среды, в которой этот процесс происходит. При трансформации волны из одного пространства в другое ее скорость кардинально изменяется.

В физике под длиной волны подразумевают расстояние, на которое может распространиться волна за время, равное общему периоду колебаний в ней.

Определение 3

Скорость волны — это абсолютная и постоянная величина для определенной среды, равная произведению скорости на время ее генерализации.

Таким образом, чтобы измерить длину волны, надо скорость волнового процесса умножить на фазу его колебаний в ней: где $v$ — скорость конкретной волны, $T$ — период общих колебаний в волне, $\lambda$ — длина самой волны.

Указанная формула определяет связь длины волны с ее скоростью и фазой. Учитывая, что промежуток колебаний в волновых процессах всегда пропорционален частоте, можно утверждать, что что скорость волны равна созданию длины на стабильную частоту колебаний в ней.

Замечание 1

Волны способны передавать силу и энергию, а также обладают конкретикой, что способствует одному волновому процессу не влиять на колебания другого.

В результате, эти две гранитизации могут легко проходить параллельно и не мешать друг другу.

Виды волн

Волны с точки зрения физики передают общую звуковую энергию, которая легко может существовать в любой среде. Благодаря разнообразию существующих волновых процессов, их невозможно точно определить и выделить основные характеристики, присущи только этому явлению.

Волновой процесс имеет многогранную природу в физике, сюда относят:

• химическую;
• механическую;
• электромагнитную;
• спиновую волны;
• гравитационную;
• плотность вероятности.

Американские ученые два года назад получили Нобелевскую премию за изобретение уникального детектора, которые способен с точностью измерить указанные показатели. Устройство в лазерной гравитационно-волновой обсерватории в первый раз зафиксировало гравитационную волну. Чтобы указанный вид волн долететь до нашей планеты, ему понадобилось более одного миллиарда лет. Далеко за видимым горизонтом галактики произошло мощное столкновение двух черных дыр, после чего прошло уже полтора миллиарда лет.

Звуковыми волнами принято считать волны, которые легко воспринимаются человеческим ухом. Диапазон этих частот находятся в границах примерно от 20 Гц до 20 кГц, а волновые процессы с частотой менее указанных показателей называются инфразвуком, а с частотой более 20 кГц – ультразвуком. Волны звукового диапазона могут находится не только в газе, но и в жидкости, и в других состояниях. Однако волны в газообразном пространстве – среде нашего обитания – представляют собой особый интерес.

Типы волн

Все звуковые колебания оснащены постоянной амплитудой, фазой и частотой. Звуки могут проходить абсолютно разные расстояния, а затем передаваться в пространстве в виде неких механических колебаний молекул конкретного вещества. Они распространяются постепенно, а с определенной скоростью, а после мгновенно исчезают. Их скорость непосредственно зависит от среды, в которой они расположены: в жидких и твердых состояниях звуковой процесс простирается лучше и быстрее, чем в воздухе.

Типы волн бывают следующими:

• бегущая — обуславливается периодом, скоростью и длиной, а также характеризуется распространением фаз в пространственном времени, зависящим от частоты и среды;
• стоячая – подразумевает суммарность двух волн: отраженной и падающей, для образования которых необходима одинаковая интенсивность волновых процессов;
• звуковая – характеризуется важным фактором, так как только благодаря этому типу волны люди могут общаться и получать необходимую информацию.

В целом, можно сделать вывод, что причиной всех звуковых процессов являются вибрации, для стабильного распространения звука требуется определенное пространство, источником данного явления выступает тело, имеющее свойство колебаться и вибрировать с правильной, постоянной частотой.

Однако не каждые физические тела, которые перемещаются, могут быть источниками звука. Интересным фактом из истории считается то, что расширение инфразвука на огромные расстояния дает возможность более точно предсказывать стихийные бедствия. А морские животные, такие как раки или медузы, крайне чувствительны к указанным процессам, поэтому способны еще за несколько дней до наступления шторма предвидеть его и спрятаться в безопасное место. Звуки также представляют собой частоту гармонических и абсолютных колебаний.

Длина волны — это… Что такое Длина волны?

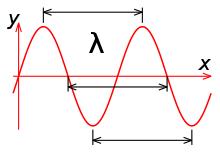
Длина волны λ может быть измерена между любыми двумя точками волны с одинаковой фазой, максимумами, минимумами или узлами волны.

Длина́ волны́ — расстояние между двумя ближайшими друг к другу точками, колеблющимися в одинаковых фазах, обычно длина волны обозначается греческой буквой .^[1] По аналогии с волнами, возникающими в воде от брошенного камня, длиной волны является расстояние между двумя соседними гребнями волны. Одна из основных характеристик колебаний. Измеряется в единицах расстояния (метры, сантиметры и т. п.). Величина , обратная длине волны, называется волновым числом и имеет смысл пространственной частоты.

Получить соотношение, связывающее длину волны с фазовой скоростью () и частотой () можно из определения. Длина волны соответствует пространственному периоду волны, то есть расстоянию, которое точка с постоянной фазой проходит за время, равное периоду колебаний , поэтому

Волнам де Бройля также соответствует определенная длина волны. Частице с энергией Е и импульсом p, соответствуют:

• частота:
• длина волны:

где h — постоянная Планка.

Примеры

Приближённо, с ошибкой около 0,07%, рассчитать длину радиоволны можно так: 300 делим на частоту в мегагерцах, получаем длину волны в метрах, например для 80 Гц, длина волны 3750 километра, для 89 МГц — 3,37 метра, для 2,4 ГГц — 12,5 см.

Точная формула для расчёта длины волны электромагнитного излучения в вакууме выглядит так:

где — скорость света, равная в Международной системе единиц (СИ) 299 792 458 м/с точно.

Для определения длины волны электромагнитного излучения в какой-либо среде следует использовать формулу:

где — показатель преломления среды для излучения с данной частотой.

Примечания

1. ↑ Мякишев Г. Я., Буховцев Б. Б. Колебания и волны // Физика. Учебник для 11 класса общеобразовательных учреждений. — 12-е изд. — М.: Просвещение, 2004. — С. 121. — 336 с. — 50 000 экз. — ISBN 5-09-013165-1

Литература

Комптоновская длина волны — Википедия

Ко́мптоновская длина́ волны́ (λ_C) — параметр элементарной частицы: величина размерности длины, характерная для релятивистских квантовых процессов, идущих с участием этой частицы. Комптоновская длина волны эквивалентна длине волны фотона, чья энергия равна энергии покоя самой частицы. Название параметра связано с именем А. Комптона и комптоновским эффектом.

Формула комптоновской длины волны получается из формулы де-бройлевской длины волны путём замены скорости частицы v на скорость света c:

λC=2πℏmc=hmc.{\displaystyle \lambda _{C}={\frac {2\pi \hbar }{mc}}={\frac {h}{mc}}.}

Для электрона, λe
C ≈ 0,0242 Å ≈ 2,4263102367(11)⋅10⁻¹²м;^[1] для протона, λp
C ≈ 0,0000132 Å ≈ 1,32140985396(61)⋅10⁻¹⁵ м.^[1]

Можно также сказать, что комптоновская длина волны частицы равна длине волны фотона с энергией, равной энергии покоя данной частицы.

Приведённая комптоновская длина волны[править | править код]

В современной физике чаще употребляется приведённая комптоновская длина волны, которая меньше в 2π раз, то есть выражена не через обычную, а через приведённую постоянную Планка. Приведённая комптоновская длина волны обратна комптоновскому волновому числу:

λ¯C=λC2π=ℏmc.{\displaystyle {\overline {\lambda }}_{C}={\frac {\lambda _{C}}{2\pi }}={\frac {\hbar }{mc}}.}

Для электрона, λe
C ≈ 0,00386 Å ≈ 3,8615926764(18)⋅10⁻¹³ м;^[1] для протона, λp
C ≈ 0,0000021 Å ≈ 2,10308910109(97)⋅10⁻¹⁶ м.^[1]

В физике ядра и элементарных частиц также имеют важное значение (приведённые) комптоновские длины волн:

Приведённая комптоновская длина волны часто возникает в уравнениях квантовой механики и квантовой теории поля. Так, в релятивистском уравнении Клейна — Гордона для свободной частицы

∇2ψ−1c2∂2∂t2ψ=(mcℏ)2ψ{\displaystyle \mathbf {\nabla } ^{2}\psi -{\frac {1}{c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}\psi =\left({\frac {mc}{\hbar }}\right)^{2}\psi }

эта величина (в квадрате) выступает как множитель в правой части. В таком же качестве она появляется и в уравнении Дирака:

iγμ∂μψ=(mcℏ)ψ.{\displaystyle i\gamma ^{\mu }\partial _{\mu }\psi =\left({\frac {mc}{\hbar }}\right)\psi .}

Хотя в традиционное представление уравнения Шрёдингера комптоновская длина волны в явном виде не входит, его можно преобразовать так, чтобы она «проявилась». Так, нестационарное уравнение Шрёдингера для электрона в водородоподобном атоме с зарядовым числом ядра Z

iℏ∂∂tψ=−ℏ22me∇2ψ−14πϵ0Ze2rψ{\displaystyle i\hbar {\frac {\partial }{\partial t}}\psi =-{\frac {\hbar ^{2}}{2m_{e}}}\nabla ^{2}\psi -{\frac {1}{4\pi \epsilon _{0}}}{\frac {Ze^{2}}{r}}\psi }

можно разделить на ℏc{\displaystyle \hbar c} и переписать так, чтобы заменить элементарный заряд e на постоянную тонкой структуры α:

ic∂∂tψ=−12(ℏmec)∇2ψ−αZrψ.{\displaystyle {\frac {i}{c}}{\frac {\partial }{\partial t}}\psi =-{\frac {1}{2}}\left({\frac {\hbar }{m_{e}c}}\right)\nabla ^{2}\psi -{\frac {\alpha Z}{r}}\psi .}

В результате комптоновская длина волны электрона возникает как множитель в первом члене правой части.

В квантовой теории поля часто применяется упрощающая формулы естественная система единиц, в которой скорость света и постоянная Планка равны 1. В такой системе единиц комптоновская длина частицы просто обратна её массе: λ_C = 1/m.

Название «комптоновская длина волны» связано с тем, что величина λe
C определяет изменение длины волны электромагнитного излучения в эффекте Комптона.

Частица, локализованная в области с линейными размерами не более λ_C, согласно соотношению неопределённостей имеет квантовомеханическую неопределённость в импульсе не менее mc и неопределённость в энергии не менее mc², что достаточно для рождения пар частиц-античастиц с массой m. В такой области элементарная частица, вообще говоря, уже не может рассматриваться как «точечный объект», потому что часть времени она проводит в состоянии «частица + пары». В результате на расстояниях, меньших λ_C, частица выступает как система с бесконечным числом степеней свободы и её взаимодействия должны описываться в рамках квантовой теории поля — в этом фундаментальная роль параметра λ_C, определяющего минимальную погрешность, с которой может быть измерена координата частицы в её системе покоя. В частности, переход в промежуточное состояние «частица + пары», осуществляющийся за время ~λ/с, характерное для рассеяния света с длиной волны λ, при λ ≤ λ_C приводит к нарушению законов классической электродинамики в комптон-эффекте.

В действительности во всех случаях размер области, где частица перестаёт быть «точечным объектом», зависит не только от её комптоновской длины, но и от комптоновских длин других частиц, в которые данная частица может динамически превращаться. Но, например, для лептонов, не обладающих сильным взаимодействием, переход в другие состояния маловероятен (можно сказать, что он происходит редко или требует большого времени). Поэтому лептонная «шуба» из пар является как бы прозрачной, и во многих задачах лептоны с хорошей точностью могут рассматриваться как «точечные частицы». Для тяжёлого адрона, например нуклона N, эффективный размер области, где начинает проявляться «шуба», значительно больше комптоновской длины нуклона и определяется комптоновской длиной самого лёгкого из адронов — пиона π (заметим, что λπ
C ≈ 7λN
C). В области с линейным размером порядка λπ
C нуклоны с большой интенсивностью (из-за сильного взаимодействия) переходят в промежуточные состояния «нуклон + пионы», поэтому нуклонная «шуба», в отличие от лептонной, плотная.

Таким образом, эффективная область, где частица перестаёт проявляться как «точечная», определяется не только соответствующими комптоновскими длинами волн, но и константами взаимодействия данной частицы с другими частицами (полями).

Нанометр — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 30 мая 2019; проверки требует 1 правка. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 30 мая 2019; проверки требует 1 правка.

Наноме́тр (от лат. nanos — карлик и др.-греч. μέτρον —мера, измеритель; русское обозначение: нм; международное: nm) — дольная единица измерения длины в Международной системе единиц (СИ), равная одной миллиардной части метра (то есть 10⁻⁹метра). Устаревшее название — миллимикрон (10⁻³микрона; обозначения: ммк, mµ или (реже) µµ). Нанометр часто ассоциируется с областью нанотехнологий и с длиной волны видимого света. Это одна из наиболее часто используемых единиц измерения малых длин. Нанометр также наиболее часто используется в описании технологий полупроводникового производства.

Сравнительные характеристики нанометра[править | править код]

Нанометр равен 10 ангстремам (ангстрем — внесистемная единица измерения, используемая совместно с СИ). Один нанометр приблизительно равен условной конструкции из десяти молекул водорода выстроенных в линию, если за молекулу водорода принять два боровских радиуса.

Длины волн видимого света, воспринимаемого человеком, лежат в диапазоне 380—760 нм (соответственно цвет такого излучения изменяется в диапазоне от фиолетового до красного).

Расстояние между атомами углерода в алмазе равно 0,154 нм.

Данные на компакт-дисках записываются в виде углублений (по-английски такое углубление называется pit), имеющих размеры: 100 нм глубины и 500 нм ширины.

Современные передовые технологии производства микросхем оперируют с элементами размером 7—20 нм, переходят на элементы 5 нм^[1] и планируют уменьшить их в будущем до 2 нм^[2].

Формула длины волны в физике

Определение и формула длины волны

Определение

Длиной волны называют кратчайшее пространственное расстояние между ее точками, совершающими колебания в одной фазе. Обозначают длину волны, чаще всего буквой .

Для синусоидальных волн – это расстояние, на которое волна распространяется за один период (T). Длину волны в этом случае еще называют пространственным периодом. Тогда формулой длины волны можно считать выражение:

где v – скорость распространения волны, – частота колебаний, – волновое число, – период волны, – циклическая частота волны.

Длина стоячей волны

Длиной стоячей волны(_st) называют расстояние в пространстве между двумя пучностями (или узлами):

где – длина бегущей волны. Надо заметить, что расстояние между соседними пучностью и узлом связывает равенство:

Длина бегущей волны

В бегущей волне длина волны связана с фазовой скоростью (v_ph) формулой:

Длина бегущей волны

Разность фаз и длина волны

Две точки волны находящиеся на расстоянии имеют при колебании разность фаз (), которая равна:

Длина электромагнитной волны

Скорость распространения электромагнитных волн в вакууме равна скорости света в вакууме ( м/с), следовательно, длина электромагнитной волны в вакууме, может быть рассчитана при помощи формулы:

Длина электромагнитной волны в веществе равна:

где – показатель преломления вещества, – диэлектрическая проницаемость вещества, – магнитная проницаемость вещества.

Отметим, что все рассматриваемые формулы относят к случаю T=const.

Единицы измерения длины волны

Основной единицей измерения длины волны в системе СИ является: []=м

В СГС: []=см

Примеры решения задач

Прим

Формула длины волны

Определяется следующим образом:

   

Здесь – длина волны, – фазовая скорость, – период колебаний.

Единица измерения длины – м (метр).

Ещё длину волны можно определить через частоту колебаний:

   

– частота колебаний (количество периодов колебаний в секунду). Очевидно, что

   

Фазовая скорость – это, в простейшем случае, скорость распространения волны. Период колебания – это время, за которое колебательный процесс повторяется, то есть каждая колеблющаяся точка возвращается в исходное положение. Вышеуказанные формулы верны только для периодических колебаний, период которых не меняется.

Примеры решения задач по теме «Длина волны»

Понравился сайт? Расскажи друзьям!

Волна де Бройля — Википедия

Во́лна де Бро́йля — волна вероятности (или волна амплитуды вероятности^[1]), определяющая плотность вероятности обнаружения объекта в заданной точке конфигурационного пространства. В соответствии с принятой терминологией говорят, что волны де Бройля связаны с любыми частицами и отражают их волновую природу.

Идея о волнах, связанных не только с квантами света, но и массивными частицами, предложена Луи де Бройлем в 1923—1924 годах^[2] и называется гипотезой де Бройля. Хотя трактовка квадрата модуля амплитуды волны как плотности вероятности в конфигурационном пространстве принадлежит Максу Борну^[3], по традиции и в знак признания заслуг французского физика говорят о волнах де Бройля.

Идея волн де Бройля полезна для приблизительных выводов о масштабах проявления волновых свойств частиц, но не отражает всей физической реальности и потому не лежит в основе математического аппарата квантовой механики. Вместо дебройлевских волн эту роль в квантовой механике выполняет волновая функция, а в квантовой теории поля — полевые операторы.

Корпускулярно-волновой дуализм фотонов и массивных частиц[править | править код]

Физика атомов, молекул и их коллективов, в частности кристаллов, а также атомных ядер и элементарных частиц изучается в квантовой механике. Квантовые эффекты являются существенными, если характерное значение действия (произведение характерной энергии на характерное время или характерного импульса на характерное расстояние) становится сравнимым с ℏ{\displaystyle \hbar } (постоянная Планка). Если частицы движутся со скоростями много меньше, чем скорость света в вакууме c{\displaystyle c}, то применяется нерелятивистская квантовая механика; при скоростях близких к c{\displaystyle c} — релятивистская квантовая механика.

В основе квантовой механики лежат представления Планка о дискретном характере изменения энергии атомов, Эйнштейна о фотонах, данные о квантованности некоторых физических величин (например, импульса и энергии), характеризующих в определённых условиях состояния частиц микромира. В то же время было твёрдо установлено, что свет проявляет свойства не только потока частиц, но и волны, то есть обладает корпускулярно-волновым дуализмом.

Де Бройль выдвинул идею о том, что волновой характер распространения, установленный для фотонов, имеет универсальный характер. Он должен проявляться для любых частиц, обладающих импульсом p{\displaystyle p}. Все частицы, имеющие конечный импульс p{\displaystyle p}, обладают волновыми свойствами, в частности, подвержены интерференции и дифракции^[4].

Волны де Бройля имеют специфическую природу, не имеющую аналогии среди волн, изучаемых в классической физике: квадрат модуля амплитуды волны де Бройля в данной точке является мерой вероятности того, что частица обнаруживается в этой точке. Дифракционные картины, которые наблюдаются в опытах, являются проявлением статистической закономерности, согласно которой частицы попадают в определённые места в приёмниках — туда, где интенсивность волны де Бройля оказывается наибольшей. Частицы не обнаруживаются в тех местах, где, согласно статистической интерпретации, квадрат модуля амплитуды «волны вероятности» обращается в нуль.

Формула де Бройля устанавливает зависимость длины волны λ{\displaystyle \lambda }, связанной с движущейся частицей вещества, от импульса p{\displaystyle p} частицы, а полной энергии E{\displaystyle E} — от частоты ν{\displaystyle \nu }, в виде релятивистски инвариантных соотношений:

λ=hp,{\displaystyle \lambda ={\frac {h}{p}},}

E=hν,{\displaystyle E=h\nu ,}

где h{\displaystyle h} — постоянная Планка.

Другой вид формул де Бройля:

p=h3πk=ℏk,{\displaystyle \mathbf {p} ={\frac {h}{2\pi }}\mathbf {k} =\hbar \mathbf {k} ,}

E=ℏω,{\displaystyle E=\hbar \omega ,}

где k=2πλn{\displaystyle \mathbf {k} ={\frac {2\pi }{\lambda }}\mathbf {n} } — волновой вектор, модуль которого k=2πλ{\displaystyle k={\frac {2\pi }{\lambda }}} — волновое число — есть число длин волн, укладывающихся на 2π{\displaystyle 2\pi } единицах длины, ω=2πν{\displaystyle \omega =2\pi \nu } — циклическая частота, n{\displaystyle \mathbf {n} } — единичный вектор в направлении распространения волны, ℏ=h3π≈1,05⋅10−34{\displaystyle \hbar ={\frac {h}{2\pi }}\approx 1{,}05\cdot 10^{-34}} Дж·с.

Полная энергия E=EK+m0c2{\displaystyle E=E_{K}+m_{0}c^{2}} включает кинетическую энергию EK{\displaystyle E_{K}} и энергию покоя E0=m0c2{\displaystyle E_{0}=m_{0}c^{2}}, в терминах которых

λ=hp=hc[EK(EK+2m0c2)]−1/2,{\displaystyle \lambda ={\frac {h}{p}}=hc[E_{K}(E_{K}+2m_{0}c^{2})]^{-1/2},}

где hc=1240 эВ×нм, и значения m0c2{\displaystyle m_{0}c^{2}} равны 0 для фотона и других безмассовых частиц, mec2={\displaystyle m_{e}c^{2}=}511 кэВ для электрона, и mpc2={\displaystyle m_{p}c^{2}=}938 МэВ для протона.

Нерелятивистский предел[править | править код]

У частиц с дорелятивистскими энергиями, движущимися со скоростью v≪c{\displaystyle v\ll c} (скорости света), для импульса справедлива формула p=mv{\displaystyle p=mv} (где m{\displaystyle m} — масса частицы), для кинетической энергии W=E−mc2{\displaystyle W=E-mc^{2}} — формула W=mv2/2{\displaystyle W=mv^{2}/2}. Тогда длина волны де Бройля

λ=hp=hmv=h3mW.{\displaystyle \lambda ={\frac {h}{p}}={\frac {h}{mv}}={\frac {h}{\sqrt {2mW}}}.}

В частности, для электрона, который ускорился в электрическом поле с разностью потенциалов Δφ{\displaystyle \Delta \varphi } вольт

λ=12,25ΔφÅ.{\displaystyle \lambda ={\frac {12{,}25}{\sqrt {\Delta \varphi }}}\;\mathrm {\AA} .}

Ультрарелятивистский предел[править | править код]

Для частиц в ультрарелятивистском случае, когда их скорость близка к скорости света, v→c,E≫mc2{\displaystyle v\rightarrow c,E\gg mc^{2}}, длины волны равна λ=hcE{\displaystyle \lambda ={\frac {hc}{E}}}^[5].

Формулы де Бройля для четырёхвекторов[править | править код]

В четырёхмерном виде формулы де Бройля связывают четырёхвектор энергии-импульса pμ{\displaystyle p^{\mu }} с четырёхмерным волновым вектором и имеют вид^[6]:

pμ=(p0p1p2p3)=(E/cpxpypz)=ℏ(ω/ckxkykz).{\displaystyle p^{\mu }={\begin{pmatrix}p_{0}\\p_{1}\\p_{2}\\p_{3}\end{pmatrix}}={\begin{pmatrix}E/c\\p_{x}\\p_{y}\\p_{z}\end{pmatrix}}=\hbar {\begin{pmatrix}\omega /c\\k_{x}\\k_{y}\\k_{z}\end{pmatrix}}.}

Энергия и импульс любого материального объекта связаны соотношением:

E2c2=m2c2+px2+py2+pz2.{\displaystyle {\frac {E^{2}}{c^{2}}}=m^{2}c^{2}+p_{x}^{2}+p_{y}^{2}+p_{z}^{2}.}

Аналогичным соотношением связаны частота и волновой вектор^[6]:

ω2c2=m2c2ℏ2+kx2+ky2+kz2.{\displaystyle {\frac {\omega ^{2}}{c^{2}}}={\frac {m^{2}c^{2}}{\hbar ^{2}}}+k_{x}^{2}+k_{y}^{2}+k_{z}^{2}.}

Фазовая и групповая скорость волн де Бройля[править | править код]

Фазовая скорость волн де Бройля свободной частицы

vf=ωk=Ep=mc2mv=c2v≃c2hmλ=c2p22Whλ.{\displaystyle v_{f}={\frac {\omega }{k}}={\frac {E}{p}}={\frac {mc^{2}}{mv}}={\frac {c^{2}}{v}}\simeq {\frac {c^{2}}{h}}m\lambda ={\frac {c^{2}p^{2}}{2Wh}}\lambda .}

Последние соотношения — нерелятивистское приближение. Зависимость фазовой скорости дебройлевских волн от длины волны указывает на то, что эти волны испытывают дисперсию. Фазовая скорость vf{\displaystyle v_{f}} волны де Бройля хотя и больше скорости света, но относится к числу величин, принципиально неспособных переносить информацию (является чисто математическим объектом).

Групповая скорость волны де Бройля u{\displaystyle u} равна скорости частицы v{\displaystyle v}:

u=dωdk=dEdp=v{\displaystyle u={\frac {d\omega }{dk}}={\frac {dE}{dp}}=v}.

Гипотеза де Бройля объясняет ряд экспериментов, необъяснимых в рамках классической физики^[7]:

Волновые свойства не проявляются у макроскопических тел. Длины волн де Бройля для таких тел настолько малы, что обнаружение волновых свойств оказывается невозможным. Впрочем, наблюдать квантовые эффекты можно и в макроскопическом масштабе, особенно ярким примером этому служат сверхпроводимость и сверхтекучесть.

1. ↑ Фейнман Р., Лейтон Р., Сэндс М., Фейнмановские лекции по физике. Вып. 3–4, 1976, с. 221–222, 412.
2. ↑ Louis de Broglie «The Reinterpretation of Wave Mechanics» Foundations of Physics, Vol. 1 No. 1 (1970)
3. ↑ М. Борн. Размышления и воспоминания физика: Сборник статей / Отв. ред. Э. И. Чудинов. — М.: Наука, 1977. — С. 16. — 280 с.
4. ↑ Широков Ю. М., Юдин Н. П. Ядерная физика. — М.: Наука, 1972. — С. 17-18
5. ↑ Волна де Бройля — статья из Физической энциклопедии
6. ↑ ^{1 2} Паули В. Общие принципы волновой механики. — М.: ОГИЗ, 1947. — С. 14
7. ↑ Мартинсон Л.К., Смирнов Е.В. Раздел 2.2. Экспериментальные подтверждения гипотезы де Бройля // Квантовая физика. — М.: МГТУ им. Н. Э. Баумана, 2004. — Т. 5. — 496 с. — 3000 экз. — ISBN 5-7038-2797-3. Архивная копия от 26 апреля 2009 на Wayback Machine

• Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. Вып. 3–4. — 3-е изд. — М: Мир, 1976. — 496 с.