5.1. Напряжение, ток, сопротивление и мощность катушки индуктивности
5.1.1. Общие сведения
Когда по катушке индуктивности протекает переменный ток, в ней наводится встречная ЭДС самоиндукции:
При синусоидальном токе i = I m s i n ω t напряжение на катушке ul = -eL = ωLImcosωt опережает
ток на 90°. Соответственно, мгновенное значение тока переходит через ноль на четверть периода
позже, чем мгновенное значение напряжения (рис. 5.1.1). В этом рассуждении пренебрегается
активным сопротивлением катушки, т.е. катушка считается идеальной.
Рис. 5.1.1
Амплитуда синусоидального напряжения на катушке пропорциональна амплитуде тока: UCm = I
Также пропорциональны и действующие значения тока и напряжения.
Коэффициент пропорциональности ωL
называется
индуктивным
реактивным
сопротивлением катушки и обозначается XL. Таким образом, амплитуды и действующие
значения тока и напряжения на катушке индуктивности связаны выражением аналогичным закону Ома:
ILm или UL = XL •
Индуктивное сопротивление увеличивается с увеличением частоты.
Реактивному сопротивлению катушки присваивают знак + в отличие от ёмкостного реактивного сопротивления, которому приписывают знак -.
фазовый
сопротивления
активного
наличия
В реальной катушки из-за
энергию другим элементам цепи, являясь источником энергии. Величина QL
•
—
Мгновенная мощность, потребляемая идеальной катушкой, определяется как произведение напряжения и тока:
p = u · i
График изменения этой мощности можно построить, перемножая попарно ординаты графиков u(t) и i(t), взятые в один и тот же момент времени. Полученная таким образом кривая (рис.
без учёта активного сопротивления катушки представляет собой синусоиду двойной частоты с амплитудой:
QL= ULm·ILm/2 = UL·IL.
Когда р>0, катушка потребляет энергию, запасая ее в магнитном поле. Когда р<0, она отдает
является максимальной мощностью, потребляемой или отдаваемой катушкой, и называется индуктивной
реактивной мощностью.
Средняя (активная) мощность, потребляемая идеальной катушкой индуктивности, равна нулю.
сдвиг уменьшается, синусоида мгновенной мощности смещается вверх и среднее значение
мощности становится больше нуля.
5.1.2. Экспериментальная часть
Задание
Выведите кривые тока и напряжения катушки на экран осциллографа и определите фазовый сдвиг между синусоидами uL(t) и iL(t), постройте график изменения мощности, определите
реактивные сопротивления катушек различной индуктивности.
Порядок выполнения эксперимента
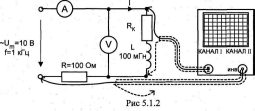
Соберите цепь согласно схеме (рис. 5.1.2), где RK
активное сопротивление катушки.
Включите регулируемый источник синусоидального напряжения и установите напряжение максимальной амплитуды с частотой 0,5 кГц. Напряжение с катушки подаётся на первый
канал осциллографа, а инвертированное напряжение с сопротивления, пропорциональное току — на второй.
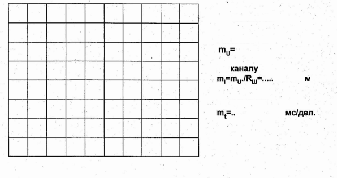



























































По времени: т4=..
По каналу
По каналу II: ти=
Масштабы
»
*
I: т,=ти./Кш=…..
.
•
(не
•
*
1
г1
•
Установите параметры развёртки и усиления осциллографа так, чтобы на экране было изображение примерно одного периода напряжения и тока. Примечание: для измерения
разности фаз необходимо использовать режим изображения сигналов двух каналов осциллографа.
прерывистого
поочерёдного!)
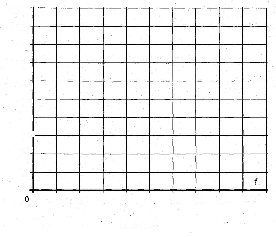
Перенесите кривые на график (рис. 5.1,3) и определите период и фазовый сдвиг между напряжением uL(t) и током iL(t) в катушке.
1 У. I
*
В/дел.
»
м
А/дел.
мс/дел
Рис. 5.1.3
Период:
T = Cmt ………………………. мс,
г д е С = ………………… дел. — период в делениях сетки осциллографа,
m t =. ……………… мс/дел. — чувствительность осциллограф по каналу развёртки. Фазовый сдвиг:
= 360·D·/C = …………………. град.
где D = ………………… дел. — сдвиг тока и напряжения в делениях сетки осциллографа,
С = ………………… дел. — период в делениях сетки осциллографа.
Примечание: фазовый сдвиг меньше 90° из-за влияния активного сопротивления катушки.
Постройте график изменения мощности, потребляемой катушкой, и определите по нему реактивную мощность как амплитуду переменной составляющей мгновенной мощности:
QL = ………………………………. вар.
Измерьте действующие значения тока и напряжения на конденсаторе мультиметра-ми и определите реактивную мощность как
QL = U L · IL= …………………………… вар.
Сравните результаты.

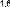

1,4 1,
6 кГ
•
•
/
I
и по
•
f
(
f
)
f= 0,6 кГц ω= . | f= 1,0 кГц ω= . | f= 1,4 кГц ω= . | f= 1,8 кГц ω= . | |||||
100 мГн | U, В | |||||||
I, мА | ||||||||
U/I, кОм | ||||||||
ωL, кОм | ||||||||
40 мГн | U, В | |||||||
I, мА | ||||||||
U/I, кОм | ||||||||
ωL, кОм | ||||||||
10 м Г н | U, В | |||||||
I, мА | ||||||||
U/I, кОм | ||||||||
ωL, кОм | ||||||||

кО
м
0,9
0,8
0,7
0,6
0,5
0,4

XI
.
•
•
— .
• ‘
• . .
—
•
•
• —
—
•
•
—
•
.-
—
•
—
•
0,3 4
0,2
0,1
0,2
0,8

ц
Измерьте действующие значения тока и напряжения на катушке мультиметрами при различных значениях индуктивности и частоты, указанных в табл. 5.1.1.
Рассчитайте индуктивные сопротивления, по результатам этих измерений как U
формуле: ХC =ωL. Сравните результаты.
На рис. 5.1.4 постройте расчётные и экспериментальные графики ХL = индуктивности. Объясните расхождение.
для каждой
Таблица 5.1.1
0,4 0,6
1,0 1,2
Рис. 5.1.4
Э
Э
Э
•
•
Э
L=
U
L/I
L.
•
1/с.
•
С ,
Э
Сначала рассмотрим идеальную индуктивную катушку, активное сопротивление которой равно нулю. Пусть по идеальной катушке с индуктивностью L протекает синусоидальный ток 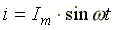 . Этот ток создает в индуктивной катушке переменное магнитное поле, изменение которого вызывает в катушке ЭДС самоиндукции
. Этот ток создает в индуктивной катушке переменное магнитное поле, изменение которого вызывает в катушке ЭДС самоиндукции
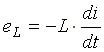 (6.9)
(6.9)
Эта ЭДС уравновешивается напряжением, подключенным к катушке: u = eL = 0.
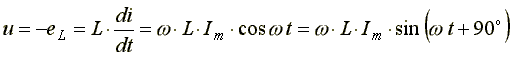 (6.10)
(6.10)
Таким образом, ток в индуктивности отстает по фазе от напряжения на 90o из-за явления самоиндукции.
Уравнение вида (6.10) для реальной катушки, имеющей активное сопротивление R, имеет следующий вид:
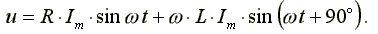 (6.11)
(6.11)
Анализ выражения (6.11) показывает, что ЭДС самоиндукции оказывает препятствие (сопротивление) протеканию переменного тока, из-за чего ток в реальной индуктивной катушке отстает по фазе от напряжения на некоторый угол φ (0o< φ < 90o), величина которого зависит от соотношения R и L. Выражение (6.11) в комплексной форме записи имеет вид:
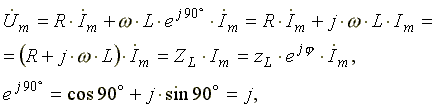 (6.12)
(6.12)
где ZL — полное комплексное сопротивление индуктивной катушки 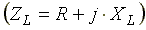 ;
;
ZL — модуль комплексного сопротивления; 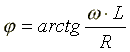 — начальная фаза комплексного сопротивления;
— начальная фаза комплексного сопротивления; 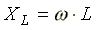 — индуктивное сопротивление (фиктивная величина, характеризующая реакцию электрической цепи на переменное магнитное поле).
— индуктивное сопротивление (фиктивная величина, характеризующая реакцию электрической цепи на переменное магнитное поле).
Полное сопротивление индуктивной катушки или модуль комплексного сопротивления
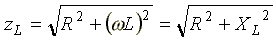 .
.
Комплексному уравнению (6.12) соответствует векторная диаграмма (рис.6.5).
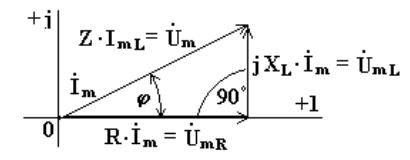
Рис. 6.5
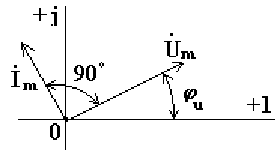
Из анализа диаграммы видно, что вектор напряжения на индуктивности опережает вектор тока на 90o.
В цепи переменного тока напряжения на участках цепи складываются не арифметически, а геометрически.
Если мы поделим стороны треугольника напряжений на величину тока Im, то перейдем к подобному треугольнику сопротивлений (рис. 6.6).
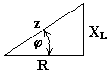 Из треугольника сопротивлений получим несколько формул:
Из треугольника сопротивлений получим несколько формул: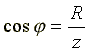 ;
; 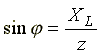 ;
;
Рис. 6.6
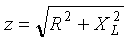 ;
;
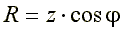 ;
; 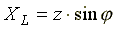 .
.
Идеальная индуктивность при синусоидальном токе
/Под идеальной будем понимать катушку, активное сопротивление которой равно нулю (Rк=0). Пусть под действием приложенного напряжения по катушке течет синусоидальный ток i=ImSinωt (рис.7.6,а). Этот ток создает переменное электромагнитное поле, изменение которого индуцирует в катушке ЭДС самоиндукции (3) В любой момент времени, согласно второму закону Кирхгофа, эта ЭДС должна компенсировать приложенное напряжение, т.е.
где Um=ωLIm откуда Im=Um/ωL или I=U/ωL
Рисунок 2.6 – Идеальная индуктивность в цепи синусоидального тока: а) цепь с идеальной индуктивностью; б) временные диаграммы тока
Величина ωL=XL имеет размерность [Ом] и называется индуктивным сопротивлением катушки.
Выражение (2.12) показывает, что для поддержания в цепи синусоидального тока, напряжение в цепи должно быть синусоидальным, но по фазе опережать ток на угол π/2=900.
Временные диаграммы тока, напряжения и мгновенной мощности представлены на рисунке 2.6,б.
Мгновенная мощность рассматриваемой цепи:
Из полученного выражения видно, что мгновенная мощность рассматриваемой цепи изменяется по синусоидальному закону, но с двойной частотой. В течение первой четверти периода, когда ток в цепи нарастает от нуля до максимального значения, направления тока и ЭДС самоиндукции противоположны, а направления тока и напряжения совпадают. Мгновенная мощность положительна. Это означает, что в этом интервале времени катушка потребляет энергию от источника и запасает ее в своем магнитном поле (WM=Li2/2).
Во второй четверти периода ток убывает от максимального значения до нуля. ЭДС самоиндукции и ток совпадают по направлению. Напряжение и ток направлены противоположно и мгновенная мощность отрицательна. Это означает, что в этом интервале времени катушка становится источником электрической энергии и отдает в цепь запасенную в магнитном поле энергию. Так как активное сопротивление катушки равно нулю (по условию), то есть, активных потерь в цепи нет, то вся запасенная энергия полностью возвращается. В третьей и четвертой четвертях периода процессы повторяются. Катушка вновь запасает энергию и возвращает ее источнику.
Таким образом, в цепи с идеальной катушкой индуктивности происходит периодический обмен энергией между катушкой и источником. Средняя (активная) мощность оказывается равной нулю. Источник не расходует энергии, т.к. активные потери отсутствуют.
Для количественной оценки интенсивности обмена электрической энергией между источником и катушкой вводят понятие реактивная мощность. Она равна амплитудному значению мгновенной мощности:
Единицей измерения реактивной мощности является Вольт Ампер реактивный [ВАр].
/Другие разделы главы 2:
Сначала
рассмотрим идеальную индуктивную
катушку, активное сопротивление которой
равно нулю. Пусть по идеальной катушке
с индуктивностью L протекает синусоидальный
ток 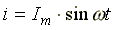 .
Этот ток создает в индуктивной катушке
переменное магнитное поле, изменение
которого вызывает в катушке ЭДС
самоиндукции
.
Этот ток создает в индуктивной катушке
переменное магнитное поле, изменение
которого вызывает в катушке ЭДС
самоиндукции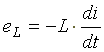
Эта ЭДС уравновешивается напряжением, подключенным к катушке: u = eL =0.
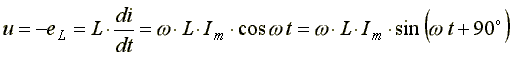
Таким
образом, ток в индуктивности отстает
по фазе от напряжения на 90o из-за явления самоиндукции.
Уравнение вида для реальной катушки,
имеющей активное сопротивление R, имеет
следующий вид: 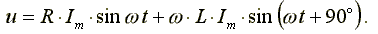
Анализ выражения показывает, что ЭДС самоиндукции оказывает препятствие (сопротивление) протеканию переменного тока, из-за чего ток в реальной индуктивной катушке отстает по фазе от напряжения на некоторый угол φ (0o < φ < 90o), величина которого зависит от соотношения R и L. Выражение в комплексной форме записи имеет вид:
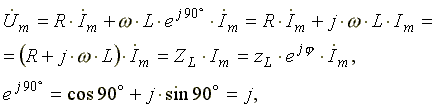
где ZL — полное комплексное сопротивление
индуктивной катушки 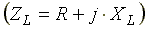 ;
ZL — модуль комплексного сопротивления;
;
ZL — модуль комплексного сопротивления; 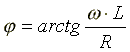 — начальная фаза комплексного сопротивления;
— начальная фаза комплексного сопротивления;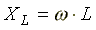 — индуктивное сопротивление (фиктивная
величина, характеризующая реакцию
электрической цепи на переменное
магнитное поле).
Полное
сопротивление индуктивной катушки или
модуль комплексного сопротивления
— индуктивное сопротивление (фиктивная
величина, характеризующая реакцию
электрической цепи на переменное
магнитное поле).
Полное
сопротивление индуктивной катушки или
модуль комплексного сопротивления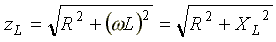 .
.
Комплексному
уравнению соответствует векторная
диаграмма . 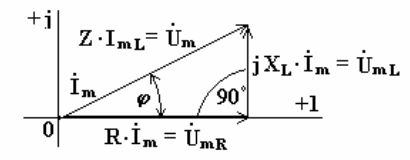
Из анализа диаграммы видно, что вектор напряжения на индуктивности опережает вектор тока на 90o. В цепи переменного тока напряжения на участках цепи складываются не арифметически, а геометрически. Если мы поделим стороны треугольника напряжений на величину тока Im, то перейдем к подобному треугольнику сопротивлений.
Из
треугольника сопротивлений получим
несколько формул: 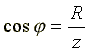
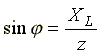
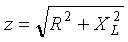 ;
;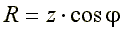
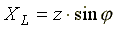
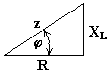
19 Емкость в цепи синусоидального тока
Если к конденсатору емкостью C подключить синусоидальное напряжение, то в цепи протекает синусоидальный ток
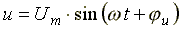
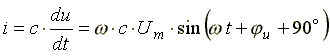
Из анализа выражений следует, что ток опережает напряжение по фазе на 90o.
Выражение в комплексной форме записи имеет вид:
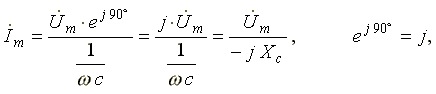
где 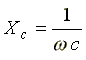 —
емкостное сопротивление, фиктивная
расчетная величина, имеющая размерность
сопротивления.
—
емкостное сопротивление, фиктивная
расчетная величина, имеющая размерность
сопротивления.
Если
комплексное сопротивление индуктивности
положительно
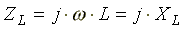 ,
то комплексное сопротивление емкости
отрицательно
,
то комплексное сопротивление емкости
отрицательно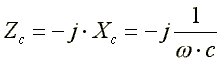 .Вектор
тока опережает вектор напряжения на
90o.
.Вектор
тока опережает вектор напряжения на
90o.
20 Последовательно соединенные реальная индуктивная катушка и конденсатор в цепи синусоидального тока
Катушка
с активным сопротивлением R
и индуктивностью
L и конденсатор
емкостью С
включены последовательно. В схеме
протекает синусоидальный ток 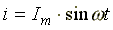 .
.
Определим напряжение на входе схемы. В соответствии со вторым законом Кирхгофа,
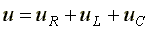
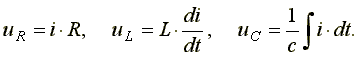
Подставим эти формулы в уравнение. Получим:
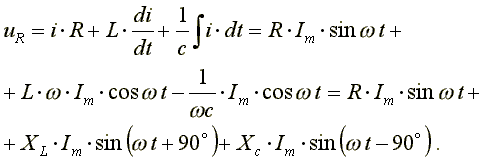
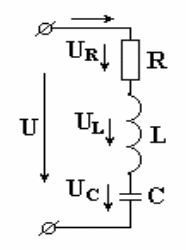
Из выражения видно: напряжение в активном сопротивлении совпадает по фазе с током, напряжение на индуктивности опережает по фазе ток на 90o, напряжение по емкости отстает по фазе от тока на 90o. Запишем уравнение в комплексной форме:
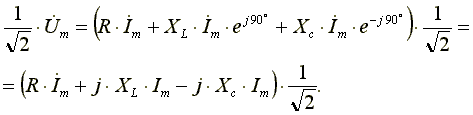
Поделим левую и правую части уравнения на √2. Получим уравнение для комплексов действующих значений токов и напряжений
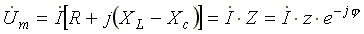
где 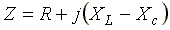 —
комплексное сопротивление цепи;
—
комплексное сопротивление цепи;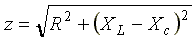 —
модуль комплексного сопротивления, или
полное сопротивление цепи;
—
модуль комплексного сопротивления, или
полное сопротивление цепи;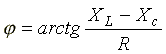 — начальная фаза комплексного сопротивления.
— начальная фаза комплексного сопротивления.
При построении векторных диаграмм цепи рассмотрим три случая.
XL > XC, цепь носит индуктивный характер. Векторы напряжений на индуктивности и емкости направлены в противоположные стороны, частично компенсируют друг друга. Вектор напряжения на входе схемы опережает вектор тока.
Индуктивное сопротивление меньше емкостного. Вектор напряжения на входе схемы отстает от вектора тока. Цепь носит емкостный характер .
Индуктивное и емкостное сопротивления одинаковы. Напряжения на индуктивности и емкости полностью компенсируют друг друга. Ток в цепи совпадает по фазе с входным напряжением. В электрической цепи наступает режим резонансного напряжения.
Ток в резонансном режиме достигает максимума, так как полное сопротивление (z) цепи имеет минимальное значение.
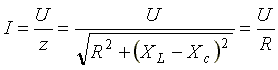
Условие
возникновения резонанса: 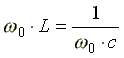 ,
отсюда резонансная частота равна
,
отсюда резонансная частота равна 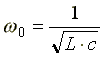 .
.
Из формулы следует, что режима резонанса можно добиться следующими способами:
изменением частоты;
изменением индуктивности;
изменением емкости.
В резонансном режиме входное напряжение равно падению напряжения в активном сопротивлении. На индуктивности и емкости схемы могут возникнуть напряжения, во много раз превышающие напряжение на входе цепи. Это объясняется тем, что каждое напряжение равно произведению тока I0 (а он наибольший), на соответствующее индуктивное или емкостное сопротивление (а они могут быть большими).
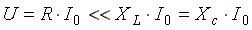 .
.
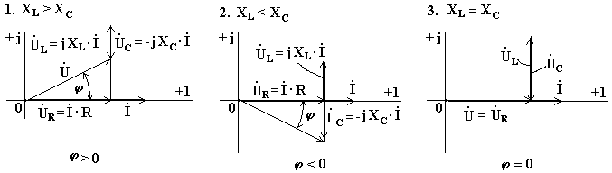
Сначала
рассмотрим идеальную индуктивную
катушку, активное сопротивление которой
равно нулю. Пусть по идеальной катушке
с индуктивностью L протекает синусоидальный
ток 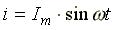 .
Этот ток создает в индуктивной катушке
переменное магнитное поле, изменение
которого вызывает в катушке ЭДС
самоиндукции
.
Этот ток создает в индуктивной катушке
переменное магнитное поле, изменение
которого вызывает в катушке ЭДС
самоиндукции
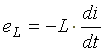 (6.9)
(6.9)
Эта ЭДС уравновешивается напряжением, подключенным к катушке: u = eL = 0.
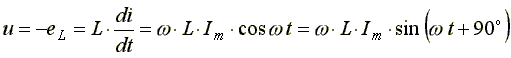 (6.10)
(6.10)
Таким образом, ток в индуктивности отстает по фазе от напряжения на 90o из-за явления самоиндукции. Уравнение вида (6.10) для реальной катушки, имеющей активное сопротивление R, имеет следующий вид:
(6.11)
Анализ выражения (6.11) показывает, что ЭДС самоиндукции оказывает препятствие (сопротивление) протеканию переменного тока, из-за чего ток в реальной индуктивной катушке отстает по фазе от напряжения на некоторый угол φ (0o< φ < 90o), величина которого зависит от соотношения R и L. Выражение (6.11) в комплексной форме записи имеет вид:
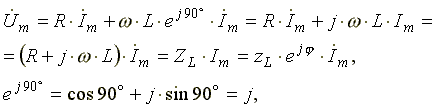 (6.12)
(6.12)
где
ZL — полное комплексное сопротивление
индуктивной катушки 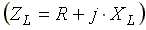 ; ZL — модуль комплексного сопротивления;
; ZL — модуль комплексного сопротивления; 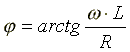 —
начальная фаза комплексного сопротивления;
—
начальная фаза комплексного сопротивления;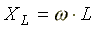 —
индуктивное сопротивление (фиктивная
величина, характеризующая реакцию
электрической цепи на переменное
магнитное поле).
Полное сопротивление
индуктивной катушки или модуль
комплексного сопротивления
—
индуктивное сопротивление (фиктивная
величина, характеризующая реакцию
электрической цепи на переменное
магнитное поле).
Полное сопротивление
индуктивной катушки или модуль
комплексного сопротивления
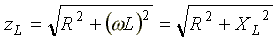 .
.
Комплексному уравнению (6.12) соответствует векторная диаграмма (рис.6.5).
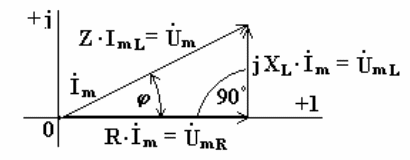 Рис.
6.5
Рис.
6.5
Из анализа диаграммы видно, что вектор напряжения на индуктивности опережает вектор тока на 90o. В цепи переменного тока напряжения на участках цепи складываются не арифметически, а геометрически. Если мы поделим стороны треугольника напряжений на величину тока Im, то перейдем к подобному треугольнику сопротивлений (рис. 6.6).
И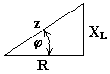 з
треугольника сопротивлений получим
несколько формул:
з
треугольника сопротивлений получим
несколько формул: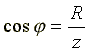 ;
;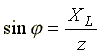 ;
Рис.
6.6
;
Рис.
6.6
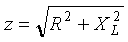 ;
;
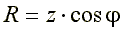 ;
; 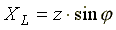 .
.
6.6. Емкость в цепи синусоидального тока
Если к конденсатору емкостью C подключить синусоидальное напряжение, то в цепи протекает синусоидальный ток
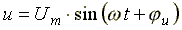 ;
;
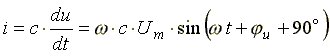 .
(6.13)
.
(6.13)
Из анализа выражений 6.13 следует, что ток опережает напряжение по фазе на 90o.
Выражение (6.13) в комплексной форме записи имеет вид:
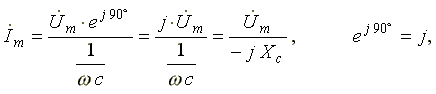 ,
(6.14)
,
(6.14)
где 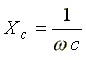 —
емкостное сопротивление, фиктивная
расчетная величина, имеющая размерность
сопротивления.
—
емкостное сопротивление, фиктивная
расчетная величина, имеющая размерность
сопротивления.
Если
комплексное сопротивление индуктивности
положительно 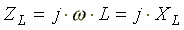 ,
то комплексное сопротивление емкости
отрицательно
,
то комплексное сопротивление емкости
отрицательно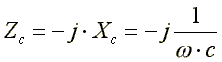 .
.
На рис. 6.7 изображена векторная диаграмма цепи с емкостью. Вектор тока опережает вектор напряжения на 90o.
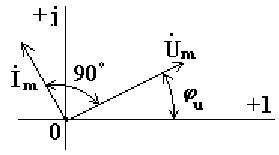 Рис.
6.7
Рис.
6.7
6.7. Последовательно соединенные реальная индуктивная катушка и конденсатор в цепи синусоидального тока
Катушка с активным сопротивлением R и индуктивностью L и конденсатор емкостью С включены последовательно (рис.6.8). В схеме протекает синусоидальный ток
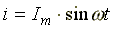 .
.
Определим напряжение на входе схемы. В соответствии со вторым законом Кирхгофа,
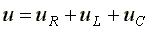
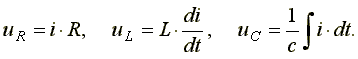 (6.15)
(6.15)
Подставим эти формулы в уравнение (6.15). Получим:
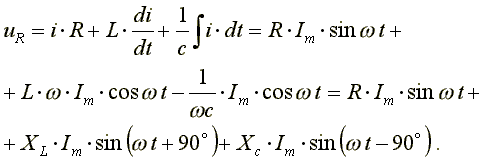 (6.16)
(6.16)
И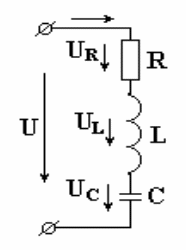 з
выражения (6.16) видно: напряжение в
активном сопротивлении совпадает по
фазе с током, напряжение на индуктивности
опережает по фазе ток на 90o,
напряжение по емкости отстает по фазе
от тока на 90o. Запишем уравнение (6.16) в комплексной
форме:
з
выражения (6.16) видно: напряжение в
активном сопротивлении совпадает по
фазе с током, напряжение на индуктивности
опережает по фазе ток на 90o,
напряжение по емкости отстает по фазе
от тока на 90o. Запишем уравнение (6.16) в комплексной
форме:
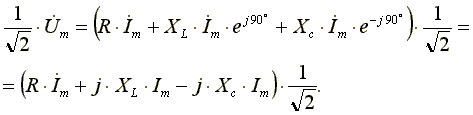 (6.17)
(6.17)
Рис. 6.8
Поделим левую и правую части уравнения (6.17) на √2. Получим уравнение для комплексов действующих значений токов и напряжений
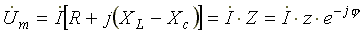 ,
(6.18)
,
(6.18)
где 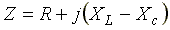 —
комплексное сопротивление цепи;
—
комплексное сопротивление цепи;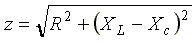 —
модуль комплексного сопротивления, или
полное сопротивление цепи;
—
модуль комплексного сопротивления, или
полное сопротивление цепи;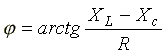 —
начальная фаза комплексного сопротивления.
—
начальная фаза комплексного сопротивления.
При построении векторных диаграмм цепи рассмотрим три случая.
XL > XC, цепь носит индуктивный характер. Векторы напряжений на индуктивности и емкости направлены в противоположные стороны, частично компенсируют друг друга. Вектор напряжения на входе схемы опережает вектор тока (рис.6.9).
Индуктивное сопротивление меньше емкостного. Вектор напряжения на входе схемы отстает от вектора тока. Цепь носит емкостный характер (рис.6.10).
Индуктивное и емкостное сопротивления одинаковы. Напряжения на индуктивности и емкости полностью компенсируют друг друга. Ток в цепи совпадает по фазе с входным напряжением. В электрической цепи наступает режим резонансного напряжения (рис.6.11).
Ток в резонансном режиме достигает максимума, так как полное сопротивление (z) цепи имеет минимальное значение.
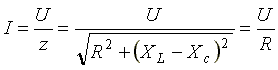
Условие
возникновения резонанса: 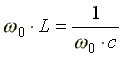 ,
отсюда резонансная частота равна
,
отсюда резонансная частота равна
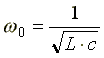 .
.
Из формулы следует, что режима резонанса можно добиться следующими способами:
изменением частоты;
изменением индуктивности;
изменением емкости.
В резонансном режиме входное напряжение равно падению напряжения в активном сопротивлении. На индуктивности и емкости схемы могут возникнуть напряжения, во много раз превышающие напряжение на входе цепи. Это объясняется тем, что каждое напряжение равно произведению тока I0 (а он наибольший), на соответствующее индуктивное или емкостное сопротивление (а они могут быть большими).
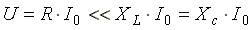 .
.
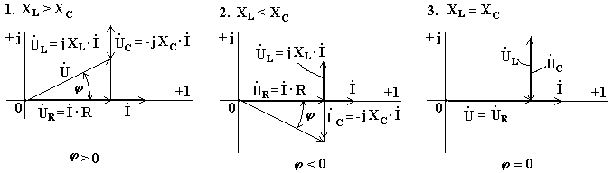 Рис.
6.9 Рис. 6.10 Рис. 6.11
Рис.
6.9 Рис. 6.10 Рис. 6.11
5. Цепи синусоидального с катушками индуктивности
5.1. Напряжение и ток катушки индуктивности
5.1.1. Общие сведения
Когда к катушке индуктивности подведено синусоидальное напряжение, ток в ней отстает от синусоиды напряжения на ней на 900. Соответственно, мгновенное значение тока достигает амплитудного значения на четверть периода позже, чем мгновенное значение напряжения (рис. 5.1.1). В этом рассуждении пренебрегается активным сопротивлением катушки.
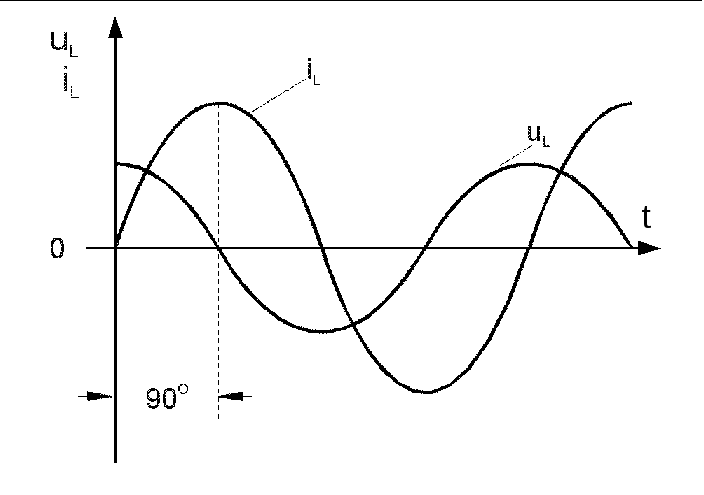
Рис. 5.1.1
5.1.2. Экспериментальная часть
Задание
Выведите на дисплей виртуального осциллографа кривые изменения во времени мгновенных значений тока iLи напряженияuLкатушки индуктивности и определите фазовый сдвиг между ними.
Порядок выполнения эксперимента
Соберите цепь согласно схеме (рис. 5.1.2), подключите к ее входу регулируемый источник синусоидального напряжения с параметрами: U=5В, f= 1 кГц.
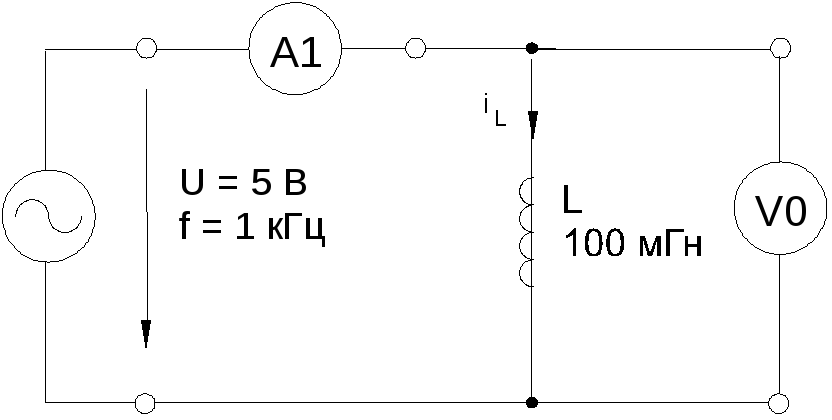
Рис. 5.1.2
Включите виртуальные приборы V0,A1 и осциллограф.
«Подключите» два входа осциллографа к приборам V0 иA1, а остальные отключите.
Установите параметры развёртки осциллографа так, чтобы на экране было изображение примерно одного-двух периодов напряжения и тока.
Перенесите данные осциллографирования напряжения и тока катушки на график (рис. 5.1.3), определите фазовый сдвиг между синусоидами напряжения и тока катушки индуктивности.
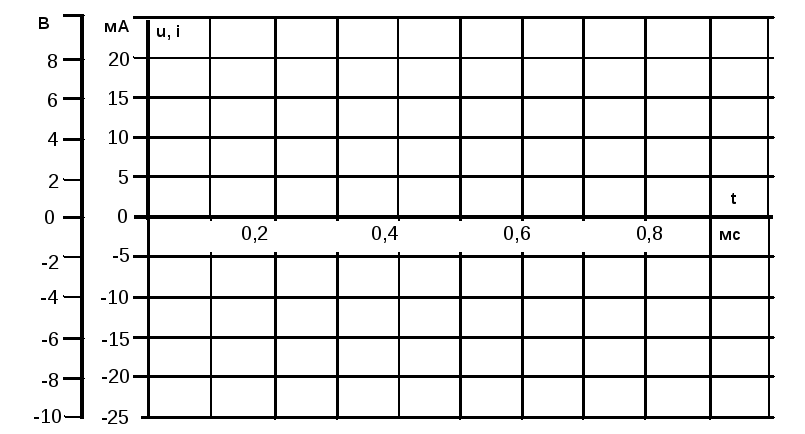
Рис. 5.1.3
Период
T =
Фазовый сдвиг
=
Примечание: фазовый сдвиг меньше 90оиз-за влияния активного сопротивления катушки.
Включите блок дополнительных приборов, выберите из меню прибор «Угол сдвига фаз» и «подключите» его к V1 и А1. Убедитесь, что вы правильно определили фазовый сдвиг по осциллографу.
5.2. Реактивное сопротивление катушки индуктивности
5.2.1. Общие сведения
Катушка индуктивности в цепи переменного тока оказывает токоограничивающий эффект благодаря индуктируемой в ней противоЭДС. Этот токоограничивающий эффект принято выражать как индуктивное реактивное сопротивление (индуктивный реактанс) XL.
Величина индуктивного реактанса XLзависит от величины индуктивности катушки, измеряемой в Генри, и частоты приложенного напряжения переменного тока. В случае синусоидального напряжения имеем
XL = L = 2fL ,
где XL —реактивное индуктивное сопротивление, Ом,
L — индуктивность катушки, Гн.
Если активное сопротивление катушки мало и им можно пренебречь, то реактивное (индуктивное) сопротивление можно определить через действующие значения или амплитуды напряжения и тока:
XL = UL IL или XL = ULm ILm.
5.2.2. Экспериментальная часть Задание
Выведите на дисплей виртуального осциллографа кривые тока и напряжения различных катушек индуктивности при различных частотах и постройте зависимость XL = f(f). Соответствующий индуктивный реактанс находится по амплитудным значениям тока и напряжения из осциллограмм и проверяется по формулеXL = L.
Порядок выполнения эксперимента
Соберите цепь согласно схеме (рис. 5.2.1.), подсоедините к ее входу регулируемый источник синусоидального напряжения с параметрами U = 5 В, f= 1 кГц.
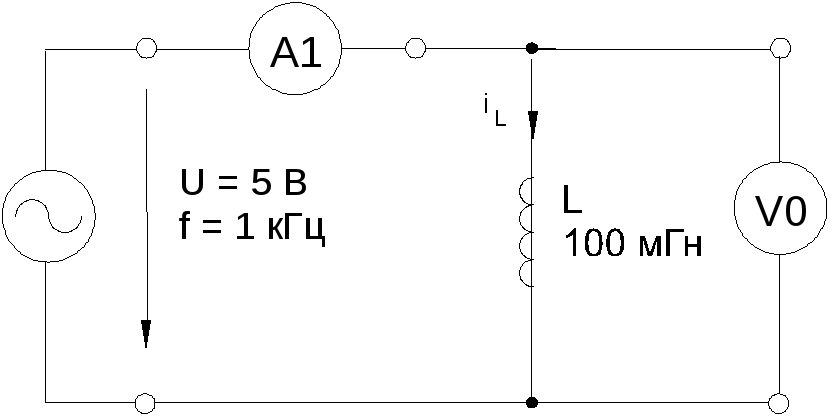
Рис. 5.2.1.
Включите виртуальные приборы V0,A1 и осциллограф.
«Подключите» два входа осциллографа к приборам V0 иA1, а остальные отключите.
Установите параметры развёртки осциллографа так, чтобы на экране было изображение примерно одного-двух периодов напряжения и тока.
Снимите с осциллограммы амплитудные значения Um иIm для индуктивностей и частот, указанных в табл. 4.2.1, и занесите их в соответствующие ячейки таблицы.
Таблица 5.2.1
f, кГц | 0,5 | 1 | 1,5 | 2 | |||||||||||
UmL, В | 100 мГн | ||||||||||||||
UmL, В | 40 мГн | ||||||||||||||
UmL, В | 10 мГн | ||||||||||||||
ImL, мА | 100 мГн | ||||||||||||||
ImL, мА | 40 мГн | ||||||||||||||
ImL, мА | 10 мГн | ||||||||||||||
XL = Um Im, кОм | 100 мГн | ||||||||||||||
40 мГн | |||||||||||||||
10 мГн | |||||||||||||||
XL =L, Ком | 100 мГн | ||||||||||||||
40 мГн | |||||||||||||||
10 мГн | |||||||||||||||
Вычислите величины XL по формуламUm ImиLи занесите их в табл. 5.2.1.
Перенесите величины XL на график (рис. 5.2.2) для построения кривойXL = f(f).
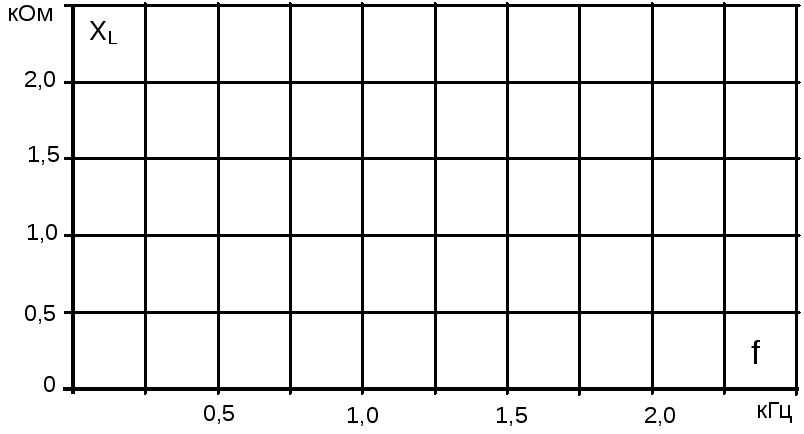
Рис. 5.2.2
Здесь полное комплексное сопротивление катушки : Z=R+jL
Реальная катушка индуктивности, кроме индуктивности, обладает активным сопротивлением витков провода, из которого она изготовлена. Поэтому комплексная схема замещения будет состоять из последовательно соединенных индуктивного и активного сопротивлений, рис. 1.11.
По второму закону Кирхгофа для комплексов действующих значений напряжений общее напряжение
U= UL+ UR=jLI+RI=( jL+R)I=Z I
состоит из активной и реактивной (индуктивной) составляющих.
Рис. 1.11.
Модуль и аргумент сопротивления : Z= ,
,

определяют
соответственно соотношение амплитуд
и сдвиг фаз между напряжением и током.
Комплекс тока равен  ,
,
где u-начальная фаза приложенного напряжения.
Следовательно, выражение для мгновенного значения синусоидального тока в реальной катушке индуктивности имеет вид:
 .
.
Ток отстает по фазе от приложенного к цепи напряжения на угол , зависящий от соотношения между активным и индуктивным сопротивлениями катушки.
Полученные комплексные соотношения можно изобразить на векторной диаграмме, рис. 1.12 .

Рис. 1.12.
Вектор тока, общего для последовательно включенных элементов, принимается за исходный и откладывается в произвольном направлении, обычно горизонтальном.
Вектор URнаправляется вдоль вектора I, поскольку он совпадает по фазе, а векторUL, опережающий вектор тока на 90о, строим перпендикулярно току против часовой стрелки. Геометрическая сумма этих двух векторов дает векторU напряжения, приложенного к катушке индуктивности. ВекторU опережает по фазе вектор Iна угол. Если начальная фаза напряженияu задана, можно нанести оси комплексной системы координат и путем геометрических измерений определитьi и другие интересующие нас параметры.
Необходимо однако помнить, что представление общего напряжения на зажимах реальной катушки индуктивности в виде суммы активной и индуктивной составляющих, является формальным и в реальной цепи они не существуют и не поддаются непосредственному измерению вольтметром.
1.9. Последовательное включение реальной катушки индуктивности и конденсатора без потерь в цепь синусоидального тока
Последовательную цепь переменного тока с индуктивной катушкой и конденсатором можно представить комплексной схемой замещения R, L, C элементами, рис. 1.13.

Рис. 1.13.
Приложенное напряжение запишем как сумму напряжений на элементах цепи :
u= uR +uL+uC
или в комплексной форме : U= UR + UL+UC .
Выразив напряжения через ток и сопротивления , получим :
Замечательной особенностью здесь является то, что реaктивная составляющая полного комплексного сопротивления контура равна разности индуктивного и емкостного сопротивлений и поэтому может принимать разные знаки или обращаться в нуль. Это является следствием того, что при протекании через оба элемента одного и того же тока, напряжения на них находятся в противофазе: напряжение на индуктивности опережает ток по фазе на 90о, а на емкости — отстает на 90о.
Цепи переменного тока — конденсаторы и индукторы
Электрорезонанс
 Электрорезонанс (схема серии R-L-C) ПРИБОР 1. Печатная плата R-L-C 2. Генератор сигналов 3. Осциллограф Tektronix TDS1002 с двумя наборами выводов (см. Введение в осциллограф) ВВЕДЕНИЕ
Электрорезонанс (схема серии R-L-C) ПРИБОР 1. Печатная плата R-L-C 2. Генератор сигналов 3. Осциллограф Tektronix TDS1002 с двумя наборами выводов (см. Введение в осциллограф) ВВЕДЕНИЕ
Резонанс серии RLC
 RLC Series Resonance 11EM Object: Целью данной лабораторной работы является изучение резонанса в цепи резистор-индуктор-конденсатор (RLC) путем проверки тока через цепь как функции
RLC Series Resonance 11EM Object: Целью данной лабораторной работы является изучение резонанса в цепи резистор-индуктор-конденсатор (RLC) путем проверки тока через цепь как функции
Использование осциллографа
 Использование осциллографа Осциллограф используется для измерения напряжения, которое изменяется во времени.У него есть два датчика, как вольтметр. Вы помещаете эти датчики по обе стороны от того, что вы хотите измерить
Использование осциллографа Осциллограф используется для измерения напряжения, которое изменяется во времени.У него есть два датчика, как вольтметр. Вы помещаете эти датчики по обе стороны от того, что вы хотите измерить
RC & RL переходный ответ
 EE 2006 Университет Миннесоты, Дулут, аб 8 1. Введение R & R Transient Response Учащийся будет анализировать цепи R и R серии. Шаговый вход будет возбуждать эти соответствующие схемы, создавая переходный процесс
EE 2006 Университет Миннесоты, Дулут, аб 8 1. Введение R & R Transient Response Учащийся будет анализировать цепи R и R серии. Шаговый вход будет возбуждать эти соответствующие схемы, создавая переходный процесс
Lab 3 Выпрямительные схемы
 ECET 242 Electronic Circuits Lab 3 Выпрямительные цепи Страница 1 из 5 Название: Цель: Учащиеся, успешно завершившие это лабораторное упражнение, выполнят следующие задачи: 1.Узнайте, как построить
ECET 242 Electronic Circuits Lab 3 Выпрямительные цепи Страница 1 из 5 Название: Цель: Учащиеся, успешно завершившие это лабораторное упражнение, выполнят следующие задачи: 1.Узнайте, как построить
Лабораторная работа № 9: анализ устойчивого состояния переменного тока
 Теория и введение Лабораторная работа № 9: Цели анализа устойчивого состояния переменного тока для лабораторной работы № 9 Основная задача лабораторной работы 9 состоит в том, чтобы познакомить учащихся с анализом устойчивого состояния переменного тока, шкалой дБ и частотным анализатором NI ELVIS.
Теория и введение Лабораторная работа № 9: Цели анализа устойчивого состояния переменного тока для лабораторной работы № 9 Основная задача лабораторной работы 9 состоит в том, чтобы познакомить учащихся с анализом устойчивого состояния переменного тока, шкалой дБ и частотным анализатором NI ELVIS.
СЕРИЙНО-ПАРАЛЛЕЛЬНЫЕ ЦЕПИ DC
 Имя: Дата: Курс и Секция: Преподаватель: ЭКСПЕРИМЕНТ 1 СЕРИЯ-ПАРАЛЛЕЛЬНЫЕ ЦЕПИ ЦЕЛИ ЦЕЛИ 1.Проверьте теоретический анализ последовательно-параллельных сетей с помощью прямых измерений. 2. Улучшить навыки
Имя: Дата: Курс и Секция: Преподаватель: ЭКСПЕРИМЕНТ 1 СЕРИЯ-ПАРАЛЛЕЛЬНЫЕ ЦЕПИ ЦЕЛИ ЦЕЛИ 1.Проверьте теоретический анализ последовательно-параллельных сетей с помощью прямых измерений. 2. Улучшить навыки
Использование метода импеданса
 Использование метода импеданса Метод импеданса позволяет полностью исключить подход дифференциального уравнения для определения отклика цепей. На самом деле метод импеданса даже
Использование метода импеданса Метод импеданса позволяет полностью исключить подход дифференциального уравнения для определения отклика цепей. На самом деле метод импеданса даже
Индукторы в цепях переменного тока
 Индукторы в цепях переменного тока Наименование раздела Резисторы, катушки индуктивности и конденсаторы влияют на изменение величины тока в цепи переменного тока и времени, в которое ток достигает своего максимума
Индукторы в цепях переменного тока Наименование раздела Резисторы, катушки индуктивности и конденсаторы влияют на изменение величины тока в цепи переменного тока и времени, в которое ток достигает своего максимума
Частотная характеристика фильтров
 Инженерная школа, факультет электротехники и вычислительной техники 332: 224 Принципы электротехники II Лабораторный эксперимент 2 Частотная характеристика фильтров 1 Введение Цели До
Инженерная школа, факультет электротехники и вычислительной техники 332: 224 Принципы электротехники II Лабораторный эксперимент 2 Частотная характеристика фильтров 1 Введение Цели До
Шаговая реакция цепей RC
 Шаговая реакция цепей RC 1.ЦЕЛИ … 2 2. ССЫЛКИ … 2 3. ЦЕПИ … 2 4. КОМПОНЕНТЫ И ТЕХНИЧЕСКИЕ ХАРАКТЕРИСТИКИ … 3 КОЛИЧЕСТВО … 3 ОПИСАНИЕ … 3 КОММЕНТАРИИ … 3 5. ОБСУЖДЕНИЕ … 3 5.1 ИСТОЧНИКОВОЕ СОПРОТИВЛЕНИЕ … 3
Шаговая реакция цепей RC 1.ЦЕЛИ … 2 2. ССЫЛКИ … 2 3. ЦЕПИ … 2 4. КОМПОНЕНТЫ И ТЕХНИЧЕСКИЕ ХАРАКТЕРИСТИКИ … 3 КОЛИЧЕСТВО … 3 ОПИСАНИЕ … 3 КОММЕНТАРИИ … 3 5. ОБСУЖДЕНИЕ … 3 5.1 ИСТОЧНИКОВОЕ СОПРОТИВЛЕНИЕ … 3
Лабораторная работа E1: введение в схемы
 E1.1 Лабораторная работа E1: Введение в схемы Целью этой лабораторной работы является знакомство с некоторыми базовыми приборами, используемыми в электрических цепях. Вы научитесь использовать источник питания постоянного тока, цифровой мультиметр
E1.1 Лабораторная работа E1: Введение в схемы Целью этой лабораторной работы является знакомство с некоторыми базовыми приборами, используемыми в электрических цепях. Вы научитесь использовать источник питания постоянного тока, цифровой мультиметр
Смотри Хоренштейн 4.3 и 4.4
 EE 462: Лаборатория № 4 Цепи питания постоянного тока с использованием диодов от Drs. СРЕДНИЙ. Радун и К.Д. Донохью (14.02.07) Кафедра электротехники и вычислительной техники Университета Кентукки Лексингтон, KY 40506 Обновлено
EE 462: Лаборатория № 4 Цепи питания постоянного тока с использованием диодов от Drs. СРЕДНИЙ. Радун и К.Д. Донохью (14.02.07) Кафедра электротехники и вычислительной техники Университета Кентукки Лексингтон, KY 40506 Обновлено
АНАЛИТИЧЕСКИЕ МЕТОДЫ ДЛЯ ИНЖЕНЕРОВ
 ЕДИНИЦА 1: Код единицы: QCF Уровень: 4 Значение кредита: 15 АНАЛИТИЧЕСКИЕ МЕТОДЫ ДЛЯ ИНЖЕНЕРОВ A / 601/1401 РЕЗУЛЬТАТ — ТРИГОНОМЕТРИЧЕСКИЕ МЕТОДЫ ОБУЧЕНИЕ 1 СИНУЗОИДНАЯ ФУНКЦИЯ Уметь анализировать и моделировать инженерные ситуации
ЕДИНИЦА 1: Код единицы: QCF Уровень: 4 Значение кредита: 15 АНАЛИТИЧЕСКИЕ МЕТОДЫ ДЛЯ ИНЖЕНЕРОВ A / 601/1401 РЕЗУЛЬТАТ — ТРИГОНОМЕТРИЧЕСКИЕ МЕТОДЫ ОБУЧЕНИЕ 1 СИНУЗОИДНАЯ ФУНКЦИЯ Уметь анализировать и моделировать инженерные ситуации
= V пик 2 = 0.Пик 707В
 ОСНОВНАЯ ЭЛЕКТРОНИКА — РЕКТИФИКАЦИЯ И ЦЕЛЬ ФИЛЬТРАЦИИ Предположим, что вы хотите создать простой электронный источник постоянного тока, работающий от входа переменного тока (например, что-то, что вы могли бы подключить к стандартному
ОСНОВНАЯ ЭЛЕКТРОНИКА — РЕКТИФИКАЦИЯ И ЦЕЛЬ ФИЛЬТРАЦИИ Предположим, что вы хотите создать простой электронный источник постоянного тока, работающий от входа переменного тока (например, что-то, что вы могли бы подключить к стандартному
Глава 12: Трехфазные цепи
 Глава 12. Трехфазные цепи. 12.1. Что такое трехфазные цепи? 12.2 Баланс трехфазных напряжений 12.3 Балансные трехфазные соединения Y-Y 12.4 Другие балансные трехфазные соединения 12.5 Питание в
Глава 12. Трехфазные цепи. 12.1. Что такое трехфазные цепи? 12.2 Баланс трехфазных напряжений 12.3 Балансные трехфазные соединения Y-Y 12.4 Другие балансные трехфазные соединения 12.5 Питание в
Постоянная времени RC цепи
 Постоянная времени RC-цепи 1 Задачи 1. Определить постоянную времени RC-цепи и 2. Определить емкость неизвестного конденсатора. 2 Введение Какого черта конденсатор?
Постоянная времени RC-цепи 1 Задачи 1. Определить постоянную времени RC-цепи и 2. Определить емкость неизвестного конденсатора. 2 Введение Какого черта конденсатор?
7.1 МОЩНОСТЬ В ЦЕПЯХ
 П Р И М Е Ч Е Н И Е 7 ЦЕЛЬ ПЕРЕМЕННОГО ТОКА Цель этой главы — познакомить слушателя с простыми расчетами мощности переменного тока, а также с выработкой и распределением электроэнергии. Глава построена на материале
П Р И М Е Ч Е Н И Е 7 ЦЕЛЬ ПЕРЕМЕННОГО ТОКА Цель этой главы — познакомить слушателя с простыми расчетами мощности переменного тока, а также с выработкой и распределением электроэнергии. Глава построена на материале
Операционный усилитель — IC 741
 Операционный усилитель — IC 741 Tabish Декабрь 2005 г. Цель: изучить работу операционного усилителя 741 путем проведения следующих экспериментов: (a) Измерение входного тока смещения (b) Смещение входного сигнала
Операционный усилитель — IC 741 Tabish Декабрь 2005 г. Цель: изучить работу операционного усилителя 741 путем проведения следующих экспериментов: (a) Измерение входного тока смещения (b) Смещение входного сигнала
Основы анализа подписи
 Основы анализа сигнатур Углубленный обзор тестирования на отключение питания с использованием Аналогового анализа сигнатур www.huntron.com 1 www.huntron.com 2 Содержание РАЗДЕЛ 1. ВВЕДЕНИЕ … 7 ЦЕЛЬ …
Основы анализа сигнатур Углубленный обзор тестирования на отключение питания с использованием Аналогового анализа сигнатур www.huntron.com 1 www.huntron.com 2 Содержание РАЗДЕЛ 1. ВВЕДЕНИЕ … 7 ЦЕЛЬ …
Блок 2: Резистор / Конденсатор-Фильтры
 Модуль 2: Резистор / конденсатор-фильтры Физика335 Студент 3, 27 октября Физика 335-секционный профессор Дж. Хоббс Партнер: Физика335 Студент2 Аннотация Были сконструированы базовые RC-фильтры и созданы такие свойства, как
Модуль 2: Резистор / конденсатор-фильтры Физика335 Студент 3, 27 октября Физика 335-секционный профессор Дж. Хоббс Партнер: Физика335 Студент2 Аннотация Были сконструированы базовые RC-фильтры и созданы такие свойства, как
Глава 7 Цепи постоянного тока
 Глава 7 Цепи постоянного тока 7.Введение … 7-7. Электродвижущая сила … 7-3 7.3 Резисторы последовательно и параллельно … 7-5 7.4 Правила цепи Кирхгофа … 7-7 7.5 Измерения напряжения-тока … 7-9
Глава 7 Цепи постоянного тока 7.Введение … 7-7. Электродвижущая сила … 7-3 7.3 Резисторы последовательно и параллельно … 7-5 7.4 Правила цепи Кирхгофа … 7-7 7.5 Измерения напряжения-тока … 7-9
Основные схемы операционного усилителя
 Основные операционные усилители Manuel Toledo INEL 5205 Контрольно-измерительные приборы 3 августа 2008 г. Введение Операционный усилитель (операционный усилитель или сокращенно OA) является, пожалуй, самым важным строительным блоком для конструкции
Основные операционные усилители Manuel Toledo INEL 5205 Контрольно-измерительные приборы 3 августа 2008 г. Введение Операционный усилитель (операционный усилитель или сокращенно OA) является, пожалуй, самым важным строительным блоком для конструкции
Электронный учебник WorkBench
 Электронное учебное пособие WorkBench Введение Electronic WorkBench (EWB) — это пакет моделирования для электронных схем.Это позволяет проектировать и анализировать схемы без использования макетов, реальных компонентов
Электронное учебное пособие WorkBench Введение Electronic WorkBench (EWB) — это пакет моделирования для электронных схем.Это позволяет проектировать и анализировать схемы без использования макетов, реальных компонентов
Положительные отзывы и осцилляторы
 Физика 3330 Эксперимент № 6 Осень 1999 г. Положительная обратная связь и осцилляторы Цель В этом эксперименте мы изучим, как спонтанные колебания могут быть вызваны положительной обратной связью. Вы построите активный
Физика 3330 Эксперимент № 6 Осень 1999 г. Положительная обратная связь и осцилляторы Цель В этом эксперименте мы изучим, как спонтанные колебания могут быть вызваны положительной обратной связью. Вы построите активный
Аналоговая электроника I.лаборатория
 Аналоговая электроника I Лабораторное упражнение 1 Цепи электропитания постоянного тока Цель упражнения Цель этого лабораторного упражнения — ознакомиться с выпрямительными цепями и методами стабилизации напряжения
Аналоговая электроника I Лабораторное упражнение 1 Цепи электропитания постоянного тока Цель упражнения Цель этого лабораторного упражнения — ознакомиться с выпрямительными цепями и методами стабилизации напряжения
Лабораторная работа 1: Цифровой осциллограф
 ФИЗИКА 220 Физическая электроника Лаборатория 1. Объект цифрового осциллографа. Познакомиться с осциллографом, повсеместно распространенным инструментом для наблюдения и измерения электронных сигналов.Аппарат: Tektronix
ФИЗИКА 220 Физическая электроника Лаборатория 1. Объект цифрового осциллографа. Познакомиться с осциллографом, повсеместно распространенным инструментом для наблюдения и измерения электронных сигналов.Аппарат: Tektronix
Глава 22 Дальнейшая электроника
 Глава 22 Далее Электронная стиральная машина имеет задержку открытия дверцы после цикла стирки. Часть этой схемы показана ниже. Когда цикл заканчивается, переключатель S замыкается. т этой ступени конденсатора
Глава 22 Далее Электронная стиральная машина имеет задержку открытия дверцы после цикла стирки. Часть этой схемы показана ниже. Когда цикл заканчивается, переключатель S замыкается. т этой ступени конденсатора
СХЕМА ЛАБОРАТОРНОГО ЭКСПЕРИМЕНТА 2
 ЦЕПЬ ЛАБОРАТОРНОГО ЭКСПЕРИМЕНТА 2 Осциллограф и анализ переходных процессов 2.1 Введение В первом эксперименте была продемонстрирована полезность цифрового мультиметра для измерения многих простых величин постоянного тока. Тем не менее,
ЦЕПЬ ЛАБОРАТОРНОГО ЭКСПЕРИМЕНТА 2 Осциллограф и анализ переходных процессов 2.1 Введение В первом эксперименте была продемонстрирована полезность цифрового мультиметра для измерения многих простых величин постоянного тока. Тем не менее,
Лабораторная работа 5 операционных усилителей
 Лабораторная работа 5 Операционные усилители Автор: Гари А. Ибарра, Кристофер Э. Крамер, Университет Дьюка, факультет электротехники и вычислительной техники, Дарем, Северная Каролина. Цель Цель этой лаборатории состоит в том, чтобы исследовать свойства
Лабораторная работа 5 Операционные усилители Автор: Гари А. Ибарра, Кристофер Э. Крамер, Университет Дьюка, факультет электротехники и вычислительной техники, Дарем, Северная Каролина. Цель Цель этой лаборатории состоит в том, чтобы исследовать свойства
30.Земельные участки Боде. Введение
 0. Графики Боде Введение Каждая из цепей в этом наборе задач представлена диаграммой Боде по величине. Функция сети обеспечивает связь между графиком Боде и схемой. Чтобы решить эти
0. Графики Боде Введение Каждая из цепей в этом наборе задач представлена диаграммой Боде по величине. Функция сети обеспечивает связь между графиком Боде и схемой. Чтобы решить эти
Домашнее задание 03
 Вопрос 1 (по 2 балла, если не указано иное) Задание по домашнему заданию 03 1.Источник питания постоянного тока 9 В генерирует 10 Вт на резисторе. Какую амплитуду от пика до пика должен иметь источник переменного тока для генерации того же
Вопрос 1 (по 2 балла, если не указано иное) Задание по домашнему заданию 03 1.Источник питания постоянного тока 9 В генерирует 10 Вт на резисторе. Какую амплитуду от пика до пика должен иметь источник переменного тока для генерации того же
Глава 11: Вьетнамки
 ГЛАВА 11: Триггеры В этой главе вы будете строить часть схемы, которая контролирует последовательность команд. Требуемая схема должна управлять счетчиком и микросхемой памяти. Когда учат
ГЛАВА 11: Триггеры В этой главе вы будете строить часть схемы, которая контролирует последовательность команд. Требуемая схема должна управлять счетчиком и микросхемой памяти. Когда учат
Лабораторная работа 3 — Цепи постоянного тока и закон Ома
 Лабораторная работа 3: Цепи постоянного тока и закон Ома L3-1 Имя Дата Партнеры Лабораторная работа 3 — Цепи постоянного тока и закон Ома ЦЕЛИ Научиться применять концепцию разности потенциалов (напряжения) для объяснения действия батареи в
Лабораторная работа 3: Цепи постоянного тока и закон Ома L3-1 Имя Дата Партнеры Лабораторная работа 3 — Цепи постоянного тока и закон Ома ЦЕЛИ Научиться применять концепцию разности потенциалов (напряжения) для объяснения действия батареи в
Основные операции осциллографа
 Работа с осциллографом asic Эта рабочая таблица и все связанные с ней файлы лицензированы в соответствии с версией Creative Commons Ttribution License.0. Чтобы просмотреть копию этой лицензии, посетите http://creativecommons.org/licenses/by/.0/,
Работа с осциллографом asic Эта рабочая таблица и все связанные с ней файлы лицензированы в соответствии с версией Creative Commons Ttribution License.0. Чтобы просмотреть копию этой лицензии, посетите http://creativecommons.org/licenses/by/.0/,
АМЕРИКАНСКИЙ НАЦИОНАЛЬНЫЙ СТАНДАРТ
 ИНЖИНИРИНГОВЫЙ КОМИТЕТ Подкомитет по практическому взаимодействию АМЕРИКАНСКИЙ НАЦИОНАЛЬНЫЙ СТАНДАРТ ANSI / SCTE 46 2014 Метод испытаний для наружных источников питания переменного тока в постоянный ток УВЕДОМЛЕНИЕ Общество инженеров кабельной электросвязи
ИНЖИНИРИНГОВЫЙ КОМИТЕТ Подкомитет по практическому взаимодействию АМЕРИКАНСКИЙ НАЦИОНАЛЬНЫЙ СТАНДАРТ ANSI / SCTE 46 2014 Метод испытаний для наружных источников питания переменного тока в постоянный ток УВЕДОМЛЕНИЕ Общество инженеров кабельной электросвязи
Германий Диод AM Радио
 Германий Диод AM Radio LAB 3 3.1 Введение В этом лабораторном упражнении вы создадите радио AM (Medium Wave) на основе германиевых диодов. Самые ранние радиостанции использовали простые схемы диодного детектора. Диоды
Германий Диод AM Radio LAB 3 3.1 Введение В этом лабораторном упражнении вы создадите радио AM (Medium Wave) на основе германиевых диодов. Самые ранние радиостанции использовали простые схемы диодного детектора. Диоды
Интерференция звуковых волн
 1/2016 Звук 1/8 ИНТЕРФЕРЕНЦИЯ ЗВУКОВЫХ ВОЛН НАЗНАЧЕНИЕ: для измерения длины волны, частоты и скорости распространения ультразвуковых звуковых волн и для наблюдения явлений интерференции с ультразвуковыми звуковыми волнами.
1/2016 Звук 1/8 ИНТЕРФЕРЕНЦИЯ ЗВУКОВЫХ ВОЛН НАЗНАЧЕНИЕ: для измерения длины волны, частоты и скорости распространения ультразвуковых звуковых волн и для наблюдения явлений интерференции с ультразвуковыми звуковыми волнами.
Что такое чисто индуктивная цепь? — Phasor Diagram & Waveform
Цепь, которая содержит только индуктивность (L), а не любые другие величины, такие как сопротивление и емкость в цепи, называется Pure индуктивной цепью. В схеме этого типа ток отстает от напряжения на угол 90 градусов.
Содержание:
Катушка индуктивности — это тип катушки, которая запасает электрическую энергию в магнитном поле, когда через нее протекает ток.Индуктор состоит из провода, который намотан в виде катушки. Когда ток, протекающий через индуктор, изменяется, изменяющееся во времени магнитное поле вызывает ЭДС, которая препятствует протеканию тока. Индуктивность измеряется в Генри . Противостояние потока тока известно как индуктивное сопротивление .
Объяснение и вывод индуктивной схемы
Схема, содержащая чистую индуктивность, показана ниже:
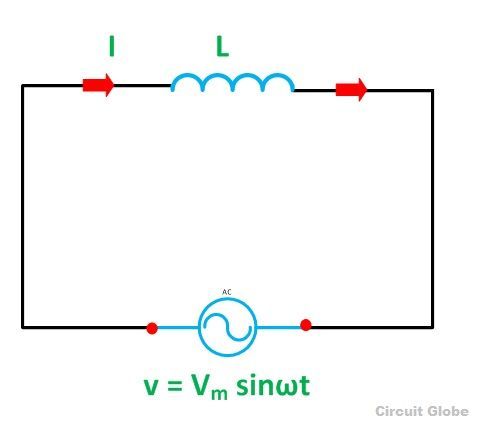 Схема
Схемачистой индуктивной схемы
Пусть переменное напряжение, подаваемое на цепь, определяется уравнением:
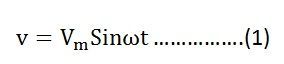
В результате переменный ток i протекает через индуктивность, которая индуцирует в нем ЭДС.Уравнение показано ниже:
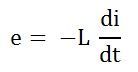
ЭДС, которая индуцируется в цепи, равна и противоположна приложенному напряжению. Следовательно, уравнение становится,

Положив значение е в уравнении (2), получим уравнение как
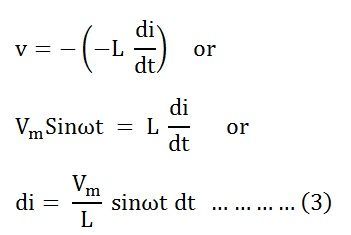
Интегрируя обе части уравнения (3), мы получим
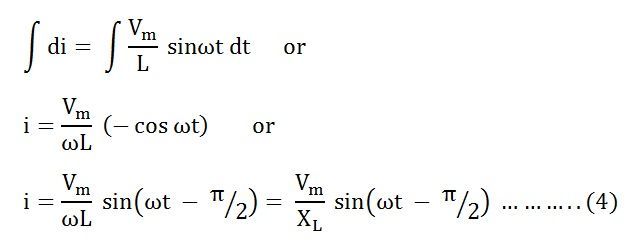 , где X L = ω L — сопротивление, предлагаемое потоку переменного тока чистой индуктивностью и называемое индуктивным реактивным сопротивлением.
, где X L = ω L — сопротивление, предлагаемое потоку переменного тока чистой индуктивностью и называемое индуктивным реактивным сопротивлением.
Значение тока будет максимальным, когда sin (ωt — π / 2) = 1
Следовательно,
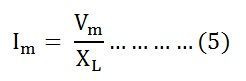
Подставляя это значение в I м из уравнения (5) и подставляя его в уравнение (4), мы получим 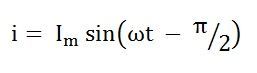
Диаграмма вектора и кривая мощности индуктивной цепи
Ток в чистой индуктивной цепи переменного тока отстает от напряжения на 90 градусов. Форма волны, кривая мощности и фазовая диаграмма чисто индуктивного контура показаны ниже
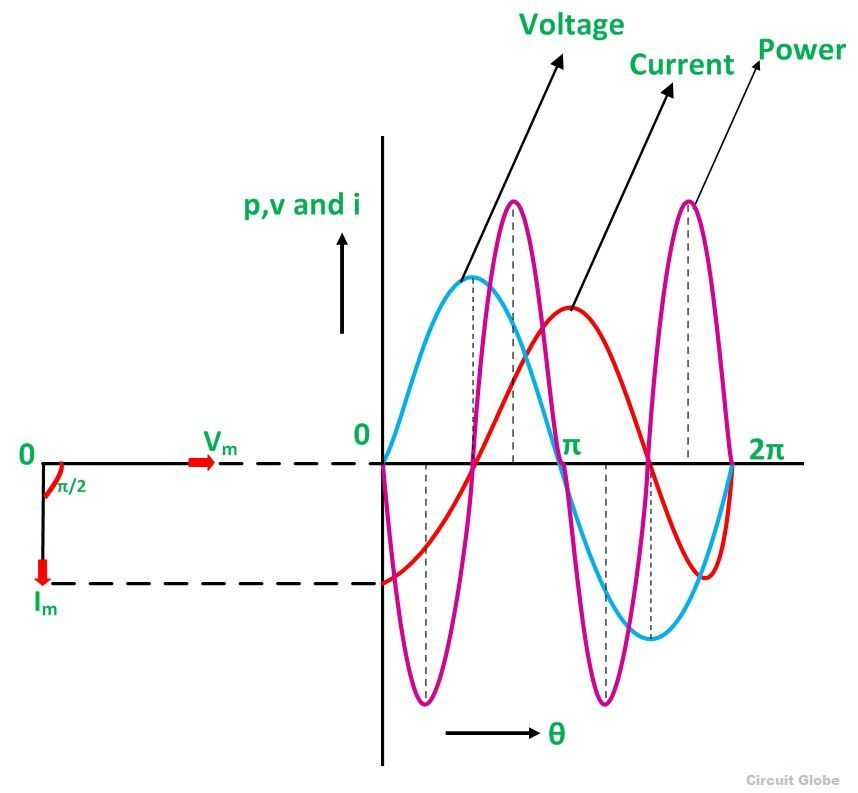
Диаграмма вектора и форма волны чистой индуктивной цепи
Форма волны напряжения, тока и мощности показана синим, красным и розовым цветами соответственно.Когда значения напряжения и тока находятся на своем пике в качестве положительного значения, мощность также является положительной, и аналогично, когда напряжение и ток дают отрицательный сигнал, мощность также станет отрицательной. Это из-за разности фаз между напряжением и током.
Когда напряжение падает, значение тока изменяется. Когда значение тока достигает своего максимального или максимального значения, напряжение в этот момент времени будет равно нулю, и, следовательно, напряжение и ток не совпадают по фазе друг с другом на угол 90 градусов.
Диаграмма вектора также показана на левой стороне формы сигнала, где текущее (I м ) запаздывающее напряжение (V м ) под углом π / 2.
Власть в чистой индуктивной цепи
Мгновенная мощность в индуктивной цепи задается
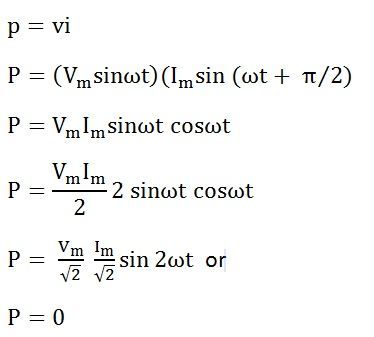
Следовательно, средняя мощность, потребляемая в чисто индуктивной цепи, равна нулю.
Средняя мощность в одном изменении, то есть в полупериоде, равна нулю, так как отрицательная и положительная петли находятся под кривой мощности, то же самое.
В чисто индуктивной цепи в течение первой четверти цикла мощность, подаваемая источником, сохраняется в магнитном поле, установленном вокруг катушки. В следующем цикле четверти магнитное поле уменьшается, и энергия, которая была сохранена в цикле первой четверти, возвращается источнику.
Этот процесс продолжается в каждом цикле, и, таким образом, в цепи не расходуется энергия.
,
