Электричество и магнетизм

Чтобы понять механизм поведения диэлектриков в поле на микроскопическом уровне, нам надо сначала объяснить, как может электрически нейтральная система реагировать на внешнее электрическое поле. Простейший случай — полное отсутствие зарядов — нас не интересует. Мы знаем наверняка, что в диэлектрике имеются электрические заряды — в составе атомов, молекул, ионов кристаллической решетки и т. д. Поэтому мы рассмотрим следующую по простоте конструкции электронейтральную систему — два равных по величине и противоположных по знаку точечных заряда +q и –q, находящихся на расстоянии l друг от друга. Такая система называется электрическим диполем. 

Электрический диполь — это система, состоящая из двух точечных равных по величине и противоположных по знаку зарядов, находящихся на расстоянии l друг от друга (рис. 3.6).

  

Рис. 3.6. Электрический диполь 

Линии напряженности электрического поля и эквипотенциальные поверхности электрического диполя выглядят следующим образом (рис. 3.7, 3.8, 3.9)

Рис. 3.7. Линии напряженности электрического поля электрического диполя

 

Рис. 3.8. Эквипотенциальные поверхности электрического диполя

 

 

 Рис. 3.9. Линии напряженности электрического поля и эквипотенциальные поверхности

 Основной характеристикой диполя является

электрический дипольный момент. Введем вектор l, направленный от отрицательного заряда (–q) к положительному (+q), тогда вектор р, называемый электрическим моментом диполя или просто дипольным моментом, определяется как

(3. 5)

Рассмотрим поведение «жесткого» диполя — то есть расстояние  которого не меняется — во внешнем поле

Е (рис. 3.10).

Рис. 3.10. Силы, действующие на электрический диполь, помещенный во внешнее поле 

Пусть направление дипольного момента составляет с вектором Е угол . На положительный заряд диполя действует сила, совпадающая по направлению с Е и равная F₁ = +qE, а на отрицательный — противоположно направленная и равная F₂ = –qE. Вращающий момент этой пары сил равен

(3.6)

Так как ql = р, то М = рЕ sin или в векторных обозначениях 

(Напомним, что символ

 

означает векторное произведение векторов а и b.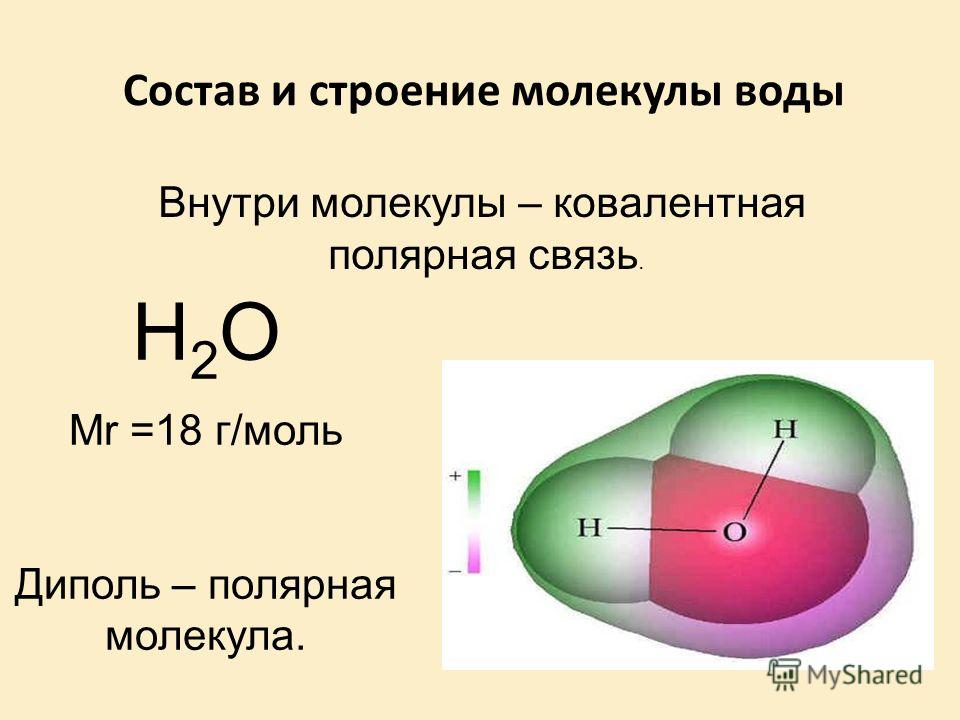 ) Таким образом, при неизменном дипольном моменте молекулы () механический момент, действующий на нее, пропорционален напряженности Е внешнего электрического поля и зависит от угла между векторами

р и E.

 Под действием момента сил М диполь поворачивается, при этом совершается работа

(3.7)

которая идет на увеличение его потенциальной энергии. Отсюда получаем потенциальную энергию диполя в электрическом поле 

откуда

 

или

(3.8)

если положить const = 0.  

Из рисунка видно, что внешнее электрическое поле стремится повернуть диполь таким образом, чтобы вектор его электрического момента р совпал по направлению с вектором Е. В этом случае  , а, следовательно, и М = 0. С другой стороны, при  потенциальная энергия диполя во внешнем поле принимает минимальное значение  , что соответствует положению устойчивого равновесия. При отклонении диполя от этого положения снова возникает механический момент, который возвращает диполь в первоначальное положение. Другое положение равновесия, когда дипольный момент направлен против поля  является

неустойчивым. Потенциальная энергия в этом случае принимает максимальное значение  и при небольших отклонениях от такого положения возникающие силы не возвращают диполь назад, а еще больше отклоняют его. 

На рис. 3.11 показан опыт, иллюстрирующий возникновение момента электрических сил, действующих на диэлектрик в электрическом поле.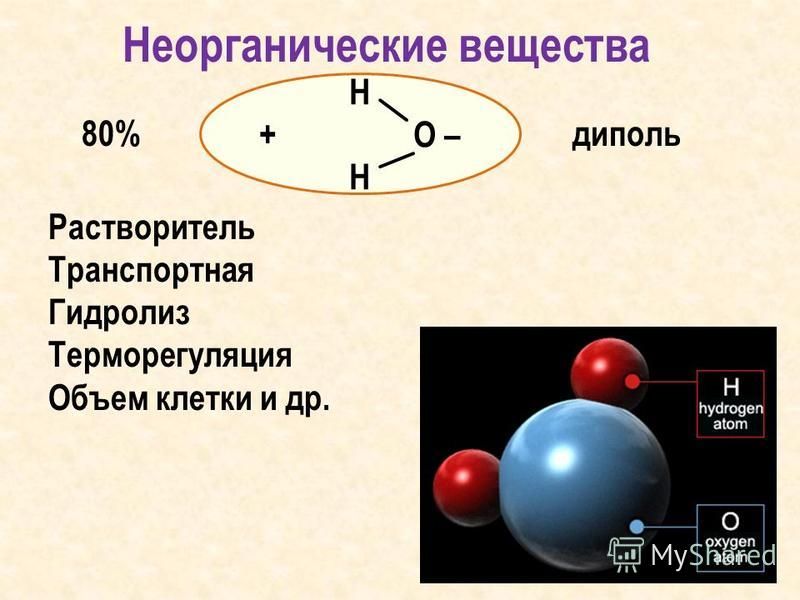 На удлиненный диэлектрический образец, расположенный под некоторым углом к силовым линиям электростатического поля, действует момент сил, стремящийся развернуть этот образец вдоль поля. Диэлектрическая палочка, подвешенная за середину внутри плоского конденсатора, разворачивается перпендикулярно его пластинам после подачи на них высокого напряжения от электростатической машины. Появление вращающего момента обусловлено взаимодействием поляризовавшейся палочки с электрическим полем конденсатора.

 

Рис. 3.11. Момент электрических сил, действующих на диэлектрик в электрическом поле 

В случае неоднородного поля на рассматриваемый диполь будет действовать еще и равнодействующая сила F_paвн, стремящаяся его сдвинуть. Мы рассмотрим здесь частный случай. Направим ось х вдоль поля

Е. Пусть диполь под действием поля уже повернулся вдоль силовой линии, так что отрицательный заряд находится в точке с координатой x, а положительный заряд расположен в точке с координатой х + l. Представим себе, что величина напряженности поля зависит от координаты х. Тогда равнодействующая сила F_paвн  равна

(3.9)

Такой же результат может быть получен из общего соотношения

 

где энергия П определена в (3.8). Если Е увеличивается с ростом x, то

 

и проекция   равнодействующей силы положительна. Это значит, что она стремиться втянуть диполь в область, где напряженность поля больше. Этим объясняется известный эффект, когда нейтральные кусочки бумаги притягиваются к наэлектризованной расческе. В плоском конденсаторе с однородным полем они остались бы неподвижными. 

Рассмотрим несколько опытов, иллюстрирующих возникновение силы, действующей на диэлектрик, помещенный в неоднородное электрическое поле.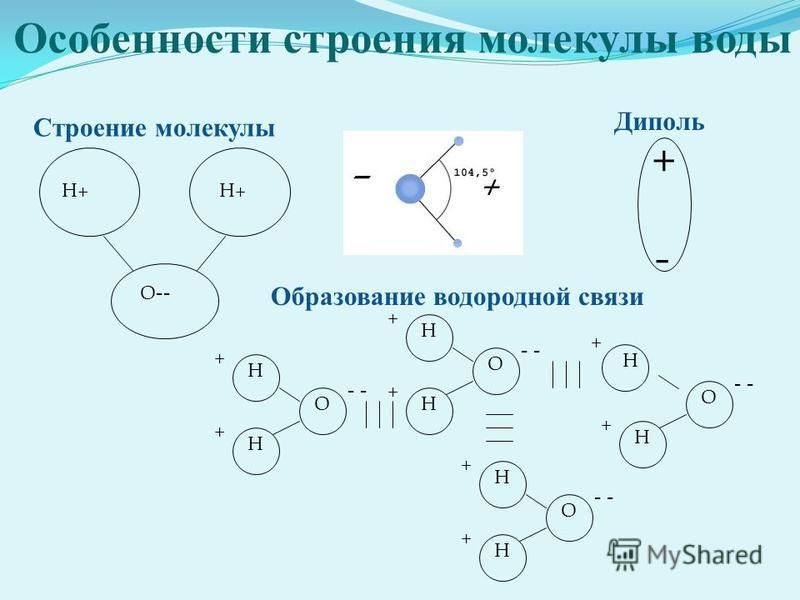

 

На рис. 3.12 показано втягивание диэлектрика в пространство между обкладками плоского конденсатора. В неоднородном электростатическом поле на диэлектрик действуют силы, втягивающие его в область более сильного поля.

 

Рис. 3.12. Втягивание жидкого диэлектрика в плоский конденсатор 

Это демонстрируется при помощи прозрачного сосуда, в который помещен плоский конденсатор, и налито некоторое количество жидкого диэлектрика — керосина (рис.3.13). Конденсатор присоединен к высоковольтному источнику питания — электростатической машине. При ее работе на нижнем краю конденсатора, в области неоднородного поля, на керосин действует сила, втягивающая его в пространство между пластинами. Поэтому уровень керосина внутри конденсатора устанавливается выше, чем снаружи. После выключения поля уровень керосина между пластинами падает до его уровня в сосуде. 

 

Рис. 3.13. Втягивание керосина в пространство между обкладками плоского конденсатора 

Видео 3. 1. Эксперимент по втягиванию жидкого диэлектрика в конденсатор.

В реальных веществах нечасто встречаются диполи, образованные только двумя зарядами. Обычно мы имеем дело с более сложными системами. Но понятие электрического дипольного момента применимо и к системам со многими зарядами. В этом случае дипольный момент  определяется как

(3.10)

где , — величина заряда с номером i и радиус-вектор, определяющий его местоположение, соответственно. В случае двух зарядов  мы приходим к прежнему выражению

 

Пусть наша система зарядов электрически нейтральна. В ней есть положительные заряды, величины которых и местоположения мы обозначим индексом «+». Индексом «–» мы снабдим абсолютные величины отрицательных зарядов и их радиус-векторы. Тогда выражение (3.10) может быть записано в виде

(3. 11)

В (3.11) в первом слагаемом суммирование ведется по всем положительным зарядам, а во втором — по всем отрицательным зарядам системы.

Электрическая нейтральность системы означает равенство полного положительного заряда и суммы абсолютных величин всех отрицательных зарядов

(3.12)

Введем теперь понятие «центр зарядов» — положительных R⁺ и отрицательных R^–

(3.13)

Выражения (3.13) аналогичны формулам для центра масс в механике, и потому мы назвали их центрами положительных и отрицательных зарядов, соответственно. С этими обозначениями и с учетом соотношения (3.12) мы записываем электрический дипольный момент (3.11) системы зарядов в виде

(3.14)

где l-вектор, проведенный из центра отрицательных зарядов в центр положительных зарядов. Смысл нашего упражнения заключается в демонстрации, что любую электрически нейтральную систему зарядов можно представить как некий эквивалентный диполь.

 

Дополнительная информация 

 http://webmath.exponenta.ru/dnu/lc/age/pyartli1/node9.htm —  Векторное произведение.

Фейнмановские лекции по физике. Т.5. Электричество и магнетизм

Фейнмановские лекции по физике. Т.5. Электричество и магнетизм

Фейнмановские лекции по физике. Т. 5. Электричество и магнетизм Это лекции по общей физике, которые читал физик-теоретик. Они совсем не похожи ни на один известный курс. Это может показаться странным: основные принципы классической физики, да и не только классической, но в квантовой, давно установлены, курс общей физики читается во всем мире в тысячах учебных заведений уже много лет и ему пора превратиться в стандартную последовательность известных фактов и теорий, подобно, например, элементарной геометрии в школе. Однако даже математики считают, что их науке надо учить по-другому. А уж о физике и говорить нечего: она столь интенсивно развивается, что даже лучшие педагоги все время сталкиваются с большими трудностями, когда им надо рассказывать студентам о современной пауке. Они жалуются, что им приходится ломать то, что принято называть старыми или привычными представлениями. Но откуда берутся привычные представления? Обычно они попадают в молодые головы в школе от таких же педагогов, которые потом будут говорить о недоступности идей современной науки. Поэтому прежде чем подойти к сути дела, приходится тратить много времени на то, чтобы убедить слушателей в ложности того, что было ранее внушено им как очевидная и непреложная истина. Оглавление От редактора Предисловие Глава 1. Электромагнетизм § 1. Электрические силы § 2. Электрические и магнитные поля § 3. Характеристики векторных полей § 4. Законы электромагнетизма § 5. Что это такое — «поля»? § 6. Электромагнетизм в науке и технике Глава 2. Дифференциальное исчисление векторных полей § 1. Понимание физики § 2. Скалярные и векторные поля — T и h § 3. Производные полей — градиент § 4. Оператор § 5. Операции с § 6. Дифференциальное уравнение потока тепла § 7. Вторые производные векторных полей § 8. Подвохи Глава 3. Интегральное исчисление векторов § 1. Векторные интегралы; криволинейный интеграл от § 2. Поток векторного поля § 3. Поток из куба; теорема Гаусса § 4. Теплопроводность; уравнение диффузии § 5. Циркуляция векторного поля § 6. Циркуляция по квадрату; теорема Стокса § 7. Поля без роторов и поля без дивергенций § 8. Итоги Глава 4. Электростатика § 1. Статика § 2. Закон Кулона; наложение сил § 3. Электрический потенциал § 4. E = – fi § 5. Поток поля E § 6. Закон Гаусса; дивергенция поля E § 7. Поле заряженного шара § 8. Линии поля; эквипотенциальные поверхности Глава 5. Применения закона Гаусса § 1. Электростатика — это есть закон Гаусса плюс… § 2. Равновесие в электростатическом поле § 3. Равновесие с проводниками § 4. Устойчивость атомов § 5. Поле заряженной прямой линии § 6. Заряженная плоскость; пара плоскостей § 7. Однородно заряженный шар; заряженная сфера § 8. Точен ли закон Кулона? § 9. Поля проводника § 10. Поле внутри полости проводника Глава 6. Электрическое поле в разных физических условиях § 1. Уравнения электростатического потенциала § 2. 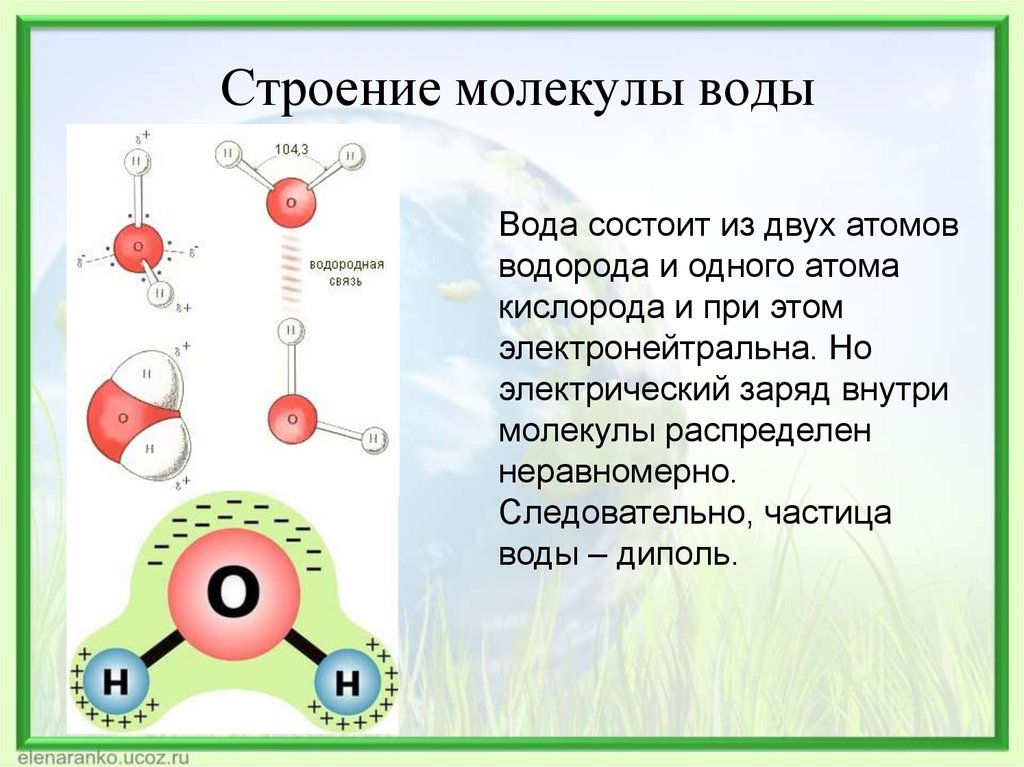Электрический диполь § 3. Замечания о векторных уравнениях § 4. Дипольный потенциал как градиент § 5. Дипольное приближение для произвольного распределения § 6. Поля заряженных проводников § 7. Метод изображений § 8. Точечный заряд у проводящей плоскости § 9. Точечный заряд у проводящей сферы § 10. Конденсаторы; параллельные пластины § 11. Пробой при высоком напряжении § 12. Ионный микроскоп Глава 7. Электрическое поле в разных физических условиях (продолжение) § 1. Методы определения электростатического поля § 2. Двумерные поля; функции комплексного переменного § 3. Колебания плазмы § 4. Коллоидные частицы в электролите § 5. Электростатическое поле сетки Глава 8. Электростатическая энергия § 1. Электростатическая энергия зарядов. Однородный шар § 2. Энергия конденсатора. Силы, действующие на заряженные проводники § 3. Электростатическая энергия ионного кристалла § 4. Электростатическая энергия ядра § 5. Энергия в электростатическом поле § 6. Энергия точечного заряда Глава 9. Электричество в атмосфере § 1. Градиент электрического потенциала § 2. Электрические токи в атмосфере § 3. Происхождение токов в атмосфере § 4. Грозы § 5. Механизм распределения зарядов § 6. Молния Глава 10. Диэлектрики § 1. Диэлектрическая проницаемость § 2. Вектор поляризации P § 3. Поляризационные заряды § 4. Уравнения электростатики для диэлектриков § 5. Поля и силы в присутствии диэлектриков Глава 11. Внутреннее устройство диэлектриков § 1. Молекулярные диполи § 2. Электронная поляризация § 3. Полярные молекулы; ориентационная поляризация § 4. Электрические поля в пустотах диэлектрика § 5. Диэлектрическая проницаемость жидкостей; формула Клаузиуса — Моссотти § 6. Твердые диэлектрики § 7. Сегнетоэлектричество; титанат бария Глава 12. Электростатические аналогии § 1. Одинаковые уравнения — одинаковые решения § 2. Поток тепла; точечный источник вблизи бесконечной плоской границы § 3. Натянутая мембрана § 4. Диффузия нейтронов; сферически-симметричный источник в однородной среде § 5. Безвихриевое течение жидкости; обтекание шара § 6. Освещение; равномерное освещение плоскости § 7. «Фундаментальное единство» природы Глава 13. Магнитостатика § 1. Магнитное поле § 2. Электрический ток; сохранение заряда § 3. Магнитная сила, действующая на ток § 4. Магнитное поле постоянного тока; закон Ампера § 5. Магнитное поле прямого провода и соленоида; атомные токи § 6. Относительность магнитных и электрических полей § 7. Преобразование токов и зарядов § 8. Суперпозиция; правило правой руки Глава 14. Магнитное поле в разных случаях § 1. Векторный потенциал § 2. Векторный потенциал заданных токов § 3. Прямой провод § 4. Длинный соленоид § 5. Поле маленькой петли; магнитный диполь § 6. Векторный потенциал цепи § 7. Закон Био — Савара

Диполь-дипольные взаимодействия — Химия LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

1658

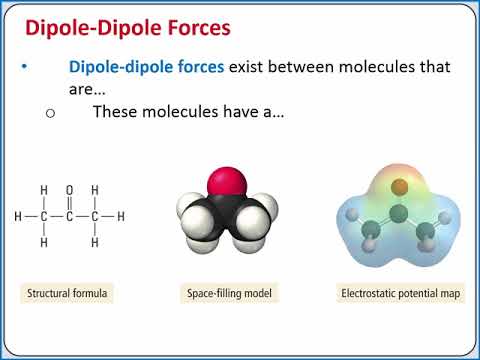
Диполь-дипольные взаимодействия возникают, когда две диполярные молекулы взаимодействуют друг с другом в пространстве. Когда это происходит, частично отрицательная часть одной из полярных молекул притягивается к частично положительной части второй полярной молекулы. Этот тип взаимодействия между молекулами объясняет многие физически и биологически значимые явления, такие как повышенная температура кипения воды.

Определение диполя

Молекулярные диполи возникают из-за неравного распределения электронов между атомами в молекуле. Те атомы, которые являются более электроотрицательными, притягивают связанные электроны ближе к себе. Нарастание электронной плотности вокруг атома или дискретной области молекулы может привести к молекулярному диполю, в котором одна сторона молекулы имеет частично отрицательный заряд, а другая сторона частично положительный заряд. Молекулы с диполями, которые не компенсируются их молекулярной геометрией, называются полярными.

Пример \(\PageIndex{1}\): Углекислый газ и фтороводород

Рисунок \(\PageIndex{1}\).

На рис. 1 выше более электроотрицательные атомы кислорода притягивают к себе электронную плотность, как показано стрелками. Однако углекислый газ неполярен из-за своей линейной геометрии. Общий диполь молекулы является направленным и определяется векторной суммой диполей между атомами. Если бы мы представили молекулу углекислого газа с центром в 0 координатной плоскости XY, общий диполь молекулы был бы задан следующим уравнением:0024

\[\mu \cos(0) + -\mu \cos(0) = 0. \]

Где \(μ\) — дипольный момент связи (задается как μ=Q x r, где Q — заряд, а r — расстояние разноса). Следовательно, два диполя компенсируют друг друга, образуя молекулу без чистого диполя.

Рисунок \(\PageIndex{2}\).

Напротив, на рис. 2 показана ситуация, когда молекулярный диполь действительно возникает. Нет противоположного дипольного момента, который компенсировал бы момент, показанный выше. Если бы мы представили молекулу фтористого водорода, расположенную так, что водород находился бы в начале координат в координатной плоскости XY, диполь был бы задан как \(\mu \cos(0)=\mu\).

Потенциальная энергия дипольного взаимодействия

Потенциальная энергия — это максимальная энергия, доступная объекту для выполнения работы. В физике работа — это величина, описывающая энергию, затрачиваемую на действие силы на расстоянии. Потенциальная энергия является позиционной, поскольку зависит от сил, действующих на объект в его положении в пространстве. Например, мы могли бы сказать, что объект, удерживаемый над землей, имеет потенциальную энергию, равную его массе, умноженной на ускорение под действием силы тяжести, умноженной на его высоту над землей (т. е. \(mgh\)). Эта потенциальная энергия, которую объект имеет в результате своего положения, может быть использована для совершения работы. Например, мы могли бы использовать систему шкивов с большим весом, удерживаемым над землей, чтобы поднимать меньший вес в воздух. Когда мы сбрасываем большой груз, он преобразует свою потенциальную энергию в кинетическую и совершает работу с веревкой, которая поднимает меньший груз в воздух. Важно помнить, что в соответствии со вторым законом термодинамики количество работы, совершаемой объектом, никогда не может превышать (а часто значительно меньше) потенциальной энергии объекта.

На субатомном уровне заряженные атомы обладают электрическим потенциалом, который позволяет им взаимодействовать друг с другом. Электрический потенциал относится к энергии, удерживаемой заряженной частицей в результате ее положения относительно второй заряженной частицы. Электрический потенциал зависит от полярности заряда, силы заряда и расстояния. Молекулы с одинаковым зарядом будут отталкиваться друг от друга по мере сближения, а молекулы с противоположными зарядами будут притягиваться.

Для двух положительно заряженных частиц, взаимодействующих на расстоянии r, потенциальная энергия, которой обладает система, может быть определена с помощью закона Кулона:

\[V = \dfrac{kQq}{r} \label{1}\]

где

• \(k\) — постоянная Кулона, а
• \(Q\) и \(q\) относятся к величине заряда каждой частицы в кулонах.

Приведенное выше уравнение можно также использовать для расчета расстояния между двумя заряженными частицами (\(r\)), если мы знаем потенциальную энергию системы. Хотя закон Кулона важен, он дает только потенциальную энергию между двумя точечными частицами. Поскольку молекулы намного больше точечных частиц и имеют заряд, сосредоточенный на большей площади, нам нужно придумать новое уравнение. 9{3}}{(\cos\theta_{12}- 3\cos\theta_{1}\cos\theta_{2})} \label{3}\]

В этой формуле \(\theta_{12} \) — это угол между двумя противоположно заряженными диполями, а \(r_{12}\) — это расстояние между двумя молекулами. Кроме того, \(\theta_{1}\) и \(\theta_{2}\) — это углы, образованные двумя диполями относительно линии, соединяющей их центры.

Также важно найти потенциальную энергию дипольного момента для более чем двух взаимодействующих молекул. При работе с несколькими взаимодействующими заряженными молекулами важно помнить, что одинаковые заряды отталкиваются, а противоположные притягиваются. Итак, для системы, в которой взаимодействуют три заряженные молекулы (2 положительно заряженные молекулы и 1 отрицательно заряженная молекула), нам необходимо рассмотреть угол между силами притяжения и отталкивания. 9{2}} \label{4}\]

, где

• \(k\) — постоянная Кулона, а
• \(r\) — расстояние между молекулами.

Рисунок \(\PageIndex{3}\): Взаимодействие диполь-диполь в газовой фазе. изображение используется с разрешения (Гэри Л. Бертран).

Пример \(\PageIndex{2}\)

Рассчитать потенциальную энергию диполь-дипольного взаимодействия между 2 молекулами \(\ce{HF}\), ориентированными вдоль оси x в координатной плоскости XY, площадь положительного заряда которой отстоит на 5,00 Ангстрем от площади отрицательного заряда соседней молекулы: 9{-20}J\end{align*}\]

Диполь-дипольные взаимодействия в макроскопических системах

Исходя из вышеизложенного, казалось бы, что в системе, состоящей из большого числа диполярных молекул, случайно в другом V должно стремиться к нулю, потому что молекулы принимают все возможные ориентации. Таким образом, отрицательная потенциальная энергия двух молекулярных диполей, участвующих в благоприятном взаимодействии, компенсируется положительной энергией двух молекулярных диполей, участвующих во взаимодействии с высокой потенциальной энергией. Вопреки нашему предположению, в объемных системах более вероятно взаимодействие диполярных молекул таким образом, чтобы минимизировать их потенциальную энергию (т. е. диполи образуют менее энергетические, более вероятные конфигурации в соответствии с распределением Больцмана). Например, частично положительная область молекулярного диполя, удерживаемая рядом с частично положительной областью второго молекулярного диполя, представляет собой конфигурацию с высокой потенциальной энергией, и лишь немногие молекулы в системе будут иметь достаточную энергию, чтобы принять ее при комнатной температуре. Как правило, конфигурации с более высокой потенциальной энергией могут быть заселены только при повышенных температурах. Следовательно, взаимодействия диполей в объемном растворе не случайны, а вместо этого принимают более вероятные конфигурации с более низкой энергией. Это учитывается в следующем уравнении: 96}\dfrac{1}{k_{B}T} \label{5}\]

Пример \(\PageIndex{4}\)

Глядя на уравнение \ref{5}, что происходит с потенциальной энергией взаимодействия при повышении температуры.

Решение

Потенциальная энергия диполь-дипольного взаимодействия уменьшается с увеличением T. Это видно из формы приведенного выше уравнения, но объяснение этому наблюдению относительно простое. По мере повышения температуры системы большее количество молекул имеет достаточную энергию, чтобы занимать менее благоприятные конфигурации. Более высокие, менее благоприятные конфигурации — это те, которые обеспечивают менее благоприятные взаимодействия между диполями (т. Е. Конфигурации с более высокой потенциальной энергией). 9{-1}) \\[4pt] &=-3288\dfrac{J}{mol}=3.29\dfrac{kJ}{mol} \end{align*}\]

Биологическое значение дипольных взаимодействий

потенциальная энергия от дипольных взаимодействий важна для живых организмов. Наибольшее влияние дипольных взаимодействий на живые организмы наблюдается при сворачивании белков. Каждый процесс образования белка, от связывания отдельных аминокислот до вторичных структур, третичных структур и даже образования четвертичных структур, зависит от диполь-дипольных взаимодействий.

Ярким примером взаимодействия четвертичных диполей, жизненно важного для здоровья человека, является образование эритроцитов. Эритроциты, широко известные как эритроциты, представляют собой тип клеток, ответственных за газообмен (то есть дыхание). Внутри эритроцитов молекула, участвующая в этом решающем процессе, представляет собой «гемоглобин», образованный четырьмя белковыми субъединицами и гемовой группой. Чтобы гем сформировался должным образом, должно пройти несколько этапов, каждый из которых включает дипольные взаимодействия. Четыре белковые субъединицы — две альфа-цепи, две бета-цепи — и гемовая группа взаимодействуют друг с другом посредством ряда диполь-дипольных взаимодействий, которые позволяют эритроциту принять свою окончательную форму. Любая мутация, которая разрушает эти диполь-дипольные взаимодействия, препятствует правильному формированию эритроцитов и ухудшает их способность переносить кислород к тканям организма. Таким образом, мы видим, что без диполь-дипольных взаимодействий белки не смогли бы правильно складываться, и вся жизнь, какой мы ее знаем, прекратила бы свое существование.

Ссылки

1. Le Fèvre, RJW (1953). дипольные моменты; их измерение и применение в химии. Лондон, Метуэн.
2. Аткинс, П. В. и Дж. Де Паула (2006). Физическая химия для наук о жизни. Нью-Йорк, издательство Оксфордского университета; Фриман.
3. Петруччи Р. Х., В. С. Харвуд и др. (2002). Общая химия: принципы и современные приложения. Река Аппер-Сэдл, Нью-Джерси, Прентис-холл.
4. Блумфилд, Массачусетс (1992). Химия и живой организм. Нью-Йорк, Уайли.
5. Силби, Р. Дж., Р. А. Альберти и др. (2005). Физическая химия. Хобокен, Нью-Джерси, Уайли.
6. Гиперфизика. http://hyperphysics.phy-astr.gsu.edu/hbase/hframe.html Университет штата Джорджия, факультет физики и астрономии. 2008.
7. Кэмпбелл, Н. А. и Дж. Б. Рис (2005). Биология. Сан-Франциско, Пирсон Бенджамин Каммингс.
8. Чанг, Рэймонд. (2005). Физическая химия для биологических наук. Саусалито, Калифорния, Университетские научные книги.

---

Dipole-Dipole Interactions распространяется под лицензией CC BY-NC-SA 4.0, авторами, ремиксами и/или кураторами являются Гэри Л. Бертран, Дэвид Джонс, Джоэл Гуэсс и Джоэл Гусс.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или страница

   Лицензия

   CC BY-NC-SA

   Версия лицензии

   4,0

   Показать страницу TOC

   № на стр.

2. Теги

   1. автор@Дэвид Джонс
   2. автор@Гэри Л. Бертран
   3. автор @ Джоэл Угадай
   4. диполь
   5. диполь-дипольные взаимодействия

Молекулярный диполь — общая полярность молекулы

Структура и связь

Молекулярный диполь — общая полярность молекулы

Дипольный момент молекулы и ее общая полярность зависят от величины и направления индивидуальных полярных связей и их дипольные моменты.

Помните, что для молекул с одной полярной связью молекулярный диполь определяется просто на основе дипольного момента этой связи: определяется векторной суммой 90 246 90 247 этих дипольных моментов.

Например, если мы заменим еще один атом водорода в дихлорметане (CH ₂ Cl ₂ , показанный выше), нам нужно найти векторная сумма двух диполей C-Cl для определения общего диполя молекулы:

Важно отметить, что неподеленных пар электронов также влияют на величину и направление молекулярного диполя .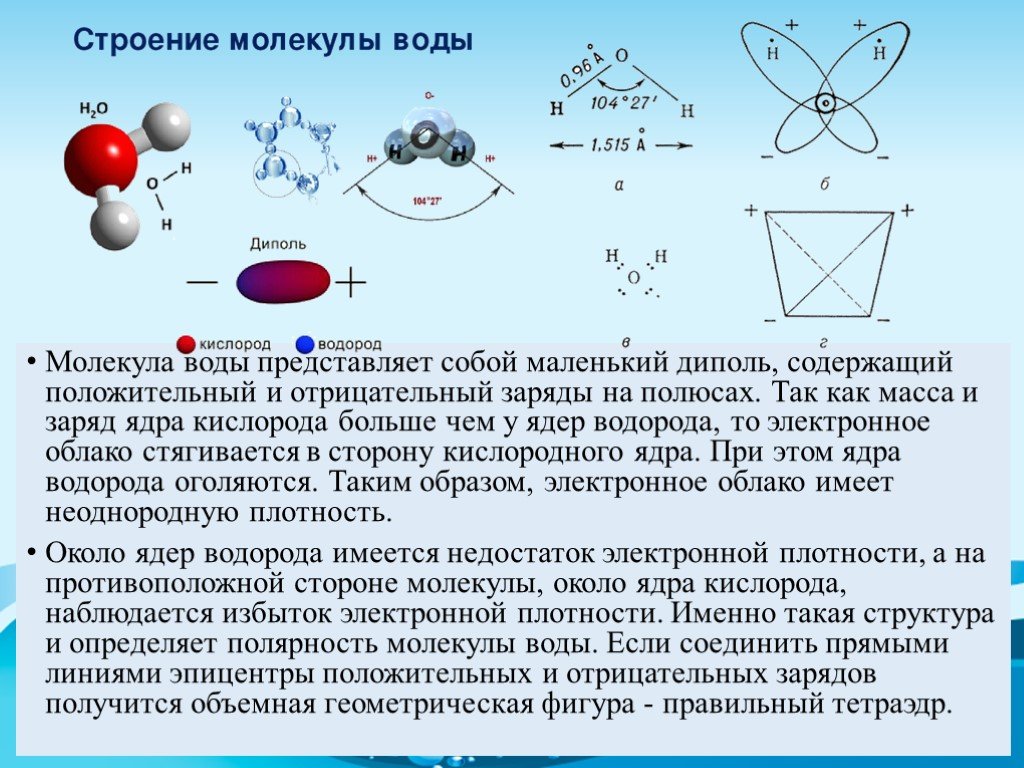

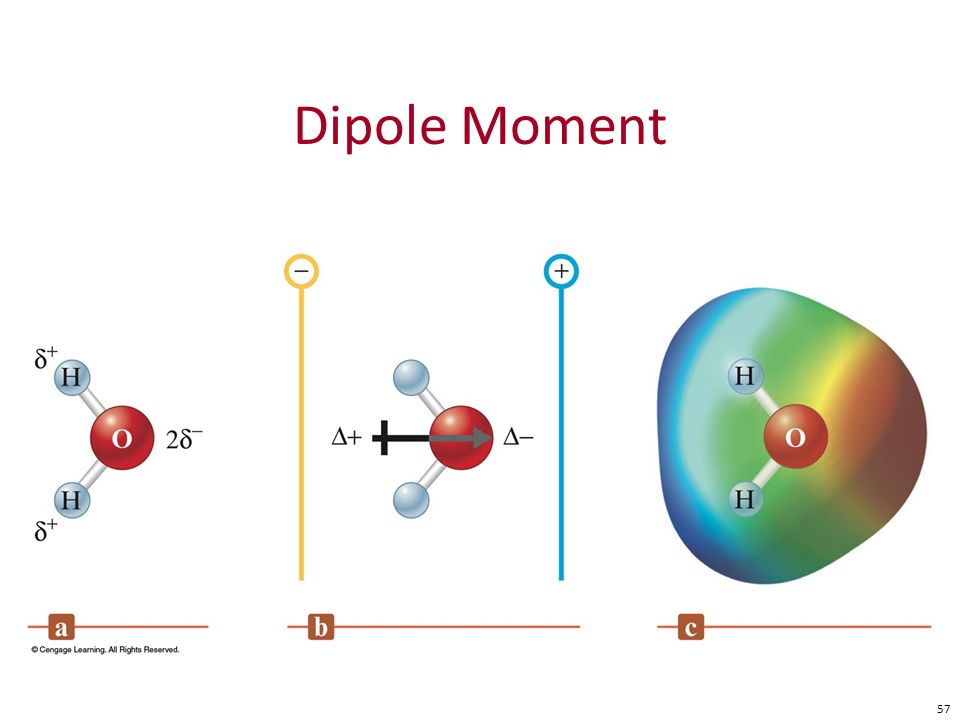
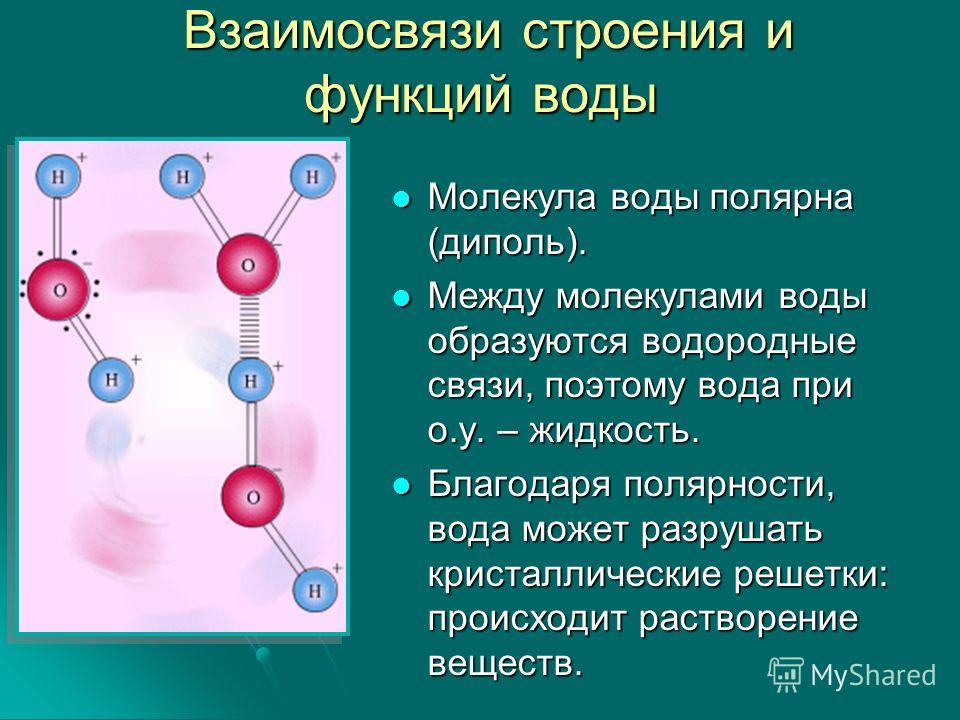
Например, молекула воды имеет две полярные связи и одну неподеленную пару электронов. Кислород тянет связывающие электроны, общие с атомами водорода, поскольку он более электроотрицательный. С другой стороны, неподеленные пары направляют дипольный момент на них. Хотя результирующие дипольные векторы не выровнены линейно в точке 0 ^o , все они направлены в одну сторону, и при их объединении мы видим, что все диполей усиливают друг друга. Об этом свидетельствует большее значение дипольного момента воды (1,85 Д) по сравнению с дипольным моментом отдельных связей ОН (1,5 Д).

Очень полезно изучить теории гибридизации и VSEPR, которые предполагают, что водороды и неподеленные пары кислорода находятся в sp ³ орбитали на ~109,5 ^{o _.}

Таким образом, 1,85 D является векторной суммой двух диполей 1,5 D при 104,5 ^o плюс усиливающий эффект неподеленных пар.

 

Аналогично, аммиак имеет больший дипольный момент (1,47 Д), чем каждая связь NH (1,3 Д). Дипольный момент неподеленной пары усиливается векторной суммой трех связей N-H:

Мы только что обсудили примеры, когда дипольные моменты усиливались друг другом в соответствии с их векторной суммой. Так что насчет молекул, когда дипольные моменты направлены в противоположную сторону?

Здесь есть два сценария. Если дипольные моменты имеют одинаковую величину при 180 ^o , то молекула неполярна, так как дипольные моменты компенсируются.

Итак, чтобы обобщить, помните, что симметричных молекул не имеют дипольного момента независимо от того, насколько полярны ковалентные связи, потому что общий дипольный момент молекулы зависит от величины и направления отдельных диполей.

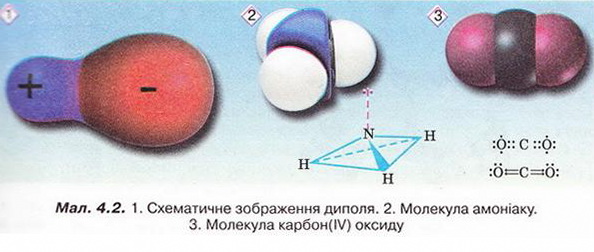
Например, двуокись углерода имеет две полярные связи C=O, однако их дипольные моменты , находящиеся при 180 ^o , сокращены, и, следовательно, молекула не имеет чистого диполя и является неполярной :

 

Если дипольные моменты имеют разную величину, но в противоположных направлениях, то суммарный дипольный момент будет векторной суммой (вычитанием) этих дипольных моментов. См. практический вопрос ниже.

 

Во многих случаях молекула не нарисована или не задана геометрия , и вас просят определить полярна ли данная молекула или нет .

Чтобы ответить на этот вопрос, необходимо сначала определить геометрию молекулы по правилам теории ВСЕПР . Они сведены в следующую таблицу, но также подробно описаны здесь, так что не стесняйтесь проверить их и структуры Льюиса, прежде чем мы перейдем к следующему примеру:0024

 

 

  Пример:

Определите, является ли молекула полярной, показав соответствующие дипольные моменты.

Эта молекула представляет собой формальдегид и имеет тригональную планарную геометрию в соответствии с правилами VSEPR: из С=О связь . Кислород, будучи более электроотрицательным, тянет электронную плотность связи С=О, определяя тем самым направление молекулярного диполя: молекулярный диполь определяется суммой этих дипольных моментов.

Например, диэтиловый эфир обладает суммарным дипольным моментом, который представляет собой векторную сумму двух полярных связей C-O :

 

 

Для более крупных молекул с множеством сигма-связей сложнее определить суммарный дипольный момент из-за свободного вращения вокруг этих одинарных связей. Однако наличие двойных связей , которые ограничивают постоянное изменение направления дипольного момента, позволяет определить молекулярный дипольный момент.

Это можно проиллюстрировать, сравнив точки кипения cis – and trans -1,2-Dichloroethene :

 

 

The dipole moments of the C-Cl bonds in cis -1,2-Dichloroethene reinforce and молекула имеет чистый диполь . Напротив, изомер транс не имеет молекулярного диполя , поскольку связи C-Cl направлены в противоположном направлении и их дипольные эффекты компенсируются:

 

 

В результате транс-изомер представляет собой неполярную молекулу с более низкой температурой кипения (48 ^o против 60 ^o C), чем цис цис диполь-дипольные взаимодействия в последнем.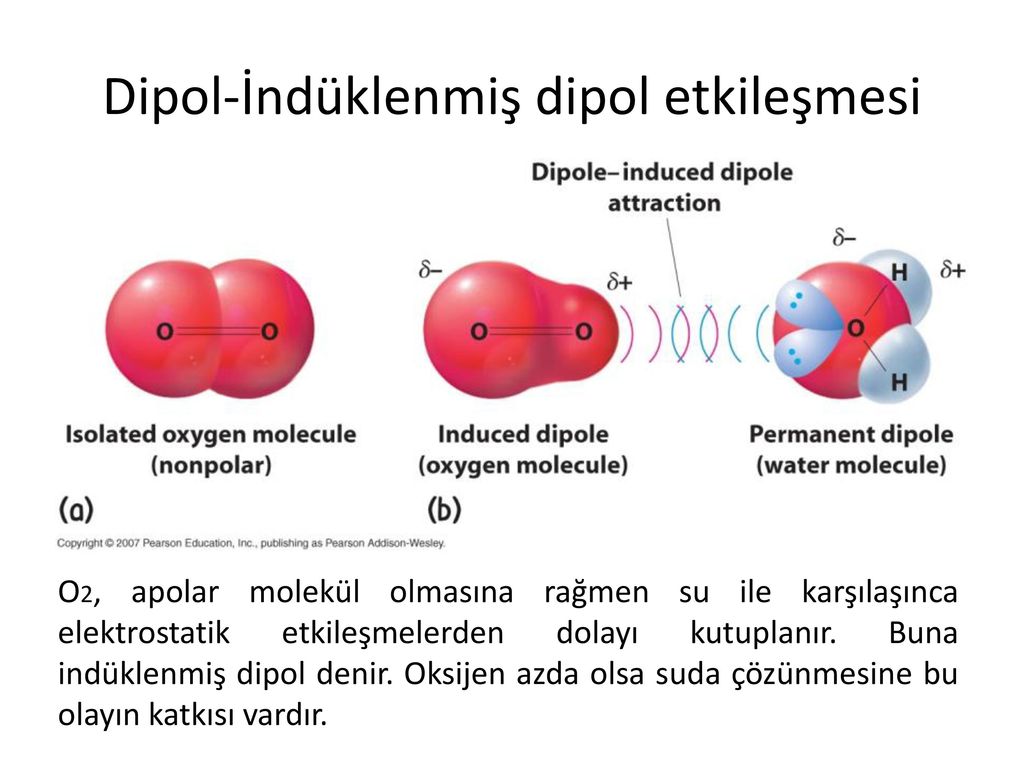

Интересно, что изомер транс имеет температуру плавления на выше ! Почему так?

Ответим на этот вопрос в следующем посте про температуры кипения и плавления.

Подводя итог , молекулярный дипольный момент зависит от величины и направления всех дипольных моментов в молекуле. Чем больше молекулярный диполь, тем более полярна молекула. Симметричные молекулы с сопоставимой структурой менее полярны, чем , поскольку их индивидуальный диполь компенсируется и нет результирующего дипольного момента.

Как всегда, ниже приведены некоторые практические задачи на молекулярный дипольный момент.

1.

Определите полярные связи и укажите направление чистого молекулярного дипольного момента, если он есть.

ответ

Этот контент предназначен только для зарегистрированных пользователей.

Нажмите здесь, чтобы зарегистрироваться!

Присоединившись к Chemistry Steps, вы получите мгновенный доступ к ответам и решениям для всех практических задач , включая более 20 часов видео по решению задач, викторин с несколькими вариантами ответов, головоломок, и мощный набор Органическая химия 1 и 2 Краткие учебные пособия .

2.

Учитывая, что водород более электроотрицателен, чем дейтерий, какая из следующих молекул, по вашему мнению, будет иметь больший дипольный момент?

ответ

Этот контент предназначен только для зарегистрированных пользователей.

Нажмите здесь, чтобы зарегистрироваться!

Присоединившись к Chemistry Steps, вы получите мгновенный доступ к ответов и решений для всех практических задач , включая более 20 часов видео по решению задач, викторин с несколькими вариантами ответов, головоломок, и мощный набор Органическая химия 1 и 2 сводных учебных пособий .