Условия потенциальности электрического поля. Вихри (ротор)

Условие возможности выражения напряженности поля через скалярную функцию, называемую потенциалом.

Выражение потенциала в интегральной форме:

Интеграл от вектора по замкнутому контуру должен быть равен нулю в потенциальном поле. Однако, рассматривая процессы движения жидкости или газа, можно заметить, что интеграл по замкнутому контуру от вектора скорости не равен нулю, если контур охватывает вихри или водовороты:

Таким образом, равенство (или не равенство) нулю конкретного интеграла служит признаком отсутствия (наличия) вихрей.

В случае плоского контура (контура, который лежит в одной плоскости) величина интеграла, отнесенного к площади, ограниченной контуром, характеризует среднюю плотность вихревого движения, ось которого направлена нормально к плоскости контура.

Вихрем или ротором называют векторную величину, определяющую интенсивность вихревого характера какого-либо вектора Е. Составляющая вектора n⁰ определяется выражением:

Где интеграл берется по контуру, лежащему в плоскости и ограничивающему площадь S, каждый линейный размер которой стремится к нулю. Нормаль n⁰ к площадке S связана с направлением обхода контура правилом правоходового винта.

Как вектор, вихрь rotE, может быть определен в декартовой системе координат по своим составляющим:

Данное уравнение выводится из формулы (2).

Пользуясь оператором Гамильтона, можно представить дифференциальную операцию rot E как векторное произведение рассматриваемого вектора и оператора набла:

Безвихревый характер потенциальных полей, помимо условия интегрального (формула (1)), приводящего, как это видно из формулы (2) к отсутствию вихрей:

Данное выражение может быть получено путем следующих рассуждений.

Если в формуле (1) слагающие напряженности могут быть представлены как соответствующие частные производные от некоторой скалярной функции φ(x, y, z), то есть если E = -grad φ, то:

Это следует из условия независимости порядка дифференцирования:

Если данное условие соблюдается, то произведя вычисления по формуле (3) придем к формуле (6). Также стоит обратить внимание и на следующее: из-за формального обращения с оператором Гамильтона по правилам векторной алгебры:

И немного практики.

Пример 1

В области электрического поля E_x = — Cy, E_y = Cx, E_z = 0 можно ли представить напряженность поля как градиент потенциала?

Решение

Если условие rot E = 0 выполняется, то мы можем представить Е как –grad φ. Произведя вычисления вихря по формуле (3) получим:

Как видим из результата, напряженность такого поля не может быть представлена в виде градиента – поле оказывается вихревым.

Подобное электрическое поле существует внутри длинной катушки, питаемой переменным током.

 Пример 2

То же самое, что и в предыдущем примере, но:

E_x = Cy, E_y = Cx, E_z = 0

Решение

Поле безвихревое, что подтверждается прямым вычислением. Его потенциал может быть представлен выражением φ = -Cxy и оно удовлетворяет уравнению Лапласа. Такое поле создается в первом квадранте плоскости xy, если по координатным осям расположены электроды с нулевым потенциалом, а электрод в виде гиперболического цилиндра xy = A = const, имеет потенциал φ = — AC.

Потенциальность электростатического поля

Потенциальность  электростатического  поля.

1. Условие потенциальности поля.

Силовое поле называется потенциальным, если работа сил поля при перемещении в нем зависит только от начальных и конечных точек пути и не зависит от формы траектории.

или:

 если работа сил поля при перемещении по  замкнутому контуру равна нулю.    

 

 В  _{электростатическое поле потенциально.}

 

А   _{— дифференциальная формулировка}

потенциальности поля.

2.) Скалярный потенциал

Так как  работа при перемещении заряда не зависит от траектории, то ее можно выразить через скалярную функцию _{, разность значений которой и определяет эту работу.}

Так как  _{всегда, то общим решением  уравнения будет:}

    _,

      где   _{(3. 1)}

Знак  «-» в (3.1) возник исторически  и означает, что  _{направлен в сторону убывания потенциала .}

Потенциал _{описывает тоже поле , т.е. потенциал определен с точностью до произвольной постоянной φ0 и не имеет определенного числового значения. Поэтому можно произвольно задать в любой точке пространства. Эта процедура называется нормировкой. Обычно (но не обязательно) полагается или}  

2

  

1

При перемещении заряда из точки 1 в точку 2 удельная работа: 

Таким образом, физический смысл имеет не абсолютное значение потенциала, а разность потенциалов между точками: разность потенциалов между двумя точками _{равна работе по перемещению единичного положительного заряда между ними.}

Здесь мы учли, что

3). Потенциал точечного заряда.

 

 

при  _:   

4. Потенциал системы точечных зарядов.
, где 
5. Потенциал непрерывно распределенного по объему заряда.

Разбиваем весь объем  _{на элементы , в каждом из которых находится заряд , и используем формулу из п.4:}

,

где _{— расстояние от объёма до точки вычисления потенциала.}

6. Потенциал поля поверхностно распределенного заряда.

Аналогично п5:

7. Свойства скалярного потенциала:

а) Конечность потенциала при распределении  заряда с конечной плотностью.

Запишем формулу  п.5 в сферических  координатах:

 

Потенциал _{системы зарядов, распределенной в конечной области пространства с конечной плотностью — конечен.}

Напомним, что  бесконечно большой  потенциал  _{точечного заряда в точке нахождения заряда обусловлен мнимой бесконечностью его плотности заряда}

.

б) Непрерывность потенциала.

_{, но     — должно быть конечно во всей области пространства.}

Т.о. Потенциал является непрерывной и конечной функцией с конечными производными по координатам.

 

Эти условия и свойства важны при решении дифференциальных уравнений для потенциала _.

8. Теорема Ирншоу:

Не существует такой  конфигурации неподвижных зарядов, которая была бы устойчивой, если нет  других сил, кроме кулоновских.

Или:

Замкнутая система неподвижных  зарядов не может находиться в  состоянии устойчивого 

равновесия (при условии, что между зарядами действуют только силы Кулона).

Доказательство.

Если положение устойчиво, то при  любом смещении должна существовать «возвращающая»  сила _{вблизи каждого заряда направлена по}  

_{— создается зарядом  внутри объема, что противоречит предложению о создании такого поля зарядами, находящимся вне поверхности.}

 

 

 




E-полей и потенциалов

E-полей и потенциалов

Рассчитать

Коэффициент сверхрелаксации: 1,0


Настройка

Предустановки: ДипольДиполь 2КругТочкаКонцентрическийКонцентрический 2КонденсаторКрышка2БанкаЗаряд в банкеЗаряд в банке 2УгловойУгловой и ЛинияУгловой, острый

Инструменты: Вытягивающий электрод
Стирающий электрод
Размер инструмента: Потенциал электрода: 0 В

Опции

Разрешение: 128 х 128

Количество цветов: 512
Цветовая схема:
(положительный, 0, отрицательный) Красный, белый, синийОранжевый, белый, фиолетовыйПурпурный, черный, зеленый

Данные

Показать поле
Показать датчик
Потенциал зонда:
Напряженность поля зонда:
Степень сходимости:

Эта программа вычисляет и отображает электрический потенциал по заданному шаблону «электроды» (т.

е. области с постоянным напряжением) в двумерном мире. Этот мир представлен сеткой квадратных ячеек, с границами, всегда фиксируемыми на уровне 0 В. Цвет представляет потенциал, указанный в цветовой схеме. выпадающий список.

Немного справочной информации:

Используя закон Гаусса, граничное условие нулевой плотности заряда между электродами, и отношения между электрический потенциал ( В ) и электрическое поле, мы можем найти уравнение Лапласа для электрического потенциала. Используя приближения для частных производных, мы можем показать, что в двух измерениях электрический потенциал в любой данной клетке является средним значением электрических потенциалов четырех соседние клетки.

С этим результатом мы можем использовать метод релаксации аппроксимировать электрический потенциал всех ячеек сетки. Эта программа зацикливается по каждой ячейке сетки и вычисляет электрический потенциал как среднее потенциала четырех соседних клеток. После нескольких циклов по сетке, это приближение сходится к решению для данной схемы электродов.

Для работы по программе:

Выберите рисунок электрода из списка пресетов или используйте рисовать и стирать инструменты для создания собственного рисунка.

Отрегулируйте размер инструмента для рисования и стирания электроды с помощью ползунка размера инструмента и выберите потенциал электрода, который будет рисуется с помощью ползунка электродного потенциала. Очистить все электроды (кроме граничные «электроды») сразу с помощью кнопки «Очистить электроды».

Расчет электрического потенциала либо поэтапно, до схождения, либо непрерывно с помощью соответствующих кнопок. Слово «расчет» появится, когда программа вычисляет потенциал. Приостановка, возобновление или сброс вычислений в любом из этих трех режимов с помощью кнопки «Пауза»/«Возобновить». и кнопки «Сбросить поля». «Конвергенция» здесь определяется как когда самое большое изменение потенциала для любой клетки на данном шаге расчета («степень сходимости» в поле «Данные») округляется до 0,000 В.

Используйте ползунок сверхрелаксации для ускорения конвергенции. Установка коэффициента чрезмерной релаксации слишком высокое значение (обычно не менее 2,0) делает расчет нестабильным.

Чтобы увидеть электрическое поле , установите флажок «Показать поле». Чтобы увидеть вектор поля и потенциал для данной ячейки , включите зонд с помощью флажка «Показать зонд», а затем щелкните/коснитесь и перетащите зонд в ячейку. Потенциалы даны в вольтах, а поля дано в В/ячейка; одна ячейка может быть любой единицей расстояния.

Используйте ползунок разрешения , чтобы изменить разрешение сетки. Если вычисление слишком медленно, попробуйте начать с более низкого разрешения, а затем увеличить разрешение с там. Измените количество цветов , используемых на дисплее, с помощью ползунка с соответствующим названием. Это можно эффективно использовать для просмотра контурной карты потенциала, используя меньшее количество цвета. Изменить цветовую схему , используемую в раскрывающемся списке цветовой схемы.

Для лучшей производительности на настольных компьютерах используйте Chrome.

Натаниэль Клемм, Государственный университет Вебера, на средства стипендии Beishline Fellowship

18.4 Электрический потенциал | Техасский шлюз

Цели обученияElectric PotentialПрактические задачиПроверьте свое понимание

Цели обучения

К концу этого раздела вы сможете делать следующее:

• Объяснять сходства и различия между электрической потенциальной энергией и гравитационной потенциальной энергией
• Рассчитать разность электрических потенциалов между двумя точечными зарядами и в однородном электрическом поле

Основные термины раздела

электрический потенциал

электрическая потенциальная энергия

Как вы узнали при изучении гравитации, масса в гравитационном поле обладает потенциальной энергией, что означает, что она может ускоряться и тем самым увеличивать свою кинетическую энергию. Эту кинетическую энергию можно использовать для совершения работы. Например, представьте, что вы хотите использовать камень, чтобы забить гвоздь в кусок дерева. Сначала вы поднимаете камень высоко над гвоздем, что увеличивает потенциальную энергию системы камень-Земля — поскольку Земля такая большая, что она не движется, поэтому мы обычно сокращаем это, говоря просто, что потенциальная энергия камня увеличивается. Когда вы бросаете камень, гравитация преобразует потенциальную энергию в кинетическую. Когда камень попадает в гвоздь, он вбивает гвоздь в дерево. Гравитационная потенциальная энергия — это работа, которую потенциально может совершить масса в силу своего положения в гравитационном поле. Потенциальная энергия — очень полезная концепция, потому что ее можно использовать с сохранением энергии для расчета движения масс в гравитационном поле.

Электрическая потенциальная энергия работает почти так же, но она основана на электрическом поле, а не на гравитационном поле. В силу своего положения в электрическом поле заряд обладает электрической потенциальной энергией. Если заряд может двигаться свободно, сила электрического поля заставляет его ускоряться, поэтому его потенциальная энергия преобразуется в кинетическую энергию, точно так же, как масса, падающая в гравитационном поле. Эту кинетическую энергию можно использовать для совершения работы. Электрическая потенциальная энергия — это работа, которую заряд может совершить благодаря своему положению в электрическом поле.

Аналогия между потенциальной энергией гравитации и потенциальной электрической энергией показана на рис. 18.23. Слева система шар-Земля получает гравитационную потенциальную энергию, когда шар находится выше в гравитационном поле Земли. Справа двухзарядная система получает электрическую потенциальную энергию, когда положительный заряд находится дальше от отрицательного заряда.

Рис. 18.23 Слева гравитационное поле указывает на Землю. Чем выше находится шар в гравитационном поле, тем выше потенциальная энергия системы Земля-шар. Справа электрическое поле указывает на отрицательный заряд.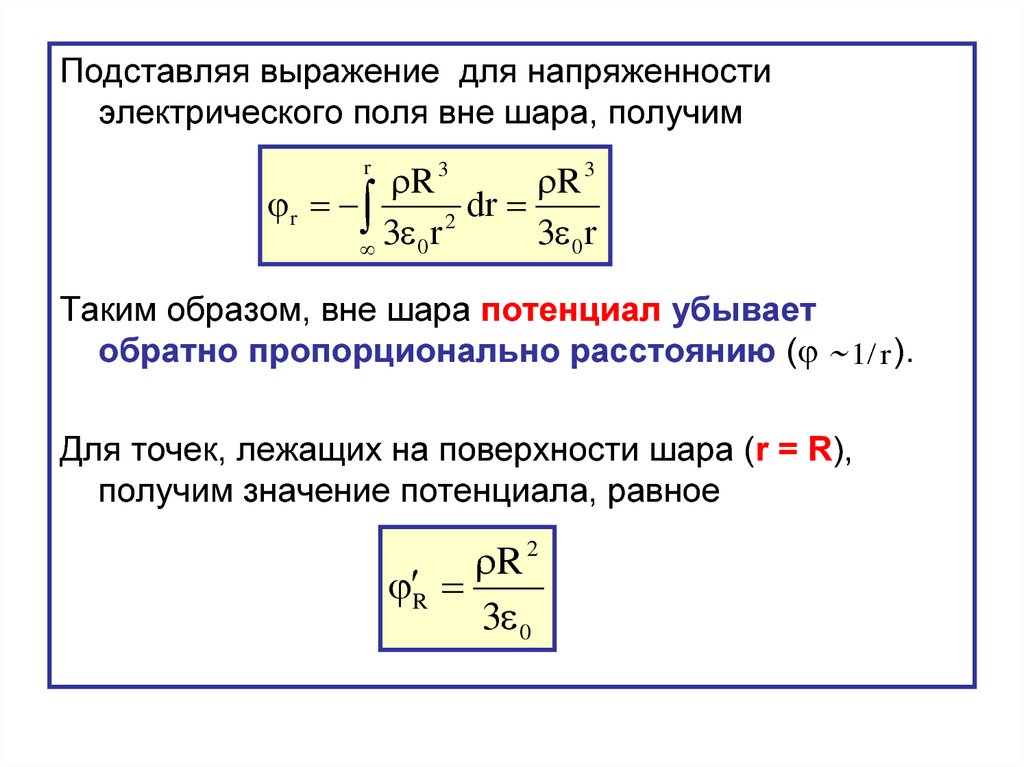 Чем дальше положительный заряд от отрицательного, тем выше потенциальная энергия двухзарядной системы.

Давайте использовать символ UGUG для обозначения гравитационной потенциальной энергии. Когда масса падает в гравитационное поле, ее гравитационная потенциальная энергия уменьшается. Закон сохранения энергии говорит нам, что работа, совершаемая гравитационным полем для ускорения массы, должна равняться потере потенциальной энергии массы. Если для обозначения этой работы использовать символ Wсовершенная гравитациейWсовершеннаягравитацией, то

18.18−ΔUG=Wсовершенная гравитацией,−ΔUG=Wсовершенная гравитацией,

где знак минус отражает тот факт, что потенциальная энергия шара уменьшается .

Работа силы тяжести над массой равна

18.19Wсовершенная гравитацией=−F(yf−yi),Wсовершенная гравитацией=−F(yf−yi),

, где F – сила тяжести , а yiyi и yfyf — начальное и конечное положения шара соответственно. Отрицательный знак потому, что гравитация направлена ​​вниз, что мы считаем отрицательным направлением. Для постоянного гравитационного поля у поверхности Земли F=mgF=mg. Изменение гравитационной потенциальной энергии массы равно 9или −mg(yf−yi), или ∆UG=mg(yf−yi).

Обратите внимание, что yf−yiyf−yi — это просто минус высоты h , с которой падает масса, поэтому мы обычно просто пишем ΔUG=−mghΔUG=−mgh.

Теперь применим те же рассуждения к заряду в электрическом поле, чтобы найти электрическую потенциальную энергию. Изменение ΔUEΔUE электрической потенциальной энергии представляет собой работу, совершаемую электрическим полем для перемещения заряда q от начального положения xixi до конечного положения xfxf (−ΔUE=Wdone по E-полю − ΔUE=Wdone по E-полю). Определение работы не меняется, за исключением того, что теперь работа выполняется электрическим полем: Для заряда, который падает через постоянное электрическое поле E , сила, приложенная к заряду электрическим полем, равна F=qEF=qE. Таким образом, изменение потенциальной электрической энергии заряда равно

18,21. −ΔUE=Wdone by E-field=Fd=qE(xf−xi)−ΔUE=Wdone by E-field=Fd=qE(xf−xi)

или

18,22 ΔUE=-qE(xf-xi).ΔUE=-qE(xf-xi).

Это уравнение дает изменение электрической потенциальной энергии заряда q при его перемещении из положения xixi в положение xfxf в постоянном электрическом поле E .

На рис. 18.24 показано, как эта аналогия работала бы, если бы мы находились близко к поверхности Земли, где гравитация постоянна. Верхнее изображение показывает ускорение заряда из-за постоянного электрического поля. Точно так же круглая масса на нижнем изображении ускоряется из-за постоянного гравитационного поля. В обоих случаях потенциальная энергия частицы уменьшается, а ее кинетическая энергия увеличивается.

Рис. 18.24 На верхнем рисунке масса ускоряется благодаря постоянному электрическому полю. На нижнем рисунке масса ускоряется из-за постоянного гравитационного поля.

Смотреть физику

Аналогия между гравитацией и электричеством

В этом видео обсуждается аналогия между потенциальной энергией гравитации и потенциальной электрической энергией. Он рассматривает понятия работы и потенциальной энергии и показывает связь между массой в однородном гравитационном поле, например, на поверхности Земли, и электрическим зарядом в однородном электрическом поле.

Нажмите, чтобы просмотреть содержимое

Если электрическое поле непостоянно, то уравнение ΔUE=−qE(xf−xi)ΔUE=−qE(xf−xi) становится неверным, и вычисление потенциальной электрической энергии становится более сложным. . Например, рассмотрим электрическую потенциальную энергию ансамбля двух точечных зарядов q1q1 и q2q2 одного знака, изначально находящихся очень далеко друг от друга. Начнем с размещения заряда q1q1 в начале нашей системы координат. Для этого не требуется электрической энергии, поскольку в начале координат нет электрического поля (поскольку заряд q2q2 находится очень далеко). Затем мы переносим заряд q2q2 с очень большого расстояния на расстояние р от центра заряда q1q1. Это требует некоторого усилия, так как электрическое поле заряда q1q1 прикладывает к заряду q2q2 силу отталкивания. Энергия, необходимая для сборки этих двух зарядов, может быть восстановлена, если мы позволим им снова разлететься. Таким образом, заряды обладают потенциальной энергией, когда они находятся на расстоянии r друг от друга. Получается, что электрическая потенциальная энергия пары точечных зарядов q1q1 и q2q2, находящихся на расстоянии r друг от друга, равна

18,23. UE=kq1q2rUE=kq1q2r

Напомним, что если заряды q1q1 и q2q2 могут свободно двигаться, они могут накапливать кинетическую энергию, разлетаясь друг от друга, и эту кинетическую энергию можно использовать для выполнения работы. Максимальное количество работы, которую могут совершить два заряда (если они летят бесконечно далеко друг от друга), определяется приведенным выше уравнением.

Обратите внимание, что если два заряда имеют противоположные знаки, то потенциальная энергия отрицательна. Это означает, что заряды имеют больший потенциал для совершения работы, когда они находятся на расстоянии 90 124 на расстоянии 90 125 друг от друга, чем когда они находятся на расстоянии р отдельно. Это имеет смысл: противоположные заряды притягиваются, поэтому заряды могут получить больше кинетической энергии, если они притягиваются друг к другу издалека, чем если бы они стартовали на небольшом расстоянии друг от друга. Таким образом, у них больше возможностей выполнять работу, когда они находятся далеко друг от друга. На рис. 18.25 показано, как потенциальная электрическая энергия зависит от заряда и разделения.

Рис. 18.25 Потенциальная энергия зависит от знака зарядов и их разделения. Стрелки на зарядах указывают направление, в котором заряды будут двигаться, если их отпустить. Когда заряды одного знака находятся далеко друг от друга, их потенциальная энергия мала, как показано на верхней панели для двух положительных зарядов. Ситуация обратная для зарядов противоположных знаков, как показано на нижней панели.

Электрический потенциал

Напомним, что для нахождения силы, приложенной фиксированным зарядом Q к любому произвольному пробному заряду q , было удобно определить электрическое поле, которое представляет собой силу на единицу заряда, приложенную Q к любому пробному заряду, который помещаем в его электрическое поле. Та же стратегия используется здесь с потенциальной электрической энергией: теперь мы определим электрический потенциал В , который представляет собой потенциальную электрическую энергию на единицу заряда.

18,24 В=UEqV=UEq

Предупреждение о неправильном понимании

Подчеркните разницу между электрической потенциальной энергией и электрическим потенциалом. Хотя последнее кажется сокращением от первого, эти два термина имеют разные значения.

Обычно электрический потенциал называют просто потенциалом или напряжением . Единицами измерения потенциала являются Дж/Кл, которые получили название 90 124 вольт 90 125 (В) в честь итальянского физика Алессандро Вольта (1745–1827). Из уравнения UE=kq1q2/rUE=kq1q2/r электрический потенциал на расстоянии р от точечной зарядки q1q1

18,25 В=UEq2=kq1r.V=UEq2=kq1r.

Это уравнение дает энергию, необходимую на единицу заряда, чтобы переместить заряд q2q2 из бесконечности на расстояние r от точечного заряда q1q1. Математически это записывается как

.

18,26 В=UEq2|R=r-UEq2|R=∞.V=UEq2|R=r-UEq2|R=∞.

Обратите внимание, что это уравнение на самом деле представляет разность электрического потенциала. Однако, поскольку второй член равен нулю, его обычно не записывают, и мы говорим об электрическом потенциале вместо разности электрических потенциалов или просто говорим о разности потенциалов или напряжении). Ниже, когда мы рассматриваем электрическую потенциальную энергию на единицу заряда между двумя точками, не бесконечно удаленными друг от друга, мы говорим об электрическом потенциале разница явно. Просто помните, что электрический потенциал и разность электрических потенциалов на самом деле одно и то же; первый используется только тогда, когда электрическая потенциальная энергия равна нулю либо в начальной, либо в конечной конфигурации заряда.

Возвращаясь теперь к электрическому потенциалу на расстоянии r от точечного заряда q1q1, обратите внимание, что q1q1 может быть любым произвольным точечным зарядом, поэтому мы можем опустить нижние индексы и написать просто

18,27 В=ккв.В=ккв.

Теперь рассмотрим электрический потенциал вблизи группы зарядов q ₁ , q ₂ и q ₃ , как показано на рис. 18.26. Электрический потенциал определяется с учетом электрического поля. Электрические поля следуют принципу суперпозиции и могут быть просто сложены вместе, поэтому электрический потенциал от разных зарядов также суммируется. Таким образом, электрический потенциал точки вблизи группы зарядов равен

18.28V=kq1r1+kq2r2+kq3r3+⋯.V=kq1r1+kq2r2+kq3r3+⋯.

, где r1, r2, r3,…,r1, r2, r3,…, — расстояния от центра зарядов q1, q2, q3,…q1, q2, q3,… до интересующей точки, как показано на рис. 18.26.

Рис. 18.26. Потенциал в красной точке представляет собой просто сумму потенциалов каждого отдельного заряда.

Теперь рассмотрим электрический потенциал в однородном электрическом поле. Из уравнения ΔUE=−qE(xf−xi)ΔUE=−qE(xf−xi) мы видим, что разность потенциалов при переходе от xixi к xfxf в однородном электрическом поле Е это

18,29 ΔV=ΔUEq=−E(xf−xi).ΔV=ΔUEq=−E(xf−xi).

Советы по достижению успеха

Из уравнения ΔV=−E(xf−xi)ΔV=−E(xf−xi) видно, что электрическое поле можно записать как

18,30E=ΔVxf−xiE=ΔVxf−xi

что означает, что электрическое поле имеет единицы В/м. Таким образом, если вы знаете разность потенциалов между двумя точками, рассчитать электрическое поле очень просто — вы просто делите разность потенциалов на расстояние!

Обратите внимание, что положительный заряд в области с высоким потенциалом испытывает силу, толкающую его к областям с более низким потенциалом. В этом смысле потенциал подобен давлению жидкости. Представьте себе трубу, содержащую жидкость, с жидкостью на одном конце трубы под высоким давлением и жидкостью на другом конце трубы под низким давлением. Если ничто не препятствует течению жидкости, она будет течь от конца высокого давления к концу низкого давления. Точно так же положительный заряд, который может свободно перемещаться, будет перемещаться из области с высоким потенциалом в область с более низким потенциалом. 9?

1. 6В
2. 12 В
3. 24 В
4. 32 В

Рабочий пример

Рентгеновская трубка

Стоматологи используют рентгеновские лучи для визуализации зубов и костей своих пациентов. Рентгеновские трубки, генерирующие рентгеновское излучение, содержат источник электронов, расположенный на расстоянии около 10 см от металлической мишени. Электроны ускоряются от источника к мишени однородным электрическим полем величиной около 100 кН/Кл, как показано на рис. 18.28. Когда электроны попадают в цель, возникает рентгеновское излучение. а) Какова разность потенциалов между источником электронов и металлической мишенью? б) Чему равна кинетическая энергия электронов, когда они достигают мишени, если предположить, что электроны стартовали из состояния покоя?

Рис. 18.28 В рентгеновской трубке через источник электронов протекает большой ток, вызывающий выброс электронов из источника электронов. Вылетевшие электроны под действием электрического поля ускоряются к мишени. Когда они попадают в цель, производится рентгеновское излучение.

СТРАТЕГИЯ ДЛЯ (A)

Используйте уравнение ΔV=-E(xf-xi)ΔV=-E(xf-xi), чтобы найти разность потенциалов при постоянном электрическом поле.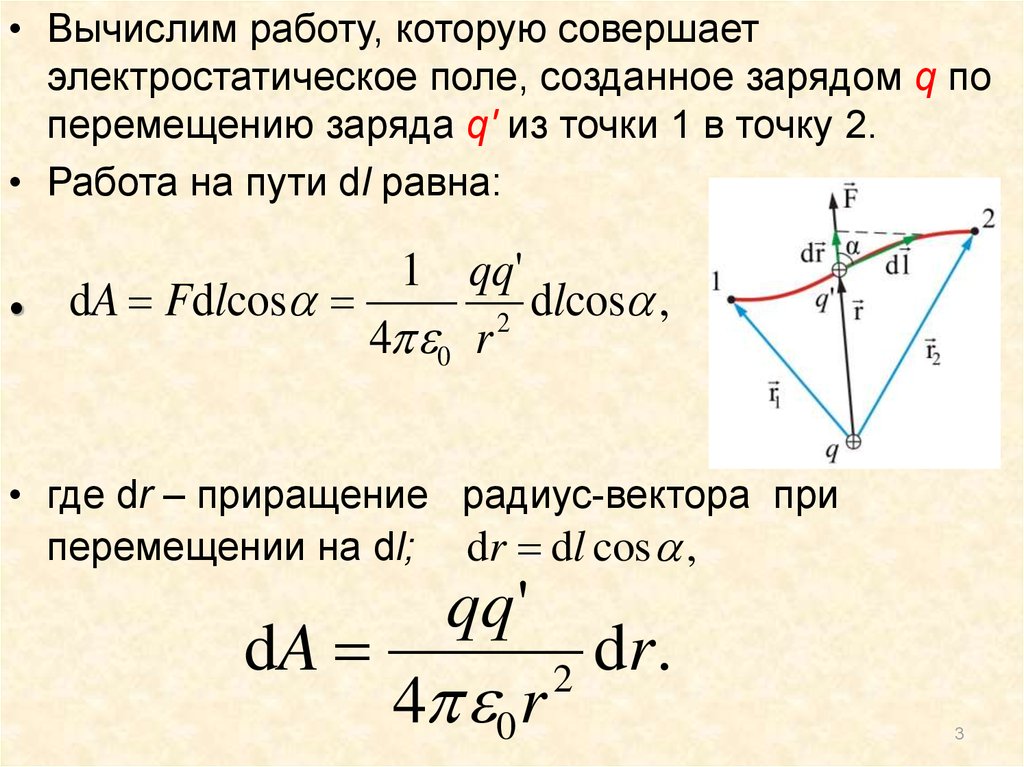 Определите исходное положение как xi=0xi=0 и целевое положение как xf=10 смxf=10 см. Для ускорения электронов в положительном x , электрическое поле должно указывать в отрицательном направлении x . Таким образом, сила F=qEF=qE, действующая на электроны, будет направлена ​​в положительном направлении x , потому что и q , и E отрицательны. Таким образом, E=-100×103 N/CE=-100×103 N/C.

Решение для (a)

Используя xi=0xi=0 и xf=10 см=0,10 mxf=10 см=0,10 м, уравнение ΔV=−E(xf−xi)ΔV=−E(xf−xi) говорит нам, что разность потенциалов между источником электронов и мишенью равна

18,31ΔV=−E(xf−xi)=−(−100×103 N/C)(0,10 m−0)=+10 кВ.ΔV=−E(xf−xi)=−(−100×103 N/C)(0,10 м−0)=+10 кВ.

Обсуждение для (a)

Разность потенциалов положительна, поэтому энергия на единицу положительного заряда выше у цели, чем у источника. Это означает, что свободные положительные заряды будут падать от мишени к источнику. Однако электроны имеют отрицательный заряд, поэтому они ускоряются от источника к цели, набирая кинетическую энергию по пути.

СТРАТЕГИЯ ДЛЯ (В)

Примените закон сохранения энергии, чтобы найти конечную кинетическую энергию электронов. При переходе от источника к мишени изменение потенциальной электрической энергии плюс изменение кинетической энергии электронов должно быть равно нулю, поэтому ΔUE+ΔK=0,ΔUE+ΔK=0. Изменение потенциальной электрической энергии при движении через постоянное электрическое поле определяется уравнением 100×103 N/CE=−100×103 N/C. Поскольку электроны начинают с покоя, их начальная кинетическая энергия равна нулю. Таким образом, изменение кинетической энергии — это просто их конечная кинетическая энергия, поэтому ΔK=KfΔK=Kf.

Решение для (b)

Снова xi=0xi=0 и xf=10 см=0,10 мxf=10 см=0,10 м. Заряд электрона равен q=-1,602×10-19 Cq=-1,602×10-19 C. Сохранение энергии дает

18,32ΔUE+ΔK=0,−qE(xf−xi)+Kf=0,Kf =qE(xf−xi. ).ΔUE+ΔK=0,−qE(xf−xi)+Kf=0,Kf=qE(xf−xi.).

Подставляя известные значения в правую часть этого уравнения, получаем 15 Дж.Кf=(−1,60×10−19 C)(−100×103 N/C)(0,10 m−0)=1,6×10−15 Дж.

Обсуждение для (б)

Это очень маленькая энергия. Однако электроны очень малы, поэтому их легко ускорить, и этой энергии достаточно, чтобы заставить электрон двигаться очень быстро. Вы можете найти их скорость, используя определение кинетической энергии, K=12mv2K=12mv2. В результате электроны движутся со скоростью более 100 миллионов миль в час!

Рабочий пример

Электрическая потенциальная энергия дверной ручки и пылинки

Снова рассмотрим дверную ручку из примера в предыдущем разделе. Дверная ручка рассматривается как сферический проводник с однородным статическим зарядом q1=-1,5 нКлq1=-1,5 нКл на его поверхности. Какова потенциальная электрическая энергия между дверной ручкой и пылинкой, несущей заряд q2=0,20 нКлq2=0,20 нКл на расстоянии 1,0 см от передней поверхности дверной ручки? Диаметр дверной ручки 5,0 см.

СТРАТЕГИЯ

Как и в предыдущем разделе, мы относимся к заряду так, как если бы он был сосредоточен в центре дверной ручки. Опять же, как вы сможете подтвердить на следующих уроках физики, мы можем сделать это упрощение, потому что заряд равномерно распределен по поверхности сферического объекта. Сделайте набросок ситуации и определите систему координат, как показано на изображении ниже. Мы используем +x+x, чтобы указать внешнее направление, перпендикулярное двери, с x=0x=0 в центре дверной ручки. Если диаметр дверной ручки 5,0 см, ее радиус равен 2,5 см. Таким образом, пылинка в 1,0 см от поверхности дверной ручки находится на расстоянии r=2,5 см+1,0 см=3,5 смr=2,5 см+1,0 см=3,5 см от центра дверной ручки. Для решения этой задачи используйте уравнение UE=kq1q2/rUE=kq1q2/r.

Решение

Заряд на дверной ручке q1=-1,5 nКл=-1,5×10-9 Кл, q1=-1,5 nКл=-1,5×10-9 Кл, а заряд на пылинке q2=0,20 nC=2,0×10−10 Cq2=0,20 nC=2,0×10−10 C. Расстояние r=3,5 см=0,035 mr=3,5 см=0,035 м. Подстановка этих значений в уравнение UE=kq1q2/rUE=kq1q2/r дает

18,34UE=kq1q2r=(8,99×109 Н⋅м2/C2)(−1,5×10−9 C)(2,0×10−10 C) (0,035 м)=-7,7×10-8J.UE=kq1q2r=(8,99×109 Н⋅м2/C2)(-1,5×10-9 C)(2,0×10-10 C)(0,035 м)=-7,7 ×10−8 Дж.

Обсуждение

Энергия отрицательная, а это значит, что энергия будет уменьшаться, то есть получать еще больше отрицательного по мере приближения пылинки к дверной ручке. Это помогает объяснить, почему пыль скапливается на объектах, несущих статический заряд. Однако обратите внимание, что изоляторы обычно собирают больше статического заряда, чем проводники, потому что любой заряд, который накапливается на изоляторах, не может перемещаться по изолятору, чтобы найти способ уйти. Они должны просто ждать, пока их уберет какая-нибудь пролетающая влажная пылинка или другой хозяин.

 

Практические задания

Каков электрический потенциал на расстоянии 10 см от заряда −10 нКл?

1. 9,0 × 10 ² В
2. 9,0 × 10 ³ В
3. 9,0 × 10 ⁴ В
4. 9,0 × 10 ⁵ В

Электрон ускоряется от 0 до 10 × 10 ⁴ м/с в электрическом поле. Через какую разность потенциалов прошел электрон? Масса электрона составляет 9,11 × 10 ^–31 кг, а его заряд равен −1,60 × 10 9возможность для двух масс совершать работу в силу их положения по отношению друг к другу. Каково аналогичное определение электрической потенциальной энергии?

1. Электрическая потенциальная энергия — это потенциальная возможность двух зарядов совершать работу благодаря их положению относительно исходной точки.
2. Электрическая потенциальная энергия — это способность двух зарядов совершать работу в силу их положения относительно бесконечности.
3. Электрическая потенциальная энергия — это способность двух зарядов совершать работу благодаря их положению относительно друг друга.
4. Электрическая потенциальная энергия — это способность отдельных зарядов совершать работу благодаря их положениям относительно их конечных положений.

Упражнение 12

Отрицательный заряд находится на расстоянии 10 м от положительного заряда.