Момент силы | 7 класс

Содержание

Момент силы зависит от длины плеча. Для многих подобная фраза — просто сухой набор фактов. На самом деле, если разобраться, за терминами «длина плеча», «момент силы» прячутся удобные и вполне понятные физические концепции. На данном уроке мы приподнимем над всем этим завесу тайны, а также откроем для себя условие равновесия и правило моментов. Нюансы а-ля в чем там измеряется момент силы и формула момента силы прилагаются!

Момент силы: вновь Архимед и его рычаг

Поговаривают, что древнейшим открытием и в какой-то степени самым первым научным достижением человека можно смело называть рычаг. Удивительно, но наши предки на уровне интуиции понимали, что увесистый камень намного проще поднять или передвинуть с помощью самой обычной палки. При этом удивляет больше не наличие палки во всей этой истории, а осознание первобытным человеком принципа простых механизмов. Ведь палки первые разумные жители планеты специально искали подлиннее. Они понимали: чем длиннее, тем будет проще совершить работу.

«Катить проще, чем тянуть» — еще одно древнейшее «научное»  открытие примитивного человека наряду с рычагом.

Принцип рычага передавался из уст в уста, от одного племени к другому, от одного поколения к следующему. Мы не знали, почему это работает. У нас не было формул, не было определений. Был лишь рычаг в самых его разных формах проявления и четкое знание — возьмись подальше от точки опоры, если тяжело.

И лишь в третьем веке до нашей эры Архимед впервые произвел необходимые математические расчеты. Он наконец описал теорию рычага, которой мы пользуемся и по сей день. Он первым связал друг с другом понятия груза, плеча и силы. Как гласит легенда, осознав масштабы своего открытия, воскликнул: «Дайте мне точку опоры, и я переверну Землю!»

Благодаря опытам Архимеда, его фундаментальному пониманию закона равновесия рычага, впоследствии возникла крайне важная физическая величина — момент силы.  

Закон равновесия: опыт с грузами

Определить момент силы можно разными способами. Мы воспользуемся самым простым. Нам достаточно вспомнить условие равновесия рычага и провести несложный опыт с подвешенными грузами. 

Во-первых, возьмем небольшую деревянную балку. К ее верхнему концу прикрепим болтом мерную линейку таким образом, чтобы крепление располагалось в центре тяжести линейки (рисунок 1). Далее к линейке прикрепим по сантиметровым делениям два крючка, за которые будем подвешивать грузики разной массы. Начнем с отметок $10 \space см$ и $20 \space см$ — по пять влево и вправо от центра тяжести в $15 \space см$. 

Рисунок 1. Простая система из линейки, балки, крепления и крючков

Возьмем грузик массой $20 \space г$ и подвесим его за крючок (рисунок 2). Очевидно, что рычаг в результате не окажется в положении равновесия. 

Рисунок 2. Справа от точки опоры рычага подвешиваем первый грузик массой $20 \space г$

Теперь с другой стороны от центра тяжести подвесим грузик массой $40 \space г$ (рисунок 3). Очевидно, что рычаг снова не окажется в положении равновесия: с левой стороны на плечо рычага действует бó‎льшая сила $mg$. 

Рисунок 3. Отклонение рычага в левую сторону при подвешивании второго грузика массой $40 \space г$

Приводим рычаг в равновесие

Интуитивно мы понимаем, что дабы соблюсти условие равновесия данной системы, один из грузиков нужно куда-то сместить. Мы так же интуитивно понимаем, что если смещать грузик массой $40 \space г$, его нужно подвесить за крючок, располагающийся ближе к точке опоры. Смещать грузик массой $20 \space г$ нужно в другую сторону — подальше от точки опоры.

Вопрос на миллион: если, скажем, мы хотим перевесить двадцатиграммовый грузик, на сколько делений должно увеличиться плечо груза?

Используем стандартный метод проб и ошибок. Перевешивая крючок с грузиком по разным отметкам на линейке, мы обнаружим, что рычаг придет в положение равновесия, если двадцатиграммовый грузик подвесить на расстоянии десяти сантиметров от точки опоры — на отметке $25 \space см$ (рисунок 4). Обратите внимание на то, как пропорциональны получаемые величины: грузики массой $40 \space г$ и $20 \space г$ уравновешивают друг друга на плечах длиной $5 \space см$ и $10 \space см$ соответственно. 

Рисунок 4. Рычаг в положении равновесия

Условие равновесия

Именно таким образом Архимедом было сформулировано условие равновесия рычага. Можно долго перевешивать грузики, пользоваться различными массами, рычагами короткими, рычагами длинными, но одна вещь всегда будет объединять все элементы и переменные:

Рычаг находится в положении равновесия при условии, что отношение масс, подвешенных грузов, будет обратно пропорционально отношению расстояний от точки опоры до центров тяжести грузов:
$\frac{m_1}{m_2}=\frac{l_2}{l_1}$.

Если от масс перейти к силам, формулу можно улучшить до следующего вида:
$\frac{m_1g}{m_2g} = \frac{l_2}{l_1}$.

Лучше, но все равно не то. Где гарантии, что на наш абстрактный грузик будет действовать только сила тяжести? Ведь на грузик можно и надавить. Так что улучшим пропорцию еще раз и придем к окончательному математическому выражению под условие равновесия:
$\frac{F_1}{F_2} = \frac{l_2}{l_1}$,
где $F_1$ и $F_2$ — силы, действующие на рычаг, $l_1$ и $l_2$ — плечи сил.

Таким образом: 

Рычаг находится в положении равновесия, когда отношение сил, действующих на рычаг, обратно пропорционально отношению плеч этих сил.  

А теперь заметим, что согласно основному свойству пропорции из формулы выше получается следующее равенство:
$F_1\cdot l_1 = F_2\cdot l_2$.

Ранее мы с подобным не сталкивались — с произведением силы на плечо силы. Именно это произведение и называется в физике момент силы.

Определение момента силы

Момент силы — физическая величина, характеризующая действие силы. Равняется произведению модуля силы на ее плечо.

Формула момента силы соответственно следующая:

$M = F \cdot l$,

где $F$ — модуль силы, $l$ — длина плеча.

Обратите внимание на то, как выглядит формула момента силы: в физике момент силы обозначается заглавной латинской литерой $M$ и измеряется в $Н \cdot м$ — в ньютонах на метр. Характеризует момент силы, как мы указали в определении, действие силы.

Так-так, в чем измеряется момент силы?

Еще раз, формула момента силы включает в себя произведение модуля силы на длину плеча. Сила $F$ измеряется в ньютонах. Длина плеча, как и любая другая длина, согласно СИ измеряется в метрах. Ну и в чем же тогда измеряется момент силы? В ньютонах на метр ($H\cdot м$), разумеется.

И как понять, что характеризует момент силы?

Возьмем гаечный ключ. Ухватимся рукой за его конец и приложим некоторое усилие, чтобы провернуть гайку. После перехватим гаечный ключ примерно до середины ручки и также попробуем приложить некоторое усилие. Во втором случае провернуть гайку будет сложнее, чем если бы мы держались за конец ручки инструмента.

Рисунок 5. Опыт с гаечным ключом. Обратите внимание на направление момента силы $M$

Причина? Образуются разные величины момента силы! Помните, как мы говорили о механическом выигрыше на прошлом уроке? При нем образуется бóльший момент силы.

Иными словами, момент силы — это и есть в своем роде величина усилия. Чем больше момент, тем быстрее двигается предмет, тем проще он проворачивается, тем легче выполняется действие. Формула момента силы наглядно это демонстрирует.

Как рассчитать момент силы

Момент силы всегда рассчитывается как произведение модуля силы на плечо силы:
$M = F \cdot l$.

Иногда определять приходится результирующий момент — когда на тело действует несколько разнонаправленных сил. Однако подобные «превратности» нам встретятся в программе лишь через пару лет.

Момент силы трапеции

Для примера возьмем нечто отвлеченное от привычных нам двуплечих рычагов — ясно, что внутри подобной механической системы плечо силы чаще всего будет совпадать с плечом рычага, так что сложности как таковой с расчетом плеча силы не возникнет. Представим вместо этого, что мы раскручиваем прикрепленную к поверхности фигуру в форме трапеции. Ого!.. 

Итак, наша вращающаяся трапеция. Силу мы прикладываем к концу фигуры — направление силы указано на изображении (рисунок 6). Согласитесь, увидеть плечо силы для подобной схемы движения уже не так просто, особенно когда глаз привык к рычагам.

Рисунок 6. Приложение силы к трапеции

Не паникуем и вспоминаем, что плечо силы есть перпендикуляр к линии действия силы, опущенный из точки опоры или, вернее сказать, из оси вращения (рисунок 7).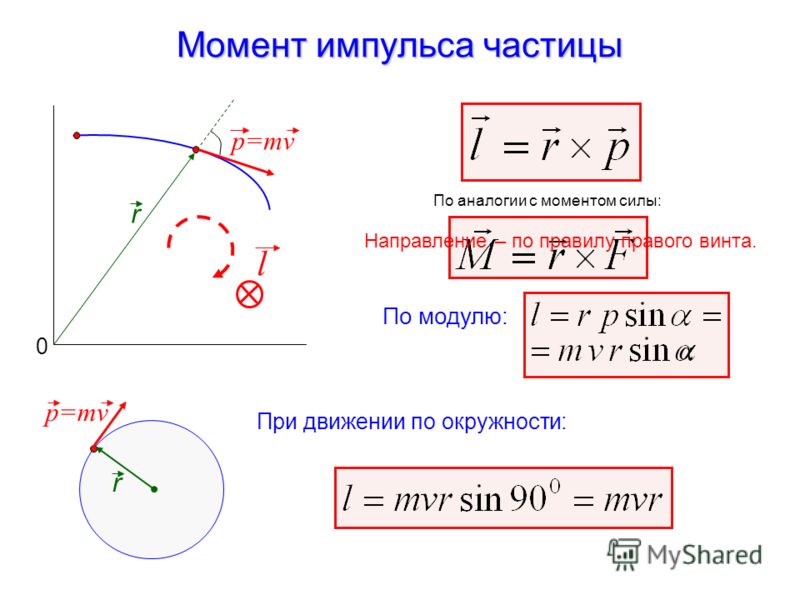

Рисунок 7. Плечо силы трапеции

Плечо силы будет равно длине отрезка $OA$. Ось вращения трапеции находится в точке $О$. Все гениальное просто, согласны?

Знак момента силы

Еще один немаловажный момент при расчете момента силы — знак величины. Момент может быть отрицательным или положительным. Это зависит от того, в каком направлении действует сила, приложенная к телу. Если она вращает тело по часовой стрелке, то момент силы считается положительным. Если наоборот — против часовой стрелки, то момент считается отрицательным. 

Рисунок 8. Знак момента силы

Может ли момент быть нулевым? Конечно, почему нет. Логично предположить, что в случае, если плечо силы равно нулю, то сила не создает никакого момента. Например, если вы надавите на ось вращения, сдвинуть при таком приложении силы что-либо невозможно.

Задача на моменты

Образавр предлагает решить задачу самостоятельно!

На земле лежит палка массой $20 \space кг$ и длиной $4 \space м$. Палку приподнимают за конец, прикладывая усилие в $120 \space Н$. Какие моменты при этом создают силы, действующие на доску? Моменты силы тяжести в поднятом положении палки и в вертикальном положении к земле равны.

Дано:
$m = 20 \space кг$
$d = 4 \space м$
$F = 120 \space Н$

$M — ?$

Рисунок 9. Схема рычага к задаче

Решение задачи на моменты

Показать решение и ответ

Скрыть

На палку действуют: сила реакции опоры $\vec{N}$, сила тяжести $m\vec{g}$ и внешняя сила, которую мы прикладываем к концу, $\vec{F}$. Ось вращения при этом располагается в точке $B$: мысленно представим, что палка совершает вращательное движение, а так как точка $B$ будет находиться в центре полученной окружности, она и будет считаться осью вращения.

Плечо силы реакции опоры $\vec{N}$ равно нулю: точка приложения силы и ось вращения совпадают. Следовательно $M_N$ силы реакции опоры мы можем определить сразу. Он равен нулю:
$M_N = 0$.

Далее опускаем перпендикуляр из оси вращения $B$ к внешней силе $\vec{F}$.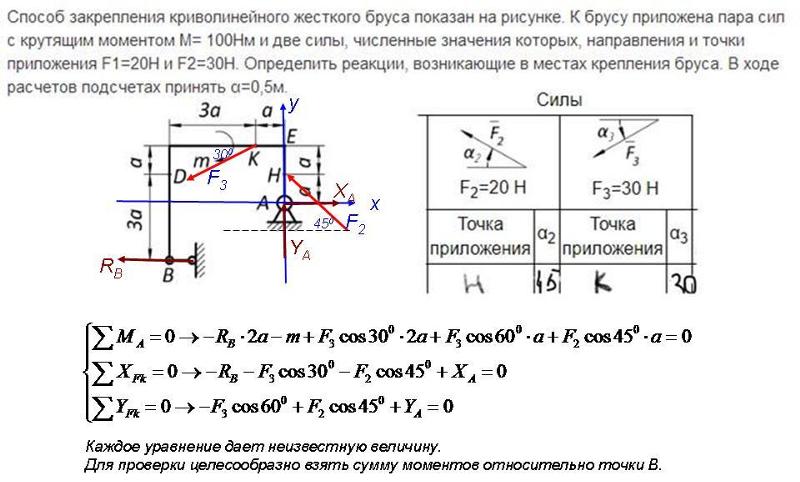 Получаем, что плечо внешней силы $\vec{F}$ равно длине палки $d$:
$l_F = d$.

По формуле $M = F \cdot l$, зная, что по условию задачи длина палки составляет $4 \space м$, а модуль внешней силы равен $120 \space Н$, рассчитаем момент внешней силы $M_F$. Вращение происходит по часовой стрелке, следовательно, момент будет положительным по знаку.

Считаем:
$M_F = 120 \cdot 4 = 480 \space H \cdot м$.

Нюанс и финальный расчет

Если допустить, что момент силы тяжести $M_{mg}$ в поднятом положении палки равен моменту в вертикальном положении к земле, то плечо силы тяжести $l_{mg}$ равно половине длины палки:
$l_{mg} = \frac{1}{2} \cdot d =2 \space м$.

Примечание. Подобное допущение необходимо исключительно для простоты расчетов. Если бы пришлось определять плечо силы тяжести «честно», в задаче также должны фигурировать как минимум высота подъема палки и угол подъема. Для вычисления плеча в треугольнике понадобились бы теорема косинусов и признаки подобия треугольников. Такие дела… Поэтому считаем «нечестно». Нахождением сложных плеч вы будете заниматься в курсе статики для 10 класса.

Теперь рассчитаем момент силы тяжести $M_{mg}$ по формуле моментов, учитывая, что движение происходит против часовой стрелки. Момент отрицательный:

$M_{mg}=-\frac{1}{2}\cdot mg\cdot l_{mg}=-0.5 \cdot 20 \cdot 9.8 \cdot 2 =-196~Н \cdot м$.

Ответ: $M_N = 0$, $M_F = 480 \space Н\cdot м$, $M_{mg} = -196 \cdot Н \cdot м$.

Правило моментов

Остается последнее — разобраться, зачем нужно отрицательное значение момента силы.

Ранее мы говорили о том, что условие равновесия рычага — обратная пропорциональность отношений сил к плечам этих сил. Однако условие равновесия можно задать и через смежное понятие момента силы. В некоторых случаях даже удобнее для вычислений. 

Рисунок 10. Трапеции в состоянии равновесия

Вернемся к нашей вращающейся трапеции. Представим, что вы стоите и прикладываете к одному концу трапеции силу $\vec{F}_1$. Ваш друг берется за другой конец трапеции и тянет фигурку в противоположную сторону c силой $\vec{F}_2$. Вы в одну сторону, он в другую. При этом трапеция вращаться никуда не хочет. Она упрямо находится в положении равновесия. Но, казалось бы, моменты сил создаются. Где движение?

Правило моментов — формула

Дело в том, что один момент силы, условно говоря, «гасит» другой. Математически вычитается. Как только создаваемый вами момент силы превысит тот, что создается вашим другом, фигурка начнет движение по часовой стрелке, к вам. Если друг поднажмет, то трапеция пойдет против часовой стрелки, от вас.

Таким образом, мы можем складывать все моменты, действующие на тело, чтобы понимать, движется ли тело, и если да, то в какую сторону. Знак числа — удобный математический инструмент, позволяющий работать с направлениями. Если сумма всех моментов положительна, вращательное движение идет по часовой стрелке.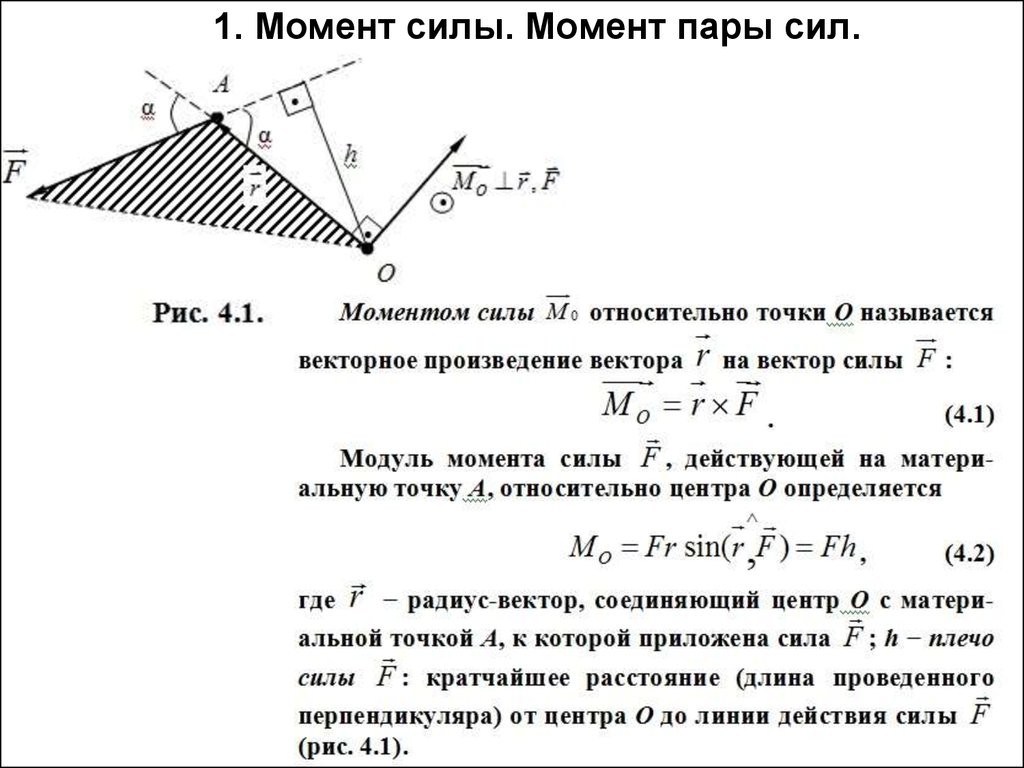 Если отрицательна — против часовой.

А если сумма моментов равна нулю?

Логично, что тогда тело находится в положении равновесия. Оно не двигается. Вот как мы можем получить условие равновесия (неважно — рычага или другого тела), выраженное через момент силы.

Подобное равенство называется правило моментов.

Тело находится в состоянии покоя, если алгебраическая сумма всех моментов сил, приложенных к телу, равняется нулю:
$\sum_i M_i= M_1+M_2+…+M_i =0$. 

{"questions":[{"content":"Момент силы рассчитывается по формуле[[choice-1]]","widgets":{"choice-1":{"type":"choice","options":["$M = \\frac{F}{l}$","$M = Fl$","$M = \\frac{F_1l_1}{F_2l_2}$","$M = Al$"],"answer":[1]}},"hints":[]}]}

Момент силы – формула, определение, свойства кратко (7 класс)

4.3

Средняя оценка: 4.3

Всего получено оценок: 88.

4.3

Средняя оценка: 4.3

Всего получено оценок: 88.

Из курса физики в 7 классе известно, что сила имеет три параметра: точку приложения, модуль и направление. Для вращательного движения точка приложения приобретает особое значение. В расчетах оказывается целесообразным заменить силу другим, более удобным понятием, учитывающим точку приложения, — моментом силы. Рассмотрим его суть, дадим определение, выведем формулу момента силы.

Сила при вращательном движении

Вращательное движение отличается от поступательного тем, что различные точки проходят различное расстояние и имеют различную мгновенную скорость, в зависимости от расстояния до оси вращения. Сила, приложенная к вращающемуся телу, также по-разному влияет на точки, лежащие на разном расстоянии от оси.

Фактически тело, начинающее вращение под действием силы, представляет собой рычаг второго рода с точкой опоры на оси вращения. И чем дальше от опоры находится точка приложения силы, тем меньшая сила требуется для движения рычага. Если приложить силу вдвое дальше от точки опоры, то для поворота рычага на один и тот же угол потребуется сила вдвое меньше. То есть для одного и того же поворота произведение силы на радиус поворота оказывается одинаковым.

Рис. 1. Рычаг второго рода.

Момент силы

В динамике вращательного движения важна не непосредственно величина силы, а произведение этой величины на расстояние от точки вращения. Это произведение называется моментом силы, обозначается буквой $M$:

$$M=F_\tau R$$

Из приведенной формулы можно получить размерность момента: поскольку сила измеряется в ньютонах, а радиус — в метрах, единица измерения момента силы получается равной ньютон-метру. Радиус вращения при этом нередко называют «плечом силы» $l$.

Рис. 2. Момент силы.

Обратите внимание, что вращательное движение создает только компонента силы, направленная перпендикулярно радиусу поворота, — тангенциальная составляющая силы:

$$F_\tau = F sin \alpha,$$

где $\alpha$ — это угол между радиус-вектором точки, к которой приложена сила $F$, и вектором приложения этой силы.

В самом деле, если сила направлена от точки приложения точно в сторону оси вращения, никакого вращательного движения создать с помощью этой силы не получится, какой бы модуль у этой силы не был. Формула также подтверждает это — синус угла между вектором силы, направленной точно на ось, и радиус-вектором точки приложения равен нулю, а значит, и тангенциальная составляющая силы также будет равна нулю. Момент такой силы, соответственно, также будет нулевым. Создать вращение будет невозможно.

Вращение невозможно создать также в случае, когда сила приложена непосредственно к оси вращения, независимо от ее направления. Радиус-вектор точки приложения силы при этом равен нулю, и определить тангенциальную составляющую приложенной силы невозможно. Момент такой силы оказывается нулевым.

Знак момента силы

Тангенциальная составляющая силы, входящая в формулу момента силы, может иметь два направления. В зависимости от направления такой момент силы может как увеличивать скорость вращения тела, так и уменьшать ее.

Для учета этой разницы вводится такое свойство момента, как знак.

Поскольку угол на координатной плоскости отсчитывается в направлении против часовой стрелки, то момент силы, поворачивающий тело в этом направлении, считается положительным.

Если момент силы поворачивает тело по часовой стрелке, он принимается отрицательным.
Рис. 3. Угол поворота.

Что мы узнали?

Для вращательного движения особую роль играет точка приложения силы. Поэтому при исследовании вращательного движения используется не понятие силы, а понятие момента силы, который равен произведению тангенциальной составляющей силы на радиус поворота и измеряется в ньютон-метрах.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4.3

Средняя оценка: 4.3

Всего получено оценок: 88.

---

А какая ваша оценка?

Формула момента

с решенными числами

Момент относится к очень короткому периоду времени. Если вы рассматриваете качели, размещение грузов с обеих сторон делает их сбалансированными. Если вы прибавите дополнительный или меньший вес, с одной стороны, качели перестанут быть сбалансированными, и это называется моментом неуравновешенности.

Мерой эффекта поворота является крутящий момент. Сила, действующая на тело крутящего момента, называется моментом силы.

Формула момента дается

Момент силы = F x d

Где,

F — приложенная сила,

d — расстояние от неподвижной оси,

Момент силы выражается в ньютон-метрах (Нм).

Формула момента силы может применяться для расчета момента силы как для уравновешенных, так и для неуравновешенных сил.

Решенные примеры

Пример 1

Метровая линейка 200 см поворачивается в средней точке (в точке 50 см). Если гиря в 10 Н подвешена к отметке 30 см, а гиря в 20 Н подвешена к отметке 60 см, определите, будет ли измерительная линейка оставаться сбалансированной над своей точкой опоры или нет.

Решение:

Согласно принципу моментов, когда тело находится в вращательном равновесии, то

Суммарные моменты против часовой стрелки = Суммарные моменты по часовой стрелке

Всего моментов против часовой стрелки:

Длина плеча рычага = (50 – 30) = 20 см

= 0,20 м

Поскольку длина плеча рычага равна расстоянию от его середины, где приложена уравновешенная сила = 10 Н

Момент против часовой стрелки = плечо рычага x прилагаемое усилие

= 0,20 х 10 = 2 Нм

Момент по часовой стрелке: Длина плеча рычага = (60 – 50)

= 10 см

= 0,10 м.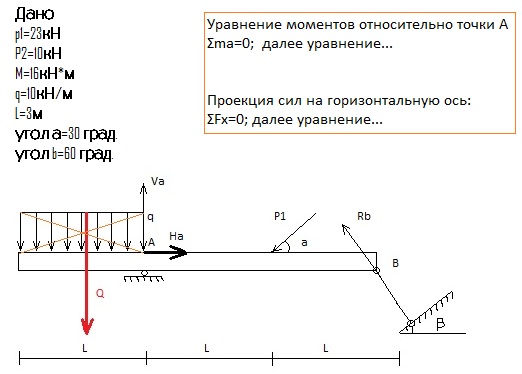

Поскольку длина плеча рычага равна расстоянию от средней точки, относительно которой приложена уравновешенная сила = 20 Н

Момент по часовой стрелке = плечо рычага x приложенная сила

                             = 0,10 × 20 = 2 Н·м

Следовательно,

Поскольку общий момент против часовой стрелки = общий момент по часовой стрелке = 2 Нм, в соответствии с принципом моментов он находится в равновесии вращения, т. е. измерительная линейка остается сбалансированной относительно своей оси.

Пример 2

Метровая линейка длиной 500 см повернута в средней точке. Если к точке 20 см подвешен груз массой 2 Н, рассчитайте, какой вес необходимо приложить к отметке 80 см, чтобы удерживать его в равновесном положении.

Решение:

В соответствии с принципом моментов, чтобы объект находился в равновесии вращения, сумма моментов, действующих против часовой стрелки, и моментов, действующих по часовой стрелке, должна быть равна. Таким образом, груз, подвешенный к отметке 80 см, должен создавать момент по часовой стрелке, равный моменту против часовой стрелки, создаваемому грузом, подвешенным на левой стороне измерительной линейки.

Момент против часовой стрелки:

Длина плеча рычага = (50 – 20)

= 30 см

= 0,30 м

Поскольку длина плеча рычага равна расстоянию от его средней точки, в которой оно уравновешено

Приложенная сила = 2 Н

Момент против часовой стрелки = плечо рычага x приложенная сила

= 0,30 х 2 Н

= 0,6 Н·м

Момент по часовой стрелке:

длина плеча рычага = (80 – 50)

= 30 см

= 0,30 м

Поскольку длина плеча рычага равна расстоянию от приложенной к нему Силы.

Пусть это будет «F».

Таким образом, момент по часовой стрелке = F x 0,30

= 0,30 Ф Н·м

Момент по часовой стрелке = Момент против часовой стрелки

0,30 F = 0,6

Ф = 2 Н

Груз массой 2 Н необходимо повесить на высоте 80 см, чтобы линейка была сбалансирована.

Следите за новостями BYJU’S, чтобы не пропустить такие интересные статьи. Кроме того, зарегистрируйтесь в «BYJU’S — The Learning App», чтобы получить множество интерактивных, увлекательных видеороликов, связанных с физикой, и неограниченную академическую помощь.

 

Формула момента

— GeeksforGeeks

Момент — это в основном сила, которая определяется как движение, направленное на вращение тела вокруг определенного положения. Давайте разберемся в этом моменте на примерах. Если кто-то хочет закрыть окно, он просто отталкивает ручку пальцем, и окно плавно закрывается. Теперь попробуйте снова закрыть окно, но на этот раз поднесите палец слишком близко к петле и посмотрите, не слишком ли тяжело. Силы используются для того, чтобы заставить любое тело или объект вращаться. Следовательно, поворотное действие силы известно как момент силы. Есть еще много примеров моментов в нашей повседневной жизни, и это

• Осмотр достопримечательностей в парке
• Открытие консервной банки
• Использование рычага для подъема большого груза
• Молоток используется для удаления гвоздей и т. д.

Момент силы   

Момент силы – это движение который заставляет тело или объект вращаться и также известен как крутящий момент. Он также определяется как произведение силы и перпендикулярного расстояния. Момент имеет как величину, так и направление.

Формула момента

Рассчитывается по формуле

M = F × d

Где M — момент силы,

F — приложенная сила

d — расстояние от фиксированного положения.

Эта формула применима как для уравновешенных, так и для неуравновешенных сил. Единицей измерения момента в системе СИ является ньютон-метр (Нм). Его размеры составляют [ML ² T ^-2 ], а его направление задается правилом большого пальца правой руки.

Принцип момента

Он утверждает, что если система находится в равновесии, то сумма ее моментов по часовой стрелке будет равна сумме ее моментов против часовой стрелки.

Момент по часовой стрелке = момент против часовой стрелки.

F ₁ × d ₁ = F ₂ × d _2.

• Момент по часовой стрелке. Сила заставляет объект или тело вращаться по часовой стрелке. Это воспринимается как положительное.
• Момент против часовой стрелки. Сила заставляет объект или тело поворачиваться против часовой стрелки. Он воспринимается как отрицательный.

Термин Равновесие определяется как «это происходит, когда все силы, действующие на тело, уравновешены».

Применение принципа моментов

• Мы можем найти массу объекта.
• В простых машинах.
• Помогает понять, как расположены и организованы физические величины.

Пара 

Пара определяется как пара двух сил, которые равны по величине, но их направления противоположны друг другу, а движения линий не совпадают.

Формула пары:

τ = F × d.

S.I единица пары = ньютон-метр (Нм) и размеры [ML ² T ² ].

Здесь силы равны и противоположны, поэтому мы получаем, что сила равна нулю, а линейное ускорение отсутствует.

Несколько применений пары

• Открытие и закрытие крышки бутылки.
• С помощью ключа откройте шкафчик.
• Поворот отвертки.
• Штурвал, установленный водителем автобуса.

Импульс 

Называется свойством движения объекта. Импульс определяется как произведение массы и скорости объекта. Обозначается символом «р».

Формула импульса,

p = m × v

Где p = импульс тела или объекта

m = масса объекта

v = скорость объекта.

Единица количества движения в системе СИ – кг м/с.

Вот несколько задач на данный момент.

Примеры задач Найдите момент, если вес мальчика 20 Н.



Решение: 

Учитывая, что вес мальчика создавал момент, направленный против часовой стрелки.

Момент = Сила × расстояние0003

М = 20 × 3

М = 60 Нм.

Вопрос 2: Момент силы 20 Н относительно неподвижной точки равен 2 Нм. Вычислите расстояние от точки до линии действия силы.

Решение :

Дано, Сила = 20 Н и Момент = 2 Нм.

Используя формулу момента M = F × d

2 = 20 × d 

d = 2/20

d = 0,1 м.

Вопрос 3: Найдите силу, приложенную к двери, вызывающую момент 10 Нм, если расстояние от оси петли до точки на двери, где была приложена сила, составляет 2 м.

 Решение:

Дано, момент (М) = 10 Нм 

Расстояние (d) = 2 м.

Как известно, M = F × d

10 = F × 2

F = 10/2

F = 5N.

Вопрос 4: Балочные весы имеют длину плеч 100см и 80см. Какой вес, помещенный на сковороду с более длинным плечом, уравновесит предмет весом 200 г, находящийся на других кастрюлях?

Решение:

По принципу моментов

Момент по часовой стрелке = Момент против часовой стрелки

Вт × 100 = 200 × 80

Вт = (200 × 80)/100

Вт = 160 г.

Вопрос 5: Два человека сидят на качелях противоположными сторонами, один человек весит 100 Н и находится на расстоянии 2 м от оси вращения, а вес другого человека составляет 200 Н. найти, где человек сидит, чтобы сбалансировать качели.

Решение:

Согласно принципу моментов,

Момент по часовой стрелке = Момент против часовой стрелки

100 × 2 = 200 × d

d = (100 × 2)/200

d = 1 м.

Вопрос 6: Является ли момент скалярной или векторной величиной? Объясните

Решение:

По формуле момента это произведение силы и расстояния от фиксированной точки или M = F × d.