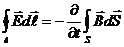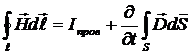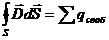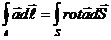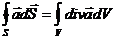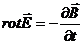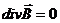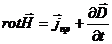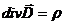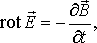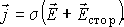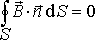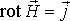Система уравнений Максвелла для электромагнитного поля в интегральной и дифференциальной форме. Уравнения связи.
Стр 1 из 4Следующая ⇒Система уравнений Максвелла для электромагнитного поля в интегральной и дифференциальной форме. Уравнения связи.


Уравнения связи:



2. Методы расчета электрических полей дискретных зарядов. Поле двух точечных зарядов, поле диполя.

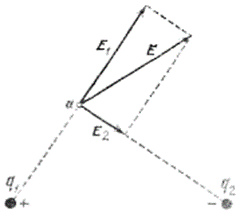
Поле двух точечных заряда для умных:
Пишем закон Кулона:
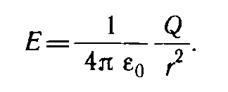
Для каждого зарядов.
Пишем теорему косинусов для зарядов, теорему косинусов для расстояния между зарядами и расстоянием между зарядом и точкой (на рис. т. α). Из второго уравнения находим косинус и его подставляем в первое уравнение, затем находим общую напряженность.
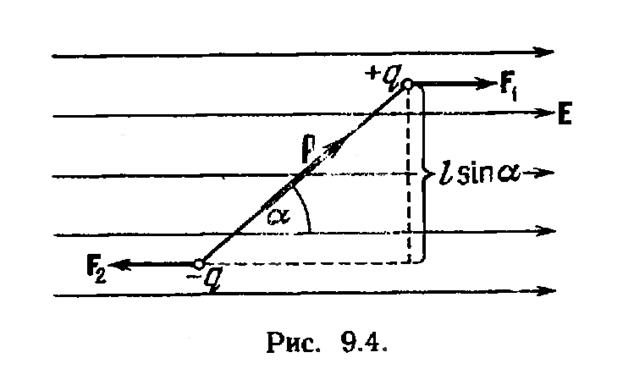
Поле диполя:




Диполь во внешнем электрическом поле.



4. Расчет электрических полей методом «зеркального» изображения.

Теорема Гаусса для электрического поля. Поле равномерно заряженного цилиндра. Поле объемно заряженного шара.


Цилиндр:

Шар:

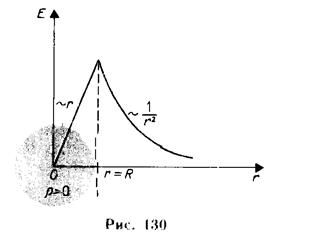
Дополнение:

7,8. Закон Био-Савара-Лапласа. Принцип суперпозиции. Магнитное поле в центре и на оси кругового тока. Магнитное поле отрезка прямолинейного проводника.




Магнитное поле на оси кругового витка с током.
Согласно закону Био-Савара-Лапласа, индукция магнитного поля, создаваемого элементом тока dl на расстоянии r от него есть
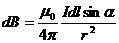
где  α – угол между элементом тока
α – угол между элементом тока 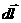 и радиус-вектором
и радиус-вектором 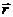 , проведенным из этого элемента в точку наблюдения; r — расстояние от элемента тока до точки наблюдения.
, проведенным из этого элемента в точку наблюдения; r — расстояние от элемента тока до точки наблюдения.
В нашем случае α = π/2, sinα = 1; 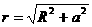 , где а – расстояние, отсчитываемое от центра витка до рассматриваемой точки на оси витка. Векторы
, где а – расстояние, отсчитываемое от центра витка до рассматриваемой точки на оси витка. Векторы 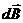
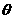 = π — 2β, где β – угол между отрезками а и r.
= π — 2β, где β – угол между отрезками а и r.
Из соображений симметрии ясно, что результирующее магнитное поле на оси витка будет направлено вдоль этой оси, то есть вклад в него дают только те составляющие, которые параллельны оси витка:
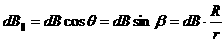 .
.
Результирующую величину индукции магнитного поля
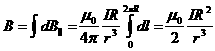
или, подставив значение r:

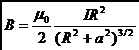 .
.
· Индукция магнитного поля в произвольной точке А, созданного отрезком проводника с током 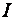
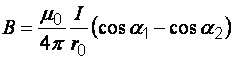 , (3)
, (3)
где 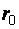 – расстояние от т. А до проводника;
– расстояние от т. А до проводника; 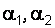 – углы, образованные радиус-вектором, проведенном в т.А соответственно из начала и конца проводника, с направлением тока.
– углы, образованные радиус-вектором, проведенном в т.А соответственно из начала и конца проводника, с направлением тока.
9, 10. Теорема о циркуляции векторов В и Н (закон полного тока). Магнитное поле бесконечно длинного соленоида. Магнитное поле тороида.


Электрическое поле в веществе. Поляризация диэлектриков. Три группы поляризации.

Характеристики поля поляризации. Связь векторов D, E, P. Теорема Гаусса для электрического поля в диэлектриках.





Условия на границе двух диэлектриков. Закон преломления векторов E и D.


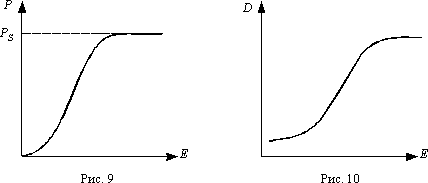
14. Сегнетоэлектрики. Зависимости P(E), D(E), ε(E). Гистерезис. Пьезоэффект.




15. Магнитное поле в веществе. Магнитный момент атома. Атом в магнитном поле. Парамагнитный и диамагнитный эффект.


Намагниченность, магнитная восприимчивость. Связь B, J, H.

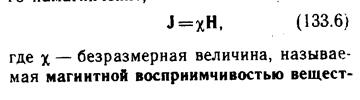


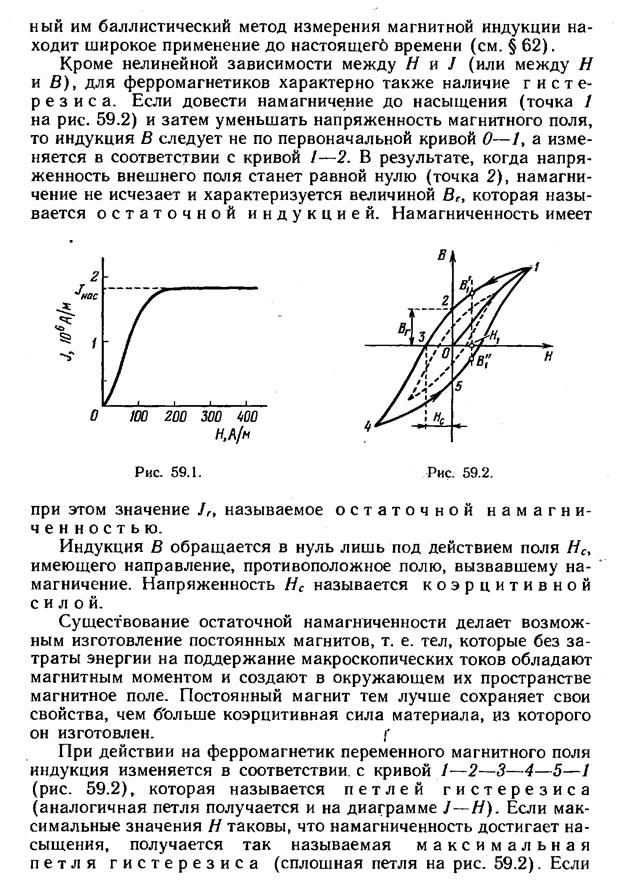
17. Ферромагнетики. Зависимости J(H), B(H), μ(Н). Гистерезис. Энергия, выделяемая в ферромагнетиках при перемагничивании.

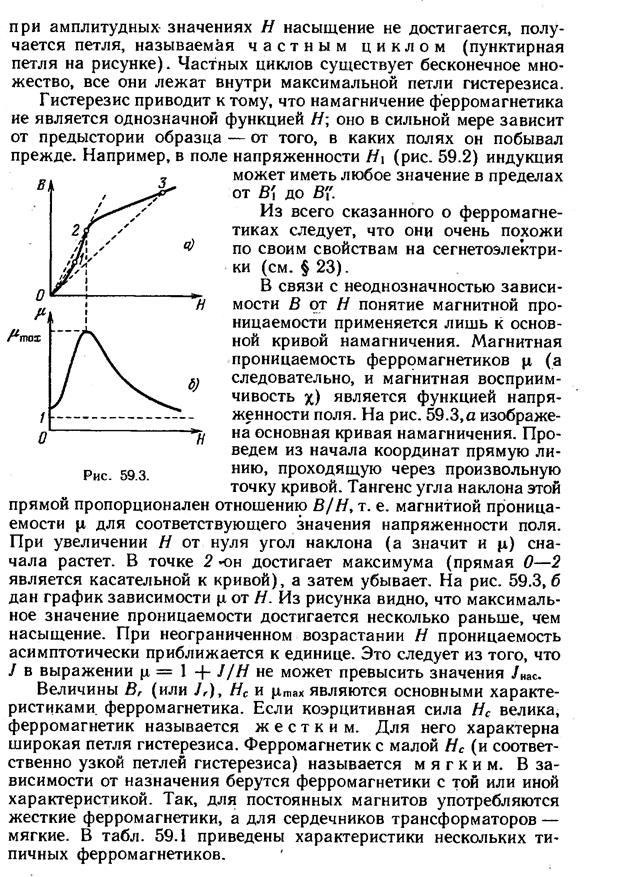


Условия на границе двух магнетиков, закон преломления векторов Н и В. Магнитная защита, лабораторные магниты.



МАГНИТНОЕ ЭКРАНИРОВАНИЕ (магнитная защита) — защита объекта от воздействия магн. полей (постоянных и переменных). Совр. исследования в ряде областей науки (физика, геология, палеонтология, биомагнетизм) и техники (космич. исследования, атомная энергетика, материаловедение) часто связаны с измерениями очень слабых магн. полей ~10-14-10-9 Тл в широком частотном диапазоне. Внешние магнитные поля (например, поле Земли 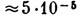 Тл с шумом
Тл с шумом 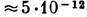 Тл, магн. шумы от электрич. сетей и городского транспорта) создают сильные помехи для работы высокочувствит. магнитометрич. аппаратуры. Уменьшение влияния магн. полей в сильной степени определяет возможности проведения магн. измерений Среди методов М. э. наиболее распространены следующие.
Тл, магн. шумы от электрич. сетей и городского транспорта) создают сильные помехи для работы высокочувствит. магнитометрич. аппаратуры. Уменьшение влияния магн. полей в сильной степени определяет возможности проведения магн. измерений Среди методов М. э. наиболее распространены следующие.
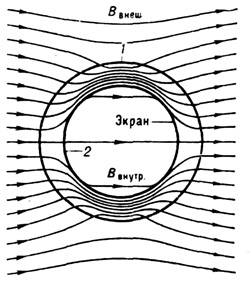
Экранирующее действие полого цилиндра из ферромагнитного вещества с 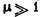 (1 — внеш. поверхность цилиндра, 2 -внутр. поверхность). Остаточное магнитное
(1 — внеш. поверхность цилиндра, 2 -внутр. поверхность). Остаточное магнитное 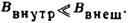 поле внутри цилиндра
поле внутри цилиндра
Движение заряженных частиц в электрическом и магнитном поле в веществе. Эффект Холла.



Электрический ток в вакууме. Виды электронных и ионных эмиссий. Классическое представление работы выходы электронов из твердых тел, как работа против сил зеркального изображения электрона в металлических проводниках.
Для получения электрического тока в вакууме необходимо наличие свободных носителей. Получить их можно за счет испускания электронов металлами — электронной эмиссии.
Виды эмиссий:
· Термоэлектронная
· Фотоэлектронная
· Вторичная электронная
· Вторичная ионно-ионная
· Термоионная
· Горячих электронов


26. Термоэлектронная эмиссия. Основное уравнение ТЭЭ. Вывод из классической теории Друде-Лоренца и статистики Максвелла-Больцмана.



27. Эффект Шоттки. Влияние поправки Шоттки на ТЭЭ.
Эмиссии электронов из металла препятствует потенциальный барьер, образованный из электрических сил изображения. Снижение этого барьера по мере увеличения прилагаемого внешнего электрического поля называется эффектом Шоттки. Рассмотрим сначала систему металл-вакуум. Минимальная энергия, которую необходимо передать электрону на уровне Ферми чтобы он покинул металл, называется работой выхода 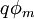 (
( 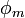 измеряется в электрон-вольтах). Для типичных металлов величина
измеряется в электрон-вольтах). Для типичных металлов величина 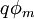 колеблется в районе 2-6 эВ и чувствительна к загрязнению поверхности.
колеблется в районе 2-6 эВ и чувствительна к загрязнению поверхности.
Электрон, который находится в условиях вакуума на некотором расстоянии 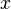 от поверхности металла, индуцирует на поверхности положительный заряд. Сила притяжения между электроном и этим индуцированным поверхностным зарядом равна по величине силе притяжения к эффективному положительному заряду
от поверхности металла, индуцирует на поверхности положительный заряд. Сила притяжения между электроном и этим индуцированным поверхностным зарядом равна по величине силе притяжения к эффективному положительному заряду 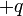 , который называют зарядом изображения. Эта сила, которая также называется силой изображения, равна:
, который называют зарядом изображения. Эта сила, которая также называется силой изображения, равна:
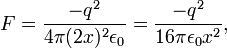
где 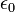 — диэлектрическая проницаемость вакуума. Работа, которую нужно совершить чтобы переместить электрон из точки
— диэлектрическая проницаемость вакуума. Работа, которую нужно совершить чтобы переместить электрон из точки 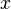 на бесконечность, равна:
на бесконечность, равна:
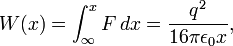
Эта работа отвечает потенциальной энергии электрона на расстоянии 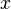 от поверхности. Зависимость
от поверхности. Зависимость 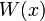 , обычно изображается на диаграммах прямой линией.
, обычно изображается на диаграммах прямой линией.
Если в системе есть внешнее электрическое поле 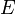 , то потенциальная энергия электрона
, то потенциальная энергия электрона 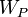 будет равна сумме:
будет равна сумме:
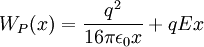 эВ.
эВ.
Снижение барьера Шоттки 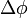 и расстояние
и расстояние 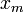 , при котором величина потенциала достигает максимума, определяется из условия
, при котором величина потенциала достигает максимума, определяется из условия 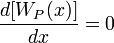 . Откуда находим:
. Откуда находим:
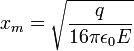 см,
см,
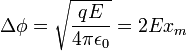 В.
В.
Из этих уравнений находим значение снижения барьера и расстояние: 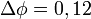 В,
В, 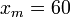 При
При 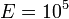 1/см и
1/см и 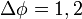 В,
В, 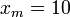 При
При 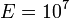 В/см. В результате, сильное электрическое поле вызывает значительное снижение барьера Шоттки. Вследствие этого эффективная работа выхода из металла для термоэлектронной эмиссии
В/см. В результате, сильное электрическое поле вызывает значительное снижение барьера Шоттки. Вследствие этого эффективная работа выхода из металла для термоэлектронной эмиссии 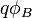 уменьшается.
уменьшается.
Полученные выше результаты могут быть перенесены на системы металл-полупроводник. В данном случае электрическое поле 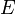 заменяется полем в полупроводнике вблизи границы раздела (где он достигает своего максимального значения), а диэлектрическая проницаемость вакуума
заменяется полем в полупроводнике вблизи границы раздела (где он достигает своего максимального значения), а диэлектрическая проницаемость вакуума 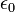 заменяется диэлектрической проницаемостью полупроводника (
заменяется диэлектрической проницаемостью полупроводника ( 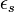 ), то есть:
), то есть:
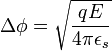
Значение ( 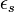 ) может отличаться от статической диэлектрической проницаемости полупроводника. Это связано с тем, что если время пролёта электрона от поверхности раздела металл-полупроводник в точку
) может отличаться от статической диэлектрической проницаемости полупроводника. Это связано с тем, что если время пролёта электрона от поверхности раздела металл-полупроводник в точку 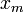 (
( 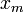 — точка, где потенциальная энергия достигает своего максимального значения) меньше времени диэлектрической релаксации полупроводника, то последний не успевает поляризоваться. Поэтому экспериментальные значение диэлектрической проницаемости могут быть меньшими статической (низкочастотной) проницаемости. В кремнии эти величины практически совпадают между собой.
— точка, где потенциальная энергия достигает своего максимального значения) меньше времени диэлектрической релаксации полупроводника, то последний не успевает поляризоваться. Поэтому экспериментальные значение диэлектрической проницаемости могут быть меньшими статической (низкочастотной) проницаемости. В кремнии эти величины практически совпадают между собой.
Эффективная диэлектрическая проницаемость  для контакта золото-кремний определённая по результатам фотоэлектрических измерений. На практике имеем, что эффективная диэлектрическая проницаемость сил изображения находится в диапазоне 11,5 — 12,5. При
для контакта золото-кремний определённая по результатам фотоэлектрических измерений. На практике имеем, что эффективная диэлектрическая проницаемость сил изображения находится в диапазоне 11,5 — 12,5. При 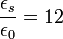 расстояние
расстояние 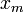 меняется от 10 до 50А в диапазоне изменений электрического поля около
меняется от 10 до 50А в диапазоне изменений электрического поля около 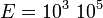 В/см. Если учесть, что скорость носителей около
В/см. Если учесть, что скорость носителей около 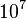 см/с, их время пролёта будет
см/с, их время пролёта будет 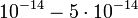 с. Оказывается, что диэлектрическая проницаемость, полученная при учёте силы изображения, близко к значений проницаемости (~12) для электромагнитного излучения соответствующих частот (с длиной волны 3-15 мкм). Поскольку диэлектрическая проницаемость кремния практически постоянна в диапазоне частот от нуля, соответствующей длине волны
с. Оказывается, что диэлектрическая проницаемость, полученная при учёте силы изображения, близко к значений проницаемости (~12) для электромагнитного излучения соответствующих частот (с длиной волны 3-15 мкм). Поскольку диэлектрическая проницаемость кремния практически постоянна в диапазоне частот от нуля, соответствующей длине волны 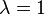 , в пролёта электрона через обеднённый слой решётка успевает поляризоваться. Поэтому значение диэлектрической проницаемости, полученные в фотоэлектрических и оптических опытах, близки друг к другу. Германий и арсенид галлия имеют аналогичные частотные зависимости диэлектрической проницаемости. Поэтому можно предположить, что в случае этих полупроводников значение диэлектрической проницаемости, определяющего силы изображения, в указанном выше интервале полей примерно совпадает со статичными значениями.
, в пролёта электрона через обеднённый слой решётка успевает поляризоваться. Поэтому значение диэлектрической проницаемости, полученные в фотоэлектрических и оптических опытах, близки друг к другу. Германий и арсенид галлия имеют аналогичные частотные зависимости диэлектрической проницаемости. Поэтому можно предположить, что в случае этих полупроводников значение диэлектрической проницаемости, определяющего силы изображения, в указанном выше интервале полей примерно совпадает со статичными значениями.
Эффект Шоттки используется в полупроводниковой технике и реализован в т. н. диодах Шоттки, имеющих высокие частотные характеристики.
Система уравнений Максвелла для электромагнитного поля в интегральной и дифференциальной форме. Уравнения связи.


Уравнения связи:



2. Методы расчета электрических полей дискретных зарядов. Поле двух точечных зарядов, поле диполя.


Поле двух точечных заряда для умных:
Пишем закон Кулона:
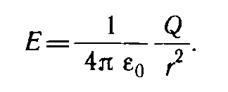
Для каждого зарядов.
Пишем теорему косинусов для зарядов, теорему косинусов для расстояния между зарядами и расстоянием между зарядом и точкой (на рис. т. α). Из второго уравнения находим косинус и его подставляем в первое уравнение, затем находим общую напряженность.
Поле диполя:




Уравнения Максвелла в дифференциальной и интегральной формах
Система уравнений, состоящая из уравнений Максвелла для электромагнитного поля и уравнений Ньютона для частиц, представляет собой единую систему уравнений, описывающую все явления, обусловленные электромагнитным взаимодействием (без учёта релятивистских и квантовых эффектов). Поэтому, строго говоря, их необходимо решать совместно в задачах электродинамики. Однако в такой наиболее общей постановке решать задачи о взаимодействии электромагнитного поля с веществом чрезвычайно трудно. Сложность проблемы заключается в том, что вещество состоит из громадного количества частиц, движение которых каждой в отдельности невозможно описать. С такой проблемой сталкиваются в классической механике при попытках описать механическое движение газов, жидкостей и твёрдых тел. Чтобы обойти эту трудность физикам приходилось строить определённые модели механических систем: модель абсолютно твёрдого тела, модель сплошной среды и др. При изучении взаимодействия заряженных частиц с электромагнитным полем также приходится вводить некоторые модели. Одной из таких широко употребляемых, является модель сплошной среды, состоящая из электрических диполей (диэлектрик). Эта модель электрического диполя играет очень важную роль в физике, так как атомы и молекулы представляют собой системы заряженных частиц, которые в целом нейтральны, но могут обладать отличным от нуля дипольным моментом и поэтому создавать электрическое поле.
Открытие тока смещения позволило Максвеллу создать единую теорию электрических и магнитных явлений. Эта теория объяснила все известные в то время экспериментальные факты и предсказала ряд новых явлений, существование которых подтвердилось впоследствии. Основным следствием теории Максвелла был вывод о существовании электромагнитных волн, распространяющихся со скоростью света.
Основу теории образуют уравнения Максвелла. В учении об электромагнетизме эти уравнения играют такую же роль, как законы Ньютона в механике или основные законы (начала) в термодинамике. Ниже приведена полная система уравнений Максвелла классической электродинамики в сплошной среде.
Первую пару уравнений Максвелла образуют уравнения:
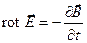 (1)
(1)
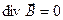 (2)
(2)
Здесь вектор — вектор напряжённости электрического поля, — вектор индукции магнитного поля.
Первое из этих уравнений связывает значение с изменениями вектора во времени и является по существу выражением закона электромагнитной индукции. Оно показывает, что источником вихревого поля вектора является меняющееся со временем вихревое магнитное поле. Второе уравнение указывает на отсутствие источников магнитного поля, т.е. магнитных зарядов, как в вакууме, так и в намагниченном веществе.
Вторую пару уравнений Максвелла образуют уравнения:
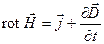 (3)
(3)
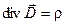 (4)
(4)
Где — вектор электрического смещения, 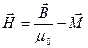 — напряжённость магнитного поля,
— напряжённость магнитного поля, 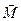 — намагниченность вещества,
— намагниченность вещества, 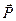 — поляризованность,
— поляризованность, 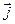 — вектор плотности тока, ρ- объёмная плотность заряда.
— вектор плотности тока, ρ- объёмная плотность заряда.
Первое уравнение устанавливает связь между токами проводимости и токами смещения, и порождаемым ими магнитным полем. Второе показывает, что источниками вектора служат сторонние заряды.
Вышеперечисленные уравнения представляют собой дифференциальную форму уравнений Максвелла. Можно отметить, что в первую пару уравнений входят только основные характеристики поля — и . Во второй паре фигурируют только вспомогательные величины и .
Можно отметить, что вид уравнений (2) и (4) не зависит от наличия среды, в то время как векторы и , а также величины и 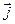 , входящие в уравнения (3) и (4), зависят от свойств вещества и условий, в которых оно находится. Любое макроскопическое тело, рассматриваемое как сплошная среда, состоит из заряженных частиц – электронов и ядер, обладающих также и магнитными моментами, и поэтому взаимодействующих с электромагнитным полем, являясь в то же время и его источниками. Таким образом, величины , , и
, входящие в уравнения (3) и (4), зависят от свойств вещества и условий, в которых оно находится. Любое макроскопическое тело, рассматриваемое как сплошная среда, состоит из заряженных частиц – электронов и ядер, обладающих также и магнитными моментами, и поэтому взаимодействующих с электромагнитным полем, являясь в то же время и его источниками. Таким образом, величины , , и 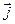 следует определять, исходя из электрических и магнитных свойств вещества.
следует определять, исходя из электрических и магнитных свойств вещества.
Выводя формулу (1), Максвелл предположил, что изменяющегося со временем магнитное поле обусловливает появление в пространстве поля 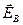 , независимо от присутствия в пространстве проволочного контура. Наличие контура лишь позволяет обнаружить по возникновению в нем индукционного тока существование в соответствующих точках пространства электрического поля.
, независимо от присутствия в пространстве проволочного контура. Наличие контура лишь позволяет обнаружить по возникновению в нем индукционного тока существование в соответствующих точках пространства электрического поля.
Рассмотрим случай электромагнитной индукции, когда проволочный контур, в котором индуцируется ток, неподвижен, а изменения магнитного потока обусловлены изменениями магнитного поля. Возникновение индукционного тока свидетельствует о том, что изменения магнитного поля вызывают появление в контуре сторонних сил, действующих на носители тока. Эти сторонние силы не связаны ни с химическими, ни с тепловыми процессами в проводе; они также не могут быть магнитными силами, потому что такие силы над зарядами работы не совершают. Остаётся заключить, что индукционный ток обусловлен возникающим в проводе электрическим полем. Обозначим напряжённость этого поля 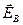 (это обозначение является вспомогательным так же как и
(это обозначение является вспомогательным так же как и 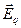 ). Электродвижущая сила равна циркуляции вектора
). Электродвижущая сила равна циркуляции вектора 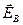 по данному контуру:
по данному контуру:
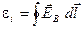 (1.1)
(1.1)
Подстановка в формулу 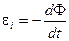 выражения (1.1) для
выражения (1.1) для 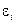 и выражения
и выражения 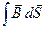 для
для 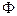 приводит к соотношению
приводит к соотношению
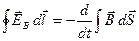
(интеграл в правой части берётся по произвольной поверхности, опирающейся на контур). Поскольку контур и поверхность неподвижны, операции дифференцирования по времени и по поверхности можно поменять местами:
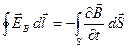 (1.2)
(1.2)
В связи с тем, что вектор зависит, вообще говоря, как от времени, так и от координат, то можно написать под знаком интеграла символ частной производной по времени (интеграл 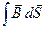 является функцией только времени).
является функцией только времени).
Левую часть равенства (1.2) преобразуем по теореме Стокса. В результате получится:
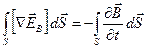 .
.
Ввиду произвольности выбора поверхности интегрирования должно выполняться равенство
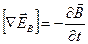 .
.
Ротор поля 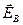 в каждой точке пространства равен взятой с обратным знаком производной по времени от вектора .
в каждой точке пространства равен взятой с обратным знаком производной по времени от вектора .
Это поле 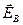 , порождающееся изменением магнитного поля, существенно отличается от порождаемого электрическими зарядами электрического поля
, порождающееся изменением магнитного поля, существенно отличается от порождаемого электрическими зарядами электрического поля 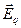 . Электростатическое поле потенциально, его линии начинаются и заканчиваются на зарядах. Ротор вектора
. Электростатическое поле потенциально, его линии начинаются и заканчиваются на зарядах. Ротор вектора 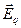 в любой
в любой
точке равен нулю:
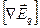 =0.
=0.
Согласно (1.2) ротор вектора 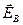 отличен от нуля. Следовательно, поле
отличен от нуля. Следовательно, поле 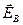 так же, как и магнитное является вихревым. Линии напряжённости
так же, как и магнитное является вихревым. Линии напряжённости 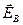 замкнуты.
замкнуты.
Таким образом, электрическое поле может быть как потенциальным ( 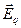 ) так и вихревым (
) так и вихревым ( 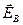 ). В общем случае электрическое поле слагается из этих двух полей. Сложив вместе
). В общем случае электрическое поле слагается из этих двух полей. Сложив вместе 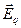 и
и 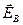 , получим следующее уравнение:
, получим следующее уравнение:
 . (1.3)
. (1.3)
Существование взаимосвязи между электрическим и магнитным полями служит причиной того, что раздельное рассмотрение электрического и магнитного полей имеет лишь относительный смысл. Действительно, электростатическое поле создаётся системой неподвижных зарядов в одной системе координат, однако они могут двигаться относительно другой инерциальной системы отсчёта и тогда они будут во второй системе подвижными, следовательно, будут создавать магнитное поле. Таким образом, поле, которое относительно некоторой системы отсчёта оказывается «чисто» электрическим или «чисто» магнитным, относительно других систем отсчёта будет представлять собой совокупность электрического и магнитных полей, образующих единое электромагнитное поле.
Выводя формулу (3), Максвелл пересмотрел уравнения для ротора вектора для случая стационарного (не изменяющегося со временем) электромагнитного поля, где ротор вектора равен в каждой точке плотности тока проводимости:
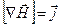 , (3.1)
, (3.1)
где вектор 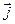 связан с плотностью заряда в той же точке уравнением непрерывности:
связан с плотностью заряда в той же точке уравнением непрерывности:
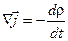 (3.2)
(3.2)
Электромагнитное поле может быть стационарным лишь при условии, что плотность заряда и плотность тока 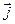 не зависят от времени. В этом случае согласно (3.2) дивергенция
не зависят от времени. В этом случае согласно (3.2) дивергенция 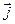 равна нулю.
равна нулю.
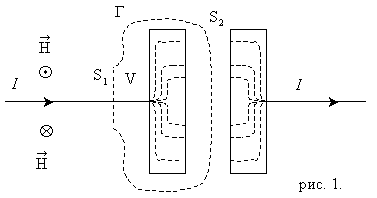
Поэтому можно выяснить, является ли справедливым уравнение (3.2) справедливым в случае изменяющихся со временем полей. Рассмотрим магнитное поле, создаваемое током, текущим при зарядке конденсатора от источника постоянного напряжения U (рис. 1).
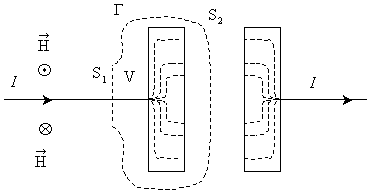
Этот ток непостоянен во времени (в момент, когда напряжение на конденсаторе становится равным U, ток прекращается). Линии тока проводимости терпят разрыв в промежутке между обкладками конденсатора.
Возьмём круговой контур Г, охватывающий провод, по которому течёт ток к конденсатору, и проинтегрируем соотношение (3.1) по пересекающеё провод поверхности S1, ограниченной контуром:
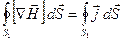 .
.
Преобразовав левую часть по теореме Стокса, получим циркуляцию вектора по контуру Г:
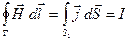 (3.3)
(3.3)
(I – сила тока заряжающего конденсатор). Проделав такие же вычисления для поверхности S2, придём к явно неверному соотношению:
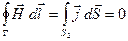 (3.4)
(3.4)
Полученный результат указывает на то, что в случае изменяющихся со временем полей уравнение (3.1) перестаёт быть справедливым. Напрашивается вывод, что в этом уравнении отсутствует слагаемое, зависящее от произвольных полей во времени. Для стационарных полей это слагаемое обращается в нуль.
На неправомерность уравнения (3.1) в случае нестационарных полей указывает также, следующие соображения. Возьмём дивергенцию от обеих частей соотношения (3.1):
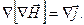
Дивергенция ротора должна быть обязательно равна нулю. Таки образом, можно прийти к выводу, что дивергенция вектора 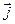 также должна быть всегда равной нулю. Однако этот вывод
также должна быть всегда равной нулю. Однако этот вывод
противоречит уравнению непрерывности, где 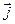 отлична от нуля.
отлична от нуля.
Чтобы согласовать уравнения (3.1) и (3.2), Максвелл ввел в правую часть уравнения (3.1) дополнительное слагаемое. Естественно, что это слагаемое должно иметь размерность плотности тока. Максвелл назвал его плотностью тока смещения. Таким образом, согласно Максвеллу уравнение (3.1) должно иметь вид:
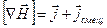 (3.5)
(3.5)
Сумму тока проводимости и тока смещения принято называть полным током. Плотность полного тока равна:
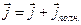 (3.6)
(3.6)
Если положить дивергенцию тока смещения равной дивергенции тока проводимости, взятой с обратным знаком,
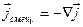 (3.7)
(3.7)
то дивергенция правой части уравнения (3.5), так же как и дивергенция левой части, всегда будет равна нулю.
Заменив в (3.7) 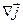 согласно (3.2) через
согласно (3.2) через 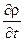 , получим следующее выражение для дивергенции тока смещения:
, получим следующее выражение для дивергенции тока смещения:
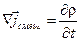 . (3.8)
. (3.8)
Чтобы связать ток смещения с величинами, характеризующими изменение электрического поля со временем, воспользуемся соотношением:
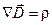
Продифференцировав это соотношение по времени, получим:
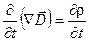
Теперь поменяем в левой части порядок дифференцирования по времени и по координа -там. В результате придём к следующему выражения для производной по 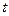 .
.
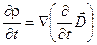 .
.
Подстановка этого выражения в формулу (3.8) даёт:
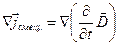 .
.
Отсюда
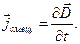 (3.9)
(3.9)
Подставив выражение (3.9) в формулу (3.6), придём к уравнению
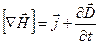 .
.
Каждое из векторных уравнений (1) и (3) эквивалентно трем скалярным уравнениям, связывающим компоненты векторов, стоящих в левой и правой частях равенств. Воспользовавшись правилом раскрытия дифференциальных операторов, можно записать их в следующем виде:
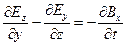 ;
; 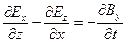 ;
; 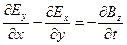 (5)
(5)
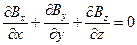 (6)
(6)
для первой пары уравнений, и:
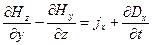 ;
; 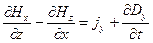 ;
; 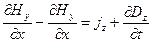 (7)
(7)
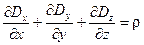 (8)
(8)
для второй.
Всего получилось 8 уравнений, в которых входят 12 функций (по три компоненты векторов , , , .) Поскольку число уравнений меньше числа известных функций, уравнений (1) — (4) недостаточно для нахождения полей по заданным распределениям зарядов и токов. Чтобы осуществить расчёт полей, нужно дополнить уравнения Максвелла уравнениями, связывающими и 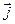 с , а также с . Эти уравнения имеют вид.
с , а также с . Эти уравнения имеют вид.
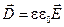 (9)
(9)
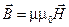 (10)
(10)
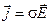 (11)
(11)
Совокупность уравнений (1) – (11) образуют основу электродинамики покоящихся сред.
Уравнения:
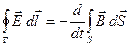 (12)
(12)
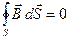 (13)
(13)
(первая пара) и
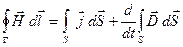 (14)
(14)
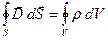 (15)
(15)
(вторая пара) представляют собой уравнения Максвелла в интегральной форме.
Уравнение (12) получается путём интегрирования соотношения (1) по произвольной поверхности S с последующим преобразованием левой части по теореме Стокса в интеграл по контуру Г, ограничивающему поверхность S. Уравнение (14) получается таким же способом из соотношения (3). Уравнения (13) и (15) получаются из соотношений (2) и (4) путём интегрирования по произвольному объёму V с последующим преобразованием левой части по теореме Остроградского-Гаусса в интеграл по замкнутой поверхности S, ограничивающей объём V.
Граничные условия
При решении задач электродинамики, учитывается, что все макроскопические тела ограничены поверхностями. При переходе через эти поверхности физические свойства макроскопических тел изменяются скачком и поэтому также скачком могут изменяться электромагнитные поля, создаваемые этими телами. Другими словами векторные функции и являются кусочно-непрерывными функциями координат, т.е. они непрерывны вместе со своими производными внутри каждой однородной области, но могут претерпевать разрывы на границах раздела двух сред. В связи с этим представляется удобным решать уравнения Максвелла (1) — (4) в каждой области, ограниченной некоторой поверхностью раздела отдельно, а затем полученные решения объединять с помощью граничных условий.
При нахождении граничных условий удобно исходить из интегральной формы уравнений Максвелла. Согласно уравнению (4) и теореме Остроградского-Гаусса:
, (16)
где Q – полный заряд внутри объёма интегрирования.
Рассмотрим бесконечно малый объём в виде цилиндра с высотой h и площадью основания S, расположенный в средах 1 и 2 (рис. 2).
Соотношение (16) в этом случае можно записать виде:
(17)
здесь — нормаль к границе раздела двух сред, направленная из среды 2 в среду 1. Знак «минус» во втором слагаемом обусловлен тем, что внешняя нормаль поверхности интегрирования в среде 2 направлена противоположно нормали в среде 1. Пусть основание цилиндра стремится к границе раздела двух сред. Так как площадь боковой стремится к нулю, то , и поэтому (17) приобретёт вид:
(18)
где и — значения нормальных составляющих вектора по разные стороны поверхности раздела; — поверхностная плотность зарядов, избыточных по отношению к связанным зарядам самого вещества. Если поверхность раздела не заряжена, то в формуле (18) необходимо положить =0. Пользоваться понятием поверхностной плотности удобно тогда, когда избыточные (сторонние) заряды расположены в очень тонком слое вещества d, а поле рассматривается на расстояниях от поверхности r>>d. Тогда из определения объёмной плотности заряда следует:
= d = .
Если учесть, что , а — поверхностная плотность поляризационных зарядов, то формулу (18) можно записать в виде:
где , а величина , которая входит в граничное условие (18), есть поверхностная плотность зарядов, избыточных по отношению к связанным зарядам самого вещества.
Используя уравнение (2) и проводя аналогичные рассуждения, получаем граничное условие для вектора :
(19)
Выражения (18) и (19) – граничные условия для нормальных составляющих векторов и . Чтобы получить условия для тангенциальных составляющих можно использовать уравнения (1) и (3). Умножим уравнение (3) скалярно на положительную нормаль к поверхности S, ограниченной контуром L, имеющим вид прямоугольника (рис. 3).
Используя теорему Стокса, получим:
Перепишем это уравнение в виде:
(20)
Здесь и — значения вектора соответственно в средах 1 и 2, — единичный вектор, касательный к поверхности раздела, — нормаль к поверхности раздела, направленная из среды 2 в среду 1.
Пусть теперь при малом, но фиксированном l. Тогда , и соотношение (20) примет вид:
и после сокращения на l имеем:
здесь . Вектор , как следует из рисунка 2, можно записать как в виде . Тогда
предыдущее выражение можно записать, как
.
Поскольку эта формула справедлива для любой ориентации поверхности , а следовательно, и
вектора , то имеем
(21)
В граничном условии (21) присутствует поверхностная плотность тока, избыточная по отношению к токам намагничивания. Если токи отсутствуют, то следует положить =0. Учитывая, что , а есть поверхностная плотность тока намагничивания, запишем формулу (21) в виде:
где .
Используя уравнение (1) и проводя аналогичные рассуждения, получаем граничные условия для вектора :
(22)
Таким образом, уравнения Максвелла (1) — (4) должны быть дополнены граничными условиями (18), (19), (21) и (22). Эти условия означают непрерывность тангенциальных составляющих вектора (22) и нормальной составляющей вектора (19) при переходе через границу раздела двух сред. Нормальная составляющая вектора при переходе через границу раздела испытывает скачок, тангенциальная составляющая вектора , если имеются поверхностные токи (21).
Ещё одно граничное условие можно получить, используя уравнение непрерывности ( 0) и уравнение (4), из которых следует:
Так как граничное условие (19) является следствием уравнения (2), то по аналогии находим:
(23)
Если же на поверхности раздела нет зарядов, поверхностная плотность которых зависит от времени, то из (18) и (23) следует непрерывность нормальных составляющих плотности тока:
.
Итак, граничные условия на поверхности раздела двух сред имеют вид:
; (24)
;
где — нормаль к границе раздела, направленная из среды 2 в среду 1, и должны выполняться в любой момент времени и в каждой точке поверхности раздела.
Система уравнений Максвелла в интегральной и дифференциальной формах. Электромагнитное поле.
В законе электромагнитной индукции (ЭМИ) ℇ 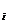 = —dФ/dt ЭДС можно представить по определению как циркуляцию поля сторонних сил
= —dФ/dt ЭДС можно представить по определению как циркуляцию поля сторонних сил
ℇ = 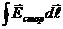 (см. часть 2, лекция №20), в данном случае (ЭМИ) сторонние силы не связаны ни с химическими, ни с тепловыми процессами, они также не могут быть магнитными силами, по тому, что такие силы работу над зарядами не совершают. Остается заключить, что индукционный ток обусловлен возникающим в проводе электрическим полем, тогда ЭДС
(см. часть 2, лекция №20), в данном случае (ЭМИ) сторонние силы не связаны ни с химическими, ни с тепловыми процессами, они также не могут быть магнитными силами, по тому, что такие силы работу над зарядами не совершают. Остается заключить, что индукционный ток обусловлен возникающим в проводе электрическим полем, тогда ЭДС
|
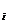 =
= 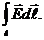 Магнитный поток по определению Ф =
Магнитный поток по определению Ф = 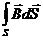 . Подставляя в закон ЭМИ получим
. Подставляя в закон ЭМИ получим(30-4)
Это первое уравнение Максвелла.

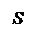
 Интеграл в правой части берется по произвольной поверхности S, опирающейся на контур ℓ (рис. 30.3).
Интеграл в правой части берется по произвольной поверхности S, опирающейся на контур ℓ (рис. 30.3).

 (Поскольку в общем случае
(Поскольку в общем случае 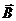 может быть
может быть
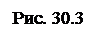

 функцией и координат, то берем частную
функцией и координат, то берем частную
производную 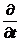 )
)
Смысл первого уравнения соответствует
максвелловской трактовке явления ЭМИ, то
есть, изменяющееся со временем магнитное поле порождает вихревое электрическое поле.
Второе уравнение Максвелла
|
(30-5)
Это уравнение выражает тот факт, что силовые линии магнитного поля не имеют источника (нет «магнитных зарядов») и всегда замкнуты и, что оно имеет вихревой характер, поток вектора магнитной индукции равен нулю.
Третье уравнение Максвелла
|
(30-6)
Это обобщенный закон полного тока (см. часть 3, лекция №24), который подчеркивает тот факт, что магнитное поле может создаваться не только токами проводимости ( 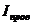 ), но и перемещенным электрическим полем («ток смещения»
), но и перемещенным электрическим полем («ток смещения» 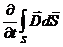 ).
).
Четвертая теорема Максвелла (см. часть 3, лекция №18).
|
(30-7)
Физически эта теорема подчеркивает тот факт, что электрическое поле может создаваться зарядами, то есть источниками силовых линий электрического поля являются электрические заряды.
Уравнения (30-3,5,6,7) представляют уравнения Максвелла в интегральной форме.
Уравнения Максвелла подчеркивают тот факт, что электрическое поле может создаваться как зарядами, так и переменным магнитным полем, а магнитное поле может создаваться как токами проводимости, так и переменным электрическим полем. При этом магнитное поле всегда носит вихревой характер, о чем говорит второе уравнение Максвелла. Электрическое поле, создаваемое зарядами и переменным магнитным полем носят различный характер.Силовые линии в первом случае начинаются и кончаются на зарядах (четвертое уравнение Максвелла). А электрическое поле, создаваемое переменным магнитным полем не имеет источников и носит вихревой характер, также как магнитное поле (первое уравнение Максвелла).
В вакууме, где нет зарядов и токов, магнитное поле может создаваться только переменным электрическим полем, а электрическое поле только переменным магнитным полем.
Эту совокупность непрерывно изменяющихся и порождающих друг друга электрического и магнитного полей Максвелл назвал электромагнитным полем.
Кроме четырех рассмотренных уравнений в полную систему уравнений Максвелла входят еще три уравнения, называемых материальными. В них входят характеристики вещества («материи»), такие как диэлектрическая и магнитная проницаемости ℰ и µ, проводимость σ.
Связь 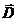 и
и 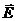 (лекция №18, часть 3)
(лекция №18, часть 3)
Связь 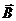 и
и 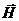 (лекция №23, часть 3)
(лекция №23, часть 3)
|
Закон Ома в локальной форме (лекция №20, часть 3)
Уравнения Максвелла (30-4) ÷ (30-7) можно представить в дифференциальной форме, т.е. в виде системы дифференциальных уравнений. Для этого используем теоремы Стокса
|
(30-8)
и Остроградского – Гаусса:
|
где 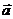 — некоторый вектор в нашем случае:
— некоторый вектор в нашем случае: 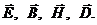 (О функции rot
(О функции rot 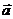 см. примечание к п.2).
см. примечание к п.2).
Первое уравнение Максвелла
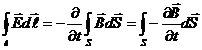
С другой стороны, используя теорему Стокса, получим
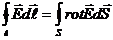
Поскольку равны левые части, равны и правые
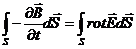
откуда следует
|
(30-10)
Второе уравнение Максвелла
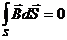
С другой стороны из теоремы Остроградского – Гаусса
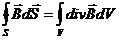
|
Третье уравнение запишем, предварительно выразив токи проводимости через плотность токов проводимости 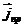
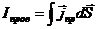 ,
,
тогда
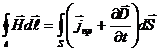
с другой стороны
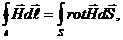
получим
|
(30-12)
Аналогичный подход для четвертого уравнения дает систему уравнений
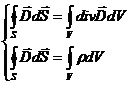 ,
,
|
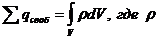 — объемная плотность заряда) из которой следует:
— объемная плотность заряда) из которой следует:(30-13)
Сведем четыре уравнения Максвелла в интегральной и дифференциальной формах, а также три материальных уравнения в таблицу:
Уравнения Максвелла
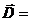 ℰℰ
ℰℰ 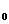
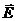 ;
; 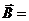 μμ
μμ 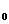
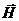 ;
; 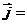 σ
σ 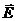
Отметим, что физический смысл уравнений в дифференциальной форме такой же, что и соответствующих уравнений в интегральной форме. Интегрируя их, можно получить 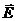 ,
, 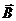 ,
, 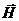 ,
, 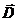 .
.
Примечание.Вихревое электрическое поле характеризуется особой векторной величиной, называемой ротором напряженности поля: 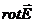 . Вектор ротора приложен в центре поля перпендикулярно плоскости его силовых линий (в случае круговых линий – в центре окружностей) и направлен относительно них согласно правилу правого винта.
. Вектор ротора приложен в центре поля перпендикулярно плоскости его силовых линий (в случае круговых линий – в центре окружностей) и направлен относительно них согласно правилу правого винта.
По определению
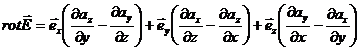 .
.
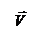










 Наглядное представление о роторе вектора можно получить, представив себе небольшую легкую турбинку, помещенную в данную точку текущей жидкости.
Наглядное представление о роторе вектора можно получить, представив себе небольшую легкую турбинку, помещенную в данную точку текущей жидкости.


 |
3. Волновые уравнения для электромагнитного поля и их решения. Скорость распространения электромагнитных волн в средах. Основные свойства электромагнитных волн.
Пусть имеется однородная и изотропная среда вдали от зарядов и токов. Возбудим в какой-либо точке пространства переменное электрическое гармоническое поле 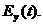 (Предположим
(Предположим 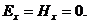 Для простоты рассматриваем этот частный случай).
Для простоты рассматриваем этот частный случай).
Из уравнений Максвелла при условии сделанных предположений можно получить волновые уравнения электромагнитного поля



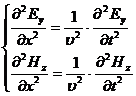 , (30-14)
, (30-14)
где — скорость распространения электро-
магнитной волны.
Процесс распространения электромагнитного поля в пространстве называется электромагнитной волной.
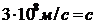 Подставим ℰ
Подставим ℰ 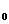 = 8,85
= 8,85 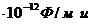 μ
μ  =
= 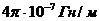 в выражение для скорости u. Если среда – вакуум, то ℰ = 1, μ = 1, тогда получим u = ,то есть скорость электромагнитной волны в вакууме равна скорости света в вакууме. Это обстоятельство приводит к выводу, что свет — электромагнитная волна.
в выражение для скорости u. Если среда – вакуум, то ℰ = 1, μ = 1, тогда получим u = ,то есть скорость электромагнитной волны в вакууме равна скорости света в вакууме. Это обстоятельство приводит к выводу, что свет — электромагнитная волна.
Решения уравнений (30-14)
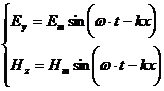 (30-15)
(30-15)
Выражения (30-15) – уравнения электромагнитной волны. Их графическое



Как показывает опыт, электромагнитные волны проходят через диэлектрики и отражаются от металлов. Для них свойственны такие явления как интерференция, дифракция, поляризация, дисперсия (рассмотрим далее в разделе «Оптика»).
Итак, из решения уравнений Максвелла получаются следующие выводы:
– если в какой-либо ограниченной области пространства возникает электромагнитное поле, то оно не остается локализованным в этой области, а распространяется с конечной скоростью, зависящей от свойств среды;
– если электрическое и магнитные поля меняются по простому гармоническому закону, то электромагнитное поле распространяется в пространстве в виде плоской электромагнитной волны.
Система уравнений Максвелла в интегральной и дифференциальной форме.
В основе современной классической электродинамики лежит система уравнений
Максвелла. Дифференциальная форма системы уравнений Максвелла в
системе единиц СИ имеет вид:
| (7.1) |
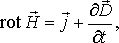
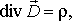
| (7.3) |
Уравнениям (7.1)— (7.4) соответствуют интегральные формы записи:
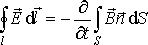

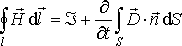
| (7.2′) |
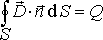
где 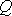 — величина свободного заряда в объеме,
охватываемом замкнутой
— величина свободного заряда в объеме,
охватываемом замкнутой
поверхностью 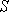 ,
а величина «сила тока»
,
а величина «сила тока»  определена соотношением
определена соотношением
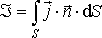
Обратим внимание читателя на то обстоятельство, что выбор положительного
направления
обхода контуров 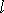 в левых частях уравнений (7.1′) и (7.2′)
в левых частях уравнений (7.1′) и (7.2′)
согласован
с выбором направления нормали 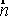 к элементу
к элементу 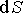 поверхности
поверхности
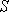 в
поверхностных интегралах правой части
упомянутых уравнений:
в
поверхностных интегралах правой части
упомянутых уравнений:
обход контура должен производиться против часовой стрелки, если смотреть
с
конца вектора 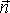 .
Иначе, если тело человека ориентировано
по вектору
.
Иначе, если тело человека ориентировано
по вектору 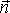 ,
то двигаться вдоль
,
то двигаться вдоль
контура надо так, чтобы область внутри контура оставалась слева.
В уравнениях (7.3′) и (7.4′) используется внешняя нормаль по отношению к
объему, ограниченному рассматриваемой замкнутой поверхностью.
В
определении (7.8) направление нормали 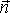 в поверхностном
в поверхностном
интеграле задает положительное направление, с учетом которого определяется
алгебраическая
величина силы тока  .
.
Интегральная форма записи уравнения (7.7) представляет собой хорошо
известный из элементарного курса физики закон Ома:
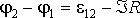
Уравнение (7.7′) записано для неразветвленного участка цепи, который
содержит
ЭДС (электродвижущую силу) 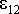 ,
имеет сопротивление
,
имеет сопротивление 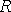 ,
,
ток
по которому течет от сечения 1 к сечению
2, 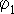 и
и 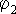 — потенциалы
— потенциалы
электрического поля для рассматриваемых сечений. В отсутствие ЭДС
из уравнения (7.7′) следует уравнение закона Ома в форме
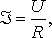
где 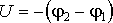 — напряжение между граничными
— напряжение между граничными
сечениями участка цепи.
Наиболее последовательное представление о природе электромагнитного
поля состоит в том, что система уравнений Максвелла принимается
как постулат, как теоретическое обобщение всех известных экспериментальных
законов электромагнетизма, как то целое, из которого как частные случаи
следуют отдельные физические закономерности.
Значимость системы уравнений Максвелла для электродинамики можно
сравнить со значимостью законов Ньютона для механики и открытием закона
всемирного тяготения.
В чем принципиальная новизна представлений Максвелла о природе
электромагнитного поля? Явление электромагнитной индукции было описано
законом электромагнитной индукции Фарадея и правилом Ленца:
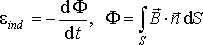
Внешне оно похоже на уравнение (7.1′) системы уравнений Максвелла.
Но М. Фарадей и Э.Х. Ленц рассматривали явление электромагнитной индукции
как явление в электропроводящем контуре. Д.К. Максвелл постулировал, что
циркуляция напряженности электрического поля по замкнутому контуру
возникает всегда, когда меняется величина потока магнитной индукции через
поверхность, натянутую на этот контур, безотносительно к тому, возникает
ли в контуре электрический ток под действием электродвижущей силы индукции.
Особенно наглядно проявляется новизна представлений Максвелла о
природе электромагнетизма в записи уравнения (7.1). В переменном
векторном
поле 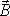 частная производная по времени от
вектора
частная производная по времени от
вектора 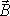
не
равна нулю. Это означает, что переменное
векторное поле 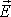 ,
в отличие
,
в отличие
от электростатики, становится вихревым, оно перестает быть потенциальным!
(Не надо думать, что для переменного электромагнитного поля нельзя
ввести
понятие потенциала, но силовые
характеристики 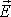 и
и 
описываются
при этом совокупностью скалярного
потенциала 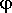 ,
переменного
,
переменного
во
времени, и векторного потенциала 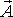 ,
тоже переменного во времени.
,
тоже переменного во времени.
Работа по перемещению точечного заряда по замкнутому контуру в этих
условиях может оказаться не равной нулю).
В магнитостатике (электрические токи не меняют своей величины и
направления, в рассматриваемой системе не накапливаются электрические
заряды) известно уравнение
| (7.10) |
и его интегральный аналог — теорема о циркуляции вектора напряженности
магнитного поля по замкнутому контуру:
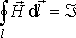
где  — сила тока, пронизывающая произвольную
поверхность, натянутую
— сила тока, пронизывающая произвольную
поверхность, натянутую
на рассматриваемый замкнутый контур.
Использование уравнения (7.11) затруднено при анализе процесса
зарядки-разрядки
конденсатора: на замкнутый контур 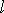 ,
расположенный в
,
расположенный в
пространстве между обкладками конденсатора, можно натянуть поверхность,
оторая целиком находится между обкладками, ток проводимости через нее
не течет. Вторая возможность — поверхность охватывает одну из обкладок
конденсатора,
через нее течет сила тока проводимости  .
.
В соответствии с уравнением (7.11) мы должны получить различные
значения
циркуляции поля 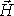 по рассматриваемому замкнутому
контуру.
по рассматриваемому замкнутому
контуру.
Такая неоднозначность противоречит физическому принципу, согласно
которому физическая величина должна определяться независимо от метода
расчета.
Уравнения Максвелла
Значение уравнений Максвелла
Уравнения Дж. Максвелла создают основу для предложенной им теории электромагнитных явлений, которая объяснила все известные в то время эмпирические факты, некоторые эффекты предсказала. Главным выводом теории Максвелла стало положение о существовании электромагнитных волн, которые распространяются со скоростью света.
Замечание
Уравнения, предложенные Максвеллом, в электромагнетизме играют роль подобную роли законов Ньютона в классической механике. Они явились обобщением экспериментальных законов и продолжением идей ученых (Кулона, Ампера, Фарадея и др.) изучавших электромагнетизм до Максвелла.
Замечание 1
Сам Максвелл предложил двадцать уравнений в дифференциальной форме с двадцатью неизвестными величинами. В современном виде мы имеем систему уравнений Максвелла благодаря немецкому физику Г. Герцу и англичанину О. Хэвисайду. С помощью этих уравнений можно описать все электромагнитные явления.
Система уравнений Максвелла
Определение 1
Систему уравнений Максвелла составляют:
\[rot\overrightarrow{H}=\overrightarrow{j}+\frac{\partial \overrightarrow{D}}{\partial t}\left(1\right),\] \[rot\overrightarrow{E}=-\frac{\partial \overrightarrow{B}}{\partial t}\left(2\right),\] \[div\overrightarrow{B}=0\left(3\right),\] \[div\overrightarrow{D}=\rho \left(4\right).\]Готовые работы на аналогичную тему
Выражения (1)-(4) называют полевыми уравнениями, они применимы для описания всех макроскопических электромагнитных явлений. Иногда уравнения системы Максвелла группируют в пары, первую пару составляют из второго и третьего уравнения, вторую пару — из первого и четвертого уравнений. При этом говорят, что в первую пару уравнений входят только основные характеристики поля ($\overrightarrow{E}\ и\ \overrightarrow{B}$), а во вторую пару — вспомогательные ($\overrightarrow{D}\ и\ \overrightarrow{H}$).
Каждое из векторных уравнений (1) и (2) эквивалентно трем скалярным уравнениям. Эти уравнения связывают компоненты векторов, которые находятся в левой и правой частях выражений. Так, в скалярном виде уравнение (1) представляется как:
В скалярном виде уравнение (2) запишем как:
Третье уравнение из системы Максвелла в скалярном виде:
Четвертое уравнение в скалярной форме примет следующий вид:
Для того чтобы рассмотреть конкретную ситуацию, систему уравнений (1)-(4) дополняют следующими материальными уравнениями, которые учитывают электромагнитные свойства среды:
Замечание 2
Необходимо отметить, что существует целый ряд явлений, в которых материальные уравнения существенно отличны от уравнений (5), например, если речь идет о нелинейных явлениях. В таких случаях получение материальных уравнений составляет отдельную научную задачу.
Физический смысл уравнений Максвелла
Уравнение (1) системы указывает на то, что двумя возможными источниками магнитного поля являются токи проводимости ($\overrightarrow{j}$) и токи смещения ($\frac{\partial \overrightarrow{D}}{\partial t}$).
Уравнение (2) является законом электромагнитной индукции и отображает тот факт, что переменное магнитное поле — один из источников возникновения электрического поля.
Следующим источником электрического поля служат электрические заряды, что и отображает уравнение (4), которое является, по сути, законом Кулона.
Уравнение (3) означает, что линии магнитной индукции не имеют источников (они либо замкнуты, либо уходят в бесконечность), что приводит к выводу об отсутствии магнитных зарядов, которые создают магнитное поле.
Материальные уравнения (5) — это соотношения между векторами поля и токами. Диэлектрические свойства среды заключены в диэлектрической проницаемости ($\varepsilon $). Магнитные свойства, которые описывает намагниченность, учтены в магнитной проницаемости ($\mu $). Проводящие свойства среды сосредоточены в удельной проводимости ($\sigma $).
Уравнения поля линейны и учитывают принцип суперпозиции.
Границы применимости уравнений Максвелла
Система уравнений Максвелла ограничена следующими условиями:
Материальные тела должны быть неподвижны в поле.
Постоянные $\varepsilon ,\ \mu ,\sigma $ могут зависеть от координат, но не должны зависеть от времени и векторов поля.
В поле не должно находиться постоянных магнитов и ферромагнитных тел.
Если существует необходимость учета движения среды, то уравнения системы Максвелла оставляют неизменными, а движение учитывается в материальных уравнениях, которые становятся зависимыми от скорости среды и существенно усложняются. Кроме прочего материальные уравнения перестают быть соотношениями между парами величин, как в (5). Например, плотность тока проводимости становится зависимой от индукции магнитного поля, а не только от напряженности электрического поля.
Замечание 3
Магнитное поле постоянных магнитов, например, можно описать, используя систему Максвелла, если известна намагниченность. Но, если заданы токи, то в присутствии ферромагнетиков описать поле при помощи данных уравнений не получится.
Пример 1
Задание: Докажите, что из уравнений Максвелла следует закон сохранения заряда.
Решение:
В качестве основания для решения задачи используем из системы Максвелла уравнение:
\[rot\overrightarrow{H}=\overrightarrow{j}+\frac{\partial \overrightarrow{D}}{\partial t}\left(1.1\right).\]Проведем операцию дивергирования в обеих частях выражения (1.1):
\[div\left(rot\overrightarrow{H}\right)=div\left(\overrightarrow{j}+\frac{\partial \overrightarrow{D}}{\partial t}\right)\left(1.2\right).\]Для выражения (1.2) в соответствии с теоремой равенстве нулю дивергенции ротора имеем:
\[div\left(rot\overrightarrow{H}\right)=0\ \left(1.3\right).\]Следовательно, получаем:
\[0=div\left(\overrightarrow{j}\right)+div\left(\frac{\partial \overrightarrow{D}}{\partial t}\right)\left(1.4\right).\]Рассмотрим второе слагаемое в правой части. Мы можем поменять порядок дифференцирования, так как время и пространственные координаты независимы, то есть записать:
\[div\left(\frac{\partial \overrightarrow{D}}{\partial t}\right)=\frac{\partial div(\overrightarrow{D)}}{\partial t}\left(1.5\right).\]В соответствии с системой Максвелла мы знаем, что источниками электрических полей служат заряды или:
\[div\overrightarrow{D}=\rho \left(1.6\right).\]Что позволяет нам записать уравнение (1.4) в виде:
\[0=div\left(\overrightarrow{j}\right)+\left(\frac{\partial \rho }{\partial t}\right)\left(1.7\right).\]Что дает нам закон сохранения заряда, который записан в виде:
\[div\left(\overrightarrow{j}\right)=-\frac{\partial \rho }{\partial t}(1.8).\]Данное уравнение называют уравнением непрерывности тока, оно содержит в себе закон сохранения заряда, что совершенно очевидно, если выражение (1.8), записать в интегральной форме:
\[\oint\limits_S{\overrightarrow{j}}d\overrightarrow{S}=-\frac{\partial }{\partial t}\int{\rho dV}(1.9).\]тогда если области замкнуты и изолированы получаем:
\[\oint\limits_S{\overrightarrow{j}}d\overrightarrow{S}=0\to \int{\rho dV}=const.\]Что требовалось доказать.
Пример 2
Задание: Покажите, что уравнения $rot\overrightarrow{E}=-\frac{\partial \overrightarrow{B}}{\partial t}$ и $div\overrightarrow{B}=0$ , входящие в систему Максвелла не противоречат друг другу.
Решение:
За основу решения примем уравнение:
\[rot\overrightarrow{E}=-\frac{\partial \overrightarrow{B}}{\partial t}\left(2.1\right).\]Возьмём дивергенцию от обеих частей уравнения:
\[div(rot\overrightarrow{E)}=-div(\frac{\partial \overrightarrow{B}}{\partial t})\left(2.2\right).\]В соответствии с теоремой равенстве нулю дивергенции ротора имеем:
\[div(rot\overrightarrow{E)}=0.\]Соответственно, получаем, что
\[div\left(\frac{\partial \overrightarrow{B}}{\partial t}\right)=\frac{\partial div\overrightarrow{B}}{\partial t}=0\to div\overrightarrow{B}=const.\]Выражение $div\overrightarrow{B}=const$ не противоречит тому, что $div\overrightarrow{B}=0$.
Мы получили, что уравнения $rot\overrightarrow{E}=-\frac{\partial \overrightarrow{B}}{\partial t}$ и $div\overrightarrow{B}=0$ совместны, что требовалось показать.
Лекция № 3 Система уравнений Максвелла в сплошной среде. Граничные условия”
17
1. Уравнения Максвелла в дифференциальной и интегральной формах
Система уравнений, состоящая из уравнений Максвелла для электромагнитного поля и уравнений Ньютона для частиц, представляет собой единую систему уравнений, описывающую все явления, обусловленные электромагнитным взаимодействием (без учёта релятивистских и квантовых эффектов). Поэтому, строго говоря, их необходимо решать совместно в задачах электродинамики. Однако в такой наиболее общей постановке решать задачи о взаимодействии электромагнитного поля с веществом чрезвычайно трудно. Сложность проблемы заключается в том, что вещество состоит из громадного количества частиц, движение которых каждой в отдельности невозможно описать. С такой проблемой сталкиваются в классической механике при попытках описать механическое движение газов, жидкостей и твёрдых тел. Чтобы обойти эту трудность физикам приходилось строить определённые модели механических систем: модель абсолютно твёрдого тела, модель сплошной среды и др. При изучении взаимодействия заряженных частиц с электромагнитным полем также приходится вводить некоторые модели. Одной из таких широко употребляемых, является модель сплошной среды, состоящая из электрических диполей (диэлектрик). Эта модель электрического диполя играет очень важную роль в физике, так как атомы и молекулы представляют собой системы заряженных частиц, которые в целом нейтральны, но могут обладать отличным от нуля дипольным моментом и поэтому создавать электрическое поле.
Открытие тока смещения позволило Максвеллу создать единую теорию электрических и магнитных явлений. Эта теория объяснила все известные в то время экспериментальные факты и предсказала ряд новых явлений, существование которых подтвердилось впоследствии. Основным следствием теории Максвелла был вывод о существовании электромагнитных волн, распространяющихся со скоростью света.
Основу теории образуют уравнения Максвелла. В учении об электромагнетизме эти уравнения играют такую же роль, как законы Ньютона в механике или основные законы (начала) в термодинамике. Ниже приведена полная система уравнений Максвелла классической электродинамики в сплошной среде.
Первую пару уравнений Максвелла образуют уравнения:
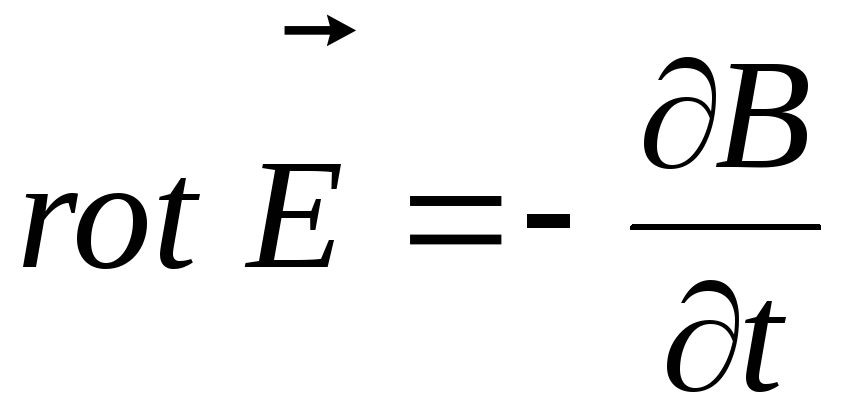 (1)
(1)
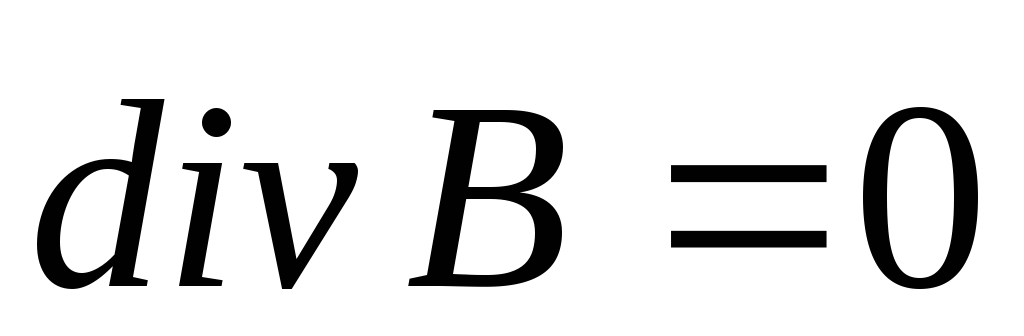 (2)
(2)
Здесь
вектор  — вектор напряжённости электрического
поля,
— вектор напряжённости электрического
поля,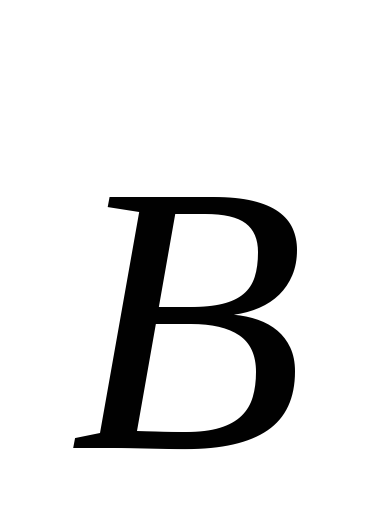 — вектор индукции магнитного поля.
— вектор индукции магнитного поля.
Первое
из этих уравнений связывает значение  с изменениями вектора
с изменениями вектора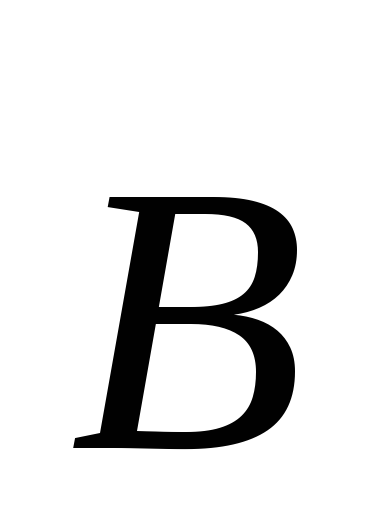 во времени и является по существу
выражением закона электромагнитной
индукции. Оно показывает, что источником
вихревого поля вектора
во времени и является по существу
выражением закона электромагнитной
индукции. Оно показывает, что источником
вихревого поля вектора является меняющееся со временем вихревое
магнитное поле. Второе уравнение
указывает на отсутствие источников
магнитного поля, т.е. магнитных зарядов,
как в вакууме, так и в намагниченном
веществе.
является меняющееся со временем вихревое
магнитное поле. Второе уравнение
указывает на отсутствие источников
магнитного поля, т.е. магнитных зарядов,
как в вакууме, так и в намагниченном
веществе.
Вторую пару уравнений Максвелла образуют уравнения:
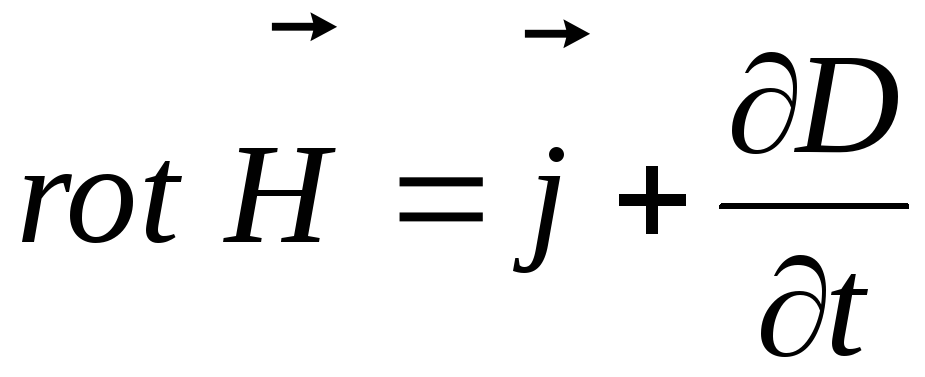 (3)
(3)
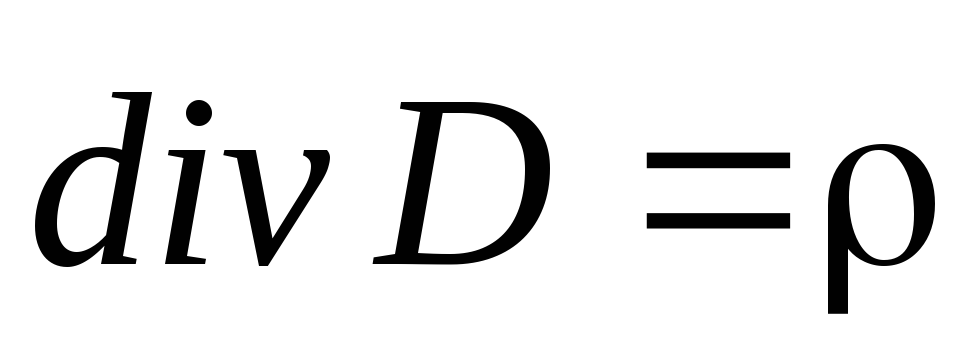 (4)
(4)
Где 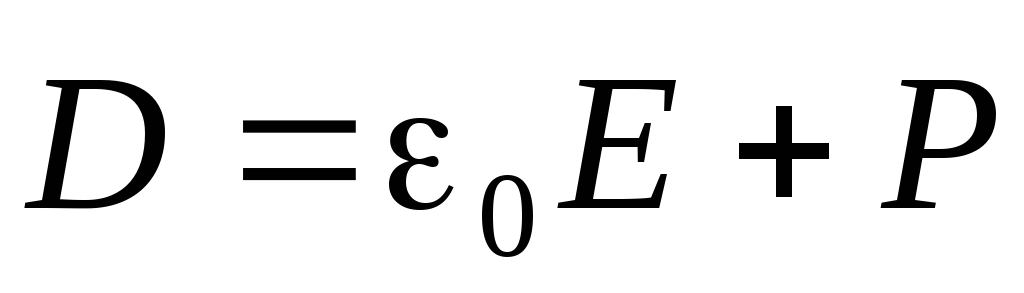 —
вектор электрического смещения,
—
вектор электрического смещения,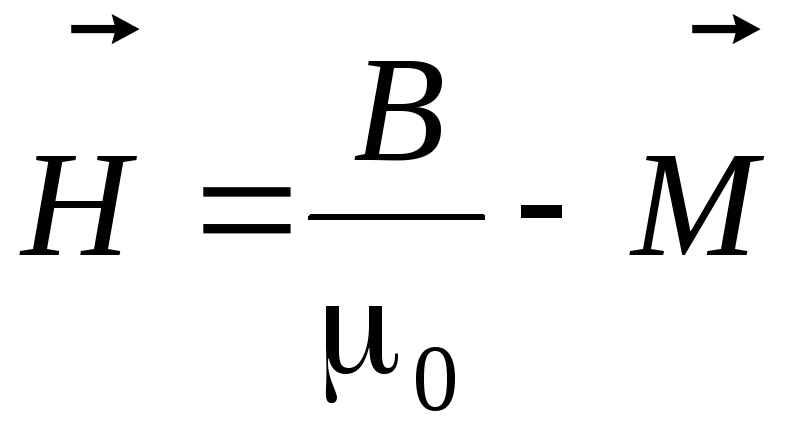 —
напряжённость магнитного поля,
—
напряжённость магнитного поля,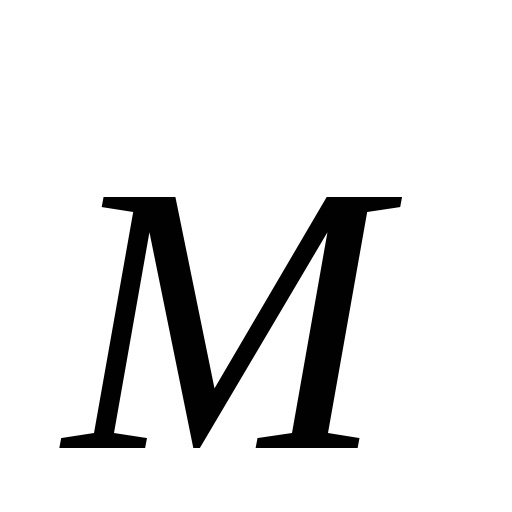 —
намагниченность вещества,
—
намагниченность вещества,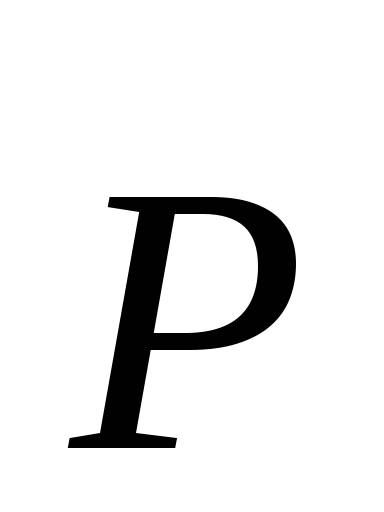 — поляризованность,
— поляризованность,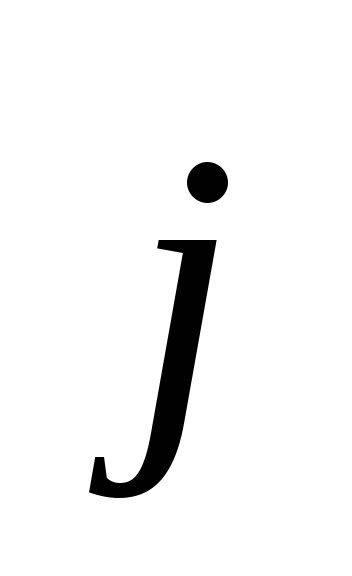 —
вектор плотности тока,
—
вектор плотности тока, — объёмная плотность заряда.
— объёмная плотность заряда.
Первое
уравнение устанавливает связь между
токами проводимости и токами смещения,
и порождаемым ими магнитным полем.
Второе показывает, что источниками
вектора 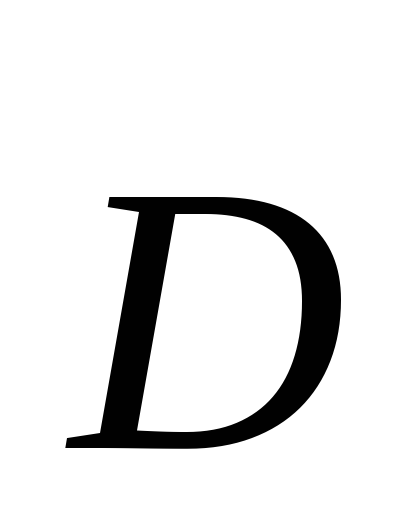 служат сторонние заряды.
служат сторонние заряды.
Вышеперечисленные
уравнения представляют собой
дифференциальную форму уравнений
Максвелла. Можно отметить, что в первую
пару уравнений входят только основные
характеристики поля —  и
и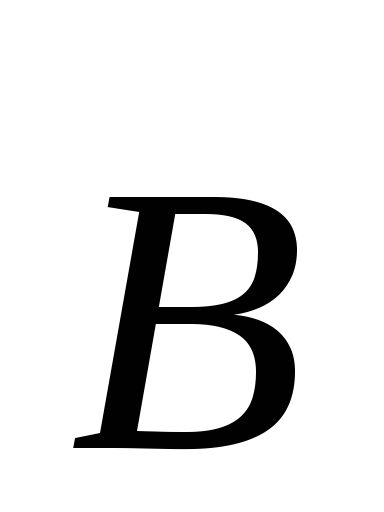 .
Во второй паре фигурируют только
вспомогательные величины
.
Во второй паре фигурируют только
вспомогательные величины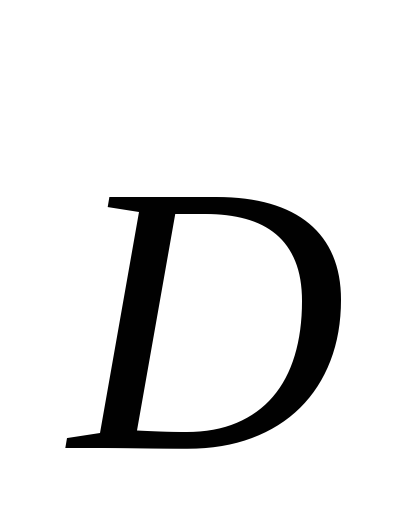 и
и .
.
Можно
отметить, что вид уравнений (2) и (4) не
зависит от наличия среды, в то время как
векторы 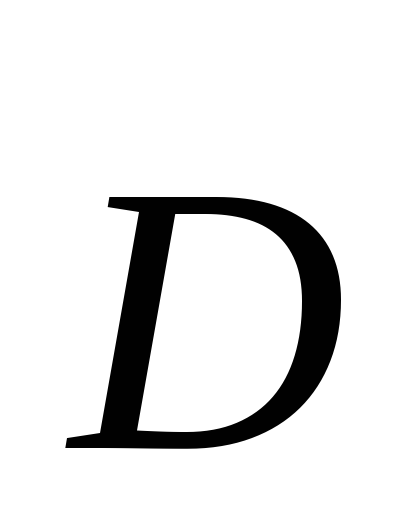 и
и ,
а также величины
,
а также величины и
и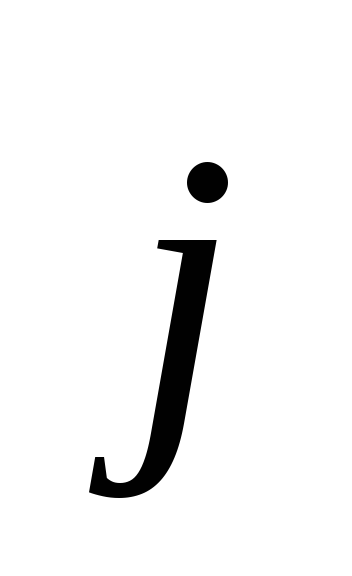 ,
входящие в уравнения (3) и (4), зависят от
свойств вещества и условий, в которых
оно находится. Любое макроскопическое
тело, рассматриваемое как сплошная
среда, состоит из заряженных частиц –
электронов и ядер, обладающих также и
магнитными моментами, и поэтому
взаимодействующих с электромагнитным
полем, являясь в то же время и его
источниками. Таким образом, величины
,
входящие в уравнения (3) и (4), зависят от
свойств вещества и условий, в которых
оно находится. Любое макроскопическое
тело, рассматриваемое как сплошная
среда, состоит из заряженных частиц –
электронов и ядер, обладающих также и
магнитными моментами, и поэтому
взаимодействующих с электромагнитным
полем, являясь в то же время и его
источниками. Таким образом, величины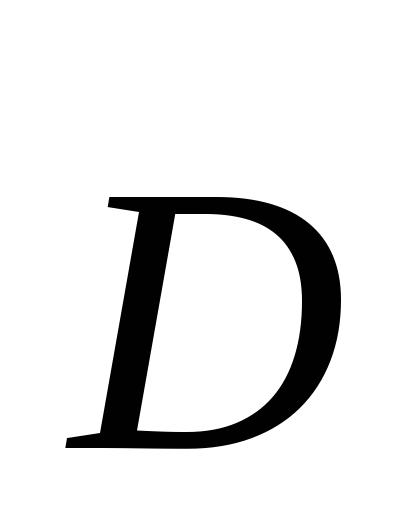 ,
, ,
, и
и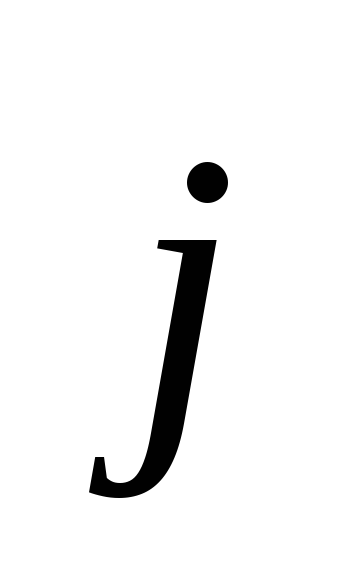 следует определять, исходя из электрических
и магнитных свойств вещества.
следует определять, исходя из электрических
и магнитных свойств вещества.
Выводя
формулу (1), Максвелл предположил, что
изменяющегося со временем магнитное
поле обусловливает появление в
пространстве поля 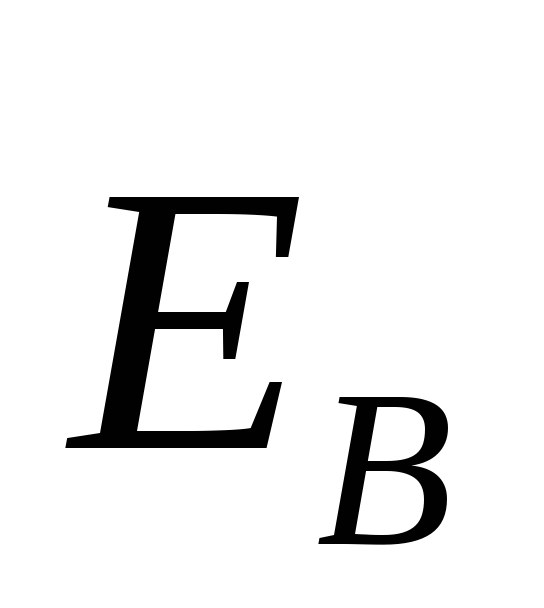 ,
независимо от присутствия в пространстве
проволочного контура. Наличие контура
лишь позволяет обнаружить по возникновению
в нем индукционного тока существование
в соответствующих точках пространства
электрического поля.
,
независимо от присутствия в пространстве
проволочного контура. Наличие контура
лишь позволяет обнаружить по возникновению
в нем индукционного тока существование
в соответствующих точках пространства
электрического поля.
Рассмотрим
случай электромагнитной индукции, когда
проволочный контур, в котором индуцируется
ток, неподвижен, а изменения магнитного
потока обусловлены изменениями магнитного
поля. Возникновение индукционного тока
свидетельствует о том, что изменения
магнитного поля вызывают появление в
контуре сторонних сил, действующих на
носители тока. Эти сторонние силы не
связаны ни с химическими, ни с тепловыми
процессами в проводе; они также не могут
быть магнитными силами, потому что такие
силы над зарядами работы не совершают.
Остаётся заключить, что индукционный
ток обусловлен возникающим в проводе
электрическим полем. Обозначим
напряжённость этого поля 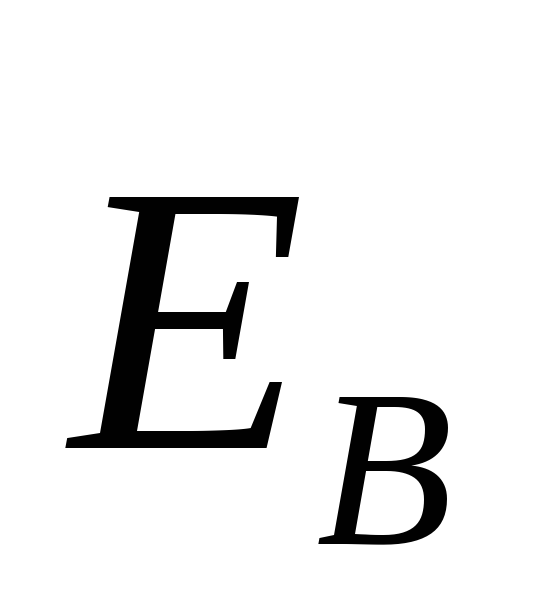 (это обозначение является вспомогательным
так же как и
(это обозначение является вспомогательным
так же как и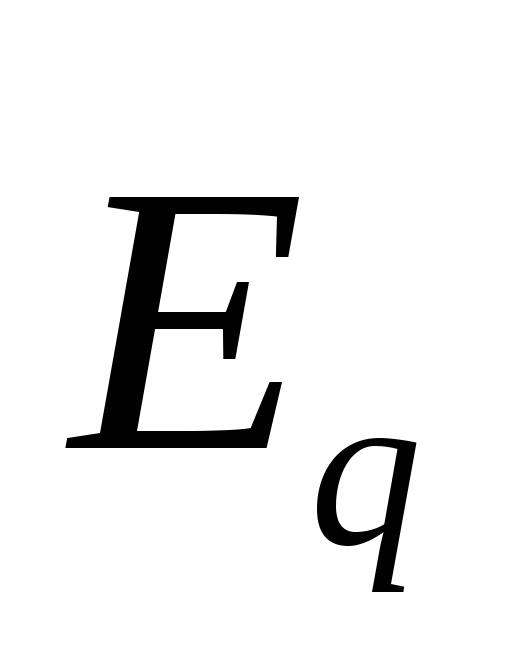 ).
Электродвижущая сила равна циркуляции
вектора
).
Электродвижущая сила равна циркуляции
вектора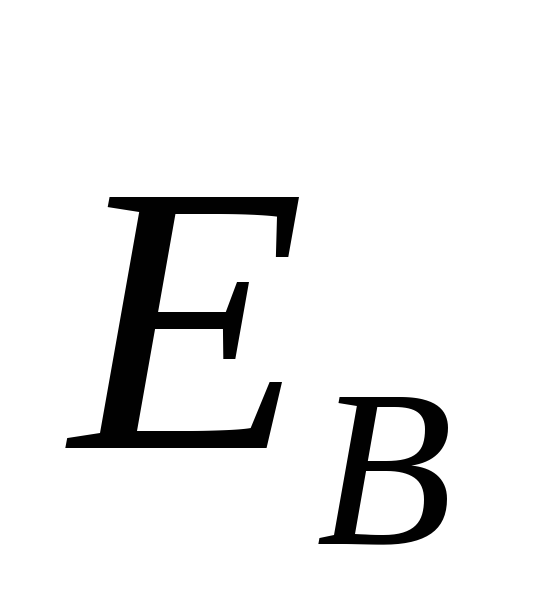 по
данному контуру:
по
данному контуру:
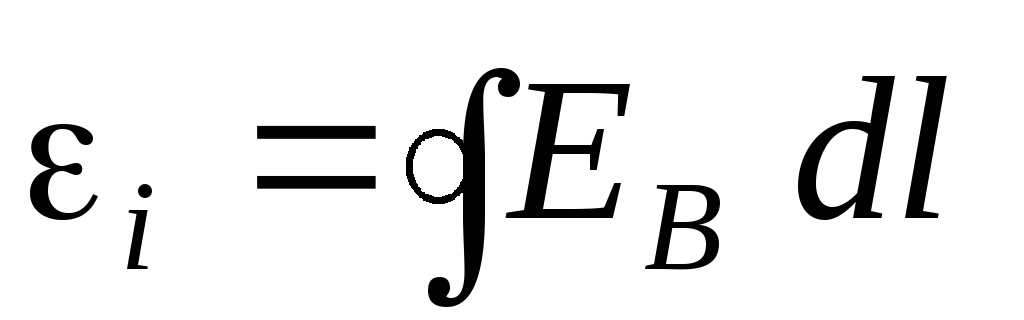 (1.1)
(1.1)
Подстановка
в формулу 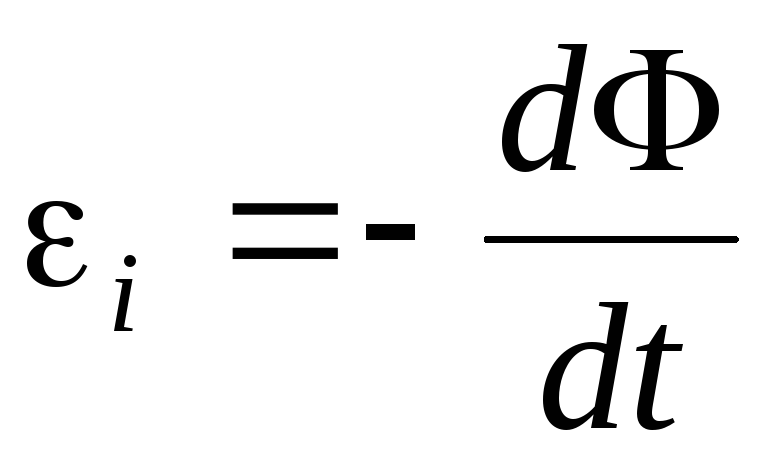 выражения (1.1) для
выражения (1.1) для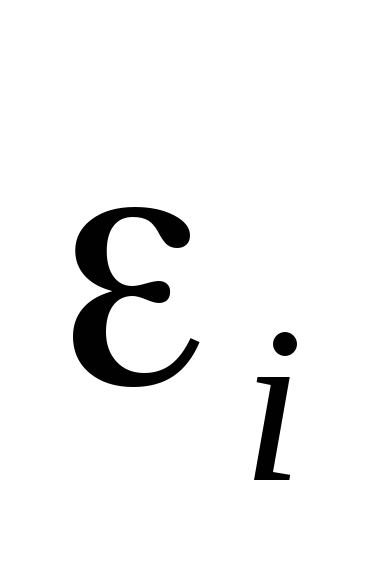 и
выражения
и
выражения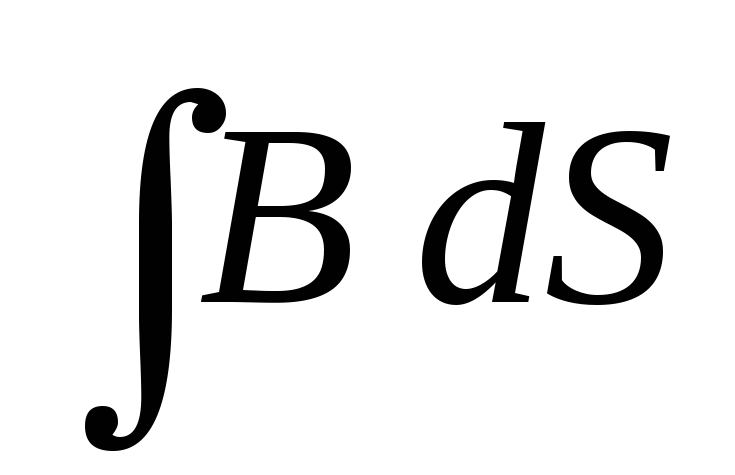 для
для приводит к соотношению
приводит к соотношению
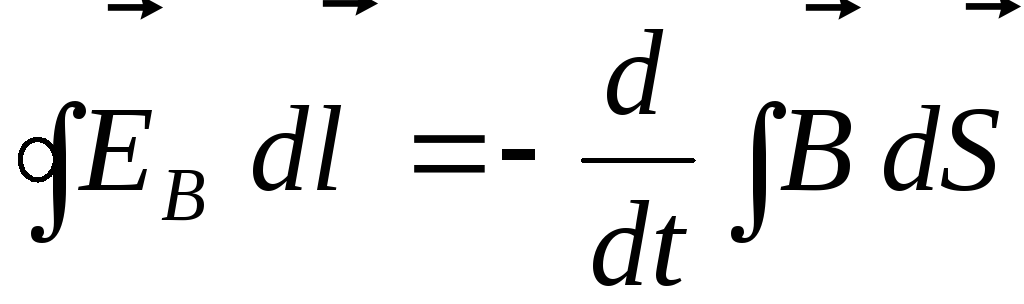
(интеграл в правой части берётся по произвольной поверхности, опирающейся на контур). Поскольку контур и поверхность неподвижны, операции дифференцирования по времени и по поверхности можно поменять местами:
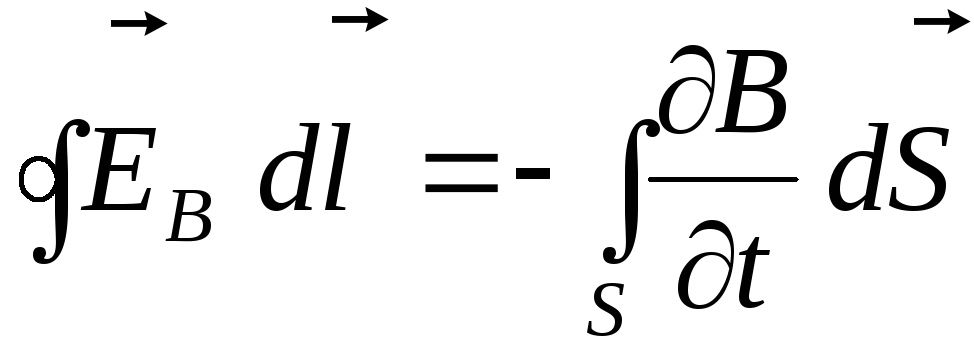 (1.2)
(1.2)
В
связи с тем, что вектор 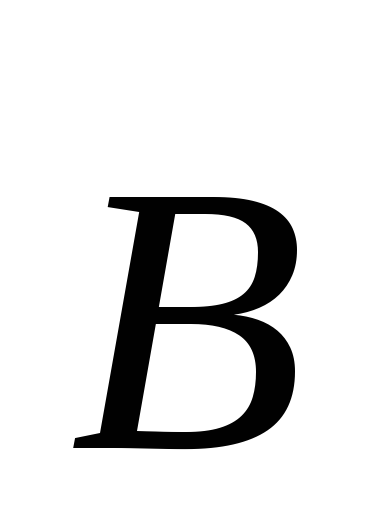 зависит, вообще говоря, как от времени,
так и от координат, то можно написать
под знаком интеграла символ частной
производной по времени (интеграл
зависит, вообще говоря, как от времени,
так и от координат, то можно написать
под знаком интеграла символ частной
производной по времени (интеграл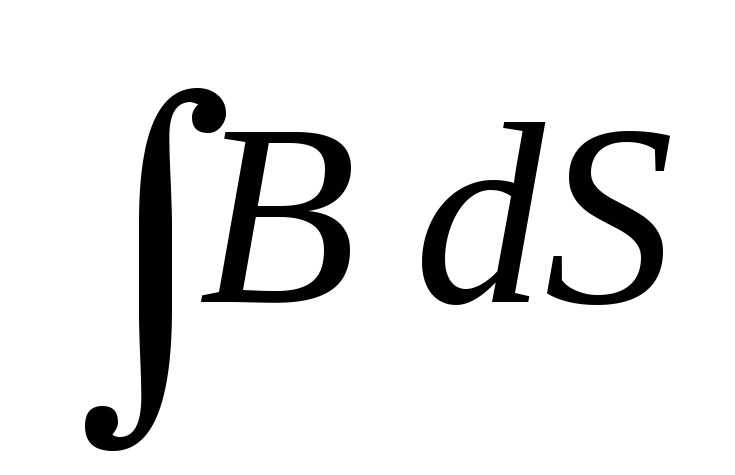 является функцией только времени).
является функцией только времени).
Левую часть равенства (1.2) преобразуем по теореме Стокса. В результате получится:
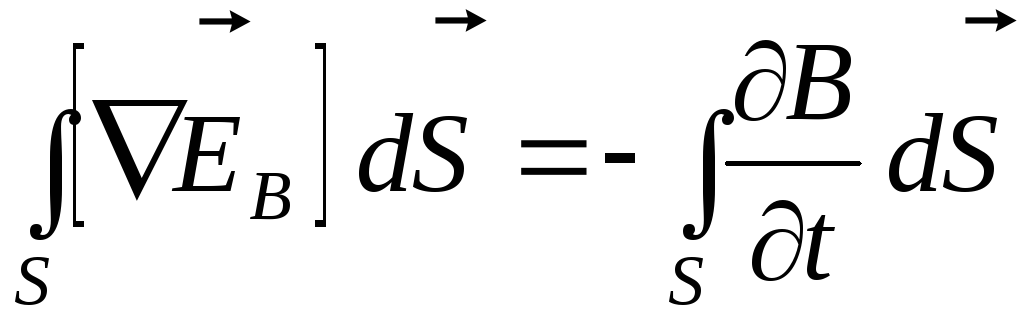 .
.
Ввиду произвольности выбора поверхности интегрирования должно выполняться равенство
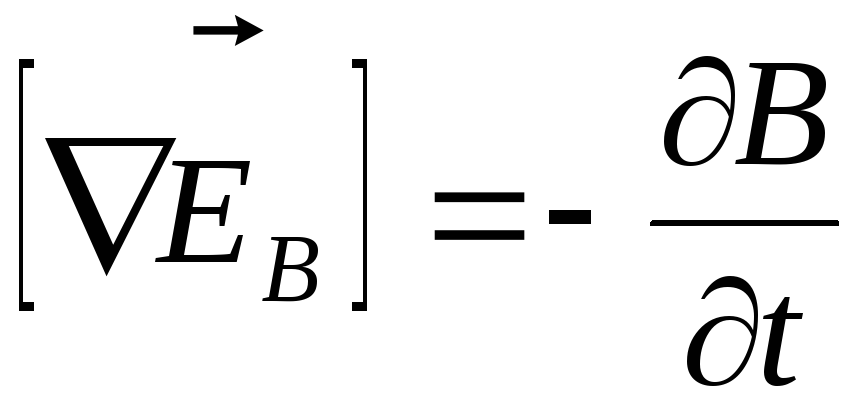 .
.
Ротор
поля 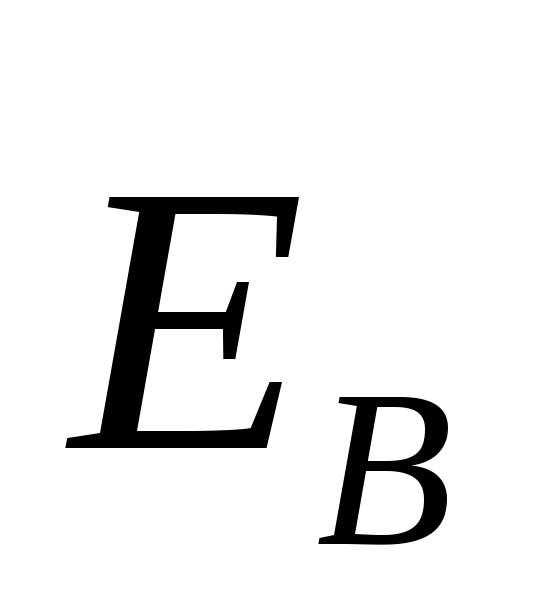 в
каждой точке пространства равен взятой
с обратным знаком производной по времени
от вектора
в
каждой точке пространства равен взятой
с обратным знаком производной по времени
от вектора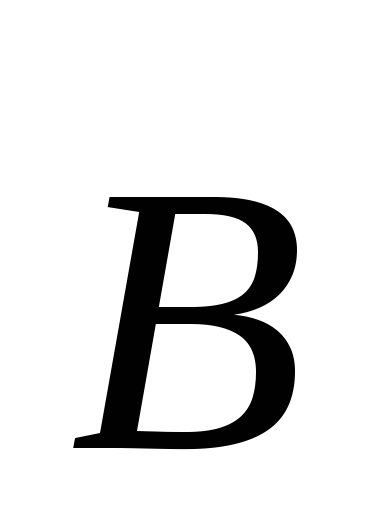 .
.
Это
поле 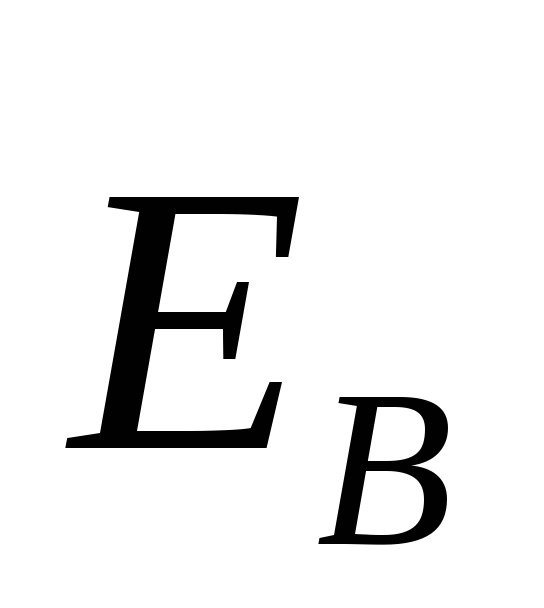 ,
порождающееся изменением магнитного
поля, существенно отличается от
порождаемого электрическими зарядами
электрического поля
,
порождающееся изменением магнитного
поля, существенно отличается от
порождаемого электрическими зарядами
электрического поля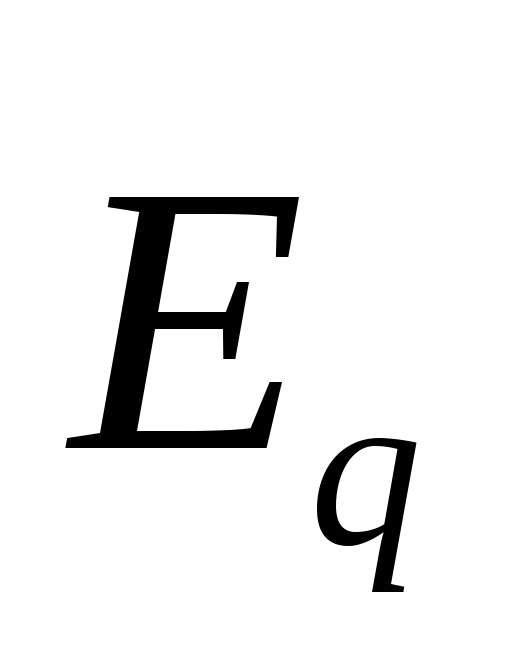 .
Электростатическое поле потенциально,
его линии начинаются и заканчиваются
на зарядах. Ротор вектора
.
Электростатическое поле потенциально,
его линии начинаются и заканчиваются
на зарядах. Ротор вектора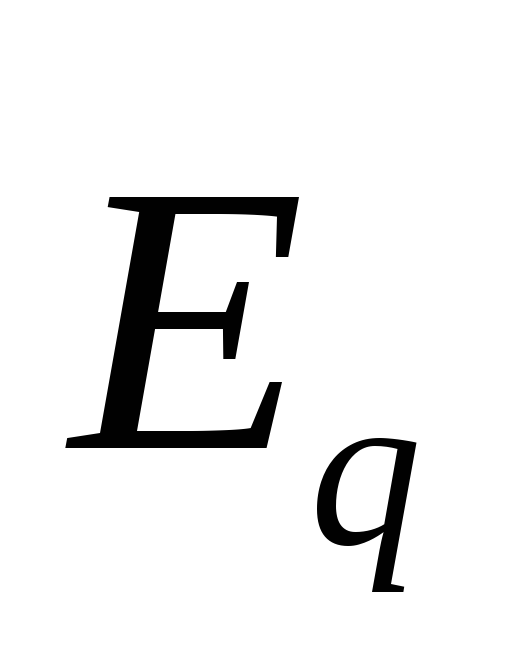 в любой точке равен нулю:
в любой точке равен нулю:
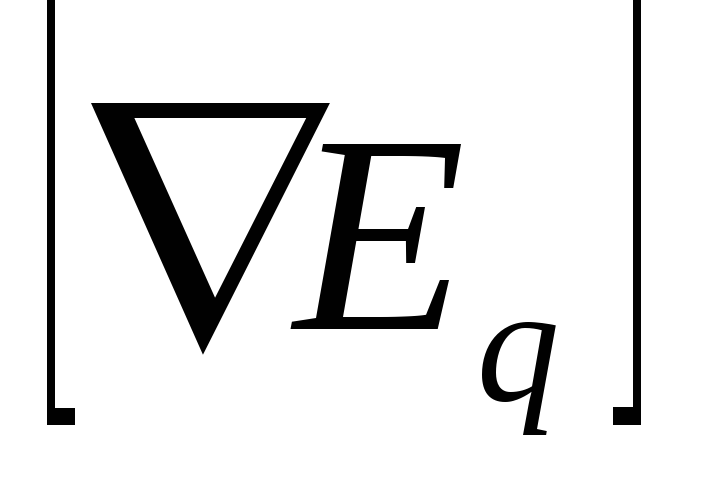 =0.
=0.
Согласно
(1.2) ротор вектора 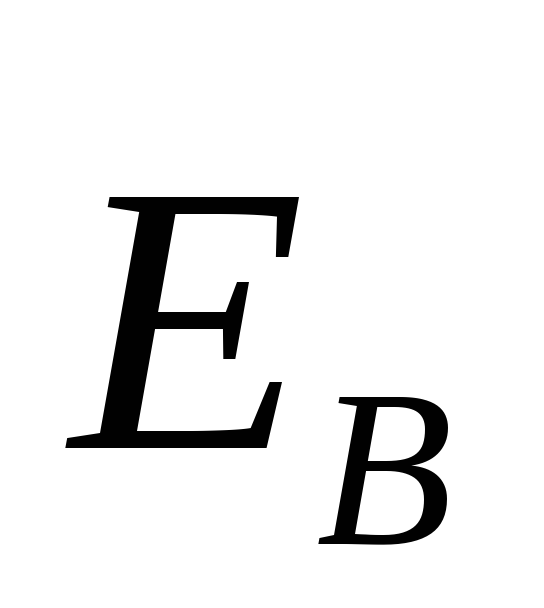 отличен от нуля. Следовательно, поле
отличен от нуля. Следовательно, поле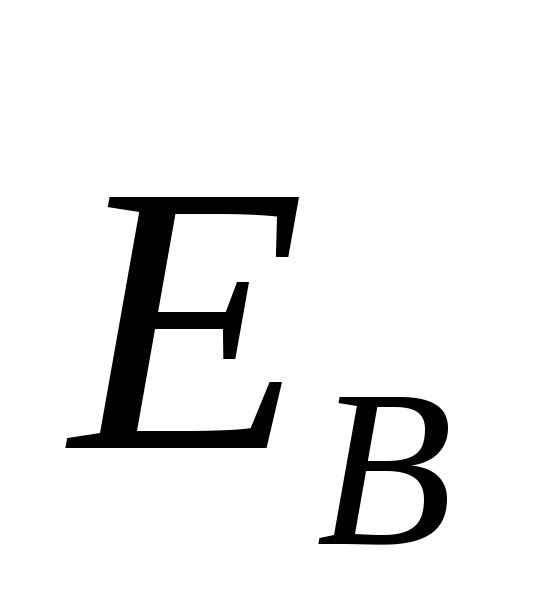 так же, как и магнитное является вихревым.
Линии напряжённости
так же, как и магнитное является вихревым.
Линии напряжённости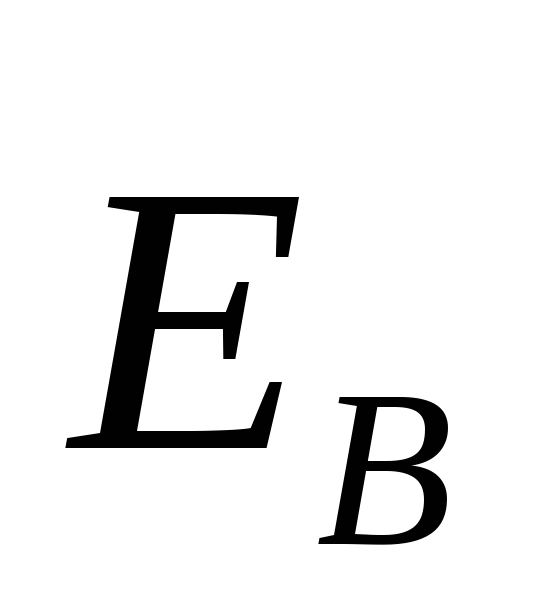 замкнуты.
замкнуты.
Таким
образом, электрическое поле может быть
как потенциальным (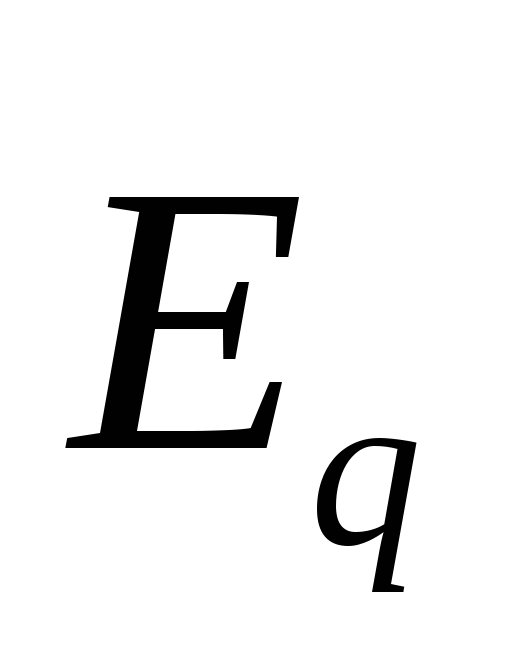 )
так и вихревым (
)
так и вихревым (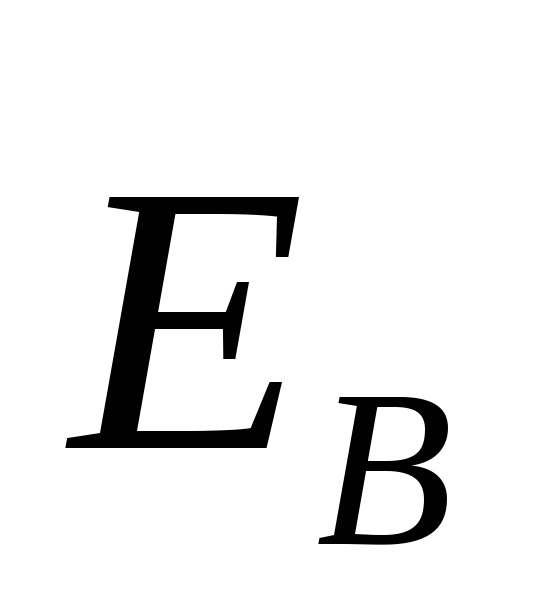 ).
В общем случае электрическое поле
слагается из этих двух полей. Сложив
вместе
).
В общем случае электрическое поле
слагается из этих двух полей. Сложив
вместе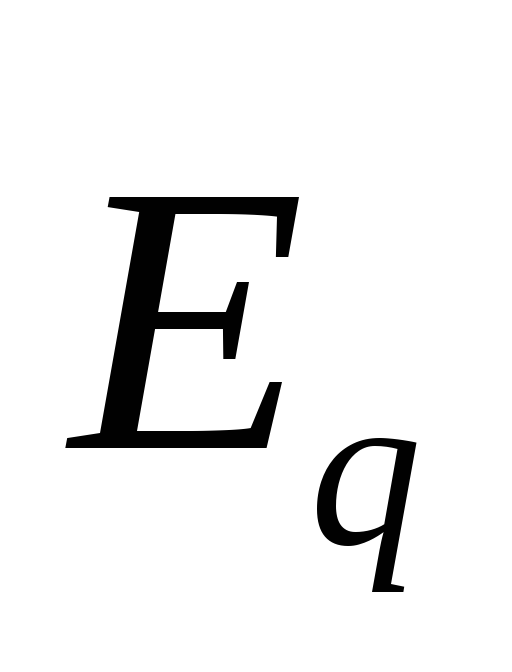 и
и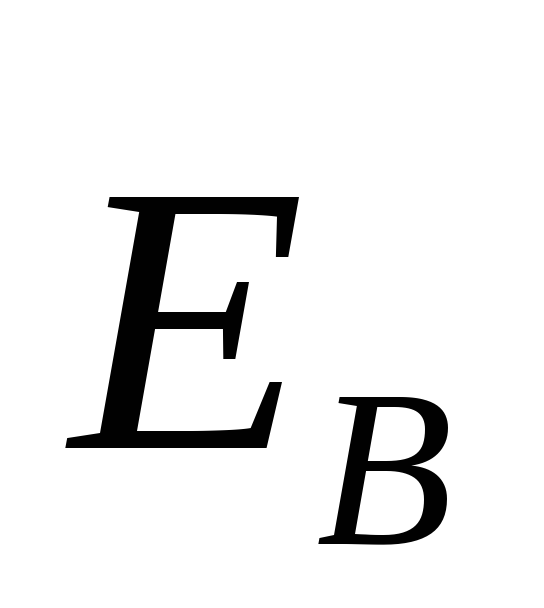 ,
получим следующее уравнение:
,
получим следующее уравнение:
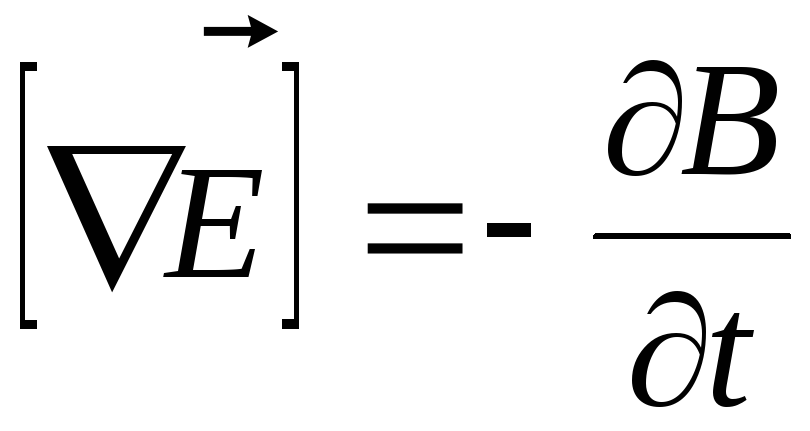 .
(1.3)
.
(1.3)
Существование взаимосвязи между электрическим и магнитным полями служит причиной того, что раздельное рассмотрение электрического и магнитного полей имеет лишь относительный смысл. Действительно, электростатическое поле создаётся системой неподвижных зарядов в одной системе координат, однако они могут двигаться относительно другой инерциальной системы отсчёта и тогда они будут во второй системе подвижными, следовательно, будут создавать магнитное поле. Таким образом, поле, которое относительно некоторой системы отсчёта оказывается «чисто» электрическим или «чисто» магнитным, относительно других систем отсчёта будет представлять собой совокупность электрического и магнитных полей, образующих единое электромагнитное поле.
Выводя
формулу (3), Максвелл пересмотрел уравнения
для ротора вектора  для случая стационарного (не изменяющегося
со временем) электромагнитного поля,
где ротор вектора
для случая стационарного (не изменяющегося
со временем) электромагнитного поля,
где ротор вектора равен в каждой точке плотности тока
проводимости:
равен в каждой точке плотности тока
проводимости:
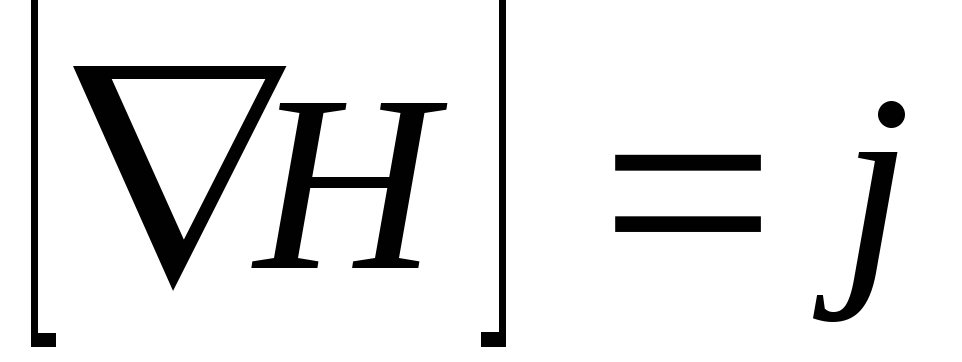 ,
(3.1)
,
(3.1)
где
вектор 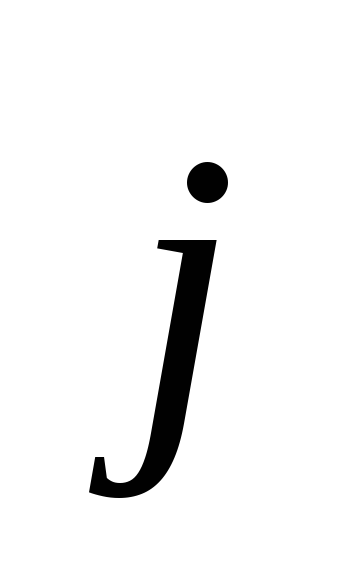 связан с плотностью заряда в той же
точке уравнением непрерывности:
связан с плотностью заряда в той же
точке уравнением непрерывности:
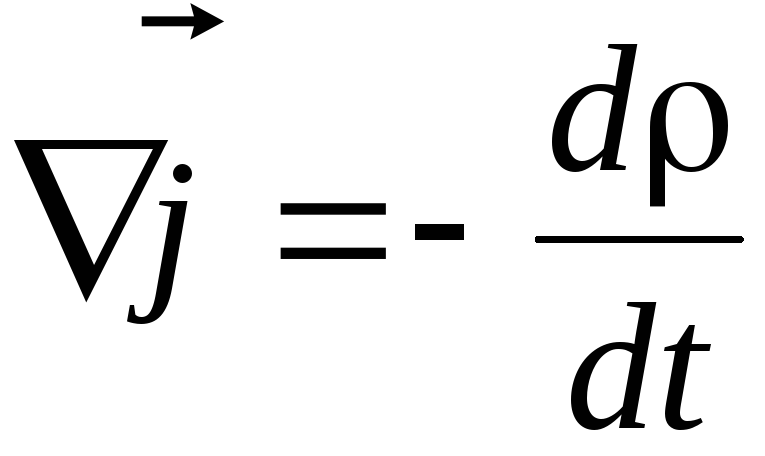 (3.2)
(3.2)
Электромагнитное
поле может быть стационарным лишь при
условии, что плотность заряда  и плотность тока
и плотность тока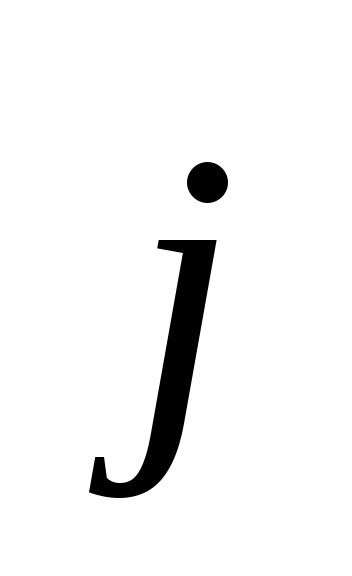 не зависят от времени. В этом случае
согласно (3.2) дивергенция
не зависят от времени. В этом случае
согласно (3.2) дивергенция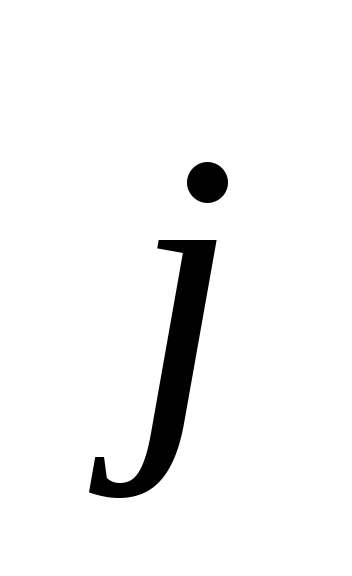 равна нулю.
равна нулю.
Поэтому можно выяснить, является ли справедливым уравнение (3.2) справедливым в случае изменяющихся со временем полей. Рассмотрим магнитное поле, создаваемое током, текущим при зарядке конденсатора от источника постоянного напряжения U (рис. 1).
 Э
Э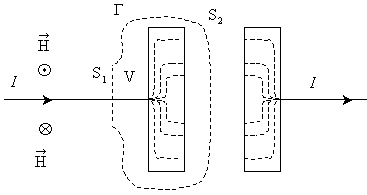 тот
ток непостоянен во времени (в момент,
когда напряжение на конденсаторе
становится равнымU,
ток прекращается). Линии тока проводимости
терпят разрыв в промежутке между
обкладками конденсатора.
тот
ток непостоянен во времени (в момент,
когда напряжение на конденсаторе
становится равнымU,
ток прекращается). Линии тока проводимости
терпят разрыв в промежутке между
обкладками конденсатора.
Возьмём круговой контур Г, охватывающий провод, по которому течёт ток к конденсатору, и проинтегрируем соотношение (3.1) по пересекающеё провод поверхности S1, ограниченной контуром:
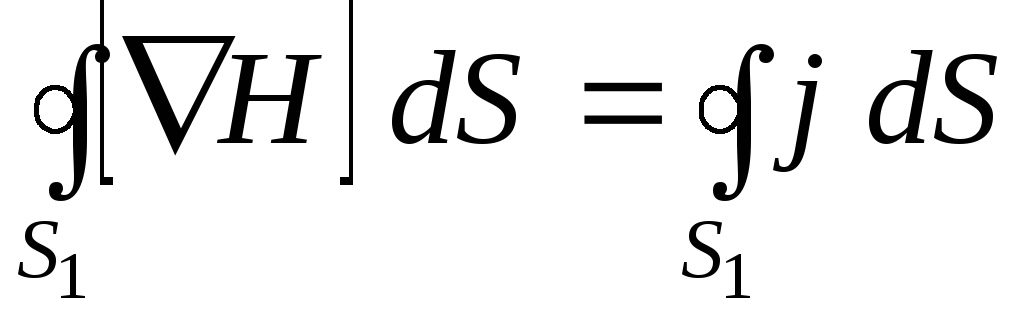 .
.
Преобразовав
левую часть по теореме Стокса, получим
циркуляцию
вектора  по
контуру Г:
по
контуру Г:
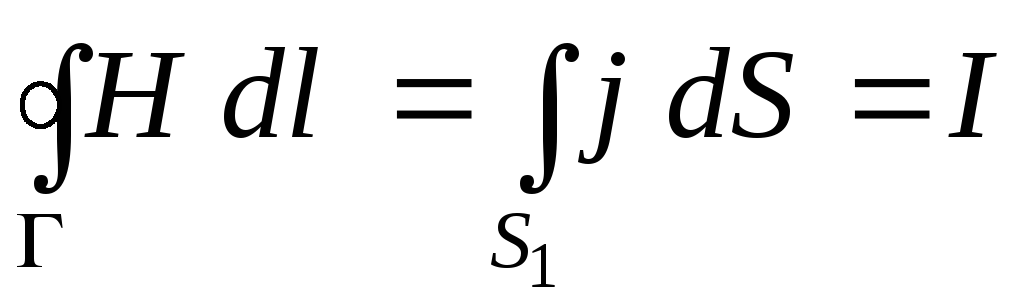 (3.3)
(3.3)
(I – сила тока заряжающего конденсатор). Проделав такие же вычисления для поверхности S2, придём к явно неверному соотношению:
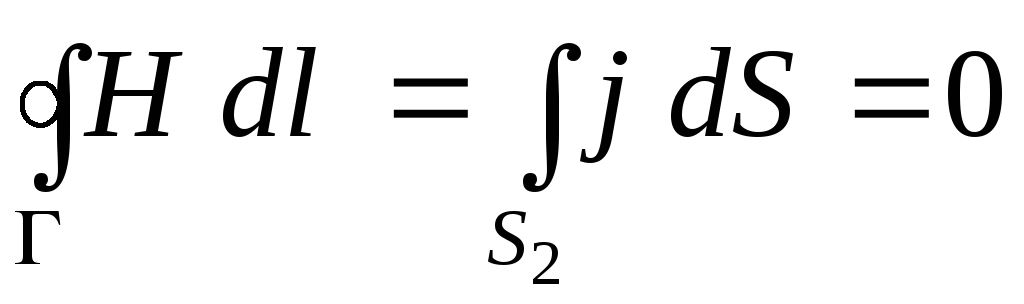 (3.4)
(3.4)
Полученный результат указывает на то, что в случае изменяющихся со временем полей уравнение (3.1) перестаёт быть справедливым. Напрашивается вывод, что в этом уравнении отсутствует слагаемое, зависящее от произвольных полей во времени. Для стационарных полей это слагаемое обращается в нуль.
На неправомерность уравнения (3.1) в случае нестационарных полей указывает также, следующие соображения. Возьмём дивергенцию от обеих частей соотношения (3.1):
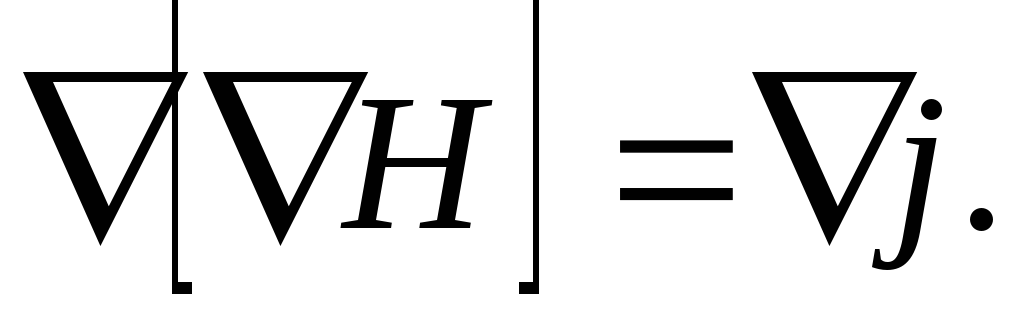
Дивергенция
ротора должна быть обязательно равна
нулю. Таки образом, можно прийти к выводу,
что дивергенция вектора 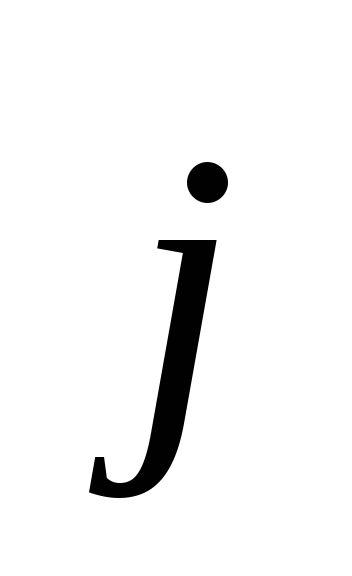 также должна быть всегда равной нулю.
Однако этот вывод
также должна быть всегда равной нулю.
Однако этот вывод
противоречит
уравнению непрерывности, где 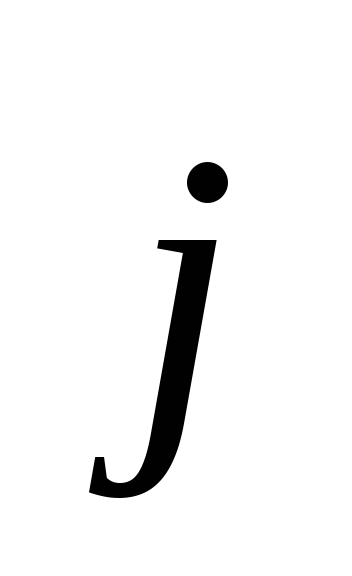 отлична от нуля.
отлична от нуля.
Чтобы согласовать уравнения (3.1) и (3.2), Максвелл ввел в правую часть уравнения (3.1) дополнительное слагаемое. Естественно, что это слагаемое должно иметь размерность плотности тока. Максвелл назвал его плотностью тока смещения. Таким образом, согласно Максвеллу уравнение (3.1) должно иметь вид:
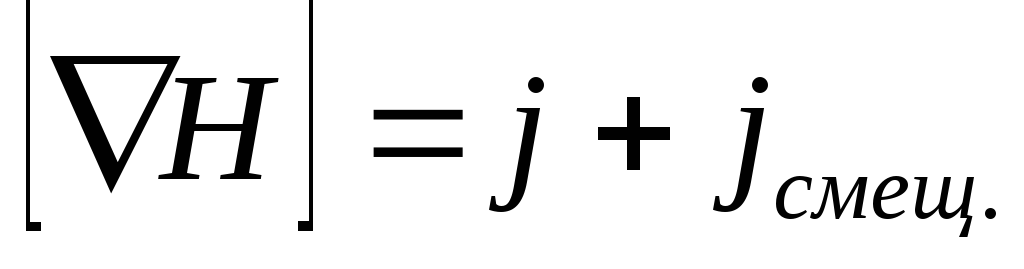 (3.5)
(3.5)
Сумму тока проводимости и тока смещения принято называть полным током. Плотность полного тока равна:
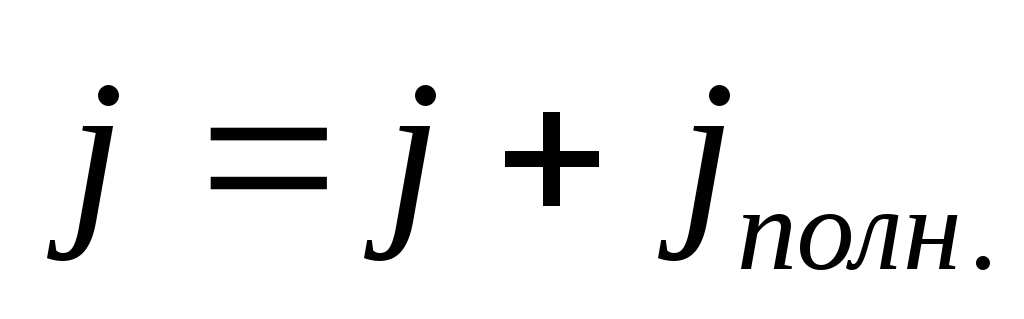 (3.6)
(3.6)
Если положить дивергенцию тока смещения равной дивергенции тока проводимости, взятой с обратным знаком,
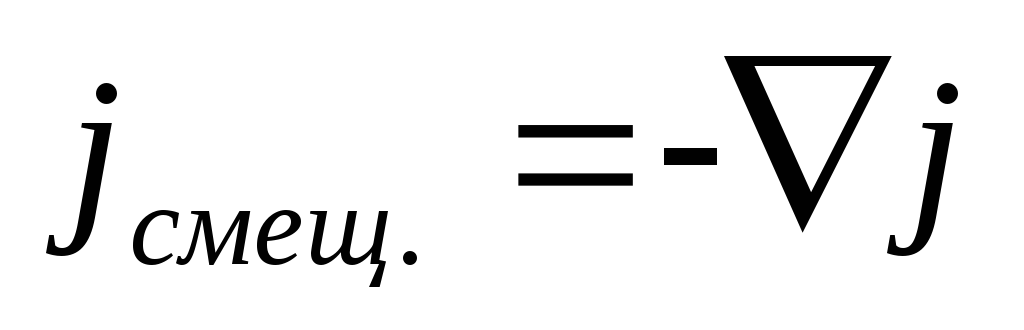 (3.7)
(3.7)
то дивергенция правой части уравнения (3.5), так же как и дивергенция левой части, всегда будет равна нулю.
Заменив
в (3.7)  согласно (3.2) через
согласно (3.2) через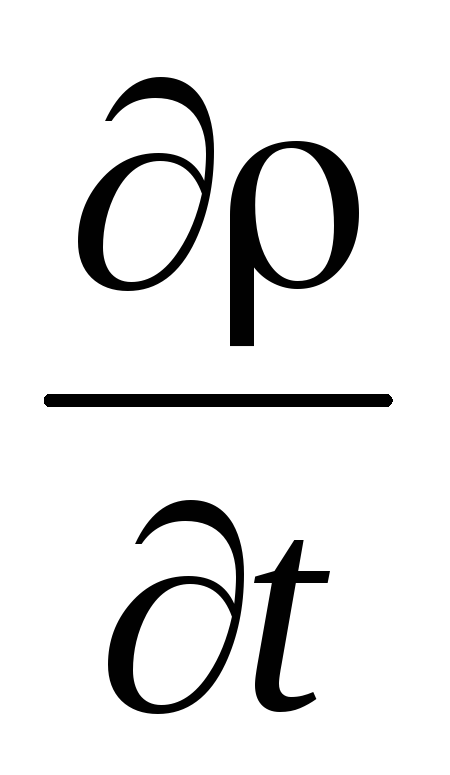 ,
получим следующее выражение для
дивергенции тока смещения:
,
получим следующее выражение для
дивергенции тока смещения:
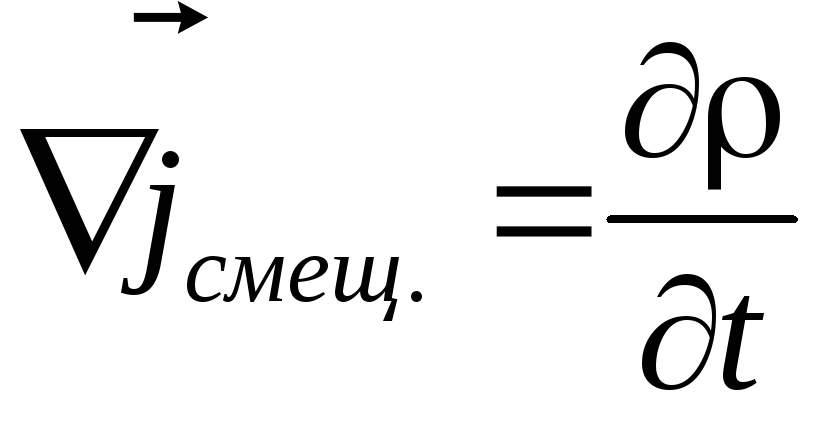 .
(3.8)
.
(3.8)
Чтобы связать ток смещения с величинами, характеризующими изменение электрического поля со временем, воспользуемся соотношением:
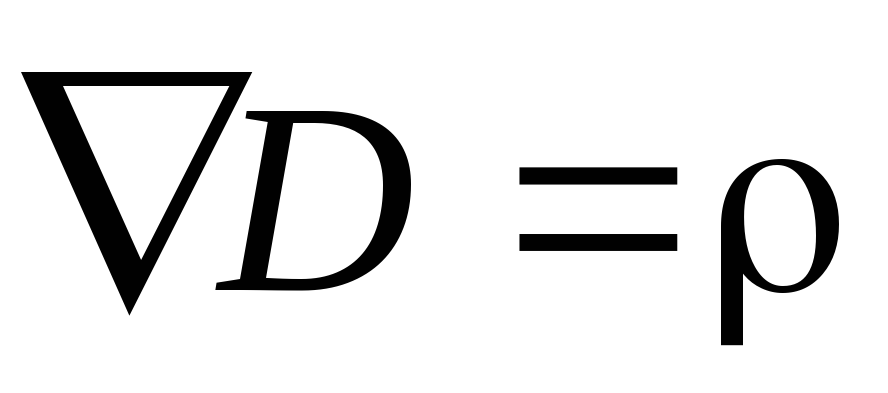
Продифференцировав это соотношение по времени, получим:
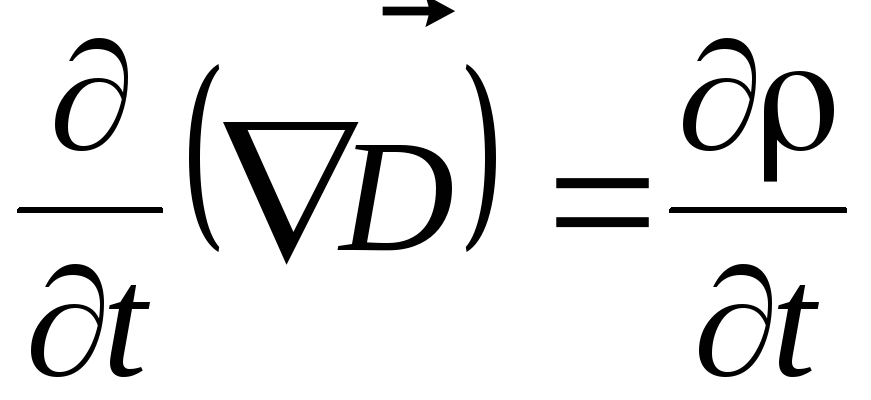
Теперь
поменяем в левой части порядок
дифференцирования по времени и по
координатам. В результате придём к
следующему выражения для производной  по
по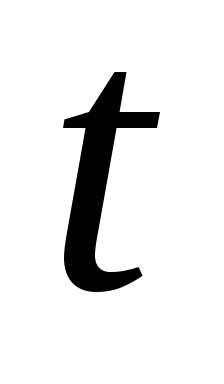 .
.
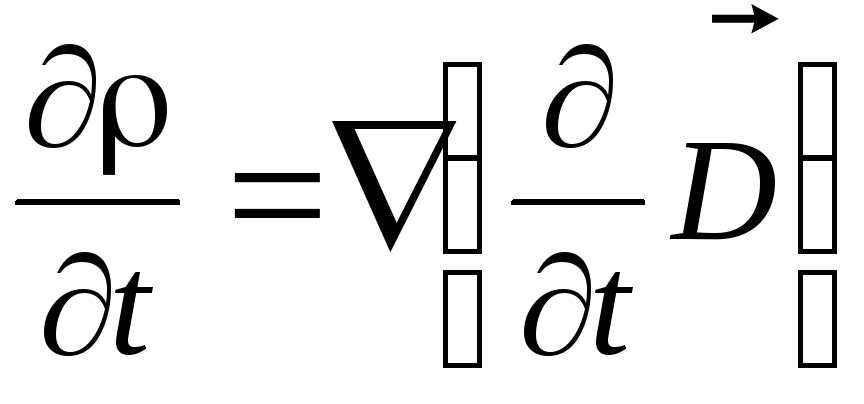 .
.
Подстановка этого выражения в формулу (3.8) даёт:
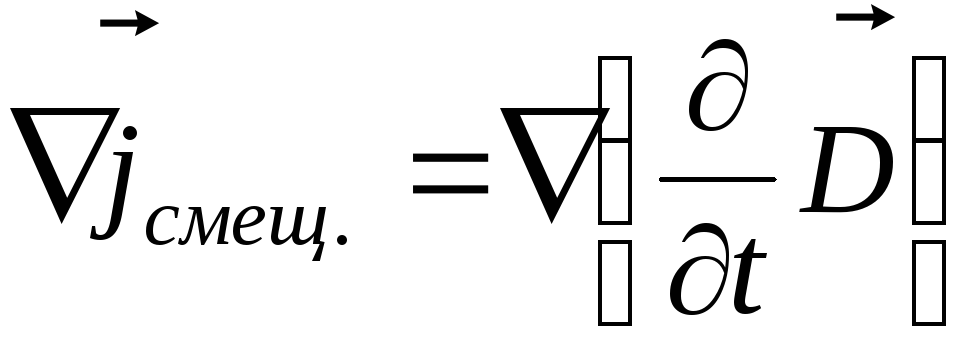 .
.
Отсюда
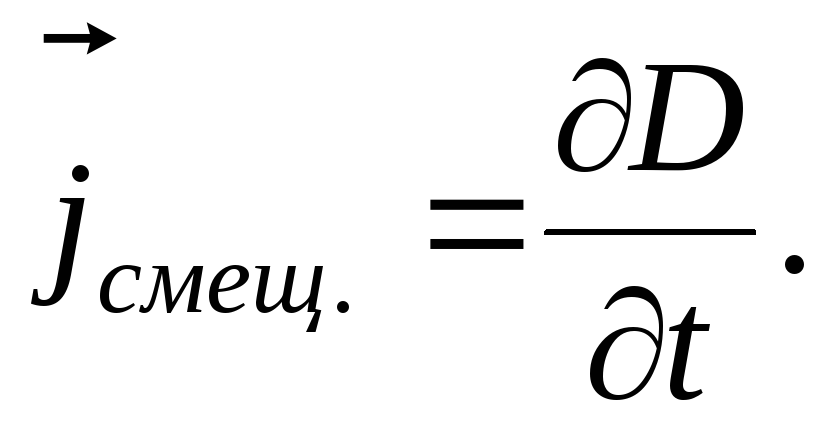 (3.9)
(3.9)
Подставив выражение (3.9) в формулу (3.6), придём к уравнению
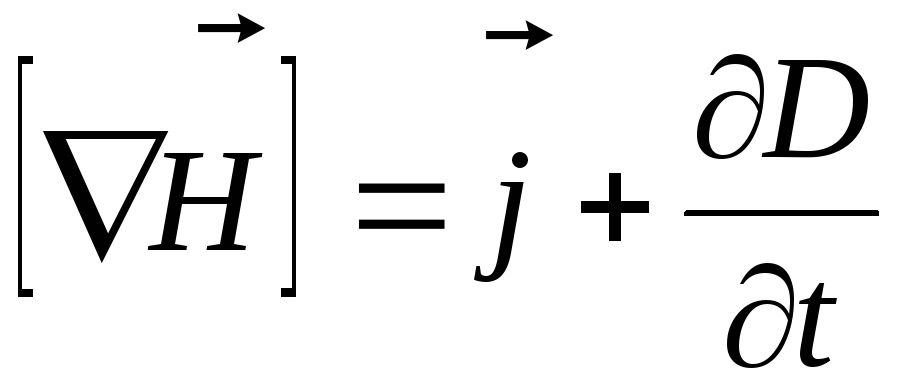 .
.
Каждое из векторных уравнений (1) и (3) эквивалентно трем скалярным уравнениям, связывающим компоненты векторов, стоящих в левой и правой частях равенств. Воспользовавшись правилом раскрытия дифференциальных операторов, можно записать их в следующем виде:
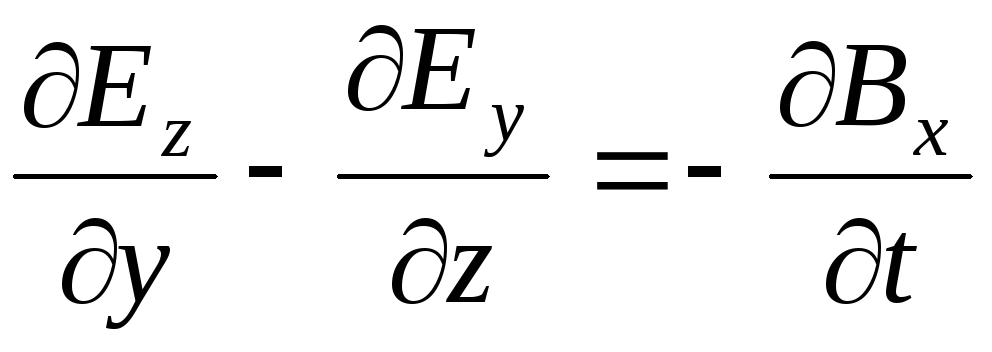 ;
; 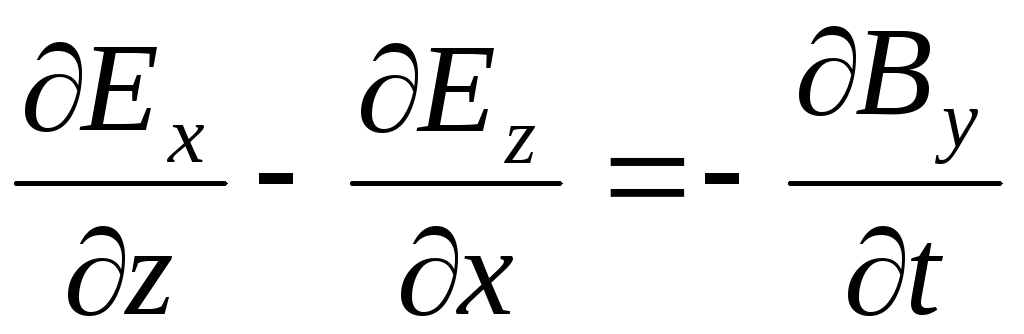 ;
;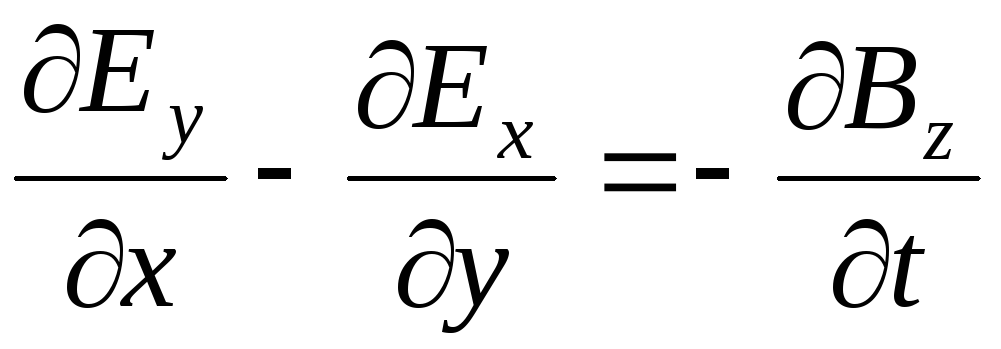 (5)
(5)
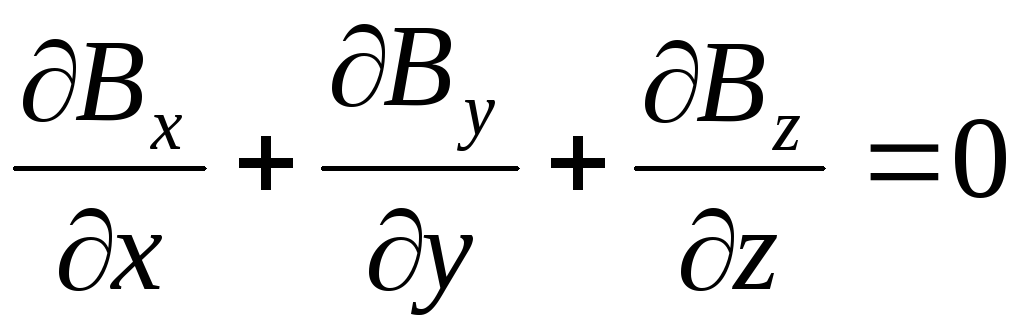 (6)
(6)
для первой пары уравнений, и:
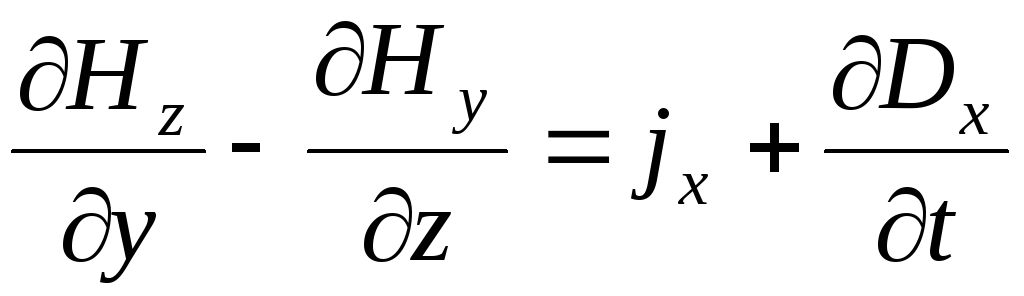 ;
; 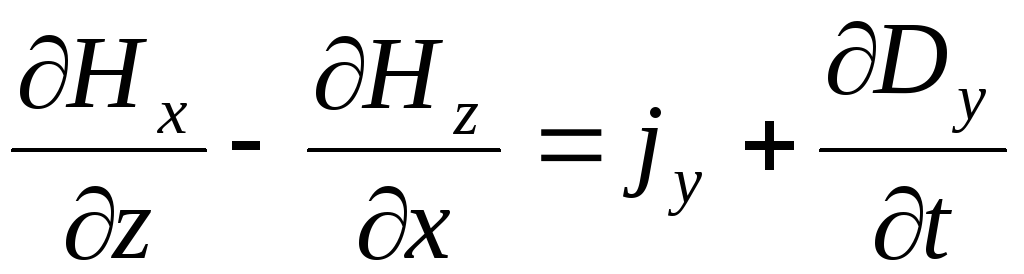 ;
;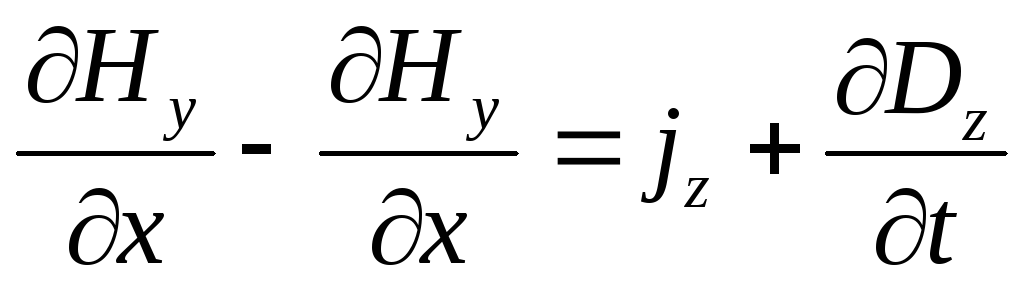 (7)
(7)
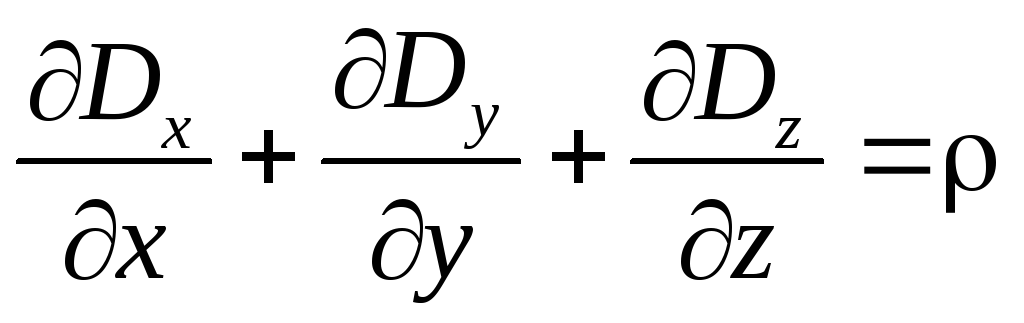 (8)
(8)
для второй.
Всего
получилось 8 уравнений, в которых входят
12 функций (по три компоненты векторов  ,
,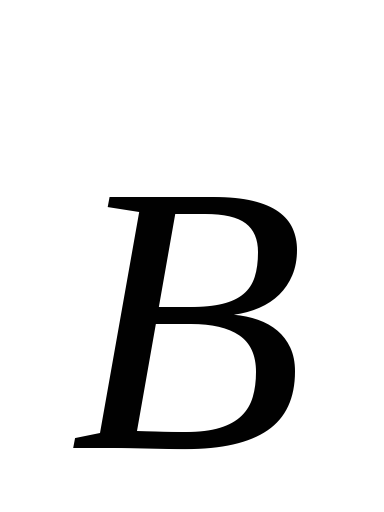 ,
,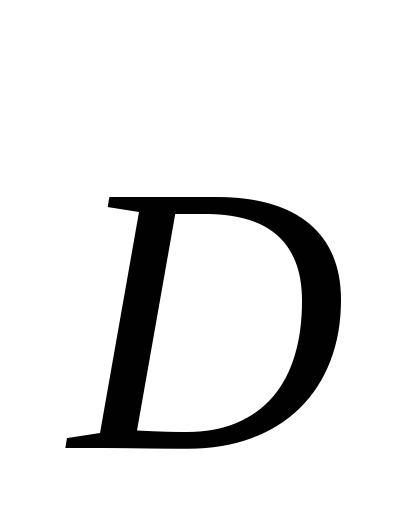 ,
, .)
Поскольку число уравнений меньше числа
известных функций, уравнений (1) — (4)
недостаточно для нахождения полей по
заданным распределениям зарядов и
токов. Чтобы осуществить расчёт полей,
нужно дополнить уравнения Максвелла
уравнениями, связывающими
.)
Поскольку число уравнений меньше числа
известных функций, уравнений (1) — (4)
недостаточно для нахождения полей по
заданным распределениям зарядов и
токов. Чтобы осуществить расчёт полей,
нужно дополнить уравнения Максвелла
уравнениями, связывающими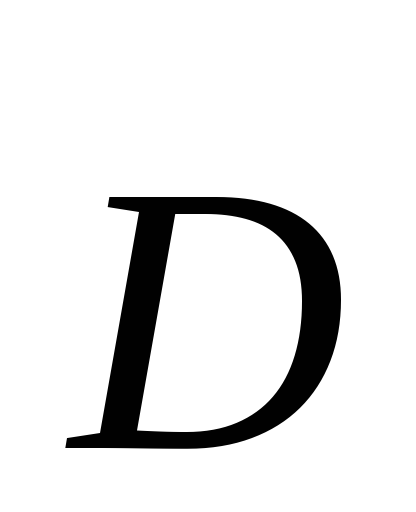 и
и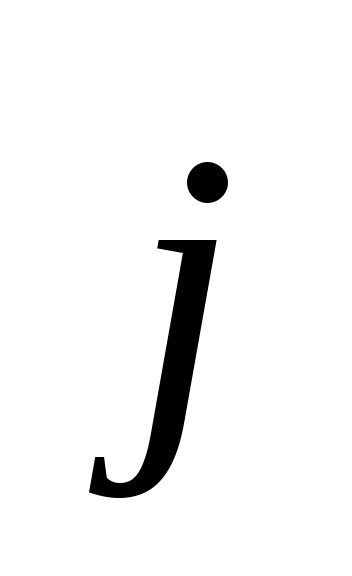 с
с ,
а также
,
а также с
с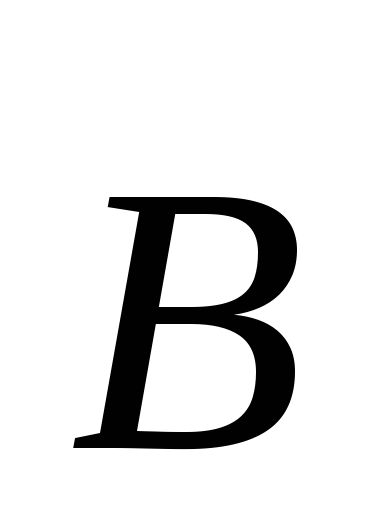 .
Эти уравнения имеют вид.
.
Эти уравнения имеют вид.
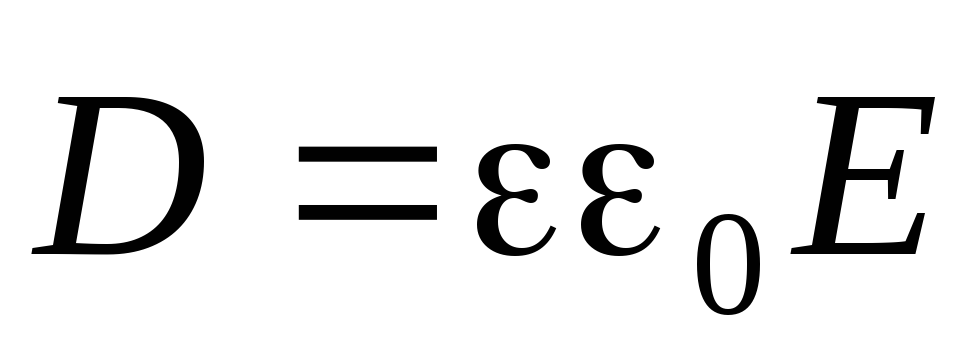 (9)
(9)
 (10)
(10)
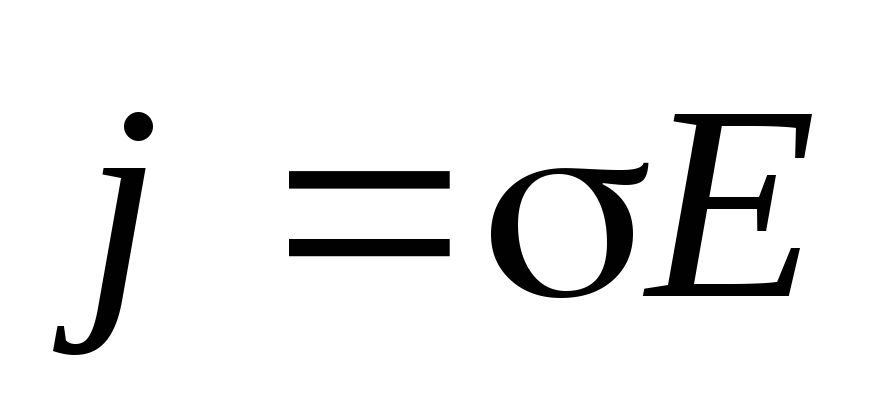 (11)
(11)
Совокупность уравнений (1) – (11) образуют основу электродинамики покоящихся сред.
Уравнения:
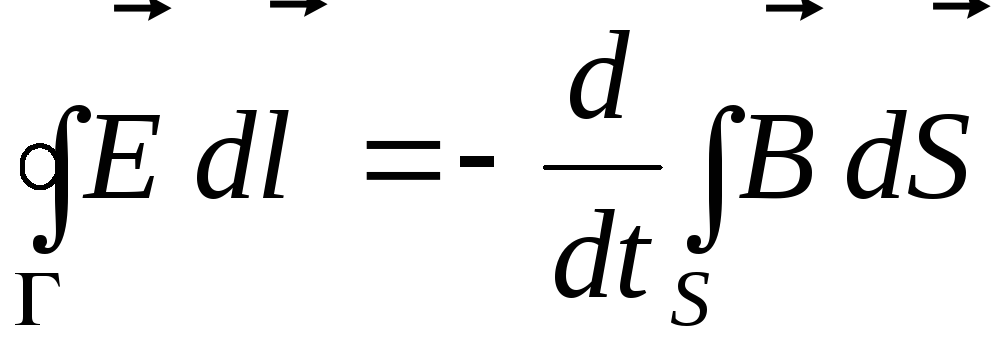 (12)
(12)
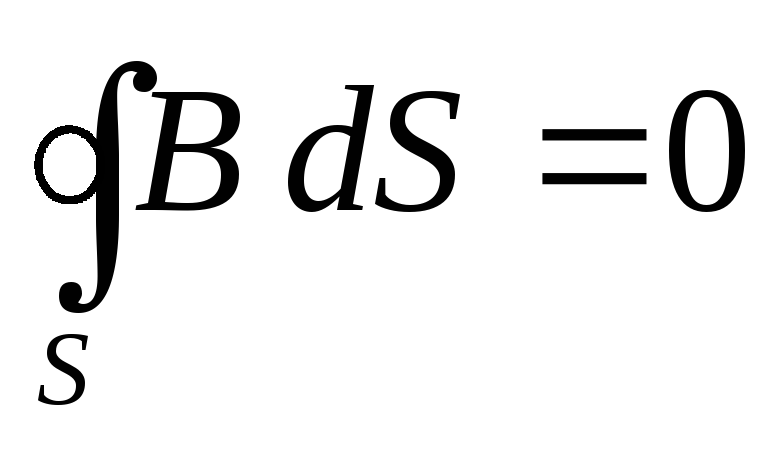 (13)
(13)
(первая пара) и
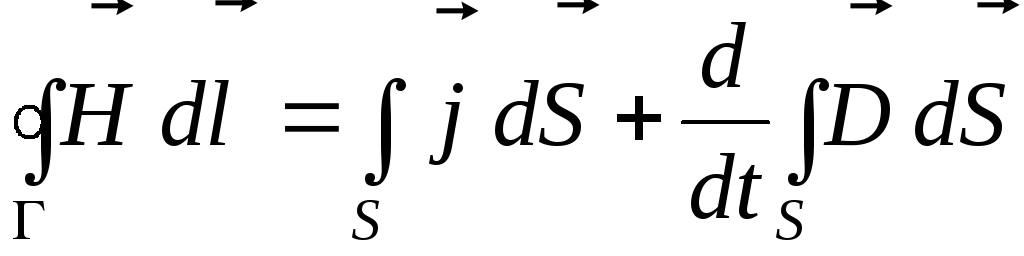 (14)
(14)
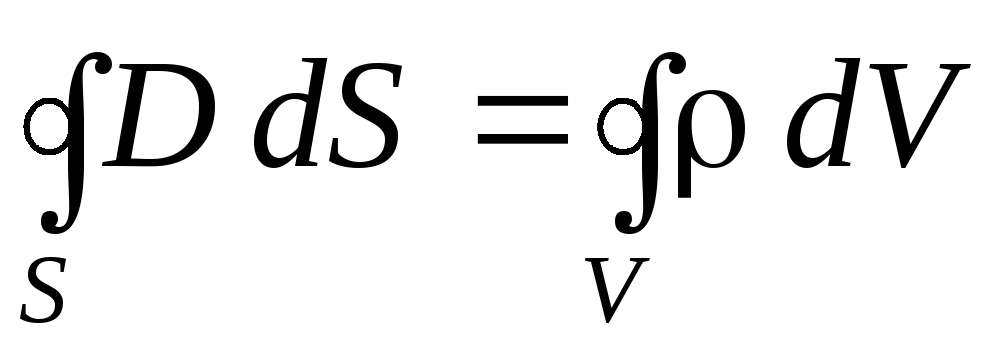 (15)
(15)
(вторая пара) представляют собой уравнения Максвелла в интегральной форме.
Уравнение (12) получается путём интегрирования соотношения (1) по произвольной поверхности S с последующим преобразованием левой части по теореме Стокса в интеграл по контуру Г, ограничивающему поверхность S. Уравнение (14) получается таким же способом из соотношения (3). Уравнения (13) и (15) получаются из соотношений (2) и (4) путём интегрирования по произвольному объёму V с последующим преобразованием левой части по теореме Остроградского-Гаусса в интеграл по замкнутой поверхности S, ограничивающей объём V.
39. Уравнения Максвелла в интегральной форме.
Введение Максвеллом понятия полного тока смещения привело его к завершению созданной им макроскопической теории электромагнитного поля, позволившей с единой точки зрения объяснить электрические и магнитный явления и предсказать новые.
В основе теории Максвелла лежат четыре уравнения, полученные нами ранее:
1. Циркуляция
вектора напряженности суммарного поля 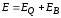 (циркуляция вектора
(циркуляция вектора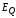 равна нулю):
равна нулю):
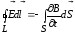 (12)
(12)
Это уравнение показывает, что источниками электрического поля могут быть не только электрические заряды, но и изменяющиеся во времени магнитные поля.
2. Обобщенная
теорема о циркуляции вектора 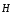 :
:
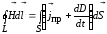 .(13)
.(13)
Это уравнение показывает, что магнитные поля могут возбуждаться либо движущимися зарядами (электрическими токами), либо переменными электрическими полями.
3. Теорема Гаусса
для поля 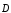 :
:
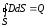 (14)
(14)
или, если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью ρ:
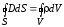 . (15)
. (15)
Это уравнение показывает, что в природе существуют электрические заряды.
4. Теорема Гаусса
для поля 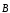 :
:
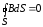 . (16)
. (16)
Это уравнение показывает, что в природе не существуют магнитные заряды.
Дополнительные уравнения, используемые с уравнениями Максвелла. Величины, входящие в уравнения Максвелла, не являются независимыми и между ними существует связь:
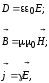
где 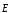 — напряженность электрического поля;
— напряженность электрического поля;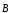 — магнитная индукция;
— магнитная индукция;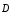 — электрическое смещение;
— электрическое смещение;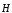 —
напряженность магнитного поля;
—
напряженность магнитного поля;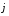 —
плотность тока проводимости; γ – удельная
проводимость вещества;
—
плотность тока проводимости; γ – удельная
проводимость вещества;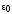 и
и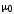 – электрическая и магнитная постоянная;
ε и μ – электрическая и магнитная
проницаемости.
– электрическая и магнитная постоянная;
ε и μ – электрическая и магнитная
проницаемости.
Совокупность этих 7 уравнений составляют основу электродинамики покоящихся сред.
Уравнения
Максвелла для стационарных полей (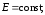
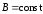 ).
).
1. ; 2.;
3. ; 4..
Источниками электрического поля являются только электрические заряды, источниками магнитного поля – только токи проводимости. В этом случае электрические и магнитные поля независимы друг от друга, что позволяет изучать отдельно постоянные электрическое и магнитное поля.
40. Уравнения Максвелла в дифференциальной форме
Теоремы векторного анализа, используемые при переходе от интегральной формы уравнения к дифференциальной
1. Теорема Стокса: зная ротор вектора 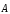 в каждой точке некоторой поверхностиS можно вычислить циркуляцию этого вектора
по контуру L,
ограничивающему S:
в каждой точке некоторой поверхностиS можно вычислить циркуляцию этого вектора
по контуру L,
ограничивающему S:
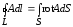 .
.
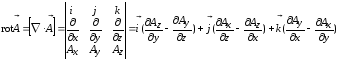 .
.
2. Теорема
Гаусса: зная
дивергенцию вектора 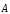 в каждой точке пространства, можно
вычислить поток этого вектора через
произвольную замкнутую поверхностьS конечных размеров.
в каждой точке пространства, можно
вычислить поток этого вектора через
произвольную замкнутую поверхностьS конечных размеров.
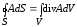 .
.
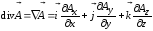 ;
;
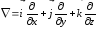 .
.
Уравнения Максвелла в дифференциальной форме характеризуют поле в каждой точке пространства. Физический смысл уравнений Максвелла в дифференциальной форме тот же, что и уравнения Максвелла в интегральной.
Если заряды и токи распределены в пространстве непрерывно, то обе формы уравнений Максвелла эквивалентны. Однако, если имеются поверхности разрыва (поверхности, на которых свойства среды меняются скачкообразно), то интегральная форма уравнений является более общей.
Уравнения Максвелла в дифференциальной форме предполагают, что все величины в пространстве и времени изменяются непрерывно. Чтобы достичь математической эквивалентности обеих форм уравнений Максвелла, дифференциальную форму дополняют граничными условиями, которым должно удовлетворять электромагнитное поле на границе раздела двух сред:
1. 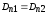 ;
(на границе раздела нет свободных
зарядов)
;
(на границе раздела нет свободных
зарядов)
2. 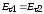 ;
;
3. 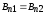 ;
;
4. 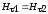 (на границе раздела нет токов проводимости).
(на границе раздела нет токов проводимости).
Некоторые следствия из уравнений Максвелла
Уравнения Максвелла – наиболее общие уравнения для электрических и магнитных полей в покоящихся средах. Они играют в электродинамике такую же роль, как законы Ньютона в механике.
1. Согласно идеям Максвелла, переменное магнитное поле всегда связано с порождаемым им электрическим полем, а переменное электрическое поле всегда связано с порождаемым им магнитным полем, т.е. электрические и магнитные поля неразрывно связаны друг с другом – они образуют единое электромагнитное поле.
2. Теория Максвелла не только смогла объяснить уже известные экспериментальные факты, но и предсказала новые явления: существование магнитного поля токов смещения позволило предсказать существование электромагнитных волн – переменного электромагнитного поля, распространяющегося в пространстве с конечной скоростью (скоростью света). Этот вывод и теоретическое исследование свойств электромагнитных волн привели Максвелла к созданию электромагнитной теории света, согласно которой свет представляет собой также электромагнитные волны.
Теория Максвелла была экспериментально подтверждена: электромагнитные волны были получены на практике немецким физиком Герцем, который доказал, что законы их возбуждения и распространения полностью подчиняются уравнениям Максвелла.
3. К электромагнитному полю применим только принцип относительности Эйнштейна, согласно которому, механические, оптические и электромагнитные явления во всех инерциальных системах отсчета протекают одинаково, т.е. описываются одинаковыми уравнениями. Из принципа относительности следует, что раздельное рассмотрение электрического и магнитного полей имеет лишь относительный смысл. Так если электрическое поле создается системой неподвижных зарядов, то эти заряды, являясь неподвижными относительно одной системы отсчета, движутся относительно другой и, следовательно, будут порождать не только электрическое, но и магнитное поле. Аналогично, неподвижный проводник с постоянным током, возбуждая в каждой точке пространства постоянное магнитное поле, движется относительно других инерциальных систем, и создаваемое им переменное магнитное поле возбуждает вихревое электрическое поле. Таким образом, поле, которое относительно некоторой системы отсчета оказывается чисто электрическим или чисто магнитным, относительно других систем отсчета будет представлять собой совокупность электрического и магнитного полей.
Вывод: теория Максвелла, ее экспериментальное подтверждение, а также принцип относительности Эйнштейна приводят к единой теории электрических, магнитных и оптических явлений, основанных на представлении об электромагнитном поле
Обзор уравнений Максвелла — Электромагнитная геофизика
Назначение
Представив набор формирующих законов для электромагнетизма, мы представляем четыре распространенных представления уравнений Максвелла. Эта страница предназначена для использования в качестве краткого руководства. Для решения конкретных задач может быть полезно начать с менее распространенных форм уравнений Максвелла. Обратите внимание, однако, что все формы могут быть получены из представленных здесь выражений.
Эта страница предназначена для быстрого доступа к соответствующим уравнениям с соответствующими обозначения и единицы.Уравнения подходят для электромагнитных полей в веществе. Если поля находятся в свободном пространстве, то используются те же определяющие отношения, но с \ (\ sigma = 0 \), \ (\ mu_0 \) и \ (\ varepsilon_0 \). Определяющие уравнения также записываются в предположении, что физические свойства изотропны и недисперсионны. Дополнительную информацию об этом можно найти в [WH88] (стр. 133) или на странице физических свойств.
Переменные и единицы
Здесь приведены переменные и единицы измерения соответствующих величин в уравнениях Максвелла.
Поля
Поле | Частотная область | во временной области | Шт. |
|---|---|---|---|
Электрическое поле | \ (\ mathbf {E} \) | \ (\ mathbf {e} \) | В / м |
Магнитное поле | \ (\ mathbf {H} \) | \ (\ mathbf {h} \) | А / м |
Флюсы
Поток | Частотная область | во временной области | Шт. |
|---|---|---|---|
Плотность тока | \ (\ mathbf {J} \) | \ (\ mathbf {j} \) | А / м \ (\! ^ 2 \) |
Электродвигатель | \ (\ mathbf {D} \) | \ (\ mathbf {d} \) | С / м \ (\! ^ 2 \) |
Плотность магнитного потока | \ (\ mathbf {B} \) | \ (\ mathbf {b} \) | т |
Физические свойства
Недвижимость | Обозначение | Шт. |
|---|---|---|
Электропроводность | \ (\ sigma \) | См / м |
Удельное сопротивление | \ (\ rho \) | \ (\ Омега м \) |
Проницаемость | \ (\ му \) | H / м |
Разрешающая способность | \ (\ varepsilon \) | Ф / м |
Дифференциальная форма во временной области
Здесь мы представляем дифференциальные формы закона Гаусса для электрических полей, закона Гаусса для магнитных полей, закона Фарадея и уравнения Ампера-Максвелла во временной области.
\ [\ begin {split} \ begin {align} \ textbf {Гаусс для E-поля:} \; \; & \ набла \ cdot \ mathbf {d} = \ rho_f \\ \ textbf {Гаусс для B-поля:} \; \; & \ набла \ cdot \ mathbf {b} = 0 \\ \ textbf {Фарадей:} \; \; & \ nabla \ times \ mathbf {e} = — \ dfrac {\ partial \ mathbf {b}} {\ partial t} \\ \ textbf {Ампера-Максвелла:} \; \; & \ набла \ раз \ mathbf {h} = \ mathbf {j} + \ dfrac {\ partial \ mathbf {d}} {\ partial t} \ end {align} \ end {split} \]
где \ (\ rho_f \) — плотность свободного изменения, а \ (\ mathbf {j} \) — плотность свободного тока.Следующие определяющие отношения могут использоваться для замены полей и потоков:
\ [\ begin {split} \ begin {align} \ mathbf {j} & = \ sigma \ mathbf {e} \\ \ mathbf {b} & = \ mu \ mathbf {h} \\ \ mathbf {d} & = \ varepsilon \ mathbf {e} \ end {align} \ end {split} \]
Дифференциальная форма в частотной области
Здесь мы представляем дифференциальные формы закона Гаусса для электрических полей, закона Гаусса для магнитных полей,
.PPT — Уравнения Максвелла: дифференциальные и интегральные формы Презентация в PowerPoint
Уравнения Максвелла: дифференциальные и интегральные формы Название закона Дифференциальная форма Интегральная форма Закон Гаусса Закон Фарадея Закон Гаусса о магнетизме Закон Ампера Эта версия интегральных форм является наиболее полезен для реализации численных методов
Уравнения Максвелла: альтернативные интегральные формы • Закон Фарадея: • F = = магнитный поток • Закон Ампера: • Ic = ток проводимости; Id = ток смещения • Эта версия интегральных форм • имеет историческое и концептуальное значение • является основой для понимания двигателей и генераторов
Закон Фарадея • Электродвижущая сила: • Когда изменяющийся магнитный поток проходит через проволочную петлю, он индуцирует петлевое напряжение VEMF, которое называется электродвижущей силой.• Есть два возможных источника изменений: • Плотность магнитного потока изменяется во времени, что приводит к ЭДС трансформатора, • Площадь контура, перпендикулярная плотности потока, изменяется во времени, что приводит к двигательной ЭДС, • У нас есть Улаби Рисунок 6- 1
Закон Фарадея ds –dl dl q udt • Электродвижущая сила: • Когда контур имеет N витков, эффект наведенной ЭДС умножается в N раз, поэтому мы имеем: Ulaby 2001
Фарадея Закон • Закон Ленца: • Ток в контуре всегда имеет такое направление, что препятствует изменению магнитного потока F (t) • Этот закон позволяет нам быстро определять направление тока, индуцируемого ЭДС Улаби. 2001
Техническое описание 12: Датчики ЭМП Датчики ЭДС Генерируют индуцированное напряжение в ответ на внешний раздражитель Пьезоэлектрические преобразователи Некоторые кристаллы, такие как кварц, становятся электрически поляризованными при воздействии механического давления, тем самым проявляясь кусает разность напряжений.Без приложенного давления полярные домены ориентированы случайным образом, но при сжимающем или растягивающем напряжении домены выстраиваются вдоль главной оси кристалла. Сжатие и растяжение создают противоположные напряжения. Открыт в 1880 году братьями Кюри. В 1881 году Липпман предсказал обратное свойство (что электрический стимул изменит форму кристалла).
Техническая информация 12: Датчики ЭМП Пьезоэлектрические преобразователи Используются в микрофонах, громкоговорителях, позиционных датчиках для сканирующих туннельных микроскопов (могут измерять деформации величиной до нанометров), акселерометрах (может измерять от 10-4 г до 100 г), генераторах искр , часы и электронные схемы (прецизионные генераторы), медицинские ультразвуковые преобразователи и множество других приложений
Tech Brief 12: Датчики ЭДС Датчик магнитного потока Фарадея Согласно закону Фарадея, напряжение ЭДС, индуцируемое на выводах проводящей петли прямо пропорциональна скорости изменения магнитного потока, проходящего через контур.В приведенной ниже конфигурации Vemf и его производная напрямую указывают скорость и ускорение контура.
Техническое описание 12: Датчики ЭДС Термопара Зеебек обнаружил в 1821 году, что соединение двух проводящих материалов будет генерировать термически индуцированную ЭДС (называемую потенциалом Зеебека) при нагревании. Беккерель в 1826 году использовал эту концепцию для измерения неизвестной температуры относительно холодного эталонного спая. Традиционно холодным эталоном является ледяная ванна, но в современных термопарах электрическая цепь генерирует опорный потенциал.
Закон Фарадея • Трансформаторы: • Они используются для преобразования напряжений, токов и, следовательно, импедансов. • На практике они создаются путем наматывания токовых петель с разным числом витков вокруг общего магнитного сердечника, который фиксирует магнитный поток F. • ПРИМЕЧАНИЕ: направление обмотки определяет полярность выхода. Ulaby Рисунок 6-5
Закон Фарадея • Трансформаторы: • Преобразование напряжения: • В первичной обмотке: колеблющееся напряжение создает осциллирующий поток, обнаруживаемый путем интегрирования • Во вторичной обмотке: • Мы заключаем Ulaby Рисунок 6-5
Закон Фарадея • Двигатели и генераторы: • Преобразование тока: • В идеальном трансформаторе мощность сохраняется, поэтому P1 = P2.Поскольку P1 = I1V1 и P2 = I2V2, мы имеем • Преобразование импеданса: • Выходное сопротивление, RL = V2 / I2 • Эквивалентное входное сопротивление, Rin = V1 / I1 • Мы делаем вывод Ulaby Рис. 6-5
Магнитные силы • Двигатели и генераторы • Ранее мы обсуждали двигатели и генераторы как применение магнитостатики. Это возможно, потому что магнитное поле фиксировано, а токи движутся, так что VEMF является чисто двигательным. • Вместо этого мы можем напрямую использовать закон Фарадея! Ulaby Рисунок 6-11
Магнитные силы • Двигатели и генераторы • Вместо этого мы можем напрямую использовать закон Фарадея! • Сначала мы вычисляем магнитный поток. • Таким образом, мы находим • тот же результат, что и для ЭДС движения. Ulaby Рис. 6-12
Ток смещения •… или великое понимание Максвелла! • Исходная (статическая) версия закона Ампера: • Эта версия закона Ампера несовместима! Зачем? • Различные поверхности, прикрепленные к одной и той же замкнутой кривой C, дают разные результаты! — Сравните • Максвелл предположил, что добавление к закону Ампера исправит ситуацию •… и все экспериментальные данные показывают, что это так.C Изменено из Ulaby Рис. 6-12
Ток смещения Пример: Ток протекает через конденсатор с параллельными пластинами Вопрос: В течение интервала времени t постоянный ток Ic течет по конденсатору с параллельными пластинами площадью A, разделение d, и диэлектрическая постоянная e, показывают, что ток смещения Id равен току проводимости. Ответ: Заряд, который накапливается на верхней пластине конденсатора, определяется как где t0 — начальное время, в которое начинает течь ток.Пренебрегая краевыми полями, мы получаем Ic D Ic
Непрерывность заряда-тока • Сохранение заряда • Заряд не может быть создан или уничтожен!
Непрерывность заряда и тока время отношения материалов • Рассеяние тока в проводниках • В реальных проводниках с конечной проводимостью избыточный заряд рассеивается за конечное время. Использование соотношений • Хороший проводник — медь: • Хороший изолятор — слюда:
Электромагнитные потенциалы • Динамические потенциалы • Как и раньше: • Из закона Фарадея: • Следовательно, мы должны иметь
Электромагнитные потенциалы • Запаздывающие потенциалы • В статическом случае • В динамическом случае мы должны учитывать конечную временную задержку: • Для векторного потенциала мы имеем
Поля векторов • Потенциалы гармоники времени • Строительные блоки для понимание динамических систем — это синусоидально изменяющиеся сигналы (фазоры).• В линейной системе любое изменение во времени может быть найдено путем сложения векторов • Уравнения Максвелла линейны, предполагая линейные отношения материалов • Таким образом, мы пишем • Для плотности запаздывающего заряда у нас есть ПРИМЕЧАНИЕ: В этом разделе его книги Улаби использует k и обозначение волнового числа вместо диапазона обозначения фазовой постоянной.
Фазорные поля • Потенциалы временной гармоники • Для поля напряжения мы имеем • что подразумевает
фазорных полей • Временные гармонические потенциалы • Для полей векторного потенциала и плотности тока мы имеем аналогичный • который подразумевают
Фазорные поля • Электрические и магнитные поля — в непроводящей среде (J = 0) • Исходя из определения векторного потенциала, мы имеем • Из закона Ампера имеем • Из закона Фарадея мы имеют
Фазорные поля Амплитуды поля и отношения дисперсии: Пример Улаби 6-8 Вопрос: В непроводящей среде с e = 16e0 и m = m0 напряженность электрического поля задается следующим образом: Определить соответствующую напряженность магнитного поля H и значение k.Ответ: У нас есть так, что Из закона Фарадея: Из закона Ампера:
Фазорных полей Амплитуды поля и дисперсионные отношения: Улаби Пример 6-8 Ответ (продолжение): Приравнивая два выражения для, мы получаем дисперсионное соотношение. такое же дисперсионное соотношение, которое мы нашли с линиями передачи! Это не случайно !! В явном виде, мы теперь находим для магнитного поля
Назначение • Чтение: Ulaby, Глава 7 • Набор задач 6: Некоторые примечания.• Есть 6 проблем. Как всегда, ЧТОБЫ ПОЛУЧИТЬ ПОЛНЫЙ КРЕДИТ, ВЫ ДОЛЖНЫ ПОКАЗАТЬ СВОЮ РАБОТУ! • Все проблемы исходят от Улаби. • Обратите внимание на значащие цифры. • Начни рано!