Введение тока смещения позволило Максвеллу блестяще завершить единую теорию электромагнитного поля. Эта теория не только позволила объяснить все разрозненные явления электричества и магнетизма, но и предсказала ряд новых явлений, которые были подтверждены впоследствии.
Эта теория базируется на единой системе четырех уравнений Максвелла, которая может быть записана в интегральной и дифференциальной форме.
Уравнения Максвелла в интегральной форме:
1. 
;
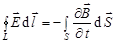2. 
;
3. 
;
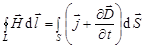4. 
.
Содержание этих уравнений заключается в следующем:
1. Циркуляция вектора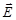 
по любому замкнутому контуру равна со знаком минус производной по времени от магнитного потока через любую поверхность, ограниченную данным контуром. При этом под 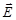понимается не только вихревое электрическое поле, но и электростатическое (циркуляция такого поля равна нулю).
2. Поток вектора 
сквозь любую замкнутую поверхность равен алгебраической сумме сторонних зарядов, охватываемых этой поверхностью. (Фактически это теорема Гаусса для поля заряда, распределенного внутри замкнутой поверхности с объемной плотностью 
3. Циркуляция вектора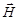 
по любому замкнутому контуру равна полному току (току проводимости и току смещения) через произвольную поверхность, ограниченную данным контуром.
4. Поток вектора 
сквозь произвольную замкнутую поверхность всегда равна нулю. Данное уравнение постулирует отсутствие в природе «магнитных» зарядов. (Это теорема Гаусса для магнитного поля)
Из уравнений Максвелла для циркуляции векторов 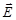и 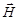следует, что электрическое и магнитное поле нельзя рассматривать как независимые: изменение во времени одного из них приводит к появлению другого. Таким образом, следует рассматривать единое электромагнитное поле.
В то же время в случае стационарных поле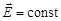й (
и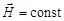 
; 
;
; .
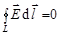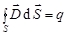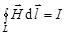В этом случае электрическое и магнитное поля независимы друг от друга, поэтому могут рассматриваться физически и математически раздельно.
Уравне́ния Ма́ксвелла — система уравнений в дифференциальной или интегральной форме, которые описывают электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах. Вместе с выражением для силы Лоренца образуют полную систему уравнений классической электродинамики, называемую иногда уравнениями Максвелла — Лоренца. Уравнения, сформулированные Джеймсом Клерком Максвеллом на основе накопленных к середине XIX века экспериментальных результатов, сыграли ключевую роль в развитии представлений теоретической физики и оказали сильное, зачастую решающее, влияние не только на все области физики, непосредственно связанные с электромагнетизмом, но и на многие возникшие впоследствии фундаментальные теории, предмет которых не сводился к электромагнетизму (одним из ярчайших примеров здесь может служить специальная теория относительности).
Дифференциальная формаУравнения Максвелла представляют собой в векторной записи систему из четырёх уравнений, сводящуюся в компонентном представлении к восьми (два векторных уравнения содержат по три компоненты каждое плюс два скалярных[28]) линейных дифференциальных уравнений в частных производных первого порядка для 12 компонент четырёх векторных функций ( ):
Жирным шрифтом в дальнейшем обозначаются векторные величины, курсивом — скалярные. Введённые обозначения:
означает ротор вектора,
означает дивергенцию вектора.
Приведённые выше уравнения Максвелла не составляют ещё полной системы уравнений электромагнитного поля, поскольку они не содержат свойств среды, в которой возбуждено электромагнитное поле. Соотношения, связывающие величины , , , и и учитывающие индивидуальные свойства среды, называются материальными уравнениями.
Интегральная форма
При помощи формул Остроградского — Гаусса и Стокса дифференциальным уравнениям Максвелла можно придать форму интегральных уравнений:
Поток электрического поля через замкнутую поверхность
Введённые обозначения:
При интегрировании по замкнутой поверхности вектор элемента площади направлен из объёма наружу. Ориентация при интегрировании по незамкнутой поверхности определяется направлением правого винта, «вкручивающегося» при повороте в направлении обхода контурного интеграла по .
Словесное описание законов Максвелла, например, закона Фарадея, несёт отпечаток традиции, поскольку вначале при контролируемом изменении магнитного потока регистрировалось возникновение электрического поля (точнее электродвижущей силы). В общем случае в уравнениях Максвелла (как в дифференциальной, так и в интегральной форме) векторные функции являются равноправными неизвестными величинами, определяемыми в результате решения уравнений.
Рассмотрим физический смысл этих 4 уравнений: силовые линии электрического поля электромагнитной волны замкнуты, как и силовые линии магнитного поля.
Одно из уравнений гласит, что электрическое поле образуется зарядами и его силовые линии начинаются и заканчиваются на зарядах.
Другое уравнение описывает магнитные силовые линии — это кольцеобразные замкнутые линии.
Третье уравнение представляет собой общий случай закона электромагнитной индукции Фарадей: любое изменение магнитного поля генерирует в соответствии с этим уравнением вихревое электрическое поле.
Четвертое уравнение. До Максвелла была известно часть этого уравнения, которая годилась для постоянных токов — это закон Ампера, утверждающий, что текущие по проводам электрические заряды (т.е. постоянный ток) создают определяемое уравнением Ампера магнитное поле.
Связав с помощью уравнений открытые до него законы, Максвелл увидел, что система несовершенна. Чтобы система имела решение, Максвелл добавил в четвертое уравнение одно слагаемое, а именно к току движущихся зарядов (ток проводимости) добавил воображаемый им ток смещения. Так он назвал изменяющееся во времени электрическое поле.
Ток смещения подобно электрическому току зарядов порождает магнитное поле. Т.об. Максвелл ввел в уравнение Ампера слагаемое, которое убывает. Это волновое слагаемое — часть поля, которое угасает гараздо медленнее обратного квадрата расстояния.
17. Свободные колебания в колебательном контуре. Дифференциальное уравнение затухающих электромагнитных колебаний и его решения.
Свободные колебания — колебания в системе под действием внутренних тел, после того как система выведена из положения равновесия.
Колебания груза, подвешенного на нити, или груза, прикрепленного к пружине, — это примеры свободных колебаний. После выведения этих систем из положения равновесия создаются условия, при которых тела колеблются без воздействия внешних сил.
Внутренние силы — силы, действующие между телами системы.
Внешние силы — силы, действующие на тела системы со стороны тел, не входящих в нее.
Условия возникновения свободных колебаний.
При выведении тела из положения равновесия в системе должна возникать сила, направленная к положению равновесия и, следовательно, стремящаяся возвратить тело в положение равновесия.
Пример: при перемещении шарика, прикрепленного к пружине, влево и при его перемещении вправо сила упругости направлена к положению равновесия.
Трение в системе должно быть достаточно мало. Иначе колебания быстро затухнут или вовсе не возникнут. Незатухающие колебания возможны лишь при отсутствии трения.
Если рассматривать колебательный контур, то для получения вынужденных колебаний (рис. 8.4), нужно включить последовательно с элементами контура переменную эдс или, разорвав контур, подать напряжение:
Рис. 8.4. Вынужденные колебания в колебательном контуре
U = Umcosw, тогда уравнение будет иметь вид:
<!—[if !supportEmptyParas]—> <!—[endif]—> <!—[if !vml]—> <!—[endif]—>, (8.15)
<!—[if !supportEmptyParas]—> <!—[endif]—>
после замены получим
<!—[if !supportEmptyParas]—> <!—[endif]—> <!—[if !vml]—> <!—[endif]—>. (8.16)
Решение полученного неоднородного дифференциального уравнения находим прибавлением к его частному решению общего решения соответствующего однородного уравнения. Частное решение имеет вид
<!—[if !vml]—> <!—[endif]—>,
где <!—[if !vml]—> <!—[endif]—>.
Подставив в эти выражения значения <!—[if !vml]—> <!—[endif]—>, получим:
<!—[if !supportEmptyParas]—> <!—[endif]—> <!—[if !vml]—> <!—[endif]—>. (8.17)
<!—[if !supportEmptyParas]—> <!—[endif]—>Разделив заряд на емкость, получим напряжение на конденсаторе:
<!—[if !vml]—> <!—[endif]—>,
где <!—[if !vml]—> <!—[endif]—>. Установившийся ток в контуре <!—[if !vml]—> <!—[endif]—>. Амплитуда тока имеет вид
<!—[if !supportEmptyParas]—> <!—[endif]—> <!—[if !vml]—> <!—[endif]—>. (8.18)
<!—[if !supportEmptyParas]—> <!—[endif]—>
Резонансная частота для контура
<!—[if !supportEmptyParas]—> <!—[endif]—> <!—[if !vml]—> <!—[endif]—> <!—[if !vml]—> <!—[endif]—>. (8.19)
Резонансные кривые для UC и тока I имеют такой вид, как показано на рис. 8.5.
Рис. 8.5. Явление резонанса напряжений и токов в колебательном контуре: кривые 1, 2, 3 соответствуют всё бóльшему активному сопротивлению контура
<!—[if !supportEmptyParas]—> <!—[endif]—>
При <!—[if !vml]—> <!—[endif]—> резонансные кривые стремятся к Um – напряжению, возникающему на конденсаторе при подключению его к источнику постоянного напряжения. Максимум при резонансе получается тем выше и острее, чем меньше <!—[if !vml]—> <!—[endif]—>, т. е. чем меньше активное сопротивление и больше индуктивность контура. Тогда амплитуда силы тока имеет максимальное значение при <!—[if !vml]—> <!—[endif]—>. Следовательно, резонансная частота для силы тока совпадает с собственной частотой контура <!—[if !vml]—> <!—[endif]—>.
В статье мы, используя теорему Гаусса-Остроградского и теорему Стокса приведем четыре уравнения Максвелла к дифференциальной форме. В конце статьи вы сможете посмотреть видео-лекцию для закрепления информации.
Четыре фундаментальных уравнения электромагнетизма сформулированы Джеймсом Клерком Максвеллом. Они описывают свойства электрического и магнитного полей и отношения между этими полями. Из уравнений Максвелла можно вывести уравнение электромагнитной волны, распространяющейся в вакууме со скоростью света
Первое уравнение Максвелла, дифференциальной формы Фарадея
Закон Фарадея — интегральная форма:
На основании теоремы Стокса мы меняем линейный интеграл (циркуляцию) в левой части уравнения на поверхностный интеграл:
Мы можем оставить правую сторону в законе Фарадея в виде:
Теперь мы можем сравнить оба поверхностных интеграла:
Итак, мы получаем закон Фарадея — дифференциальную форму:
Второе уравнение Максвелла, дифференциальной формы обобщенного закона Ампера
Обобщенный закон Ампера — интегральная форма:
На основании теоремы Стокса мы меняем линейный интеграл (циркуляцию) с левой части уравнения на поверхностный интеграл:
Мы можем представить правую часть в обобщенном законе Ампера как поверхностный интеграл:
С учетом того, что прямой ток I можно выразить плотностью тока j :
записываем правую сторону как один поверхностный интеграл:
Теперь мы сравним оба поверхностных интеграла друг с другом:
Чтобы это уравнение было истинным для каждой поверхности A, независимо от ее размера и формы, подфункции с обеих сторон уравнения должны быть равны.
Таким образом, мы получаем обобщенный закон Ампера — дифференциальную форму :
Третье уравнение Максвелла, дифференциальной формы закона Гаусса для электрического поля
Закон Гаусса для электрического поля — интегральная форма:
Основываясь на теореме Гаусса — Остроградского, мы меняем поверхностный интеграл в левой части уравнения на интеграл объема:
Нагрузка Q также представлена как интеграл объема от плотности заряда ρ :
Из равенства обоих интегралов объема:
получаем закон Гаусса для электрического поля — дифференциальную форму:
Четвертое уравнение Максвелла,
дифференциальная форма закона Гаусса для магнитного поля
Закон Гаусса для магнитного поля — интегральная форма:
Основываясь на теореме Гаусса — Остроградского, мы меняем поверхностный интеграл в левой части уравнения на интеграл объема:
Поскольку на основе закона Гаусса для магнитного поля оба этих интеграла равны нулю, то подфункции также равны нулю, поэтому мы сразу получаем закон Гаусса для магнитного поля — дифференциальную форму:
Финальный вывод уравнений Максвелла
Видео-лекция
В данном видео подробно разберем уравнения Максвелла.
Используя Гаусса — Остроградского формулу и С такса формулу, ур-ниям (1) — (4) можно придать форму интегральных:
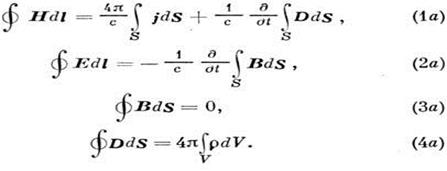
Криволинейные интегралы в (1a), (2a) берутся по произвольному замкнутому контуру (их наз. циркуляция-ми векторных полей), а стоящие в правых частях поверхностные интегралы — по поверхностям, ограниченным этими контурами (опирающимся на них), причём направление циркуляции (направление элемента контура 
) связано с направлением нормали к S (вектор 
) правовинтовым соотношением (если в качестве исходного выбрано пространство с правыми системами координат). В интегралах по замкнутым поверхностям (S) в (3а), (4а) направление вектора элемента площади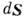 
совпадает с наружной нормалью к поверхности; V — объём, ограниченный замкнутой поверхностью S.
M. у. в форме (1a) — (4a) предназначаются не только для изучения топологич. свойств эл—магн. полей, но и являются удобным аппаратом решения конкретных задач электродинамики в системах с достаточно высокой симметрией или с априорно известными распределениями полей. Кроме того, в матем. отношении эта система ур-ний содержательнее системы (1) — (4), поскольку пригодна для описания разрывных, нодиффе-ренцируемых распределений полей. Но в отношении физ. пределов применимости обе системы ур-ний равнозначны, т. к. любые скачки полей в макроэлектродинамике должны рассматриваться как пределы микромасштабно плавных переходов, с тем чтобы внутри них сохранялась возможность усреднения ур-ний Лоренца — Максвелла. С этими оговорками резкие скачки можно описывать и в рамках M. у. (1) — (4), прибегая к аппарату обобщённых функций.
Наконец, M. у. в интегральной форме облегчают физ. интерпретацию MH. эл—магн. явлений и поэтому нагляднее сопоставляются с теми экспериментально установленными законами, к-рым они обязаны своим происхождением. Так, ур-ние (1a) есть обобщение Био — Савара закона (с добавлением к току 
максвелловского смещения тока).
Ур-ние (2a) выражает закон индукции Фарадея; иногда его правую часть переобозначают через «магн. ток смещения»
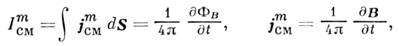
где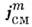 
— плотность «магн. тока смещения», ФВ — магн. поток. Ур-ние (За) связывают с именем Гаусса 
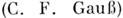, установившим соленоидальность поля В, обусловленную отсутствием истинных магн. зарядов. Впрочем вопрос о существовании магнитных монополей пока остаётся открытым. Но соответствующее обобщение M. у. произведено (Хевисайд, 1885) на основе принципа двойственной симметрии M. у. (см. в разделе 9), для чего в (2) и (2a) наряду с магн. током смещения вводится ещё и «истинный» магн. ток (процедура, обратная проделанной когда-то Максвеллом с электрич. током в первом ур-нии), а в ур-ние Гаусса (3), (За) — магн. заряд
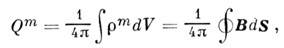
где 
— плотность магн. заряда. Фактически все экспериментальные установки для регистрации ожидаемых магнитных монополей основаны на этом предположении. Наконец, ур-ние (4a) определяет поле свободного электрич. заряда; его иногда называют законом Кулона (Ch. A. Coulomb), хотя, строго говоря, оно не содержит утверждения о силе взаимодействия между зарядами, да и к тому же справедливо не только в электростатике, но и для систем с произвольным изменением поля во времени. На тех же основаниях иногда и ур-нпе (Ia) связывают с именем Ампера (A. Ampere).
Введение тока смещения позволило Дж. Максвеллу создать теорию, которая объяснила все известные на тот момент явления из области электромагнетизма и позволила выдвинуть ряд новых гипотез, которые позднее были подтверждены.
В основу данной теории легли уравнения Максвелла, которые в электромагнетизме играют такую же роль, как начала в термодинамике или законы Ньютона в классической механике.
Уравнения Максвелла в дифференциальной форме.
В настоящей интерпретации система уравнений Максвелла имеет четыре структурных векторных уравнения:
Первое уравнение устанавливает связь между полным током (суммой тока проводимости и током смещения) и магнитным полем, которое они вызывают.
Второе уравнение является выражением закона электромагнитной индукции в интерпретации Максвелла (переменное магнитное поле — один из источников возникновения электрического поля).
Третье уравнение — указывает на факт отсутствия магнитных зарядов.
Четвертое уравнение говорит о том, что источниками электрического поля являются электрические заряды.
Готовые работы на аналогичную тему
Уравнения (1) — (4) являются уравнениями Максвелла в дифференциальной форме. Каждое из векторных уравнений эквивалентно трем скалярным уравнениям, которые связывают компоненты векторов в правых и левых частях выражений.
Для того, чтобы применять систему уравнений Максвелла для расчета конкретных полей, уравнения данной системы дополняются материальными уравнениями, которые связывают векторы $\overrightarrow{D}\ и\ \overrightarrow{j}$ c вектором $\overrightarrow{E}$, а вектор $\overrightarrow{H}$ c вектором $\overrightarrow{B}$. Эти равнения имеют вид:
где величины $\varepsilon $,$\ \mu $, $\sigma $ — материальные постоянные, характеризующие свойства среды.
Если уравнения (1) — (4) являются фундаментальными, то относительно уравнений (5) надо отметить, что они выполняются совсем не всегда. Так, если речь идет о нелинейных явлениях, получение материальных уравнений составляет отдельную научную задачу.
Уравнения Максвелла в интегральной форме
Систему структурных уравнений Максвелла можно представить в интегральной форме. Так, если проинтегрировать уравнение (1) по произвольной поверхности $S$:
По теореме Стокса левая часть выражения (6) преобразуется к виду:
где интеграл в правой части берется по контуру $L$, который ограничивает поверхность $S$. Если считать, что контур и поверхность неподвижны, то операции дифференцирования по времени и интегрирования по поверхности можно поменять местами в выражении (6) левой части, получим:
здесь интеграл $\int\limits_S{\overrightarrow{D}d\overrightarrow{S}}$ является функцией только от времени, поэтому можно заменить частную производную обычной. Интегрируя уравнение (2) подобным образом, получим второе уравнение системы Максвелла:
Если проинтегрировать уравнение (3) по объему $V$, и использовать для преобразования левой части теорему Остроградского — Гаусса в интеграл по замкнутой поверхности $S$, которая ограничивает объем $V$, то получим:
Аналогичную процедуру проводят с уравнением (4). Получается:
Так получают систему уравнений Максвелла в интегральной форме:
Замечание
Уравнения Максвелла применимы к поверхностям любого размера. Эти уравнения описывают электрические и магнитные поля в покоящихся средах.
Пример 1
Задание: Ток, текущий по обмотке прямого соленоида, который имеет радиус $R$, изменяется так, что модуль индуктивности магнитного поля внутри соленоида растет в соответствии с законом: $B=Ct^2,\ $где $C=const.$ Запишите функцию тока смещения $j_{sm}\left(r\right),$ где $r$ — расстояние от оси соленоида.
Решение:
По определению, плотность тока смещения можно записать как:
\[j_{sm}=\frac{\partial D}{\partial t}\left(1.1\right).\]Используя одно из уравнений системы Максвелла:
\[\int\limits_S{\overrightarrow{E}d\overrightarrow{l}}=-\int\limits_S{\frac{\partial \overrightarrow{B}}{\partial t}d\overrightarrow{S}}\ (1.2),\]найдем напряженность электрического поля, которое порождается переменным магнитным полем, а зная связь напряжённости электрического поля и электрического смещения:
\[\overrightarrow{D}=\varepsilon {\varepsilon }_0\overrightarrow{E}(1.3)\]получим функцию $D(r)$.
Итак, используя уравнение изменения индукции магнитного поля из условий задачи, найдем частную производную $\frac{\partial \overrightarrow{B}}{\partial t}:$
\[\frac{\partial \overrightarrow{B}}{\partial t}=2Ct\left(1.4\right).\]Для $r \[2\pi rE=-\pi r^22Ct\to E=-rCt\to D=-C\varepsilon {\varepsilon }_0rt\to j_{sm}=-C\varepsilon {\varepsilon }_0r.\]
Для $r>R$, из (1.2) — (1.4) получим:
\[2\pi rE=-\pi R^22Ct,\ E=-C\frac{R^2t}{r}\to j_{sm}=-C\varepsilon {\varepsilon }_0\frac{R^2}{r}.\]Для $r=R$, из (1.2) — (1.4) найдем ток смещения:
\[E=-RCt\to D=-C\varepsilon {\varepsilon }_0Rt\to j_{sm}=-C\varepsilon {\varepsilon }_0R.\]Ответ: $j_{sm}=-C\varepsilon {\varepsilon }_0r\ \left(rR\right),\ j_{sm}=-C\varepsilon {\varepsilon }_0R\ \left(r=R\right).$
Пример 2
Задание: Запишите систему уравнений Максвелла для стационарных полей ($\overrightarrow{E}=const,\overrightarrow{H}=const\ $) в интегральной форме.
Решение:
В том случае, если поля стационарны, система уравнений максвелла распадается на две группы независимых уравнений. Первую группу составляют уравнения электростатики:
\[\int\limits_S{\overrightarrow{E}d\overrightarrow{l}}=0\ \ и\] \[\oint\limits_S{\overrightarrow{D}d\overrightarrow{S}=\int\limits_V{\rho }dV.}\]Вторая группа — уравнения магнитостатики:
\[\int\limits_L{\overrightarrow{H}d\overrightarrow{l}}=\int\limits_S{\overrightarrow{j}d\overrightarrow{S}}\ и\] \[\oint\limits_S{\overrightarrow{B}d\overrightarrow{S}=0}.\]Итак, переменное магнитное поле вызывает появление вихревого электрического поля. Переменное электрическое поле вызывает появление магнитного поля. Взаимно порождаясь, они могут существовать независимо от источников заряда или токов, которые первоначально создали одно из них. В сумме это есть электромагнитное поле (ЭМП). Превращение одного поля в другое и распространение в пространстве есть способ существования ЭМП. Конкретные проявления ЭМП – радиоволны, свет, гамма-лучи и т.д.
В 1860 г. знаменитый английский физик Джеймс Клерк Максвелл создал единую теорию электрических и магнитных явлений, в которой он использовал понятие ток смещения, дал определение ЭМП и предсказал существование в свободном пространстве электромагнитного излучения, которое распространяется со скоростью света.
Теорию ЭМП Максвелл сформулировал в виде системы нескольких уравнений. В учении об электромагнетизме эти уравнения Максвелла играют такую же роль, как уравнения (или законы) Ньютона в механике.
1) Мы знаем теорему о циркуляции вектора напряжённости магнитного поля:
,
но: ; т.е. , тогда
| , | (7.3.1) |
Это уравнение является обобщением закона Био–Савара–Лапласа и показывает, что циркуляция вектора по произвольному замкнутому контуру L равна сумме токов проводимости и токов смещения сквозь поверхность, натянутую на этот контур. Или другими словами, показывает связь между полным током и порождаемым им магнитным полем.
В дифференциальной форме это уравнение Максвелла выглядит так:
где2) Рассматривая явление электромагнитной индукции, мы сделали вывод, что ЭДС индукции . Перейдем от вихревого электрического поля к магнитному:
| , | (7.3.2) |
Это уравнение описывает явление электромагнитной индукции (закон Фарадея) и устанавливает количественную связь между электрическими и магнитными полями: переменное электрическое поле порождает переменное магнитное поле. В этом физический смысл уравнения.
В дифференциальной форме это уравнение выглядит так:
Различие в знаках этого уравнения Максвелла соответствует закону сохранения энергии и правилу Ленца. Если бы знаки при и были одинаковы, то бесконечно малое увеличение одного из полей вызвало бы неограниченное увеличение обоих полей, а бесконечно малое уменьшение одного из полей, приводило бы к полному исчезновению обоих полей. То есть различие в знаках является необходимым условием существования устойчивого ЭМП.3) Ещё два уравнения выражают теорему Остроградского–Гаусса для электрического и магнитного полей (статических полей)
| , | (7.3.3) |
Поток вектора электрического смещения через замкнутую поверхность S равен сумме зарядов внутри этой поверхности. Это уравнение показывает также, что силовые линии вектора и начинаются и заканчиваются на зарядах.
В дифференциальной форме
где
4) И для магнитного поля
| , | (7.3.4) |
Это уравнение выражает то свойство магнитного поля, что линии вектора магнитной индукции всегда замкнуты и что магнитных зарядов нет.
В дифференциальной форме
| , | (7.3.5) |
5, 6, 7) Наконец надо помнить, что величины, входящие в эти четыре уравнения не независимы, и между ними существует связь:
| , | (7.3.6) |
| , | (7.3.7) |
| , | (7.3.8) |
здесь σ – удельная проводимость, – плотность сторонних токов.
Эти уравнения называются уравнениями состояния или материальными уравнениями. Вид этих уравнений определяется электрическими и магнитными свойствами среды. В общем случае уравнения состояния очень сложны и нелинейны.
Уравнения (7.3.1 – 7.3.8) составляют полную систему уравнений Максвелла. Они являются наиболее общими для электрических и магнитных полей в покоящихся средах. Уравнения Максвелла – инвариантны относительно преобразований Лоренца. Физический смысл уравнений Максвелла в дифференциальной и интегральной формах полностью эквивалентен.
Таким образом, полная система уравнений Максвелла в дифференциальной и интегральной формах имеет вид:
;
– обобщенный закон Био–Савара–Лапласа;
; – закон Фарадея;
; – теорема Гаусса; – отсутствие магнитных зарядов;
, ,
Аудио-видео демонстрации по теме или смежным темам: 1. Солнечная корона. 2. Солнечная плазма.с которой электромагнитное поле действует на точечный электрический заряд q, движущийся со скоростью v.
Исходя из симметрии физических процессов в природе, можно предположить, что переменное во времени электрическое поле порождает магнитное поле. К этому же выводу пришел Дж. К. Максвелл, применяя теорему о циркуляции вектора напряженности магнитного поля для анализа протекания квазистационарного тока через конденсатор. Пусть квазистационарный ток I(t) протекает через конденсатор ёмкостью C (рис.). Запишем теорему о циркуляции вектора , используя контур L, который охватывает проводник с током I(t), и две поверхности S1 и S2, опирающиеся на контур, как показано на рисунке,Ток проводимости не пересекает поверхность S2 (между обкладками конденсатора нет тока проводимости), поэтому при выборе поверхности S2 циркуляция вектора должна равняться нулю. Поскольку циркуляция вектора по контуру L не должна зависеть от выбора поверхности, опирающейся на этот контур, то для устранения возникающего противоречия необходимо каким-то образом изменить выражение в правой части теоремы о циркуляции вектора . Выход был найден Максвеллом, который ввел понятие тока смещения с вектором плотности . Согласно Максвеллу ток смещения необходимо учитывать в теореме о циркуляции вектора наряду с обычным током проводимости, создаваемым движущимися электрическими зарядами. Обобщенная с учетом тока смещения теорема о циркуляции вектора записывается следующим образом Здесь при наблюдении с конца единичного вектора нормали n к поверхности S, опирающейся на контур L, обход контура должен совершаться против хода часовой стрелки. Согласно последней формуле переменное во времени электрическое смещение является таким же источником магнитного поля, что и ток проводимости.
Дополнив основные факты из области электромагнетизма установлением магнитных действий токов смещения, Максвелл написал систему фундаментальных уравнений электродинамики в интегральной форме:
и дифференциальной форме:
Закон сохранения заряда не вошел в число фундаментальных, т.к. является следствием уравнений 2 и 3.
Для описания электромагнитных явлений в среде к четырем уравнениям необходимо добавить материальные уравнения, определяющие отклик среды на действие электромагнитного поля. В области относительно слабых полей для большинства изотропных сред справедливы следующие материальные уравненияЗдесь и — относительная диэлектрическая проницаемость и относительная магнитная проницаемость среды соответственно, — электропроводность среды и — сторонняя сила, действующая на свободные заряды среды, q – величина свободного заряда. Если имеется поверхность раздела двух сред, на которой скачком меняются электрические и магнитные характеристики этих сред, то из системы уравнений Максвелла следуют граничные условия, которые выражают непрерывность тангенциальных компонент векторов и , а также нормальных компонент векторов и , при переходе через границу раздела двух сред. Граничные условия получаются в отсутствие на поверхности раздела двух сред поверхностных зарядов и токов проводимости. Уравнения Максвелла показывают, что источниками электрического поля могут быть либо электрические заряды, либо магнитные поля, меняющиеся во времени. Магнитные же поля могут возбуждаться либо движущимися электрическими зарядами (токами), либо переменными электрическими полями. Уравнения не симметричны относительно электрического и магнитного полей, т.к. в отличие от электрических зарядов пока не обнаружено магнитных зарядов — магнитных монополей, хотя такие теории есть.
физический смысл уравнений Максвелла:
В первом уравнении (.1) утверждается, что электростатическое поле может быть создано только электрическими зарядами. В этом уравнении — вектор электрического смещения, ρ — объемная плотность электрического заряда.Поток вектора электрического смещения через любую замкнутую поверхность равен заряду, заключенному внутри этой поверхности.
Как свидетельствует эксперимент, поток вектора магнитной индукции через замкнутую поверхность всегда равен нулю (.2)
Сопоставление уравнений (.2) и (.1) позволяет сделать вывод о том, что магнитные заряды в природе отсутствуют.
Огромный интерес и важность представляют уравнения (.3) и (.4). Здесь рассматриваются циркуляции векторов напряженности электрического () и магнитного () полей по замкнутому контуру. В уравнении (.3) утверждается, что переменное магнитное поле () является источником вихревого электрического поля (). Это не что иное, как математическая запись явления электромагнитной индукции Фарадея.В уравнении (.4) устанавливается связь магнитного поля и переменного электрического. Согласно этому уравнению магнитное поле может быть создано не только током проводимости (), но и переменным электрическим полем .
Справочно:
Уравнения Максвелла
Уравнения Максвелла представляют собой основные уравнения электромагнетизма, которые представляют собой совокупность закона Гаусса для электричества, закона Гаусса для магнетизма, закона электромагнитной индукции Фарадея и закона Ампера для токов в проводниках. Уравнения Максвелла дают математическую модель для электрических, оптических и радиотехнологий, таких как производство электроэнергии, электродвигатели, беспроводная связь, радар, линзы и т. Д.Эти уравнения объясняют, как магнитные и электрические поля создаются из зарядов.
Эти уравнения являются частью всеобъемлющей и симметричной теории электромагнетизма, которая необходима для понимания электромагнитных волн, оптики, радио- и телевизионной передачи, микроволновых печей и поездов с магнитной подвеской.
Каковы четыре уравнения Максвелла?
Четыре уравнения Максвелла для свободного пространства:
Первое уравнение Максвелла (закон Гаусса для электричества)
Закон Гаусса гласит, что поток, проходящий через любую замкнутую поверхность, равен 1 / ε0 от общего заряда, приложенного этим поверхность.
Интегральная форма 1-го уравнения Максвелла
Это интегральная форма 1-го уравнения Максвелла.
Первое уравнение Максвелла в дифференциальной форме
Это называется дифференциальной формой первого уравнения Максвелла.
Второе уравнение Максвелла (закон Гаусса для магнетизма)
Закон Гаусса для магнетизма гласит, что суммарный поток магнитного поля через замкнутую поверхность равен нулю, поскольку монополи магнита не существуют.
Третье уравнение Максвелла (закон электромагнитной индукции Фарадея)
Согласно закону электромагнитной индукции Фарадея
Это дифференциальная форма третьего уравнения Максвелла.
Посетите нашу страницу для связанных тем: Электромагнетизм
Рекомендуемое видео:
Четвертое уравнение Максвелла (закон Ампера)
Величина магнитного поля в любой точке прямо пропорциональна силе тока и обратно пропорциональна пропорционально расстоянию точки от прямых проводников называется законом Ампера.
Третье уравнение Максвелла говорит, что изменяющееся магнитное поле создает электрическое поле. Но в четвертом уравнении Максвелла нет никакой подсказки, создает ли изменяющееся электрическое поле магнитное поле? Чтобы преодолеть этот недостаток, Максвелл утверждал, что если изменяющийся магнитный поток может создавать электрическое поле, то при симметрии должно существовать соотношение, при котором изменяющееся электрическое поле должно создавать изменяющийся магнитный поток.
Для получения дополнительной информации по темам посетите нашу страницу: Электричество и магнетизм
Похожие темы:
Физика Ссылки по теме:
.Уравнения Максвелла (интегральная форма)
Иногда легче понять уравнения Максвелла в их интегральной форме; версия, которую мы обрисовали в прошлый раз, является дифференциальной формой.
Для закона Гаусса и закона Гаусса для магнетизма, мы фактически уже сделали это. Сначала запишем их в дифференциальной форме:
Мы выбираем любой регион, который мы хотим, и интегрируем обе части каждого уравнения по этому региону:
В левой части мы можем использовать теорему расхождения, в то время как правые части можно просто оценить:
где общий заряд, содержащийся в регионе.Закон Гаусса говорит нам, что поток электрического поля, проходящего через замкнутую поверхность, (в основном) равен заряду, содержащемуся внутри поверхности, в то время как закон Гаусса для магнетизма говорит нам, что не существует такого понятия, как магнитный заряд.
Закон Фарадея был в основном дан нам в интегральной форме, но мы можем получить его из дифференциальной формы:
Мы выбираем любую поверхность и объединяем через нее поток обеих сторон:
Слева мы можем использовать теорему Стокса, а справа мы можем вывести производную за пределы интеграла:
где — поток магнитного поля через поверхность.Закон Фарадея говорит нам, что изменяющееся магнитное поле индуцирует ток вокруг цепи.
Аналогичный анализ помогает с законом Ампера:
Подбираем поверхность и интегрируем:
Тогда мы упростим каждую сторону.
где — поток электрического поля через поверхность и общий ток, протекающий через поверхность. Закон Ампера говорит нам, что текущий ток вызывает магнитное поле вокруг тока, а поправка Максвелла говорит нам, что изменяющееся электрическое поле ведет себя так же, как ток, состоящий из движущихся зарядов.
Мы собираем их вместе в интегральную форму уравнений Максвелла:
Нравится:
Нравится Загрузка …
Связанные
2 февраля 2012 г. — Отправленный Джоном Армстронгом | Электромагнетизм, Математическая физика
,альтернативных формул уравнений Максвелла
Уравнения Максвелла обычно пишутся несколькими разными способами. Форма у нас на фронте этого сайта известна в виде точки:
Приведенные выше уравнения известны как «точечная форма», потому что каждое равенство истинно в каждой точке пространства. Тем не менее, если мы интегрируем Форма точки над объемом, мы получаем интегральную форму. Существует также Форма Гармонии Времени, и Уравнения Максвелла записаны только с E и H .И одна форма использует воображаемый магнитный заряд, который может быть полезен для решения некоторых задач. Мы обсудим это ниже.
Интегральная форма уравнений Максвелла
Если точечная форма уравнений Максвелла верна в каждой точке, то мы можем интегрировать их по любому объему ( В, ) или через любая поверхность и они все равно будут правдой. Есть несколько трюков векторного исчисления, перечисленных в уравнении [1].
| [Уравнение 1] |
|---|
Я не буду проходить вывод, но вы используете теорему дивергенции для первых двух уравнений Максвелла (законы Гаусса) и интегрируете через объем V с граничной поверхностью ( S ).Ты используешь Теорема Стокса о законе Фарадея и Ампера на открытой поверхности ( S ) с границей ( L ). Результат ниже:
Уравнения Максвелла в интегральной форме.
Обратите внимание, что в первых двух уравнениях поверхность S является замкнутой поверхностью (как поверхность сферы), что означает, что она включает в себя объем 3D. В последних двух уравнениях поверхность S представляет собой открытую поверхность (как круг), которая имеет граничную линию L (периметр открытой или незамкнутой поверхности).
Гармонически-временная форма уравнений Максвелла
Мы знаем из теории преобразований Фурье что каждый сигнал во времени может быть переписан как сумма синусоид (знак или косинус). Используя немного более сложная математика, и мы можем указать изменение во времени в терминах суммы синусоид написано в сложной форме:
| [Уравнение 2] |
|---|
В уравнении [2] f — это интересующая нас частота, которая равно .Следовательно, производная по времени функции в Уравнение [2] совпадает с исходной функцией, умноженной на. Это означает, что мы можем заменить производные по времени в точечной форме уравнений Максвелла [1] как в следующем:
Уравнения Максвелла в гармонической форме времени.
Это известно как вектор-форма или гармоническая форма уравнений Максвелла. Это совершенно законно, потому что эта форма говорит нам, как ведут себя волны если они колеблются с частотой f , и все волны могут быть разложены в сумму простые колебательные волны.
Уравнения Максвелла, записанные только с E и H
Мы также можем переписать уравнения Максвелла, используя только E и H . Это означает, что мы собираемся избавиться от D , B и Плотность электрического тока Дж . Мы можем сделать это с помощью уравнений:
| [Уравнение 3] |
|---|
Если мы подставим их в уравнение [1], мы сможем получить уравнения Максвелла только с электрическим и Магнитные поля:
Уравнения Максвелла, написанные только для E и H .
Симметричная форма уравнений Максвелла — с магнитным зарядом
Что если кто-то найдет магнитные монополи? Тогда нам придется изменить уравнения Максвелла. И тогда мы также должны были бы изменить уравнения, чтобы учесть Магнитный ток (то есть поток магнитного заряда).
Это не чисто абстрактное упражнение — некоторые проблемы в инженерии могут быть решены проще, предполагая, что данное распределение поля на самом деле является фиктивным магнитным заряд или магнитный ток — это облегчает решение.Так что вы также можете прийти через следующую форму уравнений Максвелла, но вы должны знать, что некоторые термины не существуют в реальности:
Уравнения Максвелла, записанные с магнитным зарядом и магнитным током.
Как видите, мы ввели объемную плотность магнитного заряда во второе уравнение, и плотность магнитного тока в третьем уравнении.
Уравнения Максвелла
Эта страница, посвященная формам уравнений Максвелла, защищена авторским правом.Никакая часть не может быть воспроизведена кроме как с разрешения. Авторское право принадлежит Maxwells-Equations.com, 2012.
.уравнений Максвелла — Викиверситет
уравнения Максвелла [править]
Уравнения Максвелла , сформулированные примерно в 1861 году Джеймсом Клерком Максвеллом, описывают взаимосвязь между электрическим и магнитным полями. Они представляли собой синтез того, что было известно в то время об электричестве и магнетизме, особенно опираясь на работы Майкла Фарадея, Чарльза-Августина Кулона, Андре-Мари Ампера и других. Эти уравнения предсказывали существование электромагнитных волн, придавая им свойства, которые были признаны свойствами света, что привело к (правильному) пониманию того, что свет является электромагнитной волной.Другие формы электромагнитных волн, такие как радиоволны, не были известны в то время, но впоследствии они были продемонстрированы Генрихом Герцем в 1888 году. Эти уравнения считаются одними из самых элегантных сооружений математической физики.
Уравнения Максвелла служат многим целям и принимают различные формы. С одной стороны, они используются при решении реальных реальных проблем электромагнитных полей и излучения. С другой стороны, они вызывают восхищение своей элегантностью.Есть много футболок, которые обычно можно приобрести в студенческих городках, с различными формами этих уравнений.
Ниже приводится обзор различных форм, которые принимают эти уравнения, начиная с самых утилитарных и заканчивая самыми элегантными. Какую форму вы предпочитаете, зависит от вашего научного мировоззрения и, возможно, от вашего вкуса в футболках. Различные ∇ ⋅ Е {\ displaystyle \ nabla \ cdot \ mathbf {E}} и ∇ × Е {\ displaystyle \ nabla \ times \ mathbf {E}} Символы, фигурирующие в некоторых уравнениях, являются операторами дивергенции и скручивания соответственно.
Они обычно формулируются как четыре уравнения (но позже мы увидим некоторые особенно элегантные версии только с двумя), а уравнения обычно выражаются в дифференциальной форме , то есть в виде дифференциальных уравнений в частных производных, включающих операторы дивергенции и скручивания. Они также могут быть выражены с помощью интегралов.
Они часто выражаются через четыре векторных поля: E, B, D и H, хотя в более простых формах используются только E и B.
Уравнения Максвелла, выраженные в дифференциальной форме [править]
В этих
- E обозначает электрическое поле,
- B обозначает магнитное поле,
- D обозначает поле электрического смещения и
- H обозначает напряженность магнитного поля или вспомогательное поле .
- J обозначает свободную плотность тока, а
- ρ {\ displaystyle \ rho} обозначает плотность свободного электрического заряда.
Диэлектрическая поляризуемость, магнитная проницаемость и скорость света [править]
Использование отдельных полей D и H иногда полезно в инженерных задачах, связанных с диэлектрической поляризуемостью и магнитной проницаемостью используемых материалов. Но более элегантная «чистая» форма удаляет D и H через уравнения:
- D знак равно ε Е {\ displaystyle \ mathbf {D} = \ varepsilon \ mathbf {E}}
- ЧАС знак равно В / μ {\ displaystyle \ mathbf {H} = \ mathbf {B} / \ mu}
где ε знак равно ε р ε 0 {\ displaystyle \ varepsilon = \ varepsilon _ {r} \ varepsilon _ {0} \,} диэлектрическая проницаемость и μ знак равно μ р μ 0 {\ displaystyle \ mu = \ mu _ {r} \ mu _ {0} \,} это проницаемость, ε р {\ displaystyle \ varepsilon _ {r} \,} относительная диэлектрическая проницаемость, μ р {\ displaystyle \ mu _ {r} \,} относительная проницаемость, ε 0 {\ displaystyle \ varepsilon _ {0} \,} электрическая постоянная или диэлектрическая проницаемость вакуума , μ 0 {\ displaystyle \ mu _ {0} \,} это магнитная постоянная или проницаемость вакуума .
Количество ε μ {\ displaystyle \ varepsilon \ mu \,} имеет единицы секунд в квадрате на квадратный метр. Итак, позволяя
- v знак равно 1 ε μ {\ displaystyle v = {\ frac {1} {\ sqrt {\ varepsilon \ mu}}} \,}
мы получаем v {\ displaystyle v \,} как фазовая скорость в материале.Лабораторные измерения ε {\ displaystyle \ varepsilon \,} и μ {\ displaystyle \ mu \,} получить значение около 3 × {\ displaystyle \ times} 10 8 метров в секунду, что близко к скорости света. Тщательный математический анализ Максвелла показал, что эти уравнения предсказывают электромагнитное излучение с такой скоростью.
уравнения Максвелла в интегральной форме [править]
В то время как дифференциальные версии часто рассматриваются как «реальные» уравнения Максвелла, интегральная форма, как правило, является первой, с которой сталкиваются студенты.Можно показать, что две формы эквивалентны дифференциальным формам с помощью общей теоремы Стокса. Форма, известная как теорема Гаусса (k = 3), заботится об уравнениях, связанных с расходимостью, а форма, известная как Теорема Стокса (k = 2), заботится о уравнениях, связанных с ротором.
Что означают четыре уравнения [править]
Закон Кулона [править]
Первое уравнение — это просто закон электростатики Кулона, очень элегантно (как обычно) управляемый Фарадеем и Гауссом.Закон Кулона просто гласит, что электрическая сила между двумя заряженными частицами действует в направлении линии между ними, отталкивает, если они имеют одинаковые заряды, и притягивает, если не совпадает, пропорциональна произведению зарядов и обратно пропорциональна квадрату. расстояния между ними:
- F знак равно Q 1 Q 2 4 π ε d 2 {\ displaystyle F = {\ frac {q_ {1} q_ {2}} {4 \ pi \ varepsilon \ d ^ {2}}}}
Константа, которая определяет силу электрической силы 4 π ε {\ displaystyle 4 \ pi \ varepsilon \,} в знаменателе.В единицах СИ заряды измеряются в кулонах, сила в ньютонах, расстояние в метрах, ε знак равно ε р ε 0 {\ displaystyle \ varepsilon = \ varepsilon _ {r} \ varepsilon _ {0} \,} и значение ε 0 {\ displaystyle \ varepsilon _ {0}} является 8.{-12}} Кулоны 2 на метр Ньютона 2 или Фарады на метр.
Майкл Фарадей переформулировал электрические и магнитные силы в терминах полей . Он предположил, что каждый заряд создает электрическое поле (называемое E), которое действует на другой заряд. Поле, созданное зарядом q 1 , наблюдаемое на расстоянии d, имеет вид
- Е знак равно Q 1 4 π ε d 2 {\ displaystyle E = {\ frac {q_ {1}} {4 \ pi \ varepsilon \ d ^ {2}}}}
и указывает прямо наружу от этого заряда, во всех направлениях.Сила, ощущаемая зарядом q 2 , составляет
- F знак равно Q 2 Е {\ displaystyle F = q_ {2} E \,}
Теперь рассмотрим сферу радиуса d с зарядом в центре. Если ρ {\ displaystyle \ rho} плотность заряда в кулонах на кубический метр (уравнения Максвелла в терминах плотностей), общий заряд в некотором объеме является интегралом по этому объему ρ {\ displaystyle \ rho} ,
Итак, мы имеем
- Q знак равно ∫ В ρ d В {\ displaystyle q = \ int _ {V} \ rho \, \ mathrm {d} V}
Теперь поле на поверхности сферы
- Q 1 4 π ε d 2 {\ displaystyle {\ frac {q_ {1}} {4 \ pi \ varepsilon \ d ^ {2}}}} , или 1 4 π ε d 2 ∫ В ρ d В {\ displaystyle {\ frac {1} {4 \ pi \ varepsilon \ d ^ {2}}} \ int _ {V} \ rho \, \ mathrm {d} V}
Это поле находится прямо наружу, перпендикулярно поверхности сферы и равномерно по всей поверхности.{2}} ; Вот почему у нас есть противный фактор 4 π {\ displaystyle 4 \ pi} в различных формулах; помните, что d — это расстояние, а следовательно, радиус сферы (, а не ее диаметр), поэтому
- ∫ В ρ ε d В знак равно ∮ S Е ⋅ d {\ displaystyle \ int _ {V} {\ frac {\ rho} {\ varepsilon}} \, \ mathrm {d} V = \ oint _ {S} \ mathbf {E} \ cdot \ mathrm {d} \ mathbf {A}}
Но по теореме Гаусса
- ∮ S Е ⋅ d знак равно ∫ В ∇ ⋅ Е d В {\ displaystyle \ oint _ {S} \ mathbf {E} \ cdot \ mathrm {d} \ mathbf {A} = \ int _ {V} \ nabla \ cdot \ mathbf {E} \ \ mathrm {d} V}
Так
- ∫ В ∇ ⋅ Е d В знак равно ∫ В ρ ε d В {\ displaystyle \ int _ {V} \ nabla \ cdot \ mathbf {E} \ \ mathrm {d} V = \ int _ {V} {\ frac {\ rho} {\ varepsilon}} \, \ mathrm {d } V}
Так как это верно для любого объема, мы имеем
- ∇ ⋅ Е знак равно ρ ε {\ displaystyle \ nabla \ cdot \ mathbf {E} = {\ frac {\ rho} {\ varepsilon}}}
Отсутствие магнитных монополей [править]
Второе из уравнений аналогично первому, но для магнитного поля.Дивергенция B должна быть пространственной плотностью магнитных монополей. Так как они никогда не наблюдались (хотя различные Великие Объединенные Теории могли бы их учесть), значение равно нулю.
Первоначально это не было сформулировано в терминах монополей, но фактически было утверждением, что магнитные «силовые линии» (линии, которые интуитивно описывают поле) никогда не заканчиваются. Они просто циркулируют вокруг различных проводников, несущих электрический ток. В противоположность этому, можно считать, что линии электрического поля «начинаются» и «заканчиваются» на заряженных частицах.
Закон Фарадея [править]
Третье уравнение содержит результат экспериментов Фарадея с «электромагнитной индукцией» — изменяющееся магнитное поле создает электрическое поле, и это электрическое поле циркулирует вокруг области, испытывающей изменение общего магнитного потока. (Помните, что оператор curl измеряет степень, в которой векторное поле движется по кругу.) Мы не будем вдаваться в подробности его экспериментов, за исключением того, что он обнаружил, что движется катушка с проволокой (петля, чтобы подобрать циркуляция электрического поля) через магнитное поле (например, поместив его на вал и повернув его), привели к созданию электрических генераторов и, следовательно, внесли большой вклад в индустриализацию мира.
Закон Био-Савара [править]
Закон Био-Савара, в котором говорится, как электрический ток порождает магнитное поле. Форма, которая нам полезна, — это «закон циркуляции Ампера», который гласит, что вблизи бесконечно длинного прямого провода, несущего электрический ток, магнитное поле движется по кругу вокруг провода, следуя правилу правой руки. Напряженность поля составляет:
- В знак равно μ я 2 π р {\ displaystyle B = {\ frac {\ mu \ I} {2 \ pi R}}}
Теперь рассмотрим интеграл по траектории магнитного поля вокруг окружности, перпендикулярной проволоке, с радиусом R и центрированной по проволоке.Магнитное поле везде параллельно этому пути, а длина пути 2 π р {\ displaystyle 2 \ pi R \,} , так:
- ∮ С В → ⋅ d L → знак равно 2 π р В знак равно μ я {\ displaystyle \ oint _ {C} {\ vec {B}} \ cdot {\ vec {dl}} = 2 \ pi RB = \ mu I}
Теперь, по теореме Стокса, этот интеграл по траектории поля B такой же, как и поверхностный интеграл скручивания поля B:
- ∬ ( ∇ × В → ) ⋅ d → знак равно ∮ С В → ⋅ d L → знак равно μ я знак равно ∬ μ J → ⋅ d → {\ displaystyle \ iint (\ nabla \ times {\ vec {B}}) \ cdot {\ vec {dA}} = \ oint _ {C} {\ vec {B}} \ cdot {\ vec {dl}} = \ mu \ I = \ iint \ mu {\ vec {J}} \ cdot {\ vec {dA}}}
Где J → {\ displaystyle {\ vec {J}} \,} плотность тока , в амперах на квадратный метр.Интеграл от J → {\ displaystyle {\ vec {J}} \,} на любой поверхности просто общее количество тока, протекающего по этой поверхности. Поскольку вклад плотности тока в магнитное поле является линейным, эта формула должна работать для любой поверхности, поэтому имеем:
- ∇ × В → знак равно μ J → {\ displaystyle \ nabla \ times {\ vec {B}} = \ mu {\ vec {J}}}
В четвертом уравнении Максвелла есть еще один член, называемый Ток смещения Максвелла .Это обеспечивает вклад в магнитное поле от изменения во времени электрического поля. Это явление трудно продемонстрировать экспериментально и было добавлено Максвеллом на теоретической основе, чтобы удовлетворить сохранение заряда. Итак, окончательная форма:
- ∇ × В → знак равно μ J → + 1 с 2 ∂ Е → ∂ T {\ displaystyle \ nabla \ times {\ vec {B}} = \ mu \ {\ vec {J}} + {\ frac {1} {c ^ {2}}} {\ frac {\ частичный {\ vec { E}}} {\ частичный t}}}
Составы в относительности [править]
Относительность обеспечивает объединение электрического и магнитного полей в тензор второго ранга, определенный в четырехмерном пространстве-времени.{\ alpha} \,} является релятивистской «плотностью четырех тока» — ее пространственные компоненты являются обычной плотностью тока J → {\ displaystyle {\ vec {J}} \,} , а его временной компонент является плотность заряда ρ {\ displaystyle \ rho \,} , Точка с запятой в первом уравнении является «ковариантным градиентом» тензорного исчисления.Индекс со скобками во втором уравнении является «антисимметризатором».
На языке Внешнего исчисления уравнения можно переписать еще более компактно:
- d F знак равно 0 {\ displaystyle \ mathrm {d} \ mathbf {F} = 0}
- d * F знак равно * J {\ displaystyle \ mathrm {d} \ * \ \ mathbf {F} = * \ \ mathbf {J}}
, где d — оператор внешней производной, * — оператор звезды Ходжа, а F — тензор Фарадея.
См. Также [править]
Ссылки [редактировать]
,