1.5. Операции над векторами, заданными в координатной форме
Если векторы заданы в координатной форме, то операции сложения и вычитания векторов, умножения вектора на число можно заменить более простыми арифметическими операциями над координатами этих векторов по следующим правилам.
Правило 1. При сложении векторов их одноименные координаты складываются:
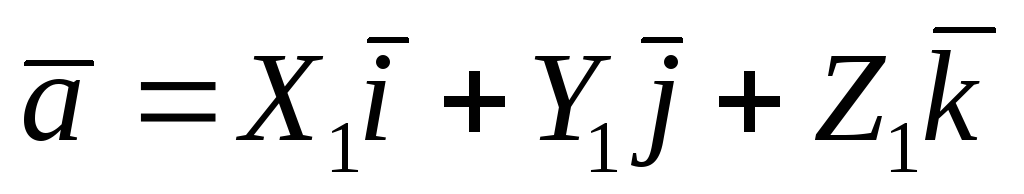 ,
,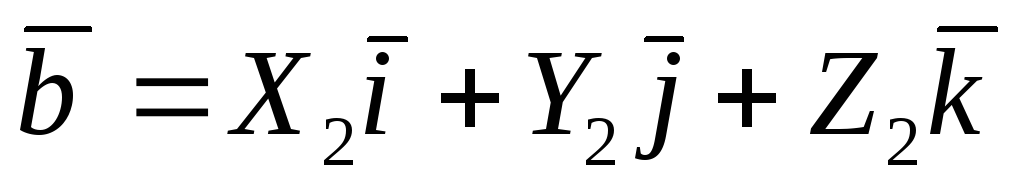 ,
,
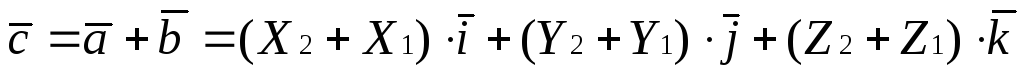 (1.5.1)
(1.5.1)

Правило 2. Чтобы вычесть из вектора
 ,
нужно вычест координаты вектора
,
нужно вычест координаты вектора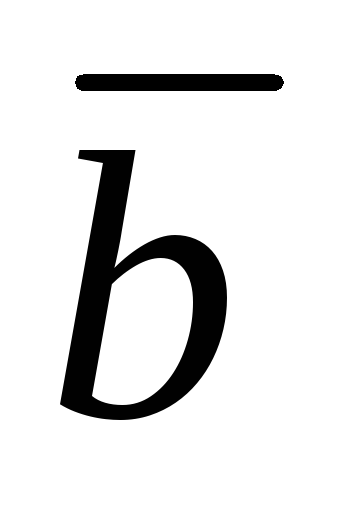 из соответствующих координат вектора
из соответствующих координат вектора ,
т.е.
,
т.е. 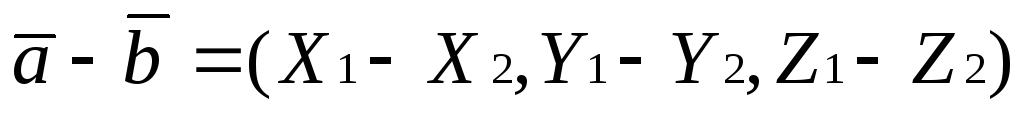 или
или (1.5.2)
(1.5.2)
Правило 3.Чтобы умножить вектор
 ,
нужно умножить на это число его координаты
, т.е. если
,
нужно умножить на это число его координаты
, т.е. если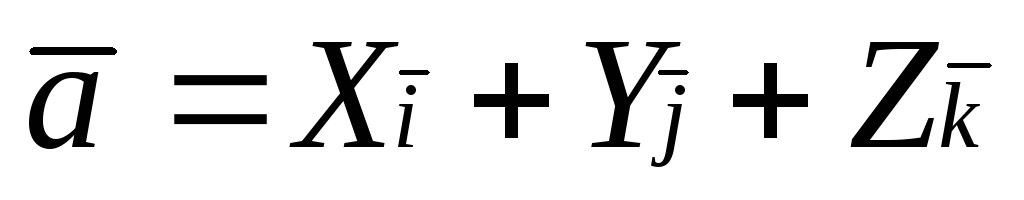 ,
то
,
то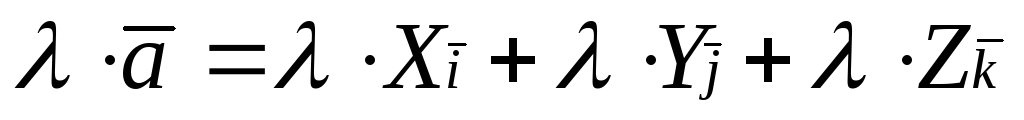 .
.1.6. Скалярное произведение векторов
Скалярным произведением двух векторов  и
и называется
число ,(обозначаемое
называется
число ,(обозначаемое
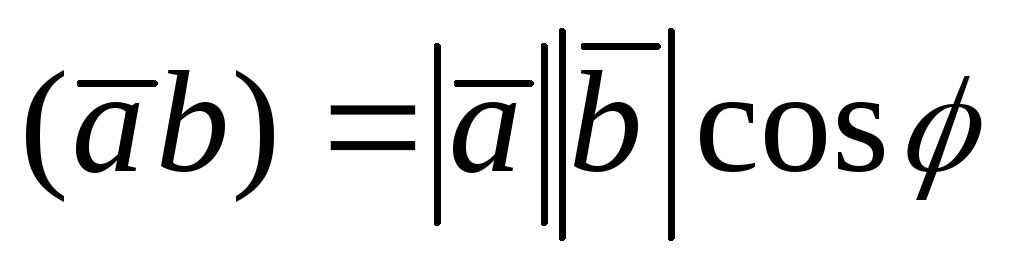 , (1.6.1)
, (1.6.1)
где  — угол между векторами
— угол между векторами и
и (рис.1.10).
(рис.1.10).

Рис. 1.10
1.6.1. Свойства скалярного произведения:
1). 
2).  и
и перпендикулярны; (или
перпендикулярны; (или ,
или
,
или )
)
3). 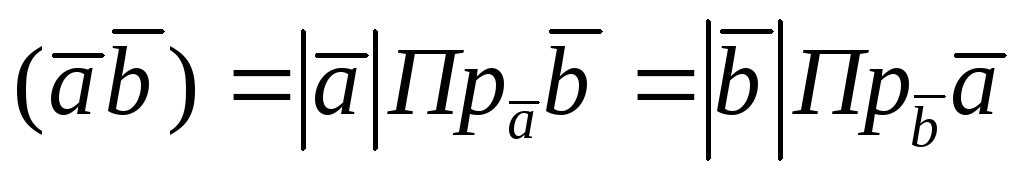
4). 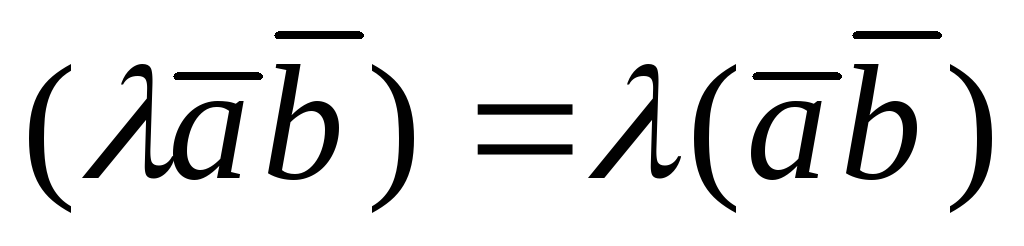 ,
где
,
где — число
— число
5).  ,
если
,
если
6). 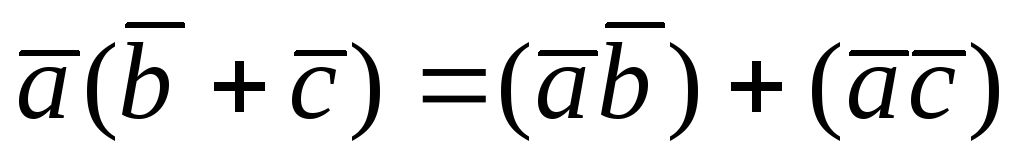
Докажем свойство 6. Имеем
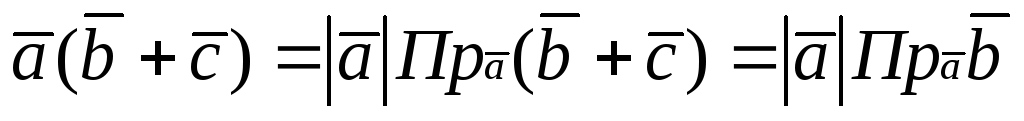
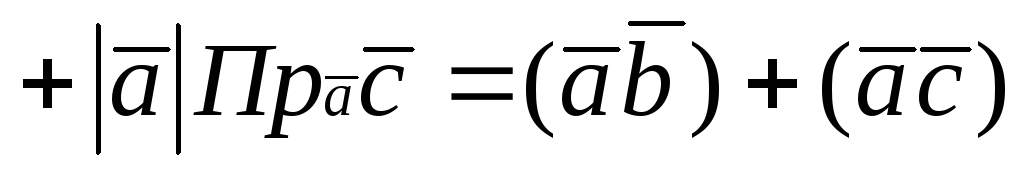
Замечание 1. Остальные свойства доказываются на основании определения.
Замечание 2. Свойства1, 3, 4, 6 дают право при скалярном умножении векторных многочленов выполнять действия так же, как при умножении алгебраических многочленов.
Замечание 3. Скалярное умножение не
распространяется на три и большее число
векторов. Произведение, например, трех
векторов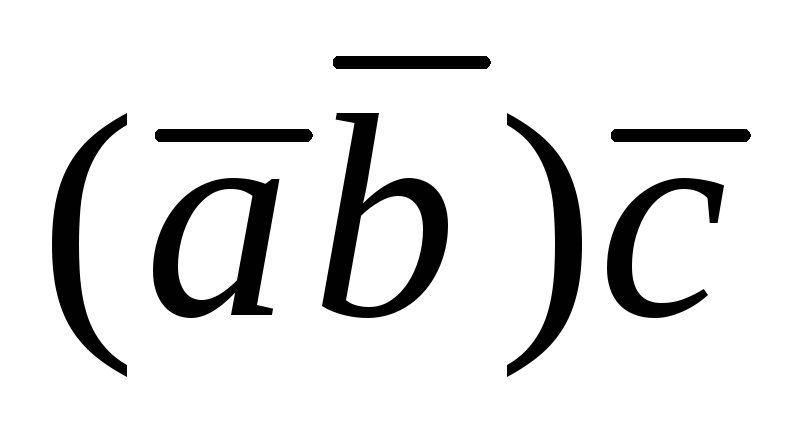 не является числом, оно будет вектором,
коллинеарным вектору
не является числом, оно будет вектором,
коллинеарным вектору
 на число
на число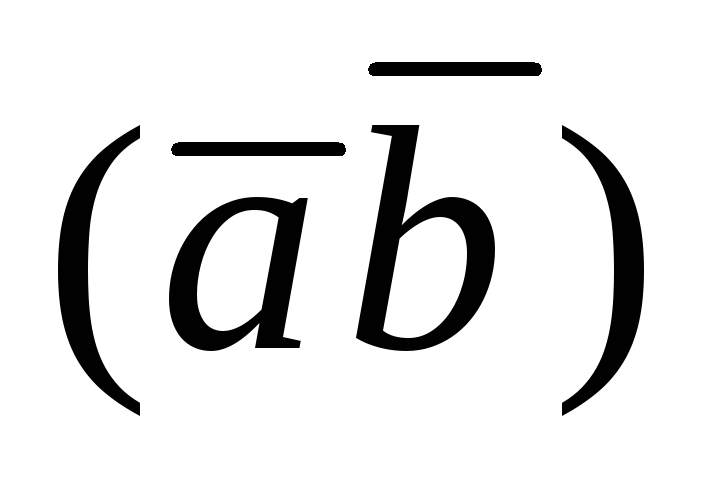 .
.1.6.2. Скалярное произведение векторов, заданных координатами
Так как единичные векторы (орты)  осейOx, Oy, Oz прямоугольной системы
координат взаимноперпендикулярны, то
по формуле (1.6.1) получим :
осейOx, Oy, Oz прямоугольной системы
координат взаимноперпендикулярны, то
по формуле (1.6.1) получим :
 ,
,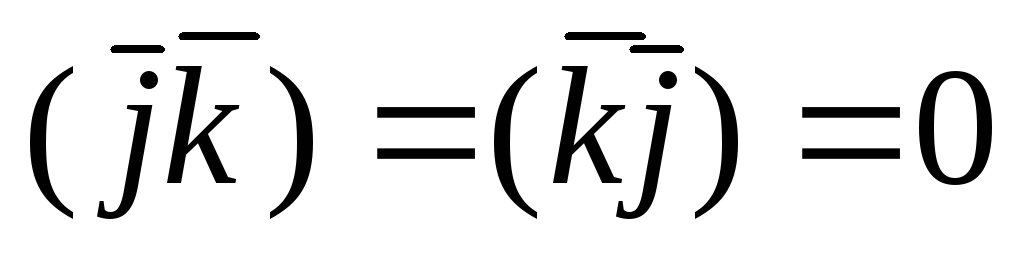
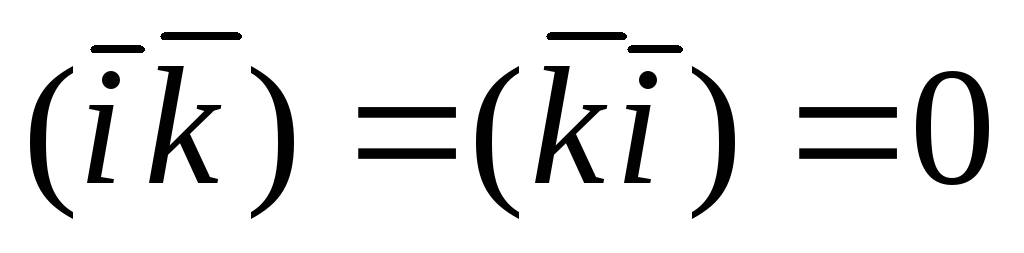 (1.6.2.1)
(1.6.2.1) Далее, используя свойство скалярного
произведения 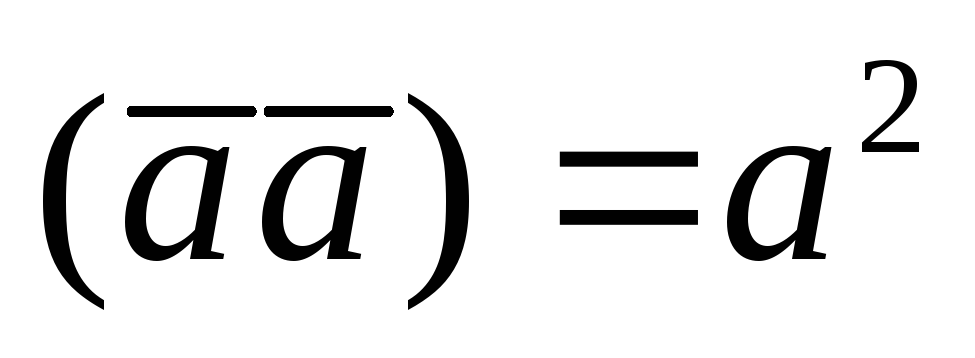 имеем:
имеем:
 (1.6.2.2)
(1.6.2.2)
Пусть, 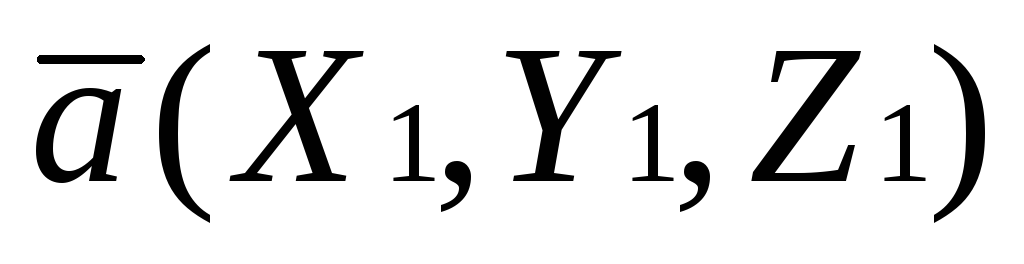 ,
,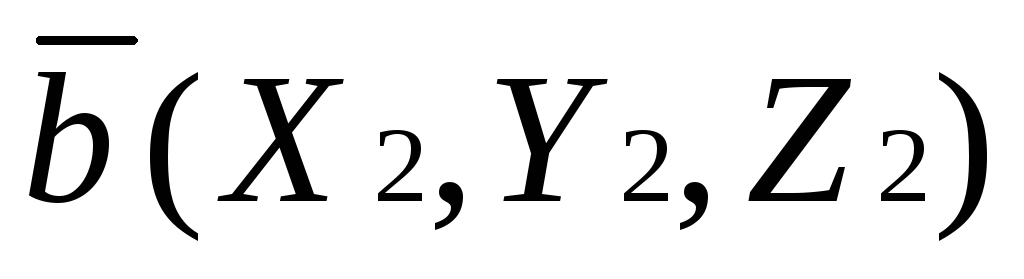 .
Найдем произведение этих векторов (с
учетом формул 1.6.2.1 и 1.6.2.2 ):
.
Найдем произведение этих векторов (с
учетом формул 1.6.2.1 и 1.6.2.2 ):
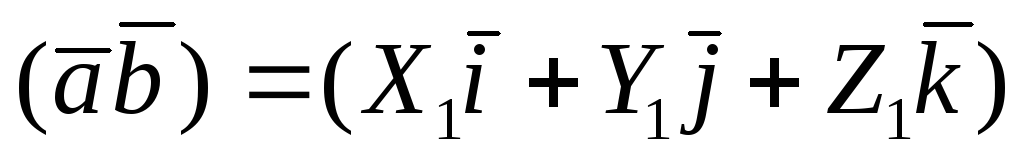

 (1.6.2.3)
(1.6.2.3)
Таким образом, скалярное произведение двух векторов равно сумме произведений одноименных координат этих векторов.
Из равенства (1.6.2.3) и равенства векторов получим:
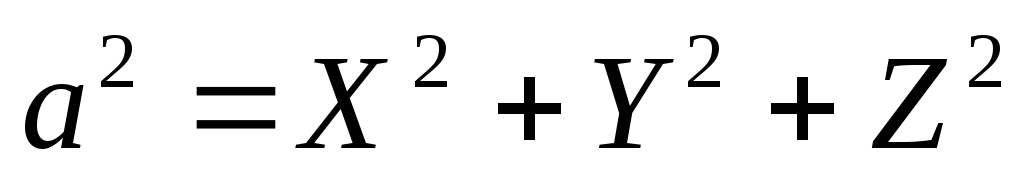 (1.6.2.4)
(1.6.2.4)
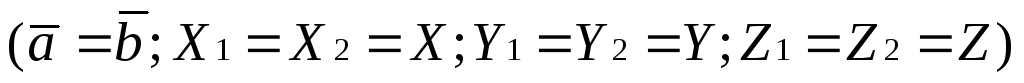
т.е. квадрат длины вектора равен сумме его координат .
Из равенства (1.6.2.4) найдем длину вектора  :
:
 (1.6.2.5)
(1.6.2.5)
Длина вектора равна квадратному корню из суммы квадратов его координат.
1.6.3. Угол между векторами
Из определения скалярного произведения двух векторов следует, что
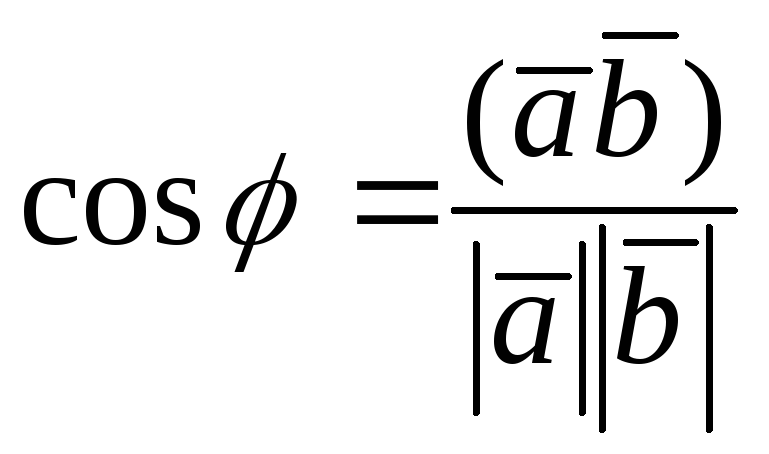
Если векторы  и
и заданы координатами
заданы координатами и
и ,
то формула (1.6.3.1) запишется в виде:
,
то формула (1.6.3.1) запишется в виде:
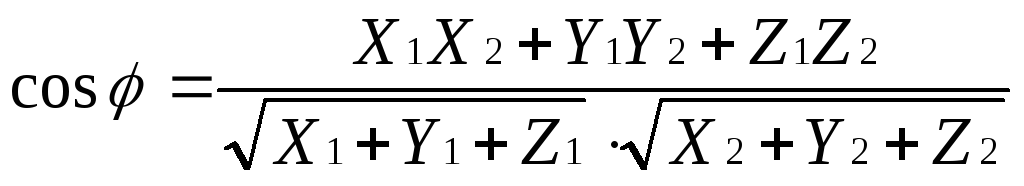 (1.6.3.2)
(1.6.3.2)
1.6.4. Условия коллинеарности и перпендикулярности векторов
Как известно, необходимым и достаточным
условием коллинеарности двух ненулевых
векторов 
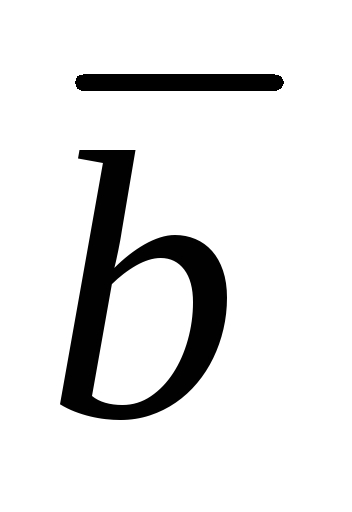 является равенство:
является равенство: 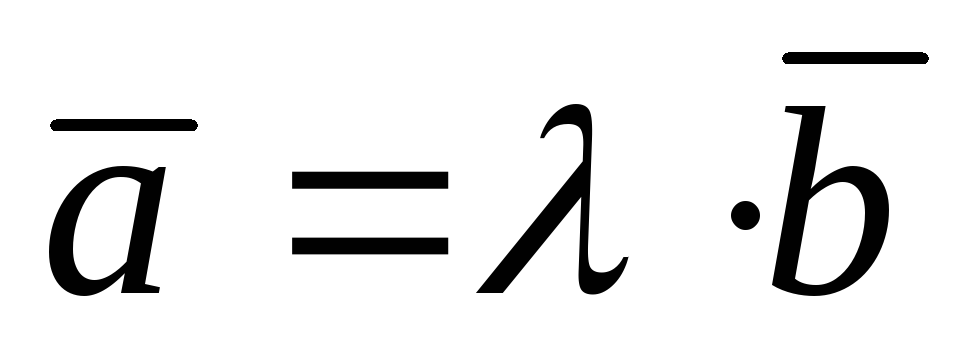 , (1.6.4.1)
, (1.6.4.1)
где скалярный множитель  >0,
если векторы
>0,
если векторы и
и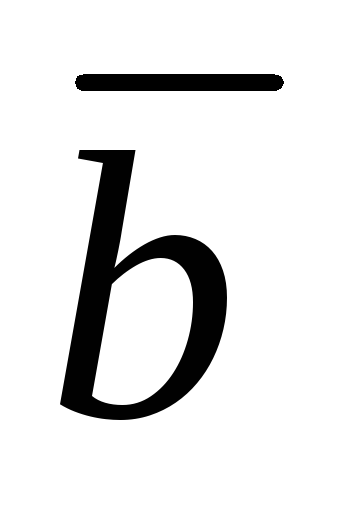 имеют
одинаковые направления и
имеют
одинаковые направления и
Пусть заданны два вектора в координатной
форме:  и
и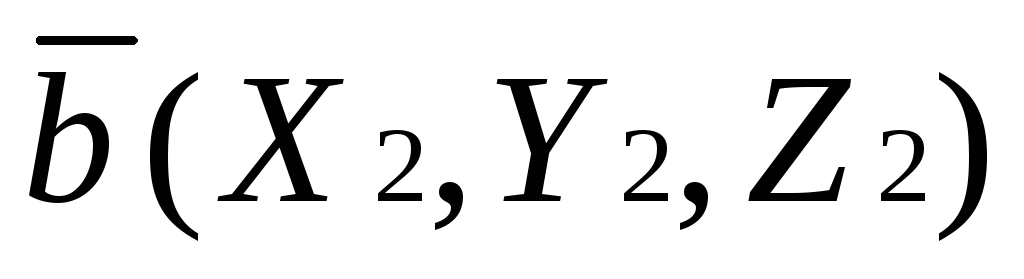 .
.
В этом случае из равенства (1.6.4.1) следует, что
 , (1.6.4.2)
, (1.6.4.2)
откуда  (1.6.4.3)
(1.6.4.3)
Следовательно, если ненулевые векторы  и
и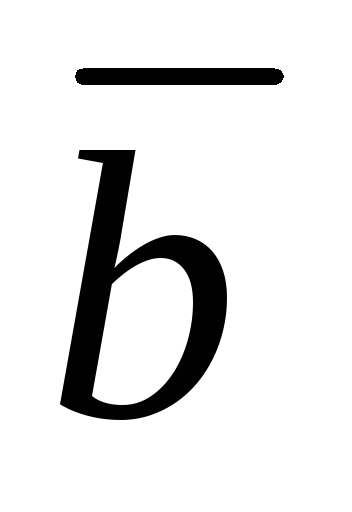 коллинеарны, то и их одноименные
координаты пропорциональны.
коллинеарны, то и их одноименные
координаты пропорциональны.
Необходимым и достаточным условием
перпендикулярности векторов 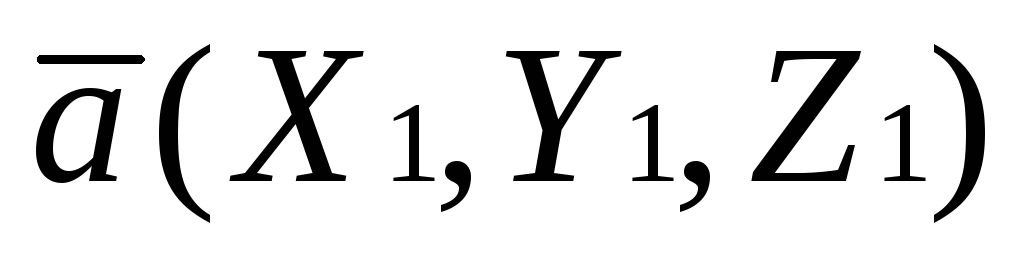 и
и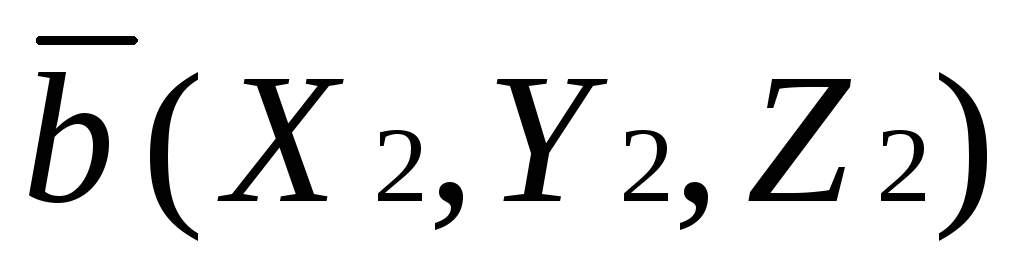 является равенство:
является равенство:
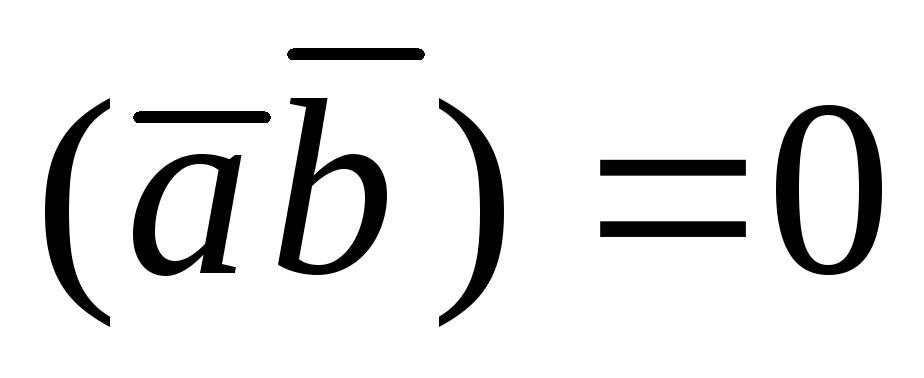 (1.6.4.4)
(1.6.4.4)
или в координатной форме условие (1.6.4.4) имеет вид:
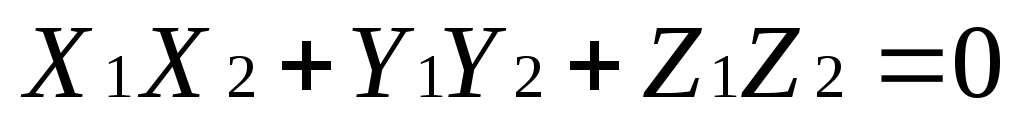 (1.6.4.5)
(1.6.4.5)
1.7. Векторное произведение двух векторов
Векторным произведением вектора  на вектор
на вектор называется новый вектор
называется новый вектор ,
обозначаемый символом
,
обозначаемый символом
 или(1.7.1)
или(1.7.1)
и определяемый следующими тремя условиями:
1) Модуль вектора  равен площади параллелограмма,
построенного на векторах
равен площади параллелограмма,
построенного на векторах и
и (после совмещения их начал), т.е.
(после совмещения их начал), т.е.
 ,
(1.7.2)
,
(1.7.2)
где  — угол между векторами
— угол между векторами и
и (рис.1.11).
(рис.1.11).

Рис.1.11
2). Вектор  перпендикулярен
к плоскости этого параллелограмма (т.е.
перпендикулярен обоим векторам
перпендикулярен
к плоскости этого параллелограмма (т.е.
перпендикулярен обоим векторам и
и ).
).
3). Вектор  направлен
в ту сторону от этой плоскости, что
кратчайший поворот от вектора
направлен
в ту сторону от этой плоскости, что
кратчайший поворот от вектора к вектору
к вектору вокруг вектора
вокруг вектора (после смещения начал всех трех векторов)
кажется происходящим против часовой
стрелки, если смотреть из конца вектора
(после смещения начал всех трех векторов)
кажется происходящим против часовой
стрелки, если смотреть из конца вектора .
Векторы
.
Векторы ,
, ,
, образуют
правую тройку векторов.
образуют
правую тройку векторов.
Замечание. Правую тройку образуют,
например, большой, указательный, и
средний пальцы правой руки; при пользовании
левой системой координат в определении
векторного произведения вместо правой
берут левую тройку ,
, ,
, .
.
Своим прообразом произведение двух
векторов имеет в механике операцию
отыскания момента силы относительно
точки. Именно, если в некоторой точке А
приложена сила  ,
то момент
,
то момент этой силы относительно определенной
точки О есть вектор, который в принятом
нами обозначении (1.7.1) должен быть записан
в виде
этой силы относительно определенной
точки О есть вектор, который в принятом
нами обозначении (1.7.1) должен быть записан
в виде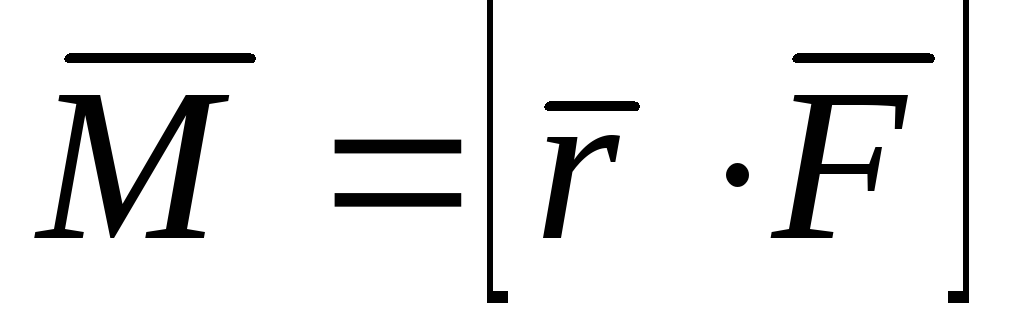 ,
где
,
где — вектор, идущий из точки О в точку А.
— вектор, идущий из точки О в точку А.
7. Векторы. Сложение, вычитание векторов, умножение вектора на число.
Вектор – это объект, кот.имеет длину и направление. Это пара точек, про кот.известно, какая является началом, а какая концом.
Векторы
бывают: 1) свободными (начало несущественно
для рассмотрения задачи, их можно
переносит пар-но самому себе как угодно.)
2) связанными (начало существенно для
рассмотрениязадачи).
Длина вектора обозначается: |AB|
Если начало и конец совпад, то вектор наз-ся нулевой. Его направление считается неопределенным.
Сложение векторов: по правилу параллелограмма.








 Умножение
вектора на число: результатом умножения
свобод.вектора на положительное число
Умножение
вектора на число: результатом умножения
свобод.вектора на положительное число  будет вектор, имеющий то же направление,
что и исходный, но с длиной в
будет вектор, имеющий то же направление,
что и исходный, но с длиной в раз больше.
раз больше.

8. Операции над векторами, заданными в координатной форме.
Равенство векторов и линейные операции (сложение векторов и умножение вектора на число) удобно представлять в координатной форме. При этом справедливы следующие свойства.
1. Равные векторы имеют равные координаты (в одном и том же базисе).
2. Каждая координата суммы векторов равна сумме соответствующих координат слагаемых.
3. Каждая координата произведения вектора на число равна произведению этого числа на соответствующую координату вектора.
4. Каждая координата линейной комбинации векторов равна линейной комбинации соответствующих координат векторов.
Вектора можно:
1. Складывать и вычитать.
2. Умножать на число.
3. Искать их скалярное произведение.
4. Искать угол между векторами.

9. Скалярное произведение векторов, его свойства.
Скал.произведение
( )
– число, равное произвед.длин этих
векторов наcos
угла между ними.
)
– число, равное произвед.длин этих
векторов наcos
угла между ними.
Свойства скал.произведения:
1.Не зависит от порядка умножения.
2.Скал.произведение вектора на самого себя = квадрату этого вектора.
3.Скал.произведение взаимоперпендикулярных векторов = 0.

10. Векторное произведение векторов, его свойства.
Векторное произвед.векторов – операция над ними, результатом кот.явл-ся вектор, обладающий след.свойствами:
1.Векторное произвед.вектора на самого себя = 0.
2.Постоянный множитель можно выносить за знак векторного произведения.
3. [ ]
= [
]
= [ ;
;
[ ]
= ([
]
= ([ )
+ [
)
+ [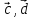 ]
]
[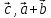 ]
=[
]
=[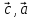 ]
+ [
]
+ [ ]
]
 =
= 
 =
= 
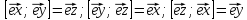 –правые тройки
векторов.
–правые тройки
векторов.
Если в декартовой системе координат 1 напр-е изменилось на противоположное, то получается левая тройка векторов.
Смысл векторного
произвед.: длина векторного произв. 2х
векторов = площади параллел-ма,
построенного на этих векторах: 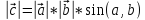

11. Системы линейных алгебраических уравнений. Решение их методами Гаусса, Крамера, матричным.
Метод Гаусса: Процедура решает неоднородную систему n линейных алгебраических уравнений с n неизвестными: a11 x1+a12 x2+ . . .+a1n xn=a1n+1
a21 x1+a22 x2+ . . .+a2n xn=a2n+1 . .
an1 x1+an2 x2+ . . .+ann xn=ann+1
Вначале находим отличный от нуля коэффициент при x1. Соответствующее уравнение переставляем с первым (если это необходимо). Получаем систему с a11 отличным от нуля. Разделив коэффициенты этого уравнения на a11, получим:
x1+b12 x2+ . . .+b1n xn=b1n+1
При помощи этого уравнения исключаем x1 из исходной системы:
a(1)22 x2+a(1)23 x3+ . . .+a(1)2n xn=a(1)2n+1 .
a(1)n2 x2+a(1)n3 x3+ . . .+a(1)nn xn=a(1)nn+1
где
a(1)i j=ai j-ai 1b1 j, i,j= 2…n
Полученная система содержит n-1 уравнение. Применяем описанную выше процедуру к этой системе. Операции повторяем требуемое число раз, пока не приведем систему к треугольному виду:
x1+с12 x2+ . . .+с1n xn=с1n+1
x2+ . . .+c2n xn=c2n+1
xn=cnn+1
Теперь легко определить xn,xn-1, . . ., x1.
Если det(A)=0, то исходная система не имеет решений и процедура выдает S=0 иначе S=1 и решения находятся в массиве X.
Метод Крамера: каждый из неизвестных x – дробь, в знаменателе кот.нах-ся определитель системы, а в числителе определитель, получ.из определителя системы путем замены столбца, №кот. = № x на столбц свободных членов. a11 x1+a12 x2+ . . .+a1n xn=a1n+1
a21 x1+a22 x2+ . . .+a2n xn=a2n+1 . .
an1 x1+an2 x2+ . . .+ann xn=ann+1


Матричный метод: 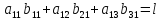
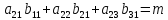
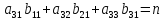
Пусть знаменатель
=  =
=
А числитель = D.
Для  =
=
 =
= =
=
 .
Для остальных – аналогично.
.
Для остальных – аналогично.
Алгебра векторов, страница 10
1.5.2. Линейные операции в координатной форме.
Рассмотрим, как преобразуются координаты при сложении векторов и при умножении вектора на число.
Теорема 1.5.2. При сложении векторов их соответствующие координаты складываются.
Док-во. Пусть 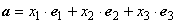 и
и 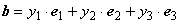 .
Тогда
.
Тогда 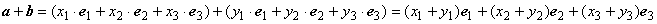 , что и требовалось доказать.
, что и требовалось доказать.
Теорема 1.5.3. При умножении вектора на число все его координаты умножаются на это число.
Док-во. Пусть 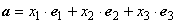 . Тогда
. Тогда 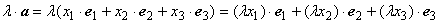 ,
что и требовалось доказать.
,
что и требовалось доказать.
При доказательстве обеих теорем используются свойства операций сложения векторов и умножения вектора на число, входящие в определение векторного пространства.
Следствие из теор. 1.5.3: Критерий коллинеарности векторов. Два ненулевых вектора коллинеарны тогда и только тогда, когда их координаты в любом базисе пропорциональны.
Док-во. Необходимость. Пусть векторы а(х1, х2, х3) и b(y1, y2, y3) коллинеарны. Тогда по теореме
1.4.6. 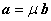 , т.е.
, т.е. 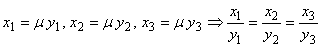 .
.
Достаточность. Если координаты
векторов пропорциональны, т.е. 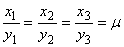 , то
, то 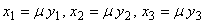 , и
, и 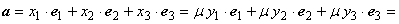
 .
.
 1.5.3.
Ортонормированный базис. Направляющие косинусы.
1.5.3.
Ортонормированный базис. Направляющие косинусы.
Опр.1.5.4. Базис векторного пространства называется ортонормированным, если составляющие его векторы взаимно перпендикулярны и имеют единичную длину.
 Ортонормированный базис на
плоскости обычно вводят парой ортов i, j. Прежде чем ввести ортонормированный базис в
пространстве, дадим определение ориентации тройки векторов.
Ортонормированный базис на
плоскости обычно вводят парой ортов i, j. Прежде чем ввести ортонормированный базис в
пространстве, дадим определение ориентации тройки векторов.
Опр. 1.5.5. Упорядоченная тройка некомпланарных векторов a, b, c называется правой, если при приведении этих векторов к общему началу кратчайший поворот от a к b виден из конца вектора c против часовой стрелки (если кратчайший поворот от a к b совершается по часовой стрелке, то тройка векторов a, b, c называется левой).
Заметим, что если тройка a, b, c – правая (левая), то правыми (левыми) являются тройки b, c, a и c, a, b, т.е. ориентация не меняется при циклической перестановке векторов. В тоже время перестановка двух векторов меняет ориентацию: если тройка a, b, c – правая (левая), то тройка b, a, c (и, как следствие, тройки a, c, b и c, b,a) – левая (правая).
Ортонормированный базис в пространстве
будем задавать правой тройкой ортов i, j, k. Произвольный
вектор пространства a теперь
может быть представлен в виде 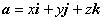 . На рисунке
справа х = ОА2, у = ОА3, z = ОА4, все три координаты положительны.
Если х, у, z – координаты вектора а в ортонормированном базисе, то
. На рисунке
справа х = ОА2, у = ОА3, z = ОА4, все три координаты положительны.
Если х, у, z – координаты вектора а в ортонормированном базисе, то 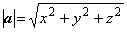 (док-во: |a|2 = ОА2 = ОА12 + A1А2 (так как
тр-к OAA1 – прямоугольный) = (ОА22 + A2А12)
+ A1А2 = ОА22 + ОА32 + ОА42).
(док-во: |a|2 = ОА2 = ОА12 + A1А2 (так как
тр-к OAA1 – прямоугольный) = (ОА22 + A2А12)
+ A1А2 = ОА22 + ОА32 + ОА42).
Множення вектора на число
Геометрична інтерпретація.
Добуток ненульового вектора на число — це вектор, колінеарний заданому (співнаправлений з заданим, якщо число додатне, протилежно направлений, якщо число від’ємне), а його модуль дорівнює модулю заданого вектора, помноженому на модуль числа.Алгебраїчна інтерпретація. Добуток ненульового вектора на число — це вектор, координати якого дорівнюють відповідним координатам даного вектора, помноженим на число.
Формули множення вектора на число
Формула множення вектора на число для плоских задач
У випадку плоскої задачі добуток вектора a = {ax ; ay} та числа k можна знайти скориставшись наступною формулою:
k · a = {k · ax; k · ay}
Формула множення вектора на число для просторових задач
У випадку просторової задачі добуток вектора a = {ax ; ay ; az} і числа k можна знайти скориставшись наступною формулою:
k · a = {k · ax ; k · ay ; k · az}
Формула множення n -вимірного вектора
У випадку n-вимірного простору добуток вектора a = {a1 ; a2; … ; an} і числа k можна знайти скориставшись наступною формулою:
k · a = {k · a1; k · a2; … ; k · an}
Властивості добутку вектора на число
Якщо вектор b дорівнює добутку ненульового числа k і ненульового вектора a, тобто b = k · a, тоді:
b || a — вектори b і a паралельні
a↑↑b, якщо k > 0 — вектори b і a співнаправлені, якщо число k > 0
a↑↓b, якщо k < 0 — вектори b и a протилежно направлені, якщо число k < 0
|b| = |k| · |a| — модуль вектора b дорівнює модулю вектора a помноженому на модуль числа k
Будь-які нецензурні коментарі будуть видалені, а їх автори занесені в чорний список!
Определение координат вектора заданного координатами его начальной и конечной точки.
Основное соотношение.Чтобы найти координаты вектора AB, зная координаты его начальной точек А и конечной точки В, необходимо из координат конечной точки вычесть соответствующие координаты начальной точки.
 |
Формулы определения координат вектора заданного координатами его начальной и конечной точки
Формула определения координат вектора для плоских задач
В случае плоской задачи вектор AB заданный координатами точек A(Ax ; Ay) и B(Bx ; By) можно найти воспользовавшись следующей формулой
AB = {Bx — Ax ; By — Ay}
Формула определения координат вектора для пространственных задач
В случае пространственной задачи вектор AB заданный координатами точек A(Ax ; Ay ; Az) и B(Bx ; By ; Bz) можно найти воспользовавшись следующей формулой
AB = {Bx — Ax ; By — Ay ; Bz — Az}
Формула определения координат вектора для n -мерного пространства
В случае n-мерного пространства вектор AB заданный координатами точек A(A1 ; A2 ; … ; An) и B(B1 ; B2 ; … ; Bn) можно найти воспользовавшись следующей формулой
AB = {B1 — A1 ; B2 — A2 ; … ; Bn — An}
Примеры задач связанных с определением координат вектора по двум точкам
Примеры для плоских задач
Пример 1. Найти координаты вектора AB, если A(1; 4), B(3; 1).Решение: AB = {3 — 1; 1 — 4} = {2; -3}.
Пример 2. Найти координаты точки B вектора AB = {5; 1}, если координаты точки A(3; -4).Решение:
ABx = Bx — Ax => Bx = ABx + Ax => Bx = 5 + 3 = 8ABy = By — Ay => By = ABy + Ay => By = 1 + (-4) = -3
Ответ: B(8; -3).
Пример 3. Найти координаты точки A вектора AB = {5; 1}, если координаты точки B(3; -4).Решение:
ABx = Bx — Ax => Ax = Bx — ABx => Ax = 3 — 5 = -2ABy = By — Ay => Ay = By — ABy => Ay = -4 — 1 = -5
Ответ: A(-2; -5).
Примеры для пространственных задач
Пример 4. Найти координаты вектора AB, если A(1; 4; 5), B(3; 1; 1).Решение: AB = {3 — 1; 1 — 4; 1 — 5} = {2; -3; -4}.
Пример 5. Найти координаты точки B вектора AB = {5; 1; 2}, если координаты точки A(3; -4; 3).Решение:
ABx = Bx — Ax => Bx = ABx + Ax => Bx = 5 + 3 = 8ABy = By — Ay => By = ABy + Ay => By = 1 + (-4) = -3
ABz = Bz — Az => Bz = ABz + Az => Bz = 2 + 3 = 5
Ответ: B(8; -3; 5).
Пример 6. Найти координаты точки A вектора AB = {5; 1; 4}, если координаты точки B(3; -4; 1).Решение:
ABx = Bx — Ax => Ax = Bx — ABx => Ax = 3 — 5 = -2ABy = By — Ay => Ay = By — ABy => Ay = -4 — 1 = -5
ABz = Bz — Az => Az = Bz — ABz => Az = 1 — 4 = -3
Ответ: A(-2; -5; -3).
Примеры для n -мерного пространства
Пример 7. Найти координаты вектора AB, если A(1; 4; 5; 5; -3), B(3; 0; 1; -2; 5).Решение: AB = {3 — 1; 0 — 4; 1 — 5; -2 — 5; 5 — (-3)} = {2; -4; -4; -7; 8}.
Пример 8. Найти координаты точки B вектора AB = {5; 1; 2; 1}, если координаты точки A(3; -4; 3; 2).Решение:
AB1 = B1 — A1 => B1 = AB1 + A1 => B1 = 5 + 3 = 8AB2 = B2 — A2 => B2 = AB2 + A2 => B2 = 1 + (-4) = -3
AB3 = B3 — A3 => B3 = AB3 + A3 => B3 = 2 + 3 = 5
AB4 = B4 — A4 => B4 = AB4 + A4 => B4 = 1 + 2 = 3
Ответ: B(8; -3; 5; 3).
Пример 9. Найти координаты точки A вектора AB = {5; 1; 4; 5}, если координаты точки B(3; -4; 1; 8).Решение:
AB1 = B1 — A1 => A1 = B1 — AB1 => A1 = 3 — 5 = -2AB2 = B2 — A2 => A2 = B2 — AB2 => A2 = -4 — 1 = -5
AB3 = B3 — A3 => A3 = B3 — AB3 => A3 = 1 — 4 = -3
AB4 = B4 — A4 => A4 = B4 — AB4 => A4 = 8 — 5 = 3
Ответ: A(-2; -5; -3; 3).

