Сложение и вычитание векторов. Умножение на число
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Назовите
Назовите
коллинеарные
векторысонаправленные векторы
Назовитеравные
коллинеарные
противоположнонаправленные векторы
A
B
C
D
N
M
R
E
S
F
Q
V
T
Y
U
I
O
P
X
G
H
J
K
L
Z
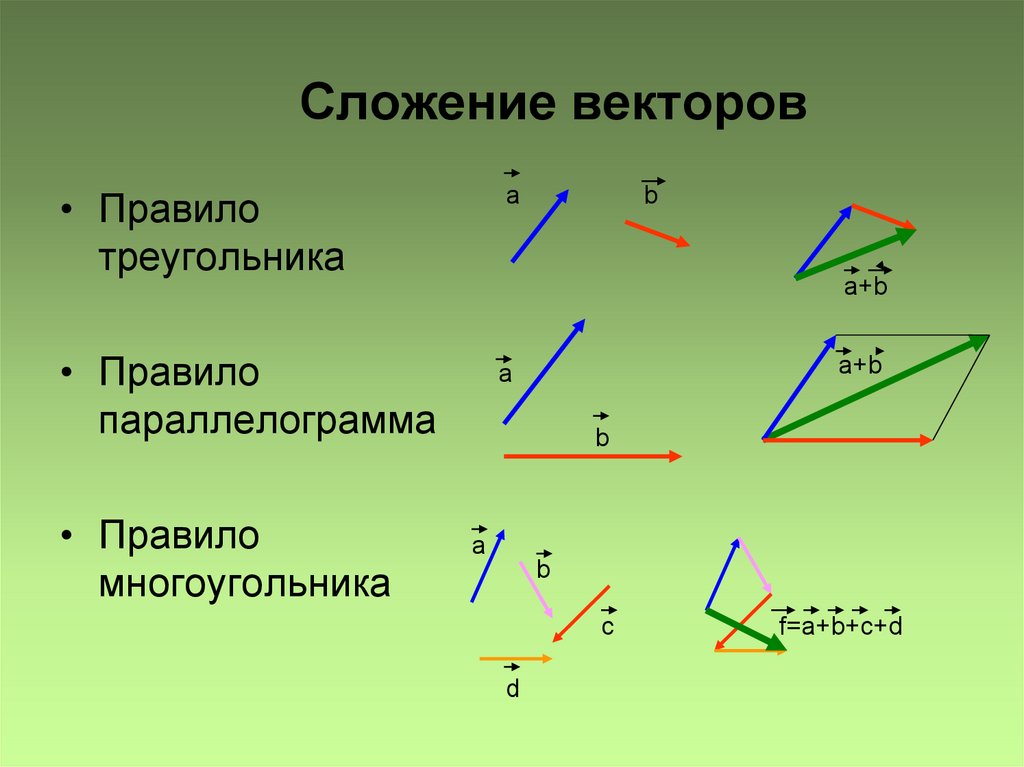
По правилу треугольника складываются и
коллинеарные векторы, хотя при их сложении
b
a+b
a
b
a
b
a+b
a
f
c
c+ f
Законы сложения векторов
Теорема
Для любых векторов
1
a, b, c справедливы равенства:
a+b=b+a
!
переместительный закон
2 (a + b) + c = a + (b + c)
сочетательный закон
!
Сложение векторов.
 Правило параллелограмма.
Правило параллелограмма.11
10
12
a
8
a
b
2
a+b
b
9
1
3
4
7
6
5
Сложение векторов.
Правило многоугольника.
АВ + ВС + СD + DO = АO
n
m
a
m
c
c
a
n
Правило многоугольника можно сформулировать также
следующим образом: если А1, А2, …, Аn – произвольные
А6
А7
А1
А4
А5
А3
А2
!
Если начало первого вектора совпадает с концом
последнего вектора, то сумма данных векторов равна
1
2
3
4
5
нулевому вектору.
a +a +a +a +a
=0
a3
a3
a5
a2
a4
a4
a1
a2
a1
a5
a1 называется противоположным
вектору a, если векторы a и a1 имеют равные
Вектор
длины и противоположно направлены.
a1
a
А
-b
a1
-b, противоположный вектору b
Вектор
b
a = a1 ; a
А
Вектор ВА, противоположный
вектору АВ
ВА = – АВ
В
В
a + (-a) = 0
№ 766 На рисунке изображены векторы
ХУ.
 Представьте вектор ХУ в виде суммы остальных или им
Представьте вектор ХУ в виде суммы остальных или импротивоположных векторов.
–b
–a
c
Х
d
– a – b + c + d = ХУ
У
Вычитание векторов.
a – b = a +(–b)
-b
b
-b
a
a
a- b
Вычитание векторов.
MF — SF =
MF + FS = MS
RO — RM = RO + MR = MR + RO = MO
MD — SD =
MD + DS = MS
RO — AO = RO + OA = RA
RO — RO = RO + OR = RR = 0
— OS — ST =
SO + TS = TS + SO = TO
1) Постройте сумму а + b,
Дано:
c
b
а
Построение:
1)
a+b
b
а
d
2) Постройте сумму с + d,
используя правило параллелограмма .
Дано:
c
b
а
Построение:
2)
с
d
c+d
d
3) Постройте разность с — b, используя
правило разности векторов.
Дано:
c
b
а
Построение:
3)
с
-b
с-b
d
4) Постройте разность d — а,
используя правило вычитания векторов .
Дано:
а
c
d
b
Построение:
4) = d – a, значит х = d +(-а)
х
d
-а
d-a
Что получается при умножении
вектора на число?
c
а
d
b
2а
3b
— 0,5d
5) Упростите выражение:
1 вариант.
2 вариант.
CA – OB – CD + AB =
BA + CD – OD – CA =
= CA + BO + DC + AB =
= BA + CD + DO + AC =
= DC + CA + AB + BO =
= BA + AC + CD + DO =
= DO.
= BO.
АВ + ВС =
АS + SС =
АО + ОР =
NM + ML =
MN + NR =
RP + PR =
MK + KM =
ZK + KZ =
MK + OM =
DE + KD =
из ОВN
из ASR
ON =
AS =
из XKH XH =
из АMD MD =
из FPO OP =
из ОВN
из ASR
OB =
RA =
из XKH KX =
из АMD
из FPO
AD =
FO =
№ 768 Точки М и N – середины сторон АВ и АС
через векторы
a = АМ и b = АN
В
М
a
ВМ =
-a
NC =
b
из AMN
MN = MA + AN =
А
b
N
С
-a + b
из ABN
BN = BA + AN =
-a-a + b
Найдите
АВ + AD – DC – OD
ABCD — прямоугольник
B
C
5
О
А
(
4
)
3
D
= АС – DC – OD = АС + CD + DO = АО
1
АО 5 2,5
2
English Русский Правила
Сообщество Экспонента
- вопрос
- 28.
 12.2022
12.2022
Математика и статистика
Подскажите, пожалуйста, ссылки на видео и/или другую информацию (на русском) для того чтоб быстрее разобраться — как, после обучения модели и сохранив ее в виде скрипта , — использовать эт…
Подскажите, пожалуйста, ссылки на видео и/или другую информацию (на русском) для того чтоб быстрее разобраться — как, после обучения модели и сохранив ее в виде скрипта , — использовать эт…
- модель
28.12.2022
- Публикация
- 24.12.2022
Системы связи
Скачать материалы семинара можно тут.
Недавно у нас в офисе прошел офлайн-семинар, который собрал на одной площадке специалистов данной тематики для обмена знаниями и опытом, чтобы вооружившись последними технологиями дать быстрый старт в развитии отечественного оборудования систем связи 5G.
- 5G
- ИИ
- Искусственный интеллект
24.12.2022
- вопрос
- 23.
 12.2022
12.2022
Глубокое и машинное обучение(ИИ), Робототехника и беспилотники, ПЛИС и СнК, Системы управления, Электропривод и силовая электроника, Радиолокация, Автоматизация испытаний, Системы связи, Цифровая обработка сигналов, Верификация и валидация, Математика и статистика, Изображения и видео
Здравствуйте! Есть такая вот статья. Мне в Matlab надо написать формулу, чтобы в результате получить диаграмму, как на рисунке 4 на статье. Только вот я не понимаю, какую формулу можно было бы написат…
Здравствуйте! Есть такая вот статья. Мне в Matlab надо написать формулу, чтобы в результате получить диаграмму, как на рисунке 4 на статье. Только вот я не понимаю, какую формулу можно было бы написат…
3 Ответа
- Отвеченный вопрос
- 21.12.2022
Другое, Математика и статистика, Цифровая обработка сигналов
Есть массив экспериментальных данных (9 спектров при разных концентрациях), который я пытаюсь описать спектрами нескольких форм (в данном примере для упрощения только одна форма со спектром x(2,: ) и.
1 Ответ
- ПЧ
- Скалярное управление
- АД
14.12.2022
- Отвеченный вопрос
- 13.12.2022
Другое, Математика и статистика, Цифровая обработка сигналов
Здравствуйте. Подскажите пожалуйста как (и можно ли вообще) решить систему квадратных уравнений. eqn1=(x-y)/(A0-x-y)/(m0-x-2*y)==K1; eqn2=y/(x-y)/(m0-x-2*y)==K2; То есть выразить переменные x и y чер…
Здравствуйте. Подскажите пожалуйста как (и можно ли вообще) решить систему квадратных уравнений. eqn1=(x-y)/(A0-x-y)/(m0-x-2*y)==K1; eqn2=y/(x-y)/(m0-x-2*y)==K2; То есть выразить переменные x и y чер…
7 Ответов
- Публикация
- 07.12.2022
Электропривод и силовая электроника
Наша команда представила решение для электроэнергетической отрасли на базе КПМ РИТМ.
В очередной раз мы провели демонстрацию работы стенда с терминалами РЗиА (ВАЖНО! — мы не занимаемся рекламой сипротеков, на их месте может быть любой терминал, в том числе и В.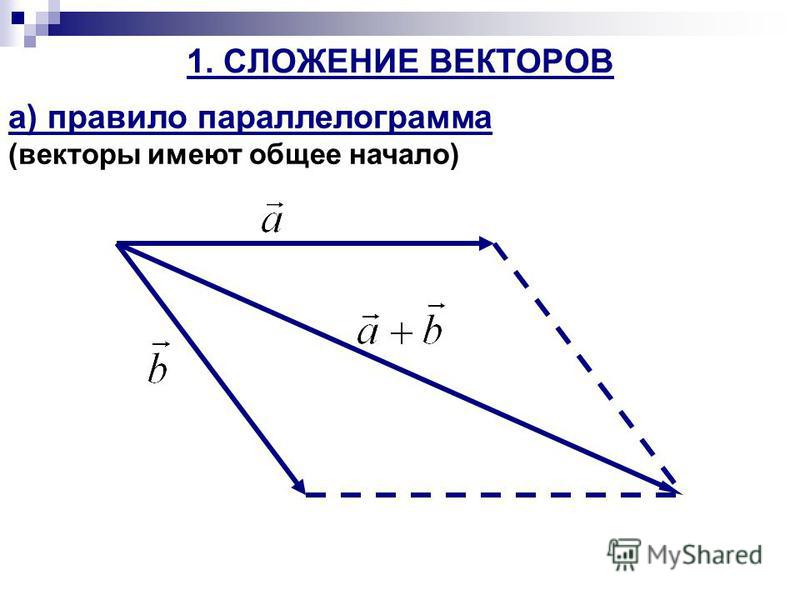
На прошлой неделе прошел международный форум «Электрические сети», который объединил десятки ведущих представителей профессионального сообщества электроэнергетики, а также задал вектор развития для внедрения новых прорывных технологий.
- Электропривод
- электроэнергетика
07.12.2022
- Публикация
- 07.12.2022
Робототехника и беспилотники
В докладе будет рассказано о применении алгоритмов обучения с подкреплением к различным задачам: от простых игровых задач до задачи навигации мобильного робота. Также будут представлены результаты сравнения различных алгоритмов в задачах избежания столкновения…
Приглашаем на вебинар «Обучение с подкреплением: от игр к реальным задачам», который пройдет 13 декабря в 10:00.
В настоящее время технологии обучения с подкреплением активно применяются во многих сферах: от ритейла до автономных транспортных средств. Может быть лучше: основной сложностью этого подхода является отсутствие размеченных данных, и, к сожалению, нет формализованного подхода как данные могут быть размечены для этой задачи. Другая сложность — это формализация функции вознаграждения. От удачного ее выбора зависит конечный успех настройки алгоритма управления.
Другая сложность — это формализация функции вознаграждения. От удачного ее выбора зависит конечный успех настройки алгоритма управления.
- MATLAB
- Simulink
- САУ
- МОП
- Модельно ориентированное проектирование
- Искусственный интеллект
07.12.2022
- вопрос
- 07.12.2022
Системы связи, Цифровая обработка сигналов, ПЛИС и СнК, Другое
Здравствуйте! У меня вопрос по поводу дифференциальной квадратурной фазовой модуляции (DQPSK), которая применяется в стандарте связи TETRA. Мне необходимо построить сигнал с данной модуляцией и…
Здравствуйте! У меня вопрос по поводу дифференциальной квадратурной фазовой модуляции (DQPSK), которая применяется в стандарте связи TETRA. Мне необходимо построить сигнал с данной модуляцией и…
13 Ответов
Сложение векторов, вычитание и скалярное умножение
Перейти к основному содержанию
Домашняя страница Технологического института Онтарио
nool
Пример:
youtube.com/embed/jvdu7J3iLCE»>Графические методы — физика Колледжа Дугласа 1104 Индивидуальный учебник — зима и лето 2020
Глава 3 Двумерная кинематика
Сводка
- Определение и применение правил сложения, вычитания и умножения векторов.

- Применять графические методы сложения и вычитания векторов для определения перемещения движущихся объектов.
Вектор — это величина, которая имеет величину и направление. Например, перемещение, скорость, ускорение и сила — все это векторы. В одномерном или прямолинейном движении направление вектора может быть задано просто знаком плюс или минус. Однако в двух измерениях (2-d) мы указываем направление вектора относительно некоторой системы отсчета (т. е. системы координат), используя стрелку, длина которой пропорциональна величине вектора и указывает направление вектора.
На рис. 2 показано такое графическое представление вектора на примере полного перемещения человека, идущего по городу, рассмотренного в главе 3.1 «Кинематика в двух измерениях: введение». Мы будем использовать обозначение, что символ со стрелкой над ним, такой как $$\vec{\text{D}}$$, обозначает вектор. Его величина представлена курсивным символом , D , , а его направление — θ .
2 показано такое графическое представление вектора на примере полного перемещения человека, идущего по городу, рассмотренного в главе 3.1 «Кинематика в двух измерениях: введение». Мы будем использовать обозначение, что символ со стрелкой над ним, такой как $$\vec{\text{D}}$$, обозначает вектор. Его величина представлена курсивным символом , D , , а его направление — θ .
ВЕКТОРА В ЭТОМ ТЕКСТЕ
В этом тексте мы будем представлять вектор со стрелкой над символом. Например, мы представим количественную силу вектором $$\vec{\text{F}}$$, который имеет как величину, так и направление. Величина вектора будет представлена переменной, выделенной курсивом, например, F , а направление переменной будет задано углом θ .
Рисунок 2. Человек проходит 9 кварталов на восток и 5 кварталов на север. Водоизмещение 10,3 блока под углом 29. 1 o к северу от востока. Рисунок 3. Чтобы графически описать результирующий вектор для человека, идущего по городу, показанному на рисунке 2, нарисуйте стрелку, представляющую общий вектор смещения D . С помощью транспортира начертите линию под углом θ относительно оси восток-запад. Длина D стрелки пропорциональна модулю вектора и измеряется линейкой вдоль линии. В этом примере магнитуда D вектора составляет 10,3 единицы, а направление θ равно 29,1 o к северу от востока.
1 o к северу от востока. Рисунок 3. Чтобы графически описать результирующий вектор для человека, идущего по городу, показанному на рисунке 2, нарисуйте стрелку, представляющую общий вектор смещения D . С помощью транспортира начертите линию под углом θ относительно оси восток-запад. Длина D стрелки пропорциональна модулю вектора и измеряется линейкой вдоль линии. В этом примере магнитуда D вектора составляет 10,3 единицы, а направление θ равно 29,1 o к северу от востока.Метод «голова к хвосту» представляет собой графический способ добавления векторов, описанный на рис. 4 ниже и в следующих шагах. Конец вектора является начальной точкой вектора, а заголовок (или кончик) вектора является конечным заостренным концом стрелки.
Рисунок 4.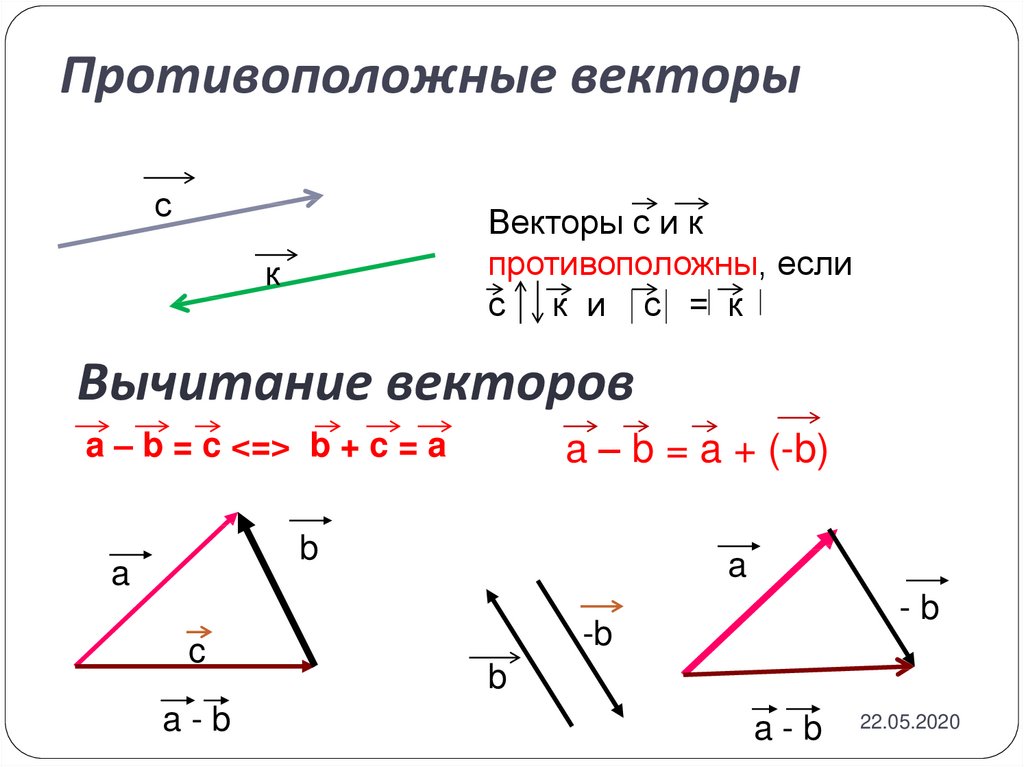 Метод «голова к хвосту»: метод «голова к хвосту» графического сложения векторов проиллюстрирован для двух перемещений человека, идущего по городу, рассмотренного на рисунке 2. (a) Нарисуйте вектор, представляющий перемещение на восток. (b) Нарисуйте вектор, представляющий смещение на север. Хвост этого вектора должен исходить из головы первого вектора, указывающего на восток. (c) Проведите линию от хвоста вектора, указывающего на восток, к началу вектора, указывающего на север, чтобы получить сумму или результирующий вектор D . Длина стрелки D пропорциональна модулю вектора и составляет 10,3 единицы. Его направление, описываемое как угол относительно востока (или горизонтальной оси) θ , измеренное с помощью транспортира, равно 29,1 0 .
Метод «голова к хвосту»: метод «голова к хвосту» графического сложения векторов проиллюстрирован для двух перемещений человека, идущего по городу, рассмотренного на рисунке 2. (a) Нарисуйте вектор, представляющий перемещение на восток. (b) Нарисуйте вектор, представляющий смещение на север. Хвост этого вектора должен исходить из головы первого вектора, указывающего на восток. (c) Проведите линию от хвоста вектора, указывающего на восток, к началу вектора, указывающего на север, чтобы получить сумму или результирующий вектор D . Длина стрелки D пропорциональна модулю вектора и составляет 10,3 единицы. Его направление, описываемое как угол относительно востока (или горизонтальной оси) θ , измеренное с помощью транспортира, равно 29,1 0 . Шаг 1. Нарисуйте стрелку, представляющую первый вектор (9 блоков на восток), используя линейку и транспортир .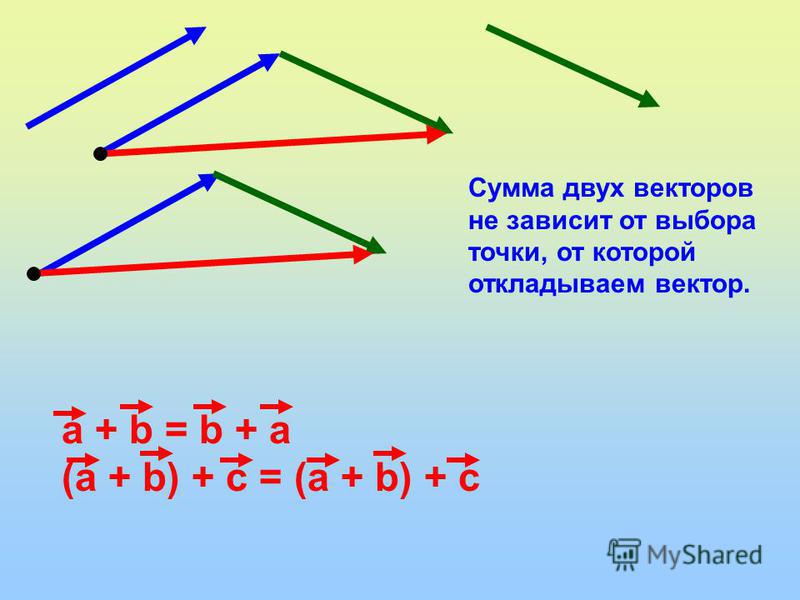
Шаг 2. Теперь нарисуйте стрелку, представляющую второй вектор (5 кварталов на север). Поместите конец второго вектора в начало первого вектора .
Рисунок 6.Шаг 3. Если имеется более двух векторов, продолжайте этот процесс для каждого добавляемого вектора. Обратите внимание, что в нашем примере у нас есть только два вектора, поэтому мы закончили размещать стрелки от начала до конца .
Шаг 4. Проведите стрелку от хвоста первого вектора к началу последнего вектора . Это результат или сумма других векторов.
Рисунок 7. Шаг 5. Чтобы получить величину равнодействующей, измерьте ее длину линейкой. (Обратите внимание, что в большинстве вычислений мы будем использовать теорему Пифагора для определения этой длины. )
)
Шаг 6. Чтобы получить направление равнодействующей, измерьте угол, который она образует с системой отсчета, используя транспортир. (Обратите внимание, что в большинстве расчетов мы будем использовать тригонометрические отношения для определения этого угла.)
Точность графического сложения векторов ограничена только точностью, с которой могут быть выполнены чертежи, и точностью измерительных инструментов. Это справедливо для любого количества векторов.
Пример 1. Графическое добавление векторов методом «голова к хвосту»: женщина на прогулке
Используйте графический метод сложения векторов, чтобы найти полное перемещение человека, который проходит следующие три пути (перемещения) по плоскому полю. Сначала она проходит 25,0 м в направлении 49,0° к северу от востока. Затем она проходит 23,0 м в направлении 15,0° к северо-востоку. Наконец, она поворачивается и проходит 32,0 м в направлении 68,0° к югу от востока.
Стратегия
Представьте каждый вектор смещения графически со стрелкой, обозначив первый $$\vec{\text{A}}$$, второй $$\vec{\text{B}}$$ и третий $$\vec{\text{C}}$$, делая длины пропорциональными расстоянию и направлениям, указанным относительно линии восток-запад. Описанный выше прямой метод позволяет определить величину и направление результирующего смещения, обозначаемого $$\vec{\text{R}}$$.
Решение
(1) Нарисуйте три вектора смещения.
Рисунок 8.(2) Разместите векторы от начала до конца, сохранив их первоначальную величину и направление.
Рис. 9.(3) Нарисуйте результирующий вектор $$\vec{\text{R}}$$.
Рисунок 10. (4) Используйте линейку для измерения величины $$\vec{\text{R}}$$ и транспортир для измерения направления $$\vec{\text{R}} $$. Хотя направление вектора можно указать разными способами, проще всего измерить угол между вектором и ближайшей горизонтальной или вертикальной осью.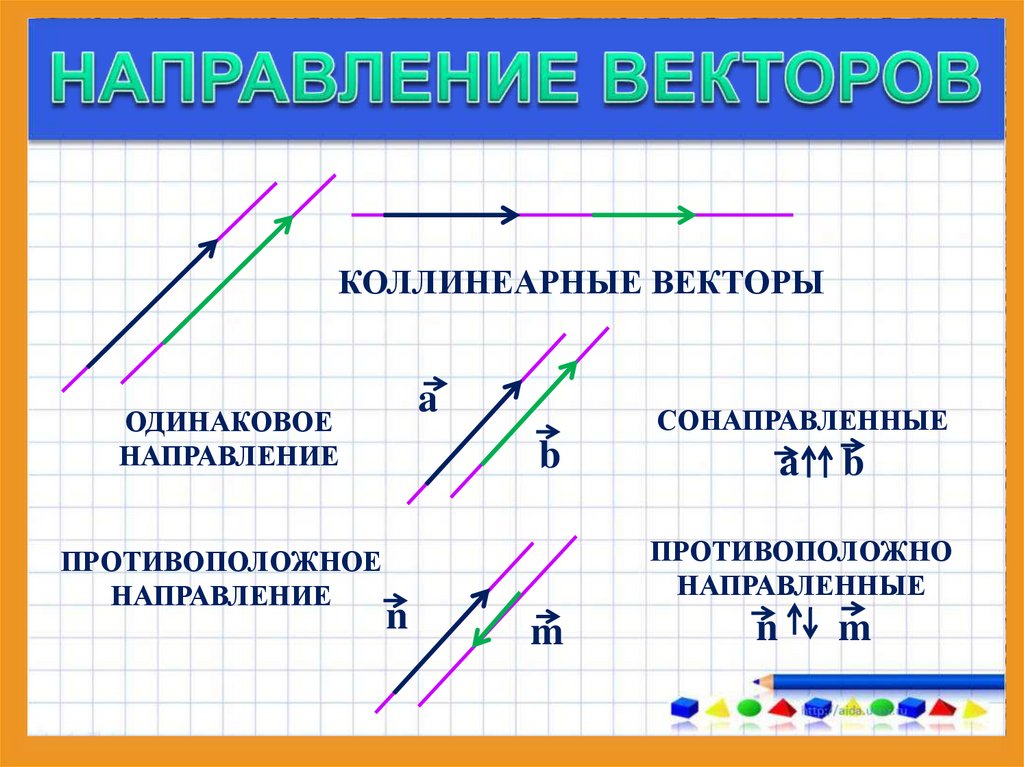 Поскольку результирующий вектор находится к югу от оси, направленной на восток, мы переворачиваем транспортир вверх ногами и измеряем угол между осью, направленной на восток, и вектором.
Поскольку результирующий вектор находится к югу от оси, направленной на восток, мы переворачиваем транспортир вверх ногами и измеряем угол между осью, направленной на восток, и вектором.
В этом случае видно, что полное смещение R имеет величину 50,0 м и лежит в направлении 7,0° к югу от востока. Используя его величину и направление, этот вектор можно выразить как R = 50,0 м и θ = 7,0° к югу от востока.
Обсуждение
Графический метод сложения векторов «голова к хвосту» работает для любого количества векторов. Также важно отметить, что результирующая не зависит от порядка добавления векторов. Следовательно, мы можем добавлять векторы в любом порядке, как показано на рис. 12, и все равно получим то же решение.
Рисунок 12. Здесь мы видим, что при добавлении одних и тех же векторов в другом порядке результат будет тот же. Эта характеристика верна в любом случае и является важной характеристикой векторов. Сложение векторов коммутативно . Векторы можно добавлять в любом порядке.
Эта характеристика верна в любом случае и является важной характеристикой векторов. Сложение векторов коммутативно . Векторы можно добавлять в любом порядке.
[латекс]\vec{\text{A}}+\vec{\text{B}}=\vec{\text{B}}+\vec{\text{A}}.[/latex]
(Это верно и для сложения обычных чисел — вы получите тот же результат, если сложите 2+3 или 3+2 , например).
Вычитание векторов — это прямое расширение сложения векторов. Чтобы определить вычитание (скажем, мы хотим вычесть $$\vec{\text{B}}$$ из $$\vec{\text{A}}$$, записанного $$\vec{\text{A}}- \vec{\text{B}}$$, мы должны сначала определить, что мы подразумеваем под вычитанием. отрицательных вектора $$\vec{\text{B}}$$ определяется как $$-\ vec{\text{B}}$$, то есть графически отрицательное значение любого вектора имеет ту же величину, но противоположное направление , как показано на рисунке 13. Другими словами, $$\vec{\text{B}}$$ имеет ту же длину, что и $$-\vec{\text{B}}$$, но указывает на противоположное направление.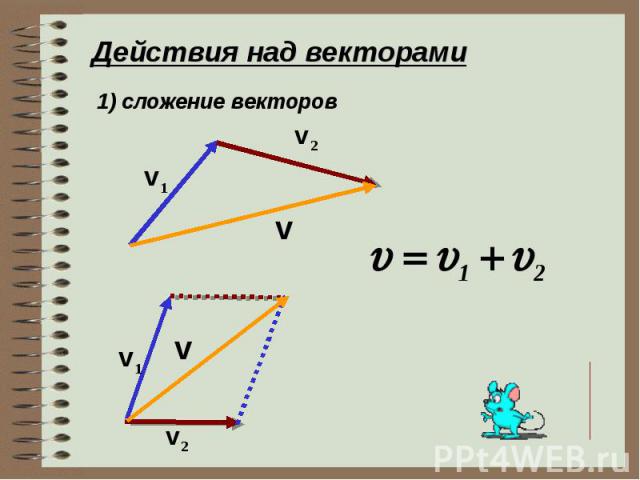 По сути, мы просто переворачиваем вектор так, чтобы он указывал в противоположном направлении.
По сути, мы просто переворачиваем вектор так, чтобы он указывал в противоположном направлении.
Вычитание 9Затем 0038 вектора $$\vec{\text{B}}$$ из вектора $$\vec{\text{A}}$$ просто определяется как сложение $$-\vec{\text{ B}}$$ в $$\vec{\text{A}}$$. Обратите внимание, что вычитание вектора — это добавление отрицательного вектора. Порядок вычитания не влияет на результат.
$$\vec{\text{A}}-\vec{\text{B}}=\vec{\text{A}}+(-\vec{\text{B}})$$
Это аналогично вычитанию скаляров (где, например, 5-2=5+(-2) ). Опять же, результат не зависит от порядка, в котором производится вычитание. Когда векторы вычитаются графически, используются описанные выше методы, как показано в следующем примере.
Пример 2: графическое вычитание векторов: женщина, плывущая на лодке
Женщина, плывущая на лодке ночью, следует указаниям к причалу. Инструкции гласили: сначала пройти 27,5 м в направлении 66,0° к северо-востоку от ее текущего местоположения, а затем пройти 30,0 м в направлении 112° к северу от востока (или 22,0° к западу от севера). Если женщина совершит ошибку и поедет в направлении , противоположном , на второй этап пути, где она окажется? Сравните это место с расположением дока.
Рисунок 14.Стратегия
Мы можем представить первый этап пути вектором $$\vec{\text{A}}$$, а второй этап пути вектором $$ \vec{\text{B}}$$. Док расположен в месте $$\vec{\text{A}}+\vec{\text{B}}$$. Если женщина по ошибке едет в направлении , противоположном , для второго этапа путешествия, она проедет расстояние $$\vec{\text{B}}$$ (30,0 м) в направлении 180°-112°.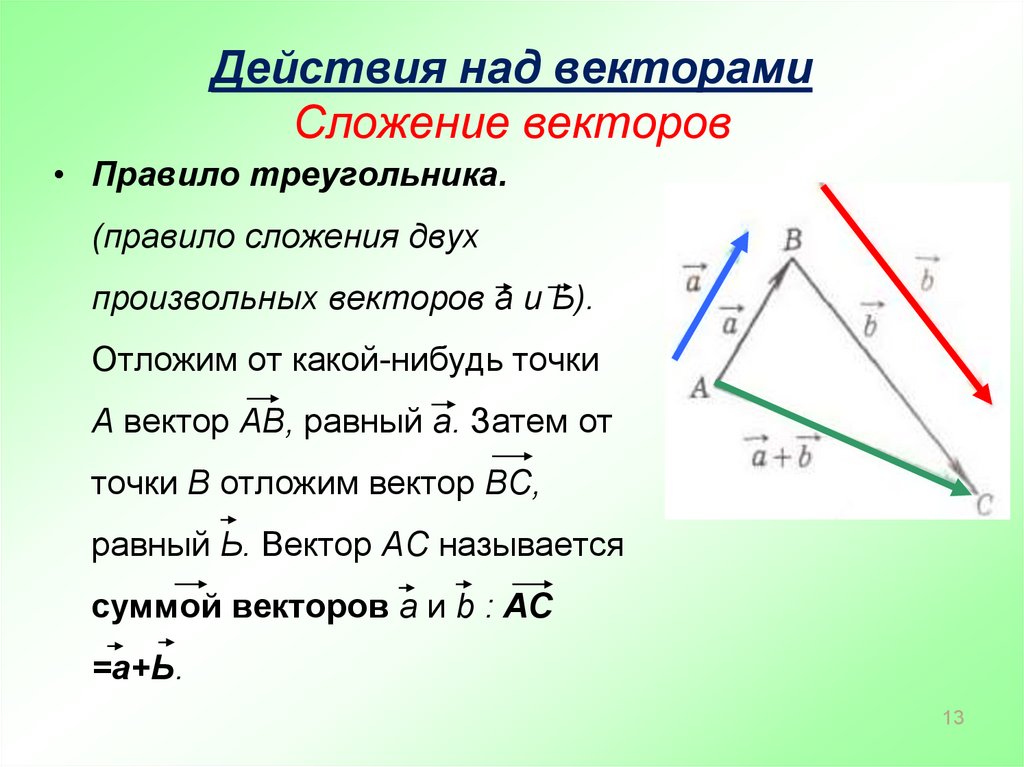 = 68 ° к югу от востока. Мы представляем это как $$-\vec{\text{B}}$$, как показано ниже. Вектор $$-\vec{\text{B}}$$ имеет ту же величину, что и $$\vec{\text{B}}$$, но имеет противоположное направление. Таким образом, она окажется в месте $$\vec{\text{A}}+(-\vec{\text{B}})$$ или $$\vec{\text{A}}-\ vec{\text{B}}$$.
= 68 ° к югу от востока. Мы представляем это как $$-\vec{\text{B}}$$, как показано ниже. Вектор $$-\vec{\text{B}}$$ имеет ту же величину, что и $$\vec{\text{B}}$$, но имеет противоположное направление. Таким образом, она окажется в месте $$\vec{\text{A}}+(-\vec{\text{B}})$$ или $$\vec{\text{A}}-\ vec{\text{B}}$$.
Выполним сложение векторов, чтобы сравнить положение дока, $$\vec{\text{A}}+\vec{\text{B}}$$, с положением, в котором по ошибке приходит женщина, $$\vec{\text{A}}+(-\vec{\text{B}})$$.
Решение
(1) Чтобы определить место, куда случайно попала женщина, начертите векторы $$\vec{\text{A}}$$ и $$-\vec{\text{B}} $$.
(2) Разместите векторы лицом к хвосту.
(3) Нарисуйте результирующий вектор $$\vec{\text{R}}$$. 9\prime$$:
Рис. 17.В данном случае R =52,9 м и θ=90,1° к северу от востока.
Мы видим, что женщина окажется на значительном расстоянии от пристани, если она отправится в противоположном направлении на второй этап поездки.
Обсуждение
Поскольку вычитание вектора аналогично сложению вектора с противоположным направлением, графический метод вычитания векторов работает так же, как и сложение.
Если бы мы решили пройти в три раза большее расстояние на первом этапе пути, рассматриваемого в предыдущем примере, то мы бы прошли 3 × 27,5 м , или 82,5 м, в направлении 66,0° к северу от востока. Это пример умножения вектора на положительный скаляр . Обратите внимание, что величина меняется, но направление остается прежним.
Если скаляр отрицательный, то умножение вектора на него изменяет величину вектора и дает новому вектору в противоположном направлении . Например, если умножить на -2, величина удвоится, но изменится направление. Мы можем обобщить эти правила следующим образом: когда вектор $$\vec{\text{A}}$$ умножается на скаляр c ,
- величина вектора становится абсолютной величиной c $$\vec{\text{A}}$$,
- , если c положительно, направление вектора не меняется,
- , если c отрицательно, направление меняется на противоположное.

В нашем случае c=3 и A=27,5 м . Векторы умножаются на скаляры во многих ситуациях. Обратите внимание, что деление является обратным умножению. Например, деление на 2 равносильно умножению на значение (1/2). Правила умножения векторов на скаляры такие же, как и при делении; просто рассматривайте делитель как скаляр от 0 до 1.
В приведенных выше примерах мы добавляли векторы для определения результирующего вектора. Однако во многих случаях нам нужно будет сделать обратное. Нам нужно будет взять один вектор и найти, какие другие векторы, сложенные вместе, дают его. В большинстве случаев это связано с определением перпендикуляра компоненты одного вектора, например x – и y -компоненты, или компоненты север-юг и восток-запад.
Например, мы можем знать, что общее перемещение человека, идущего по городу, составляет 10,3 квартала в направлении 29,0° к северу от востока, и мы хотим узнать, сколько кварталов ему пришлось пройти на восток и север.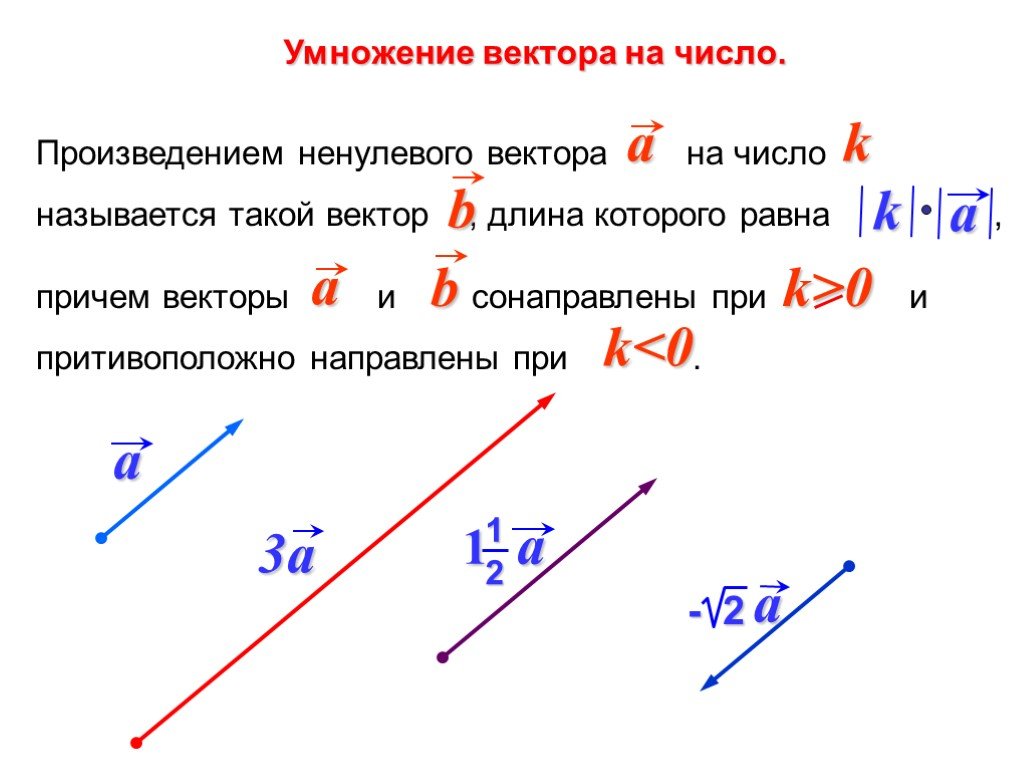 Этот метод называется поиск компонентов (или деталей) смещения в восточном и северном направлениях, и это процесс, обратный процессу, которому следовали, чтобы найти полное перемещение. Это один из примеров нахождения компонентов вектора. В физике есть много приложений, где это может оказаться полезным. Мы скоро увидим это в главе 3.4 Движение снаряда и многое другое, когда мы рассмотрим сил в главе 4 Динамика: законы движения Ньютона. Большинство из них включают поиск компонентов вдоль перпендикулярных осей (например, север и восток), так что задействованы прямоугольные треугольники. Аналитические методы, представленные в главе 3.3 Сложение и вычитание векторов: аналитические методы, идеально подходят для нахождения компонент вектора.
Этот метод называется поиск компонентов (или деталей) смещения в восточном и северном направлениях, и это процесс, обратный процессу, которому следовали, чтобы найти полное перемещение. Это один из примеров нахождения компонентов вектора. В физике есть много приложений, где это может оказаться полезным. Мы скоро увидим это в главе 3.4 Движение снаряда и многое другое, когда мы рассмотрим сил в главе 4 Динамика: законы движения Ньютона. Большинство из них включают поиск компонентов вдоль перпендикулярных осей (например, север и восток), так что задействованы прямоугольные треугольники. Аналитические методы, представленные в главе 3.3 Сложение и вычитание векторов: аналитические методы, идеально подходят для нахождения компонент вектора.
PHET EXPLORATIONS: MAZE GAME
Узнайте о положении, скорости и ускорении на «Арене боли». Используйте зеленую стрелку, чтобы переместить мяч. Добавьте больше стен на арену, чтобы усложнить игру.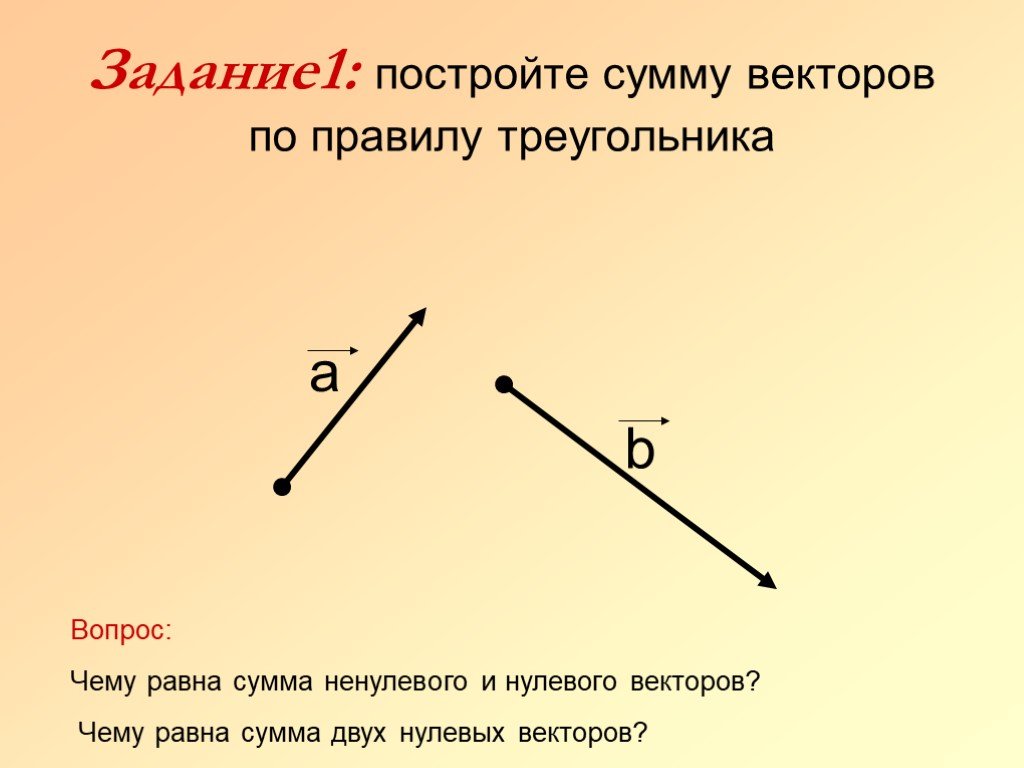 Постарайтесь достичь цели как можно быстрее.
Постарайтесь достичь цели как можно быстрее.
- Графический метод сложения векторов $$\vec{\text{A}}$$ и $$\vec{\text{B}}$$ включает рисование векторов на графике и их сложение с помощью метод «к хвосту». Результирующий вектор $$\vec{\text{R}}$$ определяется таким образом, что $$\vec{\text{A}}+\vec{\text{B}}=\vec{\text{R} }$$. Затем с помощью линейки и транспортира определяются величина и направление $$\vec{\text{R}}$$.
- Графический метод вычитания вектора $$\vec{\text{B}}$$ из $$\vec{\text{A}}$$ включает добавление вектора, противоположного вектору $$\vec{\text{ B}}$$, который определяется как $$-\vec{\text{B}}$$. В этом случае $$\vec{\text{A}}-\vec{\text{B}}=\vec{\text{A}}+(-\vec{\text{B}})=\ vec{\text{R}}$$. Затем обычным образом применяется метод сложения головы к хвосту для получения результирующего вектора $$\vec{\text{R}}$$.
- Сложение векторов равно коммутативным , таким что $$\vec{\text{A}}+\vec{\text{B}}=\vec{\text{B}}+\vec{\text{A} }$$.



 12.2022
12.2022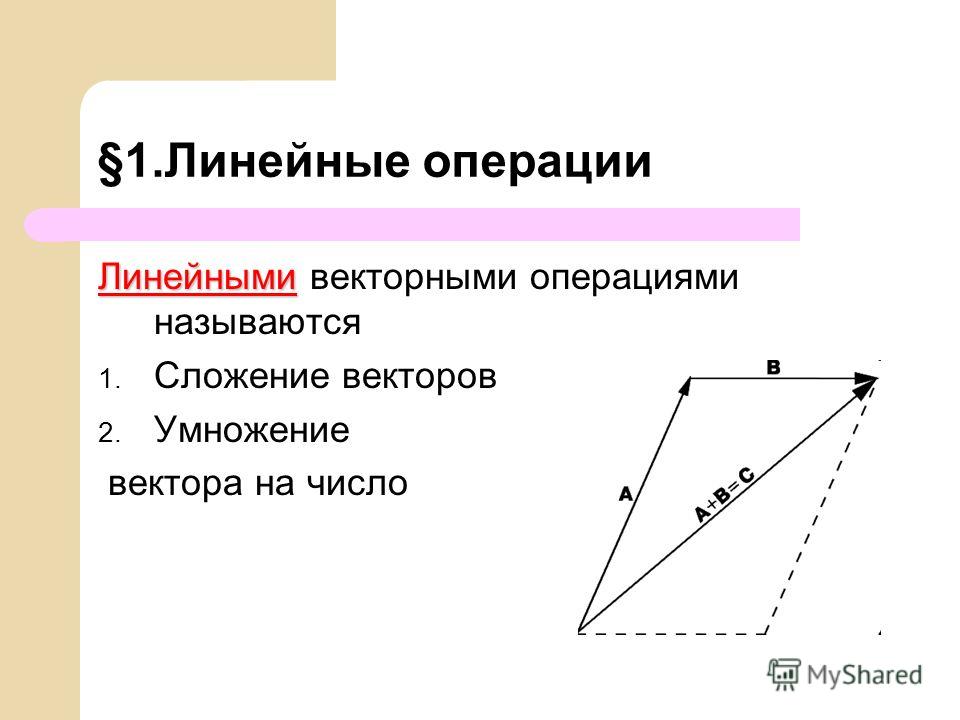 12.2022
12.2022

