применение двоичной системы счисления — двоичная система счисления
Двоичная система счисления — позиционная система счисления с основанием 2, иначе говоря, используются лишь две цифры: 1 и 0 > применение двоичной системы счисления
|
Особенности двоичной системы счисления
Дата Автор ElectricianКомментироватьПросмотров: 10 355
В повседневной жизни мы используем десятичную систему счисления, которая состоит всего лишь из десяти цифр от 0 до 9, а все остальные числа являются комбинацией этих чисел. Данная комбинация получила название позиционной системы. Суть данной системы заключается в том, что число разбивают на части, кратные десяти, и записывают каждую часть на соответствующем месте, считая справа налево. Разберем на примере 365. Эта запись будет иметь следующий вид: где его разбивают на части и в такой же последовательности записывают множители при степенях десяти.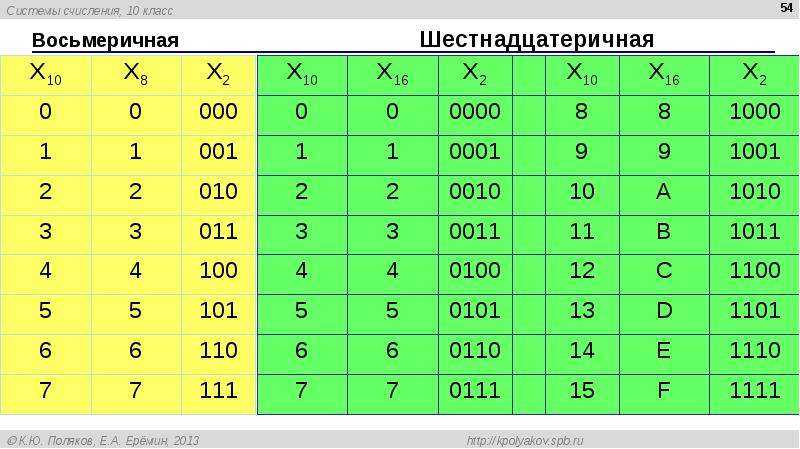
Если мы при построении счетчиков используем триггеры, то нам необходимо учитывать и то, что триггеры могут находится только в двух состояниях – либо единица, либо ноль. Поэтому любое число для них может быть записано только в двоичной системе счисления. По аналогии с десятичной системой, каждое число разбивают на части, которые будут кратны уже не десяти, а двум. Такое выражение будет иметь вид:
Давайте рассмотрим на примере все того же 365 и определим все степени двойки, которые в этом числе могут быть:
20=1; 21=2; 22=4; 23=8; 24=16; 25=32; 26=64; 27= 128; 28=256; 29=512;
Поскольку 29=512 – а это больше чем 365, то мы берем ближайшее меньшее к 365 – а это 28=256. Последовательно отнимая от заданного числа степени двойки получим:
365 — 256(28)=109; 109 — 64(26)=45; 45 – 32(25)=13; 13 – 8(23) =5; 5 – 4(22) =1; 1 – 1(20)=0;
А это значит что:
365=256+64+32+8+4+1 =
То есть запись в позиционной системе будет иметь вид:
101101101
Проще переход к двоичной системе можно произвести еще таким способом:
Заданное число делят на два.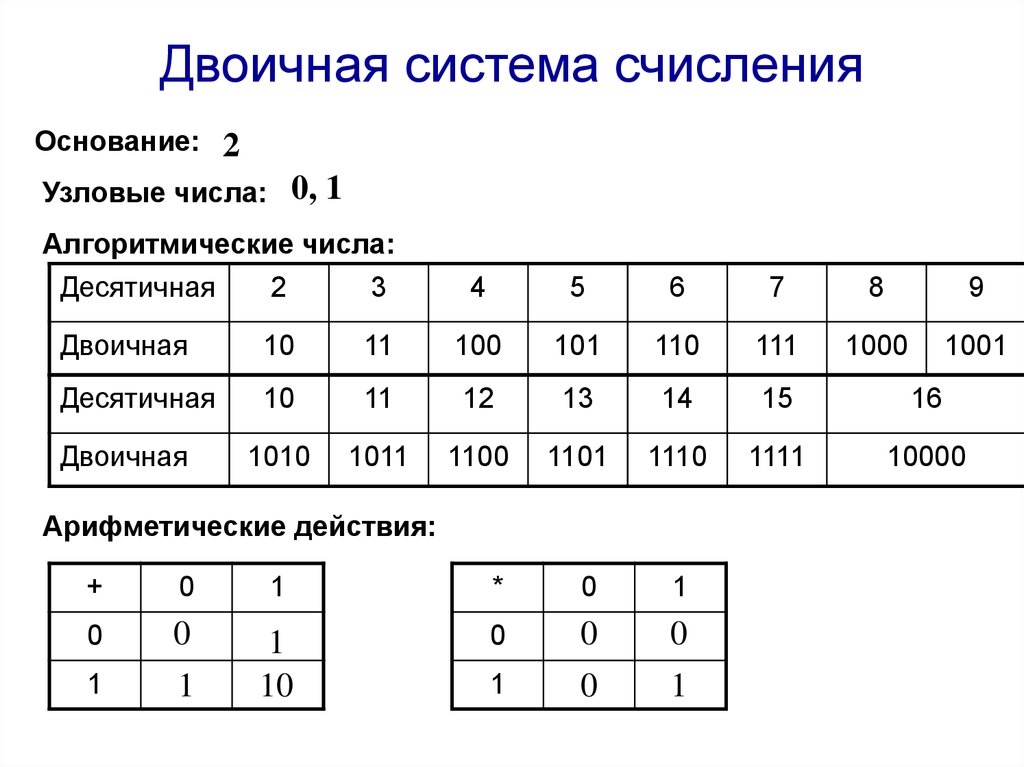 Если оно получается непарным, то от него отнимают единицу, которую записывают справа от числа за вертикальной чертой как показано выше. После того, как оно стало парным (365-1=364), его делят на два и результат записывают ниже заданного (364:2=182). Поскольку 182 парное, то справа записываем ноль и снова делим на два. Подобные действия проделывают до конца, а потом выписывают единицы и нули в направлении снизу вверх и получают 101101101.
Если оно получается непарным, то от него отнимают единицу, которую записывают справа от числа за вертикальной чертой как показано выше. После того, как оно стало парным (365-1=364), его делят на два и результат записывают ниже заданного (364:2=182). Поскольку 182 парное, то справа записываем ноль и снова делим на два. Подобные действия проделывают до конца, а потом выписывают единицы и нули в направлении снизу вверх и получают 101101101.
Для перехода к десятичной системе счисления над каждой цифрой числа, записанного в двоичной системе, сверху надписывают справа налево степень двойки:
1 0 1 1 0 1 1 0 1
Подсчитывают степени соответствующие единице и суммируют результат:
28+26+25+23+22+20 = 256+ 64+32+8+4+1 =365
Каждый разряд двоичного числа называет «бит». В нашем случае использовано девять бит. Биты группируются в старшие разряды. Так, восемь битов составляют «байт». Число, состоящее из байтов и битов называют «словом». Для записи больших чисел удобно использовать так называемую двоично – десятичную систему. Для осуществления этого каждую цифру в десятичной системе записывают в двоичном коде отдельно: 3 – 0011; 6 – 0110; 5 – 0101. Итак, 365 в двоично – десятичной системе будет иметь вид:
Число, состоящее из байтов и битов называют «словом». Для записи больших чисел удобно использовать так называемую двоично – десятичную систему. Для осуществления этого каждую цифру в десятичной системе записывают в двоичном коде отдельно: 3 – 0011; 6 – 0110; 5 – 0101. Итак, 365 в двоично – десятичной системе будет иметь вид:
365 – 0011 0110 0101
При этом понадобится не девять бит, а двенадцать, но в таком виде гораздо удобней осуществлять перевод из одной системы в другую.
Posted in СхемотехникаДвоичная система счисления | Почему компьютер использует двоичный номер, логические ворота
Двоичная система счисления
Компьютерная система понимает только двоичную систему счисления. И поэтому нам нужно общаться с компьютером только с помощью двоичного кода
. Двоичный код также попеременно называют машинным языком или машинным кодом. В двоичной системе счисления все числа представляются с использованием только двух числовых чисел: либо 0 (ноль), либо 1 (единица).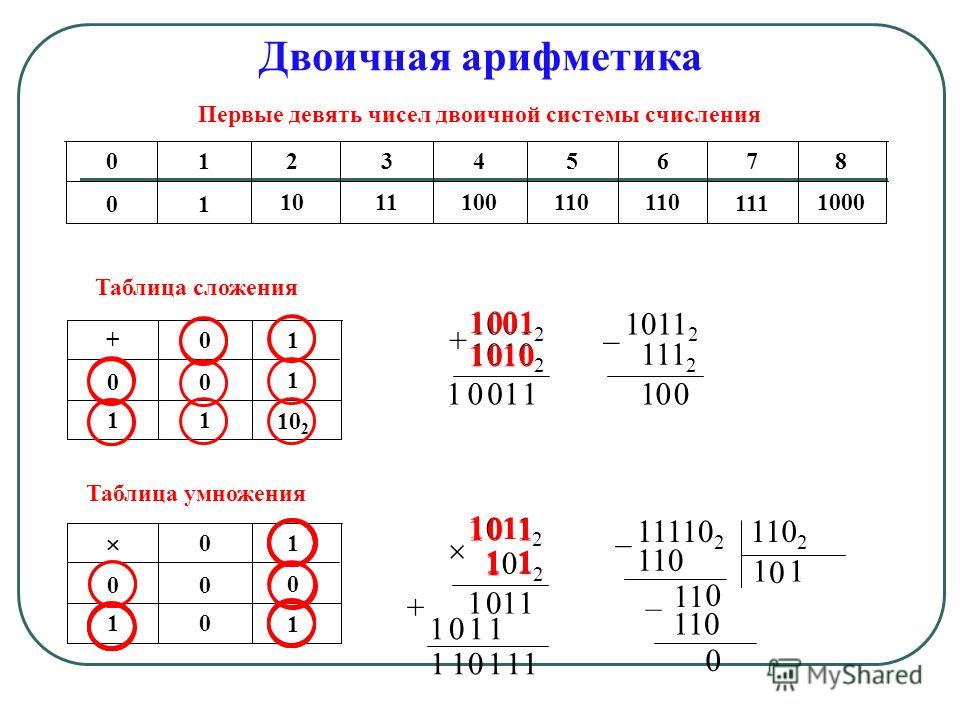
Все компьютерные программы, написанные на любом языке программирования высокого уровня, должны быть сначала преобразованы в машинный код в двоичном формате, который может быть непосредственно выполнен центральным процессором компьютера — ЦП.
В этом уроке мы подробно обсудим и найдем ответы на некоторые важные темы в двоичной системе счисления.
Эти вопросы включают в себя: почему компьютер понимает только двоичный код, почему двоичный код состоит только из двух чисел: 0 (ноль) и 1 (единица), различные типы систем счисления, что такое логические вентили и булева алгебра.
Как работает компьютер?
Система двоичных чисел
Содержание
Что такое системы счисления?
Бинарные номера Система
Как данные, представленные в двоичном
Двоичные числа и логические ворота
Типы чисел систем
Почему компьютер использует бинарные номера?
Двоичный код и двоичные единицы
Двоичная и булева алгебра
Система двоичных чисел и логические вентили
Вопросы для интервью
- Что такое двоичная система счисления?
- Какие существуют типы систем счисления?
- Почему компьютерная система использует только двоичную систему счисления?
- Почему компьютерные программы компилируются?
- Как данные представлены в двоичном виде?
- Двоичный код и двоичные единицы
- Двоичные числа и логические элементы
- Двоичное число и булева алгебра
Изучение информатики в настоящее время считается одним из лучших вариантов карьеры.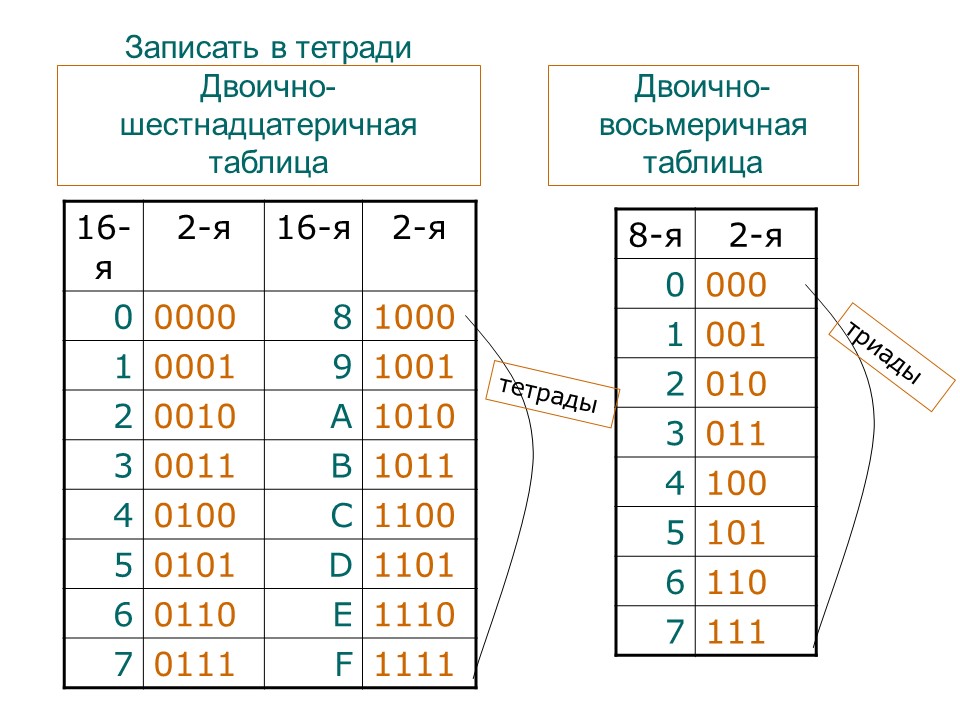 Карьера в области компьютерных наук дает возможность не только работать с некоторыми первоклассными корпоративными компаниями, но и работать в качестве предпринимателя.
Карьера в области компьютерных наук дает возможность не только работать с некоторыми первоклассными корпоративными компаниями, но и работать в качестве предпринимателя.
Карьера в области компьютерных наук также дает вам возможность ускорить свою карьеру с отличным финансовым вознаграждением.
Что такое система счисления?
Мы все знакомы с широко используемой числовой системой счисления (десятичной системой счисления, в которой используются цифры от 0 до 9), которую мы все используем в нашей повседневной жизни.
Однако существует множество систем счисления, которые можно использовать при общении с компьютерной системой и которые поддерживаются большинством языков программирования.
Система счисления — это система, которой следует определять набор значений, используемых для измерения количества. С помощью системы счисления мы можем выразить количественное измерение любого объекта.
Например, чтобы выразить вес 75 кг, возраст как 26 лет, расстояние как 100 км и так далее.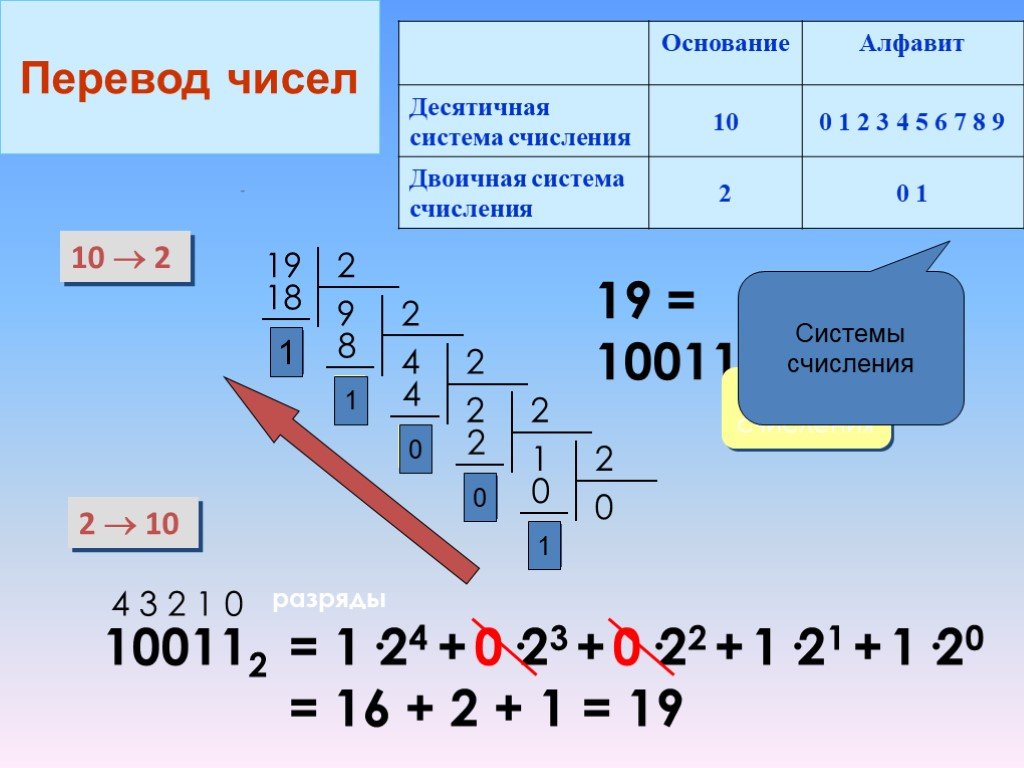
Однако из-за аппаратной архитектуры компьютерной системы обычно используемая десятичная система счисления не подходит.
Из-за ограничений аппаратной архитектуры компьютера десятичная система не может быть реализована для функционирования компьютерной системы.
Типы системы счисления
Система счисления определяется как система, которая позволяет представить любое число с помощью набора комбинаций символов, цифр и алфавитов. Центральный процессор компьютерной системы может интерпретировать и выполнять только инструкции машинного кода в двоичном формате.
И поэтому весь программный код на любом языке должен быть преобразован в машинный код в двоичном виде с помощью компилятора. Однако большинство языков программирования поддерживают эти четыре системы счисления при написании программного кода.
Двоичная система счисления
В двоичной системе счисления используются только две цифры: 0 и 1 . В двоичной системе счисления любое число представляется двумя цифрами: 0 и 1.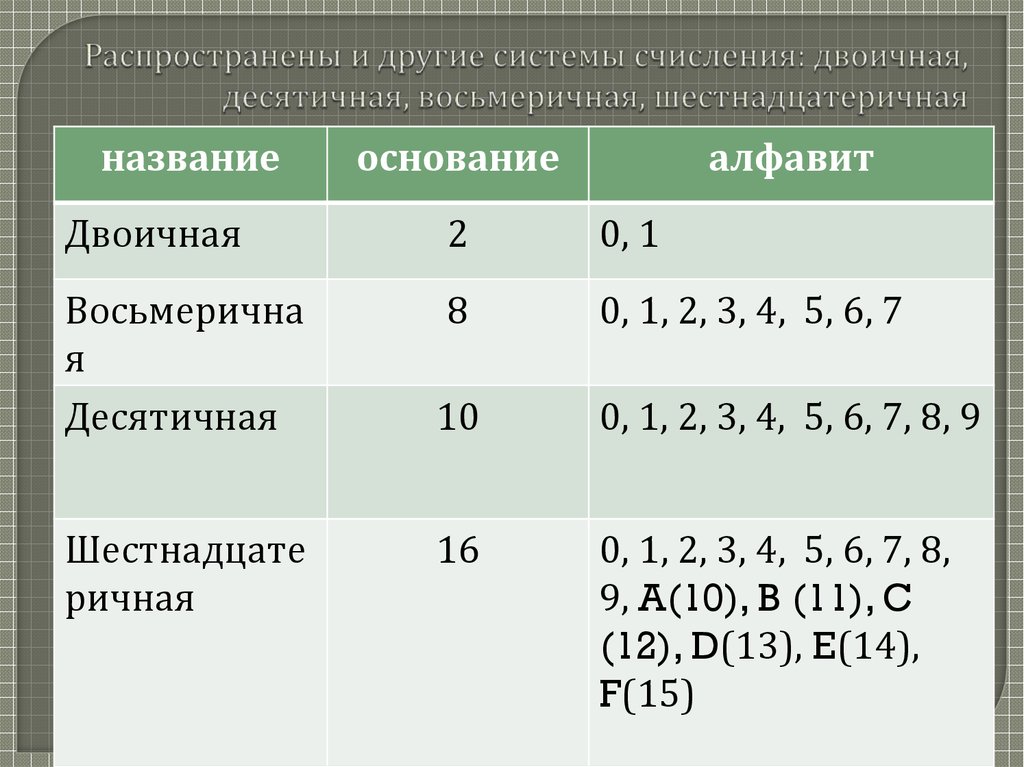
Двоичная система счисления имеет основание 2, потому что в ней всего две цифры для представления любого числа.
Восьмеричная система счисления
Восьмеричная система счисления использует только восемь ( 8 ) цифр от 0 до 7 для представления любого числа. В восьмеричной системе счисления любое число (значение) может быть представлено комбинацией любых 8 цифр (0,1,2,3,4,5,6, 7).
Восьмеричная система счисления имеет основание 8, поскольку в ней всего 8 цифр для представления любого числа
Десятичная система счисления
Десятичная система счисления является наиболее часто используемой системой счисления, в которой используются десять (10) цифр от 0 до 9.для представления любого числа.
В десятичной системе любое число может быть представлено комбинацией 10 цифр (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). Десятичная система счисления имеет основание 10, потому что в ней есть 10 цифр для представления любого числа
.Шестнадцатеричная система счисления
Шестнадцатеричная система счисления имеет шестнадцать ( 16 ) буквенно-цифровых значений от 0 до 9 и от A до F для представления любого числа.
Шестнадцатеричная система счисления использует девять ( 10 ) цифр ( 0, 1, 2, 3, 4, 5, 6, 7, 8, 9) и семь ( 6 ) алфавитов ( A, B, C, D, E, F ) для представления любого числа в этой системе счисления.
Шестнадцатеричная система счисления имеет основание 16, так как использует 16 буквенно-цифровых значений.
Двоичная система счисления
В математике и цифровой электронике двоичное число — это число, выраженное с использованием двоичной системы счисления или системы счисления с основанием 2.
Двоичная система счисления представляет любые числовые значения, используя комбинацию только двух возможных значений, то есть 0 (ноль) и 1 (единица). В цифровой электронике это лучше всего подходит для представления двух состояний: ВКЛ или ВЫКЛ.
Двоичная система счисления использует только две цифры для представления любого числа . Из-за простой реализации в цифровых электронных схемах с использованием логических вентилей двоичная система используется внутри почти всех современных компьютеров и компьютерных устройств.
Таким образом, компьютерная система представляет собой цифровое электронное устройство, которое может понимать и выполнять программные инструкции, передаваемые в двух состояниях: ВКЛ или ВЫКЛ. Эти два состояния лучше всего можно представить с помощью двоичной системы счисления.
Почему компьютер использует двоичную систему счисления
Компьютеры были изобретены благодаря их высокой вычислительной мощности. Компьютеры используются для обработки больших объемов данных с молниеносной скоростью. Компьютерная система состоит из ряда компонентов.
Каждый из этих компонентов выполняет определенную задачу. Одним из наиболее важных компонентов компьютерной системы является ЦП.
ЦП (центральный процессор) в компьютерной системе отвечает за выполнение всех арифметических вычислений и логических решений.
ЦП также называют микропроцессором, микросхемой процессора или просто процессором.
Микросхема процессора состоит из миллионов крошечных электронных компонентов, называемых транзисторами. Транзистор является основным строительным блоком для всех цифровых электронных устройств, включая компьютеры.
Транзистор является основным строительным блоком для всех цифровых электронных устройств, включая компьютеры.
Транзистор изготовлен из кремния, полупроводникового материала. Транзисторы используются в качестве микропереключателя, который может быть либо включен, либо выключен.
Процессор компьютера, который является мозгом компьютерной системы, состоит из миллионов этих транзисторов.
И, следовательно, процессор компьютера может понимать и выполнять инструкции, передаваемые только в виде двух состояний: включено или выключено.
И, следовательно, для связи с компьютерной системой нам нужна система счисления, способная представить любое число, используя только две цифры.
Двоичная система счисления идеально соответствует этому условию, потому что в двоичной системе счисления мы используем только две цифры: 0 и 1.
В двоичном формате включенное состояние представлено 1 (единица), а выключенное состояние представлено как 0 (ноль).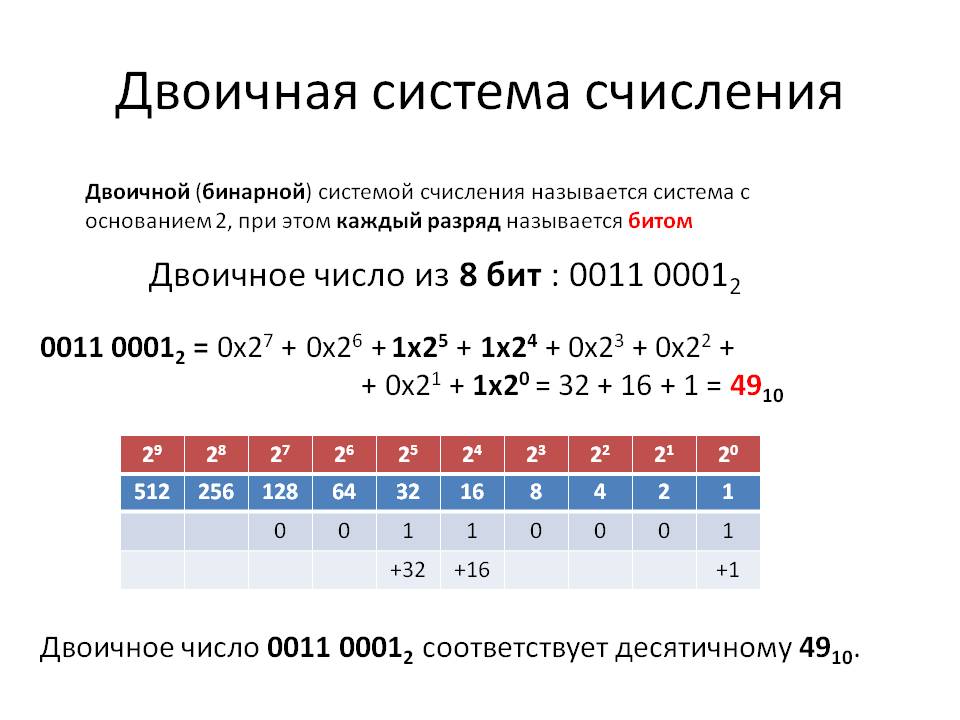
И по этой причине архитектура компьютера поддерживает двоичную систему счисления, и все компьютерные программы должны быть сначала скомпилированы в инструкции машинного кода в двоичном формате, которые может выполнять ЦП компьютера.
Почему компьютер использует двоичную систему счисления
Как данные представлены в двоичном виде
Компьютер хранит всю информацию и программные данные только в двоичном цифровом виде. Это означает, что все данные, будь то текст, фотографии, аудио, видео или что-то еще, состоят только из наборов единиц и нулей.
Однако операционная система представляет эти данные в графическом формате в графическом интерфейсе, который удобочитаем.
Двоичный код и двоичные единицы
Поскольку ЦП компьютера может выполнять только инструкции машинного кода и работать с данными в двоичном формате, весь программный код и данные должны быть представлены в двоичной форме.
Процессор обрабатывает данные, и результат этой операции может быть отправлен либо на устройство вывода (монитор, принтер и т. д.), либо сохранен в постоянном запоминающем устройстве для использования в будущем.
д.), либо сохранен в постоянном запоминающем устройстве для использования в будущем.
Фундаментальным строительным блоком цифровой информации является двоичная цифра или бит, который представляет одно состояние 0 (ноль) или 1 (единица). Это представлено битом в памяти компьютера, который является наименьшей единицей памяти.
Для представления большого объема данных биты могут быть организованы в группы по четыре, восемь, шестнадцать, 32 или 64 бита, называемые полубайтами/полубайтами, байтами, словами, длинными словами и очень длинными словами соответственно. Они называются двоичными единицами измерения.
Компьютеры распознают только два дискретных состояния: включено и выключено. Эти состояния могут быть представлены двумя цифрами: 0 и 1. Каждый 0 или 1 называется битом в двоичной системе. Бит — это наименьшая единица данных, которую может обработать компьютер.
A Бит — это сокращение от двоичной цифры. Двоичная система имеет основание 2 с двумя цифрами (0 и 1). Используя комбинации нулей и единиц, мы можем представлять большие числа.
Используя комбинации нулей и единиц, мы можем представлять большие числа.
Двоичные числа и логические элементы
Компьютерная система выполняет различные задания, выполняя инструкции программы в соответствии с логикой программы. ЦП — это основной компонент внутри компьютерной системы, который выполняет все арифметические вычисления, а также логические операции.
ЦП компьютера отвечает за выполнение как арифметических вычислений, так и логических операций. Центральный процессор состоит из миллионов крошечных схем, называемых транзисторами, которые могут функционировать как микропереключатели.
Логические элементы построены с использованием транзисторов внутри микросхемы процессора, в основном используемых ЦП для выполнения логических операций.
Компьютеры — это цифровые машины, а логические элементы — основные компоненты цифровой электроники. Логические элементы используются для создания цифровых схем и даже сложных интегральных схем.
ЦП компьютера состоит из миллионов этих крошечных схем, которые позволяют ЦП выполнять логические операции.
Процессор работает, реагируя на ввод 0 и 1 определенным образом, а затем возвращая вывод на основе решения.
Само решение происходит в схеме, называемой логическим вентилем, для каждого из которых требуется как минимум один транзистор с входами и выходами, расположенными по-разному для разных операций.
Двоичные числа и логическая алгебра
Булева алгебра в математике и математической логике — это раздел алгебры, в котором значения переменных являются значениями истинности ( true и false ) и обычно обозначается в двоичном формате 1 и 0 соответственно.
Булева алгебра была введена Джорджем Булем в 1854 году, британским математиком. Булева алгебра сыграла фундаментальную роль в развитии цифровой электроники.
В алгебре мы используем десятичные числа, тогда как в булевой алгебре используются значения истинности, истина (1) и ложь (0).
Логический вентиль — это крошечная схема, используемая в процессорах для принятия логического решения, основанного на булевой алгебре.
Булева алгебра используется для анализа и упрощения цифровых (логических) схем. Он использует только двоичные числа, то есть 0 и 1. Его также называют двоичной алгеброй или логической алгеброй.
Изучение основ информатики и программирования.
Онлайн-курс — Udemy
Это наиболее полный и уникальный онлайн-курс C по компьютерным наукам и основам программирования , который даст вам глубокое понимание наиболее важных фундаментальных концепций информатики и программирования.
Что такое двоичный код? Понимание того, как компьютеры используют Base 2
Двоичные числа необходимы для вычислений, поскольку все данные, которые проходят через ваш телефон или компьютер, представлены в двоичном виде. Но поскольку люди естественным образом не используют двоичную систему счисления, ее может быть трудно понять.
Давайте рассмотрим, что такое двоичный файл. К концу вы узнаете, чем двоичная система отличается от нашей обычной системы счета, как работают двоичные числа, что означают «32-битные» и «64-битные» и почему все это имеет значение.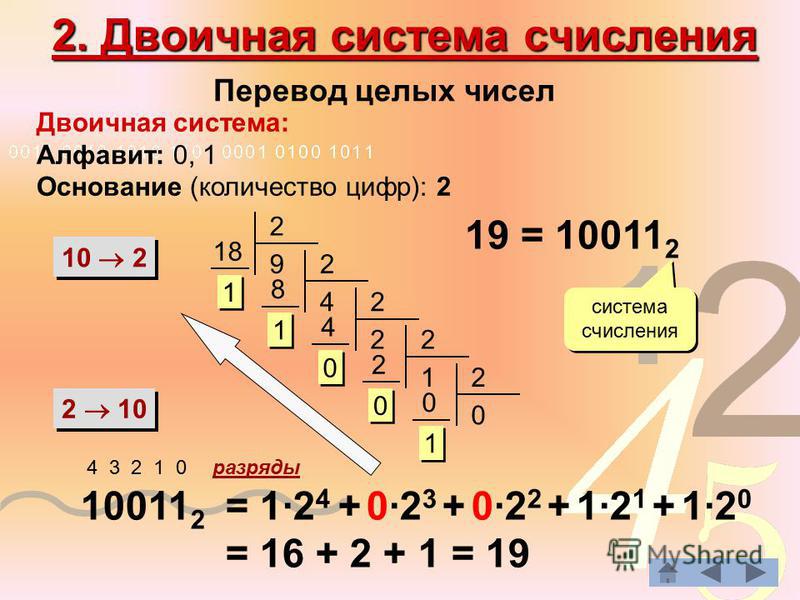
Понимание базы 10: десятичная дробь
Прежде чем мы приступим к изучению двоичной системы, полезно рассмотреть систему счисления, используемую в современном мире. Десятичная система, или основание 10, — это система, в которой каждое возможное место в числе может быть одной из 10 цифр.
Чтобы выразить однозначное число в десятичном виде, мы используем цифры от 0 до 9. Чтобы подняться выше, мы добавляем еще один разряд, дойдя до 10, 100, 1000 и выше. Например, запись числа 1972 в разбивке представляет следующее:
1,000 | 100 | 10 | 1 |
|---|---|---|---|
1 | 9 | 7 | 2 |
Таким образом, число 1972 состоит из 1х1000, 9х100, 7х10 и 2х1. Поскольку вы использовали эту систему с детства, это то, как вы думаете о числах.
Поскольку вы использовали эту систему с детства, это то, как вы думаете о числах.
Binary — это другой подход к числам: меняется не значение, а то, как мы его представляем.
Счет по основанию 2 с двоичным кодом
Двоичная система счисления использует только два числа для каждого разряда: 0 и 1. Двоичная система также известна как «основание 2». В двоичном формате для представления большего числа, чем 1, вам нужно второе место.
В то время как каждый дополнительный разряд в десятичной системе умножается на 10, каждый дополнительный разряд в двоичной системе умножается на 2. Таким образом, когда вы добавляете единицы в двоичной системе, они представляются следующим образом, считая справа налево от первых 10 разрядов:
512, 256, 128, 64, 32, 16, 8, 4, 2, 1
Другими словами, самое правое значение в двоичном числе показывает, сколько в нем единиц. Цифра слева от нее представляет, сколько двоек, следующая сколько четверок и так далее.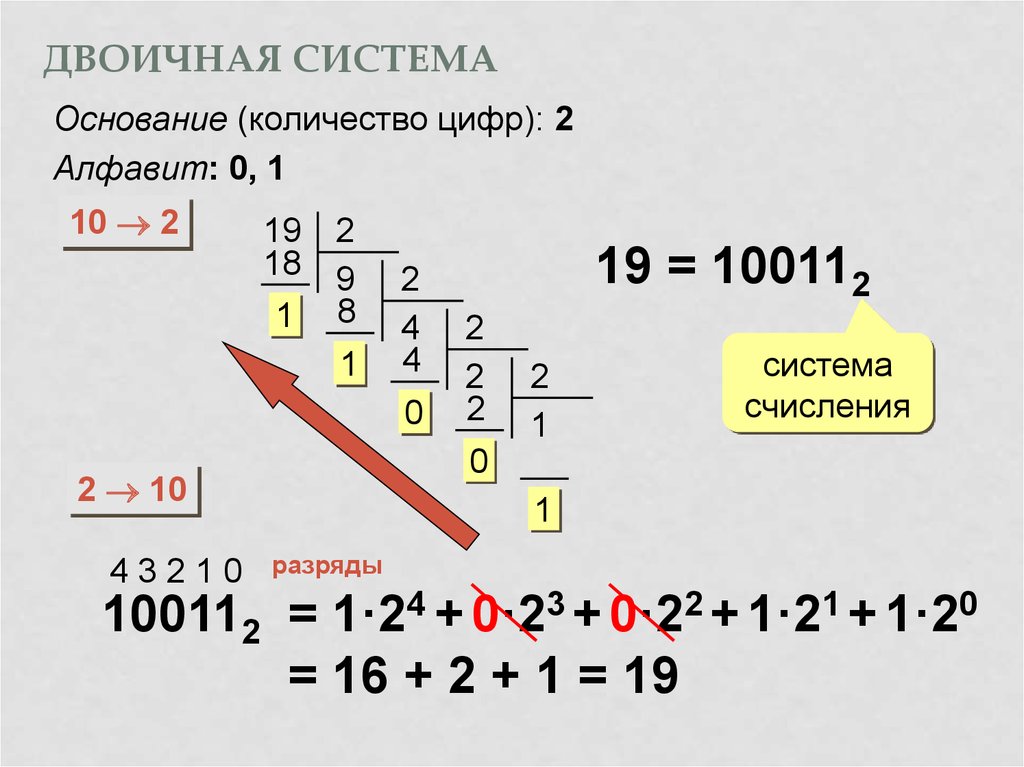 Эти значения могут показаться знакомыми, поскольку варианты хранения доступны на телефонах и других носителях — вот откуда они берутся.
Эти значения могут показаться знакомыми, поскольку варианты хранения доступны на телефонах и других носителях — вот откуда они берутся.
Запись чисел в двоичном формате очень помогает их пониманию, так как это не естественный способ счета для нас. См. приведенную ниже диаграмму, иллюстрирующую двоичный счет:
Decimal Value | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 319 | 319 | 1 | |||||||||||||||||||||||
2 | 1 | ||||||||||||||||||||||||
3 | 1 930185 0315 1 | ||||||||||||||||||||||||
4 | 1 | ||||||||||||||||||||||||
5 | 1 | 1 | |||||||||||||||||||||||
6 | 1 | 1 | |||||||||||||||||||||||
7 | 1 | 1 | 1 | ||||||||||||||||||||||
8 | 1 | 55 9 | 1 | 1 | |||||||||||||||||||||
10 | 1 | 1 | |||||||||||||||||||||||
11 | 9 00315 | 1 | 1 | ||||||||||||||||||||||
12 | 1 | 1 | |||||||||||||||||||||||
13 | 1 | 1 | 02 9 | 5 9503551 | 1 | 1 | |||||||||||||||||||
15 | 1 | 1 | 1 | 1 | |||||||||||||||||||||
16 | 0318 | 1 | |||||||||||||||||||||||
17 | 1 | 1 | |||||||||||||||||||||||
18 | 1 | 1 | 9 | 1 | 1 | 1 | |||||||||||||||||||
20 | 1 | 1 | |||||||||||||||||||||||
21 | 9 031518 9 00318 | 1 | 1 | ||||||||||||||||||||||
22 | 1 | 1 | 1 | ||||||||||||||||||||||
23 | 1 | 1 | 1 | 1 20095 | 90000315|||||||||||||||||||||
24 | 1 | 1 | |||||||||||||||||||||||
25 | 1 | 1 | 1 | ||||||||||||||||||||||
26 5 | 80318 | 1 | 1 | 1 | |||||||||||||||||||||
27 | 1 | 1 | 1 | 1 | |||||||||||||||||||||
28 | 1 | 918 | 1 | 9000 288888 1 | 1 | 9000 288 1 | 1 | . 0005 0005 | 1 | ||||||||||||||||
29 | 1 | 1 | 1 | 1 | |||||||||||||||||||||
30 | 1 | 1 | 1 | 1 | 1 | 1 9000 9000 0318 | |||||||||||||||||||
31 | 1 | 1 | 1 | 1 | 1 | ||||||||||||||||||||
… | |||||||||||||||||||||||||
254 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||||||||||
255 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||||||||||
| 9 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Взгляните на таблицу и убедитесь, что вы поняли идею. Например, если вы посмотрите на десятичное число 25, вы сможете разбить его двоичный аналог (11001) на 16 + 8 + 1 .
Например, если вы посмотрите на десятичное число 25, вы сможете разбить его двоичный аналог (11001) на 16 + 8 + 1 .
Преобразование из двоичного в десятичное и обратно
Чтобы выяснить, что представляет собой двоичное число в десятичном виде, вы можете нарисовать диаграмму, подобную приведенной выше. Это медленно, но поможет вам надежно это проверить.
Поработав некоторое время с двоичным кодом, вы сможете вычислять небольшие значения в уме. Например, если вы видите число 1101001, вы можете изменить его, добавив 1, 8, 32 и 64, чтобы в сумме получить 105.
Переход от десятичного числа к двоичному отличается. Для этого нужно сначала вычислить наибольшую двоичную единицу, которая вписывается в ваше число. Например, если вы хотите узнать, что такое 73 в двоичном формате, самое большое двоичное значение под этим числом — 64, поэтому место 64 — это 1,9.0005
Разница между 73 и 64 равна 9, а это означает, что нам нужна 1 на месте 8 и 1 на месте 1, чтобы получить 9. Собрав все это вместе, двоичное значение для 73 равно 1001001.
Собрав все это вместе, двоичное значение для 73 равно 1001001.
Когда вы привыкнете к местам, вы сможете выполнять эти вычисления быстрее. Однако со значениями больше 512 или 1024 становится трудно работать вручную.
При работе с большими числами помогут такие инструменты, как калькулятор Programmer в Windows и macOS. Они позволяют вводить число в десятичном виде и видеть его эквивалент в двоичном формате (или наоборот). Существует также удобный режим переключения битов, который позволяет включать и выключать отдельные двоичные цифры, чтобы увидеть обновление значения в режиме реального времени.
Биты, байты и более крупные единицы
Мы используем определенные термины для обозначения размера двоичных чисел. Одна цифра — это бит ; как мы видели выше, один бит сам по себе может представлять только 1 или 0. Этого достаточно для хранения булевой переменной, где 0 — ложь, а 1 — истина.
Восемь бит вместе известны как байт , что является наименьшим объемом памяти, с которым может работать большинство компьютеров.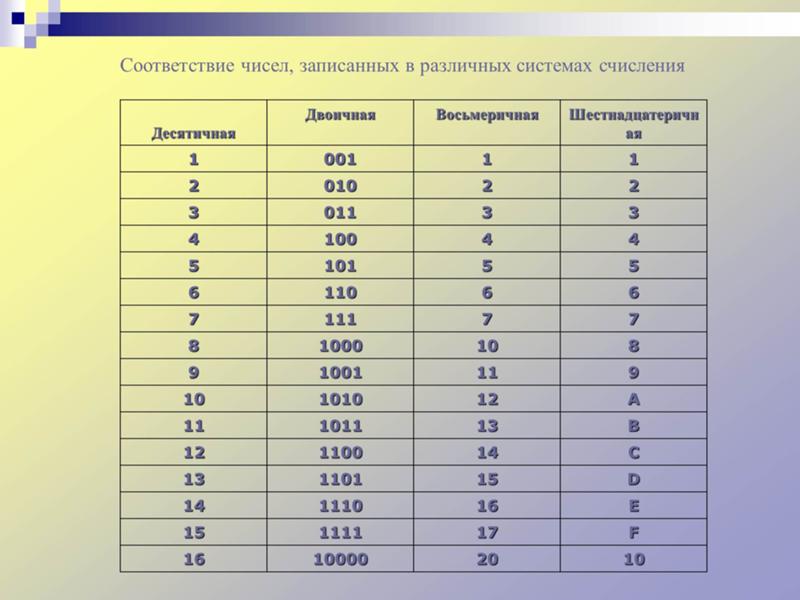 С помощью одного байта вы можете представить десятичные числа от 0 до 255, что составляет 256 возможных значений.
С помощью одного байта вы можете представить десятичные числа от 0 до 255, что составляет 256 возможных значений.
Для подсчета более высоких двоичных чисел в области современных объемов памяти мы используем стандартные префиксы СИ, такие как кило-, мега- и гига-. Килобайт — это тысяча байтов, мегабайт — миллион байтов, а гигабайт — миллиард байтов. Это продолжается с терабайтами и далее.
Как ни странно, поскольку мы измеряем эти размеры в десятичном виде, а компьютеры — в двоичном, иногда вы обнаружите, что устройство имеет меньше памяти, чем заявлено. Наше объяснение различий в размерах жестких дисков подробно объясняет, почему это происходит.
Как двоичный код используется на практике
байта являются важной точкой отсчета. В первых компьютерах один байт использовался для хранения одного текстового символа.
Многие ранние видеоигры ограничивали количество счетчиков до 255 по той же причине. Например, такие аркадные игры, как Pac-Man, вылетают после 255-го уровня, потому что игре не хватает памяти. В оригинальной Zelda для NES максимальное количество рупий (игровой валюты) равно 255, потому что для хранения этого числа игра использует один байт. Из-за ограниченной памяти программисты не хотели выделять больше места для этих значений, поскольку необходимо учитывать множество других факторов. 98 или примерно 18 квинтиллионов возможных адресов. Это число находится за пределами человеческого понимания, а это означает, что предел оперативной памяти намного превышает все, что мы используем сейчас.
В оригинальной Zelda для NES максимальное количество рупий (игровой валюты) равно 255, потому что для хранения этого числа игра использует один байт. Из-за ограниченной памяти программисты не хотели выделять больше места для этих значений, поскольку необходимо учитывать множество других факторов. 98 или примерно 18 квинтиллионов возможных адресов. Это число находится за пределами человеческого понимания, а это означает, что предел оперативной памяти намного превышает все, что мы используем сейчас.
Точно так же адреса IPv4 состоят из четырех байтов (каждая цифра в адресе, например 192.168.100.47, может принимать значения от 0 до 255). Сегодня в сети насчитывается более четырех миллиардов устройств, подключенных к Интернету, поэтому у нас закончились адреса IPv4. Мир медленно движется к IPv6, у которого такой же гораздо более высокий лимит.
Теперь, когда вы понимаете двоичную систему, вы можете понять, почему при ее обсуждении появляются одни и те же числа (степени двойки).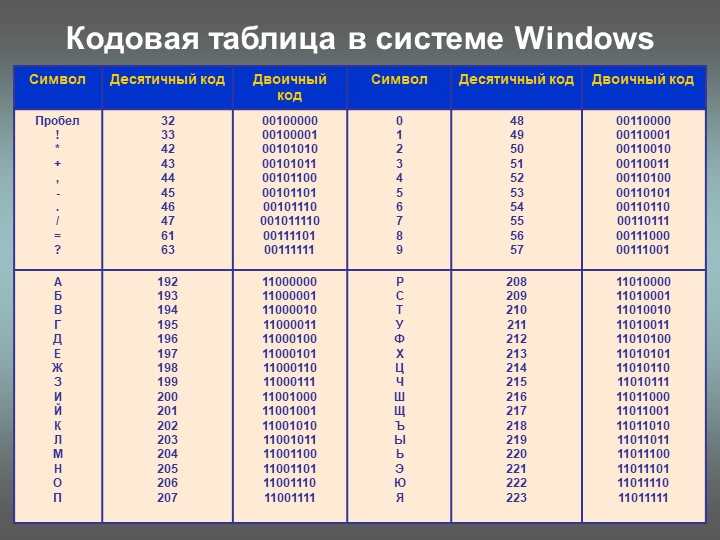


 д.
д.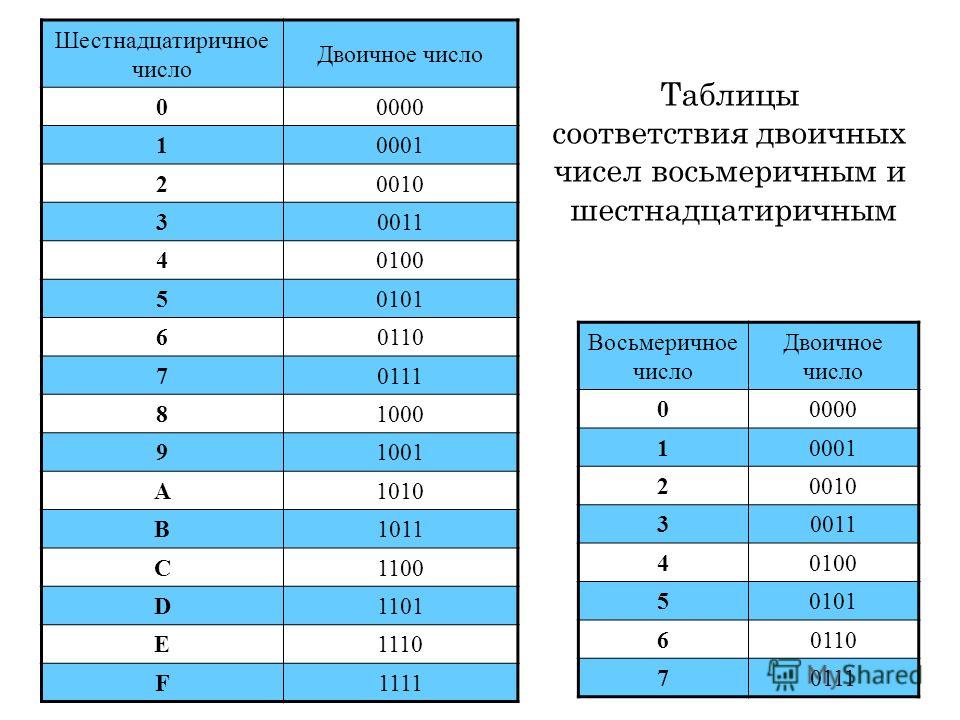 д.
д.