Понятие удельного сопротивления веществ, таблица сопротивления металлов и свойств меди • Мир электрики

Содержание

1. Понятие удельного сопротивления вещества
2. Применение меди
3. Таблица сопротивления металлов
4. Медь. Ее характеристики и свойства
5. Описание вещества и свойства
6. Марки меди
7. Влияние примесей на свойства меди

Что такое удельное сопротивление вещества? Чтобы ответить простыми словами на этот вопрос, нужно вспомнить курс физики и представить физическое воплощение этого определения. Через вещество пропускается электрический ток, а оно, в свою очередь, препятствует с какой-то силой прохождению тока.

Понятие удельного сопротивления вещества

Именно эта величина, которая показывает насколько сильно препятствует вещество току и есть удельное сопротивление (латинская буква «ро»). В международной системе единиц сопротивление выражается в Омах, умноженных на метр. Формула для вычисления звучит так: «Сопротивление умножается на площадь поперечного сечения и делится на длину проводника».

Возникает вопрос: «Почему при нахождении удельного сопротивления используется еще одно сопротивление?». Ответ прост, есть две разных величины — удельное сопротивление и сопротивление. Второе показывает насколько вещество способно препятствовать прохождению через него тока, а первое показывает практически то же самое, только речь идет уже не о веществе в общем смысле, а о проводнике с конкретной длиной и площадью сечения, которые выполнены из этого вещества.

Обратная величина, которая характеризует способность вещества пропускать электричество именуется удельной электрической проводимостью и формула по которой вычисляется удельная сопротивляемость напрямую связана с удельной проводимостью.

Применение меди

Понятие удельного сопротивления широко применяется в вычисление проводимости электрического тока различными металлами. На основе этих вычислений принимаются решения о целесообразности применения того или иного металла для изготовления электрических проводников, которые используются в строительстве, приборостроении и других областях.

Таблица сопротивления металлов

Существуют определенные таблицы? в которых сведены воедино имеющиеся сведения о пропускании и сопротивлении металлов, как правило, эти таблицы рассчитаны для определенных условий.

В частности, широко известна таблица сопротивления металлических монокристаллов при температуре двадцать градусов по Цельсию, а также таблица сопротивления металлов и сплавов.

Этими таблицами пользуются для вычисления различных данных в так называемых идеальных условиях, чтобы вычислить значения для конкретных целей нужно пользоваться формулами.

Медь. Ее характеристики и свойства

Описание вещества и свойства

Медь — это металл, который очень давно был открыт человечеством и также давно применяется для различных технических целей. Медь очень ковкий и пластичный металл с высокой электрической проводимостью, это делает ее очень популярной для изготовления различных проводов и проводников.

Физические свойства меди:

• температура плавления — 1084 градусов по Цельсию;
• температура кипения — 2560 градусов по Цельсию;
• плотность при 20 градусах — 8890 килограмм деленный на кубический метр;
• удельная теплоемкость при постоянном давлении и температуре 20 градусов — 385 кДж/Дж*кг
• удельное электрическое сопротивление — 0,01724;

Марки меди

Данный металл можно разделить на несколько групп или марок, каждая из которых имеет свои свойства и свое применение в промышленности:

1. Марки М00, М0, М1 — отлично подходят для производства кабелей и проводников, при ее переплавке исключается перенасыщение кислородом.
2. Марки М2 и М3 — дешевые варианты, которые предназначены для мелкого проката и удовлетворяют большинству технических и промышленных задач небольшого масштаба.
3. Марки М1, М1ф, М1р, М2р, М3р — это дорогие марки меди, которые изготавливаются для конкретного потребителя со специфическими требованиями и запросами.

Между собой марки отличаются по нескольким параметрам:

• вид поставки;
• насыщение кислородом;
• разница в показателе сопротивления;
• наличие примесей;
• степень теплопроводности;

Влияние примесей на свойства меди

Примеси могут влиять на механические, технические и эксплуатационные свойства продукции.

1. Механические свойства. Такие вещества, как железо, висмут, свинец или кислород, оказывают влияние на пластичность меди. Некоторые малорастворимые примеси влияют на сохранение структуры вещества при увеличении температуры. Например, свинец или висмут делает медь очень хрупкой, а вот добавление хотя бы незначительного количества серебра (пять сотых процента) значительно повышает плавкость меди, то есть даже при высоких температурах ее кристаллическая решетка остается неизменной, при этом не происходит потереть тепло- или электропроводимости.
2. Технические свойства . К ним относят обработку давлением при разных температурах и сплавляемость (сварка) вещества. При наличии малорастворимых примесей в меди появляются зоны особой хрупкости при большой температуре, это делает обработку давлением очень трудной, однако, в марках М1 и М2 нужная пластичность достигается за счет низкого содержания примесей. Если говорить о давлении при низких температурах, то данная технология применяется при производстве катанки (проволоки) и для разных марок способность к вытяжке также различна.
3. Эксплуатационные свойства. При стандартных условиях эксплуатации разные марки ведут себя вполне одинаково, но из-за содержания водорода и кислорода в разных марках условия применяются при повышении температуры. В частности, кислород начинает отрицательно влиять на медь при повышении температуры окружающей среды, а водород при нагреве самого вещества до двухсот градусов.

В заключение следует подчеркнуть, что медь — это уникальный металл с уникальными свойствами. Она применяется в автомобилестроении, изготовлении элементов для электроиндустрии, электроприборов, предметов потребления, часов, компьютеров и многого другого. Со своим низким удельным сопротивлением данный металл является отличным материалом для изготовления проводников и прочих электрических приборов. Этим свойством медь обгоняет только серебро, но из-за более высокой стоимости оно не нашло такого же применения в электроиндустрии.

Зависимость удельного сопротивления проводника от температуры

Электрическое сопротивление — физическая величина, которая указывает, какое препятствие создается току при его прохождении по проводнику. Единицами измерения служат Омы, в честь Георга Ома. В собственном законе он вывел формулу для нахождения сопротивления, которая приведена ниже.

Разглядим сопротивление проводников на примере металлов. Металлы имеют внутреннее строение в виде кристаллической решетки. Эта решетка имеет строгую упорядоченность, а её узлами являются положительно заряженные ионы. Носителями заряда в металле выступают “свободные” электроны, которые не принадлежат определенному атому, а беспорядочно передвигаются между узлами решетки. Из квантовой физики понятно, что движение электронов в металле это распространение электромагнитной волны в жестком теле. Другими словами электрон в проводнике движется со скоростью света (фактически), и подтверждено, что он проявляет характеристики не только лишь как частичка, но к тому же как волна. А сопротивление металла появляется в итоге рассеяния электромагнитных волн (другими словами электронов) на термических колебаниях решетки и её недостатках. При столкновении электронов с узлами кристаллической решетки часть энергии передается узлам, вследствие чего выделяется энергия. Эту энергию можно вычислить при неизменном токе, благодаря закону Джоуля-Ленца – Q=I 2 Rt. Видите ли чем больше сопротивление, тем больше энергии выделяется.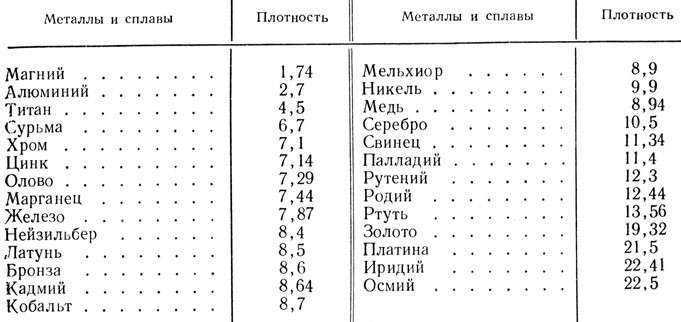

Удельное сопротивление

Существует такое принципиальное понятие как удельное сопротивление, это тоже самое сопротивление, исключительно в единице длины. У каждого металла оно свое, к примеру у меди оно равно 0,0175 Ом*мм2/м, у алюминия 0,0271 Ом*мм2/м . Это означает, брусок из меди длиной 1 м и площадью поперечного сечения 1 мм2 будет иметь сопротивление 0,0175 Ом, а таковой же брусок, но из алюминия будет иметь сопротивление 0,0271 Ом. Выходит что электропроводность меди выше чем у алюминия. У каждого металла удельное сопротивление свое, а высчитать сопротивление всего проводника можно по формуле

где p – удельное сопротивление металла, l – длина проводника, s – площадь поперечного сечения.

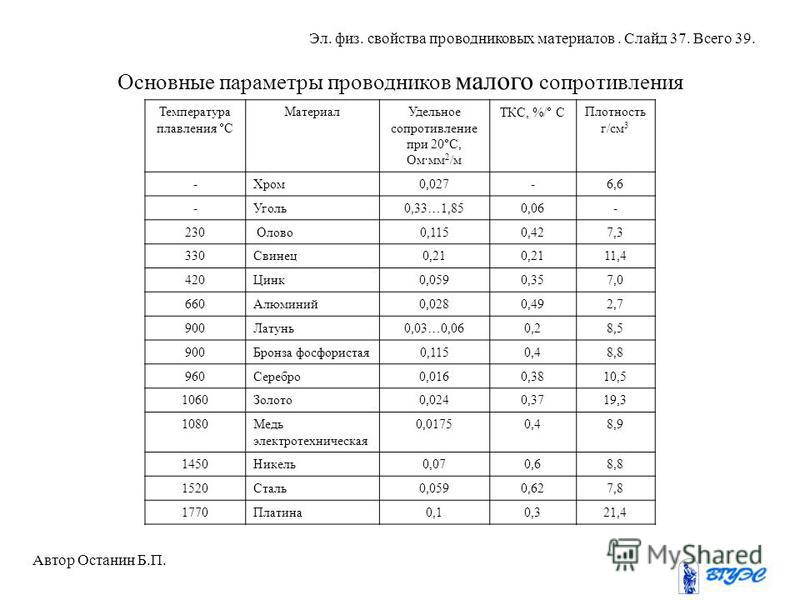
Значения удельных сопротивлений приведены в таблице удельных сопротивлений металлов (20°C)

Не считая удельного сопротивления в таблице есть значения ТКС, об этом коэффициенте чуток позднее.

Зависимость удельного сопротивления от деформаций

При холодной обработке металлов давлением, металл испытывает пластическую деформацию.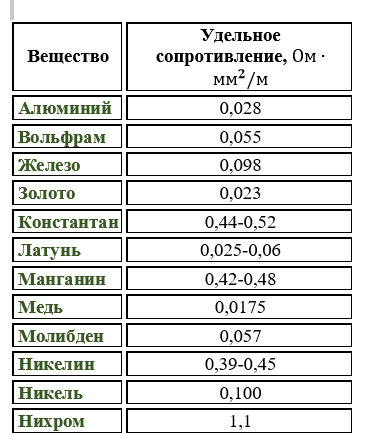 При пластической деформации кристаллическая решетка искажается, количество изъянов становится больше. С повышением изъянов кристаллической решетки, сопротивление течению электронов по проводнику вырастает, поэтому, удельное сопротивление металла возрастает. Например, проволоку изготавливают способом протяжки, это означает, что металл испытывает пластическую деформацию, в итоге чего, удельное сопротивление вырастает. На практике для уменьшения сопротивления используют рекристаллизационный отжиг, это непростой технологический процесс, после которого кристаллическая решетка вроде бы, “расправляется” и количество изъянов миниатюризируется, поэтому, и сопротивление металла тоже.

При растяжении либо сжатии, металл испытывает упругую деформацию. При упругой деформации вызванной растяжением, амплитуды термических колебаний узлов кристаллической решетки растут, поэтому, электроны испытывают огромные затруднения, и в связи с этим, возрастает удельное сопротивление. При упругой деформации вызванной сжатием, амплитуды термических колебаний узлов уменьшаются, поэтому, электронам проще двигаться, и удельное сопротивление миниатюризируется.

Воздействие температуры на удельное сопротивление

Как мы уже узнали выше, предпосылкой сопротивления в металле являются узлы кристаллической решетки и их колебания. Итак вот, при увеличении температуры, термические колебания узлов растут, а означает, удельное сопротивление также возрастает. Существует такая величина как температурный коэффициент сопротивления (ТКС), который указывает как возрастает, либо миниатюризируется удельное сопротивление металла при нагреве либо охлаждении. К примеру, температурный коэффициент меди при 20 градусах по цельсию равен 4.1 · 10 − 3 1/градус. Это значит что при нагреве, например, медной проволоки на 1 градус цельсия, её удельное сопротивление возрастет на 4.1 · 10 − 3 Ом. Удельное сопротивление при изменении температуры можно вычислить по формуле

где r это удельное сопротивление после нагрева, r0 – удельное сопротивление до нагрева, a – температурный коэффициент сопротивления, t2 – температура до нагрева, t1 — температура после нагрева.

Подставив наши значения, мы получим: r=0,0175*(1+0.0041*(154-20))=0,0271 Ом*мм 2 /м. Видите ли наш брусок из меди длиной 1 м и площадью поперечного сечения 1 мм 2 , после нагрева до 154 градусов, имел бы сопротивление, как у того же бруска, только из алюминия и при температуре равной 20 градусов цельсия.

Свойство конфигурации сопротивления при изменении температуры, применяется в указателях температуры сопротивления. Эти приборы могут определять температуру основываясь на показаниях сопротивления. У термометров сопротивления высочайшая точность измерений, но малые спектры температур.

На практике, характеристики проводников препятствовать прохождению тока применяются очень обширно. Примером может служить лампа накаливания, где нить из вольфрама, греется за счет высокого сопротивления металла, большой длины и узенького сечения. Либо хоть какой нагревательный устройство, где спираль разогревается благодаря высочайшему сопротивлению. В электротехнике, элемент основным свойством которого является сопротивление, именуется – резистор.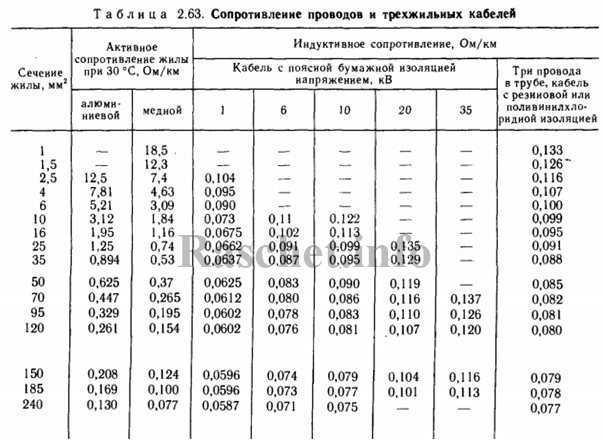 Резистор применяется фактически в хоть какой электрической схеме.

Вещества и материалы, способные проводить электрический ток, именуют проводниками. Другие относят к диэлектрикам. Но незапятнанных диэлектриков не бывает, они все тоже проводят ток, но его величина очень мала.

Но и проводники по-разному проводят ток. Согласно формуле Георга Ома, ток, протекающий через проводник, линейно пропорционален величине приложенного к нему напряжения, и назад пропорционален величине, именуемой сопротивлением.

Единицу измерения сопротивления окрестили Омом в честь ученого, открывшего эту зависимость. Но выяснилось, что проводники, сделанные из различных материалов и имеющие однообразные геометрические размеры, владеют различным электрическим сопротивлением. Дабы найти сопротивление проводника известного длины и сечения, ввели понятие удельного сопротивления — коэффициента, зависящего от материала.

В конечном итоге сопротивление проводника известной длины и сечения будет равно

Определение сопротивления проводника при помощи его удельного сопротивления

Удельное сопротивление применимо не только лишь к жестким материалам, но и к жидкостям.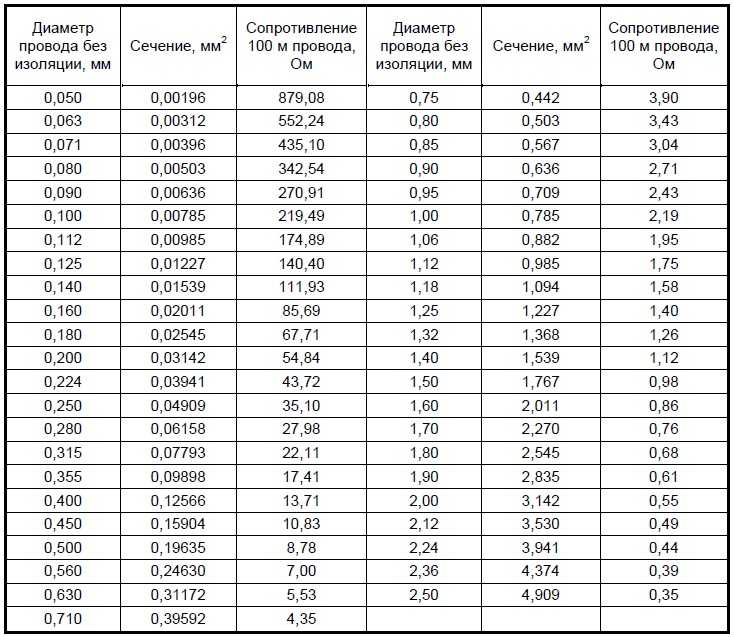 Но его величина зависит к тому же от примесей либо других компонент в начальном материале. Незапятнанная вода не проводит электрический ток, являясь диэлектриком. Но в природе дистиллированной воды не бывает, в ней всегда встречаются соли, бактерии и другие примеси. Этот коктейль – проводник электрического тока, владеющий удельным сопротивлением.

Удельные сопротивления некоторых материалов

Внедряя в металлы разные добавки, получают новые материалы – сплавы, удельное сопротивление которых отличается от того, что было у начального материала, даже если добавка в него в процентном соотношении малозначительна.

Зависимость удельного сопротивления от температуры

Удельные сопротивления материалов приводятся в справочниках для температуры, близкой к комнатной (20 °С). При увеличении температуры возрастает сопротивление материала. Почему так происходит?

Электрического тока снутри материала проводят свободные электроны. Они под действием электрического поля отрываются от собственных атомов и передвигаются между ними в направлении, данным этим полем. Атомы вещества образуют кристаллическую решетку, между узлами которой и движется поток электронов, именуемый еще «электронным газом». Под действием температуры узлы решетки (атомы) колеблются. Сами электроны тоже движутся не по прямой, а по запутанной линии движения. При всем этом они нередко сталкиваются с атомами, меняя траекторию перемещения. В некоторые моменты времени электроны могут двигаться в сторону, оборотную направлению электрического тока.

С повышением температуры амплитуда колебаний атомов возрастает. Соударение электронов с ними происходит почаще, движение потока электронов замедляется. На физическом уровне это выражается в увеличении удельного сопротивления.

Примером применения зависимости удельного сопротивления от температуры служит работа лампы накаливания. Вольфрамовая спираль, из которой изготовлена нить накала, в момент включения имеет маленькое удельное сопротивление. Бросок тока в момент включения стремительно ее разогревает, удельное сопротивление возрастает, а ток – миниатюризируется, становясь номинальным.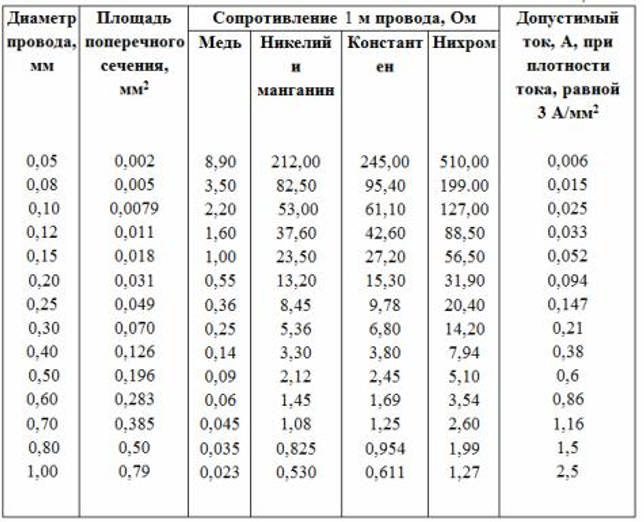

Тот же процесс происходит и с нагревательными элементами из нихрома. Потому и высчитать их рабочий режим, определив длину нихромовой проволоки известного сечения для сотворения требуемого сопротивления, не выходит. Для расчетов необходимо удельное сопротивление нагретой проволоки, а в справочниках приведены значения для комнатной температуры. Потому итоговую длину спирали из нихрома подгоняют экспериментально. Расчетами же определяют примерную длину, а при подгонке понемногу укорачивают нить участок за участком.

Температурный коэффициент сопротивления

Но не во всех устройствах наличие зависимости удельного сопротивления проводников от температуры приносит пользу. В измерительной технике изменение сопротивления частей схемы приводит к возникновению погрешности.

Для количественного определения зависимости сопротивления материала от температуры введено понятие температурного коэффициента сопротивления (ТКС). Он указывает, как меняется сопротивление материала при изменении температуры на 1°С.

Для производства электронных компонент – резисторов, применяемых в схемах измерительной аппаратуры, используются материалы с низким ТКС. Они стоят дороже, но зато характеристики устройства не меняются в широком спектре температур окружающей среды.

Но характеристики материалов с высочайшим ТКС тоже применяются. Работа некоторых датчиков температуры базирована на изменении сопротивления материала, из которого сделан измерительный элемент. Для этого необходимо поддерживать размеренное напряжение питания и определять ток, проходящий через элемент. Откалибровав шкалу устройства, измеряющего ток, по примерному указателю температуры, получают электронный измеритель температуры. Этот принцип применяется не только лишь для измерений, но и для датчиков перегрева. Отключающих устройство при появлении ненормальных режимов работы, приводящих к перегреву обмоток трансформаторов либо силовых полупроводниковых частей.

Применяются в электротехнике и элементы, изменяющие свое сопротивление не от температуры окружающей среды, а от тока через них – терморезисторы. Пример их применения – системы размагничивания электронно-лучевых трубок телевизоров и мониторов. При подаче напряжения сопротивление резистора мало, ток через него проходит в катушку размагничивания. Но тот же ток нагревает материал терморезистора. Его сопротивление возрастает, понижая ток и напряжение на катушке. И так – до полного его исчезновения. В конечном итоге на катушку подается синусоидальное напряжение с плавненько уменьшающейся амплитудой, создающее в ее пространстве такое же магнитное поле. Итог – к моменту разогрева нити накала трубки она уже размагничена. А схема управления остается в запертом состоянии, пока аппарат не выключат. Тогда терморезисторы остынут и будут готовы к работе опять.

Явление сверхпроводимости

А что будет, если температуру материала уменьшать? Удельное сопротивление будет уменьшаться. Есть предел, до которого миниатюризируется температура, именуемый абсолютным нулем. Это —273°С. Ниже этого предела температур не бывает. При всем этом значении удельное сопротивление любого проводника равно нулю.

При абсолютном нуле атомы кристаллической решетки перестают колебаться. В конечном итоге электронное скопление движется между узлами решетки, не соударяясь с ними. Сопротивление материала становится равным нулю, что открывает способности для получения нескончаемо огромных токов в проводниках маленьких сечений.

Явление сверхпроводимости открывает новые горизонты для развития электротехники. Но еще пока есть трудности, связанные с получением в бытовых критериях сверхнизких температур, нужных для сотворения этого эффекта. Когда задачи будут решены, электротехника перейдет на новый уровень развития.

Примеры применения значений удельного сопротивления при расчетах

Мы уже познакомились с принципами расчета длины нихромовой проволоки для производства нагревательного элемента. Но есть и другие ситуации, когда нужны познания удельных сопротивлений материалов.

Для расчета контуров заземляющих устройств применяются коэффициенты, надлежащие типовым грунтам. Если же тип грунта в месте устройства контура заземления неизвестен, то для правильных расчетов за ранее определяют его удельное сопротивление. Так результаты расчетов оказываются поточнее, что исключает подгонку характеристик контура при изготовлении: добавление числа электродов, приводящее к повышению геометрических размеров заземляющего устройства.

Удельные сопротивления грунтов

Удельное сопротивление материалов, из которых сделаны кабельные полосы и шинопроводы, применяется для расчетов их активного сопротивления. В предстоящем при номинальном токе нагрузки с его помощью рассчитывается величина напряжения в конце полосы. Если его величина окажется недостаточной, то заранее наращивают сечения токопроводов.

Удельное электрическое сопротивление | Свойства материалов: анизотропия, симметрия, структура

Фильтр поиска панели навигации Oxford AcademicСвойства материалов: анизотропия, симметрия, структураГеохимияКнигиЖурналы Термин поиска мобильного микросайта

Закрыть

Фильтр поиска панели навигации Oxford AcademicСвойства материалов: анизотропия, симметрия, структураГеохимияКнигиЖурналы Термин поиска на микросайте

Расширенный поиск

• Иконка Цитировать Цитировать

• Разрешения

• Делиться
  • Твиттер
  • Подробнее

Cite

Newnham, Robert E,

‘Electrical resistivity’

,

Properties of Materials: Anisotropy, Symmetry, Structure

(

Oxford,

2004;

online edn,

Oxford Academic

, 12 ноября 2020 г.

), https://doi.org/10.1093/oso/9780198520757.003.0019,

, по состоянию на 1 февраля 2023 г.

Выберите формат Выберите format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)

Закрыть

Фильтр поиска панели навигации Oxford AcademicСвойства материалов: анизотропия, симметрия, структураГеохимияКнигиЖурналы Термин поиска мобильного микросайта

Закрыть

Фильтр поиска панели навигации Oxford AcademicСвойства материалов: анизотропия, симметрия, структураГеохимияКнигиЖурналы Термин поиска на микросайте

Advanced Search

Abstract

Следующие шесть глав описывают явления переноса, связанные с потоком заряда, тепла и вещества.

В каждом случае есть векторный поток, управляемый векторным полем. Линейные зависимости между потоком и полем включают удельное электрическое сопротивление (глава 17), теплопроводность (глава 18), диффузию (глава 19).) и термоэлектричество (глава 21). Все они представлены тензорами второго ранга, подобными диэлектрической проницаемости (глава 9), но основная физика несколько отличается. Транспортные свойства — это неравновесные явления, управляемые статистической механикой и концепцией микроскопической обратимости, а не вторым законом термодинамики, который применяется к равновесным свойствам, таким как удельная теплоемкость, диэлектрическая проницаемость и упругость. Тензоры более высокого порядка появляются, когда транспортные эксперименты проводятся в присутствии магнитных полей или механических напряжений. Гальваномагнитные, термомагнитные (глава 20) и пьезорезистивные эффекты (глава 22) требуют тензоров третьего и четвертого рангов. Когда к проводнику приложено электрическое поле, через образец протекает электрический ток. Поле Ei (в В/м) связано с плотностью тока Jj (в А/м2) по закону Ома, где ρij — удельное электрическое сопротивление (в Ом·м). В тензорной форме … Ei = ρijJj … Ei и Jj — полярные векторы (полярные тензоры первого ранга), а ρij — свойство полярного тензора второго ранга, которое обычным образом следует закону Неймана. Иногда удобнее использовать обратное соотношение, связанное с электропроводностью σij : … Ji = σijEj ….

Ключевые слова: Анизотропные проводники, Запрещенная зона и подвижность, Рост кристаллов, Электродные металлы, Колебания решетки, Матричные соотношения, NTC

Предмет

Геохимия

В настоящее время у вас нет доступа к этой главе.

Войти

Получить помощь с доступом

Получить помощь с доступом

Доступ для учреждений

Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок.

Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:

Доступ на основе IP

Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.

Войдите через свое учреждение

Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.

1. Нажмите Войти через свое учреждение.
2. Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
3. При посещении сайта учреждения используйте учетные данные, предоставленные вашим учреждением. Не используйте личную учетную запись Oxford Academic.
4. После успешного входа вы вернетесь в Oxford Academic.

Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.

Войти с помощью читательского билета

Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.

Члены общества

Доступ члена общества к журналу достигается одним из следующих способов:

Войти через сайт сообщества

Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:

1. Щелкните Войти через сайт сообщества.
2. При посещении сайта общества используйте учетные данные, предоставленные этим обществом. Не используйте личную учетную запись Oxford Academic.
3. После успешного входа вы вернетесь в Oxford Academic.

Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.

Войти с помощью личного кабинета

Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. Смотри ниже.

Личный кабинет

Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.

Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.

Просмотр учетных записей, вошедших в систему

Щелкните значок учетной записи в правом верхнем углу, чтобы:

• Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью.
• Просмотр институциональных учетных записей, предоставляющих доступ.

Выполнен вход, но нет доступа к содержимому

Oxford Academic предлагает широкий ассортимент продукции. Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ. Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю.

Ведение счетов организаций

Для библиотекарей и администраторов ваша личная учетная запись также предоставляет доступ к управлению институциональной учетной записью. Здесь вы найдете параметры для просмотра и активации подписок, управления институциональными настройками и параметрами доступа, доступа к статистике использования и т. д.

Покупка

Наши книги можно приобрести по подписке или приобрести в библиотеках и учреждениях.

Информация о покупке

Теплопроводность и электрическое сопротивление платиновых металлов

Теплопроводность и электрическое сопротивление платиновых металлов — technology. matthey.com

Теплопроводность и электрическое сопротивление платиновых металлов

Архив журнала

Platinum Metals Rev., 1962, 6 , (4), 138

Теплопроводность и электрическое сопротивление платиновых металлов

---

Поделиться этой страницей:

• Твиттер
• Фейсбук
• LinkedIn
• Реддит
• Дигг
• СМЕШИВАНИЕ

---

Краткое содержание статьи

Представлены и обсуждены новые значения теплопроводности и удельного электрического сопротивления рутения, осмия, родия, иридия, палладия и платины в приблизительном диапазоне температур от 80° до 500°К.

Во время недавней ревизии одним из авторов раздела о теплопроводности известной книги таблиц физических констант Кея-Лаби стало очевидным, что приведенные до сих пор значения теплопроводности некоторых металлов, в частности родия и иридий явно ошибались.

При изучении ранее представленных данных было обнаружено, что значения числа Лоренца (теплопроводность, умноженная на удельное электрическое сопротивление, деленная на абсолютную температуру) дают необычно низкие значения для этих металлов, и были проведены исследования для получения новых определений. теплопроводности и удельного электрического сопротивления. О новых значениях, найденных для иридия и родия, уже сообщалось (1), и можно отметить, что при комнатной температуре значение теплопроводности для иридия выше значения, приведенного ранее, примерно в 2,5 раза, а для родия примерно в 2,5 раза. 1.7.

Из четырех металлов платиновой группы, которые еще предстоит рассмотреть, значения теплопроводности, по-видимому, не были измерены при нормальных температурах или выше для осмия и рутения, а для палладия в диапазоне от 0° до 100°C (2, 3 , 4) показывают различия до 27 %, и, в то время как большинство доступных значений для платины показывают более близкое соответствие в этом температурном диапазоне (2, 4, 5, 6, 7), различия примерно в 30 % возникают между меньшим количеством измерений. изготовлены при 1000°С (8, 9, 10).

Теплопроводность осмия и рутения была измерена Уайтом и Вудсом (11), но только ниже 150°К. Эти исследователи отмечают, что экстраполяция их тепловых данных предполагает теплопроводность при комнатной температуре около 0,9±0,1 Вт см ^-1 град ^-1 для осмия и около 1,1±0,1 Вт см ^-1 град ^-1 . для рутения. В то же время они призывают к точным определениям теплопроводности при 300° или 400°К.

Подробная информация об образцах

Все образцы, изученные в данной работе, были поставлены компанией Johnson, Matthey – Co., Limited в виде небольших стержней, размеры которых указаны в Таблице I. Эта таблица также содержит значения плотности и такие подробности. как были поставлены в отношении химических примесей и способа приготовления.

Таблица I

Детали образцов

Металл	Длина см	Диаметр см	Примеси %										Плотность г/мл	Другая информация
			Au	Аг	Cu	Фе	Ni	ПД	Rh	Ир	Ру	Пт
Рутений	«> 2,5	0,660			.001	.01	.001	.0005	.03			.002	12.36	Аргонно-дуговая плавка и шлифовка
Осмий	2,7	0,489		.0001	0,002	.0005		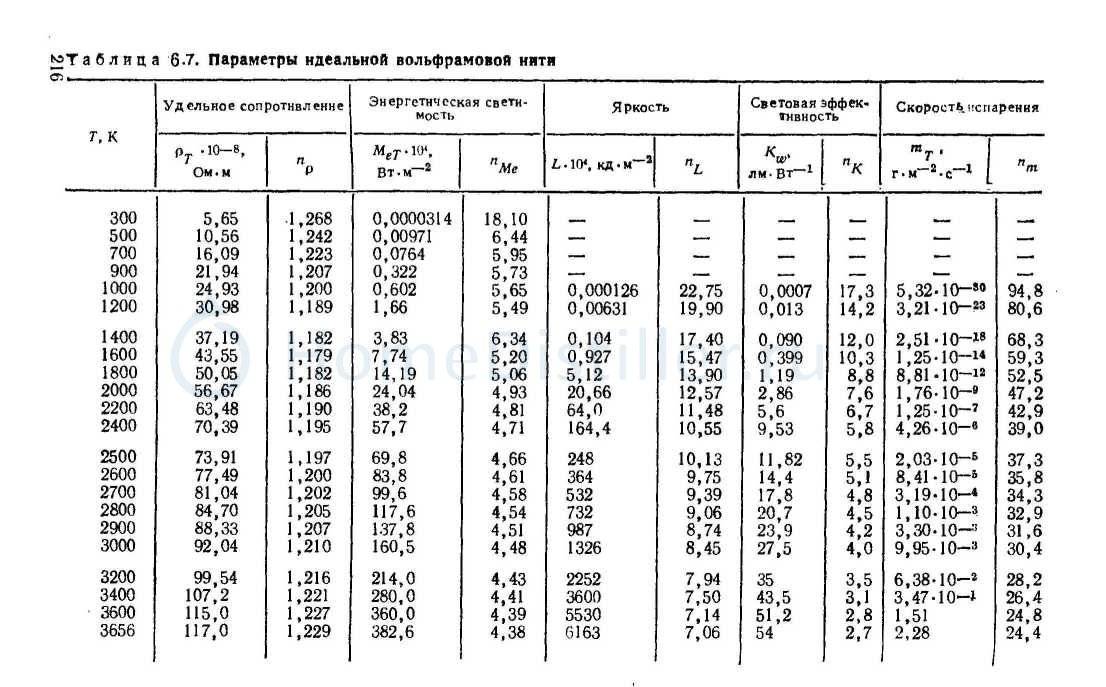	. 002		.03		22.45	» »
Родий	5.0	0,348		от 0,002 до 0,005		.005		от 0,001 до 0,003		от 0,03 до 0,1			12.44
Иридий ‥	5.0	«> 0,318						.001	от 0,02 до 0,05		от 0,002 до 0,005		22.43
Палладий	6.1	0,636	.0005	<.000 л	.0001	.0005			.005		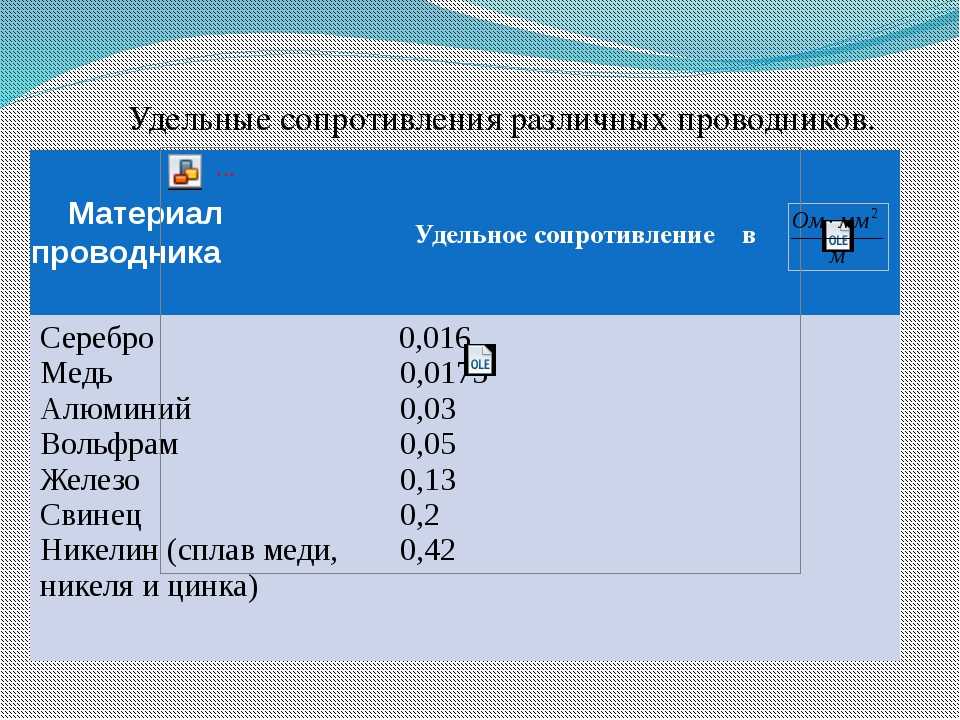	. 0002	12.02
Платина ‥	6.1	0,635			.0001	.0001		<.000 л					21.51	Отожжен при ~1000°C

Экспериментальные методы и результаты

Используемые экспериментальные методы аналогичны описанным ранее (1, 12). Сначала определяли удельное электрическое сопротивление при комнатной температуре, при этом образцы располагались на лезвиях ножей на фиксированном расстоянии друг от друга и служили потенциальными контактами. Удельное сопротивление, полученное путем сравнения этого падения потенциала с падением напряжения на стандартном сопротивлении, позже использовалось для получения эффективного коэффициента формы, отношения площади к длине, когда термопары, прикрепленные к стержням, служили для измерения температуры, а также в качестве потенциальных выводов.

Таким образом были проведены определения удельного электрического сопротивления до высоких температур и вплоть до температур жидкого азота. Для измерения удельного сопротивления при температурах жидкого гелия применялся метод сравнения, в котором капли потенциала действовали противоположно через гальванометр, а токи в эталонном сопротивлении и цепях образца регулировались таким образом, чтобы не было отклонения.

Значения удельного электрического сопротивления, полученные на жидком гелии, ρ _{0 9В табл. В эту таблицу включены некоторые результаты других работников. Отношение остаточного сопротивления, указанное в последней колонке, часто можно рассматривать как показатель состояния чистоты образца, причем отношение становится ниже по мере увеличения чистоты или уменьшения степени деформации. Лишь для иридия и платины это отношение наименьшее в образцах, использованных в настоящей работе.}

Кривые, показывающие изменение удельного электрического сопротивления в зависимости от температуры для каждого металла в исследованном диапазоне, приведены в нижней части рис. 1.

Таблица II при жидком гелии,

ρ ₀ и температурах льда, ρ ₂₇₃

Металл	Наблюдатель	Сведения об образце	Удельное электрическое сопротивление
			ρ 273	р 0	10 3 ρ 0 /ρ 273
Рутений	Настоящая работа ‥	При получении ‥	«> 7.13	0,566	79,4
	Мейснер-Фойгт (15)‥	__ ‥ ‥ ‥	__	__	8.3
	Юсти (16) ‥ ‥	99,99%: спеченный 2200°C ‥	7.157	0,501	70
	Халм – Гудман (17)	— ‥ ‥ ‥ ‥	—	—	60
	Белый — Лес (11) ‥	Дуговой переплав Ru2 ‥ ‥	«> 7,9*	0,235	30*
		„ Ru3 ‥	6,8*	0,02	3 *
Осмий	Настоящая работа ‥ ‥	В состоянии получения‥ ‥ ‥	8.532	0,272	32
		После нагрева до 1540°С ‥	8.12	0,244	30
	Халм – Гудман (17)	‥ ‥ ‥ ‥	—	—	40
	Белый– Вудс (II) ‥	Дугоплавкий Ос2	«> 8,5*	0,0996	11,7*
		„ Ос3 ‥	8,5*	0,0873	10,3*
Родий	Настоящая работа ‥ ‥	После нагрева до 1336°С ‥	4.33	0,024	5,5
	Мейснер – Фойгт (15)	—	—	—	3.0
	Белый — Вудс (18) ‥	J. M., отожженная 1300°C	4,4*	0,0084	1,9*
	Кемп и др. и (19)	Образец № 1 Griineisen
		– Гоенс (20)	4,63*	0,0155	3,3*
Иридий	Настоящая работа ‥	После нагрева до 1310°С	4,71	0,055	11,7
	Мейснер – Фойгт (15) ‥	—	—	—	«> 47,7
	Белый — Вудс (18) ‥	J.M., отожженная 1300°C	4,75*	0,1034	21,8*
Палладий	Настоящая работа ‥ ‥	В состоянии получения ‥ ‥	9,93	0,144	14,5
	Мейснер – Фойгт (15) ‥	— ‥ ‥ ‥ ‥	—	—	35,3
	Кемп и др. (21)	Отожжен при 450°C	«> 9,9*	0,0182	1,8*
	Макдональд и др. (22) ‥	Подготовлено J.M., 0,031%	—	—	14,3*
		примесь
Платина	Настоящая работа	В состоянии получения	9,85	0,013	1.3
	Мейснер – Фойгт(15)‥	—	—	—	«> 1.6
	Белый – Вудс(18) ‥	Отожженный 1050°C	9,6*	0,0125	1,3*
	Макдональд и др. (22) ‥	Подготовлено JM	—	—	4,3*

С поправкой на 273°K, из опубликованного значения

Рис. 1 Нижний диапазон исследуемых температур. Однако для палладия и платины кривые все еще слишком близки, чтобы их можно было показать отдельно, и для этих металлов показаны некоторые экспериментальные точки.

Для измерения теплопроводности использовались четыре варианта метода продольного теплового потока. В приблизительном температурном диапазоне от 50° до 25°С использовались следующие варианты защищенного сравнительного метода теплового потока, но все с водяным охлаждением на нижнем конце, что обеспечивает дополнительную абсолютную меру теплового оттока из образец:

Метод умеренной температуры I:

Испытуемый образец был присоединен к верхней части стержня из армко-железа с известной теплопроводностью, основание которого охлаждалось водой. Измерения оттока тепла от испытуемого образца проводились по градиенту температуры в чугуне и водопроточном калориметре. Этот метод применялся для иридия и родия.

Метод II при умеренной температуре:

В этом варианте стержень из армко-железа располагался вверху, а калориметр потока воды присоединялся к нижнему концу испытуемого образца. Таким образом, приток тепла к исследуемому образцу измерялся по установившемуся градиенту температуры в чугуне, а отток тепла — с помощью проточного калориметра. Этот метод применялся для иридия, родия, палладия и платины.

Метод умеренной температуры III:

Для двух самых коротких экземпляров необходимо было соединить еще один стержень, на который можно было намотать нагревательный элемент. Для этой цели использовали стержень из армко-железа достаточной длины, чтобы можно было измерить приток тепла по градиенту температуры, установившемуся на участке этого стержня. Отток тепла определялся как по градиенту в другом железном стержне Армко, прикрепленном к нижнему концу образца, так и по калориметру потока воды в основании этого железного стержня. Этот метод был использован для осмия и рутения.

Все соединения выполнены с помощью горячей посадки в небольшие стальные хомуты. Пространство между композитным центральным стержнем и защитной трубкой было заполнено теплоизолирующим порошком с теплопроводностью около 0,00033 Дж см/см ² с град С. замеры расхода обычно согласованы в пределах примерно 2%.

Низкотемпературный метод

Определения проводились с образцом, прикрепленным к основанию металлического контейнера с внутренней полировкой, который можно было непрерывно откачивать через тонкостенную медно-никелевую трубку. Контейнер по очереди погружали в кипящую воду, тающий лед, измельченную твердую двуокись углерода, жидкий кислород или жидкий азот в ходе эксперимента. Сверху на образец была намотана нагревательная спираль, которая была покрыта оберткой из алюминиевой фольги. Энергия, подводимая к этому нагревателю, измерялась, корректировалась на проводимость свинца и использовалась для определения теплового потока в рабочем сечении стержня. Поправки на перенос излучения были получены из второй серии экспериментов, проведенных при сравнимых средних температурах, но с образцом, свободно подвешенным в камере.

Из данной группы металлов этот метод использовался только для иридия и родия. Следует, однако, отметить, что этот метод применялся также к армко-железу (13) и рению (14) и дал значения, хорошо согласующиеся с данными других исследователей.

На рис. 2 показано изменение теплопроводности в зависимости от температуры с помощью плавных кривых или прямых линий, проведенных через аналогичные наборы экспериментальных точек для каждого металла.

Рис. 2

Изменение теплопроводности с температурой

Кривые для иридия и родия мало отличаются от ранее опубликованных авторами результатов (1), особенно при самых низких температурах. Это связано с использованием пересмотренной калибровки никель-хромовых и константановых термопар.

Значения пар металлов, принадлежащих к одной и той же подгруппе, рутения и осмия, родия и ирида, палладия и платины, имеют тенденцию совпадать.

При температуре выше нормальной теплопроводность каждого металла относительно постоянна. Значения для рутения хорошо согласуются с предсказанным значением Уайта и Вудса (11), упомянутым ранее, в то время как значение для осмия лежит на нижней границе диапазона значений, которые они дали.

Кривые зависимости числа Лоренца от температуры воспроизведены на рис. 3. Интересно отметить, что в диапазоне от 323° до 500°К числа Лоренца металлов платиновой группы превышают теоретическое значение в размере от 0 до 15 процентов. Казалось бы, используя значение 2,6 × 10 ^-8 Дж ом/с град С °К должна быть возможность рассчитать их теплопроводность при более высоких температурах по значениям удельного электрического сопротивления и достичь точности в пределах 10%. Этот порядок точности является хорошим по сравнению с большими различиями между доступными данными, как указано во введении. Этот вывод вызывает сомнение в достоверности опубликованных значений теплопроводности платины (8, 10) и числа Лоренца платины (23) и палладия (24) в более высокой области температур. Например, данные Холма и Штормера дают числа Лоренца, которые возрастают от 2,6×10 ^-8 примерно при 100°C до 3,0×10 ^-8 примерно при 1000°C, в то время как Hopkins (23) и Hopkins and Griffiths (24) получают значения несколько выше 3×10 ^-8 для платины и палладия между 1000°С и их температурами плавления.

Рис. 3

Изменение числа Лоренца в зависимости от температуры

По мере снижения температуры до характеристической температуры 8 и ниже нее времена релаксации, связанные с электрическим и тепловым электронным переносом, больше не сопоставимы, поэтому наблюдается уменьшение числа Лоренца в сторону меньших значений, начинающееся в диапазоне от 300° до 400°К. При температурах, превышающих θ, где должно сохраняться теоретическое значение числа Лоренца, любое превышение теоретического значения можно объяснить увеличением теплопроводности за счет фононной или решеточной проводимости.

Полученные значения для этого компонента решетки имеют самые высокие численные значения около 0,13 Дж см/см ² с град С для образцов иридия и рутения. В целом составляющая решетки показывает небольшое уменьшение с повышением температуры, что подтверждает сомнения, уже высказанные относительно высокотемпературных данных для платины и палладия.

Каталожные номера

1. 1

   Р. В. Пауэлл и Р. П. Тай, Проц. 9-й Международный Конгресс Холодильщиков, 1955 г., 1 , 2149

2. 2

   Т. Барретт и Р. М. Винтер, Проц. физ. Soc., 1914, 26, 347; Энн. Физик, 1925 г., 77 , 1

3. 3

   Э. Седстрём Диссертация, Стокгольм 1924

4. 4

   В. Ягер и Х. Диссельхорст, Абх. д. физ. Тех. Рейхсанштальт, 1900 г., 3 , 269

5. 5

   Дж. Х. Грей Фил. Транс. (А), 1895 186 , 165

6. 6

   В. Мейснер, Энн. Физик, 1915, 47 , 1001

7. 7

   В. Г. Каннулуйк и Э. Х. Кармен Австралийская J. Sci. рез., 1951, г. 4 , 303

8. 8

   Р. Хольм и Р. Штормер, Висс. Veroffentl Siemens-Konzern, 1930, 312

9. 9

   К. С. Кришнан и К. С. Джейн, Брит. Дж. Приложение. физ., 1954 г., 5 , 426

10. 10

    К. Х. Боде, «Прогресс в международных исследованиях термодинамических и транспортных свойств», ASME, 1962, 481

11. 11

    Г. К. Уайт и С. Б. Вудс Canadian J. of Physics, 1958 г., 36 , 875

12. 12

    Р. В. Пауэлл и Р. П. Тай Инженер , 1960 г., 209 , 729

13. 13

    Р. В. Пауэлл, М. Дж. Хикман, Р. П. Тай Мисс и М. Дж. Вудман, «Прогресс в международных исследованиях термодинамических и транспортных свойств», ASME, 1962, 466

14. 14

    Р. В. Пауэлл, Р. П. Тай Мисс и М. Дж. Вудман В процессе публикации.

15. 15

    В. Мейснер и Б. Фойгт Энн. Физик, 1930 г., 7 , 892

16. 16

    Э. Юсти Z.f.Naturforsch., 1949, 4а , 472

17. 17

    Дж. К. Халм и Б. Б. Гудман Физ. Реп., 1957 г., 106 , 659

18. 18

    Г. К. Уайт и С. Б. Вудс Canadian J. of Phys., 1957, 35 , 248

19. 19

    В. Р. Г. Кемп, П. Г. Клеменс и Р. Дж. Тайнш, Annalen der Physik, 1959, 5 , 35

20. 20

    Э.