Логические операции. Построение таблиц истинности

Логические
операции.
Построение таблиц
истинности
Цель: узнать что такое логика?
какая существует связь между двоичным
кодированием и алгеброй логики? как можно
использовать логические операции?
Введение
• Слово «логика» произошло от греческих слов «легос»
и «логос». «Легос» означает – «говорить»,
«пояснять», «логос» – «мудрость».
• Логикой называется наука о формах и законах
правильного мышления.
• Мышление – высшая форма познавательной
деятельности человека. Правильное мышление
играет решающую роль в деятельности людей. Чтобы
человек правильно мыслил, он должен подчиняться
определенным правилам и закономерностям.
Введение
Основные формы мышления:
• Понятие – это форма мышления, которая отражает
существенные признаки предметов. Объем понятия может
быть представлен как множество объектов. Основу
современной математики составляют логика и теория
множеств.
• Высказывание – это форма мышления, содержащая
утверждение или отрицание чего-либо. Высказывания
могут быть ложными или истинными. Вопросительные и
побудительные предложения не выражают высказываний.
Высказывания бывают простыми и сложными.
• Умозаключение – это форма мышления, при которой
мысль формируется в результате синтеза и обработки
нескольких высказываний и понятий.
Введение
Основатель логической алгебры — Джордж Буль. Он
изобрел своеобразную алгебру – систему обозначений и
правил, применимую к объектам, числам, буквам и
предложениям.
В основе булевой алгебры лежат операции
конъюнкция (И), дизъюнкция (ИЛИ) и отрицание (НЕ).
В XX веке ученые объединили двоичную систему
счисления с алгеброй логики Джорджа Буля, создав тем
самым основу для разработки современного цифрового
электронного компьютера.
Логика
Высказывание в математической логике может быть
истинным или ложным, третий случай не
рассматривается.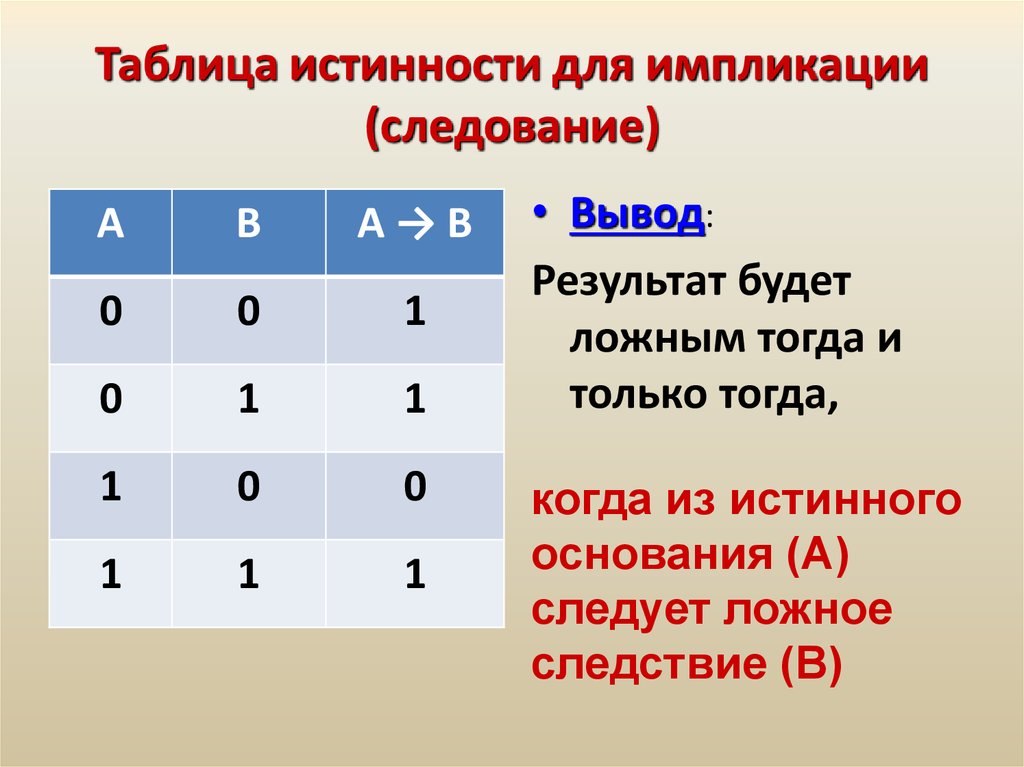
Если обозначим «истину» как 1, «ложь» как 0, тогда
можно выполнять операции с 1 и 0 или, другими
словами, в двоичном коде.
Алгебра логики – математический аппарат записи
логических высказываний, вычислений, упрощений и
преобразований.
Алгебра логики определяет правила вычислений
логических условий 1 (истина) и 0 (ложь).
Логические операции
Логическое сложение (дизъюнкция, показывается
символом ∨). Операция, соединяющая два или более
высказываний при помощи операции «ИЛИ»
(например, «А или В») называется логическим
сложением, или дизъюнкцией. Дизъюнкция в обычном
языке означает «или (or)».
Таблица 1
Дизъюнкция
A
B
A˅B
0
0
0
1
0
1
0
1
1
1
1
1
Логические операции
Логическое умножение (конъюнкция, обозначается
символом ∧). Операция, связывающая два или более
высказываний при помощи операции «И», называется
логическим умножением или конъюнкцией.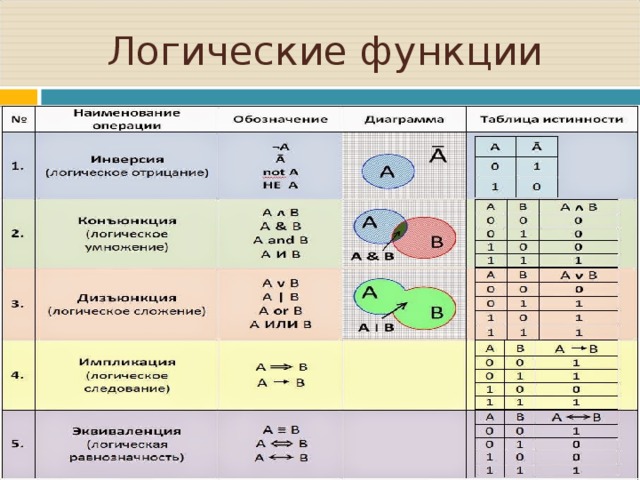
Конъюнкция в обычном языке означает «и (and)»
Таблица 2
Конъюнкция
A
B
A˄B
0
0
0
1
0
0
0
1
0
1
1
1
Логические операции
Логическое отрицание (инверсия). Отрицание «НЕ»,
которым логическое высказывание обращается в
обратное, называется логическим отрицанием или
инверсией (таблица 3). Инверсия в обычном языке
соответствует выражениям «неверно», «обращение в
обратное» и приставке «не (not)».
Таблица 3
Инверсия
A
B
0
1
1
0
Задания для закрепления:
Задание № 1.
Обратите в противоположное следующие высказывания.
1. Четные числа бывают простыми.
2. Самат выполнил заданные ему пять заданий.
Задание № 2.
Даны следующие простые высказывания.
1) А = {Монитор – устройство для печати информации на
бумаге},
2) В = {Принтер – устройство для ввода информации},
3) С = {Процессор – устройство обработки информации},
4) D = {Мышь – устройство хранения информации},
Используя таблицы 1, 2, 3 найдите значения следующих
логических операций. 1) (А∧В) 2) (С∨D) 3) (В∧С).
Таблица истинности
Таблица истинности – это таблица, в которой
представлены все значения, которые может принимать
высказывание при всех возможных значениях простых
высказываний, входящих в нее. В таблице истинности
отражаются четыре возможных исхода для двух
переменных. Это пары:
(0, 0), (0, 1), (1, 0), (1, 1).
Если в формуле три переменных, то количество
возможных комбинаций будет равно 8-ми, так как 23= 8.
(0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1),
(1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1,1).
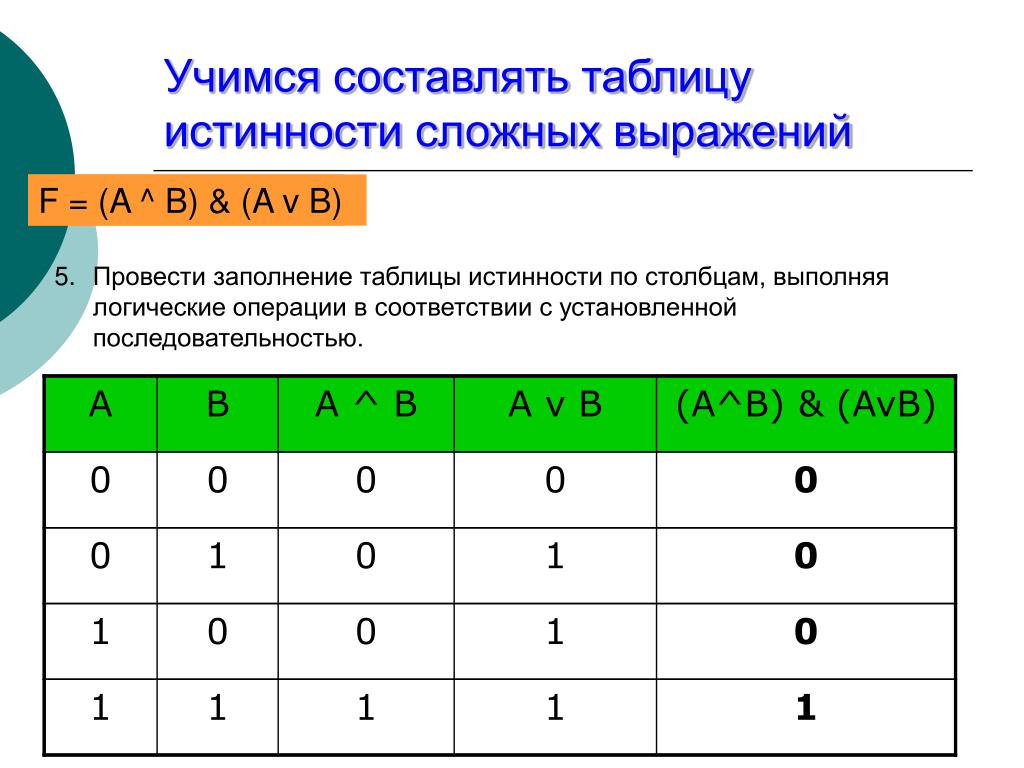
Логическое выражение
Логическое выражение – это составное
выражение, записанное в виде формулы.
При решении задач с логическими
высказываниями необходимо построение таблицы
истинности.
Приоритеты при выполнении логических
операций
1) выражения в скобках;
2) инверсия;
3) конъюнкция;
4) дизъюнкция.
Алгоритм построения таблицы
истинности для логических
элементов
1. Определить количество переменных n в логическом
выражении.
2. Подсчитать количество строк m=2n , n – количество
переменных.
3. Подсчитать количество логических операций в
выражении.
4. Для подсчета количества столбцов в таблице сложить
число переменных и число логических операций.
5. Установить последовательность выполнения логических
операций с учетом приоритетов.
6. Выписать наборы входных переменных.
7. Заполнить таблицы.
Пример
Для высказываний А = {22 – четное число} и В = {3 – четное
число} вычислите значения логических операций.
Пояснение решения задачи:
1. Если применить для двух простых высказываний
операцию (И) А∧В, тогда высказывание А – истинно, так как
число 22 – четное. А высказывание В – ложно, так как 3 –
нечетное число. Таким образом, согласно правилу для
операции И будет 1∧0 =0 (ложь).
2. Если применить для двух простых высказываний
операцию (ИЛИ) А∨В, тогда высказывание А – истинно, тогда
как В – ложно.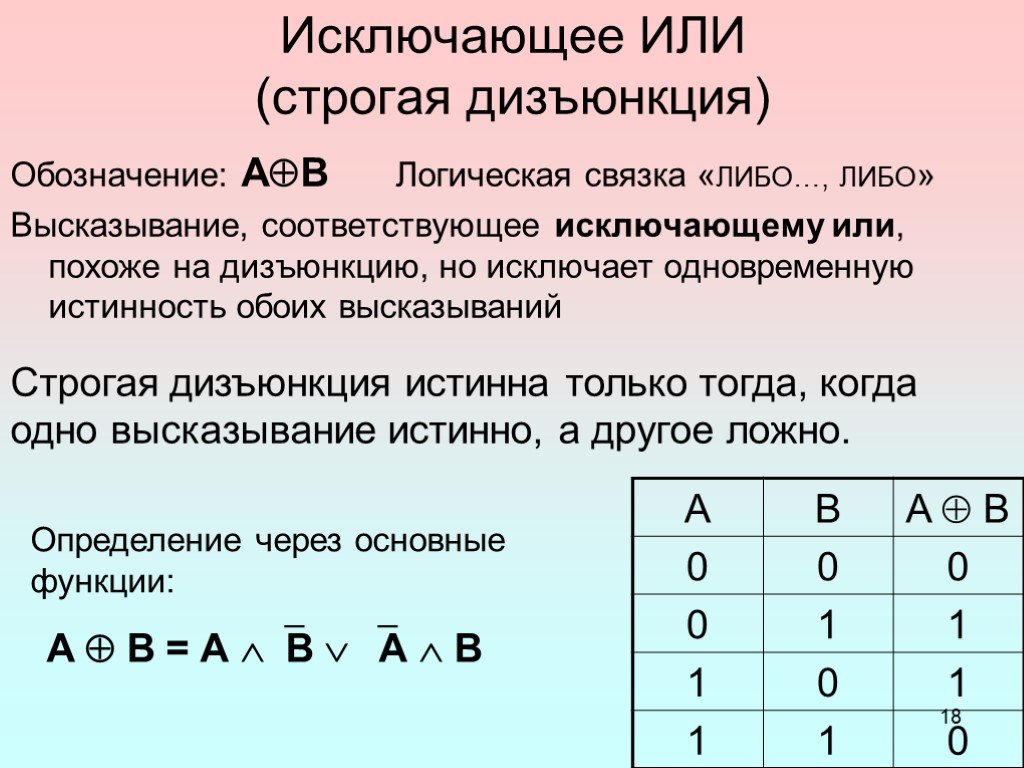 Таким образом, операция 1∨0 =1 (Истина).
3. Если высказывание А подвергнуть инверсии, то оно
будет ложным, так как обратится в высказывание «число 22
нечетное». Точно так же инверсия высказывания В «число 3
нечетное» будет истинным.
A∧B
Ложь (0)
A∨B
Истина (1)
A
Ложь (0)
B
Истина(1)
Задания для закрепления:
Постройте таблицу истинности (НЕ А ИЛИ В) И А
А
В
НЕ А
НЕ А ИЛИ В
(НЕ А ИЛИ В) И А
0
0
1
1
0
Домашнее задание:
Уровень А.
Найдите значения логических функций, приведенных ниже.
1) F = ((0>5) and (2>3)) or(4<5))
2) F = (1<5) and (1>0)
3) F = (3>2) or (3<1)
4) F = (3>2) or (2>0)
5) F = ((1>2) or (1<0)) and((–1>2) or (–1<0))
6) F = (2>5) and (2>3)
7) F = not (5>6)
8) F = not (6>5)
9) F = (2=0) or (2>0)
10) F = (3>0) or (2>0)
Примечание. Образец выполнения задания представлен в
таблице.
0>4
2>5
4<7
(0>4) and (2>5)
F = (0>4) and (2>5) or(4<7)
0
0
1
0
1
Домашнее задание:
Уровень В.
Найдите значения логических функций, приведенных ниже.
1. F = (1∨1)∨(1∨0)
2. F = (0∧0)∧(1∧1)
3. F = (0∧1)∨(0∧1)
4. F = (0∨0)∧(1∧1)
5. F = (1∨0)∧(0∧1)
Уровень С.
Даны высказывания – А = {4+19=21} и B = {8 + 3 = 9}.
Определите истинность следующих выражений:
А∧В, А, В, А∨В

Основные логические операции и таблицы истинности

Как мы уже знаем, используя логические связки можно строить сложные высказывания, или, говоря по-другому, определять логические операции над логическими переменными. Простые высказывания – это аргументы логической операции (независимые переменные). Результат такой логической операции можно задать, используя таблицу истинности.

Значения логической операции для всех сочетаний значений логических переменных — или, как это иначе называют, наборов логических переменных — называется таблицей истинности.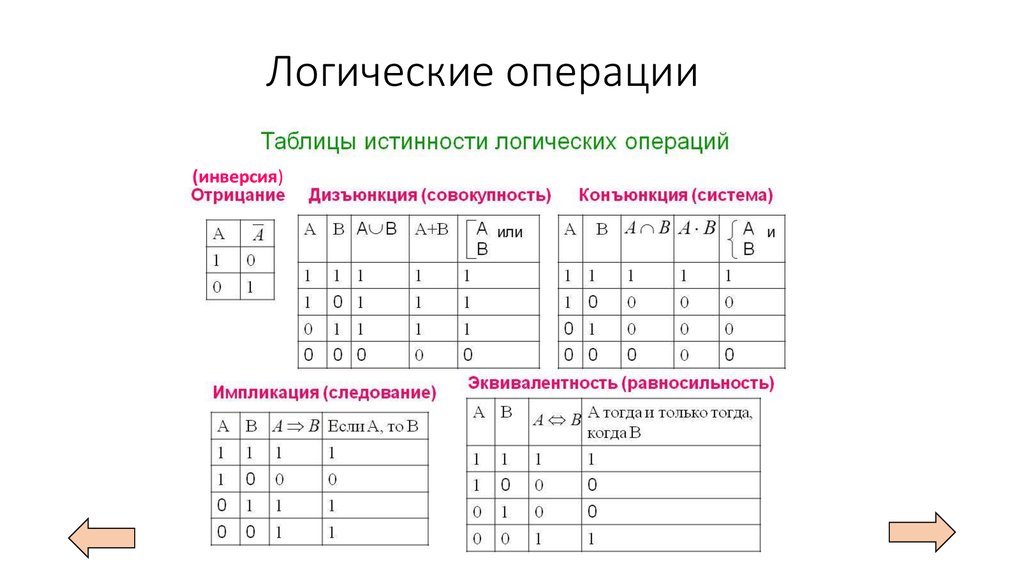 Таблица истинности полностью и однозначно определяет логическую операцию.

Таким образом, в любой логической операции имеются аргумент(ы), значения которых мы задаём и, соответствующее этим аргументам, значение логической операции. Набор логических переменных – это конкретное значение всех аргументов операции.

Так как каждая логическая переменная может принимать только два значения (0 или 1), то легко подсчитать полное количество наборов для любой логической операции. Тогда, если набор состоит из одной переменной, то таких наборов два. Если переменных две, то количество наборов четыре. В целом, количество наборов логических переменных (K) для сложного высказывания можно определить по формуле: K=2ⁿ, где n — количество логических переменных.

Рассмотрим подробнее наиболее интересные логические операции над одной или двумя переменными.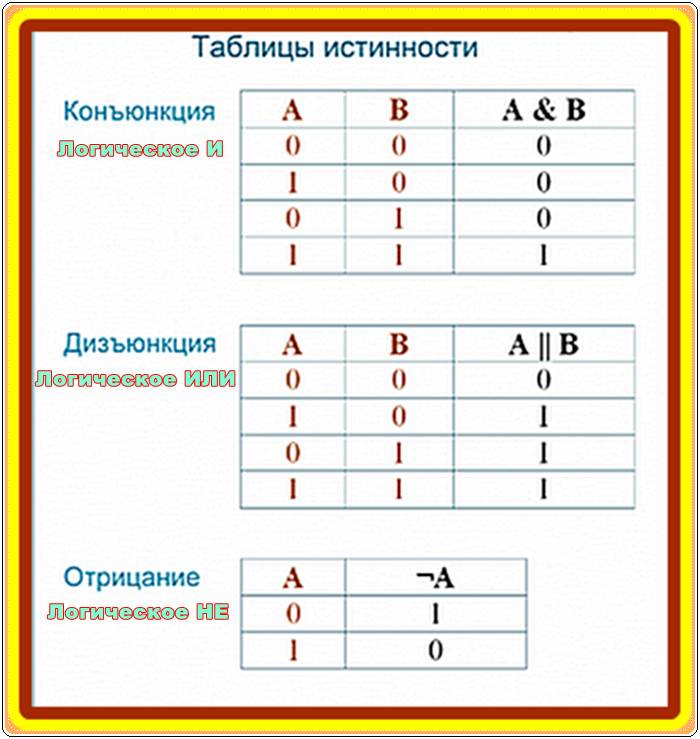

Логическое отрицание

Присоединение частицы «не» к сказуемому данного простого высказывания A называется операцией логического отрицания или инверсией. Обозначается илиA .

Иногда вместо приведенного определения используют другое, ему эквивалентное: присоединение слов «Неверно, что …» ко всему данному высказыванию A называется операцией логического отрицания. В результате выполнения операции логического отрицания получается новое высказывание. Например:

Таблица истинности инверсии имеет вид:

Инверсия логической переменной истинна, если сама переменная ложна, и, наоборот, инверсия ложна, если переменная истинна.

Логическое умножение

Соединение двух простых высказываний A и B в одно составное с помощью союза «и» называют логическим умножением или конъюнкцией, а результат операции — логическим произведением.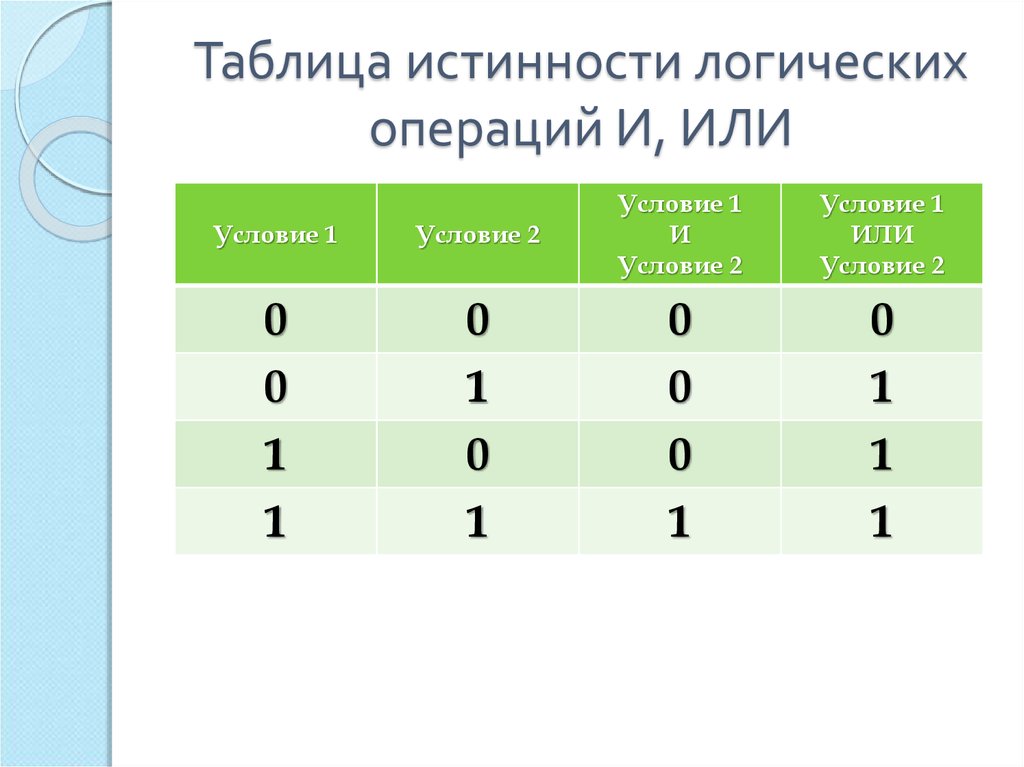

Указание о логическом перемножении простых высказываний A и B обозначается так: A ∙B

, AB, A Λ B, A & B.

Например:

В русском языке в качестве операции «логическое умножение» помимо союза «и» используются союзы «но» и «а».

Таблица истинности конъюнкции имеет следующий вид:

Конъюнкция двух логических переменных истинна тогда и только тогда, когда оба высказывания истинны.

Это определение можно обобщить для любого количества логических переменных, объединенных конъюнкцией.

A∙ B∙ C = 1, только если A = 1, B

= 1, C = 1. (1)

Логическое сложение

Перед тем как привести определение этой операции, дадим некоторые разъяснения.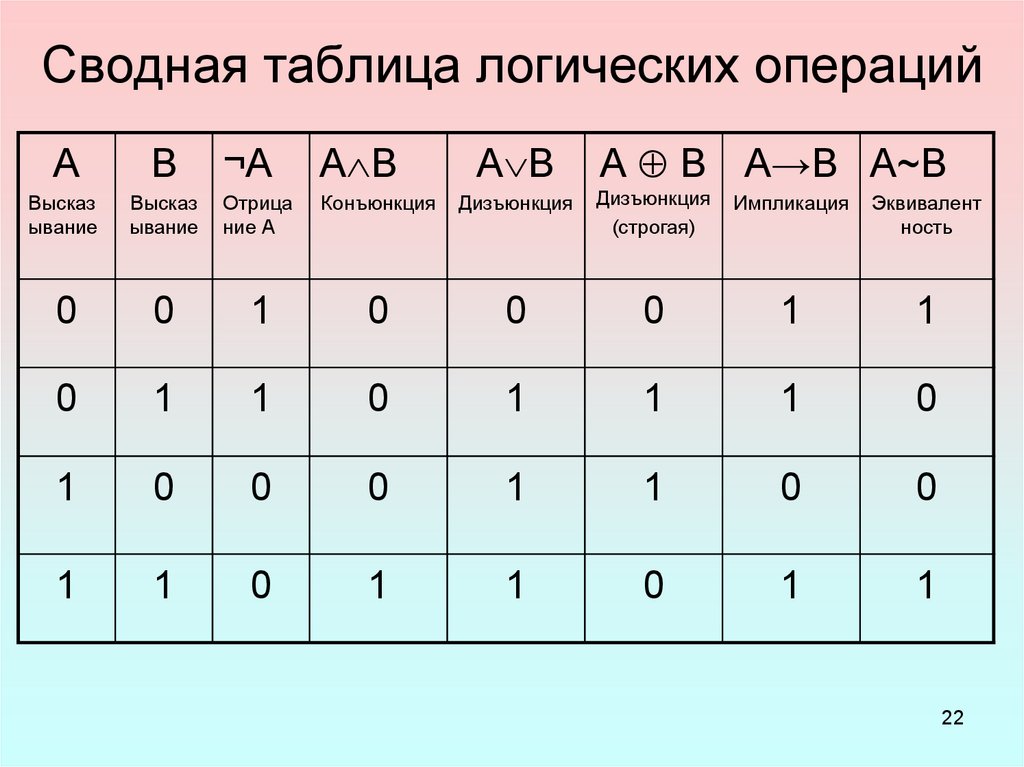 Союз «или» в обиходе мы применяем в двух значениях: исключающем и неисключающем. Разъясним это примерами.

Рассмотрим повествовательное предложение: «Володя вчера в шесть часов вечера читал книгу или ехал в автобусе на стадион.». Союз «или» использован в этом предложении в неисключающем смысле — Володя мог читать и одновременное ехать в автобусе. Одно не исключает другого.

Рассмотрим еще одно повествовательное предложение. «Володя вчера наблюдал за ходом матча с западной или восточной трибуны». Здесь союз «или» имеет исключающий характер — две описываемые ситуации исключают друг друга: нельзя наблюдать один и тот же матч одновременно с двух противоположных трибун.

Соединение двух простых высказываний A и B в одно составное с помощью союза «или», употребляемого в неисключающем смысле, называется логическим сложением или дизъюнкцией, а полученное составное высказывание — логической суммой.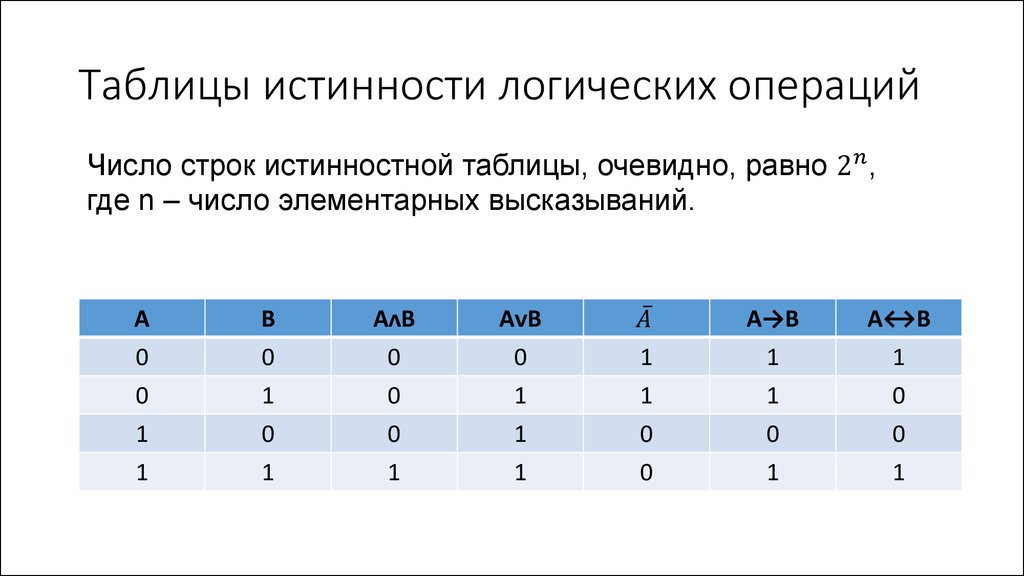

Указание о необходимости выполнить логическое сложение высказываний

A и B записывается так: A + B или A v B. Например:

Таблица истинности дизъюнкции имеет следующий вид:

Дизъюнкция двух логических переменных ложна тогда и только тогда, когда оба высказывания ложны.

Это определение можно обобщить для любого количества логических переменных, объединенных дизъюнкцией.

A + B + C = 0, только если A = 0, B = 0, C = 0. (2)

3.1: Предложения и логические операторы

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

80504

• Al Doerr & Ken Levasseur
• Массачусетский университет Лоуэлл

Propositions

Определение \(\PageIndex{1}\): Proposition

Предложение — это предложение, к которому может быть осмысленно применено одно и только одно из условий true или false .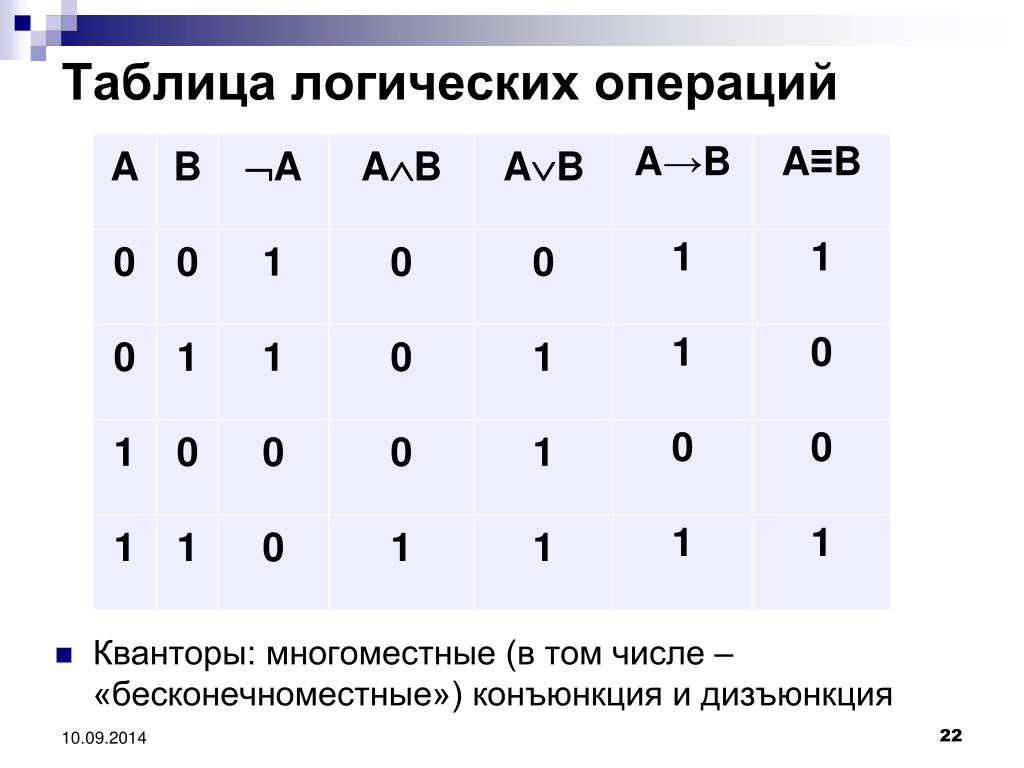

Пример \(\PageIndex{1}\): некоторые утверждения

«Четыре четные», «\(4 \in \{1,3, 5\}\)» и «\(43 > 21\) )» являются предложениями.

В традиционной логике декларативное утверждение с определенным значением истинности считается предложением. Хотя нашей конечной целью является обсуждение математической логики, мы не будем полностью отделяться от традиционной обстановки. Это естественно, потому что основные предположения или постулаты математической логики моделируются по образцу логики, которую мы используем в повседневной жизни. Поскольку в повседневной речи часто используются сложные предложения, мы ожидаем, что логические предложения содержат такие связки, как слово «и». Утверждение «Европа поддерживает жизнь или Марс поддерживает жизнь» является предложением и, следовательно, должно иметь определенное истинностное значение. Каким бы ни было это истинное значение, оно должно быть таким же, как истинное значение «Марс поддерживает жизнь или Европа поддерживает жизнь».

Логические операции

Существует несколько способов объединения простых операторов в составные. Слова/фразы и , или , не , если… то… , и …если и только если… можно добавить к одному или нескольким предложениям для создания новое предложение. Чтобы избежать путаницы, мы точно определим значение каждого из них и введем его стандартный символ. За исключением отрицания (

не ), все операции действуют на пары предложений. Поскольку каждое предложение имеет два возможных значения истинности, существует четыре способа, которыми истинность может быть присвоена двум утверждениям. При определении эффекта, который логическая операция оказывает на два предложения, результат должен быть указан для всех четырех случаев. Удобнее всего это сделать с помощью таблицы истинности, которую мы проиллюстрируем определением слова 9.0036 и .

Определение \(\PageIndex{2}\): Логическая конъюнкция

Если \(p\) и \(q\) являются высказываниями, их конъюнкция \(p \textrm{ и } q\) (обозначается \( p \land q\)) определяется таблицей истинности

\begin{equation*} \begin{array}{ccc} p & q & p\land q \\ \hline 0 & 0 & 0 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \\ 1 & 1 & 1 \\ \end{array} \end{equation*}

Примечание \(\PageIndex{1}\)

1. Чтобы прочитать эту правду таблицы, вы должны понимать, что любая строка представляет случай: один возможный набор значений для \(p\) и \(q\text{. }\)
2. Цифры 0 и 1 используются для обозначения ложных и истинных значений соответственно. Это согласуется со способом, которым многие языки программирования обрабатывают логические или логические переменные, поскольку один бит, 0 или 1, может представлять значение истинности.
3. В каждом случае символ под \(p\) представляет истинное значение \(p\text{.}\) То же верно для \(q\text{.}\) Символ под \(p \ land q\) представляет его истинное значение для этого случая. Например, вторая строка таблицы истинности представляет случай, когда \(p\) ложно, \(q\) истинно, а результирующее значение истинности для \(p \land q\) ложно. Как и в повседневной речи, \(p \land q\) истинно только тогда, когда оба предложения истинны.
4. Буквы \(x\text{,}\) \(y\) и \(z\) часто используются в алгебре для обозначения числовых переменных, \(p\text{,}\) \(q\ ) и \(r\) кажутся наиболее часто используемыми символами для логических переменных. Когда мы говорим, что \(p\) является логической переменной, мы имеем в виду, что любое предложение может занять место \(p\text{.
   }\)
5. И последнее замечание: порядок, в котором мы перечисляем случаи в таблице истинности, в этой книге стандартизирован. Если таблица истинности включает два простых предложения, числа под простыми предложениями можно интерпретировать как двузначные двоичные целые числа в возрастающем порядке: 00, 01, 10 и 11 для 0, 1, 2 и 3 соответственно.

Определение \(\PageIndex{3}\): Логическая дизъюнкция

Если \(p\) и \(q\) являются высказываниями, их дизъюнкция \(p \textrm{ или } q\) (обозначается \( p \lor q\)), определяется таблицей истинности

\begin{equation*} \begin{array}{ccc} p & q & p\lor q \\ \hline 0 & 0 & 0 \\ 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 1 \\ \end{массив} \end{уравнение*}

Определение \(\PageIndex{4}\): логическое отрицание

Если \ (p\) есть предложение, его отрицание, \(\textrm{not } p\text{,}\) обозначается \(\neg p\text{,}\) и определяется таблицей истинности

\begin{equation*} \begin{array}{cc} p & \neg p \\ \hline 0 & 1 \\ 1 & 0 \\ \end{array} \end{equation*}

Примечание \ (\PageIndex{2}\)

Отрицание — единственный стандартный оператор, который действует на одно предложение; следовательно, необходимы только два случая.

Рассмотрим следующие предложения из повседневной речи:

1. Я уволюсь, если не получу повышения.
2. Если я пройду финал, я закончу школу.
3. Я пойду в кино, если моя машина заведется.

Все три суждения условны, их все можно переформулировать так, чтобы они соответствовали форме «Если Условие , то Заключение ». Например, первое утверждение можно переписать так: «Если я не получу повышения, я уволюсь».

Условное утверждение следует интерпретировать как гарантию; если условие истинно, то ожидается, что заключение будет истинным. Говорит не больше и не меньше.

Определение \(\PageIndex{5}\): условное выражение

Условное утверждение «Если \(p\), то \(q\text{,}\)», обозначаемое \(p \rightarrow q\text{,}\), определяется таблицей истинности

Таблица \(\ PageIndex{1}\: Таблица истинности для \(p\стрелка вправо q\)

\(p\)	\(к\)	\(p\стрелка вправо q\)
\(0\)	\(0\)	\(1\)
\(0\)	\(1\)	\(1\)
\(1\)	\(0\)	\(0\)
\(1\)	\(1\)	\(1\)

Пример \(\PageIndex{2}\): Анализ условного суждения

Предположим, ваш преподаватель сказал вам: «Если вы получите оценку 95 или выше на выпускном экзамене, вы получите пятерку на этом экзамене».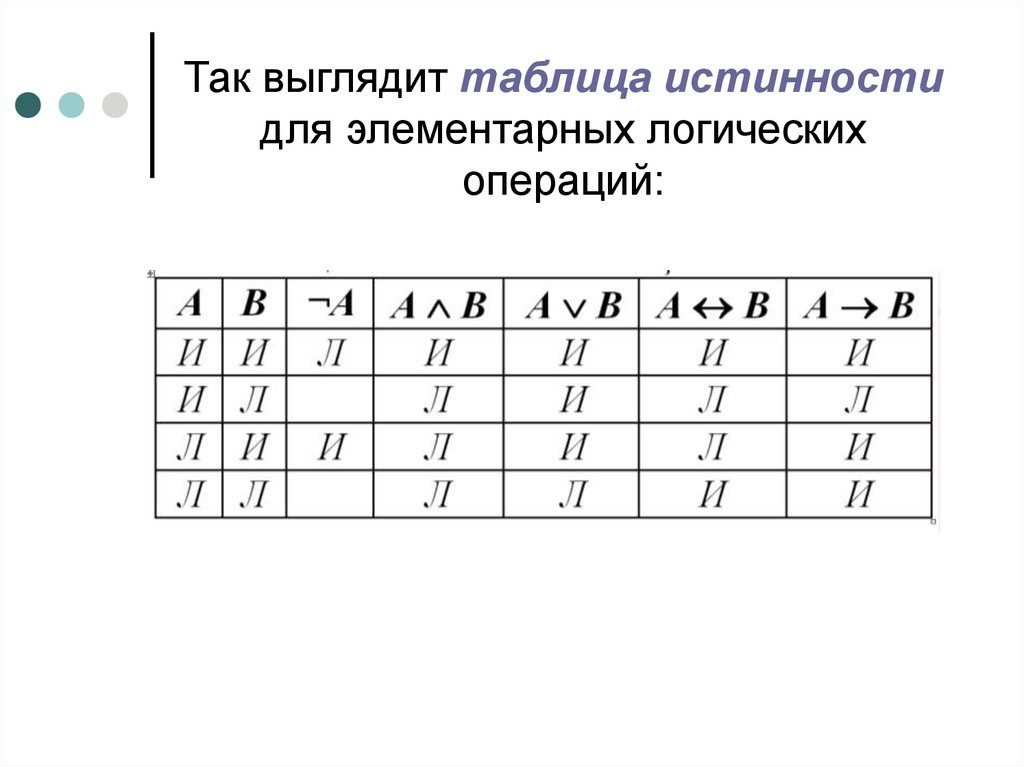 курс.» Ваш инструктор дал вам обещание. Если вы выполняете его условие, вы ожидаете, что вывод (получение пятерки) будет не за горами. Предположим, вам вернули итоговую оценку. Ваш инструктор сказал правду или он виновен во лжи?

Случай I: Ваш итоговый балл за экзамен был меньше 95 (условие ложно), и вы не получили пятерку (заключение ложно). Инструктор сказал правду.

Случай II: Ваш итоговый балл на экзамене был ниже 95, но вы получили пятерку за курс. Инструктор сказал правду. (Возможно, ваш общий средний балл по курсу был превосходным.)

Случай III: Ваш итоговый экзаменационный балл был выше 95, но вы не получили пятерку. Преподаватель солгал.

Случай IV: Ваш итоговый балл за экзамен был выше 95, и вы получили пятерку. Инструктор сказал правду.

Подводя итог, единственный случай, когда условное суждение ложно, это когда условие истинно, а заключение ложно.

Порядок условия и заключения в условном суждении важен. Если поменять местами условие и заключение, получится другое предложение.

Определение \(\PageIndex{6}\): Обратное

Обратное предложение \(p \rightarrow q\) есть предложение \(q \rightarrow p\text{.}\)

Обратное выражение «Если вы получите оценку 95 или выше на выпускном экзамене, то вы получите пятерку по этому курсу»: «Если вы получите пятерку по этому курсу, то вы получите оценку 95 или выше. лучше на выпускном экзамене». Должно быть ясно, что эти два утверждения говорят о разных вещах.

Здесь есть предложение, связанное с \(p \rightarrow q\), которое имеет тот же логический смысл. Это противопоставление.

Определение \(\PageIndex{7}\): Противоположный

Противоположным высказыванию \(p \rightarrow q\) является высказывание \(\neg q \rightarrow \neg p\text{.}\)

Как мы увидим при обсуждении логических доказательств, мы можем доказать условное суждение, доказывая его противоположность, что может быть несколько проще.

Определение \(\PageIndex{8}\): Биусловное высказывание

Если \(p\) и \(q\) являются высказываниями, биусловное высказывание «\(p\) тогда и только тогда, когда \(q\text {,}\)», обозначаемый \(p \leftrightarrow q\text{,}\), определяется таблицей истинности

\begin{equation*} \begin{array}{ccc} p & q & p\leftrightarrow q \\ \hline 0 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \\ 1 & 1 & 1 \\ \end{массив} \end{уравнение*}

Обратите внимание, что \(p \leftrightarrow q\) истинно, когда \(p\) и \(q\) имеют одинаковые значения истинности.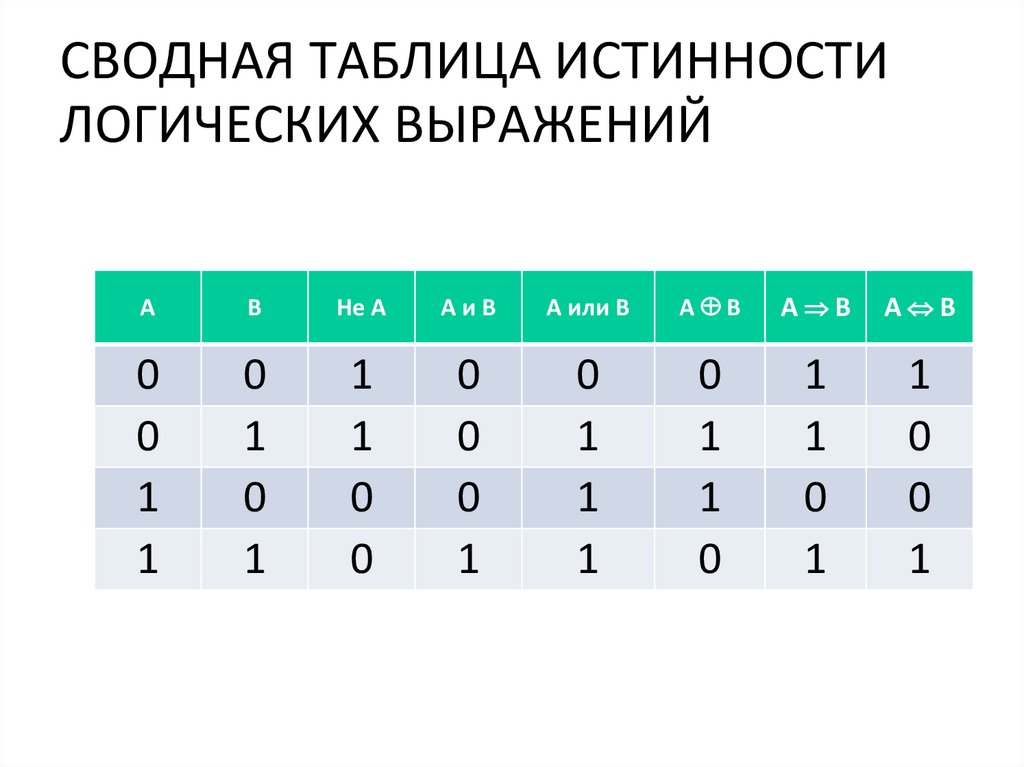 Обычно «если и только если» сокращают до «iff».

Хотя выражения «если…, то…» и «…если и только если…» часто используются в повседневной речи, существует несколько альтернативных форм, о которых вам следует знать. Они сведены в следующие списки.

Все следующие эквиваленты «Если \(p\), то \(q\)»:

• \(p\) подразумевает \(q\text{.}\)
• \(q\) следует из \(p\text{.}\)
• \(p\text{,}\) только если \(q\text{.}\)
• \(q\text{,}\) если \(p\text{.}\)
• \(p\) достаточно для \(q\text{.}\)
• \(q\) необходимо для \(p\text{.}\)

Все следующие эквиваленты «\(p\) тогда и только тогда, когда \(q\)»:

• \(p\) необходимо и достаточно для \(q\text{.}\)
• \(p\) эквивалентно \(q\text{.}\)
• Если \(p\text{,}\), то \(q\text{,}\), а если \(q\text{,}\), то \(p\text{.}\)
• Если \(p\text{,}\), то \(q\) и наоборот.

Упражнения

Упражнение \(\PageIndex{1}\)

Пусть \(d\) = «Мне нравятся дискретные структуры», \(c\) = «Я пройду этот курс» и \(s\) = «Я буду выполнять свои задания». Выразите каждое из следующих утверждений в символической форме:

1. Мне нравятся дискретные структуры, и я пройду этот курс.
2. Я буду выполнять задания или не пройду этот курс.
3. Неправда, что я люблю дискретные структуры и буду выполнять свои задания.
4. Я не буду выполнять задание и не пройду этот курс.

Ответить

1. \(\displaystyle d\land c\)
2. \(\displaystyle s\lor \neg c\)
3. \(\displaystyle \neg (d\land s)\)
4. \(\displaystyle \neg s\land \neg c\)

Упражнение \(\PageIndex{2}\)

Для каждого из следующих предложений определите простые предложения, выразите составное предложение в символической форме и определите, истинно оно или ложно:

1. Мир плоский или ноль — четное целое число.
2. Если 432 802 кратно 4, то 432 802 четно.
3. 5 — простое число, а 6 не делится на 4.
4. \(3 \in \mathbb{Z}\) и \(3 \in \mathbb{Q}\text{.}\)
5. \(2/3 \in \mathbb{Z}\) и \(2/3 \in \mathbb{Q}\text{.}\)
6. Сумма двух четных целых чисел четна, а сумма двух нечетных целых чисел нечетна.

Упражнение \(\PageIndex{3}\)

Пусть \(p =\)»\(2 \leq 5\)», \(q\) = «8 — четное целое число» и \(r \) = «11 — простое число». Выразите следующее в виде утверждения на английском языке и определите, верно оно или нет:

1. \(\displaystyle \neg p \land q\)
2. \(\displaystyle p\стрелка вправо q\)
3. \(\displaystyle (p\land q)\to r\)
4. \(\displaystyle p \rightarrow (q \lor (\neg r))\)
5. \(\displaystyle p \rightarrow ((\neg q)\lor (\neg r))\)
6. \(\displaystyle (\neg q) \rightarrow (\neg p)\)

Ответить

1. \(2>5\), а 8 — четное целое число. ЛОЖЬ.
2. Если \(2\leqslant 5\), то 8 — четное целое число. Истинный.
3. Если \(2\leqslant 5\) и 8 — четное целое число, то 11 — простое число. Истинный.
4. Если \(2\leqslant 5\), то либо 8 — четное целое число, либо 11 — не простое число. Истинный.
5. Если \(2\leqslant 5\), то либо 8 является нечетным целым числом, либо 11 не является простым числом. ЛОЖЬ.
6. Если 8 не является четным целым числом, то \(2>5\text{.}\) Истинно.

Упражнение \(\PageIndex{4}\)

Перепишите каждое из следующих утверждений, используя другие условные формы:

1. Если целое число кратно 4, то оно четное. 92\) является необходимым условием для \(x = y\text{.}\)

Упражнение \(\PageIndex{5}\)

Напишите обратное предложение из упражнения \(\PageIndex{4}\). Сравните истинность каждого предложения и его обратного.

Ответить

Верно только обратное \(d\).

---

Эта страница под названием 3.1: Предложения и логические операторы распространяется по лицензии CC BY-NC-SA, автором, ремиксом и/или куратором этой страницы являются Эл Доерр и Кен Левассер.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Эл Дорр и Кен Левассер

   Лицензия

   CC BY-NC-SA

   Показать страницу TOC

   нет

2. Теги

   На этой странице нет тегов.

Определение истины с помощью логических операторов с примерами кода

Определение истины с помощью логических операторов с примерами кода

Используя язык программирования, мы вместе решим головоломку «Определение истины с помощью логических операторов» на этом уроке. Это демонстрируется в следующем коде.

 Помните также, что логические операторы имеют
приоритет, как и арифметические операторы.
! имеет наивысший приоритет, за ним следует &&, а затем ||.
Если вам нужно переопределить приоритет, вы можете обернуть все, что хотите.
хотите выполнить первым в круглых скобках, чтобы дать ему приоритет.
Скобки всегда выполняются первыми. вот несколько примеров
демонстрируя, как вы можете контролировать порядок операций:
пусть а = истина;
пусть б = истина;
пусть с = ложь;
пусть д = ложь;
a && b && c && d // Операторы выполняются слева направо
а || б && в || d // b && c оценивается первым
(a || b) && (c || d) // a || b вычисляется, затем c || д, затем &&
!(a || b) && (c || d) // то же, что и выше, но (a || b) инвертируется перед вычислением &&
 

На множестве иллюстративных примеров мы продемонстрировали, как решать задачу определения истины с помощью логических операторов.

Что такое логические операторы с таблицей истинности?

Таблица истинности используется для выполнения логических операций в математике. Эти операции включают булеву алгебру или булевы функции. В основном он используется для проверки того, является ли пропозициональное выражение истинным или ложным в соответствии с входными значениями. Это основано на булевой алгебре.

Как найти истинностное значение?

Какие 5 логических операторов?

Существует пять символов логических операторов: тильда, точка, клин, подкова и тройная черта.

Что такое ∧ в таблице истинности?

Символ, который используется для представления оператора AND или логической конъюнкции, — ∧. Это похоже на перевернутую букву V. Если у нас есть два простых оператора P и Q, и мы хотим сформировать составной оператор, соединенный оператором AND, мы можем записать его так: P ∧ Q \large{P \wedge Q} P ∧Q.

Каковы примеры логических операторов?

Логические операторы

Что такое таблица истинности в логике?

Таблица истинности представляет собой разбивку логической функции путем перечисления всех возможных значений, которые может получить функция. Такая таблица обычно содержит несколько строк и столбцов, причем верхняя строка представляет собой логические переменные и их комбинации, по возрастающей сложности ведущие к конечной функции.

Каковы значения истинности для P ∧ Q → Q?

Итак, поскольку у нас нет утверждений по обе стороны от символа «и», которые оба верны, утверждение ~p∧q ложно. Итак, ~p∧q=F. Теперь, когда мы знаем значение истинности всего в скобках (~p∧q), мы можем соединить это утверждение с ∨p, чтобы получить окончательное утверждение (~p∧q)∨p. Таблицы истинности.

Каковы значения истинности для P ∨ Q?

Истинность или ложность предложения называется его истинностным значением. Обратите внимание, что ∨ представляет собой неисключающее или, т. Е. p ∨ q истинно, когда любое из p, q истинно, а также когда оба истинны. С другой стороны, ⊕ представляет собой исключающее или, т. е. p ⊕ q истинно только тогда, когда истинно одно из p и q. 1.1.

Как узнать истинность условного оператора?

Шаг 1.