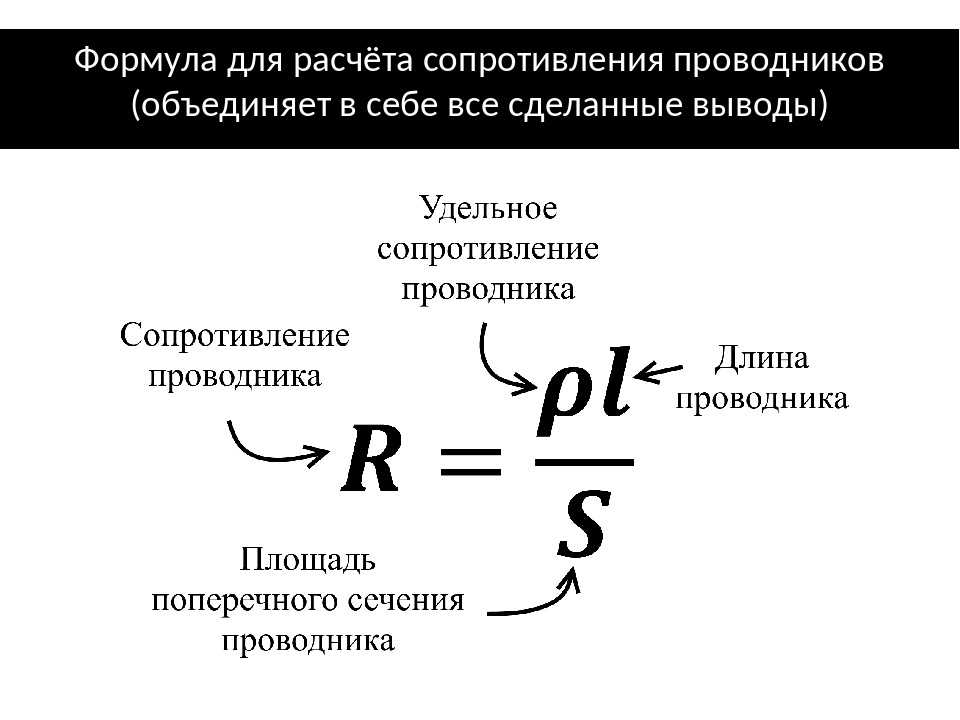
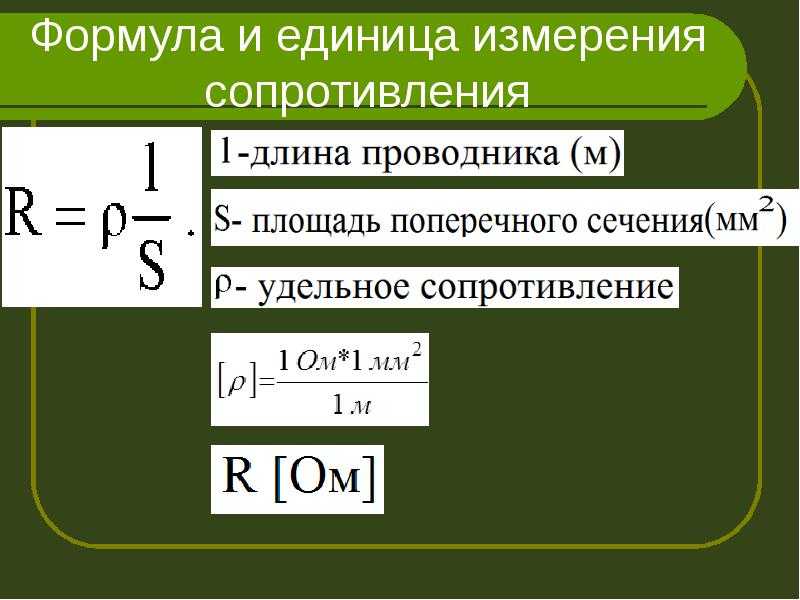
| ЛАБОРАТОРНАЯ РАБОТА №2. ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО СОПРОТИВЛЕНИЯ ПРОВОДНИКА. Электрический ток есть упорядоченное движение зарядов. Эти заряды в учениях о токах называются носителями тока. В металлах и полупроводниках носителями тока являются электроны, в электролитах и ионизованных газах – положительные и отрицательные ионы. Одним из главных способов возбуждения электрического тока в телах является создание и поддержание в них электрического поля. Как показывает опыт, для многих тел (например, металлов) в широких пределах плотность электрического тока j пропорциональна напряженности электрического поля Е. Это – один из важнейших, хотя и не фундаментальных, законов электродинамики. Он называется законом Ома (1787-1854). Математически закон Ома выражается формулой: (1) где λ — постоянная для данного материала величина, называемая его удельной проводимостью или электропроводностью. Строго говоря, закон Ома справедлив лишь для физически однородных тел. Величина, обратная электропроводности, называется удельным сопротивлением материала: (2) Рассмотрим случай, когда электрические токи текут вдоль тонких проводов (проволок). Направление тока будет совпадать с направлением оси провода. Через поперечное сечение S провода в единицу времени проходит количества электричества (3) называемое силой тока и просто током. Если ток постоянен, то из-за сохранения заряда величина I будет одна и та же вдоль всего провода. Пусть и – потенциалы концов 1 и 2 провода длиной (4) (5) Величина, определяемая формулой (5), называется электрическим сопротивлением или просто сопротивлением провода. Формула (4) выражает закон Ома для участка цепи в интегральной форме, в отличие о формулы (1) выражающей этот же закон в дифференциальной форме. Сопротивление проводника можно измерить двумя способами:
При измерении по первому методу используется схема №1, по второму схема №2. При работе с данной схемой воспользуемся следующими формулами: Где — общее сопротивление, — внутреннее сопротивление амперметра, U – показания вольтметра, I – показания амперметра. Рассмотрим теперь схему 2: Где — общее сопротивление, — внутреннее сопротивление амперметра, U – показания вольтметра, I – показания амперметра. Точность расчетов по этим схемам определяется точностью амперметра и вольтметра. Теперь если мы в качестве сопротивления возьмем проводник длинной , поперечным сечением S, то, зная R, сможем определить удельное сопротивление: (6)
Таблица1
Измерение удельного сопротивления по методу с точным определением напряжения.
Таблица 2
4. Пользуясь формулой , определите R; =2500 Ом – внутренне сопротивление проводника. 5. Рассчитать погрешность измерений.
Литература:
Каталог: win1251 win1251 -> Диалектика добра и зла: социально-философский аспект win1251 -> Изменение структуры ночного сна при наземном моделировании межпланетного полета win1251 -> Оценка функционального состояния человека в условиях космического полета на основе анализа вариабельности сердечного ритма 14.  03. 08 авиационная, космическая и морская медицинаwin1251 -> Совершенствование врачебно-летной экспертизы при сердечно-сосудистой патологии (клинико-психологическое исследование) 14. 00. 32 авиационная, космическая и морская медицина win1251 -> Психофизиологические корреляты стрессоустойчивости оператора 14. 00. 32 Авиационная, космическая и морская медицина 19. 00. 03 Психология труда. Инженерная психология, эргономика win1251 -> Физиологические факторЫ, определяющие физическую работоспособность человека в процессе многолетней адаптации к специфической мышечной деятельности 03. 00. 13 физиология Скачать 46.91 Kb. Поделитесь с Вашими друзьями: |
Формула натяжения с примерами решений
Формула натяжения
Сила, действующая на длину гибкого участка, такого как веревка, кабель или цепь, известна как сила формулы натяжения.
Сила, притягиваемая и передаваемая в осевом направлении с помощью веревки, троса, цепи или другого подобного одномерного непрерывного объекта, или каждого конца стержня или другого подобного трехмерного объекта; напряжение также может быть описано как пара сил действие-реакция, действующих на каждом конце вышеупомянутых элементов.
Сила натяжения
На латыни «натяжение» означает «растяжение». В физике сила, приложенная к длине гибкого участка, такого как веревка, кабель или цепь, известна как сила формулы натяжения. Мы знаем, что сила натяжения указывает на толчок или натяжение. В физике мы сталкиваемся с несколькими видами сил, такими как вес, нормальная сила, толчок и удар. В зависимости от того, как он работает и взаимодействует, сила или мощность могут быть контактными или бесконтактными. Сила натяжения представляет собой контактную силу, передаваемую отрезком гибкого материала.
Суммарная энергия равна: Fnet = T − W = 0
T = W ± ma
Если тело движется вверх, напряжение называется T = W + ma
3 тело опускается T = W – ma
Напряжение, также известное как мощность пары «действие-противодействие», применяется к каждому компоненту адаптивного предмета.
Если мы исследуем сшивание, то часть струны на одной стороне поперечного сечения будет использовать силу действия на часть струны на противоположной стороне поперечного сечения. Точно так же второй сегмент троса использует силу реакции предыдущего сегмента.
В каждом поперечном сечении силы растяжения видны с обеих сторон. На концах веревка будет оказывать давление на привязанный к ней предмет (гравитация), и объект будет использовать силу реакции веревки, чтобы подтянуться ближе к веревке. Направление этой силы коррелирует с длиной веревки.
Когда атомы или молекулы расходятся на атомном уровне и накапливают потенциальную энергию, в то время как восстанавливающая сила все еще присутствует, восстанавливающая сила может создавать напряжение.
В случае тел, подвешенных на цепи, тросе, веревке и т. д., натяжение может быть ясно объяснено. Он обозначается буквой T (иногда также обозначается как Ft).
Решаемые примеры
В.
Легкая нерастяжимая струна выдерживает 15-килограммовый груз, свисающий с ее нижнего конца. Каково натяжение струны, если верхний конец струны надежно закреплен на крюке на крыше?
A. Из-за того, что тело не движется, а просто болтается, натяжение нити прямо пропорционально весу тела.
м = 15 кг
T = W = мг = 15 × 9,8 = 147 Н
Измерение удельного сопротивления с помощью четырехточечного датчика
Четырехточечный датчик представляет собой простой прибор для измерения удельного сопротивления образцов полупроводников. Пропуская ток через два внешних датчика и измеряя напряжение через внутренние датчики, можно измерить удельное сопротивление подложки. Концентрация легирования может быть рассчитана по удельному сопротивлению с использованием формул, обсуждаемых в Приложениях, и калькулятора удельного сопротивления PV Lighthouse 9.0005
Измерение поверхностного удельного сопротивления
Поверхностное сопротивление верхнего эмиттерного слоя очень легко измерить экспериментально с помощью «четырехточечного датчика».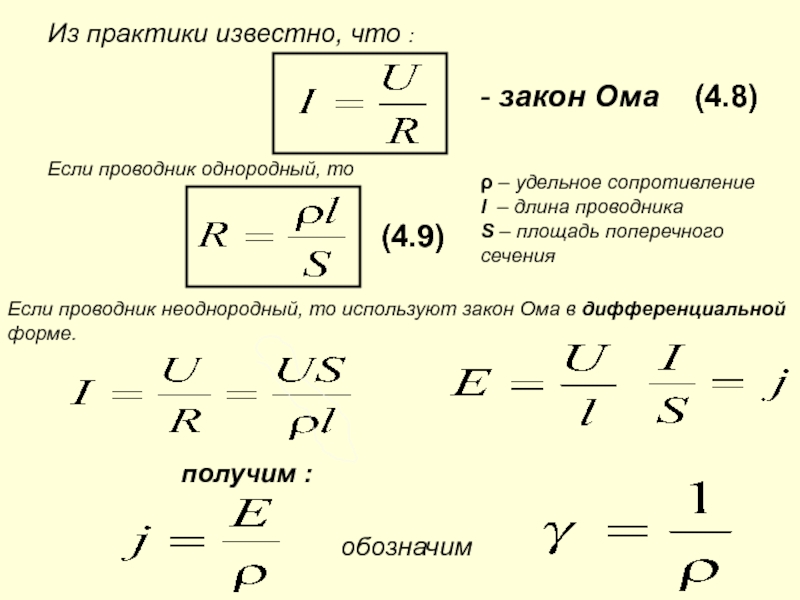
Ток проходит через внешние датчики и индуцирует напряжение во внутренних датчиках напряжения. Соединение между материалами типа n и p ведет себя как изолирующий слой, и ячейка должна находиться в темноте.
Использование четырехточечного датчика для измерения поверхностного сопротивления солнечного элемента.
Используя показания напряжения и тока датчика:1
Где:
πln2=4,532
Типичное удельное сопротивление слоя эмиттера кремниевых солнечных элементов находится в диапазоне 30-100 Ом/□.
При обычном использовании ток устанавливается равным 4,53 мА, поэтому удельное сопротивление представляет собой просто показание напряжения в мВ.
Измерение удельного объемного сопротивления
Измерение удельного объемного сопротивления аналогично измерению поверхностного удельного сопротивления, за исключением того, что удельное сопротивление в см -3 сообщается с использованием толщины пластины, t:
ρ=πln2VIt=4,532VIt
Где t — толщина слоя/пластины в см.
Приведенная выше простая формула работает, когда толщина пластины меньше половины расстояния между датчиками ( t < s /2) 2. Для более толстых образцов формула принимает следующий вид:
.
Следующий калькулятор реализует приведенное выше уравнение:
Калькулятор удельного сопротивления четырехточечного датчикаНапряжение на внутренних датчиках, В = Вольт Ток на внешних датчиках, I = Толщина пластины, Вт = Расстояние между датчиками, с =
Удельное сопротивление листа, ρ квадрат = Ом/квадрат Удельное сопротивление пластины, ρ = Ом-см Удельное сопротивление с поправкой на толщину, ρ = Ом-см
Проблемы с измерениями
Несмотря на простоту в принципе, существуют экспериментальные проблемы, которые необходимо учитывать при использовании четырехточечного датчика. В частности, нанесение металла на полупроводник образует диод Шоттки, а не омический контакт.
Образцы с очень высоким или очень низким удельным сопротивлением требуют регулировки тока возбуждения для получения надежных показаний. Образцы с обрезанными или притертыми поверхностями легче измерить, чем образцы с полированными поверхностями
Образцы с высоким удельным сопротивлением
Для образцов с высоким удельным сопротивлением ток уменьшают, чтобы не создавать чрезмерно высокое напряжение на контактах. Рекомендуется, чтобы напряжение на внутренних датчиках было менее 100 мВ/мм (см. ссылку)
Образцы с низким удельным сопротивлением
Образцы с низким удельным сопротивлением обычно намного легче измерять, поскольку контакты с кремнием являются омическими. Для очень низкого удельного сопротивления вам придется увеличить ток до 45,3 мА и установить вольтметр на более низкую шкалу. Для образцов с очень низким удельным сопротивлением ток, проходящий через образец, вызывает резистивный нагрев, который, в свою очередь, увеличивает измеренное удельное сопротивление.
