Электрическое сопротивление — металл — Большая Энциклопедия Нефти и Газа, статья, страница 3

Cтраница 3

При повышении температуры электрическое сопротивление металлов увеличивается, а угля, электролитов и полупроводниковых приборов уменьшается. Насколько изменяется сопротивление, можно вычислить с помощью температурного коэффициента сопротивления. Если он положителен, то с ростом температуры сопротивление увеличивается, следовательно, ток уменьшается, но в обмотках электромагнитов, сетях, измерительных устройствах, лампах — в разной степени. Поэтому последствия изменения тока различны.  [31]

Роль примесей в электрическом сопротивлении металлов мы не обсуждаем.  [32]

Схема расположения энергетических зон в металле, изоляторе и.  [33]

Поэтому с повышением температуры электрическое сопротивление металлов возрастает.  [34]

Схема расположения энергетических зон в металле, изоляторе и.  [35]

Поэтому с по-вышением температуры электрическое сопротивление металлов возрастает.  [36]

В том, что электрическое сопротивление металлов обусловлено взаимодействиями электронов проводимости с различными дефектами решетки, убеждает и тот факт, что удельное сопротивление кристаллов металлов сильно зависит от наличия в них примесей. Например, введение 1 % примеси марганца увеличивает удельное сопротивление меди в три раза.  [37]

Схема расположения энергетических зон в металле, изоляторе и.  [38]

Поэтому с повышением температуры электрическое сопротивление металлов возрастает.  [39]

Под действием всестороннего давления электрическое сопротивление R металлов и полупроводников изменяется.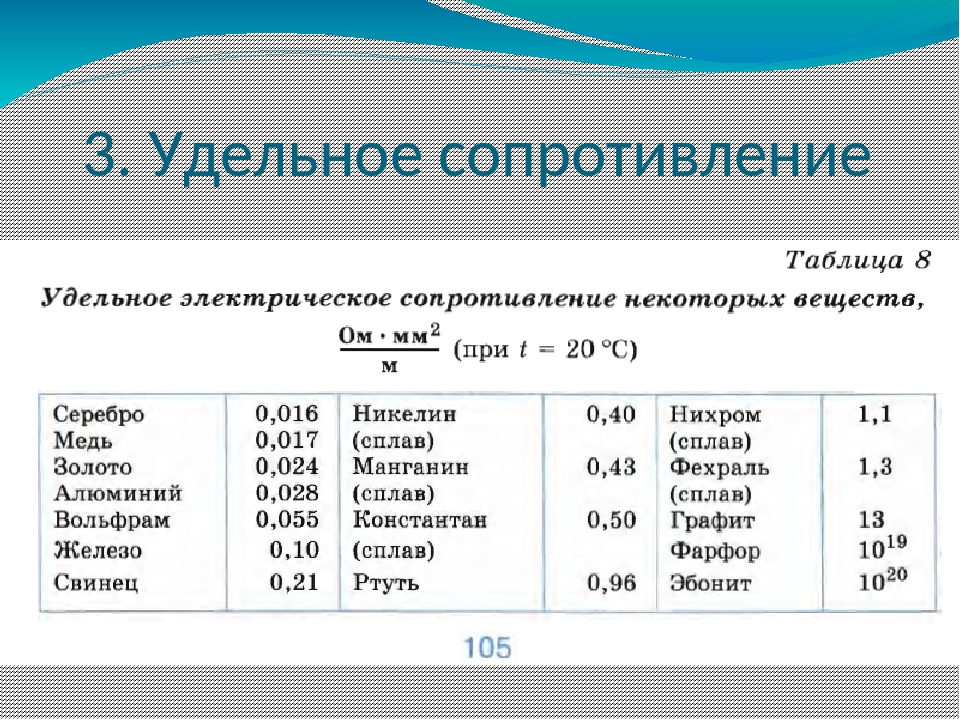  [40]

Излагаются особенности методики исследования электрического сопротивления металлов при высоких температурах с использованием образцов в виде стержней диаметром 8 — 14 мм, длиной 50 — 70 мм. Достаточно равномерный нагрев по длине и сечению образца осуществляется электронной бомбардировкой при помощи простой катодной системы. Приводятся результаты экспериментального исследования сопротивления молибдена ( поли — монокристаллического), ниобия и тантала.  [41]

Исследование изотопического эффекта в остаточном электрическом сопротивлении металлов показало, что в кристалле без физических дефектов и химических примесей возникает благодаря наличию изотопов конечное остаточное электрическое сопротивление.  [42]

При не очень низких температурах электрическое сопротивление металлов обусловливается главным образом рассеянием электронов на атомах кристаллической решетки металла. В результате актов рассеяния электронов происходит в среднем передача энергии от электронов к атомам кристаллической решетки.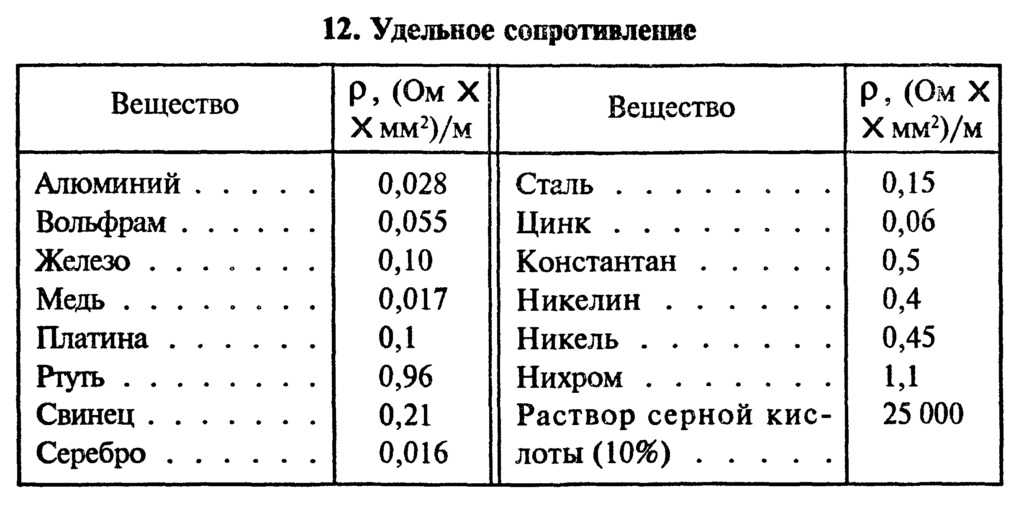

Передача энергии обусловливает возникновение электрического сопротивления. Атомы колеблются в узлах кристаллической решетки, и полученная ими энергия преобразуется в энергию колебаний. Колебания решетки описываются как возбуждения твердого тела, называемые фононами, а вся совокупность колебаний успешно описывается понятием фононного газа. Электрическое сопротивление в этой картине является результатом элект-рон-фононного взаимодействия.  [43]

Из того факта, что электрическое сопротивление металла

без примесных атомов и дефектов при абсолютном нуле температуры равно нулю, следует, что сопротивление возникает в результате взаимодействия электрона, его столкновениями с тепловыми колебаниями решетки. Наложение электрического поля ускоряет движение коллективизированных электронов. Температурная зависимость длины свободного пробега / обусловлена взаимодействием движущихся под действием внешнего электрического поля электронов с ионным остовом решетки.  [44]

Радиоактивное облучение оказывает влияние на электрическое сопротивление металлов, используемых в различных измерительных преобразователях, в зависимости от строения их кристаллической решетки и энергии Эа межатомных связей.

 [45]

Страницы:      1    2    3    4

2.3.3. Удельное электрическое сопротивление металлов в магнитоупорядоченном состоянии.

Для ферромагнетиков (железа, кобальта, никеля) и антиферромагнетиков (хрома, марганца) на величину удельного электрического сопротивления дополнительное влияние оказывает взаимодействие собственного магнитного момента электронов проводимости с магнитными моментами атомов кристаллической решётки. Это взаимодействие исчезает при температуре, соответствующей точкам магнитного разупорядочения. Для ферромагнетиков это точки Кюри, Т_с(Fe α-β)=1024К, Т_с(Со α)=1394К, Т_с( β)=1130К, Т

с(Ni)=629,63K (рис.9,10). Для антиферромагнетиков это точки Нееля, Т_н(Cr)=311К, T_H(Mn α)=95K, Т_н (Mn β)=580K, Т_н (Mn γ)=660К.

Таким образом, выше точки магнитного разупорядочения общее сопротивление чистого металла имеет температурную зависимость

ρ = ρ_e—ph – ρ_m , (15)

где ρ_m — магнитная составляющая удельного электрического сопротивления.

В окрестности Т_с и Т_н рассеяние электронов приобретает специфический, скачкообразный характер.

2.3.4. Удельное электрическое сопротивление металлов при температуре плавления.

При плавлении для металлов с температурной зависимостью, подобной кривой 1 на рис. 6, проявляется сильное, в 1,5-2 раза, увеличение удельного электрического сопротивления; для металлов с зависимостью, подобной кривой 2, характерно небольшое увеличение ρ, а для полуметаллов — сильное уменьшение ρ (рис.7,8,9,10).

2.3.5. Удельное электрическое сопротивление в окрестностях точки полиморфных превращений.

При полиморфных превращениях в большинстве случаев наблюдается скачкообразное увеличение или уменьшение удельного электрического сопротивления, возможен гистерезис, т.е. различное значение сопротивления при нагреве и охлаждении в окрестностях точки полиморфного превращения. В некоторых случаях кривая температурной зависимости удельного электрического сопротивления пересекает точку полиморфного превращения плавно, без скачкообразных изменений (рис.

10).

Рис. 10. Температурная зависимость удельного электросопротивления (ρ) железа. Стрелками показаны точка Кюри, точки полиморфных превращений, точка плавления.

2.3.6. Влияние внешнего давления на удельное электрическое сопротивление.

Влияние внешнего давления на удельное электрическое сопротивление оценивается коэффициентом сопротивления по давлению α

rp=(-1/ρ)·(dρ/dP),Па^-1. Для большинства металлов этот коэффициент находится в пределах α_rp=(1÷5)·10^-11 Па^-1, т.е. сопротивление уменьшается на 0,1÷0,5 % при всестороннем сжатии на каждые 10⁸ Па внешнего давления. При всестороннем сжатии уменьшается атомный объем и амплитуда тепловых колебаний атомов в узлах кристаллической решетки, что является основной причиной уменьшения сопротивления.

2.3.7. Гальваномагнитные и термомагнитные явления.

Гальваномагнитные явления возникают при одновременном воздействии на металл электрического и магнитного полей.

При «скрещенных» полях, когда вектора Е и В перпендикулярны, вследствие отклонения магнитным полем упорядоченно движущихся носителей заряда, возникает эффект Холла. Эффект Холла характеризуется разностью потенциалов на боковых гранях проводника (ЭДС Холла). ЭДС Холла пропорциональна плотности тока и индукции магнитного поля, а знаки заряда на боковых гранях зависят от типа носителей (электроны или дырки). При отклонении от прямого угла между Е и В ЭДС Холла уменьшается. Воздействие магнитного поля на проводник приводит также к уменьшению длины свободного пробега носителей заряда и, как следствие, — к увеличению электросопротивления. Это явление называют эффектом магнетосопротивления.

Термомагнитные явления возникают при создании градиента температуры по длине проводника с одновременным воздействием магнитного поля. При этом на боковых гранях проводника возникает ЭДС Нернста-Эттинсгаузена в результате действия носителей заряда, участвующих в переносе теплоты.

Электрическое сопротивление металлов | СпрингерЛинк

Авторы:

• Джордж Теренс Миден ⁰

1. Джордж Теренс Миден

   1. Centre de Recherches sur les Très Basses Températures, Faculté des Sciences, Université de Grenoble, France
      

   Посмотреть публикации автора

   Вы также можете искать этого автора в пабмед Google ученый

Часть серии книг: Международная серия монографий по криогенике (INCMS)

• 1348 доступов

• 251 Цитаты

Секции

• Содержание
• Ключевые слова
• Авторы и филиалы
• Библиографическая информация

‘) var head = document. getElementsByTagName(«head»)[0] var script = document.createElement(«сценарий») script.type = «текст/javascript» script.src = «https://buy.springer.com/assets/js/buybox-bundle-abe5f44a67.js» script.id = «ecommerce-scripts-» ​​+ метка времени head.appendChild (скрипт) var buybox = document.querySelector(«[data-id=id_»+ метка времени +»]»).parentNode var сейчас = новая дата().getTime() вар начало = 1650956400000 вар конец = 1652338800000 var isMeasuringTime = now > start && now -1) { ;[].slice.call(buybox.querySelectorAll(«.кнопка варианта покупки[тип=отправить]»)).forEach(функция (кнопка, индекс) { button.removeAttribute(«отключено») }) ;[].slice.call(buybox.querySelectorAll(«.Информация-предварительного-заказа-опций-покупки»)). forEach(функция (эл., индекс) { el.style.display = ‘нет’ }) ;[].slice.call(buybox.querySelectorAll(«.вариант покупки-информация о предварительном заказе.новая-функция»)).forEach(функция (эл., индекс) { эл.стиль.дисплей = » }) } функция initMetrics (начало, конец) { var metricsKey = «abMetricsCampaignPrices-v1» переменная кампанияPricesMetricsGroup = «X» if (!window.localStorage || !window.fetch) вернуть командуPricesMetricsGroup если (! isMeasuringTime) { window.localStorage.removeItem(metricsKey) вернуть «НЕТ» } пытаться { var metricsValue = window.localStorage.getItem(metricsKey) кампанияPricesMetricsGroup = metricsValue || случайное распределение (метрический ключ) } поймать (ошибиться) { console.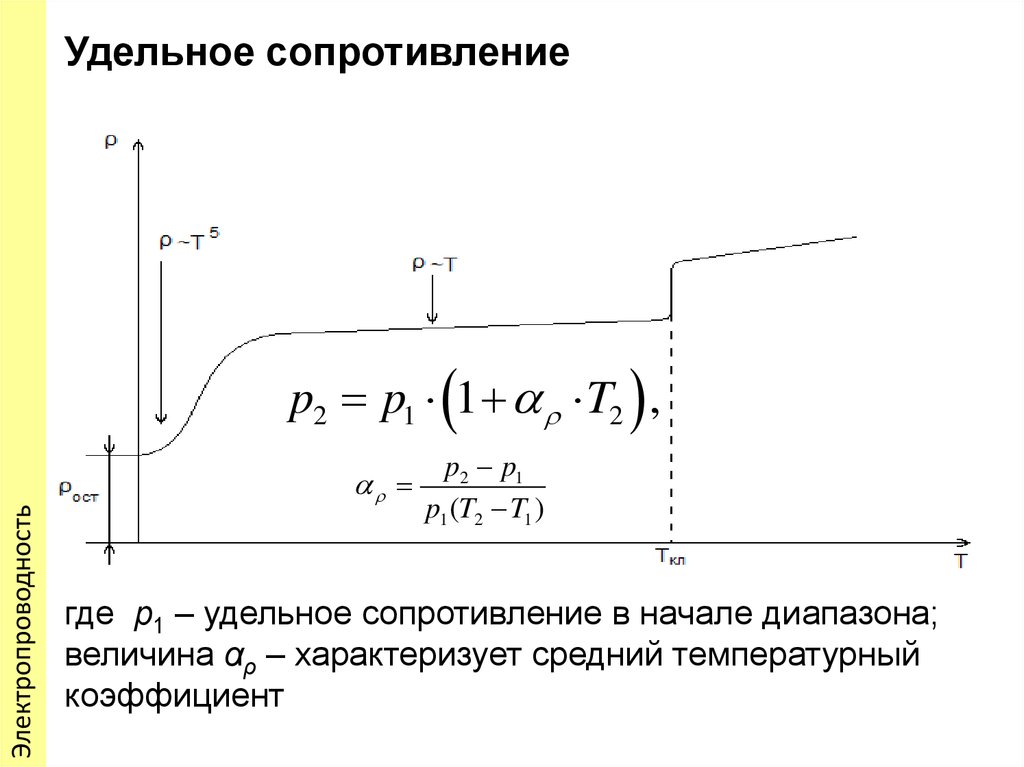 log(ошибка) } обратная кампанияPricesMetricsGroup } функция случайного распределения (метрический ключ) { var randomGroup = Math.random() -1 ;[].slice.call(buybox.querySelectorAll(«.опция покупки»)).forEach(функция (опция, индекс) { var toggle = option.querySelector(priceNS + «.buying-option-price») var form = option.querySelector(«.форма-варианта-покупки») var priceInfo = option.querySelector(priceNS + «.price-info») если (allOptionsInitiallyCollapsed || узкаяBuyboxArea && индекс > 0) { toggle.setAttribute («ария-расширенная», «ложь») form.hidden = «скрытый» priceInfo.hidden = «скрытый» } еще { переключить.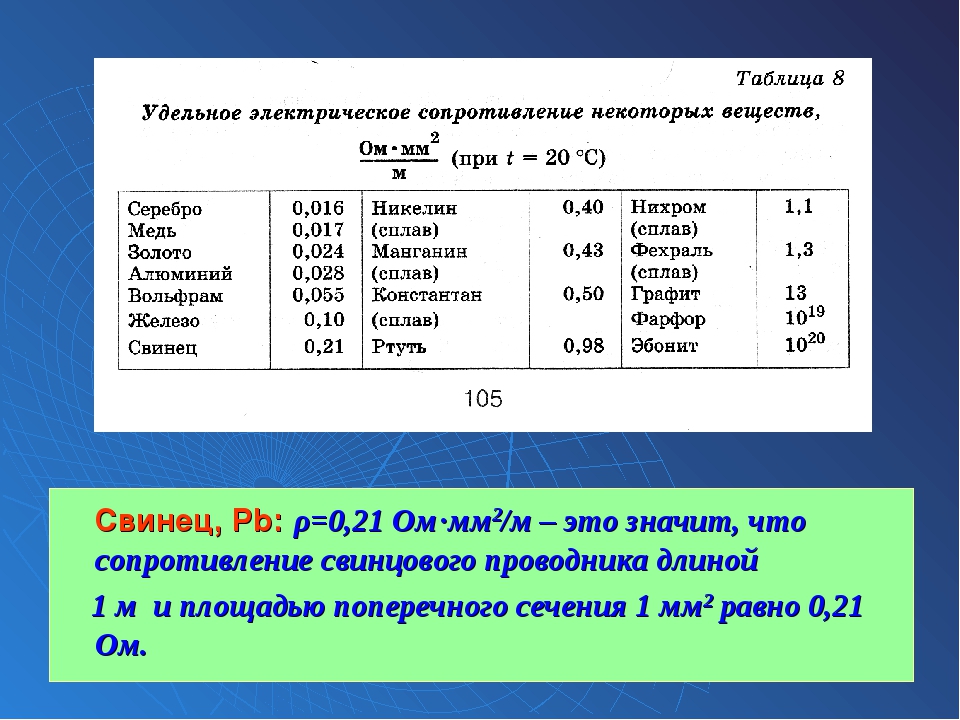 щелчок() } }) } начальное состояниеОткрыть() если (window.buyboxInitialized) вернуть window.buyboxInitialized = истина initKeyControls() если (window.fetch && isMeasuringTime) { var свернутый = buybox.querySelector(«.buying-option.expanded») === ноль var metricsAppendix = «» metricsAppendix += «&discount=» + (buybox.querySelector(«.Цена-кампания-покупки-варианта»).className.indexOf(«со скидкой») !== -1).toString() metricsAppendix += «&metricsGroup=» + кампанияPricesMetricsGroup metricsAppendix += «&collapsed=» +collapsed.toString() window.fetch(«https://test-buckets.springer.com/log?v3&time=» + сейчас + приложение metrics) .затем (функция (разрешение) { вернуть рез. 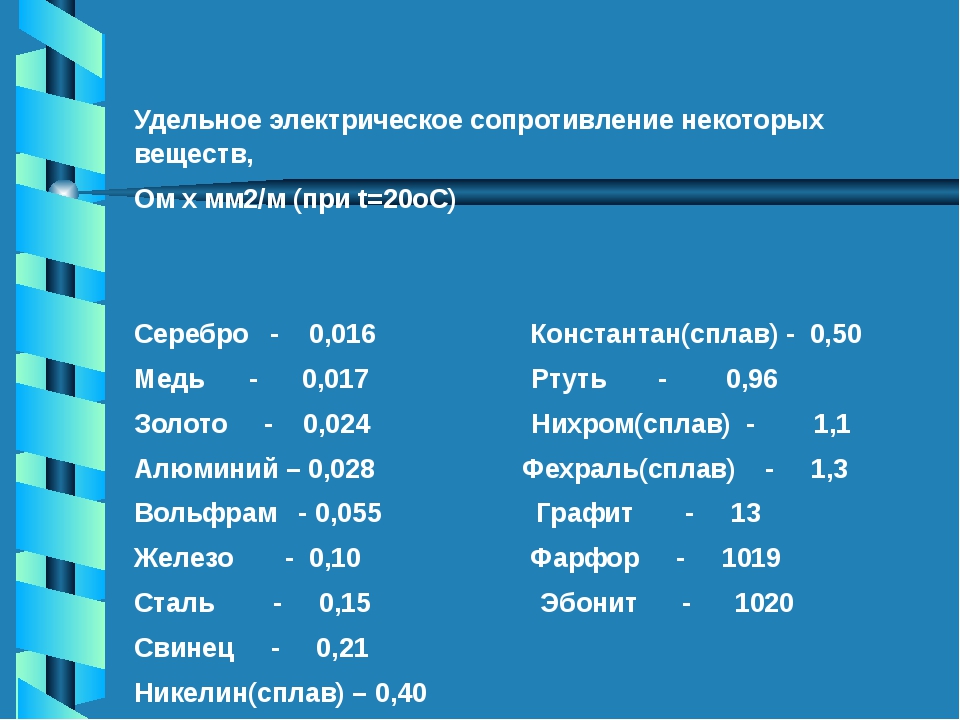текст() }) .поймать (функция () { }) } })()

Доступ через ваше учреждение

‘) var head = document.getElementsByTagName(«head»)[0] var script = document.createElement(«сценарий») script.type = «текст/javascript» script.src = «https://buy.springer.com/assets/js/buybox-bundle-abe5f44a67.js» script.id = «ecommerce-scripts-» ​​+ метка времени head.appendChild (скрипт) var buybox = document.querySelector(«[data-id=id_»+ метка времени +»]»).parentNode var сейчас = новая дата().getTime() вар начало = 1650956400000 вар конец = 1652338800000 var isMeasuringTime = now > start && now -1) { ;[]. slice.call(buybox.querySelectorAll(«.кнопка варианта покупки[тип=отправить]»)).forEach(функция (кнопка, индекс) { button.removeAttribute(«отключено») }) ;[].slice.call(buybox.querySelectorAll(«.Информация-предварительного-заказа-опций-покупки»)).forEach(функция (эл., индекс) { el.style.display = ‘нет’ }) ;[].slice.call(buybox.querySelectorAll(«.вариант покупки-информация о предварительном заказе.новая-функция»)).forEach(функция (эл., индекс) { эл.стиль.дисплей = » }) } функция initMetrics (начало, конец) { var metricsKey = «abMetricsCampaignPrices-v1» переменная кампанияPricesMetricsGroup = «X» if (!window.localStorage || !window.fetch) вернуть командуPricesMetricsGroup если (! isMeasuringTime) { window. localStorage.removeItem(metricsKey) вернуть «НЕТ» } пытаться { var metricsValue = window.localStorage.getItem(metricsKey) кампанияPricesMetricsGroup = metricsValue || случайное распределение (метрический ключ) } поймать (ошибиться) { console.log(ошибка) } обратная кампанияPricesMetricsGroup } функция случайного распределения (метрический ключ) { var randomGroup = Math.random() -1 ;[].slice.call(buybox.querySelectorAll(«.опция покупки»)).forEach(функция (опция, индекс) { var toggle = option.querySelector(priceNS + «.buying-option-price») var form = option.querySelector(«.форма-варианта-покупки») var priceInfo = option. querySelector(priceNS + «.price-info») если (allOptionsInitiallyCollapsed || узкаяBuyboxArea && индекс > 0) { toggle.setAttribute («ария-расширенная», «ложь») form.hidden = «скрытый» priceInfo.hidden = «скрытый» } еще { переключить.щелчок() } }) } начальное состояниеОткрыть() если (window.buyboxInitialized) вернуть window.buyboxInitialized = истина initKeyControls() если (window.fetch && isMeasuringTime) { var свернутый = buybox.querySelector(«.buying-option.expanded») === ноль var metricsAppendix = «» metricsAppendix += «&discount=» + (buybox.querySelector(«. Цена-кампания-покупки-варианта»).className.indexOf(«со скидкой») !== -1).toString() metricsAppendix += «&metricsGroup=» + кампанияPricesMetricsGroup metricsAppendix += «&collapsed=» +collapsed.toString() window.fetch(«https://test-buckets.springer.com/log?v3&time=» + сейчас + приложение metrics) .затем (функция (разрешение) { вернуть рез.текст() }) .поймать (функция () { }) } })()

Аномальное падение удельного электрического сопротивления при легировании монокристалла Ag примесями

Металлы считаются идеальными материалами для электроники из-за их превосходных электрических свойств ¹ . Серебро (Ag) является лучшим проводником при комнатной температуре с удельным сопротивлением 1,59 мкОм·см при 293  K, что может быть выражено как 108% в соответствии с Международным стандартом отожженной меди (IACS).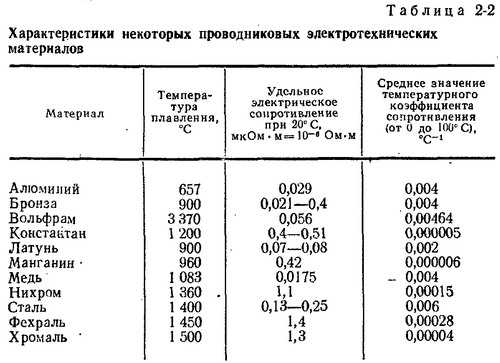 Высокая электропроводность металлов, особенно серебра, делает их идеальными для многих промышленных применений, где необходимы превосходные печатные, термические, электрические свойства, свойства соединения проводов и пайки ^2,3,4,5,6 . В последнее время многие исследователи пытались разработать передовые металлические материалы с большим энергопотреблением и более высокой эффективностью для аэрокосмической и медицинской промышленности ^{7,8,9,10,11,12,13,14} . Хотя сверхпроводники идеально подходят для этой цели, их низкая критическая температура перехода ( T _c ) остается ограничивающим фактором для практических приложений. Таким образом, значительные исследования были сосредоточены на разработке новых материалов с более высокой проводимостью при комнатной температуре (КТ) ^15,16,17 .

Удельное сопротивление материала увеличивается в результате дефектов, таких как дефекты, примеси, границы зерен и дислокации ¹⁸ .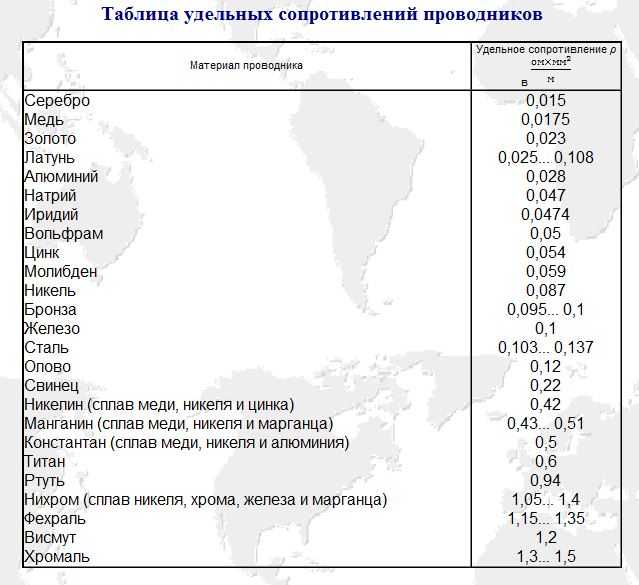 Удельное сопротивление монокристаллической меди (Cu) (1,52 мкОм·см при 293 K, 113,4% IACS) на 12 % ниже, чем у поликристаллической Cu, что даже ниже, чем у поликристаллического Ag, за счет устранения границ зерен. посредством процесса выращивания кристаллов ¹⁹ . Другой подход к снижению удельного сопротивления включает одновременное приложение тепла и давления после выращивания кристаллов, что может повысить кристалличность металла и, таким образом, значительно снизить удельное сопротивление (например, для меди снижение удельного сопротивления на 14%: 1,472 мкОм·см при 29°С).3 K, 117,1% IACS) ²⁰ .

Удельное сопротивление сплавов обычно выше, чем у чистых металлов, и увеличивается при загрязнении примесями ^21,22 . Однако здесь мы сообщаем об удивительном уменьшении удельного сопротивления при добавлении определенного количества примеси Cu к монокристаллу Ag, который является идеальным проводником при комнатной температуре. Медная проволока высокой чистоты имеет проводимость чуть более 103 % по IACS, что близко к значению, ожидаемому для меди без примесей.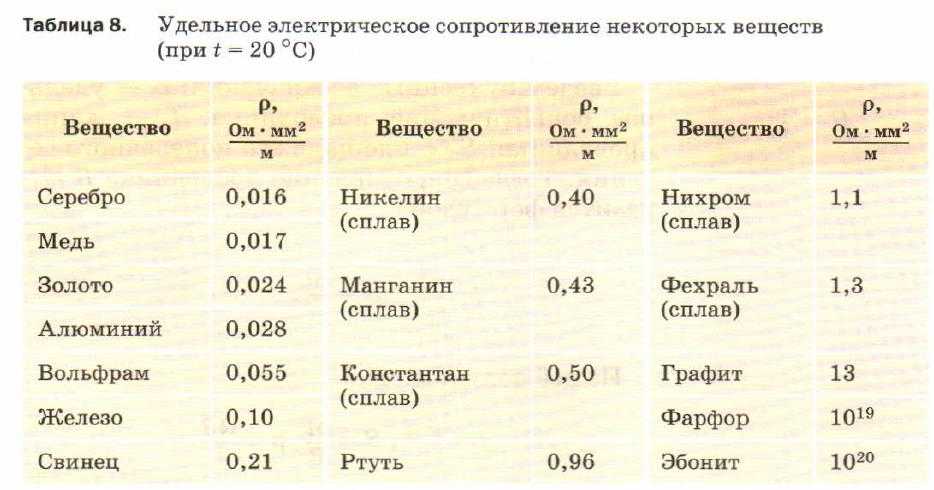 Здесь мы сообщаем о нехарактерном увеличении проводимости до 127% IACS в результате примесей Cu в монокристаллическом Ag.

Монокристаллы Cu, монокристаллы Ag и Ag _1-x Cu _x смешанные кристаллы (x = 1, 2, 3, 5 и 10 моль%) выращены методом Чохральского (все оборудование поддерживалось Crystal Bank в Пусанском национальном университете). На рис. 1 показан пример смешанного кристалла Ag _0,95 Cu _0,05 . Эти полярные изображения, полученные с помощью рентгеновской дифракции (XRD) (рис. 1б, в), подтверждают кристалличность кристаллов Ag _1-x Cu _x (дополнительные полярные изображения других Ag _1-x Cu _x смешанные кристаллы представлены в дополнительной информации на рис. 1). Качество кристаллов смешанных кристаллов Ag-Cu было немного ниже, чем у чистых монокристаллов Cu и Ag, но смешанные кристаллы демонстрировали хорошо выраженный рост в направлении (111) вплоть до соотношения меди и сплава 10 моль.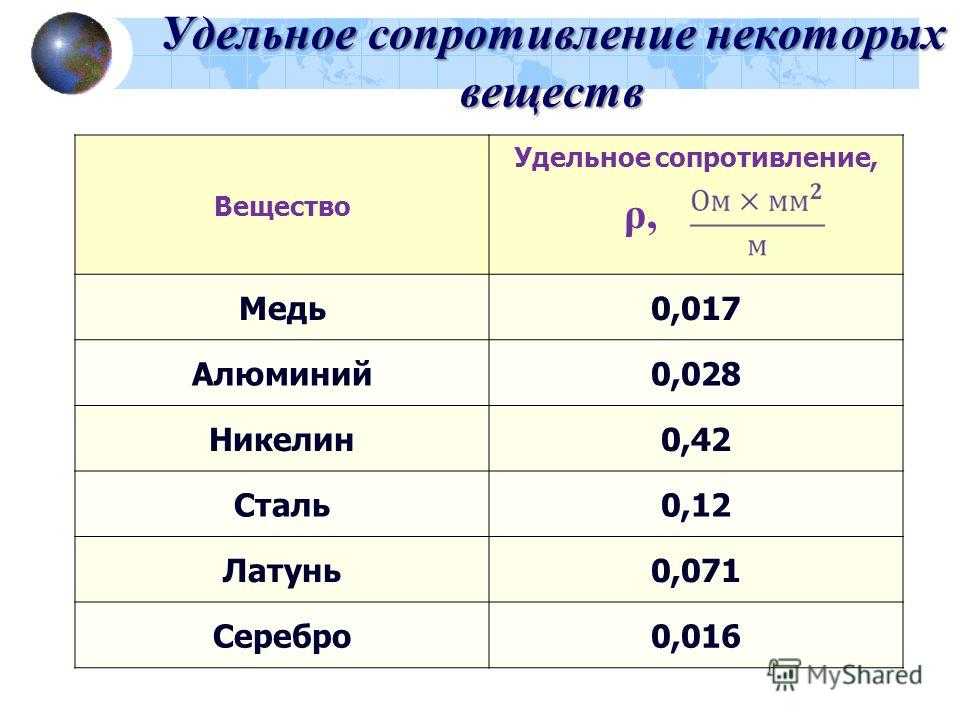 % и большая часть атомов меди замещена в позиции Ag. Образцы для измерения удельного сопротивления были подготовлены путем резки проволокой с использованием электроэрозионной обработки (EDM), как показано на вставке к рисунку 1e.

Рисунок 1

Выращенный смешанный кристалл Ag-Cu и его изготовление.

(a): Фотография смешанного кристалла Ag, легированного 5% меди, выращенного методом Чохральского. (b) и (c): 2.5D и 2D-изображения полюсной фигуры, полученные из металлического смешанного кристалла. (d) и (e): Образец вырезания изображения с использованием проволочной электроэрозионной машины (EDM). Вставка к (e): Образец для измерения удельного электрического сопротивления методом четырехточечного зонда. Все фотографии сделаны S.Y.J. и соавторы.

Увеличенное изображение

Композиционный анализ проведен методом спектрометрии тлеющего разряда (ГДС). Мы подтвердили, что атомы Cu равномерно распределены в предполагаемом количестве.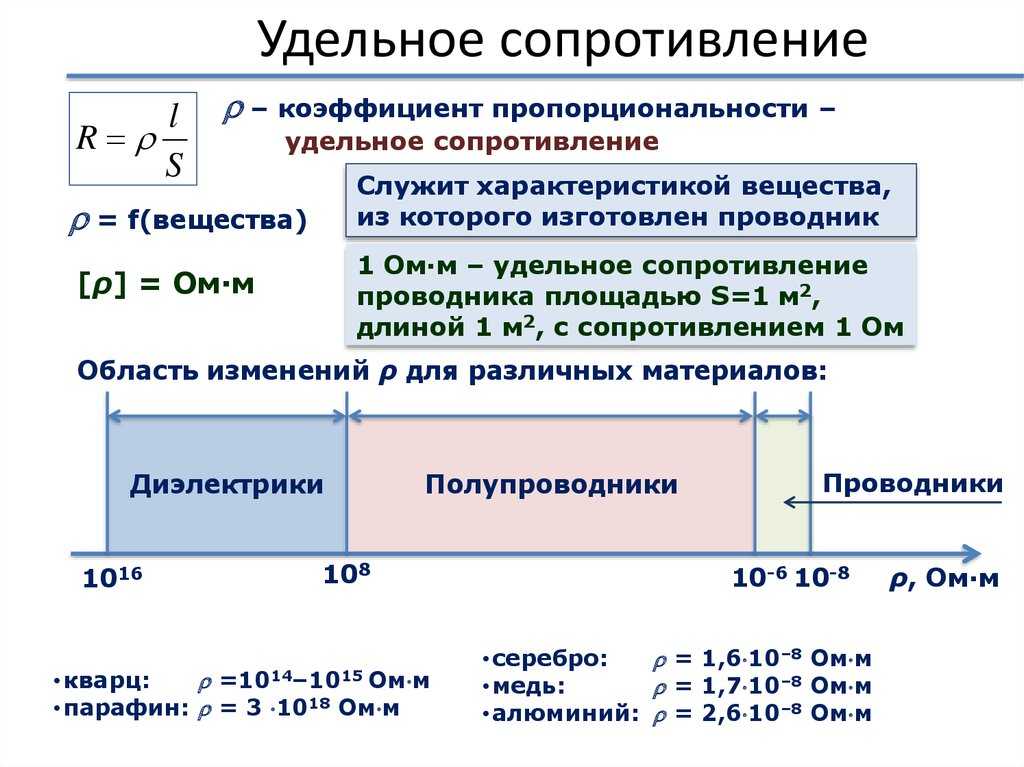 Концентрации примесей, отличных от Cu, были пренебрежимо малы по сравнению с концентрациями Cu. Распределение непреднамеренных примесей, кроме Ag и Cu, показано в разделе «Дополнительная информация» (рис. S2 и таблица 1).

Таблица 1 Оптимизированные параметры решетки (a ₀ ), объемный модуль ( B ), расчетная температура Дебая (Θ _D ) и константа электрон-фононного взаимодействия (λ _tr ) для Ag, Cu и смешанного кристалла

Полноразмерная таблица

14 На рис. 2а показано удельное электрическое сопротивление различных материалов Ag/Cu при комнатной температуре. Известно, что удельное сопротивление металлов увеличивается с добавлением примесей, а также выше в смешанных кристаллах или сплавах, чем в чисто кристаллических материалах.
Рисунок 2

Удельное электрическое сопротивление кристаллов.

(a): Удельное электрическое сопротивление чистого монокристалла Ag, смешанных кристаллов Ag-Cu и поликристаллического сплава Ag _0,97 Cu _0,03 , измеренное при 300 K, и поликристаллического Cu, монокристаллического Cu и поликристаллического Ag, измеренное при 293 К ^19,23 .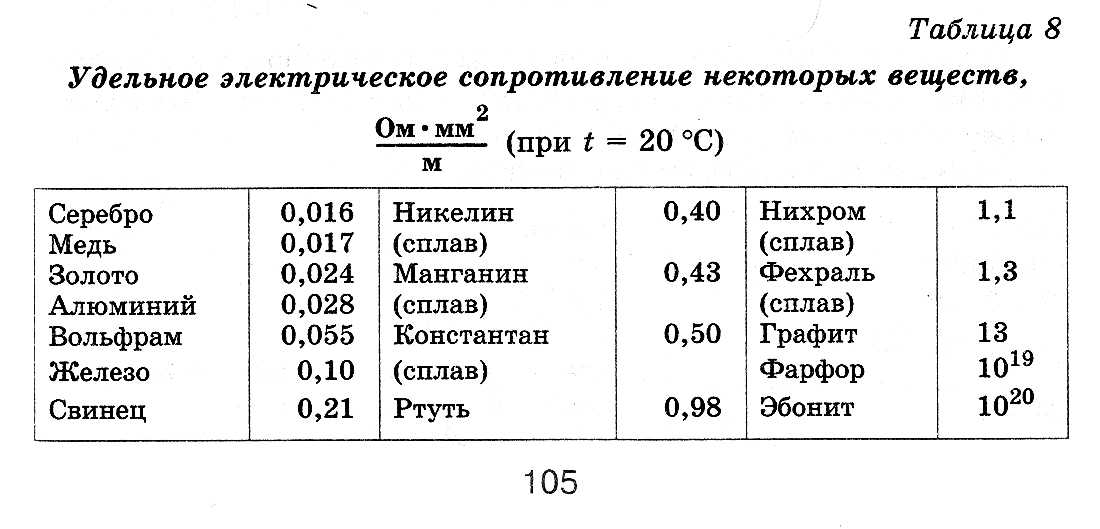 (б): Температурные зависимости удельного электросопротивления поликристаллического сплава Ag _0,97 Cu _0,03 , монокристаллического Ag и Ag _0,97 Cu _0,03 смешанный кристалл.

Изображение полного размера

Однако мы неожиданно обнаружили, что удельное сопротивление уменьшилось после легирования небольшими количествами меди до 3 мол.%. Наименьшее удельное сопротивление было получено в смешанном кристалле Ag, легированном 3 mol.% Cu (); его удельное сопротивление составило 1,35 мкОм·см, что на 9,4% ниже, чем у монокристаллического Ag () (1,49 мкОм·см). Удельное сопротивление около 3  мольных % (± 0,1, 0,2 %) Cu было немного выше, чем у 3  мольных % (вставка, рис. 2 (а)). Удельное сопротивление серебра, легированного медью более чем на 5  мольных %, было несколько выше, чем у монокристаллического серебра. Удельное сопротивление немного увеличилось при более чем 5  мольных % Ag, легированного медью. Удельное сопротивление кристаллов Ag, легированных 5 моль. % Cu () и 10 моль.% Cu (), составило 1,51 и 1,66 мкОм·см соответственно, что несколько выше, чем у чистого монокристаллического Ag. Это первое сообщение о таком нехарактерном падении удельного сопротивления из-за легирования медью.

Напротив, сплав (, а не , выращенный как монокристалл) показал увеличение удельного сопротивления в результате добавления Cu. Сплав готовили печным охлаждением из расплавленного состояния. Сплав, легированный 3 мол.% Cu (), имел удельное сопротивление 1,76 мкОм·см, что на 23,3% больше, чем у смешанного кристалла Ag _0,97 Cu _0,03 .

Различные последствия легирования меди в сплаве и монокристалле могут быть связаны с ближним порядком меди в смешанном кристалле и уменьшенным числом границ зерен. Скорость жидкостного охлаждения намного ниже при росте кристаллов, что приводит к увеличению вероятности ближнего упорядочения.

На рис. 2б представлены температурные зависимости удельного электросопротивления поликристаллического сплава Ag _0,97 Cu _0,03 , монокристалла Ag и смешанного кристалла Ag _0,97 Cu _0,03 (другие образцы см. на рис. S3). Пониженное удельное сопротивление при низкой температуре 10 K отражает тот факт, что легированные примеси меди не вносили вклада в электронно-примесное рассеяние.

Чтобы понять изменение удельного сопротивления после добавления Cu в монокристалл Ag, мы сначала рассмотрели экспериментальные данные Маттиссена ^24,25 . Согласно правилу Маттиссена, удельное электрическое сопротивление нечистого металла можно разделить на два вклада, определяемых как:

, где ρ ₀ — остаточное сопротивление, не зависящее от температуры, вызванное в основном электронно-примесным ( el-imp ) рассеяния на дефектах электронов ( el-def ) и зависит от концентрации примесей c 0064 эль-ф ) рассеивание ²⁶ . Для ρ ₀ бинарной системы твердый раствор и с учетом правила Нордгейма, заданного как ρ ₀ ∝ c (1 — c) , где c — мольная доля Cu, увеличение ρ для Смешанные кристаллы, легированные медью >5%, можно объяснить увеличенным рассеянием el-imp .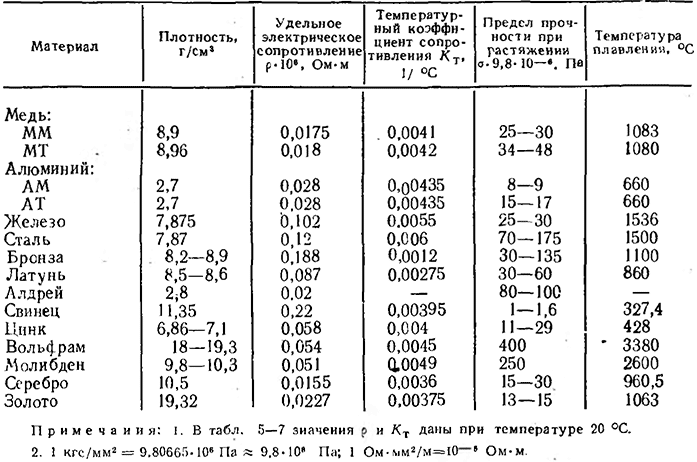 Однако изменение ρ _i необходимо учитывать для понимания падения ρ в смешанных кристаллах, легированных <5% Cu. Собственное сопротивление ρ _I может быть аппроксимирован уравнением Bloch-Grüneisen:

, где θ _D -температура Debye, x -это переменный диатащен. Константа α _EL-PH пропорциональна λ _TR ω _D /ω _P ^{2 9007, P 2 9007, P 2 9007, P _{966666666666666666666666666666666666666666666666666666666666. константа связи и ω D и ω p — дебаевская и плазменная частоты соответственно 18,27 . Это уравнение предпочтительно для металлических элементов, таких как одновалентные металлы со сферической поверхностью Ферми 28 . Уравнение состоит из трех частей: электронный член (ω p ), член, связанный с фононами (Θ D , ω D ) и член электрон-фононного взаимодействия (λ т. р. ).}}

Сначала рассмотрим электронный термин. Известно, что значение ω _p определяется исключительно концентрацией носителей заряда n и эффективной массой электронов m* (ω _p ^{/4m* 90 ). Таким образом, электронный вклад в удельное электрическое сопротивление можно понять на основе электронной структуры. Удельное электрическое сопротивление (ρ) может быть описано уравнением переноса Больцмана в виде:}

где e — заряд носителя, N — количество k-точек, использованных в расчетах, Ω — объем элементарной ячейки, f ₀ — равновесная ферми- Функция распределения Дирака, τ _n,k – время релаксации, обозначает групповую скорость, ε _n,k обозначает энергию зоны, а δ – дельта-функцию ²⁹ . Нижние индексы n и k представляют индекс полосы и импульс кристалла в случае твердого кристалла соответственно. может быть получено из зонной структуры с использованием следующего соотношения:

Таким образом, значение ρ может быть получено из электронной структуры и точного значения τ. В принципе, значение τ зависит от энергии зоны ε _n,k и температуры; однако мы предполагали, что значение было постоянным, чтобы оценить, как изменение электронной структуры смешанного кристалла влияет на удельное электрическое сопротивление. Кроме того, мы приняли приближение жесткой полосы. Уровень Ферми был получен из общего числа электронов в элементарных ячейках и использовался для расчета ρ.

Электрические сопротивления оценивались по электронным структурам Ag, Cu и смешанного кристалла, в которых для всех систем использовались электронные структуры модели суперячейки. Модель с составом 3,125 мол.% Cu была использована для оценки электросопротивления смешанных кристаллов с 3 мол.% Cu. Конфигурация атомов Cu рассматривалась для исследования влияния взаимодействия Cu-Cu на электронную структуру и удельное электрическое сопротивление. Мы смоделировали две крайние системы: i) димеризованное состояние двух атомов Cu (расстояние между Cu-Cu (d _Cu-Cu ) = 2,824   ) и ii) самая дальняя разделенная система Cu-Cu в суперячейке (d _Cu-Cu = 8,300   ). Состояние димера было более стабильным на 12 мэВ, чем в последнем случае (рис. S4 в SI). Плотность состояний двух систем сравнивается на рисунке S5 (в системе СИ) и показывает четкую разницу между системами, что указывает на влияние упорядочения на электронную структуру. Расчетное электросопротивление по электронной структуре димерной системы при комнатной температуре может быть на ~1% ниже, чем у Ag (рис. 3). Для всех систем использовалось одно и то же значение τ. Эти результаты показали, что кластеризация Cu может привести к снижению электронного сопротивления по сравнению с чистым Ag. Величина уменьшения ρ из электронной структуры была меньше, чем экспериментальное значение на рис. 2.

Рисунок 3

Расчетное удельное электрическое сопротивление Ag, Cu, Cu-Cu димеризованных и Cu-Cu разделенных систем.

Электронные структуры суперячейки использовались для оценки свойств. Все значения были получены с использованием уравнения переноса Больцмана с постоянным значением времени релаксации 3,4 × 10 ⁻¹⁴  с, выбранным в соответствии с экспериментальным удельным сопротивлением Ag.

Изображение полного размера

Пониженное электрическое сопротивление в смешанном кристалле не может быть полностью объяснено только изменением электронной структуры. Таким образом, помимо электронного члена, связанный с фононами член, Θ _D и ω _D , считалась причиной падения ρ. Из уравнения (2) и уравнение ω _D = K _B θ _D /H , где K _{/H , где K 9 B. постоянной, мы видим, что температура Дебая Θ D оказывает существенное влияние на ρ. Θ D рассчитано из фононной плотности состояний (табл. 1). Величина Θ D для смешанного кристалла системы Cu-выделения была несколько больше, чем у Ag, а система Cu-димер была значительно меньше. Эти результаты показывают, что свойства фононов также сильно зависят от упорядочения Cu.}

Известно, что λ _tr не зависит от температуры и может быть получено из соотношения между Θ _D и τ при температуре выше 0,7 Θ _D ^33,34 , приведенные в уравнении. (5):

где .

Для вычисления λ необходимо знать значение τ _tr . В этом исследовании значение τ оценивалось путем сравнения экспериментального ρ с полученным с использованием уравнения (3). Оцененные значения λ _tr с τ и Θ _D показаны в таблице 1. Расчетные значения Ag и Cu соответствовали значениям, приведенным в литературе. Значение λ _tr для смешанного кристалла ниже, чем у Ag. Пониженные значения были в основном связаны с увеличением времени релаксации и ограничением влияния температуры Дебая. Время релаксации связи (или рассеяния) электронов с акустическим фононом зависит от потенциала деформации, плотности материалов и средней скорости продольного звука ^35,36 . Мы определили, что оценка скорости звука по дисперсии фононов и измеренная плотность не приводят к увеличению времени релаксации в смешанном кристалле. Таким образом, уменьшение рассеяния (т. е. увеличение времени релаксации) в основном объяснялось уменьшением деформационного потенциала при добавлении Cu. С другой стороны, добавление Cu уменьшало плотность, что приводило к уменьшению времени релаксации. Таким образом, по мере увеличения количества Cu изменение деформационного потенциала оказывало меньшее влияние. Из-за компромисса между этими двумя эффектами минимум наблюдался в удельном сопротивлении смешанного кристалла при ~ 3  мол.% Cu.

В дополнение к этим внутренним механизмам образование вакансий, внешний эффект, также может способствовать низкому значению удельного сопротивления. Наши расчеты показали, что образование вакансии может быть значительно подавлено в присутствии Cu в составе Ag. Мы оценили энергию образования вакансии на основе расчетов полной энергии кубической сверхъячейки, содержащей 32 атома. Энергия образования вакансии в Ag была оценена в 0,74 эВ, что указывает на то, что концентрация вакансий может быть достаточно высокой, ~6,56 × 10 ¹⁹  см ⁻³ при температуре роста 900°С. Интересным открытием является то, что при замене одного Ag на Cu энергия образования вакансии сильно возрастает и оценивается в 1,19 эВ для вакансии, расположенной в ближайшем узле Cu, и 1,13 эВ для вакансии, отделенной от Cu. Это указывает на то, что небольшая добавка Cu в Ag может значительно снизить концентрацию вакансий. Поскольку вакансия должна быть сильным рассеивающим центром, это подавление может объяснить уменьшение удельного сопротивления при добавлении Cu. Образование других дефектных состояний, связанных с Cu, из-за низкого предела растворимости Cu может привести к увеличению удельного сопротивления, так как концентрация Cu превышает 3 мол.%.

Таким образом, мы наблюдали нехарактерное падение удельного сопротивления монокристаллического Ag, выращенного методом Чохральского, в результате добавления небольшого количества примеси Cu (до 3 мол.