Позиционные системы счисления — что это, определение и ответ
Системы счисления — одна из самых базовых тем в информатике. Знание систем счисления позволяет успешно решать задание№14. Также системы счисления лежат в основах логики, программирования и кодирования. В этой теме надо разбираться по порядку.
Допустим, необходимо посчитать количество цветов на поляне. Можно загибать пальцы, делать зарубки на дереве, как это делали древние люди, и так далее. Можно сделать вывод, что форма счета может быть любой, также, как и форма записи. Для способа записи чисел ввели такое понятие, как система счисления.
Существует два типа систем счисления:
Нас будут интересовать именно позиционные системы счисления с различными основаниями. Самые популярные системы счисления: двоичная, восьмеричная, десятичная, шестнадцатеричная. Позиционные системы счисления основаны на том, что «вес» цифры зависит от её положения — или позиции — в числе, отсюда и такое название.
Для успешной подготовки к экзамену необходимо уметь переводить любое число из десятичной системы счисления в любую другую n‑ричную и из n‑ричной в десятичную. Далее приведена информация по каждому случаю.
Десятичная система счисления
Исторически сложилось, что это самая распространенная система счисления. Именно её мы используем, когда мы делаем покупки в магазине, набираем номер телефона или открываем страницу в книге. На каждой позиции может стоять только одна цифра из диапазона от 0 до 9. Основанием (то есть, количество цифр) является число 10. Это значит, что «вес» любой цифры в числе будет кратен 10 в степени, равной позиции этой цифры. При этом позиции (их называют разрядами) отсчитываются с правого конца числа, начиная с нуля.
Пример. Чтобы разобраться подробнее, возьмем число 123. Давайте «разложим» это число по разрядам. Для этого каждую цифру числа умножим на основание системы, в данном случае число 10, возведенное в степень, равную номеру разряда.
Цифра 3 стоит в нулевом разряде, цифра 2 — в первом, а цифра 1 — во втором. Получается, значение равно:1 * 102 + 2 * 101 + 3 * 100 = 100 + 20 + 3 = 123.
При работе с разными системами счисления, чтобы избежать путаницы, справа от числа приписывают нижний индекс с основанием: 12310.
Двоичная система счисления
Эта система счисления используется в вычислительной технике. Десятичную систему счисления в компьютерах не стали использовать, потому что требовалось производство устройств, способных работать в десяти состояниях, а это сильно увеличило бы цену и размер таких устройств. Двоичная же система позволяла экономить на всем.
Двоичная система счисления, как следует из названия, имеет основание 2 и использует только цифры 0 и 1.
Пример. Возьмем число 1001 — это число 9 в десятичной системе счисления. Для того, чтобы перевести число из 2-ичной в 10-ичную систему счисления, необходимо точно так же «разложить» число на разряды, т.
е. каждую цифру двоичного числа умножить на основание 2, возведенное в степень, равную разряду:10012 = 1 * 23 + 0 * 22 + 0 * 21 + 1 * 20 = 8 + 0 + 0 + 1 = 9.
Точно так же выполняется перевод из любой n-ричной системы счисления в десятичную. Для этого надо:
1. определить количество разрядов;
2. умножить каждую цифру n-ричной системы счисления на основание «n», возведенное в степень, равную разряду.
Пример. Посмотрим на то, как переводить число из десятичной системы счисления в n-ричную. Сейчас сделаем это опять на примере двоичной системы. Пусть нужно перевести число 24010 в двоичную систему счисления. Для этого надо последовательно делить число 240 на 2, фиксируя получающиеся остатки (удобнее всего делать это «лесенкой»), пока не дойдем до последнего частого, которое на 2 уже не делится.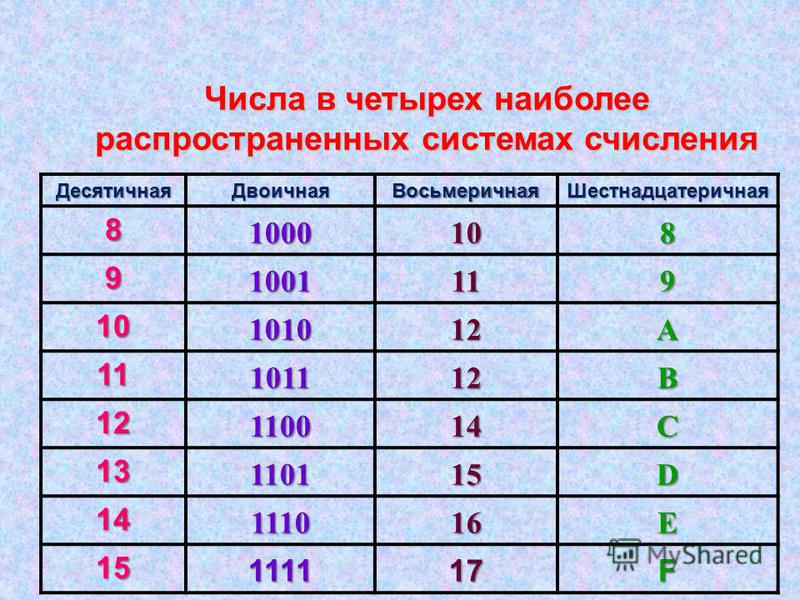
Это будет первая цифра числа в двоичной системе. А остальные цифры — это получившиеся остатки, записанные в обратном порядке:Осталось записать обведенные кружком цифры в обратном порядке, начиная с самой правой (выделена жирным). Получаем, что число 24010 = 111100002.
Точно так же выполняется перевод из десятичной системы счисления в любую n-ричную. Для этого надо:
целую часть числа последовательно делить на основание новой системы счисления, пока не останется число или цифра, которая уже делиться не будет;
эта оставшаяся цифра будет первой цифрой нового числа. Остальные цифры — это остатки от всех делений, записанные в обратном порядке.
Восьмеричная система счисления
Имеет основание 8, использует цифры от 0 до 7.
Для того, чтобы перевести из восьмеричной системы счисления в десятичную, необходимо умножить каждую цифру восьмеричного числа на основание 8, возведенное в степень, равную разряду.
Пример. 6718 = 6 * 82 + 7 * 81 + 1 * 80 = 384 + 56 + 1 = 44110.
Перевод из десятеричной системы счисления в восьмеричную осуществляется аналогично переводу в двоичную, только делителем в данном случае является 8.
Пример. Пусть надо перевести число 16310 в восьмеричную систему:Получаем, что 16310 = 2438.
Шестнадцатеричная система счисления
Имеет основание 16, использует цифры от 0 до 9 и буква A, B, C, D, E, F, где буква А = 10, В = 11, С = 12, D = 13, Е = 14, F = 15.
Для того, чтобы перевести из шестнадцатеричной системы счисления в десятичную, нужно необходимо умножить каждую цифру восьмеричного числа на основание 16, возведенное в степень, равную разряду.
Пример. 12716 = 1 * 162 + 2 * 161 + 7 * 160 = 256 + 32 + 7 = 29510.
Для того, чтобы перевести из десятичной системы счисления в шестнадцатеричную, нужно целую часть числа находить делением на основание новой.
Пример. 19110 переведем в шестнадцатеричную систему:Получаем, что 19110 = BF16
Перевод между системами счисления, основания которых являются степенью двойки.
Для перевода чисел, записанных в восьмеричной системе в двоичный код, необходимо каждую цифру восьмеричного числа представить триадой двоичных символов.
Триады — числа, состоящие из трех цифр, грубо говоря, это перевод восьмеричных чисел от 0 до 7 в двоичную систему счисления. Тетрады состоят из четырех, и это, грубо говоря, перевод шестнадцатеричных чисел от 0 до F в двоичную систему счисления. Триады и тетрады переводятся, начиная с конца числа (т.
е. с младших разрядов). Если крайние триады (тетрады) оказались неполными, они дополняются нулями. Если при переводе в двоичную систему в начале числа (слева) возникают нули, их следует отбросить (они незначащие).
Пример. 123456678 = 001 010 011 100 101 110 110 1112 = 1 010 011 100 101 110 110 1112
Таблица с триадами и тетрадами, которую надо знать наизусть.
| Число | Триада | Тетрада |
|---|---|---|
| 0 | 000 | 0000 |
| 1 | 001 | 0001 |
| 2 | 010 | 0010 |
| 3 | 011 | 0011 |
| 4 | 100 | 0100 |
| 5 | 101 | 0101 |
| 6 | 110 | 0110 |
| 7 | 111 | 0111 |
| 8 | 1000 | |
| 9 | 1001 | |
| A (10) | 1010 | |
| B (11) | 1011 | |
| C (12) | 1100 | |
| D (13) | 1101 | |
| E (14) | 1110 | |
| F (15) | 1111 |
Перевод чисел с большими степенями
В задании №14 в ЕГЭ по информатике важно знать еще пару особенностей систем счисления.
В десятичной системе счисления вы привыкли к тому, что 10a (десять в степени a) равно единице с a нулями. Важно то, что во всех других позиционных системах это работает точно так же. Сформулируем соответствующее правило:
| Десятичное число вида na в n-ричной системе счисления будет выглядеть как единица с a нулями. |
Пример. Десятичное число 27 в двоичной системе счисления будет выглядеть как единица и семь нулей: 100000002, десятичное число 54 в пятеричной системе счисления будет выглядеть как единица и четыре нуля: 100005 и т.д.
Еще одна важная вещь касается вычитания маленьких чисел из больших круглых чисел в разных системах счисления. Если мы в десятичной системе счисления из 1000000 вычтем 1, мы получим 999999 – это никого не удивляет. Однако, в двоичной и других системах счисления понимание этого дается многим с трудом, хотя принцип абсолютно тот же самый.
Сформулируем соответствующее правило:
| Если необходимо из числа 1000…000n+1, содержащего единицу и a нулей, вычесть 1n+1, то результат будет nnn…nnnn+1, где количество цифр n будет равно a. |
Пример. 100006 – 16 = 55556, 100000003 – 13 = 22222223.
В форматных заданиях №16 часто встречаются прототипы, где нужно складывать и вычитать десятичные числа с большими показателями. Давайте посчитаем количество «шестерок» в выражении 725 – 73, где числа записали в семеричной системе счисления. При переводе чисел получим, что 725 = 1000…0007 (25 нулей), 73 = 10007. Запишем решение через столбик:
Видим, что младшие 3 разряда остаются нулями, остальные разряды превращаются в шестерки.
Заметим, что в получившемся числе 25 разрядов, 3 из которых – это нули, а оставшиеся 22 разряда – шестерки. Таким образом, ответом является 22.
Отметим, что мы искали количество цифр, имеющих максимальное значение в данной системе счисления. Можно заметить, что мы взяли 25 — показатель старшей степени, и вычли из него 3 — показатель младшей степени, и получили верный ответ. Такое правило работает с любым выражением, где числа имеют одинаковое основание. Сформулируем соответствующее правило:
| Если необходимо десятичное число, имеющее вид an – am, перевести в a–ричную систему счисления, то количество цифр (a-1) будет равно разности показателей, то есть n-m. |
Пример. Сколько будет единиц в двоичной записи числа 2234 -2217? Нам нужно посчитать количество максимальных цифр в двоичной записи данного выражения. Числа имеют одинаковое основание 2, поэтому воспользуемся правилом, которое мы вывели выше, то есть 234 – 217 = 17.
Десятичные и шестнадцатеричные цифры и целые числа — Информатика, информационные технологии
Целые числовые константы в исходном коде Java (так называемые литерные константы) могут быть десятичными или шестнадцатеричными. Они записываются либо символами ASCII, или символами Unicode следующим образом.
Десятичные константы записываются как обычно. Например, -137.
Шестнадцатеричная константа начинается с символов 0x или 0X (цифра 0, после которой следует латинская буква X), а затем идёт само число в шестнадцатеричной нотации. Например, 0x10 соответствует 1016=16; 0x2F соответствует 2F16=47, и т.д. О шестнадцатеричной нотации рассказано чуть ниже.
Ранее иногда применялись восьмеричные числа, и в языках C/C++, а также старых версиях Java можно было их записывать в виде числа, начинающегося с цифры 0. То есть 010 означало 108=8. В настоящее время в программировании восьмеричные числа практически никогда не применяются, а неадекватное использование ведущего нуля может приводить к логическим ошибкам в программе.
Целая константа в обычной записи имеет тип int. Если после константы добавить букву L (или l, что хуже видно в тексте, хотя в среде разработки выделяется цветом), она будет иметь тип long, обладающий более широким диапазоном значений, чем тип int.
Поясним теперь, что такое шестнадцатеричная нотация записи чисел и зачем она нужна.
Информация представляется в компьютере в двоичном виде – как последовательность бит. Бит – это минимальная порция информации, он может быть представлен в виде ячейки, в которой хранится или ноль, или единица. Но бит – слишком мелкая единица, поэтому в компьютерах информация хранится, кодируется и передаётся байтами — порциями по 8 бит.
В данной книге под “ячейкой памяти” будет пониматься непрерывная область памяти (с последовательно идущими адресами), выделенная программой для хранения данных. На рисунках мы будем изображать ячейку прямоугольником, внутри которого находятся хранящиеся в ячейке данные. Если у ячейки имеется имя, оно будет писаться рядом с этим прямоугольником.
Мы привыкли работать с числами, записанными в так называемой десятичной системе счисления. В ней имеется 10 цифр (от 0 до 9), а в числе имеются десятичные разряды. Каждый разряд слева имеет вес 10 по сравнению с предыдущим, то есть для получения значения числа, соответствующего цифре в каком-то разряде, стоящую в нём цифру надо умножать на 10 в соответствующей степени. То есть 52=5•10+2, 137=1•102+3•101+7, и т.п.
В программировании десятичной системой счисления пользоваться не всегда удобно, так как в компьютерах информация организована в виде бит, байт и более крупных порций. Человеку неудобно оперировать данными в виде длинных последовательностей нулей и единиц. В настоящее время в программировании стандартной является шестнадцатеричная система записи чисел. Например, с её помощью естественным образом кодируется цвет, устанавливаются значения отдельных бит числа, осуществляется шифрование и дешифрование информации, и так далее. В этой системе счисления всё очень похоже на десятичную, но только не 10, а 16 цифр, и вес разряда не 10, а 16.
В качестве первых 10 цифр используются обычные десятичные цифры, а в качестве недостающих цифр, больших 9, используются заглавные латинские буквы A, B, C, D, E, F:
0 1 2 3 4 5 6 7 8 9 A B C D E F
То есть A=10, B=11, C=12, D=13, E=14, F=15.
Заметим, что в шестнадцатеричной системе счисления числа от 0 до 9 записываются одинаково, а превышающие 9 отличаются. Для чисел от 10 до 15 в шестнадцатеричной системе счисления используются буквы от A до F, после чего происходит использование следующего шестнадцатеричного разряда. Десятичное число 16 в шестнадцатеричной системе счисления записывается как 10. Для того, чтобы не путать числа, записанные в разных системах счисления, около них справа пишут индекс с указанием основания системы счисления. Для десятичной системы счисления это 10, для шестнадцатеричной 16. Для десятичной системы основание обычно не указывают, если это не приводит к путанице. Точно так же в технической литературе часто не указывают основание для чисел, записанных в шестнадцатеричной системе счисления, если в записи числа встречаются не только “обычные” цифры от 0 до 9, но и “буквенные” цифры от A до F.
Обычно используют заглавные буквы, но можно применять и строчные.
Рассмотрим примеры.
0x10 = 1016 =16 ;
0x100 = 10016 =16 •16=256;
0x1000 = 100016 =(16)3=4096;
0x20 = 2016 =2•16 =32;
0x21 = 2116 =2•16 +1=33;
0xF = F16 =15 ;
0x1F = 1F16 =1•16 +15=31 ;
0x2F = 2F16 =2•16 +15=47 ;
0xFF = FF16 =15 •16+15=255;
Более подробно вопросы представления чисел в компьютере будут рассмотрены в отдельном разделе.
Статьи к прочтению:
- Детское кафе «санмаринушка» (в кафе «la gusto»).
- Диагностика состояния аппаратуры и устройств.
Перевод чисел из десятичной в двоичную систему счисления. Лекция по информатике №1
Похожие статьи:
Пустьв десятичной системе задано число 37510.
Арифметические основы компьютера Системы счисления Для автоматизации работы с данными, которые относятся к разным типам, унифицируют их форму…
Разложение целого числа по степеням основания в различных системах счисления
Системы счисления.
Совокупность приемов наименования и записи чисел называется счислением. Под системой счисления понимается способ представления любого…
Совокупность приемов наименования и записи чисел называется счислением. Под системой счисления понимается способ представления любого…Что такое шестнадцатеричная система счисления?
Если вы новичок в программировании или просто хотите понять, как работает шестнадцатеричная система счисления, то этот блог для вас! Шестнадцатеричные числа представлены строкой букв и цифр, состоящей из 16 различных символов. Например, шестнадцатеричное число «FFFF» часто отображается как «255», поскольку каждый шестнадцатеричный символ представляет собой четыре двоичных разряда. Читайте дальше, чтобы узнать больше о шестнадцатеричной системе счисления.
Что такое шестнадцатеричная система счисления? Шестнадцатеричная система счисления — это система счисления с основанием 16, в которой для представления чисел используются цифры 0–9 и буквы A–F. Шестнадцатеричная система счисления имеет 16 возможных значений для каждой цифры, что позволяет представлять более широкий диапазон чисел, чем в десятичной системе счисления.
Шестнадцатеричная система счисления широко используется в компьютерных науках, поскольку она обеспечивает простой способ представления двоичных данных. При преобразовании из двоичного в шестнадцатеричный каждая группа из четырех битов представляется одной шестнадцатеричной цифрой. Например, двоичное число 1010 можно представить как шестнадцатеричное число А. Это упрощает преобразование между двумя системами при работе с компьютерным кодом.
Шестнадцатеричная система счисления также может использоваться для представления цветов на экране компьютера. Каждый цвет представлен шестизначным шестнадцатеричным кодом, который включает в себя сочетание цифр 0-9 и букв A-F. Например, черный цвет может быть представлен как #000000, а белый цвет может быть представлен как #FFFFFF.
Как работает шестнадцатеричная система счисления Шестнадцатеричная система счисления основана на шестнадцатеричном основании. Это означает, что существует 16 возможных цифр, которые можно использовать для представления числа.
Чаще всего используются цифры от 0 до 9.и А-Ф.
Чтобы понять, как работает шестнадцатеричная система счисления, сначала важно понять, как работает десятичная система счисления. В десятичной системе счисления существует 10 возможных цифр, которые можно использовать для представления числа (0-9). Каждая цифра в десятичном числе имеет разрядное значение. Позиция цифры определяется ее положением в числе. Например, в числе 123 1 имеет разрядное значение 100, 2 имеет разрядное значение 10, а 3 имеет разрядное значение 1.
Шестнадцатеричная система счисления работает аналогично десятичной системе счисления, за исключением того, что вместо 10 можно использовать 16 возможных цифр. Как и в десятичной системе, каждая цифра в шестнадцатеричном числе имеет разрядное значение. Однако, поскольку в шестнадцатеричной системе цифр больше, разрядные значения различаются. В шестнадцатеричной системе счисления разрядные значения цифр увеличиваются на 16-ю степень при движении справа налево, а не на 10-ю степень, как в десятичной системе.
3=409.6 ,the2hasaplacevalue
Шестнадцатеричная система счисления представляет собой систему счисления с основанием 16, в которой для представления чисел используются цифры 0–9 и буквы A–F. Эта система счисления используется во многих приложениях, таких как компьютерное программирование, потому что ее легко преобразовать между двоичной (язык, используемый компьютерами) и шестнадцатеричной.
Основным преимуществом шестнадцатеричной системы счисления является ее простота. Поскольку для представления чисел используется всего 16 символов, их легко преобразовать между различными основаниями (например, двоичными и десятичными). Шестнадцатеричная система счисления также более компактна, чем другие системы счисления, что делает ее идеальной для хранения и передачи.
Шестнадцатеричная таблица преобразования Шестнадцатеричная система счисления является системой счисления с основанием 16.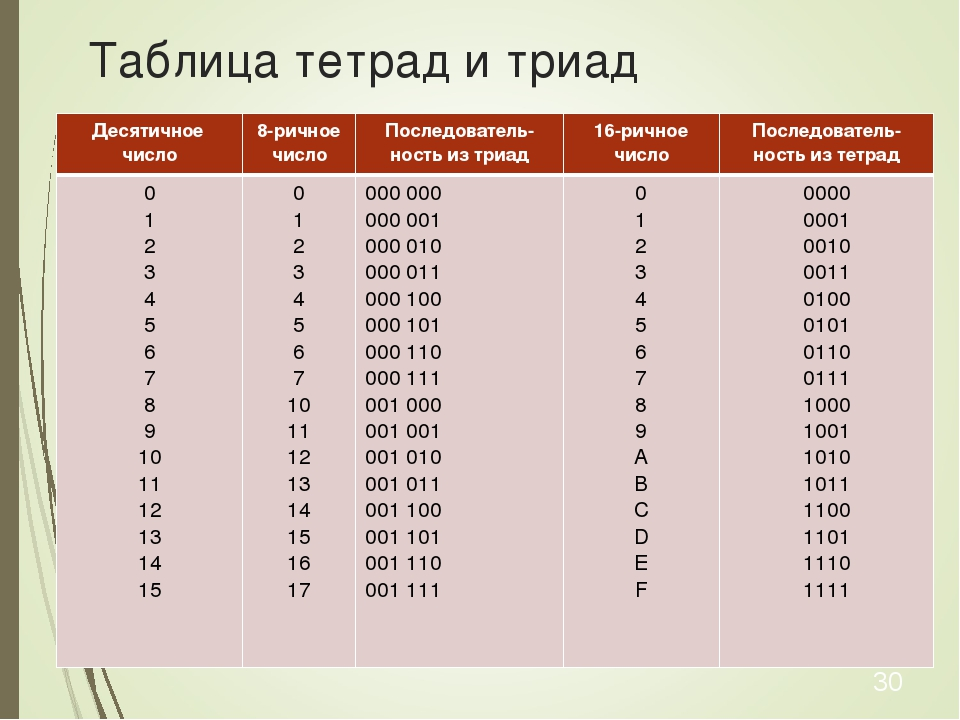
Это означает, что в системе 16 цифр, 0-9 и A-F. В приведенной ниже таблице шестнадцатеричных преобразований показаны десятичные значения для каждой из шестнадцатеричных цифр:
Таблица шестнадцатеричных преобразований
Десятичное значение цифр
0 0
1 1
2 2
3 3
4 4
5 5
6 6
7 7
8 8
9 9
A 10
B 11
C 12
D 13
E 14
9000 4 Как преобразовать шестнадцатеричный формат в двоичный?Шестнадцатеричная система счисления представляет собой систему счисления с основанием 16, в которой используются буквы A-F для представления значений 10-15. Чтобы преобразовать шестнадцатеричное число в двоичное, просто запишите шестнадцатеричное число, как если бы оно было обычным числом с основанием 10, а затем разбейте его на группы из 4 двоичных цифр.
Например, шестнадцатеричное число «AF» будет записано как «10» с основанием 10, которое затем можно разбить на две группы по 4 двоичных цифры: «1000» и «1111».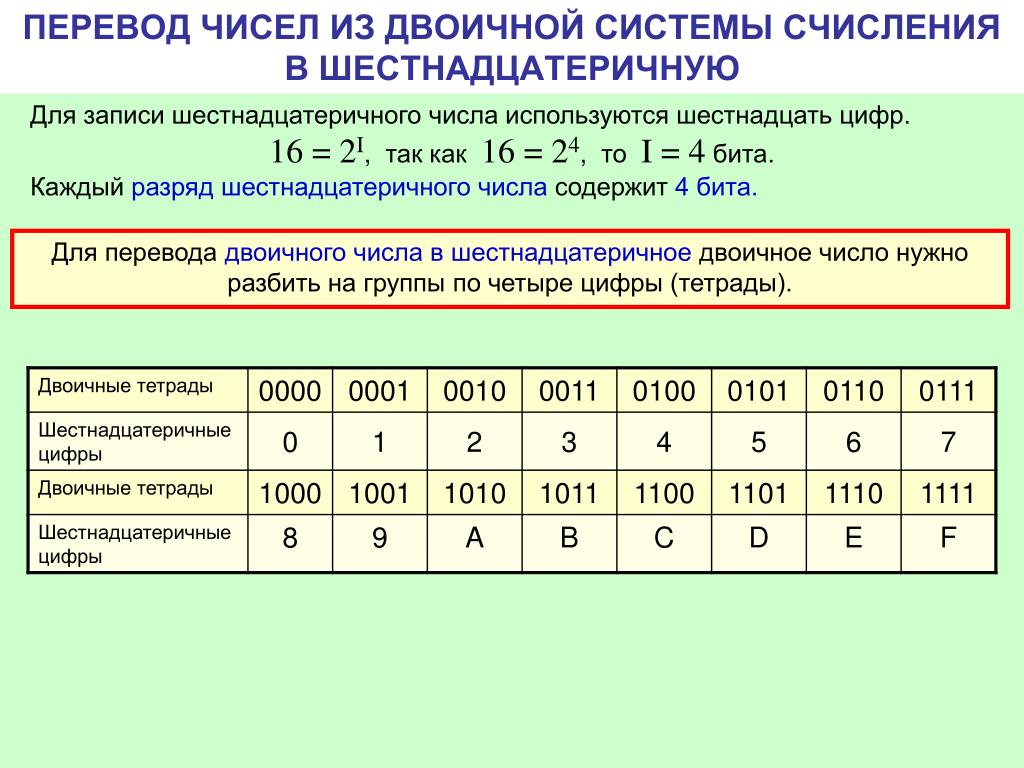
Следовательно, двоичный эквивалент «AF» — «10001111».
Шестнадцатеричная система счисления является прекрасной альтернативой более традиционной десятичной системе счисления. Это особенно полезно для представления чисел в компьютерном коде. Если вы работаете с большими числами, шестнадцатеричная система может быть удобным способом отслеживать их.
Если вы хотите узнать о других предметах, нет лучшего места для начала, чем приложение Noon. Доступно более 10 000 лекций, и вы можете учиться в своем собственном темпе и из любой точки мира. Кроме того, с преподавателями со всего мира вы обязательно найдете идеального педагога для своих нужд. И так, чего же ты ждешь? Загрузите приложение Noon прямо сейчас и начните учиться уже сегодня!
шестнадцатеричных чисел
шестнадцатеричных чиселПри работе с учебником не используйте полосу прокрутки. Вместо этого перемещайтесь по документу, нажимая на горячие ссылки.
Вы когда-нибудь задумывались о происхождении слова «цифра»? Оно происходит от латинского слова «digitus», что означает «палец».
Мы привыкли к тому, что цифры обозначают числа, и, конечно же,
достаточно, в нашей десятичной системе столько же цифр, сколько
пальцы на наших руках. Представьте себе следующий сценарий: Племя инопланетян
под названием «Гексаны» решает иммигрировать на планету Земля. как можно было бы
ожидать, они оседают в США, точнее, на юго-востоке
Огайо. Гексаны похожи на людей во всех отношениях, за исключением того, что они
иметь по восемь пальцев на каждой руке. Они быстро адаптируются к американцам
цивилизация. Через несколько лет они начинают чувствовать, что их племя
подвергается дискриминации со стороны преобладающей системы нумерации, основанной на
количество пальцев, типичное для землян. Они обращаются к губернатору
Огайо, чтобы придать равный вес в государственном образовании обучению
альтернативная система нумерации, основанная на 16 цифрах, и называемая вполне
соответственно «шестнадцатеричная» система.
Теперь предположим, что губернатор штата Огайо поручил вам разработку
соответствующей учебной программы общеобразовательной школы.
Первое, что у вас есть
решить, какими будут цифры новой системы.
Конечно, первые десять цифр будут от 0 до 9, но теперь вы также
нужны цифры для чисел от 10 до 15. Вы могли бы изобрести новые
символы для тех, но вы понимаете, что это повлекло бы, среди прочего
вещи, переделывая все используемые в штате клавиатуры. Гораздо больше
целесообразное решение состоит в том, чтобы существующие буквы обозначали дополнительные цифры.
Итак, вы решили использовать заглавную букву А для цифры, соответствующей 10,
B для 11 и так далее.
Какое число представлено шестнадцатеричной цифрой D?
- 9
- 13
- 14
- Д
Извините, вы выбрали неправильный ответ.
Это не может быть правильным, так как цифры от 0 до 9 представлены одинаково в десятичной системе и в шестнадцатеричной системе.
Пожалуйста, попробуйте еще раз.
Извините, вы выбрали неправильный ответ.
Пожалуйста, попробуйте еще раз.
Извините, вы выбрали неправильный ответ.
Строго говоря, вы не дали неправильного ответа, только один на что автор этого урока не надеялся. Формулировка мой вопрос неточен. Я спросил тебя: «Какой номер…?» В шестнадцатеричном системы, D очень много является (одноразрядным) числом. Если бы я спросил вместо этого «Какое десятичное число …?», ответ «D» был бы просто неправильным.
Пожалуйста, попробуйте еще раз.
ПРАВИЛЬНО!
Какой буквой обозначается самая большая шестнадцатеричная цифра?
- ф
- Н
- Э
- ч
- Ф
- е
Извините, вы выбрали неправильный ответ.
Помните, что дополнительные цифры представлены ЗАГЛАВНЫМИ буквами.
Пожалуйста, попробуйте еще раз.
Извините, вы выбрали неправильный ответ.
Пожалуйста, попробуйте еще раз.
Извините, вы выбрали неправильный ответ.
Пожалуйста, попробуйте еще раз.
Извините, вы выбрали неправильный ответ.
Помните, что дополнительные цифры представлены ЗАГЛАВНЫМИ буквами.
Пожалуйста, попробуйте еще раз.
Извините, вы выбрали неправильный ответ.
Помните, что дополнительные цифры представлены ЗАГЛАВНЫМИ буквами.
Пожалуйста, попробуйте еще раз.
ПРАВИЛЬНО!
А какому выражению в десятичной системе соответствует «F»?
- 16
- 15
- 17
Извините, вы выбрали неправильный ответ.
Напомним, что в нашей системе, основанной на 10 цифрах, самый большой цифра 10-1 = 9.
Пожалуйста, попробуйте еще раз.
Извините, вы выбрали неправильный ответ.
Пожалуйста, попробуйте еще раз.
ПРАВИЛЬНО!
Хорошо, мы установили, что шестнадцатеричные цифры 0—F соответствуют
к нашим знакомым десятичным числам 0—15. Но как мы будем представлять
число 16? Обратите внимание, что это тот момент, когда у Hexans заканчиваются
пальцы.
Конечно, мы, люди, сталкиваемся с той же проблемой, когда получаем
до 9 + 1. Некоторые из наших предков нашли гениальное решение:
Запишем следующее число после 9 как 10, что можно интерпретировать как:
«1 полный набор из (10) цифр и 0 остатков»,
или «1 x 10 + 0» для сокращения. Конечно, гексан был бы склонен
думать об «1 полном наборе цифр и 0 остатках» скорее как о
«1 x 16 + 0», а это именно то число, которое стоит после «F»!
Таким образом, десятичное число 16 будет представлено как 10 в шестнадцатеричном формате. система. Наше число 17, то есть «1 полный набор цифр и 1 остаток» в Hexan будет представлен как 11 в шестнадцатеричной системе, и скоро.
Что означает десятичное число 21 для Hexan?
- «Два полных набора цифр и один лишний».
- «Один полный набор цифр и пять оставшихся».
Извините, вы выбрали неправильный ответ.
Число 21 полагалось давать в десятичной системе счисления.
ШЕСТНАДЦАТЕРИЧНОЕ число 21 означало бы для Hexan
«Два полных набора цифр и один лишний».
Пожалуйста, попробуйте еще раз.
ПРАВИЛЬНО!
Так как же Hexan будет представлять десятичное число 21?
- 15
- 17
- 14
Извините, вы выбрали неправильный ответ.
Шестнадцатеричное число 17 — это способ Hexan сказать «Один полный набор цифр и семь остатков». Это соответствует до десятичного числа 1 х 16 + 7 = 23.
Пожалуйста, попробуйте еще раз.
Извините, вы выбрали неправильный ответ.
Шестнадцатеричное число 14 — это способ Hexan сказать «Один полный набор цифр и четыре остатка». Это соответствует до десятичного числа 1 х 16 + 4 = 20.
Пожалуйста, попробуйте еще раз.
ПРАВИЛЬНО!
Какое десятичное число соответствует идее Гексана о «1 полный набор цифр и остатки E»?
- 1Е
- 30
- 32
- 29
Извините, вы выбрали неправильный ответ.
Это правильный ответ на другой вопрос, а именно: ‘Какое ШЕСТНАДЦАТЕРИЧНОЕ число соответствует гексанскому представлению о «1 полный набор цифр и E остатков»?
Пожалуйста, попробуйте еще раз.
Извините, вы выбрали неправильный ответ.
Обратите внимание, что 32 — это два полных набора шестнадцатеричных цифр.
Пожалуйста, попробуйте еще раз.
Извините, вы выбрали неправильный ответ.
Пожалуйста, попробуйте еще раз.
ПРАВИЛЬНО!
Какое шестнадцатеричное число соответствует десятичному числу 27?
- 1Б
- 19
- 1Н
- 1С
Извините, вы выбрали неправильный ответ.
«Один полный набор шестнадцатеричных цифр и 9 оставшихся» 1 х 16 + 9 = 25.
Пожалуйста, попробуйте еще раз.
Извините, вы выбрали неправильный ответ.
Буква H не представляет собой шестнадцатеричную цифру.
Пожалуйста, попробуйте еще раз.
Извините, вы выбрали неправильный ответ.
«Один полный набор шестнадцатеричных цифр и остатки C» 1 х 16 + 12 = 28.
Пожалуйста, попробуйте еще раз.
ПРАВИЛЬНО!
Десятичное число 34 — это наш способ выразить понятие
«3 полных набора цифр и 4 остатка».
Какое десятичное число соответствует представлению Hexan о «3 полных набора цифр и 4 остатка»?
- С4
- 160
- 52
- 59
Извините, вы выбрали неправильный ответ.
Ответ должен быть десятичным, а не шестнадцатеричным числом.
Пожалуйста, попробуйте еще раз.
Извините, вы выбрали неправильный ответ.
160 будет «Десять полных наборов шестнадцатеричных цифр и никаких остатков», или, говоря более понятным для Hexan языком, «Полный набор цифр и никаких остатков», то есть А0.
Пожалуйста, попробуйте еще раз.
Извините, вы выбрали неправильный ответ.
59 будет «три полных набора шестнадцатеричных цифр и 11 оставшихся», или, говоря более понятным для Hexan языком, «3 полных набора цифр и оставшиеся B», то есть 3В.
Пожалуйста, попробуйте еще раз.
ПРАВИЛЬНО!
Когда гексан пишет число «BC», он думает о
«B полных наборов цифр и C остатков».
Какому десятичному числу это соответствует?
- 159
- 172
- 188
Извините, вы выбрали неправильный ответ.
159 соответствует «9 полных наборов цифр и F остатков».
Пожалуйста, попробуйте еще раз.
Извините, вы выбрали неправильный ответ.
172 соответствует «полным наборам цифр и C остаткам».
Пожалуйста, попробуйте еще раз.
ПРАВИЛЬНО!
Хорошо, мы видим, что существует двузначное число. шестнадцатеричное число. Каждая из цифр является либо «нормальной» цифрой, или заглавная буква. Если мы увеличим вторую цифру на единицу, число увеличивается на единицу, как в нашей десятичной системе. Но если мы увеличить первую цифру шестнадцатеричного числа на единицу, число увеличивается не на десять, как в нашей системе, а на целых шестнадцать.
Самое большое двузначное шестнадцатеричное число — FF. Какое десятичное число это соответствует?
- 1616
- 1515
- 255
Извините, вы выбрали неправильный ответ.
Пожалуйста, попробуйте еще раз.
Извините, вы выбрали неправильный ответ.
Конечно, мы рассматриваем «15 полных наборов шестнадцатеричных цифр и 15 остатков». Но десятичное число 1515 означает «151 полный набор десятичных цифр и пять оставшихся».
Пожалуйста, попробуйте еще раз.
ПРАВИЛЬНО!
Сколько чисел можно представить двумя шестнадцатеричными цифрами?
- 255
- 256
- 240
Извините, вы выбрали неправильный ответ.
Подсказка: 00 также представляет число.
Пожалуйста, попробуйте еще раз.
Извините, вы выбрали неправильный ответ.
Подсказка: первая из этих цифр также может быть нулем.
Пожалуйста, попробуйте еще раз.
ПРАВИЛЬНО!
Не знаю, есть ли во вселенной Гексаны, но есть
являются шестнадцатеричными числами, и они встречаются даже здесь, на планете Земля.
Среди прочего двузначный шестнадцатеричный
цифры используются для кодирования отображаемых цветов
на экранах телевизоров и компьютеров.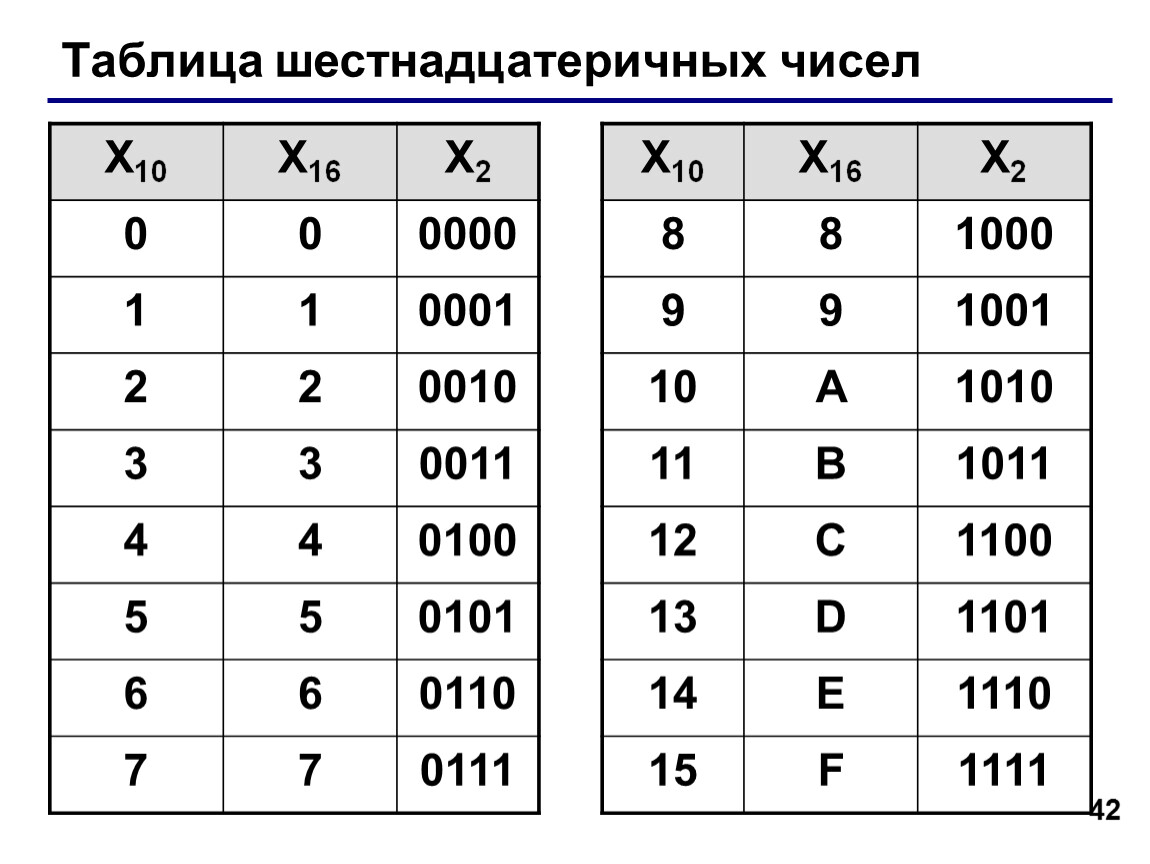
Это работает следующим образом:
Экран разделен на небольшие области, называемые пикселями. Каждый пиксель
имеет красную, зеленую и синюю составляющие, а цветное изображение кодируется
указание сильных сторон этих компонентов для каждого пикселя.
Если для каждого компонента установлена максимальная сила, появится белый пиксель.
на экране. Отключение зеленого и синего компонентов и настройка
красный компонент до максимальной силы, конечно, приведет к ярко-красному
пиксель. Желтый пиксель можно получить как смесь красного и зеленого,
с выключенным синим компонентом.
Теперь сильные стороны красного, зеленого,
и синие компоненты кодируются двузначными шестнадцатеричными числами. Как мы видели
выше, это означает, что
каждый из этих компонентов может иметь 256 различных
оттенки, что дает вашему компьютеру возможность отображать
256 х 256 х 256 = 16 миллионов и 777 216 различных цветов!
Почему для этого используются шестнадцатеричные числа, а не десятичные числа? кодирование?
- Компьютерщики просто обожают неясные коды.
- Эта система делает цвета более яркими и привлекательными для человеческого глаза.
- Шестнадцатеричными числами можно закодировать больше цветов, чем десятичными. числа.
- Для оптимального использования памяти компьютера.
Извините, вы выбрали неправильный ответ.
Конечно, программисты любят неясные коды. Но это не причина, по которой цвета кодируются в шестнадцатеричной системе.
Пожалуйста, попробуйте еще раз.
Извините, вы выбрали неправильный ответ.
Что делает цвета яркими и привлекательными, так это тот факт, что многие из них. Особый способ, которым эти более 16 миллионов цветов закодированы, не имеет значения для их яркости.
Пожалуйста, попробуйте еще раз.
Извините, вы выбрали неправильный ответ.
В десятичной системе можно выразить столько чисел, сколько в
шестнадцатеричная система. Но в этом ответе есть доля правды: вы можете кодировать
больше цветов с тремя двузначными шестнадцатеричными числами, чем с тремя
двузначные десятичные числа.
