Третий закон кирхгофа: 3. Законы Кирхгофа для электрических цепей. — RC74 — интернет-магазин радиоуправляемых моделей

3-й закон Кирхгофа — dmagin — LiveJournal

3.Законы кирхгофа

4.4: Законы Кирхгофа — Физика LibreTexts

Законы Кирхгофа и спектроскопия

Второй закон Кирхгофа

И методы их расчета Последовательное соединение — это совокупность связанных элементов электрической цепи, не имеющая узлов.

4.4.1 Спектроскопия

4.4.2 Законы излучения Кирхгофа

Одной из самых важных вещей, которые мы можем делать с помощью телескопа, является спектроскопия. Исторически появление спектроскопии в конце 19 в.20-м веке послужила такой главной мотивацией, что привела к изобретению нового термина — астрофизика. Спектроскопия следует некоторым основным правилам. Они известны как законы Кирхгофа. Давайте узнаем больше об этом.

Законы

Получение спектра поглощения

Темные линии

Потемнение конечностей

Наша линия обзора и оптическая глубина

Общие вопросы о законах Кирхгофа и спектроскопии

Джошуа Н. Винн, Принстонский университет

Содержание

Previous Entry | Next Entry

Продвижение по теме потоков в почти симметричных графах продолжается.
Было (кратко, ес-но) изучено состояние дел в теории электрических сетей (по работам «Random Walks and Electrical Networks», «Inverse Problems for Electrical Networks»). Обнаружено, что люди почему-то не используют мой прием — задание разности потенциалов в сети через введение асимметричного ребра. А мучаются со стандартной задачей Дирихле — то есть через задание краевых условий на потенциалы. Зря. Теряется общность и простота «графического» подхода. (Правда меня немного смущает, что такую асимметрию можно задать, просто воткнув в землю диод, без всяких источников тока).

Что еще понято. Наконец-то постиг, как доказывается пресловутый инвариант для графа любой размерности. Для этого пришлось, правда, ввести 3-й закон Кирхгофа )).

Ну и наиболее интересная часть — продвинулся в решении обратной задачи для электрических сетей — вычисление проводимостей графа на основе известных разностей потенциала. Поскольку материала много, то разобью на несколько постов.

Начнем с Кирхгофа.

Как известно, Кирхгофу приписывают два правила, которые полезны для расчета электрических цепей:
1) Сумма токов в каждом узле равна нулю — мы это называем балансом потоков.
2) Сумма разностей потенциалов по замкнутому контуру равна нулю (про всякие ЭДС и пр. мы здесь намеренно опускаем,- они нам без надобности).- Это тоже очевидность, на которой не останавливаемся.

А вот про 3-й закон (скорее, правило), похоже никто не знает. Включая самого Кирхгофа. А он, оказывается, тоже полезен. И важен для всех, кто занимается электроразведкой, кто подает ток/напряжение в одном месте, а снимает в другом.

В электротехнике известен принцип эквивалентности — если мы меняем местами питающие электроды (по которым подаем ток) и съемные (снимаем напряжение), то результат остается тот же самым. Вроде бы очевиден,- связан с линейностью уравнений. Для графов я особо не вникал — почему так происходит. Проверил — действительно так.
Как проверяется. Берем симметричный граф (аналог электрической сети). И вводим асимметрию, например, ребра ij,- то есть вводим разность между проводимостями: dC = Cij — Сji. Смотрим — чему равна разность потенциалов между любыми произвольными узлами графа (m и n, например). Потом восстанавливаем симметричность ребра ij и вводим асимметрию между узлами m и n. А разность меряем между i и j (как много приходится писать) — полученные разности Umn (в 1-м случае) и Uij (во 2-м) — равны. Это и есть принцип эквивалентности.

Теперь допустим, что мы снимаем разность потенциалов Umn с одних и тех же узлов (измерительные электроды фиксированы), но при этом последовательно меням расположение питающих электродов. Например, сначала задали ток через узлы 12 (измерили Umn), потом через 23 (снова измерили Umn), потом — через 34 и т.д. Теперь мы можем сформулировать 3-е правило:

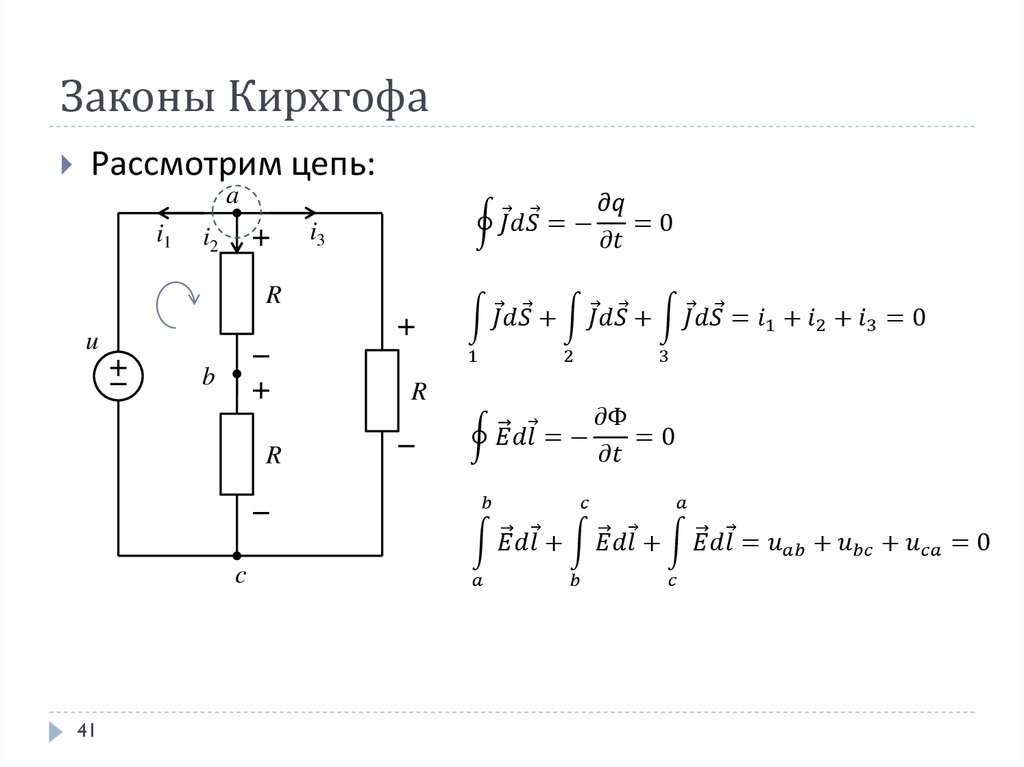
Если путь, по которому меняются питающие электроды,- замкнут (12-23-34-41), то сумма измеренных разностей потенциалов Umn будет равна нулю.

Фактически, 3-е правило — это использование 2-го закона совместно с принципом эквивалентности.
Почему данное правило не пользуется популярностью (неизвестно)? Скорее всего потому, что в традиционной электротехнике (и электроразведке тоже) редко меняют положение питающих электродов.

Где мы можем применить данное правило?

Ну, доказать, наконец-то наш инвариант (след. пост).
Но более интересно — понять — какие же измерения нам нужно провести (а какие, наборот — уже будут лишними), чтобы решить обратную задачу (для электрических сетей, например). Результаты данного исследования планируется изложить через пост.

dmagin

dmagin

Заметки о структурах данных

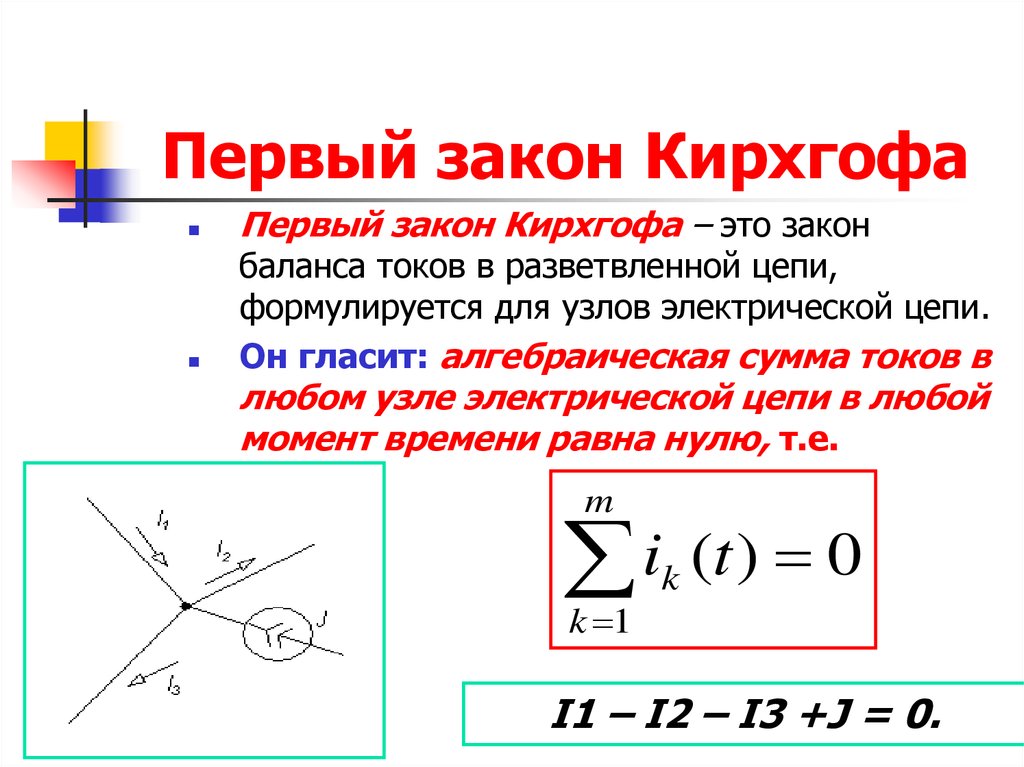
Первый закон Кирхгофа

Данный закон применим к любому узлу электрической цепи.

Первый закон Кирхгофа — алгебраическая сумма всех токов, сходящихся в узле равна нулю. Токи, наравленные к узлу, условно принимаются положительными, а направленные от него — отрицательными (или наоборот). На рисунке ниже изображен пример применения первого закона Кирхгофа для узла, в котором сходится 5 ветвей.Более понятна для понимания другая формулировка первого закона Кирхгофа: сумма токов, направленных к узлу электрической цепи равна сумме токов, направленных от него.

Данный закон применим к любому замкнутому контуру электрической цепи.

Второй закон Кирхгофа — в любом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений в отдельных сопротивлениях. Для применения данного закона на практике, сначала необходимо выбрать замкнутый контур электрической цепи.

Далее в нем произвольно выбирают направление обхода (по часовой стрелке, или наоборот). При записи левой части равенства ЭДС, направления которых совпадают с выбранным направлением обхода, принимаются положительными, в обратном случае — отрицательными. При записи правой части равенства положительными считают падения напряжения в тех сопротивлениях, в которых выбранное положительное направление тока совпадает с направлением обхода. В противном случае, падению напряжения следует присвоить знак «минус».

На рисунке ниже наглядно представлены примеры составления равенств для нескольких контуров электрической цепи.

4-5. ЭКВИВАЛЕНТНЫЕ ПРЕОБРАЗОВАНИЯ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

В последовательное соединение в общем случае может входить любое количество резисторов и источников ЭДС (рис. 1), но не может входить более одного источника тока, т.к. это противоречило бы свойству каждого из источников создавать в цепи ток не зависящий от внешних элементов.

Падение напряжения между точками

a и b рис. 1 можно представить разностью потенциалов этих точек U_ab = j _a — j _b . Формально в эту разность можно включить произвольное число значений потенциалов (например, потенциалов точек соединения элементов) с противоположными знаками, а затем попарно объединить их —

U_ab = j _a — j _b = j _a -j _с +j _с -j _d +j _d -…-j _i +j _i -j _k

+j _k-… -j _q +j _q — j _b =

= (j _a -j _с)+(j _с-j _d)+(j _d -. ..-j _i)+(j _i -j _k)+(j _k-… -j _q)+(j _q — j _b) =

= U_ac+ U_cd+ U_de+…+ U_ik+ U_kl+ U

lm+…+ U_qb =

= Ir₁+ Ir₂+ Ir₃+…+ Ir_m+E₁+ E₂+…-E_n =

= I(r₁+ r₂+ r₃+…+ r_m)+( E₁+ E₂+…-E_n) = IR + E

(1)

Таким образом, любое последовательное соединение можно преобразовать к последовательному соединению одного эквивалентного резистора и одного источника ЭДС.

Причем, сопротивление эквивалентного резистора равно сумме всех сопротивлений входящих в соединение, а ЭДС эквивалентного источника равна алгебраической сумме ЭДС источников входящих в соединение.

Параллельное соединение элементов — это совокупность элементов электрической цепи, объединенных двумя узлами и не имеющих связей с другими узлами.

В параллельное соединение элементов в общем случае могут входить резисторы и источники тока (рис. 2), но не может входить более одного источника ЭДС, т.к. это противоречило бы их свойству создавать на выходе разность потенциалов не зависящую от внешней цепи.

I = Ug₁+Ug₂+…+Ug_n —J₁+J₂+…+J_m=

=U(g₁+g₂+…+g_n) -(J₁+J₂+.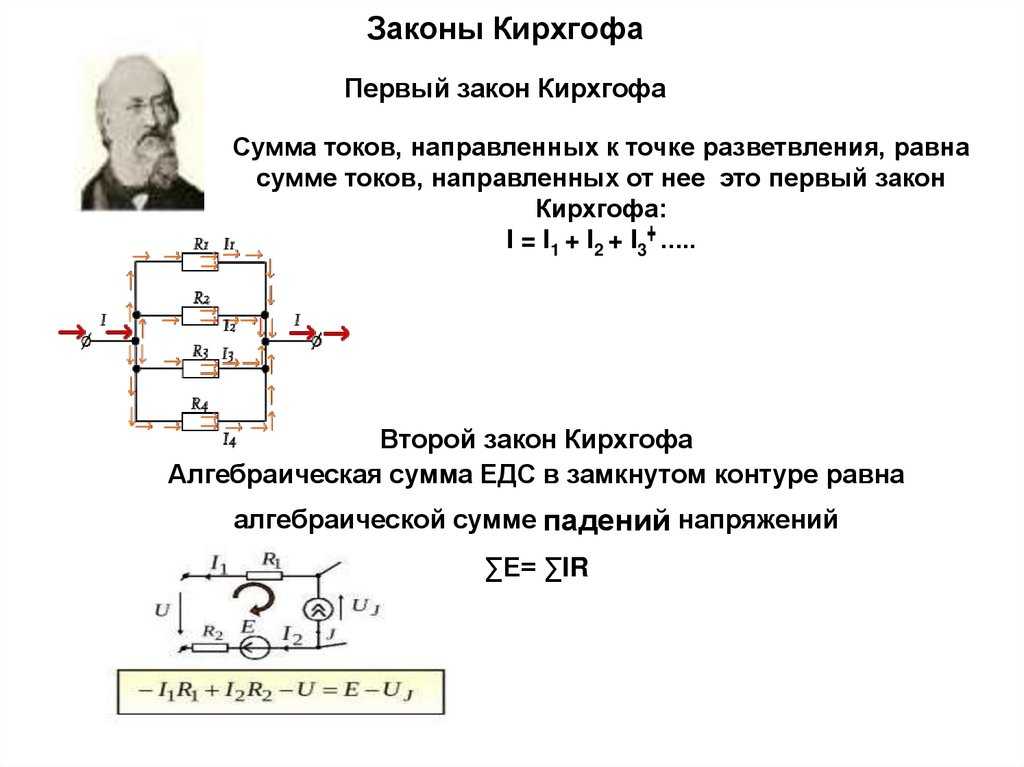 ..+J_m)=UG+J

Преобразование треугольника сопротивлений в эквивалентную звездуВстречаются схемы, в которых отсутствуют сопротивления, включенные последовательно или параллельно, например, мостовая схема, изображенная на рис. 2.4. Определить эквивалентное сопротивление этой схемы относительно ветви с источником ЭДС описанными выше методами нельзя. Если треугольник сопротивлений R1-R2-R3, включенных между узлами 1-2-3 заменить трехлучевой звездой сопротивлений, лучи которой расходятся из точки 0 в те же узлы 1-2-3, эквивалентное сопротивление полученной схемы легко определяется.

Рис. 2.4 Сопротивление луча эквивалентной звезды сопротивлений равно произведению сопротивлений прилегающих сторон треугольника, деленному на сумму сопротивлений всех сторон треугольника. В соответствии с указанным правилом, сопротивления лучей звезды определяются по формулам:

Эквивалентное соединение полученной схемы определяется по формуле

Сопротивления R0 и Rλ1 включены последовательно, а ветви с сопротивлениями Rλ1 + R4 и Rλ3 + R5 соединены параллельно.

Преобразование звезды сопротивлений в эквивалентный треугольник

Иногда для упрощения схемы полезно преобразовать звезду сопротивлений в эквивалентный треугольник. Рассмотрим схему на рис. 2.5. Заменим звезду сопротивлений R1-R2-R3 эквивалентным треугольником сопротивлений RΔ1-RΔ2-RΔ3, включенных между узлами 1-2-3.

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 30875

Исаак Ньютон продемонстрировал, что белый свет можно разделить на составляющие его цвета. Чистый белый свет содержит шесть цветов видимого спектра: красный, оранжевый, желтый, зеленый, синий и фиолетовый. А 9Спектроскоп 0026 состоит из призмы для разделения цветов, а затем проецирует их на экран или детектор для анализа. Астрономы используют спектроскопы для изучения света, исходящего от звезд и других тел. Однако происходит любопытная вещь, когда мы исследуем свет, исходящий, скажем, от облака разреженного горячего газа. Вместо того, чтобы видеть непрерывный спектр, мы видим ряд дискретных линий. Эти эмиссионных линий создаются электронами, переходящими из возбужденного состояния в более низкое состояние. Излучаемые длины волн, как объясняется в модели Бора, уникальны для каждого элемента. В результате, исследуя эмиссионные линии, мы можем определить, из каких элементов состоит облако.

Спектроскоп анализирует свет, используя призму, чтобы разделить его на различные цвета.

https://commons.wikimedia.org/wiki/F…oscopy_pic.png

Атомно-эмиссионный спектр гелия.

https://commons.wikimedia.org/wiki/F…_of_helium.svg

Если мы исследуем свет после того, как он пройдет через холодный газ, мы увидим то, что кажется почти непрерывным спектром, но с несколькими пустыми линиями, в которых исчезли определенные длины волн света. Эти линий поглощения являются результатом поглощения света электронами и перехода из более низкого состояния в более высокое энергетическое состояние. Конкретные длины волн в линиях поглощения элемента такие же, как длины волн в линиях излучения того же элемента. Таким образом, мы можем идентифицировать элементы либо по их спектрам излучения, либо по спектрам поглощения. 900:30 Мы можем видеть, как спектр объекта смещается по мере того, как объект движется к нам или от нас. https://commons.wikimedia.org/wiki/F…ectroscopy.gif Спектр поглощения некоторых элементов.

https://commons.wikimedia.org/wiki/F…w_elements.PNG

Бор разработал свою модель атома частично путем изучения спектров излучения и поглощения водорода. Водород является простейшим из атомов, поскольку он имеет только одну электронную орбиту вокруг ядра. Многоэлектронные атомы имеют более сложные спектры. Молекулы имеют еще более сложные спектры, например, спектры молекулярного водорода, состоящего из двух связанных вместе атомов водорода, более сложны, чем спектры одного атома водорода. Тем не менее, все эти различные спектры ведут себя предсказуемым образом, поэтому каждый из них действует как окончательный «отпечаток пальца», который можно использовать для идентификации присутствующего элемента или соединения.

Как отмечалось выше, спектр испускания или поглощения вещества зависит частично от его температуры, а также от его состояния и плотности. Законы Кирхгофа формально описывают, какие виды спектра излучаются, следующим образом:

1. Горячее твердое тело, жидкость или газ под высоким давлением испускает непрерывный спектр.

2. Горячий газ под низким давлением дает спектр с яркими линиями или эмиссионными линиями.

3. Спектр темной линии или линии поглощения виден, когда источник непрерывного спектра рассматривается позади холодного газа под давлением.

Законы Кирхгофа оказались полезными при определении состава и температуры всего, от атмосферы планет до звезд и межзвездных туманностей. Но они ничего не говорят нам о движении этих объектов. Для этого нам нужно будет рассмотреть еще одно свойство электромагнитных волн — эффект Доплера.

Законы Кирхгофа описывают свет, излучаемый светящимся твердым телом, горячим газом и холодным рассеянным газом.

https://commons.wikimedia.org/wiki/F…chhof_laws.svg

4.4: Законы Кирхгофа распространяются в соответствии с лицензией CC BY-NC-SA и были созданы, изменены и/или курированы LibreTexts.

Наверх

Была ли эта статья полезной?

Тип изделия
Раздел или страница
Лицензия
CC BY-NC-SA
Теги

Второй закон Кирхгофа заключается в том, что оптически тонкие источники производят эмиссионные линии, такие как туманность Ориона. (Изображение: Любинко Йованович/общественное достояние)

Закон Кирхгофа номер один гласит, что оптически толстые источники излучают непрерывный планковский спектр. Это потому, что плотность достаточно высока, чтобы фотоны достигли теплового равновесия с атомами. Второй закон Кирхгофа заключается в том, что оптически тонкие источники производят эмиссионные линии, такие как туманность Ориона.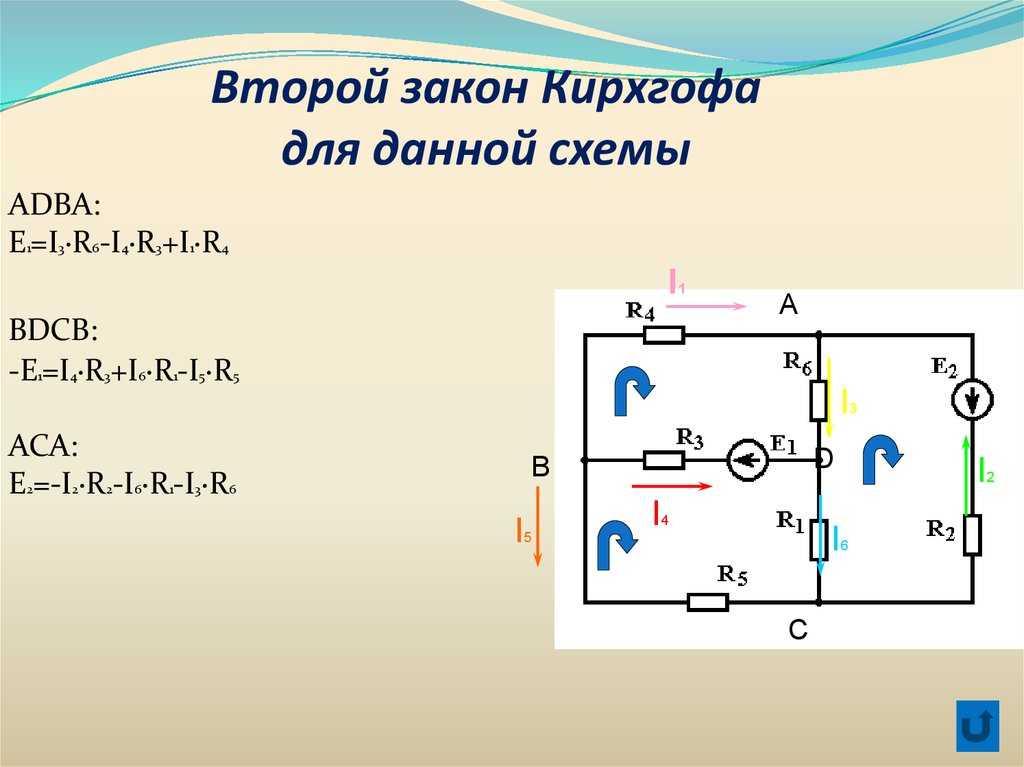 Фотоны не взаимодействуют с атомами на своем пути, поэтому у них нет возможности достичь равновесия.

И, в-третьих, если есть горячий, оптически толстый источник, окруженный более холодным, оптически тонким слоем, тогда получается спектр поглощения.

Этот третий закон Кирхгофа представляет собой наиболее интересный случай и требует дополнительных пояснений. Как известно, внутри звезды горячее и плотнее, чем снаружи. Итак, звезда является примером горячего, оптически толстого источника — звездного недра — окруженного более холодным, оптически тонким слоем — фотосферой. Важным моментом является то, что длина свободного пробега не одинакова для всех фотонов. Сильно зависит от длины волны. Фотоны с длиной волны, подходящей для поглощения окружающими атомами, имеют гораздо более короткую длину свободного пробега, чем фотоны с некоторой случайной длиной волны.

Например, у звезды с фотосферой при температуре 10 000° Кельвина длина свободного пробега при 0,656 мкм намного короче, чем при 0,6 или 0,7 мкм. Фотоны с этим специфическим красным цветом не могут распространяться так далеко, как другие фотоны. Когда мы направляем наш телескоп на звезду, мы видим до оптической глубины 2/3, но фактическая глубина в километрах, на которой оптическая толщина составляет 2/3, зависит от длины волны. При размере 0,656 мкм звезда более непрозрачна, и мы не можем заглянуть так далеко внутрь.

Эта статья взята непосредственно из серии видео Введение в астрофизику . Смотрите прямо сейчас на Wondrium .

Это означает, что фотоны этой длины волны, достигающие нашего телескопа, происходят из более мелкого и холодного слоя звезды. И излучение черного тела от этого более холодного газа менее интенсивно, чем излучение из более глубоких слоев. Таким образом, на длине волны 0,656 мкм звезда выглядит тусклее и темнее, чем на соседних длинах волн. Получаем темную полосу в спектре.

Если бы мы могли как-то разглядеть звездный диск и если бы у нас были специальные очки для наблюдения за звездой на любой длине волны, которую мы хотим, то когда мы смотрим на 0,656 микрона, звезда выглядела бы тусклее и немного больше, может быть, на 1000 километров, потому что фотосфера не такая глубокая. Это происходит на большей высоте от центра звезды.

Это ясно объясняет, почему было бы слишком упрощенно говорить, что темные линии появляются в результате поглощения. Это правда, что эти фотоны поглощаются, но они испускаются с той же скоростью. Точнее сказать, что темные линии есть, потому что звезда более непрозрачна на этих длинах волн. Мы не можем заглянуть так далеко в звездный туман. 900:30 Изображение Солнца с помощью соответствующего телескопа показывает, что оно становится тусклее вблизи края круга. (Изображение: Дилан О’Доннелл, deography.com/Public domain)

Есть еще одно интересное явление. Изображение Солнца с помощью соответствующего телескопа показывает, что оно становится тусклее у края круга; так называемая «конечность» солнечного диска. Удивительно, но это не обман зрения. Излучение от конечности действительно менее интенсивно, чем излучение из центра диска. Это явление называется потемнением конечностей.

Нашей первой реакцией может быть то, что это просто потому, что Солнце — сфера, а не плоский круг.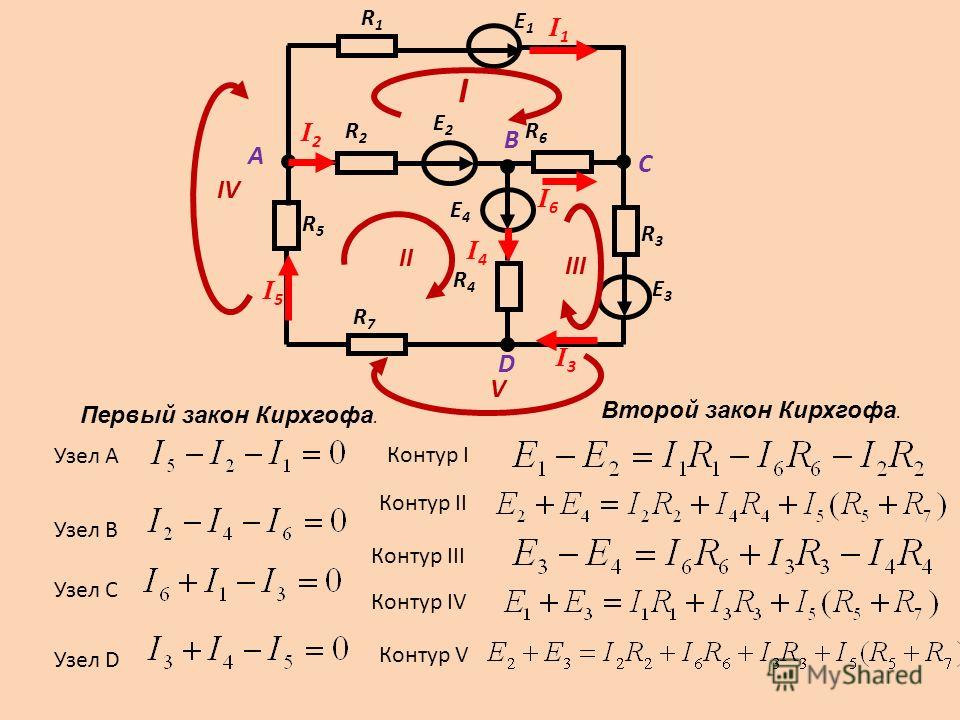 То, что мы видим, — это эффект затенения, который всегда получается, когда светят на сферу. Но мы не проливаем свет на Солнце. Солнце светит нам. Он светится изнутри, посылая энергию одинаково во все стороны.

Не сферическая форма Солнца вызывает потемнение конечностей. На самом деле можно доказать, что равномерно яркая сфера не показывает никакого потемнения к краю. Под любым углом он выглядит как равномерно яркий круглый диск. Это можно продемонстрировать с помощью «светящейся декоративной сферы». Люди используют их, чтобы украсить свои дворы и сады. Они не показывают потемнение конечностей.

Причиной потемнения конечностей является то, что Солнце, как и все звезды, представляет собой газовую сферу, более горячую и плотную внутри, чем снаружи. Когда мы смотрим на центр Солнца, наш луч зрения проходит через Солнце почти перпендикулярно фотосфере. Фотоны, приходящие к нам с этого направления, возникли на оптической глубине около 2/3, что соответствует определенной глубине в километрах внутри Солнца.

Но когда мы смотрим на конечность, наш взгляд скользит по поверхности. Если мы будем следовать этому скользящему лучу зрения, мы достигнем оптической глубины 2/3 на большей высоте, дальше от центра Солнца, и на большей высоте температура ниже, а излучение менее интенсивно. Вот почему мы получаем потемнение конечностей.

Это интересный эффект, и это полезный способ проверить модели фотосферы Солнца. Наблюдая потемнение края в разные цвета, мы можем узнать, как температура увеличивается с глубиной и как общая непрозрачность Солнца меняется в зависимости от длины волны.

April 2016

В: Что утверждает первый закон ирхгофа?

Первый закон Кирхгофа состоит в том, что оптически толстые источники излучают непрерывный планковский спектр. Это потому, что плотность достаточно высока, чтобы фотоны достигли теплового равновесия с атомами.

В: Что наблюдается на «конце» солнечного диска?

Изображение Солнца в соответствующий телескоп показывает, что оно становится тусклее у края круга; так называемая «конечность» солнечного диска.