Лекции по вычислительной технике (Информатика и программирование)
СУММАТОРЫ
Одноразрядный двоичный сумматор.
Из рассмотренного в § 3.2 принципа сложения многоразрядных двоичных чисел следует, что в каждом из разрядов производятся однотипные действий: определяется цифра суммы путем сложения по модулю 2 цифр слагаемых и поступающего в данный разряд переноса и формируется перенос, передаваемый в следующий разряд. Эти действия реализуются одноразрядным двоичным сумматором. Символическое изображение такого сумматора показано на рис. 9.61.а. Он имеет три входа для подачи цифр разрядов слагаемых , и переноса на выходах формируются сумма и перенос , предназначенный для передачи в следующий разряд.
рис 9.61
В одноразрядном сумматоре могут предусматриваться входы для подачи как прямых , , , так и инверсных значений , , входных переменных, а также выходы, на которых формируются инверсные значения выходных переменных. Пример такого одноразрядного сумматора приведен на рис. 9.61,6.
Пример такого одноразрядного сумматора приведен на рис. 9.61,6.
В табл. 9.34 показано функционирование одноразрядного сумматора. Пользуясь этой таблицей истинности, запишем логические выражения для выходных величин и в базисе И-ИЛИ-НЕ:
;
На рис. 9.62 приведена схема сумматора, построенного с использованием этих логических выражений.
Многоразрядные двоичные сумматоры
В зависимости от способа ввода кодов слагаемых сумматоры делятся на два типа: последовательного и параллельного действия. В сумматоры первого типа коды чисел вводятся в последовательной форме, т. е. разряд за разрядом (младшим разрядом вперед), в сумматоры (второго типа каждое из слагаемых подается в параллельной форме, т. е. одновременно всеми разрядами.
Сумматор последовательного действия (рис. 9.63).
Состоит из одноразрядного сумматора, выход которого соединен с входом через D-триггер. Изображенные на рисунке сдвиговые регистры не входят непосредственно в схему сумматора, они служат для подачи на входы сумматоров разрядов слагаемых (регистры и ) и приема выдаваемых сумматором разрядов суммы (регистр ).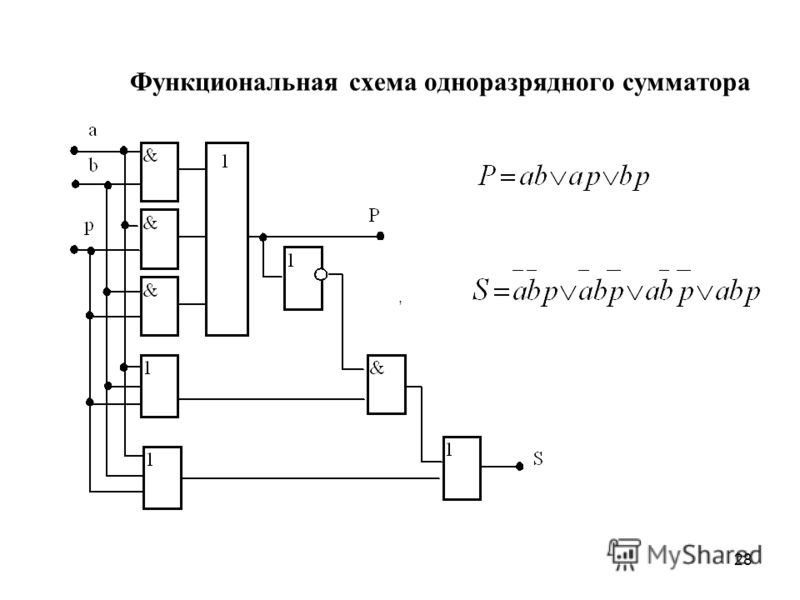 Операция суммирования во всех разрядах слагаемых осуществляется с помощью одного и того же одноразрядного сумматора. Такое построение сумматора возможно за счет того, что слагаемые поступают в последовательной форме.
Операция суммирования во всех разрядах слагаемых осуществляется с помощью одного и того же одноразрядного сумматора. Такое построение сумматора возможно за счет того, что слагаемые поступают в последовательной форме.
С первым тактовым импульсом на входы сумматора поступают из регистров и цифры первого разряда слагаемых и , из D-триггера на вход подается лог. 0. Суммируя поданные на входы цифры, одноразрядный сумматор формирует первый разряд суммы , выдаваемый на вход регистра , и перенос , принимаемый в D-триггер. Второй тактовый импульс осуществляет в регистрах сдвиг на один разряд вправо; при этом на входы одноразрядного сумматора подаются цифры второго разряда слагаемых , и перенос , получающаяся цифра второго разряда суммы вдвигается в регистр , перенос принимается в триггер и т. д.
Очевидное достоинство сумматора последовательного действия заключается в малом объеме оборудования, требуемого для его построения. Однако связанная с этим необходимость в последовательной обработке разрядов приводит к низкому быстродействию.
Сумматор параллельного действия. Состоит из отдельных разрядов, каждый из которых содержит одноразрядный сумматор (рис. 9.64).
При подаче слагаемых цифры их разрядов поступают на соответствующие одноразрядные сумматоры. Каждый из одноразрядных сумматоров формирует на своих выходах цифру соответствующего разряда суммы и перенос, передаваемый на вход одноразрядного сумматора следующего (более старшего) разряда.
Повышение быстродействия параллельных сумматоров.
Для обеспечения высокого быстродействия параллельные сумматоры должны строиться на элементах, обладающих высоким быстродействием.
Трудности в достижении высокого быстродействия сумматора, построенного по схеме на рис. 9.64, связаны с тем, что процесс распространения переносов в нем имеет последовательный характер. Импульс переноса в каждом разряде формируется после того, как будет сформирован и передан импульс переноса из предыдущего разряда. В наиболее неблагоприятном случае возникший в младшем разряде перенос может последовательно вызывать переносы во всех остальных разрядах.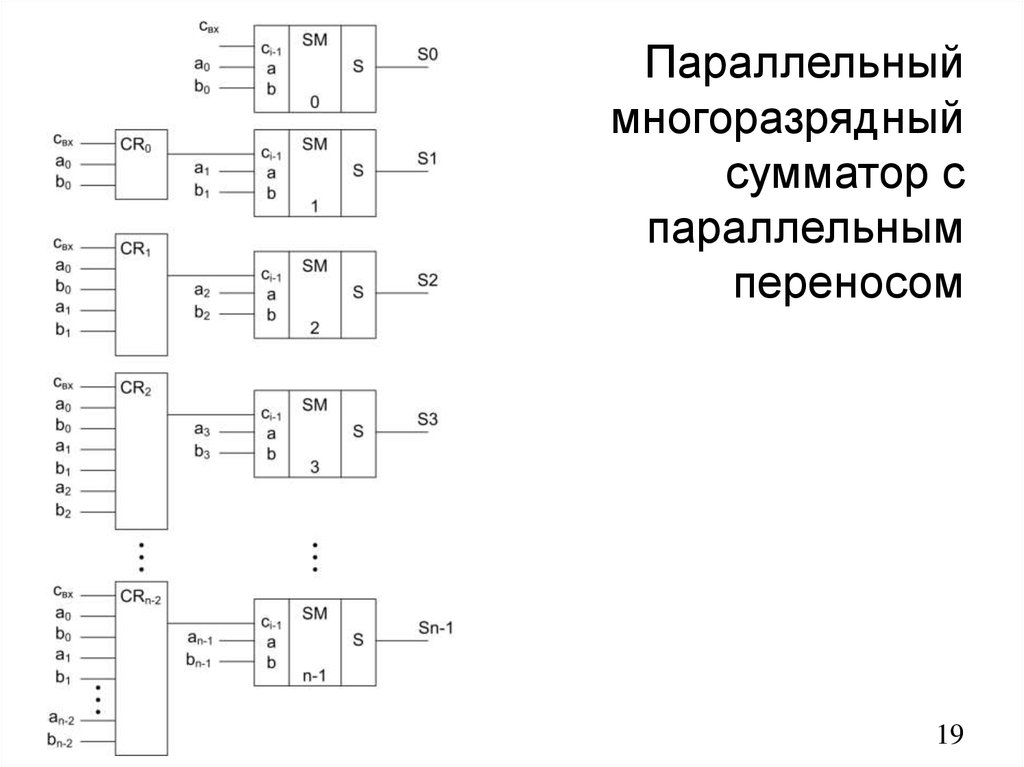 При этом время передачи переносов,где — задержка распространения переноса в одном разряде.
При этом время передачи переносов,где — задержка распространения переноса в одном разряде.
рис 9.64
Уменьшение достигается следующими приемами.
1. При построении схем одноразрядных сумматоров стремятся к уменьшению числа элементов в цепи между входом, на который поступает импульс переноса , и выходом, на котором формируется передаваемый в следующий разряд импульс переноса . Этот принцип реализован в схеме сумматора на рис. 9.62, в которой цепь от к содержит один логический элемент И-ИЛИ-НЕ.
2. В цепях от к применяют элементы с повышенным быстродействием.
3. Схемы сумматоров следует строить таким образом, чтобы сигналы с выхода каждого логического элемента в цепи от pi к pi+i поступали на возможно меньшее число других логических элементов, так как присоединение каждого дополнительного элемента к той или иной точке цепи переносов, как правило, приводит к увеличению паразитной емкости, удлинению фронтов сигналов и, следовательно, к увеличению задержки распространения сигнала и снижению быстродействия сумматора.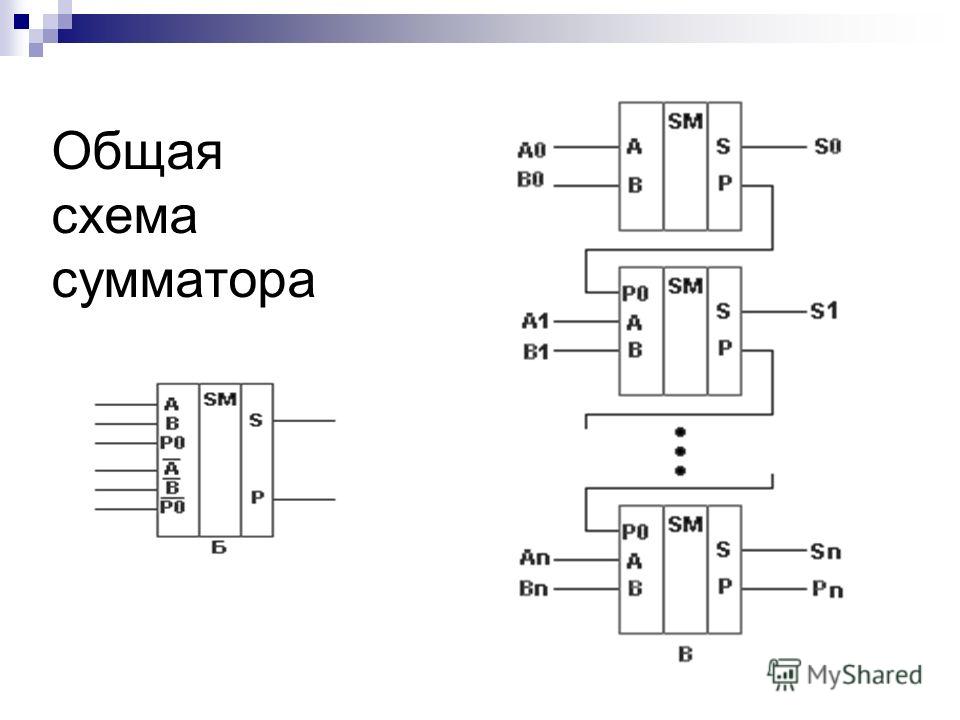
4. Применяют устройства формирования переносов в параллельной форме. В показанном на рис. 9.65 сумматоре с помощью устройства, называемого блоком ускоренного переноса, производится формирование переносов в параллельной форме, т. е. одновременно для всех разрядов. Переносы из этого блока поступают во все разрядные сумматоры одновременно. При этом разрядные сумматоры не содержат цепей формирования переносов, они формируют только сумму s, и величины и , для .получения которых переносы не требуются. Эти величины и необходимы для формирования переносов в блоке ускоренного переноса, они определяют следующие ситуации: означает, что в i-м разряде перенос в следующий (i+1)-й разряд необходимо формировать независимо от поступления в данный разряд переноса из предыдущего разряда; означает, что в i-м разряде перенос должен формироваться только при условии поступления переноса из предыдущего разряда.
рис 9.65
Рассмотрим принцип построения блока ускоренного переноса.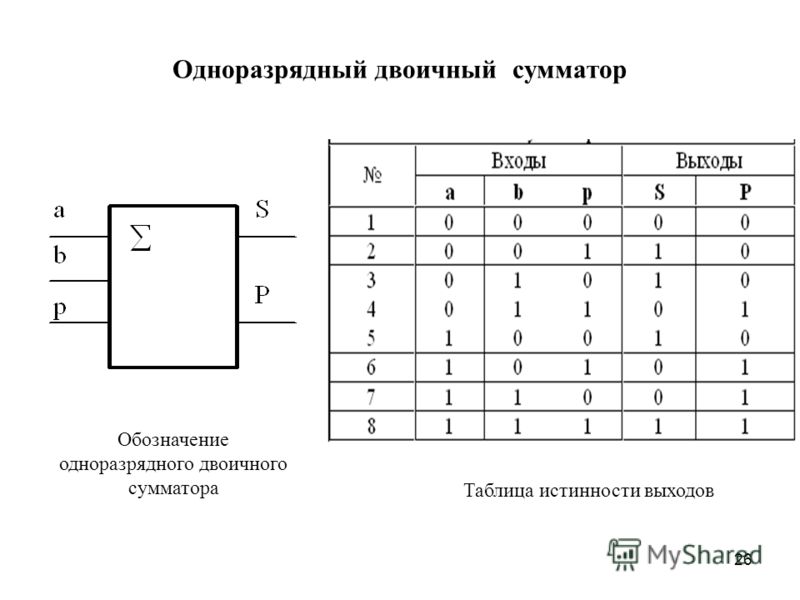 Перенос во второй разряд должен формироваться при условии или при условии и наличии переноса на входе , т.е. . После преобразований получим
Перенос во второй разряд должен формироваться при условии или при условии и наличии переноса на входе , т.е. . После преобразований получим
Аналогичные выражения можно построить для переносов в другие разряды:
;
На рис. 9.66,а и б показаны схема блока ускоренного переноса и его условное обозначение.
Входящие в выражения величины , формируются одновременно во всех разрядных сумматорах, одновременно поступают на входы блока ускоренного переноса и, следовательно, в этом блоке одновременно формируются переносы, подаваемые в разрядные сумматоры. После поступления переносов из блока ускоренного переноса в разрядных сумматорах формируются суммы .
Формирование инверсных значений и и суммы в разом сумматоре может быть выполнено с использованием следующих логических выражений:
; ;
рис 9.66
рис 9.66
Схема разрядного сумматора, построенного в соответствии с этими выражениями, показана на рис. 9.66,в.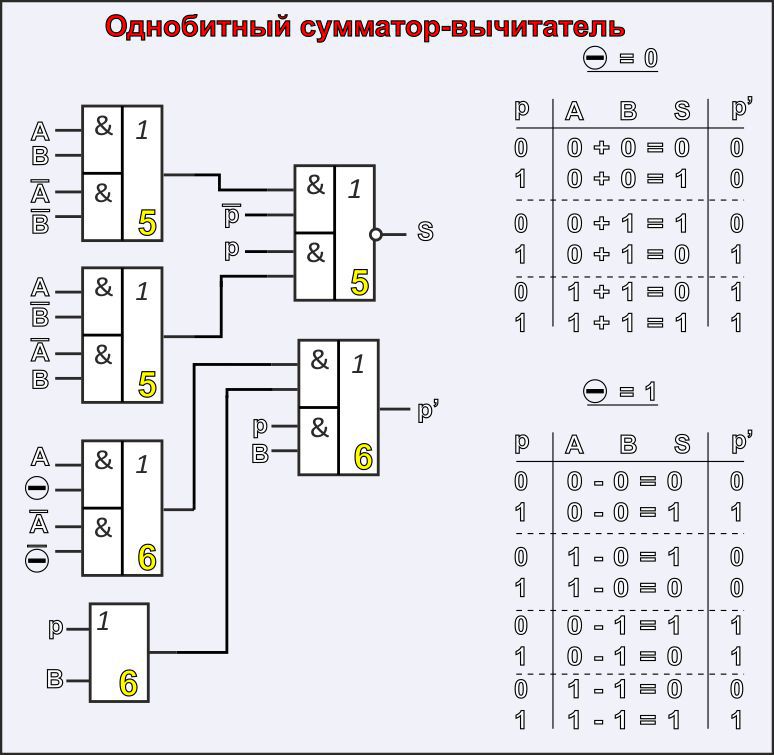
Десятичные сумматоры
Для построения многоразрядных двоичных сумматоров, как было показано выше, необходимы одноразрядные двоичные сумматоры строятся с использованием одноразрядных десятичных сумматоров. Последние выполняют операцию суммирования .десятичных цифр , и переноса , поступающих в разряд, и формируют на выходах десятичную цифру суммы и перенос для передачи в следующий десятичный разряд.
При использовании десятичной системы счисления цифры разрядов десятичного числа представляются в некоторой двоичной форме (см. § 3.2). В связи с этим одна из особенностей одноразрядных десятичных сумматоров связана с тем, что суммируемые Десятичные цифры и представляются многоразрядными двоичными числами (переносы независимо от используемой системы счисления могут иметь лишь значения 0 либо 1). Рассмотрим построение одноразрядного сумматора десятичных цифр, представляемых в коде 8421.
Сумматор для кода 8421.
В работе сумматора этого типа имеются особенности в формировании переноса и суммы, отличающие его от работы двоичного сумматора.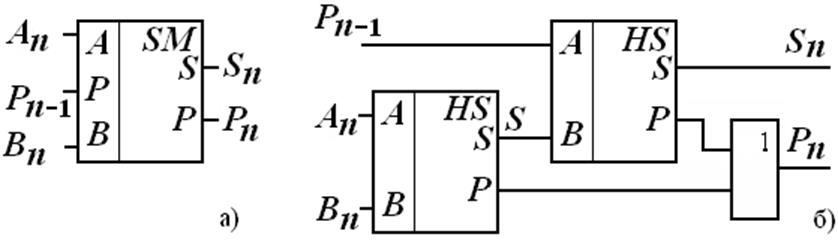
Правила сложения в десятичной системе счисления с использованием кода 8421 рассмотрены в § 3.3. Построенная в соответствии с этими правилами схема одноразрядного десятичного сумматора (рис. 9.67) включает в себя четырехразрядный двоичный сумматор(1), схему формирования переноса в следующий десятичный разряд (2) и схему коррекции суммы (3). Последняя представляет собой трехразрядный сумматор, в котором при производится прибавление единицы в разрядах нескорректированной суммы с весовыми коэффициентами 2 и 4.
Операция суммирования в случае, когда слагаемые (одно либо оба) имеют отрицательные значения, может производиться с представлением таких слагаемых в обратном коде.
Схема формирования обратного кода.
В десятичной системе счисления обратный код образуется путем преобразования каждой цифры числа в дополнение до 9. В табл. 9.35 приведены для десятичных цифр 0, 1,…, 9 прямые коды и соответствующие им обратные.
рис 9.67
Из сопоставления приведенных в таблице значений и соответствующих им нетрудно заключить, что .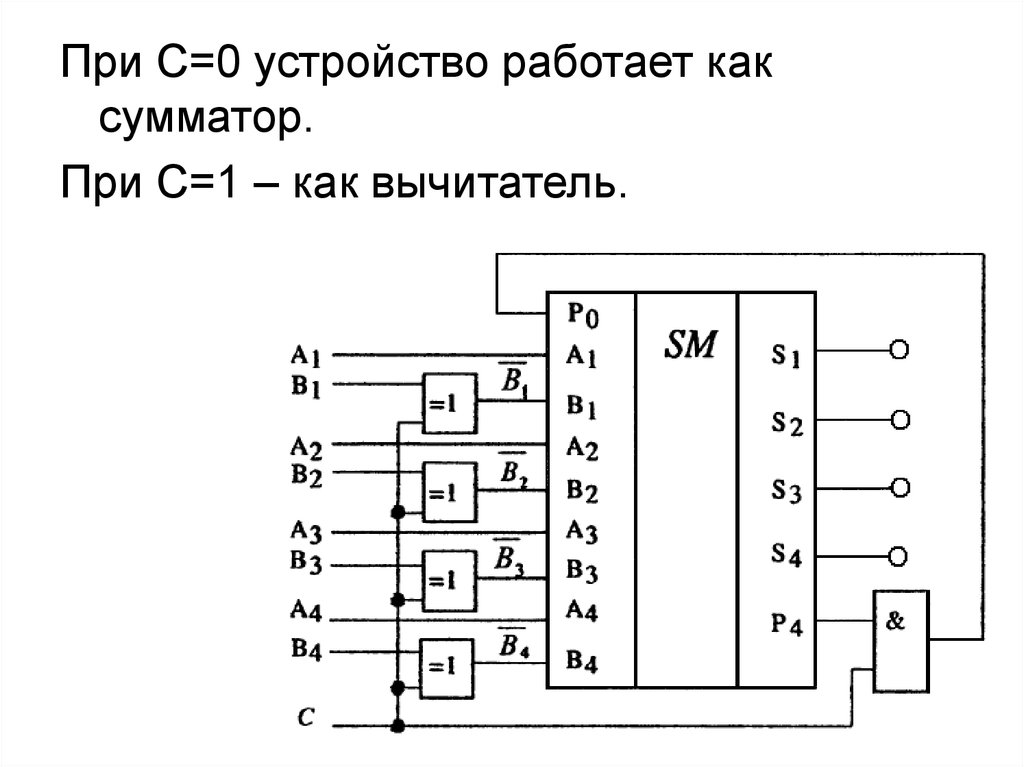
Логические выражения для и можно получить из карт Вейча (табл. 9.36):
; .
На рис. 3,68 приведена схема, формирующая обратный код по полученным выше логическим выражениям,
рис 9.68
рис 9.69
3.3 Сумматоры
Сумматор – это узел ЭВМ, предназначенный для сложения кодов двоичных чисел. Сумматоры делятся на последовательные (накапливающие) и параллельные (комбинационные). Накапливающие сумматоры имеют низкое быстродействие, поэтому они рассматриваться не будут. В комбинационных сумматорах слагаемые поступают на входы одновременно, а на выходе получается код суммы. После снятия слагаемых результат пропадает. Эти устройства не обладают памятью и строятся на логических элементах.
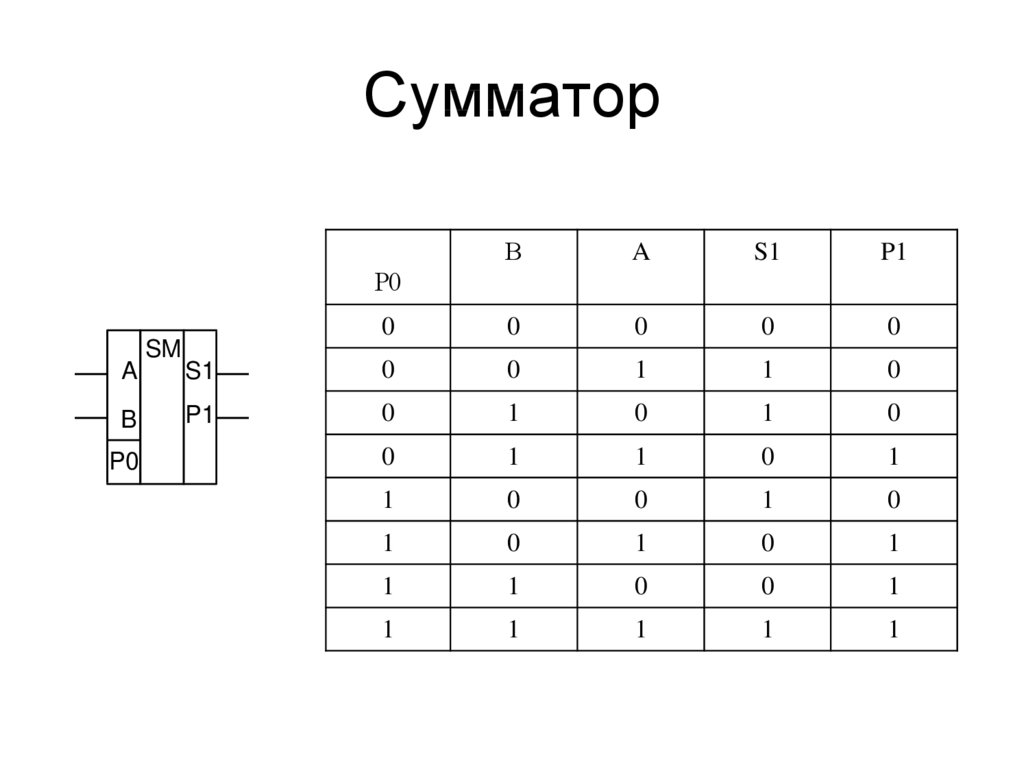
Составим таблицу истинности устройства для сложения двух одноразрядных чисел a и b (рис. 3.19)
№
a
b
p
s
0
0
0
0
0
1
0
1
0
1
2
1
0
0
1
3
1
1
1
0
Рисунок
3.
Здесь р – перенос в старший разряд, s – значение суммы. Устройство, реализующее эту таблицу истинности, называют двоичным полусумматором. Его можно синтезировать по ФАЛ для каждого из выходов
Составим схему на произвольных элементах (рис. 3.20)
Рисунок 3.20 – Схемная реализация и условное обозначение
полусумматора
№
ai
bi
Pi-1
Pi
0
0
0
0
0
0
1
0
0
1
0
1
2
0
1
0
0
1
3
0
1
1
1
0
4
1
0
0
0
1
5
1
0
1
1
0
6
1
1
0
1
0
7
1
1
1
1
1
Рисунок
3.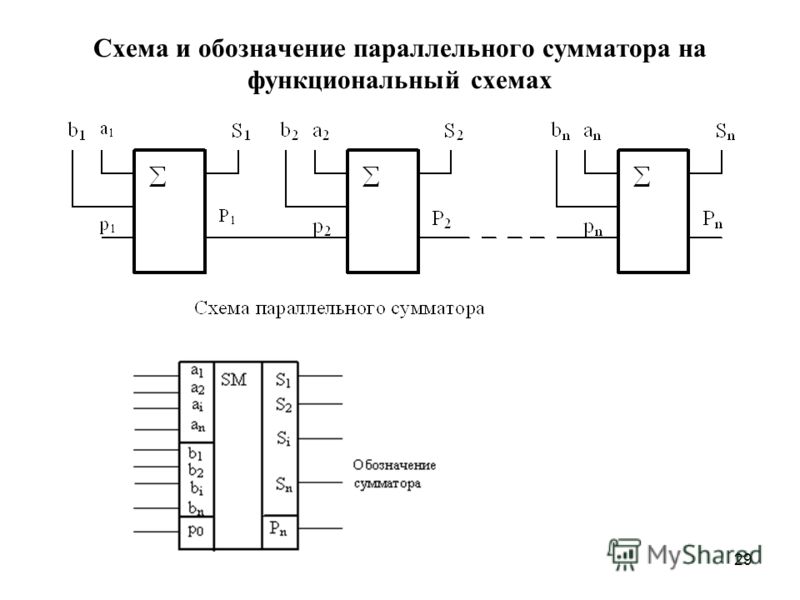 21 – Таблица истинности для сложения
трёх цифр
21 – Таблица истинности для сложения
трёх цифр
Система собственных функций:
для суммы:
для переноса (рис. 3.22):
Рисунок 3.22 – Карта Карно для цепи переноса
Минимальная форма по этой карте .
Уравнение для Si не минимизируется. Устройство, реализующее эти ФАЛ называется сумматор (полный сумматор ). Он имеет три входа и два выхода. Цена сумматора по уравнениям составляет Ц = 25. Путем совместной минимизации уравнений Si и Pi , удается снизить цену до 20 и, в таком виде, выпускаются микросхемы сумматоров. Например, К155ИМ1 – полный одноразрядный сумматор (рис. 3.23).
Рисунок 3.23 – Полный сумматор
Для сложения многоразрядных чисел сумматор составляют из одноразрядных. Пусть требуется сложить два четырёхразрядных двоичных числа: А и В
Составим схему
сумматора (рис.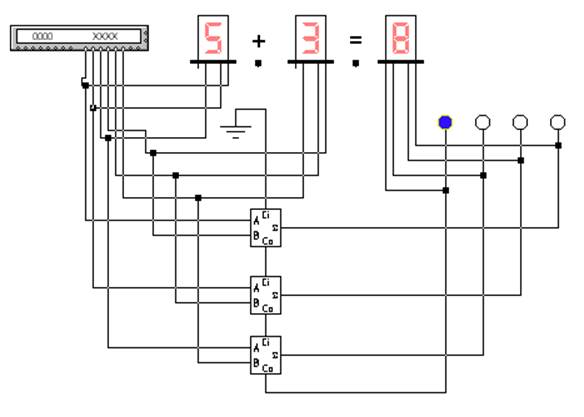 3.24)
3.24)
Рисунок 3.24 – Многоразрядный сумматор
Получился многоразрядный сумматор с последовательным переносом. Такие сумматоры выпускают в виде отдельных микросхем. Например, ИМС К155 ИМ3 — четырёхразрядный сумматор с последовательным переносом. Время сложения чисел определяется временем распространения переноса и равно 55 нсек (для четырёх разрядов).
уменьшается, так как цепь переноса последовательная.
Вспомним формулу переноса
Найдём эти переносы
Видно,
что имея только слагаемые можно
формировать перенос в любом разряде не
дожидаясь его появления в предыдущем
разряде, причём с помощью только
двухуровневой схемы (один слой
конъюнкторов и один дизъюнктор ).
При большом числе разрядов сложность схемы ускоренного переноса сильно возрастает. Поэтому сумматор разбивают на группы по 4 или 8 разрядов. Внутри группы выполняют параллельный перенос, а между группами — параллельный или последовательный. Такие сумматоры называют сумматоры с групповым переносом.
Многоразрядный сумматор условно обозначают так (рис. 3.25)
Рисунок 3.25 – Условное обозначение многоразрядного сумматора
С
помощью сумматоров можно не только
складывать, но и вычитать двоичные
числа. При использовании дополнительных
кодов операцию вычитания двух положительных
чисел заменяют операцией суммирования
положительного и отрицательного чисел,
при этом получение дополнительного
кода числа является элементарной
операцией.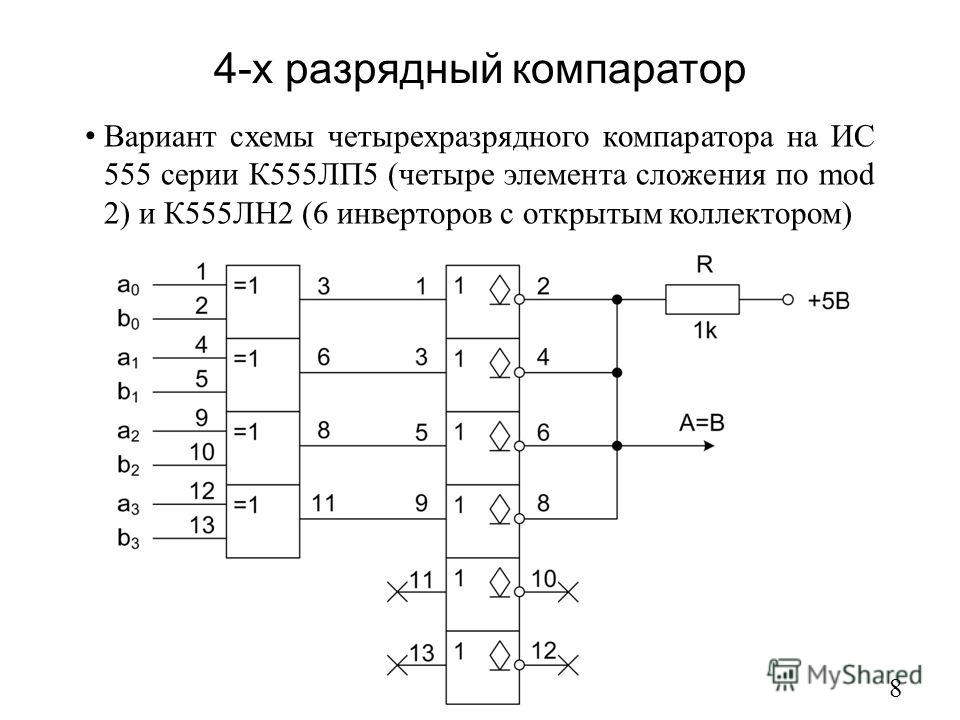 Для этого необходимо
проинвертировать число и прибавить к
нему в младший разряд 1.
Для этого необходимо
проинвертировать число и прибавить к
нему в младший разряд 1.
Схема вычитателя числа A из числа B приведена на рисунке 3.26, а схема вычитателя числа B из числа A приведена на рисунке 3.27.
Рисунок 3.26. Схема вычитателя числа A из числа B
Рисунок 3.27. Схема вычитателя числа B из числа A.
Схема инкремент/декремент.
Возьмём три полусумматора и соединим их следующим образом (рис.3.28)
Рисунок 3.28 – Схема инкремент / декремент
Подавая на управляющий вход Z ноль или единицу, проанализируем состояние выхода при различных входных сигналах (рис. 3.29)
Z
Входной код
ааа
Выходной код
S S S
0
1
1
0
1
1
0
0
0
0
1
0
0
1
1
1
1
0
1
1
1
1
0
0
1
0
1
0
Рисунок
3. 29 – Соответствие сигналов схемы
инкремент / декремент
29 – Соответствие сигналов схемы
инкремент / декремент
Если на вход Z поступает 0, то число на выходе будет без изменений. Если на вход Z подать 1, то эта единица добавляется к младшему разряду числа (инкремент +1).
Если числа на входе и выходе проинвертировать, то мы получаем схему декремент (декремент -1).
A2 A1 A0 S2 S1 S0
Число на входе 1 1 0 1 0 1 получился ответ
Выполняем инверсию
0 0 1 инкремент 0 1 0
Эта схема самостоятельного значения не имеет, но широко используется как составная часть арифметико – логических устройств.
NumberNut.
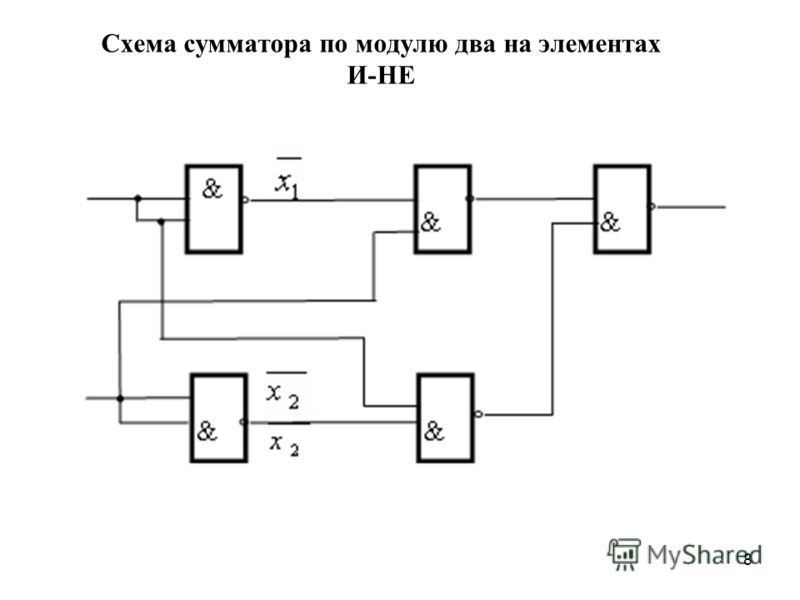 com: Арифметика: Сложение: Трехзначные числа
com: Арифметика: Сложение: Трехзначные числа Числа и подсчет| Арифметика |Дроби и десятичные дроби|Предварительная алгебра|Карта сайта
Цифры становятся больше. Теперь, когда у вас под контролем однозначное и двузначное сложение, вам нужно двигаться вверх и начать работать со значениями в столбце сотен (трехзначные числа). Запомните процесс и работайте справа налево. Вместо того, чтобы останавливаться на столбце десятков, у вас будет еще один столбец для работы. Давайте рассмотрим несколько примеров без ношения.
456 + 123 = 579
281 + 715 = 996
809 + 150 = 959
И в вертикальном формате…
| 462 + 516 978 |
Эти примеры дали вам меньше тысячи (1000) ответов.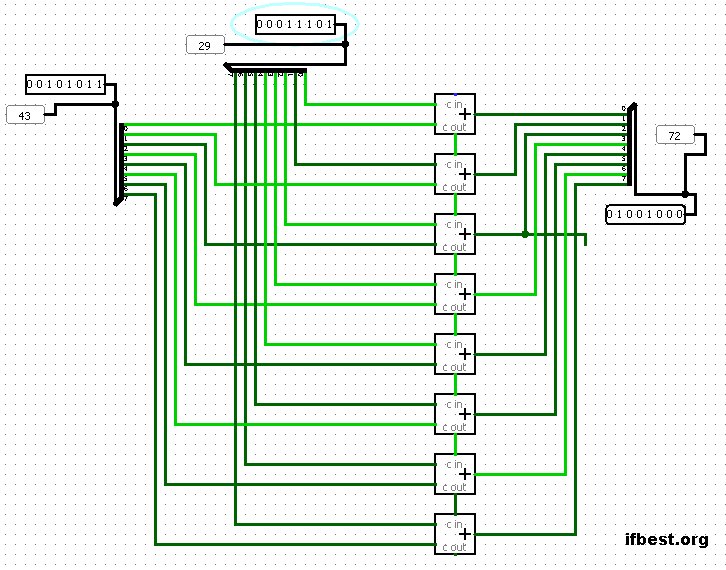 Должно быть очевидно, что многие из сложенных вами трехзначных чисел дадут вам сумму , которая больше 1000. Как ты доехал? Верните эти навыки ношения/перегруппировки.
Должно быть очевидно, что многие из сложенных вами трехзначных чисел дадут вам сумму , которая больше 1000. Как ты доехал? Верните эти навыки ношения/перегруппировки.
Когда общее количество столбцов превышает «9» вам нужно будет перенести «1» в следующий столбец слева. Сумма из столбца единиц , которая больше «9», перенесет «1» в столбец десятков . Если вы получите если в столбце десятков больше 9, то в столбце сотен появится 1. От сотен вы перейдете к тысячам . Это тот же процесс, что и с двузначными числами. Если вам кажется, что это слишком сложно, просто помните, что вы складываете только однозначные числа. Мы не просим вас складывать все числа за один раз. Разбейте задачу на несколько простых шагов. В математике есть правила, позволяющие делать вещи. очень просто.
Пример:
573 + 769 = ?
Шаги для решения:
• Колонка единиц: 3 + 9 = 12
• Напишите «2» и перенесите «1».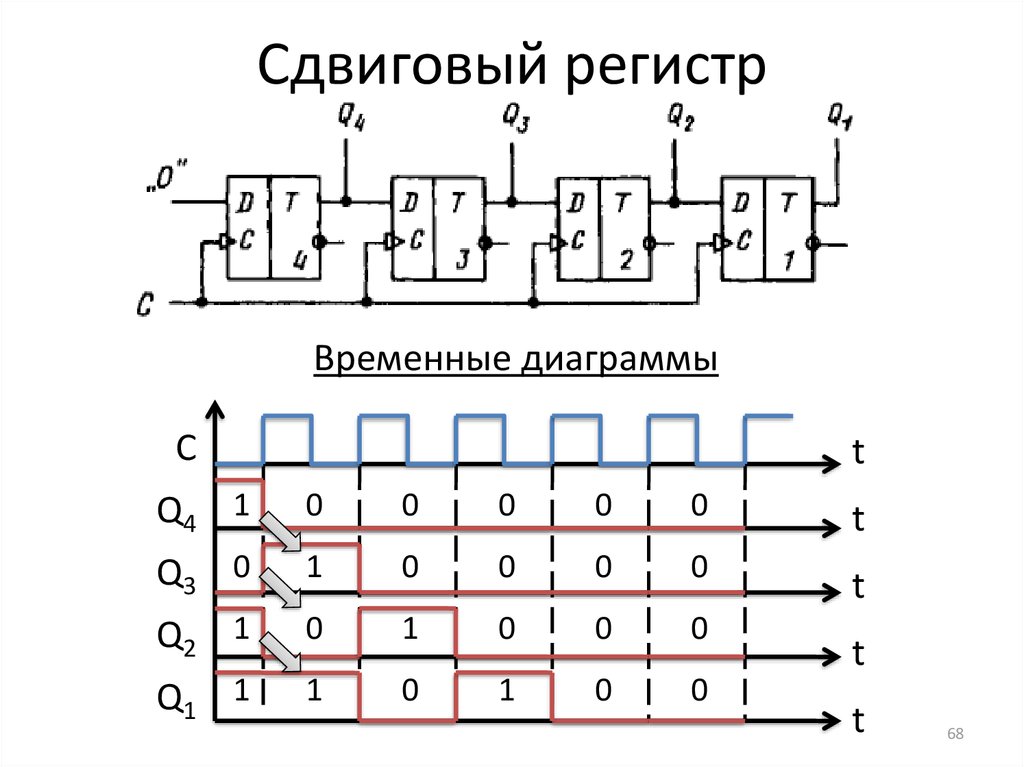
• Столбец десятков: 1 (переносится) + 7 + 6 = 14
• Напишите «4» и перенесите «1».
• Столбец сотен: 1 (перенесено) + 5 + 7 = 13
• Напишите «13», и ваш окончательный ответ будет «1342».
Ответ:
573 + 769 = 1342
Разбейте на этапы…
| 573 + 769 ? | 1 573 + 769 2 | 1 1 573 + 769 4 2 | 573 + 769 13 42 |
Теперь, когда вы знаете основы перехода от одного столбца к другому, вы сможете складывать вместе любые два значения. Вы всегда будете использовать один и тот же процесс: начните с крайнего правого столбца (столбца единиц) и двигайтесь влево.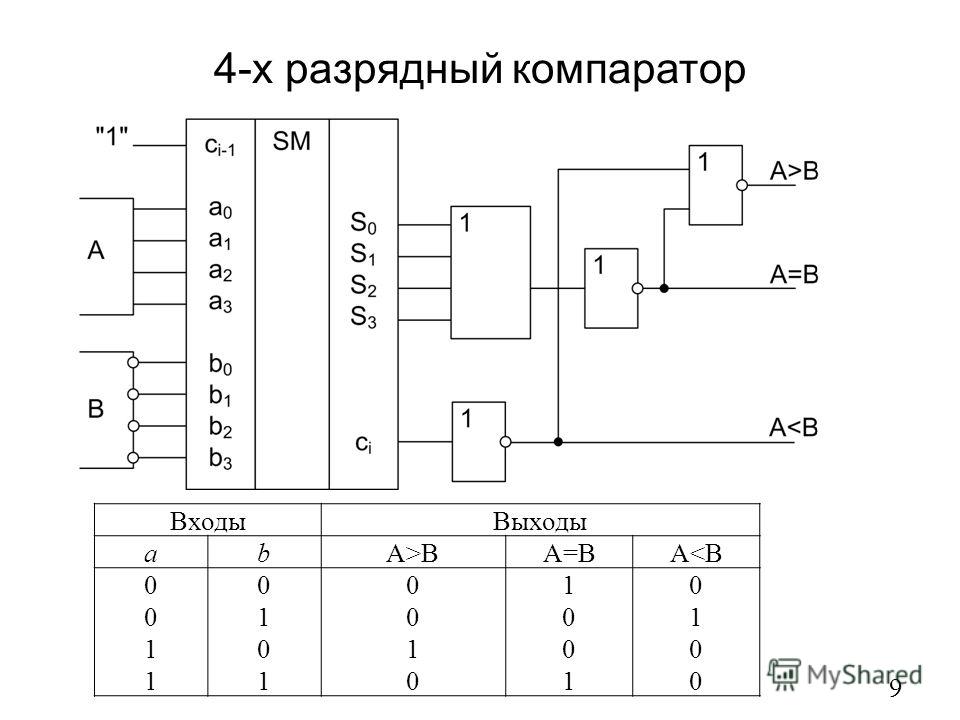 Когда вы достигнете чисел, называемых десятичными, правила останутся прежними. Но с десятичными знаками вам нужно выровнять десятичные точки, прежде чем начать.
Когда вы достигнете чисел, называемых десятичными, правила останутся прежними. Но с десятичными знаками вам нужно выровнять десятичные точки, прежде чем начать.
С имеющимися у вас навыками вы легко справитесь с этими задачами.
1234 + 4231 = 5465
20 567 + 35 411 = 55 978
И в вертикальном формате:
| 65 872 + 2 781 68 653 |
Разбейте его на этапы…
| 65 872 + 2 781 3 | 1 65 872 + 2 781 5 3 | 1 1 65 872 + 2 781 6 53 | 1 1 65 872 + 2 781 68 653 |
Помните, что это только один столбец за раз.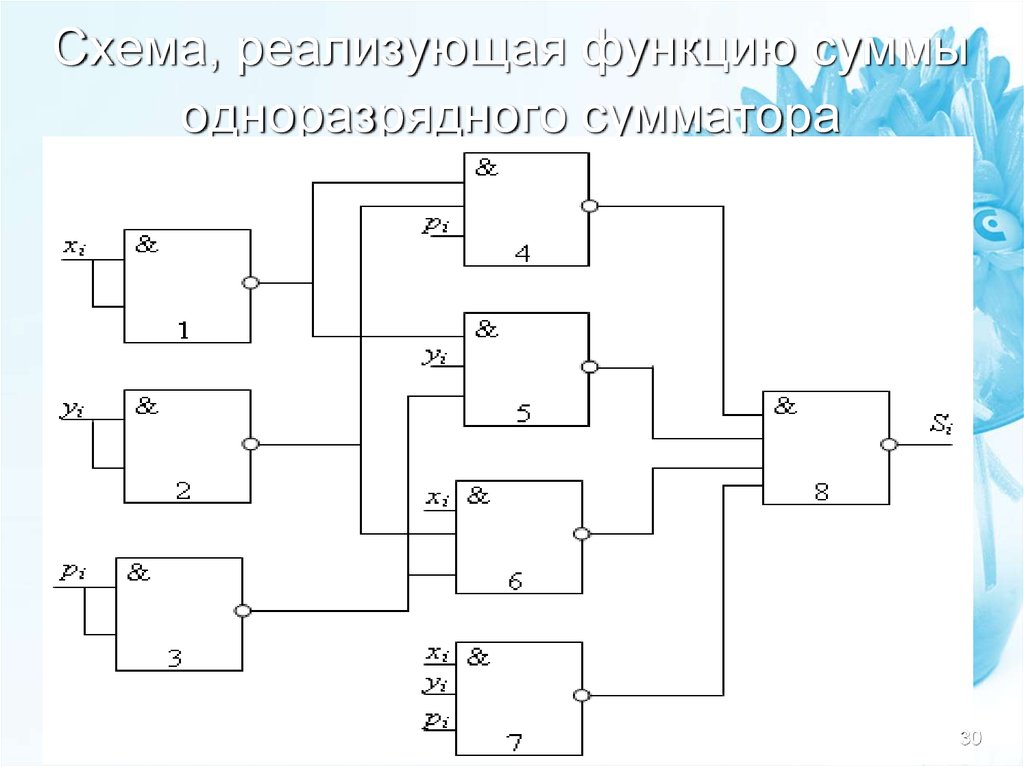 После некоторой практики это будет намного легче.
После некоторой практики это будет намного легче.
► СЛЕДУЮЩАЯ СТРАНИЦА ПО АРИФМЕТИКЕ
► ВЕРНУТЬСЯ НА НАЧАЛО СТРАНИЦЫ
► Или выполните поиск на сайтах…
- Обзор
- Операции
- Дополнение
- от 1 до 10
- Переноска
- 2-значные номера
- Трехзначные номера
- Несколько дополнений
- Целые числа
- Рабочие тетради
- Вычитание
- Умножение
- Подразделение
- Мероприятия
Википедия:
https://en.wikipedia.org/wiki/arithmetic
Encyclopædia Britannica:
22229303. com:
http://www.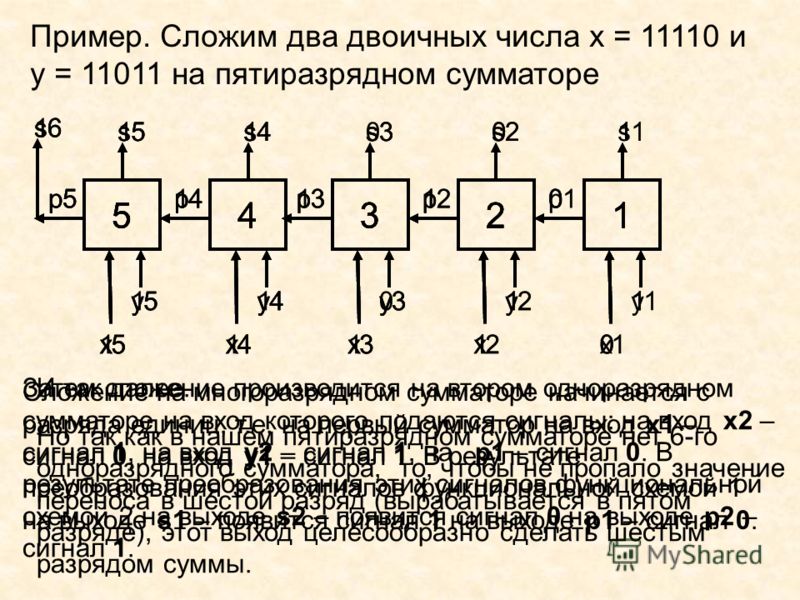 encyclopedia.com/topic/arithmetic.aspx
encyclopedia.com/topic/arithmetic.aspx
Просмотреть образовательные ресурсы по сложению и перегруппировке трехзначных чисел
0007
50 filtered results
50 filtered results
Three-Digit Addition and Regrouping
Sort byPopularityMost RecentTitleRelevance
-
Filter Results
- clear all filters
By Grade
- Дошкольное учреждение
- Детский сад
- 1-й класс
- 2-й класс
- 3-й класс
- 4-й класс
- 5-й класс
- 6th grade
- 7th grade
- 8th grade
By Subject
- Coding
- Fine arts
- Foreign language
Math
- Number Sense
Дополнение
- Стратегии добавления
- Факты
.
 0007
0007- Two-Digit Addition
- Two-Digit by One-Digit Addition
- Two-Digit Addition and Regrouping
- Three-Digit Addition
Three-Digit Addition and Regrouping
- Addition and Отсутствующие дополнения
- Вычитание
- Умножение
- Дивизион
- .0182
- Decimals
- Percents, Ratios, and Rates
- Algebra
- Geometry
- Measurement
- Time
- Money Math
- Данные и графики
- Math Word Words
- Math Buzzles
- Снятие и написание
-
-
-
-
-
-
-
-
- .
 0181 Social emotional
0181 Social emotional - Social studies
- Typing
By Topic
- Coloring
By Standard
- Common Core
Сложение 4
Урок с подсказкой
Сложение 4
На этом уроке детям предлагаются различные стратегии нахождения суммы двух чисел. Стратегии сложения, подобные этим, помогают третьеклассникам глубже понять и бегло выполнять эту операцию. Урок включает в себя инструкции и множество практических задач для применения того, что изучается. Чтобы еще больше попрактиковаться, попробуйте наши листы сложения для третьего класса, рекомендованные к этому уроку.
3-й класс
Математика
Пошаговый урок
Поиск трехзначного сложения и перегруппировка образовательных ресурсов
Существуют различные подходы к решению трехзначного сложения. Ресурсы Education.com представляют собой набор уроков и заданий, которые охватывают их все. Учителя могут выбирать из печатных рабочих листов со стандартными вертикальными уравнениями, планов уроков с упором на метод плацентарной стоимости и многое другое. Откройте для себя различные трехзначные системы сложения и перегруппировки, доступные в Учебной библиотеке.
Ресурсы Education.com представляют собой набор уроков и заданий, которые охватывают их все. Учителя могут выбирать из печатных рабочих листов со стандартными вертикальными уравнениями, планов уроков с упором на метод плацентарной стоимости и многое другое. Откройте для себя различные трехзначные системы сложения и перегруппировки, доступные в Учебной библиотеке.
Ресурсы для сложения и перегруппировки трехзначных чисел
Некоторые учащиеся могут столкнуться с препятствиями при сложении трехзначных чисел, но инструменты в Учебной библиотеке помогают детям преодолевать любые затруднения, с которыми они могут столкнуться. Трехзначные ресурсы для добавления и перегруппировки включают в себя все, от эффективных онлайн-упражнений до подробных планов уроков.
Один из планов, «Обзор стратегии сложения трехзначных чисел», предлагает учащимся три разных подхода к сложению высоких цифр. «Свободное сложение в пределах 1000» учит учащихся складывать, используя стратегию разряда, которая использует положение цифры в числе.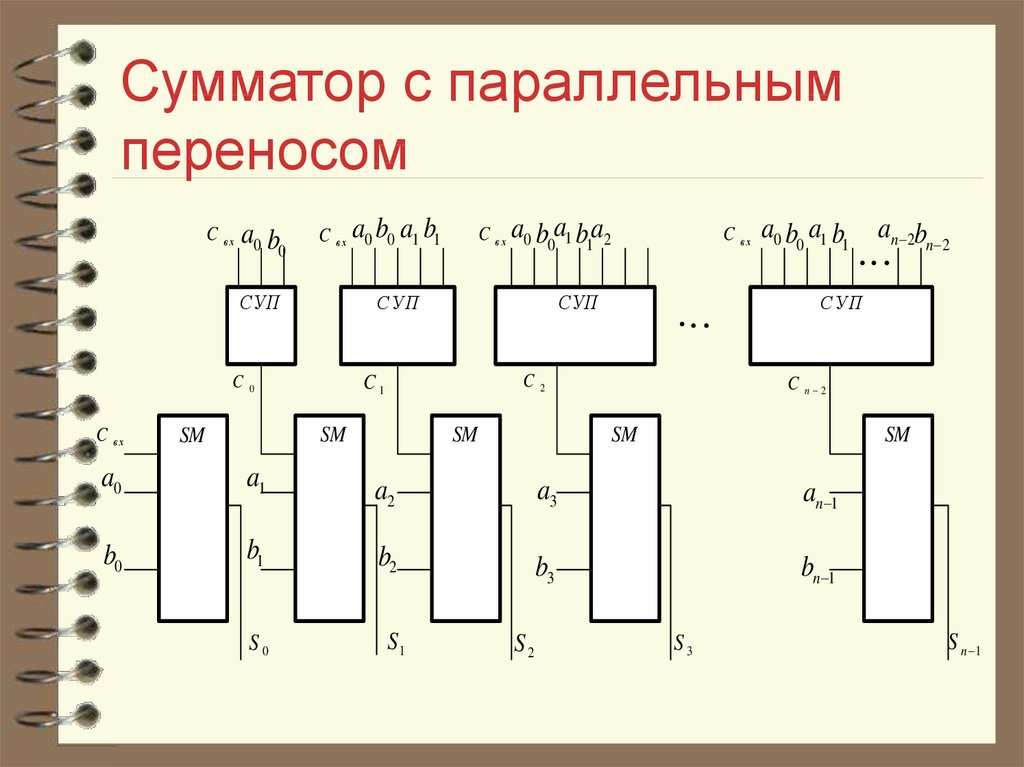


 0007
0007 0181 Social emotional
0181 Social emotional