ОглавлениеВВЕДЕНИЕ§ 1.2. Физика и техника. § 1.3. Понятие о величине и измерении. Физические величины. § 1.4. Прямое и косвенное измерения. § 1.5. Звездное небо и его видимое вращение. § 1.6. Угловые измерения на небе. § 1.7. Определение расстояний до небесных тел на основе измерения параллаксов. § 1.8. Основные единицы времени и их связь с движением Земли. § 1.9. Правило вывода единиц физических величин из формул. Международная система единиц СИ. § 1.10. Плотность вещества. Раздел I. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕПЛОТА Глава 2. ОСНОВЫ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ СТРОЕНИЯ ВЕЩЕСТВА § 2.2. Диффузия. § 2.3. Силы молекулярного взаимодействия. § 2.5. Агрегатное состояние вещества. § 2.6. Понятие о температуре и внутренней энергии тела. Глава 3. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗООБРАЗНОГО СОСТОЯНИЯ ВЕЩЕСТВА § 3.  2. Броуновское движение.§ 3.3. Измерение скорости движения молекул газа. Опыт Штерна. § 3.4. Распределение молекул по скоростям их хаотического движения. § 3.5. Размеры и массы молекул и атомов. § 3.6. Постоянная Авогадро и постоянная Лошмидта. § 3.7. Число столкновений и длина свободного пробега молекул в газе. § 3.9. Понятие вакуума. § 3.10. Межзвездный газ. Глава 4. ИДЕАЛЬНЫЙ ГАЗ. АБСОЛЮТНАЯ ТЕМПЕРАТУРА И ЕЕ СВЯЗЬ С ЭНЕРГИЕЙ МОЛЕКУЛ ГАЗА § 4.2. Основное уравнение молекулярно-кинетической теории газов. § 4.3. Зависимость давления газа от температуры при постоянном объеме. § 4.4. Абсолютный нуль. § 4.5. Термодинамическая шкала температур. Абсолютная температура. § 4.6. Связь между температурой и кинетической энергией молекул газа. Постоянная Больцмана. Глава 5. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА § 5.2. Объединенный газовый закон. Приведение объема газа к нормальным условиям. § 5.3. Молярная газовая постоянная. 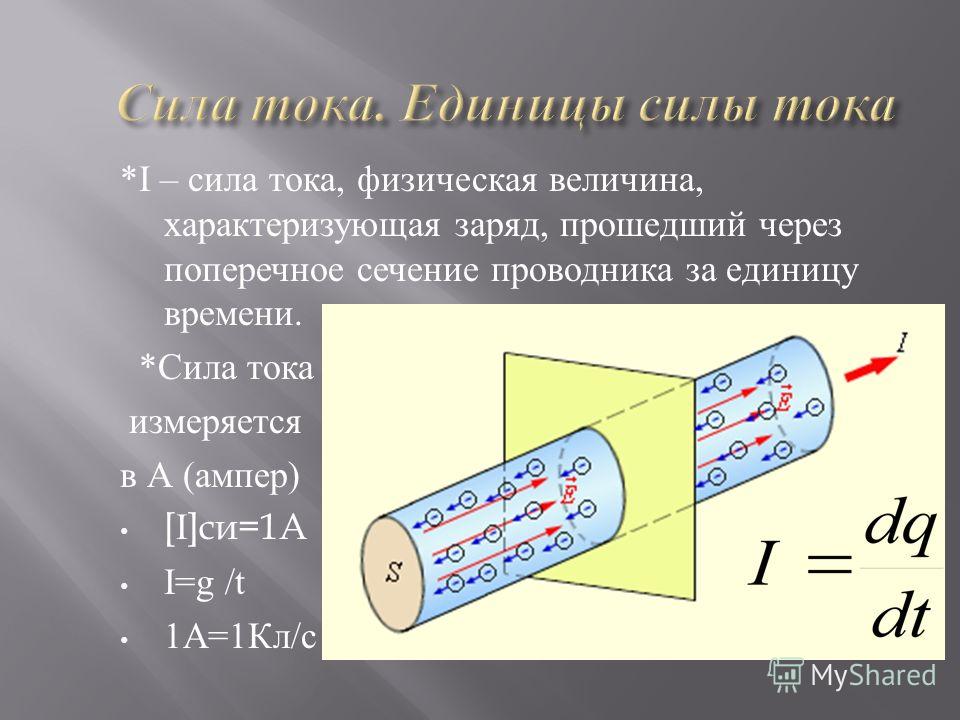 § 5.4. Уравнение Клапейрона — Менделеева. Плотность газа. § 5.5. Зависимость средней квадратичной скорости молекул газа от температуры. § 5.6. Изохорический процесс. § 5.7. Изобарический процесс. § 5.8. Изотермический процесс. § 5.9. Внутренняя энергия идеального газа. § 5.10. Работа газа при изменении его объема. Физический смысл молярной газовой постоянной. Глава 6. ИЗМЕНЕНИЕ ВНУТРЕННЕЙ ЭНЕРГИИ. ЗАКОН СОХРАНЕНИЯ И ПРЕВРАЩЕНИЯ ЭНЕРГИИ § 6.2. Теплообмен. § 6.3. Виды теплообмена. § 6.4. Изменение внутренней энергии при нагревании и охлаждении. § 6.6. Подсчет теплоты, выделяемой при сжигании топлива. К. п. д. нагревателя. § 6.7. Изменение внутренней энергии при выполнении механической работы. Опыт Джоуля. § 6.8. Закон сохранения и превращения энергии в механике. § 6.9. Закон сохранения и превращения энергии в механических и тепловых процессах. 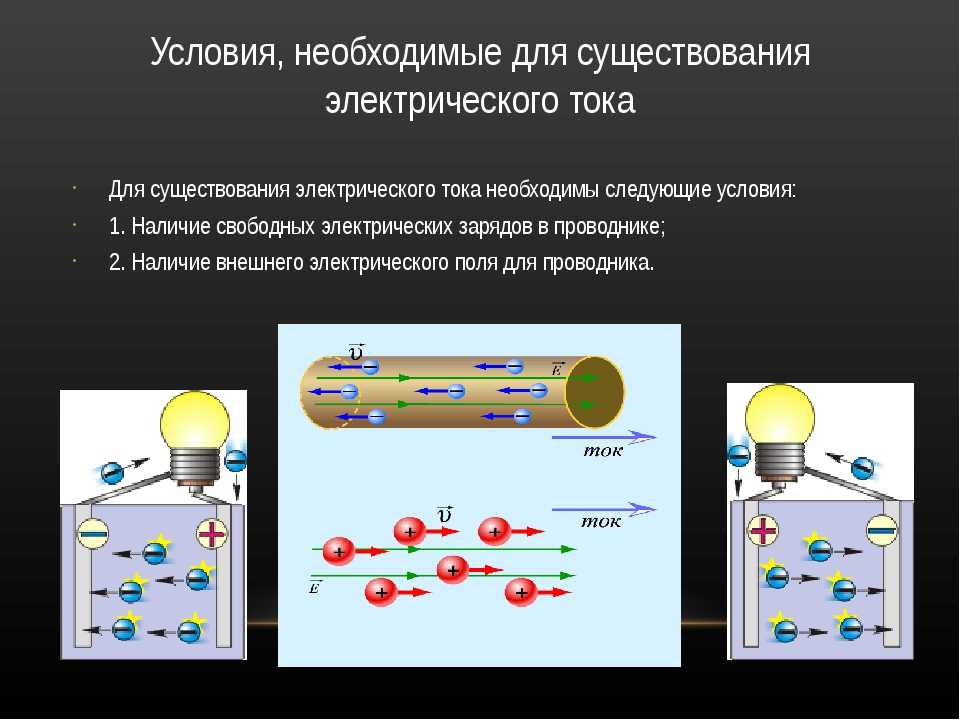 § 6.10. Первое начало термодинамики. § 6.11. Применение первого начала термодинамики к изопроцессам в идеальном газе. § 6.12. Адиабатный процесс. § 6.13. Понятие о строении Солнца и звезд. Глава 7. ПЕРЕХОД ВЕЩЕСТВА ИЗ ЖИДКОГО СОСТОЯНИЯ В ГАЗООБРАЗНОЕ И ОБРАТНО § 7.3. Теплота парообразования. Глава 8. СВОЙСТВА ПАРОВ. КИПЕНИЕ. КРИТИЧЕСКОЕ СОСТОЯНИЕ ВЕЩЕСТВА § 8.2. Свойства паров, насыщающих пространство. § 8.3. Свойства паров, не насыщающих пространство. § 8.4. Процесс кипения жидкости. § 8.5. Зависимость температуры кипения жидкости от внешнего давления. Точка кипения. § 8.6. Уравнение теплового баланса при парообразовании и конденсации. § 8.7. Перегретый пар и его использование в технике. § 8.8. Критическое состояние вещества. § 8.9. Сжижение газов и использование жидких газов в технике. Глава 9. ВОДЯНОЙ ПАР В АТМОСФЕРЕ § 9.2. Абсолютная и относительная влажность воздуха. Точка росы.  § 9.4. Понятие об атмосферах планет. Глава 10. СВОЙСТВА ЖИДКОСТЕЙ § 10.2. Поверхностный слой жидкости. § 10.3. Энергия поверхностного слоя жидкости. Поверхностное натяжение. § 10.4. Сила поверхностного натяжения. § 10.5. Смачивание. Краевой угол. § 10.6. Мениск. Давление, создаваемое искривленной поверхностью жидкости. § 10.7. Капиллярность. Капиллярные явления в природе и технике. § 10.8. Понятие о вязкости среды. Ламинарное течение жидкости. § 10.9. Закон Ньютона для внутреннего трения. Динамическая вязкость. Глава 11. СВОЙСТВА ТВЕРДЫХ ТЕЛ. ДЕФОРМАЦИИ § 11.2. Анизотропия кристаллов. Пространственная решетка и ее дефекты. § 11.3. Виды кристаллических структур. § 11.4. Виды деформаций. § 11.5. Механическое напряжение. § 11.6. Упругость, пластичность, хрупкость и твердость. § 11.7. Закон Гука. Модуль упругости. § 11.8. Энергия упруго деформированного тела. Глава 12. ПЛАВЛЕНИЕ И КРИСТАЛЛИЗАЦИЯ.  СУБЛИМАЦИЯ. ДИАГРАММА СОСТОЯНИЙ ВЕЩЕСТВА§ 12.2. Удельная теплота плавления. § 12.3. Изменение объема и плотности вещества при плавлении и отвердевании. § 12.5. Уравнение теплового баланса при плавлении и кристаллизации. § 12.6. Растворы и сплавы. Охлаждающие смеси. § 12.7. Испарение твердых тел (сублимация). § 12.8. Диаграмма состоянии вещества. Тройная точка. Глава 13. ТЕПЛОВОЕ РАСШИРЕНИЕ ТЕЛ § 13.2. Линейное расширение твердых тел при нагревании. § 13.3. Объемное расширение тел при нагревании. Зависимость плотности вещества от температуры. § 13.4. Особенности теплового расширения твердых тел. § 13.5. Некоторые особенности теплового расширения жидкостей. § 13.6. Значение теплового расширения тел в природе и технике. Глава 14. ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ. ЗАКОН КУЛОНА § 14.2. Явления, подтверждающие сложное строение атома.  § 14.3. Опыты Резерфорда. Ядерная модель строения атома. § 14.4. Понятие о строении атомов различных химических элементов. § 14.5. Электризация при соприкосновении незаряженных тел. § 14.6. Сила взаимодействия электрических зарядов. Закон Кулона. § 14.7. Диэлектрическая проницаемость среды. § 14.8. Международная система единиц СИ в электричестве. Электрическая постоянная. § 14.9. Электроскоп. § 15.2. Напряженность электрического поля. § 15.3. Линии напряженности электрического поля. § 15.4. Однородное поле. Поверхностная плотность заряда. § 15.5. Работа электрического поля при перемещении заряда. Потенциальная энергия заряда. § 15.6. Потенциал. Разность потенциалов и напряжение. Эквипотенциальные поверхности. § 15.7. Связь между напряженностью поля и напряжением. Градиент потенциала. § 15.8. Проводник в электрическом поле. § 15.9. Электрометр. § 15.10. Диэлектрик в электрическом поле. Поляризация диэлектрика.  § 15.11. Понятие о сегнетоэлектриках. § 15.12. Пьезоэлектрический эффект. § 15.14. Условия, от которых зависит электроемкость проводника. § 15.15. Конденсаторы. § 15.16. Соединение конденсаторов в батарею. § 15.17. Энергия заряженного конденсатора. Плотность энергии электрического поля. § 15.18. Опыт Милликена. Глава 16. ЭЛЕКТРИЧЕСКИЙ ТОК В МЕТАЛЛАХ. ЗАКОНЫ ПОСТОЯННОГО ТОКА § 16.2. Сила тока и плотность тока в проводнике. § 16.3. Замкнутая электрическая цепь. § 16.4. Электродвижущая сила источника электрической энергии. § 16.5. Внешняя и внутренняя части цепи. § 16.6. Закон Ома для участка цепи без э. д. с. Сопротивление проводника. Падение напряжения. § 16.7. Зависимость сопротивления от материала, длины и площади поперечного сечения проводника. § 16.9. Сверхпроводимость. § 16.10. Эквивалентное сопротивление. § 16.11. Последовательное соединение потребителей энергии тока. 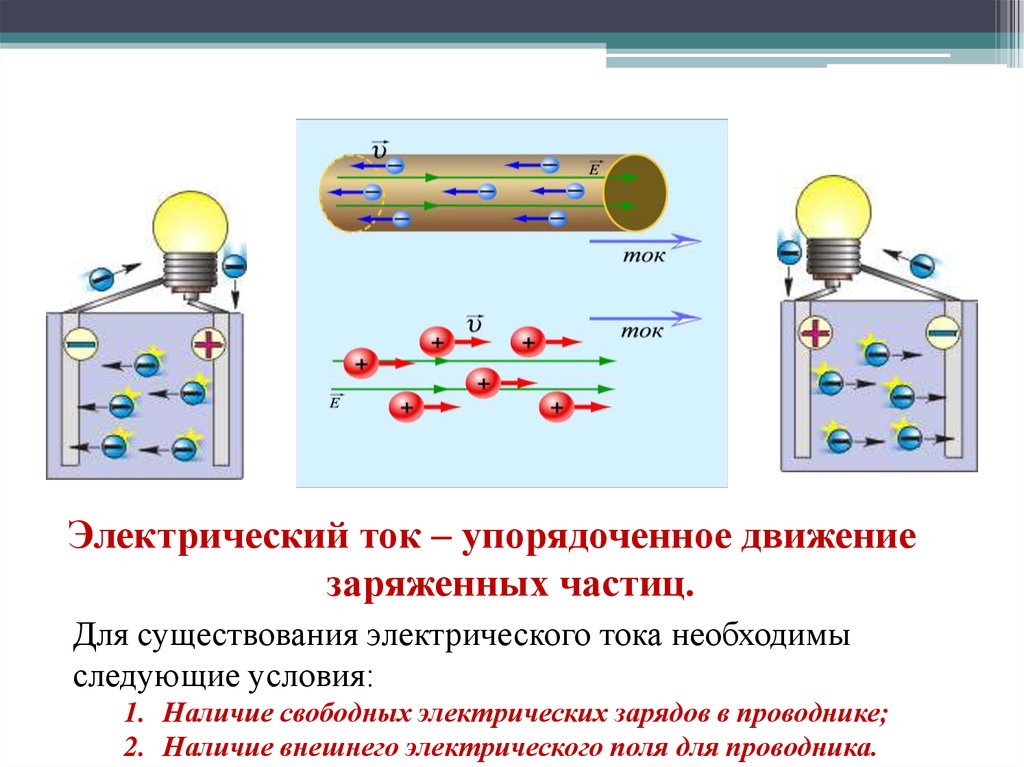 § 16.12. Параллельное соединение потребителей энергии тока § 16.13. Закон Ома для всей цепи. § 16.14. Соединение одинаковых источников электрической энергии в батарею. § 16.15. Закон Ома для участка цепи с э. д. с. и для всей цепи при нескольких э. д. с. Глава 17. РАБОТА, МОЩНОСТЬ И ТЕПЛОВОЕ ДЕЙСТВИЕ ЭЛЕКТРИЧЕСКОГО ТОКА § 17.2. Мощность электрического тока. § 17.3. Тепловое действие электрического тока. Закон Джоуля — Ленца. § 17.4. Короткое замыкание. Практическое применение теплового действия тока. Глава 18. ТЕРМОЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ § 18.2. Контактная разность потенциалов. § 18.3. Термоэлектродвижущая сила. § 18.4. Явление Пельтье. § 18.5. Применение термоэлектрических явлений в науке и технике. Глава 19. ЭЛЕКТРИЧЕСКИЙ ТОК В ЭЛЕКТРОЛИТАХ § 19.2. Электролиз. § 19.3. Электролиз, сопровождающийся растворением анода. § 19.4. Количество вещества, выделяющегося при электролизе. Первый закон Фарадея. § 19.5. Второй закон Фарадея.  Определение заряда иона.§ 19.6. Использование электролиза в технике. § 19.7. Гальванические элементы. § 19.8. Аккумуляторы. § 19.9. Применение гальванических элементов и аккумуляторов в технике. Явление электрокоррозии. Глава 20. ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ И В ВАКУУМЕ § 20.2. Зависимость силы тока в газе от напряжения. § 20.3. Электрический разряд в газе при атмосферном давлении. § 20.4. Электрический разряд в разреженных газах. Газосветные трубки и лампы дневного света. § 20.5. Излучение и поглощение энергии атомом. § 20.6. Катодные лучи. § 20.7. Понятие о плазме. § 20.8. Электрический ток в вакууме. § 20.9. Двухэлектродная лампа (диод). § 20.10. Трехэлектродная лампа (триод). § 20.11. Электронно-лучевая трубка. Глава 21. ЭЛЕКТРИЧЕСКИЙ ТОК В ПОЛУПРОВОДНИКАХ § 21.2. Чистые (беспримесные) полупроводники. Термисторы. § 21.3. Примесные полупроводники. § 21.4. Электронно-дырочный переход. § 21.5. Полупроводниковый диод. 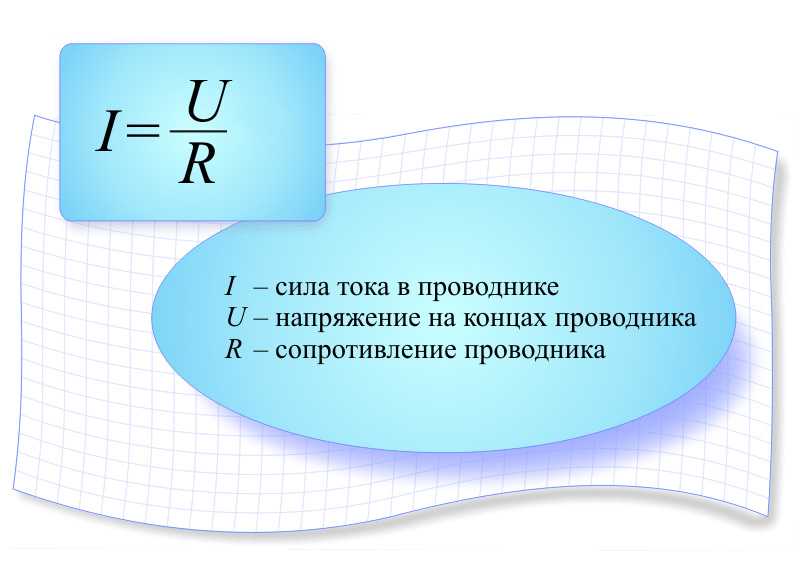 § 21.6. Полупроводниковый триод (транзистор). Глава 22. ЭЛЕКТРОМАГНЕТИЗМ § 22.2. Магнитное поле как особый вид материи. § 22.3. Магниты. § 22.4. Линии магнитной индукции. Понятие о вихревом поле. § 22.5. Магнитное поле прямолинейного тока, кругового тока и соленоида. § 22.6. Сравнение магнитных свойств соленоида и постоянного магнита. § 22.7. Сила взаимодействия параллельных токов. Магнитная проницаемость среды. § 22.8. Определение ампера. Магнитная постоянная. § 22.9. Действие магнитного поля на прямолинейный проводник с током. § 22.10. Однородное магнитное поле. § 22.11. Магнитный момент контура с током. § 22.12. Работа при перемещении проводника с током в магнитном поле. Магнитный поток. § 22.13. Индукция магнитного поля, создаваемая в веществе проводниками с током различной формы. § 22.14. Напряженность магнитного поля и ее связь с индукцией и магнитной проницаемостью среды. § 22.15. Парамагнитные, диамагнитные и ферромагнитные вещества.  § 22.16. Намагничивание ферромагнетиков. Электромагнит. § 22.17. Работа и устройство амперметра и вольтметра. § 22.18. Сила Лоренца. Движение заряда в магнитном поле. § 22.19. Постоянное и переменное магнитные поля. Глава 23. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ § 23.2. Явление электромагнитной индукции. § 23.3. Э. д. с. индукции, возникающая в прямолинейном проводнике при его движении в магнитном поле. Правило правой руки. § 23.4. Опыты Фарадея. § 23.5. Закон Ленца для электромагнитной индукции. Объяснение диамагнитных явлений. § 23.6. Величина э. д. с. индукции. § 23.7. Вихревое электрическое поле и его связь с магнитным полем. § 23.8. Вихревые токи. § 23.9. Роль магнитных полей в явлениях, происходящих на Солнце и в космосе. § 23.10. Явление самоиндукции. Э. д. с. самоиндукции. § 23.11. Энергия магнитного поля. Раздел III. КОЛЕБАНИЯ И ВОЛНЫ Глава 24. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ § 24.2. Условия возникновения колебаний. § 24.  3. Классификация колебательных движений тела в зависимости от действующей на него силы.§ 24.4. Параметры колебательного движения. § 24.5. Величины, характеризующие мгновенное состояние колеблющейся точки. § 24.6. Гармоническое колебание. § 24.7. Уравнение гармонического колебания и его график. § 24.8. Математический маятник. § 24.9. Законы колебания математического маятника. Формула маятника. § 24.10. Физический маятник. § 24.11. Практические применения маятников. § 24.12. Упругие колебания. Превращение энергии при колебательном движении. § 24.13. Распространение колебательного движения в упругой среде. § 24.14. Перенос энергии бегущей волной. § 24.15. Поперечные и продольные волны. § 24.16. Волна и луч. Длина волны. § 24.17. Скорость распространения волн и ее связь с длиной волны и периодом (частотой) колебаний. § 24.18. Сложение колебаний, происходящих по одной прямой. § 24.19. Отражение волн. § 24.20. Стоячие волны.  § 24.21. Интерференция волн. § 24.22. Сложение колебаний с кратными частотами. Разложение сложного колебания на гармонические составляющие. § 24.23. Вынужденные колебания. Механический резонанс и его роль в технике. Глава 25. ЗВУК И УЛЬТРАЗВУК § 25.3. Громкость и интенсивность звука. § 25.4. Высота тона и тембр звука. § 25.5. Интерференция звуковых волн. § 25.6. Отражение и поглощение звука. § 25.7. Звуковой резонанс. § 25.8. Ультразвук и его применение в технике. Глава 26. ПЕРЕМЕННЫЙ ТОК § 26.2. Понятие об устройстве индукционных генераторов. § 26.3. Действующие значения э. д. с., напряжения и силы переменного тока. § 26.4. Индуктивность и емкость в цепи переменного тока. § 26.5. Преобразование переменного тока. Трансформатор. § 26.6. Индукционная катушка. § 26.7. Трехфазный ток. § 26.8. Получение, передача и распределение электрической энергии в народном хозяйстве СССР. Глава 27. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ § 27.  2. Затухающие электромагнитные колебания. Электрический резонанс.§ 27.3. Получение незатухающих колебаний с помощью лампового генератора. § 27.4. Токи высокой частоты и их применение. § 27.5. Электромагнитное поле как особый вид материи. § 27.6. Открытый колебательный контур. Излучение. § 27.7. Электромагнитные волны. Скорость их распространения. § 27.8. Опыты Герца. § 27.9. Изобретение радио А С. Поповым. Радиотелеграфная связь. § 27.10. Радиотелефонная связь. Амплитудная модуляция. § 27.11. Устройство простейшего лампового радиоприемника с усилителем низкой частоты. § 27.12. Понятие о радиолокации. Раздел IV. ОПТИКА. ОСНОВЫ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ Глава 28. ПРИРОДА СВЕТА. РАСПРОСТРАНЕНИЕ СВЕТА § 28.2. Понятие об электромагнитной теории света. Диапазон световых волн. § 28.3. Понятие о квантовой теории света. Постоянная Планка. § 28.4. Источники света. § 28.5. Принцип Гюйгенса. Световые лучи. § 28.6. Скорость распространения света в вакууме.  Опыт Майкельсона.§ 28.7. Скорость распространения света в различных средах. Глава 29. ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ СВЕТА § 29.2. Законы отражения света. § 29.3. Зеркальное и диффузное отражение. Плоское зеркало. § 29.4. Сферические зеркала. § 29.5. Построение изображений, получаемых с помощью сферических зеркал. Формула сферического зеркала. § 29.6. Законы преломления света. § 29.7. Абсолютный показатель преломления и его связь с относительным показателем преломления. § 29.8. Полное отражение света. Предельный угол. § 29.9. Прохождение света через пластинку с параллельными гранями и через трехгранную призму. Призма с полным отражением. Глава 30. ЛИНЗЫ. ПОЛУЧЕНИЕ ИЗОБРАЖЕНИЙ С ПОМОЩЬЮ ЛИНЗ § 30.2. Главные фокусы и фокальные плоскости линзы. § 30.3. Оптическая сила линзы. § 30.4. Построение изображения светящейся точки, расположенной на главной оптической оси линзы. § 30.5. Вывод формулы для сопряжеппых точек тонкой линзы. § 30.  6. Построение изображения светящейся точки, расположенной на побочной оптической оси линзы.§ 30.7. Построение изображений предмета, создаваемых линзой. § 30.8. Линейное увеличение, полученное с помощью линзы. § 30.9. Недостатки линз. Выясним, какие существенные недостатки встречаются у линз. Глава 31. ОПТИЧЕСКИЕ ПРИБОРЫ. ГЛАЗ § 31.2. Фотографический аппарат. § 31.3. Глаз как оптическая система. § 31.4, Длительность зрительного ощущения. § 31.5. Угол зрения. § 31.6. Расстояние наилучшего зрения. Оптические дефекты глаза. § 31.7. Увеличение оптического прибора. Лупа. § 31.8. Микроскоп. § 31.9. Труба Кеплера. Телескопы. § 31.10. Труба Галилея. Бинокль. Глава 32. ЯВЛЕНИЯ, ОБЪЯСНЯЕМЫЕ ВОЛНОВЫМИ СВОЙСТВАМИ СВЕТА § 32.2. Цвета тонких пленок. § 32.3. Интерференция в клинообразной пленке. Кольца Ньютона. § 32.4. Интерференция света в природе и технике. § 32.5. Дифракция света. § 32.6. Дифракционная решетка и дифракционный спектр.  Измерение длины световой волны.§ 32.7. Поляризация волн. § 32.8. Поляризация света. Поляроиды. § 32.9. Поляризация при отражении и преломлении света. Глава 33. ФОТОМЕТРИЯ § 33.2. Световой поток. § 33.3. Сила света. Единицы силы света и светового потока. § 33.4. Освещенность. § 33.5. Яркость. § 33.6. Законы освещенности. § 33.7. Сравнение силы света двух источников. Фотометр. Люксметр. Глава 34. ИЗЛУЧЕНИЕ И СПЕКТРЫ. РЕНТГЕНОВСКИЕ ЛУЧИ § 34.2. Разложение белого света призмой. Сплошной спектр. § 34.3. Сложение спектральных цветов. Дополнительные цвета. § 34.4. Цвета тел. § 34.5. Ультрафиолетовая и инфракрасная части спектра. § 34.6. Роль ультрафиолетовых и инфракрасных лучей в природе. Их применение в технике. § 34.7. Приборы для получения и исследования спектров. § 34.8. Виды спектров. § 34.9. Спектры поглощения газов. Опыты Кирхгофа. § 34.10. Закон теплового излучения Кирхгофа. § 34.11. Законы теплового излучения Стефана — Больцмана, Вина, Планка. § 34.12. Спектры Солнца и звезд. Их связь с температурой. § 34.13. Спектральный анализ. § 34.14. Понятие о принципе Доплера. § 34.15. Рентгеновские лучи и их практическое применение. § 34.16. Шкала электромагнитных волн. § 34.17. Виды космического излучения. Глава 35. ЯВЛЕНИЯ, ОБЪЯСНЯЕМЫЕ КВАНТОВЫМИ СВОЙСТВАМИ ИЗЛУЧЕНИЯ § 35.2. Давление световых лучей. Опыты П. Н. Лебедева. § 35.3. Тепловое действие света. § 35.4. Химическое действие света. § 35.5. Использование химического действия света при фотографировании. Понятие о квантовой природе химического действия излучения. § 35.6. Внешний фотоэлектрический эффект. Опыты Столетова. § 35.7. Законы внешнего фотоэффекта. § 35.8. Объяснение фотоэффекта на основе квантовой теории. § 35.9. Фотоэлементы с внешним фотоэффектом. § 35.10. Внутренний фотоэффект. § 35.11. Фотосопротивления. § 35.12. Фотоэлементы с внутренним фотоэффектом. § 35.13. Использование фотоэлементов в науке и технике. § 35.14. Понятие о телевидении. § 35.15. Понятие о теории Бора. Строение атома водорода. § 35.16. Излучение и поглощение энергии атомами. § 35.17. Явление люминесценции. § 35.18. Понятие о квантовых генераторах. Глава 36. ОСНОВЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ § 36.2. Экспериментальные основы специальной теории относительности Эйнштейна. Постулаты Эйнштейна. § 36.3. Понятие одновременности. § 36.4. Относительность понятий длины и промежутка времени § 36.5. Теорема сложения скоростей Эйнштейна. § 36.6. Масса и импульс в специальной теории относительности. § 36.7. Связь между массой и энергией. Уравнение Эйнштейна. § 36.8. Связь между импульсом и энергией. Импульс и энергия фотонов. Раздел V. ФИЗИКА АТОМНОГО ЯДРА Глава 37. СТРОЕНИЕ АТОМНОГО ЯДРА § 37.2. Радиоактивность. § 37.3. Понятие о превращении химических элементов. § 37.4. Понятие об энергии и проникающей способности радиоактивного излучения. § 37.5. Эффект Вавилова — Черенкова. § 37.6. Открытие искусственного превращения атомных ядер. § 37.7. Открытие нейтрона. § 37.8. Состав атомного ядра. Запись ядерных реакций. § 37.9. Изотопы. § 37.10. Понятие о ядерных силах. § 37.11. Дефект массы атомных ядер. Энергия связи. Глава 38. КОСМИЧЕСКИЕ ЛУЧИ. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ § 38.2. Открытие позитрона. § 38.3. Нейтрино. § 38.4. Открытие новых элементарных частиц. § 38.5. Классификация элементарных частиц. § 38.6. Античастицы. Взаимные превращения вещества и поля. § 38.7. Гипотеза кварков. Глава 39. АТОМНАЯ ЭНЕРГИЯ И ЕЕ ИСПОЛЬЗОВАНИЕ § 39.2. Деление тяжелых атомных ядер. § 39.3. Цепная реакция деления. Ядерный взрыв. § 39.4. Ядерный реактор. § 39.5. Развитие ядерной энергетики в СССР. § 39.6. Понятие о термоядерной реакции. Энергия Солнца и звезд. § 39.7. Понятие об управляемой термоядерной реакции. § 39.8. Получение радиоактивных изотопов и их применение. Раздел VI. ОСНОВНЫЕ СВЕДЕНИЯ ПО АСТРОНОМИИ Глава 40. СТРОЕНИЕ И РАЗВИТИЕ ВСЕЛЕННОЙ§ 40.2. Происхождение и развитие небесных тел. § 40.3. Понятие о космологии. |
Электрический ток. В проводниках при определенных условиях… | by NikolayGolovko
В проводниках при определенных условиях может возникнуть непрерывное упорядоченное движение свободных носителей электрического заряда. Такое движение называется электрическим током. За направление электрического тока принято направление движения положительных свободных зарядов, хотя в большинстве случае движутся электроны — отрицательно заряженные частицы.
Количественной мерой электрического тока служит сила тока I — скалярная физическая величина, равная отношению заряда q, переносимого через поперечное сечение проводника за интервал времени t, к этому интервалу времени:
Если ток не постоянный, то для нахождения количества прошедшего через проводник заряда рассчитывают площадь фигуры под графиком зависимости силы тока от времени.
Если сила тока и его направление не изменяются со временем, то такой ток называется постоянным. Сила тока измеряется амперметром, который включается в цепь последовательно. В Международной системе единиц СИ сила тока измеряется в амперах [А]. 1 А = 1 Кл/с.
Средняя сила тока находится как отношение всего заряда ко всему времени (т.е. по тому же принципу, что и средняя скорость или любая другая средняя величина в физике):
Если же ток равномерно меняется с течением времени от значения I1 до значения I2, то можно значение среднего тока можно найти как среднеарифметическое крайних значений:
Плотность тока — сила тока, приходящаяся на единицу поперечного сечения проводника, рассчитывается по формуле:
При прохождении тока по проводнику ток испытывает сопротивление со стороны проводника. Причина сопротивления — взаимодействие зарядов с атомами вещества проводника и между собой. Единица измерения сопротивления 1 Ом. Сопротивление проводника R определяется по формуле:
где: l — длина проводника, S — площадь его поперечного сечения, ρ — удельное сопротивление материала проводника (будьте внимательны и не перепутайте последнюю величину с плотностью вещества), которое характеризует способность материала проводника противодействовать прохождению тока. То есть это такая же характеристика вещества, как и многие другие: удельная теплоемкость, плотность, температура плавления и т.д. Единица измерения удельного сопротивления 1 Ом·м. Удельное сопротивление вещества — табличная величина.
Сопротивление проводника зависит и от его температуры:
где: R0 — сопротивление проводника при 0°С, t — температура, выраженная в градусах Цельсия, α — температурный коэффициент сопротивления. Он равен относительному изменению сопротивления, при увеличении температуры на 1°С. Для металлов он всегда больше нуля, для электролитов наоборот, всегда меньше нуля.
Диод в цепи постоянного тока
Диод — это нелинейный элемент цепи, сопротивление которого зависит от направления протекания тока. Обозначается диод следующим образом:
Стрелка в схематическом обозначении диода показывает, в каком направлении он пропускает ток. В этом случае его сопротивление равно нулю, и диод можно заменить просто на проводник с нулевым сопротивлением. Если ток течет через диод в противоположном направлении, то диод обладает бесконечно большим сопротивлением, то есть не пропускает ток совсем, и является разрывом в цепи. Тогда участок цепи с диодом можно просто вычеркнуть, так как ток по нему не идет.
Немецкий физик Г.Ом в 1826 году экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (то есть проводнику, в котором не действуют сторонние силы) сопротивлением R, пропорциональна напряжению U на концах проводника:
Величину R принято называть электрическим сопротивлением. Проводник, обладающий электрическим сопротивлением, называется резистором. Это соотношение выражает закон Ома для однородного участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.
Проводники, подчиняющиеся закону Ома, называются линейными. Графическая зависимость силы тока I от напряжения U (такие графики называются вольт-амперными характеристиками, сокращенно ВАХ) изображается прямой линией, проходящей через начало координат. Следует отметить, что существует много материалов и устройств, не подчиняющихся закону Ома, например, полупроводниковый диод или газоразрядная лампа. Даже у металлических проводников при достаточно больших токах наблюдается отклонение от линейного закона Ома, так как электрическое сопротивление металлических проводников растет с ростом температуры.
Проводники в электрических цепях можно соединять двумя способами: последовательно и параллельно. У каждого способа есть свои закономерности.
1. Закономерности последовательного соединения:
Формула для общего сопротивления последовательно соединенных резисторов справедлива для любого числа проводников. Если же в цепь последовательно включено n одинаковых сопротивлений R, то общее сопротивление R0 находится по формуле:
2. Закономерности параллельного соединения:
Формула для общего сопротивления параллельно соединенных резисторов справедлива для любого числа проводников. Если же в цепь параллельно включено n одинаковых сопротивлений R, то общее сопротивление R0находится по формуле:
Электроизмерительные приборы
Для измерения напряжений и токов в электрических цепях постоянного тока используются специальные приборы — вольтметры и амперметры.
Вольтметр предназначен для измерения разности потенциалов, приложенной к его клеммам. Он подключается параллельно участку цепи, на котором производится измерение разности потенциалов. Любой вольтметр обладает некоторым внутренним сопротивлением RB. Для того чтобы вольтметр не вносил заметного перераспределения токов при подключении к измеряемой цепи, его внутреннее сопротивление должно быть велико по сравнению с сопротивлением того участка цепи, к которому он подключен.
Амперметр предназначен для измерения силы тока в цепи. Амперметр включается последовательно в разрыв электрической цепи, чтобы через него проходил весь измеряемый ток. Амперметр также обладает некоторым внутренним сопротивлением RA. В отличие от вольтметра, внутреннее сопротивление амперметра должно быть достаточно малым по сравнению с полным сопротивлением всей цепи.
Для существования постоянного тока необходимо наличие в электрической замкнутой цепи устройства, способного создавать и поддерживать разности потенциалов на участках цепи за счет работы сил неэлектростатического происхождения. Такие устройства называются источниками постоянного тока. Силы неэлектростатического происхождения, действующие на свободные носители заряда со стороны источников тока, называются сторонними силами.
Природа сторонних сил может быть различной. В гальванических элементах или аккумуляторах они возникают в результате электрохимических процессов, в генераторах постоянного тока сторонние силы возникают при движении проводников в магнитном поле. Под действием сторонних сил электрические заряды движутся внутри источника тока против сил электростатического поля, благодаря чему в замкнутой цепи может поддерживаться постоянный электрический ток.
При перемещении электрических зарядов по цепи постоянного тока сторонние силы, действующие внутри источников тока, совершают работу. Физическая величина, равная отношению работы Aст сторонних сил при перемещении заряда q от отрицательного полюса источника тока к положительному к величине этого заряда, называется электродвижущей силой источника (ЭДС):
Таким образом, ЭДС определяется работой, совершаемой сторонними силами при перемещении единичного положительного заряда. Электродвижущая сила, как и разность потенциалов, измеряется в вольтах (В).
Закон Ома для полной (замкнутой) цепи: сила тока в замкнутой цепи равна электродвижущей силе источника, деленной на общее (внутреннее + внешнее) сопротивление цепи:
Сопротивление r — внутреннее (собственное) сопротивление источника тока (зависит от внутреннего строения источника). Сопротивление R — сопротивление нагрузки (внешнее сопротивление цепи).
Падение напряжения во внешней цепи при этом равно (его еще называют напряжением на клеммах источника):
Важно понять и запомнить: ЭДС и внутреннее сопротивление источника тока не меняются, при подключении разных нагрузок.
Если сопротивление нагрузки равно нулю (источник замыкается сам на себя) или много меньше сопротивления источника, то тогда в цепи потечет ток короткого замыкания:
Сила тока короткого замыкания — максимальная сила тока, которую можно получить от данного источника с электродвижущей силой ε и внутренним сопротивлением r. У источников с малым внутренним сопротивлением ток короткого замыкания может быть очень велик, и вызывать разрушение электрической цепи или источника. Например, у свинцовых аккумуляторов, используемых в автомобилях, сила тока короткого замыкания может составлять несколько сотен ампер. Особенно опасны короткие замыкания в осветительных сетях, питаемых от подстанций (тысячи ампер). Чтобы избежать разрушительного действия таких больших токов, в цепь включаются предохранители или специальные автоматы защиты сетей.
Несколько источников ЭДС в цепи
Если в цепи присутствует несколько ЭДС подключенных последовательно, то:
1. При правильном (положительный полюс одного источника присоединяется к отрицательному другого) подключении источников общее ЭДС всех источников и их внутреннее сопротивление может быть найдено по формулам:
Например, такое подключение источников осуществляется в пультах дистанционного управления, фотоаппаратах и других бытовых приборах, работающих от нескольких батареек.
2. При неправильном (источники соединяются одинаковыми полюсами) подключении источников их общее ЭДС и сопротивление рассчитывается по формулам:
В обоих случаях общее сопротивление источников увеличивается.
При параллельном подключении имеет смысл соединять источники только c одинаковой ЭДС, иначе источники будут разряжаться друг на друга. Таким образом суммарное ЭДС будет таким же, как и ЭДС каждого источника, то есть при параллельном соединении мы не получим батарею с большим ЭДС. При этом уменьшается внутреннее сопротивление батареи источников, что позволяет получать большую силу тока и мощность в цепи:
В этом и состоит смысл параллельного соединения источников. В любом случае при решении задач сначала надо найти суммарную ЭДС и полное внутреннее сопротивление получившегося источника, а затем записать закон Ома для полной цепи.
Работа A электрического тока I, протекающего по неподвижному проводнику с сопротивлением R, преобразуется в теплоту Q, выделяющееся на проводнике. Эту работу можно рассчитать по одной из формул (с учетом закона Ома все они следуют друг из друга):
Закон преобразования работы тока в тепло был экспериментально установлен независимо друг от друга Дж.Джоулем и Э.Ленцем и носит название закона Джоуля–Ленца. Мощность электрического тока равна отношению работы тока A к интервалу времени Δt, за которое эта работа была совершена, поэтому она может быть рассчитана по следующим формулам:
Работа электрического тока в СИ, как обычно, выражается в джоулях (Дж), мощность — в ваттах (Вт).
Рассмотрим теперь полную цепь постоянного тока, состоящую из источника с электродвижущей силой ε и внутренним сопротивлением r и внешнего однородного участка с сопротивлением R. В этом случае полезная мощность или мощность, выделяемая во внешней цепи:
Максимально возможная полезная мощность источника достигается, если R = r и равна:
Если при подключении к одному и тому же источнику тока разных сопротивлений R1 и R2 на них выделяются равные мощности то внутреннее сопротивление этого источника тока может быть найдено по формуле:
Мощность потерь или мощность внутри источника тока:
Полная мощность, развиваемая источником тока:
Сила магнитного поля, действующая на проводник с током
Цели обучения
К концу этого раздела вы сможете:
- Описывать воздействие магнитной силы на проводник с током.
- Рассчитайте магнитную силу, действующую на проводник с током.
Поскольку обычно заряды не могут покинуть проводник, магнитная сила, действующая на заряды, движущиеся в проводнике, передается самому проводнику.
Рис. 1. Магнитное поле действует на проводник с током в направлении, определяемом правилом правой руки 1 (то же направление, что и на отдельные движущиеся заряды). Эта сила легко может быть достаточно большой, чтобы сдвинуть провод, поскольку типичные токи состоят из очень большого количества движущихся зарядов.
Мы можем получить выражение для магнитной силы, действующей на ток, взяв сумму магнитных сил, действующих на отдельные заряды. (Силы складываются, поскольку они имеют одинаковое направление.) Сила, действующая на отдельный заряд, движущийся со скоростью дрейфа v d , определяется формулой F = qv d B sin θ . Принимая B равномерным по всей длине провода l и равным нулю в других местах, общая магнитная сила на проводе тогда равна F = ( qv d B sin θ )( N ), где N — число носителей заряда на отрезке провода длиной l 8 . Теперь Н = нВ, где n — число носителей заряда в единице объема, а В — объем проволоки в поле. Учитывая, что В = Al , где A — площадь поперечного сечения провода, тогда сила, действующая на провод, равна F = ( qv d B sin θ ) ( nAl ). Собираем термины,
[латекс]F=(nqAv_{\text{d}})lB\sin\theta\\[/latex].
Потому что nqAv d = I (см. Ток),
[латекс]F=IlB\sin\theta\\[/латекс]
уравнение для 0 магнитной силы на длине провода с током I в однородном магнитном поле B , как показано на рисунке 2. Если мы разделим обе части этого выражения на l , находим, что магнитная сила на единицу длины провода в однородном поле равна [латекс]\frac{F}{l}=IB\sin\theta\\[/latex]. Направление этой силы задается RHR-1, с большим пальцем в направлении тока I . Затем пальцами в направлении B , перпендикуляр к ладони указывает в направлении F , как на рисунке 2.
Рисунок 2. Сила, действующая на проводник с током в магнитном поле, равна F = IlB грех θ . Его направление задает RHR-1.
Пример 1. Расчет магнитной силы, действующей на провод с током: сильное магнитное поле
= 20,0 А.Стратегия
Силу можно найти с помощью данной информации, используя [латекс]F=IlB\sin\theta\\[/latex] и отметив, что угол θ между I and B is 90º, so that sin θ = 1.
Solution
Entering the given values into F = IlB sin θ yields
F = IlB sin θ = (20,0 А)(0,0500 м)(1,50 Тл)(1).
Единицы тесла: [латекс]1\текст{Т}=\фракция{\текст{N}}{\текст{А}\cdot\текст{м}}\\[/латекс]; таким образом,
F = 1,50 Н.
Обсуждение
Это сильное магнитное поле создает значительную силу на проводе небольшой длины.
Сила магнитного поля, действующая на проводники с током, используется для преобразования электрической энергии в работу. (Ярким примером являются двигатели — в них используются петли из проволоки, и они рассматриваются в следующем разделе.) Магнитогидродинамика (МГД) — это техническое название, данное умному приложению, в котором магнитная сила перекачивает жидкости без движущихся механических частей. (См. рис. 3.)
Рис. 3. Магнитогидродинамика. Магнитная сила тока, проходящего через эту жидкость, может быть использована в качестве немеханического насоса.
Сильное магнитное поле прикладывается к трубке, и ток проходит через жидкость под прямым углом к полю, в результате чего на жидкость действует сила, параллельная оси трубки, как показано на рисунке. Отсутствие движущихся частей делает его привлекательным для перемещения горячего химически активного вещества, такого как жидкий натрий, используемый в некоторых ядерных реакторах. Экспериментальные искусственные сердца тестируются с использованием этой техники для перекачивания крови, возможно, для обхода неблагоприятных последствий механических насосов. (Однако на клеточные мембраны влияют большие поля, необходимые для МГД, что задерживает его практическое применение у людей.) Был предложен двигатель МГД для атомных подводных лодок, потому что он может быть значительно тише, чем обычные гребные двигатели. Сдерживающая ценность атомных подводных лодок основана на их способности скрыться и пережить первый или второй ядерный удар. По мере того, как мы постепенно разбираем наши арсеналы ядерного оружия, подводная ветвь будет выведена из эксплуатации последней из-за этой способности (см. рис. 4). Существующие МГД-приводы тяжелые и неэффективные — требуется много доработок.
Рис. 4. Двигательная установка МГД на атомной подводной лодке может создавать значительно меньшую турбулентность, чем гребные винты, и обеспечивать более тихую работу. Разработка бесшумной подводной лодки была драматизирована в книге и фильме «Охота на Красный Октябрь ».
- Магнитная сила, действующая на проводники с током, определяется выражением
[латекс]F=IIB\sin\theta\\[/латекс]
где I — сила тока, l — длина прямого проводника в однородном магнитном поле B и θ — это угол между I и B .
Сила следует за RHR-1 большим пальцем в направлении I .
Концептуальные вопросы
- Нарисуйте схему ситуации на рисунке 1, показав направление электронов, несущих ток, и используйте RHR-1, чтобы проверить направление силы, действующей на провод.
- Убедитесь, что направление силы в МГД-приводе, таком как на рис. 3, не зависит от знака зарядов, переносящих ток через жидкость.
- Почему магнитогидродинамический привод лучше работает в морской воде, чем в пресной? Кроме того, зачем нужны сверхпроводящие магниты?
- Что больше мешает показаниям компаса, переменный ток в вашем холодильнике или постоянный ток, когда вы заводите машину? Объяснять.
Задачи и упражнения
1. Каково направление действия магнитной силы на ток в каждом из шести случаев на рис. 5?
Рисунок 5.
2. Каково направление тока, на который действует магнитная сила, показанная в каждом из трех случаев на рисунке 6, если предположить, что ток течет перпендикулярно 9?0017 Б ?
Рисунок 6.
3. Каково направление магнитного поля, которое создает магнитную силу, показанную на токах в каждом из трех случаев на рисунке 7, если предположить, что B перпендикулярно I ?
Рисунок 7.
4. (a) Какова сила на метр, действующая на молнию на экваторе, которая несет 20 000 А перпендикулярно земному полю 3,00 × 10 −5 -T? б) Каково направление силы, если течение направлено прямо вверх, а направление поля Земли строго на север, параллельно земле?
5. (a) Линия электропередачи постоянного тока для системы легкорельсового транспорта передает ток 1000 А под углом 30º к полю Земли 5,00 × 10 −5 -T. Какая сила действует на отрезке этой линии длиной 100 м? (b) Обсудите практические проблемы, которые это вызывает, если таковые имеются.
6. Какая сила действует на воду в МГД-приводе с трубкой диаметром 25,0 см, если через трубку, перпендикулярную магнитному полю напряженностью 2,00 Тл, пропускают ток силой 100 А? (Относительно небольшой размер этой силы указывает на необходимость очень больших токов и магнитных полей для создания практических МГД-приводов. )
7. Провод, по которому течет ток силой 30,0 А, проходит между полюсами сильного магнита, перпендикулярного его полю, и испытывает силу 2,16 Н на 4,00 см провода в поле. Какова средняя напряженность поля?
8. (a) Участок кабеля длиной 0,750 м, по которому подается ток к стартеру автомобиля, образует угол 60º с полем Земли 5,50 × 10 −5 Тл. Какова сила тока, когда на провод действует сила 7,00 × 10 90 233 −3 90 234 Н? б) Если пропустить провод между полюсами сильного подковообразного магнита и подвергнуть его 5,00 см воздействию поля силой 1,75 Тл, какая сила будет действовать на этот отрезок провода?
9. а) Чему равен угол между проводом, по которому течет ток 8,00 А, и полем 1,20 Тл, в котором он находится, если на 50 см провода действует магнитная сила 2,40 Н? б) Какова сила, действующая на проволоку, если ее повернуть под углом 90º к полю?
10. Сила, действующая на прямоугольную проволочную петлю в магнитном поле на рисунке 8, может использоваться для измерения напряженности поля. Поле однородно, и плоскость петли перпендикулярна полю. а) Как направлена магнитная сила, действующая на петлю? Обоснуйте утверждение, что силы на сторонах петли равны и противоположны, независимо от того, какая часть петли находится в поле, и не влияют на результирующую силу, действующую на петлю. (b) Если используется ток 5,00 А, какова сила на тесла на петле шириной 20,0 см?
Рис. 8. Прямоугольная проволочная петля, по которой течет ток, перпендикулярна магнитному полю. Поле однородно в показанной области и равно нулю вне этой области.
Избранные решения задач и упражнений
1. (a) на запад (слева)
(b) на страницу
(c) на север (вверх)
(d) без силы
(e) на восток (справа)
(е) юг (вниз)
3. (а) на стр.
(б) запад (слева)
(в) со стр.
5. (a) 2,50 Н (b) Это примерно полфунта силы на 100 м проволоки, что намного меньше веса самой проволоки. Поэтому особых опасений не вызывает.
7. 1,80 Т
9. (а) 30º (б) 4,80 Н
Проводник с током: определение, значение, примеры
Проводник с током: проводник, по которому протекает электрический ток при нормальных условиях [этот термин определен в IEC TS 62257-5-2015].
Примечание 1 к записи: Линейный проводник (L), нейтральный проводник (N), средний проводник (M), PEN-проводник, PEM-проводник и PEL-проводник являются токонесущими проводниками. Защитный проводник (PE) не является проводником с током.
Защитный проводник в нормальных условиях почти не проводит электрический ток, потому что в нем нет повреждений и наведенных токов, таких как токи замыкания на землю. Поэтому он не считается токонесущей жилой и не включается в общее количество проводников в электрических цепях, сетях и системах.
Примеры токонесущих проводников
Термин «токонесущий проводник» выделяет из совокупности проводников такие проводники, по которым в нормальных условиях, характеризующихся отсутствием замыканий, протекает электрический ток.
Во-первых, к токонесущим проводникам относятся проводники под напряжением, такие как фазный проводник (L), полюсный проводник (L), нейтральный проводник (N) и средний проводник (M).
Во-вторых, это PEN-проводник, PEM-проводник и PEL-проводник, которые не являются проводниками под напряжением, но по которым в нормальных условиях протекает электрический ток. Защитный проводник (PE) не является проводником с током, так как в нормальных условиях по нему почти не протекает электрический ток.
При указании общего количества проводников в электрической цепи, сети или системе учитываются только токонесущие проводники. Например, 3-фазная 4-проводная цепь переменного тока может состоять из трех фазных проводников и четвертого нейтрального проводника или PEN-проводника. В одну и ту же электрическую цепь могут входить три фазных провода, нулевой провод и защитный провод, который не учитывается в общем числе проводников.
Эти схемы показаны на рисунках 31A1 и 31C стандарта IEC 60364-1 (см.
