Физика для углубленного изучения. 2. Электродинамика. Оптика
Физика для углубленного изучения. 2. Электродинамика. Оптика
ОглавлениеВведениеI. ЭЛЕКТРОСТАТИКА § 1. Электрический заряд. Закон Кулона § 2. Электрическое поле. Напряженность поля § 3. Теорема Гаусса § 4. Потенциал электростатического поля. Энергия системы зарядов § 5. Расчет электрических полей § 6. Проводники в электрическом поле § 7. Силы в электростатическом поле § 8. Конденсаторы. Электроемкость § 9. Энергия электрического поля II. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК § 10. Характеристики электрического тока. Закон Ома § 11. Соединение проводников в электрические цепи § 12. Закон Ома для неоднородной цепи § 14. Работа и мощность постоянного тока § 15. Магнитное поле постоянного тока § 16. Действие магнитного поля на движущиеся заряды III. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ § 17. Явление электромагнитной индукции § 18. Электрические машины постоянного тока § 19. Энергия магнитного поля § 20.  Основы теории электромагнитного поля§ 21. Квазистационарные явления в электрических цепях IV. ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК § 22. Цепи переменного тока. Закон Ома § 23. Работа и мощность переменного тока. Передача электроэнергии V. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ § 25. Колебательный контур § 26. Вынужденные колебания в контуре. Резонанс § 27. Незатухающие электромагнитные колебания § 28. Электромагнитные волны § 29. Свойства и применения электромагнитных волн VI. ОПТИКА § 30. Свет как электромагнитные волны. Интерференция § 31. Дифракция света § 32. Спектральные приборы. Дифракционная решетка § 33. Протяженные источники света § 34. Интерференция немонохроматического света § 35. Физические принципы голографии § 36. Геометрическая оптика § 37. Оптические приборы, формирующие изображение |
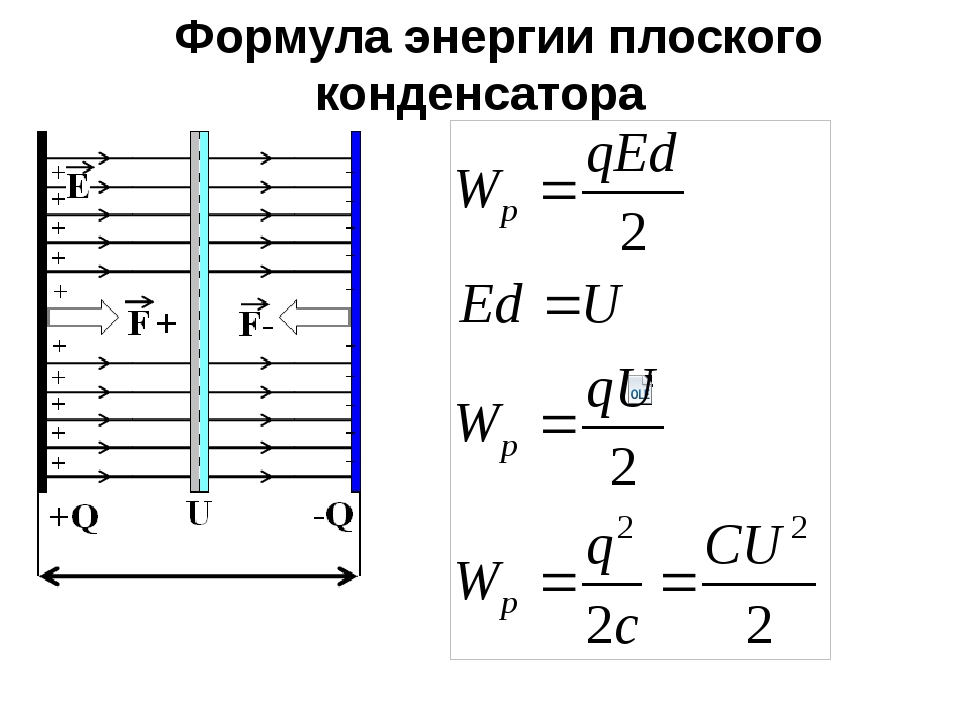
Энергия заряженного конденсатора.
Калькулятор онлайн для любых конденсаторов.
| 0 | ||||
| AC | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
Онлайн калькулятор вычисления энергии электростатического поля заряженного конденсатора, позволит найти энергию заряженного конденсатора через напряжение, емкость и электрический заряд на одной из обкладок.
Калькулятор произведет вычисление и даст подробное решение. Единицы измерения, могут включать любые приставки Си. Калькулятор автоматически переведет одни единицы в другие.
Калькулятор вычислит:
Энергию заряженного конденсатора через напряжение (разность потенциалов), до которого заряжен конденсатор и емкость.
Энергию заряженного конденсатора через электрический заряд на одной из обкладок и емкость
Так же для вычисления энергии электростатического поля плоского, цилиндрического и сферического конденсаторов, можно воспользоваться калькулятором вычисления энергии заряженного конденсатора для плоского, цилиндрического и сферического конденсаторов.
Энергия заряженного конденсатора через напряжение (разность потенциалов), до которого заряжен конденсатор и емкость
Энергия заряженного конденсатора через напряжение (разность потенциалов), до которого заряжен конденсатор и емкость определяется формулой, где C — емкость конденсатора Единицей измерения энергии является — Джоуль (Дж, J). Механика Оптика Электричество и магнетизм Конденсаторы Содержание: Мы уже знаем, что конденсатор используется для хранения энергии. В этом модуле мы обсудим, сколько энергии может храниться в конденсаторе, параметры, от которых зависит накопленная энергия, и их соотношение. Необходимо совершить работу по переносу зарядов на проводник против силы отталкивания от уже имеющихся на нем зарядов. Эта работа, совершаемая для заряда от одной пластины к другой, запасается в виде потенциальной энергии электрического поля проводника. Предположим, что заряд переносится с пластины B на A. В данный момент заряд на пластинах равен Q’ и –Q’. Затем, чтобы передать заряд dQ’ от B к A. Работа, совершенная внешней силой, будет равна
U — напряжение (разность потенциалов), до которого заряжен конденсатор
-24]Вам могут также быть полезны следующие сервисы Калькуляторы (физика) Калькулятор вычисления скорости, времени и расстояния Калькулятор вычисления ускорения, скорости и перемещения Калькулятор вычисления времени движения Калькулятор времени Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. Импульс тела. Калькулятор вычисления импульса, массы и скорости Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения Калькулятор отражения и преломления света Калькулятор Закона Ома Калькулятор Закона Кулона Калькулятор напряженности E электрического поля Калькулятор нахождения точечного электрического заряда Q Калькулятор нахождения силы F действующей на заряд q Калькулятор вычисления расстояния r от заряда q Калькулятор вычисления потенциальной энергии W заряда q Калькулятор вычисления потенциала φ электростатического поля Калькулятор вычисления электроемкости C проводника и сферы Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе Калькулятор вычисления энергии W заряженного конденсатора
Калькулятор вычисления энергии W заряженного конденсатора. 
Для плоского, цилиндрического и сферического конденсаторов
Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов Калькуляторы по астрономии Вес тела на других планетах Ускорение свободного падения на планетах Солнечной системы и их спутниках Конвертеры величин Конвертер единиц длины Конвертер единиц скорости Конвертер единиц ускорения Цифры в текст Калькуляторы (Теория чисел) Калькулятор выражений Калькулятор упрощения выражений Калькулятор со скобками Калькулятор уравнений Калькулятор суммы Калькулятор пределов функций Калькулятор разложения числа на простые множители Калькулятор НОД и НОК Калькулятор НОД и НОК по алгоритму Евклида Калькулятор НОД и НОК для любого количества чисел Калькулятор делителей числа Представление многозначных чисел в виде суммы разрядных слагаемых Калькулятор деления числа в данном отношении Калькулятор процентов Калькулятор перевода числа с Е в десятичное Калькулятор экспоненциальной записи чисел Калькулятор нахождения факториала числа Калькулятор нахождения логарифма числа Калькулятор квадратных уравнений Калькулятор остатка от деления Калькулятор корней с решением Калькулятор нахождения периода десятичной дроби Калькулятор больших чисел Калькулятор округления числа Калькулятор свойств корней и степеней Калькулятор комплексных чисел Калькулятор среднего арифметического Калькулятор арифметической прогрессии Калькулятор геометрической прогрессии Калькулятор модуля числа Калькулятор абсолютной погрешности приближения Калькулятор абсолютной погрешности Калькулятор относительной погрешности Дроби Калькулятор интервальных повторений Учим дроби наглядно Калькулятор сокращения дробей Калькулятор преобразования неправильной дроби в смешанную Калькулятор преобразования смешанной дроби в неправильную Калькулятор сложения, вычитания, умножения и деления дробей Калькулятор возведения дроби в степень Калькулятор перевода десятичной дроби в обыкновенную Калькулятор перевода обыкновенной дроби в десятичную Калькулятор сравнения дробей Калькулятор приведения дробей к общему знаменателю Калькуляторы (тригонометрия) Калькулятор синуса угла Калькулятор косинуса угла Калькулятор тангенса угла Калькулятор котангенса угла Калькулятор секанса угла Калькулятор косеканса угла Калькулятор арксинуса угла Калькулятор арккосинуса угла Калькулятор арктангенса угла Калькулятор арккотангенса угла Калькулятор арксеканса угла Калькулятор арккосеканса угла Калькулятор нахождения наименьшего угла Калькулятор определения вида угла Калькулятор смежных углов Калькуляторы систем счисления Калькулятор перевода чисел из арабских в римские и из римских в арабские Калькулятор перевода чисел в различные системы счисления Калькулятор сложения, вычитания, умножения и деления двоичных чисел Системы счисления теория N2 | Двоичная система счисления N3 | Троичная система счисления N4 | Четырехичная система счисления N5 | Пятеричная система счисления N6 | Шестеричная система счисления N7 | Семеричная система счисления N8 | Восьмеричная система счисления N9 | Девятеричная система счисления N11 | Одиннадцатиричная система счисления N12 | Двенадцатеричная система счисления N13 | Тринадцатеричная система счисления N14 | Четырнадцатеричная система счисления N15 | Пятнадцатеричная система счисления N16 | Шестнадцатеричная система счисления N17 | Семнадцатеричная система счисления N18 | Восемнадцатеричная система счисления N19 | Девятнадцатеричная система счисления N20 | Двадцатеричная система счисления N21 | Двадцатиодноричная система счисления N22 | Двадцатидвухричная система счисления N23 | Двадцатитрехричная система счисления N24 | Двадцатичетырехричная система счисления N25 | Двадцатипятеричная система счисления N26 | Двадцатишестеричная система счисления N27 | Двадцатисемеричная система счисления N28 | Двадцативосьмеричная система счисления N29 | Двадцатидевятиричная система счисления N30 | Тридцатиричная система счисления N31 | Тридцатиодноричная система счисления N32 | Тридцатидвухричная система счисления N33 | Тридцатитрехричная система счисления N34 | Тридцатичетырехричная система счисления N35 | Тридцатипятиричная система счисления N36 | Тридцатишестиричная система счисления Калькуляторы площади геометрических фигур Площадь квадрата Площадь прямоугольника КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ Калькуляторы (Комбинаторика) Калькулятор нахождения числа перестановок из n элементов Калькулятор нахождения числа сочетаний из n элементов Калькулятор нахождения числа размещений из n элементов Калькуляторы линейная алгебра и аналитическая геометрия Калькулятор сложения и вычитания матриц Калькулятор умножения матриц Калькулятор транспонирование матрицы Калькулятор нахождения определителя (детерминанта) матрицы Калькулятор нахождения обратной матрицы Длина отрезка. 
Онлайн калькулятор расстояния между точками Онлайн калькулятор нахождения координат вектора по двум точкам Калькулятор нахождения модуля (длины) вектора Калькулятор сложения и вычитания векторов Калькулятор скалярного произведения векторов через длину и косинус угла между векторами Калькулятор скалярного произведения векторов через координаты Калькулятор векторного произведения векторов через координаты Калькулятор смешанного произведения векторов Калькулятор умножения вектора на число Калькулятор нахождения угла между векторами Калькулятор проверки коллинеарности векторов Калькулятор проверки компланарности векторов Генератор Pdf с примерами Тренажёры решения примеров Тренажёр таблицы умножения Тренажер счета для дошкольников Тренажер счета на внимательность для дошкольников Тренажер решения примеров на сложение, вычитание, умножение, деление. 
Найди правильный ответ. Тренажер решения примеров с разными действиями Тренажёры решения столбиком Тренажёр сложения столбиком Тренажёр вычитания столбиком Тренажёр умножения столбиком Тренажёр деления столбиком с остатком Калькуляторы решения столбиком Калькулятор сложения, вычитания, умножения и деления столбиком Калькулятор деления столбиком с остатком Генераторы Генератор примеров по математике Генератор случайных чисел Генератор паролей Энергия, запасенная в конденсаторе
Как рассчитать энергию, запасенную в конденсаторе?
Проблемы с энергией, запасенной в конденсаторе
Проблема 1: Батарея на 20 В подключена к 3 конденсаторам последовательно, как показано на рисунке. Два конденсатора по 20 мкФ и один по 10 мкФ. Рассчитайте энергию, запасенную в конденсаторах в установившемся режиме.
Соль:
\(\begin{array}{l}\frac{1}{{{C}_{eff}}}=\frac{1}{20}+\frac{1}{20}+\frac{1 }{10}=\frac{4}{20}=\frac{1}{5}\end{массив} \) 9{-3}}J\конец{массив} \)
Задача 2: Конденсатор с плоскими пластинами имеет пластины площадью 4 м 2 , разделенные расстоянием 0,5 мм.
Конденсатор подключен через ячейку ЭДС 100 вольт. Найти емкость, заряд и энергию, запасенные в конденсаторе, если внутрь этого конденсатора после отсоединения от ячейки вставить диэлектрическую пластину с диэлектрической проницаемостью k = 3 и толщиной 0,5 мм.
Sol: Если конденсатор без диэлектрика 9{-6}}J\конец{массив} \)
Вас также может заинтересовать:
- ХК Верма Солюшнс
- Решения HC Verma, часть 1
- Решения HC Verma, часть 2
Электростатический потенциал и емкость
Часто задаваемые вопросы об энергии, хранящейся в конденсаторе
Q1
Накопляется ли энергия в конденсаторе?
В конденсаторе энергия накапливается в пространстве между двумя пластинами.
Q2
Какой вид энергии хранится в конденсаторе?
Электростатическая потенциальная энергия накапливается в конденсаторе. Таким образом, это связано с зарядом и напряжением между пластинами конденсатора.
Q3
Где хранится энергия в конденсаторе?
При отключении заряженного конденсатора от батареи его энергия остается в поле в пространстве между его пластинами.
Q4
Как увеличить энергию, запасенную в конденсаторе?
Энергия конденсатора зависит от емкости и напряжения конденсатора. Если емкость, напряжение или и то и другое увеличиваются, энергия, хранящаяся в конденсаторе, также увеличивается. Между пластинами конденсатора можно добавить диэлектрическую пластину, чтобы увеличить емкость конденсатора.
Capacitor Energy — AP Physics 2
Все ресурсы AP Physics 2
6 Диагностические тесты 149 практических тестов Вопрос дня Карточки Учитесь по концепции
AP Физика 2 Справка » Электричество и магнетизм » Схемы » Компоненты схемы » Энергия конденсатора
Рассмотрим схему:
Если падение напряжения на C2 равно 5 В, какова общая энергия, накопленная в C2 и C3?
Возможные ответы:
Правильный ответ:
Пояснение:
В параллельных ветвях цепи падения напряжения одинаковы.
Следовательно, мы знаем, что падение напряжения на C3 также равно 5В.
Затем мы можем использовать следующее уравнение для расчета общей накопленной энергии:
Поскольку напряжение обоих конденсаторов одинаково, мы можем просто сложить две емкости, чтобы сделать один расчет энергии:
Отчет Ошибка
Конденсатор подключен к аккумулятору. Когда конденсатор полностью заряжен, сколько энергии запасается?
Возможные ответы:
Ни один из других ответов не правильный
Правильный ответ:
Пояснение:
Чтобы найти количество энергии, хранящейся в конденсаторе, мы используем уравнение
.
Нам известны емкость () и напряжение (), поэтому воспользуемся третьим уравнением.
Сообщить об ошибке
У вас есть 4 конденсатора, , , , и , , расположенные, как показано на схеме ниже.
Их емкости следующие:
Если к цепи подключена батарея на 6 В, какая общая энергия сохраняется в конденсаторах?
Возможные ответы:
Правильный ответ:
Объяснение:
Уравнение для энергии, запасенной в конденсаторе, выглядит так:
При добавлении конденсаторов помните, как добавлять последовательно и параллельно.
Конденсаторы и соединены последовательно, и соединены параллельно, и и соединены параллельно.
Теперь, когда у нас есть уравнение полной емкости, мы можем найти уравнение полной емкости.
Суммарная накопленная энергия составляет 121,5 Дж.
Сообщить об ошибке
Если , и , сколько энергии хранится в ?
Возможные ответы:
Правильный ответ:
Объяснение:
В этой цепи источник напряжения, и , и параллельны, то есть имеют одинаковое напряжение.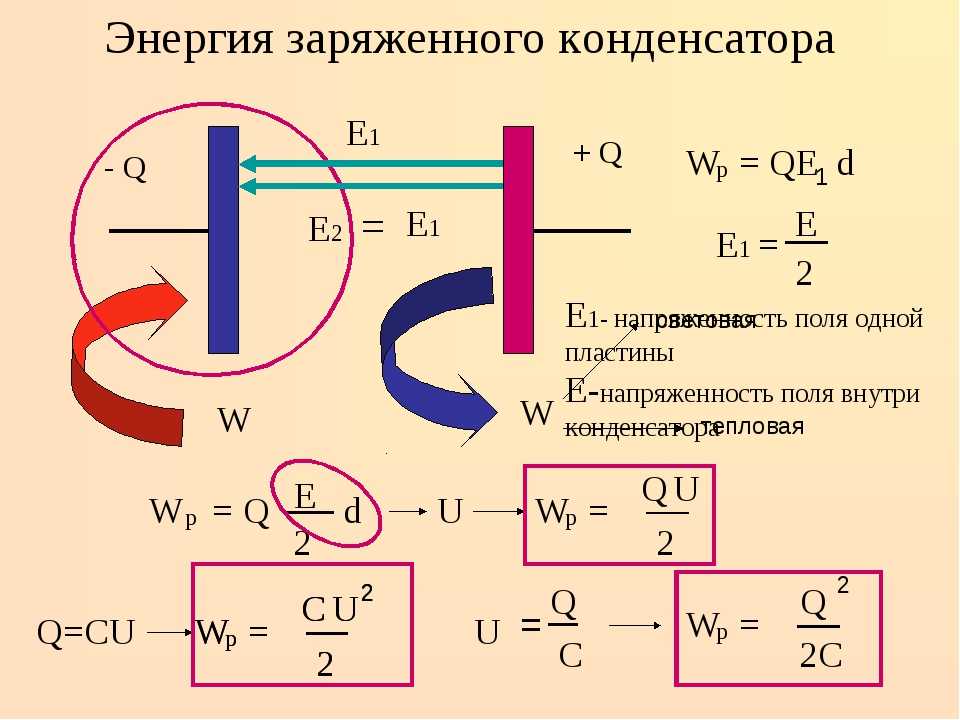
Чтобы найти энергию, мы можем использовать формулу
, где это энергия, это емкость и это падение напряжения на этом конденсаторе.
Чтобы использовать формулу, нам нужно напряжение на .
Еще одна подсказка, которую мы можем использовать, заключается в том, что и имеют одинаковый заряд, поскольку они соединены последовательно. Сначала найдем эквивалентную емкость:
Теперь мы можем использовать формулу
для расчета заряда конденсатора.
Теперь, когда мы знаем, что в обоих конденсаторах имеется заряд , мы можем снова использовать формулу, чтобы найти напряжение только в .
Наконец, мы подставляем это в первое уравнение для расчета энергии.
Сообщить об ошибке
Представьте конденсатор с величиной заряда Q на каждой пластине. Этот конденсатор имеет площадь A, разделительное расстояние D и не подключен к батарее. Если какое-то внешнее воздействие разорвет конденсатор так, что D удвоится, увеличится, уменьшится или останется неизменной внутренняя энергия U, хранящаяся в конденсаторе?
Возможные ответы:
Остается постоянной
Увеличивается
Уменьшается
Мы должны знать диэлектрическую проницаемость
Правильный ответ:
Увеличивается
Объяснение:
Необходимые уравнения:
Из первого уравнения видно, что при удвоении D C уменьшится вдвое (поскольку и постоянны).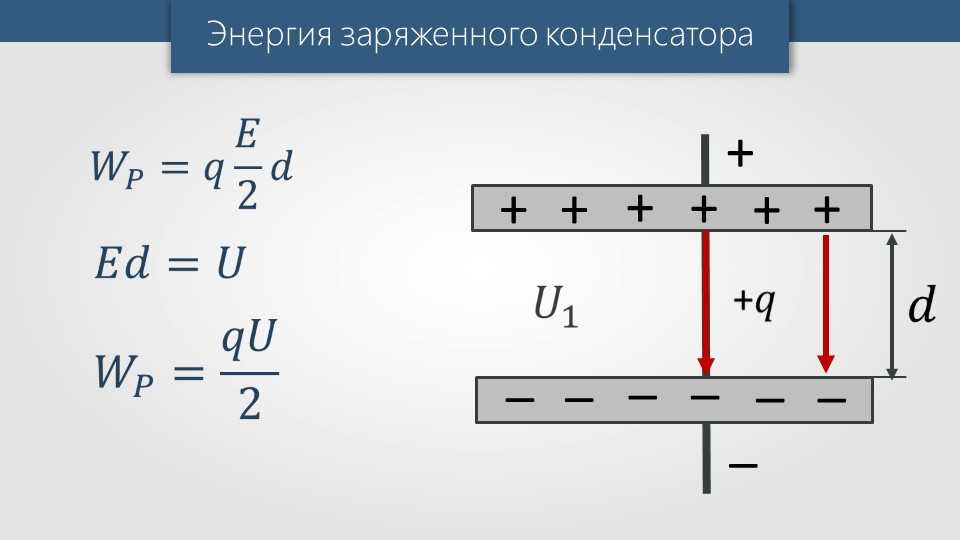
Из третьего уравнения мы исходим из того, что при уменьшении C вдвое потенциальная энергия U удвоится.
Сообщить об ошибке
Представьте конденсатор с величиной заряда Q на каждой пластине. Этот конденсатор имеет площадь A, разделительное расстояние D и подключен к батарее с напряжением V. Если какое-то внешнее воздействие разъединит конденсатор, так что D удвоится, внутренняя энергия U, хранящаяся в конденсаторе, увеличится, уменьшится или останется на прежнем уровне? такой же?
Возможные ответы:
Увеличивается ровно в 2 раза
Остается постоянным
Уменьшается
Увеличивается
Правильный ответ: 9001 0 5
5 Уменьшается 49 Объяснение:
Соответствующие уравнения:
В этой задаче мы должны отметить, что напряжение V поддерживается батареей постоянным. Глядя на второе уравнение, если C изменяется (за счет изменения D), то Q должен измениться, когда V поддерживается постоянным.
