Трёхфазная система электроснабжения — Википедия

Трёхфазная система электроснабжения — частный случай многофазных систем электрических цепей переменного тока, в которых действуют созданные общим источником синусоидальные ЭДС одинаковой частоты, сдвинутые друг относительно друга во времени на определённый фазовый угол. В трёхфазной системе этот угол равен 2π/3 (120°).

Многопроводная (шестипроводная) трёхфазная система переменного тока изобретена Николой Теслой. Значительный вклад в развитие трёхфазных систем внёс М. О. Доливо-Добровольский, который впервые предложил трёх- и четырёхпроводную системы передачи переменного тока, выявил ряд преимуществ малопроводных трёхфазных систем по отношению к другим системам и провёл ряд экспериментов с асинхронным электродвигателем.

Каждая из действующих ЭДС находится в своей фазе периодического процесса, поэтому часто называется просто «фазой». Также «фазами» называют проводники — носители этих ЭДС. В трёхфазных системах угол сдвига равен 120 градусам. Фазные проводники обозначаются в РФ латинскими буквами L с цифровым индексом 1…3, либо A, B и C

[1].

Распространённые обозначения фазных проводов:

Россия, EC (выше 1000 В)	Россия, ЕС (ниже 1000 В)	Германия	Дания
А	L1	L1	R
B	L2	L2	S
C	L3	L3	T

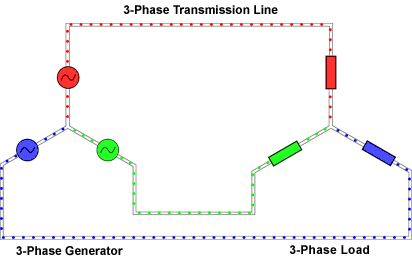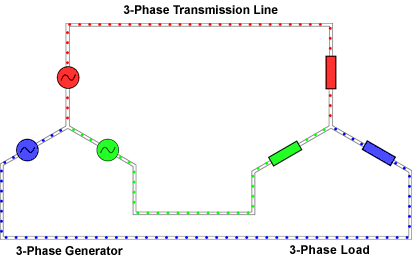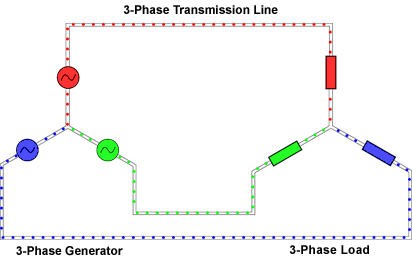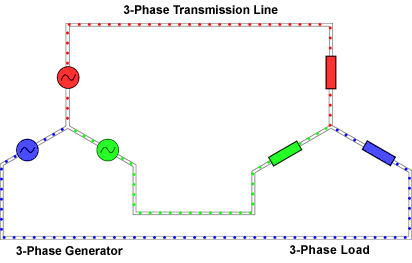Анимированное изображение течения токов по симметричной трёхфазной цепи с соединением типа «звезда»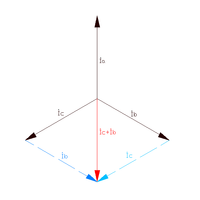

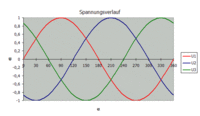Векторная диаграмма фазных токов. Симметричный режим. Графическое представление зависимости фазных токов от времени 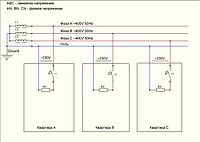Возможная схема разводки трёхфазной сети в многоквартирных жилых домах

• Экономичность.
  • Экономичность передачи электроэнергии на значительные расстояния.
  • Меньшая материалоёмкость 3-фазных трансформаторов.
  • Меньшая материалоёмкость силовых кабелей, так как при одинаковой потребляемой мощности снижаются токи в фазах (по сравнению с однофазными цепями).
• Уравновешенность системы. Это свойство является одним из важнейших, так как в неуравновешенной системе возникает неравномерная механическая нагрузка на энергогенерирующую установку, что значительно снижает срок её службы.
• Возможность простого получения кругового вращающегося магнитного поля, необходимого для работы электрического двигателя и ряда других электротехнических устройств. Двигатели 3-фазного тока (асинхронные и синхронные) устроены проще, чем двигатели постоянного тока, одно- или 2-фазные, и имеют высокие показатели экономичности.
• Возможность получения в одной установке двух рабочих напряжений — фазного и линейного, и двух уровней мощности при соединении на «звезду» или «треугольник».
• Возможность резкого уменьшения мерцания и стробоскопического эффекта светильников на люминесцентных лампах путём размещения в одном светильнике трёх ламп (или групп ламп), питающихся от разных фаз.

Благодаря этим преимуществам, трёхфазные системы наиболее распространены в современной электроэнергетике.

Звезда[править | править код]

Звездой называется такое соединение, когда концы фаз обмоток генератора (G) соединяют в одну общую точку, называемую нейтральной точкой или нейтралью. Концы фаз обмоток потребителя (M) также соединяют в общую точку.

Провода, соединяющие начала фаз генератора и потребителя, называются линейными. Провод, соединяющий две нейтрали, называется нейтральным.

Трёхфазная цепь, имеющая нейтральный провод, называется четырёхпроводной. Если нейтрального провода нет — трёхпроводной.

Если сопротивления Za, Zb, Zc потребителя равны между собой, то такую нагрузку называют симметричной.

Линейные и фазные величины[править | править код]

Напряжение между фазным проводом и нейтралью (Ua, Ub, Uc) называется фазным. Напряжение между двумя фазными проводами (UAB, UBC, UCA

) называется линейным. Для соединения обмоток звездой, при симметричной нагрузке, справедливо соотношение между линейными и фазными токами и напряжениями:

IL=IF;UL=3×UF{\displaystyle I_{L}=I_{F};\qquad U_{L}={\sqrt {3}}\times {U_{F}}}

Несложно показать, что линейное напряжение сдвинуто по фазе на π/6{\displaystyle \pi /6} относительно фазных:

uLab=uFa−uFb=UF[cos⁡(ωt)−cos⁡(ωt−2π/3)]=2UFsin⁡(−π/3)sin⁡(ωt−π/3)=3UFcos⁡(ωt+π−π/3−π/2){\displaystyle u_{L}^{ab}=u_{F}^{a}-u_{F}^{b}=U_{F}[\cos(\omega t)-\cos(\omega t-2\pi /3)]=2U_{F}\sin(-\pi /3)\sin(\omega t-\pi /3)={\sqrt {3}}U_{F}\cos(\omega t+\pi -\pi /3-\pi /2)}

uL=3UFcos⁡(ωt+π/6){\displaystyle u_{L}={\sqrt {3}}U_{F}\cos(\omega t+\pi /6)}

Мощность трёхфазного тока[править | править код]

Для соединения обмоток звездой, при симметричной нагрузке, мощность трёхфазной сети равна P=3UFIFcosφ=3UL3ILcosφ=3ULILcosφ{\displaystyle P=3U_{F}I_{F}cos\varphi =3{\frac {U_{L}}{\sqrt {3}}}I_{L}cos\varphi ={\sqrt {3}}U_{L}I_{L}cos\varphi }

Последствия отгорания (обрыва) нулевого провода в трёхфазных сетях[править | править код]

Существующие виды защиты от линейного напряжения, которые можно найти в продаже в электротехнических магазинах Шины для раздачи нулевых проводов (синяя) и проводов заземления (зелёная)

При симметричной нагрузке в трёхфазной системе питание потребителя линейным напряжением возможно даже при отсутствии нейтрального провода. Несмотря на это, при питании нагрузки фазным напряжением, когда нагрузка на фазы не является строго симметричной, наличие нейтрального провода обязательно. При его обрыве или значительном увеличении сопротивления (плохом контакте) происходит так называемый перекос фаз, в результате которого подключенная нагрузка, рассчитанная на фазное напряжение, может оказаться под произвольным напряжением в диапазоне от нуля до линейного (конкретное значение зависит от распределения нагрузки по фазам в момент обрыва нулевого провода). Это зачастую является причиной выхода из строя бытовой электроники в квартирных домах, который может приводить к пожарам. Пониженное напряжение также может послужить причиной выхода из строя техники.

Проблема гармоник, кратных третьей[править | править код]

Современная техника всё чаще оснащается импульсными сетевыми источниками питания. Импульсный источник без корректора коэффициента мощности потребляет ток узкими импульсами вблизи пиков синусоиды питающего напряжения на интервалах зарядки конденсатора входного выпрямителя. Большое количество таких источников питания в сети создаёт повышенный ток третьей гармоники питающего напряжения. Токи гармоник, кратных третьей, вместо взаимной компенсации, математически суммируются в нейтральном проводнике (даже при симметричном распределении нагрузки) и могут привести к его перегрузке даже без превышения допустимой мощности потребления по фазам. Такая проблема существует, в частности, в офисных зданиях с большим количеством одновременно работающей оргтехники. Решением проблемы третьей гармоники является применение корректора коэффициента мощности (пассивного или активного) в составе схемы производимых импульсных источников питания. Требования стандарта IEC 1000-3-2 накладывают ограничения на гармонические составляющие тока нагрузки устройств мощностью от 50 Вт. В России количество гармонических составляющих тока нагрузки нормируется стандартами ГОСТ Р 54149-2010, ГОСТ 32144-2013 (с 1.07.2014), ОСТ 45.188-2001.

---

Треугольник[править | править код]

Треугольник — такое соединение, когда конец первой фазы соединяется с началом второй фазы, конец второй фазы с началом третьей, а конец третьей фазы соединяется с началом первой.

Соотношение между линейными и фазными токами и напряжениями[править | править код]

Для соединения обмоток треугольником, при симметричной нагрузке, справедливо соотношение между линейными и фазными токами и напряжениями:

IL=3×IF;UL=UF{\displaystyle I_{L}={\sqrt {3}}\times {I_{F}};\qquad U_{L}=U_{F}}

Мощность трёхфазного тока при соединении треугольником[править | править код]

Для соединения обмоток треугольником, при симметричной нагрузке, мощность трёхфазного тока равна:

P=3UFIFcosφ=3ULIL3cosφ=3ULILcosφ{\displaystyle P=3U_{F}I_{F}cos\varphi =3U_{L}{\frac {I_{L}}{\sqrt {3}}}cos\varphi ={\sqrt {3}}U_{L}I_{L}cos\varphi }

Распространённые стандарты напряжений[править | править код]

Страна	Частота, Гц	Напряжение (фазное/линейное), Вольт
Россия [2]	50	220/230 [3] (бытовые сети) 230/400, 380/660, 400/690, 380, 400, 220/380, 3000, 6000, 10000 (промышленные сети)[источник не указан 544 дня]
Страны ЕС	50	230/400, 400/690 (промышленные сети) 660 450
Япония	50 (60)	120/208
США	60	120/208, 277/480 240 (только треугольник)

Проводники, принадлежащие разным фазам, маркируют разными цветами. Разными цветами маркируют также нейтральный и защитный проводники. Это делается для обеспечения надлежащей защиты от поражения электрическим током, а также для удобства обслуживания, монтажа и ремонта электрических установок и электрического оборудования — фазировка (чередование фаз, то есть очерёдность протекания токов по фазам) принципиальна, так как от неё зависит направление вращения трёхфазных двигателей, правильная работа управляемых трёхфазных выпрямителей и некоторых других устройств. В разных странах маркировка проводников имеет свои различия, однако многие страны придерживаются общих принципов цветовой маркировки проводников, изложенных в стандарте Международной Электротехнической Комиссии МЭК 60445:2010.

Трёхфазная двухцепная линия электропередачи

Цвета фаз[править | править код]

Каждая фаза в трёхфазной системе имеет свой цвет. Он меняется в зависимости от страны. Используются цвета международного стандарта IEC 60446 (IEC 60445).

Страна	L1	L2	L3	Нейтраль / ноль	Земля / защитное заземление
Россия, Белоруссия, Украина, Казахстан (до 2009), Китай	Белый	Черный	Красный	Голубой	Жёлто/зелёный (в полоску)
Европейский союз и все страны которые используют европейский стандарт CENELEC с апреля 2004 (IEC 60446), Гонконг с июля 2007, Сингапур с марта 2009, Украина, Казахстан с 2009, Аргентина, Россия с 2009	Коричневый	Чёрный	Серый	Голубой	Жёлто/зелёный (в полоску)[4]
Европейский союз до апреля 2004[5]	Красный	Жёлтый	Голубой	Чёрный	Жёлто/зелёный (в полоску) (зелёный в установках до 1970)
Индия, Пакистан, Великобритания до апреля 2006, Гонконг до апреля 2009, ЮАР, Малайзия, Сингапур до февраля 2011	Красный	Жёлтый	Голубой	Чёрный	Жёлто/зелёный (в полоску) (зелёный в установках до 1970)
Австралия и Новая Зеландия	Красный (или коричневый)[6]	Белый (или чёрный) (ранее — жёлтый)	Тёмно синий (или серый)	Чёрный (или голубой)	Жёлто/зелёный (в полоску) (зелёный в очень старых установках)
Канада (обязательный)[7]	Красный	Чёрный	Голубой	Белый или серый	Зелёный или цвета меди
Канада (в изолированных трехфазных установках)[8]	Оранжевый	Коричневый	Жёлтый	Белый	Зелёный
США (альтернативная практика)[9]	Коричневый	Оранжевый (в системе треугольник), или фиолетовый (в системе звезда)	Жёлтый	Серый или белый	Зелёный
США (распространённая практика)[10]	Чёрный	Красный	Голубой	Белый или серый	Зелёный, жёлто/зелёный (в полоску),[11] или провод цвета меди
Норвегия	Чёрный	Белый/серый	Коричневый	Голубой	Жёлто/зелёный (в полоску), в более старых установках может встречаться только жёлтый или цвета меди

1. ↑ Действующий в РФ ГОСТ 2.709-89 предписывает обозначение цепей фазных проводников трёхфазного переменного тока: L1, L2, L3, и при этом допускает обозначения A, B, C.
2. ↑ Согласно ГОСТ 29322-2014
3. ↑ Согласно ГОСТ 29322-2014
4. ↑ Жёлто-зелёная маркировка была принята как международный стандарт для защиты от поражения эл.током дальтоников. От 7 % до 10 % людей не могут точно распознать красный и зелёные цвета.
5. ↑ В Европе ещё осталось много установок со старой цветовой схемой начала 1970-х. В новых установках используются жёлто/зелёные шины заземления в соответствии с IEC 60446. (Фаза/ноль+земля; Германия: чёрный/серый + красный; Франция зелёный/красный + белый; Россия: красный/серый + чёрный; Швейцария: красныйd/серый + жёлтый или жёлтый и красный; Дания: белый/чёрный + красный
6. ↑ В Австралии и Новой Зеландии фазы могут быть люього цвета, но только не жёлто-зелёного, зелёного, жёлтого, чёрного или голубого цвета.
7. ↑ Canadian Electrical Code Part I, 23rd Edition, (2002) ISBN 1-55324-690-X, rule 4-036 (3)
8. ↑ Canadian Electrical Code (англ.)русск. 23-е издание 2002 года, правила 24-208(c)
9. ↑ Начиная с 1975 в США National Electric Code (англ.)русск. не имел специальных обозначений фаз. По сложившейся практике для соединения звезда 120/208 фазы маркировались чёрным, красным и голубым цветом, а при соединении звезда или треугольник 277/480 фазы обозначались коричневым, оранжевым и жёлтым. В системе 120/240 треугольник с наибольшим напряжением 208 вольт (обычно фаза B) всегда обозначалась оранжевым, общая фаза A была чёрного цвета, а фаза C — красной или голубой.
10. ↑ See Paul Cook: Harmonised colours and alphanumeric marking Архивная копия от 4 марта 2016 на Wayback Machine. IEE Wiring Matters, Spring 2006.
11. ↑ В США провод жёлто-зелёного цвета (в полоску) может обозначать изолированную землю^{[неизвестный термин]}. Сегодня в большинстве стран, жёлто-зелёные (в полоску) провода используются для защитного заземления и не могут быть отсоеденины и использованы для других целей.

Переменный ток Википедия

     Синусоидальный Три примера переменных токов:      Синусоидальный ток      Пульсирующий ток, снимаемый с двух полуколец генератора постоянного тока      Выпрямленный и сглаженный ток, снимаемый с якоря генератора постоянного тока с большим количеством контуров и коллекторных пластин

Переме́нный ток — электрический ток, который с течением времени изменяется по величине и направлению или, в частном случае, изменяется по величине, сохраняя своё направление в электрической цепи неизменным^[1].

Хотя переменный ток часто переводят на английский как alternating current, эти термины не эквивалентны. Термин alternating current (AC) в узком смысле означает синусоидальный ток, в широком смысле — периодический знакопеременный ток (то есть периодический двунаправленный ток). Условное обозначение на электроприборах: ∼{\displaystyle \thicksim } или ≈{\displaystyle \thickapprox } (знак синусоиды), или латинскими буквами AC{\displaystyle AC}.

Содержание

• 1 Общее понятие о переменном токе
• 2 Периодический переменный ток
  • 2.1 Стандарты частоты
• 3 Переменный синусоидальный ток
• 4 Многофазный переменный ток
  • 4.1 Трёхфазный ток
  • 4.2 Двухфазный ток
• 5 Действующее значение переменного синусоидального тока
• 6 Генерирование переменного тока
  • 6.1 Инверторы
  • 6.2 Фазорасщепитель
• 7 Сети переменного тока
• 8 Электрификация железных дорог на переменном токе
• 9 См. также
• 10 Примечания
• 11 Ссылки

Общее понятие о переменном токе[ |

Переменный ток — Википедия

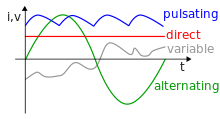     Постоянный ток Три примера переменных токов:      Синусоидальный ток      Пульсирующий ток, форма импульсов близка к пилообразной      Случайно изменяющийся ток

Переме́нный ток  — электрический ток, который с течением времени изменяется по величине и направлению или, в частном случае, изменяется по величине, сохраняя своё направление в электрической цепи неизменным^[1].

Хотя переменный ток часто переводят на английский как alternating current, эти термины не являются эквивалентными. Термин alternating current (AC) в узком смысле означает синусоидальный ток, в широком смысле — периодический знакопеременный ток (то есть периодический двунаправленный ток). Условное обозначение на электроприборах: ∼{\displaystyle \thicksim } или ≈{\displaystyle \thickapprox } (знак синусоиды), или латинскими буквами AC{\displaystyle AC}.

Общее понятие о переменном токе

Так как переменный ток в общем случае меняется в электрической цепи не только по величине, но и по направлению, то одно из направлений переменного тока в цепи считают условно положительным, а другое, противоположное первому, условно отрицательным. В соответствии с этим и величину мгновенного значения переменного тока в первом случае считают положительной, а во втором случае — отрицательной.

Переменный ток — величина алгебраическая, знак его определяется тем, в каком направлении в рассматриваемый момент времени протекает ток в цепи — в положительном или отрицательном.

Величина переменного тока, соответствующая данному моменту времени, называется мгновенным значением переменного тока.

Максимальное мгновенное значение переменного тока, которое он достигает в процессе своего изменения, называется амплитудой тока Im{\displaystyle I_{m}}.

График зависимости переменного тока от времени называется развёрнутой диаграммой переменного тока.

Развёрнутая диаграмма переменного синусоидального тока

На рисунке приведена развёрнутая диаграмма переменного тока, изменяющегося с течением времени по величине и направлению. На горизонтальной оси 0t{\displaystyle 0t} отложены в определённом масштабе отрезки времени, а по вертикальной оси — величины тока, вверх — от начальной точки 0{\displaystyle 0} — положительные, вниз — отрицательные. Часть развёрнутой диаграммы тока, расположенная выше оси времени 0t{\displaystyle 0t}, характеризует изменение положительных величин во времени, а часть, расположенная ниже оси времени 0t{\displaystyle 0t}, — изменение отрицательных величин.

В начальный момент времени t=0{\displaystyle t=0} ток равен нулю (i=0){\displaystyle (i=0)}. Затем он с течением времени растёт в положительном направлении, в момент времени t=T4{\displaystyle t={\frac {T}{4}}} достигает максимального значения, после чего убывает по величине и в момент времени t=T2{\displaystyle t={\frac {T}{2}}} становится равным нулю. Затем, пройдя через нулевое значение, ток меняет свой знак на противоположный, то есть становится отрицательным, затем растёт по абсолютной величине, затем достигает максимума при t=34T{\displaystyle t={\frac {3}{4}}T}, после чего убывает и при t=T{\displaystyle t=T} становится равным нулю.

Видео по теме

Периодический переменный ток

Развёрнутая диаграмма периодического переменного тока

Периодическим переменным током называется такой электрический ток, который через равные промежутки времени повторяет полный цикл своих изменений, возвращаясь к своей исходной величине.

На представленной диаграмме мы видим, что через равные промежутки времени T{\displaystyle T} график тока воспроизводится полностью без каких-либо изменений.

Время T{\displaystyle T}, в течение которого переменный периодический ток совершает полный цикл своих изменений, возвращаясь к своей исходной величине, называется периодом переменного тока.

Величина, обратная периоду, называется частотой переменного тока:

f=1T{\displaystyle f={\frac {1}{T}}}, где

f{\displaystyle f} — частота переменного тока;

T{\displaystyle T} — период переменного тока.

Если выразить время T{\displaystyle T} в секундах (sec), то будем иметь:

f=1T[1sec]{\displaystyle f={\frac {1}{T}}\left[{\frac {1}{sec}}\right]}, то есть размерность частоты переменного тока выражается в 1/с..

Частота переменного тока численно равна числу периодов в секунду.

За единицу измерения частоты переменного тока принят 1 герц (1 гц, 1 Гц, 1 Hz).

Герц — единица Международной системы единиц (СИ), названа в честь Генриха Герца. Через основные единицы СИ герц выражается следующим образом: 1 Гц = 1 с⁻¹. Десятичные кратные и дольные единицы образуют с помощью стандартных приставок СИ.

Частота переменного тока равна одному герцу, если период тока равен одной секунде (один полный цикл за одну секунду).

Стандарты частоты

В большинстве стран в электротехнике применяются частоты 50 или 60 Гц (60 Гц — этот вариант принят в США и Канаде). В некоторых странах, например, в Японии, используются оба стандарта (см. Промышленная частота переменного тока).

Частота 16 ⅔ Гц до сих пор используется в некоторых европейских железнодорожных сетях (Австрия, Германия, Норвегия, Швеция и Швейцария), частота 25 Гц — на старых железнодорожных линиях США. (См. Электрификация железных дорог переменным током пониженной частоты).

В авиации и военной технике для снижения массы устройств или с целью повышения частоты вращения электродвигателей переменного тока применяется частота 400 Гц.

Число оборотов

ЭСБЕ/Переменный ток — Викитека

Переменный ток. — Если какой-либо источник тока вызывает в данном проводнике или в данной замкнутой цепи электродвижущую силу и эта электродвижущая сила непрерывно изменяется по величине и по направлению, т. е. представляется периодической функцией времени, то в рассматриваемом проводнике или в рассматриваемой замкнутой цепи появляется электрический ток, сила которого и направление изменяются также непрерывно со временем. Такой ток и носит название П. тока. Возникновение такого тока в проводнике осложняется явлениями индукции. В самом деле, вследствие непрерывного изменения силы П. тока возбуждается в проводнике, в котором происходит этот ток, особая электродвижущая сила, происходящая: 1) от самоиндукции, т. е. от индукции самого данного проводника с П. током, и 2) от индукции на этот проводник других проводников, находящихся вблизи первого проводника, так как в таких проводниках возникают также П. токи от индуктивного действия на них рассматриваемого проводника с П. током. Итак, полная электродвижущая сила, возбуждающая в какой-либо момент времени в данном проводнике электрический ток, представляет собой сумму электродвижущей силы источника тока и всех других электродвижущих сил, возникающих вследствие индукции. Обозначая через Е электродвижущую силу источника тока, причем, по условию, Е выражается какой-либо периодической функцией времени f(t), через L коэффициент самоиндукции данного проводника (см. Самоиндукция), через i силу тока в этом проводнике, через M₁, M₂, … коэффициенты взаимной индукции данного проводника и других соседних с ним проводников, в которых силы токов суть i₁, i₂…, и пользуясь законами индукции токов, мы будем иметь для полной электродвижущей силы в данном проводнике выражение

E=E−Ldidt−M1di1dt−M2di2dt…{\displaystyle E=E-L{\frac {di}{dt}}-M_{1}{\frac {di_{1}}{dt}}-M_{2}{\frac {di_{2}}{dt}}…}

Обозначая сопротивление данного проводника через R, мы получаем по закону Ома для силы тока в этом проводнике выражение

i=E−Ldidt−M1di1dt−M2di2dt…R{\displaystyle i={\frac {E-L{\frac {di}{dt}}-M_{1}{\frac {di_{1}}{dt}}-M_{2}{\frac {di_{2}}{dt}}…}{R}}} . . . (1)

Положим, что вблизи данного проводника не имеется никаких других проводников. В этом случае мы имеем

i=E−LdidtR{\displaystyle i={\frac {E-L{\frac {di}{dt}}}{R}}} . . . . . (2)

Здесь по условию E = f(t), причем f(t) есть периодическая функция времени. Но по теореме Фурье всякая периодическая функция t может быть представлена в виде следующего ряда:

f(t)=A+E0sin⁡(2πtT−α)+E0′sin⁡(4πtT−α′)+E0″sin⁡(6πtT−α″)+…{\displaystyle f(t)=A+E_{0}\sin \left(2\pi {\frac {t}{T}}-\alpha \right)+E’_{0}\sin \left(4\pi {\frac {t}{T}}-\alpha ‘\right)+E»_{0}\sin \left(6\pi {\frac {t}{T}}-\alpha »\right)+…}

т. е. электродвижущая сила Е может быть рассматриваема как сумма постоянной электродвижущей силы А и электродвижущих сил, которые изменяются со временем по закону гармонического колебания (т. е. пропорционально синусам углов, непрерывно изменяющихся со временем) и которых периоды суть T, ½T, ⅓T…, а наибольшие величины суть Е₀, Е′₀, Е″₀ …, причем моменты, когда эти отдельные электродвижущие силы достигают своих наибольших величин или когда они обращаются в 0, различны, т. е. фазы этих электродвижущих сил неодинаковы. При таком характере электродвижущей силы E, действующей в проводнике, ток i, появляющийся в нем, может быть рассматриваем как ток, слагающийся из отдельных токов j, i₀, i′, i″…, которые возбуждаются в этом проводнике вследствие действия отдельных электродвижущих сил:

A, E0sin⁡(2πtT−α), E0′sin⁡(2πt12T−α′), E0″sin⁡(2πt13T−α″)…{\displaystyle A,\ E_{0}\sin \left(2\pi {\frac {t}{T}}-\alpha \right),\ E’_{0}\sin \left(2\pi {\frac {t}{{\frac {1}{2}}T}}-\alpha ‘\right),\ E»_{0}\sin \left(2\pi {\frac {t}{{\frac {1}{3}}T}}-\alpha »\right)…}

Наиболее простой и к тому же наиболее часто рассматриваемый в практике случай будет тот, когда электродвижущая сила, действующая в проводнике, выражается через

E=E0sin⁡2πtT{\displaystyle E=E_{0}\sin 2\pi {\frac {t}{T}}} . . . (3)

т. е. эта электродвижущая сила изменяется со временем гармонически. Такую электродвижущую силу представляет электродвижущая сила, которая вследствие индукции появляется в какой-либо катушке, приготовленной из изолированной проволоки и приводимой в однородном магнитном поле в равномерное вращение около оси, лежащей в плоскости какого-либо оборота этой катушки и не совпадающей с направлением силовых линий поля. Такая же электродвижущая сила возбуждается и многими динамо-машинами П. тока. В данном случае мы получаем из выражения для i следующее дифференциальное уравнение:

didt+RLi=E0Lsin⁡2πtT{\displaystyle {\frac {di}{dt}}+{\frac {R}{L}}i={\frac {E_{0}}{L}}\sin 2\pi {\frac {t}{T}}} . . . (4)

Интегрируя это уравнение и принимая во внимание, что при стационарном характере изменения величины электродвижущей силы и изменение силы тока должно быть также стационарного характера, получаем

i=E0sin⁡(2πtT−θ)R2+4π2L2T2{\displaystyle i={\frac {E_{0}\sin \left(2\pi {\frac {t}{T}}-\theta \right)}{\sqrt {R^{2}+{\frac {4\pi ^{2}L^{2}}{T^{2}}}}}}} . . . . (5),

причем tgθ=2πLTR{\displaystyle {\mbox{tg}}\,\theta ={\frac {2\pi L}{TR}}} . . . . (6)

или, обозначая через n число полных изменений электродвижущей силы в течение одной секунды, т. е. полагая n = t/T, имеем

i=E0sin⁡(2πnt−θ)R2+4π2n2L2{\displaystyle i={\frac {E_{0}\sin(2\pi nt-\theta )}{\sqrt {R^{2}+4\pi ^{2}n^{2}L^{2}}}}} . . . . (5′)

и tgθ=2πnLR{\displaystyle {\mbox{tg}}\,\theta ={\frac {2\pi nL}{R}}} . . . . (6′)

Полученное выражение для силы П. тока показывает, что продолжительность одного полного изменения силы этого тока (период этого тока) одинакова с продолжительностью одного полного изменения вызывающей этот ток электродвижущей силы Е. Но если только проводник, в котором является П. ток, не неиндуктивен, т. е. для этого проводника величина коэффициента самоиндукции L не равна 0, то развитие тока не совпадает по времени с развитием электродвижущей силы. В своем изменении ток запаздывает относительно электродвижущей силы. Между фазами электродвижущей силы и тока получается постоянная разность, выраженная через θ и удовлетворяющая равенству tgθ=2πnLR{\displaystyle {\mbox{tg}}\,\theta ={\frac {2\pi nL}{R}}}. Как видно из этой формулы, при большом числе перемен тока в единицу времени, при значительной величине L и малом сопротивлении R, разность фаз θ мало отличается от π2{\displaystyle {\frac {\pi }{2}}}, т. е. в тот момент, когда электродвижущая сила Е достигает своей наибольшей величины, сила тока весьма близка к 0, и обратно. Итак, явление П. тока в проводнике происходит так, как будто в данный момент t действует в этом проводнике электродвижущая сила не E=E0sin⁡2πtT{\displaystyle E=E_{0}\sin 2\pi {\frac {t}{T}}}, а сила, равная E=E0sin⁡(2πtT−θ){\displaystyle E=E_{0}\sin \left(2\pi {\frac {t}{T}}-\theta \right)}, и, кроме того, как будто проводник имеет сопротивление не R, но большее, равное R2+4π2n2L2{\displaystyle {\sqrt {R^{2}+4\pi ^{2}n^{2}L^{2}}}}. Последнее сопротивление, т. е. R2+4π2n2L2{\displaystyle {\sqrt {R^{2}+4\pi ^{2}n^{2}L^{2}}}}, носит название кажущегося сопротивления проводника при существовании в нем П. тока. Кажущееся сопротивление проводника при значительной величине L, как это будет в том случае, когда проводник имеет форму спирали или намотан в виде катушки и в особенности когда внутри такой катушки находится железо (пучок железных проволок или сложенные вместе железные полосы), может во много раз превышать сопротивление R, т. е. сопротивление, оказываемое этим проводником постоянному току. Но и при небольшой величине L кажущееся сопротивление будет большое, когда n велико. Нужно еще заметить, что при очень больших величинах n (тысячи для железных проволок и стержней, миллионы для проводников из немагнитных металлов) кажущееся сопротивление проводника должно быть выражено через R′2+4π2n2L′2{\displaystyle {\sqrt {R’^{2}+4\pi ^{2}n^{2}L’^{2}}}}, т. е. входящие в выражение кажущегося сопротивления величины R′ и L′ отличаются от величин R и L, определяемых из опытов с токами, постоянными и П. со сравнительно небольшой величиной n. Это происходит оттого, что при очень большой величине n П. токи не проникают, как показывает теория и подтверждают опыты, всей внутренней массы проводника. В этом случае такие П. токи, т. е. П. токи очень большой частоты, распространяются только по поверхностным слоям проводника, а потому сплошной цилиндр или проволока являются по отношению к этим токам эквивалентными проводникам, имеющим форму трубок того же внешнего диаметра, как сплошной цилиндр или проволока. Для цилиндрических проводников с поперечным сечением в виде круга найдены Рэлэем следующие выражения для R′ и L′:

R′=R(1+112μ2l2p2R2−1180μ4l4p4R4+…){\displaystyle R’=R\left(1+{\frac {1}{12}}{\frac {\mu ^{2}l^{2}p^{2}}{R^{2}}}-{\frac {1}{180}}{\frac {\mu ^{4}l^{4}p^{4}}{R^{4}}}+…\right)},

L′=l{A+μ(12−148μ2l2p2R2+138640μ4l4p4R4−…)}{\displaystyle L’=l\left\{A+\mu \left({\frac {1}{2}}-{\frac {1}{48}}{\frac {\mu ^{2}l^{2}p^{2}}{R^{2}}}+{\frac {13}{8640}}{\frac {\mu ^{4}l^{4}p^{4}}{R^{4}}}-…\right)\right\}}.

Здесь μ обозначает магнитную проницаемость вещества проводника, l обозначает длину его, p = 2πn. Эти формулы значительно упрощаются, если положить, что n очень велико. В последнем случае мы получим

R′=12μlpR, L′=l(A+μR2lp){\displaystyle R’={\sqrt {{\frac {1}{2}}\mu lpR}},\ L’=l\left(A+{\sqrt {\frac {\mu R}{2lp}}}\right)}.

Возникновение в проводнике П. токов с очень большим числом перемен происходит в случае колебательных разрядов через этот проводник какого-либо наэлектризованного тела или конденсатора (см. Колебательный разряд). Такое же явление встречается при ударе молнии в громоотвод (см.). П. токи чрезвычайно большой частоты (например, токи Тесла) не вызывают никакого болевого ощущения в человеческом организме, тогда как П. токи со сравнительно небольшим числом n производят весьма сильные физиологические действия на нервную систему человека и животных.

Вместо выражения (5′) можно написать

i=Jsin⁡(2πtT−θ)=Jsin⁡2πt′T{\displaystyle i=J\sin \left(2\pi {\frac {t}{T}}-\theta \right)=J\sin 2\pi {\frac {t’}{T}}} . . . (7).

Здесь J обозначает наибольшую величину силы П. тока. Из формулы (7) мы получаем для средней арифметической величины силы тока (i_m) (средней для всех значений i между 0 и J) выражение:

im=114T∫014Tidt=2πJ=0,637J{\displaystyle i_{m}={\frac {1}{{\frac {1}{4}}T}}\int _{0}^{{\frac {1}{4}}T}idt={\frac {2}{\pi }}J=0,637J}.

Средняя квадратичная сила П. тока (i_e), или, по современной номенклатуре, действующая сила переменного тока (intensité efficace) получается по формуле

ie=(i2)m{\displaystyle i_{e}={\sqrt {(i^{2})_{m}}}}, где (i2)m=1T∫0Ti2dt=J22{\displaystyle (i^{2})_{m}={\frac {1}{T}}\int _{0}^{T}i^{2}dt={\frac {J^{2}}{2}}}

Итак, имеемie=J2=0,707J{\displaystyle i_{e}={\frac {J}{\sqrt {2}}}=0,707J},

откуда, обратно, получаем J=2⋅ie=1,414ie{\displaystyle J={\sqrt {2}}\cdot i_{e}=1,414i_{e}}.

Приборы, служащие для измерения силы П. тока (электродинамометры и амметры), обыкновенно и показывают величину i_e, так как эти приборы основаны на действиях, пропорциональных квадрату силы тока. В самом деле, эти приборы основаны или на электродинамическом действии тока, или на тепловом его действии, или на действии тока на намагничиваемое им железо.

Подобным же образом, как при определении i_m и i_e, мы находим для средней арифметической величины (Е_m) электродвижущей силы выражение

Em=2πE0=0,637E0{\displaystyle E_{m}={\frac {2}{\pi }}E_{0}=0,637E_{0}},

и для средней квадратичной величины (Е_e ) или, по современной номенклатуре, для действующей электродвижущей силы Е_e (force électromotrice efficace) выражение

Ee=E02=0,707E0{\displaystyle E_{e}={\frac {E_{0}}{\sqrt {2}}}=0,707E_{0}}

Средняя работа в единицу времени (W_m), необходимая для поддержания в проводнике П. тока, выражается через

Wm=1T∫0TEidt=E0J2cos⁡θ{\displaystyle W_{m}={\frac {1}{T}}\int _{0}^{T}Eidt={\frac {E_{0}J}{2}}\cos \theta }

Такая же работа в течение единицы времени совершается в среднем и током. Эта работа будет очень мала, когда разность фаз θ близка к π2{\displaystyle {\frac {\pi }{2}}}.

Положим, что вблизи данного неизменяемого проводника с П. током находится другой неизменяемый замкнутый проводник, в котором появляются индукционные токи, происходящие от действия на этот проводник данного проводника с П. током в нем.

Обозначая через R₁ и R₂ сопротивления первого и второго проводников, через L₁ и и L₂ — коэффициенты самоиндукции этих проводников, через M — коэффициент взаимной индукции их, через E=E0sin⁡2πtT{\displaystyle E=E_{0}\sin 2\pi {\frac {t}{T}}} — электродвижущую силу в первом проводнике и через i₁, i₂ силы токов в них, мы получаем при помощи выражения (1) следующие дифференциальные уравнения:

L1di1dt+Mdi2dt+R1i1−E0sin⁡2πnt=0{\displaystyle L_{1}{\frac {di_{1}}{dt}}+M{\frac {di_{2}}{dt}}+R_{1}i_{1}-E_{0}\sin 2\pi nt=0},

L2di2dt+Mdi1dt+R2i2=0{\displaystyle L_{2}{\frac {di_{2}}{dt}}+M{\frac {di_{1}}{dt}}+R_{2}i_{2}=0}.

Отсюда находим

i1=E0sin⁡(2πnt−θ1)(R1+4π2n2M2R2R22+4π2n2L22)2+4π2n2(L1−4π2n2ML2R22+4π2n2L22)2{\displaystyle i_{1}={\frac {E_{0}\sin(2\pi nt-\theta _{1})}{\sqrt {\left(R_{1}+4\pi ^{2}n^{2}{\frac {M^{2}R_{2}}{R_{2}^{2}+4\pi ^{2}n^{2}L_{2}^{2}}}\right)^{2}+4\pi ^{2}n^{2}\left(L_{1}-4\pi ^{2}n^{2}{\frac {ML_{2}}{R_{2}^{2}+4\pi ^{2}n^{2}L_{2}^{2}}}\right)^{2}}}}} . . . (8).

Итак, присутствие какого-либо замкнутого проводника вблизи данного проводника, в котором действует гармонически изменяющаяся электродвижущая сила, производит изменение кажущегося сопротивления этого проводника так, как будто истинное сопротивление (R₁) этого проводника увеличивается, а коэффициент самоиндукции (L₁) его уменьшается. На этом основано регулирование П. токов, употребляемых в электротехнике, при помощи вдвигания или выдвигания замкнутой катушки внутрь другой катушки, введенной в цепь регулируемого тока.

Влияние самоиндукции цепи на силу тока в этой цепи, когда возбуждающая ток электродвижущая сила изменяется гармонически, т. е. выражается через Е = E₀Sin2πnt, может быть уменьшено употреблением конденсатора. В самом деле, поместив в цепь П. тока конденсатор, емкость которого пусть будет обозначена через С, а разность потенциалов в какой-либо момент времени через V, мы получаем для силы тока в цепи выражения

i=E−Ldidt−VR{\displaystyle i={\frac {E-L{\frac {di}{dt}}-V}{R}}} . . . . (9)

и

i=CdVdt{\displaystyle i=C{\frac {dV}{dt}}} . . . . . . (10).

Так как при E=E0sin⁡2πtT{\displaystyle E=E_{0}\sin 2\pi {\frac {t}{T}}} должно быть i=Jsin⁡(2πnt−θ){\displaystyle i=J\sin(2\pi nt-\theta )}, то получается

V=−J2πnCcos⁡(2πnt−θ)=−14π2n2Cdidt{\displaystyle V=-{\frac {J}{2\pi nC}}\cos(2\pi nt-\theta )=-{\frac {1}{4\pi ^{2}n^{2}C}}{\frac {di}{dt}}} . . . (11).

При помощи формул (9) и (11) находим i=E−(L−14π2n2C)didtR{\displaystyle i={\frac {E-\left(L-{\frac {1}{4\pi ^{2}n^{2}C}}\right){\frac {di}{dt}}}{R}}} . . . (12).

Отсюда получаемi=E0sin⁡(2πnt−θ)R2+4π2n2(L−14π2n2C)2{\displaystyle i={\frac {E_{0}\sin(2\pi nt-\theta )}{\sqrt {R^{2}+4\pi ^{2}n^{2}\left(L-{\frac {1}{4\pi ^{2}n^{2}C}}\right)^{2}}}}} . . . (13)

и tgθ=2πn(L−14π2n2C)R{\displaystyle {\mbox{tg}}\theta ={\frac {2\pi n\left(L-{\frac {1}{4\pi ^{2}n^{2}C}}\right)}{R}}} . . . (14).

Итак, введение конденсатора с емкостью С в цепь П. (гармонически изменяющегося) тока производит уменьшение коэффициента самоиндукции цепи на величину 14π2n2C{\displaystyle {\frac {1}{4\pi ^{2}n^{2}C}}}, т. е. конденсатор, введенный в такую цепь, может быть уподоблен проводнику, сопротивление которого равно 0, а коэффициент самоиндукции равен −14π2n2C{\displaystyle -{\frac {1}{4\pi ^{2}n^{2}C}}}. Введение конденсатора в цепь изменяет также и разность фаз электродвижущей силы и тока, как это видно из формул (6′) и (14). Введение конденсатора с емкостью С в ответвление цепи можно рассматривать, как помещение в это ответвление проводника, сопротивление которого равно 0, а коэффициент самоиндукции равен −14