Точечный заряд. Единицы измерения заряда. Закон Кулона
В электростатике одним из основополагающих является закон Кулона. Он применяется в физике для определения силы взаимодействия двух неподвижных точечных зарядов или расстояния между ними. Это фундаментальный закон природы, который не зависит ни от каких других законов. Тогда форма реального тела не влияет на величину сил. В этой статье мы расскажем простым языком закон Кулона и его применение на практике.
История открытия
Ш.О. Кулон в 1785 г. впервые экспериментально доказал взаимодействия описанные законом. В своих опытах он использовал специальные крутильные весы. Однако еще в 1773 г. было доказано Кавендишем, на примере сферического конденсатора, что внутри сферы отсутствует электрическое поле. Это говорило о том, что электростатические силы изменяются в зависимости от расстояния между телами. Если быть точнее — квадрату расстояния. Тогда его исследования не были опубликованы. Исторически сложилось так, что это открытие было названо в честь Кулона, аналогичное название носит и величина, в которой измеряется заряд.
Формулировка
Определение закона Кулона гласит: В вакууме F взаимодействия двух заряженных тел прямо пропорционально произведению их модулей и обратно пропорционально квадрату расстояния между ними.
Звучит кратко, но может быть не всем понятно. Простыми словами: Чем больший заряд имеют тела и чем ближе они находятся друг к другу, тем больше сила.
И наоборот: Если увеличить расстояние межу зарядами — сила станет меньше.
Формула правила Кулона выглядит так:
Обозначение букв: q — величина заряда, r — расстояние межу ними, k — коэффициент, зависит от выбранной системы единиц.
Величина заряда q может быть условно-положительной или условно-отрицательной. Это деление весьма условно. При соприкосновении тел она может передаваться от одного к другому. Отсюда следует, что одно и то же тело может иметь разный по величине и знаку заряд. Точечным называется такой заряд или тело, размеры которого много меньше, чем расстояние возможного взаимодействия.
Стоит учитывать что среда, в которой расположены заряды, влияет на F взаимодействия. Так как в воздухе и в вакууме она почти равна, открытие Кулона применимо только для этих сред, это одно из условий применения этого вида формулы. Как уже было сказано, в системе СИ единица измерения заряда — Кулон, сокращено Кл. Она характеризует количество электричества в единицу времени. Является производной от основных единиц СИ.
1 Кл = 1 А*1 с
Стоит отметить, что размерность 1 Кл избыточна. Из-за того что носители отталкиваются друг от друга их сложно удержать в небольшом теле, хотя сам по себе ток в 1А небольшой, если он протекает в проводнике. Например в той же лампе накаливания на 100 Вт течет ток в 0,5 А, а в электрообогревателе и больше 10 А. Такая сила (1 Кл) примерно равна действующей на тело массой 1 т со стороны земного шара.
Вы могли заметить, что формула практически такая же, как и в гравитационном взаимодействии, только если в ньютоновской механике фигурируют массы, то в электростатике — заряды.
Формула Кулона для диэлектрической среды
Коэффициент с учетом величин системы СИ определяется в Н 2 *м 2 /Кл 2 . Он равен:
Во многих учебниках этот коэффициент можно встретить в виде дроби:
Здесь Е 0 = 8,85*10-12 Кл2/Н*м2 — это электрическая постоянная. Для диэлектрика добавляется E — диэлектрическая проницаемость среды, тогда закон Кулона может применяться для расчетов сил взаимодействия зарядов для вакуума и среды.
С учетом влияния диэлектрика имеет вид:
Отсюда мы видим, что введение диэлектрика между телами снижает силу F.
Как направлены силы
Заряды взаимодействуют друг с другом в зависимости от их полярности — одинаковые отталкиваются, а разноименные (противоположные) притягиваются.
Кстати это главное отличие от подобного закона гравитационного взаимодействия, где тела всегда притягиваются. Силы направлены вдоль линии, проведенной между ними, называют радиус-вектором. В физике обозначают как r 12 и как радиус-вектор от первого ко второму заряду и наоборот. Силы направлены от центра заряда к противоположному заряду вдоль этой линии, если заряды противоположны, и в обратную сторону, если они одноименные (два положительных или два отрицательных). В векторном виде:
Силы направлены от центра заряда к противоположному заряду вдоль этой линии, если заряды противоположны, и в обратную сторону, если они одноименные (два положительных или два отрицательных). В векторном виде:
Сила, приложенная к первому заряду со стороны второго обозначается как F 12. Тогда в векторной форме закон Кулона выглядит следующим образом:
Для определения силы приложенной ко второму заряду используются обозначения F 21 и R 21 .
Если тело имеет сложную форму и оно достаточно большое, что при заданном расстоянии не может считаться точечным, тогда его разбивают на маленькие участки и считают каждый участок как точечный заряд. После геометрического сложения всех получившихся векторов получают результирующую силу. Атомы и молекулы взаимодействуют друг с другом по этому же закону.
Применение на практике
Работы Кулона очень важны в электростатике, на практике они применяется в целом ряде изобретений и устройств. Ярким примером можно выделить молниеотвод. С его помощью защищают здания и электроустановки от грозы, предотвращая тем самым пожар и выход из строя оборудования. Когда идёт дождь с грозой на земле появляется индуцированный заряд большой величины, они притягиваются в сторону облака. Получается так, что на поверхности земли появляется большое электрическое поле. Возле острия молниеотвода оно имеет большую величину, в результате этого от острия зажигается коронный разряд (от земли, через молниеотвод к облаку). Заряд от земли притягивается к противоположному заряду облака, согласно закону Кулона. Воздух ионизируется, а напряженность электрического поля уменьшается вблизи конца молниеотвода. Таким образом, заряды не накапливаются на здании, в таком случае вероятность удара молнии мала. Если же удар в здание и произойдет, то через молниеотвод вся энергия уйдет в землю.
С его помощью защищают здания и электроустановки от грозы, предотвращая тем самым пожар и выход из строя оборудования. Когда идёт дождь с грозой на земле появляется индуцированный заряд большой величины, они притягиваются в сторону облака. Получается так, что на поверхности земли появляется большое электрическое поле. Возле острия молниеотвода оно имеет большую величину, в результате этого от острия зажигается коронный разряд (от земли, через молниеотвод к облаку). Заряд от земли притягивается к противоположному заряду облака, согласно закону Кулона. Воздух ионизируется, а напряженность электрического поля уменьшается вблизи конца молниеотвода. Таким образом, заряды не накапливаются на здании, в таком случае вероятность удара молнии мала. Если же удар в здание и произойдет, то через молниеотвод вся энергия уйдет в землю.
В серьезных научных исследованиях применяют величайшее сооружение 21 века – ускоритель частиц. В нём электрическое поле выполняет работу по увеличению энергии частицы.
Полезное
Понятие электричества. Электризация. Проводники, полупроводники и диэлектрики. Элементарный заряд и его свойства. Закон Кулона. Напряженность электрического поля. Принцип суперпозиции. Электрическое поле как проявления взаимодействия. Электрическое поле элементарного диполя.
Термин электричество происходит от греческого слова электрон (янтарь).
Электризацией называют процесс сообщения телу электрического
заряда. Этот термин ввел в 16 веке английский ученый и врач Джилберт.
ЭЛЕКТРИЧЕСКИЙ ЗАРЯД – ЭТО ФИЗИЧЕСКАЯ СКАЛЯРНАЯ ВЕЛИЧИНА, ХАРАКТЕРИЗУЮЩАЯ СВОЙСТВА ТЕЛ ИЛИ ЧАСТИЦ ВСТУПАТЬ И ЭЛЕКТРОМАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ, И ОПРЕДЕЛЯЮЩАЯ СИЛУ И ЭНЕРГИЮ ЭТИХ ВЗВИМОДЕЙСТВИЙ.
Свойства электрических зарядов:
1.В природе существуют два типа электрических зарядов. Положительные (возникают на стекле потертом о кожу) и отрицательные(возникают на эбоните потертом о мех).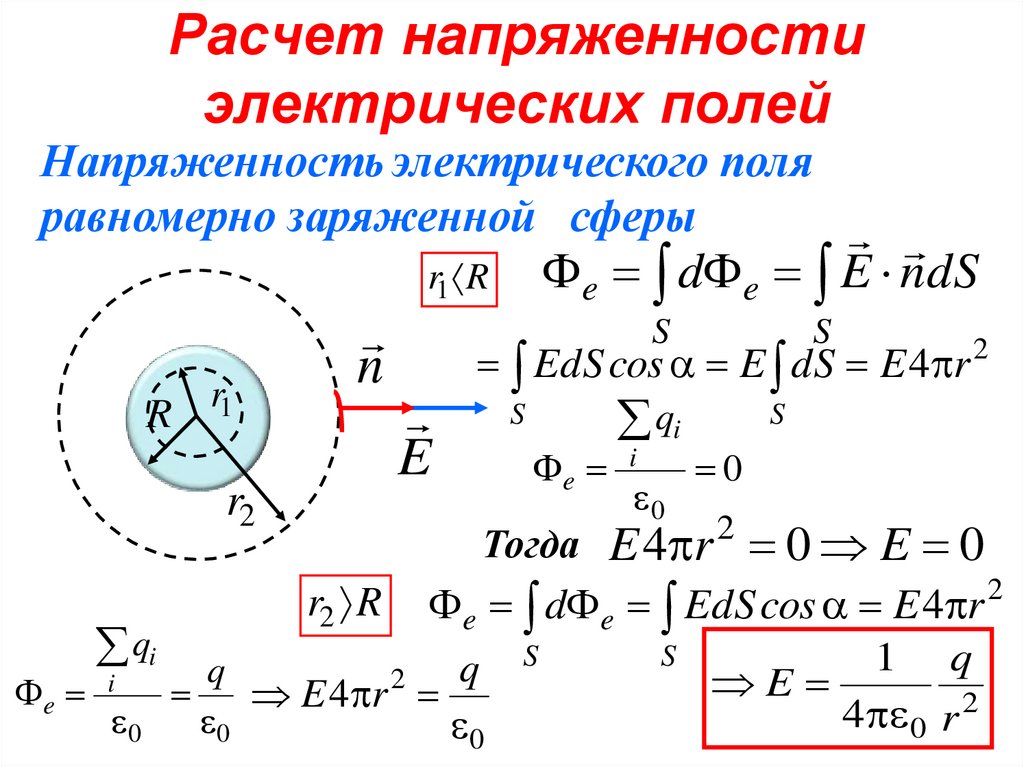
2. Одноименные заряды отталкиваются, разноименные притягиваются.
3. Электрический заряд НЕ СУЩЕСТВУЕТ БЕЗ ЧАСТИЦ НОСИТЕЛЕЙ ЗАРЯДА (электрон, протон, позитрон и др.).Например с электрона и др. элементарных заряженных частиц нельзя снять э/заряд.
4.Электрический заряд дискретен, т.е. заряд любого тела составляет целое кратное от элементарного электрического заряда е (е = 1,6 10 -19 Кл). Электрон (т е = 9,11 10 -31 кг) и протон (т р = 1,67 10 -27 кг ) являются соответственно носителями элементарных отрицательного и положительного зарядов.(Известны частицы с дробным электрическим зарядом: – 1/3
5. Электрический заряд — величина релятивистски инвариантная , т.е. не зависит от системы отсчета, а значит, не зависит от того, движется этот заряд или покоится.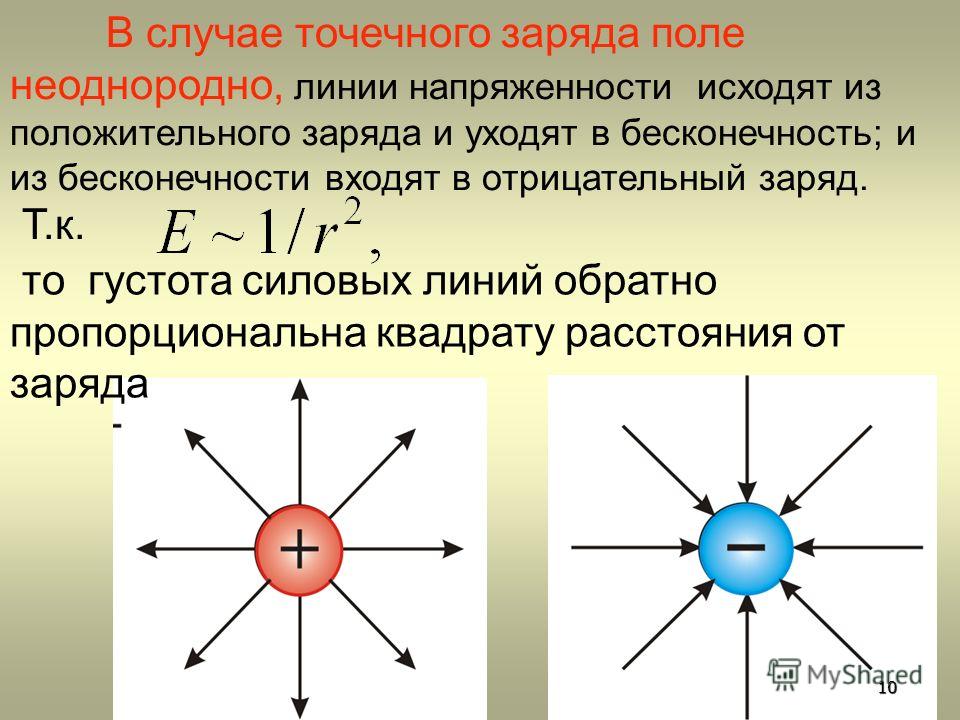
6. Из обобщения опытных данных установлен фундаментальный закон природы — закон сохранения заряда: алгебраическая сум-
ма электрических зарядов любой замкнутой системы (системы, не обменивающейся зарядами с внешними телами) остается неизменной, какие бы процессы ни происходили внутри этой системы.
Закон экспериментально подтвержден в 1843 г. английским физиком
М. Фарадеем ( 1791- 1867) и др., подтвержден рождением и аннигиляцией частиц и античастиц.
Единица электрического заряда (производная единица, так как определяется через единицу силы тока) — кулон (Кл): 1 Кл — электрический заряд,
проходящий через поперечное сечение проводника при силе тока 1 А за время 1с.
Все тела в природе способны электризоваться, т.е. приобретать электрический заряд. Электризация тел может осуществляться различными способами: соприкосновением (трением), электростатической индукцией
и др. Всякий процесс заряжения сводится к разделению зарядов, при котором на одном из тел (или части тела) появляется избыток положительного заряда, а на другом (или другой части тела) — избыток отрицательного заряда.
Электризация тел возможна потому, что тела состоят из заряженных частиц. В процессе электризации тел могут перемещаться, находящиеся в свободном состоянии, электроны и ионы. Протоны остаются в ядрах.
В зависимости от концентрации свободных зарядов тела делятся на проводники, диэлектрики и полупроводники
Проводники — тела, в которых электрический заряд может перемешаться по всему его объему. Проводники делятся на две группы:
1) проводники первого рода (металлы) — перенос в
них зарядов (свободных электронов) не сопровождается химическими
превращениями;
2) проводники второго рода (например, расплавленные соли, ра-
створы кислот) — перенос в них зарядов (положительных и отрицательных
ионов) ведет к химическим изменениям.
Диэлектрики (например, стекло, пластмассы) — тела, в которых практически отсутствуют свободные заряды.
Полупроводники (например, германий, кремний) занимают
промежуточное положение между проводниками и диэлектриками. Указанное деление тел является весьма условным, однако большое различие в них концентраций свободных зарядов обусловливает огромные качественные различия в их поведении и поэтому оправдывает деление тел на проводники, диэлектрики и полупроводники.
ЭЛЕКТРОСТАТИКА — наука о неподвижных зарядах
Закон Кулона.
Закон взаимодействия неподвижных точечных электрических зарядов
Экспериментально установлен в 1785 г. Ш. Кулоном с помощью крутильных весов.
подобных тем, которые использовались Г. Кавендишем для определения гравитационной постоянной (ранее этот закон был открыт Г. Кавендишем, однако его работа оставалась неизвестной более 100 лет).
Точечным зарядом, называется заряженное тело или частица, размерами которых можно пренебречь, по сравнению с расстоянием до них.
Закон Кулона: сила взаимодействия между двумя неподвижными точечными зарядами, находящимися в вакууме, пропорциональна зарядам q 1 и q 2 , и обратно пропорциональна квадрату расстояния r между ними :
k — коэффициент пропорциональности, зависящий от выбора системы
В СИ
Величина ε 0 называется электрической постоянной; она относится к
числу фундаментальных физических постоянных и равна:
ε 0 = 8,85 ∙10 -12 Кл 2 /Н∙м 2
векторной форме закон Кулона в вакууме имеет вид:
где — радиус вектор, соединяющий второй заряд с первым, F 12 – сила, действующая со стороны второго заряда на первый.
Точность выполнения закона Кулона на больших расстояниях, вплоть до
10 7 м, установлена при исследовании магнитного поля с помощью спутников
в околоземном пространстве. Точность же его выполнения на малых расстояниях, вплоть до 10 -17 м, проверена экспериментами по взаимодействию элементарных частиц.
Закон Кулона в среде
Во всех средах сила кулоновского взаимодействия меньше по сравнению с силой взаимодействием в вакууме или воздухе. Физическая величина, показывающая во сколько раз сила электростатического взаимодействия в вакууме больше, чем в данной среде, называется диэлектрической проницаемостью среды и обозначается буквой ε.
ε = F в вакууме / F в среде
Закон кулона в общем виде в СИ:
Свойства Кулоновских сил.
1.Кулоновские силы — это силы центрального типа, т.к. направлены вдоль прямой, соединяющей заряды
Кулоновская сила является силой притяжения, если знаки зарядов разные и силой отталкивания, если знаки зарядов одинаковые
3. Длякулоновских сил справедлив 3 закон Ньютона
Длякулоновских сил справедлив 3 закон Ньютона
4.Кулоновские силы подчиняются принципу независимости или суперпозиции, т.к. сила взаимодействия между двумя точечными зарядами не изменятся при появлении вблизи других зарядов. Результирующая сила электростатического взаимодействия, действующая на данный заряд, равна векторной сумме сил взаимодействия данного заряда с каждым зарядом системы отдельно.
F= F 12 +F 13 +F 14 + ∙∙∙ +F 1 N
Взаимодействия между зарядами осуществляются посредством электрического поля. Электрическое поле – это особая форма существования материи, посредством которой осуществляется взаимодействие электрических зарядов. Электрическое поле проявляет себя тем, что на любой другой заряд внесенный в это поле оно действует с силой. Электростатическое поле создается неподвижными электрическими зарядами и распространяется в пространстве с конечной скоростью с.
Силовая характеристика электрического поля называется напряженностью.
Напряженностью электрического в некоторой точке называют физическую величину, равную отношению силы, с которой поле действует на положительный пробный заряд, помещённый в данную точку, к модулю этого заряда.
Напряженность поля точечного заряда q:
Принцип суперпозиции: напряженность электрического поля, создаваемого системой зарядов в данной точке пространства, равна векторной сумме напряженностей электрических полей, создаваемых в этой точке каждым зарядом в отдельности (в отсутствие других зарядов).
Закон Кулона количественно описывает взаимодействие заряженных тел. Он является фундаментальным законом, то есть установлен при помощи эксперимента и не следует ни из какого другого закона природы. Он сформулирован для неподвижных точечных зарядов в вакууме. В реальности точечных зарядов не существует, но такими можно считать заряды, размеры которых значительно меньше расстояния между ними. Сила взаимодействия в воздухе почти не отличается от силы взаимодействия в вакууме (она слабее менее чем на одну тысячную).
Электрический заряд – это физическая величина, характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия.
Впервые закон взаимодействия неподвижных зарядов был открыт французским физиком Ш. Кулоном в 1785 г. В опытах Кулона измерялось взаимодействие между шариками, размеры которых много меньше расстояния между ними. Такие заряженные тела принято называть точечными зарядами .
На основании многочисленных опытов Кулон установил следующий закон:
Сила взаимодействия двух неподвижных точечных электрических зарядов в вакууме прямо пропорциональна произведению их модулей и обратно пропорциональна квадрату расстояния между ними. Она направлена вдоль прямой, соединяющей заряды, и является силой притяжения, если заряды разноименные, и силой отталкивания, если заряды одноименные.
Если обозначить модули зарядов через |q 1 | и |q 2 |, то закон Кулона можно записать в следующей форме:
\[ F = k \cdot \dfrac{\left|q_1 \right| \cdot \left|q_2 \right|}{r^2} \]
Коэффициент пропорциональности k
в законе Кулона зависит от выбора системы единиц. 9 \)
— Коэффициент пропорциональности в законе Кулона
9 \)
— Коэффициент пропорциональности в законе Кулона
Силы взаимодействия подчиняются третьему закону Ньютона: \(\vec{F}_{12}=\vec{F}_{21} \) . Они являются силами отталкивания при одинаковых знаках зарядов и силами притяжения при разных знаках.
Электрический заряд обычно обозначается буквами q или Q .
Совокупность всех известных экспериментальных фактов позволяет сделать следующие выводы:
Существует два рода электрических зарядов, условно названных положительными и отрицательными.
Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд.
Одноименные заряды отталкиваются, разноименные – притягиваются. В этом также проявляется принципиальное отличие электромагнитных сил от гравитационных. Гравитационные силы всегда являются силами притяжения.
Взаимодействие неподвижных электрических зарядов называют электростатическим или кулоновским взаимодействием. Раздел электродинамики, изучающий кулоновское взаимодействие, называют электростатикой.
Раздел электродинамики, изучающий кулоновское взаимодействие, называют электростатикой.
Закон Кулона справедлив для точечных заряженных тел. Практически закон Кулона хорошо выполняется, если размеры заряженных тел много меньше расстояния между ними.
Отметим, чтоб выполнялся закон Кулона необходимо 3 условия:
- Точечность зарядов — то есть расстояние между заряженными телами много больше их размеров.
- Неподвижность зарядов . Иначе вступают в силу дополнительные эффекты: магнитное поле движущегося заряда и соответствующая ему дополнительная сила Лоренца, действующая на другой движущийся заряд.
- Взаимодействие зарядов в вакууме .
В Международной системе СИ за единицу заряда принят кулон (Кл) .
Кулон – это заряд, проходящий за 1 с через поперечное сечение проводника при силе тока 1 А . Единица силы тока (Ампер) в СИ является наряду с единицами длины, времени и массы основной единицей измерения.
В вашем браузере отключен Javascript. {-2}\,{\text{м}}} \)
{-2}\,{\text{м}}} \)
\(\displaystyle{\varepsilon = 1} \)
\(\displaystyle{q} — ? \)
Решение
Поскольку шарики одинаковы, то на каждый шарик действуют одинаковые силы: сила тяжести \(\displaystyle{m \vec g} \), сила натяжения нити \(\displaystyle{\vec T} \)и сила кулоновского взаимодействия (отталкивания) \(\displaystyle{\vec F} \). На рисунке показаны силы, действующие на один из шариков. Поскольку шарик находится в равновесии, сумма всех сил, действующих на него, равна 0. Кроме того, сумма проекций сил на оси \(\displaystyle{OX} \) и \(\displaystyle{OY} \)равна 0:
\(\begin{equation} {{\mbox{на ось }} {OX} : \atop { \mbox{ на ось }} {OY} : }\quad \left\{\begin{array}{ll} F-T\sin{\alpha} & =0 \\ T\cos{\alpha}-mg & =0 \end{array}\right. \quad{\text{или}}\quad \left\{\begin{array}{ll} T\sin{\alpha} & =F \\ T\cos{\alpha} & = mg \end{array}\right. \end{equation} \)
Решим совместно эти уравнения. Разделив первое равенство почленно на второе, получим:
\(\begin{equation} {\mbox{tg}\,}= {F\over mg}\,. {-9}\,{\text{Кл}}} \)\(\displaystyle{\ell=10\,{\text{см}}} \)\(\displaystyle{\varphi_{\text{ш}}=200\,{\text{В}}} \)\(\displaystyle{R=2\,{\text{см}}} \) \(\displaystyle{\varepsilon = 1} \) \(\displaystyle{A} \) — ?
{-9}\,{\text{Кл}}} \)\(\displaystyle{\ell=10\,{\text{см}}} \)\(\displaystyle{\varphi_{\text{ш}}=200\,{\text{В}}} \)\(\displaystyle{R=2\,{\text{см}}} \) \(\displaystyle{\varepsilon = 1} \) \(\displaystyle{A} \) — ?
Решение
Работа, которую необходимо совершить, чтобы перенести заряд из точки с потенциалом \(\displaystyle{\varphi_1} \) в точку с потенциалом \(\displaystyle{\varphi_2} \) , равна изменению потенциальной энергии точечного заряда, взятому с обратным знаком:
\(\begin{equation} A=-\Delta W_n\,. \end{equation} \)
Известно, что \(\displaystyle{A=-q(\varphi_2-\varphi_1) } \) или
\(\begin{equation} A=q(\varphi_1-\varphi_2) \,. \end{equation} \)
Поскольку точечный заряд первоначально находится на бесконечности, то потенциал в этой точке поля равен 0: \(\displaystyle{\varphi_1=0} \) .
Определим потенциал в конечной точке, то есть \(\displaystyle{\varphi_2} \) .
Пусть \(\displaystyle{Q_{\text{ш}}} \) – заряд шарика. По условию задачи потенциал шарика известен (\(\displaystyle{\varphi_{\text{ш}}=200\,{\text{В}}} \)) , тогда:
\(\begin{equation} \varphi_{\text{ш}}={Q_{\text{ш}}\over 4\pi\varepsilon_o\varepsilon R}\, \end{equation} \)
\(\begin{equation} {\text{откуда}}\quad Q_{\text{ш}}=\varphi_{\text{ш}}\cdot 4\pi\varepsilon_o\varepsilon R\,. 9\) Н·м 2 /Кл 2 , где ε 0 – электрическая постоянная, равная 8,85·10 -12 Кл 2 /Н·м 2 .
9\) Н·м 2 /Кл 2 , где ε 0 – электрическая постоянная, равная 8,85·10 -12 Кл 2 /Н·м 2 .
Формулировка закона :
сила взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними.
Эту силу называют кулоновской .
Закон Кулона в данной формулировке справедлив только для точечных заряженных тел, т.к. только для них понятие расстояния между зарядами имеет определенный смысл. Точечных заряженных тел в природе нет. Но если расстояние между телами во много раз больше их размеров, то ни форма, ни размеры заряженных тел существенно, как показывает опыт, не влияют на взаимодействие между ними. В этом случае тела можно рассматривать как точечные.
Легко обнаружить, что два заряженных шарика, подвешенные на нитях, либо притягиваются друг к другу, либо отталкиваются. Отсюда следует, что силы взаимодействия двух неподвижных точечных заряженных тел направлены вдоль прямой, соединяющей эти тела. 3_{1,2}} \cdot \vec r_{1,2}\) . (2)
3_{1,2}} \cdot \vec r_{1,2}\) . (2)
Если знаки зарядов q 1 и q 2 одинаковы, то направление силы \(~\vec F_{1,2}\) совпадает с направлением вектора \(~\vec r_{1,2}\) ; в противном случае векторы \(~\vec F_{1,2}\) и \(~\vec r_{1,2}\) направлены в противоположные стороны.
Зная закон взаимодействия точечных заряженных тел, можно вычислить силу взаимодействия любых заряженных тел. Для этого тела нужно мысленно разбить на такие малые элементы, чтобы каждый из них можно было считать точечным. Складывая геометрически силы взаимодействия всех этих элементов друг с другом, можно вычислить результирующую силу взаимодействия.
Открытие закона Кулона – первый конкретный шаг в изучении свойств электрического заряда. Наличие электрического заряда у тел или элементарных частиц означает, что они взаимодействуют друг с другом по закону Кулона. Никаких отклонений от строгого выполнения закона Кулона в настоящее время не обнаружено.
Опыт Кулона
Необходимость проведения экспериментов Кулона была вызвана тем, что в середине XVIII в.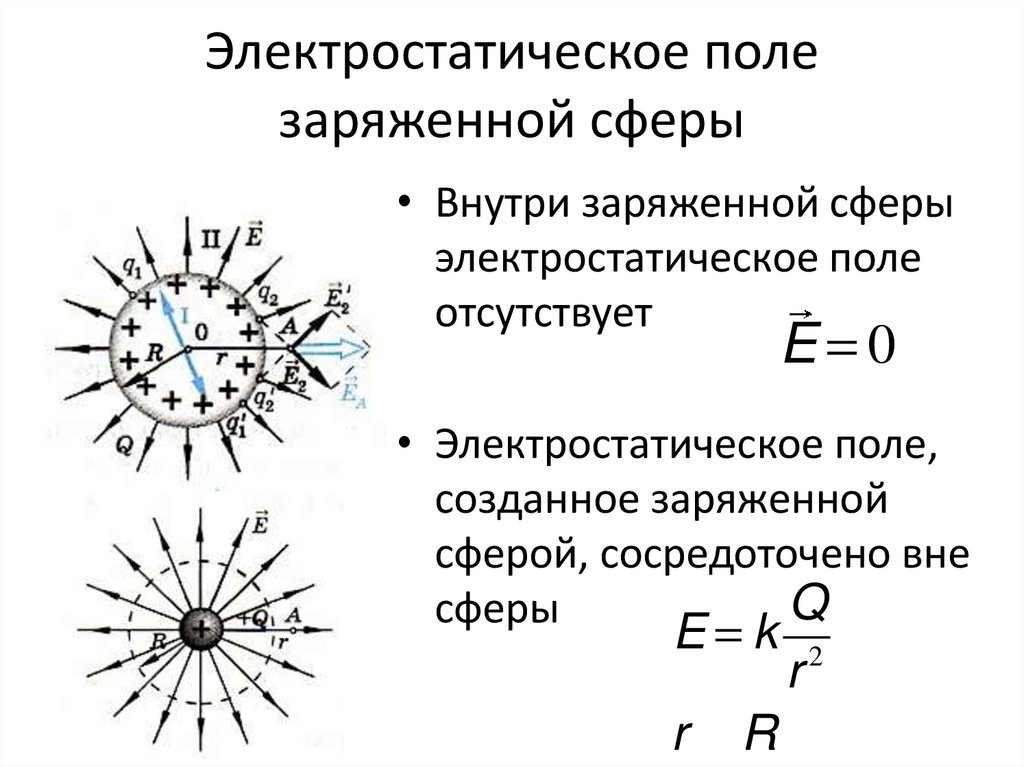 4}{l} \cdot \varphi\) ,
4}{l} \cdot \varphi\) ,
где d – диаметр, l – длина проволоки, φ – угол закручивания. В приведенном математическом выражении коэффициент пропорциональности k находился опытным путем и зависел от природы материала, из которого изготавливалась проволока.
Данная закономерность была использована в так называемых крутильных весах. Созданные весы позволили измерить ничтожно малые силы порядка 5·10 -8 Н.
Рис. 3
Крутильные весы (рис. 3, а) состояли из легкого стеклянного коромысла 9 длиной 10,83 см, подвешенного на серебряной проволоке 5 длиной около 75 см, диаметром 0,22 см. На одном конце коромысла располагался позолоченный бузиновый шарик 8 , а на другом – противовес 6 – бумажный кружок, смоченный в скипидаре. Верхний конец проволоки прикреплялся к головке прибора 1 . Здесь же имелся указатель 2 , с помощью которого отсчитывался угол закручивания нити по круговой шкале 3 . Шкала была проградуирована. Вся эта система размещалась в стеклянных цилиндрах 4 и 11 . В верхней крышке нижнего цилиндра имелось отверстие, в которое вставлялась стеклянная палочка с шариком 7 на конце. В опытах применялись шарики с диаметрами в пределах 0,45 – 0,68 см.
Шкала была проградуирована. Вся эта система размещалась в стеклянных цилиндрах 4 и 11 . В верхней крышке нижнего цилиндра имелось отверстие, в которое вставлялась стеклянная палочка с шариком 7 на конце. В опытах применялись шарики с диаметрами в пределах 0,45 – 0,68 см.
Перед началом эксперимента указатель головки устанавливался на нулевой отметке. Затем шарик 7 заряжался от предварительно наэлектризованного шарика 12 . При соприкосновении шарика 7 с подвижным шариком 8 происходило перераспределение заряда. Однако из-за того, что диаметры шариков были одинаковыми, одинаковыми были и заряды на шариках 7 и 8 .
Вследствие электростатического отталкивания шариков (рис. 3, б) коромысло 9 поворачивалось на некоторый угол γ (по шкале 10 ). С помощью головки 1 это коромысло возвращалось в исходное положение. По шкале 3 указатель 2 позволял определять угол α закручивания нити.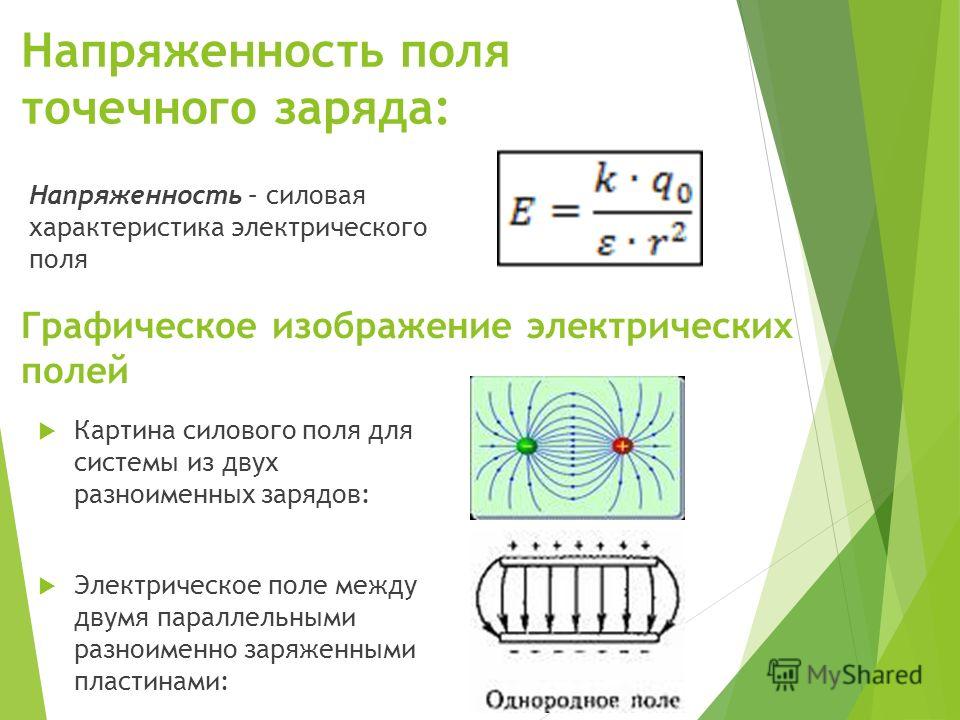 Общий угол закручивания нити φ = γ + α . Сила же взаимодействия шариков была пропорциональна φ , т. е. по углу закручивания можно судить о величине этой силы.
Общий угол закручивания нити φ = γ + α . Сила же взаимодействия шариков была пропорциональна φ , т. е. по углу закручивания можно судить о величине этой силы.
При неизменном расстоянии между шариками (оно фиксировалось по шкале 10 в градусной мере) исследовалась зависимость силы электрического взаимодействия точечных тел от величины заряда на них.
Для определения зависимости силы от заряда шариков Кулон нашел простой и остроумный способ изменения заряда одного из шариков. Для этого он соединял заряженный шарик (шарики 7 или 8 ) с таким же по размерам незаряженным (шарик 12 на изолирующей ручке). Заряд при этом распределялся поровну между шариками, что и уменьшало исследуемый заряд в 2, 4 и т. д. раз. Новое значение силы при новом значении заряда опять определялось экспериментально. При этом выяснилось, что сила прямо пропорциональна произведению зарядов шариков :
\(~F \sim q_1 \cdot q_2\) .
Зависимость силы электрического взаимодействия от расстояния была обнаружена следующим образом.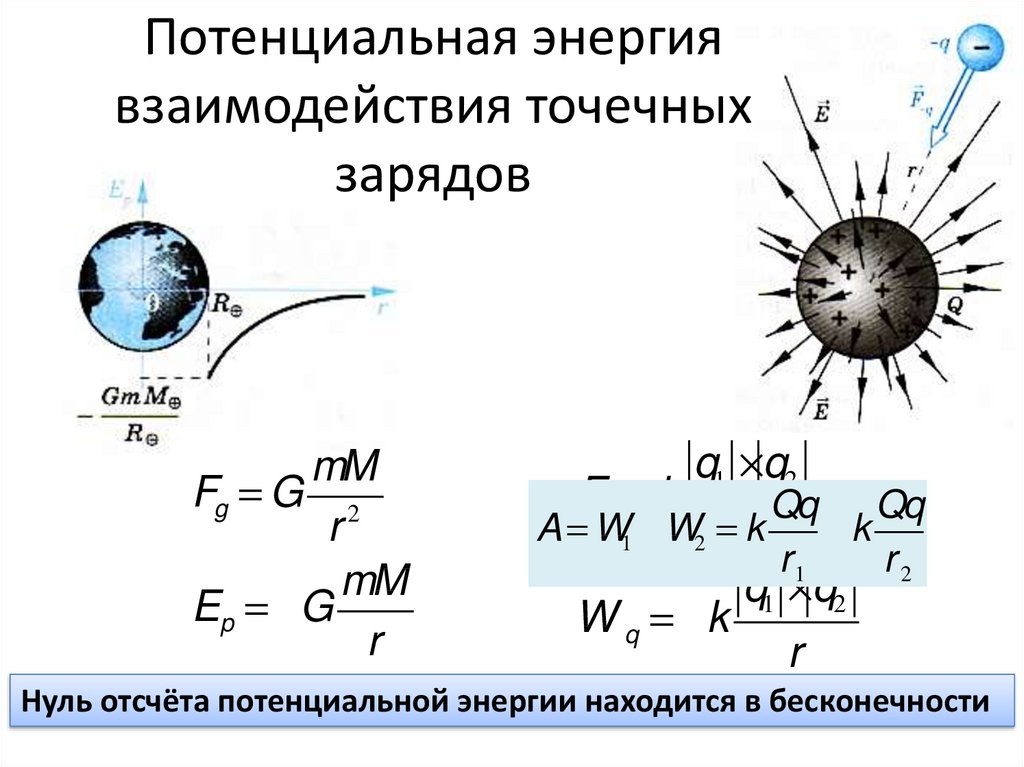 2}\) .
2}\) .
Литература
- Мякишев Г.Я. Физика: Электродинамика. 10-11 кл.: учеб. для углубленного изучения физики / Г.Я. Мякишев, А.З. Синяков, Б.А. Слободсков. – М.: Дрофа, 2005. – 476 с.
- Вольштейн С. Л. и др. Методы физической науки в школе: Пособие для учителя / С.Л. Вольштейн, С.В. Позойский, В.В. Усанов; Под ред. С.Л. Вольштейна. – Мн.: Нар. асвета, 1988. – 144 с.
Самые часто задаваемые вопросы
Возможно ли, изготовить печать на документе по предоставленному образцу? Ответ Да, возможно. Отправьте на наш электронный адрес скан-копию или фото хорошего качества, и мы изготовим необходимый дубликат.
Какие виды оплаты вы принимаете?
Ответ
Вы можете оплатить документ во время получения на руки у курьера, после того, как проверите правильность заполнения и качество исполнения диплома. Также это можно сделать в офисе почтовых компаний, предлагающих услуги наложенного платежа.
Все условия доставки и оплаты документов расписаны в разделе «Оплата и доставка». Также готовы выслушать Ваши предложения по условиям доставки и оплаты за документ.
Также готовы выслушать Ваши предложения по условиям доставки и оплаты за документ.
Могу ли я быть уверена, что после оформления заказа вы не исчезнете с моими деньгами? Ответ В сфере изготовления дипломов у нас достаточно длительный опыт работы. У нас есть несколько сайтов, который постоянно обновляются. Наши специалисты работают в разных уголках страны, изготавливая свыше 10 документов день. За годы работы наши документы помогли многим людям решить проблемы трудоустройства или перейти на более высокооплачиваемую работу. Мы заработали доверие и признание среди клиентов, поэтому у нас совершенно нет причин поступать подобным образом. Тем более, что это просто невозможно сделать физически: Вы оплачиваете свой заказ в момент получения его на руки, предоплаты нет.
Могу я заказать диплом любого ВУЗа?
Ответ
В целом, да. Мы работаем в этой сфере почти 12 лет. За это время сформировалась практически полная база выдаваемых документов почти всех ВУЗов страны и за разные года выдачи. Все, что Вам нужно – выбрать ВУЗ, специальность, документ, и заполнить форму заказа.
Все, что Вам нужно – выбрать ВУЗ, специальность, документ, и заполнить форму заказа.
Что делать при обнаружении в документе опечаток и ошибок?
Ответ
Получая документ у нашего курьера или в почтовой компании, мы рекомендуем тщательно проверить все детали. Если будет обнаружена опечатка, ошибка или неточность, Вы имеете право не забирать диплом, при этом нужно указать обнаруженные недочеты лично курьеру или в письменном виде, отправив письмо на электронную почту.
В кратчайшие сроки мы исправим документ и повторно отправим на указанный адрес. Разумеется, пересылка будет оплачена нашей компанией.
Чтобы избежать подобных недоразумений, перед тем, как заполнять оригинальный бланк, мы отправляем на почту заказчику макет будущего документа, для проверки и утверждения окончательного варианта. Перед отправкой документа курьером или почтой мы также делаем дополнительное фото и видео (в т. ч. в ультрафиолетовом свечении), чтобы Вы имели наглядное представление о том, что получите в итоге.
Что нужно сделать, чтобы заказать диплом в вашей компании?
Ответ
Для заказа документа (аттестата, диплома, академической справки и др.) необходимо заполнить онлайн-форму заказа на нашем сайте или сообщить свою электронную почту, чтобы мы выслали вам бланк анкеты, который нужно заполнить и отправить обратно нам.
Если вы не знаете, что указать в каком-либо поле формы заказа/анкеты, оставьте их незаполненными. Всю недостающую информацию мы потому уточним в телефонном режиме.
Последние отзывы
Валентина:
Вы спасли нашего сына от увольнения! Дело в том что недоучившись в институте, сын пошел в армию. А вернувшись, восстанавливаться не захотел. Работал без диплома. Но недавно начали увольнять всех, кто не имеет «корочки. Поэтому решили обратиться к вам и не пожалели! Теперь спокойно работает и ничего не боится! Спасибо!
Электростатическое поле точечного заряда и заряженной сферы
теория по физике 🧲 электростатика
Любые заряженные тела создают вокруг себя электростатическое поле. Рассмотрим особенности электростатического поля, создаваемого точечным зарядом и заряженной сферой.
Рассмотрим особенности электростатического поля, создаваемого точечным зарядом и заряженной сферой.
Электростатическое поле точечного заряда
Направление силовых линий электростатического поля точечного заряда| Положительный заряд +Q | Отрицательный заряд –Q |
| У положительного заряда силовые линии направлены по радиальным линиям от заряда. | У отрицательного заряда силовые линии направлены по радиальным линиям к заряду. |
Модуль напряженности не зависит от значения пробного заряда q0:
E=FKq0..=kQq0r2q0..=kQr2..
Модуль напряженности точечного заряда в вакууме:
E=kQr2..
Модуль напряженности точечного заряда в среде:
E=kQεr2..
Сила Кулона:
−FKулона=q−E
Потенциал не зависит от значения пробного заряда q0:
φ=Wpqo.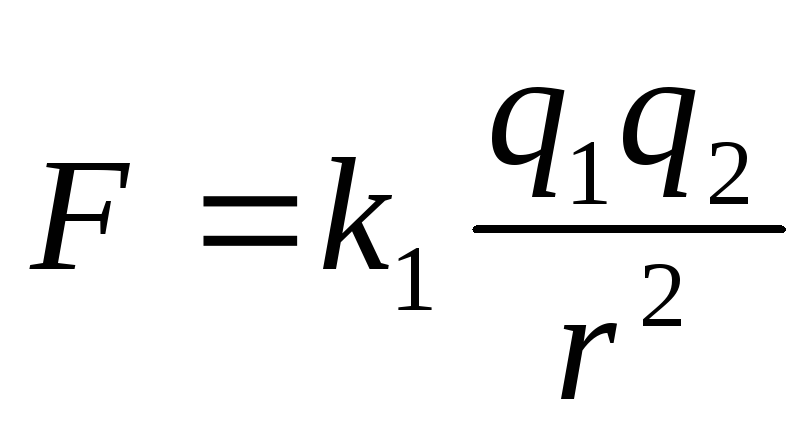 .=±kQq0rq0..=±kQr..
.=±kQq0rq0..=±kQr..
Потенциал точечного заряда в вакууме:
φ=±kQr..
Потенциал точечного заряда в среде:
φ=±kQεr..
Внимание! Знак потенциала зависит только от знака заряда, создающего поле.
Эквипотенциальные поверхности для данного случая — концентрические сферы, центр которых совпадает с положением заряда.
Работа электрического поля по перемещению точечного заряда:
A12=±q(φ1−φ2)
Пример №1. Во сколько раз увеличится модуль напряженности электрического поля, созданного точечным зарядом Q в некоторой точке, при увеличении значения этого заряда в 5 раз? Модуль напряженности электрического поля, созданного точечным зарядом, определяется формулой:
E=kQεr2..
Формула показывает, что модуль напряженности и электрический заряд — прямо пропорциональные величины.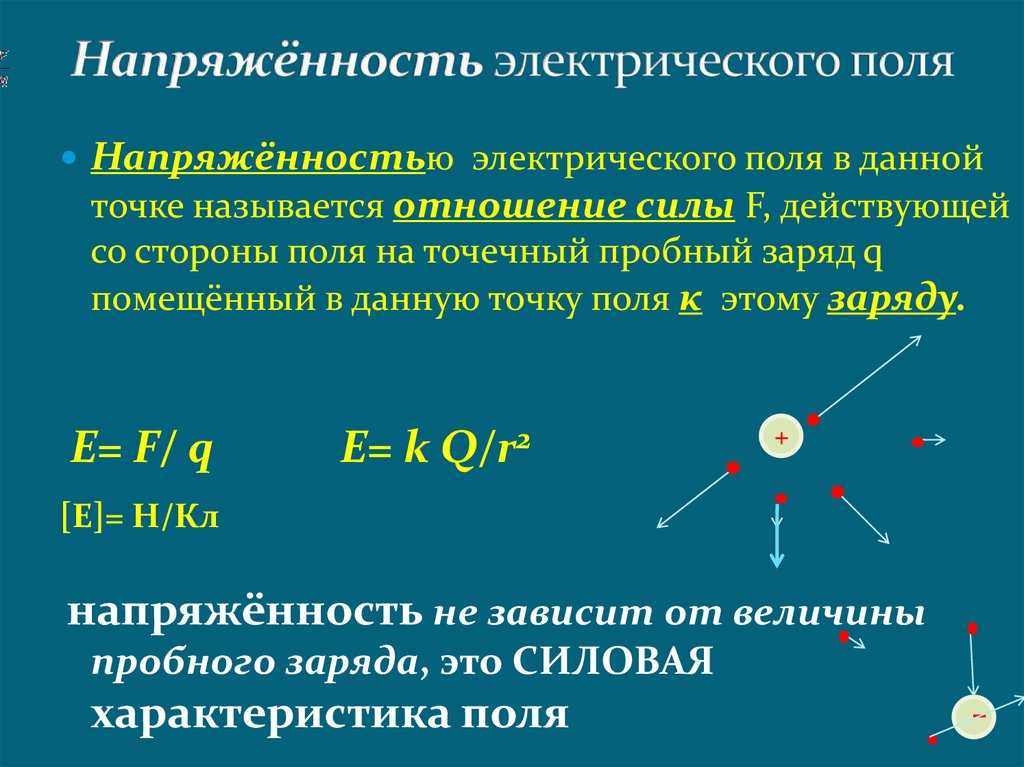 Следовательно, если заряд, который создает поле, увеличится в 5 раз, то модуль напряженности создаваемого поля тоже увеличится в 5 раз.
Следовательно, если заряд, который создает поле, увеличится в 5 раз, то модуль напряженности создаваемого поля тоже увеличится в 5 раз.
Электростатическое поле заряженной сферы
Направление силовых линий электростатического поля заряженной сферы:
| Положительно заряженная сфера +Q | Отрицательно заряженная сфера –Q |
| У положительно заряженной сферы силовые линии — это радиальные линии, которые начинаются из этой сферы. | У отрицательно заряженной сферы силовые линии — это радиальные линии, которые заканчиваются в этой сфере. |
Модуль напряженности электростатического поля заряженной сферы:
| Внутри проводника (расстояние меньше радиуса сферы, или r < R) | E=0 |
| На поверхности проводника (расстояние равно радиусу сферы, или r = R) | E=kQR2. |
| Вне проводника (расстояние больше радиуса сферы, или r > R) | E=kQr2..=kQ(R+a)2.. a — расстояние от поверхности сферы до изучаемой точки. r — расстояние от центра сферы до изучаемой точки. |
Сила Кулона:
−FK=q−E
Потенциал:
| Внутри проводника и на его поверхности (r < R или r = R) | φ=±kQR.. |
| Вне проводника (r > R) | φ=±kQr..=±φ=±kQR+a.. |
Пример №2. Определить потенциал электростатического поля, создаваемого заряженной сферой радиусом 0,1 м, в точке, находящейся на расстоянии 0,2 м от этой сферы. Сфера заряжена положительна и имеет заряд, равный 6 нКл.
6 нКл = 6∙10–9 Кл
Так как сфера заряжена положительно, то потенциал тоже положителен:
Задание EF18107Два неподвижных точечных заряда действуют друг на друга с силами, модуль которых равен F. Чему станет равен модуль этих сил, если один заряд увеличить в n раз, другой заряд уменьшить в n раз, а расстояние между ними оставить прежним?
Чему станет равен модуль этих сил, если один заряд увеличить в n раз, другой заряд уменьшить в n раз, а расстояние между ними оставить прежним?
Ответ:
а) F
б) nF
в) Fn
г) n2F
Алгоритм решения
1.Записать исходные данные.
2.Записать закон Кулона.
3.Применить закон Кулона к обоим зарядам для 1 и 2 случая.
4.Установить, как меняется сила, с которой заряды действуют друг на друга.
Решение
Запишем исходные данные:
• Первая пара зарядов: q1 и q2.
• Вторая пара зарядов: q1’ = nq1 и q2’=q2/n.
• Расстояние между зарядами: r1 = r2 = r.
Закон Кулона:
FK=k|q1||q2|r2..
Применим закон Кулона к парам зарядов. Закон Кулона для первой пары:
FK1=k|q1||q2|r2..
Закон Кулона для второй пары:
FK2=k|nq1|∣∣q2n.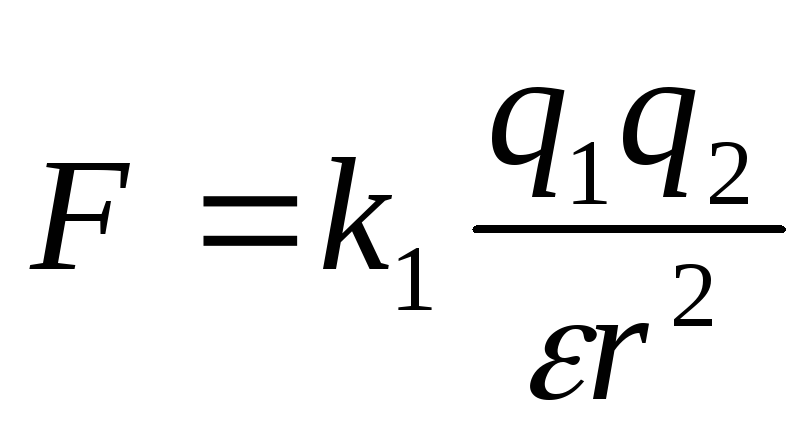 .∣∣r2..=k|q1||q2|r2..
.∣∣r2..=k|q1||q2|r2..
Коэффициент n сократился. Следовательно, силы, с которыми заряды взаимодействуют друг с другом, не изменятся:
FK1=FK2
После изменения зарядов модуль силы взаимодействия между ними останется равным F.pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18591В трёх вершинах квадрата размещены точечные заряды: +q, –q, +q (q >0) (см. рисунок). Куда направлена кулоновская сила, действующая со стороны этих зарядов на точечный заряд +2q, находящийся в центре квадрата?
Ответ:
а) ↘
б) →
в) ↖
г) ↓
Алгоритм решения
1.Сделать чертеж. Обозначить все силы, действующие на центральный точечный заряд со стороны остальных точечных зарядов.
2.Найти равнодействующую сил геометрическим способом.
3.Выбрать верный ответ.
Решение
Сделаем чертеж. В центр помещен положительный заряд. Он будет отталкиваться от положительных зарядов и притягиваться к отрицательным:
В центр помещен положительный заряд. Он будет отталкиваться от положительных зарядов и притягиваться к отрицательным:
Модули всех векторов сил, приложенных к центральному точечному заряду равны, так как модули точечных зарядов, расположенных в вершинах квадрата равны, и находятся они на одинаковом расстоянии от этого заряда.
Складывая векторы геометрически, мы увидим, что силы, с которыми заряд +2q отталкивается от точечных зарядов +q, компенсируют друг друга. Поэтому на заряд действует равнодействующая сила, равная силе, с которой он притягивается к отрицательному точечному заряду –q. Эта сила направлена в ту же сторону (к нижней правой вершине квадрата).
Ответ: аpазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF22574На неподвижном проводящем уединённом шарике радиусом R находится заряд Q. Точка O – центр шарика, OA = 3R/4, OB = 3R, OC = 3R/2. Модуль напряжённости электростатического поля заряда Q в точке C равен EC. Определите модуль напряжённости электростатического поля заряда Q в точке A и точке B?
Определите модуль напряжённости электростатического поля заряда Q в точке A и точке B?
Установите соответствие между физическими величинами и их значениями.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
Алгоритм решения
1.Записать формулы для нахождения напряженности электростатического поля внутри и снаружи заряженной сферы.
2.Определить величину напряженности поля в указанных точках.
3.Установить соответствие между величинами и их значениями.
Решение
Внутри заряженной сферы напряженность электростатического поля равна 0. Поэтому напряженность в точке А равна 0.
EA=0
Снаружи заряженной сферы напряженность электростатического поля равна:
E=kQr2..=kQ(R+a)2..
Найдем напряженность электростатического поля в точке В, которая находится на расстоянии 3R от центра заряженной сферы:
EB=kQr2.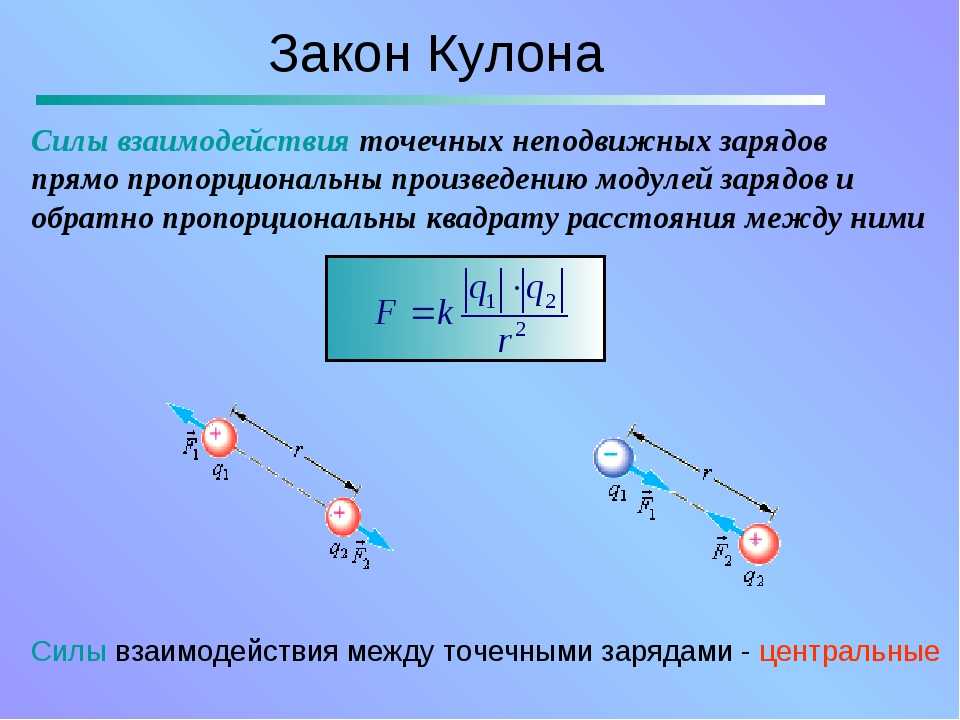 .=kQ(3R)2..=kQ9R2..
.=kQ(3R)2..=kQ9R2..
Чтобы выразить EB через Eс, найдем напряженность электростатического поля в точке С, которая находится на расстоянии 3R/2 от центра заряженной сферы:
EС=kQr2..=kQ(32..R)2..=4kQ9R2..
Найдем отношение EB к Eс:
EBEС..=kQ9R2..÷4kQ9R2..=kQ9R2..·9R24kQ..=14..
Следовательно:
EB=EС4..
Ответ: 14pазбирался: Алиса Никитина | обсудить разбор | оценить
Алиса Никитина | Просмотров: 5.3k | Оценить:
Сила отталкивания двух зарядов. Закон Кулона. Точечный заряд
Страница 56
ЗАКОН КУЛОНА(уч.10кл.стр.354-362)
Основной закон электростатики. Понятие точечного заряженного тела.
Измерение силы взаимодействия зарядов с помощью крутильных весов. Опыты Кулона
Определение точечного заряда
Закон Кулона. Формулировка и формула
Сила Кулона
Определение единицы заряда
Коэффициент в законе Кулона
Сравнение электростатических и гравитационных сил в атоме
Равновесие статических зарядов и его физический смысл (на примере трех зарядов)
Основной закон электростатики – закон взаимодействия двух неподвижных точечных заряженных тел.
Установлен Шарлем Огюстеном Кулоном в 1785 году и носит его имя.
В природе точечных заряженных тел не существует, но если расстояние между телами во много раз больше их размеров, то ни форма, ни размеры заряженных тел существенно не влияют на взаимодействия между ними. В током случае эти тела можно рассматривать, как точечные.
Сила взаимодействия заряженных тел зависит от свойств среды между ними. Опыт показывает, что воздух очень мало влияет на силу этого взаимодействия и она оказывается почти такой же как в вакууме.
Опыт Кулона
Первые результаты по измерению силы взаимодействия зарядов получены в 1785 г. французским ученым Шарлем Огюстеном Кулоном
Для измерения силы использовались крутильные весы.
Маленькая тонкая незаряженная золотая сфера на одном конце изолирующего коромысла, подвешенного на упругой серебряной нити, уравновешивалась на другом концу коромысла бумажным диском.
Поворотом коромысла она приводилась в контакт с такой же неподвижной заряженной сферой, в результате чего ее заряд делился поровну между сферами.
Диаметр сфер выбирался много меньше расстояния между ними, чтобы исключить влияние размеров и формы заряженных тел на результаты измерений.
Точечный заряд – заряженное тело, размер которого много меньше расстояния его возможного действия на другие тела.
Сферы, имеющие одноименные заряды, начинали отталкиваться, закручивая нить. Угол поворота был пропорционален силе, действующей на подвижную сферу.
Расстояние между сферами измерялось по специальной градуировочной шкале.
Разряжая сферу 1 после измерения силы и соединяя ее вновь с неподвижной сферой, Кулон уменьшал заряд на взаимодействующих сферах в 2,4,8 и т.д. раз,
Закон Кулона:
Сила взаимодействия между двумя неподвижными точечными зарядами, находящимися в вакууме, прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними, и направлена по прямой, соединяющей заряды.
k – коэффициент пропорциональности, зависящий от выбора системы единиц.
Силу F12 называю силой Кулона
Сила Кулона центральная, т.е. направлена по линии соединяющей центры зарядов.
В СИ единица заряда является не основной, а производной, и определяется с помощью Ампера – основной единицы СИ.
Кулон – электрический заряд, проходящий через поперечное сечение проводника при силе тока в 1 А за 1 с
В СИ коэффициент пропорциональности в законе Кулона для вакуума:
k = 9*109 Нм2/Кл2
Часто коэффициент записывают в виде:
e0 = 8,85*10-12 Кл2/(Нм2) – электрическая постоянная
Закон Кулона записывается в форме:
Если точечный заряд поместить в среду с относительной диэлектрической проницаемостью e, отличную от вакуума, кулоновская сила уменьшится в e раз.
У любой среды кроме вакуума e > 1
Согласно закону Кулона два точечных заряда по 1 Кл, на расстоянии 1 м в вакууме, взаимодействуют с силой
Из этой оценки видно, что заряд в 1 Кулон – очень большая величина.
На практике пользуются дольными единицами – мкКл (10-6), мКл (10-3)
1 Кл содержит 6*1018 зарядов электронов.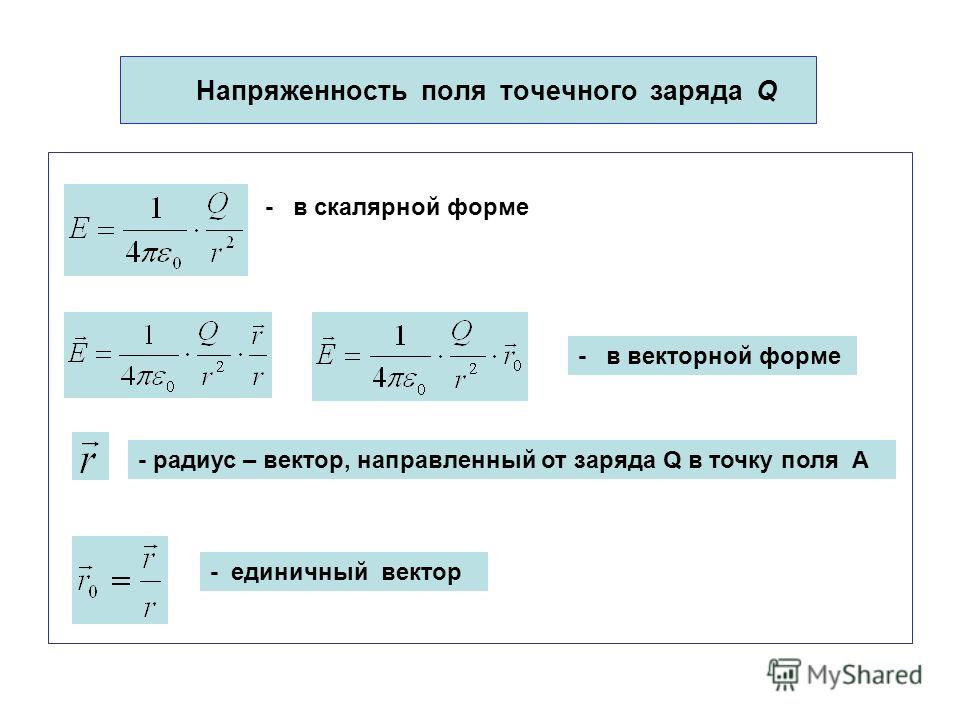
На примере сил взаимодействия электрона и протона в ядре можно показать, что электростатическая сила взаимодействия частиц больше гравитационной примерно на 39 порядков. Однако электростатические силы взаимодействия макроскопических тел (в целом электронейтральных) определяются лишь очень малыми избыточными зарядами, находящимися на них, и поэтому не велики по сравнению с гравитационными, зависящими от массы тел.
Возможно ли равновесие статических зарядов?
Рассмотрим систему из двух положительных точечных зарядов q1 и q2.
Найдем, в какую точку следует поместить третий заряд, чтобы он находился в равновесии, а так же определим величину и знак этого заряда.
Статическое равновесие возникает тогда, когда геометрическая (векторная) сумма сил, действующих на тело, равна нулю.
Точка, в которой силы, действующие на третий заряд q3, могут компенсировать друг друга, находится на прямой между зарядами.
При этом заряд q3 может быть как положительным так и отрицательным. В первом случае компенсируются силы отталкивания, во втором – силы притяжения.
В первом случае компенсируются силы отталкивания, во втором – силы притяжения.
Учитывая закон Кулона статическое равновесие зарядов будет в случае:
Равновесие заряда q3 не зависит ни от его величины, ни от знака заряда.
При изменении заряда q3 в равной мере меняются как силы притяжения (q3 положительный), так и силы отталкивания (q3 отрицательный)
Решив квадратное уравнение относительно x можно показать, что заряд любого знака и величины будет находится в равновесии в точке на расстоянии x1 от заряда q1:
Выясним устойчивым или неустойчивым будет положение третьего заряда.
(При устойчивом равновесии тело, выведенное из положения равновесия, возвращается к нему, при неустойчивом – удаляется от него)
При горизонтальном смещении силы отталкивания F31, F32 меняются из-за изменения расстояний между зарядами, возвращая заряд к положению равновесия.
При горизонтальном смещении равновесие заряда q3 устойчивое.
При вертикальном смещении, равнодействующая F31, F32 выталкивает q3
Перейти на страницу:
Два точечных заряда действуют друг на друга с силой, которая обратно пропорциональна квадрату расстояния между ними и прямо пропорциональна произведению их зарядов (без учета знака зарядов)
В различных средах, например в воздухе и в воде, два точечных заряда взаимодействуют с разной силой. Относительная диэлектрическая проницаемость среды характеризуют это различие. Это известная табличная величина . Для воздуха .
Относительная диэлектрическая проницаемость среды характеризуют это различие. Это известная табличная величина . Для воздуха .
Постоянная k определяется как
Направление силы Кулона
Согласно третьему закону Ньютона , силы одной природы возникают попарно, равны по величине, противоположны по направлению. Если взаимодействуют два неодинаковых заряда, сила, с которой больший заряд действует на меньший (В на А) равна силе, с которой меньший действует на больший (А на В).
Интересно, что у различных законов физики есть некоторые общие черты. Вспомним закон тяготения . Сила гравитации также обратно пропорциональны квадрату расстояния, но уже между массами , и невольно возникает мысль, что в этой закономерности таится глубокий смысл. До сих пор никому не удалось представить тяготение и электричество как два разных проявления одной и той же сущности.
Сила и тут изменяется обратно пропорционально квадрату расстояния, но разница в величине электрических сил и сил тяготения поразительна. Пытаясь установить общую природу тяготения и электричества, мы обнаруживаем такое превосходство электрических сил над силами тяготения, что трудно поверить, будто у тех и у других один и тот же источник. Как можно говорить, что одно действует сильнее другого? Ведь все зависит от того, какова масса и каков заряд. Рассуждая о том, насколько сильно действует тяготение, вы не вправе говорить: «Возьмем массу такой-то величины», потому что вы выбираете ее сами. Но если мы возьмем то, что предлагает нам сама Природа (ее собственные числа и меры, которые не имеют ничего общего с нашими дюймами, годами, с нашими мерами), тогда мы сможем сравнивать. Мы возьмем элементарную заряженную частицу, такую, например, как электрон. Две элементарные частицы, два электрона, за счет электрического заряда отталкивают друг друга с силой, обратно пропорциональной квадрату расстояния между ними, а за счет гравитации притягиваются друг к другу опять-таки с силой, обратно пропорциональной квадрату расстояния.
Пытаясь установить общую природу тяготения и электричества, мы обнаруживаем такое превосходство электрических сил над силами тяготения, что трудно поверить, будто у тех и у других один и тот же источник. Как можно говорить, что одно действует сильнее другого? Ведь все зависит от того, какова масса и каков заряд. Рассуждая о том, насколько сильно действует тяготение, вы не вправе говорить: «Возьмем массу такой-то величины», потому что вы выбираете ее сами. Но если мы возьмем то, что предлагает нам сама Природа (ее собственные числа и меры, которые не имеют ничего общего с нашими дюймами, годами, с нашими мерами), тогда мы сможем сравнивать. Мы возьмем элементарную заряженную частицу, такую, например, как электрон. Две элементарные частицы, два электрона, за счет электрического заряда отталкивают друг друга с силой, обратно пропорциональной квадрату расстояния между ними, а за счет гравитации притягиваются друг к другу опять-таки с силой, обратно пропорциональной квадрату расстояния.
Вопрос: каково отношение силы тяготения к электрической силе? Тяготение относится к электрическому отталкиванию, как единица к числу с 42 нулями. Это вызывает глубочайшее недоумение. Откуда могло взяться такое огромное число?
Это вызывает глубочайшее недоумение. Откуда могло взяться такое огромное число?
Люди ищут этот огромный коэффициент в других явлениях природы. Они перебирают всякие большие числа, а если вам нужно большое число, почему не взять, скажем, отношение диаметра Вселенной к диаметру протона — как ни удивительно, это тоже число с 42 нулями. И вот говорят: может быть, этот коэффициент и равен отношению диаметра протона к диаметру Вселенной? Это интересная мысль, но, поскольку Вселенная постепенно расширяется, должна меняться и постоянная тяготения. Хотя эта гипотеза еще не опровергнута, у нас нет никаких свидетельств в ее пользу. Наоборот, некоторые данные говорят о том, что постоянная тяготения не менялась таким образом. Это громадное число по сей день остается загадкой.
Основной закон взаимодействия электрических зарядов был найден Шарлем Кулоном в 1785 г. экспериментально. Кулон установил, что сила взаимодействия между двумя небольшими заряженными металлическими шариками обратно пропорциональна квадрату расстояниямежду ними и зависит от величины зарядови:
где
—коэффициент
пропорциональности .
Силы, действующие на заряды , являются центральными , то есть они направлены вдоль прямой, соединяющей заряды.
Закон Кулона можно записать в векторной форме :,
где —вектор силы, действующей на заряд со стороны заряда,
Радиус-вектор, соединяющий заряд с зарядом;
Модуль радиус-вектора.
Сила, действующая на заряд со стороныравна,.
Закон Кулона в такой форме
справедлив только для взаимодействия точечных электрических зарядов , то есть таких заряженных тел, линейными размерами которых можно пренебречь по сравнению с расстоянием между ними.
выражает силу взаимодействия между неподвижными электрическими зарядами, то есть это электростатический закон.
Формулировка закона Кулона :
Сила
электростатического взаимодействия
между двумя точечными электрическими
зарядами прямо пропорциональна
произведению величин зарядов и обратно
пропорциональна квадрату расстояния
между ними .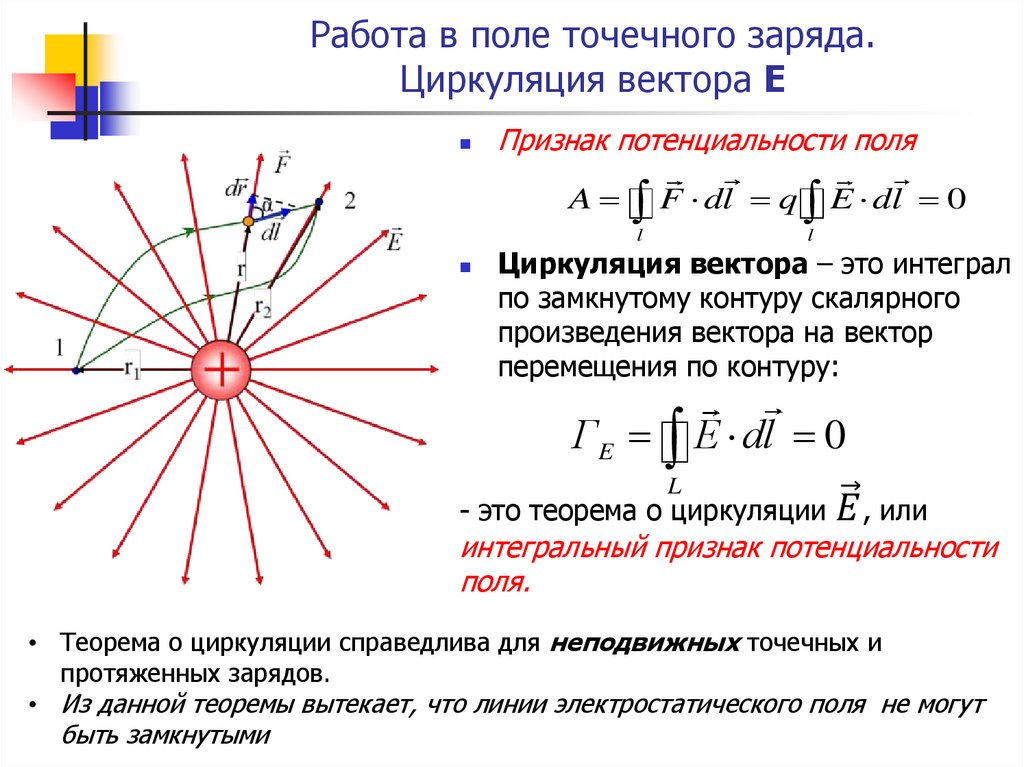
Коэффициент пропорциональности в законе Кулоназависит
от свойств среды
выбора единиц измерения величин, входящих в формулу.
Поэтому можно представить отношением,
где —коэффициент, зависящий только от выбора системы единиц измерения ;
Безразмерная величина, характеризующая электрические свойства среды, называется относительной диэлектрической проницаемостью среды . Она не зависит от выбора системы единиц измерения и равна единице в вакууме.
Тогда закон Кулона примет вид:,
для вакуума ,
тогда —относительная диэлектрическая проницаемость среды показывает, во сколько раз в данной среде сила взаимодействия между двумя точечными электрическими зарядами и, находящимися друг от друга на расстоянии, меньше, чем в вакууме.
В системе СИ коэффициент , и
закон Кулона имеет вид :.
Это рационализированная запись закона К улона.
Электрическая
постоянная,
.
В системе СГСЭ ,.
В векторной форме закон Кулона принимает вид
где —вектор силы, действующей на заряд со стороны заряда ,
Радиус-вектор, соединяющий заряд с зарядом
r –модуль радиус-вектора .
Всякое заряженное тело состоит из множества точечных электрических зарядов, поэтому электростатическая сила, с которой одно заряженное тело действует на другое, равна векторной сумме сил, приложенных ко всем точечным зарядам второго тела со стороны каждого точечного заряда первого тела.
1.3.Электрическое поле. Напряженность.
Пространство, в котором находится электрический заряд, обладает определенными физическими свойствами .
На всякий другой заряд, внесенный в это пространство, действуют электростатические силы Кулона.
Если в каждой точке пространства действует сила, то говорят, что в этом пространстве существует силовое поле.
Поле наряду с
веществом является формой материи.
Если поле стационарно, то есть не меняется во времени, и создается неподвижными электрическими зарядами, то такое поле называется электростатическим.
Электростатика изучает только электростатические поля и взаимодействия неподвижных зарядов.
Для характеристики электрического поля вводят понятие напряженности . Напряженность ю в каждой точке электрического поля называется вектор , численно равный отношению силы, с которой это поле действует на пробный положительный заряд, помещенный в данную точку, и величины этого заряда, и направленный в сторону действия силы.
Пробный заряд , который вносится в поле, предполагается точечным и часто называется пробным зарядом.
— Он не участвует в создании поля, которое с его помощью измеряется.
Предполагается, что этот заряд не
искажает исследуемого поля, то есть он достаточно мал и не вызывает
перераспределения зарядов, создающих
поле.
Если на пробный точечный заряд поле действует силой, то напряженность.
Единицы напряженности:
В системе СИ выражение для поля точечного заряда :
В векторной форме:
Здесь – радиус-вектор, проведенный из зарядаq , создающего поле, в данную точку.
Таким образом,векторы напряженности электрического поля точечного заряда q во всех точках поля направлены радиально (рис.1.3)
— от заряда, если он положительный, «исток»
— и к заряду, если он отрицательный «сток»
Для графической интерпретации электрического поля вводят понятие силовой линии или линии напряженности . Это
кривая , касательная в каждой точке к которой совпадает с вектором напряженности .
Линия напряженности начинается на положительном заряде и заканчивается на отрицательном.
Линии напряженности
не пересекаются, так как в каждой точке
поля вектор напряженности имеет лишь
одно направление.
Самые часто задаваемые вопросы
Возможно ли, изготовить печать на документе по предоставленному образцу? Ответ Да, возможно. Отправьте на наш электронный адрес скан-копию или фото хорошего качества, и мы изготовим необходимый дубликат.
Какие виды оплаты вы принимаете?
Ответ
Вы можете оплатить документ во время получения на руки у курьера, после того, как проверите правильность заполнения и качество исполнения диплома. Также это можно сделать в офисе почтовых компаний, предлагающих услуги наложенного платежа.
Все условия доставки и оплаты документов расписаны в разделе «Оплата и доставка». Также готовы выслушать Ваши предложения по условиям доставки и оплаты за документ.
Могу ли я быть уверена, что после оформления заказа вы не исчезнете с моими деньгами?
Ответ
В сфере изготовления дипломов у нас достаточно длительный опыт работы. У нас есть несколько сайтов, который постоянно обновляются. Наши специалисты работают в разных уголках страны, изготавливая свыше 10 документов день. За годы работы наши документы помогли многим людям решить проблемы трудоустройства или перейти на более высокооплачиваемую работу. Мы заработали доверие и признание среди клиентов, поэтому у нас совершенно нет причин поступать подобным образом. Тем более, что это просто невозможно сделать физически: Вы оплачиваете свой заказ в момент получения его на руки, предоплаты нет.
За годы работы наши документы помогли многим людям решить проблемы трудоустройства или перейти на более высокооплачиваемую работу. Мы заработали доверие и признание среди клиентов, поэтому у нас совершенно нет причин поступать подобным образом. Тем более, что это просто невозможно сделать физически: Вы оплачиваете свой заказ в момент получения его на руки, предоплаты нет.
Могу я заказать диплом любого ВУЗа? Ответ В целом, да. Мы работаем в этой сфере почти 12 лет. За это время сформировалась практически полная база выдаваемых документов почти всех ВУЗов страны и за разные года выдачи. Все, что Вам нужно – выбрать ВУЗ, специальность, документ, и заполнить форму заказа.
Что делать при обнаружении в документе опечаток и ошибок?
Ответ
Получая документ у нашего курьера или в почтовой компании, мы рекомендуем тщательно проверить все детали. Если будет обнаружена опечатка, ошибка или неточность, Вы имеете право не забирать диплом, при этом нужно указать обнаруженные недочеты лично курьеру или в письменном виде, отправив письмо на электронную почту.
В кратчайшие сроки мы исправим документ и повторно отправим на указанный адрес. Разумеется, пересылка будет оплачена нашей компанией.
Чтобы избежать подобных недоразумений, перед тем, как заполнять оригинальный бланк, мы отправляем на почту заказчику макет будущего документа, для проверки и утверждения окончательного варианта. Перед отправкой документа курьером или почтой мы также делаем дополнительное фото и видео (в т. ч. в ультрафиолетовом свечении), чтобы Вы имели наглядное представление о том, что получите в итоге.
Что нужно сделать, чтобы заказать диплом в вашей компании?
Ответ
Для заказа документа (аттестата, диплома, академической справки и др.) необходимо заполнить онлайн-форму заказа на нашем сайте или сообщить свою электронную почту, чтобы мы выслали вам бланк анкеты, который нужно заполнить и отправить обратно нам.
Если вы не знаете, что указать в каком-либо поле формы заказа/анкеты, оставьте их незаполненными. Всю недостающую информацию мы потому уточним в телефонном режиме.
Последние отзывы
Валентина:
Вы спасли нашего сына от увольнения! Дело в том что недоучившись в институте, сын пошел в армию. А вернувшись, восстанавливаться не захотел. Работал без диплома. Но недавно начали увольнять всех, кто не имеет «корочки. Поэтому решили обратиться к вам и не пожалели! Теперь спокойно работает и ничего не боится! Спасибо!
Тема 1.1 ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ.
Раздел 1 ОСНОВЫ ЭЛЕКТРОДИНАМИКИ
1. Электризация тел. Понятие о величине заряда.
Закон сохранения заряда.
2. Силы взаимодействия между зарядами.
Закон Кулона.
3. Диэлектрическая проницаемость среды.
4. Международная система единиц в электричестве.
1. Электризация тел. Понятие о величине заряда.
Закон сохранения заряда.
Если две поверхности привести в плотное соприкосновение, то возможен переход электронов с одной поверхности на другую, при этом на этих поверхностях появляются электрические заряды.
Это явление называется ЭЛЕКТРИЗАЦИЕЙ. При трении площадь плотного соприкосновения поверхностей увеличивается, увеличивается и величина заряда на поверхности – такое явление называют ЭЛЕКТРИЗАЦИЕЙ ТРЕНИЕМ.
В процессе электризации происходит перераспределение зарядов, в результате которого обе поверхности заряжаются равными по величине, противоположными по знаку зарядами.
Т.к. все электроны имеют одинаковые заряды (отриц.) е = 1,6 10Кл, то для того, чтобы определить величину заряда на поверхности (q), необходимо знать, сколько электронов в избытке или недостатке на поверхности (N) и заряд одного электрона.
В процессе электризации новые заряды не появляются и не исчезают, а только происходит их перераспределение между телами или частями тела, поэтому суммарный заряд замкнутой системы тел остается постоянным, в этом и заключается смысл ЗАКОНА СОХРАНЕНИЯ ЗАРЯДА.
2. Силы взаимодействия между зарядами.
Закон Кулона.
Электрические заряды взаимодействуют между собой, находясь на расстоянии, при этом одноименные заряды отталкиваются, а разноименные – притягиваются.
Впервые выяснил опытным путем отчего зависит сила взаимодействия между зарядами французский ученый Кулон и вывел закон, названный законом КУЛОНА. Закон фундаментальный т.е. основан на опытах. При выводе этого закона Кулон использовал крутильные весы.
3) k – коэффициент, выражающий зависимость от окружающей среды.
Формула закона Кулона.
Сила взаимодействия между двумя неподвижными точечными зарядами прямо пропорциональны произведению величин этих зарядов и обратно пропорциональна квадрату расстояний между ними, и зависит от среды, в которой находятся эти заряды, и направлена вдоль прямой, соединяющей центры этих зарядов.
3. Диэлектрическая проницаемость среды.
Е — диэлектрическая проницаемость среды, зависит от окружающей заряды среды.
Е = 8,85*10 — физическая постоянная, диэлектрическая проницаемость вакуума.
Е – относительная диэлектрическая проницаемость среды, показывает во сколько раз сила взаимодействия между точечными зарядами в вакууме больше чем в данной среде.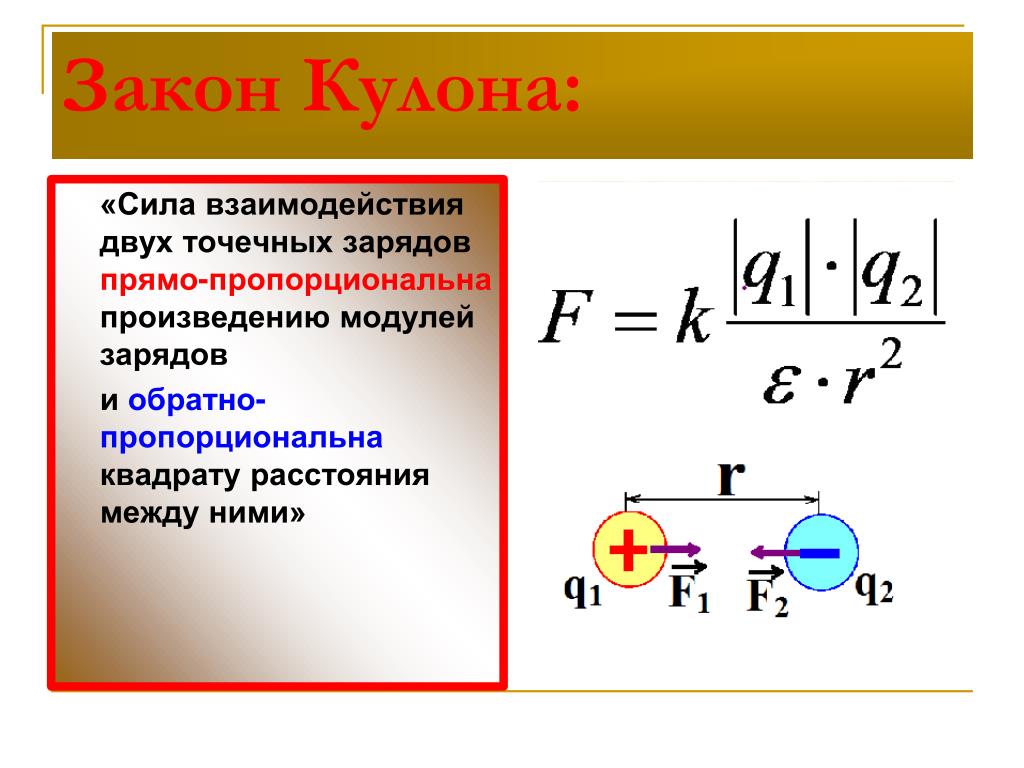 В вакууме самое сильное взаимодействие между зарядами.
В вакууме самое сильное взаимодействие между зарядами.
4. Международная система единиц в электричестве.
Основной единицей для электричества в системе «СИ» является сила тока в 1А, все остальные единицы измерения являются производными от 1Ампера.
1Кл – количество электрического заряда, переносимого заряженными частицами через поперечное сечение проводника при силе тока в 1А за 1с.
Тема 1.2 ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
1. Электрическое поле – как особый вид материи.
6. Связь разности потенциалов с напряженностью электрического поля.
1. Электрическое поле – как особый вид материи.
В природе как вид материи существует электромагнитное поле. В разных случаях электромагнитное поле проявляет себя по — разному, так например около неподвижных зарядов проявляет себя только электрическое поле, которое называют электростатическим. Около подвижных зарядов можно обнаружить как электрическое, так и магнитное поля, которые в совокупности представляют ЭЛЕКТРОМАГНИТНЫЕ ПОЛЯ.
Рассмотрим свойства электростатических полей:
1) Электростатическое поле создается неподвижными зарядами, обнаружить такие поля можно
с помощью пробных зарядов (небольшой по величине положительный заряд), т.к. только на них электрическое поле оказывает силовое действие, которое подчиняется закону Кулона.
2. Напряженность электрического поля.
Эл.поле как вид материи обладает энергией, массой, распространяется в пространстве с конечной скоростью и теоретических границ не имеет.
Практически считается, что поля нет если оно не оказывает заметного действия на пробные заряды.
Так как обнаружить поле можно с помощью силового действия на пробные заряды, то основной характеристикой электрического поля является напряженность.
Если в одну и ту же точку электрического поля вносить разные по величине пробные заряды, то между действующей силой и величиной пробного заряда прямая пропорциональная зависимость.
Коэффициентом пропорциональности между действующей силой и величиной заряда является напряженность Е.
Е = -формула расчета напряженности электрического поля, если q = 1 Кл, то | E | = | F |
Напряженность является силовой характеристикой точек электрического поля, т.к. она численно равна силе, действующей на заряд в 1 Кл в данной точке электрического поля.
Напряженность – величина векторная, вектор напряженности по направлению совпадает с вектором силы, действующей на положительный заряд в данной точке электрического поля.
3. Линии напряженности электрического поля. Однородное электрическое поле.
Для того, чтобы наглядно можно было изображать электрическое поле, т.е. графически, используют линии напряженности электрического поля. Это такие линии, иначе называемые силовыми линиями, касательные к которым по направлению совпадают с векторами напряженности в точках электрического поля через которые эти линии проходят,
Линии напряженности обладают следующими свойствами:
1) Начинаются на полож. зарядах, заканчиваются – на отрицательных, или начинаются на положител. зарядах и уходят в бесконечность, или приходят из бесконечности и заканчиваются на положительных зарядах..
зарядах и уходят в бесконечность, или приходят из бесконечности и заканчиваются на положительных зарядах..
2) Эти линии непрерывны и нигде не пересекаются.
3) Густота линий (кол-во линий на единицу площади поверхности) и напряженность электрического поля находятся в прямой и пропорциональной зависимости.
В однородном электрическом поле напряженность во всех точках поля одинакова, графически такие поля изображаются параллельными линиями на равном расстоянии друг от друга. Такое поле можно получить между двумя параллельными плоскими заряженными пластинами на маленьком расстоянии друг от друга.
4. Работа по перемещению заряда в электрическом поле.
Поместим в однородное электрическое поле электрический заряд. Со стороны поля на заряд будут действовать силы. Если заряд перемещать, то может совершаться работа.
Совершенная работа на участках:
А = q E d — формула расчета работы по перемещению заряда в электрическом поле.
Вывод: Работа по перемещению заряда в электрическом поле от формы траектории не зависит, а она зависит от величины перемещаемого заряда (q) , напряженности поля (Е), а также от выбора начальной и конечной точек перемещения (d).
Если заряд в электрическом поле перемещать по замкнутому контуру, то совершаемая работа будет равна 0. Такие поля называются потенциальными полями. Тела в таких полях обладают потенциальной энергией, т.о. электрический заряд в любой точке электрического поля обладает энергией и совершаемая работа в электрическом поле равна разности потенциальных энергий заряда в начальной и конечной точках перемещения.
5. Потенциал. Разность потенциалов. Напряжение.
Если в данную точку электрического поля помещать разные по величине заряды, то потенциальная энергия заряда и его величина находятся в прямой пропорциональной зависимости.
-(фи) потенциал точки электрического поля
Потенциал является энергетической характеристикой точек электрического поля, т.к. он численно равен потенциальной энергии заряда в 1 Кл в данной точке электрического поля.
На равных расстояниях от точечного заряда потенциалы точек поля одинаковы. Эти точки образуют поверхность равного потенциала, и такие поверхности называются эквипотенциальными поверхностями.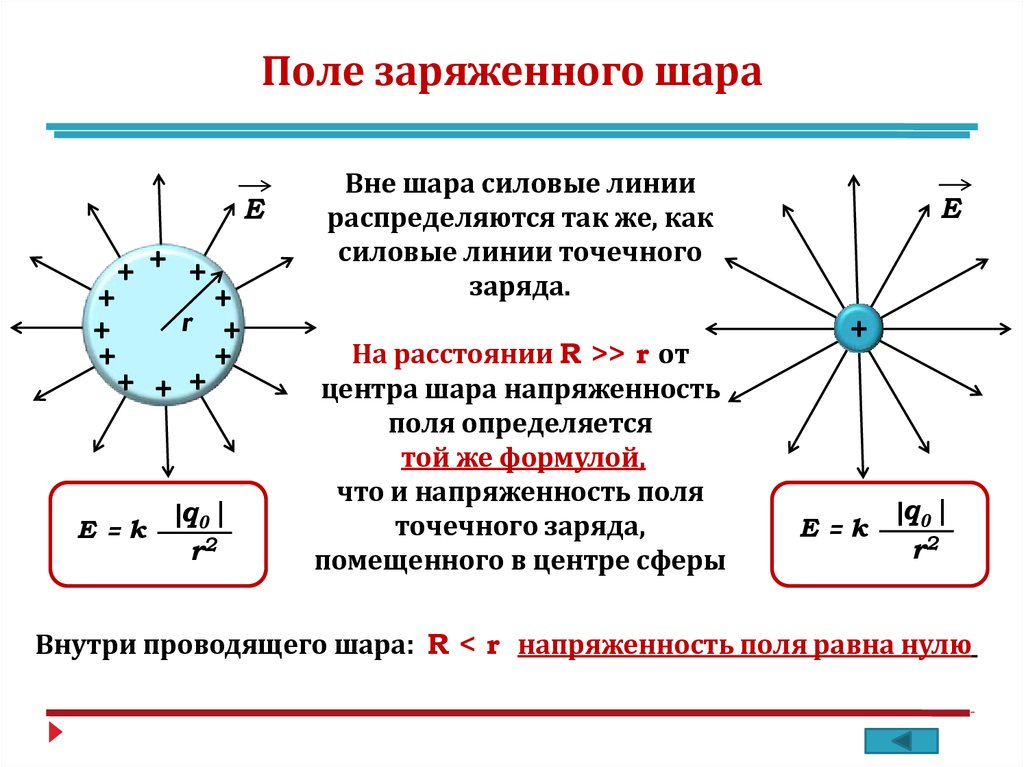 На плоскости это окружности, в пространстве – это сферы.
На плоскости это окружности, в пространстве – это сферы.
Напряжение
Формулы расчета работы по перемещению заряда в электрическом поле.
1В – напряжение между точками электрического поля при перемещении в которых заряда в 1Кл совершается работа в 1 Дж.
Формула, устанавливающая связь между напряженностью электрического поля, напряжением и разностью потенциалов.
Напряженность численно равна напряжению или разности потенциалов между двумя точками поля взятыми вдоль одной силовой линии на расстоянии 1м. Знак (-) означает, что вектор напряженности всегда направлен в сторону точек поля с уменьшающимся потенциалом.
19.3 Электрический потенциал, обусловленный точечным зарядом – College Physics
Глава 19 Электрический потенциал и электрическое поле
Резюме
- Объясните точечные заряды и составьте уравнение для электрического потенциала точечного заряда.
- Различать электрический потенциал и электрическое поле.

- Определите электрический потенциал точечного заряда при заданном заряде и расстоянии.
Точечные заряды, такие как электроны, являются одними из основных строительных блоков материи. Кроме того, сферические распределения заряда (как на металлическом шаре) создают внешние электрические поля точно так же, как точечный заряд. Электрический потенциал, обусловленный точечным зарядом, является, таким образом, случаем, который нам необходимо рассмотреть. Использование вычислений для определения работы, необходимой для перемещения пробного заряда [латекс]{q}[/латекс] с большого расстояния на расстояние [латекс]{r}[/латекс] от точечного заряда [латекс]{Q }[/latex], и учитывая связь между работой и потенциалом [латекс]{(W = -q \Delta V)}[/latex], можно показать, что 92 .}[/латекс]
Электрический потенциал
В точечного зарядаЭлектрический потенциал [латекс] {В}[/латекс] точечного заряда определяется выражением
[латекс] {В =}[/латекс] [латекс]{\ frac{kQ}{r}}[/latex] [latex]{( \text{Point Charge} ),}[/latex]
Потенциал на бесконечности выбран равным нулю. 2}}.[/латекс]
2}}.[/латекс]
Напомним, что электрический потенциал [латекс]{V}[/латекс] является скаляром и не имеет направления, тогда как электрическое поле [латекс]\textbf{E}[/латекс] является вектором. Чтобы найти напряжение из-за комбинации точечных зарядов, вы складываете отдельные напряжения в виде чисел. Чтобы найти полное электрическое поле, вы должны сложить отдельные поля в виде векторов , принимая во внимание величину и направление. Это согласуется с тем фактом, что [латекс]{V}[/латекс] тесно связан с энергией, скаляром, тогда как [латекс]\текстbf{Е}[/латекс] тесно связан с силой, вектором.
Пример 1. Какое напряжение создает небольшой заряд на металлическом шарике?
Заряды статического электричества обычно находятся в диапазоне от нанокулонов (нКл) до микрокулонов [латекс]{( \mu \text{C})}[/latex]. Чему равно напряжение на расстоянии 5,00 см от центра металлического шара диаметром 1 см, имеющего статический заряд -3,00 нКл?
Стратегия
Как мы обсуждали в главе 18 Электрический заряд и электрическое поле, заряд на металлическом шаре распространяется равномерно и создает поле, похожее на поле точечного заряда, расположенного в его центре.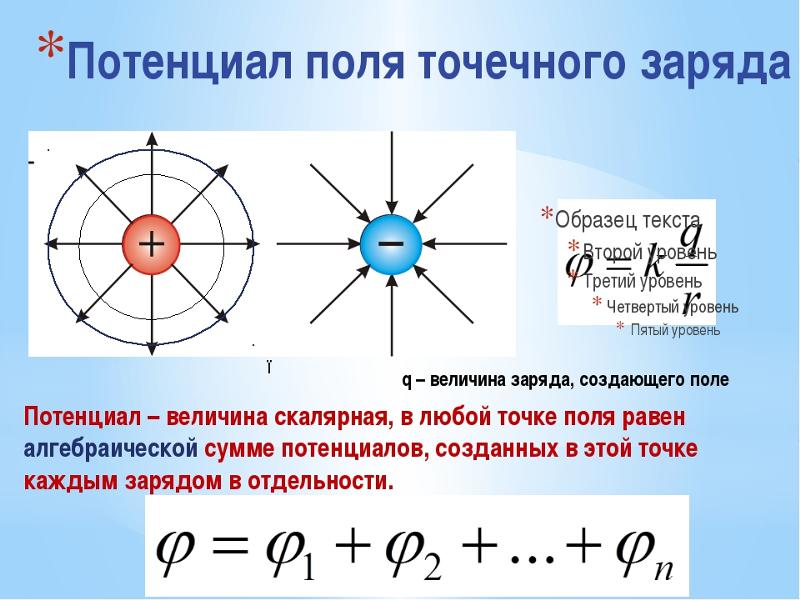 Таким образом, мы можем найти напряжение, используя уравнение [latex]{V = kQ/r}[/latex] . 9{2} \;\text{m}})} \\[1em] & {-539 \;\text{V}}. \end{array}[/latex]
Таким образом, мы можем найти напряжение, используя уравнение [latex]{V = kQ/r}[/latex] . 9{2} \;\text{m}})} \\[1em] & {-539 \;\text{V}}. \end{array}[/latex]
Обсуждение
Отрицательное значение напряжения означает, что положительный заряд будет притягиваться с большего расстояния, поскольку потенциал ниже (более отрицательный), чем на больших расстояниях. И наоборот, отрицательный заряд будет отталкиваться, как и ожидалось.
Пример 2. Что такое избыточный заряд генератора Ван де Граафа
Демонстрационный генератор Ван де Граафа имеет металлическую сферу диаметром 25,0 см, которая создает напряжение 100 кВ вблизи своей поверхности. (См. рис. 1.) Какой избыточный заряд находится на сфере? (Предположим, что каждое числовое значение здесь показано тремя значащими цифрами.)
Рисунок 1. Напряжение этого демонстрационного генератора Ван де Граафа измеряется между заряженной сферой и землей. Потенциал Земли принимается равным нулю в качестве эталона.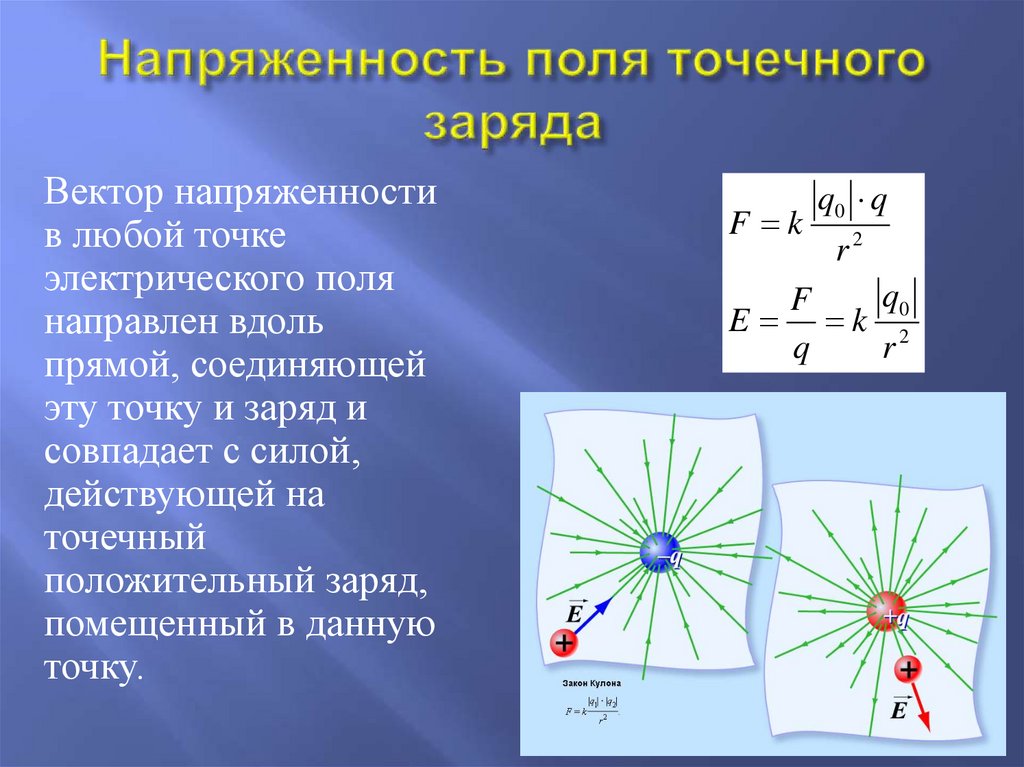 Потенциал заряженной проводящей сферы такой же, как и у равного точечного заряда в ее центре.
Потенциал заряженной проводящей сферы такой же, как и у равного точечного заряда в ее центре.Стратегия
Потенциал на поверхности будет таким же, как у точечного заряда в центре сферы на расстоянии 12,5 см. (Радиус сферы равен 12,5 см.) Таким образом, мы можем определить избыточный заряд, используя уравнение 9{-6} \;\text{C} = 1,39 \;\mu \text{C}}. \end{array}[/latex]
Обсуждение
Это относительно небольшой заряд, но он производит довольно большое напряжение. У нас есть еще одно указание на то, что трудно хранить изолированные заряды.
Напряжения в обоих этих примерах можно измерить с помощью измерителя, который сравнивает измеренный потенциал с потенциалом земли. Потенциал земли часто принимается равным нулю (вместо того, чтобы принимать потенциал на бесконечности равным нулю). Важна именно разность потенциалов между двумя точками, и очень часто неявно предполагается, что какая-то точка отсчета, например Земля или очень удаленная точка, имеет нулевой потенциал.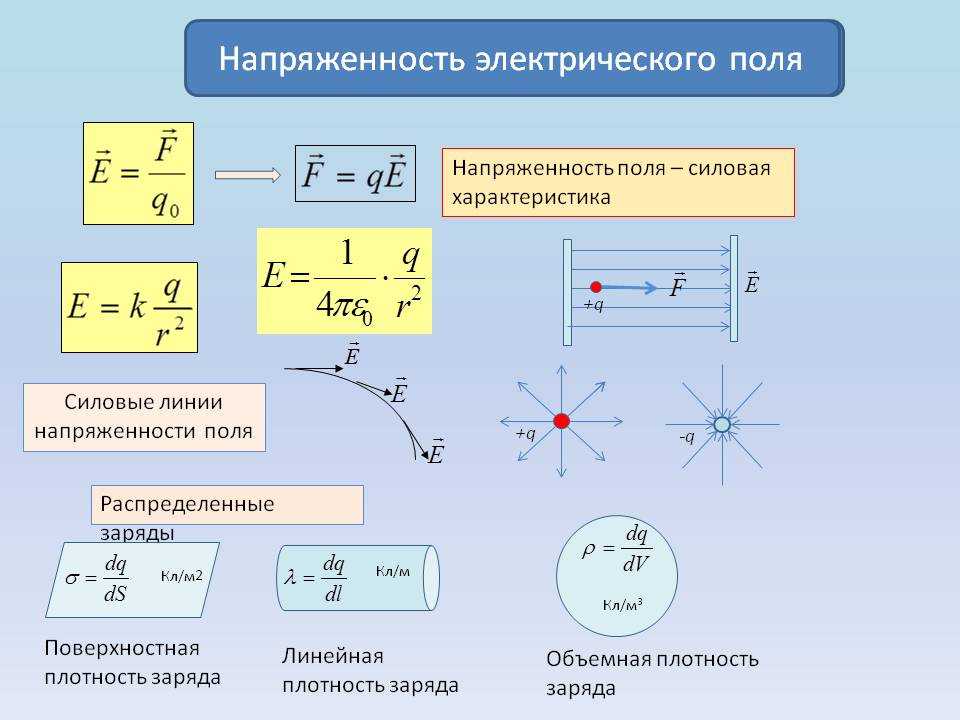 Как отмечалось в главе 19.1 Электрическая потенциальная энергия: разность потенциалов, это аналогично принятию уровня моря как [латекс]{h = 0}[/латекс] при рассмотрении потенциальной энергии гравитации, [латекс]{\текст{PE}_g = mgh}[/ латекс].
Как отмечалось в главе 19.1 Электрическая потенциальная энергия: разность потенциалов, это аналогично принятию уровня моря как [латекс]{h = 0}[/латекс] при рассмотрении потенциальной энергии гравитации, [латекс]{\текст{PE}_g = mgh}[/ латекс].
- Электрический потенциал точечного заряда равен [латекс]{В = кОм/р}[/латекс].
- Электрический потенциал — это скаляр, а электрическое поле — это вектор. Сложение напряжений в виде чисел дает напряжение, обусловленное комбинацией точечных зарядов, тогда как сложение отдельных полей в виде векторов дает общее электрическое поле. 9{-10} \;\text{m}}[/latex] от протона (среднее расстояние между протоном и электроном в атоме водорода)?
3: (а) Шар имеет поверхность, равномерно заряженную 1,00 Кл. На каком расстоянии от его центра находится потенциал 5,00 МВ? б) Что ваш ответ говорит о практическом аспекте выделения такого большого заряда?
4: На каком расстоянии от точечного заряда [латекс]{1,00 мкм \текст{С}}[/латекс] будет потенциал 100 В? На каком расстоянии это будет [латекс]{2.
 2 \;\text{V}}[/латекс]? 9{-14} \;\text{m}}[/latex] из фрагмента, содержащего 46 протонов? б) Какова потенциальная энергия в МэВ одноименно заряженного фрагмента на этом расстоянии?
2 \;\text{V}}[/латекс]? 9{-14} \;\text{m}}[/latex] из фрагмента, содержащего 46 протонов? б) Какова потенциальная энергия в МэВ одноименно заряженного фрагмента на этом расстоянии?8: Исследовательский генератор Ван де Граафа имеет металлический шар диаметром 2,00 м с зарядом 5,00 мКл. а) Каков потенциал вблизи его поверхности? б) На каком расстоянии от его центра находится потенциал 1,00 МВ? (в) Атом кислорода с тремя недостающими электронами высвобождается вблизи генератора Ван де Граафа. Какова его энергия в МэВ на этом расстоянии?
9: Электростатический распылитель краски представляет собой металлическую сферу диаметром 0,200 м с потенциалом 25,0 кВ, которая отбрасывает капли краски на заземленный объект. а) Какой заряд находится на шаре? б) Какой заряд должен иметь капля краски массой 0,100 мг, чтобы достичь предмета со скоростью 10,0 м/с?
10: В одном из классических экспериментов по ядерной физике в начале ХХ века альфа-частица была ускорена к ядру золота, и ее траектория была существенно отклонена кулоновским взаимодействием.
 Если энергия двухзарядного альфа-ядра была 5,00 МэВ, насколько близко к ядру золота (79протоны) может ли он прийти до того, как отклонится?
Если энергия двухзарядного альфа-ядра была 5,00 МэВ, насколько близко к ядру золота (79протоны) может ли он прийти до того, как отклонится?11: а) Каков потенциал между двумя точками, расположенными на расстоянии 10 см и 20 см от точечного заряда [латекс]{3,0 мкм \text{C}}[/латекс]? б) В какое место следует переместить точку на расстоянии 20 см, чтобы разность потенциалов увеличилась в два раза?
12: необоснованные результаты
(a) Какова конечная скорость электрона, ускоренного из состояния покоя при напряжении 25,0 МВ отрицательно заряженным выводом Ван де Граафа?
(b) Что неразумного в этом результате?
(c) Какие допущения ответственны?
19.3 Электрический потенциал, обусловленный точечным зарядом – College Physics 2e
Цели обучения
К концу этого раздела вы сможете:
- Объясните точечные заряды и составьте уравнение для электрического потенциала точечного заряда.

- Различать электрический потенциал и электрическое поле.
- Определите электрический потенциал точечного заряда при заданном заряде и расстоянии.
Точечные заряды, такие как электроны, являются одними из основных строительных блоков материи. Кроме того, сферические распределения заряда (как на металлическом шаре) создают внешние электрические поля точно так же, как точечный заряд. Электрический потенциал, обусловленный точечным зарядом, является, таким образом, случаем, который нам необходимо рассмотреть. Использование исчисления для нахождения работы, необходимой для перемещения пробного заряда qq с большого расстояния на расстояние rr от точечного заряда QQ , и учитывая связь между работой и потенциалом W=–qΔVW=–qΔV, можно показать, что электрический потенциал VV точечного заряда равен
В знак равно kQ р ( Начисление очков ) , В знак равно kQ р ( Начисление очков ) ,
19,37
где k — константа, равная 9,0×109Н·м2/C29,0×109 Н·м2/C2.

Электрический потенциал VV точечного заряда
Электрический потенциал VV точечного заряда определяется как
В знак равно kQ р ( Начисление очков ) . В знак равно kQ р ( Начисление очков ) .
19,38
Потенциал на бесконечности выбран равным нулю. Таким образом, VV для точечного заряда уменьшается с расстоянием, тогда как EE для точечного заряда уменьшается с квадратом расстояния:
E=Fq=kQr2.E=Fq=kQr2.
19,39
Напомним, что электрический потенциал VV является скаляром и не имеет направления, тогда как электрическое поле EE является вектором. Чтобы найти напряжение из-за комбинации точечных зарядов, вы складываете отдельные напряжения в виде чисел. Чтобы найти полное электрическое поле, вы должны сложить отдельные поля в виде векторов , принимая во внимание величину и направление.
 Это согласуется с тем фактом, что VV тесно связан с энергией, скаляром, тогда как EE тесно связан с силой, вектором.
Это согласуется с тем фактом, что VV тесно связан с энергией, скаляром, тогда как EE тесно связан с силой, вектором.Пример 19,6
Какое напряжение создает небольшой заряд на металлическом шаре?
Заряды статического электричества обычно находятся в диапазоне от нанокулонов nCnC до микрокулонов µCµC. Чему равно напряжение на расстоянии 5,00 см от центра металлического шара диаметром 1 см, имеющего статический заряд от −3,00 нКл до 3,00 нКл?
Стратегия
Как мы обсуждали в разделе «Электрический заряд и электрическое поле», заряд на металлическом шаре распространяется равномерно и создает поле, похожее на поле точечного заряда, расположенного в его центре. Таким образом, мы можем найти напряжение, используя уравнение V=kQ/rV=kQ/r.
Решение
Подставляя известные значения в выражение для потенциала точечного заряда, получаем –539 В.В=kQr=8,99×109 Н·м2/C2–3,00×10–9 C5,00×10–2 м=–539 В.

19,40
Обсуждение
Отрицательное значение напряжения означает положительный заряд будет притягиваться с большего расстояния, так как потенциал ниже (более отрицательный), чем на больших расстояниях. И наоборот, отрицательный заряд будет отталкиваться, как и ожидалось.
Пример 19,7
Что такое избыточный заряд генератора Ван де Граафа
Демонстрационный генератор Ван де Граафа имеет металлическую сферу диаметром 25,0 см, которая производит напряжение 100 кВ вблизи своей поверхности. (См. рис. 19.7.) Какой избыточный заряд находится на сфере? (Предположим, что здесь каждое числовое значение представлено тремя значащими цифрами.)
Рисунок 19,7 Напряжение этого демонстрационного генератора Ван де Граафа измеряется между заряженной сферой и землей. Потенциал Земли принимается равным нулю в качестве эталона. Потенциал заряженной проводящей сферы такой же, как и у равного точечного заряда в ее центре.

Стратегия
Потенциал на поверхности будет таким же, как у точечного заряда в центре сферы на расстоянии 12,5 см. (Радиус сферы равен 12,5 см.) Таким образом, мы можем определить избыточный заряд, используя уравнение
V=kQr.V=kQr.
19,41
Решение
Решение для QQ и ввод известных значений дают
Q=rVk=0,125м100×103В8,99×109 Н·м2/C2=1,39×10–6C=1,39 мкКл. m100×103V8,99×109 Н·м2/C2=1,39×10–6C=1,39 мкКл.
19.42
Обсуждение
Это относительно небольшой заряд, но выдает довольно большое напряжение. У нас есть еще одно указание на то, что трудно хранить изолированные заряды.
Напряжения в обоих этих примерах можно измерить с помощью измерителя, который сравнивает измеренный потенциал с потенциалом земли. Потенциал земли часто принимается равным нулю (вместо того, чтобы принимать потенциал на бесконечности равным нулю).
 Важна именно разность потенциалов между двумя точками, и очень часто неявно предполагается, что какая-то точка отсчета, например Земля или очень удаленная точка, имеет нулевой потенциал. Как отмечено в книге «Электрическая потенциальная энергия: разность потенциалов», это аналогично принятию уровня моря как h=0h=0 при рассмотрении потенциальной энергии гравитации, PEg=mghPEg=mgh.
Важна именно разность потенциалов между двумя точками, и очень часто неявно предполагается, что какая-то точка отсчета, например Земля или очень удаленная точка, имеет нулевой потенциал. Как отмечено в книге «Электрическая потенциальная энергия: разность потенциалов», это аналогично принятию уровня моря как h=0h=0 при рассмотрении потенциальной энергии гравитации, PEg=mghPEg=mgh.Новый взгляд на концепцию поля – Колледж физики, главы 1-17
18 Электрический заряд и электрическое поле
Резюме
- Описать силовое поле и рассчитать напряженность электрического поля, создаваемого точечным зарядом.
- Рассчитайте силу, действующую на пробный заряд со стороны электрического поля.
- Объясните взаимосвязь между электрической силой (F) на испытательном заряде и напряженностью электрического поля (E).
Контактные силы, такие как между бейсбольным мячом и битой, объясняются в малом масштабе взаимодействием зарядов в атомах и молекулах в непосредственной близости.
 Они взаимодействуют через силы, включающие Кулоновская сила . Действие на расстоянии — это сила между объектами, которые находятся недостаточно близко, чтобы их атомы могли «соприкоснуться». То есть они разделены более чем несколькими атомными диаметрами.
Они взаимодействуют через силы, включающие Кулоновская сила . Действие на расстоянии — это сила между объектами, которые находятся недостаточно близко, чтобы их атомы могли «соприкоснуться». То есть они разделены более чем несколькими атомными диаметрами.Например, заряженная резиновая расческа притягивает нейтральные кусочки бумаги на расстоянии под действием кулоновской силы. Очень полезно представить объект, окруженный в пространстве силовым полем . Силовое поле переносит силу на другой объект (называемый тестовым объектом) на некотором расстоянии.
Поле — это способ концептуализации и отображения силы, которая окружает любой объект и действует на другой объект на расстоянии без видимой физической связи. Например, гравитационное поле, окружающее Землю (и все другие массы), представляет собой гравитационную силу, которая могла бы возникнуть, если бы в данной точке поля была помещена другая масса.
Точно так же кулоновское силовое поле, окружающее любой заряд, распространяется по всему пространству.
Рис. 1. Поле кулоновских сил, обусловленное положительным зарядом Q , действует на два разных заряда. Оба заряда находятся на одинаковом расстоянии от Q . (a) Поскольку q 1 положительна, сила F 1 , действующая на нее, является отталкивающей. (b) Заряд Q 2 является отрицательным и больше по величине, чем Q 1 , и поэтому сила F 2 ACTIDE AT IT ATTS ATTRY IS ATTRY ATS 7777777777777 2 . 2}[/latex], для точечный заряд (частица, имеющая заряд [латекс]\boldsymbol{Q}[/латекс]), действующий на пробный заряд [латекс]\boldsymbol{q}[/латекс] на расстоянии [латекс]\boldsymbol {r}[/latex] (см. [ссылка]). Как величина, так и направление кулоновского силового поля зависят от [латекс]\boldsymbol{Q}[/латекс] и пробного заряда [латекс]\boldsymbol{q}[/латекс].
2}[/latex], для точечный заряд (частица, имеющая заряд [латекс]\boldsymbol{Q}[/латекс]), действующий на пробный заряд [латекс]\boldsymbol{q}[/латекс] на расстоянии [латекс]\boldsymbol {r}[/latex] (см. [ссылка]). Как величина, так и направление кулоновского силового поля зависят от [латекс]\boldsymbol{Q}[/латекс] и пробного заряда [латекс]\boldsymbol{q}[/латекс]. Ф 1 . Таким образом, кулоновское силовое поле не является уникальным в любой точке пространства, поскольку оно зависит от пробных зарядов 9.0047 q 1 и q 2 а также плата Q .
Ф 1 . Таким образом, кулоновское силовое поле не является уникальным в любой точке пространства, поскольку оно зависит от пробных зарядов 9.0047 q 1 и q 2 а также плата Q .Для упрощения мы бы предпочли иметь поле, зависящее только от [латекс]\boldsymbol{Q}[/латекс], а не от тестового заряда [латекс]\жирныйсимвол{q}[/латекс]. Электрическое поле определяется таким образом, что оно представляет собой только создающий его заряд и уникально в каждой точке пространства. В частности, электрическое поле [латекс]\boldsymbol{E}[/латекс] определяется как отношение кулоновской силы к пробному заряду:
[латекс]\boldsymbol{E =}[/латекс] [латекс]\boldsymbol{\frac{F}{q}}[/латекс],
где [латекс]\boldsymbol{F}[/латекс] — электростатическая сила (или кулоновская сила), действующая на положительный пробный заряд
[латекс]\boldsymbol{q}[/латекс]. 2 }[/латекс] . Таким образом, величина электрического поля [латекс]\boldsymbol{E}[/латекс] для точечного заряда равна 92}}[/латекс]
2 }[/латекс] . Таким образом, величина электрического поля [латекс]\boldsymbol{E}[/латекс] для точечного заряда равна 92}}[/латекс]Таким образом видно, что электрическое поле зависит только от заряда [латекс]\boldsymbol{Q}[/латекс] и расстояния [латекс]\boldsymbol{r}[/латекс]; он полностью не зависит от тестового заряда [латекс]\boldsymbol{q}[/латекс].
Расчет электрического поля точечного заряда
Расчет напряженности и направления электрического поля [латекс]\boldsymbol{E}[/латекс], создаваемого точечным зарядом 2,00 нКл (нанокулоны) на расстоянии 5,00 мм от заряда. 95 \;\textbf{N} / \textbf{C}.} \end{array}[/latex]
Обсуждение
Эта напряженность электрического поля одинакова в любой точке на расстоянии 5,00 мм от заряда [latex]\boldsymbol{Q}[/latex], который создает поле. Он положительный, что означает, что он имеет направление, указывающее в сторону от заряда [латекс]\boldsymbol{Q}[/латекс].
Расчет силы, действующей на точечный заряд электрическим полем
Какую силу электрическое поле, найденное в предыдущем примере, действует на точечный заряд [латекс]\boldsymbol{-0,250 \;\mu \textbf{C}} [/латекс]?
Стратегия
Поскольку мы знаем напряженность электрического поля и заряд в поле, силу, действующую на этот заряд, можно рассчитать, используя определение электрического поля [латекс]\boldsymbol{\textbf{E} = \textbf{ F}/q}[/latex] заменены на [latex]\boldsymbol{ \textbf{F} = q \textbf{E}}[/latex].
 5}[/latex] N/C, таким образом, 95 \;\textbf{N} / \textbf{C})} \\[1em] & \boldsymbol{0.180 \;\textbf{N}.} \end{массив}[/latex]
5}[/latex] N/C, таким образом, 95 \;\textbf{N} / \textbf{C})} \\[1em] & \boldsymbol{0.180 \;\textbf{N}.} \end{массив}[/latex]Потому что [латекс] \boldsymbol{q}[/latex] отрицательна, сила направлена против направления поля.
Обсуждение
Сила притяжения, как и ожидалось для разных зарядов. (Поле было создано положительным зарядом, а здесь действует на отрицательный заряд.) Заряды в этом примере типичны для обычного статического электричества, а полученная небольшая сила притяжения аналогична силам, возникающим при статическом прилипании и подобных ситуациях.
PhET Explorations: Electric Field of Dreams
Играй в мяч! Добавьте заряды в Поле Снов и посмотрите, как они реагируют на электрическое поле. Включите фоновое электрическое поле и отрегулируйте направление и величину.
Рисунок 2. Электрическое поле мечты- Поле электростатической силы, окружающее заряженный объект, распространяется в пространстве во всех направлениях.

- Объясните точечные заряды и составьте уравнение для электрического потенциала точечного заряда.


 .
.
 2 \;\text{V}}[/латекс]? 9{-14} \;\text{m}}[/latex] из фрагмента, содержащего 46 протонов? б) Какова потенциальная энергия в МэВ одноименно заряженного фрагмента на этом расстоянии?
2 \;\text{V}}[/латекс]? 9{-14} \;\text{m}}[/latex] из фрагмента, содержащего 46 протонов? б) Какова потенциальная энергия в МэВ одноименно заряженного фрагмента на этом расстоянии? Если энергия двухзарядного альфа-ядра была 5,00 МэВ, насколько близко к ядру золота (79протоны) может ли он прийти до того, как отклонится?
Если энергия двухзарядного альфа-ядра была 5,00 МэВ, насколько близко к ядру золота (79протоны) может ли он прийти до того, как отклонится?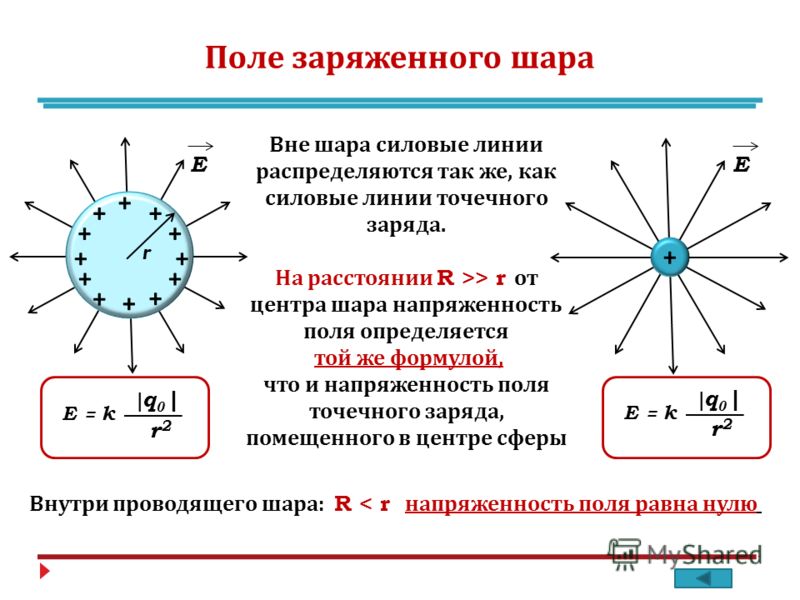

 Это согласуется с тем фактом, что VV тесно связан с энергией, скаляром, тогда как EE тесно связан с силой, вектором.
Это согласуется с тем фактом, что VV тесно связан с энергией, скаляром, тогда как EE тесно связан с силой, вектором.

 Важна именно разность потенциалов между двумя точками, и очень часто неявно предполагается, что какая-то точка отсчета, например Земля или очень удаленная точка, имеет нулевой потенциал. Как отмечено в книге «Электрическая потенциальная энергия: разность потенциалов», это аналогично принятию уровня моря как h=0h=0 при рассмотрении потенциальной энергии гравитации, PEg=mghPEg=mgh.
Важна именно разность потенциалов между двумя точками, и очень часто неявно предполагается, что какая-то точка отсчета, например Земля или очень удаленная точка, имеет нулевой потенциал. Как отмечено в книге «Электрическая потенциальная энергия: разность потенциалов», это аналогично принятию уровня моря как h=0h=0 при рассмотрении потенциальной энергии гравитации, PEg=mghPEg=mgh. Они взаимодействуют через силы, включающие Кулоновская сила . Действие на расстоянии — это сила между объектами, которые находятся недостаточно близко, чтобы их атомы могли «соприкоснуться». То есть они разделены более чем несколькими атомными диаметрами.
Они взаимодействуют через силы, включающие Кулоновская сила . Действие на расстоянии — это сила между объектами, которые находятся недостаточно близко, чтобы их атомы могли «соприкоснуться». То есть они разделены более чем несколькими атомными диаметрами. 2}[/latex], для точечный заряд (частица, имеющая заряд [латекс]\boldsymbol{Q}[/латекс]), действующий на пробный заряд [латекс]\boldsymbol{q}[/латекс] на расстоянии [латекс]\boldsymbol {r}[/latex] (см. [ссылка]). Как величина, так и направление кулоновского силового поля зависят от [латекс]\boldsymbol{Q}[/латекс] и пробного заряда [латекс]\boldsymbol{q}[/латекс].
2}[/latex], для точечный заряд (частица, имеющая заряд [латекс]\boldsymbol{Q}[/латекс]), действующий на пробный заряд [латекс]\boldsymbol{q}[/латекс] на расстоянии [латекс]\boldsymbol {r}[/latex] (см. [ссылка]). Как величина, так и направление кулоновского силового поля зависят от [латекс]\boldsymbol{Q}[/латекс] и пробного заряда [латекс]\boldsymbol{q}[/латекс]. Ф 1 . Таким образом, кулоновское силовое поле не является уникальным в любой точке пространства, поскольку оно зависит от пробных зарядов 9.0047 q 1 и q 2 а также плата Q .
Ф 1 . Таким образом, кулоновское силовое поле не является уникальным в любой точке пространства, поскольку оно зависит от пробных зарядов 9.0047 q 1 и q 2 а также плата Q . 2 }[/латекс] . Таким образом, величина электрического поля [латекс]\boldsymbol{E}[/латекс] для точечного заряда равна 92}}[/латекс]
2 }[/латекс] . Таким образом, величина электрического поля [латекс]\boldsymbol{E}[/латекс] для точечного заряда равна 92}}[/латекс] 5}[/latex] N/C, таким образом, 95 \;\textbf{N} / \textbf{C})} \\[1em] & \boldsymbol{0.180 \;\textbf{N}.} \end{массив}[/latex]
5}[/latex] N/C, таким образом, 95 \;\textbf{N} / \textbf{C})} \\[1em] & \boldsymbol{0.180 \;\textbf{N}.} \end{массив}[/latex]