ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ДВИЖУЩИЙСЯ ЗАРЯД. СИЛА ЛОРЕНЦА — Студопедия

Поделись  

Электрический ток — это упорядоченно движущиеся наряженные частицы. Поэтому действие магнитного поля на проводник с током есть результат действия поля на движущиеся заряженные частицы внутри проводника. Найдем силу, действующую на одну частицу.

 

Модульсилы Лоренца равен отношению модуля силы F, действующей на участок проводника длиной , к числу N заряженных частиц, упорядоченно движущихся в этом участке проводника:

Рассмотрим отрезок тонкого прямого проводника с током (рис. 1.23). Пусть длина отрезка и площадь поперечного сечения проводника S настолько малы, что вектор индукции магнитного поля можно считать одинаковым в пределах этого отрезка проводника. Сила тока l в проводнике связана с зарядом частиц q, концентрацией заряженных частиц (числом зарядов в единице объема) и скоростью их упорядоченного движения следующей формулой:

Модуль силы, действующей со стороны магнитного поля на выбранный элемент тока, равен:

Подставляя в эту формулу выражение (1. 4) для силы тока, получаем:

где N = nS — число заряженных частиц в рассматриваемом объеме. Следовательно, на каждый движущийся заряд со стороны магнитного поля действует сила Лоренца, равная:

где — угол между вектором скорости и вектором магнитной индукции. Сила Лоренца перпендикулярна векторам и . Ее направление определяется с помощью того же правила левой руки, что и направление силы Ампера: если левую руку распололсить так, чтобы составляющая магнитной индукции , перпендикулярная скорости заряда, входила в ладонь, а четыре вытянутых пальца были направлены по движению положительного заряда (против движения отрицательного), то отогнутый на 90° большой палец укажет направление действующей на заряд силыЛоренца

F_л (рис. 1.24).

Электрическое поле действует на заряд q с силой . Следовательно, если есть и электрическое поле, и магнитное поле, то суммарная сила , действующая на заряд, равна:

= _эл + _л.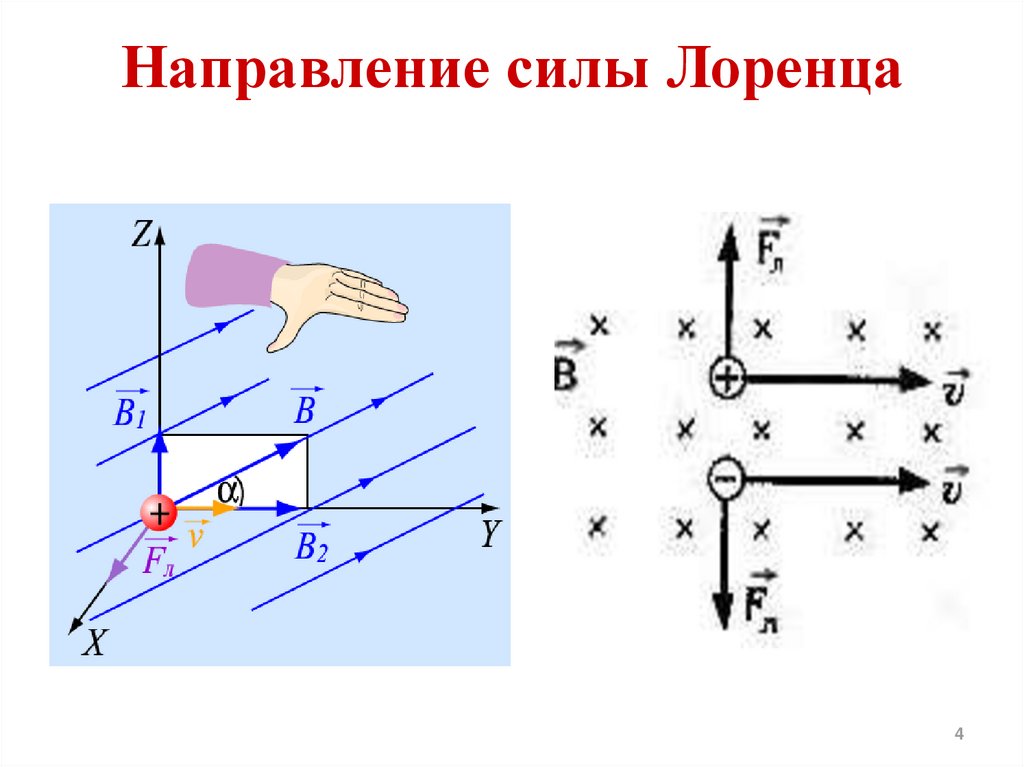

Так как сила Лоренца перпендикулярна скорости частицы, то она не совершает работы. Согласно теореме о кинетической энергии (см. учебник физики для 10 класса) это означает, что сила Лоренца не меняет кинетическую энергию частицы и, следовательно, модуль ее скорости. Под действием силы Лоренца меняется лишь направление скорости частицы.

Движение заряженной частици в однородном магнитном поле. Рассмотрим движение частицы с зарядом q в однородном магнитном поле , направленном перпендикулярно к начальной скорости частицы (рис. 1.25).

Сила Лоренца зависит от модулей векторов скорости частицы и индукции магнитного поля.
Так как магнитное поле не меняет модуль скорости движущейся частицы, то остается неизменным и модуль силы Лоренца. Эта сила перпендикулярна скорости и, следовательно, определяет центростремительное ускорение частицы. Неизменность по модулю центростремительного ускорения частицы, движущейся с постоянной по модулю скоростью, означает, что частица равномерно движется по окружности радиусом r.

Определим этот радиус.

Использование действия магнитного поля на движущийся заряд. Действие магнитного поля на движущийся заряд широко используют в современной технике. Достаточно упомянуть телевизионные трубки (кинескопы), в которых летящие к экрану электроны отклоняются с помощью магнитного поля, создаваемого особыми катушками.

Сила Лоренца используется и ускорителе заряженных частиц (циклотрон) для получения частиц с большими энергиями. Циклотрон состоит из двух полых полуцилиндров (дуантов) 3, находящихся в однородном магнитном поле (рис. 1.26). Между дуантами создается переменное электрическое поле. Согласно формуле (1.6) при увеличении скорости частицы / радиус окружности (траектории 2), по которой движется частица, увеличивается. Период обращения частицы не зависит от скорости (см. формулу (1.7)), и, следовательно, через полпериода, вследствие изменения направления электрического поля, частица снова оказывается в ускоряющем ее поле и т.

д. На последнем витке частица вылетает из циклотрона.

На действии магнитного поля основано также и устройство приборов, позволяющих разделять заряженные частицы по их уденьиым зарядам, т. е. по отношению заряда частицы к ее массе, и по полученным результатам точно определять массы частиц. Такие приборы получили название масс-электрографов.

На рисунке 1.27 изображена принципиальная схема простейшего масс-электрографа. Вакуумная камера прибора помещена в магинитое поле (вектор индукции перпендикулярен рисунку). Ускорение электрическим полем заряженные частицы (электроны или ионы), описав дугу, попадают на фотопластинку, где оставляют след, позволяющий с высокой точностью измерить радиус траектории r. По этому радиусу определяется удельный заряд иона. Зная заряд иона, легко вычислить его массу.

На движущуюся заряженную часчицу со стороны магнитного поля действует сила Лоренца. Эта сила перпендикулярна скорости и не совершает работы.

 

1. Чему равен модуль силы Лоренца!
2. Как движется заряженная частица в однородном магнитном поле, если начальная скорость частицы перпендикулярна линиям магнитной индукции!
3. Как определить направление силы Лоренца!

Дей­ствие маг­нит­но­го поля на дви­жу­щий­ся элек­три­че­ский заряд

1. «Модели эфиров»

Если бы Андре Мари Ампер (рис. 1) знал о дей­ствии элек­три­че­ско­го тока, то про­дви­нул­ся го­раз­до даль­ше в своих от­кры­ти­ях.

Рис. 1. Андри Мари Ампер (Ис­точ­ник)

Как и мно­гие учё­ные того пе­ри­о­да Ампер при­дер­жи­вал­ся «мо­де­ли эфира»: элек­три­че­ский ток – эфир, некая жид­кость, ко­то­рая про­те­ка­ет по про­вод­ни­кам. Имен­но от­сю­да и сам тер­мин «элек­три­че­ский ток» — то, что течёт. Толь­ко в самом конце XIX века – вна­ча­ле ХХ мо­де­ли эфи­ров стали от­хо­дить, а на смену им стали по­яв­лять­ся новые мо­де­ли адек­ват­нее от­ра­жа­ю­щие на­блю­да­е­мые яв­ле­ния. В част­но­сти были от­кры­ты ка­тод­ные лучи, была вы­яв­ле­на ра­дио­ак­тив­ность, про­ве­де­ны ис­сле­до­ва­ния Фа­ра­дея по элек­тро­ли­зу – всё это на­во­ди­ло на мысль о су­ще­ство­ва­нии за­ря­жён­ных ча­стиц, ко­то­рые как-то дви­жут­ся.

 

2. Электронная модель Хендрика Лоренца

Се­рьёз­ную мо­дель пред­ло­жил учё­ный Хенд­рик Ло­ренц (рис. 2) так на­зы­ва­е­мую «элек­трон­ную мо­дель». При об­ра­зо­ва­нии кри­стал­ли­че­ской ре­шёт­ки ме­тал­лов, от каж­до­го атома ме­тал­ла от­ры­ва­ет­ся по од­но­му внеш­не­му элек­тро­ну, таким об­ра­зом, в узлах кри­стал­ли­че­ской ре­шёт­ки на­хо­дят­ся по­ло­жи­тель­ные ионы, а в объ­ё­ме этой ре­шёт­ки почти сво­бод­но могут дви­гать­ся элек­тро­ны (рис. 3).

Рис. 2. Хенд­рик Ло­ренц (Ис­точ­ник)

Такая мо­дель яв­ля­ет­ся до­ста­точ­но устой­чи­вой, по­то­му что дей­ству­ют элек­тро­ста­ти­че­ские силы между по­ло­жи­тель­но за­ря­жён­ной ре­шёт­кой и элек­трон­ным окру­же­ни­ем. Имен­но по­это­му ме­тал­лы до­ста­точ­но проч­ны для раз­ря­же­ния, но в то же время, ковки.

Рис. 3. Кри­стал­ли­че­ская ре­шет­ка (Ис­точ­ник)

Мо­дель, пред­ло­жен­ная Ло­рен­цом, хо­ро­ша хотя бы тем, что до­ста­точ­но легко объ­яс­ня­ла воз­ник­но­ве­ние элек­три­че­ско­го тока в ме­тал­лах.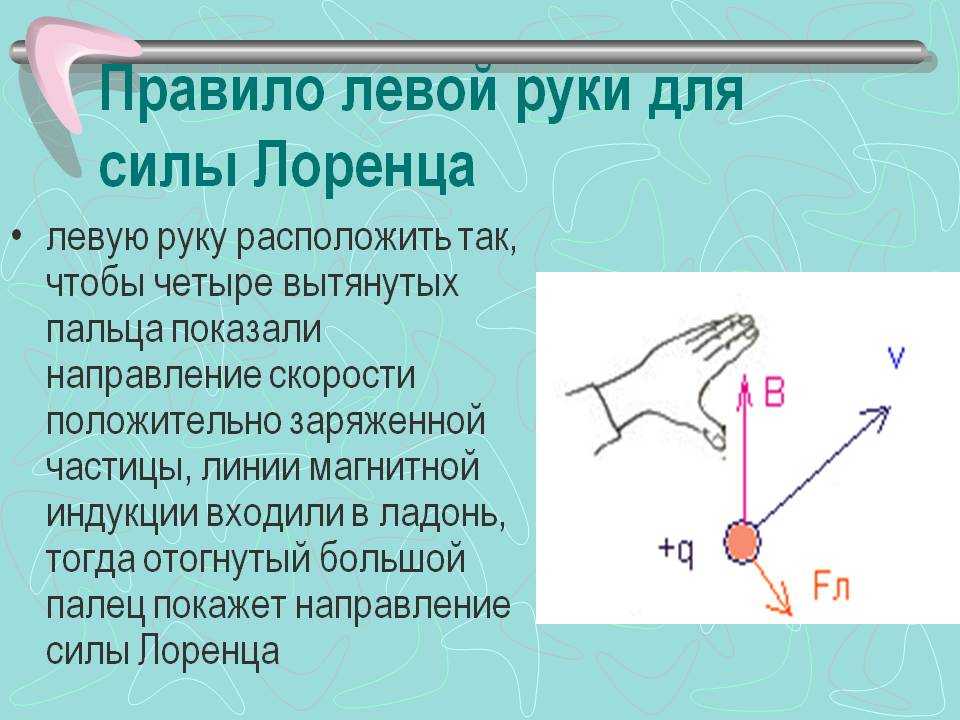

При обыч­ных усло­ви­ях эти элек­тро­ны на­хо­дят­ся в бес­по­ря­доч­ном дви­же­нии во­круг кри­стал­ли­че­ской ре­шёт­ки. И толь­ко при по­да­че раз­но­сти по­тен­ци­а­лов на конце про­вод­ни­ка, когда внут­ри про­вод­ни­ка по­яв­ля­ет­ся элек­три­че­ское поле, кроме этой ха­о­ти­че­ской со­став­ля­ю­щей по­яв­ля­ет­ся дру­гая – упо­ря­до­чен­ная со­став­ля­ю­щая или на­прав­лен­ное дви­же­ние. Имен­но это дви­же­ние, со­глас­но мо­де­ли Ло­рен­ца, пред­став­ля­ет собой элек­три­че­ский ток.

Так, со сто­ро­ны маг­нит­но­го поля на про­вод­ник с током (I), дей­ству­ет сила Ам­пе­ра пер­пен­ди­ку­ляр­ная на­прав­ле­нию тока и на­прав­ле­нию линии маг­нит­но­го поля. (Рис. 4)

Рис. 4. На­прав­лен­ное дви­же­ние (Ис­точ­ник)

«Если элек­три­че­ский ток пред­став­ля­ет собой на­прав­лен­ное дви­же­ние за­ря­дов, то не будет ли со сто­ро­ны маг­нит­но­го поля дей­ство­вать такая же сила» — при­мер­но, так рас­суж­дал Ло­ренц. В вы­ра­же­ние для силы Ам­пе­ра (1.1.) вме­сто силы тока под­ста­вим опре­де­ле­ние силы тока – от­но­ше­ние пе­ре­не­сен­но­го за­ря­да в про­вод­ни­ке ко вре­ме­ни, за ко­то­рое было осу­ществ­ле­но дан­ное пе­ре­не­се­ние.

(1.1)

(1.2)

Также за­ме­тим, что от­но­ше­ние эле­мен­та длины про­вод­ни­ка к ин­тер­ва­лу вре­ме­ни – ско­рость дви­же­ния за­ря­да.

(1.3)

Тогда вы­ра­же­ние при­ни­ма­ет вид (6.4.). Мо­дуль силы равен про­из­ве­де­нию ве­ли­чи­ны маг­нит­ной ин­дук­ции поля на ко­ли­че­ство пе­ре­но­си­мо­го через про­вод­ник за­ря­да на ско­рость ча­стиц, ко­то­рые пе­ре­но­сят заряд и на синус угла между на­прав­ле­ни­ем дви­же­ния за­ря­да и на­прав­ле­ни­ем век­то­ра маг­нит­ной ин­дук­ции.

(1.4)

Учтём, что но­си­те­ля­ми элек­три­че­ско­го тока в про­вод­ни­ке яв­ля­ют­ся элек­тро­ны, ве­ли­чи­на за­ря­дов ко­то­рых оди­на­ко­ва. По­это­му можно за­пи­сать, что со­во­куп­ный заряд, пе­ре­но­си­мый через по­пе­реч­ное се­че­ние про­вод­ни­ка – про­из­ве­де­ние эле­мен­тар­но­го за­ря­да на ко­ли­че­ство элек­тро­нов пе­ре­но­си­мых через по­пе­реч­ное се­че­ние про­вод­ни­ка.

(1.5)

(1.6)

Вывод при­ве­ден­ной фор­му­лы был су­гу­бо фор­маль­ным, од­на­ко, даже такой вывод поз­во­лял пред­по­ло­жить, что не толь­ко на про­вод­ник с током, но и на от­дель­ный заряд в маг­нит­ном поле будет дей­ство­вать сила со сто­ро­ны этого поля. Пред­по­ло­жим, что число за­ря­дов равно еди­ни­це и этот заряд дви­жет­ся не внут­ри кри­стал­ли­че­ской ре­шёт­ки, а в сво­бод­ном про­стран­стве. Воз­ни­ка­ет во­прос: что про­изой­дёт с этим за­ря­дом, если он вой­дёт в об­ласть, где су­ще­ству­ет од­но­род­ное маг­нит­ное поле? Со­глас­но нашей ги­по­те­зе, на ча­сти­цу, дви­жу­щу­ю­ся в од­но­род­ном маг­нит­ном поле, долж­на дей­ство­вать сила, ко­то­рая пер­пен­ди­ку­ляр­на ско­ро­сти этой ча­сти­цы (по­сколь­ку имен­но так будет на­прав­лен элек­три­че­ский ток, свя­зан­ный с дви­же­ни­ем этих ча­стиц) и пер­пен­ди­ку­ляр­на ли­ни­ям маг­нит­но­го поля. Ве­ли­чи­на этой силы будет опре­де­лять­ся так:

3. Проверка гипотезы Лоренца – принцип работы электронно-лучевой трубки

От­кры­тие ка­тод­ных лучей, а также ра­дио­ак­тив­но­сти поз­во­ли­ли про­ве­рить экс­пе­ри­мен­таль­но ги­по­те­зу Ло­рен­ца. Вос­поль­зу­ем­ся элек­трон­но-лу­че­вой труб­кой (рис. 5)

Рис. 5. Элек­трон­но-лу­че­вая труб­кой (Ис­точ­ник).

В ва­ку­ум­ной труб­ке раз­ме­ще­ны две пла­сти­ны: анод и катод. На катод по­да­ёт­ся от­ри­ца­тель­ный по­тен­ци­ал, на анод – по­ло­жи­тель­ный. Для того чтобы в труб­ке воз­ник­ли сво­бод­ные элек­тро­ны, катод на­гре­ва­ет­ся нитью на­ка­ла. Сво­бод­ные элек­тро­ны ме­тал­ли­че­ско­го ка­то­да вб­ли­зи его по­верх­но­сти могут по­ки­дать эту по­верх­ность, об­ла­дая вы­со­кой ки­не­ти­че­ской энер­ги­ей за счёт на­гре­ва­ния – яв­ле­ние тер­мо­элек­трон­ной эмис­сии. Сво­бод­ные элек­тро­ны, по­ки­нув­шие по­верх­ность ка­то­да, по­па­да­ют в зону дей­ствия элек­три­че­ско­го поля между ано­дом и ка­то­дом. Линии на­пря­жён­но­сти этого поля на­прав­ле­ны от анода к ка­то­ду. Элек­тро­ны, бу­дучи от­ри­ца­тель­но за­ря­жен­ны­ми ча­сти­ца­ми, дви­жут­ся от ка­то­да к аноду – про­тив линии на­пря­жён­но­сти поля. Так в труб­ке воз­ни­ка­ет элек­три­че­ский ток, на­прав­лен­ный от анода к ка­то­ду. Если ис­поль­зо­вать анод, по­кры­тый спе­ци­аль­ным ма­те­ри­а­лом, ко­то­рый све­тит­ся при по­па­да­нии на него за­ря­жён­ных ча­стиц, можно про­на­блю­дать место по­па­да­ния элек­тро­нов по све­то­во­му пятну. Имен­но так и ра­бо­та­ет элек­трон­но-лу­че­вая труб­ка. При по­да­че на­пря­же­ния на анод и катод мы видим неболь­шое зе­лё­ное пятно на аноде – это место бом­бар­ди­ров­ки экра­на элек­тро­на­ми.

4. Опыты с осциллографом

Если вос­поль­зо­вать­ся ос­цил­ло­гра­фом (рис.6), то будет по­ка­за­но не све­то­вое пятно, а све­тя­ща­я­ся линия. Когда одним из по­лю­сов под­во­дят к го­ри­зон­таль­ной линии, на­хо­дя­щей­ся на ос­цил­ло­гра­фе – она от­кло­ня­ет­ся от сво­е­го пер­во­на­чаль­но­го зна­че­ния в на­прав­ле­нии пер­пен­ди­ку­ляр­ном на­прав­ле­нию ско­ро­сти и на­прав­ле­нию линий маг­нит­но­го поля, по­сколь­ку маг­нит­ное поле на­прав­ле­но от се­вер­но­го по­лю­са к юж­но­му. Это на ка­че­ствен­ном уровне под­твер­жда­ет ги­по­те­зу.

По­пы­та­ем­ся по­лу­чить не толь­ко ка­че­ствен­ные, но и ко­ли­че­ствен­ные ре­зуль­та­ты. Для этого будем про­ве­рять за­ви­си­мость силы дей­ству­ю­щей со сто­ро­ны маг­нит­но­го поля от раз­лич­ных фак­то­ров. В част­но­сти от ско­ро­сти дви­же­ния элек­тро­нов. Каким об­ра­зом можно по­ме­нять ско­рость дви­же­ния элек­тро­нов в ос­цил­ло­гра­фе? При по­мо­щи ре­гу­ли­ров­ки яр­ко­сти линии на ос­цил­ло­гра­фе можно из­ме­нить ско­рость дви­же­ния элек­тро­нов в ос­цил­ло­гра­фе. Чем ярче линия – тем быст­рее дви­жет­ся элек­тро­ны внут­ри труб­ки. Если под­не­сти маг­нит к ос­цил­ло­гра­фу се­вер­ным по­лю­сом и ме­нять ско­рость дви­же­ния элек­тро­нов – то по мере умень­ше­ния яр­ко­сти – ис­ка­же­ние лини также будет умень­шать­ся. Это озна­ча­ет, что сила, дей­ству­ю­щая со сто­ро­ны маг­нит­но­го поля на элек­тро­ны, при умень­ше­нии ско­ро­сти элек­тро­нов тоже умень­ша­ет­ся. Более точ­ные из­ме­ре­ния дадут нам пря­мую про­пор­ци­о­наль­ность между силой, дей­ству­ю­щей со сто­ро­ны маг­нит­но­го поля на дви­жу­щи­е­ся за­ря­ды и ско­ро­стью этих за­ря­дов. Сила, дей­ству­ю­щая на за­ря­ды со сто­ро­ны маг­нит­но­го поля, про­пор­ци­о­наль­на ин­дук­ции – если под­не­сти несколь­ко маг­ни­тов к ос­цил­ло­гра­фу, то ис­ка­же­ние будет го­раз­до силь­нее.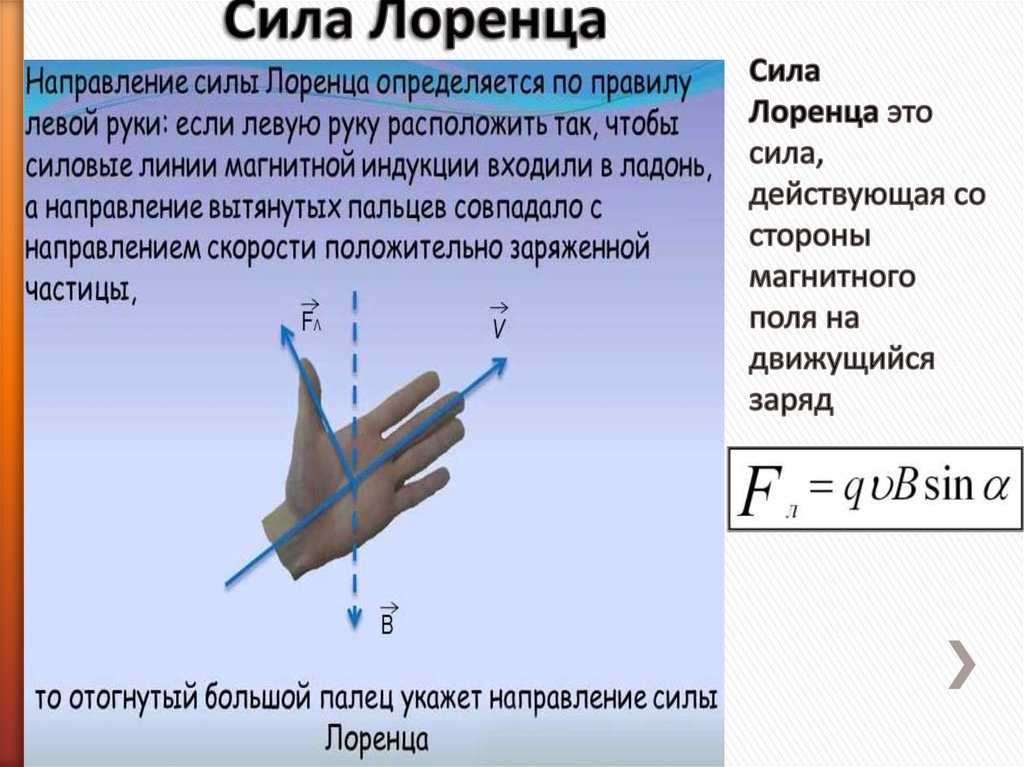 Ве­ли­чи­на силы дей­ству­ю­щей со сто­ро­ны маг­нит­но­го поля на дви­жу­щий­ся заряд за­ви­сит от вза­им­но­го на­прав­ле­ния век­то­ра маг­нит­ной ин­дук­ции и век­то­ра ско­ро­сти дви­же­ния ча­стиц – при под­не­се­нии маг­ни­тов к ос­цил­ло­гра­фу южным по­лю­сом – линия будет ис­ка­жать­ся в про­ти­во­по­лож­ном на­прав­ле­нии.

Рис. 6. Ос­цил­ло­граф (Ис­точ­ник)

5. Электромагниты

Обоб­щим вы­во­ды из про­де­лан­ных экс­пе­ри­мен­тов. На дви­жу­щий­ся в маг­нит­ном поле заряд (q) со сто­ро­ны маг­нит­но­го поля дей­ству­ет сила (F), на­прав­ле­ние ко­то­рой за­ви­сит от вза­им­но­го на­прав­ле­ния век­то­ра ско­ро­сти дви­же­ния ( ) за­ря­да и век­то­ра маг­нит­ной ин­дук­ции поля (В). Ве­ли­чи­на силы про­пор­ци­о­наль­на ско­ро­сти дви­же­ния за­ря­да и мо­ду­лю маг­нит­ной ин­дук­ции. На­прав­ле­ние силы опре­де­ля­ет­ся по пра­ви­лу «Левой руки» (рис. 4).

(1.7)

Таким об­ра­зом, по­лу­чен­ное ранее вы­ра­же­ние для силы, опи­сы­ва­ет вза­и­мо­дей­ствие маг­нит­но­го поля с дви­жу­щим­ся в этом поле элек­три­че­ским за­ря­дом.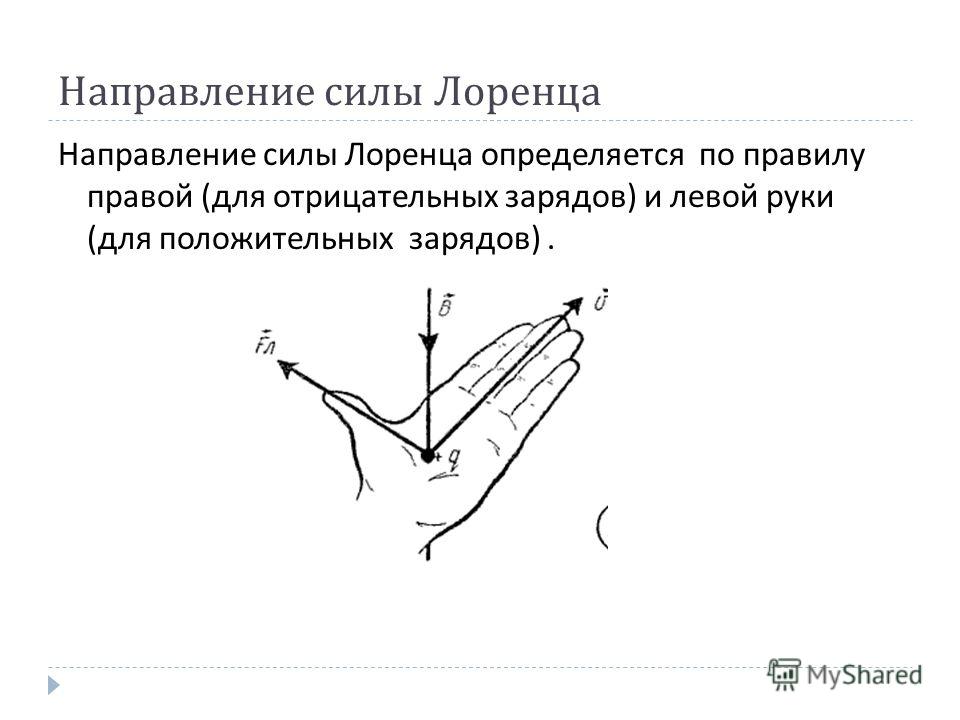 От­кры­тие силы дей­ствия маг­нит­но­го поля на дви­жу­щий­ся в нём заряд стало воз­мож­ным толь­ко бла­го­да­ря улуч­ше­нию пред­став­ле­ний о стро­е­нии ве­ще­ства, элек­три­че­ском токе в ме­тал­лах, дви­же­нии за­ря­жен­ных ча­стиц. И огром­ную роль во всех этих за­да­чах сыг­рал Ло­ренц, по­это­му от­кры­тая сила и по­лу­чи­ла на­зва­ние – сила Ло­рен­ца.

6. Выводы

Сде­ла­ем ещё несколь­ко за­ме­ча­ний.

1. Век­тор силы Ло­рен­ца пер­пен­ди­ку­ля­рен век­то­ру ско­ро­сти

(1.8)

(1.9)

(1.10)

2. Если сила пер­пен­ди­ку­ляр­на век­то­ру ско­ро­сти, то такая сила на­зы­ва­ет­ся цен­тро­стре­ми­тель­ной. И тогда под её дей­стви­ем – тело дви­жет­ся по окруж­но­сти. Сле­до­ва­тель­но, сила Ло­рен­ца – цен­тро­стре­ми­тель­ная сила:

(1.11)

3. Из-за того, что под дей­стви­ем силы Ло­рен­ца заряд дви­жет­ся по дуге окруж­но­сти, сле­до­ва­тель­но, он об­ла­да­ет цен­тро­стре­ми­тель­ным уско­ре­ни­ем.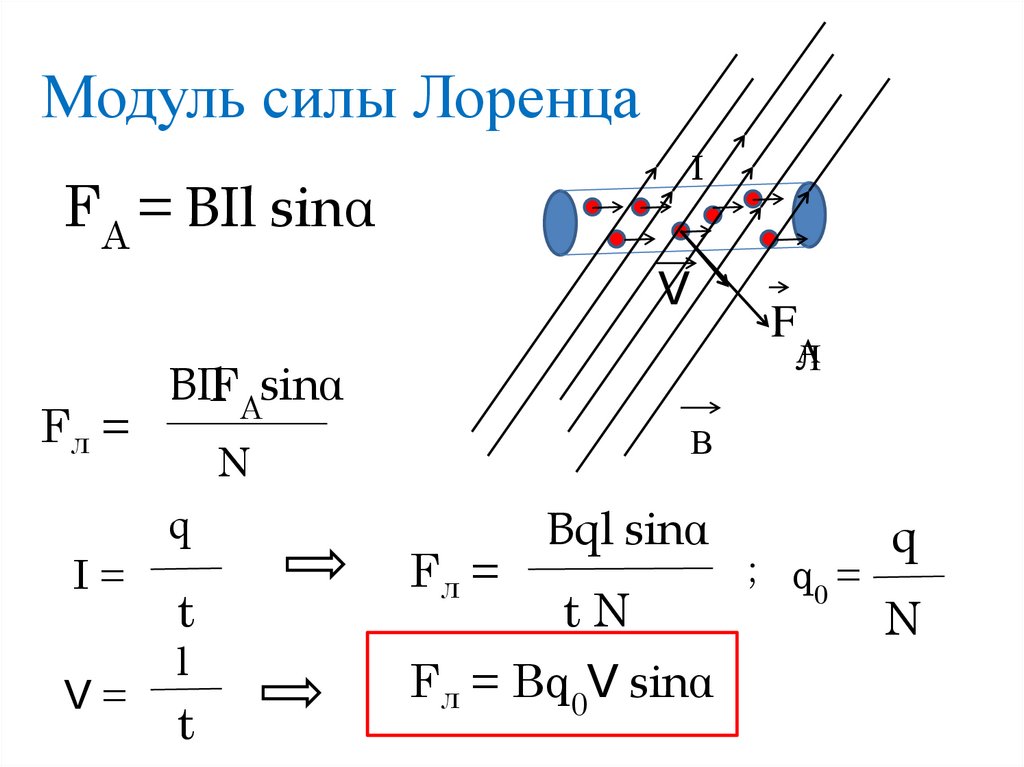 Цен­тро­стре­ми­тель­ное уско­ре­ние может быть рас­счи­та­но как квад­рат ско­ро­сти дви­же­ния, де­лён­ный на ра­ди­ус окруж­но­сти, ко­то­рый опи­сы­ва­ет тело:

(1.12)

4. Так, со­глас­но вто­ро­му за­ко­ну Нью­то­на сила может быть опре­де­ле­на как про­из­ве­де­ние массы тела на при­об­ре­та­е­мое им уско­ре­ние:

(1.13)

После под­ста­нов­ки урав­не­ния 1.12 в 1.13 по­лу­чим:

(1.14)

После со­кра­ще­ния ско­ро­сти по­лу­чим сле­ду­ю­щие со­от­но­ше­ния:

(1.15)

(1.16)

(1.17.)

Действие магнитного поля на движущийся заряд. Сила Лоренца

Электрический ток – это совокупность упорядоченно движущихся заряженных частиц. Поэтому действие магнитного поля на проводник с током есть результат действия поля на движущиеся заряженные частицы внутри проводника.

Силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют силой Лоренца.

Модуль силы Лоренца равен отношению модуля силы Ампера, действующей на участок проводника, к числу заряженных частиц в этом участке проводника:

Сила Ампера равна , сила тока равна (см. стр. 12). Подставив эти выражения в формулу для силы Лоренца, получим:

где — угол между векторами скорости и магнитной индукции.

Направление силы Лоренца определяют для положительного заряда по правилу левой руки. (Для отрицательного заряда сила Лоренца будет направлена в противоположную сторону).

Так как сила Лоренца перпендикулярна скорости частицы, то она не совершает работу. А, согласно теореме о кинетической энергии, это означает, что сила Лоренца не меняет кинетическую энергию частицы и, следовательно модуль ее скорости. Под действием силы Лоренца меняется лишь направление скорости частицы.

 

Закон Ампера

Поместим в магнитное поле проводник длинной l, по которому течет ток I. На проводник действует сила, прямо пропорциональная силе тока, текущего по проводнику, индукции магнитного поля, длине проводника, и зависящая от ориентации проводника в магнитном поле. |F|=IBlsina, где a — угол между направлением тока в проводнике и направлением вектора магнитной индукции B, Направление силы Ампера определяется по правилу левой руки: если левую руку расположить так, что магнитные силовые линии входят в ладонь, четыре вытянутых пальца направить по току, то отогнутый большой палец укажет направление силы. Очевидно, что сила Ампера равна нулю, если проводник расположен вдоль силовых линий поля и максимальна, если проводник перпендикулярен силовым линиям. Движение заряженных частиц в магнитном поле. На проводник с током в магнитном поле действует сила Ампера F_А IBlsina.Ток, в свою очередь, это направленное движение заряженных частиц. Сила тока равна I=qnvS, где q – заряд частицы, n-концентрация движущихся заряженных частиц, v-средняя скорость их направленного движения, S-площадь поперечного сечения проводника. Подставив I в выражение для F_А, получим F_А= qnvSBlsina, где nsl=N – общее число частиц, создающих ток. Тогда сила, действующая на отдельный движущийся заряд – сила Лоренца, равна Fл=qvBsina. где a — угол между векторами скорости и магнитной индукции. Направление силы Лоренца определяется для положительно заряженной частицы по правилу левой руки.

Закон Ампера

Сила, действующая на проводник с током в магнитном поле, называется силой Ампера.

Экспериментальное изучение магнитного взаимодействия показывает, что модуль силы Ампера пропорционален длине проводника с током, силе тока и зависит от ориентации проводника в магнитном поле.

Опыт показывает, что магнитное поле, вектор индукции которого направлен вдоль проводника с током, не оказывает влияния на ток. Поэтому модуль силы зависит лишь от модуля составляющей вектора магнитной индукции, перпендикулярной проводнику.

Закон Ампера заключается в следующем. Сила Ампера равна произведению магнитной индукции поля на силу тока, длину участка проводника и на синус угла между магнитной индукцией и участком проводника:

 

Направление силы ампера определяется по правилу левой руки: если левую руку расположить так, чтобы перпендикулярная составляющая магнитной индукции входила в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 90 большой палец покажет направление силы, действующей на отрезок проводника.

Магнитное взаимодействие проводников с током используется в Международной системе для определения единицы сила тока –ампера.

Ампер –сила неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малого кругового сечения, расположенным на расстоянии 1 м друг от друга в вакууме, вызывал бы между этими проводниками силу магнитного взаимодействия, равную Н на каждый метр длины.



Генератор переменного тока и синусоида

Устройство, позволяющее получить переменный ток, называется генератором переменного тока. Задача генератора переменного тока создать изменяющиеся со временем ЭДС или напряжение.

Принцип работы генератора переменного тока

Чтобы понять принцип работы генератора переменного тока необходимо изучить поведение системы под действием ЭДС или напряжения в зависимости от времени по закону гармонических колебаний (ξ(t) = ξmax×cosωt; U(t) = Umax×cosωt). Создавая в колебательной системе переменную ЭДС (или подавая напряжение) мы получим ток I(t), который протекает в этой системе. Ток тоже будет меняться по гармоническому закону I(t) = Imax×cos(ωt+φ), и он будет переменным.

В основе практически всех генераторов тока лежит проводящая рамка, вращающаяся в магнитном поле. В этой рамке может быть много витков. Для общего понимания можно рассмотреть рамку, состоящую из одного витка.

В примере магнитное поле создается постоянным магнитом. Рамка находится между полюсами, подключена к внешней цепи и вращается вокруг своей оси. Линии магнитного поля выходят из северного полюса и входят в южный полюс магнита (направление вектора магнитной индукции (B) на схеме сверху вниз). Нормаль к рамке (n) в данный момент тоже направлена сверху вниз.

Подсоединим эту рамку к цепи через кольцевые контакты и щетки. Рамка — это контур, находящийся в магнитном поле. Через этот контур магнитным полем создается магнитный поток Φ = B×S×cosα (B — модуль вектора магнитной индукции; S — площадь рамки; α — угол между направлением нормали и направлением магнитного поля). Если рамка вращается с угловой скоростью ω, то угол α меняется с течением времени α = ω×t+φ0. φ0 — это начальный угол между нормалью к рамке и вектором магнитной индукции. С учетом приведенной схемы (рамка расположена так, что ее плоскость перпендикулярна магнитному полю) φ0 = 0. Если α меняется с течением времени, то и магнитный поток будет меняться с течением времени Φ(t) = B×S×cos(ω×t+φ0). Если в рамке меняется магнитный поток, то в ней по закону Фарадея возникает электродвижущая сила электромагнитной индукции ξi = -Φ’ (Φ’ — производная по времени магнитного потока). Получаем следующую формулу ξi(t) = -(B×S×cos(ω×t+φ0))’ = +B×S×sin(ω×t+φ0)×ω.

Пусть φ0 = π/2, тогда sin(α+π/2) = cosα. Соответственно ξi(t) = B×S×ω×cos(ω×t) или ξi(t) = ξmax×cos(ω×t) (ξmax = B×S×ω). Эта формула относится к рамке, состоящей из одного витка. Для рамки из N последовательно соединенных витков ξi(t) = ξmax×cos(ω×t) (ξmax = N×B×S×ω).

В идеальном генераторе (внутреннее сопротивление обмотки равно 0 Ом) напряжение на выходе будет совпадать с ЭДС. U(t) = Umax×cos(ω×t) (Umax = N×B×S×ω).

На выходе генератора напряжение (ЭДС) меняется по гармоническому закону. Циклическая частота напряжения (ЭДС) равна угловой скорости вращения рамки. Амплитуда напряжения (ЭДС) на выходе генератора прямо пропорциональна числу витков в рамке, площади рамки, величине магнитного поля, частоте вращения рамки.

Рассмотренная модель позволяет понять принцип работы генератора переменного тока. В реальных генераторах, как правило, вращается не рамка, а магнит вокруг рамки. Также вместо постоянного магнита используется электромагнит. Вращающийся электромагнит называется ротором, а неподвижная часть с рамкой — статором.

Проводник в магнитном поле — сила Лоренца

Рассмотрев теоретические основы работы генератора переменного тока перейдем к более детальному объяснению. Для этого разберемся с проводником, передвигающимся в магнитном поле. Ведь, по сути, рамку можно представить как систему проводников, а вращение — как движение.

Если передвигать проводник в магнитном поле таким образом, чтобы он пересекал силовые линии поля, то в проводнике будет индуктироваться ЭДС. Для определения направления индуктированной ЭДС в проводнике служит правило правой руки.

Если мысленно расположить правую руку в магнитном поле вдоль проводника так, чтобы магнитные линии, выходящие из северного полюса, входили в ладонь, а большой отогнутый палец совпадал с направлением движения проводника, то четыре вытянутых пальца будут указывать направление индуктированной ЭДС в проводнике.

Если проводник замкнуть на какую-либо нагрузку, то в нем возникнет ток. Ток создаст свой магнитный поток. Взаимодействие тока и магнитного поля полюсов создаст тормозящую силу (сила Лоренца), действующую на проводник в направлении противоположном его движению.

Сила Лоренца – это сила, которая действует на электрически заряженную частицу при ее движении в магнитном поле. Ее направление ортогонально плоскости, в которой лежат векторы скорости частицы и напряженности магнитного поля. Для определения направления силы Лоренца можно пользоваться правилом левой руки.

Если левую руку расположить так, чтобы линии магнитного поля входили в ладонь перпендикулярно ей, а четыре пальца были направлены по движению положительно заряженной частицы (или против движения отрицательно заряженной частицы), то отставленный большой палец покажет направление действующей на проводник силы. Если заряд отрицателен, то направление силы нужно сменить на противоположное.

Рассмотрим пример, в котором цилиндрический проводник движется в постоянном магнитном поле. Его вектор скорости υ→ перпендикулярен оси цилиндра, а вектор индукции магнитного поля B→ перпендикулярен, как оси проводника, так и его скорости.

Вместе проводником движутся и свободные заряды, находящиеся внутри него. Со стороны магнитного поля на эти заряды будут действовать силы Лоренца, направленные вдоль оси проводника. В металлах свободными зарядами являются отрицательно заряженные частицы — электроны. Однако мы будем рассматривать движение положительно заряженных частиц, так как за направление тока принимают направление положительных частиц.

В неподвижном проводнике свободные заряды движутся хаотически равновероятно во все стороны, поэтому среднее значение вектора силы Лоренца равно нулю. При движении проводника на хаотическое тепловое движение свободных зарядов накладывается направленное движение проводника. Благодаря движению появляется отличная от нуля результирующая сила Лоренца, одинаковая для всех частиц проводника и приводящая к возникновению электрического тока.

Под действием силы Лоренца свободные заряды смещаются к торцам цилиндра. Такое перераспределение зарядов на концах проводника приводит к созданию электрического поля. Здесь важно отметить, что действие поля на заряженные частицы будет направлено в сторону противоположную силе Лоренца. Но при постоянной скорости движения проводника установится равновесие, при котором движение зарядов прекратится несмотря на наличие электрического поля. В таких условиях сила Лоренца FL=qυB, действующая на частицу, будет уравновешена силой со стороны электрического поля Fel=qE.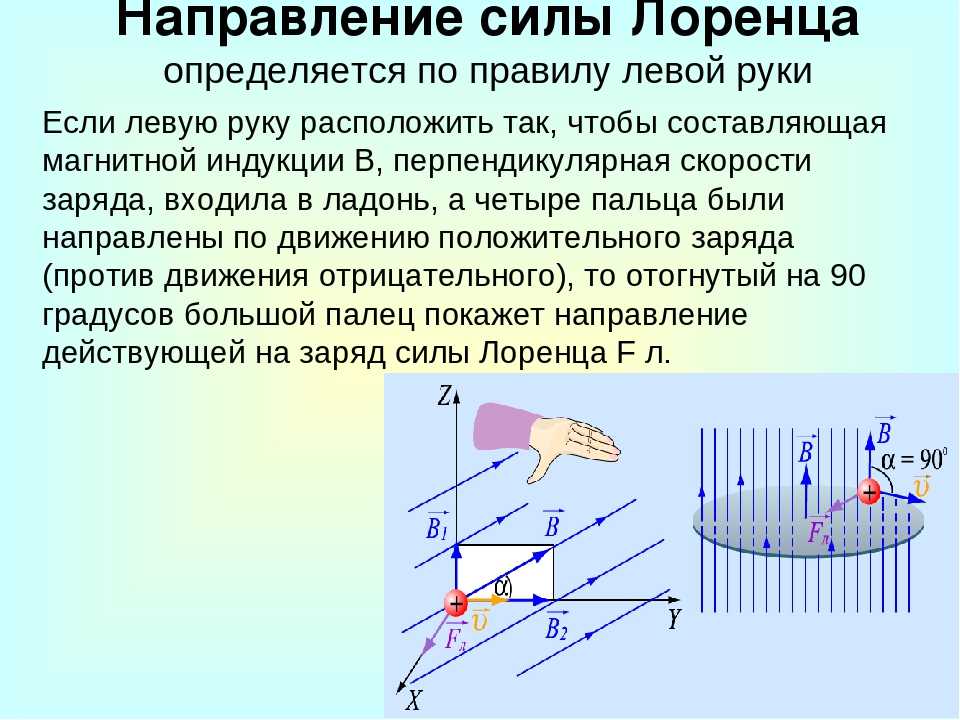 Приравнивая эти силы, можно определить напряженность электрического поля в проводнике E=υB.

Так как сила Лоренца одинакова во всех точках проводника, то и электрическая сила также должна быть постоянна, то есть возникшее электрическое поле является однородным. Это электрическое поле можно также характеризовать разностью потенциалов между торцами цилиндра, которая равна Δφ=El=υBl, где l — длина проводника.

Сила Лоренца, действующая на свободные заряды в проводнике, может являться сторонней силой. Тем самым она будет приводить к возникновению электрического тока в замкнутом контуре, если к движущемуся проводнику подключить нагрузку.

Для создания замкнутой цепи с нагрузкой-резистором R дадим проводнику AC скользить по двум параллельным шинам (рельсам), соединенным между собой. Вся система помещена в однородное магнитное поле, вектор индукции которого B→ перпендикулярен плоскости шин. Для упрощения примем, что сопротивления шин и движущегося проводника (перемычки) пренебрежимо малы по сравнению с сопротивлением соединяющего резистора R.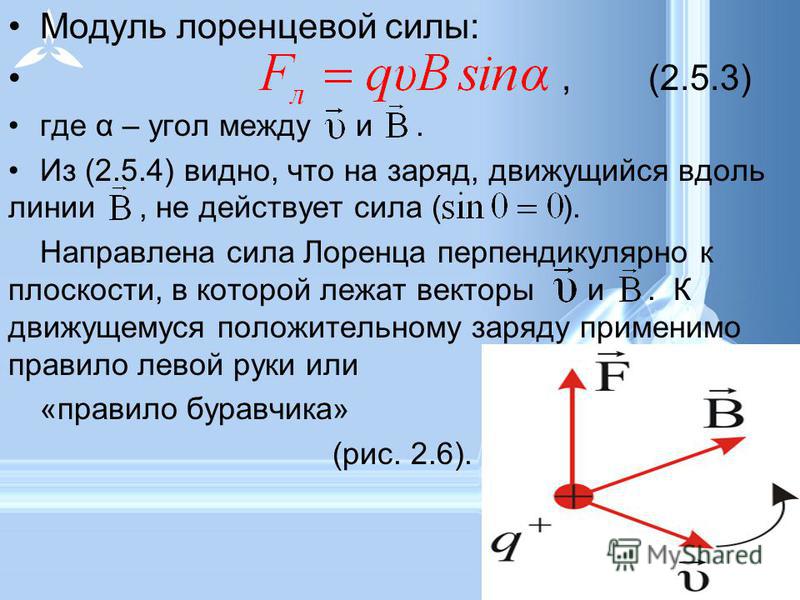 Если к подвижному проводнику приложить внешнюю силу F→, то он придет в движение.

Под действие силы Лоренца свободные заряды в проводнике придут в движение, создавая избыточные заряды на концах. Эти заряды создадут электрическое поле во всем контуре, образованном перемычкой, шинами и соединяющим резистором, поэтому в контуре возникнет электрический ток. Сила Лоренца, действующая на заряды движущегося проводника, будет играть роль сторонней, преодолевающей силы, действующие со стороны электрического поля. Работа этой силы (ЭДС) по перемещению единичного заряда равна произведению силы Лоренца на расстояние между шинами ε = (1/q)FLl=υBl.

Несмотря на то, что это выражение для ЭДС полностью совпадает с формулой (Δφ=El=υBl) для разности потенциалов, ее смысл принципиально иной. Разность потенциалов — это возможная работа сил электрического поля. В рассматриваемой цепи направление движения заряженных частиц противоположно направлению силы со стороны электрического поля. То есть сила Лоренца совершает стороннюю работу против сил электрического поля, а электрическое поле совершает положительную работу, проталкивая заряженные частицы по шинам и соединяющему резистору (внешней цепи).

Работа генератора и синусоида переменного напряжения (ЭДС) — самое простое объяснение

Минимально вдаваясь в теоретические особенности работы генератора, вектора магнитной индукции, силу Лоренца, закон Фарадея, сложные для восприятия формулы, попробуем как можно проще все объяснить на простых примерах. После того как вы поймете все процессы генерации напряжения и тока на микроуровне, можно смело переходить к прочтению академической писанины с кучей умных слов и непонятных формул. У вас появится шанс что-то понять и осмыслить. И когда вы услышите фразу индуцированная ЭДС, вы будете четко понимать ее смысл, а не будете оперировать размытыми определениями.

Начнем с классической рамки, вращающейся в магнитном поле. В реальных генераторах как правило магнитное поле вращается вокруг рамки (обмоток), но от перемены мест слагаемых сумма не меняется, поэтому для простоты моделирования будем рассматривать именно вращение рамки.

Линии магнитного поля выходят из северного полюса и входят в южный полюс магнита. Мы не будем акцентировать внимание на конкретное направление линий магнитного поля, так как это для упрощенной модели объяснения не принципиально.

Изобразим схематически рамку в магнитном поле:

Несмотря на то, что в магнитное поле, условно показанном красными линиями, помещено нечто похожее на букву «П», это нечто и есть рамка из проводника. В электротехнике рамка — это проводник, согнутый в форме прямоугольника. Можно конечно было продлить проводник от точек A и D навстречу, но это опять-таки непринципиально пока цепь не замкнута.

Вернемся к рамке. По сути она состоит из трех отрезков проводника AB, BC и CD. При вращении рамки линии магнитного поля пересекают только участки AB и CD. То есть отрезок BC можно откинуть.

Известно, что если перемещать проводник в магнитном поле из стороны в сторону, то при движении в одну сторону свободные заряды (электроны) смещаются к одному концу проводника, при движении в другую сторону — к другому концу проводника.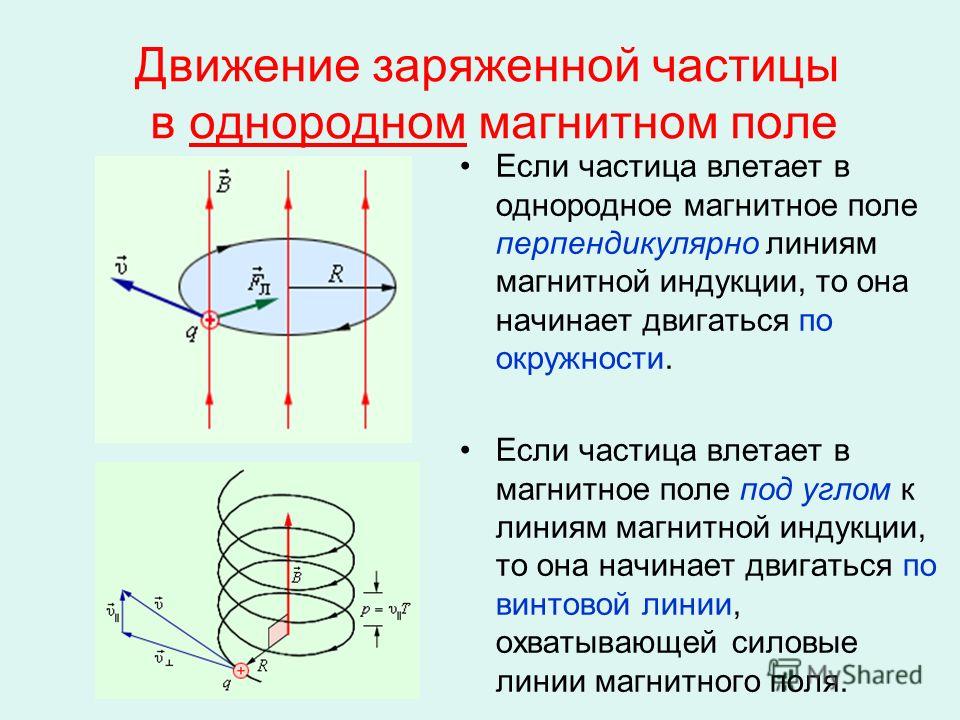 Вращение рамки — это тоже движение, при котором участок AB перемещается в одну сторону в то время, как участок CD перемещается в другую сторону:

Так как у нас простое объяснение, то на данном этапе целесообразно перейти от рассмотрения вращающейся рамки к вращающемуся (движущемуся) проводнику в магнитном поле. Для этого оставим только участок АС. Для понимания отметим, что участок CD просто увеличивал ЭДС, а убрав его ЭДС цепи уменьшилась в два раза. Чтобы получить ту же ЭДС с одним проводником (в нашем случае участок AB), его длину следовало бы увеличить в два раза:

Теперь важно уточнить особенность вращения в разрезе движения проводника. Для этого приведем следующую модель:

Проводник AB перемещается в магнитном поле по траектории окружности. Конец проводника A мы видим, а конец B находится за плоскостью чертежа. Двигаясь по окружности проводник с разной скоростью пересекает линии магнитного поля и это наглядно видно.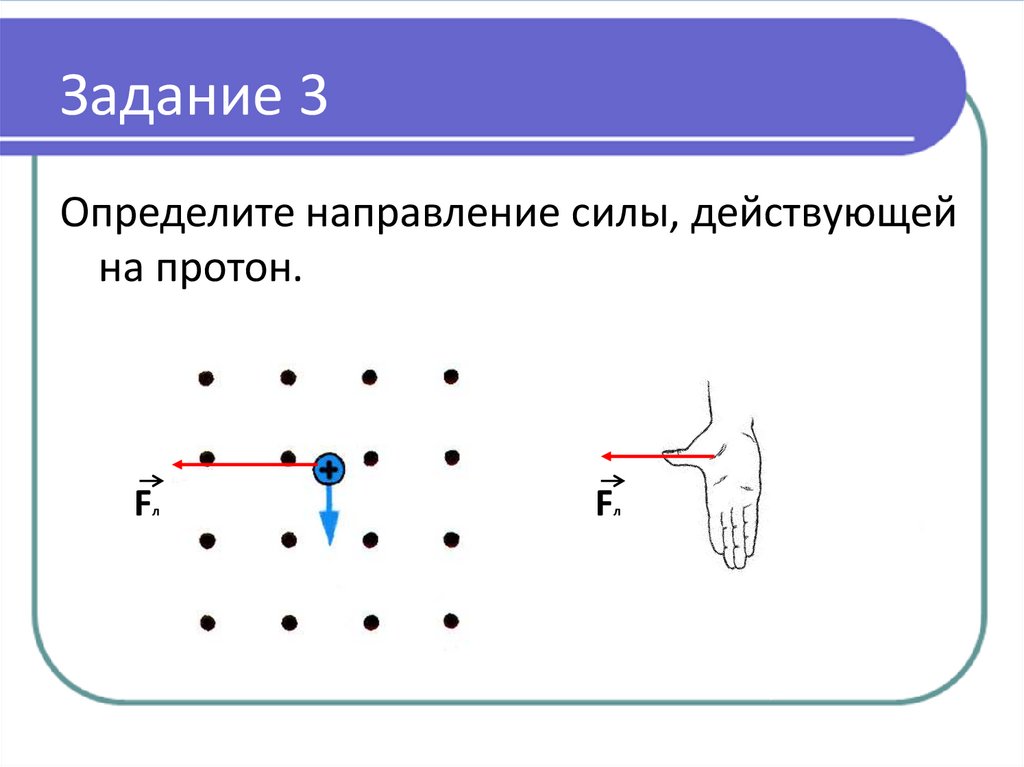 Так путь от точки 0 до точки 1 больше пути от точки 1 до точки 2. И так далее вплоть до точки 5. От точки 5 и далее по траектории скорость пересечения линий магнитного поля уменьшается, потом, проводник уже движется в другую сторону, опять увеличивается и уменьшается до точки 0.

Что нам дает скорость пересечения проводника с линиями магнитного поля? Чем она больше, тем сильнее воздействие магнитного поле на свободные электроны в проводнике, и тем больше электронов переместятся к одному из концов проводника. Чем больше электронов скопиться у одного из концов проводника, тем большая будет разность потенциалов между точками A и B.

Сделаем проводником один оборот по окружности в магнитном поле и проанализируем разность потенциалов между его концами (синусоида):

Точка 0	В данной точке изначально находится проводник. Заряды в проводнике движутся хаотически равновероятно во все стороны, но при этом они равномерно распределены по всей длине. Потенциал на конце A = 0 Вольт, на конце B = 0 Вольт. То есть разности потенциалов между концами проводника нет.
Точка 1	Дойдя до точки 1 проводник пересечет определенное количество линий магнитного поля, что вызовет смещение определенного количества электронов к одному из концов проводника, например к концу A. Соответственно конец A будет заряжен отрицательно, а конец B — положительно. Образуется разность потенциалов (ЭДС), как показано схематически на графике (синусоида). Если проводник прекратит движение, то электроны вернутся на свои места и равномерно перераспределятся, пропадет разность потенциалов. Но проводник продолжает двигаться.
Точка 2	Время потраченное на прохождение от точки 1 до точки 2 значительно меньше времени прохождения от точки 0 до точки 1. Соответственно двигаясь в этом секторе проводник намного быстрее будет пересекать линии магнитного поля. Электроны продолжат скапливаться у конца A, но делать они это будут намного интенсивнее.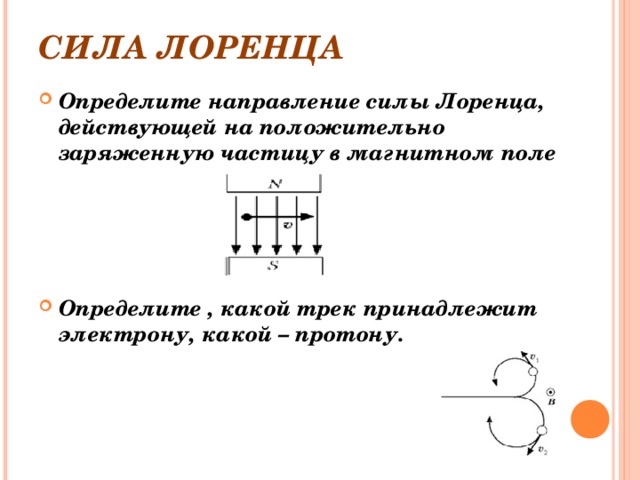 Также увеличится разность потенциалов (ЭДС) между концами A и B.
Точка 5	Возле точки 5 проводник пересекает линии магнитного с максимальной скоростью. В точке 5 будет наибольшая разность потенциалов (ЭДС) между концами A и B.
Точка 11	От точки 5 до точки 11 скорость пересечения проводником линий магнитного поля уже будет постепенно убывать. Электроны постепенно будут возвращаться в исходное положение и в точке 11 между концами A и B пропадет разность потенциалов.
Точка 15	От точки 11 к точке 15 и далее к точке 0 проводник уже будет двигаться в другом направлении. Соответственно картина перераспределения зарядов будет аналогичной, только электроны уже будут накапливаться у конца B и затем возвращаться в исходное положение в точке 0.

Один оборот проводника за секунду — это 1 Гц. Соответственно 50 Гц — это 50 оборотов в секунду, и за это время электроны 50 раз сконцентрируются у одного конца проводника и 50 раз — у другого конца проводника.

Мы разобрались, что при движении проводника (вращении рамки) в магнитном поле на концах проводника образуется переменная электродвижущая сила (разность потенциалов между концами A и B), которую графически можно представить синусоидой. Если подсоединить к концам проводника нагрузку (замкнуть цепь), то имеющаяся разность потенциалов создаст электрическое поле и во внешней цепи появится переменный ток.

Важно отметить следующую интересную особенность — при движении проводника (вращении рамки) в магнитном поле разность потенциалов создает электрическое поле не только во внешней (подключенной к проводнику) цепи, но и в самом проводнике. Но движение зарядов в проводнике происходит против силы электрического поля. Этому способствует сила Лоренца, совершающая стороннюю работу. Сила Лоренца не появится, если проводник не будет двигаться в магнитном поле. А чтобы проводник двигался, кто-то или что-то должно его двигать. В этом и заключается основная особенность работы генератора переменного тока.

Общая физика. Оптика / Шпоргалки / 17-19 н

17. Действие магнитного поля на проводник и контур с током.

Закон Ампера

Рассмотрим проводник с током, помещенный в магнитное поле. Поскольку электрический ток – это направленное движение заряженных частиц в одну сторону, то на каждую из них будет действовать магнитная составляющая силы Лоренца, причем все эти силы будут сонаправлены. Следовательно, результирующая сила, действующая со стороны магнитного поля на элемент проводника с током, может быть найдена так: , где dN – количество свободных электронов в элементе проводника. Сила определяется выражением (5.29). Если длина элемента dl, площадь поперечного сечения S, а концентрация свободных электронов в металле п, то

.

Таким образом, сила, действующая со стороны магнитного поля на бесконечно малый элемент проводника с током, помещенный в магнитное поле, определяется как

. (5.32)

Полученное соотношение выражает закон Ампера, а сила, определяемая по (5.32), называется силой Ампера. Направление силы Ампера можно определить по правилу “левой руки”: если расположить ладонь левой руки так, чтобы четыре пальца показывали направление тока в проводнике, а линии магнитной индукции входили в раскрытую ладонь, то отогнутый под прямым углом большой палец покажет направление силы, действующей на элемент проводника с током. Опишем взаимодействие двух параллельных бесконечно длинных проводников с токами (рис. 5.22). Каждый из проводников создает магнитное поле, индукция которого определяется по (5.12). Рассмотрим левый проводник с током , находящийся в поле правого проводника. Во всех точках первого проводника магнитная индукция поля второго проводника , где а – расстояние между проводниками. Учтем, что вектор направлен перпендикулярно плоскости рисунка “на нас”.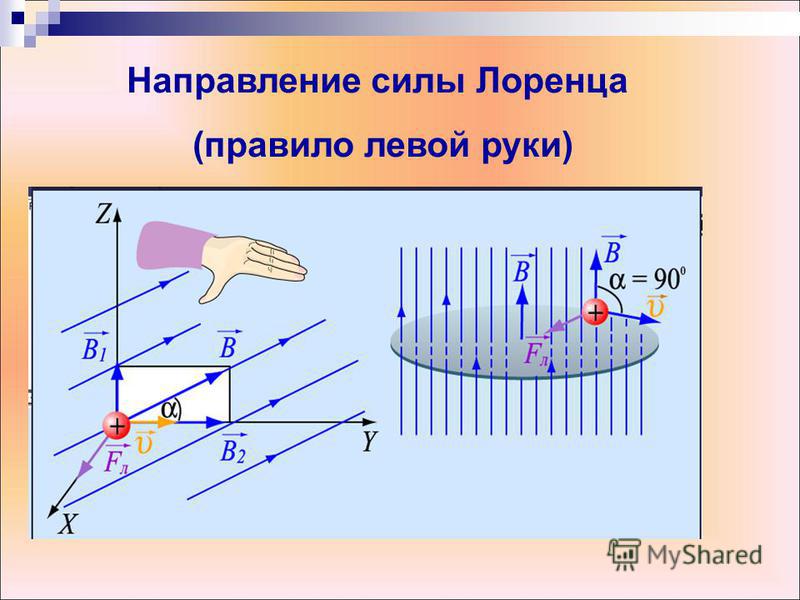 Если выделить в проводнике элемент с током , то, по правилу левой руки, сила , действующая на него, будет направлена вправо. Это означает, что левый проводник притягивается к правому. Модуль силы определяется таким образом:

.

Если теперь рассмотреть правый проводник с током , находящийся в поле левого проводника, то выводы будут аналогичными. Во всех точках второго проводника магнитная индукция поля первого проводника . Вектор направлен перпендикулярно плоскости рисунка “к нам”. Если выделить в проводнике элемент с током , то, по правилу левой руки, сила , действующая на него, будет направлена влево. Это означает, что правый проводник притягивается к левому. Модуль силы определяется таким образом:

.

Нетрудно видеть, что выполняется третий закон Ньютона: силы, с которыми взаимодействуют равные отрезки проводников одинаковы:

. (5. 33)

Таким образом, параллельные проводники с сонаправленными токами притягиваются друг к другу. Если направления тока в проводниках противоположны, то направления действующих между проводниками сил изменятся на противоположное, и проводники будут отталкиваться.

Из (5.33) следует определение основой единицы измерения электрических величин в СИ – ампера. 1 ампер – сила неизменяющегося тока, который, протекая по двум параллельным бесконечно длинным проводникам ничтожно малого кругового сечения, расположенным в вакууме на расстоянии 1 м друг от друга, вызывает между ними силу взаимодействия 210^–7 Н на каждый метр длины проводников.

Рассмотрим теперь поведение контура с током в магнитном поле. Пусть прямоугольная рамка с током находится в однородном магнитном поле, причем направления магнитного момента рамки и индукции поля совпадают (рис.5.23). Со стороны магнитного поля на каждую сторону рамки будет действовать сила, направления всех сил указаны на рисунке. Действие сил приводит к растяжению рамки. Если изменить направление тока (или направление ), то действие сил будет приводить к сжатию рамки. Однако в любом случае, поскольку , то

, .

Нетрудно увидеть, что , т.е. первоначально покоившаяся рамка в целом будет сохранять состояние покоя в однородном магнитном поле. Таким образом, действие магнитного поля на рамку сводится в данном случае только к ее деформации.

Повернем плоскость рамки на угол  относительно положения, указанного на рис. 5.23. На такой же угол повернется вектор относительно вектора магнитной индукции. На рис. 5.24 показан вид сверху на рамку. Видно, что векторы сил и изменили свои направления (мы предлагаем вам самостоятельно убедиться в том, что направления и остались прежними). Несмотря на то, что в таком положении рамки по-прежнему , рамка не будет сохранять положение покоя. Если предоставить рамке возможность вращения, то она будет вращаться под действием моментов сил и вокруг оси z, перпендикулярной плоскости рис. 5.24, против часовой стрелки. Определим эти моменты:

; ;

; ,

где – радиусы-векторы, проведенные от оси вращения в точки приложения соответствующих сил.

Направления векторов моментов указаны на рисунке. Ясно, что суммарный момент сил, действующих на рамку, определится как

.

Поскольку (площадь рамки), то, воспользовавшись (5.16), получим

, . (5.34)

Таким образом, если направления магнитного момента рамки с током и магнитной индукции поля, в которое она помещена, не совпадают, то действие поля на рамку приведет к ее повороту вокруг оси, перпендикулярной вектору индукции. Поскольку при выполнении условий или вращающий момент станет равным нулю, то поворот рамки будет продолжаться до достижения рамкой положений, указанных на рис. 5.25. Однако нетрудно видеть, что положение, указанное на рис. 5.25, а – это положение устойчивого равновесия. При выведении рамки из этого положения действие момента сил возвращает рамку обратно (рис. 5.26, а). Положение рамки на рис. 5.25, б – это положение неустойчивого равновесия. При выведении рамки из этого положения действие момента сил разворачивает рамку еще больше (рис. 5.26, б).

Определим работу сил Ампера по повороту рамки на некоторый угол . Воспользуемся выводом п.4.7 первой части курса: . Тогда . С точки зрения закона сохранения энергии положительная работа внешних сил увеличивает энергию рамки с током в магнитном поле: . Поэтому энергия рамки с током в поле выразится так:

. (5.35)

Если теперь рассмотреть поведение рамки с током в неоднородном поле, то необходимо учесть, что на различные элементы рамки будут действовать силы, направленные по-разному (рис.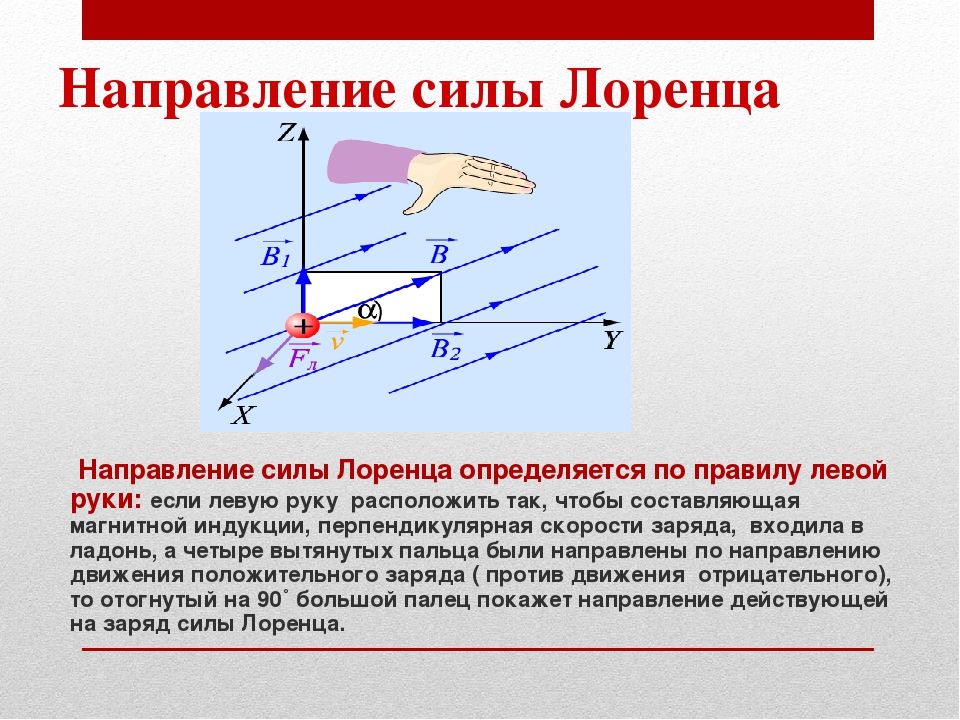 5.27). В результате суммирования элементарных сил можно получить результирующую силу, действующую на рамку в неоднородном поле. Поскольку далее будет показано, что силы Ампера потенциальны, то справедливо соотношение (3.12) из первой части курса: . Тогда, если неоднородность магнитного поля проявляется вдоль какой-нибудь оси Ох, то

,

где первый сомножитель – это проекция магнитного момента на выбранную ось. Таким образом, мы получили вывод: если магнитный момент рамки и индукция поля сонаправлены, то рамка втягивается в область более сильного поля (туда, где модуль больше, т.е. влево на рис. 5.27). Если направления магнитного момента рамки и индукции поля противоположны, то рамка выталкивается в область слабого поля.

Суммируя все сделанные выводы, резюмируем: в наиболее общем случае поведение контура с током во внешнем магнитном поле описывается его поступательным движением, вращением и деформацией.

Рассмотрим движение элемента проводника с током в магнитном поле под действием силы Ампера, действующей на этот элемент со стороны поля (рис. 5.28). Для простоты изображения сначала допустим, что линии магнитной индукции перпендикулярны проводнику, а поле однородное. Если перемещение элемента проводника равно , то элементарная работа силы Ампера будет равна

.

Поскольку в смешанном произведении векторов допустима циклическая перестановка сомножителей, то

,

где – вектор площади элемента поверхности, очерчиваемой при движении элемента проводника (она заштрихована на рис. 5.28), а dФ – элементарный магнитный поток чрез заштрихованную поверхность.

Полная работа по перемещению всего проводника может быть найдена так:

. (5.36)

Работа сил магнитного поля по перемещению проводника с током равна произведению силы тока в проводнике и магнитного потока через поверхность, очерчиваемую проводником при своем движении

18. Работа сил магнитного поля

по перемещению проводника и контура с током

Рассмотрим теперь перемещение замкнутого контура с током (рис. 5.29). Пусть контур произвольной формы перемещается из положения abcda в положение . Разделим контур abcda на две части abc и cda. Найдем работы по перемещению каждой части.

, где Ф₁ – магнитный поток через поверхность, ограниченную контуром в его начальном положении, – магнитный поток через поверхность, ограниченную контуром . Знак “–” в этой формуле вызван тем, что векторы перемещения и силы Ампера образуют друг с другом тупые углы для всех элементов проводника abc.

, где Ф₂ – магнитный поток через поверхность, ограниченную контуром в его конечном положении.

Работа по перемещению всего замкнутого контура найдется так: . Работа сил магнитного поля по перемещению контура с током равна произведению силы тока в контуре и изменения магнитного потока через площадь, ограниченную контуром:

. (5.37)

Если при вычислении работы сил магнитного поля рассмотреть самый общий случай произвольной ориентации элемента проводника с током и вектора магнитной индукции поля, то результат не изменится. Действительно, произвольно направленный вектор всегда можно разложить по трем взаимно перпендикулярным направлениям (рис. 5.30) так, что , , . Эти три составляющие магнитной индукции определяют выражения для трех составляющих силы Ампера , , . Однако, согласно (5.32), , причем , а поэтому работа данной составляющей силы Ампера по перемещению проводника будет равна нулю. Кроме того, . Поэтому работу по перемещению проводника будет совершать только сила , а именно этот случай мы и рассматривали раньше.

Заметим, что при перемещении контура с током в магнитном поле работа сил Ампера определяется магнитными потоками через контур только в начальном и конечном его положениях. Поэтому силы Ампера можно отнести к потенциальным.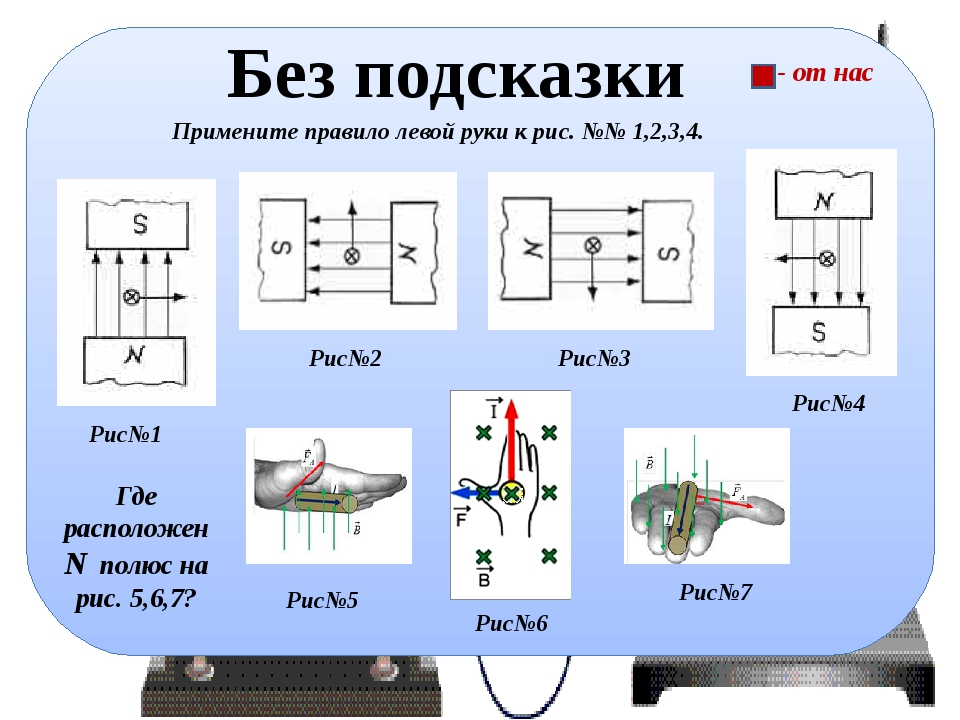

19. Явление электромагнитной индукции.

Закон Фарадея–Максвелла

Содержание опытов Фарадея можно пояснить следующими рисунками. Разместим на одном сердечнике две проводящие катушки (рис.6.1, а). Одну из них замкнем на гальванометр, а другую будем подключать к источнику тока при помощи ключа К. В момент замыкания (или размыкания) цепи ключом К гальванометр будет давать показания, т.е. в цепи второй катушки будет возникать электрический ток. Итак, по результатам такого опыта можно сделать вывод, что первая катушка электрически влияет на вторую. Однако, что было причиной появления тока в катушке 2: возникновение (или исчезновение) тока в катушке 1 или магнитного поля этого тока?

Для ответа на этот вопрос поставим второй опыт (рис. 6.1, б). Теперь катушка 1 постоянно подключена к источнику, а поэтому ток в ней неизменен. Однако в процессе смещения катушек друг относительно друга гальванометр дает показания, т.е. причиной появления тока в катушке 2 является изменение магнитного поля, в котором она находилась.

Чтобы подтвердить этот вывод, Фарадей проводит третий опыт (рис.6.1, в), в котором первая катушка заменяется постоянным магнитом. Результаты опыта при смещении магнита относительно катушки 2 полностью аналогичны предыдущим. Однако в этом случае видно, что причиной всех электрических явлений в катушке 2 является исключительно поведение магнитного поля, в которое она помещена, а источник создания магнитного поля никак не влияет на результат наблюдений.

Общим для всех трех опытов было то, что при осуществлении действий, описанных выше, изменялся магнитный поток через вторую катушку, в которой создавался (индуцировался) электрический ток. Важно также и то, что появление тока наблюдалось только в процессе изменения магнитного потока.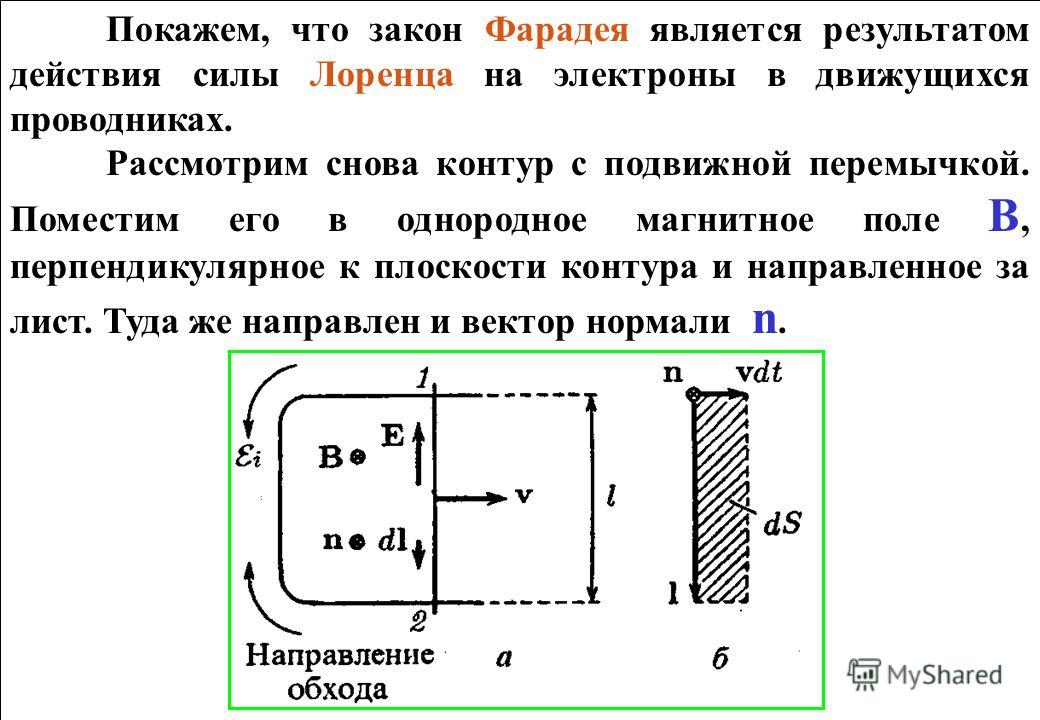 Как только изменение магнитного потока прекращалось (полностью замыкался ключ, прекращалось относительное смещение катушек или останавливался магнит), стрелка гальванометра занимала нулевое положение. Если гальванометр заменить вольтметром, то он аналогично будет показывать появление разности потенциалов на концах катушки 2.

Наблюдаемое явление Фарадей назвал электромагнитной индукцией, т.е. явлением возникновения ЭДС индукции (а также индукционного тока в замкнутом контуре) при любом изменении магнитного потока через площадь, ограниченную контуром.

Экспериментально обнаружено, что величина возбуждаемой ЭДС определяется только скоростью изменения магнитного потока через контур и не зависит от способа его изменения. Напомним, что, согласно определению магнитного потока (5.18), его величина может изменяться при изменении модуля индукции в точках поверхности, ограниченной контуром, при изменении ориентации контура относительно линий магнитной индукции поля, при изменении площади контура.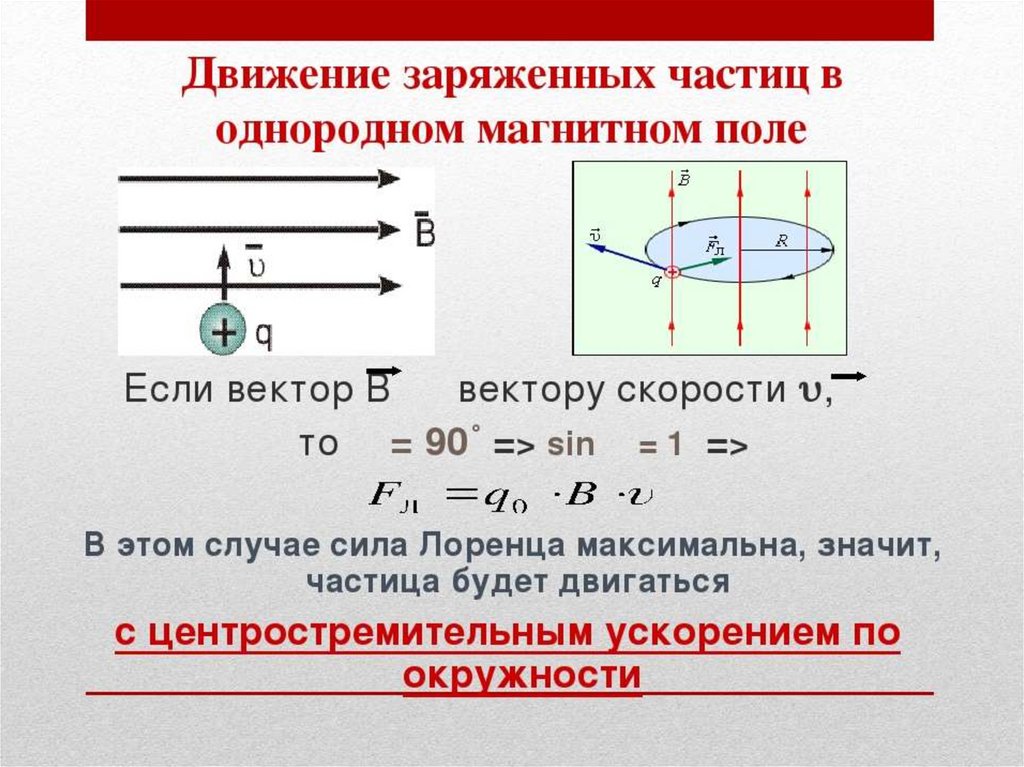

Также экспериментально выяснено, что направление индукционного тока в контуре таково, что своим магнитным полем он компенсирует изменение магнитного потока, вызвавшего его появление (правило Ленца). На рис. 6.2 показано, что при увеличении тока в контуре 1 будет увеличиваться магнитная индукция поля, создаваемого этим контуром. В этом случае магнитный поток этого поля через контур 2 также возрастает. Это приводит к появлению в контуре 2 электромагнитной индукции, т.е. в контуре создается индукционный ток . Его направление таково, что линии индукции создаваемого им магнитного поля () направлены противоположно внешнему. Тогда суммарный магнитный поток через контур 2 определяется разностью потоков внешнего и индуцированного полей. Поэтому величина магнитного потока через контур 2 увеличивается слабее. Если же ток в контуре 1 будет уменьшаться, то явление электромагнитной индукции создаст ток в контуре 2, направленный в противоположную сторону.

Таким образом, процессы, происходящие при электромагнитной индукции, приводят к тому, что магнитный поток через исследуемый контур стремится остаться неизменным. Можно показать, что это – следствие закона сохранения энергии. Итак, правило Ленца показывает, что следствие процесса (появляющийся индукционный ток) всегда препятствует причине, его вызывающей (изменению магнитного потока).

Поясним это еще на одном примере (рис.6.3). Поместим в однородное магнитное поле с индукцией систему двух параллельных проводников, замкнутых на резистор сопротивлением R. Пусть между проводниками располагается перемычка, способная перемещаться по ним без нарушения электрического контакта. Тогда при ее движении вправо со скоростью будет увеличиваться площадь проводящего контура, образованного проводниками, резистором и перемычкой. Соответственно, будет увеличиваться и магнитный поток через этот контур, что приведет к появлению индукционного тока.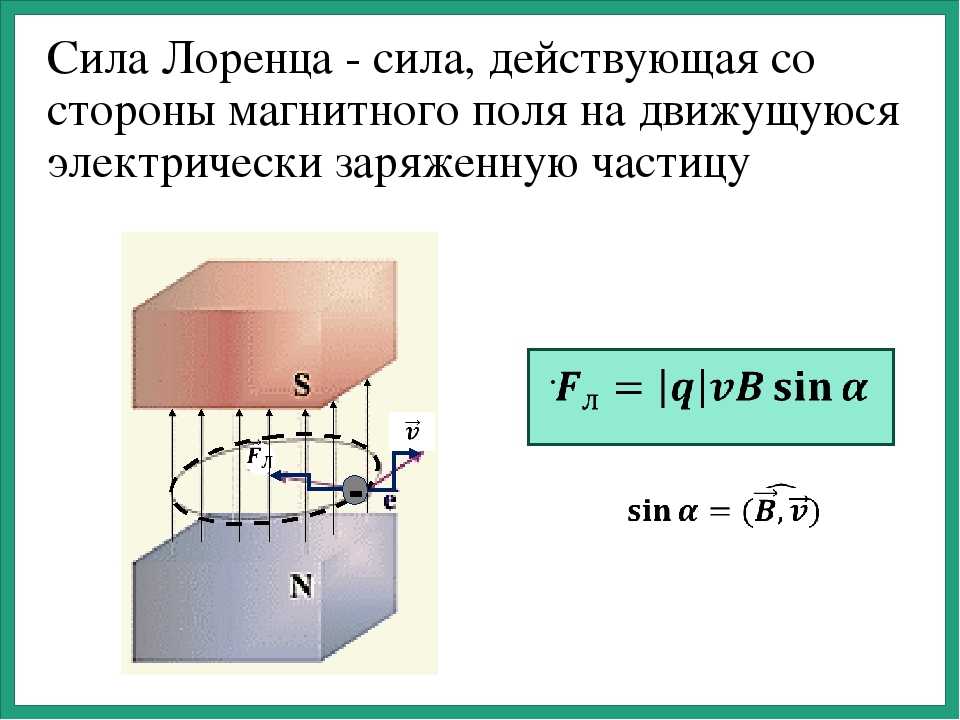 Индукционный ток в контуре будет иметь такое направление (против часовой стрелки), что вектор его магнитной индукции будет противоположен вектору индукции внешнего магнитного поля. В магнитном поле с индукцией на перемычку с индукционным током будет действовать сила Ампера, направление которой определим по правилу левой руки (см. рис. 6.3). Появившаяся сила стремится замедлить движение перемычки, т.е. препятствует ее движению. Поскольку причиной электромагнитной индукции в контуре было движение перемычки, то следствие явления – появившаяся сила Ампера – препятствует причине своего появления.

Выведем количественные соотношения, описывающие содержание явления электромагнитной индукции.

1 способ (на основе закона сохранения энергии). Рассмотрим схему, аналогичную предыдущей. На рис.6.4 показан проводящий контур, образованный двумя параллельными проводниками, замкнутыми свободно двигающейся по ним перемычкой. В контур включен источник тока с ЭДС E и резистор сопротивлением R. Поместим контур в однородное магнитное поле с индукцией . Поскольку в контуре существует электрический ток, то на перемычку будет действовать сила Ампера, что вызовет движение перемычки вправо. Поэтому площадь контура будет возрастать, а, следовательно, магнитный поток через площадь, ограниченную контуром, также будет увеличиваться. Это будет причиной появления электромагнитной индукции.

Согласно закону сохранения энергии работа, совершенная источником тока за время , равна работе сил магнитного поля по перемещению перемычки и выделившемуся в контуре за это время количеству теплоты: , т.е.

,

где – заряд, перенесенный источником за время . Поскольку , то ,

откуда сила тока в контуре.

Поскольку, согласно закону Ома, числитель последнего выражения должен определять суммарную ЭДС в контуре, то, следовательно, второе слагаемое выражает ЭДС индукции, возникшую в нем: .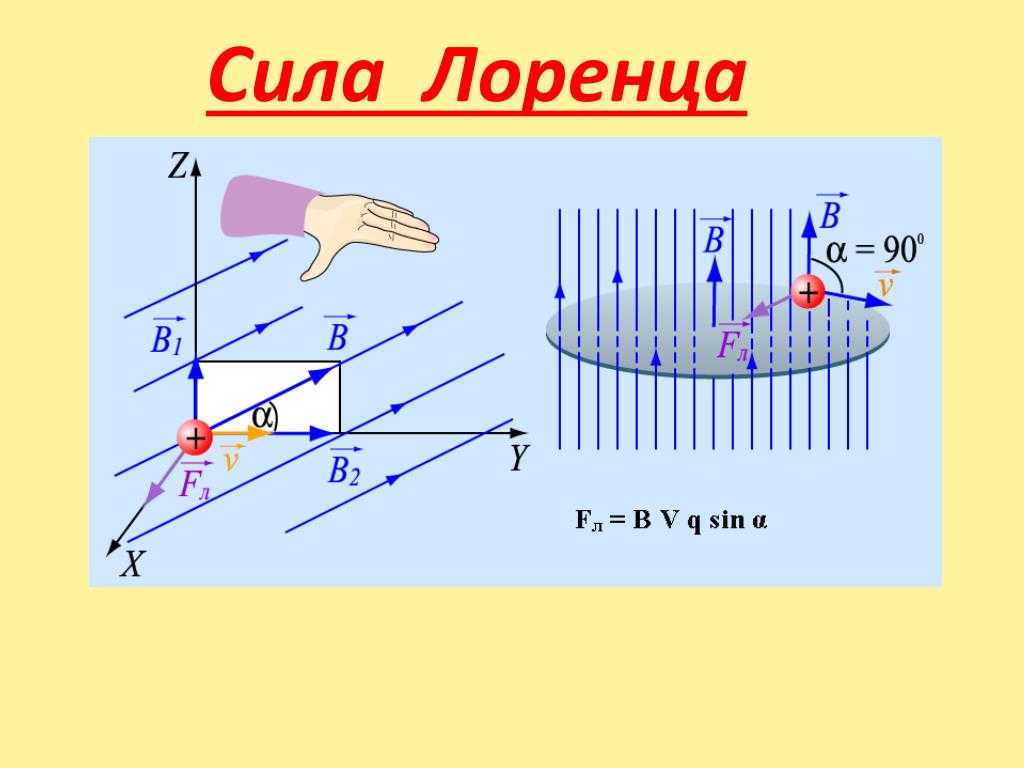 (6.1)

2 способ (на основе электронных представлений). Рассмотрим процессы, происходящие внутри перемычки (рис.6.5, а). Поскольку все свободные электроны двигаются вместе с ней вправо, то со стороны магнитного поля на них действует магнитная составляющая силы Лоренца (5.29). Ее действие приводит к смещению электронов к нижнему краю перемычки, в результате чего происходит разделение зарядов внутри нее. Между разделенными зарядами возникает электрическое поле напряженностью , которое действует на электроны с силой (рис.6.5, б). В стационарном режиме . Следовательно, , т.е. . Найдем разность потенциалов между концами перемычки: ,

поскольку – площадь, очерчиваемая проводником за время при движении (рис.6.5, в). Перемычка играет роль источника индукционного тока, а положительным направлением тока внутри источника считается направление от “–” к “+”. Поэтому ЭДС индукции, возникшая при движении перемычки, определится как

. (6.2)

Мы видим, что оба рассмотрения приводят к одному и тому же результату. Обобщим его на произвольный случай движения контура во внешнем магнитном поле (рис.6.6). Поскольку ЭДС – это удельная работа сторонних сил по переносу заряда вдоль контура, а роль сторонней силы выполняет , то. Преобразуем это выражение, используя свойства смешанного произведения векторов:

5.1: Силы свободных зарядов и токов

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

25005

• Дэвид Х. Стаелин
• Массачусетский технологический институт через MIT OpenCourseWare

Уравнение силы Лоренца и введение в силу

Уравнение силы Лоренца (1. 2.1) полностью характеризует электромагнитные силы на неподвижные и движущиеся заряды. Несмотря на простоту этого уравнения, оно очень точное и важное для понимания всех электрических явлений, потому что эти явления можно наблюдать только в результате действия сил на заряды. Иногда эти силы приводят в движение двигатели или другие исполнительные механизмы, а иногда они направляют электроны через материалы, которые нагреваются, освещаются или претерпевают другие физические или химические изменения. Эти силы также управляют токами, необходимыми для всех электронных схем и устройств.

Когда известны электромагнитные поля, местоположение и движение свободных зарядов, расчет сил, действующих на эти заряды, не представляет сложности и поясняется в разделах 5.1.2 и 5.1.3. Когда эти заряды и токи ограничены проводниками, а не изолированы в вакууме, обычно можно использовать подходы, представленные в разделе 5.2. Наконец, когда интересующие заряды и движение зарядов связаны внутри стационарных атомов или вращающихся заряженных частиц, необходимо добавить выражения для плотности сил Кельвина, разработанные в разделе 5. 3. Проблема обычно выходит за рамки этого текста, когда электромагнитные поля, производящие силы, не заданы, а определяются теми же зарядами, на которые действуют силы (например, физика плазмы), и когда скорости релятивистские.

В простейшем случае действуют силы, возникающие из-за действия известных электромагнитных полей на свободные заряды в вакууме. Этот случай можно рассмотреть, используя уравнение силы Лоренца (5.1.1) для вектора силы \(\overline{\mathrm{f}}\), действующего на заряд q [кулонов]:

\[ \ overline{\ mathrm {f}} = \ mathrm {q} \ left (\ overline {\ mathrm {E}} + \ overline {\ mathrm {v}} \ times \ mu _ {\ mathrm {o}} \ overline { \mathrm{H}}\right) \quad [\text { Ньютоны }]\qquad\qquad\qquad \text { (уравнение силы Лоренца) }\]

где \(\overline{\mathrm{E}}\) и \(\overline{\mathrm{H}}\) — локальные электрические и магнитные поля, а \(\overline{\mathrm{v}}\ ) — вектор скорости заряда [м с ^-1 ].

Электрические силы Лоренца, действующие на свободные электроны

Электронно-лучевая трубка (ЭЛТ), используемая для дисплеев в старых компьютерах и телевизорах, как показано на рисунке 5.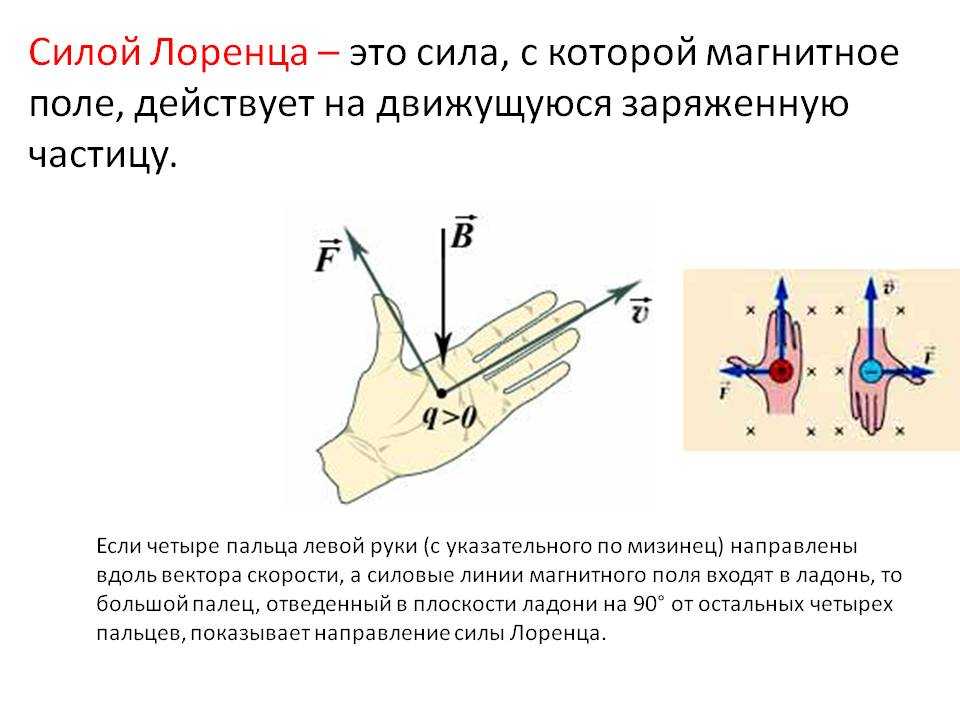 1.1, представляет собой простой пример закона силы Лоренца (5.1. 1). Электроны, термически возбужденные нагретым катода при -В вольт вылетают при низкой энергии и ускоряются в вакууме с ускорением \(\overline{\mathrm{a}}\) [м с ^-2 ] по направлению к заземленному аноду электрическим полем \( \overline{\mathrm{E}} \cong-\hat{z} \mathrm{V} / \mathrm{s}\) между анодом и катодом ¹³ ; V и s — напряжение на трубке и расстояние между катодом и анодом соответственно. В электронике анод по определению всегда имеет более положительный потенциал \(\Phi\), чем катод.

¹³ Анод заземлен по соображениям безопасности; он находится на лицевой стороне трубки, где пользователи могут положить пальцы на другую сторону стеклянной лицевой панели. Кроме того, катод и анод иногда имеют такую ​​форму, что электрическое поле \(\overline{\mathrm{E}}\), сила \(\overline{\mathrm{f}}\) и ускорение \(\ overline{\mathrm{a}}\) являются функциями от z, а не постоянными; т.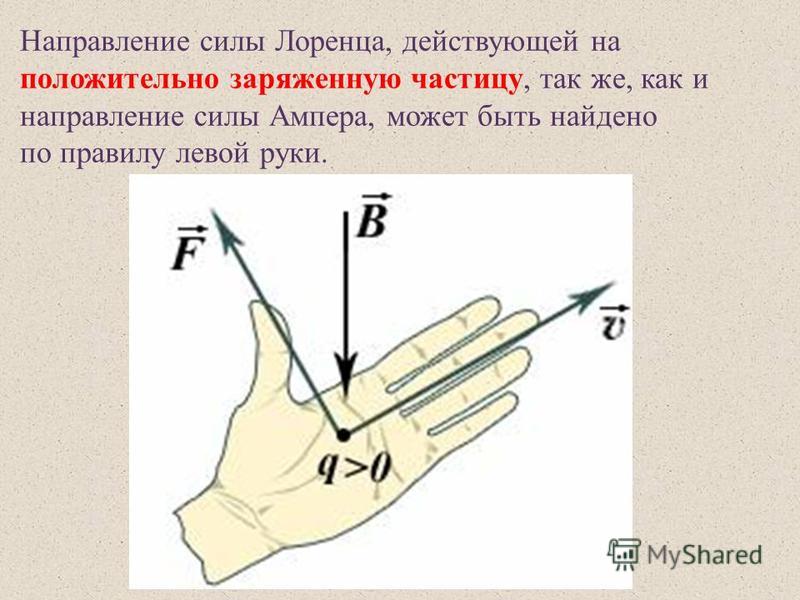 е. \(\overline{\mathrm E} \neq-\hat{z} V / D\).

Рисунок \(\PageIndex{1}\): Электронно-лучевая трубка. 9{2} / 2 \ \text{[m]}\]

, где мы определили начальное положение и скорость электрона при t = 0 как z _o и \(\overline{\mathrm{v}}_{ \mathrm{o}}\) соответственно.

Увеличение w _k кинетической энергии электрона равно сумме работы, совершаемой над ним электрическим полем \(\overline{\mathrm{E}}\). То есть увеличение кинетической энергии электрона является произведением постоянной силы f, действующей на него, и расстояния s, которое электрон прошел в направлении \(\overline{\mathrm{f}}\), испытывая это сила. Если s — расстояние между анодом и катодом, то:

\[\mathrm{w} _{\mathrm{k}}=\mathrm{fs}=(\mathrm{eV} / \mathrm{s}) \mathrm{s}=\mathrm{eV} \ \ text{[J]}\]

Таким образом, кинетическая энергия, приобретаемая электроном при движении через разность потенциалов V, равна эВ Джоулям. Если V = 1 вольт, то wk равно единице « электрон-вольт », или «e» джоулей, где e ≅ 1,6 × 10 ^-19 кулонов. {\ mathrm {D}} \ mathrm {e} \ mathrm {E} _ {\ mathrm {z}} \ mathrm {d} \ mathrm {z} = \ mathrm {eV} \]

Типичные значения V в телевизионных ЭЛТ, как правило, меньше 50 кВ, чтобы свести к минимуму опасные рентгеновские лучи, возникающие при воздействии электронов на люминофоры на лицевой панели ЭЛТ, которая часто изготавливается из поглощающего рентгеновские лучи свинцового стекла.

На рис. 5.1.1 также показано, как изменяющиеся во времени боковые электрические поля \(\overline{\mathrm{E}}_{\perp}(\mathrm{t})\) могут быть приложены отклоняющими пластинами для сканирования электронный луч через лицевую панель ЭЛТ и «рисовать» изображение, которое будет отображаться. При более высоких напряжениях на трубке V электроны движутся так быстро, что боковые электрические силы не успевают действовать, и вместо них используется магнитное отклонение, поскольку боковые магнитные силы возрастают со скоростью электронов v.

Магнитные силы Лоренца на свободных зарядах

Альтернативный метод бокового сканирования электронного луча в ЭЛТ использует магнитное отклонение, создаваемое катушками, создающими магнитное поле, перпендикулярное электронному лучу, как показано на рис. 5.1.2. Магнитная сила Лоренца, действующая на заряд q = -e (1,6021×10 ^-19 кулонов), легко находится из (5.1.1) и равна:

\[\overline{\mathrm{f}}=-\mathrm {e} \overline{\mathrm{v}} \times \mu_{\mathrm{o}} \overline{\mathrm{H}} \\text{[N]}\]

Таким образом, показанный электронный луч ЭЛТ будет отклоняться вверх, где магнитное поле \(\overline{\mathrm{H}}\), создаваемое катушкой, направлено за пределы бумаги; величина силы, действующей на каждый электрон, равна evμ _o Гн [Н].

Рисунок \(\PageIndex{2}\): Магнитное отклонение электронов в электронно-лучевой трубке.

Боковая сила, действующая на электроны evμ _o Гн, может быть связана с напряжением ЭЛТ V. Электроны, ускоренные из состояния покоя за счет разности потенциалов V вольт, имеют кинетическую энергию eV [J], где: 9{2} / 2\]

Следовательно, скорость электрона v = (2 эВ/м) ^0,5 , где m — масса электрона (9,107×10 ^-31 кг), а боковое отклонение увеличивается с увеличением напряжения на трубке V , тогда как оно уменьшается, если вместо этого используется электростатическое отклонение.

Другой случай магнитного отклонения показан на рис. 5.1.3, где свободный электрон, движущийся перпендикулярно магнитному полю \(\overline{\mathrm{B}}\), испытывает силу \(\overline{\mathrm{f} }\) ортогонален его вектору скорости \(\overline{\mathrm{v}}\), поскольку \(\overline{\mathrm{f}}=\mathrm{q} \overline{\mathrm{v}} \ раз \ mu _ {\ mathrm {o}} \ overline {\ mathrm {H}} \). 9{2} R=m_{e} v \omega_{e}\]

, где v = ω _e R. Мы можем решить (5.1.9) для этого «электрона циклотронной частоты » ω _e :

\[\omega_{\mathrm{e}}=\mathrm{e} \mu _{\mathrm{o}} \mathrm{H} / \mathrm{m}_{\mathrm{e}} \qquad \ qquad \qquad \text { (электронная циклотронная частота) }\]

, которая не зависит от v и энергии электрона, при условии, что электрон не является релятивистским. Таким образом, величины магнитных полей можно измерить, наблюдая за частотой излучения ω _e свободных электронов в интересующей области.

Пример \(\PageIndex{B}\): Циклотронное движение

Каков радиус \(r_e\) циклотронного движения для 100 э. в. свободный электрон в земной магнитосфере ¹⁴ где B ≅ 10 ^-6 Тесла? Каков радиус \(r_p\) свободного протона с той же энергией? Массы электронов и протонов составляют ~9,1×10 ^-31 и 1,7×10 ^-27 кг соответственно.

Раствор 9{-6} \\[4pt] &\cong 34 \\mathrm{m} \end{align*}\]

для электронов и ~2,5 км для протонов.

¹⁴ Магнитосфера простирается от ионосферы на несколько планетарных радиусов; столкновения частиц редки по сравнению с циклотронной частотой.

---

Эта страница под названием 5.1: Forces on Free Charges and Currents распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Дэвидом Х. Стэлином (MIT OpenCourseWare) через исходный контент, который был отредактирован к стилю и стандартам платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Дэвид Х. Стаелин

   Лицензия

   CC BY-NC-SA

   Версия лицензии

   4,0

   Программа OER или Publisher

   MIT OpenCourseWare

2. Теги

   1. электронно-лучевая трубка (ЭЛТ)
   2. ЭЛТ
   3. сила Лоренца
   4. Первый закон Ньютона
   5. source@https://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-013-electromagnetics-and-applications-spring-2009

Сила Лоренца — BrainDuniya

Что называют Силой Лоренца?

Когда заряженное тело движется в области электрического и магнитного поля, оно испытывает силы притяжения или отталкивания. Эта сила называется силой Лоренца . Эта сила Лоренца представляет собой комбинацию двух сил –

1. Электрическая сила – Сила, действующая на движущийся заряд из-за электрического поля.
2. Магнитная сила – Сила, действующая на движущийся заряд из-за магнитного поля.

Следовательно, \text {Сила Лоренца} = \text {Сила электрического поля, действующая на движущийся заряд} + \text {Сила магнитного поля, действующая на движущийся заряд}

Или, \quad \text {Сила Лоренца} = \text {Электрическая сила} + \text {Магнитная сила}

Или, \quad \vec {F} = \vec {F_e} + \vec {F_m} ………. (2)

Таким образом, сила Лоренца — это результирующая сила, испытываемая движущимся зарядом в области, где существуют как электрическое, так и магнитное поля.

1. Электрическая сила

Предположим, что заряд ( q ) движется в области, в которой присутствует электрическое поле ( \vec E ).

Тогда из определения напряженности электрического поля –

Сила, испытываемая зарядом ( q ) в электрическом поле ( \vec {E} ), определяется как –

\vec {F_e} = q \vec { E}

Направление этой электрической силы совпадает с направлением электрического поля ( \vec {E} ) .

2.Magnetic Force

Предположим, что заряд ( q ) движется в области, в которой присутствует магнитное поле ( \vec B ).

Тогда из определения магнитной силы из-за магнитного эффекта –

Сила, действующая на движущийся заряд (q), движущийся со скоростью (v) под углом (\theta) к направлению магнитного поля (\vec {B} ) , будет –

\vec {F_m} = q ( \vec {v} \ \times \ \\vec {B} ) …….. (1)

Направление этой магнитной силы соответствует правилу векторного произведения из ( \vec {v} ) и ( \vec {B} ) .

Следовательно, сила Лоренца на заряде будет –

\vec {F} = q \vec {E} + q ( \vec {v} \ \times \ \vec {B} )

= q [ \vec {E} + ( \vec {v} \times \vec {B} ) ] ……… (3)

---

Сила Лоренца, действующая на проводник

Проводник содержит большое количество свободных электронов, являющихся носителями заряда. Эти свободные электроны движутся в проводнике с дрейфовой скоростью ( \vec {v} ). Свободные электроны движутся в направлении, противоположном направлению обычного тока, протекающего в проводнике.

Следовательно, если проводник с током поместить в магнитное поле, свободные электроны будут испытывать магнитную силу, которая передается проводнику.

Рассмотрим проводник длиной (l), по которому течет ток (I). Проводник помещен в однородное магнитное поле ( \vec {B} ), как показано на рисунке. Пусть –

• Количество свободных электронов в единице объема проводника равно (n).
• Площадь поперечного сечения проводника (А)
• Заряд одного электрона (-е)

Следовательно, магнитная сила, испытываемая одним электроном, будет равна –

\vec {f_m} = ( — e ) ( \vec {v} \ \times \ \\vec {B} )

Сила, действующая на элемент проводника

Рассмотрим небольшой элемент длиной ( dl ) проводника, как показано на рисунке.

090801 СИЛА ЛОРЕНЦА НА ПРОВОДНИКЕ С ТОКОМ

Тогда количество свободных электронов в элементе будет –

В = n \\times \ A \\times \ dl = ( nAdl )

Следовательно, магнитная сила, действующая на элемент будет –

d \vec {F_m} = \text {Сила, действующая на один электрон} \ \times \ \text {Количество электронов}

= ( n A dl ) \vec {f_m}

= n A dl [ — e ( \vec {v} \ \times \ \vec {B} ) ]

Итак, \quad d \vec {F_m} = — n A e dl ( \vec {v} \ \times \ \vec {B} )

Дрейфовая скорость электрона определяется выражением –

\vec {v} = \left ( — \frac {\vec {d l}}{dt} \right ) (Знак минус используется, потому что ( dl ) в направлении, противоположном направлению ( \vec {v} ) )

Итак, \quad d \vec {F_m} = — n A e dl \left [ \left ( — \frac {\vec {d l}}{dt} \right ) \ \times \ \vec {B} \ right ]

= n A e dl \ left ( \ frac {\ vec {d l}} {dt} \ \ times \ \ vec {B} \ right )

Но, \ quad ( n A dl ) e = dq ( Суммарный заряд в элементе. )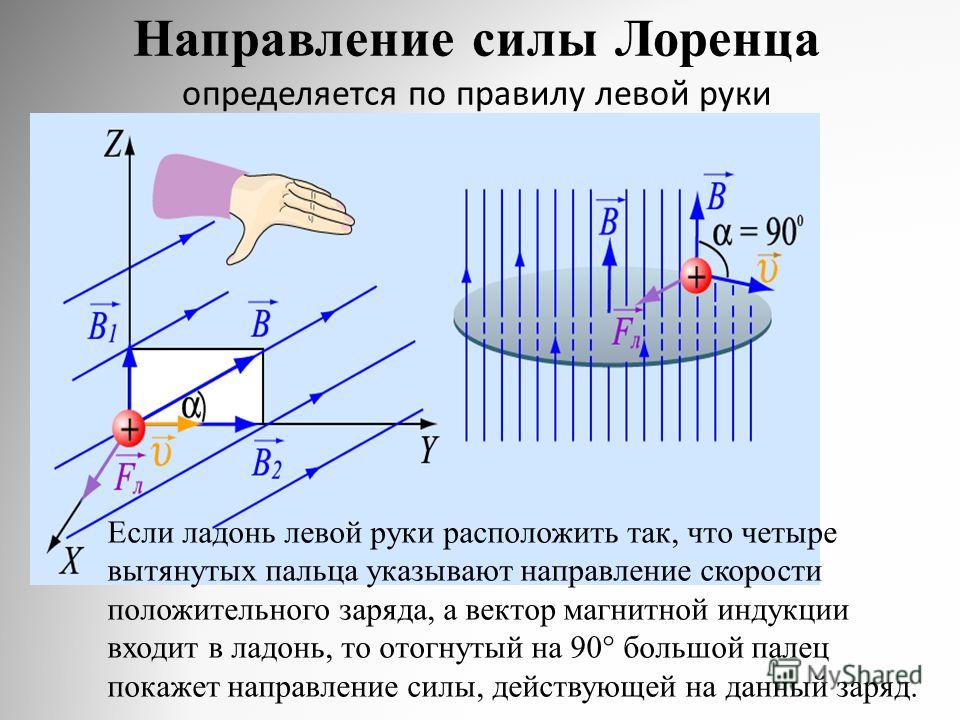

Следовательно, \quad d \vec {F_m} = dq \left ( \frac {\vec {d l}}{dt} \ \times \ \vec {B} \right )

= \left ( \frac {dq}{dt} \right ) ( \vec {d l} \\times \\vec {B} ) \quad \text {Но,} \\left ( \frac {dq}{ dt} \right ) = I

= I \ ( \vec {d l} \ \times \ \vec {B} ) ………… (4)

Суммарная сила Лоренца на проводнике

Следовательно, чистая сила Лоренца на проводнике получается интегрированием –

\vec {F_m} = \int d \vec {F_m}

= \int I \ ( \vec {d l} \ \times \ \ \vec {B} )

= I \ ( \int \vec {d l } \ \times \ \vec {B} )

= I \ ( \vec {l} \times \ \vec {B} \ ) ………. (5)

Это выражение представляет собой векторную форму из для получения величины результирующей силы, действующей на проводник.

Аналитическая форма чистой силы Лоренца

Учтите, что ось прямого проводника образует угол ( \theta ) в положительном направлении с направлением магнитного поля ( \vec {B} ), как показано на рисунке.

Тогда величина магнитной силы будет равна –

\vec {F_m} = B I l \sin \theta ……….. (6)

Теперь рассмотрим следующие ситуации –

(1) Когда ( \тета = 0 \градус) \\текст {или} \ (\тета = 180 \градус) .

Тогда ( \sin \theta = 0 ) .

Следовательно, ( F_m = 0 ) . Следовательно, на проводник не будет действовать никакая сила.

(2) Когда ( \тета = 90 \градус ) .

Тогда ( \sin \theta = 1 ) .

Следовательно, ( F_m = BIl ) . Следовательно, проводник будет испытывать максимальную силу.

(3) Если проводник не прямой, а изогнутый, то его можно рассматривать как комбинацию множества небольших прямых проводников длиной (dl) каждый.

Тогда магнитная сила [ F_m = \sum {I} ( d \vec {l} \ \times \ \vec {B} ) ]

(4) Магнитная сила, действующая на любой замкнутый контур с током или многоугольник в однородном магнитном поле, становится равной нулю. В этом случае длины элементов образуют замкнутый многоугольник.

Следовательно, [ \oint {d \vec {l}} = 0 ]

---

Сила между двумя параллельными проводниками

Рассмотрим два бесконечно длинных параллельных проводника X и Y, лежащих на горизонтальной плоскости, как показано на рисунке . Пусть –

• Ток в проводнике X равен ( I_x ) и
• Ток в проводнике Y равен (I_y).
• Направления ( I_x ) \ \text {и} \ ( I_y ) совпадают.
• Расстояние между проводниками ( d ) .

Сила, действующая на проводник Y из-за магнитного поля проводника X

Ток в проводнике X создаст вокруг себя магнитное поле, как показано на рисунке. Напряженность этого магнитного поля в любой точке проводника Y будет равна –

B_x = \left ( \frac {\mu_0}{4 \pi} \right ) \left ( \frac {2 I_x}{d} \ справа ) …….. (1)

Направление этого магнитного поля определяется правилом большого пальца правой руки . Она перпендикулярна плоскости проводника X и направлена ​​вертикально вниз (т.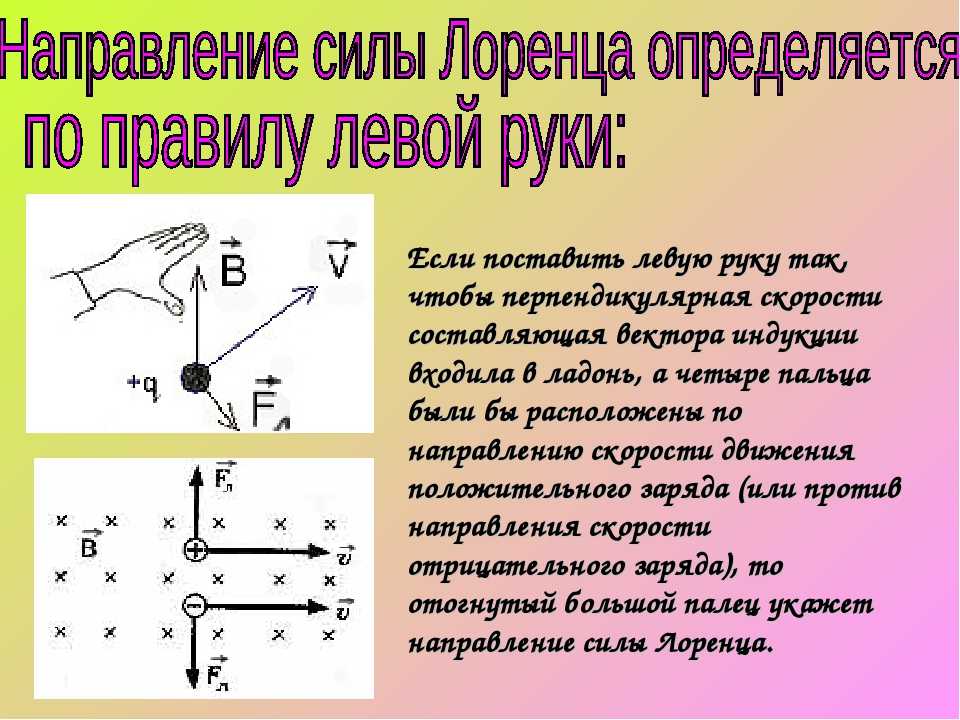 е. проникает в плоскость бумаги) в пространстве между проводниками X\\text{и}\Y.

090802 МАГНИТНАЯ СИЛА МЕЖДУ ДВУМЯ ПАРАЛЛЕЛЬНЫМИ ПРОВОДАМИ С ТОКОМ

Мы знаем, что сила Лоренца, действующая на проводник с током, равна –

F = B I l \sin \theta

Проводник Y перпендикулярен магнитному полю. Следовательно, ( \тета = 90 \градус )

Таким образом, \quad F = B I l

Следовательно, сила, действующая на единицу длины проводника Y, будет равна –

F_y = B_x \times I_y \times 1 = B_x \ I_y

Подставляя значение ( B_x ) из уравнения (1), получаем –

F_y = \left ( \frac {\mu_0}{4 \pi} \right ) \left ( \frac {2 \ I_x}{d} \right ) I_y

Или, \quad F_y = \left ( \frac {\mu_0}{4 \pi} \right ) \left ( \frac {2 \ I_x \ I_y}{d} \right ) ……….. ( 2)

Сейчас, к Правило левой руки Флеминга , направление силы ( F_y ) находится в направлении проводника X .

Сила, действующая на проводник X из-за магнитного поля проводника Y

Аналогичным образом, сила, действующая на единицу длины проводника X в магнитном поле ( B_y ) из-за проводника Y, получается как –

F_x = \left ( \frac {\mu_0}{4 \pi} \right ) \left ( \frac {2 \ I_x \ I_y}{d} \right ) ……….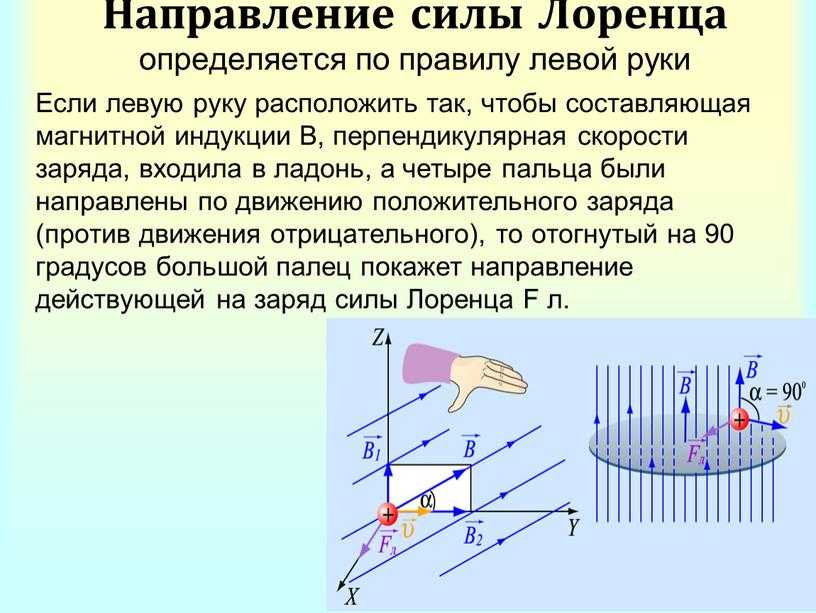 . (3)

По Правило левой руки Флеминга , направление силы (F_x) находится в направлении проводника Y.

Мы находим, что силы ( F_x ) \ \text {и} \ ( F_y ) равны, но противоположны по направлению. Таким образом, эти силы будут тянуть два проводника навстречу друг другу.

Отсюда делают вывод, что два длинных параллельных проводника, по которым текут токи одного направления, притягиваются друг к другу. Аналогично, два длинных параллельных проводника, по которым течет ток в противоположном направлении, отталкиваются друг от друга.

090803 МАГНИТНАЯ СИЛА МЕЖДУ ДВУМЯ ПРОТИВОПАРАЛЛЕЛЬНЫМИ ПРОВОДАМИ ТОКА

Магнитное поле посередине

Пространство между двумя параллельными проводниками находится под влиянием двух магнитных полей (B_x) и (B_y). Если по двум проводникам текут токи одного направления, то направления двух магнитных полей в пространстве между проводниками будут противоположными.

Величина магнитного поля на расстоянии \left ( \frac {d}{2} \right ) от проводников будет одинаковой, но противоположной по направлениям.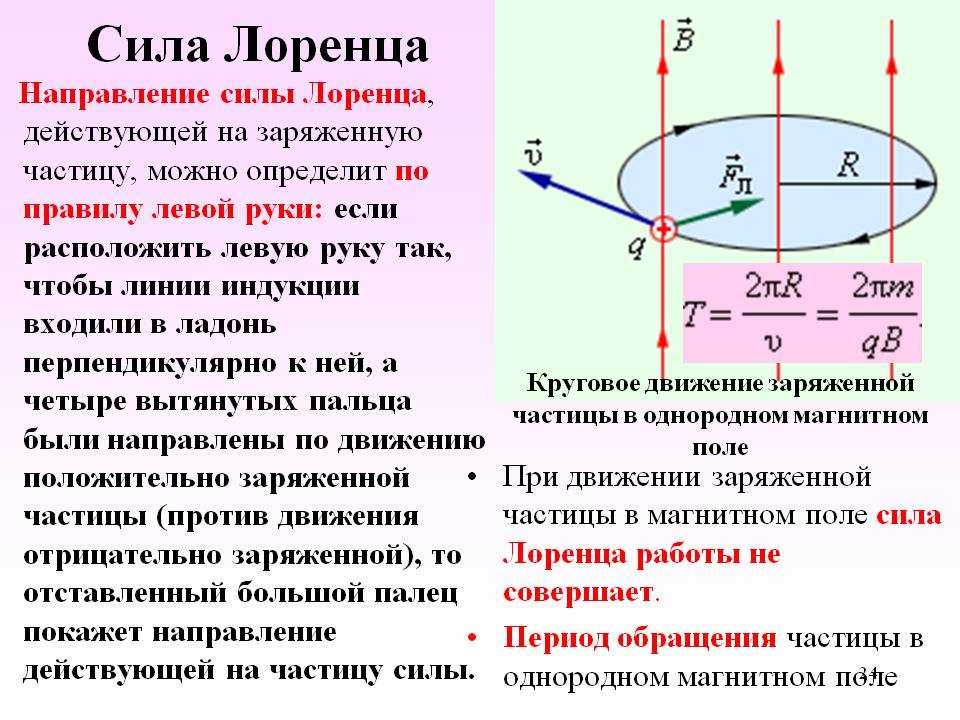 Следовательно, чистое магнитное поле на середине расстояния между двумя проводниками становится равным нулю.

Если токи в обоих проводниках текут в противоположных направлениях, то направление двух магнитных полей в пространстве между проводниками будет одинаковым. Тогда магнитное поле на расстоянии \left ( \frac {d}{2} \right ) от проводников будет одинаковым и направленным в ту же сторону. Следовательно, чистое магнитное поле в этой точке будет –

B = ( B_x + B_y )

= \left [ \left ( \frac {\mu_0}{4 \pi} \right ) \left ( \frac { 2 I}{d/2} \right ) + \left ( \frac {\mu_0}{4 \pi} \right ) \left ( \frac {2 I}{d/2} \right ) \right ]

= 4 \times \left ( \frac {\mu_0}{4 \pi} \right ) \left ( \frac {2 I}{d} \right )

---

См. числовые задачи, основанные на этой статье.

• P0
• P0

• P0

• P0

---

11,4 MAGNEL CORMIT раздел, вы сможете:
• Определить направление, в котором на проводник с током действует сила во внешнем магнитном поле
• Расчет силы, действующей на провод с током во внешнем магнитном поле

На движущиеся заряды действует сила магнитного поля. Если эти движущиеся заряды находятся в проводе, то есть если по проводу течет ток, на провод также должна действовать сила. Однако, прежде чем мы обсудим силу, действующую на ток со стороны магнитного поля, мы сначала исследуем магнитное поле, создаваемое электрическим током. Здесь мы изучаем два отдельных эффекта, которые тесно взаимодействуют друг с другом: проводник с током создает магнитное поле, и магнитное поле воздействует на проводник с током.

Магнитные поля, создаваемые электрическими токами

Обсуждая исторические открытия в области магнетизма, мы упомянули открытие Эрстеда о том, что провод, по которому течет электрический ток, вызывает отклонение расположенного поблизости компаса. Была установлена ​​связь, что электрические токи создают магнитные поля. (Эта связь между электричеством и магнетизмом обсуждается более подробно в «Источниках магнитных полей».)

На стрелку компаса рядом с проводом действует сила, которая выравнивает стрелку по касательной к окружности вокруг провода.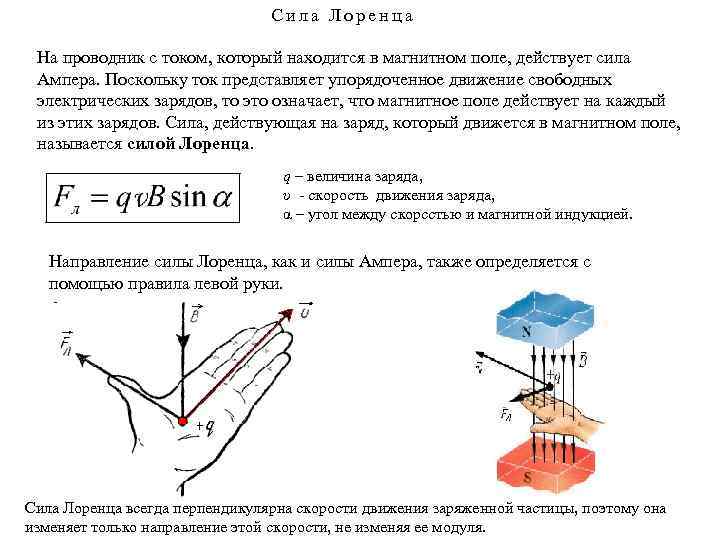 Следовательно, провод с током создает круговые петли магнитного поля. Чтобы определить направление магнитного поля, создаваемого проводом, мы используем второе правило правой руки. В RHR-2 большой палец указывает в направлении тока, а пальцы обхватывают провод, указывая направление создаваемого магнитного поля (рис. 11.11). Если магнитное поле исходило от вас или исходило от страницы, мы обозначаем это точкой. Если бы магнитное поле попадало на страницу, мы представляем это с помощью символа ×.×. Эти символы возникли при рассмотрении векторной стрелки: стрелка, направленная к вам, с вашей точки зрения выглядела бы как точка или кончик стрелки. Стрелка, направленная от вас, с вашей точки зрения выглядела бы как крестик или ×.×. Составной эскиз магнитных кругов показан на рис. 11.11, где показано, что напряженность поля уменьшается по мере удаления от провода за счет петель, которые находятся дальше друг от друга.

Рисунок 11.11 (а) Когда провод находится в плоскости бумаги, поле перпендикулярно бумаге. Обратите внимание на символы, используемые для поля, указывающего внутрь (например, хвост стрелы), и поля, указывающего наружу (например, кончик стрелки). (b) Длинный и прямой провод создает поле с силовыми линиями магнитного поля, образующими круглые петли.

Расчет магнитной силы

Электрический ток — это упорядоченное движение заряда. Следовательно, проводник с током в магнитном поле должен испытывать силу, обусловленную полем. Чтобы исследовать эту силу, давайте рассмотрим бесконечно малый отрезок провода, как показано на рис. 11.12. Длина и площадь поперечного сечения секции дл и А соответственно, поэтому его объем равен V=A·дл.V=A·дл. Проволока сформирована из материала, содержащего n носителей заряда в единице объема, поэтому число носителей заряда в сечении составляет нА·дл.нА·дл. Если носители заряда движутся со скоростью дрейфа v→d,v→d, ток I в проводе равен (из тока и сопротивления)

I=neAvd.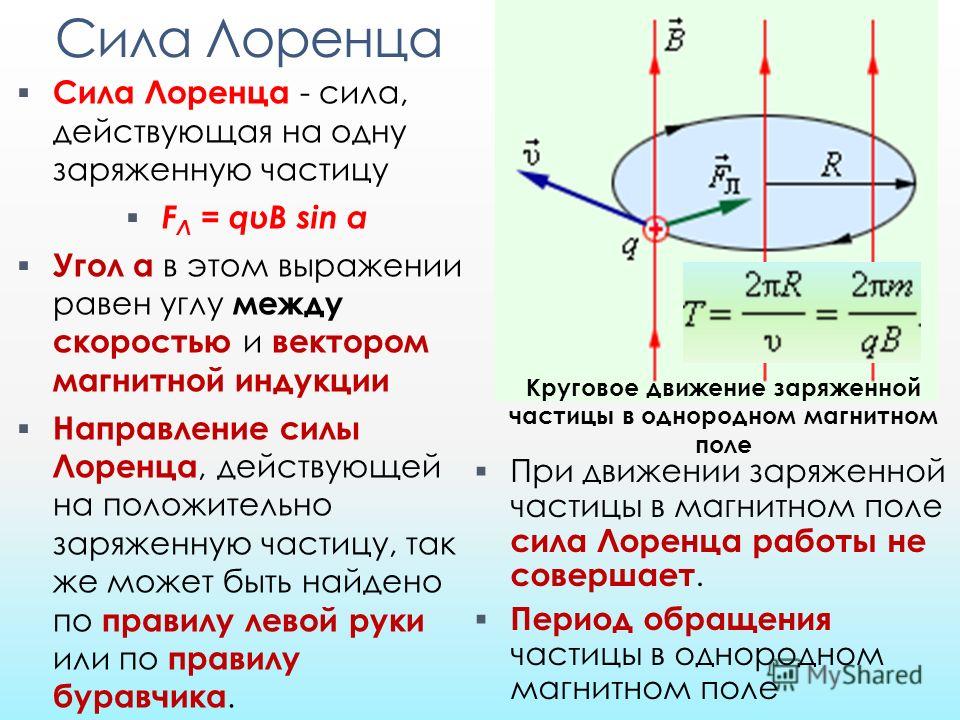 I=neAvd.

Магнитная сила, действующая на любой отдельный носитель заряда, равна ev→d×B→,ev→d×B→, поэтому общая магнитная сила dF→dF→ на носителях заряда nA·dlnA·dl в сечении провода равна

dF→=(nA·dl)ev→d×B→.dF→=(nA·dl)ev→d×B→.

11.10

Мы можем определить dl как вектор длины dl , указывающий вдоль v→d,v→d, что позволяет нам переписать это уравнение как

dF→=neAvddl→×B→,dF→=neAvddl→×B→,

11.11

или

dF→=Idl→×B→.dF→=Idl→×B→.

11.12

Это магнитная сила, действующая на сечение провода. Обратите внимание, что на самом деле это чистая сила, действующая со стороны поля на сами носители заряда. Направление этой силы задается RHR-1, где вы указываете пальцами в направлении тока и скручиваете их в сторону поля. Затем ваш большой палец указывает направление силы.

Рисунок 11.12 Бесконечно малое сечение провода с током в магнитном поле.

Чтобы определить магнитную силу F→F→ на проводе произвольной длины и формы, мы должны проинтегрировать уравнение 11.12 по всему проводу. Если сечение провода прямое, а B однородное, дифференциалы уравнения становятся абсолютными величинами, что дает нам

F→=Il→×B→.F→=Il→×B→.

11.13

Это сила, действующая на прямой провод с током в однородном магнитном поле.

Пример 11,4

Уравновешивание гравитационной и магнитной сил на проводе с током

Проволока длиной 50 см и массой 10 г подвешена в горизонтальной плоскости на паре гибких проводов (рис. 11.13). Затем провод подвергается воздействию постоянного магнитного поля величиной 0,50 Тл, которое направлено, как показано на рисунке. Каковы величина и направление тока в проводе, необходимые для снятия напряжения в опорных выводах?

Рисунок 11.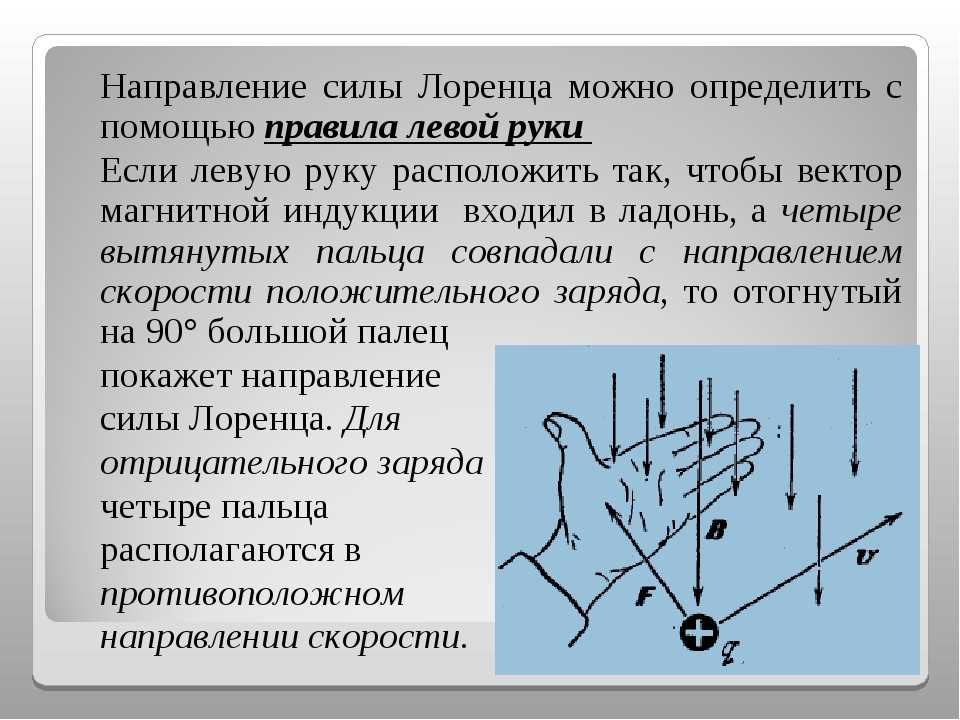 13 а) Проволока, подвешенная в магнитном поле. (b) Диаграмма свободного тела для проволоки.

Стратегия

Судя по диаграмме свободного тела на рисунке, напряжения в опорных проводах стремятся к нулю, когда гравитационные и магнитные силы уравновешивают друг друга. Используя RHR-1, мы обнаруживаем, что магнитная сила направлена ​​вверх. Затем мы можем определить ток I , приравняв две силы.

Раствор

Приравняем две силы веса и магнитной силы, действующие на провод:

мг=IIB.мг=ILB.

Таким образом,

I=mglB=(0,010 кг)(90,8 м/с2)(0,50 м)(0,50T)=0,39A.I=mglB=(0,010кг)(9,8м/с2)(0,50м)(0,50T)=0,39A.

Значение

Это большое магнитное поле создает значительную силу на длине провода, чтобы противодействовать весу провода.

Пример 11,5

Расчет силы магнитного поля на проводе с током

По длинному жесткому проводу, проложенному вдоль оси y , течет ток силой 5,0 А, текущий в положительном направлении y .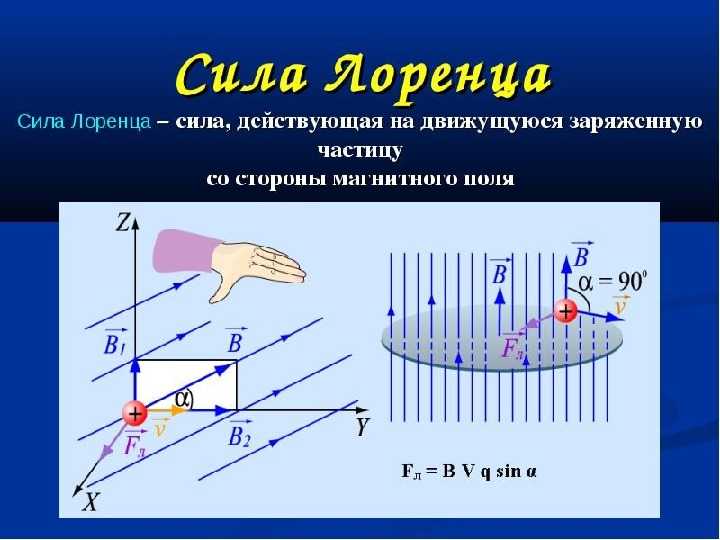 а) Если постоянное магнитное поле величиной 0,30 Тл направлено вдоль положительного x -ось, какова магнитная сила на единицу длины провода? б) Если постоянное магнитное поле с напряженностью 0,30 Тл направлено под углом 30 градусов от оси + x к оси + y , какова магнитная сила на единицу длины провода?

Стратегия

Магнитная сила, действующая на провод с током в магнитном поле, определяется как F→=Il→×B→.F→=Il→×B→. Для части а, поскольку в этой задаче ток и магнитное поле перпендикулярны, мы можем упростить формулу, чтобы получить величину и найти направление через RHR-1. Угол θ составляет 90 градусов, что означает sinθ=1.sinθ=1. Кроме того, длину можно разделить на левую часть, чтобы найти силу на единицу длины. Для части b текущая длина записывается в виде единичного вектора, а также магнитное поле.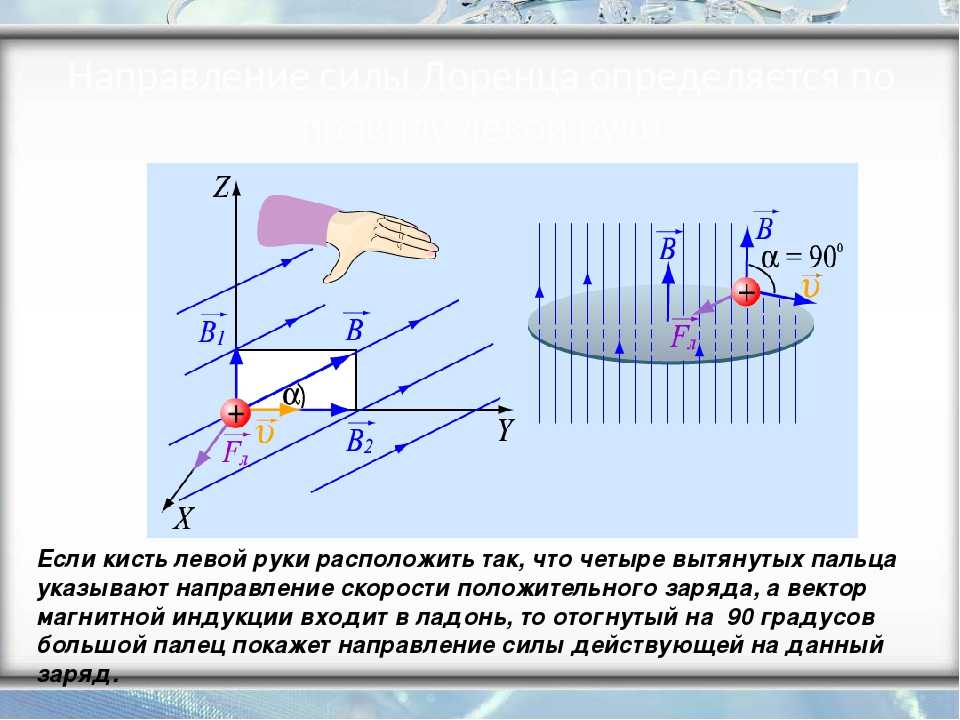 После взятия перекрестного произведения направленность очевидна по результирующему единичному вектору.

Решение

1. Начнем с общей формулы для магнитной силы, действующей на провод. Мы ищем силу на единицу длины, поэтому мы делим на длину, чтобы вывести ее в левую часть. Мы также устанавливаем sinθ=1.sinθ=1. Следовательно, решение

   F=IlBsinθFl=(5,0 А)(0,30 Т)Fl=1,5 Н/м.F=IlBsinθFl=(5,0 А)(0,30 Т)Fl=1,5 Н/м.

   Направленность: Укажите пальцами в положительном направлении y и согните пальцы в положительном направлении x . Ваш большой палец будет указывать в направлении −k→−k→. Следовательно, с направленностью решение

   F→l=-1,5k→Н/м.F→l=-1,5k→Н/м.

2. Текущая длина и магнитное поле записываются в виде единичного вектора. Затем мы используем векторное произведение, чтобы найти силу: 9Н/м.

Значение

Это большое магнитное поле создает значительную силу на проводе небольшой длины. По мере того, как угол магнитного поля становится ближе к току в проводе, на него действует меньшая сила, как видно из сравнения частей а и б.

Проверьте свое понимание 11.3

Проверьте свое понимание Прямая гибкая медная проволока погружена в магнитное поле, направленное на страницу. а) Если ток в проводе течет по + x -направление, в какую сторону будет изгибаться провод? б) В какую сторону изгибается провод, если ток течет в направлении – x ?

Пример 11,6

Сила на круглой проволоке

Круговая петля с током радиуса R , по которой течет ток I , расположена в плоскости xy . Постоянное однородное магнитное поле прорезает петлю параллельно оси y (рис. 11.14). Найдите магнитную силу, действующую на верхнюю половину петли, нижнюю половину петли и полную силу, действующую на петлю.

Рисунок 11.14 Петля из проволоки, по которой течет ток в магнитном поле.

Стратегия

Магнитная сила на верхней петле должна быть записана через дифференциальную силу, действующую на каждый сегмент петли. Если мы проинтегрируем по каждой дифференциальной части, мы найдем общую силу на этом участке петли. Аналогично находится сила на нижней петле, а полная сила есть сложение этих двух сил.

Решение

Дифференциальная сила, действующая на произвольный отрезок проволоки, расположенный на верхнем кольце, равна:

dF=IBsinθdl.dF=IBsinθdl.

, где θθ — угол между направлением магнитного поля (+ y ) и отрезком провода. Дифференциальный сегмент расположен на том же радиусе, поэтому, используя формулу длины дуги, мы имеем:

dl=RdθdF=IBRsinθdθ.dl=RdθdF=IBRsinθdθ.

Чтобы найти силу, действующую на сегмент, проинтегрируем по верхней половине круга от 0 до π.