Метод Гаусса — примеры c решением, теоремы и формулы

Карл Фридрих Гаусс – немецкий математик, основатель одноименного метода решения СЛАУ

Карл Фридрих Гаусс – был известным великим математиком и его в своё время признали «королём математики». Хотя название «метод Гаусса» является общепринятым, Гаусс не является его автором: метод Гаусса был известен задолго до него. Первое его описание имеется в китайском трактате «Математика в девяти книгах», который составлен между II в. до н. э. и I в. н. э. и представляет собой компиляцию более ранних трудов, написанных примерно в X в. до н. э.

Метод Гаусса – последовательное исключение неизвестных. Этот метод используется для решения квадратных систем линейных алгебраических уравнений. Хотя уравнения при помощи метода Гаусса решаются легко, но всё же студенты часто не могут найти правильное решение, так как путаются в знаках (плюсы и минусы). Поэтому во время решения СЛАУ необходимо быть предельно внимательным и только тогда можно легко, быстро и правильно решить даже самое сложное уравнение.

У систем линейных алгебраических уравнений есть несколько преимуществ: уравнение не обязательно заранее на совместность; можно решать такие системы уравнений, в которых число уравнений не совпадает с количеством неизвестных переменных или определитель основной матрицы равняется нулю; есть возможность при помощи метода Гаусса приводить к результату при сравнительно небольшом количестве вычислительных операций.

О чем статья

Определения и обозначения

Как уже говорилось, метод Гаусса вызывает у студентов некоторые сложности. Однако, если выучить методику и алгоритм решения, сразу же приходит понимание в тонкостях решения.

Для начала систематизируем знания о системах линейных уравнений.

Обратите внимание!

СЛАУ в зависимости от её элементов может иметь:

1. Одно решение;
2. много решений;
3. совсем не иметь решений.

В первых двух случаях СЛАУ называется совместимой, а в третьем случае – несовместима. Если система имеет одно решение, она называется определённой, а если решений больше одного, тогда система называется неопределённой.

Метод Крамера и матричный способ не подходят для решения уравнений, если система имеет бесконечное множество решений. Вот поэтому нам и нужен метод Гаусса, который поможет нам в любом случае найти правильное решение. К элементарным преобразованиям относятся:

• перемена мест уравнений системы;
• почленное умножение обеих частей на одно из уравнений на некоторое число, так, чтобы коэффициенты при первой переменной в двух уравнениях были противоположными числами;
• сложение к обеим частям одного из уравнений определённых частей другого уравнения.

Итак, когда мы знаем основные правила и обозначения, можно приступать к решению.

Теперь рассмотрим, как решаются системы методом Гаусса на простом примере:

   

где а, в, с  – заданные коэффициенты, d – заданные свободные члены, x, y, z – неизвестные. Коэффициенты и свободные члены уравнения можно называть его элементами.

Если = = = , тогда система линейных алгебраических уравнений называется однородной, в другом случае – неоднородной.

Множественные числа , , называются решением СЛАУ, если при подстановке , , в СЛАУ получим числовые тождества.

Система, которую мы написали выше имеет координатную форму. Если её переделать в матричную форму, тогда система будет выглядеть так:

– это основная матрица СЛАУ.

– матрица столбец неизвестных переменных.

– матрица столбец свободных членов.

Если к основной матрице добавить в качестве – ого столбца матрицу-столбец свободных членов, тогда получится расширенная матрица систем линейных уравнений. Как правило, расширенная матрица обозначается буквой , а столбец свободных членов желательно отделить вертикальной линией от остальных столбцов. То есть, расширенная матрица выглядит так:

Если квадратная матрица равна нулю, она называется вырожденная, а если – матрица невырожденная.

Обратите внимание!

Если с системой уравнений:          

Произвести такие действия:

• умножать обе части любого из уравнений на произвольное и отличное от нуля число ;
• менять местами уравнения;
• к обеим частям любого из уравнений прибавить определённые части другого уравнения, которые умножаются на произвольное число ,

тогда получается эквивалентная система, у которой такое же решение или нет решений совсем.

Теперь можно перейти непосредственно к методу Гаусса.

Нужна помощь в написании работы?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Цена работы

Простейшие преобразования элементов матрицы

Мы рассмотрели основные определения и уже понимаем, чем нам поможет метод Гаусса в решении системы. Теперь давайте рассмотрим простую систему уравнений. Для этого возьмём самое обычное уравнение, где и используем решение методом Гаусса:

Из уравнения запишем расширенную матрицу:

Из данной матрицы видно, по какому принципу она записана. Вертикальную черту не обязательно ставить, но просто так удобнее решать систему.

Матрица системы – это матрица, которая составляется исключительно с коэффициентами при неизвестных. Что касается расширенной матрицы системы, так, это такая матрица, в которой кроме коэффициентов записаны ещё и свободные члены. Любую из этих матриц называют просто матрицей.

На матрице, которая написана выше рассмотрим, какие существуют элементарные преобразования:

1. В матрице строки можно переставлять местами. Например, в нашей матрице спокойно можно переставить первую и вторую строки:

.

2. Если в матрице имеются (или появились) пропорциональные строки (одинаковые), тогда необходимо оставить всего лишь одну строку, а остальные убрать (удалить).

3. Если в ходе преобразований в матрице появилась строка, где находятся одни нули, тогда такую строку тоже нужно удалять.

4. Строку матрицы можно умножать (делить) на любое число, которое отличное от нуля. Такое действие желательно проделывать, так как в будущем проще преобразовывать матрицу.

5. Сейчас рассмотрим преобразование, которое больше всего вызывает затруднение у студентов. Для этого возьмём изначальную нашу матрицу:

Для удобства умножаем первую строку на (-3):

Теперь ко второй строке прибавляем первую строку, которую умножали на -3. Вот что у нас получается:

В итоге получилось такое преобразование:

Теперь для проверки можно разделить все коэффициенты первой строки на те же и вот что получается:

В матрице верхняя строка преобразовалась:

Первую строку делим на и преобразовалась нижняя строка:

И верхнюю строку поделили на то же самое число :

Как вы можете убедиться, в итоге строка, которую мы прибавляли ни капельки не изменилась, а вот вторая строка поменялась. ВСЕГДА меняется только та строка, к которой прибавляются коэффициенты.

Мы расписали в таких подробностях, чтобы было вам понятно, откуда какая цифра взялась. На практике, например, на контрольной или экзамене матрица так подробно не расписывается. Как правило, в задании решение матрицы оформляется так:

.

Обратите внимание!

Если в примере приведены десятичные дроби, метод Гаусса в этом случае также поможет решить систему линейных алгебраических уравнений. Однако, не стоит забывать, что следует избегать приближённых вычислений, так как ответ будет неверным. Лучше всего использовать десятичные дроби, а от них переходить к обыкновенным дробям.

Алгоритм решения методом Гаусса пошагово

После того, как мы рассмотрели простейшие преобразования, в которых на помощь пришёл метод Гаусса, можем вернуться к нашей системе, которую уже разложили по полочкам и пошагово распишем:

Шаг 1. Переписываем систему в виде матрицы

Записываем матрицу:

Шаг 2. Преобразовываем матрицу: вторую строку в первом столбце приводим к нулю

Как мы привели вторую строку в первом столбце к нулю описано выше. Напомним, что первую строку умножали на и вторую строку прибавили к первой , умноженной на .

Шаг 3. Приводим матрицу к ступенчатому виду

Теперь вторую строку можно поделить на 2 и получается:

Верхнюю строку делим на и приводим матрицу к ступенчатому виду:

Когда оформляют задание, так и отчёркивают простым карандашом для упрощения работы, а также обводят те числа, которые стоят на “ступеньках”. Хотя в учебниках и другой литературе нет такого понятия, как ступенчатый вид. Как правило, математики такой вид называют трапециевидным или треугольным.

Шаг 4. Записываем эквивалентную систему

После наших элементарных преобразований получилась эквивалентная система:

Шаг 5. Производим проверку (решение системы обратным путём)

Теперь систему нужно решить в обратном направлении, то есть обратным ходом, начиная с последней строки.:

находим : ,

,

.

После находим :

,

.

Тогда:

.

Как видим, уравнение решено правильно, так как ответы в системе совпадают.

Решение систем линейных уравнений методом Гаусса, в которых основная матрица невырожденная, а количество в ней неизвестных равняется количеству уравнений

Как мы уже упоминали, невырожденная матрица бывает тогда, когда .

Разберём систему уравнений невырожденной матрицы, где уравнений по количеству столько же, сколько и неизвестных. Эту систему уравнений решим другим способом.

Дана система уравнений:

Для начала нужно решить первое уравнение системы относительно неизвестной переменной . Далее подставим полученное выражение сначала во второе уравнение, а затем в третье, чтобы исключить из них эту переменную.

Теперь переходим ко второму уравнению системы относительно и полученный результат подставим в третье уравнение.. Это нужно для того, чтобы исключить неизвестную переменную :

Из последнего, третьего уравнения мы видим, что . Из второго уравнения находим . И последнее, находим первое уравнение .

Итак, мы нашли все три неизвестных при помощи последовательного исключения. Такой процесс называют – прямой ход метода Гаусса. Когда последовательно находятся неизвестные переменные, начиная с последнего уравнения, называется обратным ходом метода Гаусса.

Когда выражается через и в первом уравнении, а затем подставляется полученное выражение во второе или третье уравнения, тогда, чтобы привести в к такому же результату, необходимо проделать такие действия:

• берём второе уравнение и к его левой и правой частям прибавляем определённые части из первого уравнения, которые умножаются на ,
• берём третье уравнение и к его левой и правой частям прибавляем определённые части из первого уравнения, которые умножаются на .

И действительно, благодаря такой процедуре у нас есть возможность исключать неизвестную переменную со второго и третьего уравнения системы:

Возникают нюансы с исключением неизвестных переменных тогда, когда в уравнении системы нет каких-либо неизвестных переменных. Рассмотрим такую систему:

В этой системе в первом уравнении нет переменной и поэтому у нас нет возможности решить первое уравнение системы относительно , чтобы исключить данную переменную из остальных уравнений. В таком случае выход есть. Нужно всего лишь уравнения переставить местами.

Так как мы описываем уравнения системы, в которых определитель основных матриц отличен от нуля, тогда всегда есть такое уравнение, в котором есть необходимая нам переменная и это уравнение мы можем поставить туда, куда нам нужно.

В примере, который мы рассматриваем, достаточно всего лишь поменять местами первое и второе уравнение.

Теперь мы можем спокойно разрешить первое уравнение относительно переменной и убрать (исключить) из остальных уравнений в системе. Вот и весь принцип работы с такими, на первый взгляд, сложными системами.

Решение систем линейных уравнений методом Гаусса, в которых основная матрица вырожденная, а количество в ней неизвестных не совпадает с количеством уравнений

Метод Гаусса помогает решать системы уравнений, у которых основная матрица прямоугольная или квадратная, но основная вырожденная матрица может совсем не иметь решений, иметь бесконечное множество решений или иметь всего лишь одно единственное решение.

Рассмотрим, как при помощи метода Гаусса устанавливается совместность или несовместность систем линейных уравнений. В случае, если есть совместность определим все решения или одно решение.

В принципе, исключать неизвестные переменные можно точно так, как описано выше. Однако, есть некоторые непонятные ситуации, которые могут возникнуть в ходе решения:

1. На некоторых этапах в момент исключения неизвестных переменных некоторые уравнения могут обратиться в тождества . В данном случае такие уравнения лишние в системе и их можно смело полностью убирать, а затем продолжать решать уравнение методом Гаусса.

Например, вам попалась подобная система:

У нас получается такая ситуация

Как видим, второе уравнение . Соответственно, данное уравнение мы можем из системы удалить, так как оно без надобности.

Дальше можно продолжать решение системы линейных алгебраических уравнений уравнений традиционным методом Гаусса.

2. При решении уравнений прямым ходом методом Гаусса могут принять не только одно, но и несколько уравнений такой вид: , где – число, которое отличное от нуля. Это говорит о том, что такое уравнение никогда не сможет превратиться в тождество даже при любых значениях неизвестных переменных. То есть, можно выразить по-другому. Если уравнение приняло  вид, значит система несовместна, то есть, не имеет решений. Рассмотрим на примере:

Для начала необходимо исключить неизвестную переменную из всех уравнений данной системы, начиная со второго уравнения. Для этого нужно прибавить к левой и правой частям второго, третьего, четвёртого уравнения части (левую и правую) первого уравнения, которые соответственно, умножаются на (-1), (-2), (-3). Получается:

В третьем уравнении получилось равенство . Оно не подходит ни для каких значений неизвестных переменных , и , и поэтому, у данной системы нет решений. То есть, говорится, что система не имеет решений.

3. Допустим, что при выполнении прямого хода методом Гаусса нам нужно исключить неизвестную переменную , и ранее, на каком-то этапе у нас уже исключалась вместе с переменной . Как вы поступите в таком случае? При таком положении нам нужно перейти к исключению переменной . Если же  уже исключались, тогда переходим к ,  и т. д.

Рассмотрим систему уравнений на таком этапе, когда уже исключилась переменная :

Такая система уравнений после преобразования выглядит так:

Вы наверное уже обратили внимание, что вместе с исключились и . Поэтому решение методом Гаусса продолжаем исключением переменной из всех уравнений системы, а начнём мы с третьего уравнения:

Чтобы завершить уравнение прямым ходом метода Гаусса, необходимо исключить последнюю неизвестную переменную из последнего уравнения:

Допусти, что система уравнений стала:

В этой системе нет ни одного уравнения, которое бы сводилось к . В данном случае можно было бы говорить о несовместности системы. Дальше непонятно, что же делать? Выход есть всегда. Для начала нужно выписать все неизвестные, которые стоят на первом месте в системе:

В нашем примере это , и . В левой части системы оставим только неизвестные, которые выделены зелёным квадратом а в правую перенесём известные числа, но с противоположным знаком. Посмотрите на примере, как это выглядит:

Можно придать неизвестным переменным с правой части уравнений свободные (произвольные) значения: , , , где , ,  – произвольные числа.

Теперь в правых частях уравнений нашей системы имеются числа и можно приступать к обратному ходу решения методом Гаусса.

В последнем уравнении системы получилось: , и теперь мы легко найдём решение в предпоследнем уравнении: , а из первого уравнения получаем:

= =

В итоге, получился результат, который можно и записать.

Ответ

,

,

,

,

,

.

Примеры решения методом Гаусса

Выше мы подробно расписали решение системы методом Гаусса. Чтобы закрепить материал, решим несколько примеров, в которых опять нам поможет метод Гаусса. Соответственно, начнём с самой простой системы.

Пример 1

Задача 

Решить систему линейных алгебраических уравнений методом Гаусса:

Решение

Выписываем матрицу, куда добавляем столбец свободных членов:

Прежде всего мы смотрим на элемент, который находится в матрице в левом верхнем углу (первая строка, первый столбец). Для наглядности выделим цифру зелёным квадратом. На этом месте практически всегда стоит единица:

Так как мы должны использовать подходящее элементарное преобразование строк и сделать так, чтобы элемент, который находится в матрице под выделенной цифрой превратился в . Для этого можно ко второй строке прибавить первую строку и умножить на .Однако, не сильно хочется работать с дробями, поэтому давайте постараемся этого избежать. Для этого нужно вторую строку умножить на (разрешающий элемент данного шага).

Соответственно, первая строка остаётся неизменной, а вторая поменяется:

Подбираем такое элементарное преобразование строк, чтобы во второй строке в первом столбце образовался . Для этого первую строку нужно умножить на и только после этого ко второй строке прибавить изменённую после умножения на вторую строку. Вот что получилось:

. Теперь прибавляем со второй строки первую строку . У нас получился , который записываем во вторую строку в первый столбец. Также решаем и остальные элементы матрицы. Вот что у нас получилось:

Как всегда у нас первая строка осталась без изменений, а вторая с новыми числами.

Итак, у нас получился ступенчатый вид матрицы:

Записываем новую систему уравнений:

Для проверки решаем систему обратным ходом. Для этого находим сначала :

Так как найден, находим :

.

Подставляем в изначальную нашу систему уравнений найденные и :

и .

Как видите из решения, система уравнений решена верно. Запишем ответ.

Ответ

Выше мы решали систему уравнений в двумя неизвестными, а теперь рассмотрим систему уравнений с тремя неизвестными.

Пример 2

Задача

Решить систему уравнений методом Гаусса:

Решение

Составляем матрицу, куда вписываем и свободные члены:

Что нам надо? Чтобы вместо цифры 2 появился 0. Для этого подбираем ближайшее число. Например, можно взять цифру -2 и на неё перемножить все элементы первой строки. Значит, умножаем , а потом прибавляем, при этом задействуем вторую строку: . В итоге у нас получился нуль, который записываем во вторую строку в первый столбец. Затем , и . Аналогично, и . И умножаем свободный член . Так и запишем следующую матрицу. Не забывайте, что первая строка остаётся без изменений:

Дальше необходимо проделать те же самые действия по отношению к третьей строке. То есть, первую строку нужно умножать не на (-2), а на цифру 3, так как и в третьей строке нужно коэффициенты привести у нулю. Также первую строку умножаем на 3 и прибавляем третью строку. Получается так:

Теперь нужно обнулить элемент 7, который стоит в третьей строке во втором столбце. Для этого выбираем цифру (-7) и проделываем те же действия. Однако, необходимо задействовать вторую строку. То есть, вторую строку умножаем на (-7) и прибавляем с третьей строкой. Итак, . Записываем результат в третью строку. Такие же действия проделываем и с остальными элементами. Получается новая матрица:

В результате получилась ступенчатая система уравнений:

Сначала находим : ,

.

Обратный ход:

Итак, уравнение системы решено верно.

Ответ

,

,

.

Пример 3

Система с четырьмя неизвестными более сложная, так как в ней легко запутаться. Попробуем решить такую систему уравнений.

Задача

Решите систему уравнений методом Гаусса:

Решение                                                                

В уравнении , то есть – ведущий член и пусть  ≠ 0

Из данного уравнения составим расширенную матрицу:

Теперь нужно умножить последние три строки (вторую, третью и четвёртую) на: , , . Затем прибавим полученный результат ко второй, третьей и четвёртой строкам исключаем переменную из каждой строки, начиная не с первой, а не со второй. Посмотрите, как изменилась наша новая матрица и в теперь стоит 0.

Поменяем вторую и третью строку местами и получим:

Получилось так, что = b и тогда, умножая вторую строку на (-7/4) и результат данной строки, прибавляя к четвёртой, можно исключить переменную из третьей и четвёртой строк:

Получилась такая матрица:

Также, учитывая, что  = , умножим третью строку на: 13,5/8 = 27/16, и, полученный результат прибавим к четвёртой, чтобы исключить переменную и получаем новую систему уравнений:

Теперь необходимо решить уравнение обратным ходом и найдём из последнего, четвёртого уравнения ,

из третьего: = = =

второе уравнение находим: = = = 2,

из первого уравнения: = .

Значит, решение системы такое: (1, 2, -1, -2).

Ответ

,

,

,

.

Добавим ещё несколько примеров для закрепления материла, но без такого подробного описания, как предыдущие системы уравнений.

Пример 4

Задача

Решить систему уравнений методом Гаусса:

Решение

Записываем расширенную матрицу системы:

Сначала смотрим на левое верхнее число:

Как выше уже было сказано, на этом месте должна стоять единица, но не обязательно. Производим такие действия: первую строку умножаем на -3, а потом ко второй строке прибавляем первую:

 

Производим следующие действия: первую строку умножаем на -1. Затем к третьей строки прибавляем вторую:

Теперь вторую строку умножаем на 1, а затем к третьей строке прибавляем вторую:

Получился ступенчатый вид уравнения:

Проверяем:

,

,

,

,

.

.

  Ответ

,

,

.

Заключение

Итак, вы видите, что метод Гаусса – интересный и простой способ решения систем линейных алгебраических уравнений. Путём элементарных преобразований нужно из системы исключать неизвестные переменные, чтобы систему превратить в ступенчатый вид. Данный метод удобен тем, что всегда можно проверить, правильно ли решено уравнение. Нужно просто подставить найденные неизвестные в изначальную систему уравнений.

Если элементы определителя не равняются нулю, тогда лучше обратиться к методу Крамера, а если же элементы нулевые, тогда такие системы очень удобно решать благодаря методу Гаусса.

Предлагаем ещё почитать учебники, в которых также описаны решения систем методом Гаусса.

Литература для общего развития:

Умнов А. Е. Аналитическая геометрия и линейная алгебра, изд. 3: учеб. пособие – М. МФТИ – 2011 – 259 с.

Карчевский Е. М. Лекции по линейной алгебре и аналитической геометрии, учеб. пособие – Казанский университет – 2012 – 302 с.

принцип, теорема и примеры решения задач

Содержание:

• Историческая справка
• Принцип метода Гаусса
• Примеры решения систем уравнений

Историческая справка

Метод Гаусса был предложен известнейшим немецким математиком Карлом Фридрихом Гауссом (1777 — 1855) и является одним из наиболее универсальных методов решения СЛАУ. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении задачи, расширенная матрица системы с помощью элементарных преобразований над ее строками приводится к ступенчатому виду. Далее последовательно находятся все неизвестные, начиная снизу вверх.

Принцип метода Гаусса

Метод Гаусса включает в себя прямой (приведение расширенной матрицы к ступенчатому виду, то есть получение нулей под главной диагональю) и обратный (получение нулей над главной диагональю расширенной матрицы) ходы. Прямой ход и называется методом Гаусса, обратный — методом Гаусса-Жордана, который отличается от первого только последовательностью исключения переменных.

Метод Гаусса идеально подходит для решения систем содержащих больше трех линейных уравнений, для решения систем уравнений, которые не являются квадратными (чего не скажешь про метод Крамера и матричный метод). То есть метод Гаусса — наиболее универсальный метод для нахождения решения любой системы линейных уравнений, он работает в случае, когда система имеет бесконечно много решений или несовместна.

Примеры решения систем уравнений

Пример

Задание. Решить СЛАУ $\left\{\begin{array}{l} 2 x_{1}+x_{2}+x_{3}=2 \\ x_{1}-x_{2}=-2 \\ 3 x_{1}-x_{2}+2 x_{3}=2 \end{array}\right.$ методом Гаусса.

Решение. Выпишем расширенную матрицу системы и при помощи элементарных преобразований над ее строками приведем эту матрицу к ступенчатому виду (прямой ход) и далее выполним обратный ход метода Гаусса (сделаем нули выше главной диагонали).

Вначале поменяем первую и вторую строку, чтобы элемент $a_{11}$ равнялся 1 (это мы делаем для упрощения вычислений):

$$\tilde{A}=A \mid B=\left(\begin{array}{rrr|r} 2 & 1 & 1 & 2 \\ 1 & -1 & 0 & -2 \\ 3 & -1 & 2 & 2 \end{array}\right) \sim\left(\begin{array}{rrr|r} 1 & -1 & 0 & -2 \\ 2 & 1 & 1 & 2 \\ 3 & -1 & 2 & 2 \end{array}\right)$$

Далее делаем нули под главной диагональю в первом столбце. Для этого от второй строки отнимаем две первых, от третьей — три первых:

$$\tilde{A} \sim\left(\begin{array}{rrr|r} 1 & -1 & 0 & -2 \\ 0 & 3 & 1 & 6 \\ 0 & 2 & 2 & 8 \end{array}\right)$$

Все элементы третьей строки делим на два (или, что тоже самое, умножаем на $\frac{1}{2}$ ):

$$\tilde{A} \sim\left(\begin{array}{rrr|r} 1 & -1 & 0 & -2 \\ 0 & 3 & 1 & 6 \\ 0 & 1 & 1 & 4 \end{array}\right)$$

Далее делаем нули во втором столбце под главной диагональю, для удобства вычислений поменяем местами вторую и третью строки, чтобы диагональный элемент равнялся 1:

$$\tilde{A} \sim\left(\begin{array}{ccc|c} 1 & -1 & 0 & -2 \\ 0 & 1 & 1 & 4 \\ 0 & 3 & 1 & 6 \end{array}\right)$$

От третьей строки отнимаем вторую, умноженную на 3:

$$\tilde{A} \sim\left(\begin{array}{rrr|r} 1 & -1 & 0 & -2 \\ 0 & 1 & 1 & 4 \\ 0 & 0 & -2 & -6 \end{array}\right)$$

Умножив третью строку на $\left(-\frac{1}{2}\right)$ , получаем:

$$\tilde{A} \sim\left(\begin{array}{rrr|r} 1 & -1 & 0 & -2 \\ 0 & 1 & 1 & 4 \\ 0 & 0 & 1 & 3 \end{array}\right)$$

Проведем теперь обратный ход метода Гаусса (метод Гассу-Жордана), то есть сделаем нули над главной диагональю. Начнем с элементов третьего столбца. Надо обнулить элемент $a_{23}$, для этого от второй строки отнимем третью:

$$\tilde{A} \sim\left(\begin{array}{rrr|r} 1 & -1 & 0 & -2 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 3 \end{array}\right)$$

Далее обнуляем недиагональные элементы второго столбца, к первой строке прибавляем вторую:

$$\tilde{A} \sim\left(\begin{array}{ccc|c} 1 & 0 & 0 & -1 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 3 \end{array}\right)$$

Полученной матрице соответствует система

$\left\{\begin{array}{l}x_{1}+0 \cdot x_{2}+0 \cdot x_{3}=-1 \\ 0 \cdot x_{1}+x_{2}+0 \cdot x_{3}=1 \\ 0 \cdot x_{1}+0 \cdot x_{2}+x_{3}=3\end{array}\right.$    или   $\left\{\begin{array}{l} x_{1}=-1 \\ x_{2}=1 \\ x_{3}=3 \end{array}\right.$

Ответ. $\left\{\begin{array}{l} x_{1}=-1 \\ x_{2}=1 \\ x_{3}=3 \end{array}\right. $

Читать дальше: однородные СЛАУ. Фундаментальная система решений.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Метод Гаусса

Определение и описание метода Гаусса

Метод преобразований Гаусса (также известный как преобразование методом последовательного исключения неизвестных переменных из уравнения или матрицы) для решения систем линейных уравнений представляет собой классический методом решения системы алгебраических уравнений (СЛАУ). Также этот классический метод используют для решения таких задач как получение обратных матриц и определения ранговости матрицы.

Преобразование с помощью метода Гаусса заключается в совершении небольших (элементарных) последовательных изменениях системы линейных алгебраических уравнений, приводящих к исключению переменных из неё сверху вниз с образованием новой треугольной системы уравнений, являющейся равносильной исходной.

Определение 1

Эта часть решения носит название прямого хода решения Гаусса, так как весь процесс осуществляется сверху вниз.

После приведения исходной системы уравнений к треугольной осуществляется нахождение всех переменных системы снизу вверх (то есть первые найденные переменные занимают находятся именно на последних строчках системы или матрицы). Эта часть решения известна также как обратный ход решения методом Гаусса. Заключается его алгоритм в следующем: сначала вычисляется переменные, находящиеся ближе всего к низу системы уравнений или матрицы, затем полученные значения подставляются выше и таким образом находится ещё одна переменная и так далее.

Описание алгоритма метода Гаусса

Последовательность действий для общего решения системы уравнения методом Гаусса заключается в поочередном применении прямого и обратного хода к матрице на основе СЛАУ. Пусть исходная система уравнений имеет следующий вид:

$\begin{cases} a_{11} \cdot x_1 +…+ a_{1n} \cdot x_n = b_1 \\ . .. \\ a_{m1} \cdot x_1 + a_{mn} \cdot x_n = b_m \end{cases}$

Чтобы решить СЛАУ методом Гаусса, необходимо записать исходную систему уравнений в виде матрицы:

$A = \begin{pmatrix} a_{11} & … & a_{1n} \\ \vdots & … & \vdots \\ a_{m1} & … & a_{mn} \end{pmatrix}$, $b=\begin{pmatrix} b_1 \\ \vdots \\ b_m \end{pmatrix}$

Матрица $A$ называется основной матрицей и представляет собой записанные по порядку коэффициенты при переменных, а $b$ называется столбцом её свободных членов. Матрица $A$, записанная через черту со столбцом свободных членов называется расширенной матрицей:

$A = \begin{array}{ccc|c} a_{11} & … & a_{1n} & b_1 \\ \vdots & … & \vdots & …\\ a_{m1} & … & a_{mn} & b_m \end{array}$

Теперь необходимо с помощью элементарных преобразований над системой уравнений (или над матрицей, так как это удобнее) привести её к следующему виду:

$\begin{cases} α_{1j_{1}} \cdot x_{j_{1}} + α_{1j_{2}} \cdot x_{j_{2}}. ..+ α_{1j_{r}} \cdot x_{j_{r}} +… α_{1j_{n}} \cdot x_{j_{n}} = β_1 \\ α_{2j_{2}} \cdot x_{j_{2}}…+ α_{2j_{r}} \cdot x_{j_{r}} +… α_{2j_{n}} \cdot x_{j_{n}} = β_2 \\ …\\ α_{rj_{r}} \cdot x_{j_{r}} +… α_{rj_{n}} \cdot x_{j_{n}} = β_r \\ 0 = β_(r+1) \\ … \\ 0 = β_m \end{cases}$ (1)

Матрица, полученная из коэффициентов преобразованной системы уравнения (1) называется ступенчатой, вот так обычно выглядят ступенчатые матрицы:

$A = \begin{array}{ccc|c} a_{11} & a_{12} & a_{13} & b_1 \\ 0 & a_{22} & a_{23} & b_2\\ 0 & 0 & a_{33} & b_3 \end{array}$

Для этих матриц характерен следующий набор свойств:

1. Все её нулевые строки стоят после ненулевых
2. Если некоторая строка матрицы с номером $k$ ненулевая, то в предыдущей строчке этой же матрицы нулей меньше, чем в этой, обладающей номером $k$.

После получения ступенчатой матрицы необходимо подставить полученные переменные в оставшиеся уравнения (начиная с конца) и получить оставшиеся значения переменных.

Основные правила и разрешаемые преобразования при использовании метода Гаусса

При упрощении матрицы или системы уравнений этим методом нужно использовать только элементарные преобразования.

Таким преобразованиями считаются операции, которые возможно применять к матрице или системе уравнений без изменения её смысла:

• перестановка нескольких строк местами,
• прибавление или вычитание из одной строчки матрицы другой строчки из неё же,
• умножение или деление строчки на константу, не равную нулю,
• строчку, состоящую из одних нулей, полученную в процессе вычисления и упрощения системы, нужно удалить,
• Также нужно удалить лишние пропорциональные строчки, выбрав для системы единственную из них с более подходящими и удобными для дальнейших вычислений коэффициентами.

Все элементарные преобразования являются обратимыми.

Разбор трёх основных случаев, возникающих при решении линейных уравнений используя метод простых преобразований Гаусса

Различают три возникающих случая при использовании метода Гаусса для решения систем:

1. Когда система несовместная, то есть у неё нет каких-либо решений
2. У системы уравнений есть решение, причём единственное, а количество ненулевых строк и столбцов в матрице равно между собой.
3. Система имеет некое количество или множество возможных решений, а количество строк в ней меньше чем количество столбцов.

Исход решения с несовместной системой

Для этого варианта при решении матричного уравнения методом Гаусса характерно получение какой-то строчки с невозможностью выполнения равенства. Поэтому при возникновении хотя бы одного неправильного равенства полученная и исходная системы не имеют решений вне зависимости от остальных уравнений, которые они содержат. Пример несовместной матрицы:

$\begin{array}{ccc|c} 2 & -1 & 3 & 0 \\ 1 & 0 & 2 & 0\\ 0 & 0 & 0 & 1 \end{array}$

В последней строчке возникло невыполняемое равенство: $0 \cdot x_{31} + 0 \cdot x_{32} + 0 \cdot x_{33} = 1$.

Система уравнений, у которой есть только одно решение

Данные системы после приведения к ступенчатой матрице и удаления строчек с нулями имеют одинаковое количество строк и столбцов в основной матрице. Вот простейший пример такой системы:

$\begin{cases} x_1 — x_2 = -5 \\ 2 \cdot x_1 + x_2 = -7 \end{cases}$

Запишем её в виде матрицы:

$\begin{array}{cc|c} 1 & -1 & -5 \\ 2 & 1 & -7 \end{array}$

Чтобы привести первую ячейку второй строчки к нулю, домножим верхнюю строку на $-2$ и вычтем её из нижней строчки матрицы, а верхнюю строчку оставим в исходном виде, в итоге имеем следующее:

$\begin{array}{cc|c} 1 & -1 & -5 \\ 0 & 3 & 10 \end{array}$

Этот пример можно записать в виде системы:

$\begin{cases} x_1 — x_2 = -5 \\ 3 \cdot x_2 = 10 \end{cases}$

Из нижнего уравнения выходит следующее значение $x$: $x_2 = 3 \frac{1}{3}$. Подставим это значение в верхнее уравнение: $x_1 – 3 \frac{1}{3}$, получаем $x_1 = 1 \frac{2}{3}$.

Система, обладающая множеством возможных вариантов решений

Для этой системы характерно меньшее количество значащих строк, чем количество столбцов в ней (учитываются строки основной матрицы).

Переменные в такой системе делятся на два вида: базисные и свободные. При преобразовании такой системы содержащиеся в ней основные переменные необходимо оставить в левой области до знака “=”, а остальные переменные перенести в правую часть равенства.

У такой системы есть только некое общее решение.

Разберём следующую систему уравнений:

$\begin{cases} 2y_1 + 3y_2 + x_4 = 1 \\ 5y_3 — 4y_4 = 1 \end{cases}$

Запишем её в виде матрицы:

$\begin{array}{cccc|c} 2 & 3 & 0 & 1 & 1 \\ 0 & 0 & 5 & 4 & 1 \\ \end{array}$

Наша задача найти общее решение системы. Для этой матрицы базисными переменными будут $y_1$ и $y_3$ (для $y_1$ — так как он стоит на первом месте, а в случае $y_3$ — располагается после нулей).

В качестве базисных переменных выбираем именно те, которые первые в строке не равны нулю.

Оставшиеся переменные называются свободными, через них нам необходимо выразить базисные.

Используя так называемый обратный ход, разбираем систему снизу вверх, для этого сначала выражаем $y_3$ из нижней строчки системы:

$5y_3 – 4y_4 = 1$

$5y_3 = 4y_4 + 1$

$y_3 = \frac{4/5}y_4 + \frac{1}{5}$. 3 = 2\\ 3x_1 + 2x_2 – 3x_3 = 0 \end{cases}$

Запишем нашу систему в виде расширенной матрицы:

$\begin{array}{ccc|c} 4 & 2 & -1 & 1 \\ 5 & 3 & -2 & 2 \\ 3 & 2 & -3 & 0\\ \end{array}$

Теперь для удобства и практичности нужно преобразовать матрицу так, чтобы в верхнем углу крайнего столбца была $1$.

Для этого к 1-ой строчке нужно прибавляем строчку из середины, умноженную на $-1$, а саму среднюю строчку записываем как есть, выходит:

$\begin{array}{ccc|c} -1 & -1 & 1 & -1 \\ 5 & 3 & -2 & 2 \\ 3 & 2 & -3 & 0\\ \end{array}$

Далее к средней строчке прибавим верхнюю, умноженную на $5$, а последнюю строчку преобразуем, умножив первую строчку на 3 и сложив с последней, получаем:

$\begin{array}{ccc|c} -1 & -1 & 1 & -1 \\ 0 & -2 & 3 & -3 \\ 0 & -1 & 0 & -3\\ \end{array}$

Домножим верхнюю и последнюю строчки на $-1$, а также поменяем местами последнюю и среднюю строки:

$\begin{array}{ccc|c} 1 & 1 & -1 & 1 \\ 0 & 1 & 0 & 3 \\ 0 & -2 & 3 & -3\\ \end{array}$

Далее сложим последнюю строчку с удвоенной средней:

$\begin{array}{ccc|c} 1 & 1 & -1 & 1 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 3 & 3\\ \end{array}$

И разделим последнюю строчку на $3$:

$\begin{array}{ccc|c} 1 & 1 & -1 & 1 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 1 & 1\\ \end{array}$

Получаем следующую систему уравнений, равносильную исходной:

$\begin{cases} x_1 + x_2 – x_3 = 1\\ x_2 = 3 \\ x_3 = 1 \end{cases}$

Из верхнего уравнения выражаем $x_1$:

$x1 = 1 + x_3 – x_2 = 1 + 1 – 3 = -1$.

Пример 2

Пример решения системы, заданной с помощью матрицы 4 на 4 методом Гаусса

$\begin{array}{cccc|c} 2 & 5 & 4 & 1 & 20 \\ 1 & 3 & 2 & 1 & 11 \\ 2 & 10 & 9 & 7 & 40\\ 3 & 8 & 9 & 2 & 37 \\ \end{array}$.

В начале меняем местами верхнюю исследующую за ней строчки, чтобы получить в левом верхнем углу $1$:

$\begin{array}{cccc|c} 1 & 3 & 2 & 1 & 11 \\ 2 & 5 & 4 & 1 & 20 \\ 2 & 10 & 9 & 7 & 40\\ 3 & 8 & 9 & 2 & 37 \\ \end{array}$.

Теперь умножим верхнюю строчку на $-2$ и прибавим ко 2-ой и к 3-ьей. К 4-ой прибавляем 1-ую строку, домноженную на $-3$:

$\begin{array}{cccc|c} 1 & 3 & 2 & 1 & 11 \\ 0 & -1 & 0 & -1 & -2 \\ 0 & 4 & 5 & 5 & 18\\ 0 & -1 & 3 & -1 & 4 \\ \end{array}$

Теперь к строке с номером 3 прибавляем строку 2, умноженную на $4$, а к строке 4 прибавляем строку 2, умноженную на $-1$.

$\begin{array}{cccc|c} 1 & 3 & 2 & 1 & 11 \\ 0 & -1 & 0 & -1 & -2 \\ 0 & 0 & 5 & 1 & 10\\ 0 & 0 & 3 & 0 & 6 \\ \end{array}$

Домножаем строку 2 на $-1$, а строку 4 делим на $3$ и ставим на место строки 3.

$\begin{array}{cccc|c} 1 & 3 & 2 & 1 & 11 \\ 0 & 1 & 0 & 1 & 2 \\ 0 & 0 & 1 & 0 & 2\\ 0 & 0 & 5 & 1 & 10 \\ \end{array}$

Теперь прибавляем к последней строке предпоследнюю, домноженную на $-5$.

$\begin{array}{cccc|c} 1 & 3 & 2 & 1 & 11 \\ 0 & 1 & 0 & 1 & 2 \\ 0 & 0 & 1 & 0 & 2\\ 0 & 0 & 0 & 1 & 0 \\ \end{array}$

Решаем полученную систему уравнений:

$\begin{cases} m = 0 \\ g = 2\\ y + m = 2\ \ x + 3y + 2g + m = 11\end{cases}$

$y=2$, $x = 0$.

Занимательная математика: правило Гаусса

Цикл «Занимательная математика» посвящен деткам увлекающимся математикой и родителям, которые уделяют время развитию своих детей, «подкидывая» им интересные и занимательные задачки, головоломки.

Первая статья из этого цикла посвящена правилу Гаусса.

Немного истории

Известный немецкий математик Карл Фридрих Гаусс (1777-1855) с раннего детства отличался от своих сверстников. Несмотря на то, что он был из небогатой семьи, он достаточно рано научился читать, писать, считать. В его биографии есть даже упоминание того, что в возрасте 4-5 лет он смог скорректировать ошибку в неверных подсчетах отца, просто наблюдая за ним.

Одно из первых его открытий было сделано в возрасте 6 лет на уроке математики. Учителю было необходимо увлечь детей на продолжительное время и он предложил следующую задачку:

Найти сумму всех натуральных чисел от 1 до 100.

Юный Гаусс справился с этим заданием достаточно быстро, найдя интересную закономерность, которая получила большое распространение и применяется по сей день при устном счете.

Давайте попробуем решить эту задачку устно. Но для начала возьмем числа от 1 до 10:

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10

Посмотрите внимательно на эту сумму и попробуйте догадаться, что же необычного смог разглядеть Гаусс? Для ответа необходимо хорошо представлять себе состав чисел.

Гаусс сгруппировал числа следующим образом:

(1+10) + (2+9) + (3+8) + (4+7) + (5+6)

Таким образом маленький Карл получил 5 пар чисел, каждая из которых в отдельности в сумме дает 11. Тогда, чтобы вычислить сумму натуральных чисел от 1 до 10 необходимо

5 * 11 = 55

Вернемся к первоначальной задаче. Гаусс заметил, что перед суммированием необходимо группировать числа в пары и тем самым изобрел алгоритм, благодаря которому можно быстро сложить числа от 1 до100:

1 + 2 + 3 + 4 + 5 + … + 48 + 49 + 50 + 51 + 52 + 53 + … + 96 + 97 + 98 + 99 + 100

1. Находим количество пар в ряде натуральных чисел. В данном случае их 50.

2. Суммируем первое и последнее числа данного ряда. В нашем примере — это 1 и 100. Получаем 101.

3. Умножаем полученную сумму первого и последнего члена ряда на количество пар этого ряда. Получаем 101 * 50 = 5050

Следовательно, сумма натуральных чисел от 1 до 100 равна 5050.

Задачи на использование правила Гаусса

А сейчас вашему вниманию предлагаются задачи, в которых в той или иной степени используется правило Гаусса. Эти задачки вполне способен понять и решить четвероклассник.

Можно дать возможность ребенку порассуждать самому, чтобы он сам «изобрел» это правило. А можно разобрать вместе и посмотреть как он сможет его применить. Среди ниже приведенных задач есть примеры, в которых нужно понять как модифицировать правило Гаусса, чтобы его применить к данной последовательности.

В любом случае, чтобы ребенок мог оперировать этим в своих вычислениях необходимо понимание алгоритма Гаусса, то есть умение разбить правильно по парам и посчитать.

Важно! Если будет заучена формула без понимания, то это очень быстро будет забыто.

Задача 1

Найти сумму чисел:

• 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10;
• 1 + 2 + 3 + … + 14 + 15 + 16;
• 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9;
• 1 + 2 + 3 + 4 + 5 + … + 48 + 49 + 50 + 51 + 52 + 53 + … + 96 + 97 + 98 + 99 + 100.

Решение.

Вначале можно дать возможность ребенку самому решить первый пример и предложить найти способ, при котором это сделать легко в уме. Далее разобрать этот пример вместе с ребенком и показать как это сделал Гаусс. Лучше всего для наглядности записать ряд и соединить линиями пары чисел, дающие в сумме одинаковое число. Важно, чтобы ребенок понял как образуются пары — берем самое маленькое и самое большое из оставшихся чисел при условии, что количество чисел в ряду четно.

• 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = (1 + 10) + (2 + 9) + (3 + 8) + (4 + 7) + (5 + 6) = (1 + 10) * 5;
• 1 + 2 + 3 + … + 14 + 15 + 16 = (1 + 16) + (2 + 15) + (3 + 14) + (4 + 13) + (5 + 12) + (6 + 11) + (7 + 10) + (8 + 9) = (1 + 16) * 8 = 136;
• 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = (1 + 8) + (2 + 7) + (3 + 6) + (4 + 5) + 9 = (1+ 8) * 4 + 9 = 45;
• 1 + 2 + 3 + 4 + 5 + … + 48 + 49 + 50 + 51 + 52 + 53 + … + 96 + 97 + 98 + 99 + 100 = (1 + 100) * 50 = 5050

Задача 2

Имеется 9 гирь весом 1г, 2г, 3г, 4г, 5г, 6г, 7г, 8г, 9г. Можно ли разложить эти гири на три кучки с равным весом?

Решение.

С помощью правила Гаусса находим сумму всех весов:

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = (1 + 8) * 4 + 9 = 45 (г)

Далее смотрим, можно ли этот вес разбить на три равных веса:

45 : 3 = 15 (г)

Значит, если мы сможем сгруппировать гири так, чтобы в каждой кучке были гири суммарным весом 15г, то задача решена.

Один из вариантов:

• 9г, 6г
• 8г, 7г
• 5г, 4г, 3г, 2г, 1г

Другие возможные варианты найдите сами с ребенком.

Обратите внимание ребенка на то, что когда решаются подобные задачи лучше всегда начинать группировать с большего веса (числа).

Задача 3

Можно ли разделить циферблат часов прямой линией на две части так, чтобы суммы чисел в каждой части были равны?

Решение.

Для начала к ряду чисел 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 применим правило Гаусса: найдем сумму и посмотрим, делится ли она на 2:

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 = (1 + 12) * 6 = 78

Значит разделить можно. Теперь посмотрим как.

По правилу Гаусса у нас получается 6 пар чисел, каждая из которых в сумме дает 13:

1 и 12, 2 и 11, 3 и 10, 4 и 9, 5 и 8, 6 и 7.

Следовательно, надо провести линию на циферблате так, чтобы 3 пары попали в одну половину, а три в другую.

Ответ: линия пройдет между числами 3 и 4, а затем между числами 9 и 10.

Задача 4

Можно ли провести на циферблате часов две прямые линией так, чтобы в каждой части сумма чисел была одинаковой?

Решение.

Для начала к ряду чисел 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 применим правило Гаусса: найдем сумму и посмотрим делиться ли она на 3:

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 = (1 + 12) * 6 = 78

78 делиться на 3 без остатка, значит разделить можно. Теперь посмотрим как.

По правилу Гаусса у нас получается 6 пар чисел, каждая из которых в сумме дает 13:

1 и 12, 2 и 11, 3 и 10, 4 и 9, 5 и 8, 6 и 7.

Следовательно, надо провести линии на циферблате так, чтобы в каждую часть попали по 2 пары.

Ответ: первая линия пройдет между числами 2 и 3, а затем между числами 10 и 11; вторая линия — между числами 4 и 5, а затем между 8 и 9.

Задача 5

Летит стая птиц. Впереди одна птица (вожак), за ней две, потом три, четыре и т. д. Сколько птиц в стае, если в последнем ряду их 20?

Решение.

Получаем, что нам необходимо сложить числа от 1 до 20. А к вычислению такой суммы можно применить правило Гаусса:

1 + 2 + 3 + 4 + 5 + … + 15 + 16 + 17 + 18 + 19 + 20 = (20 + 1) * 10 = 210.

Задача 6

Как рассадить 45 кроликов в 9 клеток так, чтобы во всех клетках было разное количество кроликов?

Решение.

Если ребенок решил и с пониманием разобрал примеры из задания 1, то тут же вспоминается, что 45 это сумма чисел от 1 до 9. Следовательно, сажаем кроликов так:

• первая клетка — 1,
• вторая — 2,
• третья — 3,
• …
• восьмая — 8,
• девятая — 9.

Но если ребенок сразу не может сообразить, то попробуйте натолкнуть его на мысль о том, что подобные задачи можно решить перебором и надо начинать с минимального числа.

Задача 7

Вычислить сумму, используя прием Гаусса:

• 31 + 32 + 33 + … + 40;
• 5 + 10 + 15 + 20 + … + 100;
• 91 + 81 + … + 21 + 11 + 1;
• 1 + 2 + 3 + 4 + … + 18 + 19 + 20;
• 1 + 2 + 3 + 4 + 5 + 6;
• 4 + 6 + 8 + 10 + 12 + 14;
• 4 + 6 + 8 + 10 + 12;
• 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11.

Решение.

• 31 + 32 + 33 + … + 40 = (31 + 40) * 5 = 355;
• 5 + 10 + 15 + 20 + … + 100 = (5 + 100) * 10 = 1050;
• 91 + 81 + … + 21 + 11 + 1 = (91 + 1) * 5 = 460;
• 1 + 2 + 3 + 4 + … + 18 + 19 + 20 = (1 + 20) * 10 =210;
• 1 + 2 + 3 + 4 + 5 + 6 = (1 + 6) * 3 = 21;
• 4 + 6 + 8 + 10 + 12 + 14 = (4 + 14) * 3 = 54;
• 4 + 6 + 8 + 10 + 12 = (4 + 10) * 2 + 12 = 40;
• 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 = (1 + 10) * 5 + 11 = 66.

Задача 8

Имеется набор из 12 гирек массой 1г, 2г, 3г, 4г, 5г, 6г, 7г, 8г, 9г, 10г, 11г, 12г. Из набора убрали 4 гирьки, общая масса которых равна трети общей массы всего набора гирек. Можно ли оставшиеся гирьки расположить на двух чашках весов по 4 штуки на каждой чашке так, чтобы они оказались в равновесии?

Решение.

Применяем правило Гаусса, чтобы найти общую массу гирек:

1 + 2 + 3 + … + 10 + 11 + 12 = (1 + 12) * 6 = 78 (г)

Вычисляем массу гирек, которые убрали:

78 : 3 = 26 (г)

Следовательно, оставшиеся гирьки (общей массой 78-26 = 52г) надо расположить по 26 г на каждую чашу весов, чтобы они оказались в равновесии.

Нам не известно какие гирьки были убраны, значит мы должны рассмотреть все возможные варианты.

Применяя правило Гаусса можно разбить гирьки на 6 пар с равным весом (по 13г):

1г и 12г, 2г и 11г, 3г и 10, 4г и 9г, 5г и 8г, 6г и 7г.

Тогда лучший вариант, когда при убирании 4 гирек уберутся две пары из приведенных выше. В этом случае у нас останутся 4 пары: 2 пары на одну чашу весов и 2 пары на другую.

Худший вариант — это когда 4 убранные гирьки разобьют 4 пары. У нас останутся 2 неразбитые пары общим весом 26г, значит их помещаем на одну чашу весов, а оставшиеся гирьки можно поместить на другую чашу весов и они тоже будут 26г.

Удачи в развитии Ваших детей.

Решение систем линейных уравнений методом гаусса

Содержание

1. Введение                                                                                                     2        
2. Понятие матрицы                                                                                       5
3. Немного из биографии Гаусса                                                                  6
4. Решение систем линейных уравнений методом Гаусса                         7
5. Проведение обучающего  эксперимента                                                  12                                            
6. Заключение                                                                                                  14                                                                                                  
7. Список используемой литературы                                                            15                                                              

ВВЕДЕНИЕ

Увлечение математикой начинается с размышления над какой-то интересной задачей или проблемой.

Часто на уроках математики мы решаем различные уравнения. Многие теоретические и практические вопросы приводят не к одному уравнению, а к целой системе уравнений с несколькими неизвестными. Особенно важен случай системы линейных алгебраических уравнений. Способы  решения систем линейных уравнений – очень интересная и важная тема. В седьмом  классе на уроках алгебры мы использовали такие способы, как сложение, подстановка и графический.

Нужно  заметить,  что  не  всегда  системы  линейных  уравнений  удобно решать  данными  способами. Мы решили выяснить существуют  ли  другие  методы решения систем линейных уравнений. Изучив данную тему, мы выяснили, что существуют такие методы,  как:  метод  Крамара,  метод Гаусса, метод обратной матрицы.

Одним из самых распространенных методов решения систем линейных уравнений является метод Гаусса. Выдающегося немецкого математика Карла Фридриха Гаусса (1777–1855) современники называли «королём математики». Ещё в раннем детстве он проявлял незаурядные математические способности.

На примерах был изучен и исследован алгоритм решения систем линейных уравнений методом Гаусса. Этот метод (который также называют методом последовательного исключения неизвестных) известен в различных вариантах уже более 2000 лет.

Процесс решения по методу Гаусса состоит из двух этапов, называемых прямым и обратным ходом. На первом этапе система приводится к треугольному виду, а на втором (обратный ход) идет последовательное определение неизвестных из указанной треугольной системы.

Метод Гаусса — один из основных результатов линейной алгебры и аналитической геометрии, к нему сводятся множество других теорем и методов линейной алгебры. Поэтому поиск решения системы линейных уравнений методом Гаусса имеет не только важное значение, но и является частью алгоритма решения многих задач, что позволяет говорить об актуальности изучения метода Гаусса. В отличие от матричного метода и метода Крамера, метод Гаусса может быть применен к системам линейных уравнений с произвольным числом уравнений и неизвестных.  

Актуальность:

Системы линейных алгебраических уравнений имеют широкое применение в решении многих задач практического приложения математики. Данная тема в школьном курсе алгебры не изучается, чтобы изучить  данную тему, необходимо познакомиться с понятиями матрицы, матрица системы и расширенная матрица системы. Получение новых знаний и нового опыта способствует развитию личности, формирует некоторые особенности мышления и оказывает влияние на отношение к миру.

Цель работы:

Научиться решать системы уравнений с помощью метода Гаусса

и применять этот метод на практике,  ознакомить и научить одноклассников решать системы уравнений методом Гаусса.

Задачи исследования

1. Познакомиться с понятием «матрица» и «матрица системы».

2. Изучить метод Гаусса.

3. Научиться применять метод Гаусса на практике.

Объект(изучения):     Метод Гаусса

Предмет:  Системы линейных уравнений с двумя и более переменными. 

Методы исследования: анализ, обобщение, эксперимент, опрос.

Гипотезы:  С помощью данного метода увеличивается скорость решения систем линейных уравнений. Метод Гаусса можно изучать на уроках       алгебры в 7 — 8 классах как дополнительный метод решения систем уравнений с двумя и более переменными.

 

Глава I

ПОНЯТИЕ МАТРИЦЫ

Матрицей  размера mn, где m — число строк, n — число столбцов, называется таблица чисел, расположенных в определенном порядке. Эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы матрицы обозначаются aij, где i — номер строки, а j — номер столбца

 Матрица может состоять как из одной строки, так и из одного столбца. Вообще говоря, матрица может состоять даже из одного элемента.

Если число столбцов матрицы равно числу строк (m=n), то матрица называется квадратной.

Матрица системы – это матрица, составленная только из коэффициентов при неизвестных.

                

Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов, в данном случае.  

        

НЕМНОГО ИЗ БИОГРАФИИ ГАУССА

Иога́нн Карл Фри́дрих Га́усс (1777 — 1855) — немецкий математик, механик, физик, астроном и геодезист. Считается одним из величайших математиков всех времён, «королём математиков».

С именем Гаусса связаны фундаментальные исследования почти во всех основных областях математики: в алгебре, теории чисел, дифференциальной и неевклидовой геометрии, теории вероятностей, а также в механике, астрономии, физике и геодезии.

Гаусс чрезвычайно строго относился к своим печатным трудам и никогда не публиковал даже выдающиеся результаты, если считал свою работу над этой темой незавершённой.  Изучение архива Гаусса показало, что он медлил с публикацией ряда своих открытий, и в результате его опередили другие математики. Вот неполный перечень упущенных им трудов.

• Неевклидова геометрия
• Эллиптические функции
• Метод наименьших квадратов
• Закон распределения простых чисел

РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ МЕТОДОМ ГАУССА

Метод Гаусса представляет собой специальный алгоритм последовательного исключения неизвестных из уравнений системы. В этом алгоритме обычно различают два этапа:

Первый этап называется прямой ход,

Второй этап – обратный ход.

Цель прямого хода метода Гаусса заключается в приведение матрицы системы к треугольному виду, когда в результате некоторых элементарных преобразований уравнений системы на главной диагонали матрицы системы будут располагаться ненулевые элементы, а все элементы ниже главной диагонали будут равны нулю. В результате наших преобразований должна получаться система, равносильная исходной системе линейных уравнений. Преобразования, которые позволяют свести исходную систему к треугольной, сохраняя равносильность, называются элементарными. Что будем понимать под элементарными преобразованиями?

Определение. Элементарными преобразованиями уравнений системы называют следующие преобразования:

1) перестановка местами двух любых уравнений;

2) умножение обеих частей какого-либо уравнения на любое число, не равное нулю;

3) прибавление к обеим частям одного из уравнений соответствующих частей любого другого уравнения;

4) перестановка (перенумерация) неизвестных системы.

Примем без доказательства, что все перечисленные преобразования приводят к системам, которые равносильны (эквивалентны) исходной системе линейных уравнений.

Удобно в методе Гаусса работать не с самой системой линейных уравнений, а с основой системы – расширенной матрицей.

Элементарным преобразованиям системы соответствуют следующие элементарные преобразования расширенной матрицы:
1. умножение произвольной строки на любое число, отличное от нуля;
2.  прибавление к произвольной строке матрицы любой другой строки матрицы;

3. перестановка местами любых двух строк;

4. перестановка местами любых двух столбцов матрицы системы;

5. транспонирование.

Решение системы уравнений с двумя переменными

Пример 1. Решим систему:

Решение:

 

                         Ответ: (-4; 1)

Решение системы уравнений с тремя переменными

Пример 2. Решим систему:  

Решение:

                

        

                                             

                                                                                                       Ответ: (-3; 8; 0)                         

Пример 3. Решим систему:

Решение:

     

 

                                                                                                                   

        Ответ: (1; 2; 3).

Пробуем применять изученное к решению задач:

Кондитерская фабрика производит продукцию трех видов: торты, пирожные и рулеты. Для их производства используется сырье трех типов: мука 1 кг, сахар 1 кг, молоко 1 л. Нормы расхода каждого из них на одну продукцию и объем расхода сырья на один день заданы таблицей:

Найти ежедневный объем выпуска каждого вида продукции.

Решение. Пусть ежедневно фабрика выпускает х1 тортов, х2 пирожных и х3 рулетов. Составим систему уравнений.

Составим расширенную матрицу системы :

        

Ответ: фабрика выпускает ежедневно 50 тортов, 200 пирожных и 95 рулетов.

Глава II

Проведение обучающего  эксперимента

Одной из целей моего проекта является научить одноклассников решать системы уравнений методом Гаусса, для чего на спецкурсе по математике я показала и рассказала им о своей работе и предложила  совместно решить несколько систем, состоящих из двух строк, методом Гаусса. Ребят заинтересовал данный метод, они с интересом слушали меня, а потом совместно решали системы уравнений данным методом.  Далее ребятам были предложены системы уравнений и заданы следующие вопросы: 

   Ответ:     Ответ:  

    Ответ:          Ответ:  

 Ответ:             Ответ:

   Ответ:

1. Знакомы ли вы с методом Гаусса?

2. Применяете и вы этот метод?

3. Хотите ли вы что б этот метод был в школьной программе ?

4. Будете ли вы решать системы этим методом?

5. Считаете ли вы этот метод простым ?

Ответы на которые вы можете видеть на диаграмме.

        

Заключение.

Метод Гаусса позволяет решать любые системы линейных уравнений и существенно сократить время нахождения решений систем линейных уравнений. Метод Гаусса доступен для его изучения учащимся 7 — 8 классов при решении систем линейных уравнений  

У меня получилось самой освоить данный метод и передать свои знания одноклассникам. Таким образом,  поставленные мною цели и задачи выполнены. И ещё метод Гаусса прост тем, как мне кажется, что для его освоения не требуется много знаний. А также для матриц ограниченного размера метод Гаусса менее трудоёмкий по сравнению с другими методами, поэтому в будущем я планирую его активно применять при решении систем уравнений.

ЛИТЕРАТУРА

1. Основы высшей математики: Учеб. пособие для вузов/В.С. Шипачев; под ред.акад. А.Н. Тихонова. —5-е изд.,стер. — М. Высш. Шк., 2003. — 279с.
2. Высшая математика для экономистов: учебное пособие для студентов экономических специальностей высших учебных заведений /Н.Ш Кремер, Б.А. Путко. — М.: Банки и биржи ЮНИТИ, 1997. – 239с.
3. Математика. Задачник : учеб. Пособие для образоват. Учреждений нач. и сред. Проф. образования / М. И. Башмаков. — 3-е изд., стер. — М.: Издательский центр «Акадения», 2013. —416с.
4. http://mathprofi.ru/metod_gaussa_dlya_chainikov.html 
5. https://ru.wikipedia.org/wiki/%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_%D0%93%D0%B0%D1%83%D1%81%D1%81%D0%B0 
6. https://ru.wikipedia.org/wiki/%D0%93%D0%B0%D1%83%D1%81%D1%81,_%D0%9A%D0%B0%D1%80%D0%BB_%D0%A4%D1%80%D0%B8%D0%B4%D1%80%D0%B8%D1%85 
7. https://ru.wikipedia.org/wiki/%D0%9C%D0%B0%D1%82%D1%80%D0%B8%D1%86%D0%B0 

Метод Гаусса

Пусть задана система линейных алгебраических уравнений, которую необходимо решить (найти такие значения неизвестных хi, что обращают каждое уравнение системы в равенство).

Мы знаем, что система линейных алгебраических уравнений может:

1) Не иметь решений (быть несовместной).
2) Иметь бесконечно много решений.
3) Иметь единственное решение.

Как мы помним, правило Крамера и матричный метод непригодны в тех случаях, когда система имеет бесконечно много решений или несовместна.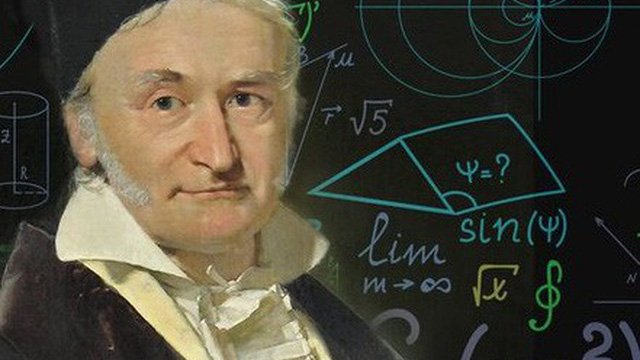 Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решения любой системы линейных уравнений, который в каждом случае приведет нас к ответу! Сам алгоритм метода во всех трёх случаях работает одинаково. Если в методах Крамера и матричном необходимы знания определителей, то для применения метода Гаусса необходимо знание только арифметических действий, что делает его доступным даже для школьников начальных классов.

Преобразования расширенной матрицы (это матрица системы —  матрица, составленная только из коэффициентов при неизвестных, плюс столбец свободных членов) системы линейных алгебраических  уравнений в методе Гаусса:

1) строки матрицы можно переставлять местами.

2) если в матрице появились (или есть) пропорциональные (как частный случай – одинаковые) строки, то следует удалить из матрицы все эти строки кроме одной.

3) если в матрице в ходе преобразований появилась нулевая строка, то ее также следует удалить.

4) строку матрицы можно умножить (разделить) на любое число, отличное от нуля.

5) к строке матрицы можно прибавить другую строку, умноженную на число, отличное от нуля.

В методе Гаусса элементарные преобразования не меняют решение системы уравнений.

Метод Гаусса состоит из двух этапов:

1. «Прямой ход» — с помощью элементарных преобразований привести расширенную матрицу системы линейных алгебраических уравнений к «треугольному» ступенчатому виду: элементы расширенной матрицы, расположенные ниже главной диагонали, равны нулю (ход «сверху-вниз»). Например, к такому виду:

Для этого выполним следующие действия:

1)   Пусть мы рассматриваем первое уравнение системы линейных алгебраических уравнений и коэффициент при х₁ равен К. Второе, третье и т.д. уравнения преобразуем следующим образом: каждое уравнение (коэффициенты при неизвестных, включая свободные члены) делим на коэффициент при неизвестном х₁, стоящий в каждом уравнении, и умножаем на К. После этого из второго уравнения (коэффициенты при неизвестных и свободные члены) вычитаем первое. Получаем при х₁ во втором уравнении коэффициент 0. Из третьего преобразованного уравнения вычитаем первое уравнение, так до тех пор, пока все уравнения, кроме первого, при неизвестном х₁ не будут иметь коэффициент 0.

2)   Переходим к следующему уравнению. Пусть это будет второе уравнение и коэффициент при х₂ равен М. Со всеми «нижестоящими» уравнениями поступаем так, как описано выше. Таким образом, «под» неизвестной х₂ во всех уравнениях будут нули.

3)   Переходим к следующему уравнению и так до тех пора, пока не останется одна последняя неизвестная и преобразованный свободный член.       

2. «Обратный ход» метода Гаусса – получение решения системы линейных алгебраических уравнений (ход «снизу-вверх»). Из последнего «нижнего» уравнения получаем одно первое решение – неизвестную х_n. Для этого решаем элементарное уравнение А*х_n = В. В примере, приведенном выше, х₃ = 4. Подставляем найденное значение в «верхнее» следующее уравнение и решаем его относительно следующей неизвестной. Например, х₂ – 4 = 1, т.е. х₂ = 5. И так до тех пор, пока не найдем все неизвестные.

Пример.

Решим систему линейных уравнений методом Гаусса, как советуют некоторые авторы:

Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

Смотрим на левую верхнюю «ступеньку». Там у нас должна быть единица. Проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Поступим так: 
1 шаг. К первой строке прибавляем вторую строку, умноженную на –1. То есть, мысленно умножили вторую строку на –1 и выполнили сложение первой и второй строки, при этом вторая строка у нас не изменилась.

Теперь слева вверху «минус один», что нас вполне устроит. Кто хочет получить +1, может выполнить дополнительное действие: умножить первую строку на –1 (сменить у неё знак).

Дальше алгоритм работает уже по апробированной методике:

2 шаг. Ко второй строке прибавили первую строку, умноженную на 5. К третьей строке прибавили первую строку, умноженную на 3.

3 шаг. Первую строку умножили на –1, в принципе, это для красоты. У третьей строки также сменили знак и переставили её на второе место, таким образом, на второй «ступеньке у нас появилась нужная единица.

4 шаг. К третьей строке прибавили вторую строку, умноженную на 2.

5 шаг. Третью строку разделили на 3.

Признаком, который свидетельствует об ошибке в вычислениях (реже – об опечатке), является «плохая» нижняя строка. То есть, если бы у нас внизу получилось что-нибудь вроде (0 0 11 |23), и, соответственно, 11x₃ = 23, x₃ = 23/11, то с большой долей вероятности можно утверждать, что допущена ошибка в ходе элементарных преобразований.

Выполняем обратный ход, в оформлении примеров часто не переписывают саму систему, а уравнения «берут прямо из приведенной матрицы». Обратный ход, напоминаю, работает «снизу вверх». В данном примере получился подарок:

x₃ = 1
x₂ = 3
x₁ + x₂ – x₃ = 1, следовательно x₁ + 3 – 1 = 1, x₁ = –1

Ответ: x₁ = –1, x₂ = 3, x₃ = 1.

Решим эту же систему по предложенному алгоритму. Получаем

4   2   –1   1
5   3   –2   2
3   2   –3   0

Разделим второе уравнение на 5, а третье – на 3. Получим:

4   2       –1    1
1   0.6    –0.4  0.4
1   0.66  –1    0

Умножим второе и третье уравнения на 4, получим:

4    2       –1    1
4    2,4    –1.6  1.6
4    2.64  –4    0

Вычтем из второго и третьего уравнений первое уравнение, имеем:

4    2       –1      1
0    0.4    –0.6   0.6
0    0.64  –3    –1

Разделим третье уравнение на 0,64:

4    2      –1              1
0    0.4   –0.6           0.6
0    1      –4.6875    –1.5625

 Умножим третье уравнение на 0,4

4    2       –1              1
0    0.4    –0.6           0.6
0    0.4    –1.875     –0.625

Вычтем из третьего уравнения второе, получим «ступенчатую» расширенную матрицу: 

4    2      –1              1
0    0.4   –0.6           0.6
0    0      –1.275      –1.225

Таким образом, так как в процессе вычислений накапливалась погрешность, получаем х₃ = 0,96 или приблизительно 1.

х_{2 = 3 и х1 = –1.}

Решая таким образом, Вы никогда не запутаетесь в вычислениях и не смотря на погрешности вычислений, получите результат.

Такой способ решения системы линейных алгебраических уравнений легко программируем и не учитывает специфические особенности коэффициентов при неизвестных, ведь на практике (в экономических и технических расчетах) приходиться иметь дело именно с нецелыми коэффициентами.

Желаю успехов! До встречи на занятиях! Репетитор Дмитрий Айстраханов.

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Карл Фридрих Гаусс | Биография, открытия и факты

Карл Фридрих Гаусс

Смотреть все СМИ

Дата рождения:

30 апреля 1777 г. Брауншвейг

Умер:

23 февраля 1855 г. (77 лет) Геттинген Ганновер

Награды и награды:

Медаль Копли (1838 г. )

Изобретения:

гелиотроп магнитометр

Известные работы:

«Арифметические исследования»

Просмотреть весь связанный контент →

Популярные вопросы

Чем знаменит Карл Фридрих Гаусс?

Гаусс считается одним из величайших математиков всех времен за его вклад в теорию чисел, геометрию, теорию вероятностей, геодезию, планетарную астрономию, теорию функций и теорию потенциала (включая электромагнетизм).

Каким было детство Карла Фридриха Гаусса?

Гаусс был единственным ребенком бедных родителей. Он был расчетливым вундеркиндом с даром к языкам. Его учителя и его преданная мать порекомендовали его герцогу Брауншвейгскому в 1791 году, который предоставил ему финансовую помощь для продолжения образования на месте, а затем для изучения математики в Геттингенском университете.

Какие награды получил Карл Фридрих Гаусс?

Гаусс получил медаль Копли, самую престижную научную награду в Соединенном Королевстве, ежегодно присуждаемую Лондонским королевским обществом в 1838 году «за свои изобретения и математические исследования в области магнетизма». За изучение карт, сохраняющих угол, он был удостоен премии Датской академии наук в 1823 г.

Какое влияние оказал Карл Фридрих Гаусс?

Гаусс написал первый систематический учебник по алгебраической теории чисел и заново открыл астероид Церера. Он опубликовал работы по теории чисел, математической теории построения карт и многим другим предметам. После смерти Гаусса в 1855 году обнаружение многих новых идей среди его неопубликованных статей распространило его влияние на оставшуюся часть века.

Сводка

Прочтите краткий обзор этой темы

Карл Фридрих Гаусс , настоящее имя Иоганн Фридрих Карл Гаусс , (родился 30 апреля 1777, Брауншвейг [Германия] — умер 23 февраля 1855, Геттинген, Ганновер), немецкий математик, обычно считается одним из величайших математиков всех времен за его вклад в теорию чисел, геометрию, теорию вероятностей, геодезию, планетарную астрономию, теорию функций и теорию потенциала (включая электромагнетизм).

Гаусс был единственным ребенком бедных родителей. Он был редкостью среди математиков тем, что был вундеркиндом и сохранял способность производить сложные вычисления в уме большую часть своей жизни. Впечатленные этой способностью и его даром к языкам, учителя и преданная мать рекомендовали его герцогу Брауншвейгскому в 179 г.1, который предоставил ему финансовую помощь для продолжения образования на месте, а затем для изучения математики в Геттингенском университете с 1795 по 1798 год. Новаторская работа Гаусса постепенно сделала его выдающимся математиком той эпохи сначала в немецкоязычном мире, а затем и за его пределами. , хотя он оставался далекой и отчужденной фигурой.

Тест «Британника»

Все об астрономии

Какой астроном предположил, что Солнце находится в центре Солнечной системы? Вокруг чего вращается большинство астероидов? От комет и планет до звезд и лун — проверьте свои знания в области астрономии в этой викторине.

Первым значительным открытием Гаусса, сделанным в 1792 году, было то, что правильный многоугольник с 17 сторонами может быть построен только с помощью линейки и циркуля. Его значение заключается не в результате, а в доказательстве, которое основывалось на глубоком анализе факторизации полиномиальных уравнений и открыло дверь более поздним идеям теории Галуа. Его докторская диссертация 1797 г. дала доказательство основной теоремы алгебры: всякое полиномиальное уравнение с действительными или комплексными коэффициентами имеет столько корней (решений), сколько его степени (наибольшей степени переменной). Доказательство Гаусса, хотя и не вполне убедительное, отличалось критикой более ранних попыток. Позже Гаусс дал еще три доказательства этого важного результата, последнее к 50-летию первого, что показывает важность, которую он придавал этой теме.

Узнайте о жизни и карьере математического гения Карла Фридриха Гаусса.

Просмотреть все видео к этой статье. по алгебраической теории чисел, Disquisitiones Arithmeticae . Эта книга начинается с первого описания модульной арифметики, дает подробное описание решений квадратных многочленов от двух переменных в целых числах и заканчивается упомянутой выше теорией факторизации. Этот выбор тем и их естественные обобщения определили повестку дня в теории чисел на протяжении большей части XIX века.веке, и постоянный интерес Гаусса к этому предмету стимулировал множество исследований, особенно в немецких университетах.

Второй публикацией было его повторное открытие астероида Церера. Его первоначальное открытие, сделанное итальянским астрономом Джузеппе Пиацци в 1800 году, вызвало сенсацию, но он исчез за Солнцем до того, как удалось провести достаточно наблюдений, чтобы рассчитать его орбиту с достаточной точностью, чтобы узнать, где он снова появится. Многие астрономы соревновались за честь найти его снова, но Гаусс победил. Его успех основывался на новом методе обработки ошибок в наблюдениях, который сегодня называется методом наименьших квадратов. После этого Гаусс много лет работал астрономом и опубликовал крупную работу по вычислению орбит — числовая сторона такой работы была для него гораздо менее обременительна, чем для большинства людей. Будучи чрезвычайно преданным подданным герцога Брауншвейгского, а после 1807 года, когда он вернулся в Геттинген в качестве астронома, герцога Ганноверского, Гаусс чувствовал, что его работа имеет общественную ценность.

Подобные мотивы побудили Гаусса принять вызов по обследованию территории Ганновера, и он часто отсутствовал в полевых условиях, отвечая за наблюдения. Проект, который длился с 1818 по 1832 год, столкнулся с многочисленными трудностями, но привел к ряду достижений. Одним из них было изобретение Гауссом гелиотропа (прибора, отражающего солнечные лучи в виде сфокусированного луча, который можно наблюдать на расстоянии нескольких миль), что повысило точность наблюдений. Другим было его открытие способа сформулировать понятие кривизны поверхности. Гаусс показал, что существует внутренняя мера кривизны, которая не меняется, если поверхность изгибается, но не растягивается. Например, круглый цилиндр и плоский лист бумаги имеют одинаковую внутреннюю кривизну, поэтому на бумаге можно делать точные копии фигур на цилиндре (как, например, в полиграфии). Но сфера и плоскость имеют разную кривизну, из-за чего невозможно составить абсолютно точную плоскую карту Земли.

Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подписаться сейчас

Гаусс опубликовал работы по теории чисел, математической теории построения карт и многим другим предметам. В 1830-х годах он заинтересовался земным магнетизмом и участвовал в первом в мире исследовании магнитного поля Земли (для его измерения он изобрел магнитометр). Вместе со своим геттингенским коллегой, физиком Вильгельмом Вебером, он сделал первый электрический телеграф, но некоторая ограниченность помешала ему энергично заняться изобретением. Вместо этого он извлек важные математические следствия из этой работы для того, что сегодня называется теорией потенциала, важной ветви математической физики, возникающей при изучении электромагнетизма и гравитации.

Гаусс также писал о картографии, теории картографических проекций. За свое исследование карт, сохраняющих угол, он был удостоен премии Датской академии наук в 1823 году. Эта работа была близка к предположению, что комплексные функции комплексной переменной обычно сохраняют угол, но Гаусс не сделал этого фундаментального утверждения. ясное понимание, оставив его Бернхарду Риману, который глубоко ценил работу Гаусса. У Гаусса были и другие неопубликованные идеи о природе сложных функций и их интегралов, некоторые из которых он поделился с друзьями.

На самом деле Гаусс часто отказывался публиковать свои открытия. Будучи студентом в Геттингене, он начал сомневаться в априорной истинности евклидовой геометрии и подозревал, что ее истинность может быть эмпирической. Для этого должно существовать альтернативное геометрическое описание пространства. Вместо того чтобы опубликовать такое описание, Гаусс ограничился критикой различных априорных защит евклидовой геометрии. Казалось, он постепенно убедился, что существует логическая альтернатива евклидовой геометрии. Однако, когда венгр Янош Бойяи и русский Николай Лобачевский опубликовали свои отчеты о новой неевклидовой геометрии около 1830 года, Гаусс не смог последовательно изложить свои собственные идеи. Можно объединить эти идеи в впечатляющее целое, в котором его концепция внутренней кривизны играет центральную роль, но Гаусс так и не сделал этого. Одни приписывали эту неудачу его врожденному консерватизму, другие — его непрекращающейся изобретательности, которая всегда влекла его к следующей новой идее, третьи — его неспособности найти центральную идею, которая управляла бы геометрией после того, как евклидова геометрия перестала быть уникальной. Все эти объяснения имеют некоторые достоинства, хотя ни одно из них не может быть исчерпывающим объяснением.

Другой темой, по которой Гаусс в значительной степени скрывал свои идеи от современников, были эллиптические функции. В 1812 году он опубликовал отчет об интересном бесконечном ряду и написал, но не опубликовал отчет о дифференциальном уравнении, которому удовлетворяет бесконечный ряд. Он показал, что ряды, называемые гипергеометрическими рядами, могут использоваться для определения многих знакомых и многих новых функций. Но к тому времени он знал, как использовать дифференциальное уравнение для создания очень общей теории эллиптических функций и полностью освободить теорию от ее истоков в теории эллиптических интегралов. Это был крупный прорыв, потому что, как обнаружил Гаусс в 179 г.0s теория эллиптических функций, естественно, трактует их как комплекснозначные функции комплексного переменного, но современная теория комплексных интегралов была совершенно неадекватна для этой задачи. Когда часть этой теории была опубликована норвежцем Нильсом Абелем и немцем Карлом Якоби примерно в 1830 году, Гаусс заметил своему другу, что Абель прошел одну треть пути. Это было точно, но это печальная мера личности Гаусса, поскольку он все еще воздерживался от публикации.

Гаусс сделал меньше, чем мог бы, и в других отношениях. Геттингенский университет был небольшим, и он не стремился расширить его или набрать дополнительных студентов. К концу его жизни через Геттинген прошли математики калибра Рихарда Дедекинда и Римана, и он был полезен, но современники сравнивали его стиль письма с жидкой кашицей: он ясен и устанавливает высокие стандарты строгости, но ему недостает мотивации и может быть медленным и утомительным, чтобы следовать. Он переписывался со многими, но не со всеми, людьми, достаточно опрометчивыми, чтобы написать ему, но мало что делал, чтобы поддерживать их публично. Редким исключением были случаи, когда Лобачевский подвергался нападкам со стороны других русских за его идеи о неевклидовой геометрии. Гаусс достаточно выучил русский язык, чтобы следить за полемикой, и предложил Лобачевского в Геттингенскую академию наук. Напротив, Гаусс написал Бойяи письмо, в котором сообщил ему, что он уже обнаружил все, что Бойяи только что опубликовал.

После смерти Гаусса в 1855 году обнаружение стольких новых идей в его неопубликованных работах распространило его влияние на оставшуюся часть века. Принятие неевклидовой геометрии произошло не с оригинальными работами Бойяи и Лобачевского, а с почти одновременной публикацией общих идей Римана о геометрии, подробного и строгого изложения ее итальянцем Эудженио Бельтрами, а также частных заметок Гаусса и переписка.

Джереми Джон Грей

Вклад Карла Фридриха Гаусса в математику — StudiousGuy

Иоганн Фридрих Карл Гаусс, также известный как Карл Фридрих Гаусс, был греческим математиком и физиком. Его иногда называли «Princeps mathematicorum », «Выдающийся математик» или «Князь математики». Он родился 30 апреля 1777 года в Брауншвейге, герцогство Брауншвейг (ныне часть Германии). Немецкий геолог Вольфганг Сарториус писал:

 Когда Гауссу едва исполнилось три года, он исправил математическую ошибку, допущенную его отцом; и что, когда ему было семь лет, он решил арифметическую задачу быстрее, чем кто-либо другой в его классе из 100 учеников».

Эта арифметическая задача заключалась в том, чтобы сложить целые числа от 1 до 100. В 1788 году Гуасс посещал гимназию (старшую среднюю школу в Германии), а затем в 1792 году поступил в Брауншвейгский коллегиум Каролинум. В 1798 г., в возрасте 21 года, он завершил свой самый известный труд «Disquisitiones Arithmeticae», который был опубликован в 1801 г. Раздел VII этого труда был в основном посвящен теории чисел. Гаусс также предсказал положение тогда еще новой малой планеты Цереры, используя метод наименьших квадратов. В 1802 году Гаусс посетил Ольберса, который открыл Палладу, а затем Гаусс открыл ее орбиту. После смерти герцога Брауншвейгского в 1807 году Гаусс покинул Брауншвейг, чтобы занять должность директора Геттингенской обсерватории. После того, как он прибыл в Геттинген, в течение двух лет умерли его отец и жена, и он был совершенно разбит. Но его проблемы никогда не сказывались на его работе. В 1809 г., он опубликовал свою вторую книгу «Theoria Motus corporum coelestium in sectionibus conicis Solem ambientium», двухтомную серию о движении небесных тел. Первый том охватывал темы, дифференциальные уравнения, конические сечения и эллиптические орбиты. Во втором томе он показал, как рассчитать и уточнить оценку орбиты планеты. Его публикации включают «Disquisitiones generales circa seriem infinitam», строгую трактовку рядов и введение в гипергеометрическую функцию, «Methodus nova Integration valores per приблизительное inveniendi», практическое эссе о приближенной интеграции, «Bestimmung der Genauigkeit der Beobachtungen», обсуждение статистических оценок и «Теория аттракции тела sphaeroidicorum ellipticorum homogeneorum methodus nova tractate». мельчайшие части. Статья «Theoria CombinedisObservationum erroribus minimis obnoxiae» (1823 г.) с приложением к ней (1828 г.) была посвящена математической статистике, в частности методу наименьших квадратов. Гаусс также доказал некоторые аксиомы, которые предполагали, что он верил в существование неевклидовой геометрии. Он никогда не публиковал статьи по неевклидовой геометрии, опасаясь, что это повлияет на его репутацию. Спустя десятилетие, когда Гаусс узнал, что Лобачевский опубликовал статью о неевклидовой геометрии, он написал письмо Шумахеру в 1846 году, в котором говорилось:

имел те же судимости в течение 54 лет».

, что показывает, что он знал о существовании неевклидовой геометрии, когда ему было всего 15 лет. Гаусс также опубликовал несколько статей по дифференциальной геометрии. Одна из статей также включала самую известную теорему Гаусса. Он в равной степени интересовался изучением физики, а также опубликовал несколько статей. 23 февраля 1855 года Гаусс умер от сердечного приступа. Рудольф Вагнер сохранил мозг Гаусса и исследовал его. Он обнаружил, что масса его мозга была немного выше средней, что объясняло его гениальность. 9{n}}[/katex] для некоторого неотрицательного целого числа n. Гаусс открыл общую формулу построения многоугольника за пределами семиугольника. Далее он заложил, 51, 85, 255, 257,….., и 4, 294, 967, 295 – гранные фигуры. Гаусс был так доволен своим результатом, что попросил каменщика нарисовать семиугольник над его могилой. Однако Стоунмен отказался, заявив, что сложная конструкция семиугольника будет выглядеть только как круг.

2. Целые числа как треугольные числа

В 1796 году Гаусс обнаружил, что любое натуральное число можно представить в виде суммы не более чем трех треугольных чисел. Он записал этот результат в свой дневник как «ΕΥΡΗΚΑ num = Δ + Δ + Δ». Этот дневник был утерян через 40 лет после его смерти. Предполагалось, что Гаусс станет последним человеком, овладевшим всеми аспектами математики.

3.

Комплексные числа

Однако комплексные числа известны с 16-го века, но Гаусс был первым математиком, который дал четкое представление о комплексных числах и функциях комплексных переменных. Хотя Эйлер работал с мнимыми и комплексными числами, до сих пор не было правильного объяснения того, как связаны между собой действительные и мнимые числа. Гаусс применил на практике комплексные числа и дал стандартное обозначение a+ib для комплексных чисел. Затем появилось больше концепций комплексных чисел.

4. Основная теорема алгебры

Гаусс дал доказательство основной теоремы алгебры, когда ему было всего 22 года. Он заявил, что

 Каждый непостоянный многочлен от одной переменной над комплексными числами один корень».

Он также доказал, что поле комплексных чисел алгебраически замкнуто (многочлен с комплексными коэффициентами даст только комплексное решение), в отличие от поля действительных чисел, где многочлен с действительными коэффициентами может дать комплексное решение.

5. Теория чисел

Гаусс внес значительный вклад в теорию чисел. Он говорил, что «Математика — королева наук, а теория чисел — королева математики». В 1801 году, в возрасте 24 лет, Гаусс опубликовал свою самую известную книгу «Disquisitiones Arithmeticae», которая считается самой влиятельной книгой в области теории чисел. В эту книгу входят:

• Символ тройной черты (≡) для соответствия
• Презентация метода модульной арифметики Гаусса
• Первые два доказательства квадратичного закона взаимности
• Теории бинарных и тернарных квадратичных форм
• Задача числа класса Гаусса
• Доказала теорему Ферма о многоугольных числах для n=5
• Правило знаков Декарта
• Гипотеза Кеплера о регулярных расположениях
• Расчет даты Пасхи
• Обнаружен алгоритм БПФ Кули-Тьюки для вычисления дискретных преобразований Фурье

6. Свойства Pentagramma Mirificum

Некоторые свойства Pentagramma mirificum обсуждались Гауссом. Pentragramma mirificum представляет собой многоугольник в форме звезды на сфере, стороны которого представляют собой дуги большого круга, а все внутренние углы прямые.

Гаусс ввел следующее выражение

(α, β, γ, δ, ε) = (tan² TP+ tan²PQ+ tan²QR+ tan²RS+ tan²ST), где выполняются следующие тождества и три величины могут быть определены оставшимися двумя.

1 + α = γδ, 1+ β = δε, 1 + γ = αε, 1 + δ = αβ, 1 + ε = βγ

Гаусс доказал следующее тождество и также дал решение в виде (α, β, γ, δ, ε) = (9, 2/3, 2, 5, 1/3)

αβγδε = 3 + α + β + γ + δ +ε = √(1+α)(1+β)(1+γ)(1+δ)(1+ε), а площадь многоугольника PQRST определяется как

{A}_{PQRST } = 2π – (|PQ| + |QR| + |RS| + |ST| + |TP|)

7. Функция Гаусса и кривая ошибки Гаусса

Гаусс ввел распределение Гаусса и продемонстрировал, как вероятность может быть представлена ​​графически по колоколообразной или нормальной кривой. Эта кривая имеет самый высокий пик около среднего и ожидаемого значения и постепенно спадает вблизи плюс и минус бесконечности. График нормальной кривой приведен ниже.

Кроме того, распределение Гаусса является типом непрерывного распределения вероятностей для случайной величины с действительным знаком, а общая форма функции плотности задается следующим образом:

Теорема Гаусса Egregium является результатом дифференциальной геометрии, которая говорит о кривизне поверхностей. Теорема утверждает, что

 Гауссова кривизна поверхности не изменится, если поверхность согнуть, не растягивая ее».

Таким образом, теорема означает, что гауссова кривизна может быть полностью определена путем измерения углов, расстояний и их скоростей на поверхности, независимо от конкретного способа размещения поверхности в окружающем трехмерном евклидовом пространстве. Теорему называют замечательной, поскольку результат не зависит от ее вложения даже после всех деформаций изгиба и кручения.

9. Теорема Гаусса

Теорема Гаусса также известна как теорема о дивергенции или теорема Остроградского. В векторном исчислении эта теорема утверждает, что

Поверхностный интеграл векторного поля по замкнутой поверхности, называемый потоком через поверхность, равен объемному интегралу дивергенции по области внутри поверхности».

Эта теорема устанавливает связь между потоком векторного поля по замкнутой поверхности и объемным интегралом дивергенции поля. Графическое представление теоремы Гаусса дается выражением

10. Лемма Гаусса

Лемма Гаусса утверждает, что произведение двух примитивных многочленов является примитивным (многочлен с целыми коэффициентами является примитивным, если он имеет 1 в качестве наибольшего общего делителя его коэффициентов). Эта лемма о целых числах формулируется как 9{n} — многочлен с целыми коэффициентами, то F называется примитивным, если наибольший общий делитель всех коэффициентов {a}_{0}, {a}_{1},…., {a}_{n} 1; другими словами, никакое простое число не делит все коэффициенты.

Далее он дал лемму Гаусса о примитивах и лемму о неприводимости. Лемма Гаусса о примитивах утверждает, что

Если P(X) и Q(X) являются примитивными полиномами над целыми числами, то произведение P(X)Q(X) также является примитивным».

Лемма о неприводимости Гаусса утверждает, что

Непостоянный полином из Z[ X ] неприводим в Z[X] тогда и только тогда, когда он одновременно неприводим в Q[X] и примитивен в Z[X]».

11. Метод приближения Гаусса

Гаусс предложил итерационный метод Гаусса-Зиделя в числовой алгебре, используемый для решения системы линейных уравнений. Этот метод назван в честь немецких математиков Гаусса и Филиппа Людвига фон Зиделя. Этот метод используется для решения системы n линейных уравнений с неизвестным x. 9{k+1} — следующая итерация x. A разлагается на нижнюю треугольную матрицу L и строго верхнюю треугольную матрицу U, т. е. A = L + U.

Суммирование Гаусса | Поговорим о науке

Суммарность Гаусса названа в честь Иоганна Карла Фридриха Гаусса. Он был немецким математиком. Гаусс — один из самых влиятельных математических мыслителей в истории. Легенда гласит, что Гаусс придумал новый метод суммирования последовательностей в очень молодом возрасте. Легенда гласит, что его учитель математики попросил класс сложить числа от 1 до 100. Другими словами, учитель хотел, чтобы они сложили 1 + 2 + 3 + 4 + 5… вплоть до 100!

Учитель предполагал, что это займет у учеников очень много времени. Подумайте, сколько времени вам понадобится, чтобы сложить все числа от 1 до 100 одно за другим. Однако Гаусс ответил 5050 почти сразу.

Эта история может быть не совсем правдой. Но это напоминает нам, что самые младшие ученики иногда открывают новые математические закономерности. Теперь давайте подумаем о шаблоне, который Гаусс использовал для быстрого решения этой проблемы.

Уловка, которую использовал Гаусс для решения этой задачи, заключается в том, что не имеет значения, в каком порядке мы складываем числа. В каком бы порядке мы ни следовали, мы получим один и тот же результат.

Например:

2 + 3 имеет тот же ответ, что и 3 + 2.

Мы можем хитрым образом изменить порядок чисел от 1 до 100. Это может помочь нам добавить их быстрее. Вот простой пример, который покажет вам, как работает эта стратегия группировки.

Допустим, вы хотите сложить числа от 1 до 10.

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = ?

 

Шаблон, показывающий сложение пар от одного до десяти (© Let’s Talk Science, 2021).

Возможно, вы заметили кое-что странное. Каждая из этих пар в сумме дает 11. Итак, мы можем думать о нашей задаче так:

(1 + 10) + (2 + 9) + (3 + 8) + (4 + 7) + (5 + 6) знак равно

(11) + (11) + (11) + (11) + (11) = ?

Поскольку у нас 5 пар, наш ответ:

11 + 11 + 11 + 11 + 11 = 11 x 5 = 55

Что ж, это куда-то идет!

Давайте посмотрим на это по-другому. Вместо того, чтобы выстраивать числа в один ряд. Расставь цифры в два ряда. В первом ряду числа увеличиваются. Во втором ряду числа уменьшаются. От 1 до 10 это будет выглядеть так.

Image — Text Version

Числа от 1 до 10 выстроены в порядке возрастания в верхнем ряду. Числа от 10 до 1 выстраиваются в порядке убывания в нижнем ряду.

 

Теперь просуммируйте каждый столбец.

Изображение — Версия текста

Сумма каждого столбца равна 11.

 

Сумма всех приведенных выше чисел равна числу пар , умноженному на сумму каждой пары . Но нам нужна сумма только одной строки, а не обеих строк. Итак, нам нужно разделить наш ответ на 2.

Мы можем записать это как: 

Изображение – Текстовая версия

Сумма – это количество пар, умноженное на сумму каждой пары, и эта сумма делится на 2. В нашем случае десять умножается на одиннадцать, а затем делится на два. . Это дает окончательную сумму 55.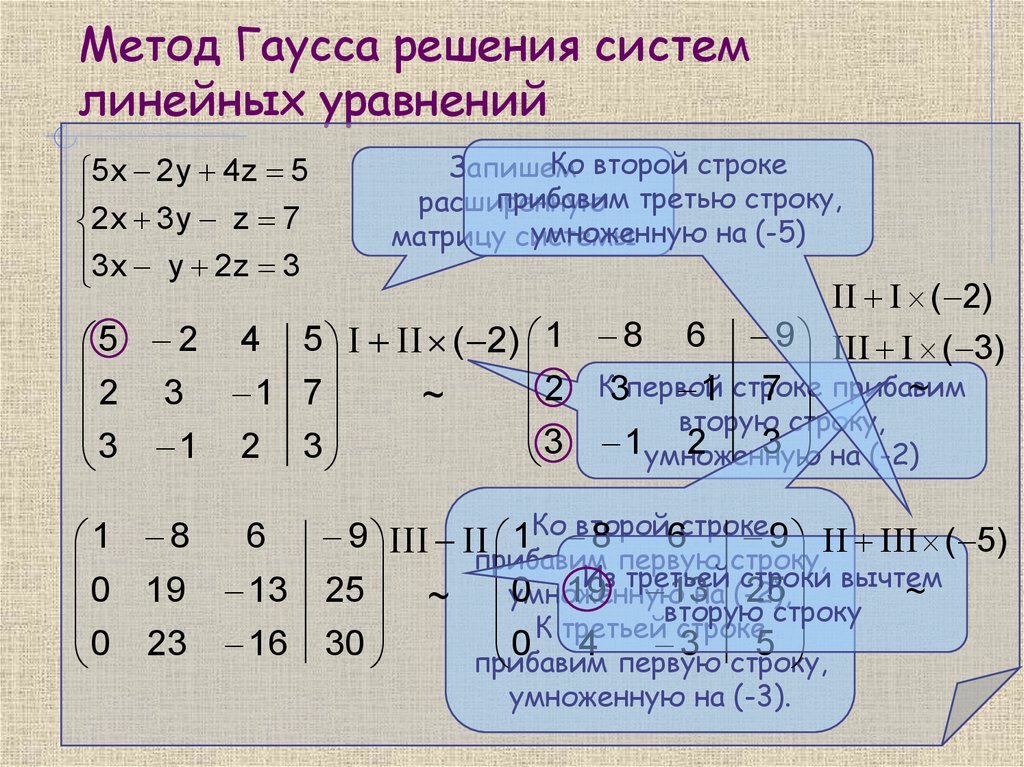

 

Мы можем использовать алгебру , чтобы представить этот шаблон. Алгебра использует буквы и другие символы для представления чисел в уравнениях. Мы можем использовать букву n , чтобы указать, сколько чисел в нашем списке. Это самое большое число. В нашем примере n будет равно 10. Количество пар будет равно этому числу, деленному на 2. Вы заметите, что размер пары равен количеству пар плюс 1. Таким образом, мы могли бы написать использовать n для записи

(количество пар) x (сумма каждой пары) = n/2 x (n +1)

Но помните, как и раньше, нам нужна сумма только одной строки, а не обеих. Таким образом, мы делим приведенную выше формулу на 2 и получаем:

Изображение — Версия текста

n вне скобки, за которой следует n плюс один внутри скобки. Это делится на 2.

 

Можем ли мы сделать то же самое для суммы, которая является нечетным числом, скажем, 67? Попробуйте сами, прежде чем смотреть ответ ниже.

Вопрос:

1 + 2 + 3 + 4 ….. 66 + 67 =?

(Ответ внизу страницы)

Шаблон, показывающий сложение пар от одного до десяти (© Let’s Talk Science, 2021).

Реальные приложения

Эта задача является примером нахождения суммы арифметической последовательности . Последовательность   – это набор упорядоченных чисел. В арифметической последовательности расстояние между любыми двумя последовательными числами одинаково. Мы можем использовать метод Гаусса, чтобы найти сумму любой арифметической прогрессии.

Последовательность извлечения кусочков пиццы (Источник: Lebazele через iStockphoto).

 

Нахождение суммы последовательности может помочь людям решить множество реальных задач. Компании находят сумму последовательностей, чтобы оценить затраты или доход. Даже расчет стоимости проезда на такси представляет собой сумму арифметической последовательности. Вы начинаете с базового тарифа. Ваша общая стоимость увеличивается на ту же сумму каждую минуту.

Нахождение суммы последовательности также является распространенным вопросом информатики. Компьютерщики используют для этого метод Гаусса. Вопрос «Отсутствующий номер» — это распространенный вопрос технического собеседования. Для ее решения нужен метод Гаусса. Многие из этих приложений используют сложные на вид формулы. Однако на самом деле они просто используют метод Гаусса для нахождения суммы последовательности.

 

ОТВЕТ

1 + 2 + 3 + 4……66 + 67 = ?

n = 67, n + 1 = 68

n(n + 1)/2

67 x 68/2

= 2 278

 

Иоганн Карл Фридрих Гаусс — Факультет математики

Родившийся 30 апреля 1777 года в Брауншвейге (Германия), Карл Фридрих Гаусс был, пожалуй, одним из самых влиятельных математических умов в истории.

Иногда его называют «Принцем математики». Он был известен своим математическим мышлением в очень молодом возрасте. Когда ему было всего 7 лет, он привлек внимание своего школьного учителя Бюттнера своей способностью складывать числа от 1 до 100 за считанные секунды. (В чем была его хитрость? Посмотрите, сможете ли вы найти ее самостоятельно, а затем посмотрите метод в нижней части страницы.) В 11 лет он начал свое формальное образование в «Гимназии» (старшей средней школе в Германии), и поступил в Брауншвейгский коллегиум Каролинум в возрасте 15 лет на стипендию от герцога Брауншвейгского — своего благодетеля. Даже в этом возрасте Гаусс, работая самостоятельно, смог вывести некоторые очень важные результаты в области теории чисел: закон Боде, биномиальную теорему, теорему о простых числах, среднее арифметическое/геометрическое и закон квадратичных чисел. взаимность. Позже его цитировали: « Математика — царица наук, а теория чисел — царица математики ». (Хотите узнать больше о некоторых из этих тем и посмотреть, насколько вы сравнимы с Гауссом? Ознакомьтесь с курсами по теории чисел.)

В возрасте 18 лет Гаусс начал учебу в Геттингенском университете у Кастнера. Он оставил школу без диплома, но по пути открыл для себя построение правильного 17-угольника (так называемого «семиугольника») с помощью только циркуля и линейки. Позже он попросил, чтобы эта форма была запечатлена на его надгробии! (Чтобы узнать больше о построениях линейки, компаса и многоугольниках, ознакомьтесь с классом «Математика в искусстве», МАТЕМАТИКА 1020.) Он получил степень в возрасте 22 лет в Брансуике, а затем получил докторскую степень в Университете Хельмштедта, обучаясь у пфафф.

За это время он открыл Фундаментальную теорему алгебры, которая утверждает, что каждый многочлен имеет корень вида  a+bi  (он придумал 4 разных доказательства этой теоремы!). (Вы можете узнать об основной теореме алгебры в Методах классической и линейной алгебры, МАТЕМАТИКА 1210.) Он также разработал метод, известный как «Исключение по Гауссу» , и использовал его для решения задач наименьших квадратов в небесных вычислениях, а затем и в вычислениях. для измерения земли и ее поверхности (мы используем этот метод для решения систем линейных уравнений в прикладной конечной математике MATH 1010 , векторной геометрии и линейной алгебре (и некоторых других)).

Он опубликовал свою первую книгу « Disquisitiones Arithmeticea » и начал заниматься астрономией в возрасте 24 лет. Астроном по имени Зак опубликовал несколько оценок орбитальных положений новой «маленькой планеты» по имени Церера. Гаусс был одним из тех, кто пытался предсказать его положение. Его предсказания сильно отличались от всех остальных и оказались почти точно верными! (Он разработал метод под названием « аппроксимация методом наименьших квадратов », чтобы делать эти предсказания, и вы можете узнать об этом и других методах аппроксимации в разделе «Введение в математическое моделирование», МАТЕМАТИКА 3820.) Он также завершил работу над Фундаментальной теоремой арифметики, в котором говорится, что каждое натуральное число может быть представлено в виде произведения простых чисел только одним способом (см. курсы по теории чисел). В 27 лет он стал членом Королевского общества, а через год женился на своей жене Джоанне Остофф (которая умерла во время родов 2 года спустя, после чего он женился на ее лучшей подруге Минне).

В 30 лет он стал директором Геттингенской обсерватории, продолжив работу по исследованию орбит различных небесных тел (возможно, это одна из причин, по которой его именем назван лунный кратер!).

Затем он опубликовал свою вторую книгу « Theoria motus corporum celestium in sectionibus conicus Solem ambientium» , в которой углубился в дифференциальные уравнения площадей (вы тоже можете, см. Ordinary Differential Equations, MATH 2800) конические сечения (см. Math in Art , МАТЕМАТИКА 1020 ) и эллиптические орбиты.

В конце 30-х и начале 40-х он закончил работы над новой обсерваторией, изобрел машину под названием «гелиотроп», которая отражала солнечные лучи на большие расстояния, чтобы отметить положение участников топографической съемки, опубликовал более 70 документы, стал членом Королевского общества Эдинборо и преследовал свои интересы в области неевклидовой геометрии (см. Математика в искусстве, МАТЕМАТИКА 1020).

Этот импульс не замедлился и в его 50-летнем возрасте, когда он начал работать с Вильгельмом Вебером в области физики, в частности, земного магнетизма. Он использовал уравнение Лапласа (см. Инженерно-математический анализ, МАТЕМАТИКА 2132), чтобы указать местоположение магнитного Южного полюса, и завершил новую «магнитную обсерваторию» (завершенную в 1833 году — без всех магнитных металлов). Он также открыл закон Кирхгофа, разработал примитивный телеграф (который мог работать на расстоянии 5000 футов), магнитометр (который измеряет силу и/или направление магнитного поля поблизости) и работал с Вебером над установлением мировой -широкая сетка магнитных точек наблюдения.

В свои 60 он разбогател на грамотных инвестициях и облигациях, а также пополнял фонд для вдов Геттингенского университета. Он также получил медаль Копли Королевского общества.

Он прочитал свою лекцию в честь Золотого Юбилея в возрасте 72 лет и продолжал свою практическую деятельность до своей смерти 23 февраля ^rd , 1855 г. в Геттингене, Ганновер.

С тех пор его работы использовались во многих различных областях математики, а его память была отмечена различными статуями, памятниками и даже на купюре в 10 немецких марок.

Ссылки:

Дж. Дж. О’Коннер, Э. Ф. Робертсон, Йохан Карл Фридрих Гаусс:

html

Weisstein, Eric W, Gauss, Karl Friedrich (1777-1855):

http://scienceworld.wolfram.com/biography/Gauss.html

Краткая история линейной алгебры и теории матриц

http: //darkwing.uoregon.edu/~vitulli/441.sp04/LinAlgHistory.html

Цитаты Гаусса:

http://www-history.mcs.st-andrews.ac.uk/history/Quotations/Gauss.html

Суммируя числа от 1 до 100:

найдите следующий шаблон:

Карл Фридрих Гаусс — Принц математики

Карл Фридрих Гаусс, картина Кристиана Альбрехта Йенсена

Карл Фридрих Гаусс, настоящее имя Иоганн Фридрих Карл Гаусс (родился 30 апреля 1777, Брауншвейг — умер 23 февраля 1855, Геттинген, Ганновер), немецкий математик, общепризнанный как один из величайших математиков всех времен за его вклад в теорию чисел, геометрию, теорию вероятностей, геодезию, планетарную астрономию, теорию функций и теорию потенциала (включая электромагнетизм).

Карла Фридриха Гаусса иногда называют «принцем математиков» и «величайшим математиком древности». Он оказал заметное влияние во многих областях математики и науки и считается одним из самых влиятельных математиков в истории.

Гаусс был вундеркиндом. Есть много анекдотов о его раннем развитии в детстве, и он сделал свои первые новаторские математические открытия еще подростком.

Всего в три года он исправил ошибку в расчетах заработной платы своего отца и к 5 годам регулярно следил за счетами отца. Сообщается, что в возрасте 7 лет он поразил своих учителей. суммируя целые числа от 1 до 100 почти мгновенно (быстро заметив, что сумма на самом деле составляет 50 пар чисел, каждая пара в сумме дает 101, всего 5050). К 12 годам он уже посещал гимназию и критиковал геометрию Евклида.

Хотя его семья была бедной и принадлежала к рабочему классу, интеллектуальные способности Гаусса привлекли внимание герцога Брауншвейгского, который отправил его в Коллегиум Каролинум в 15 лет, а затем в престижный Геттингенский университет (который он посещал с 1795 по 1798 год). ). Еще подростком, посещавшим университет, Гаусс открыл (или независимо переоткрыл) несколько важных теорем.

В 15 лет Гаусс первым обнаружил какую-либо закономерность в появлении простых чисел, задача, занимавшая умы лучших математиков с древних времен. Хотя встречаемость простых чисел казалась почти полностью случайной, Гаусс подошел к проблеме с другой стороны, нарисовав график появления простых чисел по мере увеличения чисел. Он заметил грубую закономерность или тенденцию: по мере того, как числа увеличивались на 10, вероятность появления простых чисел уменьшалась примерно в 2 раза (например, существует 1 из 4 шансов получить простое число в числе от 1 до 100, т.е. 1 шанс из 6 получить простое число от 1 до 1000, 1 шанс из 8 от 1 до 10 000, 1 шанс из 10 от 1 до 100 000 и т. д.). Однако он прекрасно осознавал, что его метод дает лишь приближение, и, поскольку он не мог окончательно доказать свои выводы, он держал их в секрете до гораздо более позднего возраста.

17-сторонний семиугольник, построенный Гауссом

Первым значительным открытием Гаусса, сделанным в 1792 году, было то, что правильный многоугольник из 17 сторон может быть построен только с помощью линейки и циркуля. Его значение заключается не в результате, а в доказательстве, которое основывалось на глубоком анализе факторизации полиномиальных уравнений и открыло дверь более поздним идеям теории Галуа. Его докторская диссертация 1797 г. дала доказательство основной теоремы алгебры: всякое полиномиальное уравнение с действительными или комплексными коэффициентами имеет столько корней (решений), сколько его степени (наибольшей степени переменной). Доказательство Гаусса, хотя и не вполне убедительное, отличалось критикой более ранних попыток. Позже Гаусс дал еще три доказательства этого важного результата, последнее к 50-летию первого, что показывает важность, которую он придавал этой теме.

Однако признание Гаусса как поистине выдающегося таланта произошло благодаря двум крупным публикациям в 1801 году. Прежде всего, это публикация им первого систематического учебника по алгебраической теории чисел, Disquisitiones Arithmeticae. Эта книга начинается с первого описания модульной арифметики, дает подробное описание решений квадратных многочленов от двух переменных в целых числах и заканчивается упомянутой выше теорией факторизации. Этот выбор тем и их естественные обобщения определили повестку дня в теории чисел на протяжении большей части XIX века.веке, и постоянный интерес Гаусса к этому предмету стимулировал множество исследований, особенно в немецких университетах.

Портрет Гаусса Эдуарда Ритмюллера на террасе Геттингенской обсерватории //Карл Фридрих Гаусс: Титан науки Дж. Уолдо Даннингтона, Джереми Грея, Фрица-Эгберта Дозе

Второй публикацией было его повторное открытие астероида Церера. Его первоначальное открытие, сделанное итальянским астрономом Джузеппе Пиацци в 1800 году, вызвало сенсацию, но он исчез за Солнцем до того, как удалось провести достаточно наблюдений, чтобы рассчитать его орбиту с достаточной точностью, чтобы узнать, где он снова появится. Многие астрономы соревновались за честь найти его снова, но Гаусс победил. Его успех основывался на новом методе обработки ошибок в наблюдениях, который сегодня называется методом наименьших квадратов. После этого Гаусс много лет работал астрономом и опубликовал крупную работу по вычислению орбит — числовая сторона такой работы была для него гораздо менее обременительна, чем для большинства людей. Будучи чрезвычайно преданным подданным герцога Брауншвейгского, а после 1807 года, когда он вернулся в Геттинген в качестве астронома, герцога Ганноверского, Гаусс чувствовал, что его работа имеет общественную ценность.

На самом деле Гаусс часто отказывался публиковать свои открытия. Будучи студентом в Геттингене, он начал сомневаться в априорной истинности евклидовой геометрии и подозревал, что ее истинность может быть эмпирической. Для этого должно существовать альтернативное геометрическое описание пространства. Вместо того чтобы опубликовать такое описание, Гаусс ограничился критикой различных априорных защит евклидовой геометрии. Казалось, он постепенно убедился, что существует логическая альтернатива евклидовой геометрии. Однако, когда венгр Янош Бойяи и русский Николай Лобачевский опубликовали свои отчеты о новой неевклидовой геометрии около 1830 года, Гаусс не смог последовательно изложить свои собственные идеи. Можно объединить эти идеи в впечатляющее целое, в котором его концепция внутренней кривизны играет центральную роль, но Гаусс так и не сделал этого. Одни приписывали эту неудачу его врожденному консерватизму, другие — его непрекращающейся изобретательности, которая всегда влекла его к следующей новой идее, третьи — его неспособности найти центральную идею, которая управляла бы геометрией после того, как евклидова геометрия перестала быть уникальной. Все эти объяснения имеют некоторые достоинства, хотя ни одно из них не может быть исчерпывающим объяснением.

Статуя Гаусса на его родине, Брансуик

Однако достижения Гаусса не ограничивались чистой математикой. Во время своих геодезических лет он изобрел гелиотроп, инструмент, который использует зеркало для отражения солнечного света на большие расстояния, чтобы отметить позиции при съемке местности. В последующие годы он сотрудничал с Вильгельмом Вебером в измерениях магнитного поля Земли и изобрел первый электрический телеграф. В знак признания его вклада в теорию электромагнетизма международная единица магнитной индукции известна как гаусс.

После смерти Гаусса в 1855 году обнаружение стольких новых идей в его неопубликованных работах распространило его влияние на оставшуюся часть века.

Личная жизнь Гаусса была омрачена ранней смертью его первой жены Йоханны Остхофф, от которой у него было трое детей, в 1809 году, за которой вскоре последовала смерть одного ребенка, Луи. Гаусс погрузился в депрессию, из которой так и не оправился. Он снова женился на лучшей подруге Джоанны, Фридерике Вильгельмине Вальдек, более известной как Минна. У них также было трое детей. Когда его вторая жена умерла в 1831 году после продолжительной болезни, одна из его дочерей, Тереза, взяла на себя домашнее хозяйство и заботилась о Гауссе до конца его жизни.

Карл Фридрих Гаусс — Принц математиков

Карл Фридрих Гаусс (1777 – 1855)

30 апреля 1777 года родился немецкий математик и ученый-физик Карл Фридрих Гаусс  . Он внес значительный вклад во многие области, включая теорию чисел, алгебру, статистику, анализ, дифференциальную геометрию, геодезию, геофизику, электростатику, астрономию и оптику. Его часто называют Princeps mathematicorum (лат. «Принц математиков»), а также «величайшим математиком древности».

«Математика — королева науки, а арифметика — королева математики» — передано Вольфгангом Сарториусом фон Вальтерсхаузеном, Gauss zum Gedächtniss, Verlag von S. Hirzel, Лейпциг, 1856 г., стр. 79

Вундеркинд

Карл Фридрих Гаусс рос единственным ребенком, его мать едва умела читать, но была известна своей невероятной сообразительностью. Слухи о Гауссе говорят, что он умел считать до того, как научился говорить, и что он поправил своего отца в расчете заработной платы в возрасте всего трех лет. Независимо от того, верны ли эти слухи на самом деле, это указывает на то, что таланты Гаусса и его любовь к сложным вычислениям были обнаружены очень рано. В возрасте семи лет он начал ходить в школу и уже разработал формулы, облегчающие его вычисления на уроках математики.

Знаменитое открытие детства Гаусса

Есть один известный рассказ об открытии Карлом Фридрихом Гауссом в детстве «трюка» для суммирования арифметической прогрессии.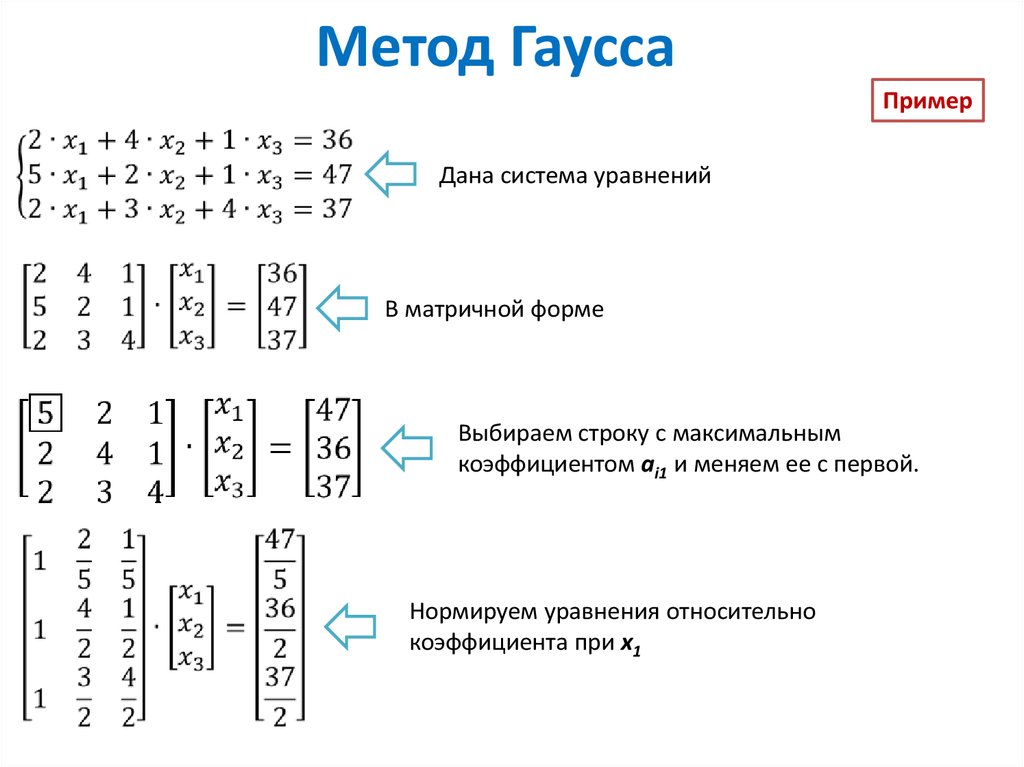 Это событие произошло, когда Гауссу было семь лет, и он посещал школу Катарины в Брансуике. Учитель, некий Бюттнер, поставил перед классом задачу вычислить сумму 1 + 2 + 3 + …. + 100 — вероятно, чтобы получить немного покоя для себя, с указанием, что каждый должен положить свой планшет на стол, как только он выполнит задание. Почти сразу же Гаусс положил свою доску на стол и сказал: « Вот оно. » Учитель презрительно посмотрел на него, в то время как остальные усердно работали. Когда инструктор, наконец, посмотрел на результаты, планшет Гаусса был единственным, кто дал правильный ответ, 5050, без дальнейших вычислений. Десятилетний мальчик, очевидно, вычислил в уме сумму арифметической прогрессии 1 + 2 + 3 + … + 99 + 100, предположительно по формуле m(m+1)/2 . Его учителя вскоре обратили внимание на талант Гаусса герцога Брауншвейгского [1].

Математика как профессия

В возрасте 14 лет Гаусса познакомили с герцогом Карлом Вильгельмом Фердинандом фон Брауншвейгом, который направил его в Коллегиум Каролинум (ныне Брауншвейгский технологический университет), который он посещал с 1792 по 1795 год, и в Геттингенский университет с 1795 по 1798 год. Во время учебы в университете Гаусс независимо заново открыл несколько важных теорем. Его прорыв произошел в 1796 году, когда он показал, что правильный многоугольник можно построить с помощью циркуля и линейки, если число его сторон является произведением различных простых чисел Ферма и степени двойки. Это было крупным открытием в важной области математики; проблемы построения занимали математиков со времен древних греков, и это открытие в конечном итоге привело Гаусса к выбору математики вместо филологии в качестве карьеры. Гаусс был так доволен этим результатом, что потребовал, чтобы на его надгробии был начертан правильный семиугольник. Каменщик отказался, заявив, что сложная конструкция, по сути, будет выглядеть как круг.

«Чарующие прелести этой возвышенной науки открываются во всей своей красоте лишь тому, кто имеет смелость углубиться в нее».
— Гаусс в письме Софи Жермен (30 апреля 1807 г.)

Работа в области теории чисел

Гаусс вернулся в Брауншвейг, где получил степень в 1799 году. После того, как герцог Брауншвейгский согласился продолжить стипендию Гаусса, он попросил, чтобы Гаусс представил докторскую диссертацию в Университете Гельмштедта. Он уже знал Пфаффа, который был выбран его советником. Диссертация Гаусса была обсуждением основной теоремы алгебры. С его стипендией, чтобы поддерживать его, Гауссу не нужно было искать работу, поэтому он посвятил себя исследованиям. Он издал книгу Disquisitiones Arithmeticae  летом 1801 года со специальным разделом, посвященным теории чисел.[7] В последующие годы Карлу Фридриху Гауссу предложили несколько должностей в зарубежных университетах, но из лояльности к герцогу и надежды получить собственную обсерваторию он остался в Геттингене, где должен был читать лекции. Несмотря на то, что ему не нравилась его профессия учителя, у него обучались несколько известных будущих математиков, таких как Рихард Дедекинд или Бернхард Риман. [8,9]

Неевклидова геометрия и простые числа

Вклад Гаусса в область математики огромен. В возрасте всего 16 лет он сделал первые попытки, ведущие к неевклидовой геометрии. Два года спустя Гаусс начал исследовать свойства распределения простых чисел, что позже привело его к вычислению площадей под графиками и к кривой Гаусса. Независимо от Каспара Весселя и Жана-Робера Аргана, Гаусс нашел геометрическое выражение комплексных чисел в одной плоскости.

Предсказание положения потерянной Цереры

Титульный лист великого труда Гаусса, Disquisitiones Arithmeticae (1801)

В июне 1801 года Зак, астроном, с которым Гаусс познакомился двумя или тремя годами ранее, опубликовал орбитальные положения Цереры, новой «малой планеты», которая была открыта Джузеппе Пьяцци, итальянским астрономом, 1 января 1801 года.[10] К сожалению, Пиацци смог наблюдать только 9 градусов его орбиты, прежде чем он скрылся за Солнцем. Зак опубликовал несколько предсказаний его положения, в том числе предсказание Гаусса, которое сильно отличалось от других. Когда Церера была заново открыта Заком 7 декабря 1801 года, она была почти в точности такой, как предсказывал Гаусс.

Борьба за приоритет с Лежандром

«Может быть, и правда, что люди, которые являются простыми математиками, имеют некоторые специфические недостатки, но это не вина математики, ибо это в равной степени верно и для любого другого исключительного занятия. Итак, есть простые филологи, простые юристы, простые солдаты, простые торговцы и т. д. К такому пустословию можно еще добавить, что всякий раз, когда известное исключительное занятие связано с определенными недостатками, оно также почти наверняка отделено от некоторых других недостатков. ”
– Gauss-Schumacher Briefwechsel (1862)

В возрасте 18 лет он открыл некоторые свойства распределения простых чисел и нашел метод наименьших квадратов, который направлен на минимизацию суммы квадратов отклонений без предварительной публикации о них. После того, как Адриан-Мари Лежандр опубликовал свой « Méthode des moindres carrés » в трактате в 1805 году, а Гаусс опубликовал свои результаты только в 1809 году, возник спор о приоритетах.

Профессор в Геттингене

Гаусс отказался от назначения в Петербургскую Академию наук из благодарности своему покровителю герцогу Брауншвейгскому и, вероятно, в надежде, что тот построит ему обсерваторию в Брауншвейге. После внезапной смерти герцога после битвы при Йене и Ауэрштедте Гаусс стал профессором Геттингенского университета Георга Августа и директором тамошней обсерватории в ноябре 1807 года. Там он должен был проводить курсы, но у него появилось отвращение к ним.

«Я разумею слово доказательство не в смысле юристов, которые ставят два полудоказательства равными целому, а в смысле математика, где ½ доказательства = 0, а от доказательства требуется, чтобы всякое сомнение становится невозможным».
— Гаусс в письме Генриху Вильгельму Матиасу Ольберсу (14 мая 1826 г.)

Геодезическая съемка

В 1818 году Гаусса попросили провести геодезическую съемку штата Ганновер, чтобы соединиться с существующей датской сетью. Гаусс с радостью согласился и взял на себя ответственность за съемку, производя измерения днем ​​и уменьшая их ночью, используя свои необычайные умственные способности для расчетов. Из-за исследования Гаусс изобрел гелиотроп, который работал, отражая солнечные лучи, используя конструкцию зеркал и небольшой телескоп. Однако для съемки использовались неточные базовые линии и неудовлетворительная сеть треугольников.[7]

Гаусс начал работать в области астрономии после завершения своего знаменитого « Арифметических исследований » и сумел рассчитать орбиты планет с помощью своего метода наименьших квадратов. Он поделился своим опытом в работе « Theoria motus corporum coelestium in sectionibus conicis solem ambientium . Его достижения в этой области сделали Гаусса всемирно известным, и некоторые из его астрономических методов используются до сих пор.

Электромагнетизм и телеграф

Вместе с Вильгельмом Эдуардом Вебером Гаусс работал в области магнетизма, начиная с 1831 года. Вместе с Вебером Гаусс изобрел магнитометр, таким образом соединив свою обсерваторию с Институтом физики в 1833 году. Он обменивался сообщениями с Вебером через стрелки компаса, на которые воздействовали электромагнитные поля: первая в мире телеграфная связь. Вместе с ним он разработал систему единиц СГС, которая была определена в 1881 году на международном конгрессе в Париже как основа для электротехнических единиц.

Гаусс работал во многих областях, но публиковал свои результаты только тогда, когда считал, что теория завершена. В результате он изредка указывал коллегам, что давно доказал тот или иной результат, но еще не представил его из-за неполноты лежащей в его основе теории или отсутствия небрежности, необходимой для быстрой работы. Многочисленные математические методы и формулы носят имя Гаусса сегодня, и на протяжении всей своей жизни и за ее пределами он заслужил репутацию одного из самых гениальных и продуктивных математиков всех времен.

Поздние годы

Он все еще занимался научной деятельностью до конца своей жизни и читал лекции по методу наименьших квадратов в 1850/51. Двое из его самых важных учеников, Бернхард Риман (который получил докторскую степень от Гаусса в 1851 году и произвел впечатление на Гаусса в 1854 году своей лекцией по основам римановой геометрии) и Рихард Дедекинд, были только в конце своей карьеры. В последние годы жизни Гаусс страдал сердечной недостаточностью (с диагнозом водянка) и бессонницей. В июне 1854 года он выехал с дочерью Терезой на строительную площадку железнодорожной ветки из Ганновера в Геттинген, где проезжавшая железная дорога распушила лошадей и опрокинула вагон, кучер был тяжело ранен, Гаусс и его дочь остались невредимы. Гаусс принял участие в открытии железнодорожной линии 31 июля 1854 года, после чего из-за болезни ему все чаще приходилось оставаться в своем доме. Он умер 23 февраля 1855 года в Геттингене в своем кресле.

Ссылки:

• [1] Бойер, Карл Б. 1968, 1991. История математики. Второе издание. Под редакцией Уты С. Мерцбах; предисловие Айзека Азимова. Нью-Йорк: Уайли. (стр. 497)
• [2] Биография Карла Фридриха Гаусса
• [3] Информационный веб-сайт Карла Фридриха Гаусса 
• [4] Карл Фридрих Гаусс из Wolfram Research
• [5] Кейли, Артур (1911). «Гаусс, Карл Фридрих». В Чисхолме, Хью (ред.). Британская энциклопедия (11-е изд.). Издательство Кембриджского университета.
• [6] Карл Фридрих Гаусс в zbMATH
• [7] О’Коннор, Джон Дж.; Робертсон, Эдмунд Ф., «Карл Фридрих Гаусс», архив MacTutor History of Mathematics, Сент-Эндрюсский университет.
• [8] Ричард Дедекинд и реальные числа, блог SciHi
.
• [9] Новый подход Бернхарда Римана к геометрии, SciHi Blog
• [10] Джузеппе Пьяцци и карликовая планета Церера, блог SciHi
• [11] Карл Фридрих Гаусс в Викиданных
• [12] Карл Фридрих Гаусс в проекте «Математическая генеалогия»
• [13] Рамамурти Шанкар, 3.