Теория электромагнетизма Максвелла. История лазера

Теория электромагнетизма Максвелла

Столетием позже, в 1864 г., Дж. К. Максвелл (1831-1879) открыл электромагнитную, а не упругую природу световых колебаний, обобщив это в знаменитых уравнениях, которые носят его имя и описывают различающиеся электрические и магнитные явления (электромагнетизм) в общей форме и из которых можно предсказать существование света. Электромагнитные волны получаются за счет колебаний в пространстве и во времени электрических и магнитных полей. Они распространяются с впечатляющей скоростью 300 000 км?с^-1, т.е. с той же скоростью, с которой, согласно измерениям, сделанным уже в 1675 г. Рёмером и позднее с высокой точностью И. Л. Физо (1819—1896) в 1849 г., распространяется свет. Максвелл предложил способ искусственного получения этих волн, и в 1887 г. Г. Герц (1857—1894) действительно смог получить электромагнитные волны с длиной волны порядка метров.

Джеймс Клерк Максвелл рассматривается вместе с Ньютоном и Эйнштейном как один из трех величайших гениев физики. Не случайно у Эйнштейна в его кабинете в Принстоне висел портрет Максвелла.

Максвелл родился в Эдинбурге (Шотландия) в семье среднего достатка. Его отец, Джон Клерк, был юристом, который унаследовал имение Максвеллов в Шотландии и стал членом их семьи. Он построил дом вблизи Глейнэйра, куда семья переехала вскоре после рождения Джеймса. Когда ему исполнилось восемь лет, его мать (с которой он был очень близок) умерла, и он остался с любящим отцом, который так и не женился больше. Максвелл любил рисовать, сочинял стихи и любил животных. У него было слабое здоровье, и он часто болел. Еще в школьные годы он заинтересовался математикой и геометрией. Его преподаватель в Эдинбургском университете профессор Джеймс Д. Форбс (1809—1868), который в течение многих лет был его наставником, представил в Эдинбургское Королевское общество одну из первых математических работ Максвелла 1846 г., касающуюся описания некоторых кривых. С 1847 по 1850 г. он учился в местном университете. В 1849 г. его профессор по математике Келланд представил в Эдинбургское Королевское общество еще одну его работу по кривым, а в 1850 г. работу по равновесию упругих тел. В эти же годы Максвелл интересовался цветным зрением. Он в 1850 г. поступил в Кембриджский университет и в 1855 г. получил ученую степень. Здесь он стал членом престижного Клуба Апостолов и в нескольких выступлениях показал свою глубокую заинтересованность в этико-философских, религиозных, логических и методологических вопросах. При подготовке к экзаменам на степень он стал интересоваться электричеством и магнетизмом. В то же время он изучил рыбий глаз и, получив математическое описание его свойств, показал условия совершенного фокусирования.

Спустя примерно полвека, Р. К. Люнебург заново открыл это, рассматривая линзы, обладающие свойствами, указанными Максвеллом. После получения степени для Максвелла в Кембридже не нашлось места, и он возвратился в Шотландию. С 1856 по 1860 г. он был профессором натуральной философии в Маришаль колледже Абердина. Эта должность хоть и не давала большого дохода, зато летние каникулы предоставляли массу свободного времени. Максвелл мог проводить шесть месяцев в своем имении Глейнэйра. В это же время он женился. Один из его студентов в Абердине, Давид Гилл (1843—1914), который позднее стал пионером применения фотографии в астрономии и Королевским Астрономом, так описывает уроки Максвелла:

«В те дни профессор был немногим лучше школьного учителя, а Максвелл не был хорошим учителем. Лишь четверо или пятеро из нас в классе с семьюдесятью или с восьмьюдесятью учениками получали от него знания. Мы оставались с ним на пару часов после лекций, до тех пор, пока его ужасная жена не утаскивала его на скудный обед в 3 часа дня. Сам он был симпатичным и очаровательным — часто задумывающимся и внезапно пробуждающимся чтобы сказать, о чем он размышлял. Многое мы не могли понять в то время, но впоследствии вспоминали и осознавали».

Исследования стабильности колец Сатурна позволили ему в 1857 г. выиграть приз и утвердили его как одного из лучших математических физиков своего времени. Проанализировав эту проблему, он получил вывод, что кольца образованы многими частицами, что в настоящее время подтверждается более точными астрономическими наблюдениями. С 1860 г. до 1865 г. он работал в Королевском колледже в Лондоне, где тщательно разрабатывал свои принципиальные работы, там же он встретился и часто общался с Майклом Фарадеем (1791—1867), отцом учения об электричестве, к которому относился с восхищением и от которого он многому научился в области электричества и магнетизма.

В 1865 г. почувствовав усталость, он на шесть лет уединился в своем доме в Гленлэре. Покидал он его только для коротких путешествий, одно из которых было в Италию в 1867 г. В Гленлэре, он закончил свою кинетическую теорию газов и написал свой знаменитый труд Treatise on Electricity and Magnetism, который содержит полностью разработанную теорию электромагнитного поля. В отношении уравнений, которые являются квинтэссенцией всей его работы, Эйнштейн сказал: «Специальная теория относительности обязана своим происхождением уравнениям Максвелла электромагнитного поля», а Больцман вопрошал: «Разве это не Бог, кто написал эти символы?»

В 1871 г. Максвелл занял кафедру экспериментальной физики в Кембридже и стал директором Кэвендишской лаборатории. Эта лаборатория была организована, в октябре 1870 г., когда герцог Девонширский, декан Кембриджского университета, решил поддержать строительство физической лаборатории и обеспечить ее оборудованием. Лаборатория была названа именем одного из родственников герцога, Генри Кэвендиша (1731—1810), который посвятил свою жизнь химии и экспериментальной физике, особенно интересуясь электричеством. Максвелл, активно работая по организации лаборатории, находил время для своего труда, который он опубликовал двумя годами позднее (1873). Он умер в Кембридже 5 ноября 1879 г.

Благодаря ему, мы обладаем фундаментальными основами теории электромагнетизма, а также термодинамики и кинетической теории газов, в которой он является одним из основателей наряду с Людвигом Больцманом (1844—1906) и Джошуа Виллардом Гиббсом (1839—1903). Кинетическая теория рассматривает газ, состоящим из огромного числа атомов или молекул, которые свободно движутся в пространстве, соударяясь друг с другом и со стенками сосуда. С помощью этой модели теория позволяет нам интерпретировать макроскопические свойства газов. Джон Херапат (1790-1868) первым установил связь между температурой газа и скоростью его молекул, хотя соотношение, которое он нашел, было ошибочным. Это также исследовалось англичанином Джеймсом П. Джоулем (1818—1889) и немцами Рудольфом Клаузиусом (1822—1888) и Людвигом Больцманом. Максвелл вывел из теории конкретные свойства газов, установив закон распределения скоростей молекул, рассматривая молекулы как маленькие бильярдные шары. Он получил выражения для давления, вязкости, диффузии и др. Он вывел теорему равнораспределения энергии, о которой мы будем говорить в дальнейшем. Максвелл рассматривал два возможных способа описания газа. Один основан на законах динамики и описывает детерминистическое поведение индивидуальных составляющих газа. Это дает полное описание системы. Другой метод является статистическим по природе и не принимает во внимание знание поведения индивидуальной молекулы, а имеет дело с огромным числом молекул. Система рассматривается, используя законы статистики. Это позволяет получить величины, которые описывают глобальные свойства газа, такие, как давление, температура и др.

Максвелл также интересовался теорией цветов, он развил и дополнил теорию физика и врача Томаса Юнга, который утверждал, что цветовое зрение получается комбинацией трех изображений в основных цветах, для которых в человеческом глазу имеются три вида соответствующих рецепторов. Максвелл идентифицировал эти три первичных цвета, из которых можно получить все цвета, как красный, синий и зеленый, и указал, что случай цветовой слепоты обусловлен отсутствием в глазу одного из трех рецепторов. Он указал, что если сделать фотографию через фильтры этих цветов, а затем соединить изображения, то получится цветная фотография объекта. Он практически продемонстрировал это собранию Королевского Общества в 1861 г., сделав фотографию закрученной в узел ткани с шотландским национальным рисунком. Эта была первая цветная фотография, полученная методом, который в существенных чертах используется и в наше время.

Однако теория электромагнитного поля — наиболее важный результат, полученный Максвеллом, и это, без сомнения, одно из важнейших достижений науки, на котором основана современная наука и техника.

В середине XIX в. электромагнетизм включал огромное число экспериментальных результатов, в которые значительный вклад внес Фарадей, но ожидалась общая теория, которая могла бы эти результаты интерпретировать.

Майкл Фарадей (1791-1867) является исключительным примером новаторского исследователя. Он был сыном кузнеца и начал работать с 13 лет подмастерьем в переплетной мастерской. Здесь он читал книги по химии и электричеству и делал эксперименты с помощью самодельных устройств. В 1813 г. он познакомился с химиком Хемфри Дэви (1778—1829) и стал его ассистентом в Королевском институте. Он был очень искусным экспериментатором и открыл фундаментальные явления, которые послужили основой электромагнитной теории Максвелла. Он разработал метод визуализации силовых линий электрических и магнитных полей. В качестве ассистента Дэви он в 1813—1815 гг. путешествовал по Европе, где знакомился с работами самых выдающихся исследователей континента.

В 1821 г. он, продолжая эксперименты датского физика Г. К. Эрстеда (1777—1851), показал, что магниты оказывают механическое действие на проводники, по которым протекает электрический ток. Позже он изучал явления электролиза, выраженные в законах, носящих его имя. В 1830— 1831 гг. он открыл явление электромагнитной индукции. Среди его последующих открытий — действие магнитного поля на поляризованный свет (эффект Фарадея) и диамагнетизм. В 1862 г. он пытался изучить действие магнитного поля на спектры света, пионерские исследования, которые позднее с успехом были выполнены П. Зееманом.

Максвелл блестящим образом интерпретировал результаты Фарадея и других исследователей, показав, что явления электрических и магнитных явлений тесно связаны, и в некоторых случаях электромагнитное поле может распространяться в виде волны. Отсюда следует, что свет является волной такого вида. Электромагнитная теория Максвелла встретила сильное сопротивление. Даже сам Максвелл и его ученики долгое время старались описать электромагнитное поле с помощью механических моделей. Только после продолжительных попыток объяснить его уравнения на основе механических моделей была окончательно принята концепция, что электрические и магнитные поля являются реальностью.

Рис. 6. Синусоидальная волна, видимая в заданный момент времени, как функция положения

Волновая теория рассматривает свет как колебания эфира и замечательно объясняет отражение, преломление, дифракцию и интерференцию, а также другие явления. Свойство света восприниматься окрашенным укладывается в свойствах волны. Белый свет есть ни что иное, как смесь всех цветов (факт, который еще Ньютон экспериментально продемонстрировал). Определенный цвет определяется длиной волны излучения (рис. 6), т.е. расстоянием между двумя соседними пиками волны. В видимой области эта длина волны обычно измеряется в ангстремах (один ангстрем или А° равен 10^-8 см) и видимая область простирается от ~3800 А° (фиолетовый свет) до 7000 А° (красный свет). Число пиков волны, проходящих в секунду через заданную точку, является частотой волны и измеряется в герцах (Гц). Произведение длины волны и частоты равно скорости распространения волны. Например, зеленый свет имеет в вакууме длину волны 5500 А°, распространяется со скоростью 300000 км с^-1 и имеет частоту 545 000 млрд. Гц. Излучения с большими длинами волн последовательно заполняют инфракрасные, микроволновые и радиоволны, А излучение с укороченными длинами волн являются ультрафиолетовым, рентгеновским и гамма-лучами (рис. 7).

Рис. 7. Электромагнитный спектр. Слева обозначены частоты, а справа — соответствующие длины волны

Поделитесь на страничке

Следующая глава >

Классическая электромагнетизма и специальная теория относительности — Classical electromagnetism and special relativity

Теория относительности играет важную роль в современной теории классического электромагнетизма . Прежде всего, это дает формулы для того, как электромагнитных объектов, в частности, электрических и магнитных полей , которые изменены в соответствии с преобразованием Лоренца из одной инерциальной системы отсчета к другой. Во- вторых, оно проливает свет на взаимосвязь между электричеством и магнетизмом, показывая , что система отсчета определяет , является ли наблюдение следующим образом электростатические или магнитные законы. В- третьих, это мотивирует компактный и удобный для обозначения законов электромагнетизма, а именно «явно ковариантной» тензорной форме.

Уравнения Максвелла, когда они впервые были изложены в их полном виде в 1865 году, оказались бы быть совместимым со специальной теорией относительности. Более того, очевидные совпадения , в которых тот же самый эффект наблюдался за счет различных физических явлений двумя различными наблюдателями будет показано, что не случайно в последнюю очередь специальную теорию относительности. На самом деле, половина 1905 года первой статье Эйнштейна о специальной теории относительности « К электродинамике движущихся тел » , объясняет , как преобразовать уравнения Максвелла.

Преобразование полей между инерциальных

Е и B полей

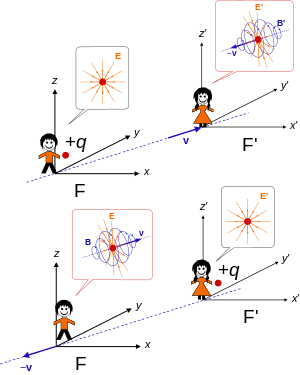Лоренц импульс электрического заряда. Вверху: Заряд находится в состоянии покоя в кадре F, так что наблюдатель видит статическое электрическое поле. Наблюдатель в другом кадре движется F ‘со скоростью об относительно F, и видит заряда движутся со скоростью — V с измененным электрическим полем E из — за длины сжатия и магнитного поля B из — за движения заряда. Внизу: Подобные установки, с зарядом в состоянии покоя в кадре F ‘.

Это уравнение, называемое также уравнение Джоулого-Бернулли , рассматривает две инерциальные . Загрунтованную рам двигается относительно нештрихованный кадр при скорости V . Поля , определенные в загрунтованном кадре обозначены штрихами, и поля определены в нештрихованных кадрах отсутствия простых чисел. Компоненты поля параллельно к скорости V обозначены и в то время как компоненты поля , перпендикулярные к V обозначены как и . В этих двух кадрах , движущихся с относительной скоростью V , то E -полями и B -полями связаны соотношением:Е∥{\ Displaystyle \ mathbf {E} _ {\ параллельно}}В∥{\ Displaystyle \ mathbf {B} _ {\ параллельно}}Е⊥{\ Displaystyle \ mathbf {E} _ {\}} преступникВ⊥{\ Displaystyle \ mathbf {B} _ {\}} преступник

Е∥’знак равноЕ∥В∥’знак равноВ∥Е⊥’знак равноγ(Е⊥+v×В)В⊥’знак равноγ(В⊥-1с2v×Е){\ Displaystyle {\ начинаются {выровнен} \ mathbf {E _ {\ параллельны}} ‘& = \ mathbf {Е _ {\ параллельны}} \\\ mathbf {B _ {\ параллельны}}’ & = \ mathbf {B _ {\ параллельны}} {\\\ mathbf E _ {\ личинка}} «& = \ гамма \ влево (\ mathbf {E} _ {\ личинка} + \ mathbf {v} \ раз \ mathbf {B}, \ справа) \\ \ mathbf {B _ {\ личинка}} «& = \ гамма \ влево (\ mathbf {B} _ {\ личинка} — {\ гидроразрыва {1} {с ^ {2}}} \ mathbf {v} \ раз \ mathbf {E} \ справа) \ {конец выровнен}}}

где

γ знак равноdее 11-v2/с2{\ Displaystyle \ Gamma \ {\ вытесненным {\ подпирать {\ mathrm {четкости}} {}} {=}} \ {\ гидроразрыва {1} {\ SQRT {1-V ^ {2} / с ^ {2} }}}}

называется фактор Лоренца и с представляет собой скорость света в свободном пространстве . Обратные преобразования являются одинаковыми , за исключением V → — v .

Эквивалентно, альтернативное выражение:

Е’знак равноγ(Е+v×В)-(γ-1)(Е⋅v^)v^В’знак равноγ(В-v×Ес2)-(γ-1)(В⋅v^)v^{\ Displaystyle {\ начинаются {выровнен} \ mathbf {Е} «& = \ гамма \ влево (\ mathbf {Е} + \ mathbf {v} \ раз \ mathbf {B}, \ справа) — \ влево ({\ гамма -1} \ справа) (\ mathbf {E} \ CDOT \ mathbf {\ {v шлем}}) \ mathbf {\ {v шлем}} \\\ mathbf {B}, «& = \ гамма \ влево (\ mathbf {В} — {\ гидроразрыва {\ mathbf {v} \ раз \ mathbf {E}} {с ^ {2}}} \ справа) — \ влево ({\ гамма -1} \ справа) (\ mathbf {B } \ CDOT \ mathbf {\ {v шлем}}) \ mathbf {\ {v шлем}} \ {конец выровнен}}}

где есть скорость единичный вектор . В предыдущих обозначениях, один на самом деле имеет и . v^знак равноv| |v| |{\ Displaystyle \ mathbf {\ Шляпа {v}} = {\ гидроразрыва {\ mathbf {v}} {\ Vert \ mathbf {v} \ Vert}}}(Е⋅v^)v^знак равноЕ∥{\ Displaystyle (\ mathbf {E} \ CDOT \ mathbf {\ {v шлем}}) \ mathbf {\ {v шлем}} = \ mathbf {E} _ {\ параллельны}}(В⋅v^)v^знак равноВ∥{\ Displaystyle (\ mathbf {B}, \ CDOT \ mathbf {\ {v шлем}}) \ mathbf {\ {v шлем}} = \ mathbf {B} _ {\ параллельны}}

Если один из полей равен нулю в одной системе отсчета, это не обязательно означает, что он равен нулю во всех остальных системах отсчета. Это можно увидеть, например, что делает нештрихованное электрическое поле нуля в переходе к штрихованному электрическому полю. В этом случае, в зависимости от ориентации магнитного поля, загрунтованную система могла видеть электрическое поле, даже если его нет в нештрихованной системе.

Это вовсе не означает , что две совершенно разные наборы событий рассматриваются в двух кадрах, но та же последовательность событий описывается двумя различными способами (см Moving магнит и проблемы проводника ниже).

Если частица заряд д движется со скоростью ¯u относительно к кадру S, то сила Лоренца в кадре S является:

Fзнак равноQЕ+QU×В{\ Displaystyle \ mathbf {F} = д \ mathbf {Е} + д \ mathbf {и} \ раз \ mathbf {B}}

В рамке S», сила Лоренца является:

F’знак равноQЕ’+QU’×В'{\ Displaystyle \ mathbf {F ‘} = д \ mathbf {Е’} + д \ mathbf {и ‘} \ раз \ mathbf {B}}

Если S и S», которые совмещены оси, то:

UИкс’знак равноUИкс+v1+(v UИкс)/с2UY’знак равноUY/γ1+(v UИкс)/с2UZ’знак равноUZ/γ1+(v UИкс)/с2{\ Displaystyle {\ {начинаются выровнены} и- {х} ‘& = {\ гидроразрыва {и- {х} + V} {1+ (v \ и- {х}) / с ^ {2}}} \\ и- { у} ‘& = {\ гидроразрыва {и- {у} / \ Gamma} {1+ (v \ и- {х}) / с ^ {2}}} \\ и- {г}’ & = {\ гидроразрыва {и- {г} / \ Gamma} {1+ (v \ и- {х}) / с ^ {2}}} \ {конец выровнен}}}

Вывод для преобразования силы Лоренца для частного случая у = 0 дается здесь. Более общий один можно увидеть здесь.

Компонент по компонентам, для относительного движения вдоль оси х, это работает, чтобы быть следующим:

ЕИкс’знак равноЕИксВИкс’знак равноВИксЕY’знак равноγ(ЕY-vВZ)ВY’знак равноγ(ВY+vс2ЕZ)ЕZ’знак равноγ(ЕZ+vВY)ВZ’знак равноγ(ВZ-vс2ЕY),{\ Displaystyle {\ {начинают выровненную} Е ‘_ {х} & = Е- {х} & \ qquad В’ _ {х} & = B_ {х} \\ Е ‘_ {у} & = \ гамма \ влево (Е- {у} -vB_ {г} \ справа) и В ‘_ {у} & = \ Gamma \ влево (B_ {у} + {\ гидроразрыва {v} {с ^ {2}}} Е- {г} \ справа) \\ Е ‘_ {г} & = \ Gamma \ влево (Е- {г} + vB_ {у} \ ​​справа) и В’ _ {г} & = \ Gamma \ влево (B_ {г} — {\ гидроразрыва {v} {с ^ {2}}} Е- {у} \ ​​справа). \\\ {конец выровнен}}}

Преобразования в этой форме могут быть сделаны более компактными, вводя электромагнитный тензор ( как определено ниже), который представляет собой ковариантный тензор .

Поля D и H

Для электрического смещения D и напряженности магнитного Н , с использованием определяющих соотношений и результат для C ² :

Dзнак равноε0Е,Взнак равноμ0ЧАС,с2знак равно1ε0μ0,{\ Displaystyle \ mathbf {D} = \ эпсилон _ {0} \ mathbf {E} \ ,, \ четырехъядерных \ mathbf {B} = \ му _ {0} \ mathbf {H} \ ,, \ четырехъядерный с ^ { 2} = {\ гидроразрыва {1} {\ эпсилон _ {0} \ му _ {0}}} \ ,,}

дает

D’знак равноγ(D+1с2v×ЧАС)+(1-γ)(D⋅v^)v^ЧАС’знак равноγ(ЧАС-v×D)+(1-γ)(ЧАС⋅v^)v^{\ Displaystyle {\ начинаются {выровнены} \ mathbf {D} «& = \ гамма \ влево (\ mathbf {D} + {\ гидроразрыва {1} {с ^ {2}}} \ mathbf {v} \ раз \ mathbf {H} \ справа) + (1- \ гамма) (\ mathbf {D} \ CDOT \ mathbf {\ {v шлем}}) \ mathbf {\ {v шлем}} {\\\ mathbf H} «& = \ гамма \ влево (\ mathbf {H} — \ mathbf {v} \ раз \ mathbf {D} \ справа) + (1- \ гамма) (\ mathbf {H} \ CDOT \ mathbf {\ шлем {v} }) \ mathbf {\ {v шлем}} \ {конец выровнен}}}

Аналогично для E и B , то D и Н образуют тензор электромагнитного смещения .

Ф и А поля

Альтернативой простой трансформации ЭМ поля используются электромагнитные потенциалы — на электрический потенциал φ и магнитный потенциал A :

φ’знак равноγ(φ-vA∥)A∥’знак равноγ(A∥-vφс2)A⊥’знак равноA⊥{\ Displaystyle {\ начинаются {выровнены} \ varphi ‘& = \ гамма \ влево (\ varphi -Va _ {\ параллельны} \ справа) \\ A _ {\ параллельны}’ & = \ гамма \ влево (A _ {\ параллельны} — {\ гидроразрыва {v \ varphi} {с ^ {2}}} \ справа) \\ A _ {\ личинка} ‘& = A _ {\ личинка} \ {конец выровнен}}}

где находится параллельная составляющая к направлению относительной скорости между кадрами V , и является перпендикулярной составляющей. Они прозрачно напоминают характерную форму других преобразований Лоренца (например , временной позиции и энергии-импульса), в то время как преобразования E и B выше , являются немного более сложными. Компоненты могут быть собраны вместе , как: A∥{\ Displaystyle \ scriptstyle A _ {\ параллельно}}A⊥{\ Displaystyle \ scriptstyle A _ {\ бот}}

A’знак равноA-γφс2v+(γ-1)(A⋅v^)v^φ’знак равноγ(φ-A⋅v){\ Displaystyle {\ начинаются {выровнен} \ mathbf {A}, «& = \ mathbf {А} — {\ гидроразрыва {\ Gamma \ varphi} {с ^ {2}}} \ mathbf {v} + \ влево (\ гамма -1 \ справа) \ влево (\ mathbf {A}, \ CDOT \ mathbf {\ {v шлет}} \ справа) \ mathbf {\ {v шлет}} \\\ varphi «& = \ гамма \ влево (\ varphi — \ mathbf {A}, \ CDOT \ mathbf {v} \ справа) \ {конец выровнен}}}

В р и J полей

Аналогично для плотности заряда р и плотность тока J ,

J∥’знак равноγ(J∥-vρ)ρ’знак равноγ(ρ-vс2J∥)J⊥’знак равноJ⊥{\ Displaystyle {\ {начинают выровненную} J _ {\ параллельный} ‘& = \ Gamma \ влево (J _ {\ параллельны} -v \ \ ро правый) \\\ Rho’ & = \ гамма \ влево (\ Rho — { \ гидроразрыва {v} {с ^ {2}}} _ {J \ параллельны} \ справа) \\ J _ {\ личинка} ‘& = J _ {\ личинка} \ {конец выровнен}}}

Сбор компонентов вместе:

J’знак равноJ-γρv+(γ-1)(J⋅v^)v^ρ’знак равноγ(ρ-J⋅vс2){\ Displaystyle {\ {начинаются выровнены} \ mathbf {j} «& = \ mathbf {j} — \ Gamma \ Rho \ mathbf {v} + \ влево (\ гамма -1 \ справа) \ слева (\ mathbf {j } \ CDOT \ mathbf {\ {v шлем}} \ справа) \ mathbf {\ {v шлем}} \\\ Rho «& = \ гамма \ влево (\ Rho — {\ гидроразрыва {\ mathbf {j} \ CDOT \ mathbf {v}} {с ^ {2}}} \ справа) \ {конец выровнен}}}

Нерелятивистская приближения

Для скорости об « с релятивистскими γ фактора ≈ 1, что дает:

Е’≈Е+v×ВВ’≈В-1с2v×ЕJ’≈J-ρvρ’≈(ρ-1с2J⋅v){\ Displaystyle {\ {начинаются выровнены} \ mathbf {E} ‘& \ ок \ mathbf {Е} + \ mathbf {v} \ раз \ mathbf {B} \\\ mathbf {B},’ & \ ок \ mathbf { B} — {\ гидроразрыва {1} {с ^ {2}}} \ mathbf {v} \ раз \ mathbf {Е} \\\ mathbf {j} «& \ приблизительно \ mathbf {j} — \ Rho \ mathbf {v} \\\ Rho «& \ ок \ слева (\ Rho — {\ гидроразрыва {1} {с ^ {2}}} \ mathbf {j} \ CDOT \ mathbf {v} \ справа) \ {конец выровнен }}}

так что нет необходимости проводить различие между пространственными и временными координатами в уравнениях Максвелла .

Отношения между электричеством и магнетизмом

«	Одна часть силы между движущимися зарядами мы называем магнитной силой. Это действительно один из аспектов электрического эффекта.	»
— Ричард Фейнман

Выведение магнетизма от электростатики

Выбирается опорный кадр определяет , если электромагнитное явление рассматривается как эффект электростатики или магнетизма. Авторы , как правило , получить магнетизм от электростатики при специальной теории относительности и заряд инвариантность принимаются во внимание. Фейнмановские лекции по физике (т. 2, гл. 13-6) использует этот метод для получения «магнитной» силой на движущийся заряд рядом с током проволокой. Смотрите также Haskell и Ландау.

Поля смешиваться в разных

Приведенные выше правила преобразования показывают , что электрическое поле в одном кадре вносит свой вклад в магнитное поле в другом кадре, и наоборот. Это часто описывается говоря , что электрическое поле и магнитное поле , два взаимосвязанных аспекта одного объекта, называется электромагнитное поле . Действительно, весь электромагнитное поле может быть закодирован в единственном тензором ранга 2 называется электромагнитный тензор ; увидеть ниже.

Перемещение магнита и проводника проблема

Известный пример перемешиванию электрических и магнитных явлений в различных системах отсчета, называется «движущийся магнит и проводник проблема», цит Эйнштейном в его работе 1905 г. по специальной теории относительности.

Если проводник движется с постоянной скоростью через поле стационарного магнита, вихревые токи будут производиться за счет магнитной силы на электроны в проводнике. В системе покоя проводника, с другой стороны, магнит будет двигаться и проводник неподвижно. Классическая электромагнитная теория предсказывает , что точно такие же микроскопические вихревые токи будут произведены, но они будут в связи с электрической силой.

Ковариантная формулировка в вакууме

Законы и математические объекты в классическом электромагнетизме можно записать в виде, явно ковариантные . Здесь, это только сделано для вакуума (или для микроскопических уравнений Максвелла, не используя макроскопические описания таких материалов , как электрическая проницаемость ), и использует единицы СИ .

В данном разделе используется Эйнштейн обозначения , включая Эйнштейн суммирование конвенцию . Смотрите также Риччи исчисления для резюме Тензора индекса нотаций и откидываемые показатели для определения верхних и нижних индексов, и как переключаться между ними. Метрический тензор Минковского здесь п имеет метрическую подпись (+ — — -).

тензор поля и 4-ток

Приведенные выше релятивистские преобразования предполагают , электрические и магнитные поля соединены друг с другом, в математическом объекте с 6 компонентов: антисимметричным вторым рангом тензором , или бивектором . Это называется тензор электромагнитного поля , обычно записывается в виде F ^μν . В матричной форме:

Fμνзнак равно(0-ЕИкс/с-ЕY/с-ЕZ/сЕИкс/с0-ВZВYЕY/сВZ0-ВИксЕZ/с-ВYВИкс0){\ Displaystyle Р ^ {\ му \ Nu} = {\ начинаются {pmatrix} 0 & -E_ {х} / с & -E_ {у} / с & -E_ {г} / с \\ Е- {х} / с & 0 & -B_ {г} & B_ {у} \\ Е- {у} / с & B_ {г} & 0 & -B_ {х} \\ Е- {г} / с & -B_ {у} & B_ {х} & 0 \ конец {pmatrix}}}

где с на скорости света — в натуральных единицах с = 1.

Существует еще один способ объединения электрических и магнитных полей в антисимметричным тензором, путем замены Е / гр → B и B → — E / C , чтобы получить двойной тензор G ^μν .

гμνзнак равно(0-ВИкс-ВY-ВZВИкс0ЕZ/с-ЕY/сВY-ЕZ/с0ЕИкс/сВZЕY/с-ЕИкс/с0){\ Displaystyle G ^ {\ му \ Nu} = {\ начинаются {pmatrix} 0 & -B_ {х} & — B_ {у} & — B_ {г} \\ B_ {х} & 0 & Е- {г} / с & -E_ {у} / с \\ B_ {у} & — Е- {г} / с & 0 & Е- {х} / с \\ B_ {г} & Е- {у} / с & -E_ {х} / с & 0 \ конец {pmatrix}}}

В контексте специальной теории относительности , обе эти преобразования в соответствии с преобразованием Лоренца в соответствии с

F’αβзнак равноΛμαΛνβFμν{\ Displaystyle F ‘^ {\ альфа \ бета} = \ Lambda _ {\ мю} ^ {\ альфа} \ Lambda _ {\ Nu} ^ {\ бета} F ^ {\ мю \ Nu}},

где Л ^{& alpha ;} _N , является преобразование Лоренца тензор для перехода от одной системы отсчета к другой. Же тензор используется дважды в суммировании.

Заряд и плотность тока, источники полей, а также объединить в четыре вектора

Jαзнак равно(сρ,JИкс,JY,JZ){\ Displaystyle J ^ {\ альфа} = \ влево (с \ Rho, J_ {х}, J_ {у}, J_ {г} \ справа)}

называется четыре тока .

Уравнения Максвелла в тензорной форме

Используя эти тензоры, уравнение Максвелла сводится к:

Уравнения Максвелла (Ковариантная формулировка) ∂Fαβ∂Иксαзнак равноμ0Jβ∂гαβ∂Иксαзнак равно0{\ Displaystyle {\ начинаются {выровнены} & {\ гидроразрыва {\ парциальное Р ^ {\ альфа \ бета}} {\ парциальное х ^ {\ альфа}}} = \ му _ {0} J ^ {\ бета} \ \ & {\ гидроразрыва {\ парциальное G ^ {\ альфа \ бета}} {\ парциальное х ^ {\ альфа}}} = 0 \ {конец выровнен}}}

где частные производные могут быть записаны различными способами, см 4-градиент . Первое уравнение , перечисленные выше , соответствует обоих закону Гаусса (при р = 0) и законом Ампера-Максвелла (при р = 1, 2, 3). Второе уравнение соответствует двум оставшимся уравнениям, Ряд Гаусса (при р = 0) и законом Фарадея (при р = 1, 2, 3).

Эти тензорные уравнения являются явно ковариантными , а это означает , что уравнения можно рассматривать в качестве ковариации на позиции индекса. Эта короткая форма записи уравнений Максвелла иллюстрирует идею общего среди некоторых физиков, а именно , что законы физики берут на себя более простой форме при записи с помощью тензоров .

При снижении индексов на F ^сф , чтобы получить F _ае (см подъема и опускания индексов ):

Fαβзнак равноηαληβμFλμ{\ Displaystyle F _ {\ альфа \ бета} = \ ETA _ {\ альфа \ Lambda} \ ETA _ {\ бета \ му} F ^ {\ Lambda \ му}}

второе уравнение можно записать в терминах F _аи как:

εδαβγ∂Fβγ∂Иксαзнак равно∂Fαβ∂Иксγ+∂Fγα∂Иксβ+∂Fβγ∂Иксαзнак равно0{\ Displaystyle \ эпсилон ^ {\ Delta \ альфа \ бета \ гамма} {\ dfrac {\ частичном F _ {\ бета \ гамма}} {\ парциальное х ^ {\ альфа}}} = {\ dfrac {\ частичная Р- { \ альфа \ бета}} {\ парциальное х ^ {\ Gamma}}} + {\ dfrac {\ парциальное F _ {\ Gamma \ альфа}} {\ парциальное х ^ {\ бета}}} + {\ dfrac {\ парциальное F _ {\ бета \ гамма}} {\ парциальное х ^ {\ альфа}}} = 0}

где контравариантный символ Леви-Чивита . Обратите внимание на циклическую перестановку индексов в этом уравнении: . εαβγδ{\ Displaystyle \ эпсилон ^ {\ альфа \ бета \ гамма \ дельта}}α⟶β↖γ↙{\ Displaystyle {\ {начинаются массив} {гс} & \ scriptstyle {\ альфа \, \, \ Longrightarrow \, \, \ бета} \\ & \ nwarrow _ {\ Gamma} \ swarrow \ {конец массива}}}

Другое ковариантное электромагнитное объектом является электромагнитным тензор энергии- , ковариантный ранга-2 тензора , который включает в себя вектор Пойнтинга , тензор напряжений Максвелла и плотность электромагнитной энергии.

4-потенциал

Тензор электромагнитного поля также могут быть записаны

Fαβзнак равно∂Aβ∂Иксα-∂Aα∂Иксβ,{\ Displaystyle Р ^ {\ альфа \ бета} = {\ гидроразрыва {\ парциальное А ^ {\ бета}} {\ парциальные х _ {\ альфа}}} — {\ гидроразрыва {\ парциальное А ^ {\ альфа}} { \ парциальное х _ {\ бета}}} \ ,,}

где

Aαзнак равно(φс,AИкс,AY,AZ),{\ Displaystyle А ^ {\ альфа} = \ влево ({\ гидроразрыва {\ varphi} {C}}, А_ {х}, А_ {у}, А_ {г} \ справа) \ ,,}

это четыре-потенциал и

Иксαзнак равно(сT,-Икс,-Y,-Z){\ Displaystyle х _ {\ альфа} = (кт, -x, -y, -z)}

это четыре-позиции .

Используя 4-потенциал в калибровке Лоренца, альтернатива является явно-ковариантным препарат может быть найдена в одном уравнении (обобщении уравнения из — за Бернхард Риман по Арнольду Зоммерфельд , известный как уравнение Римана-Зоммерфельд, или ковариантной форма уравнения Максвелла):

Уравнения Максвелла (Ковариантное Лоренц калибровочной рецептуры) ◻Aμзнак равноμ0Jμ{\ Displaystyle \ коробка А ^ {\ му} = \ му _ {0} J ^ {\ му}}

где это даламбертиан оператор, или четыре-лапласиан. Для более полного представления этих тех см ковариантной формулировки классического электромагнетизма . ◻{\ Displaystyle \ Box}

Смотрите также

Классическая теория — электромагнетизм — Большая Энциклопедия Нефти и Газа, статья, страница 1

Классическая теория — электромагнетизм

Cтраница 1

Классическая теория электромагнетизма наряду с классической и квантовой механикой является в настоящее время одной из основных теоретических дисциплин при подготовке физиков.  [1]

Классическая теория электромагнетизма имеет дело с электрическими зарядами, токами и их взаимодействиями в предположении, что все эти величины можно измерить независимо друг от друга, с неограниченной точностью. Здесь термин классическая означает просто не квантовая. Квантовые законы с их постоянной h игнорируются в классической теории электромагнетизма, так же как в обычной механике. Действительно, классическая теория была почти закончена до открытия Планка.  [2]

Но классическая теория электромагнетизма не содержит ничего, что оправдывало бы, по существу, такое неравенство электричества и магнетизма.  [3]

Из классической теории электромагнетизма следует, что это может произойти, если электроны вынуждены двигаться по спирали, причем проводник в виде правой спирали дает правое вращение. Модель Друде [7], однако, основывалась на взаимодействии вещества только с электрическим полем света и, как показали Борн [8] и Кун [9], оказалась ошибочной. Используемая в настоящей работе модель близка к модели Козмана [2], но не идентична ей; она была упрощена и приведена в соответствие с работой Козмана для удобства тех, кто желает более детально ознакомиться с математической стороной его теории. Как и Козман [2], мы используем простую классическую электромагнитную волновую модель света. Там, где он рассматривает движение двух электронов в двойной спирали, мы ( в согласии с Тиноко и Вуди [3]) рассматриваем простую спираль, имеющую свойства однородного макроскопического проводника.  [4]

Рассеяние электромагнитного излучения веществом представляет собой важную часть общей классической теории электромагнетизма. Настоящая глава посвящена другой стороне проблемы: рассеянию света газами и жидкими растворами. Существенным обстоятельством является то, что интересующие нас рассеивающие частицы располагаются относительно друг друга случайным, образом, так что каждая из них представляет собой независимый источник рассеянного излучения. Недавний обзор Гейдушека и Хольтцера9 представляет собой обстоятельное описание применения рассеяния света к изучению свойств макромолекул.  [5]

Разработка теории электромагнитных явлений Д. К. Максвеллом в Трактате об электричестве и магнетизме ( 1873 г.) завершает создание классической теории электромагнетизма.  [6]

Эти две системы уравнений — ( 14) и ( 16) — кажутся совершенно различными. В классической теории электромагнетизма уравнения ( 14) описывают электромагнитное поле в координатах Минковского. Заряды и поля в теории Максвелла существуют и изменяются в плоском пространстве. В общей теории относительности гравитационное поле является свойством пространства и определяется геометрией этого пространства. На геометрию влияет присутствие масс. Движение бесспиновых частиц, испытывающих гравитационное взаимодействие, дается геодезическими линиями. Поэтому полагали, что общая теория относительности принципиально отличается от теории электромагнетизма.  [7]

В физике существует значительное количество примеров успешного использования метода аналогий, и это является предпосылкой того, чтобы придать аналогии статус одного из основных методов научного познания. Максвелл [17] сопоставил созданную им классическую теорию электромагнетизма с гидродинамикой несжимаемых жидкостей и подчеркнул значение такого подхода в науке: Для составления физических представлений с ледует освоиться с существованием физических аналогий.  [8]

Достигнутая в результате краткость изложения помогла решению второй задачи: охвату как можно более широкого круга электромагнитных явлений. При этом пришлось использовать понятия и результаты, не относящиеся непосредственно к классической теории электромагнетизма. В основном это касается электромагнитных явлений в веществе, связанных с атомной структурой материи. Притих рассмотрении используются представления квантовой теории, лежащей в основе динамики атома: о разделении фазового пространства на элементарные ячейки определенной величины, необходимом при построении квантовых статистик; о квантовании орбитального момента количества движения; о спиновом моменте. На основе этих представлений и принципа Паули излагаются электронная теория металла и теория пара — и ферромагнетизма.  [9]

Черенков обнаружил, что направление испускания света сильно коррели-ровано с направлением падающего излучения. В 1937 г. Франк и Тамм) удачно объяснили эти результаты с помощью классической теории электромагнетизма.  [10]

Конечно, классическая теория была основательно подкреплена экспериментом и поэтому ее можно было применять без малейшего опасения к таким объектам, как катушки, конденсаторы, переменные токи и, в конце концов, радио — и световые волны. Но даже столь большой успех не гарантирует ее справедливости в других областях, например, внутри молекулы. Сохранившееся в современной физике значение классической теории электромагнетизма объясняется двумя фактами. Во-первых, специальная теория относительности не требует пересмотра классического электромагнетизма.  [11]

Классическая теория электромагнетизма имеет дело с электрическими зарядами, токами и их взаимодействиями в предположении, что все эти величины можно измерить независимо друг от друга, с неограниченной точностью. Здесь термин классическая означает просто не квантовая. Квантовые законы с их постоянной h игнорируются в классической теории электромагнетизма, так же как в обычной механике. Действительно, классическая теория была почти закончена до открытия Планка.  [12]

Магнитные свойства, обусловленные электронами, имеют двоякое происхождение. Во-первых, каждый электрон сам по себе является магнитом. С точки зрения доквантовой механики электрон можно рассматривать как маленький шарик с отрицательным зарядом, вращающийся вокруг своей оси. В соответствии с классической теорией электромагнетизма вращение любого заряда вызывает появление магнитного момента. Во-вторых, электрон движется по замкнутому пути вокруг ядра и, опять-таки по классическим представлениям, при этом должен появиться такой же магнитный момент, как при протекании электрического тока по замкнутому проводнику. Разумеется, описанную физическую картину не следует понимать буквально, поскольку она не согласуется с квантовомеханическими представлениями и не может служить основой для строгих количественных расчетов. Такая схема полезна лишь для предварительного качественного списания.  [13]

Первый из них состоит в следующем. Прежде всего заметим, что все известные силы имеют лишь несколько физических источников: либо они являются гравитационными, либо электромагнитными, либо, возможно, ядерными. Целью правильно построенной теории этих сил является дать для них соответствующие выражения, и если они будут даны в ковариантной форме, то тем самым станут ясными правила преобразования составляющих этих сил. К сожалению, однако, мы не имеем ковариантно построенных теорий для всех перечисленных сил, а что касается ядерных сил, то здесь мы вообще не имеем какой-либо теории, заслуживающей того, чтобы о ней говорить. И лишь только классическая теория электромагнетизма, можно надеяться, даст нам ковариантные выражения для сил, так как преобразования Лоренца были построены как раз так, чтобы сохранялась инвариантность электромагнитных процессов. Но этого для нас достаточно, так как правила преобразования должны быть, конечно, одинаковыми для сил любой природы. Если все силы преобразовываются по одному правилу, то утверждение точка находится в равновесии под действием двух сил должно быть справедливым во всех лоренцовых системах.  [14]

Поскольку основные положения теории относительности известны из курса механики, можно при изложении электричества и магнетизма с самого начала опираться на релятивистскую природу магнитного поля и представить электрическое и магнитное поля в их взаимной связи и единстве. Поэтому изложение материала в данной книге начинается не с электростатики, а с анализа основных понятий, связанных с зарядами, силами и электромагнитным полем. При этом определенный запас сведений о законах электромагнитных явлений, имеющийся у студента из курса физики средней школы, преобразуется в современное научное знание, а обоснование теории анализируется в свете современного состояния экспериментальных основ электромагнетизма с учетом пределов применимости используемых понятий. Это приводит иногда к необходимости выхода за пределы теории электромагнетизма в строгом смысле этого слова. Например, вопрос об экспериментальном обосновании закона Кулона для больших расстояний не может быть изложен без упоминания о его связи с нулевой массой покоя фотонов. И хотя полностью и строго этот вопрос излагается в квантовой электродинамике, его основные общие черты целесообразно изложить в классической теории электромагнетизма. Это создает у студента общее представление о проблеме и о связи изучаемого материала с материалом будущих курсов. Последнее обстоятельство имеет немаловажное методическое значите.  [15]

Страницы:      1    2

Магнетизм и электромагнетизм | Теория

Еще в глубокой древности люди заметили, что некоторые железные руды обладают свойством притягивать к себе железо, сталь, чугун и некоторые сплавы.

Это свойство получило название магнетизма, а носители этих свойств в природе — естественных магнитов. Естественные магниты имеют очень слабые силы притяжения и поэтому широкого применения в практике не нашли.

Заметив, что при соприкосновении стали, железа и некоторых сплавов с магнитом в них наводятся магнитные силы, люди научились делать из металла искусственные магниты.

Такие искусственные магниты способны сильнее, чем естественные, притягивать к себе стальные и железные предметы. Примером одного из первых искусственных магнитов может служить стрелка компаса.

Самые большие силы притяжения магнита сосредоточены на двух его концах — на так называемых полюсах магнита. В средней части магнита силы притяжения отсутствуют, и поэтому она называется нейтральной.

Рис. Расположение железных опилок по магнитным силовым линиям: 1 — лист бумаги с опилками; 2 — магнит

Если магнит подвесить на нитке за среднюю часть, то один из его полюсов повернется на север, другой — на юг. Поэтому и различают у магнита северный и южный полюса.

Пространство, в котором действуют силы магнитного притяжения, называется магнитным полем, а направления действия сил магнитного притяжения — магнитными силовыми линиями. Магнитные силовые линии отчетливо видны, если на лист бумаги равномерно насыпать железные опилки, а снизу поднести магнит.

Подобно электрическим зарядам магниты обладают свойством притягиваться один к другому или отталкиваться один от другого в зависимости от того, какими полюсами они соприкасаются. Так, например, если поднести один к другому два магнита разноименными полюсами (например, северный полюс одного магнита к южному полюсу другого), то они притянутся. Наоборот, если сблизить два магнита одноименными полюсами, магниты оттолкнутся один от другого.

Явление магнетизма может проявляться и под действием электрического тока.

Так, если по проводнику, свернутому в спираль 3, пропускать электрический ток, то такая спираль (называемая соленоидом) приобретает магнитные свойства.

Магнитное поле соленоида возрастет, если внутри него поместить железный сердечник 2. Такой соленоид называется электромагнитом, а само явление возбуждения магнитного поля электрическим током — электромагнетизмом.

Особенностью электромагнита является то, что магнитные свойства в нем проявляются лишь тогда, когда по его обмотке проходит электрический ток.

Рис. Магнитное поле соленоида: 1 — лист бумаги с опилками; 2 — железный сердечник: 3 — спираль; 4 — источник тока

Электрический ток и явление магнетизма тесно связаны между собой: с помощью электрического тока можно создать магнитное поле и, наоборот, с помощью магнитного поля можно получить электрический ток.

Так, если концы соленоида соединить с зажимами вольтметра и вводить в соленоид и выводить из него магнит или перемещать соленоид при неподвижном магните, стрелка прибора начнет отклоняться, указывая на то, что в соленоиде появился ток. Этот ток тем больше, чем большей силы магнит, чем больше витков в соленоиде и чем больше относительная скорость перемещения соленоида и магнита.

Явление возбуждения электрического тока при пересечении проводника магнитными силовыми линиями называется электромагнитной индукцией. Это явление широко используется для получения источников электрической энергии (генераторов).

Если взять несколько проводников и по одному из них пропускать ток, изменяющийся по величине или по направлению, то в соседних проводниках будет возбуждаться электродвижущая сила. Это явление называется взаимной индукцией.

Такое явление будет наблюдаться в соседних проводниках, если по одному из них то пропускать, то прерывать ток. При каждом замыкании и размыкании тока в соседних проводниках возникнет электродвижущая сила. На явлении взаимной индукции основаны устройство и действие трансформаторов переменного тока, а в электрооборудовании автомобиля — катушки зажигания с механическим прерывателем, преобразующей ток низкого напряжения генератора или аккумуляторной батареи в ток высокого напряжения для зажигания рабочей смеси в цилиндре двигателя.

При замыкании и размыкании тока электродвижущая сила возбуждается не только в соседних проводниках, но и в проводнике, в котором то пропускается, то прерывается ток. Это явление называется самоиндукцией. Направление электродвижущей силы самоиндукции при замыкании и размыкании цепи основного тока в проводнике не остается постоянным: при замыкании, когда сила основного тока увеличивается, в проводнике возбуждается электродвижущая сила направления, обратного тому, по которому движется основной ток; при размыкании, когда сила основного тока уменьшается, направление возбужденной электродвижущей силы совпадает с направлением основного тока.

Электромагнетизм Максвелла

Начала теории электромагнитного поля заложил М. Фарадей. Максвелл математически ее завершил.

Одной из самых важных идей, которую предложил Максвелл, стала идея о симметрии во взаимной зависимости электрического и магнитного полей:

Так изменяющееся со временем магнитное поле $(\frac{\partial \vec{B}}{\partial t})$ возбуждает электрическое поле, то следует ждать, что изменяющееся электрическое поле $(\frac{\partial \vec{E}}{\partial t})$ создает магнитное поле.

Открытие тока смещения $(\frac{\partial \vec{D}}{\partial t})$ дало возможность Максвеллу предложить единую теорию электромагнитных явлений. Эта теория дала объяснения разрозненным явлениям электричества и магнетизма, основываясь на единой точке зрения. Она же предсказала новые явления, наличие которых позднее подтвердилось.

Уравнения Максвелла в интегральной форме

Совокупность фундаментальных уравнений электромагнетизма – это уравнения Максвелла в неподвижных средах. В интегральной форме совокупность уравнений Максвелла записывается в виде:

$\oint {\vec{E}d\vec{l}=-\int {\frac{\partial \vec{B}}{\partial t}d\vec{S}\left( 1 \right),} }$

$\oint {\vec{H}d\vec{l}=\int {\left( \vec{j}+\frac{\partial\vec{D}}{\partial t} \right)d\vec{S}\left( 2 \right),} }$

$\oint {\vec{B}d\vec{S}=0\left( 3 \right),}$

$\oint {\vec{D}d\vec{S}=\int {\rho dV} \left( 4 \right),} $

где $\rho$ — плотность сторонних зарядов; $\ vec j$ — плотность токов проводимости.

Уравнения Максвелла в сжатой форме отображают всю систему сведений об электромагнитном поле. Смысл уравнений Максвелла:

• Первые два уравнения показывают, что переменные электрические поля возбуждают электрические поля и наоборот (1, 2).
• Поток вектора магнитной индукции через любую замкнутую поверхность всегда — ноль. Отражение отсутствия магнитных зарядов (3).
• Это известная в электростатике теорема Гаусса (4).

Уравнения Максвелла (1) и (2) означают, что электрическое и магнитное поля нельзя рассматривать как независимые. Изменение с течением времени одного поля ведет к появлению другого. Имеет смысл только совокупность электрического и магнитного полей.

В случае стационарности полей ($\vec E = const$ и $\vec B=const$) уравнения Максвелла создают две группы несвязанных уравнений:

$\oint {\vec{E}d\vec{l}} =0\, \left( 5 \right)$,

$\oint {\vec{H}d\vec{l}} =0\, \left( 6 \right),$

$\oint {\vec{B}d\vec{S}} =0\, \left( 7 \right)$,

$\oint {\vec{D}d\vec{S}} =0\, \left( 8 \right).$

Получается, что электрическое и магнитное поля независимы друг от друга.

Замечание 1

Уравнения Максвелла нельзя получить, они являются аксиомами электродинамики. Получены они обобщением экспериментальных данных. Данные постулаты имеют в электромагнетизме такое же значение, как законы Ньютона в механике.

Дифференциальная форма уравнений Максвелла

Уравнения Максвелла можно записать в локальном (дифференциальном) виде:

$\mathrm{\nabla }\times \vec{E}=-\frac{\partial \vec{B}}{\partial t}\left( 9\right)$,

$\mathrm{\nabla }\times \vec{H}=\vec{j}+\frac{\partial \vec{D}}{\partial t}\left( 10 \right),$

$\mathrm{\nabla }\vec{B}=0\, \left( 11 \right),$

$\mathrm{\nabla }\vec{D}=\rho \, \left( 12 \right)$.

Из уравнений (9)-(12) следует, что электрическое поле возникает в связи с двумя причинами:

• Источником электрического поля служат электрические заряды (сторонние и связанные). Это следует из уравнения (12).
• Поле $\vec E$ возникает всегда, когда изменяется во времени магнитное поле (закон электромагнитной индукции Фарадея).

Те же самые уравнения свидетельствуют о том, что магнитное поле порождают перемещающиеся электрические заряды (токи) или переменные электрические поля, или то и другое одновременно. Это следует из уравнений (10).

Роль уравнений Максвелла в локальном виде:

• в том, что они являются основными законами электромагнитного поля;
• при их решении могут быть найдены сами поля $\vec E$ и $\vec B$.

Уравнения Максвелла в локальной форме вместе с уравнением движения зарядов под действием силы Лоренца:

$\frac{d\vec{p}}{dt}=q\vec{E}+q\left( \vec{v}\times \vec{B} \right)\left( 13\right)$

образуют фундаментальную систему уравнений. Данная система является достаточной для характеристик всех явлений электромагнетизма, в которых отсутствуют квантовые эффекты.

Граничные условия для уравнений Максвелла

Рассматриваемые уравнения в интегральном виде имеют большую общность, чем дифференциальные, поскольку они являются справедливыми, если имеются поверхности разрыва, где свойства вещества и полей изменяются скачком.

Замечание 2

Дифференциальные уравнения Максвелла полагают, что все параметры пространства и времени изменяются непрерывно.

Достигнуть такой же общности для дифференциальных уравнений можно, если добавить к ним граничные условия. На границе веществ должны выполняться:

$D_{1n}=D_{2n}$, $B_{1n}=B_{2n}$, $E_{1\tau}=E_{2\tau}$, $H_{1\tau}=H_{2\tau}$.

Первое и последнее условия соответствуют случаям отсутствия сторонних зарядов и токов проводимости на границе раздела. Записанные выше граничные условия справедливы для постоянных и переменных полей.

Материальные уравнения

Уравнения Максвелла не содержат параметров, которые бы характеризовали индивидуальные свойства среды. Поэтому эти фундаментальные соотношения дополняют материальными уравнениями.

Материальные уравнения сложные и у них отсутствует общность и фундаментальность уравнений Максвелла. Самыми простыми они являются, если электромагнитные поля слабые и медленно изменяются в пространстве и времени. Тогда для изотропных веществ, не сегнетоэлектриков и не ферромагнетиков, материальные уравнения можно представить как:

$\vec D=\epsilon \epsilon_0 \vec E$, $\vec B=\mu \mu_0 \vec H$, $\vec j=\sigma (\vec E+\vec E’)$ (14),

где $=\epsilon, \mu, \sigma $ — известные постоянные, которые характеризуют электрические и магнитные свойства вещества. $\vec E’$ — напряженность поля сторонних сил, вызванная химическими и тепловыми процессами.

Характеристики уравнений Максвелла

Перечислим характеристики рассматриваемых нами уравнений:

1. Данные уравнения являются линейными. Они имеют только первые производные полей по времени и координатам пространства и первые степени плотности токов и плотности зарядов. Линейность уравнений связана с принципом суперпозиции.
2. В уравнения Максвелла включено уравнение непрерывности, которое отражает сохранение заряда в замкнутой системе.
3. Данные уравнения релятивистски инвариантны. Факт инвариантности уравнений Максвелла по отношению к преобразований Лоренца подтвержден множеством экспериментов.
4. Рассматриваемые нами тождества не симметричны в отношении электрических и магнитных полей. Это вызвано наличием электрических зарядов и отсутствием магнитных зарядов.

Из уравнений Максвелла следует вывод о существовании электромагнитного поля без электрических зарядов и токов. Изменение его состояния при этом имеет волновой характер. Поля этого вида называют электромагнитными волнами. В вакууме электромагнитные волны распространяются со скоростью света.

Теория Максвелла предсказала существование электромагнитных волн и дала возможность определить все их свойства.

Теория Динамическая электромагнитного поля — A Dynamical Theory of the Electromagnetic Field

« Динамическая теория электромагнитного поля » является статья Джеймса Клерка Максвелла на электромагнетизме , опубликованная в 1865 г. В статье, Максвелл получает уравнение электромагнитной волны с скоростью для света в близком согласии с измерениями , сделанных с помощью эксперимента, и делает вывод , что свет представляет собой электромагнитную волну.

публикация

После стандартной процедуры в течение времени, документ был впервые прочитал в Королевском обществе по 8 декабря 1864 года, будучи послан Maxwell Обществу 27 октября. Затем он прошел рецензирование , направляется Уильям Томпсон (позднее лорд Кельвин ) 24 декабря 1864. Затем он был отправлен в Джордж Габриэль Стокс , физических наук Секретарь Общества 23 марта 1865. Он был одобрен для публикации в Philosophical Transactions Королевского общества 15 июня 1865 года, Комитетом докладов ( по существу общества руководящего совета) и отправляется на принтер следующий день (16 июня) по. В течение этого периода, Philosophical Transactions был опубликован лишь в переплете один раз в год, и был бы готов к Юбилейному дню Общества 30 ноября (точная дата не записывается). Тем не менее, принтер будет подготовлен и доставлен Максвелл оттисков, для автора распространения , как он хотел, вскоре после того, как 16 июня.

Исходные уравнения Максвелла

В третьей части статьи, которая озаглавлена «Общие уравнения электромагнитного поля» Максвелл сформулировал двадцать уравнений , которые должны были стать известно как уравнения Максвелла , пока этот термин не стал применяться вместо Векторизованного набора из четырех уравнений , выбранный в 1884 году, что что все появились в «О физических силовых линиях».

Версии Хевисайда уравнений Максвелла различны в силу того , что они написаны в современной векторной форме . На самом деле они содержат только один из первоначальных восьми-уравнения «G» ( закон Гаусса ). Еще один из четырех уравнений Хевисайд является объединением закона Максвелла полных токов (уравнение «А») с циркуляционным законом Ампера (уравнение «C»). Это слияние, который сам Максвелл фактически первоначально сделал в уравнении (112) , в « О физических линиях сил », это то , который изменяет циркуляционный закон Ампера включить Максвелл ток смещения .

Для его оригинального текста на силу, см : О физических линиях сил  — через Викитек .

Для его оригинального текста на динамике, см : динамическая теория электромагнитного поля  — через Викитек .

Уравнения Хевисайда

Восемнадцать из двадцати исходных уравнений Максвелла может быть векторизованы на шесть уравнения, помеченный (А) до (F) ниже, каждый из которых представляет собой группу из трех исходных уравнений в компонентной форме . Девятнадцатый и двадцатые компонентных уравнений Максвелла выглядят как (G) и (H) ниже, что в общей сложности восьми векторных уравнений. Они перечислены ниже в первоначальном порядке Максвелла, обозначаемые буквами , что Максвелл присвоенных им в своей работе 1864 года.

(А) Закон полных токов

JTоTзнак равно{\ Displaystyle \ mathbf {j} _ {TOT}} = J{\ Displaystyle \, \ mathbf {j}} +∂D∂T{\ Displaystyle + \, {\ гидроразрыва {\ парциальное \ mathbf {D}} {\ парциальное т}}}

(В) Определение магнитного потенциала

μЧАСзнак равно∇×A{\ Displaystyle \ му \ mathbf {H} = \ набла \ раз \ mathbf {A}}

(С) теорема о циркуляции магнитного поля

∇×ЧАСзнак равноJTоT{\ Displaystyle \ набла \ раз \ mathbf {H} = \ mathbf {j} _ {TOT}}

(D) Силы Лоренца и закон индукции Фарадея

езнак равноμ(v×ЧАС)-∂A∂T-∇φ{\ Displaystyle \ mathbf {F} = \ мю (\ mathbf {v} \ раз \ mathbf {H}) — {\ гидроразрыв {\ парциального \ mathbf {A}} {\ парциальный т}} — \ наб \ Phi}

(Е) Уравнение электрической упругости

езнак равно1εD{\ Displaystyle \ mathbf {F} = {\ гидроразрыва {1} {\ эпсилон}} \ mathbf {D}}

(F) Закон Ома

езнак равно1σJ{\ Displaystyle \ mathbf {F} = {\ гидроразрыва {1} {\ Sigma}} \ mathbf {j}}

(Г) Закон Гаусса

∇⋅Dзнак равноρ{\ Displaystyle \ наб \ CDOT \ mathbf {D} = \ Rho}

(ЧАС) Уравнение непрерывности заряда

∇⋅Jзнак равно-∂ρ∂T{\ Displaystyle \ наб \ CDOT \ mathbf {j} = — {\ гидроразрыв {\ парциального \ Rho} {\ парциального т}} \,},

нотация

ЧАС{\ Displaystyle \ mathbf {H}}это магнитное поле , который Максвелл назвал « напряженность магнитного поля ».

J{\ Displaystyle \ mathbf {j}}это электрический ток , плотность (с того суммарная плотность тока в том числе тока смещения ).JTоT{\ Displaystyle \ mathbf {j} _ {TOT}}

D{\ Displaystyle \ mathbf {D}}это поле смещений ( так называемый « электрическое смещение » Максвелл).

ρ{\ Displaystyle \ Rho}является свободным заряд плотность (называется « количество свободного электричества » Максвелл).

A{\ Displaystyle \ mathbf {A}}это магнитный потенциал ( так называемый « угловой импульсом » Максвелл).

е{\ Displaystyle \ mathbf {F}}это сила на единицу заряда ( так называемый « электродвижущая сила » Максвелл, чтобы не путать с скалярной величиной , которую теперь называют электродвижущей силой , см ниже ).

φ{\ Displaystyle \ Phi}это электрический потенциал (который Максвелл также называет « электрическим потенциалом »).

σ{\ Displaystyle \ сигма}является электропроводность (Максвелл называется обратной проводимостью « удельное сопротивление », то , что теперь называют сопротивлением ).

∇{\ Displaystyle \ набла}вектор оператор — дель .

Разъяснения

Максвелл не считал полностью общие материалы; его исходная композиция используется линейной , изотропный , бездисперсионные среды с диэлектрической проницаемостью е и проницаемостью мкм , хотя он также обсуждал возможность анизотропных материалов.

Ряд Гаусса ( ∇⋅  B = 0 ) не входит в приведенный выше список, но непосредственно следует из уравнения  (В) , принимая расходимости (поскольку дивергенция ротора равна нулю).

Подставляя (A) в (С) дает знакомую дифференциальную форму закона Максвелла-Ампера .

Уравнение (D) неявно содержит закон для силы Лоренца и дифференциальную форму закона индукции Фарадея . Для статического магнитного поля, равна нулю, а электрическое поле Е становится консервативным и задается -∇ ф , так что (D) сводится к ∂A/∂T{\ Displaystyle \ парциальное \ mathbf {А} / \ частичная т}

езнак равноЕ+v×В{\ Displaystyle \ mathbf {F} = \ mathbf {Е} + \ mathbf {v} \ раз \ mathbf {B}, \,},

Это просто сила закон Лоренца на основе за единицей заряда — хотя уравнение Максвелла  (D) впервые появилось в уравнении ( 77 ) в « О физических линиях сил » в 1861 году, 34 лет до того, Лоренц получили свой силовой закон, в настоящее время , как правило , представляется в качестве дополнения к четырем « уравнений Максвелла ». Термин кросс-продукт в законе силы Лоренца является источником так называемой двигательной ЭДС в электрических генераторов (см также Moving магнит и проблема проводника ). Там , где нет движения через магнитное поле — например, в трансформаторах — мы можем опустить член кросс-продукта, а сила на единицу заряда ( так называемый ф ) сводится к электрическому полю Е , так что уравнение Максвелла  (D) сводится к

Езнак равно-∂A∂T-∇φ{\ Displaystyle \ mathbf {E} = — {\ гидроразрыв {\ парциального \ mathbf {A}} {\ парциальный т}} — \ наб \ Phi \,},

Принимая завитки, отметив , что завиток градиент равен нулю, получаем

∇×Езнак равно-∇×∂A∂Tзнак равно-∂∂T(∇×A)знак равно-∂В∂T,{\ Displaystyle \ набли \ раза \ mathbf {E} \, = \, — \ набла \ раз {\ гидроразрыв {\ парциального \ mathbf {A}} {\ парциального т}} \, = \, — {\ гидроразрыв { \ парциального} {\ парциального т}} {\ большое (} \ набла \ раза \ mathbf {A} {\ большой)} \, = \, — {\ гидроразрыв {\ парциального \ mathbf {B}} {\ парциальный т }} \ ,,}

которая является дифференциальной формой закона Фарадея . Таким образом, три члена в правой части уравнения  (D) может быть описан, слева направо, как термин, двигательным срок трансформатора и консервативный срок.

При выводе уравнения электромагнитной волны , Максвелл рассматривает ситуацию только из покоя среды, и , соответственно , падает термин кросс-продукта. Но он до сих пор работает из уравнения  (D) , в отличие от современных учебников , которые , как правило, работают с законом Фарадея (см ниже ).

В конститутивные уравнения (E) и (F) в настоящее время , как правило , написаны в системе покоя среды как D  = е Е  и J  = сг Е  .

Уравнение Максвелла (G) , если смотреть в изоляции , как напечатано в 1864 г. бумаги, сначала кажется, что р + ∇⋅  D = 0 . Однако, если проследить признаки через предыдущие два триплета уравнений, мы видим, что , как представляется, компоненты D фактически компоненты  — D . Обозначения , используемые в более позднем Максвелла Трактат по электричеству и магнетизму отличается, и избегает обманчивое впечатление. ‍

Максвелл — электромагнитные волны света

Отец электромагнитной теории

В части VI документа «динамической теории электромагнитного поля», с подзаголовком «Электромагнитная теория света», Максвелл использует поправку к циркуляционного закона Ампера сделано в третьей части его 1862 бумага, «О физических линиях сил», которая определяется а ток смещения , чтобы вывести уравнение электромагнитной волны .

Он получил волновое уравнение со скоростью в близком согласии с экспериментальными определениями скорости света. Он отметил,

Совпадение результатов, кажется, чтобы показать, что свет и магнетизм являются поражения одного и того же вещества, что и свет представляет собой электромагнитные помехи распространяются через поле в соответствии с электромагнитными законами.

вывод Максвелла уравнения электромагнитной волны был заменен в современной физике гораздо менее громоздкий способом, который сочетает в себе исправленную версию закона Ампера циркуляционного с законом Фарадея электромагнитной индукции.

Современные методы уравнения

Чтобы получить уравнение электромагнитной волны в вакууме, используя современный метод, мы начинаем с современной формой «Хевисайда» уравнений Максвелла. Используя (единица СИ) в вакууме, эти уравнения

∇⋅Езнак равно0{\ Displaystyle \ наб \ CDOT \ mathbf {E} = 0} ∇×Езнак равно-μо∂ЧАС∂T{\ Displaystyle \ наб \ раза \ mathbf {E} = — \ му _ {о} {\ гидроразрыва {\ парциального \ mathbf {H}} {\ парциальный т}}} ∇⋅ЧАСзнак равно0{\ Displaystyle \ наб \ CDOT \ mathbf {H} = 0} ∇×ЧАСзнак равноεо∂Е∂T{\ Displaystyle \ набла \ раз \ mathbf {H} = \ varepsilon _ {о} {\ гидроразрыва {\ парциальное \ mathbf {E}} {\ парциальное т}}}

Если мы возьмем завиток локона уравнений получим

∇×∇×Езнак равно-μо∂∂T∇×ЧАСзнак равно-μоεо∂2Е∂T2{\ Displaystyle \ набла \ раз \ набла \ раз \ mathbf {E} = — \ мю _ {O} {\ гидроразрыва {\ частичной} {\ парциальное T}} \ Nabla \ раз \ mathbf {H} = — \ му _ {O} \ varepsilon _ {о} {\ гидроразрыва {\ парциальное ^ {2} \ mathbf {E}} {\ парциальное т ^ {2}}}}

∇×∇×ЧАСзнак равноεо∂∂T∇×Езнак равно-μоεо∂2ЧАС∂T2{\ Displaystyle \ наб \ раза \ набли \ раза \ mathbf {H} = \ varepsilon _ {о} {\ гидроразрыва {\ парциальное} {\ парциального т}} \ набли \ раза \ mathbf {E} = — \ му _ {O} \ varepsilon _ {о} {\ гидроразрыва {\ парциальное ^ {2} \ mathbf {H}} {\ парциальное т ^ {2}}}}

Если мы отмечаем вектор идентичности

∇×(∇×В)знак равно∇(∇⋅В)-∇2В{\ Displaystyle \ набла \ раз \ влево (\ набла \ раз \ mathbf {V}, \ справа) = \ набла \ влево (\ набла \ CDOT \ mathbf {V}, \ справа) — \ набла ^ {2} \ mathbf { V}}

где любой вектор функция пространства, мы возвращаем волновые уравнения В{\ Displaystyle \ mathbf {V}}

∂2Е∂T2 — с2⋅∇2Е  знак равно  0{\ Displaystyle {\ парциальное ^ {2} \ mathbf {E} \ над \ частичной т ^ {2}} \ — \ с ^ {2} \ CDOT \ набла ^ {2} \ mathbf {E} \ \ = \ \ 0}

∂2ЧАС∂T2 — с2⋅∇2ЧАС  знак равно  0{\ Displaystyle {\ парциальное ^ {2} \ mathbf {H} \ над \ частичной т ^ {2}} \ — \ с ^ {2} \ CDOT \ набла ^ {2} \ mathbf {H} \ \ = \ \ 0}

где

сзнак равно1μоεознак равно2.99792458×108{\ Displaystyle с = {1 \ над {\ SQRT {\ му _ {O} \ varepsilon _ {O}}}} = 2.99792458 \ раз 10 ^ {8}} метров в секунду

является скорость света в свободном пространстве.

Наследство и влияние

Из данной статьи и связанных с ними работ Максвелла, товарищ физик Ричард Фейнман сказал: «Из длинного зрения этой истории человечества — видели, скажем, 10000 лет теперь — может быть мало сомнений в том, что наиболее значимым событием 19 — го века будет можно судить как открытие Максвелла законов электромагнетизма «.

Альберт Эйнштейн использовал уравнения Максвелла в качестве отправной точки для своей специальной теории относительности , представленной в электродинамике движущихся тел , бумаги производится во время его 1905 ANNUS Mirabilis . В нем говорится:

«Одни и те же законы электродинамики и оптики будут действительны для всех координатных систем, для которых уравнения механики справедливы»

а также

«Каждый луч света движется в„покоящейся“системе координат с определенной скоростью с, будет ли луч, испускаемых стационарным или движущимся телом».

Уравнения Максвелла могут быть также получены путем расширения общей теории относительности на пять физических размеров .

Смотрите также

Рекомендации

дальнейшее чтение

• Максвелл, Джеймс С .; Торранс, Томас Ф. (март 1996). Теория Динамическая электромагнитного поля . Eugene, OR: Випф и сток. ISBN  1-57910-015-5 .
• Нивен, WD (1952). Научные доклады Джеймса Клерка Максвелла, Том 1. Нью-Йорк: Довер.
• Джонсон, Кевин (май 2002). «Электромагнитное поле» . Джеймс Клерк Максвелл — Великий неизвестный . Проверено 7 сентября 2009 .
• Tokunaga, Kiyohisa (2002). «Часть 2, Глава V — Уравнения Максвелла» . Общий интеграл электромагнитных канонических действий . Архивировано из оригинала на 2010-11-10 . Проверено 7 сентября 2009 .
• Katz, Рэнди Х. (22 февраля 1997). « „ Посмотрите Ма, без проводов“: Маркони и изобретение радио» . История коммуникационных инфраструктур . Проверено 7 сентября 2009 .

Электромагнитное поле. Теория Максвелла. Видеоурок. Физика 11 Класс

Тема: Электромагнитная индукция

Урок: Электромагнитное поле. Теория Максвелла

Рассмотрим приведенную схему и случай, когда подключён источник постоянного тока (рис 1).

 

        

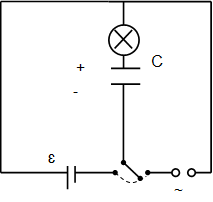
 Рис. 1. Схема

К основным элементам цепи относят лампочку, обычный проводник, конденсатор – при замыкании цепи на обкладках конденсатора возникает напряжение равное напряжению на зажимах источника.

Конденсатор представляет собой две параллельные металлические пластины, между которыми находится диэлектрик. Когда подают разность потенциалов на обкладки конденсатора, они заряжаются, и внутри диэлектрика возникает электростатическое поле. При этом тока внутри диэлектрика при небольших напряжениях быть не может.

При замене постоянного тока на переменный свойства диэлектриков в конденсаторе не меняются, и в диэлектрике по-прежнему практически отсутствуют свободные заряды, но мы наблюдаем то, что лампочка горит. Возникает вопрос: что же происходит? Возникающий в данном случае ток Максвелл назвал током смещения.

Мы знаем о том, что при помещении токопроводящего контура в переменное магнитное поле, в нём возникает ЭДС индукции.  Это обусловлено тем, что возникает вихревое электрическое поле.

 

А что если подобная же картина происходит при изменении электрического поля?

Гипотеза Максвелла: изменяющееся во времени электрическое поле вызывает появление вихревого магнитного поля.

Согласно этой гипотезе, магнитное поле после замыкания цепи образуется не только вследствие протекания тока в проводнике, но и вследствие наличия переменного электрического поля между обкладками конденсатора. Это переменное электрическое поле порождает магнитное поле в той же области между обкладками конденсатора. Причём, это магнитное поле точно такое же, как будто бы между обкладками конденсатора протекал ток, равный току во всей остальной цепи. В основе теории лежат четыре уравнения Максвелла, из которых следует, что изменение электрического и магнитного полей в пространстве и во времени происходят согласованным образом. Так, электрическое и магнитное поле образуют единое целое. Электромагнитные волны распространяются в пространстве в виде поперечных волн с конечной скоростью.

Указанная взаимосвязь между переменным магнитным и переменным электрическим полем говорит о том, что они не могут существовать обособленно друг от друга. Возникает вопрос: касается ли это утверждение статических полей (электростатического, создаваемого постоянными зарядами, и магнитостатического, создаваемого постоянными токами)? Такая взаимосвязь существует и для статических полей. Но важно понимать, что эти поля могут существовать по отношению к определённой системе отсчёта.

Покоящийся заряд создаёт в пространстве электростатическое поле (рис. 2) относительно определённой системы отсчёта. Относительно других систем отсчёта он может двигаться и, следовательно, в этих системах этот же заряд будет создавать магнитное поле.

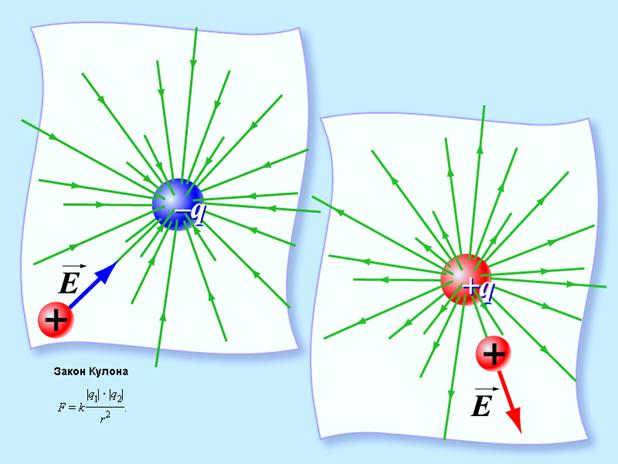
Рис. 2. Закон Кулона (Источник)

Электромагнитное поле – это особая форма существования материи, которая создаётся заряжёнными телами и проявляется по действию на заряжённые тела. В ходе этого действия их энергетическое состояние может изменяться, следовательно, электромагнитное поле обладает энергией.

1. Исследование явлений электромагнитной индукции приводит к выводу о том, что переменное магнитное поле порождает вокруг себя вихревое электрическое.

2. Анализируя прохождение переменного тока через цепи, содержащие диэлектрики, Максвелл пришёл к выводу, что переменное электрическое поле может порождать магнитное поле за счёт тока смещения.

3. Электрическое и магнитное поле – компоненты единого электромагнитного поля, которое распространяется в пространстве в виде поперечных волн с конечной скоростью.        

 

Список рекомендованной литературы

1. Буховцев Б.Б., Мякишев Г.Я, Чаругин В.М. Физика 11 кл.: Учебн. для общеобразоват. учреждений. – 17-е изд., преобраз. и доп. – М.: Просвещение, 2008.
2. Генденштейн Л.Э., Дик Ю.И., Физика 11. – М.: Мнемозина.
3. Тихомирова С.А., Яровский Б.М., Физика 11. – М.: Мнемозина.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Znate.ru (Источник).
2. Слово (Источник).
3. Физика (Источник).

 

Рекомендованное домашнее задание

1. Какое электрическое поле образуется при изменении магнитного поля?
2. Каким током объясняется свечение лампочки в цепи переменного тока с конденсатором?
3. Какое из уравнений Максвелла указывает зависимость магнитной индукции от тока проводимости и смещения?