Теорема Гаусса — Википедия

Теорема Гаусса (закон Гаусса) — один из основных законов электродинамики, входит в систему уравнений Максвелла. Выражает связь (а именно равенство с точностью до постоянного коэффициента) между потоком напряжённости электрического поля сквозь замкнутую поверхность произвольной формы и алгебраической суммой зарядов, расположенных внутри объёма, ограниченного этой поверхностью. Применяется отдельно для вычисления электростатических полей.

Аналогичная теорема, также входящая в число уравнений Максвелла, существует и для магнитного поля (см. ниже).

Также теорема Гаусса верна для любых полей, для которых верен закон Кулона или его аналог (например, для ньютоновской гравитации). При этом она является, как принято считать, более фундаментальной, так как позволяет в частности вывести степень расстояния^[1] в законе Кулона «из первых принципов», а не постулировать её (или не находить эмпирически).

В этом можно видеть фундаментальное значение теоремы Гаусса (закона Гаусса) в теоретической физике.

Существуют аналоги (обобщения) теоремы Гаусса и для более сложных полевых теорий, чем электродинамика.

Теорема Гаусса для напряжённости электрического поля в вакууме[править | править код]

Общая формулировка: Поток вектора напряжённости электрического поля через любую произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхности электрическому заряду.

СГС	СИ
ΦE=4πQ,{\displaystyle \Phi _{\mathbf {E} }=4\pi Q,}	ΦE=Qε0,{\displaystyle \Phi _{\mathbf {E} }={\frac {Q}{\varepsilon _{0}}},}

где

Данное выражение представляет собой теорему Гаусса в интегральной форме.

• Замечание: поток вектора напряжённости через поверхность не зависит от распределения заряда (расположения зарядов) внутри поверхности.

В дифференциальной форме теорема Гаусса выражается следующим образом:

СГС	СИ
divE≡∇⋅E=4πρ,{\displaystyle \mathrm {div} \,\mathbf {E} \equiv \nabla \cdot \mathbf {E} =4\pi \rho ,}	divE≡∇⋅E=ρε0.{\displaystyle \mathrm {div} \,\mathbf {E} \equiv \nabla \cdot \mathbf {E} ={\frac {\rho }{\varepsilon _{0}}}.}

Здесь ρ{\displaystyle \rho } — объёмная плотность заряда (в случае присутствия среды — суммарная плотность свободных и связанных зарядов), а ∇{\displaystyle \nabla } — оператор набла.

• Теорема Гаусса может быть доказана как теорема в электростатике исходя из закона Кулона (см. ниже). Формула, однако, также верна в электродинамике, хотя в ней она чаще всего не выступает в качестве доказываемой теоремы, а выступает в качестве постулируемого уравнения (в этом смысле и контексте её логичнее называть законом Гаусса^[2]).

Теорема Гаусса для электрической индукции (электрического смещения)[править | править код]

Для поля в диэлектрической среде электростатическая теорема Гаусса может быть записана ещё и иначе (альтернативным образом) — через поток вектора электрического смещения (электрической индукции). При этом формулировка теоремы выглядит следующим образом: поток вектора электрического смещения через замкнутую поверхность пропорционален заключённому внутри этой поверхности свободному электрическому заряду:

СГС	СИ
ΦD≡∮S⁡DdS=4πQ,{\displaystyle \Phi _{\mathbf {D} }\equiv \oint \limits _{S}\mathbf {D} \,\mathrm {d} \mathbf {S} =4\pi Q,}	ΦD≡∮S⁡DdS=Q,{\displaystyle \Phi _{\mathbf {D} }\equiv \oint \limits _{S}\mathbf {D} \,\mathrm {d} \mathbf {S} =Q,}

Важный комментарий

Важно заметить, что Q в правой части этого уравнения обозначено не то же самое, что в фундаментальной формулировке ΦE≡∮S⁡EdS=4πQ,{\displaystyle \Phi _{\mathbf {E} }\equiv \oint \limits _{S}\mathbf {E} \,\mathrm {d} \mathbf {S} =4\pi Q,} приведенной выше

[3], в начале статьи. Последняя часто называется «формулировкой для вакуума», однако это название чисто условное, она равно применимо и к случаю диэлектрической среды, только под Q здесь необходимо понимать сумму свободного заряда, находящегося внутри поверхности и поляризационного (индуцированного, связанного) заряда диэлектрика, то есть в уравнении для E надо было бы писать в правой части другую букву:

QΣ=Q+Qb,{\displaystyle Q_{\Sigma }=Q+Q_{b},}

где

• Qb=∮S⁡PdS{\displaystyle Q_{b}=\oint \limits _{S}\mathbf {P} \,\mathrm {d} \mathbf {S} } — связанный заряд внутри поверхности ^[4],
• P{\displaystyle \mathbf {P} } — вектор поляризации диэлектрика.

Мы же здесь применили одну и ту же букву в правой части просто потому, что такая запись встречается чаще всего, а поскольку та и другая форма уравнения редко используются совместно, так что путаницы не возникает.

Для случая вакуума (отсутствия диэлектрической среды) то и другое уравнения просто совпадают, поскольку тогда Q_b=0, в то время как D=E (в системе единиц СИ — пропорциональны.

В дифференциальной форме:

СГС	СИ
divD≡∇⋅D=4πρ,{\displaystyle \mathrm {div} \,\mathbf {D} \equiv \nabla \cdot \mathbf {D} =4\pi \rho ,}	divD≡∇⋅D=ρ.{\displaystyle \mathrm {div} \,\mathbf {D} \equiv \nabla \cdot \mathbf {D} =\rho .}

Важный комментарий

• Важно понимать, что Q и ρ в этом параграфе обозначены другие величины, чем в предыдущем: величина свободных зарядов и плотность свободных зарядов, то есть зарядов за исключением индуцируемых при поляризации диэлектрической среды (тогда как в предыдущем параграфе имелись в виду полный заряд и полная плотность заряда (подробнее — см. комментрарий в этом параграфе чуть выше). Совпадают эти величины только для случая вакуума (отсутствия диэлектрической среды), когда и сами уравнения этого параграфа переходят по сути в уравнения предыдущего параграфа.

Теорема Гаусса для магнитной индукции[править | править код]

Поток вектора магнитной индукции через любую замкнутую поверхность равен нулю:

ΦB≡∮S⁡B⋅dS=0,{\displaystyle \Phi _{\mathbf {B} }\equiv \oint \limits _{S}\mathbf {B} \cdot \mathrm {d} \mathbf {S} =0,}

или в дифференциальной форме

∇⋅B=0.{\displaystyle \nabla \cdot \mathbf {B} =0.}

Это эквивалентно тому, что в природе не существует «магнитных зарядов» (монополей), которые создавали бы магнитное поле, как электрические заряды создают электрическое поле^[5]. Иными словами, теорема Гаусса для магнитной индукции показывает, что магнитное поле является (полностью)

вихревым.

Теорема Гаусса для ньютоновской гравитации[править | править код]

Для напряжённости поля ньютоновской гравитации (ускорения свободного падения) теорема Гаусса практически совпадает с таковой в электростатике, за исключением только констант (впрочем, всё равно зависящих от произвольного выбора системы единиц) и, главное, знака^[6]:

Φg≡∮S⁡g⋅dS=−4πGM,{\displaystyle \Phi _{\mathbf {g} }\equiv \oint \limits _{S}\mathbf {g} \cdot \mathrm {d} \mathbf {S} =-4\pi GM,}

∇⋅g=−4πGρ,{\displaystyle \nabla \cdot \mathbf {g} =-4\pi G\rho ,}

где g — напряжённость гравитационного поля, M — гравитационный заряд (то есть масса) внутри поверхности

S, ρ — плотность массы, G — ньютоновская константа.

В терминах силовых линий[править | править код]

Теорема Гаусса может быть интерпретирована в терминах силовых линий^[7] поля так:

1. Поток поля через поверхность есть^[8] количество силовых линий, пронизывающих эту поверхность. При этом учитывается направление — силовые линии, пронизывающие поверхность в обратном направлении считаются со знаком минус.
2. Силовые линии начинаются или кончаются только на зарядах (начинаются на положительных, кончаются на отрицательных), или могут ещё уходить на бесконечность. Количество силовых линий, исходящих из заряда (начинающихся в нём) равно^[9] величине этого заряда (это определение заряда в данной модели). Для отрицательных зарядов всё так же, только заряд равен минус количеству входящих в него (кончающихся на нём) линий.
3. Исходя из этих двух положений, теорема Гаусса представляется очевидной в формулировке: количество линий, исходящих из замкнутой поверхности равно суммарному количеству зарядов внутри неё — то есть количеству линий, появившихся внутри неё. Конечно же, подразумевается учёт знаков, в частности, линия, начавшаяся внутри поверхности на положительном заряде может закончиться на отрицательном заряде также внутри неё (если такой там есть), тогда она не даст вклада в поток через эту поверхность, так как или вообще до неё не дойдёт, или выйдет, а потом войдёт обратно (или, вообще говоря, пересечёт поверхность чётное количество раз поровну в прямом и противоположном направлении), что при суммировании с учётом знака даст вклад в поток ноль. То же можно сказать о линиях, начавшихся и закончившихся вне данной поверхности — по той же причине они также дадут нулевой вклад в поток через неё.

В терминах течения несжимаемой жидкости[править | править код]

Теорема Гаусса верна для поля скоростей несжимаемой жидкости. Этот факт позволяет использовать течение несжимаемой жидкости в качестве аналогии (формальной модели), позволяющей прояснить её смысл и наглядно представить её математическое содержание.^[10]

Полезно здесь заметить, что даже сама терминология векторного анализа, используемая в электродинамике (и в частности при формулировке теоремы Гаусса) сформировалась почти целиком под влиянием этой аналогии. Достаточно указать на такие термины, как

источник поля (применительно к заряду) или поток через поверхность, которые полностью и точно соответствуют в рассматриваемой аналогии понятиям:

• источник жидкости (в смысле места, где жидкость возникает и количественной меры её возникновения — объём, возникающий в единицу времени),
• поток (в смысле количества жидкости, проходящей через поверхность в единицу времени).

В терминах течения несжимаемой жидкости теорема Гаусса формулируется так: Поток жидкости, исходящий из замкнутой поверхности, равен сумме источников, находящихся внутри этой поверхности. Или, более формально: Поток вектора скорости жидкости через замкнутую поверхность равен сумме источников, находящихся внутри этой поверхности. (В сущности, это интегральный вариант уравнения непрерывности для несжимаемой жидкости, выражающего сохранение массы жидкости с учётом постоянства её плотности).

В этой формальной аналогии напряжённость поля заменяется на скорость течения жидкости, а заряд — на источник жидкости (отрицательный заряд — на «отрицательный источник» — «сток»).

Теорема Гаусса как определение заряда[править | править код]

Теорема Гаусса^[11] может рассматриваться как определение (величины) заряда.

Так, для точечного заряда очевидно, что поток напряжённости поля через любую поверхность равен потоку через маленькую (бесконечно маленькую) сферу, окружающую этот заряд. Тогда последний (с точностью, быть может, до постоянного коэффициента, в зависимости от нашего произвольного выбора единиц измерения) может быть выбран в качестве определения величины этого заряда.

Вблизи заряда (бесконечно близко к нему) его собственное поле, очевидно, даёт подавляющий вклад в поток через бесконечно маленькую сферу (поскольку поле безгранично растёт с уменьшением расстояния). Значит, остальными полями (порождаемыми другими зарядами) можно пренебречь. Тогда можно увидеть, что данное определение согласуется с обычным (через закон Кулона).

В современной физике обычно принято считать, что определение через закон Гаусса более фундаментально (как и сам закон Гаусса по сравнению с законом Кулона — см. ниже), хотя с определённой точки зрения они просто эквивалентны.

Теорема Гаусса и закон Кулона тесно связаны, как формально, так и по физическому содержанию. В некотором смысле можно утверждать, что теорема Гаусса является интегральной формулировкой закона Кулона или наоборот, что закон Кулона является следствием теоремы (закона) Гаусса.

Что из них считать постулатом, а что следствием — зависит от того, какую аксиоматизацию для электродинамики (или электростатики, если ограничиваться ею) мы выбираем; формально тот или другой выбор практически^[12] равноправны, а в случае электростатики это полностью так. Таким образом, выбор того или другого в качестве основания построения теории — вопрос нашего произвольного выбора.

Впрочем, аксиоматизация через закон Гаусса имеет то преимущество, что в законе Гаусса не содержится никаких произвольных параметров (таких, как степень расстояния −2 в законе Кулона), степень расстояния в законе Кулона возникает при этом автоматически из размерности пространства.

Однако, следует сделать оговорку. Если наивно считать, что закон Кулона и теорема Гаусса эквивалентны, то можно рассуждать так: из теоремы Гаусса следует закон Кулона, из закона Кулона следуют уравнения Максвелла для случая электростатики, т.о. второе уравнение Максвелла (о равенстве нулю ротора электрического поля) следует из теоремы Гаусса и является излишним. На самом деле, при выводе закона Кулона из теоремы Гаусса (см. ниже) мы дополнительно используем сферическую симметрию поля точечного заряда, а также нам необходимо ввести принцип суперпозиции, в то время как уравнения Максвелла являются самодостаточными.

Исторически первым был эмпирически открыт закон Кулона. В этом (историческом) смысле теорема Гаусса является его следствием. Именно в связи с этим она называется теоремой, так как первоначально появилась как теорема.

Непосредственно ниже показано, как закон Кулона и закон Гаусса могут быть получены в рамках электростатики^[13] друг из друга.

Закон Кулона как следствие закона Гаусса[править | править код]

Исходим из теоремы Гаусса, записав её в единицах системы СИ^[14], «Поток ΦE,S{\displaystyle \Phi _{E,S}} вектора напряжённости E{\displaystyle E} через поверхность S{\displaystyle S} пропорционален заряду, заключённому в эту поверхность»:

ΦE,S=Qε0.{\displaystyle \Phi _{E,S}={\frac {Q}{\varepsilon _{0}}}.}

Для вывода Закона Кулона, будем рассматривать единственный точечный заряд в пределах замкнутой поверхности S, таким образом Q здесь будет величиной этого заряда.

Рассчитаем тот же поток прямым интегрированием по поверхности. Замечаем, что задача имеет сферическую симметрию относительно положения заряда. Из этого делаем вывод, что электрическое поле будет направлено прямо от заряда, а его величина будет одинакова для любых точек, расположенных на одинаковом расстоянии от заряда. Из этого следует, что суммарный поток будет проще всего сосчитать, если в качестве поверхности S выбрать сферу с центром в заряде. Действительно, напряжённость поля E тогда будет всюду ортогональна dS, а абсолютная величина вектора E (будем обозначать её E) будет одинакова везде на этой сфере, и её можно будет вынести за знак интеграла. Итак:

ΦE,S=∮S⁡E⋅dS=∮S⁡EdS=E∮S⁡dS=ES.{\displaystyle \Phi _{E,S}=\oint \limits _{S}\mathbf {E} \cdot \mathbf {dS} =\oint \limits _{S}EdS=E\oint \limits _{S}dS=ES.}

Имеем:

{ΦE,S=Qε0ΦE,S=ES{\displaystyle {\begin{cases}\Phi _{E,S}={\frac {Q}{\varepsilon _{0}}}\\\Phi _{E,S}=ES\end{cases}}}

Отсюда:

ES=Qε0.{\displaystyle ES={\frac {Q}{\varepsilon _{0}}}.}

Осталось подставить сюда для площади сферы S=4πr2{\displaystyle S=4\pi r^{2}} и разрешить уравнение относительно E.

Тогда получаем:

E=14πε0Qr2,{\displaystyle E={\frac {1}{4\pi \varepsilon _{0}}}{\frac {Q}{r^{2}}},}

то есть — закон Кулона.

Теорема Гаусса как следствие закона Кулона[править | править код]

Элементарное доказательство[править | править код]

Элементарное доказательство строится на двух шагах: доказательстве теоремы для случая одного точечного заряда с использованием геометрических соображений, а затем применении принципа суперпозиции, вследствие которого теорема оказывается доказана для произвольного количества точечных зарядов (а значит и в общем случае).

Исходим из закона Кулона:

E(r)=qr2er{\displaystyle \mathbf {E} (\mathbf {r} )={\frac {q}{r^{2}}}\mathbf {e} _{r}},

где er{\displaystyle \mathbf {e} _{r}} — единичный вектор в направлении радиус-вектора r{\displaystyle \mathbf {r} }, проведённого из заряда (куда мы поместили начало координат) в точку, где измеряется напряжённость поля E(r){\displaystyle \mathbf {E} (\mathbf {r} )}, r — модуль вектора r, то есть расстояние от заряда до этой точки. (В этом параграфе будем пользоваться только системой СГС, то есть кулоновская константа равна единице. Для перехода в систему СИ достаточно просто добавить множитель. Так же и переход к любой другой системе единиц будет отличаться только кулоновской константой.)

Для одного точечного заряда внутри поверхности[править | править код]

Обозначим поверхность, через которую надо вычислить поток E, буквой S. Полагаем, что наш заряд q находится внутри этой поверхности.

Окружим заряд ещё одной поверхностью — сферой S₀ с центром в заряде и радиусом R₀ столь малым, что она целиком находится внутри поверхности S. Вычислим поток через S₀:

ΦS0=4πR02E.{\displaystyle \Phi _{S_{0}}=4\pi R_{0}^{2}E.}

Выберем малый (бесконечно малый, малый не только по величине, но и «компактно», то есть так, чтобы он, скажем, мог быть покрыт круговым конусом также малого телесного угла), телесный угол ω{\displaystyle \omega } с вершиной в заряде.

Докажем, что поток ΦS,ω {\displaystyle \Phi _{S,\omega }\ } через площадку поверхности S, вырезаемую этим телесным углом ω{\displaystyle \omega }, равен потоку ΦS0,ω{\displaystyle \Phi _{S_{0},\omega }} через площадку S0,ω{\displaystyle S_{0,\omega }}, вырезаемую им же из сферы S₀. Для этого покажем, что

1. ΦS,ω =ΦS⊥,ω {\displaystyle \Phi _{S,\omega }\ =\Phi _{S_{\perp ,\omega }}\ } — поток через площадку Sω{\displaystyle S_{\omega }}, вырезаемую телесным углом ω{\displaystyle \omega } из поверхности S, равен потоку через площадку S⊥,ω,{\displaystyle S{\perp ,\omega },} вырезаемую телесным углом ω{\displaystyle \omega } из любой плоскости, перпендикулярной лучам, лежащим внутри ω{\displaystyle \omega }, которые при бесконечно малом телесном угле почти параллельны, отличаясь по направлению бесконечно мало, значит площадка будет одновременно перпендикулярна (говоря строже — почти перпендикулярна) всем им одновременно.

2. ΦS⊥,ω=ΦS0,ω.{\displaystyle \Phi _{S\perp ,\omega }=\Phi _{S_{0},\omega }.} — в пределах телесного угла ω{\displaystyle \omega }, поток через площадку, перпендикулярную лучам, равен потоку через площадку сферы S0{\displaystyle S_{0}}.

Первое доказывается замечанием о том, что поток dΦ=E⋅dS{\displaystyle d\Phi =\mathbf {E} \cdot \mathbf {dS} } через малую площадку dS может быть представлен как dΦ=E(dS)⊥{\displaystyle d\Phi =E(dS)_{\perp }}, где (dS)⊥{\displaystyle (dS)_{\perp }} — проекция вектора dS на направление вектора E, то есть площадь проекции данной площадки на плоскость, перпендикулярную E. А применительно к нашему случаю это и означает равенство ΦS⊥,ω{\displaystyle \Phi _{S\perp ,\omega }} и ΦS,ω{\displaystyle \Phi _{S,\omega }}.

Второе видно из соображений подобия и закона Кулона (обозначив r расстояние от заряда до пересечения ω{\displaystyle \omega } c S, видим, что отношение площадей S⊥,ω{\displaystyle S{\perp ,\omega }} и S0,ω{\displaystyle S_{0,\omega }} равно r2/R02{\displaystyle r^{2}/R_{0}^{2}}, в то время как E(r)/E(R0)=R02/r2{\displaystyle E(r)/E(R_{0})=R_{0}^{2}/r^{2}}, то есть обратному числу, в результате чего их произведения одинаковы, а это и есть потоки ΦS⊥,ω{\displaystyle \Phi _{S\perp ,\omega }} и ΦS0,ω{\displaystyle \Phi _{S_{0},\omega }}, равенство которых надо было доказать.

В случае, если ω{\displaystyle \omega } пересекает S неоднократно (что возможно, если последняя достаточно сложна), все эти рассуждения, если говорить коротко, повторяются столько раз, сколько пересечений имеется, и доказывается равенство по абсолютной величине потока через каждый такой элемент поверхности S. А учитывая знаки при сложении (они, очевидно, чередуются; всего же количество пересечений должно оказаться нечётным), итоговый ответ оказывается тем же, что и для случая единственного пересечения.

А поскольку равенство этих потоков выполняется для любого малого ω{\displaystyle \omega }, то есть для каждого соответственного элемента S и S₀, между которыми устанавливается однозначное соответствие, причём таким образом можно разбить всю сферу S₀ без остатка на такие элементы, то равенство верно и для потоков через полные поверхности (которые суть просто суммы потоков через описанные элементы поверхностей S и S₀). (Поскольку поверхность S замкнутая, каждому элементу на сфере находится соответствующий элемент на S — или нечётное количество элементов, как было описано выше, которые можно объединить, так как учтён поток через их все).

Итак, доказали, что для одного заряда q внутри замкнутой поверхности S поток через неё

ΦS=ΦS0=4πR02E.{\displaystyle \Phi _{S}=\Phi _{S_{0}}=4\pi R_{0}^{2}E.}

Для одного точечного заряда вне поверхности[править | править код]

Совершенно аналогичные рассуждения, проведённые для случая, когда q находится вне области, ограничиваемой поверхностью S, с учётом знака при подсчёте потока через каждую площадку, дают в результате поток ноль. (малый телесный угол теперь пересечёт S чётное число раз, потоки будут равны по абсолютной величине, но противоположны по знаку)^[15].

Суммирование элементарных потоков производится также аналогично сделанному в пункте 1, как и их вычисление.

Итак, для одного заряда вне замкнутой поверхности поток через неё нуль.

Для любого количества зарядов[править |

основные понятия, формулы, законы. Основные законы физики, которые должен знать человек

Интересоваться окружающим миром и закономерностями его функционирования и развития природно и правильно. Именно поэтому разумно обращать свое внимание на естественные науки, например, физику, которая объясняет саму сущность формирования и развития Вселенной. Основные физические законы несложно понять. Уже в очень юном возрасте школа знакомит детей с этими принципами.

Для многих начинается эта наука с учебника «Физика (7 класс)». Основные понятия и законы механики и термодинамики открываются перед школьниками, они знакомятся с ядром главных физических закономерностей. Но должно ли знание ограничиваться школьной скамьей? Какие физические законы должен знать каждый человек? Об этом и пойдет речь далее в статье.

Наука физика

Многие нюансы описываемой науки знакомы всем с раннего детства. А связано это с тем, что, в сущности, физика представляет собой одну из областей естествознания. Она повествует о законах природы, действие которых оказывает влияние на жизнь каждого, а во многом даже обеспечивает ее, об особенностях материи, ее структуре и закономерностях движения.

Термин «физика» был впервые зафиксирован Аристотелем еще в четвертом веке до нашей эры. Изначально он являлся синонимом понятия «философия». Ведь обе науки имели единую цель — правильным образом объяснить все механизмы функционирования Вселенной. Но уже в шестнадцатом веке вследствие научной революции физика стала самостоятельной.

Общий закон

Некоторые основные законы физики применяются в разнообразных отраслях науки. Кроме них существуют такие, которые принято считать общими для всей природы. Речь идет о законе сохранения и превращения энергии.

Он подразумевает, что энергия каждой замкнутой системы при протекании в ней любых явлений непременно сохраняется. Тем не менее она способна трансформироваться в другую форму и эффективно менять свое количественное содержание в различных частях названной системы. В то же время в незамкнутой системе энергия уменьшается при условии увеличения энергии любых тел и полей, которые вступают во взаимодействие с ней.

Помимо приведенного общего принципа, содержит физика основные понятия, формулы, законы, которые необходимы для толкования процессов, происходящих в окружающем мире. Их исследование может стать невероятно увлекательным занятием. Поэтому в этой статье будут рассмотрены основные законы физики кратко, а чтобы разобраться в них глубже, важно уделить им полноценное внимание.

Механика

Открывают юным ученым многие основные законы физики 7-9 классы школы, где более полно изучается такая отрасль науки, как механика. Ее базовые принципы описаны ниже.

1. Закон относительности Галилея (также его называют механической закономерностью относительности, или базисом классической механики). Суть принципа заключается в том, что в аналогичных условиях механические процессы в любых инерциальных системах отсчета проходят совершенно идентично.
2. Закон Гука. Его суть в том, что чем большим является воздействие на упругое тело (пружину, стержень, консоль, балку) со стороны, тем большей оказывается его деформация.

Законы Ньютона (представляют собой базис классической механики):

1. Принцип инерции сообщает, что любое тело способно состоять в покое или двигаться равномерно и прямолинейно только в том случае, если никакие другие тела никаким образом на него не воздействуют, либо же если они каким-либо образом компенсируют действие друг друга. Чтобы изменить скорость движения, на тело необходимо воздействовать с какой-либо силой, и, конечно, результат воздействия одинаковой силы на разные по величине тела будет тоже различаться.
2. Главная закономерность динамики утверждает, что чем больше равнодействующая сил, которые в текущий момент воздействуют на данное тело, тем больше полученное им ускорение. И, соответственно, чем больше масса тела, тем этот показатель меньше.
3. Третий закон Ньютона сообщает, что любые два тела всегда взаимодействуют друг с другом по идентичной схеме: их силы имеют одну природу, являются эквивалентными по величине и обязательно имеют противоположное направление вдоль прямой, которая соединяет эти тела.
4. Принцип относительности утверждает, что все явления, протекающие при одних и тех же условиях в инерциальных системах отсчета, проходят абсолютно идентичным образом.

Термодинамика

Школьный учебник, открывающий ученикам основные законы («Физика. 7 класс»), знакомит их и с основами термодинамики. Ее принципы мы коротко рассмотрим далее.

Законы термодинамики, являющиеся базовыми в данной отрасли науки, имеют общий характер и не связаны с деталями строения конкретного вещества на уровне атомов. Кстати, эти принципы важны не только для физики, но и для химии, биологии, аэрокосмической техники и т. д.

Например, в названной отрасли существует не поддающееся логическому определению правило, что в замкнутой системе, внешние условия для которой неизменны, со временем устанавливается равновесное состояние. И процессы, продолжающиеся в ней, неизменно компенсируют друг друга.

Еще одно правило термодинамики подтверждает стремление системы, которая состоит из колоссального числа частиц, характеризующихся хаотическим движением, к самостоятельному переходу из менее вероятных для системы состояний в более вероятные.

А закон Гей-Люссака (его также называют газовым законом) утверждает, что для газа определенной массы в условиях стабильного давления результат деления его объема на абсолютную температуру непременно становится величиной постоянной.

Еще одно важное правило этой отрасли — первый закон термодинамики, который также принято называть принципом сохранения и превращения энергии для термодинамической системы. Согласно ему, любое количество теплоты, которое было сообщено системе, будет израсходовано исключительно на метаморфозу ее внутренней энергии и совершение ею работы по отношению к любым действующим внешним силам. Именно эта закономерность и стала базисом для формирования схемы работы тепловых машин.

Другая газовая закономерность — это закон Шарля. Он гласит, что чем больше давление определенной массы идеального газа в условиях сохранения постоянного объема, тем больше его температура.

Электричество

Открывает юным ученым интересные основные законы физики 10 класс школы. В это время изучаются главные принципы природы и закономерности действия электрического тока, а также другие нюансы.

Закон Ампера, например, утверждает, что проводники, соединенные параллельно, по которым течет ток в одинаковом направлении, неизбежно притягиваются, а в случае противоположного направления тока, соответственно, отталкиваются. Порой такое же название используют для физического закона, который определяет силу, действующую в существующем магнитном поле на небольшой участок проводника, в данный момент проводящего ток. Ее так и называют – сила Ампера. Это открытие было сделано ученым в первой половине девятнадцатого века (а именно в 1820 г.).

Закон сохранения заряда является одним из базовых принципов природы. Он гласит, что алгебраическая сумма всех электрических зарядов, возникающих в любой электрически изолированной системе, всегда сохраняется (становится постоянной). Несмотря на это, названный принцип не исключает и возникновения в таких системах новых заряженных частиц в результате протекания некоторых процессов. Тем не менее общий электрический заряд всех новообразованных частиц непременно должен равняться нулю.

Закон Кулона является одним из основных в электростатике. Он выражает принцип силы взаимодействия между неподвижными точечными зарядами и поясняет количественное исчисление расстояния между ними. Закон Кулона позволяет обосновать базовые принципы электродинамики экспериментальным образом. Он гласит, что неподвижные точечные заряды непременно взаимодействуют между собой с силой, которая тем выше, чем больше произведение их величин и, соответственно, тем меньше, чем меньше квадрат расстояния между рассматриваемыми зарядами и диэлектрическая проницаемость среды, в которой и происходит описываемое взаимодействие.

Закон Ома является одним из базовых принципов электричества. Он гласит, что чем больше сила постоянного электрического тока, действующего на определенном участке цепи, тем больше напряжение на ее концах.

«Правилом правой руки» называют принцип, который позволяет определить направление в проводнике тока, движущегося в условиях воздействия магнитного поля определенным образом. Для этого необходимо расположить кисть правой руки так, чтобы линии магнитной индукции образно касались раскрытой ладони, а большой палец вытянуть по направлению движения проводника. В таком случае остальные четыре выпрямленных пальца определят направление движения индукционного тока.

Также этот принцип помогает выяснить точное расположение линий магнитной индукции прямолинейного проводника, проводящего ток в данный момент. Это происходит так: поместите большой палец правой руки таким образом, чтобы он указывал направление тока, а остальными четырьмя пальцами образно обхватите проводник. Расположение этих пальцев и продемонстрирует точное направление линий магнитной индукции.

Принцип электромагнитной индукции представляет собой закономерность, которая объясняет процесс работы трансформаторов, генераторов, электродвигателей. Данный закон состоит в следующем: в замкнутом контуре генерируемая электродвижущая сила индукции тем больше, чем больше скорость изменения магнитного потока.

Оптика

Отрасль «Оптика» также отражает часть школьной программы (основные законы физики: 7-9 классы). Поэтому эти принципы не так сложны для понимания, как может показаться на первый взгляд. Их изучение приносит с собой не просто дополнительные знания, но лучшее понимание окружающей действительности. Основные законы физики, которые можно отнести к области изучения оптики, следующие:

1. Принцип Гюйнеса. Он представляет собой метод, который позволяет эффективно определить в каждую конкретную долю секунды точное положение фронта волны. Суть его состоит в следующем: все точки, которые оказываются на пути у фронта волны в определенную долю секунды, в сущности, сами по себе становятся источниками сферических волн (вторичных), в то время как размещение фронта волны в ту же долю секунду является идентичным поверхности, которая огибает все сферические волны (вторичные). Данный принцип используется с целью объяснения существующих законов, связанных с преломлением света и его отражением.
2. Принцип Гюйгенса-Френеля отражает эффективный метод разрешения вопросов, связанных с распространением волн. Он помогать объяснить элементарные задачи, связанные с дифракцией света.
3. Закон отражения волн. Применяется в равной степени и для отражения в зеркале. Его суть состоит в том, что как ниспадающий луч, так и тот, который был отражен, а также перпендикуляр, построенный из точки падения луча, располагаются в единой плоскости. Важно также помнить, что при этом угол, под которым падает луч, всегда абсолютно равен углу преломления.
4. Принцип преломления света. Это изменение траектории движения электромагнитной волны (света) в момент движения из одной однородной среды в другую, которая значительно отличается от первой по ряду показателей преломления. Скорость распространения света в них различна.
5. Закон прямолинейного распространения света. По своей сути он является законом, относящимся к области геометрической оптики, и заключается в следующем: в любой однородной среде (вне зависимости от ее природы) свет распространяется строго прямолинейно, по кратчайшему расстоянию. Данный закон просто и доступно объясняет образование тени.

Атомная и ядерная физика

Основные законы квантовой физики, а также основы атомной и ядерной физики изучаются в старших классах средней школы и высших учебных заведениях.

Так, постулаты Бора представляют собой ряд базовых гипотез, которые стали основой теории. Ее суть состоит в том, что любая атомная система может оставаться устойчивой исключительно в стационарных состояниях. Любое излучение или поглощение энергии атомом непременно происходит с использованием принципа, суть которого следующая: излучение, связанное с транспортацией, становится монохроматическим.

Эти постулаты относятся к стандартной школьной программе, изучающей основные законы физики (11 класс). Их знание является обязательным для выпускника.

Основные законы физики, которые должен знать человек

Некоторые физические принципы, хоть и относятся к одной из отраслей данной науки, тем не менее носят общий характер и должны быть известны всем. Перечислим основные законы физики, которые должен знать человек:

• Закон Архимеда (относится к областям гидро-, а также аэростатики). Он подразумевает, что на любое тело, которое было погружено в газообразное вещество или в жидкость, действует своего рода выталкивающая сила, которая непременно направлена вертикально вверх. Эта сила всегда численно равна весу вытесненной телом жидкости или газа.
• Другая формулировка этого закона следующая: тело, погруженное в газ или жидкость, непременно теряет в весе столько же, сколько составила масса жидкости или газа, в который оно было погружено. Этот закон и стал базовым постулатом теории плавания тел.
• Закон всемирного тяготения (открыт Ньютоном). Его суть состоит в том, что абсолютно все тела неизбежно притягиваются друг к другу с силой, которая тем больше, чем больше произведение масс данных тел и, соответственно, тем меньше, чем меньше квадрат расстояния между ними.

Это и есть 3 основных закона физики, которые должен знать каждый, желающий разобраться в механизме функционирования окружающего мира и особенностях протекания процессов, происходящих в нем. Понять принцип их действия достаточно просто.

Ценность подобных знаний

Основные законы физики обязаны быть в багаже знаний человека, независимо от его возраста и рода деятельности. Они отражают механизм существования всей сегодняшней действительности, и, в сущности, являются единственной константой в непрерывно изменяющемся мире.

Основные законы, понятия физики открывают новые возможности для изучения окружающего мира. Их знание помогает понимать механизм существования Вселенной и движения всех космических тел. Оно превращает нас не в просто соглядатаев ежедневных событий и процессов, а позволяет осознавать их. Когда человек ясно понимает основные законы физики, то есть все происходящие вокруг него процессы, он получает возможность управлять ими наиболее эффективным образом, совершая открытия и делая тем самым свою жизнь более комфортной.

Итоги

Некоторые вынуждены углубленно изучать основные законы физики для ЕГЭ, другие — по роду деятельности, а некоторые — из научного любопытства. Независимо от целей изучения данной науки, пользу полученных знаний трудно переоценить. Нет ничего более удовлетворяющего, чем понимание основных механизмов и закономерностей существования окружающего мира.

Не оставайтесь равнодушными — развивайтесь!

Нерешённые проблемы современной физики — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 23 декабря 2018; проверки требуют 38 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 23 декабря 2018; проверки требуют 38 правок.

Эту статью следует сделать более понятной широкому кругу читателей. Пожалуйста, попытайтесь изложить эту статью так, чтобы она была понятна неспециалисту. Вам могут помочь советы в этом эссе. Подробности могут быть на странице обсуждения.

Ниже приведён список нерешённых пробле́м совреме́нной фи́зики^[1]. Некоторые из этих проблем носят теоретический характер. Это означает, что существующие теории оказываются неспособными объяснить определённые наблюдаемые явления или экспериментальные результаты. Другие проблемы являются экспериментальными, а это означает, что имеются трудности в создании эксперимента по проверке предлагаемой теории или по более подробному исследованию какого-либо явления.

Неразрешенные проблемы (сортировка по полю применения)[править | править код]

Общая физика / квантовая физика[править | править код]

Достоверность этого раздела статьи поставлена под сомнение. Необходимо проверить точность фактов, изложенных в этом разделе. На странице обсуждения могут быть пояснения.

Следующие проблемы являются либо фундаментальными теоретическими проблемами, либо теоретическими идеями, для которых отсутствуют экспериментальные данные. Некоторые из этих проблем тесно взаимосвязаны. Например, дополнительные измерения или суперсимметрия могут решить проблему иерархии. Считается, что полная теория квантовой гравитации способна ответить на бо́льшую часть из перечисленных вопросов (кроме проблемы острова стабильности).

Квантовая гравитация, космология, общая теория относительности[править | править код]

Распад метастабильного вакуума

Почему предсказанная масса квантового вакуума мало влияет на расширение Вселенной?

Квантовая гравитация

Можно ли квантовую механику и общую теорию относительности объединить в единую самосогласованную теорию (возможно, это квантовая теория поля)?^[3] Является ли пространство-время непрерывным или оно дискретно? Будет ли самосогласованная теория использовать гипотетический гравитон или она будет полностью продуктом дискретной структуры пространства-времени (как в петлевой квантовой гравитации)? Существуют ли отклонения от предсказаний ОТО для очень малых или очень больших масштабов или в других чрезвычайных обстоятельствах, которые вытекают из теории квантовой гравитации?

Чёрные дыры, исчезновение информации в чёрной дыре, излучение Хокинга

Производят ли чёрные дыры тепловое излучение, как это предсказывает теория? Содержит ли это излучение информацию об их внутренней структуре, как это предполагает дуальность тяготение-калибровочная инвариантность, или нет, как следует из оригинального расчета Хокинга? Если нет и чёрные дыры могут непрерывно испаряться, то что происходит с информацией, хранящейся в них (квантовая механика не предусматривает уничтожение информации)? Или излучение в какой-то момент остановится, когда от чёрной дыры мало что останется?^[4][5]. Есть ли какой-либо другой способ исследования их внутренней структуры, если такая структура вообще существует? Выполняется ли закон сохранения барионного заряда внутри чёрной дыры?^[6] Неизвестно доказательство принципа космической цензуры, а также точная формулировка условий, при которых он выполняется^[7]. Отсутствует полная и законченная теория магнитосферы черных дыр^[8]. Неизвестна точная формула для вычисления числа различных состояний системы, коллапс которой приводит к возникновению чёрной дыры с заданными массой, моментом количества движения и зарядом^[9]. Неизвестно доказательство в общем случае «теоремы об отсутствии волос» у чёрной дыры^[10].

Размерность пространства-времени

Существуют ли в природе дополнительные измерения пространства-времени, кроме известных нам четырёх?^[1] Если да, то каково их количество? Является ли размерность «3+1» (или более высокая) априорным свойством Вселенной или она является результатом других физических процессов, как предполагает, например, теория причинной динамической триангуляции? Можем ли мы экспериментально «наблюдать» высшие пространственные измерения? Справедлив ли голографический принцип, по которому физика нашего «3+1»-мерного пространства-времени эквивалентна физике на гиперповерхности с размерностью «2+1»?^[11]

Инфляционная модель Вселенной

Верна ли теория космической инфляции, и если да, то каковы подробные детали этой стадии? Что представляет собой гипотетическое инфлатонное поле, ответственное за рост инфляции? Если инфляция произошла в одной точке, является ли это началом самоподдерживающегося процесса за счёт инфляции квантово-механических колебаний, который будет продолжаться в совершенно другом, удалённом от этой точки месте?

Мультивселенная

Существуют ли физические причины существования других вселенных, которые принципиально ненаблюдаемы? Например: существуют ли квантовомеханические «альтернативные истории» или «множество миров»? Существуют ли «другие» вселенные с физическими законами, являющимися результатом альтернативных способов нарушения очевидной симметрии физических сил при высоких энергиях, расположенные, возможно, невероятно далеко из-за космической инфляции? Могли ли другие вселенные влиять на нашу, вызвав, например, аномалии в распределении температуры реликтового излучения?^[12] Является ли оправданным использование антропного принципа для решения глобальных космологических проблем?

Принцип космической цензуры и гипотеза защиты хронологии

Могут ли сингулярности, не скрывающиеся за горизонтом событий и известные как «голые сингулярности», возникать из реалистичных начальных условий, или же можно доказать какую-то версию «гипотезы космической цензуры» Роджера Пенроуза, в которой предполагается, что это невозможно?^[13] В последнее время появились факты^[14] в пользу несостоятельности гипотезы космической цензуры, а значит, голые сингулярности должны встречаться гораздо чаще, чем только лишь как экстремальные решения уравнений Керра — Ньюмена, тем не менее неоспоримых доказательств этому представлено ещё не было. Аналогично, будут ли замкнутые времениподобные кривые, которые возникают в некоторых решениях уравнений общей теории относительности (и которые предполагают возможность путешествия во времени в обратном направлении), исключены теорией квантовой гравитации, которая объединяет общую теорию относительности с квантовой механикой, как предполагает «гипотеза защиты хронологии» Стивена Хокинга?

Локальность

Существуют ли нелокальные явления в квантовой физике? Если существуют, не имеют ли они ограничения в передаче информации, или: может ли энергия и материя также двигаться по нелокальному пути? При каких условиях наблюдаются нелокальные явления? Что влечёт наличие или отсутствие нелокальных явлений для фундаментальной структуры пространства-времени? Как это связано с квантовой сцепленностью? Как это истолковать с позиций правильной интерпретации фундаментальной природы квантовой физики?

Будущее Вселенной^[15]

Движется ли Вселенная по направлению к Большому замерзанию, Большому разрыву, Большому сжатию или Большому отскоку? Является ли наша Вселенная частью бесконечно повторяющейся циклической модели?

Физика высоких энергий, физика элементарных частиц[править | править код]

Моделирование процесса обнаружения бозонов Хиггса на детекторе КМС в CERN

Нерешённые вопросы физики элементарных частиц делятся на два класса. Первый — из чего всё состоит и почему оно построено так, как построено, а также поиск возможных новых частиц и взаимодействий. Второй — как из уже известных частиц образуются уже известные явления^[16].

Механизм Хиггса^[16]

Сколько бозонов Хиггса существует? Описываются ли они в рамках Стандартной модели?^[17]

Проблема иерархии

Почему гравитация является такой слабой силой? Она становится большой только в планковском масштабе, для частиц с энергией порядка 10¹⁹ГэВ, что гораздо выше электрослабого масштаба (в физике низких энергий доминирующей является энергия в 100 ГэВ). Почему эти масштабы так сильно отличаются друг от друга? Что мешает величинам электрослабого масштаба, таким как масса бозона Хиггса, получать квантовые поправки на масштабах порядка планковских? Являются ли решением этой проблемы суперсимметрия, дополнительные измерения или просто антропная тонкая настройка?

Магнитный монополь

Существовали ли частицы — носители «магнитного заряда» в какие-либо прошлые эпохи с более высокими энергиями? Если да, то есть ли какие-либо на сегодняшний день? (Поль Дирак показал, что наличие некоторых типов магнитных монополей могло бы объяснить квантование заряда.^[18])^[19]

Распад протона и Великое объединение

Как можно объединить три различных квантово-механических фундаментальных взаимодействия квантовой теории поля? Почему легчайший барион, являющийся протоном, абсолютно стабилен? Если же протон нестабилен, то каков его период полураспада?

Суперсимметрия^[16]

Реализована ли суперсимметрия пространства в природе? Если да, то каков механизм нарушения суперсимметрии? Стабилизирует ли суперсимметрия электрослабый масштаб, предотвращая высокие квантовые поправки? Состоит ли тёмная материя из лёгких суперсимметричных частиц?

Поколения материи

Существует ли более трёх поколений кварков и лептонов? Связано ли число поколений с размерностью пространства? Почему вообще существуют поколения? Существует ли теория, которая могла бы объяснить наличие массы у некоторых кварков и лептонов в отдельных поколениях на основании первых принципов (теория взаимодействия Юкавы)?

Фундаментальная симметрия и нейтрино

Какова природа нейтрино, какова их масса и как они формировали эволюцию Вселенной? Почему сейчас во Вселенной обнаруживается вещества больше, чем антивещества?^[20] Какие невидимые силы присутствовали на заре Вселенной, но исчезли из поля зрения в процессе развития Вселенной?

Квантовая теория поля

Совместимы ли принципы релятивистской локальной квантовой теории поля с существованием нетривиальной матрицы рассеяния?^[21]

Безмассовые частицы

Почему безмассовые частицы без спина не существуют в природе?^[22]

Ядерная физика[править | править код]

Квантовая хромодинамика

Каковы фазовые состояния сильно взаимодействующей материи и какую роль они играют в космосе? Каково внутреннее устройство нуклонов? Какие свойства сильно взаимодействующей материи предсказывает КХД? Что управляет переходом кварков и глюонов в пи-мезоны и нуклоны? Какова роль глюонов и глюонного взаимодействия в нуклонах и ядрах? Что определяет ключевые особенности КХД и каково их отношение к природе гравитации и пространства-времени?

Атомное ядро и ядерная астрофизика

Какова природа ядерных сил, которая связывает протоны и нейтроны в стабильные ядра и редкие изотопы? Какова причина соединения простых частиц в сложные ядра? Какова природа нейтронных звёзд и плотной ядерной материи? Каково происхождение элементов в космосе? Что такое ядерные реакции, которые движут звёзды и приводят к их взрывам?

Остров стабильности

Какое самое тяжёлое из стабильных или метастабильных ядер может существовать?^[23]

Сверхтекучесть[править | править код]

• Не создана последовательная квантовая гидродинамическая теория сверхтекучей жидкости, объединяющая двухжидкостную теорию Ландау и теорию, учитывающую градиенты макроскопической волновой функции^[24].
• Макроскопическая теория сверхтекучести не учитывает взаимодействие между наблюдателем и квантовой системой. Существенно ли оно для сверхтекучести?^[25]
• Не решена задача учёта взаимодействия частиц при квантовом подходе^[26].
• Можно ли наблюдать релятивистские эффекты в сверхтекучих системах?^[27]
• Существующая формулировка квантовой механики не позволяет получить описание сверхтекучей системы из первых принципов. Масса сверхтекучих систем велика, а длина волны де Бройля сравнима с размерами измерительного прибора. Приведёт ли явление сверхтекучести к новому пониманию старого парадокса квантовой механики о редукции волнового пакета в процессе измерения?^[28]

Другие проблемы[править | править код]

Туннельный эффект — квантовая механика показывает, что электроны могут преодолеть потенциальный барьер, что подтверждается результатами экспериментов.
Классическая механика, наоборот, предсказывает, что это невозможно.

Квантовая механика и принцип соответствия (иногда называемый квантовым хаосом)

Есть ли предпочтительные интерпретации квантовой механики? Как квантовое описание реальности, которое включает в себя такие элементы, как квантовая суперпозиция состояний и коллапс волновой функции или квантовая декогеренция, приводят к реальности, которую мы видим? Сформулировать то же самое можно с помощью проблемы измерения: что представляет собой «измерение», которое заставляет волновую функцию сваливаться в определённое состояние?

Физическая информация

Существуют ли физические феномены, такие как чёрные дыры или коллапс волновой функции, которые безвозвратно уничтожают информацию о своих предшествующих состояниях?

Теория всего («Теории Великого объединения»)

Существует ли теория, которая объясняет значения всех фундаментальных физических констант?^[29] Существует ли теория, которая объясняет, почему калибровочная инвариантность стандартной модели такая, как она есть, почему наблюдаемое пространство-время имеет 3 + 1 измерения, и поэтому законы физики таковы, как они есть? Меняются ли с течением времени «фундаментальные физические константы»? Являются ли какие-нибудь частицы в стандартной модели физики элементарных частиц на самом деле состоящими из других частиц, связанных настолько сильно, что их невозможно наблюдать при современных экспериментальных энергиях? Существуют ли фундаментальные частицы, которые ещё не наблюдались, и если да, то какие они и каковы их свойства? Существуют ли ненаблюдаемые фундаментальные силы, которые предполагает теория, объясняющие другие нерешённые проблемы физики?

Калибровочная инвариантность

Существуют ли реально неабелевы калибровочные теории со щелью в спектре масс?

CP-симметрия

Почему не сохраняется CP-симметрия? Почему она сохраняется в большинстве наблюдаемых процессов?^[1]

Физика полупроводников

Квантовая теория полупроводников не может точно вычислить ни одной постоянной полупроводника^[30].

Квантовая физика

Неизвестно точное решение уравнения Шредингера для многоэлектронных атомов^[31].

При решении задачи о рассеянии двух пучков на одном препятствии сечение рассеяния получается бесконечно большим^[32].

Фейнманиум: Что будет происходить с химическим элементом, атомный номер которого окажется выше 137, вследствие чего 1s¹-электрону придётся двигаться со скоростью, превышающей скорость света (согласно модели атома Бора)? Является ли «Фейнманиум» последним химическим элементом, способным существовать физически? Проблема может проявиться приблизительно на 137 элементе, где расширение дистрибуции заряда ядра достигает финальной точки. Смотрите статью Расширенная периодическая таблица элементов и секцию Relativistic effects.

Статистическая физика

Отсутствует систематическая теория необратимых процессов, дающая возможность проводить количественные расчёты для любого заданного физического процесса^{[33][34][35][36]}.

Квантовая электродинамика

Существуют ли гравитационные эффекты, вызываемые нулевыми колебаниями электромагнитного поля?^[37]

Неизвестно, как при вычислениях квантовой электродинамики в области высоких частот одновременно выполнить условия конечности результата, релятивистской инвариантности и суммы всех альтернативных вероятностей, равной единице^[38].

Можно ли сопоставить нулевой энергии электромагнитного поля какую-нибудь наблюдаемую физическую величину?^[39]

Биофизика

Отсутствует количественная теория для кинетики конформационной релаксации белковых макромолекул и их комплексов^[40].

Отсутствует законченная теория электронного переноса в биологических структурах^[41].

Сверхпроводимость

Невозможно теоретически предсказать, зная структуру и состав вещества, перейдёт ли оно в сверхпроводящее состояние с понижением температуры^[42]. Возможно ли получить в стабильном состоянии материал-сверхпроводник при комнатной температуре?^[43]

Физика твёрдого тела

Невозможно даже приближённо рассчитать намагниченность, теплоёмкость, электропроводность и другие макроскопические величины, исходя из известного строения кристалла, электронных оболочек атомов в кристалле и других параметров микромира для сильно магнитных веществ (ферромагнетиков, антиферромагнетиков и ферримагнетиков)^[44].

Отсутствует количественная микроскопическая теория ацентрических твердых тел, учитывающая тип, концентрацию и характер распределения примесей и дефектов структуры^[45].

Эмпирические явления без чёткого научного объяснения[править | править код]

Космология и астрономия[править | править код]

Существование Вселенной

Каково происхождение материи, энергии и пространства-времени, сформировавших Вселенную/Мультивселенную?

Барионная асимметрия Вселенной

Почему в наблюдаемой Вселенной существует гораздо больше материи, чем антиматерии?^[23]

Проблема космологической постоянной

Почему нулевая энергия вакуума не приводит к большому значению космологической постоянной? Что отменяет эту зависимость?

Оценочное распределение тёмной материи и тёмной энергии во вселенной. 74 % — тёмная энергия, 22 % тёмная материя, 3,6 % межгалактический газ, 0,4 % — наблюдаемые звезды.

Тёмная энергия^[1]

Что является причиной наблюдаемого ускоренного расширения Вселенной (фаза де Ситтера)? Почему плотность энергии тёмной компоненты энергии — величина того же порядка, что и плотность вещества в настоящее время, тогда как эти два феномена с течением времени развивались совершенно по-разному? Может быть, это потому, что мы ведём наблюдения в нужное время? Является ли тёмная энергия космологической константой, или же она является динамическим полем — некой квинтэссенцией, такой как фантомная энергия?

Тёмная материя^[1]

Что такое тёмная материя?^[46][23] Связана ли она с суперсимметрией? Связан ли феномен тёмной материи с той или иной формой материи, или это на самом деле является расширением гравитации?

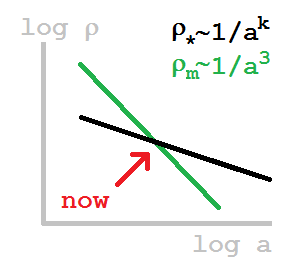Логарифмичесие графики показывают плотность тёмной энергии ρ∗{\displaystyle \rho _{*}} и плотность тёмной материи ρm{\displaystyle \rho _{m}} по горизонтали отложен временной фактор a{\displaystyle a}. Две прямые линии пересекаются в текущей эпохе^[47].

Тёмный поток

Что является причиной согласованного движения большой группы скоплений галактик к одной точке Вселенной?^[48]

Энтропия (направление времени)

Почему Вселенная имела такую низкую энтропию в прошлом, приведшую в результате к различию между прошлым и будущим и второму закону термодинамики?^[49]

Проблема горизонта^[20]

Почему удалённая от нас часть Вселенной так однородна, тогда как теория Большого взрыва предсказывает измеримую анизотропию небесной сферы больше, чем она наблюдается? Возможным подходом к решению являются гипотезы инфляции и переменной скорости света.

Изотропия реликтового излучения

Некоторые общие особенности микроволнового излучения неба на расстояниях более 13 миллиардов световых лет, по всей видимости, говорят о наличии как движения, так и ориентации Солнечной системы. Является ли это следствием систематических ошибок обработки, загрязнением результатов локальными эффектами или необъяснимым нарушением принципа Коперника?

Форма Вселенной

Что такое 3-многообразие сопутствующего пространства, то есть сопутствующее пространственное сечение Вселенной, неофициально называемое «формой» Вселенной? Ни её кривизна, ни топология в настоящее время неизвестны, хотя кривизна скорее всего «близка» к нулю на наблюдаемых масштабах. Гипотеза космической инфляции предполагает, что форма Вселенной может быть неизмеримой, но с 2003 года команда Жана-Пьера Люмине и другие группы полагают, что Вселенная может иметь форму додекаэдрического пространства Пуанкаре. Является ли форма Вселенной неизмеримой, представляет собой пространство Пуанкаре или имеет другое 3-многообразие?

Термодинамика Вселенной

Почему в наблюдаемой части Вселенной в настоящее время отсутствует термодинамическое равновесие?^[50]

Планетология

Почему с 1930-х годов снижается размер Большого красного пятна на Юпитере?^[51]

Физика высоких энергий, физика элементарных частиц[править | править код]

Нарушение симметрии электрослабого взаимодействия

Каков механизм, ответственный за нарушение электрослабой калибровочной симметрии, дающий массу W и Z бозонам? Является ли он простым механизмом Хиггса Стандартной модели^[52] или же природа использует сильную динамику при нарушении электрослабой симметрии, как это предлагается в теории техниколор?

Масса нейтрино

Какой механизм отвечает за генерацию массы нейтрино? Является ли нейтрино античастицей самой себе? Или это и есть античастица, которая просто не может соединиться и аннигилировать с нормальной частицей из-за её нестабильного состояния?^[53]

Кварки 

Почему ровно три цвета?^[1] Почему ровно три поколения кварков? Случайно ли совпадение числа цветов и числа поколений? Случайно ли совпадение этого числа с размерностью пространства в нашем мире? Откуда берётся такой разброс в массах кварков? Из чего состоят кварки?^[23] Как кварки складываются в адроны?^[16]

Отношение инерциальная масса/гравитационная масса для элементарных частиц

В соответствии с принципом эквивалентности общей теории относительности, отношение инертной массы к гравитационной для всех элементарных частиц равно единице. Однако, экспериментального подтверждения этого закона для многих частиц не существует. В частности, мы не знаем, каков будет вес макроскопического куска антивещества известной массы.

Кризис спина протона

По первоначальной оценке Европейской группы по мюонному сотрудничеству, на три основных («валентных») кварка протона приходится около 12 % от общего объёма спина. Можно ли пересчитать остаток глюонов, которые связывают кварки, а также образуют «море» пар кварков, которые постоянно создаются и аннигилируют?

Квантовая хромодинамика (КХД) в непертурбативном режиме

Уравнения КХД остаются нерешёнными на энергетических масштабах, соответствующих описанию атомных ядер, и, среди прочего, в основном численные подходы, кажется, начинают давать ответы на этот предельный случай. Подходит ли КХД для описания физики ядра и его компонентов?

Удержание цвета^[1]

Почему никогда не были зафиксированы свободный кварк или глюон, а только объекты, построенные из них, например, мезоны и барионы? Каким образом эти явления вытекают из КХД?

Сильная CP-проблема и аксионы

Почему сильное ядерное взаимодействие инвариантно к чётности и зарядовому сопряжению? Является ли теория Печчеи — Квинн решением этой проблемы?

Гипотетические частицы

Какие из гипотетических частиц, предсказываемых суперсимметричной теорией и другими известными теориями, на самом деле существуют в природе?

Теория Редже

Почему все наблюдаемые в эксперименте траектории Редже являются прямолинейными и имеют приближенно равные наклоны?^[54][55]

Радиус протона

Радиус протона, определённый в экспериментах по измерению лэмбовского сдвига в атоме водорода с заменой электрона на мюон (0,8409 фм), оказался меньше радиуса протона, определённого в экспериментах по рассеянию электронов на протонах (0,879 фм)^[56].

Магнитный момент мюона

Экспериментальное значение магнитного момента мюона не соответствует теоретическому^[56][57].

Электрический дипольный момент нейтрона

Был бы точно равен нулю, если бы имела место инвариантность всех взаимодействий, в которых участвует нейтрон, относительно операции отражения времени. Слабые взаимодействия неинвариантны относительно операции отражения времени. Вследствие этого нейтрон должен был бы обладать электрическим дипольным моментом. Причина отсутствия этого момента у нейтрона неизвестна^[58].

Спин

Почему сохраняется ненулевой момент количества движения в низшем энергетическом состоянии? Почему спины электронов и нуклонов полуцелые?^[59]

Мюон и электрон

Почему мюон и электрон различаются только массой и столь похожи во всех остальных отношениях?^[60]

Фундаментальная длина

Существует ли она в микромире и если да, то какова она по величине?^[61]

Астрономия и астрофизика[править | править код]

Закон планетарных расстояний

предложенный ещё И. Д. Тициусом и И. Э. Боде − до сих пор неизвестно, является ли это правило случайным совпадением, или существуют физические причины для закономерности расстояний до планет.

Планетная система

Отсутствует законченная теория, объясняющая происхождение Солнечной системы^[62] и Земли^[63] в частности и планетарных систем и экзопланет в целом.

Солнечная цикличность

Какова природа циклов солнечной активности; каков механизм обращений магнитного поля Солнца, Земли?

Проблема нагрева солнечной короны

Почему солнечная корона (атмосферный слой Солнца) намного горячее, чем поверхность Солнца? Почему магнитное пересоединение совершается на много порядков быстрее, чем предсказывают стандартные модели?

Скорость вращения Сатурна

Почему магнитосфера Сатурна проявляет (медленно меняющуюся) периодичность, близкую к той, на которой вращаются облака планеты? Какова истинная скорость вращения глубоких внутренних слоёв Сатурна?^[64]

Струи аккреционных дисков

Почему некоторые астрономические объекты, окружённые аккреционным диском, такие как активные ядра галактик, испускают релятивистские струи, излучаемые вдоль полярной оси?^[65] Почему у многих аккреционных дисков существуют квази-периодические колебания? Почему период этих колебаний имеет масштаб, обратно пропорциональный массе центрального объекта? Почему иногда существуют обертоны, и почему у разных объектов обертоны имеют различные соотношения частоты?

Гамма-всплески

Каково происхождение этих краткосрочных всплесков высокой интенсивности?^[66]

Сверхмассивные чёрные дыры

Какова причина отношения М-сигма между массой сверхмассивной чёрной дыры и дисперсией скорости галактики?^[67]

Наблюдаемые аномалии

Аномалия «Гиппарха»: Каково фактическое расстояние до Плеяд?

Пролётная аномалия: Почему наблюдаемая энергия спутников, совершающих гравитационный манёвр, отличается от предсказываемых теорией значений?

Проблема вращения галактик: Является ли тёмная материя ответственной за различия в наблюдаемых и теоретических скоростях вращения звёзд вокруг центра галактик, или же причина в чём-то ином?

Сверхновые

Каков точный механизм, посредством которого имплозии умирающих звёзд становятся взрывом?

Космические лучи сверхвысоких энергий^[46]

Почему некоторые космические лучи обладают невероятно высокой энергией (так называемые частицы OMG), учитывая, что вблизи Земли нет источников космических лучей с такой энергией? Почему некоторые космические лучи, испускаемые далёкими источниками, имеют энергию выше предела Грайзена-Зацепина-Кузьмина?^[68][69]

Замедление времени квазара

Почему кривые блеска квазаров в отличие от кривых блеска сверхновых^[70] не демонстрируют эффекта замедления времени на больших космологических расстояниях?^[71]

Физика конденсированного состояния[править | править код]

Аморфные тела

Какова природа перехода между жидкой или твёрдой и стекловидной фазами? Какие физические процессы приводят к основным свойствам стекла?^[72][73]

Холодный ядерный синтез

Каково объяснение спорных докладов об избыточном тепле, излучении и трансмутациях?^[74][75][76]

Криогенная электронная эмиссия

Почему в отсутствие света увеличивается эмиссия электронов фотоэлектронного умножителя при уменьшении его температуры?^[77][78]

Высокотемпературная сверхпроводимость

Каков механизм, вызывающий у некоторых материалов проявление сверхпроводимости при температурах намного выше 50 кельвинов?^[79]

Сонолюминесценция

Что является причиной выброса коротких вспышек света при схлопывании пузырьков жидкости, возбуждённых звуком?^[80]

Турбулентность

Можно ли создать теоретическую модель для описания статистики турбулентного потока (в частности, для его внутренней структуры)?^[81] При каких условиях существует гладкое решение уравнений Навье — Стокса? Это, вероятно, последняя нерешённая проблема классической или ньютоновской физики.

Физика атмосферы[править | править код]

Квазидвухлетний цикл

Какова природа колебаний с периодом порядка 26 месяцев, зарождающихся в экваториальной стратосфере?

Полугодовой цикл

Какова природа колебаний с полугодовым периодом, проявляющихся, в частности, в виде загадочного эффекта «бабьего лета»?^[82]

Равновесный градиент температуры

Существующая теория турбулентного переноса тепла в атмосфере дает значение вертикального градиента температуры −9.8 К/км, в то время как наблюдения дают значение абсолютной величины этого градиента почти на 40 % меньшее.

Отрицательная вязкость

Каков физический механизм явлений с отрицательной вязкостью?^[83]

Шаровая молния

Какова природа этого явления? Является ли шаровая молния самостоятельным объектом или подпитывается энергией извне? Все ли шаровые молнии имеют одну и ту же природу или существуют разные их типы?

Молния

Почему лишь малая часть кучевого облака перед грозой электрически заряжена?^[84] Почему ступенчатый лидер молнии перемещается с паузами?^[84] Чем объясняется чередование фаз сильного и слабого тока в процессе образования молний?^[84]

Биофизика[править | править код]

Синаптическая пластичность

Она необходима для вычислительной и физической моделей мозга, но чем это обусловлено и какую роль она играет в процессах более высокого порядка вне гиппокампа и зрительной коры?

Аксональное наведение

Как аксоны, исходящие из нейронов, находят свои цели? Этот процесс имеет решающее значение для развития нервной системы, в частности, в вопросе формирования структуры соединений в мозге.

Случайность и устойчивость к шуму при

Теорема Эренфеста — Википедия

Материал из Википедии — свободной энциклопедии

Теоре́ма Эренфе́ста (Уравнения Эренфеста) — утверждение о виде уравнений квантовой механики для средних значений наблюдаемых величин гамильтоновых систем. Эти уравнения впервые получены Паулем Эренфестом в 1927 году.

Формулировка теоремы^[1]:

В квантовой механике средние значения координат и импульсов частицы, а также силы, действующей на неё, связаны между собой уравнениями, аналогичными соответствующим уравнениям классической механики, то есть при движении частицы средние значения этих величин в квантовой механике изменяются так, как изменяются значения этих величин в классической механике.

Полная аналогия имеет место только при условии выполнения ряда требований^[2][3].

Уравнение Эренфеста для среднего значения квантовой наблюдаемой гамильтоновой системы имеет вид

ddt⟨A⟩=1iℏ⟨[A,H]⟩+⟨∂A∂t⟩,{\displaystyle {\frac {d}{dt}}\langle A\rangle ={\frac {1}{i\hbar }}\langle [A,H]\rangle +\left\langle {\frac {\partial A}{\partial t}}\right\rangle ,}

где  A{\displaystyle \ A} — квантовая наблюдаемая,  H{\displaystyle \ H} — оператор Гамильтона системы, угловыми скобками обозначено взятие среднего значения, а квадратные скобки обозначают коммутатор. Это уравнение может быть выведено из уравнения Гейзенберга.

В частном случае, средние значения координаты  q{\displaystyle \ q} и импульса  p{\displaystyle \ p} частицы описываются уравнениями

ddt⟨q⟩=1m⟨p⟩,{\displaystyle {\frac {d}{dt}}\langle q\rangle ={\frac {1}{m}}\langle p\rangle ,}

ddt⟨p⟩=−⟨∂U∂q⟩,{\displaystyle {\frac {d}{dt}}\langle p\rangle =-\left\langle {\frac {\partial U}{\partial q}}\right\rangle ,}

где  m{\displaystyle \ m} — масса частицы,  U(q){\displaystyle \ U(q)} — оператор потенциальной энергии частицы.

Уравнения Эренфеста для средних координат и импульсов являются квантовыми аналогами системы канонических уравнений Гамильтона и задают квантовое обобщение второго закона Ньютона.

1. ↑ Матвеев А. Н. Атомная физика, — М.: Высшая школа, 1989. стр.125.
2. ↑ Эренфеста теоремы // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1999. — Т. 5: Стробоскопические приборы — Яркость. — С. 636-637. — 692 с. — 20 000 экз. — ISBN 5-85270-101-7.
3. ↑ Блохинцев Д. И. Основы квантовой механики. 8-ое изд. — М.: URSS, 2014. — 664 с (параграф 34, С. 136—138)

Портал:Физика — Википедия

«Вероломная восьмёрка» (англ. The Traitorous Eight) — Джулиус Бланк (англ.)русск., Виктор Гринич (англ.)русск., Джин Кляйнер (англ.)русск., Джей Ласт (англ.)русск., Гордон Мур, Роберт Нойс, Шелдон Робертс (англ.)русск. и Жан Эрни (англ.)русск. — восемь физиков и инженеров Shockley Semiconductor Laboratory, которые уволились из-за конфликта с Уильямом Шокли и создали собственную компанию Fairchild Semiconductor. Шокли назвал случившееся «предательством» (англ. betrayal). Кто первым произнёс и кто ввёл в оборот словосочетание «вероломная восьмёрка» — до сих пор не выяснено. В 1956 году Шокли набрал команду талантливых молодых специалистов для разработки и запуска в производство новых полупроводниковых приборов. Нобелевский лауреат по физике, опытный исследователь и преподаватель не справился с управлением предприятием. Он выбрал, как оказалось позже, бесперспективную стратегию и своими руками создал нетерпимые условия для сотрудников. В марте 1957 года несогласные с диктатом Шокли начали переговоры о создании новой, своей, компании, а в августе заключили соглашение с Шерманом Фэйрчайлдом (англ.)русск.. Формальный разрыв отношений состоялся 18 сентября 1957 года. Основанная «восьмёркой» Fairchild Semiconductor вскоре выросла в крупнейшего производителя полупроводников, технологического лидера отрасли. Fairchild 1960-х стала важнейшим бизнес-инкубатором Кремниевой Долины, прямо или косвенно причастным к созданию десятков корпораций — от AMD до Zilog. (далее…) Численная относительность (англ. numerical relativity) — область общей теории относительности, которая разрабатывает и использует численные методы и алгоритмы для компьютерного моделирования физических процессов в сильных гравитационных полях, когда необходимо численно решать уравнения Эйнштейна. Основные физические системы, для описания которых необходима численная относительность, относятся к релятивистской астрофизике и включают в себя гравитационный коллапс, нейтронные звёзды, чёрные дыры, гравитационные волны и другие объекты и явления, для адекватного описания которых необходимо обращаться к полной общей теории относительности без обычных приближений слабых полей и малых скоростей (как в постньютоновских разложениях и теории возмущений на фоне точных решений уравнений Эйнштейна). Моделирование в этой области требует специальных численных методов из-за сложности и нелинейности уравнений Эйнштейна (например, гиперболичность и корректность постановки задачи Коши их временно́й эволюции зависит от представления уравнений, а также начальных и граничных условий, а также — для большинства трёхмерных задач — большой вычислительной мощности, доступной лишь современным суперкомпьютерам. На данный момент в численной относительности актуальны исследования в области моделирования релятивистских тесных двойных звёзд и связанных с ними гравитационных волн, а также многие другие математические и астрофизические проблемы. (далее…)

Антониус Йоханнес ван ден Брук (нидерл. Antonius Johannes van den Broek; 4 мая 1870, Зутермер — 25 октября 1926, Билтховен) — нидерландский юрист и физик-любитель. Несмотря на отсутствие специального образования, получил несколько результатов, оставивших след в истории науки. Ему принадлежит первая формулировка положения о равенстве порядкового номера элемента в периодической системе заряду атомного ядра. С именем ван ден Брука связано возникновение ранних теоретических представлений о составе ядра, в частности, им была предложена протон-электронная модель ядерного строения. В своих работах он неоднократно пытался найти верный принцип расположения элементов в периодической системе и разработать метод вычисления всех возможных в природе изотопов. (далее…) Сергей Гайкович Матинян (арм. Սերգեյ Հայկի Մատինյան; 8 января 1931, Тбилиси — 8 сентября 2017, Дарем, США) — советско-американский физик-теоретик. Академик АН Армянской ССР (1990, член-корреспондент с 1982), доктор физико-математических наук (1966), профессор (1969). Работы Сергея Гайковича Матиняна посвящены слабым и сильным взаимодействиям, теории элементарных частиц, квантовой теории поля, ядерной физике высоких энергий, квантовой гидродинамике (теория сверхтекучести), вопросам нейтринной астрофизики. Матинян получил важные результаты в области оптики нейтральных K{\displaystyle K}-мезонов, фоторождения векторных мезонов, обнаружил нестабильность вакуума в квантовой хромодинамике, динамический хаос неабелевых калибровочных полей. (далее…) События 1996 — в Институте тяжёлых ионов (Дармштадт, Германия) впервые синтезирован 112-й химический элемент — коперниций. Родились 1895 — Мальмгрен, Финн (125 лет назад) 1906 — Калашников, Сергей Григорьевич (114 лет назад) 1914 — Зубов, Виктор Геннадиевич (106 лет назад) 1925 — Хайм, Буркхард (95 лет назад) 1948 — Матвеенко, Валерий Павлович (72 года назад) 1953 — Кульчин, Юрий Николаевич (67 лет назад) 1954 — Вальтер, Ульрих Ханс (66 лет назад) 1954 — Рыкованов, Георгий Николаевич (66 лет назад) 1963 — Грин, Брайан Рэндолф (57 лет назад) Умерли 1975 — Нейман, Леонид Робертович (45 лет назад) 1979 — Габор, Денеш (41 год назад) 1987 — Гаммет, Луис Плак (33 года назад) 1991 — Мигдал, Аркадий Бейнусович (29 лет назад) 2013 — Барков, Лев Митрофанович (7 лет назад)

Симметрия (физика) — Википедия

Материал из Википедии — свободной энциклопедии

Симме́три́я в широком смысле — соответствие, неизменность (инвариантность), проявляемые при каких-либо изменениях, преобразованиях (например: положения, энергии, информации, другого). В физике, симметрия физической системы — это некоторое свойство, сохраняющееся после проведения преобразований.

Симме́три́я (симметрии) — одно из фундаментальных понятий в современной физике, играющее важнейшую роль в формулировке современных физических теорий. Симметрии, учитываемые в физике, довольно разнообразны, начиная с симметрий обычного трёхмерного «физического пространства» (такими, например, как зеркальная симметрия), продолжая более абстрактными и менее наглядными (такими как калибровочная инвариантность).

Некоторые симметрии в современной физике считаются точными, другие — лишь приближёнными. Также важную роль играет концепция спонтанного нарушения симметрии.

Исторически использование симметрии в физике прослеживается с древности, но наиболее революционным для физики в целом, по-видимому, стало применение такого принципа симметрии, как принцип относительности (как у Галилея, так и у Пуанкаре — Лоренца — Эйнштейна), ставшего затем как бы образцом для введения и использования в теоретической физике других принципов симметрии (первым из которых стал, по-видимому, принцип общей ковариантности, являющимся достаточно прямым расширением принципа относительности и приведшего к общей теории относительности Эйнштейна).

Группой симметрии физической задачи называется группа, каждый элемент которой является линейной операцией симметрии задачи, отображающий один элемент множества решений задачи, в другой.^[1]

Исходя из принципов симметрии, можно выводить новые законы природы дедуктивно, а не только в результате наблюдения над физическими объектами или в результате решения уравнений^[2].

В 1918 году немецкий математик Эмми Нётер доказала теорему, согласно которой каждой непрерывной симметрии физической системы соответствует некоторый закон сохранения. Наличие этой теоремы позволяет проводить анализ физической системы на основе имеющихся данных о симметрии, которой эта система обладает. Из неё, например, следует, что инвариантность уравнений движения тела с течением времени приводит к закону сохранения энергии; инвариантность относительно сдвигов в пространстве — к закону сохранения импульса; инвариантность относительно вращений — к закону сохранения момента импульса.

• Ферми Э. Квантовая механика. — М.: Мир, 1968. — 366 с.
• Любарский Г.Я. Теория групп и физика. — М.: Наука, 1986. — 224 с.

Основная теорема физики

Бывают ли теоремы в физике? Да, мы знаем, что 1) учащимся и учителям непривычно воспринимать слово “теорема” применительно к физике. Но, что делать, если здесь будет много геометрии. 2) Мы знаем, что теорема – это суждение, справедливость которого требуется доказать и придется доказывать, потому что с нашей стороны доказательств не будет, мы лишь опишем те наблюдения, которые нам удалось сделать. 3) Задача, которую мы вам предложим, содержит геометрический чертеж, а это еще один мотив для нашего заголовка. Речь идет о задаче № 1.2 из “Сборника избранных задач по физике” М.П. Шаскольский и Э.А. Эльцина стр.(5, 67): “Какую экспозицию нужно делать при фотографировании автомобиля, движущегося со V=36 км/ч, чтобы его изображение на негативе не размывалось, если для этого смещение X изображения должно быть не более 0,1 мм (рис.1).

Рис. 1

Для автомобиля L=3м, а размер изображения на негативе получается равным l=1,5 см. Пусть искомое время равно t секунд, тогда автомобиль успеет проехать за это время расстояние, равное V•t. За это же время смещение изображения должно быть не более 0,1 мм. Отношение этих величин должно, очевидно, равняться отношению длины автомобиля к размеру его изображения, т.е. L/l=300/1,5=200. Следовательно, t=(200•0,01)/10³=0,002 с. Такое решение задачи дано её авторами. Но, что если пойти чуть дальше и записать решение в буквенных обозначениях.

• или

Если подменить слагаемое V•t другим , то равенство нарушится

Введем обозначение X^‘ и запишем равенство

или

Предположим, что существует такое V^‘, что справедливо равенство

Мы видим, что появление новой величины влечет за собой появление новой величины ^.

Теперь получается формула

(1)

Если, теперь, открыть справочник по физике, содержащий данные по СТО, там найдется формула Эйнштейна

(2)

Как пишут в детективных в детективных романах “все совпадения считать случайными”. Но мы и не претендуем на многое, а всего лишь отмечаем, что оба равенства (1) и (2) имеют одинаковую структуру. “Основная теорема” теперь может быть сформулирована. Можно ли вывести (2) из (1), и наоборот (1) из (2)?

Если вам не нравятся новые элементы и , то заметим, что в их появлении состоит эвристический прием, который называется: введение вспомогательных элементов. Приведем пример: решим уравнение

+12•=10

Сразу видно, что выражение нельзя преобразовать в более простой вид. Однако, зная, что

+=1

и что 5²+12²=13², разделив все члены уравнения на 13, получим

+•=

Введем вспомогательный элемент , где 0<<90^°

Тогда . Уравнение принимает такой вид

+=  или

Это один из методов решения задач. Всего их три: разбиение задачи на подзадачи, преобразование (моделирование) задачи и уже упоминавшимся методом вспомогательных элементов. Так, во всяком случае, утверждается в книге Л.М. Фридмана и Е.Н. Турецкого “Как научиться решать задачи”. Процитируем из книги Л.М. Фридмана и Е.Н. Турецкого: Психология уже свыше ста лет занимается исследованием процессов решения задач человеком. В результате этих исследований открыто много интересных закономерностей и найдены важные характеристики процессов решения задач. Особый интерес представляет общая характеристика этого процесса, данная известным советским психологом С.В. Рубинштейном (1889-1960). Он характеризовал решение задач человеком как процесс их переформулирования, в котором непрерывно производится анализ условий и требований задачи через синтетический акт соотнесения.

Естественно возникает вопрос: а в чем состоит это переформулирование? Что получаем? Какими средствами производится переформулирование?”. Речь в этом отрывке шла о моделировании, как методе решения задачи. Применительно к нашему случаю переформулирвание (моделирование) может осуществляться вращением фотоаппарата вокруг собственной оси (воображаемой конечно).

Но, что говорят авторы о подзадачах. Они приводят такой пример.

Найти чему равна разность

  –

Подзадачи получаются из вопросов:

1. Почему под знаком первого квадратного корня стоит модуль разности ?

2. Нельзя ли избавиться от этого модуля, что для этого нужно сделать?

3. Каким числом: положительным или отрицательным является заданная разность?

Авторы исходят из концепции (способ понимания), что анализ это задавание вопросов вычленяющих какую-либо особенность. Анализ и есть вычленение. Применительно к нашему случаю можно предложить подзадачу. Что будет, если автомобиль будет двигаться по синусоидальному закону, а фотографирование производится в произвольные промежутки времени, т.е. случайно? Так и хочется забросить этот вопрос специалистам по квантовой механике (начинающим).

Подведем краткий итог нашему рассказу. На интересной проблемной задаче мы рассказали учащимся о средствах и приемах, которые помогут им осознанно ориентироваться в учебном материале.