Теорема Гаусса: применение формулы

До того, как мы рассмотрим теорему Гаусса, поговорим о том, кто же ее открыл и применил на практике.

Карл Фридрих Гаусс 1777-1855 г. Немецкий математик — один из великих, который не уступает Ньютону и Архимеду. Родился в Брауншвейге, в крестьянской семье.

Гаусс, Карл Фридрих

Гениальная способность к математике проявилась уже в детстве и, пораженный чудесным талантом, учитель начальных классов убеждал родителей Карла не отдавать мальчика в ремесленную школу, а предоставить возможность продолжить образование. В четырнадцать лет Гаусс буквально удивился своим обширным знанием графа Брауншвейгского, и он дал юноше стипендию.

Большую часть своих важных математических исследований Гаусс сделал до того, как в 1799 г. он получил ученую степень доктора наук в Гёттингенском университете, а через два года выпустил свой фундаментальный труд «Трактат о математике», посвященный его влиятельному покровителю.

Арифметические исследования» (лат. Disquisitiones Arithmeticae) — первый крупный труд 24-летнего немецкого математика К.Ф. Гаусса

В трактате речь шла об арифметике — разделе математики, который занимается, прежде всего, натуральными числами и отношениями между ним, например, такими как Великая теорема Ферма. Впоследствии Гаусс не оставил свои занятия математикой, формулируя ряд принципов теоретической вероятности и математики, в том числе распределения случайной величины вокруг средней величины, которое было названо распределением Гаусса.

В 1801 г., когда был открыт первый астероид Церера, Гаусс обратился к астрологии. Чтобы рассчитать параметры орбиты, он разработал методику наименьшего квадрата, которая позволяет полностью рассчитывать орбиту солнечного спутника по результатам только трех измерений положения его места на орбите около Солнца. Через пять лет ученый был назначен директором Гёттингенской обсерватория и остался на этом посту до конца своей жизни.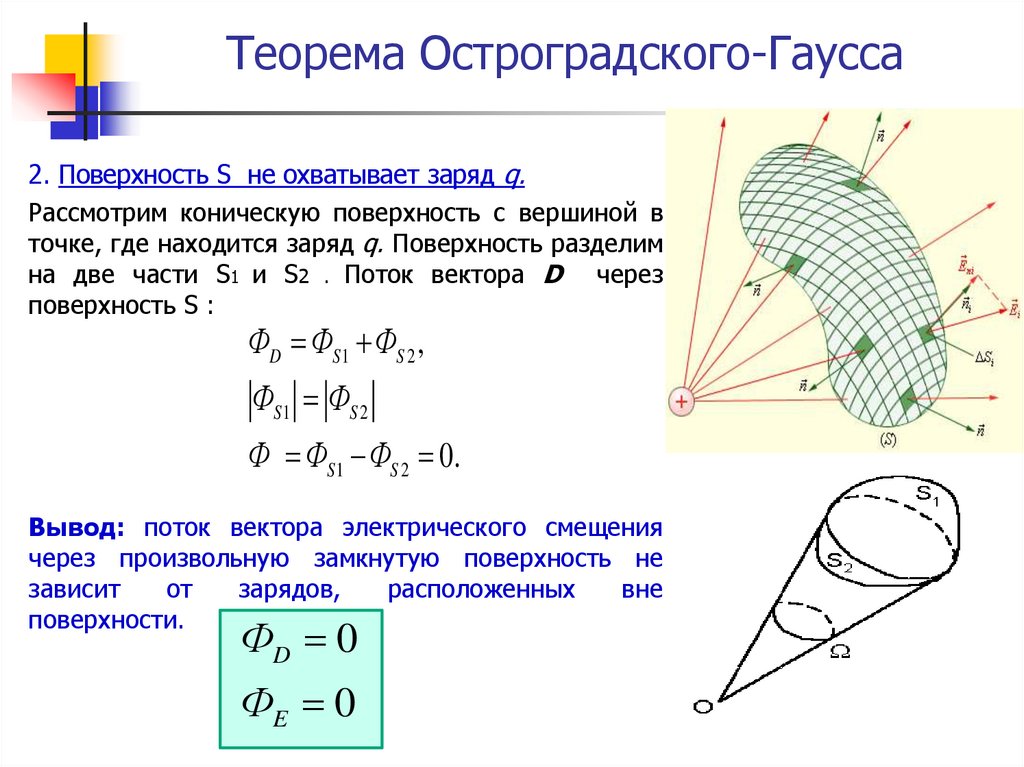 К тому же Гаусс был первым, кто всерьёз занимался изучением земной магнетизма, и именно в честь него названа единица магнитной напряженности.

В науке нередко бывает так, что один и тот же закон может быть сформулирован по-разному. В большинстве случаев формулировка закона не меняет ничего в плане его действий, но новые формулировки помогают теоретикам чуть иначе трактовать его и проверять его в отношении новых природных явлений. Именно таким образом можно рассмотреть теорему Гаусса — это, по сути, обобщение закона Кулона, который, в своей очередь, был обобщением всех знаний ученых об электростатических зарядах.

В математике, физике, астрономии найдется немного областей, развитию которых не посодействовал замечательный гений Карла Фридриха Гаусса.

В 1831 г. вместе с юным коллегой Вильгельмом Вебером (1804-1891 г.) он начал изучать электричество и магнетизм, вскоре сформулировав и доказав теорему, которая носит его имя. Для понимания её смысла представьте изолированный точечный электрический заряд Q. А сейчас представьте себе, что его окружает замкнутая поверхность. В теореме форма поверхности не важна – это может оказаться даже сдутым воздушным шариком.

В каждой точке окружающей заряд поверхности, наблюдается электрическое поле, образованное зарядом, а произведение напряженности этого электрического поля на сколь угодно малую единицу площади окружающей заряд поверхности, через которую проходят силовые линии поля, называется потоком напряженности электрического поля, и можно рассчитать поток напряженности, приходящийся на каждый элемент поверхности. В теореме Гаусса говорится, что общий поток электрической напряженности, проходящий по окружающей поверхности заряда, пропорционален величине зарядов.

Связь между законом Кулона и теоремой Гаусса можно рассмотреть на простом примере. Предположим, что заряд q окружен сферой радиуса r. На удалении r от заряда напряженность электрического поля, которая определяется силой притяжения или отталкивания единичного заряда, помещенного в соответствующую точку, составит, согласно закону Кулона:

Формула

\[E=k q / r^{2}\]

И то же самое значение мы получим для любой точки сферы заданного радиуса. {2}=4 \pi k q\]

Применение формулы Гаусса

Формула применяется для преобразования объемного интеграла в интеграл на замкнутую поверхность и обратно. В математическом анализе формула Теоремы Остроградского — Гаусса применяется для расчета дифференциации, т.е. потока вектора по поверхности окружающей среды внешними направлениями.

Принимая во внимание то, что поток векторного поля через замкнутую поверхность δδ в направлении внешней единичной нормали n0¯¯¯¯¯n0¯ равен дивергенции данного поля, вычисленной по телу TT, которое эта поверхность.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Применение теоремы Гаусса для электростатического поля

Теорема Остроградского-Гаусса применяется для расчета электростатического поля для тех задач, где поле имеет специальную симметрию. Например, плоскую, цилиндрическую или сферическую. В данном случае на эффективность применения теоремы влияют симметрия и конфигурация поля, которые должны соответствовать двум условиям:

• заряженное тело должно быть окружено простой замкнутой поверхностью;
• вычисление потока вектора напряженности необходимо свести к умножению ЕЕ (или EnEn) на площадь поверхности SS или часть нее.

Если исходные данные не соответствуют условиям, то при решении задачи необходимо использовать другие методы.

Рассмотрим применение теоремы для равномерно заряженной плоскости.

Задача

Предположим, что заряд положительный, а плоскость заряжена с постоянной поверхностной плотностью, что выражается в формуле δ=dqdSδ=dqdS. Благодаря симметрии можно сделать вывод, что напряженность в любой точке поля обладает направлением, перпендикулярным плоскости. Из этого же можно сделать вывод, что во всех точках, симметричных плоскости, напряженность поля одинакова, но ее направление противоположно.

Отметим на заряженной плоскости площадь △S△S. Определим вокруг площадки замкнутую цилиндрическую поверхность (рисунок 3) так, чтобы ее образующие основания были перпендикулярны плоскости, располагались симметрично, относительно нее и имели величину △S△S.

Рисунок 3

А теперь используем теорему Остроградского-Гаусса: ∮SEndS=1ε0∑q1∮SEndS=1ε0∑q1. Так как в этом случае En=0En=0 в каждой точке, через боковую часть потока не будет. В случае оснований En=EEn=E, а исходя из этого совокупный поток через поверхность равен 2E△S2E△S.

Посмотрим теперь внутрь поверхности. Там заключен заряд δ△Sδ△S. В соответствии с теоремой Остроградского-Гаусса, должно быть выполнено условие: 2E△S=δ△Sε02E△S=δ△Sε0, из чего следует E=δ2ε0E=δ2ε0.

Так как напряженность поля равна на любых расстояниях от плоскости, в вычисления не нужно включать длину цилиндра. Если плоскость заряжена, то направление векторов изменяется на противоположное.

Поток вектора напряженности в теореме Гаусса

Поток вектора напряженности электрического поля через замкнутую поверхность в вакууме равен алгебраической сумме всех зарядов, расположенных внутри поверхности, деленной на ε0 (поток вектора напряженности электрического поля равен числу линий напряженности, пересекающих поверхность S.)

С помощью дифференциальной формы теоремы можно рассчитать электростатическое поле при произвольном пространственном распределении зарядов. В ней установлена связь между объемной плотностью заряда ρ и изменением Е в окрестности данной точки пространства.

Теорема и формула Остроградского — Гаусса :: SYL.ru

М.В. Остроградский — российский математик и физик времен Российской империи, академик. Внес огромный вклад в развитие математического анализа, теории вероятностей, механики (раздела физики), теории чисел. В 1826 году вывел формулу, называемую сейчас формулой Остроградского — Гаусса.

История открытия

Впервые формула Остроградского — Гаусса была упомянута Жозефом Лагранжем в 1762 году.

Далее основной способ приведения тройного интеграла к поверхностному был доказан Карлом Гауссом , который использовал в качестве основы для доказательства решение проблем в электродинамике. Произошло это в первой половине XIX века.

Далее формула в общем виде была представлена Михаилом Остроградским. С ее помощью стало возможно выразить значение дифференциала по параметру от N-кратного интеграла.

Смысл формулы Остроградского

Формула Остроградского-Гаусса соотносит тройной интеграл по пространственному объему с интегралом по поверхности на его грани. Она является аналогом формулы Грина, которая соотносит двойной интеграл по плоскости с криволинейным по ее границам.

Вывод формулы

Формула Остроградского — Гаусса: вывод. Допустим, что в области W определена подынтегральная функция R (x, y, z), которая является определенной и непрерывной. Аналогичной является и ее производная во всей области W, включая ее границу. В таком виде известна сейчас теорема Остроградского — Гаусса (формула приведена ниже).

Причем S — поверхность, которая ограничивает тело, а интеграл справа распространен на ее внешнюю сторону.

И абсолютно верно,

Если аналогично брать во внимание и интегралы по поверхности, то

при этом справа находится сумма двух интегралов — первый из них соотносится с верхней частью поверхности (S₂), а второй — с нижней частью поверхности (S₁). Если приписать к данному равенству справа интеграл, указанный ниже, то его справедливость не будет нарушена:

Он соотносится с внешней частью поверхности S₃ по причине равенства нулю.

Если объединить все три вышеуказанных интеграла в один, будет получен частный случай формулы Остроградского.

Несложно осознать, что данная формула верна для более широкого класса тел и справедлива так же для фигур, ограниченных абсолютно любыми нелинейными поверхностями.

Аналогично справедливы и следующие формулы:

если функции Q и P непрерывны в области вместе со своими производными dP/dx и dQ/dy.

Если сложить оба равенства, будет получено выражение формулы Остроградского. Она отображает интеграл по поверхности, соотнесенный с внешней частью поверхности, через тройной интеграл, который берется по самому телу, границей которого является вышеуказанная поверхность.

Следует понимать, что формулы Грина, Стокса и Остроградского выражают интеграл, связанный с некоторым геометрическим телом, через интеграл, который берется на его границе. Формула Грина используется только в случае двумерности пространства, формула Стокса — к искривленному двумерному пространству.

Формулу Ньютона-Лейбница можно также рассматривать как некоторый аналог этих формул, но для одномерного пространства.

Применение данной формулы

Пусть в какой-либо незамкнутой области пространства заданы непрерывные функции A, B и C. Взяв любую замкнутую поверхность, находящуюся в данной области и ограничивающую некоторое тело, можно рассмотреть следующий интеграл по поверхности:

Необходимо найти такие значения A, B и C, чтобы при любых x, y и z данный интеграл оказывался равен нулю.

Для этого необходимо использовать формулу Остроградского-Гаусса. Одним из подразумеваемых условий является определенность и непрерывность функций A, B и C и их производных.

Так же требуется специально ввести наиболее данное для данного случая ограничение: и тело, и ограничивающая его поверхность должны содержаться одновременно в конкретной и указанной области, называемую односвязной. Основная его особенность заключается в отсутствии пустого пространства (в том числе и точечного).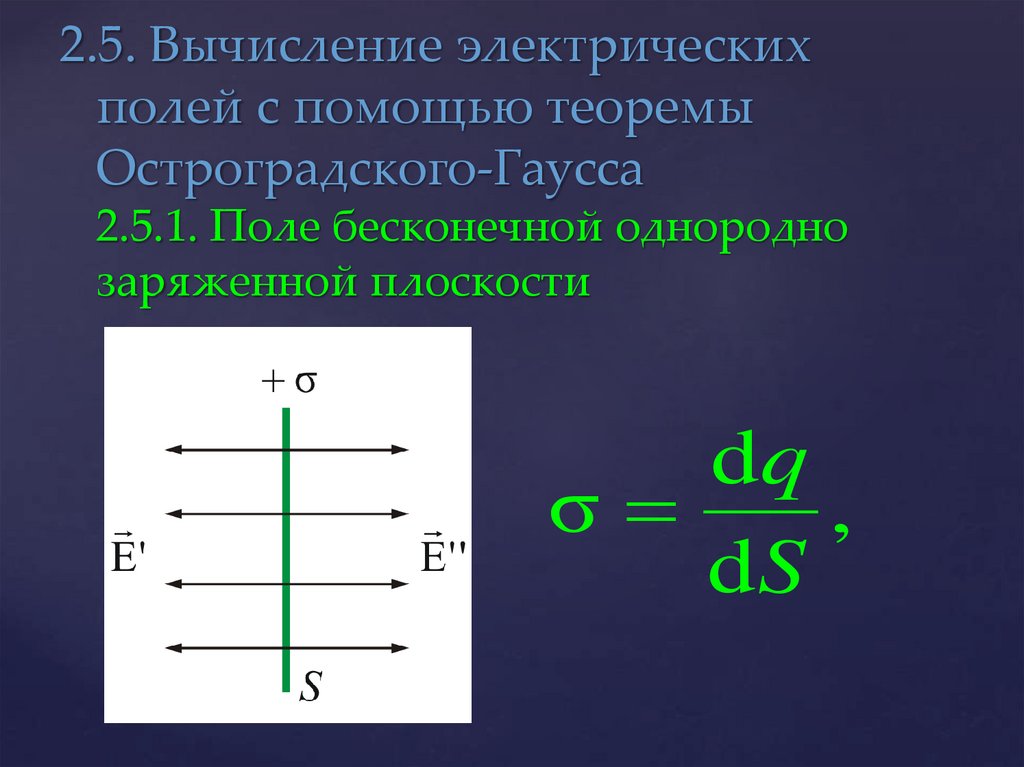 Таким образом, границей тела будет являться одна и при том единственная поверхность.

После применения формулы возможно получение следующего условия, которое является достаточным:

Чтобы доказать, что условие является так же и необходимым, достаточно воспользоваться дифференцированием тройного интеграла.

В заключении необходимо сказать об областях использования.

Как же применяется на практике формула Остроградского-Гаусса? Примеры использования можно обнаружить в самых разных сферах: для вывода некоторых формул в физике (например, уравнение диффузии), преобразования интегралов, вычисления интегралов Гаусса, доказательства некоторых формул и многого иного.

Теорема о дивергенции (Гаусса, Остроградского) для измерения потока — Обмен файлами

Сейчас вы подписаны на это сообщение

Вы можете получать электронные письма, в зависимости от ваших предпочтений в общении

Версия 1.0.0 (2,62 КБ) от Roche de Guzman

Пример, показывающий, что интеграл по объему дивергенции f = поверхностный интеграл от величины f по нормали к поверхности (f точка n)

146 загрузок За все время: 146 дюймов data-original-title=»Загрузки» aria-describedby=»popover506129″>

Обновлено 23 фев 2019

Посмотреть лицензию

• Обзор
• Функции
• История версий
• Отзывы (0)
• Обсуждения (0)

%% Теорема расходимости для измерения потока в контрольном объеме (прямоугольная призма)

% Пример Доказательство: поток = объемный интеграл дивергенции f (плотность потока * dV) = поверхностный интеграл величины f по нормали к поверхности (f точка n) (поток * dS)
% Проф. Рош К. де Гусман

Цитировать как

Рош де Гусман (2023). Теорема дивергенции (Гаусса, Остроградского) для измерения потока (https://www.mathworks.com/matlabcentral/fileexchange/70371-divergence-theorem-gauss-ostrogradsky-s-to-measure-flow), MATLAB Central File Exchange. Получено 11 января 2023 г. .

Совместимость версий MATLAB

Created with R2018b

Совместимость с любой версией

Совместимость с платформами

Windows macOS Linux

Категории

• МАТЛАБ > Графика > 2-D и 3-D графики > Поверхности, объемы и полигоны > Объемная визуализация >

Теги Добавить теги

дивергенция теорема дивергенции поток поток плотность потока поверхность интеграл вектор функция объем интеграл

Охота за сокровищами сообщества

Найдите сокровища в MATLAB Central и узнайте, как сообщество может вам помочь!

На охоту!

Версия	Опубликовано	Примечания к выпуску
1. 0.0	23 фев 2019

Выберите сеть Сайт

Выберите веб-сайт, чтобы получить переведенный контент, где он доступен, и посмотреть местные события и предложения. На основе ваше местоположение, мы рекомендуем вам выбрать:

.

Вы также можете выбрать веб-сайт из следующего списка:

Европа

Свяжитесь с местным офисом

Теорема о дивергенции

«Теорема о дивергенции» — самая важная теорема исчисления. Эта теорема используется для решения множества сложных интегральных задач. Поверхностный интеграл сравнивается с объемным интегралом. Он обозначает отношения между ними. В этой статье подробно рассматриваются формулировка теоремы о дивергенции, доказательство, теорема Гаусса о дивергенции и примеры. Теорема о дивергенции, широко известная как теорема Гаусса или теорема Остроградского в векторном исчислении, представляет собой теорему, которая связывает поток векторного поля через замкнутую поверхность с дивергенцией поля в замкнутом объеме.

Поверхностный интеграл векторного поля через замкнутую поверхность, известный как поток через поверхность, равен объемному интегралу дивергенции по области внутри поверхности согласно теореме о дивергенции. Интуитивно, в нем говорится, что сумма всех источников поля в регионе (со стоками, рассматриваемыми как отрицательные источники) дает чистый поток из региона.

Поверхностный интеграл нормальной составляющей векторной точечной функции «F» по замкнутой поверхности «S» равен объемному интегралу дивергенции функции согласно теореме о дивергенции.

  F→   

, взятые по поверхности S-замкнутого объема «V». В результате теорема о дивергенции символически обозначается следующим образом:

∬V. F .dV = ∬S. F. n.ds

Рассмотрим поверхность, обозначенную S, которая покрывает объем, обозначенный V.

Предположим, что вектор A представляет векторное поле в указанной области. Предположим, что этот объем составлен из большого количества параллелепипедов (1-6 параллелепипедов), представляющих собой элементарные объемы.

Рассмотрим объем j-го параллелепипеда ∆Vj, ограниченного поверхностью Sj площадью dSj.

Поверхностный интеграл от A по поверхности Sj будет равен

∯sA. dSj 

Рассмотрите возможность разделения всего тома на элементарные тома I, II и III.

Элементарный объем I снаружи соответствует элементарному объему II внутри, а элементарный объем II снаружи соответствует элементарному объему III внутри, и так далее.

В результате сумма составных объемных интегралов сокращается, остается только поверхностный интеграл, исходящий от поверхности S. 

 ∑ ∮∮Sj  A.dSj =∮∮S A.dS …. (1)

Умножив и разделив левую часть уравнения (1) на ΔVi

         sA.dS = ∑ 1Vi (∮∮Si   A .dSi )ΔVi

Предположим, что объем поверхности S разбивается на бесконечные составляющие объемы так, что ∆Vi →0.