Цифровые фильтры (Хемминг Р.В.)

Цифровые фильтры (Хемминг Р.В.)

Хемминг Р.В. Цифровые фильтры. Пер. с англ. / Под ред. А. М. Трахтмана — М.: Сов. радио, 1980. — 224 с. Книга представляет собой введение в цифровую фильтрацию и адресована лицам, которым приходится сталкиваться с обработкой данных на ЭВМ в различных сферах (электро- и радиотехнике, автоматике, экономике, статистике и т. д. ). Оглавление Предисловие редактора перевода Предисловие Глава 1. ВВЕДЕНИЕ 1.1. Что такое цифровой фильтр? 1.2. Почему следует интересоваться цифровыми фильтрами? 1.3. Как будет трактоваться тема? 1.4. Сравнение универсальных и специализированных ЭВМ 1.5. Необходимые статистические предпосылки 1. 6. Распределение статистики 1.7. Усиление шума в фильтре Глава 2. ЧАСТОТНЫЙ ПОДХОД 2.2. Наложение 2.3. Понятие собственной функции 2.4. Инвариантность при сдвиге 2.5. Линейные системы 2.6. Собственные функции равномерной дискретизации 2.7. Краткие выводы Глава 3. НЕКОТОРЫЕ КЛАССИЧЕСКИЕ ПРИМЕНЕНИЯ 3.2. Приближение полиномами по методу наименьших квадратов 3.3. Приближение параболами второй и четвертой степени по методу наименьших квадратов 3.4. Интегрирование. Рекурсивные фильтры 3.5. Разности и производные 3.6. Еще о сглаживании. Децибелы 3.7. Нехватка данных и интерполяция 3.8. Класс нерекурсивных сглаживающих фильтров 3.9. Пример работы фильтра 3.10. Краткие выводы Глава 4. РЯД ФУРЬЕ. НЕПРЕРЫВНЫЙ СЛУЧАЙ 4.2. Ортогональность 4.3. Формальные разложения 4.4. Нечетные и четные функции 4.5. Ряд Фурье и метод наименьших квадратов 4.6. Класс функций и скорость сходимости 4.7. Сходимость в точке непрерывности 4. 8. Сходимость в точке разрыва Глава 5. ДАЛЬНЕЙШИЕ РЕЗУЛЬТАТЫ ДЛЯ РЯДА ФУРЬЕ 5.2. Явление Гиббса 5.3. Сглаживание Ланцоша. Сигма-факторы 5.4. Комплексный ряд Фурье 5.5. Фазовая форма ряда Фурье 5.6. Образование нового ряда Фурье. Теоремы свертки 5.7. Еще о явлении Гиббса 5.8. Модифицированный ряд Фурье 5.9. Окно фон Ганна: приподнятое косинусное окно 5.10. Окно Хемминга: приподнятый косинус с подставкой 5.11. Обзор рассмотренных окон Глава 6. РАСЧЕТ НЕРЕКУРСИВНЫХ ФИЛЬТРОВ 6.2. Расчет низкочастотного фильтра 6.3. Обзор постоянно применяемых методов расчета 6.4. Дифференцирующий фильтр 6.5. Проверка дифференцирующего фильтра на примере обработки данных 6.6. Новые фильтры из старых фильтров. Обострение характеристики фильтра Глава 7. ГЛАДКИЕ НЕРЕКУРСИВНЫЕ ФИЛЬТРЫ 7.2. Гладкие фильтры 7.3. Приведение к ряду Фурье 7.4. Полиномиальная обработка в общем виде 7.5. Расчет гладкого фильтра 7.6. Гладкие полосовые фильтры Глава 8. ИНТЕГРАЛ ФУРЬЕ И ТЕОРЕМА ОТСЧЕТОВ 8.2. Краткое изложение результатов 8.3. Теорема отсчетов 8.4. Интеграл Фурье 8.5. Некоторые пары преобразований 8.6. Функции с ограниченной полосой и теорема отсчетов 8.7. Теорема свертки 8.8. Эффект конечного размера выборки 8. Окна Глава 9. ОКНА КАЙЗЕРА И ОПТИМИЗАЦИЯ 9.2. Обзор явления Гиббса и окно Ланцоша 9.3. Окно Кайзера 9.4. Вывод формул Кайзера 9.5. Расчет полосового фильтра 9.6. Снова тот же дифференциатор 9.7. Частный случай дифференцирования 9.8. Оптимизирующий расчет 9.9. Грубый метод оптимизации Глава 10. КОНЕЧНЫЙ РЯД ФУРЬЕ 10.2. Ортогональность 10.3. Связь между дискретным и непрерывным разложениями 10.4. Быстрое преобразование Фурье 10.5. Косинус разложения 10.6. Другой метод расчета 10.7. Вычисление спектра мощности Глава 11. РЕКУРСИВНЫЕ ФИЛЬТРЫ 11.2. Приведение к более простой форме 11.3. Устойчивость и z-преобразование 11.4. Фильтры Баттерворта 11.5. Простой пример расчета фильтра Баттерворта 11.6. Устранение фазовой зависимости. Двухсторонние фильтры Глава 12. ЧЕБЫШЕВСКОЕ ПРИБЛИЖЕНИЕ И ФИЛЬТРЫ ЧЕБЫШЕВА 12.2. Полиномы Чебышева 12.3. Критерий Чебышева 12.4. Фильтры Чебышева 12.5. Фильтры Чебышева типа 1 12.6. Фильтры Чебышева типа 2 12.7. Эллиптические фильтры 12.8. Выравнивание кривой ошибок 12.9. Тождество Чебышева 12.10. Пример расчета интегратора Глава 13. НЕКОТОРЫЕ ПРАКТИЧЕСКИЕ СООБРАЖЕНИЯ 13.2. Эффекты конечной арифметики 13.3. Сравнение рекурсивных и нерекурсивных фильтров 13.4. Спектральная оценка 13.5. Прореживание 13.6. Литература Список литературы

Искусство схемотехники, Т.1

Искусство схемотехники, Т.1

Хоровиц П. , Хил л .У. Искусство схемотехники: В 3-х томах: Т.1. Пер. с англ. — 4-е изд., перераб. и доп.-М.: Мир, 1993. Широко известная читателю по предыдущим изданиям монография известных американских специалистов посвящена быстро развивающимся областям электроники. В ней приведены наиболее интересные технические решения, а также анализируются ошибки разработчиков аппаратуры: внимание читателя сосредоточивается на тонких аспектах проектирования и применения электронных схем. Для специалистов в области электроники, автоматики, вычислительной техники, а также студентов соответствующих специальностей вузов и техникумов. Оглавление ПРЕДИСЛОВИЕ ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ ГЛАВА 1. ОСНОВЫ ЭЛЕКТРОНИКИ НАПРЯЖЕНИЕ, ТОК И СОПРОТИВЛЕНИЕ 1.01. Напряжение и ток 1.02. Взаимосвязь напряжения и тока: резисторы ПРИСТАВКИ ДЛЯ ОБРАЗОВАНИЯ КРАТНЫХ И ДОЛЬНЫХ ЕДИНИЦ ИЗМЕРЕНИЯ РЕЗИСТОРЫ ХАРАКТЕРИСТИКИ РЕЗИСТОРОВ ФИРМЫ ALLEN BRADLEY, (СЕРИЯ АВ, ТИП СВ) 1. 03. Делители напряжения 1.04. Источники тока и напряжения 1.05. Теорема об эквивалентном преобразовании источников (генераторов) УНИВЕРСАЛЬНЫЕ ИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ 1.06. Динамическое сопротивление СИГНАЛЫ 1.07. Синусоидальные сигналы 1.08. Измерение амплитуды сигналов 1.09. Другие типы сигналов 1.10. Логические уровни 1.11. Источники сигналов КОНДЕНСАТОРЫ И ЦЕПИ ПЕРЕМЕННОГО ТОКА 1.12. Конденсаторы КОНДЕНСАТОРЫ 1.13. RС-цепи: изменения во времени напряжения и тока 1.14. Дифференцирующие цепи 1.15. Интегрирующие цепи ИНДУКТИВНОСТИ и ТРАНСФОРМАТОРЫ 1.16. Индуктивности 1.17. Трансформаторы ПОЛНОЕ И РЕАКТИВНОЕ СОПРОТИВЛЕНИЕ 1.18. Частотный анализ реактивных схем 1.19. RC-фильтры 1.20. Векторные диаграммы 1.21. «Полюсы» и наклон в пределах октавы 1.22. Резонансные схемы и активные фильтры 1.23. Другие примеры использования конденсаторов 1.24. Обобщенная теорема Тевенина об эквивалентном преобразовании (эквивалентном генераторе) ДИОДЫ И ДИОДНЫЕ СХЕМЫ 1. 25. Диоды 1.26. Выпрямление 1.27. Фильтрация в источниках питания 1.28. Схемы выпрямителей для источников питания 1.29. Стабилизаторы напряжения 1.30. Примеры использования диодов 1.31. Индуктивные нагрузки и диодная защита ДРУГИЕ ПАССИВНЫЕ КОМПОНЕНТЫ 1.32. Электромеханические элементы 1.33. Индикаторы 1.34. Переменные компоненты ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ ГЛАВА 2. ТРАНЗИСТОРЫ 2.01. Первая модель транзистора: усилитель тока НЕКОТОРЫЕ ОСНОВНЫЕ ТРАНЗИСТОРНЫЕ СХЕМЫ 2.02. Транзисторный переключатель 2.03. Эмиттерный повторитель 2.04. Использование эмиттерных повторителей в качестве стабилизаторов напряжения 2.05. Смещение в эмиттерном повторителе 2.06. Транзисторный источник тока 2.07. Усилитель с общим эмиттером 2.08. Схема расщепления фазы с единичным коэффициентом усиления 2.09. Крутизна МОДЕЛЬ ЭБЕРСА-МОЛЛА ДЛЯ ОСНОВНЫХ ТРАНЗИСТОРНЫХ СХЕМ 2.10. Улучшенная модель транзистора: усилитель с передаточной проводимостью (крутизной) 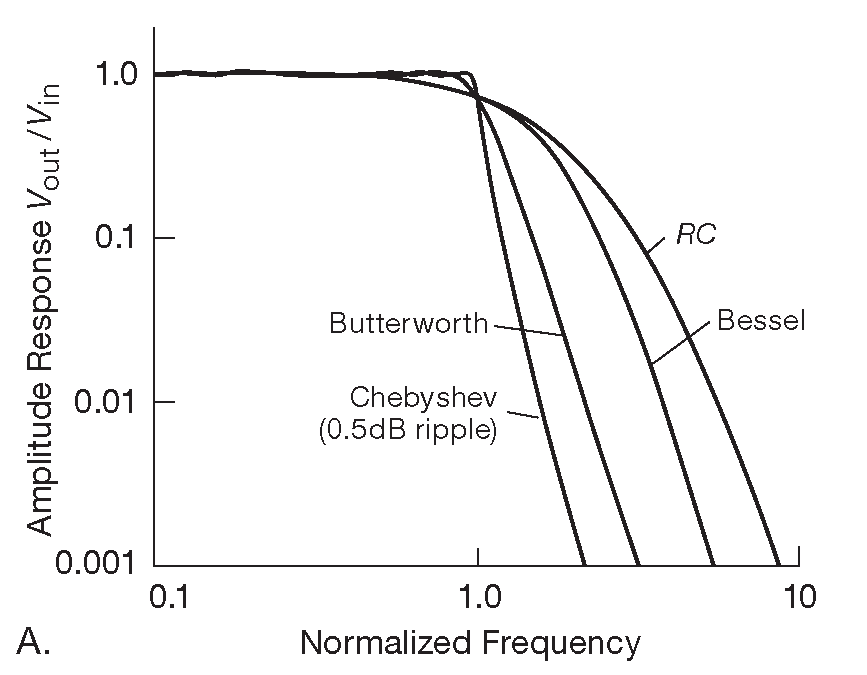2. 11. Еще раз об эмиттерном повторителе 2.13. Еще раз об усилителе с общим эмиттером 2.13. Смещение в усилителе с общим эмиттером 2.14. Токовые зеркала НЕКОТОРЫЕ ТИПЫ УСИЛИТЕЛЬНЫХ КАСКАДОВ 2.15. Двухтактные выходные каскады 2.16. Составной транзистор (схема Дарлингтона) 2.17. Следящая связь 2.18. Дифференциальные усилители 2.19. Емкость и эффект Миллера 2.20. Полевые транзисторы НЕКОТОРЫЕ ТИПИЧНЫЕ ТРАНЗИСТОРНЫЕ СХЕМЫ 2.21. Стабилизированный источник напряжения 2.22. Терморегулятор 2.23. Простая логическая схема на транзисторах и диодах СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ 2.24. Удачные схемы 2.25. Негодные схемы ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ ГЛАВА 3. ПОЛЕВЫЕ ТРАНЗИСТОРЫ 3.01. Характеристики полевых транзисторов 3.02. Типы ПТ 3.03. Общая классификация ПТ 3.04. Выходные характеристики ПТ 3.05. Производственный разброс характеристик ПТ ОСНОВНЫЕ СХЕМЫ НА ПТ 3.06. Источники тока на ПТ с р-n-переходом 3. 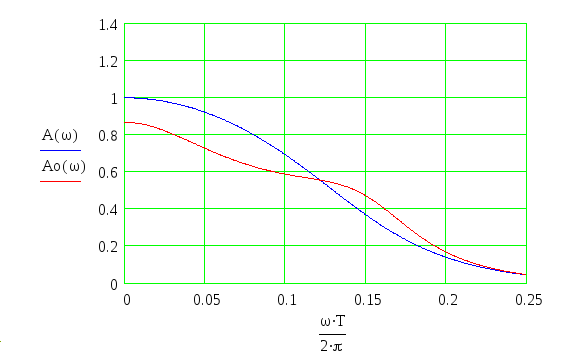07. Усилители на ПТ 3.08. Истоковые повторители 3.09. Ток затвора ПТ 3.10. ПТ в качестве переменных резисторов КЛЮЧИ НА ПТ 3.11. Аналоговые ключи на ПТ 3.12. Недостатки ПТ-ключей 3.13. Несколько схем на ПТ-ключах 3.14. Логические и мощные ключи на МОП-транзисторах 3.15. Необходимые предосторожности в обращении с МОП-транзисторами СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ ГЛАВА 4. ОБРАТНАЯ СВЯЗЬ И ОПЕРАЦИОННЫЕ УСИЛИТЕЛИ 4.01. Предварительные сведения об обратной связи 4.02. Операционные усилители 4.03. Важнейшие правила ОСНОВНЫЕ СХЕМЫ ВКЛЮЧЕНИЯ ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ 4.04. Инвертирующий усилитель 4.05. Неинвертирующий усилитель 4.06. Повторитель 4.07. Источники тока 4.08. Основные предостережения по работе с ОУ КАЛЕЙДОСКОП СХЕМ НА ОПЕРАЦИОННЫХ УСИЛИТЕЛЯХ 4.09. Линейные схемы 4.10. Нелинейные схемы ПОДРОБНЫЙ АНАЛИЗ РАБОТЫ ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ 4.11. Отличие характеристик идеального ОУ от реального 4. 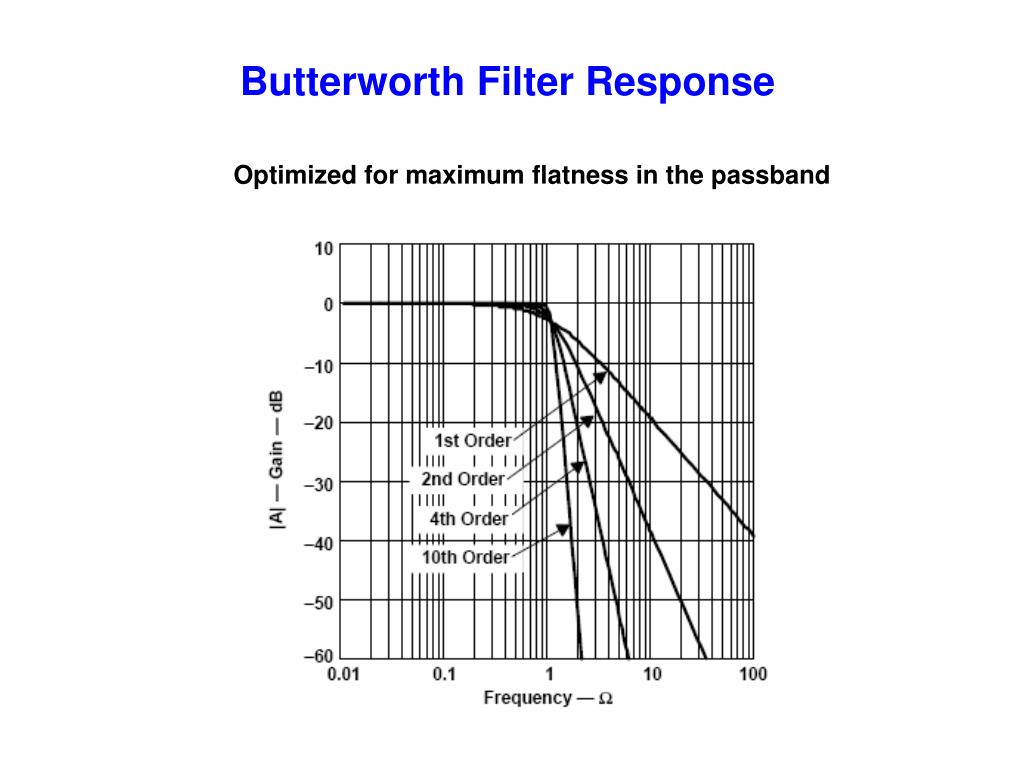12. Эффекты ограничений ОУ на работу схем на их основе 4.13. Микромощные и программируемые ОУ ПОДРОБНЫЙ АНАЛИЗ РАБОТЫ НЕКОТОРЫХ СХЕМ НА ОУ 4.14. Логарифмический усилитель 4.15. Активный пиковый детектор 4.16. Выборка-запоминание ДИЭЛЕКТРИЧЕСКОЕ ПОГЛОЩЕНИЕ 4.17. Активный ограничитель 4.18. Схема выделения модуля абсолютного значения сигнала 4.19. Интеграторы 4.20. Дифференциаторы РАБОТА ОУ С ОДНИМ ИСТОЧНИКОМ ПИТАНИЯ 4.21. Смещение усилителей переменного тока, использующих один источник питания. 4.22. Операционные усилители с одним источником питания. КОМПАРАТОРЫ И ТРИГГЕР ШМИТТА 4.23. Компараторы 4.24. Триггер Шмитта ОБРАТНАЯ СВЯЗЬ И УСИЛИТЕЛИ С КОНЕЧНЫМ УСИЛЕНИЕМ 4.25. Уравнение для коэффициента усиления 4.26. Влияние обратной связи на работу усилителей 4.27. Два примера транзисторных усилителей с обратной связью НЕКОТОРЫЕ ТИПИЧНЫЕ СХЕМЫ С ОПЕРАЦИОННЫМИ УСИЛИТЕЛЯМИ 4.28. Лабораторный усилитель общего назначения 4. 29. Генератор, управляемый напряжением 4.30. Линейный переключатель на полевом транзисторе с p-n-переходом, с компенсацией. 4.31. Детектор нуля для ТТЛ-схем 4.32. Схема измерения тока в нагрузке ЧАСТОТНАЯ КОРРЕКЦИЯ УСИЛИТЕЛЕЙ С ОБРАТНОЙ СВЯЗЬЮ 4.33. Зависимость коэффициента усиления и фазового сдвига от частоты 4.34. Методы коррекции усилителей 4.35. Частотная характеристика цепи обратной связи СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ 4.36. Некоторые полезные идеи ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ ГЛАВА 5. АКТИВНЫЕ ФИЛЬТРЫ И ГЕНЕРАТОРЫ АКТИВНЫЕ ФИЛЬТРЫ 5.01. Частотная характеристика RC-фильтров 5.02. Идеальный рабочий режим LC-фильтров 5.03. Введение в активные фильтры: обзор 5.04. Критерии режима работы фильтра Ки 5.05. Типы фильтров СХЕМЫ АКТИВНЫХ ФИЛЬТРОВ 5.06. Схемы на ИНУН 5.07. Проектирование фильтров на ИНУН с использованием наших упрощенных таблиц 5.08. Фильтры, построенные на основе метода переменных состояния 5. 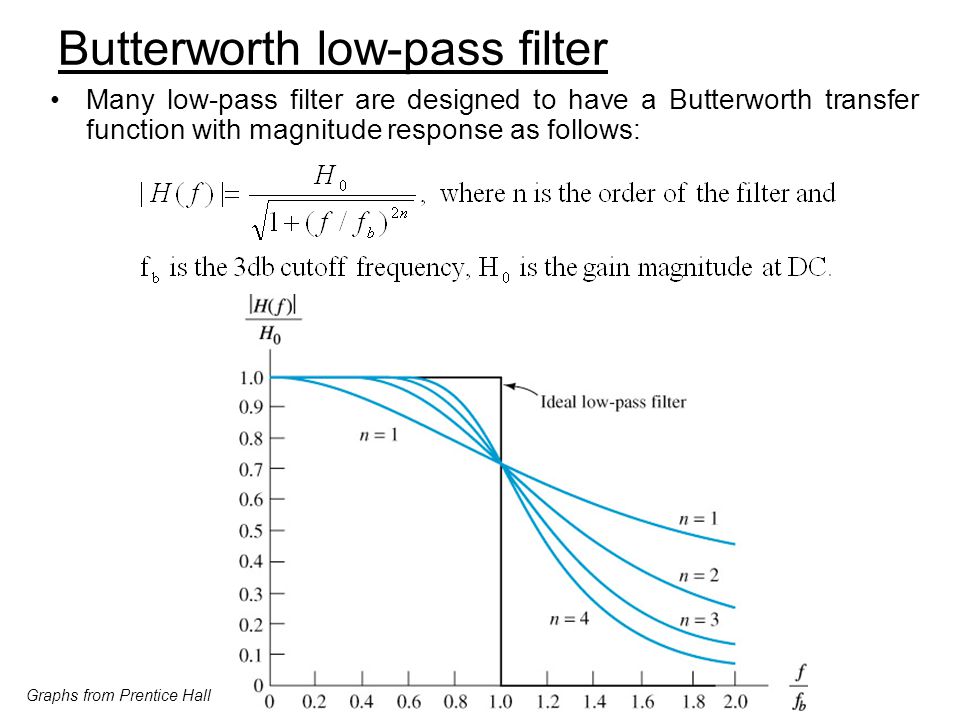09. Двойной Т-образный фильтр-пробка 5.10. Построение фильтров на гираторах 5.11. Фильтры на переключаемых конденсаторах ГЕНЕРАТОРЫ 5.13. Релаксационные генераторы 5.14. Классическая ИС таймера-555 5.15. Генераторы, управляемые напряжением 5.16. Квадратные генераторы 5.17. Мостовые генераторы Вина и L С-генераторы 5.18. LС-генераторы 5.19. Генераторы с кварцевыми резонаторами СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ ГЛАВА 6. СТАБИЛИЗАТОРЫ НАПРЯЖЕНИЯ И ИСТОЧНИКИ ПИТАНИЯ БАЗОВЫЕ СХЕМЫ СТАБИЛИЗАТОРОВ НА ОСНОВЕ КЛАССИЧЕСКОЙ ИМС 723 6.01. ИМС стабилизатора 723 6.02. Стабилизатор положительного напряжения 6.03. Стабилизаторы с большими выходными токами ПРОЕКТИРОВАНИЕ ТЕПЛООТВОДА МОЩНЫХ СХЕМ 6.04. Мощные транзисторы и отвод тепла 6.05. Ограничители тока с обратным наклоном характеристики 6.06. Защита от больших напряжений 6.07. Специальные вопросы проектирования сильноточных источников питания 6. 08. Программируемые источники питания 6.09. Пример схемы источника питания 6.10. Другие ИМС стабилизатора НЕСТАБИЛИЗИРОВАННЫЕ ИСТОЧНИКИ ПИТАНИЯ 6.11. Компоненты линии переменного тока 6.12. Трансформаторы 6.13 Элементы схемы, работающие на постоянном токе ИСТОЧНИКИ ОПОРНОГО НАПРЯЖЕНИЯ 6.14. Стабилитроны 6.15. Источник опорного напряжения на стабилитроне ТРЕХВЫВОДНЫЕ И ЧЕТЫРЕХВЫВОДНЫЕ СТАБИЛИЗАТОРЫ 6.16. Трехвыводные стабилизаторы 6.17. Трехвыводные регулируемые стабилизаторы 6.18. Дополнительные замечания относительно трехвыводных стабилизаторов 6.19. Импульсные стабилизаторы и преобразователи постоянного тока ИСТОЧНИКИ ПИТАНИЯ СПЕЦИАЛЬНОГО НАЗНАЧЕНИЯ 6.20. Высоковольтные стабилизаторы 6.21. Источники питания с малым уровнем помех и малым дрейфом 6.22. Микромощные стабилизаторы 6.23. Преобразователи напряжения с переключаемыми конденсаторами (зарядовый насос) 6.24. Источники стабилизированного постоянного тока 6. 25. Коммерческие модули источников питания СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ

Фильтры Баттерворта

Фильтры Баттерворта
Next: Растягивание единичной окружности Up: Проектирование фильтров Предыдущий: Обострительный и полосовой фильтр Содержимое Индекс

Фильтр с одним реальным полюсом и одним реальным нулем может быть сконфигурирован как полочный. фильтр, как фильтр верхних частот (поставив ноль в точке ) или как фильтр нижних частот (поставив ноль на ). Частотные характеристики этих фильтры довольно тупые; иными словами, переходные области широкие. Это часто желательно получить более резкий фильтр, полочный, низкочастотный или высокочастотный, две полосы которого более плоские и разделены более узкой переходной областью.

Процедура, заимствованная из мира аналоговой фильтрации, преобразует реальный, однополюсные, однонулевые фильтры к соответствующим Фильтры Баттерворта , которые имеют более узкие переходные области. Эта процедура четко описана и элегантно в последней главе []. Поскольку это включает проходя от дискретного времени в область непрерывного времени, вывод использует исчисление; это также требует использования понятий комплексного возведения в степень и корней единства, которого мы здесь избегаем.

Чтобы сделать фильтр Баттерворта из фильтра верхних, нижних частот или полочного фильтра фильтр, предположим, что либо полюс, либо ноль задается выражением

где параметр от 1 до . Если это точка , и если это .

Затем, по причинам, которые останутся загадочными, мы заменим точку (будь то полюс или ноль) по точкам, заданным формулой:

где диапазоны значений:

Другими словами, принимает равные углы между и . Точки расположены в комплексной плоскости, как показано на Рисунок 8.17. Они лежат на окружности, проходящей через исходную вещественную точка, которая пересекает единичный круг под прямым углом.

Хороший выбор для номинальной частоты среза или полки, определяемой эти круговые наборы полюсов или нулей — просто место, где окружность пересекает единичную окружность, соответствующую . Это дает точка

что после некоторой алгебры дает угловую частоту, равную

Рисунок 8.17: Замена полюса или нуля с действительным знаком массивом, как для фильтр Баттерворта. В этом примере мы получаем четыре новых полюса или нуля, как показаны, лежащие по окружности, где .

На рис. 8.18, часть (а), показана диаграмма полюс-ноль и частота отклик фильтра нижних частот Баттерворта с тремя полюсами и тремя нулями. Часть (b) показывает частотную характеристику фильтра нижних частот и трех других фильтры, полученные путем выбора различных значений (и, следовательно, ) для нули, оставив полюса неподвижными. По мере продвижения нулей от до , фильтр, который начинается как фильтр нижних частот, становится полочным фильтром, а затем фильтром верхних частот.

Рисунок 8.18: (а). График полюс-ноль для фильтра нижних частот Баттерворта с тремя полюсами и три нуля. Полюса выбираются по частоте среза . (б). Частотные характеристики для четырех фильтров с одинаковыми конфигурация полюсов с различным расположением нулей (но оставляя полюса исправлено). Фильтр нижних частот результаты установки на нули; два полочных фильтра соответствуют и , и, наконец, фильтр верхних частот фильтр получается установка . Фильтр верхних частот нормализован для единичное усиление на частоте Найквиста, а остальные — на единичное усиление на постоянном токе.

---

Next: Растягивание единичной окружности Up: Проектирование фильтров Предыдущий: Обострительный и полосовой фильтр Содержимое Индекс

Миллер Пакетт 21 февраля 2005 г.

КУЛИНАРНАЯ КНИГА BUTTERWORTH-FILTER

КУЛИНАРНАЯ КНИГА BUTTERWORTH-FILTER
Next: Программа поиска фильтра Баттерворта Up: Спектр и фаза Предыдущий: Отношение амплитуды к

Идеальный полосовой фильтр пропускает некоторый диапазон частот без искажений.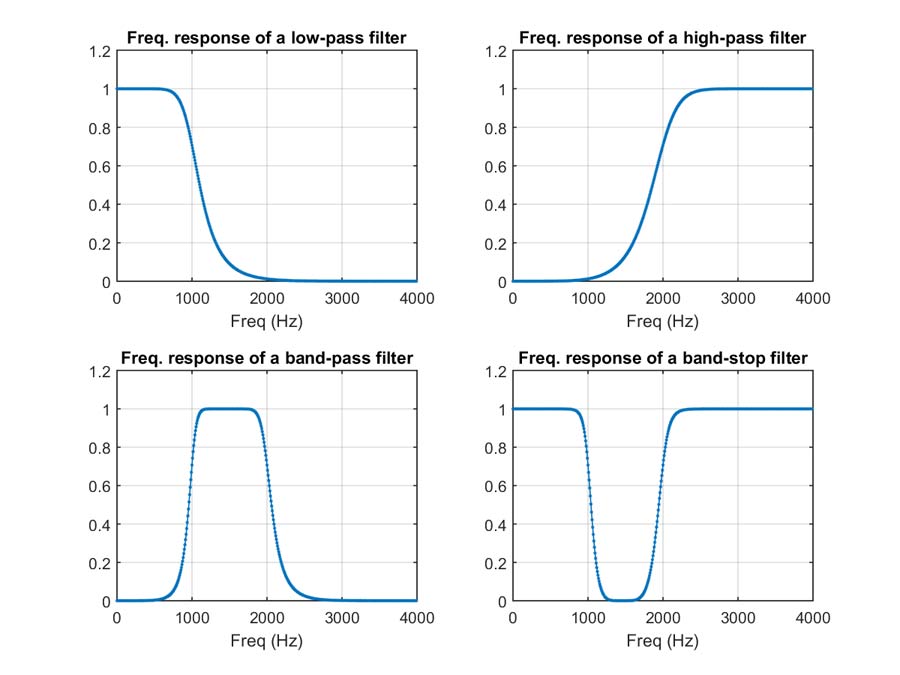 и подавляет все остальные частоты. Дальнейшие размышления показывают, что то, что мы думаем как идеальный полосовой фильтр, прямоугольная функция частоты, вместо этого далек от идеала, потому что его представление во временной области является некаузальным и слишком медленно затухает со временем для многих практических применений. Подходящим полосовым фильтром является один время затухания которого можно выбрать разумным (в сочетании с разумным необходимый компромисс по форме прямоугольника). Фильтр Баттерворта отвечает этим требованиям.

Они причинны и разного порядка, самый низкий порядок является лучшим (кратчайшим) во временной области, и более высокие порядки лучше в частотной области. Хорошо спроектированные проекты часто включают фильтры Баттерворта. К сожалению, они реже используются в экспериментальной работе. из-за сложной проблемы с настройкой что я собираюсь решить для вас здесь. Я приведу несколько примеров и расскажу ловушка с также.

Основная проблема в том, что нет простого математического выражения для коэффициентов фильтра в зависимости от порядка и частоты среза.

Анализ начинается с уравнения что для большого порядка n есть уравнение ящика:

(21)

Когда , этот спектр нижних частот Баттерворта речь идет о единстве. При спектр быстро спадает до нуля. Величина (с некоторыми эффектами усечения, которые будут описаны позже) показано на рисунке 14. для различных значений n . буф
Рисунок 14 Спектры фильтров Баттерворта различного порядка n .

Концептуально самая простая форма фильтрации Баттерворта заключается в переносе данных в частотную область и умножении на уравнение (21), где вы выбрали некоторое значение n для компромисса между требования частотной области (резкая отсечка) и временной области (быстрое затухание). Конечно, представление уравнения во временной области (21) является некаузальным.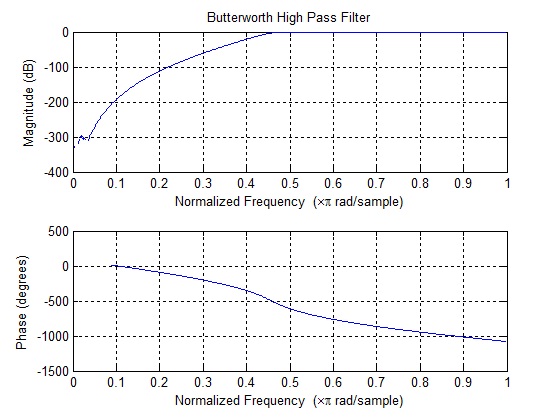 Если вы предпочитаете причинно-следственный фильтр, вы можете взять спектр Баттерворта. в программу спектральной факторизации, такую ​​как kolmogoroff().

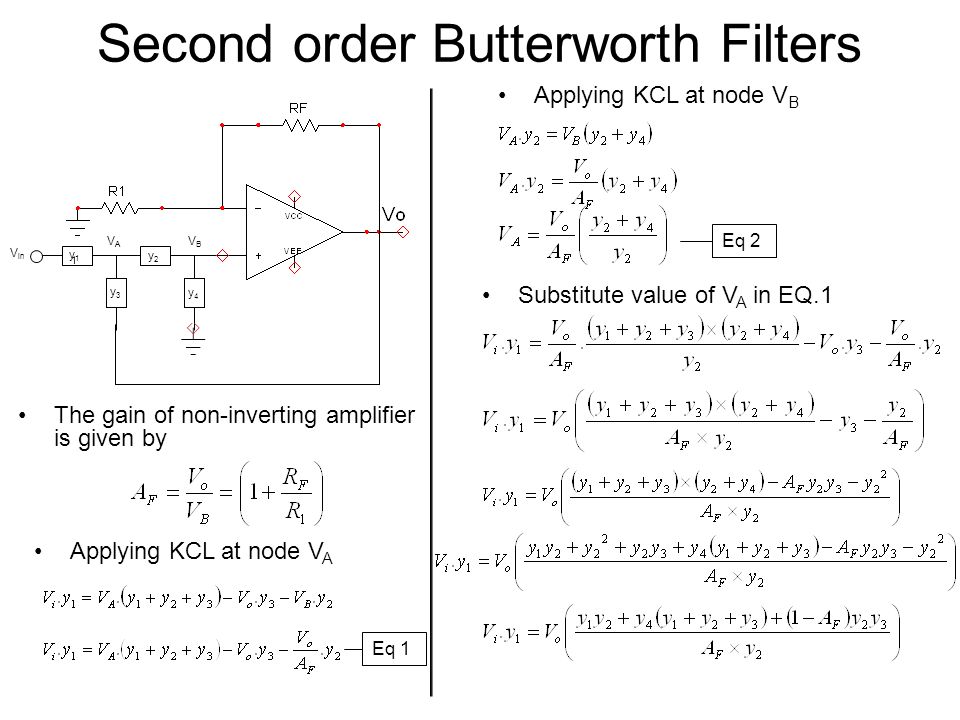
Отклик фильтра Баттерворта во временной области бесконечно велик. хотя фильтр Баттерворта степени n может быть хорошо аппроксимирован отношением полиномов -порядка. Поскольку, как мы увидим, n обычно находится в диапазоне 2-5, фильтрация во временной области быстрее, чем FT. Чтобы продолжить, нам нужно выразить через Z , где .Это делается приближенным образом, действительным для частот далеко от частоты Найквиста. Интуитивно мы знаем, что временная дифференциация подразумевается . Мы видели, что в дискретизированном времени дифференцирование обычно представлено билинейным преобразованием, уравнение (): .Таким образом, представление выборочного времени из

(22)

Подставляя уравнение (22) в (21) находим

		(23)
		(24)

где искомый причинный фильтр Баттерворта в дискретной области В ( Z ) = N ( Z )/ D ( Z ).