Эквивалентность | Введение в математическую логику
Зарегистрируйтесь для доступа к 15+ бесплатным курсам по программированию с тренажером
У современной математики есть собственный формальный язык. С его помощью мы сводим сложные высказывания к формальностям — то есть переводим рассуждения и мысли в плоскость математики. Так мы лучше понимаем мысли других людей, точнее высказываем свои рассуждения и учимся рассуждать логически.
В этом уроке мы продолжим изучать формальный язык логики высказываний. Мы разберем отношения эквивалентности и научимся определять высказывания, которые равнозначны по смыслу. Так мы сможем экономить время и заранее понимать, какие высказывания можно посчитать истинными или ложными без дополнительных рассуждений.
Логическая эквивалентность
Возьмем для примера такое предложение:
Если Вася получит прибавку к зарплате, то он пойдет в театр
С точки зрения логики в этом высказывании есть и такой смысл:
Если Вася не пошел в театр, значит он не получил прибавку к зарплате
Эти высказывания логически эквивалентны — одно можно заменить на другое без потери смысла. В этом и заключается логическая эквивалентность — два выражения считаются эквивалентными, если они имеют одинаковое истинностное значение во всех случаях.
В этом и заключается логическая эквивалентность — два выражения считаются эквивалентными, если они имеют одинаковое истинностное значение во всех случаях.
Как эквивалентность помогает доказывать
Основная польза эквивалентности в том, что она помогает доказывать математические результаты. Допустим, мы знаем, что . Попробуем это доказать.
Можно заменить выражение на другое эквивалентное выражение , которое также будет равно .
Как видите, значение составной пропозиции не изменилось. Значит, эквивалентность помогла нам доказать первоначальное высказывание — .
Как эквивалентность помогает рассуждать
Кроме доказательств, эквивалентность используется и в рассуждениях. Она помогает осмыслить предложение и отнести его к одной из трех категорий в таблице истинности.
Таблица истинности — это разбиение логической функции путем перечисления всех возможных значений, которые может принимать функция. Такая таблица обычно содержит несколько строк и столбцов. В верхней строке представлены логические переменные и комбинации, которые по возрастанию сложности приводят к конечной функции.
Такая таблица обычно содержит несколько строк и столбцов. В верхней строке представлены логические переменные и комбинации, которые по возрастанию сложности приводят к конечной функции.
В логической функции есть три основные операции:
НЕ (Инверсия или отрицание, обозначается как ¬)
ИЛИ (Дизъюнкция или сложение, обозначается как )
И (Конъюнкция или умножение, обозначается как )
Значениям функций обычно присваивается логический ноль (ложь) или логическая единица (истина).
Таблица истинности выглядит так:
¬ | ¬ | ¬ | |
Тавтология | Противоречие | Случайность | Случайность |
Рассмотрим ее подробнее:
Тавтология ( ) — высказывание, которое всегда истинно независимо от того, истинны ли значения переменных внутри него.
 По таблице вся колонка истинна
По таблице вся колонка истиннаПротиворечие или абсурд ( ) — высказывание, которое всегда ложно
Случайность — составное предложение, которое не является ни тавтологией, ни противоречием.
Тавтологии и противоречия помогают доказывать и проверять математические аргументы, а также объяснить
По такой таблице мы можем проверить, эквивалентны ли высказывания a и b.
Иногда в математике полезно заменить одно утверждение другим, но эквивалентным. Возьмем такой пример:
Если четное, то — это целое число
Эквивалентное утверждение звучит так:
Если не целое число, то — это нечетное число
Первое высказывание имело вид «Если
, то
», а второе — «Если не
, то не
».
Законы логической эквивалентности (Законы Моргана)
Ниже приведен список важных законов эквивалентности — также их называют законами алгебры высказываний. На протяжение всего курса мы будем использовать такие законы:
Эквивалентность | Закон | То же, что равенство в булевой алгебре |
Законы тождества | Высказывание с определенным значением (истина или ложь) сохраняет свою первоначальную форму | |
Законы доминирования | : Если в выражении первое И ложно, то все выражение И будет ложным | |
Законы тавтологии | Высказывание принимает только истинные значения в любом случае | |
¬ ¬ | Закон двойного отрицания | Два отрицания эквивалентны отсутствию отрицания |
Законы коммутативности | Результат операции над двумя высказываниями не зависит от того, в каком порядке берутся эти высказывания |
Применим некоторые из этих законов на практике.
Возьмем для примера составное предложение:
Я обедаю в ресторане и иду на танцы
Используем законы де Моргана — они связывают с помощью отрицания конъюнкцию и дизъюнкцию. Можно выразить отрицание так:
Я не буду есть в ресторане или не пойду танцевать
Обратите внимание, что мы отрицаем оба простых предложения и заменили «и» на «или».
В качестве еще одного примера рассмотрим следующее утверждение:
Неверно, что Глеб — доктор, а Вася — инженер
Это переводится на математический язык как:
¬ доктор инженер
Эквивалентное утверждение будет иметь вид:
¬ доктор инженер ¬доктор ¬инженер
Следовательно, мы можем сказать, что Глеб не доктор или Вася не инженер.
Приведенные выше примеры можно легко решить с помощью таблицы истинности. Но это можно сделать только для предложения с небольшим числом переменных — здесь их всего две.
Чем больше переменных, тем менее практично использовать метод таблицы истинности. Для пропозиции с 20 переменными необходимо оценить
строк в таблице истинности. Человеку будет сложно справиться с такой задачей, но можно упростить процесс и воспользоваться компьютером.
Для пропозиции с 20 переменными необходимо оценить
строк в таблице истинности. Человеку будет сложно справиться с такой задачей, но можно упростить процесс и воспользоваться компьютером.
Но если переменных будет больше 1000, вычисление на компьютере будет очень долгим.
А еще бывают случаи, когда можно не строить таблицу истинности — вместо этого можно указать причину, по которой два высказывания логически эквивалентны. При этом мы преобразуем левую часть высказывания, чтобы она соответствовала правой части, и приводим причины каждого преобразования. Как в примере выше:
Высказывание: Если четное, то — целое число
И его эквивалент: Если не целое число, то не четное
При этом преобразование справедливо для любого
Открыть доступ
Курсы программирования для новичков и опытных разработчиков. Начните обучение бесплатно
- 130 курсов, 2000+ часов теории
- 1000 практических заданий в браузере
- 360 000 студентов
Электронная почта *
Отправляя форму, вы принимаете «Соглашение об обработке персональных данных» и условия «Оферты», а также соглашаетесь с «Условиями использования»
Наши выпускники работают в компаниях:
Таблица истинности онлайн | Калькулятор логических выражений
Введите формулу и сгенерируйте таблицу истинности.
Онлайн-калькулятор таблицы истинности предоставляет значения таблицы истинности для заданных формул пропозициональной логики. Утверждения пропозициональной логики могут быть только истинными или ложными.
Разные обозначения логических символов
Для логических символов применяются различные знаки. Вот таблица соответствия, чтобы подобрать и заменить на те которые поддерживаются данным калькулятором (первый зеленый столбец):
Символ | Название | Объяснение | Примеры |
|---|---|---|---|
| Импликация | A ⇒ B ложно, только когда A истинно, а B ложно. → может означать то же самое, что и ⇒ (символ может также указывать область определения и область значений функции, см. ⊃ может означать то же самое, что и ⇒ (символ может также обозначать надмножество). | x = 2 ⇒ x2 = 4 истинно, но x2 = 4 ⇒ x = 2, в общем случае, ложно (поскольку x может быть равен −2). | |
| Тогда и только тогда | A ⇔ B истинно, только если оба значения A и B ложны, либо оба истинны. | x + 5 = y + 2 ⇔ x + 3 = y | |
| конъюнкция | Утверждение A ∧ B истинно, если и A, и B истинны, и ложно в противном случае. | n < 4 ∧ n >2 ⇔ n = 3, если n — натуральное число. | |
| логическая дизъюнкция | Утверждение A ∨ B верно, если A или B (или оба) верны. Если оба не верны, утверждение неверно. Если оба не верны, утверждение неверно. | n ≥ 4 ∨ n ≤ 2 ⇔ n ≠ 3 когда n является натуральным числом. | |
| исключающее или | Утверждение A ⊕ B верно, когда либо A, либо B верно, но не оба. A ⊻ B означает то же самое. | (¬A) ⊕ A всегда верно, A ⊕ A всегда неверно. | |
| Тавтология | Утверждение ⊤ безусловно верно. | A ⇒ ⊤ всегда верно. | |
| Противоречие | Утверждение ⊥ безусловно неверно. | ⊥ ⇒ A всегда неверно. | |
| Квантор всеобщности | ∀ x: P(x) или (x) P(x) означает P(x) верно для всех x. | ∀ n ∈ ℕ: n2 ≥ n. | |
∃ | Квантор существования | ∃ x: P(x) означает, что существует по меньшей мере один x, такой, что P(x) верно. | ∃ n ∈ ℕ: n чётно. |
∃! | Единственность | ∃! x: P(x) означает, что существует ровно один x, такой, что P(x) верно. | ∃! n ∈ ℕ: n + 5 = 2n. |
| Определение | x := y илиx ≡ y означает, что x является другим обозначением для y (но заметьте, что ≡ может означать и другое, как, например, конгруэнтность). P :⇔ Q означает, что P логически эквивалентно Q. | cosh x := (1/2)(exp x + exp (−x)) A XOR B :⇔ (A ∨ B) ∧ ¬(A ∧ B) | |
() | приоритетная группировка | Операции внутри скобок выполняются первыми. | (8 ÷ 4) ÷ 2 = 2 ÷ 2 = 1, но 8 ÷ (4 ÷ 2) = 8 ÷ 2 = 4. |
⊢ | Выводимо | x ⊢ y означает, что y выводимо из x (в некоторых формальных системах). | A → B ⊢ ¬B → ¬A |
⊨ | Модель[en] | x ⊨ y означает, что x семантически влечёт за собой y | A → B ⊨ ¬B → ¬A |
Генератор таблицы истинности
Таблица истинности – это табличное представление всех комбинаций значений для входов и соответствующих им выходов. Это математическая таблица, которая показывает все возможные результаты, которые могут возникнуть из всех возможных сценариев. Она используется для решения логических задач, в алгебре, логике и электронных схемах.
Генератор таблицы истинности выводит все комбинации истинных и ложных условий и вычисляет соответствующее содержание логического выражения.
4.2: Таблицы истинности и анализ аргументов: примеры
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 55942
Таблицы истинности
Поскольку сложные логические операторы могут быть сложными для понимания, мы можем создать таблица истинности для отслеживания того, какие значения истинности для простых утверждений делают сложное утверждение истинным, а какое ложным заявления.
Пример 1
Предположим, вы выбираете новый диван, и ваша вторая половинка говорит: «Купите что-нибудь секционное или с шезлонгом».
Это сложное утверждение состоит из двух более простых условий: «является секционным» и «имеет фаэтон». Для простоты возьмем S для обозначения «является секционным» и C для обозначения «имеет шезлонг». Условие S верно, если кушетка секционная.
Для простоты возьмем S для обозначения «является секционным» и C для обозначения «имеет шезлонг». Условие S верно, если кушетка секционная.
Таблица истинности для этого будет выглядеть так:
| S | C | S или 9003 6 С | |||||
|---|---|---|---|---|---|---|---|
| Т | Т | Т | |||||
| Т | Ф | Т |
| A | B | A ⋀ B |
|---|---|---|
| Т | Т | Т |
| Т | Ф | Ф |
| Ф | Т | Ф |
| Ф | Ф | Ф |
| А | Б | А ⋁ Б |
|---|---|---|
| Т | Т | Т |
| Т | Ф | Т |
| Ф | T | T |
| F | F | F |
| А | ~А |
|---|---|
| T | F |
| F | T |
Таблицы истинности становятся действительно полезными при анализе более сложных логических выражений.
Пример 2
Создайте таблицу истинности для утверждения A ⋀ ~( B ⋁ C )
Это помогает работать изнутри наружу при создании таблиц истинности и создавать таблицы для промежуточных операций. Начнем с перечисления всех возможных комбинаций значений истинности для 9.0036 А , В и С . Обратите внимание, что первый столбец содержит 4 T, за которыми следуют 4 F, второй столбец содержит 2 T, 2 F, затем повторяется, а последний столбец чередуется. Этот шаблон гарантирует рассмотрение всех комбинаций. Наряду с этими начальными значениями мы перечислим значения истинности для самого внутреннего выражения, B ⋁ C .
| А | Б | С | B ⋁ C |
| T | T | T | T |
| Т | Ж | Т | |
| Т | Ж | Т | Т |
| Т | Ф | Ф | Ф |
| Ф | Т | Т | Т |
| Ф | Т | Ф | Т |
| F | F | T | T |
| F | F | F | 9 0070 F
Далее находим отрицание B ⋁ C , отработка столбец B ⋁ C , который мы только что создали.
| А | Б | С | Б ⋁ С | ~( B ⋁ C ) |
| T | T | T | T | F | Т | Т | Ж | Т | Ж |
| Т | Ж | Т | Т | Ф |
| Т | Ф | Ф | Ф | Т |
| Ф | Т | Т | Т | Ф |
| Ф | Т | Ф | Т | Ф |
| Ф | Ф | 9 0070 ТТ | Ф | |
| Ф | Ф | Ф | Ф | T |
Наконец, находим значения A и ~( B ⋁ C )
| А | Б | C | B ⋁ C | ~( B ⋁ C ) | 900 36 А ⋀ ~( Б ⋁ С ) |
| Т | Т | T | T | F | F |
| T | T | F | T | 900 70 FF | |
| T | F | T | T | F | F |
| T | F | F | F | T | T |
| Т | Т | Т | Ф | Ф | |
| Ф | Т | Ф | Т | Ф | Ф |
| Ф | Ф | Т | Т 9007 1 | Ф | Ф |
| Ф | Ф | F | F | T | F |
Оказывается, это сложное выражение верно только в одном случае: если A истинно, B ложно и C ложно.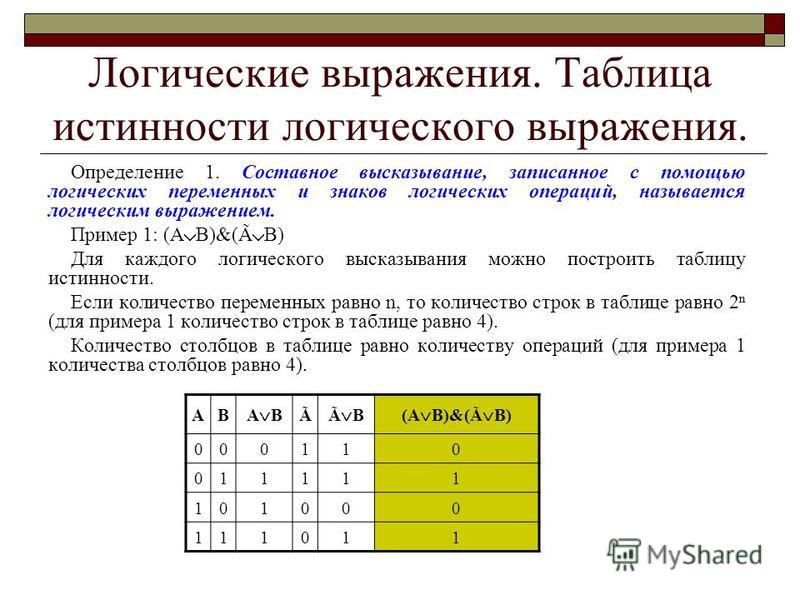
Когда мы обсуждали условия ранее, мы обсуждали тип, при котором мы предпринимаем действие на основе значения условия. Сейчас мы поговорим о более общей версии условного предложения, иногда называемой импликацией .
Импликации
Импликации — это логические условные предложения, утверждающие, что высказывание p , называемое антецедентом, подразумевает следствие q .
Импликации обычно записываются как p → q
Импликации аналогичны условным операторам, которые мы рассматривали ранее; p → q обычно записывается как «если p, то q» или «p, следовательно, q». Разница между импликациями и условными предложениями заключается в том, что условные предложения, которые мы обсуждали ранее, предполагают действие — если условие истинно, то в результате мы предпринимаем какое-то действие. Импликации — это логическое утверждение, предполагающее, что следствие должно логически следовать, если антецедент истинен.
Пример 3
Английское высказывание «Если идет дождь, то облака — это небо» является логическим следствием. Это правильный аргумент, потому что если антецедент «идет дождь» истинен, то следствие «на небе облака» также должно быть истинным.
Обратите внимание, что это утверждение ничего не говорит нам о том, чего ожидать, если не идет дождь. Если антецедент ложен, то импликация становится нерелевантной.
Пример 4
Друг говорит вам, что «если вы загрузите это изображение на Facebook, вы потеряете работу». Возможны четыре исхода:
- Вы загружаете изображение и сохраняете свою работу
- Вы загрузили картинку и потеряли работу
- Вы не загружаете картинку и сохраняете свою работу
- Вы не загрузите картинку и потеряете работу
Есть только один возможный случай, когда ваш друг солгал — первый вариант, когда вы загружаете картинку и сохраняете свою работу. В последних двух случаях ваш друг ничего не сказал о том, что произойдет, если вы не загрузите изображение, поэтому вы не можете заключить, что его заявление недействительно, даже если вы не загрузили изображение и все равно потеряли работа.
В традиционной логике импликация считается достоверной (истинной), если нет случаев, в которых антецедент истинен, а следствие ложно. Важно помнить, что символическая логика не может охватить все тонкости английского языка.
Значения истинности для импликаций
| р | q | р → q |
| Т | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
Пример 5
Построить таблица истинности утверждения ( m ⋀ ~ p ) → r
Начнем с построения таблицы истинности для антецедента.
| м | р | ~ р | м ⋀ ~ р |
| T | 900 70 ТФ | Ф | |
| Т | Ф | Т | Т |
| Ф | Т | Ф | Ф |
| Ф | Ф | Т | Ф |
Теперь мы можем построить таблицу истинности для импликации
| м | р | ~ р | м ⋀ ~ р | р | ( м ⋀ ~ р ) → р |
| Т | Т | Ж | Ж | Т | Т |
| Ф | Т | Т | Т | Т | |
| Ф | Т | Ф | Ф | Т | Т |
| Ф | Ф | Т | Ф | Т | Т |
| Т | Т | Ф | Ф | Ф | Т |
| Т | Ф | Т | Т | Ф | Ф |
| Ф | Т | Ф | Ф | Ф | Т |
| Ф | Ф | Т | Ф | Ф | Т |
В этом случае, когда m верно, p ложно, и r ложно, то антецедент m ⋀ ~ p будет истинным, но следствие ложным, что приведет к недопустимому импликации; каждый другой случай дает правильное следствие.
Для любого следствия есть три связанных утверждения: обратное, обратное и контрапозитивное.
Связанные операторы
Первоначальный вывод: «если p , то q »: p → q
Обратное: «если q 900 37 затем р ”: q → р
Обратное: «если не p , то не q »: ~ p → ~ q
Противоположное «если не q то не р ”: ~ q → ~ р
Пример 6
Снова рассмотрим верный вывод: «Если идет дождь, то на небе облака».
Обратное: «Если на небе облака, значит, идет дождь». Это, конечно, не всегда верно.
Обратное: «Если не идет дождь, то на небе нет облаков». Точно так же это не всегда верно.
Противоположным было бы: «Если на небе нет облаков, значит, не идет дождь». Это утверждение верно и эквивалентно исходному выводу.
Глядя на таблицы истинности, мы видим, что исходное условное и контрапозитивное логически эквивалентны, а обратное и обратное логически эквивалентны.
| Импликация | Конверсия | Инверсия | Контрапозитив | ||
|---|---|---|---|---|---|
| → | → | ~ p → ~ q | ~ q → ~ p | ||
| T | 9 0070 ТТ | Т | Т | Т | |
| Т | Ф | Ф | Т | Т | Ф |
| Ф | Т | Т | Ф 9007 1 | F | T |
| F | F | T | T | T | T |
Эквивалентность
Условное утверждение и его противоположность логически эквивалентны.
Обратное и обратное утверждение логически эквивалентны.
Аргументы
Логический аргумент — это утверждение о том, что набор предпосылок поддерживает вывод. Существует два основных типа аргументов: индуктивные и дедуктивные аргументы.
Существует два основных типа аргументов: индуктивные и дедуктивные аргументы.
Типы аргументов
Ан индуктивный 9Аргумент 0027 использует набор конкретных примеров в качестве посылок и использует их, чтобы предложить общий вывод.
дедуктивный аргумент использует набор общих утверждений в качестве своих предпосылок и использует их, чтобы предложить конкретную ситуацию в качестве вывода.
Пример 7
Аргумент «когда я пошел в магазин на прошлой неделе, я забыл свой кошелек, и когда я пошел сегодня, я забыл свой кошелек. Я всегда забываю свою сумочку, когда иду в магазин» — это индуктивный аргумент.
Предпосылки:
Я забыл свой кошелек на прошлой неделе
Я забыл свой кошелек сегодня
Вывод:
Я всегда забываю свой кошелек
Обратите внимание, что предпосылки представляют собой конкретные ситуации, а вывод — это общее утверждение. . В данном случае это достаточно слабый аргумент, так как он основан всего на двух случаях.
Пример 8
Аргумент «каждый день в течение последнего года в 14:00 над моим домом пролетает самолет. Каждый день в 14:00 над моим домом будет летать самолет» — более сильный индуктивный аргумент, поскольку он основан на большем наборе доказательств.
Оценка индуктивных аргументов
Индуктивный аргумент никогда не сможет доказать истинность вывода, но он может предоставить как слабое, так и сильное доказательство того, что оно может быть верным.
Многие научные теории, такие как теория большого взрыва, никогда не могут быть доказаны. Вместо этого они представляют собой индуктивные аргументы, подкрепленные широким спектром доказательств. Обычно в науке идея считается гипотезой до тех пор, пока она не будет тщательно проверена, после чего она становится теорией. Все общеизвестные научные теории, такие как теория гравитации Ньютона, выдержали годы испытаний и доказательств, хотя иногда их необходимо корректировать на основе новых данных. Для гравитации это произошло, когда Эйнштейн предложил общую теорию относительности.
Дедуктивный аргумент является более верным или нет, что облегчает его оценку.
Оценка дедуктивных аргументов
Дедуктивный аргумент считается верным, если все посылки верны и вывод логически следует из этих посылок. Другими словами, посылки истинны, и заключение обязательно следует из этих посылок.
Пример 9
Аргумент «Все кошки — млекопитающие, а тигр — кошка, значит, тигр — млекопитающее» является действительным дедуктивным аргументом.
Посылки:
Все кошки млекопитающие
Тигр есть кошка
Вывод:
Тигр есть млекопитающее
Обе посылки верны. Чтобы увидеть, что посылки должны логически вести к заключению, можно использовать диаграмму Венна. Из первой посылки мы можем заключить, что множество кошек является подмножеством множества млекопитающих. Из второй посылки нам говорят, что тигр находится в множестве кошек. Отсюда на диаграмме Венна видно, что тигр также находится внутри множества млекопитающих, так что вывод верен.
Анализ аргументов с помощью диаграмм Венна
[1]Чтобы проанализировать аргумент с помощью диаграммы Венна
- Нарисуйте диаграмму Венна на основе посылок аргумента
- Если помещения недостаточно для определения того, что определяет расположение элемента, укажите это.
- Аргумент действителен, если ясно, что вывод должен быть верным
Пример 10
Предпосылка: Все пожарные знают CPR
Посылка: Джилл знает СЛР
Вывод: Джилл — пожарный
Из первой посылки мы знаем, что все пожарные входят в группу тех, кто знает СЛР. Из второй посылки мы знаем, что Джилл является членом этого большего множества, но у нас недостаточно информации, чтобы узнать, является ли она также членом меньшего подмножества, то есть пожарных.
Поскольку вывод не обязательно следует из посылок, это неверный аргумент, независимо от того, действительно ли Джилл является пожарным.
Важно отметить, что действительно ли Джилл пожарный или нет, не имеет значения для оценки обоснованности аргумента; нас интересует только то, достаточно ли посылок для доказательства вывода.
В дополнение к этим категориальным посылкам стиля в форме «все ___», «некоторые ____» и «нет ____», также часто встречаются посылки, являющиеся импликациями.
Пример 11
Помещение: Если вы живете в Сиэтле, вы живете в Вашингтоне.
Посылка: Маркус не живет в Сиэтле
Вывод: Маркус не живет в Вашингтоне
Из первой посылки мы знаем, что множество людей, живущих в Сиэтле, находится внутри множества тех, кто живет в Вашингтоне. Из второй посылки мы знаем, что Маркус не входит в набор Сиэтла, но у нас недостаточно информации, чтобы узнать, живет ли Маркус в Вашингтоне или нет. Это неверный аргумент.
Пример 12
Рассмотрим аргумент «Вы женаты, поэтому у вас должна быть жена».
Это неверный аргумент, поскольку, по крайней мере в некоторых частях мира, есть мужчины, состоящие в браке с другими мужчинами, поэтому предпосылка не является недостаточной, чтобы подразумевать заключение.
Некоторые аргументы лучше анализировать с помощью таблиц истинности.
Пример 13
Рассмотрим аргумент:
Посылка: Если вы купили хлеб, то вы пошли в магазин
Посылка: Вы купили хлеб
Вывод: Вы пошли в магазин
Пока это пример, надеюсь, достаточно очевиден. аргумент, мы можем проанализировать его, используя таблицу истинности, представив каждую из посылок символически. Затем мы можем рассмотреть импликацию о том, что посылки вместе подразумевают заключение. Если таблица истинности является тавтологией (всегда истинной), то аргумент действителен.
Мы получим B, означающее «вы купили хлеб», а S — «вы пошли в магазин». Тогда аргумент принимает вид:
Посылка: B → S
Посылка: B
Заключение: S
Чтобы проверить достоверность, мы смотрим, подразумевает ли комбинация обеих посылок заключение; правда ли, что [( B → S ) ⋀ B ] → S ?
| B | S | B → S | ( B → S ) ⋀ Б | [( Б → С ) ⋀ Б ] → S |
| T | T | T | T | T |
| T | Ф | Ф | Ф | Т |
| Ф | Т | Т | F | T |
| F | F | T | F | T |
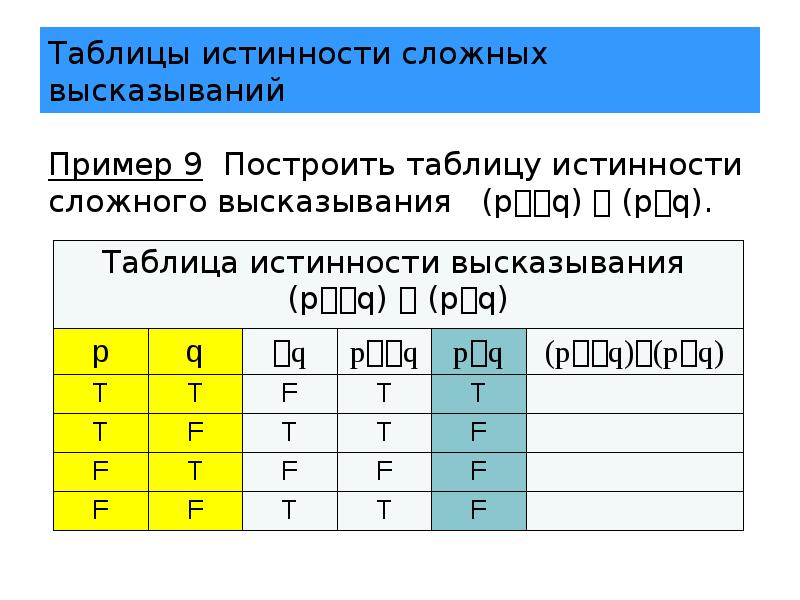
Анализ аргументов с использованием таблиц истинности
Анализ аргументов с помощью таблицы истинности:
- Символическое представление каждой из предпосылок
- Создайте условный оператор, соединив все посылки с помощью и для формирования антецедента и используя заключение в качестве следствия.
- Создайте таблицу истинности для этого утверждения. Если это всегда истинно, то аргумент действителен.
Пример 14
Предпосылка: Если я пойду в торговый центр, то я куплю новые джинсы
Предпосылка: Если я куплю новые джинсы, я куплю к ним рубашку
Вывод: Если я пойду в торговый центр , я куплю рубашку.
Let M = Я иду в торговый центр, J = Я покупаю джинсы и S = Я покупаю рубашку.
Посылки и заключение можно сформулировать так:
Посылка: M → J
Посылка: J → S
Вывод: M → S
Мы можем построить таблицу истинности для [( M → J ) ⋀ ( J → S )] → ( M → S )
| M | J | S | M → J | J → S | ( M → J ) ⋀ ( J → S ) | 9 0036 M → S | [( M → J ) ⋀ ( J → S )] → ( M → S ) |
| T | T | T 9007 1 | Т | Т | Т | Т | Т |
| Т | Т | Ф | T | F | F | F | T |
| T | F | T | F | Т | Ф | Т | Т |
| Т | Ф | F | F | T | F | F | T |
| F | T | T 9007 1 | Т | Т | Т | Т | Т |
| Ф | Т | Ф | Т | Ф | Ф | Т | Т |
| Ф | Ф | Т | Т | Т | Т | Т | Т |
| Ф | Ф | Ф | Т | Т | Т | Т | Т 9007 1 |
Из таблицы истинности мы видим, что это правильный аргумент.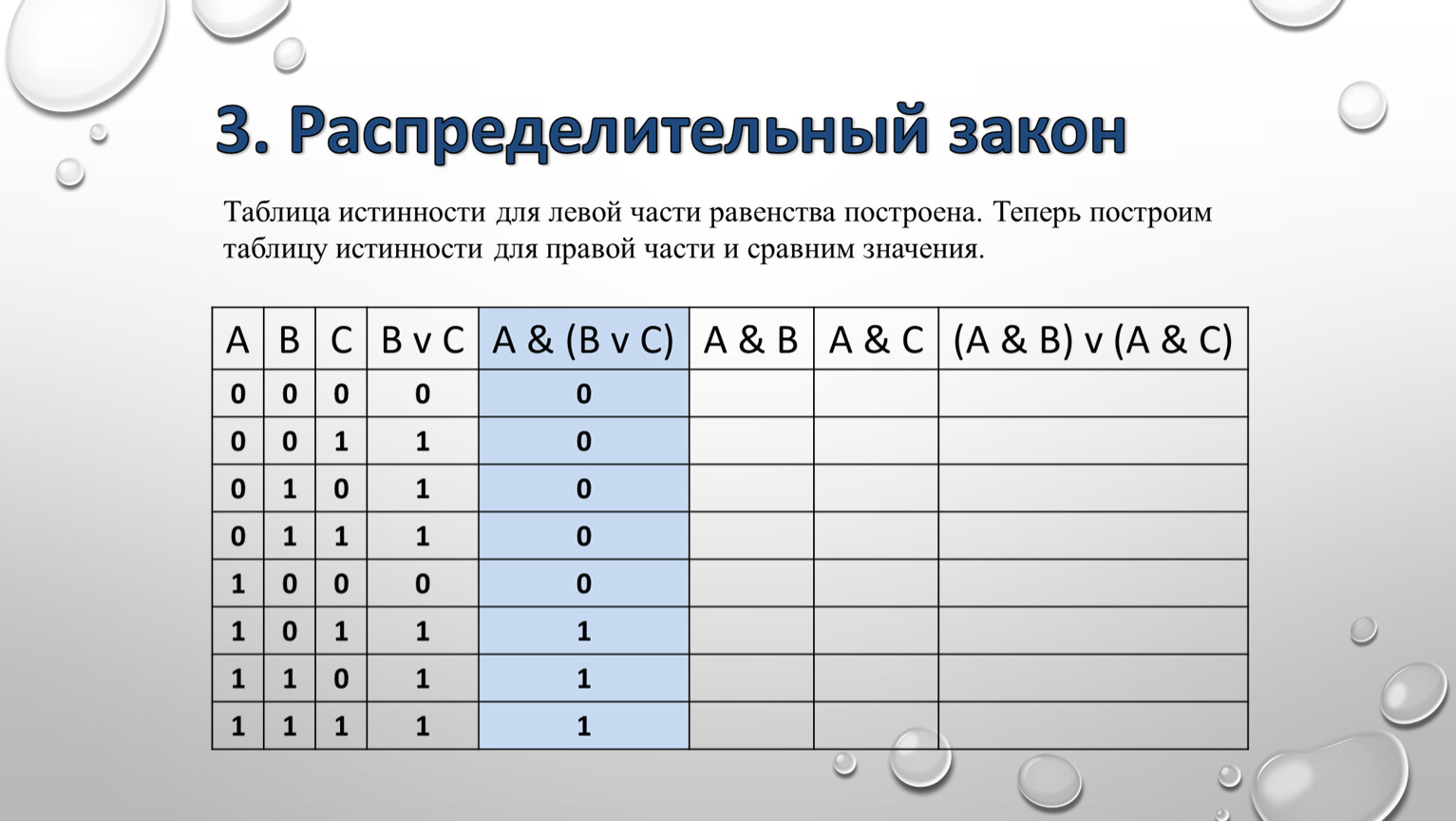
- Технически это круги Эйлера или диаграммы Эйлера, а не диаграммы Венна, но для простоты мы будем продолжать называть их диаграммами Венна. ↵
Контент с лицензией CC, ранее опубликованный
- Logic. Автор : Дэвид Липпман. Расположен по адресу : http://www.opentextbookstore.com/mathinsociety/. Проект : Математика в обществе. Лицензия : CC BY-SA: Attribution-ShareAlike
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Программа OER или Publisher
- Люмен
- Теги

1.10 Интерпретация таблиц истинности | Математика для гуманитарных специальностей
Цели обучения
Интерпретация таблиц истинности
- Тавтология
- Противоречие
- Непредвиденные обстоятельства
- Логически эквивалентен
Тавтология — это предложение, которое всегда истинно, независимо от значений истинности содержащихся в нем пропозициональных переменных. Предложение, которое всегда ложно, называется 9.0026 противоречие . Предложение, которое не является ни тавтологией, ни противоречием, называется случайностью .
Примеры
Пример тавтологии : Я собираюсь сдавать математику для гуманитарных наук в этом семестре или я не собираюсь сдавать математику для гуманитарных наук в этом семестре. Это утверждение всегда верно, так что это тавтология.
Пример внутреннего противоречия : Я получу пятерку по этому классу и не получу пятерку по этому классу. Это утверждение всегда ложно, поэтому оно противоречит самому себе.
Это утверждение всегда ложно, поэтому оно противоречит самому себе.
Предупреждение: Не делайте ошибку, считая каждое утверждение либо тавтологией, либо внутренним противоречием. Мы видели много примеров таблиц истинности, в последнем столбце которых есть смесь истин и ложностей. Эти утверждения иногда верны, а иногда нет. Они называются непредвиденными обстоятельствами .
Примеры
Заполните таблицу истинности, чтобы классифицировать утверждение как тавтологию, внутреннее противоречие или случайность.
а. р (~р)
б. (p q) (~p ~q)
Решение:
а. Это тавтология
b. Это внутреннее противоречие
Логически эквивалентные утверждения
Когда значения истинности для двух утверждений идентичны, высказывания считаются логически эквивалентными. То есть оба состава одних и тех же простых высказываний имеют одинаковое значение.
Общие эквивалентные операторы
~(~p) p г.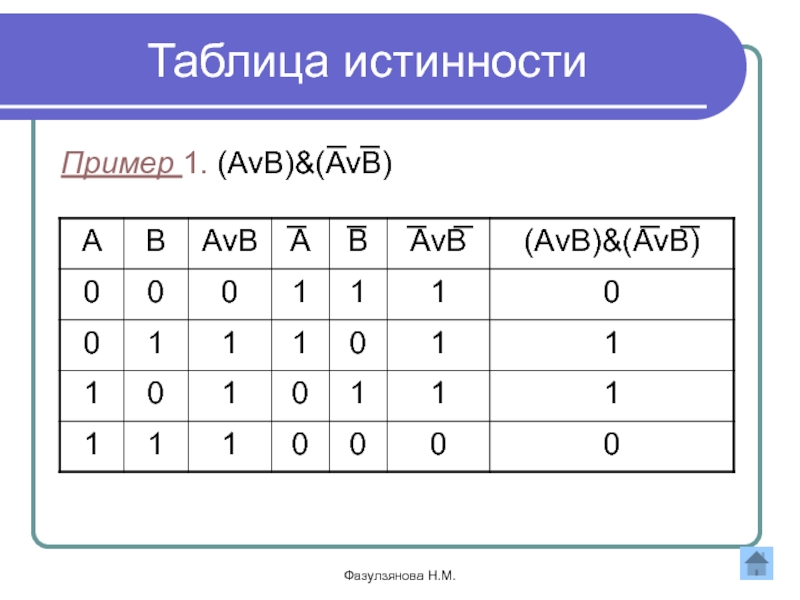


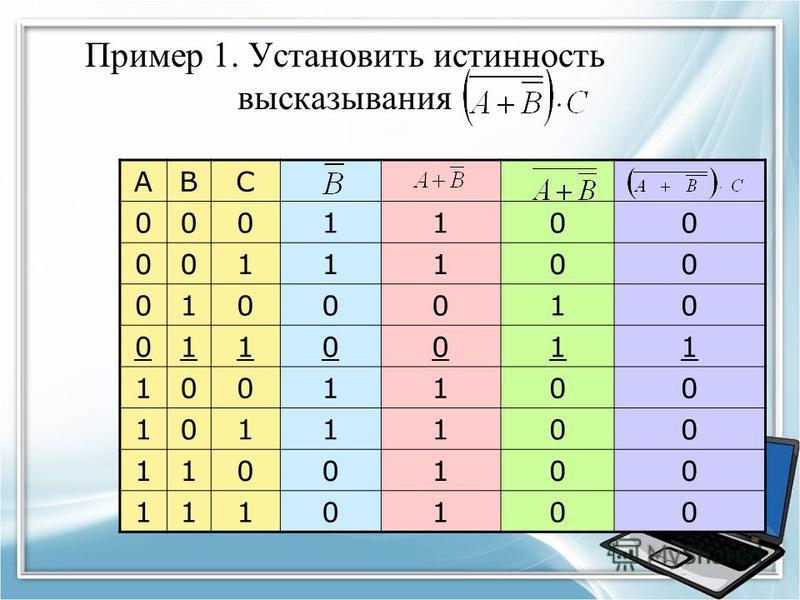 По таблице вся колонка истинна
По таблице вся колонка истинна

