2.Логические элементы и, или, не. Таблицы истинности, принципиальные схемы.
Условное обозначение на структурных схемах схемы И с двумя входами представлено на рис.1, а таблица истинности в таблице 1.
Таблица 1
х | у | х * у |
0 | 0 | 0 |
0 | 1 | 0 |
1 | 0 | 0 |
1 |
| 1 |
Единица
на выходе схемы И будет тогда и только
тогда, когда на всех входах будут единицы. Когда хотя бы на одном входе будет ноль,
на выходе также будет ноль.
Когда хотя бы на одном входе будет ноль,
на выходе также будет ноль.
Связь между выходом z этой схемы и входами х и у описывается отношением z = х * у (читается как «х и у»).
Операция конъюнкции на функциональных схемах обозначается знаком & (читается как «амперсэнд»), являющимся сокращенной записью английского слова and.
Схема ИЛИ реализует дизъюнкцию двух или более логических значений.
Когда хотя бы на одном входе схемы ИЛИ будет единица, на ее выходе также будет единица.
Условное обозначение схемы ИЛИ знак «1». Связь между выходом z этой схемы и входами х и у описывается соотношением z = х + у (читается как «х или у»). Рис.2 и таблица 2.
Таблица 2
х | у | х + у |
0 | 0 | 0 |
0 | 1 | |
1 | 0 | 1 |
1 | 1 | 1 |
Схема
НЕ (инвертор) реализует операцию
отрицания.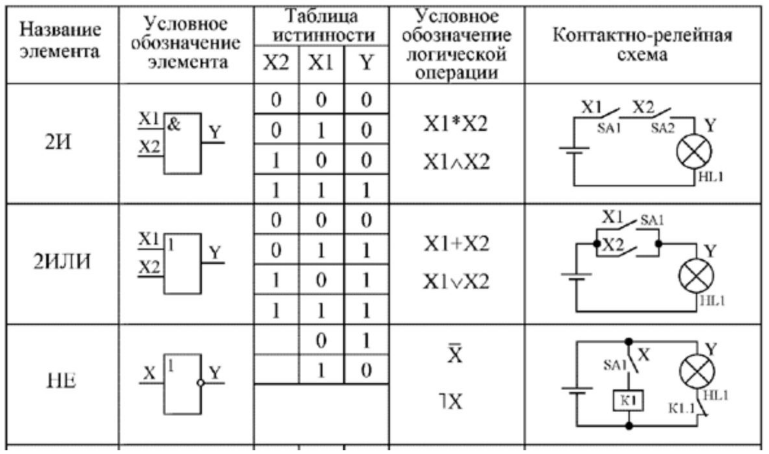
Связь между входом х этой схемы и выходом z можно записать соотношением z = , где читается как «не х» или «инверсия х».
Если на входе схемы 0, то на выходе 1. Когда на входе 1, на выходе 0. Условное обозначение инвертора — на рис.3, а таблица истинности – в таблице 3
.
Таблица 3
x | |
0 | 1 |
1 | 0 |
3.Логические элементы и — не, или — не. Таблицы истинности. Графическое представление элементов. Графики работы.
Связь между выходом z и входами х и у схемы записывают следующим образом:
z = , где читается как «инверсия х и у».
рис. 4
Таблица 4
х | у | |
0 | 0 | 1 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 0 |
Условное
обозначение схемы И-НЕ представлено на
рис.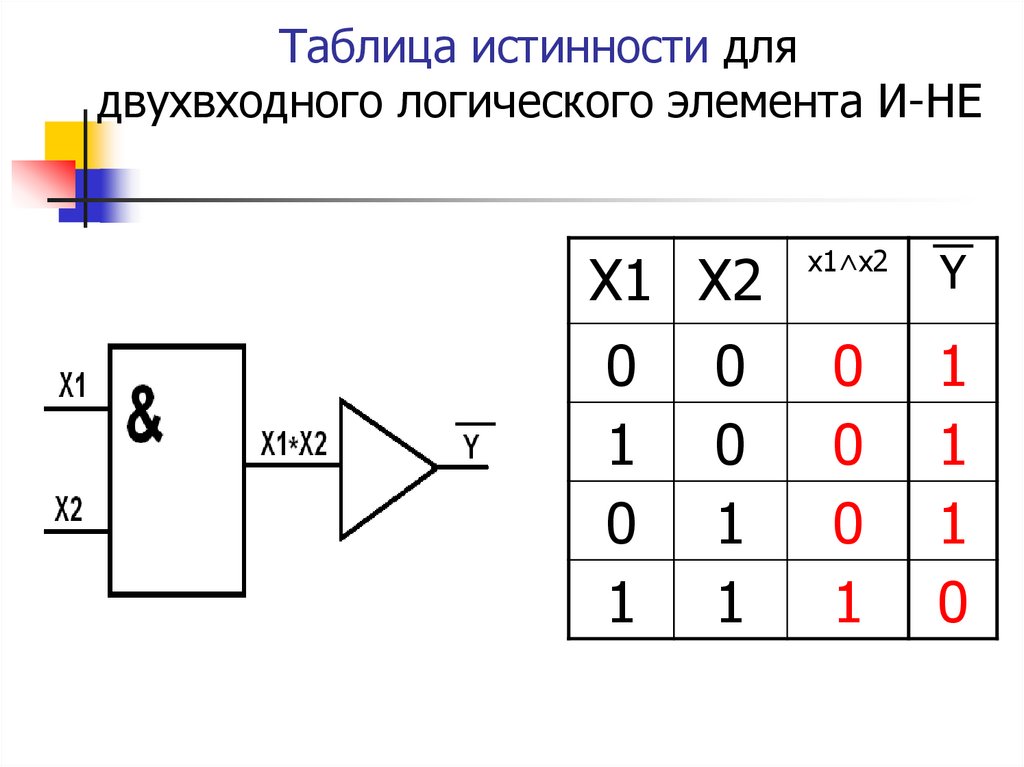 4, а таблица истинности схемы И-НЕ
– в таблице 4.
4, а таблица истинности схемы И-НЕ
– в таблице 4.
Схема ИЛИ-НЕ состоит из элемента ИЛИ и инвертора и осуществляет отрицание результата схемы ИЛИ.
Связь между выходом z и входами х и у схемы записывают следующим образом:
z = , где читается как «инверсия х или у».
Таблица 5
х | у | |
0 | 0 | 1 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 0 |
Условное
обозначение схемы ИЛИ-НЕ представлено
на рис. 5, а таблица истинности схемы
ИЛИ-НЕ – в таблице 5
5, а таблица истинности схемы
ИЛИ-НЕ – в таблице 5
4.Исключающие или, исключающие или — не. Таблицы истинности. Графическое представление элементов.
лементы Исключающее ИЛИ (по-английски — Exclusive-OR) также можно было бы отнести к простейшим элементам, но функция, выполняемая ими, несколько сложнее, чем в случае элемента И или элемента ИЛИ. Все входы элементов Исключающее ИЛИ равноправны, однако ни один из входов не может заблокировать другие входы, установив выходной сигнал в уровень единицы или нуля.
Таблица 4.1. Таблица истинности двухвходовых элементов И, И-НЕ, ИЛИ, ИЛИ-НЕ
Вход 1 | Вход 2 | Выход |
0 | 0 | 0 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 0 |
Рис.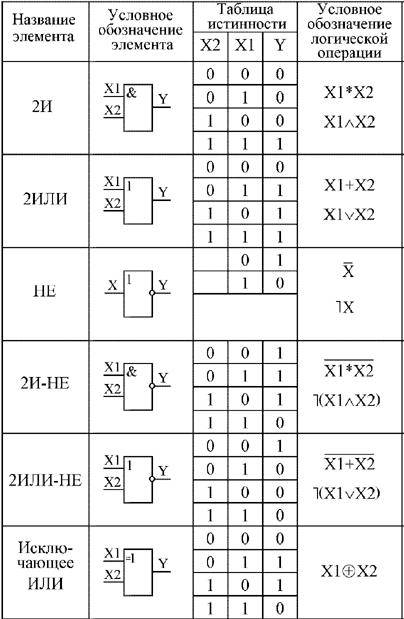 4.1.
Обозначения элементов Исключающее ИЛИ:
зарубежные (слева) и отечественные
(справа)
4.1.
Обозначения элементов Исключающее ИЛИ:
зарубежные (слева) и отечественные
(справа)
Под функцией Исключающее ИЛИ понимается следующее: единица на выходе появляется тогда, когда только на одном входе присутствует единица. Если единиц на входах две или больше, или если на всех входах нули, то на выходе будет нуль. Таблица истинности двухвходового элемента Исключающее ИЛИ приведена в табл. 4.1. Обозначения, принятые в отечественных и зарубежных схемах, показаны на рис. 4.1. Надпись на отечественном обозначении элемента Исключающее ИЛИ “=1″ как раз и обозначает, что выделяется ситуация, когда на входах одна и только одна единица.
Элементов Исключающее ИЛИ в стандартных сериях немного. Отечественные серии предлагают микросхемы ЛП5 (четыре двухвходовых элемента с выходом 2С), ЛЛ3 и ЛП12, отличающиеся от ЛП5 выходом ОК. Слишком уж специфическая функция реализуется этими элементами.
С
точки зрения математики, элемент
Исключающее ИЛИ выполняет операцию так
называемого суммирования по модулю 4.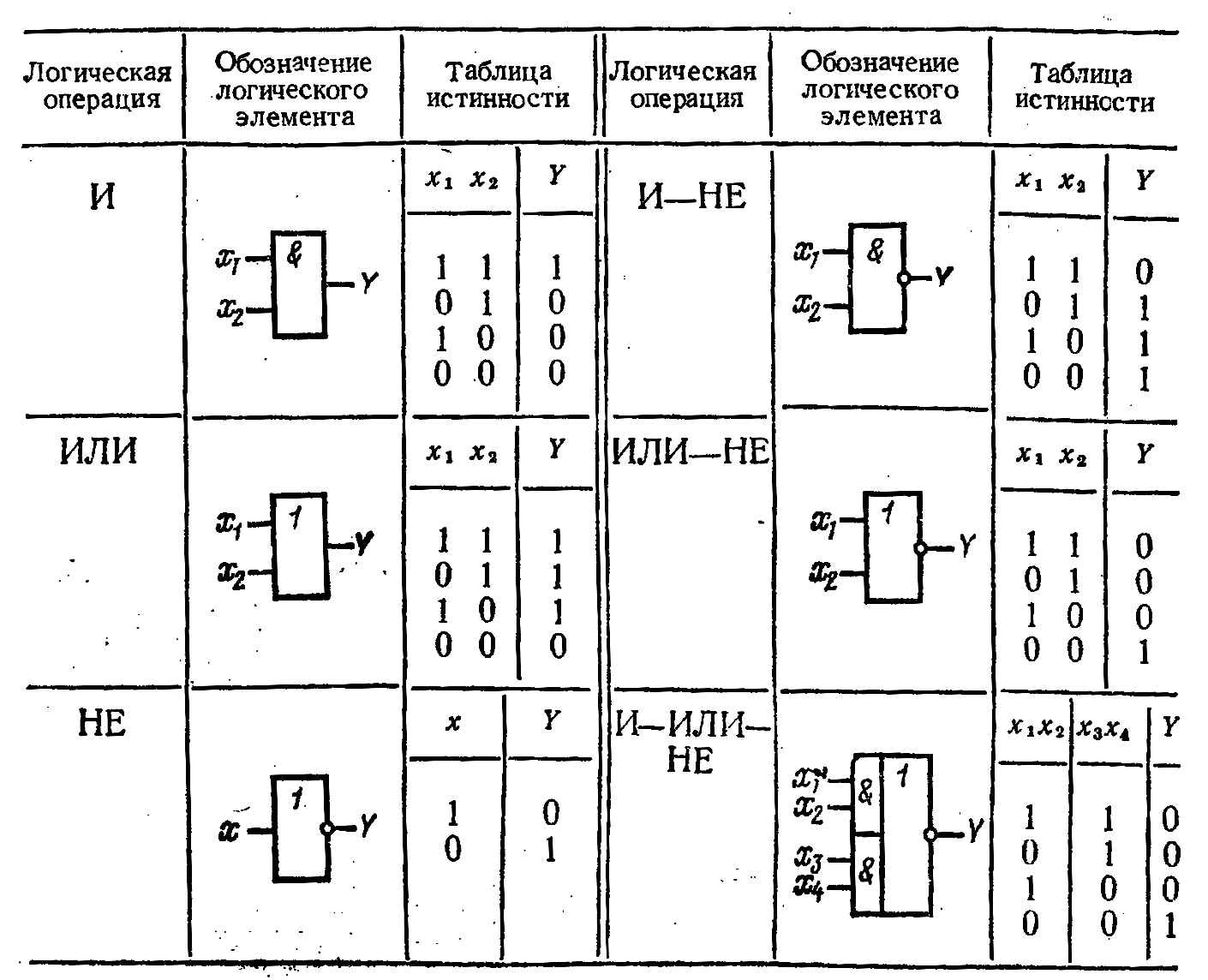 Поэтому эти элементы также называются
сумматорами по модулю два. Как уже
отмечалось в предыдущей лекции,
обозначается суммирование по модулю 2
знаком плюса, заключенного в кружок.
Поэтому эти элементы также называются
сумматорами по модулю два. Как уже
отмечалось в предыдущей лекции,
обозначается суммирование по модулю 2
знаком плюса, заключенного в кружок.
Основное применение элементов Исключающее ИЛИ, прямо следующее из таблицы истинности, состоит в сравнении двух входных сигналов. В случае, когда на входы приходят две единицы или два нуля (сигналы совпадают), на выходе формируется нуль (см. табл. 4.1). Обычно при таком применении на один вход элемента подается постоянный уровень, с которым сравнивается изменяющийся во времени сигнал, приходящий на другой вход. Но значительно чаще для сравнения сигналов и кодов применяются специальные микросхемы компараторов кодов, которые будут рассмотрены в следующей лекции.
В
качестве сумматора по модулю 2 элемент
Исключающее ИЛИ используется также в
параллельных и последовательных
делителях по модулю 2, служащих для
вычисления циклических контрольных
сумм. Но подробно эти схемы будут
рассмотрены в лекциях 14,15.
Важное применение элементов Исключающее ИЛИ — это управляемый инвертор (рис. 4.2). В этом случае один из входов элемента используется в качестве управляющего, а на другой вход элемента поступает информационный сигнал. Если на управляющем входе единица, то входной сигнал инвертируется, если же нуль — не инвертируется. Чаще всего управляющий сигнал задается постоянным уровнем, определяя режим работы элемента, а информационный сигнал является импульсным. То есть элемент Исключающее ИЛИ может изменять полярность входного сигнала или фронта, а может и не изменять в зависимости от управляющего сигнала.
Рис. 4.2. Элемент Исключающее ИЛИ как управляемый инвертор
В
случае, когда имеется два сигнала
одинаковой полярности (положительные
или отрицательные), и при этом их
одновременный приход исключается,
элемент Исключающее ИЛИ может быть
использован для смешивания этих сигналов
(рис. 4.3). При любой полярности входных
сигналов выходные сигналы элемента
будут положительными.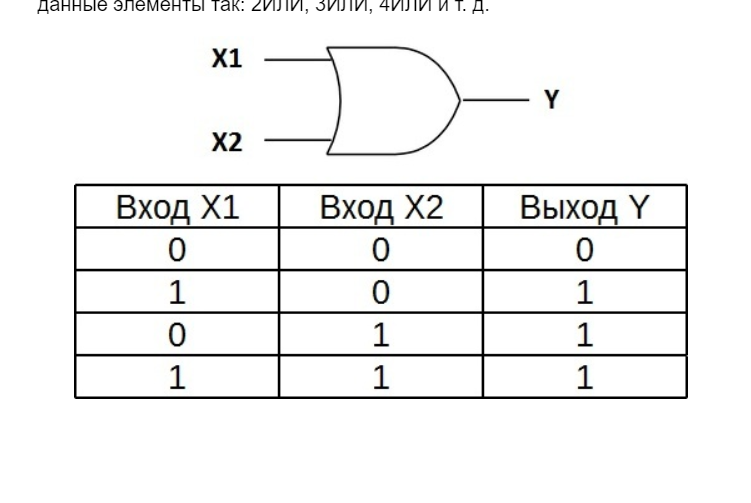 При положительных
входных сигналах элемент Исключающее
ИЛИ будет работать как элемент 2ИЛИ, а
при отрицательных он будет заменять
элемент 2И-НЕ. Такие замены могут быть
полезны в тех случаях, когда в схеме
остаются неиспользованными некоторые
элементы Исключающее ИЛИ. Правда, при
этом надо учитывать, что задержка
распространения сигнала в элементе
Исключающее ИЛИ обычно несколько больше
(примерно в 1,5 раза), чем задержка в
простейших элементах И, И-НЕ, ИЛИ, ИЛИ-НЕ.
При положительных
входных сигналах элемент Исключающее
ИЛИ будет работать как элемент 2ИЛИ, а
при отрицательных он будет заменять
элемент 2И-НЕ. Такие замены могут быть
полезны в тех случаях, когда в схеме
остаются неиспользованными некоторые
элементы Исключающее ИЛИ. Правда, при
этом надо учитывать, что задержка
распространения сигнала в элементе
Исключающее ИЛИ обычно несколько больше
(примерно в 1,5 раза), чем задержка в
простейших элементах И, И-НЕ, ИЛИ, ИЛИ-НЕ.
Рис. 4.3. Применение элемента Исключающее ИЛИ для смешивания двух неодновременных сигналов
Рис. 4.4. Выделение фронтов входного сигнала с помощью элемента Исключающее ИЛИ
Еще
одно важнейшее применение элемента
Исключающее ИЛИ — формирование коротких
импульсов по любому фронту входного
сигнала (рис. 4.4). В данном случае не
важно, положительный фронт входного
сигнала или отрицательный, на выходе
все равно формируется положительный
импульс. Входной сигнал задерживается
с помощью конденсатора или цепочки
элементов, а затем исходный сигнал и
его задержанная копия поступают на
входы элемента Исключающее ИЛИ. В обеих
схемах в качестве элементов задержки
используются также двувходовые элементы
Исключающее ИЛИ в неинвертирующем
включении (на неиспользуемый вход
подается нуль). В результате такого
преобразования можно говорить об
удвоении частоты входного сигнала, так
как выходные импульсы следуют вдвое
чаще, чем входные.
Входной сигнал задерживается
с помощью конденсатора или цепочки
элементов, а затем исходный сигнал и
его задержанная копия поступают на
входы элемента Исключающее ИЛИ. В обеих
схемах в качестве элементов задержки
используются также двувходовые элементы
Исключающее ИЛИ в неинвертирующем
включении (на неиспользуемый вход
подается нуль). В результате такого
преобразования можно говорить об
удвоении частоты входного сигнала, так
как выходные импульсы следуют вдвое
чаще, чем входные.
Данную особенность элементов Исключающее ИЛИ надо учитывать в том случае, когда на оба входа элемента поступают изменяющиеся одновременно сигналы. При этом на выходе элемента возможно появление коротких паразитных импульсов по любому из фронтов входных сигналов. Исключить их влияние на дальнейшую схему можно, например, с помощью синхронизации, подобной рассмотренной в предыдущем разделе.
Логические элементы И, или, не, и-не, или-не и их таблицы истинности
Download 196,63 Kb.
|
1 2 3 4
Bog’liqЛогические элементы И
9, Algoritm 2, 5-11 SINFLARGA ISH REJA 2020-2021 YANGI(1), DAFTAR MUQOVASI(1), Fizika 7-sinf nazorat ishlari 2016-2017, Fizika 7-sinf nazorat ishlari 2016-2017, 2 5460652021776387923, 2 5460652021776387923, Документ Microsoft Word, 6 sinf botanika imtihon javoblari, Reaksiya kitobcha, SHAHRISABZ, Korporativ boshqaruv LOTIN 2020
- Bu sahifa navigatsiya:
- Логический элемент
- Логический элемент «И» — конъюнкция, логическое умножение, AND
| Логические элементы И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ и их таблицы истинности Электрическая схема, предназначенная для выполнения какой-либо логической операции с входными данными, называется логическим элементом. Входные данные представляются здесь в виде напряжений различных уровней, и результат логической операции на выходе — также получается в виде напряжения определенного уровня. Операнды в данном случае подаются в двоичной системе счисления — на вход логического элемента поступают сигналы в форме напряжения высокого или низкого уровня, которые и служат по сути входными данными. Так, напряжение высокого уровня — это логическая единица 1 — обозначает истинное значение операнда, а напряжение низкого уровня 0 — значение ложное. 1 — ИСТИНА, 0 — ЛОЖЬ. Логический элемент — элемент, осуществляющий определенные логические зависимость между входными и выходными сигналами. Логические элементы обычно используются для построения логических схем вычислительных машин, дискретных схем автоматического контроля и управления. Для всех видов логических элементов, независимо от их физической природы, характерны дискретные значения входных и выходных сигналов. Логические элементы имеют один или несколько входов и один или два (обычно инверсных друг другу) выхода. Значения «нулей» и «единиц» выходных сигналов логических элементов определяются логической функцией, которую выполняет элемент, и значениями «нулей» и «единиц» входных сигналов, играющих роль независимых переменных. В зависимости от устройства схемы элемента, от ее электрических параметров, логические уровни (высокие и низкие уровни напряжения) входа и выхода имеют одинаковые значения для высокого и низкого (истинного и ложного) состояний. Традиционно логические элементы выпускаются в виде специальных радиодеталей — интегральных микросхем. Логические операции, такие как конъюнкция, дизъюнкция, отрицание и сложение по модулю (И, ИЛИ, НЕ, исключающее ИЛИ) — являются основными операциями, выполняемыми на логических элементах основных типов. Далее рассмотрим каждый из этих типов логических элементов более внимательно. Логический элемент «И» — конъюнкция, логическое умножение, AND «И» — логический элемент, выполняющий над входными данными операцию конъюнкции или логического умножения. Данный элемент может иметь от 2 до 8 (наиболее распространены в производстве элементы «И» с 2, 3, 4 и 8 входами) входов и один выход. Условные обозначения логических элементов «И» с разным количеством входов приведены на рисунке. В тексте логический элемент «И» с тем или иным числом входов обозначается как «2И», «4И» и т. д. — элемент «И» с двумя входами, с четырьмя входами и т. д. Таблица истинности для элемента 2И показывает, что на выходе элемента будет логическая единица лишь в том случае, если логические единицы будут одновременно на первом входе И на втором входе. В остальных трех возможных случаях на выходе будет ноль. На западных схемах значок элемента «И» имеет прямую черту на входе и закругление на выходе. На отечественных схемах — прямоугольник с символом «&». Download 196,63 Kb. Do’stlaringiz bilan baham: |
1 2 3 4
Ma’lumotlar bazasi mualliflik huquqi bilan himoyalangan ©hozir.org 2023
ma’muriyatiga murojaat qiling
Логика
. Можно ли использовать И, ИЛИ и НЕ для представления любой таблицы истинности?
Да, любая функция истинности, независимо от ее сложности и количества входных данных, может быть выражена с помощью $\land$, $\lor$ и $\neg$.
Мы можем доказать это напрямую, сгенерировав конъюнкцию для каждой строки, где функция оценивается как истина, а затем дизъюнкцией всех этих конъюнкций, и секунда размышлений прояснит, что результирующее выражение фиксирует функцию истинности (если нет строки, в которой функция оценивается как $T$, тогда просто используйте выражение $P \land \neg P$)
Например, предположим, что у нас есть функция истинности, условия истинности которой даны в следующей таблице:
\begin{array}{ccc|c} P&Q&R&f(P,Q,R)\\ \hline Т&Т&Т&Ф\\ Т&Т&Ф&Т\\ Т&Ф&Т&Ф\\ Т&Ф&Ф&Т\\ Ф&Т&Т&Т\\ Ф&Т&Ф&Ф\\ Ф&Ф&Т&Ф\\ Ж&Ж&Ж&Ж\\ \end{array}
Эта функция верна в строках 2, 4 и 5, поэтому мы порождаем термы $P \land Q \land \neg R$, $P \land \neg Q \land \neg R $ и $\neg P \land Q \land R$ соответственно. Разделение их дает нам:
$$(P \land Q \land \neg R) \lor (P \land \neg Q \land \neg R) \lor (\neg P \land Q \land R)$$
Эта формула в Дизъюнктивной нормальной форме (DNF): это обобщенная дизъюнкция, где каждая дизъюнкция является обобщенной конъюнкцией литералов, а литерал является либо атомарной переменной, либо ее отрицанием.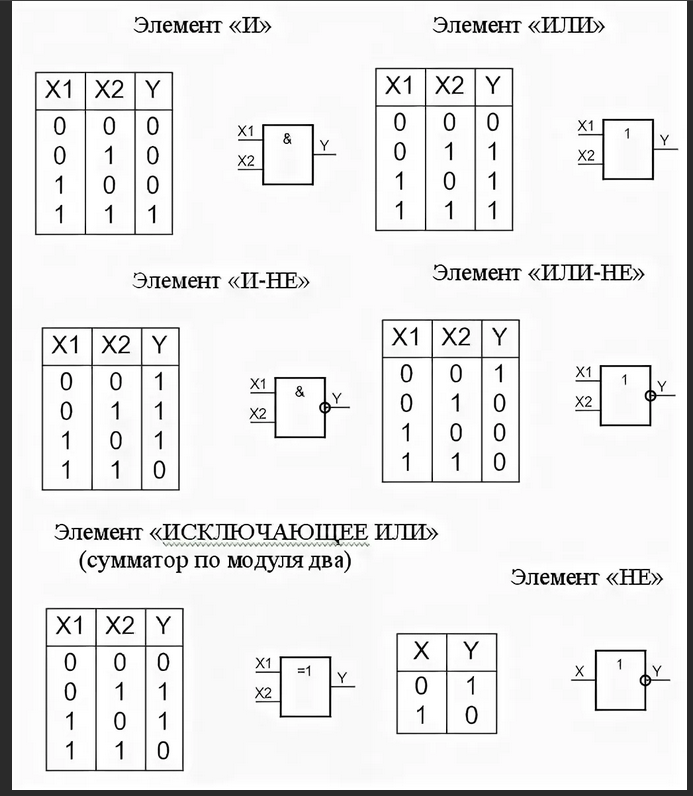
Теперь, я думаю, из этого примера должно быть ясно, что вы можете сделать это для любой функции истинности. То есть любую функцию можно представить с помощью формулы ДНФ, создав дизъюнкцию для каждой строки, где функция оценивается как $T$. Например, если в строке есть строка, в которой $P$ — True, $Q$ — True, а $R$ — false, скажем, сгенерируйте выражение $P \land Q \lor \neg R$. Когда у вас есть выражение для всех этих строк, соедините их все вместе, чтобы получить окончательное выражение. И если нет строки, в которой функция оценивается как $T$, то просто используйте выражение $P \land \neg P$, что — это в ДНФ (его можно рассматривать как обобщенную дизъюнктуру только с одной дизъюнкцией… которая является конъюнкцией литералов).
Таким образом, для любой функции истинности существует выражение ДНФ, которое фиксирует эту функцию, а ДНФ использует только $\neg, \land и \lor$
Просто для полноты, я также хочу отметить, что есть что-то, называемое конъюнктивной нормальной формой (CNF): это обобщенная конъюнкция, где каждый конъюнкт является обобщенной дизъюнкцией литералов.
Можем ли мы найти выражение, эквивалентное этой функции в КНФ? Да. Есть два способа сделать это. Во-первых, мы можем взять существующее выражение ДНФ и преобразовать его в выражение, находящееся в КНФ, используя Распределение $lor$ по $\land$. В этом случае это была бы довольно внушительная формула, начинающаяся с:
$(P \lor P \lor \neg P) \land (P \lor P \lor Q) \land (P \lor P \lor R) \land (P \lor \neg Q \lor \neg P) \land (P \lor \neg Q \lor Q) \land (P \lor \neg Q \lor R) \land (P \lor \ neg R \lor \neg P) \land …$
(посмотрите, что я здесь делаю? Я систематически нахожу все комбинации выбора одного литерала из каждого из трех дизъюнктов.. это работает как FOIL, если вы знакомы с этим)
Однако есть еще один способ сделать это: вернуться к исходной таблице истинности и сосредоточиться на случаях, когда функция оценивается как False, а не как True. То есть функция False ровно тогда, когда:
$$(P \land Q \land R) \lor (P \land \neg Q \land R) \lor (\neg P \land Q \land \neg R ) \lor (\neg P \land \neg Q \land R) \lor (\neg P \land \neg Q \land \neg R)$$
равно True, и это означает, что функция верна точно тогда, когда:
$$\neg [(P \land Q \land R) \lor (P \land \neg Q \land R) \lor (\neg P \land Q \land \neg R) \lor (\neg P \land \neg Q \land R) \lor (\neg P \land \neg Q \land \neg R)]$$
верно. Согласно ДеМоргану, это эквивалентно:
Согласно ДеМоргану, это эквивалентно:
$$(\neg P \lor \neg Q \lor \neg R) \land (\neg P \lor Q \lor \neg R) \land (P \lor \neg Q \lor R) \land (P \lor Q \lor \neg R) \land (P \lor Q \lor R)$$
и , что выражение находится в CNF, т.е. в Layer-Form.
Опять же, я думаю, из этого примера должно быть ясно, что вы можете сделать это для любой функции истинности. То есть любую функцию можно представить с помощью формулы CNF, создав дизъюнкцию для каждой строки, где функция оценивается как $F$. Например, если это строка, в которой $P$ равно True, $Q$ равно True, а $R$ равно false, скажем, сгенерируйте выражение $\neg P \lor \neg Q \lor R$ (для этого является отрицанием $P \land Q \land \neg R$). Когда у вас есть выражение для всех этих строк, соедините их все вместе, чтобы получить окончательное выражение. Если нет строки, в которой функция оценивается как $F$, то просто используйте выражение $P \lor \neg P$), которое равно в ДНФ (его можно рассматривать как обобщенную конъюнкцию только с одним конъюнктом. .. который является дизъюнктом литералов).
.. который является дизъюнктом литералов).
Мы также можем привести доказательство на основе выразительной полноты $NAND$. Поскольку $P \ NAND \ Q \Leftrightarrow \neg (P \land Q)$, мы можем просто взять любое выражение, составленное только из $NAND$, которое фиксирует некоторую функцию истинности $f$, и изменить любое из этих $ NAND$, с $\neg$ и $\land$, и результат будет эквивалентен оригиналу и, таким образом, также захватит $f$. Обратите внимание, что это на самом деле показывает, что $\{ \neg, \land \}$ является выразительно полным, поэтому нам не нужны $\lor$ (конечно, это должно быть очевидно: если $\{ \land , \lor, \neg \}$ является выразительно полным, и учитывая, что $P \lor Q \Leftrightarrow \neg (\neg P \land \neg Q)$, мы можем заменить любой $\lor$ в любом выражении, захватывающем некоторое функцию истинности $f$ на группу $\land$ и $\neg$, а также захватить эту функцию истинности). И, конечно же, мы можем также показать, что $\{ \lor, \neg \}$ является полным, и это немедленно следует из полноты $NOR$, поскольку $P \ NOR \ Q \Leftrightarrow \neg (P \ лор Q)$9n$ конечно работает, но хотелось бы понять почему и как это работает.
Кто может помочь? Спасибо!
- комбинаторика
- логика
Проблема со счетом. Он основан на следующем:
Правило продукта: Если одно четное может произойти $k$ различными способами, а второе событие может произойти $m$ различными способами, то количество способов, которыми могут произойти оба события $km$.
То есть, существует $k$ возможных исходов для первого события и $m$ для второго, поэтому общее количество возможных комбинаций исходов составляет $km$.
Таблица истинности содержит по одной строке для каждой возможности. Каждая переменная имеет два возможных результата: истина или ложь. Если есть $n$ различных переменных, то у вас есть две возможности для каждой, а общее количество комбинаций равно произведению количества возможных результатов для каждой. Это составляет произведение $2$ на себя, $n$ раз или $2^n$.




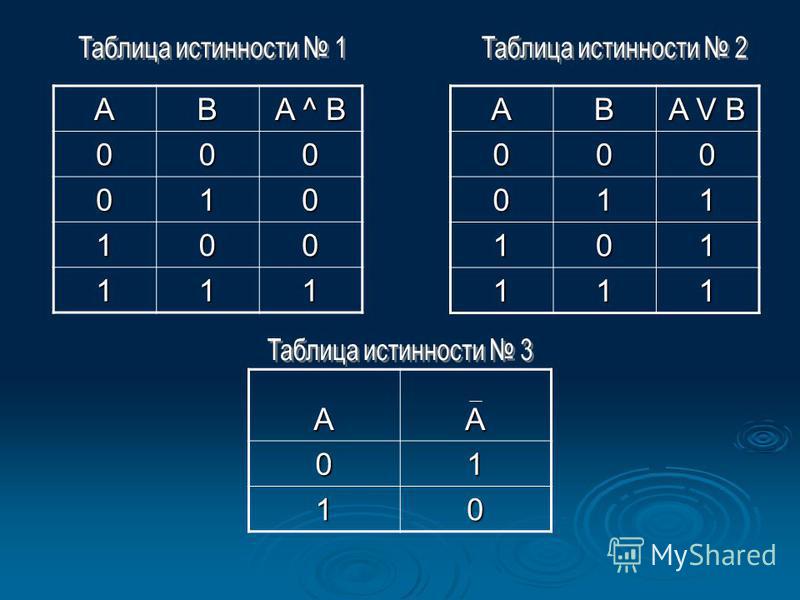 Существуют элементарные логические функции, из которых можно составить любую сложную логическую функцию.
Существуют элементарные логические функции, из которых можно составить любую сложную логическую функцию.