Рассмотрим несколько задач, которые решаются построением таблиц истинности сложных высказываний.
Задача 1.Составить таблицу истинности высказывания
Решение.Данное высказывание состоит из двух операндов A и B. Для его вычисления необходимо сначала вычислить отрицание A, то есть Ā , затем , далее выполнить логическое умножение , затем сложение и, наконец, отрицание . Таким образом, в таблице истинности будет 7 столбцов и 5 строк.
| A | B | Ā | ||||
Заполняем ячейки, соответствующие значению всем возможным сочетаниям значений высказываний A и B.
| A | B | Ā | ||||
| 0 | 0 | |||||
| 0 | 1 | |||||
| 1 | 0 | |||||
| 1 | 1 |
Далее заполняем третий и четвертый столбцы таблицы, соответственно, отрицая высказывания A и B.
| A | B | Ā | ||||
| 0 | 0 | 1 | 1 | |||
| 0 | 1 | 1 | 0 | |||
| 1 | 0 | 1 | ||||
| 1 | 1 | 0 | 0 |
При заполнении пятого столбца таблицы будьте внимательны. Операндами высказывания являются A и , значит, при заполнении пятого столбца смотреть нужно на первый и четвертый столбцы таблицы. Помните, что результат логического умножения имеет значение истина только в том случае, когда истинны оба операнда (единица будет только в четвертой строке пятого столбца).
Операндами высказывания являются A и , значит, при заполнении пятого столбца смотреть нужно на первый и четвертый столбцы таблицы. Помните, что результат логического умножения имеет значение истина только в том случае, когда истинны оба операнда (единица будет только в четвертой строке пятого столбца).
| A | B | Ā | ||||
| 0 | 0 | 1 | 1 | 0 | ||
| 0 | 1 | 1 | 0 | |||
| 1 | 0 | 0 | 1 | 1 | ||
| 1 | 1 | 0 | 0 | 0 |
При заполнении шестого столбца таблицы, следует обратить внимание на значения, стоящие в третьем и пятом столбцах, и выполнить операцию логического сложения.
| A | B | Ā | ||||
| 0 | 0 | 1 | 1 | 0 | 1 | |
| 0 | 1 | 1 | 0 | 1 | ||
| 1 | 0 | 0 | 1 | 1 | 1 | |
| 1 | 1 | 0 | 0 | 0 | 0 |
Для получения результата осталось заполнить последний столбец, где отрицается высказывание, полученное в шестом столбце.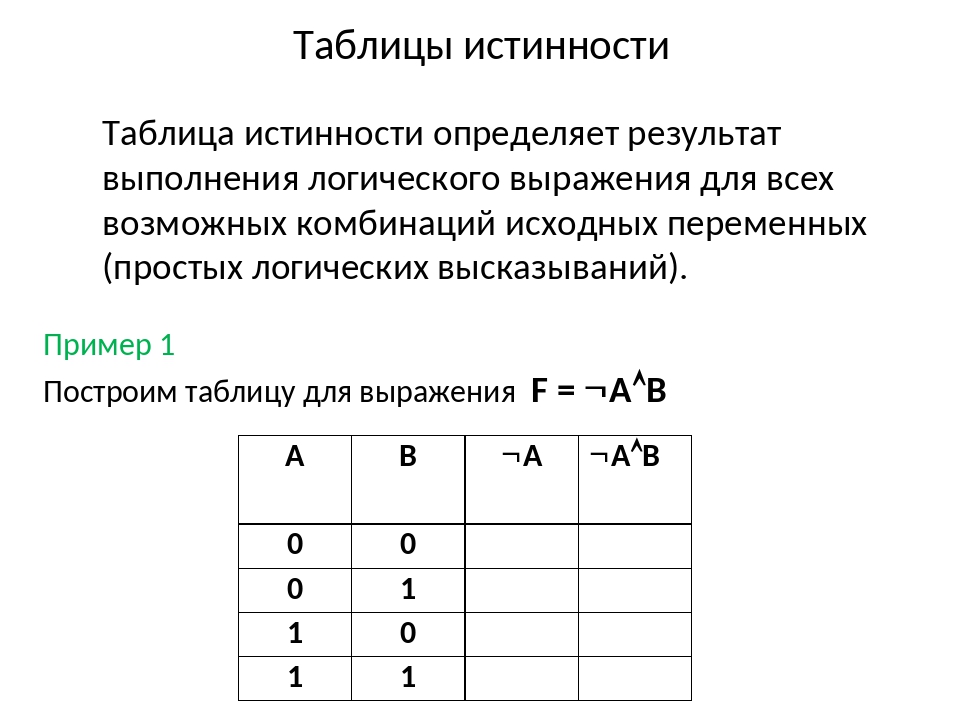
| A | B | Ā | ||||
| 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 | 1 | 0 | |
| 1 | 1 | 0 | 0 | 0 | 0 | 1 |
Ответ: Таблица истинности сложного высказывания следующая.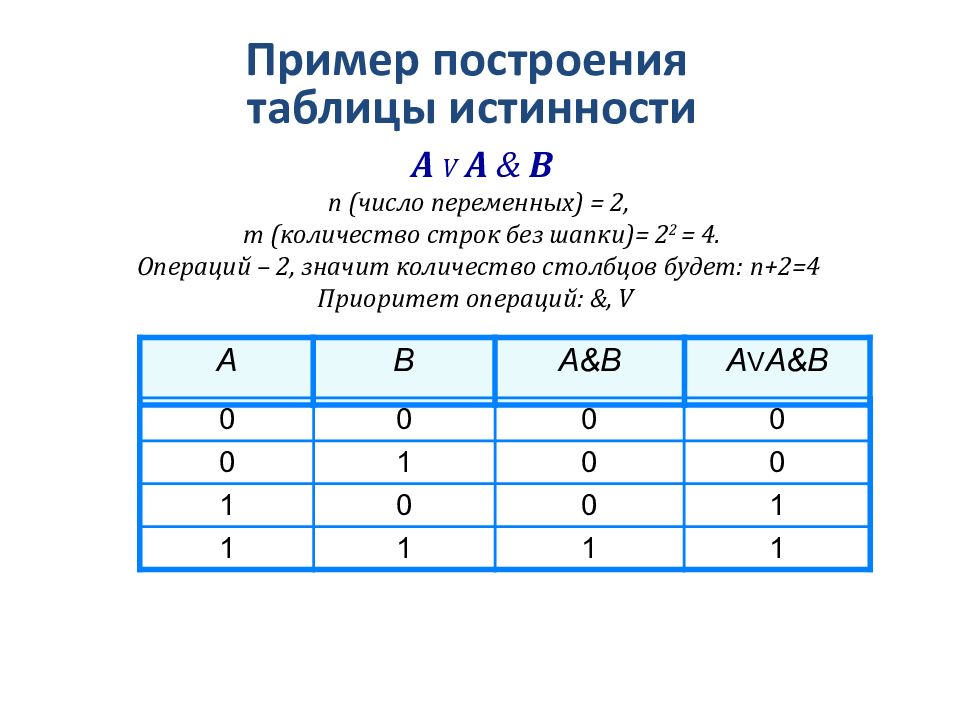
| A | ||
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Задача 2.
Установить эквивалентность двух высказываний:
   1) A V B Λ C;
   2) (А V В) Λ (А V С).
Решение.
Для установления эквивалентности двух высказываний достаточно сравнить их таблицы истинности. Если таблицы совпадают, то высказывания эквивалентны.
Построим таблицу истинности первого высказывания. В выражении участвуют три высказывания. Для того чтобы рассмотреть все возможные сочетания их значений, будем использовать следующий прием: первые три столбца таблицы заполним двоичным представлением чисел 0, 1, 2, 3,…, 23-1, дополняя слева нужное количество нулей. Выражение не содержит скобок, следовательно, воспользуемся тем, что конъюнкция выполняется раньше, чем дизъюнкция. Получим следующую таблицу.
В выражении участвуют три высказывания. Для того чтобы рассмотреть все возможные сочетания их значений, будем использовать следующий прием: первые три столбца таблицы заполним двоичным представлением чисел 0, 1, 2, 3,…, 23-1, дополняя слева нужное количество нулей. Выражение не содержит скобок, следовательно, воспользуемся тем, что конъюнкция выполняется раньше, чем дизъюнкция. Получим следующую таблицу.
| A | B | C | B Λ C | A V B Λ C |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Аналогичным образом составим таблицу истинности второго высказывания.
| A | B | C | A V B | A V C | (А V В) Λ (А V С) |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 |
Поскольку таблицы истинности совпадают, то высказывания 1 и 2 эквивалентны.
Задача 3.
Докажите тавтологию (X Λ Y) - (X VY)Решение.
Для доказательства тавтологии построим следующую таблицу истинности.| X | Y | X Λ Y | X V Y | (X Λ Y) - (X VY) |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 |

Задание 4. — Удивительный мир логики
предыдущем задании мы рассмотрели алгебру логики. А сейчас выполним задания с логическими операциями — конъюнкция, дизъюнкция, отрицание и их таблицы истинности.
Конъюнкцией называют «логическое умножение» или «логическое И» , а часто просто «И» .
В естественном языке конъюнкцию заменяют союзом И.
Для обозначения конъюнкции применяют различные символы. Это может быть знак &, AND. Но чаще всего для обозначения конъюнкции используют символ /\ .
Рассмотрим пример.
Пусть есть два высказывания:
A = «Москва — столица России» и B = «Сегодня солнечно».
Тогда конъюнкция этих высказываний будет выглядеть так «Москва — столица России И сегодня солнечно», а обозначаться так:
A /\ B
Так как на клавиатуре нет символа конъюнкции, его можно набрать из слэша ( / ) и бэкслэша ( \ ) — получится /\ — похоже на обозначение конъюнкции.
Таблица истинности для конъюнкции выглядит так:
Запомнить довольно просто — конъюнкция истинна только в одном случае — когда оба исходных высказывания истинны.
Следующая логическая операция, которую мы рассмотрим после конъюнкции — дизъюнкция.
Дизъюнкция — логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно, если оба простых логических выражений ложны.
Обозначение: A\/ B
Таблица истинности для дизъюнкции выглядит так:
Часто можно встретить другие названия этой операции — логическое сложение, логическое ИЛИ или просто ИЛИ.
В естественном языке дизъюнкция заменяется союзом ИЛИ.
Логическое отрицание или Инверсия — это сложное логическое выражение, в котором если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоброт, если исходное логическое выражение ложно, то результат отрицания будет истинным.
Другими словами, данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО…
Таблица истинности для инверсии выглядит так:
Рекомендуется к просмотру:
Видео YouTube
youtube.com/embed/3yAEUKy68lw?rel=0&wmode=opaque» frameborder=»0″ allowfullscreen=»true»>
В качестве примера решения задач с логическими выражениями рассмотрим следующую задачу:
Трое друзей, болельщиков автогонок «Формула-1», спорили о результатах предстоящих гонок.— Вот увидишь, Шумахер не придет первым, — сказал Джон. — Первым будет Хилл.
— Да нет, победителем будет, как всегда, Шумахер, — воскликнул Ник. — А об Алези и говорить нечего, ему не быть первым.
Питер, к которому обратился Ник, возмутился:
— Хиллу не видать первого места, а вот Алези пилотирует самую мощную машину.
По завершении этапа гонок оказалось, что каждое из двух предположений двоих друзей подтвердилось, а оба предположения третьего из друзей оказались неверны. Кто выиграл этап гонки?
Решение:
Введем обозначение для логических высказываний: Ш — победит Шумахер; Х — победит Хилл; А — победит Алези. Реплика Ника «Алези пилотирует самую мощную машину» не содержит никакого утверждения о месте, которое займет этот гонщик, поэтому в дальнейших рассуждениях его можно не учитывать. Зафиксируем высказывания каждого из друзей: Джон: ¬ Ш /\ Х Ник: Ш /\ ¬А Питер: ¬Х Высказывание Ш /\ ¬А /\ ¬Х истинно только при Ш=1, А=1, Х=0. ОТВЕТ: Победителем этапа гонок стал Шумахер. |
Теперь вам предстоит заполнить Google-форму и решить задания. Критерии оценивания записаны ниже:
Задачи и задания на логику
Задачи и задания на логику
КРИТЕРИИ ОЦЕНКИ:
- За полный и развернутый ответ на один вопрос вы получаете 1 балл;
- Максимум: 5 баллов.

Успехов вам!
Таблица истинности логических выражений с примерами решения
Содержание:
- Свойства логических операций
- Законы алгебры логики могут быть доказаны с помощью таблиц истинности
- Примеры с решением
Построение таблиц истинности для логических выражений
Для логического выражения можно построить таблицу истинности, показывающую, какие значения принимает выражение при всех наборах значений входящих в него переменных. Для построения таблицы истинности следует:
- подсчитать п — число переменных в выражении;
- подсчитать общее число логических операций в выражении;
- установить последовательность выполнения логических операций с учётом скобок и приоритетов;
- определить число столбцов в таблице: число переменных + число операций;
- заполнить шапку таблицы, включив в неё переменные и операции в соответствии с последовательностью, установленной в п.
 3;
3; - определить число строк в таблице (не считая шапки таблицы): ;
- выписать наборы входных переменных с учётом того, что они представляют собой ряд целых п-разрядных двоичных чисел от 0 до ;
- провести заполнение таблицы по столбцам, выполняя логические операции в соответствии с установленной последовательностью.
Построим таблицу истинности для логического выражения нём две переменные, две операции, причём сначала выполняется конъюнкция, а затем — дизъюнкция. Всего в таблице будет четыре столбца:
- Наборы входных переменных — это целые числа от 0 до 3, представленные в двухразрядном двоичном коде: 00, 01, 10, 11.
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Заполненная таблица истинности имеет вид:
Обратите внимание, что последний столбец (результат) совпал со столбцом А. В таком случае говорят, что логическое выражение равносильно логической переменной А.
Возможно вам будут полезны данные страницы:
Свойства логических операций
Рассмотрим основные свойства логических операций, называемые также законами алгебры логики.
1. Переместительный (коммутативный) закон:
• для логического умножения:
• для логического сложения:
2. Сочетательный (ассоциативный) закон:
• для логического умножения:
• для логического сложения:
При одинаковых знаках операций скобки можно ставить произвольно или вообще опускать.
3. Распределительный (дистрибутивный) закон:
• для логического умножения:
• для логического сложения:
4. Закон двойного отрицания:
Двойное отрицание исключает отрицание.
5. Закон исключённого третьего:
• для логического умножения:
• для логического сложения:
Из двух противоречивых высказываний об одном и том же предмете одно всегда истинно, а второе — ложно, третьего не дано.
6. Закон повторения:
• для логического умножения:
• для логического сложения:
7. Законы операций с 0 и 1:
• для логического умножения:
• для логического сложения:
8. Законы общей инверсии:
Законы общей инверсии:
• для логического умножения:
• для логического сложения:
Законы алгебры логики могут быть доказаны с помощью таблиц истинности
Докажем распределительный закон для логического сложения:
Совпадение значений в столбцах, соответствующих логическим выражениям в левой и правой частях равенства, доказывает справедливость распределительного закона для логического сложения.
Примеры с решением
Пример 1.
Найдём значение логического выражения для числа X = 0.
Решение:
При X = 0 получаем следующее логическое выражение: . Так как логические выражения 0 < 3, 0 < 2 истинны, то, подставив их значения в логическое выражение, получаем:
Для решения задач вам понадобится знание таблиц истинности логических операций:
А также, вы должны знать:
Порядок выполнения логических операций задается круглыми скобками
Сначала выполняется операция отрицания НЕ
затем И
после И выполняется ИЛИ
затем следование
и в последнюю очередь — эквивалентность.
Задача 1
Дан фрагмент таблицы истинности выражения F:
Какое выражение соответствует F?
Решение:
Чтобы определить верное выражение, надо значения А,В,С каждой из строк таблицы подставить в очередное выражение, определить его результат выполнения и сравнить со значением F соответствующей строки.
То выражение, значения которого совпадут со значениями столбца F, и будет искомым. Решение:
Ответ: 4
Задача 2
Дан фрагмент таблицы истинности выражения F:
Каким выражением может быть F?
Решение:
Обратите внимание:
1) В каждом из приведенных выражений логические переменные связывает только один тип логической операции. В 1 и 3 вариантах это операция И (), во 2 и 4 вариантах это операция ИЛИ ().
2) По столбцу F видно, что выражение для двух комбинаций данных истинно, а для одной — ложно. Следовательно, выражение не может быть логическим умножением (И), так как логическое умножение истинно только для одной комбинации данных, а в таблице две истины. Следовательно, искомое выражение является логическим сложением (ИЛИ) значений логических переменных.
Следовательно, искомое выражение является логическим сложением (ИЛИ) значений логических переменных.
Поэтому, в качестве ответа может быть 2 или 4 вариант. Рассмотрим их.
1) 2-й вариант: В первой строке таблицы истинности отображены только значения х1, хЗ, х5, и все они равны 0. Но в формуле 2го варианта у нас х5 отрицается, то есть значение х5 будет изменено на 1, и в результате всё выражение должно быть истинным. Что не соответствует заданной таблице. Остаётся 4-й вариант.
2) Как мы видим, переменные х1, хЗ и х5 в 4-м варианте ответа не отрицаются, что соответствует первой строке заданной таблицы.
Ответ: 4
Задача 4
Какое из приведенных имен сказочных героев удовлетворяет логическому условию:
1) АРТЕМОН
2) БАЗИЛИО
3) БУРАТИНО
4) МАЛЬВИНА
Решение:
Составим для каждого из предложенных ответов схему соответственно заданной логической формуле. Ищем истинное значение.
1) АРТЕМОН
Первая буква согласная — НЕТ (0)
Вторая буква не А — ДА (1)
Последняя буква гласная — НЕТ (0) \ / \ у
Предпоследняя буква гласная — ДА (1) X» ‘»X X»
Подставляем полученные значения в формулу и решаем ее: н 0 ->1 ) л 0 -> 1 ),= О
И так с каждым вариантом ответа, пока не найдете истину.
Задача 5
Логическая функция F задаётся выражением
Определите, какому столбцу таблицы истинности функции F соответствует каждая из
переменных X, Y, Z
Решение 1:
Последней операцией выполнения является операция . Поэтому выражение имеет значение ИСТИНА, когда
Рассмотрим все случаи, когда F = 1 (это значения в строках 1 и 3): — не рассматриваем, т.к. в табл, нет строки, где все значения логических переменных = 1.
Рассматриваем только 1 и 3 строки таблицы:
- две единицы в 3-м столбце => это значения X
- два нуля в 1-м столбце => это значения Y
- ноль единица во 2-м столбце => это значения Z
Ответ: YZX
Решение 2:
Последней операцией выполнения является операция . Поэтому выражение
Поэтому выражение
имеет значение ИСТИНА, когда
Выражение F равно 1 в 1й и Зй строках, в этих же строках только “Перем.3”=1, следовательно, значение X находится в 3-м столбце.
Теперь рассмотрим построчно значения 1-х двух столбцов:
(помним, что 1 -> 0 = 0, в остальных комбинациях =1)
1 строка: 0 и О, Y = Z. Поэтому Y и Z для столбцов не определить.
2 строка: 0 и 1. Независимо будет ли Y=0 Z=1 или Y=1 Z=0, функция F=0 т.к. уже
Х=0. Поэтому Y и Z для столбцов не определить.
3 строка: 0 и 1. В этой строке функция F=1, значит Комбинация
невозможна, иначе F будет = 0. Комбинация то, что надо. Следовательно, значение Y находится в 1-м столбце а значение Z во 2-м.
Ответ: YZX
23 задание ЕГЭ по информатике
ЕГЭ по информатике выбирают будущие работники ИТ-сферы. Но для сдачи экзамена нужно не только уметь программировать. Многие задачи связаны с математикой, анализом данных, логикой. Чтобы без проблем решить их на экзамене, необходимо много практиковаться. Вы можете учиться самостоятельно, а можете записаться на курсы подготовки к ЕГЭ и ОГЭ, где преподаватели будут объяснять все сложные моменты. В статье мы разберем тему «Логические выражения». Она встречается в 23 номере ЕГЭ по информатике.
Многие задачи связаны с математикой, анализом данных, логикой. Чтобы без проблем решить их на экзамене, необходимо много практиковаться. Вы можете учиться самостоятельно, а можете записаться на курсы подготовки к ЕГЭ и ОГЭ, где преподаватели будут объяснять все сложные моменты. В статье мы разберем тему «Логические выражения». Она встречается в 23 номере ЕГЭ по информатике.
Алгебра логики
Прежде чем приступить к разбору заданий, нужно изучить теорию. Алгеброй логики называют один из разделов математической логики. Его особенность в том, что логические выражения анализируются с использованием алгебраических законов и правил. Создание науки связано с именем Дж. Буля (1815-1864). Ученый разработал собственный математический язык, записывал с его помощью уравнений. Истинность и ложность выражений доказывал с помощью алгебраических операций. Несмотря на то, что алгебра логики продолжает развиваться, принцип остается прежним.
Основой алгебры логики (и 23 задания ЕГЭ) являются логические высказывания — не вопросительные предложения, по поводу которых можно однозначно сказать, являются они истинными или ложными. Например, высказывание «снег белый» истинно, «солнце светит ночью» — ложно. Предложение «мороженое вкусное» не является логическим высказыванием, нельзя однозначно сказать о его правдивости. Если заменить его на «я люблю мороженое», то оно может принимать как истинное, так и ложное значение, это зависит от предпочтений человека.
Например, высказывание «снег белый» истинно, «солнце светит ночью» — ложно. Предложение «мороженое вкусное» не является логическим высказыванием, нельзя однозначно сказать о его правдивости. Если заменить его на «я люблю мороженое», то оно может принимать как истинное, так и ложное значение, это зависит от предпочтений человека.
В 23 задании по информатике встречаются двузначные высказывания, принимающие значения «правда» и «неправда». Но алгебра логики рассматривает также многозначные, имеющие значения «вероятно», «невозможно», «возможно». Элементарные высказывания обозначают латинскими буквами (например, A = «осенью деревья сбрасывают листву»). Сложные высказывания составляются из элементарных с использованием частиц «и», «или», «тогда и только тогда», «если.. то» (например, А и В = «осенью деревья сбрасывают листву и некоторые птицы улетают на юг»). В цифровом представлении истине соответствует число 1, а лжи число 0. Для вычисления примеров обычно используются таблицы истинности.
Основные операции алгебры логики
Для решения номера 23 по информатике нужно знать основные операции:
- инверсия (отрицание). Операция называется унарной, так как преобразует одну величину: «переворачивает» выражение, меняет истину на ложь и наоборот. Обозначается чертой над буквой, символом ᆨ, словом «not». В результате преобразования числа A получается высказывание ᆨA. Читается «не А», «отрицание А», «А ложно». Пример: A = 1 больше 0; Ā = 1 не больше 0. На рисунке А — множество точек, Ā — все точки, не принадлежащие множеству;
- конъюнкция (умножение). Обозначает величины (2 или больше), объединенные союзом И. Для математической записи используются знаки ∧, •, &, and. Иногда знак опускают, по аналогии с математикой. Высказывание истинно, когда все его части правдивы, например, A∧B = «химия изучает вещества и молекулы». На рисунке изображается множествами, их пересечение соответствует A∧B;
- дизъюнкция (сложение).
 Связывает 2 и более выражения союзом ИЛИ. Обозначается знаками ∨, +, |, or. Выражение истинно, если правдива одна часть или сразу обе. Пример: А∨В = «звезды состоят из газа или плазмы». На рисунке изображается объединением множеств;
Связывает 2 и более выражения союзом ИЛИ. Обозначается знаками ∨, +, |, or. Выражение истинно, если правдива одна часть или сразу обе. Пример: А∨В = «звезды состоят из газа или плазмы». На рисунке изображается объединением множеств;
- строго-разделительная (исключающая) дизъюнкция. Связывает высказывания союзом ИЛИ. Особенность в том, что союз является исключающим, то есть выражение истинно, когда правдива одна из его частей. Обозначают через ∨∨, ⊕, а читают «либо А, либо В». Пример: А⊕В = «валентность серы II или IV»;
- импликация. Соединяет выражения, указывающие на причину и следствие. Обозначается ⟶, ⊃, читается «из А следует В», «если А, то В», «А влечет В». Пример является ложью, когда причина правдива, а следствие — неправда. Пример: А⟶В = «если число делится только на себя и на 1, то оно сложное».
- эквивалентность. Операция объединяет высказывания связками ТОГДА И ТОЛЬКО ТОГДА, РАВНОСИЛЬНО, НЕОБХОДИМО И ДОСТАТОЧНО.
 Обозначается ~, ↔️, читается «А эквивалентно В». Выражение истинно, когда обе части одинаковы. Например: А~В = «число делится на 5 тогда, когда его последняя цифра 0 или 5». Эквивалентность противоположна строго-разделительной дизъюнкции.
Обозначается ~, ↔️, читается «А эквивалентно В». Выражение истинно, когда обе части одинаковы. Например: А~В = «число делится на 5 тогда, когда его последняя цифра 0 или 5». Эквивалентность противоположна строго-разделительной дизъюнкции.
На самом деле, для решения номеров достаточно трех операций: сложения, умножения, отрицания. Строго-разделительную дизъюнкцию можно представить как (ᆨА∧B)∧(А∧ᆨВ), импликацию — ᆨА∨B, эквивалентность (ᆨA∧ᆨB)∨(A∧B). Порядок выполнения действий при вычислении:
- инверсия;
- конъюнкция;
- дизъюнкция;
- остальные.
Примеры решения задач
Переходим к разбору 23 задания по информатике. Решим несколько задач.
Задача 1. Вычислите логическое значение: (ᆨ(15 < 3))∧(10 > 20).
Решение: Составим таблицу.
|
15 < 3 |
10 > 20 |
ᆨ(15 < 3) |
ᆨ(15 < 3)∧(10 > 20) |
|
0 |
1 |
1 |
0 |
Ответ: ложь.
Задача 2. Запишите высказывание с помощью логических операций, определите его значение: «если часы неправильно показывают время, то вы не успеете на занятия».
Решение: Пусть «часы неправильно показывают время» = А, «успеете на занятия» = В, а «не успеете на занятия» = ᆨВ. Логическое выражение: А⟶ᆨВ. Из причины сделал верный вывод, поэтому выражение является истинным.
Ответ: истина.
Задача 3. Определить значение ((х > 10) ∨ (х < 15)) → (х < 5) для 1) x = 9 и 2) х = 4.
Решение: Для х = 9: ((9 > 10) ∨ (9 < 15)) → (9 < 5) = ложь ∨ истина → ложь = истина → ложь = ложь.
Для х = 4: ((4 > 10) ∨ (4 < 15)) → (4 < 5) = ложь ∨ истина → истина = истина → истина = истина.
Ответ: 1) ложь; 2) истина.
Мы изучили основную теорию алгебры логики и разобрались, как решать 23 номер в ЕГЭ. Эта тема очень важна, поэтому не забывайте ее и постоянно практикуйтесь, чтобы подготовиться к экзамену лучше.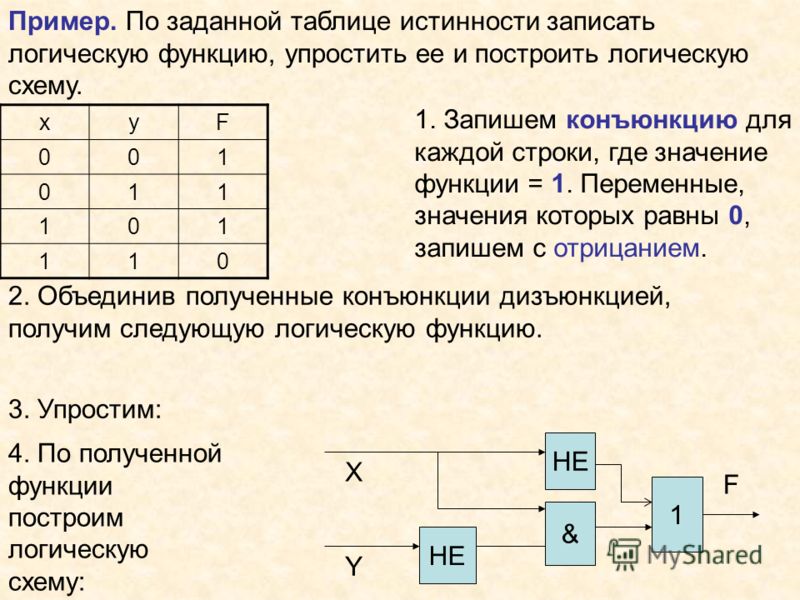 Желаем вам легких вариантов и высоких баллов!
Желаем вам легких вариантов и высоких баллов!
Урок 5. Логические законы и противоречия
В прошлом уроке были рассмотрены условия истинности для категорических атрибутивных высказываний в силлогистике. Мы показали, что разные типы высказываний при одних условиях истинны, а при других – ложны. При этом нам ни разу не встречались высказывания, которые были бы всегда истинны или всегда ложны. Между тем, такие высказывания бывают. Первые называются логическими законами, а вторые – логическими противоречиями. О них мы и поговорим в этом уроке.
Во введении к курсу было сказано, что логика – это нормативная наука о формах и приёмах рациональной познавательной деятельности. Как и любая другая наука, логика также формулирует свои законы. Однако в отличие от других наук, законы эти являются нормативными, то есть они не описывают процесс человеческого мышления, а предписывают, как человек должен мыслить, если он хочет, чтобы его рассуждение было корректным. Таким образом, логические законы представляют собой некие общие принципы, которыми люди должны руководствоваться в процессе рассуждения.
Таким образом, логические законы представляют собой некие общие принципы, которыми люди должны руководствоваться в процессе рассуждения.
Если попытаться дать более строгое определение, то:
Логический закон – это определённая логическая форма, благодаря которой высказывание в целом принимает значение «истина», независимо от конкретного содержания его частей.
По этой причине логические законы также иногда называют логическими тавтологиями: о чём бы мы не говорили, высказывания, имеющие форму логических законов, всегда оказываются истинными. К тому же они кажутся «бесплодными», потому что мы не можем извлечь из них никакой реальной информации о мире.
Логические противоречия – полная противоположность логическим законам, то есть это такая логическая форма, при которой высказывание в целом всегда принимает значение «ложь», независимо от содержания его частей.
Содержание:
Таблицы истинности
Как же определить, что определённое высказывание всегда принимает значение «истина» или «ложь»? Логики придумали для этого очень удобный метод, который получил название «таблиц истинности». Как понятно из названия, они представляют собой таблицы, в которых в верхнюю строку записывается логическая форма высказываний, а в столбцы под каждым компонентом записываются их истинностные значения. Давайте построим таблицу истинности для высказывания «Идёт дождь».
Как понятно из названия, они представляют собой таблицы, в которых в верхнюю строку записывается логическая форма высказываний, а в столбцы под каждым компонентом записываются их истинностные значения. Давайте построим таблицу истинности для высказывания «Идёт дождь».
|
Идёт дождь |
|
Истина |
|
Ложь |
Здесь всё довольно ясно: «Идёт дождь» – это простое высказывание, которое может принимать значение либо «истина», либо «ложь». Обычно для удобства логики сокращают значения до «и» и «л», а само высказывание записывают маленькой буквой латинского алфавита: p, q, r, s и т.д. Поэтому в классическом виде таблица истинности для одного простого высказывания будет выглядеть так:
Давайте теперь представим, что у нас есть два высказывания: «Идёт дождь» и «Светит солнце». Пока они никаким образом не связаны между собой. Однако поскольку их уже два, то у нас возможны уже не две, а четыре комбинации: оба высказывания истинны, оба высказывания ложны, истинно либо первое, либо второе высказывание. Таблица истинности для них будет включать уже четыре строки для значений.
Однако поскольку их уже два, то у нас возможны уже не две, а четыре комбинации: оба высказывания истинны, оба высказывания ложны, истинно либо первое, либо второе высказывание. Таблица истинности для них будет включать уже четыре строки для значений.
|
p |
q |
|
и |
и |
|
и |
л |
|
л |
и |
|
л |
л |
Если у нас есть три высказывания («Идёт дождь», «Светит солнце», «Трава зеленеет»), то таблица будет включать уже восемь строк для значений, так как в таком случае возможны восемь комбинаций.
|
p |
q |
r |
|
и |
и |
и |
|
и |
и |
л |
|
и |
л |
и |
|
и |
л |
л |
|
л |
и |
и |
|
л |
и |
л |
|
л |
л |
и |
|
л |
л |
л |
Чем больше разных высказываний вы хотите рассмотреть, тем больше комбинаций из значений возможно. Число этих комбинаций для n высказываний вычисляется по формуле 2n. Так для четырёх высказываний, число комбинаций – шестнадцать, для пяти – тридцать два и т.д.
Число этих комбинаций для n высказываний вычисляется по формуле 2n. Так для четырёх высказываний, число комбинаций – шестнадцать, для пяти – тридцать два и т.д.
Таблицы истинности строятся и в силлогистике, однако выглядят они немного иначе. В левый столбец обычно помещается диаграмма, изображающая то или иное отношение между терминами S и P, а справа помещаются различные типы высказываний и их истинностные значения.
Это сводная таблица истинности для всех типов атрибутивных высказываний, которые мы обсуждали в прошлом уроке (единичные высказывания не включены отдельно, так как их условия истинности приравниваются к условиям истинности для общих высказываний).
Далее, понятно, что обычно в рассуждении высказывания каким-то образом связаны между собой с помощью пропозициональных связок. Мы зададим истинностные значения для основных связок, которые используются чаще всего в естественном языке.
Логическое отрицание используется, когда в высказывании отрицается наличие некоторой ситуации в мире, говорится об её отсутствии. Например, «Дождь не идёт», «Комната была небольшой», «Неправда, что они друзья». В логике обычно передается через выражения «неверно, что p» или просто «не-p».
Например, «Дождь не идёт», «Комната была небольшой», «Неправда, что они друзья». В логике обычно передается через выражения «неверно, что p» или просто «не-p».
|
p |
неверно, что p |
|
и |
л |
|
л |
и |
Как видно из таблицы, если высказывание истинно, то его отрицание будет принимать значение «ложь», если же высказывание само по себе ложно, то – «истина». Предположим, что вместо p мы имеем высказывание «Маргарет Тэтчер была первой и на настоящий момент единственной женщиной-премьер-министром Великобритании». Это истинное высказывание. Соответственно, если взять его отрицание: «Маргарет Тэтчер не была первой и на настоящий момент единственной женщиной-премьер-министром Великобритании», то оно будет ложным. Если же взять высказывание «Все болезни от нервов», которое является ложным, то его отрицание «Неверно, что все болезни от нервов» будет истинным.
Если же взять высказывание «Все болезни от нервов», которое является ложным, то его отрицание «Неверно, что все болезни от нервов» будет истинным.
Конъюнкция представляет собой одновременное утверждение наличия двух ситуаций. В естественном языке она обычно передаётся союзами «и», «а», «но» и конструкциями типа «в то же время», «одновременно», «вместе» и т.д. Примеры конъюнкции можно увидеть в высказываниях «Пошёл дождь, и я спрятался под навес», «Витя хотел пойти в кино, а я хотел поиграть в футбол», «Белкин ждал директора целый час, но так и не дождался». Как видно, конъюнкция соединяет два или более простых высказываний в одно сложное.
|
p |
q |
p и q |
|
и |
и |
и |
|
и |
л |
л |
|
л |
и |
л |
|
л |
л |
л |
Конъюнктивное высказывание может быть истинным, только если все его части истинны. Если хотя бы одно простое высказывание, входящее в её состав ложно, то тогда и конъюнкция в целом ложна. Пример истинной конъюнкции: «44-го президента США зовут Барак, а его жену – Мишель». Все следующие высказывания будут ложными: «44-го президента США зовут Барак, а его жену – Мэгги», «44-го президента США зовут Борат, а его жену – Мишель», «44-го президента США зовут Джон, а его жену – Элен».
Если хотя бы одно простое высказывание, входящее в её состав ложно, то тогда и конъюнкция в целом ложна. Пример истинной конъюнкции: «44-го президента США зовут Барак, а его жену – Мишель». Все следующие высказывания будут ложными: «44-го президента США зовут Барак, а его жену – Мэгги», «44-го президента США зовут Борат, а его жену – Мишель», «44-го президента США зовут Джон, а его жену – Элен».
Дизъюнкция утверждает, что хотя бы одна из двух или более ситуаций имеет место. В естественном языке она выражается словами «или» и «либо». Примеры дизъюнктивных высказываний: «Маша была замужем за Анатолием или за Николаем», «Он работает над проектом ИК-25 либо ПФ-40». Хотя это не так очевидно, как в случае с конъюнкцией, дизъюнкция также объединяет в одно сложное высказывание два или более простых высказывания. Если мы выявляем логическую форму, то правильной была бы запись: «Маша была замужем за Анатолием, или Маша была замужем за Николаем».
|
p |
q |
p или q |
|
и |
и |
и |
|
и |
л |
и |
|
л |
и |
и |
|
л |
л |
л |
Из таблицы понятно, что дизъюнкция ложна, только когда все простые высказывания, входящие в её состав ложны. К примеру, ложным будет высказывание «Уганда находится в Центральной Америке или Западной Европе». Когда хотя бы одна из частей дизъюнкции истина, она в целом также будет истинной. Например, истинным является высказывание «Нот всего семь или шесть». При этом важно отметить, что выражение «хотя бы одна» подразумевает, что и обе части могут быть истинными. Иллюстрацией может служить следующее высказывание: «Велосипеды бывают двухколёсными или трёхколесными». Велосипеды бывают и такими, и другими, поэтому высказывание истинно. Однако нередки случаи, когда мы хотим указать, что лишь одна из альтернатив истинна, но никак не обе вместе. Рассмотрим высказывание «Картина “Герника” принадлежит кисти Пикассо или Тициана». Здесь либо одно, либо другое. Они даже не могли написать её вместе, так как жили в разных веках. В таких ситуациях говорят о строгой дизъюнкции, которая будет истинна исключительно при истинности одного из её членов. Обычно она выражается словами «либо, либо».
К примеру, ложным будет высказывание «Уганда находится в Центральной Америке или Западной Европе». Когда хотя бы одна из частей дизъюнкции истина, она в целом также будет истинной. Например, истинным является высказывание «Нот всего семь или шесть». При этом важно отметить, что выражение «хотя бы одна» подразумевает, что и обе части могут быть истинными. Иллюстрацией может служить следующее высказывание: «Велосипеды бывают двухколёсными или трёхколесными». Велосипеды бывают и такими, и другими, поэтому высказывание истинно. Однако нередки случаи, когда мы хотим указать, что лишь одна из альтернатив истинна, но никак не обе вместе. Рассмотрим высказывание «Картина “Герника” принадлежит кисти Пикассо или Тициана». Здесь либо одно, либо другое. Они даже не могли написать её вместе, так как жили в разных веках. В таких ситуациях говорят о строгой дизъюнкции, которая будет истинна исключительно при истинности одного из её членов. Обычно она выражается словами «либо, либо».
|
p |
q |
либо p, либо q |
|
и |
и |
л |
|
и |
л |
и |
|
л |
и |
и |
|
л |
л |
л |
Материальная импликация – это связка, которая передаёт отношения причинно-следственной связи между высказываниями.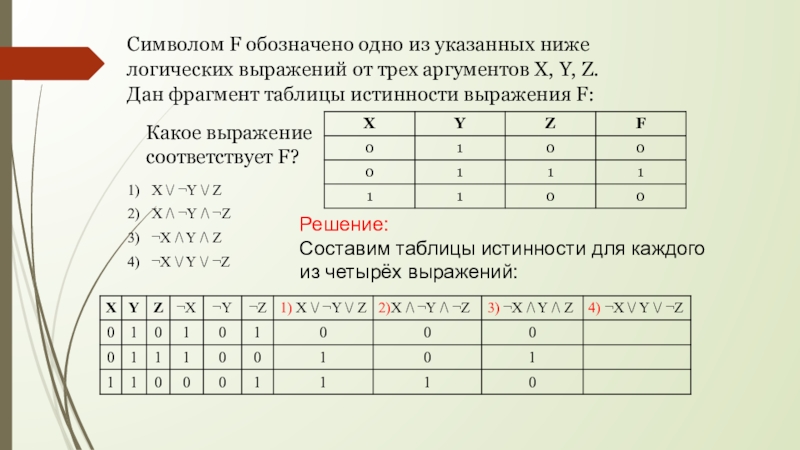 Она выражается словами «если, то». «Если Люся – полная отличница, то и по математике у неё должна быть пятёрка». Смысл импликации состоит в том, что если первое простое высказывание верно, то и второе тоже будет верным.
Она выражается словами «если, то». «Если Люся – полная отличница, то и по математике у неё должна быть пятёрка». Смысл импликации состоит в том, что если первое простое высказывание верно, то и второе тоже будет верным.
|
p |
q |
Если p, то q |
|
и |
и |
и |
|
и |
л |
л |
|
л |
и |
и |
|
л |
л |
и |
Попробуем разобраться с этой таблицей. Проблема в том, что истинностные значения материальной импликации, в отличие от значений других пропозициональных связок, совсем не являются интуитивными. С первой строкой всё ясно: если первое высказывание верно, и второе высказывание верно, то импликация в целом тоже верна. Пример: «Если птицы улетают на юг, то, значит, наступила осень». Со второй строкой тоже всё более или менее понятно: если первое высказывание истинно, а второе ложно, то отношения следования между ними нет. Вспомните отрывок из «Золотого ключика», в котором Мальвина пытается научить Буратино арифметике:
Проблема в том, что истинностные значения материальной импликации, в отличие от значений других пропозициональных связок, совсем не являются интуитивными. С первой строкой всё ясно: если первое высказывание верно, и второе высказывание верно, то импликация в целом тоже верна. Пример: «Если птицы улетают на юг, то, значит, наступила осень». Со второй строкой тоже всё более или менее понятно: если первое высказывание истинно, а второе ложно, то отношения следования между ними нет. Вспомните отрывок из «Золотого ключика», в котором Мальвина пытается научить Буратино арифметике:
– Предположим у вас в кармане два яблока, и некто забрал у вас одно из них. Сколько у вас останется яблок?
– Два.
– Но почему?
– Ведь я не отдам Некту яблоко, пусть он и дерись!
Рассуждения Буратино можно представить в виде высказывания «Если некто забрал одно из имеющихся у меня двух яблок, у меня всё равно осталось два яблока». Если первая часть истинна, то вторая, безусловно, ложна, а потому и импликация в целом ложна.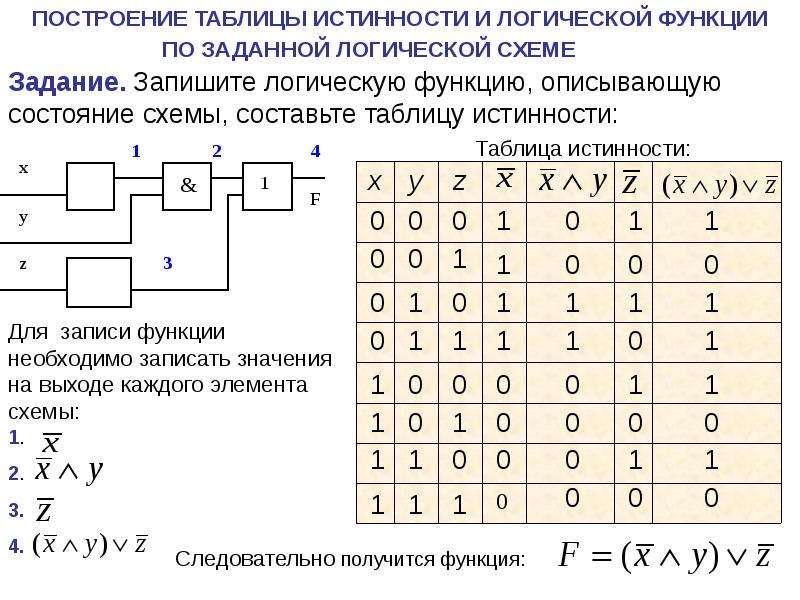 Способностей к арифметике у Буратино, действительно, не было.
Способностей к арифметике у Буратино, действительно, не было.
С последними двумя строчками дело обстоит сложнее. Проблема в том, что для них сложно придумать пример на естественном языке. Когда логики формулировали значение материальной импликации, они пользовались математическим примером. Они взяли высказывание «Для всякого числа верно, что если оно кратно 4, то оно кратно и двум». Если это высказывание верно для всякого числа, то оно должно быть верным и для любого конкретного числа: 5, 6, 8, 12 и т.д. Если подставить в высказывание 8, то получим: «если 8 кратно 4, то оно кратно и 2». Здесь и первая, и вторая части истинны. Мы получили первую строку. Если подставить число 6, «если 6 кратно 4, то оно кратно и 2», то мы получаем третью строку (первая часть ложна, а вторая истинна). Если подставить 5, «если 5 кратно 4, то 5 кратно и двум», то выходит последняя строка (обе части ложны). Однако мы всё же можем подобрать примеры для всех этих ситуации, поэтому импликация истинна. Но вот для второй строки пример подобрать нельзя: нет такого числа, которое было бы кратно 4, но некратно 2.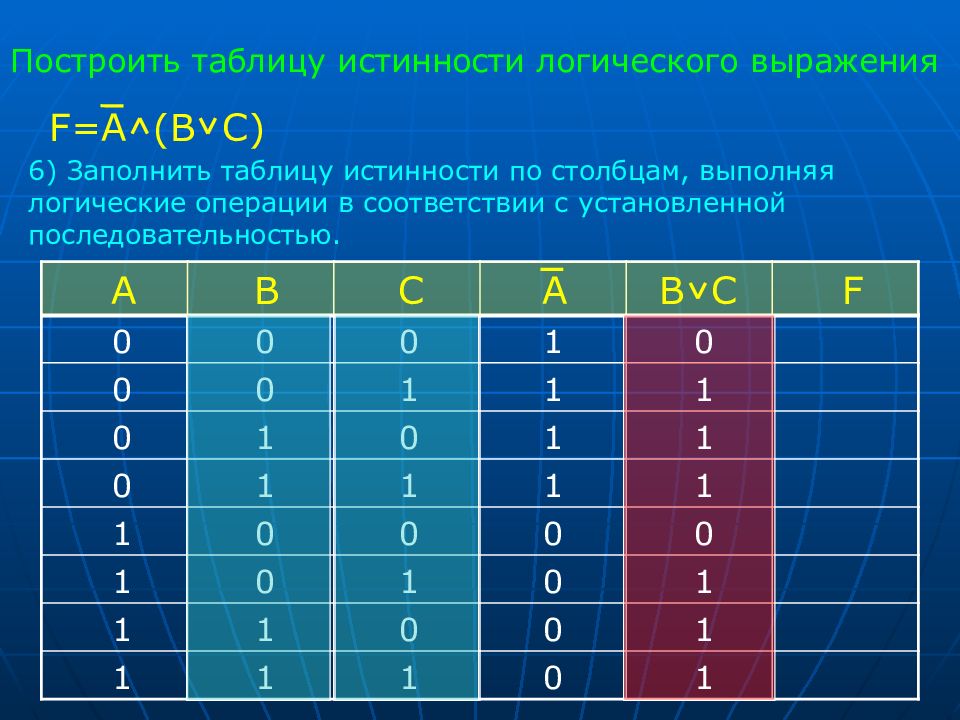 Поэтому вторая строка ложна.
Поэтому вторая строка ложна.
Итак, мы разобрали истинностные значения основных связок, теперь мы можем посмотреть, какие их комбинации приведут к тому, что высказывание подобной формы будет всегда истинным, независимо от его содержания, другими словами – будет логическим законом.
Логические законы
Сразу стоит оговориться, что логических законов довольно много. Кроме того, обычно они формулируются в рамках конкретной логической системы: логики высказываний, логики предикатов, силлогистики, модальной логики и т.д. То, что является законом в одной системе, совсем необязательно будет законом в другой системе. Однако существует несколько основных законов, которые будут верны в любой логической системе. О них мы и расскажем.
1
Закон тождества
Закон тождества обычно формулируется в виде формулы «А есть А» или «Если А, то А».
Проверим этот закон с помощью таблицы истинности. Во-первых, у нас всего одно выражение – А, поэтому таблица будет включать только две комбинации: А истинно и А ложно.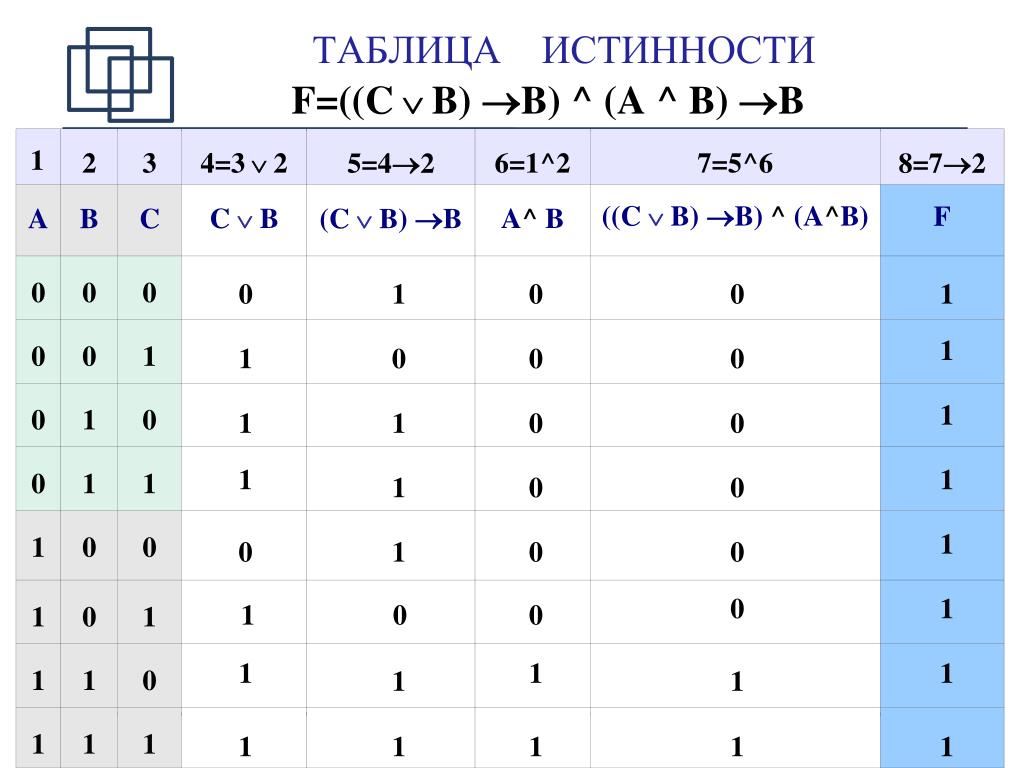 Во-вторых, связка «Если …, то …» выступает как знак материальной импликации. Таким образом, мы должны взять первую и последнюю строку из таблицы для материальной импликации.
Во-вторых, связка «Если …, то …» выступает как знак материальной импликации. Таким образом, мы должны взять первую и последнюю строку из таблицы для материальной импликации.
|
А |
Если А |
то А |
Истинностное значение импликации |
|
и |
и |
и |
и |
|
л |
л |
л |
и |
Закон тождества также может быть сформулирован и в силлогистике для высказываний «Все А есть А» и «Некоторые А есть А»:
Какой бы термин мы не подставили на место А, высказывания, имеющие эти формы, всегда будут истинными: «Все кошки – это кошки», «Все туфли – это туфли», «Некоторые автомобили – это автомобили», «Некоторые дома – это дома» и т.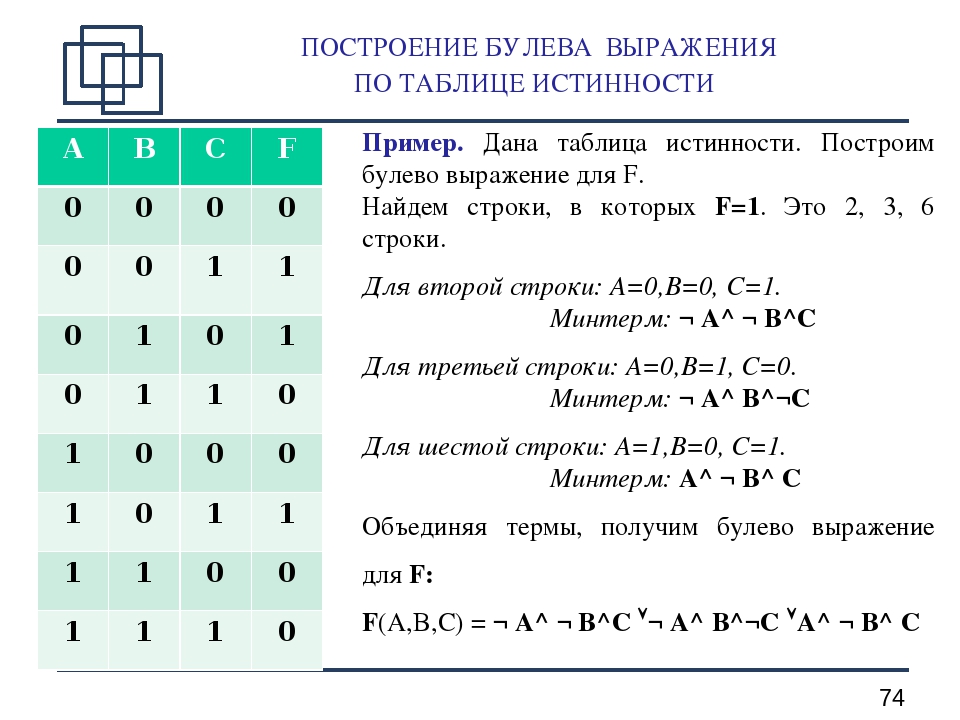 п.
п.
Как понятно из названия этого закона, он говорит о том, что А тождественно самому себе. Что это означает? Смысл этого закона состоит в утверждении того, что языковые выражения (будь то термин или целое высказывание) не могут менять своё значение в процессе рассуждения. Языковые знаки должны трактоваться однозначно, их употребление должно быть стабильным. Если я утверждаю, что какое-то высказывание истинно, например, что высказывание «Красота спасёт мир» истинно, я не могу следующим шагом утверждать, что оно ложно. И наоборот, если я утверждаю, что какое-то высказывание ложно, оно не может вдруг ни с того ни с сего превратиться в истинное. Рассуждение должно быть последовательным.
Чаще всего закон тождества нарушается при так называемой подмене понятий: в ходе рассуждения используется один и тот же термин, но значения в него вкладываются каждый раз разные. К примеру, возьмём следующее рассуждение: «Знание – сила. Сила – это векторная физическая величина, мера интенсивности воздействия на данное тело других тел и полей.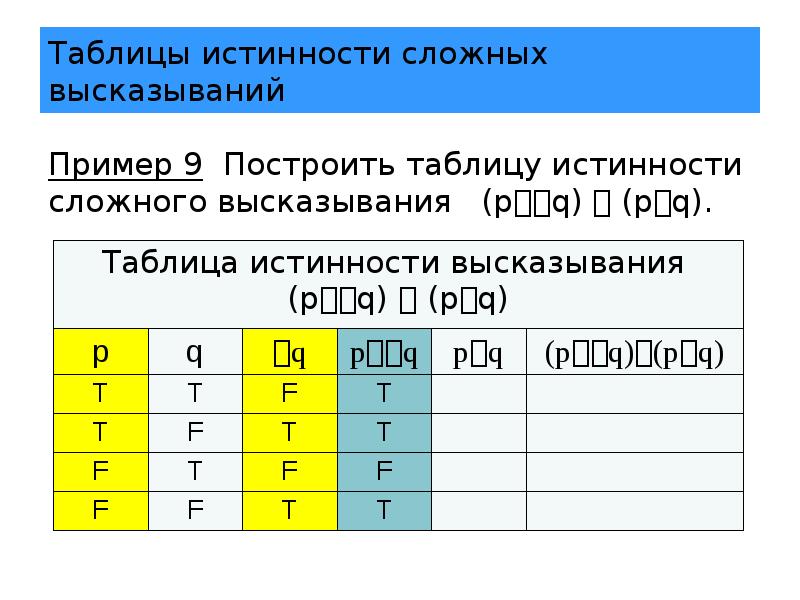 Следовательно, знание – это векторная физическая величина, мера интенсивности воздействия на данное тело других тел и полей». Такое рассуждение не может быть верным, так как здесь нарушен принцип тождества: термин «сила» употребляется в первом и втором предложении в разных значениях.
Следовательно, знание – это векторная физическая величина, мера интенсивности воздействия на данное тело других тел и полей». Такое рассуждение не может быть верным, так как здесь нарушен принцип тождества: термин «сила» употребляется в первом и втором предложении в разных значениях.
2
Закон противоречия
Закон противоречия гласит: неверно, что А и не-А.
Построим таблицу истинности.
|
А |
Неверно, что |
А |
и |
не-А |
|
и |
и |
и |
л |
л |
|
л |
и |
л |
л |
и |
В первом столбце даны значения А («истина» и «ложь»).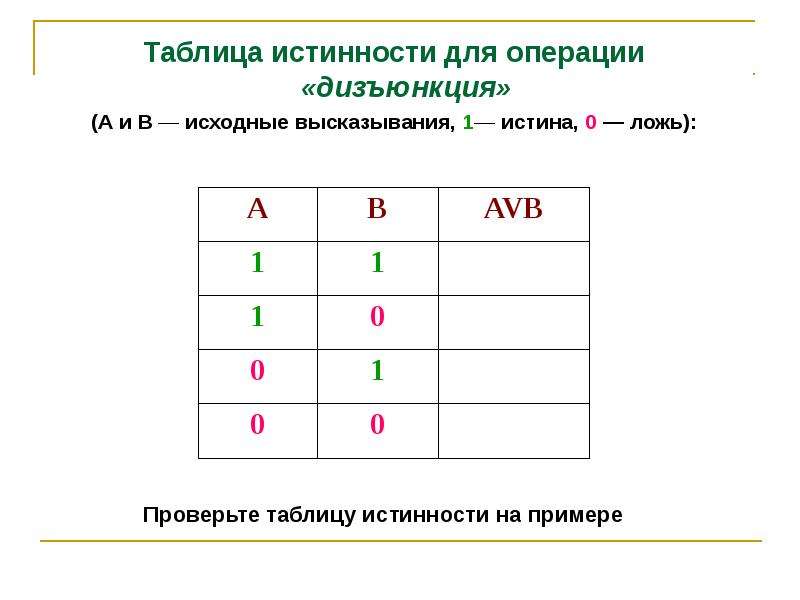 Соответственно, мы просто копируем эти значения в третий столбец. Значения для не-А в пятом столбце будут прямо обратными для значений А, поэтому получаем «ложь», «истина». В четвёртом столбце располагается конъюнкция между А и не-А. Она не может быть истинной ни в одном из случаев. Поэтому её значение всегда «ложь». Наконец, второй столбец представляет значение выражения полностью – это отрицание конъюнкции между А и не-А. Поскольку конъюнкция ложна, то её отрицание будет истинным. В итоге, мы видим, что выражение в целом всегда истинно.
Соответственно, мы просто копируем эти значения в третий столбец. Значения для не-А в пятом столбце будут прямо обратными для значений А, поэтому получаем «ложь», «истина». В четвёртом столбце располагается конъюнкция между А и не-А. Она не может быть истинной ни в одном из случаев. Поэтому её значение всегда «ложь». Наконец, второй столбец представляет значение выражения полностью – это отрицание конъюнкции между А и не-А. Поскольку конъюнкция ложна, то её отрицание будет истинным. В итоге, мы видим, что выражение в целом всегда истинно.
Если же мы возьмём выражение типа «А и не-А», то оно как раз будет представлять собой противоречие. Из таблицы мы видим, что такое выражение всегда будет принимать значение «ложь».
Согласно закону противоречия (иногда его называют законом непротиворечия) невозможно, чтобы одновременно оказались истинными высказывание и его прямое отрицание: неверно, что снег идёт и в то же время не идёт, неверно, что Катя любит ананасы и не любит ананасы. Важно сделать следующее замечание: противоречия возникает только тогда, когда утверждение и отрицание делаются об одном и том же объекте, в одно и то же время, в одном и тот же отношении. Например, высказывания «Снег идёт на Северном полюсе, но снег не идёт в Зимбабве», «Толя ходил в кино вчера, а сегодня не ходил», «Катя любит ананасы, а Петя не любит ананасы», «Вася любит кататься на коньках и не любит кататься на лыжах» не являются противоречиями. Все они говорят либо о разных предметах, либо о разных временных отрезках, либо о разных аспектах одного предмета. Поэтому не всё, что выглядит как противоречие, действительно является таковым. Такие кажущиеся противоречия называют мнимыми. Пример мнимого противоречия можно найти в дзенской притче «Бокудзю и ручей»:
Важно сделать следующее замечание: противоречия возникает только тогда, когда утверждение и отрицание делаются об одном и том же объекте, в одно и то же время, в одном и тот же отношении. Например, высказывания «Снег идёт на Северном полюсе, но снег не идёт в Зимбабве», «Толя ходил в кино вчера, а сегодня не ходил», «Катя любит ананасы, а Петя не любит ананасы», «Вася любит кататься на коньках и не любит кататься на лыжах» не являются противоречиями. Все они говорят либо о разных предметах, либо о разных временных отрезках, либо о разных аспектах одного предмета. Поэтому не всё, что выглядит как противоречие, действительно является таковым. Такие кажущиеся противоречия называют мнимыми. Пример мнимого противоречия можно найти в дзенской притче «Бокудзю и ручей»:
Один дзэнский монах, Бокудзю, говорил: «Иди и пересеки ручей, но не позволяй воде прикоснуться к тебе».
А через ручей около его монастыря не было никакого моста. Многие пытались сделать это, но когда они пересекали ручей, то, конечно же, вода прикасалась к ним. Поэтому однажды один монах пришел к нему и сказал:
Поэтому однажды один монах пришел к нему и сказал:
— Вы задали нам неразрешимую задачу. Мы пытаемся пересечь этот ручей; через него нет никакого моста. Если бы был мост, то мы, конечно же, пересекли бы ручей, и вода не прикоснулась бы к нам. Но мы вынуждены идти через поток, и вода прикасается к нам.
И Бокудзю сказал:
— Я пойду и пересеку его, а вы наблюдайте.
И Бокудзю пересёк ручей. Вода, конечно, прикоснулась к его ногам, и они сказали:
— Смотрите, вода прикоснулась к вам!
Бокудзю сказал:
— Насколько я знаю, она не прикоснулась ко мне. Я был просто свидетелем. Вода прикоснулась к моим ногам, но не ко мне. Я был просто свидетельствующим.
Между тем, чтобы пересечь ручей без моста и не позволить воде прикоснуться к себе, нет противоречия, потому что в данном случае человеческое я рассматривает в разных отношениях: как тело, и как дух. Тело проходит через ручей и намокает, но дух остаётся безмятежным и не затронутым водой.
Как и закон тождества, закон противоречия требует от нас быть последовательными в рассуждениях. Либо мы принимаем, что высказывание истинно, либо мы принимаем, что оно ложно, но не то и другое вместе. Смешение истины и лжи приводит к тому, что всё рассуждение обесценивается, так как мы уже не можем быть уверены в сделанном выводе. Противоречия опасны потому, что с точки зрения логики из них можно вывести всё что угодно, то есть высказывание формы «Если А и не-А, то В» всегда будет истинным. Вы можете сами проверить это с помощью таблицы истинности. «Если дождь идёт, и дождь не идёт, то Чехов – автор “Войны и мира”». Если допускать противоречия, подобное «рассуждение» оказывается возможным. Поэтому логика ставит запрет на противоречия.
Нужно сказать, что противоречия бывают не только явными, но и скрытыми. Очевидно, что чаще всего никто старается не допускать в своём рассуждении наличия двух прямо противоположных высказываний. Однако, не редки случаи, когда противоречие прячется за вроде бы правильными формулировками.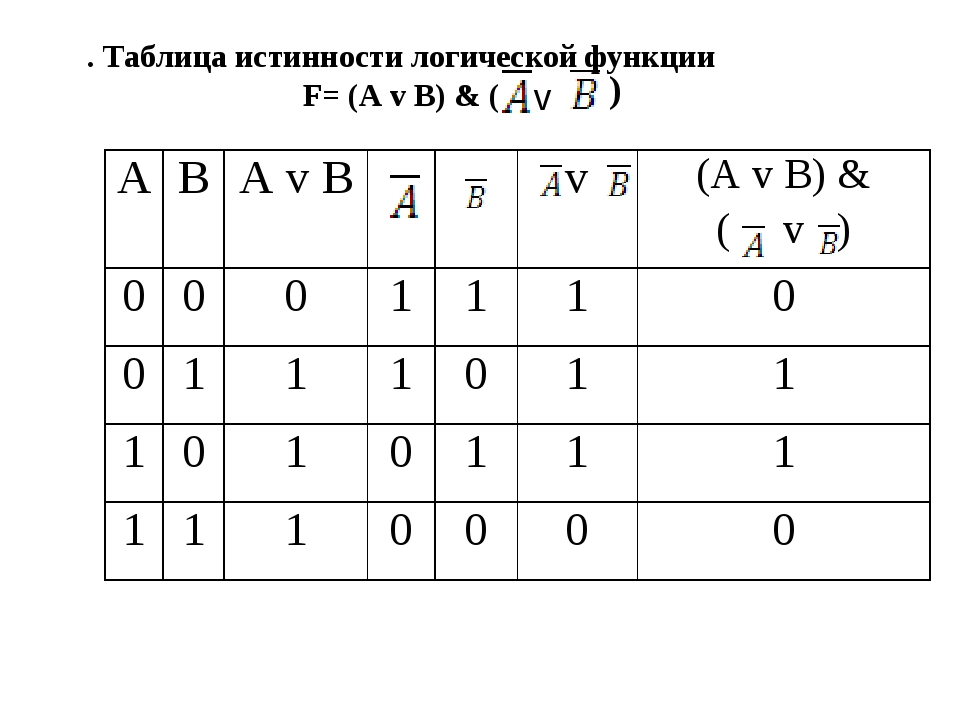 Приведём несколько примеров, которые хорошо это иллюстрируют: «Мы заставим их стать свободными», «Мы будем бороться за мир, и камня на камне не останется от нашей борьбы». Понятно, что идея свободы предполагает, что человека не заставляют, а он сам принимает решения, а идея мира предполагает отсутствия борьбы или войны.
Приведём несколько примеров, которые хорошо это иллюстрируют: «Мы заставим их стать свободными», «Мы будем бороться за мир, и камня на камне не останется от нашей борьбы». Понятно, что идея свободы предполагает, что человека не заставляют, а он сам принимает решения, а идея мира предполагает отсутствия борьбы или войны.
Обычно появление противоречия – это знак того, что в рассуждение где-то закралась ошибка. Исправление этой ошибки, снимет и противоречие. Ошибка может скрываться в сделанных умозаключениях, но может содержаться и в изначально избранных посылках. По этой причине приведение к противоречию играет ключевую роль в так называемых доказательствах от противного. Наверное, все помнят их со школьных уроков геометрии. Доказательство от противного строится на том, что нужно обосновать какой-то тезис, но прямое его доказательство найти не получается. Тогда берётся его отрицание, и в определённый момент рассуждения мы наталкиваемся на противоречие, а это знак того, что отрицание тезиса было неверным. Так что противоречие может играть и позитивную роль в рассуждении.
Так что противоречие может играть и позитивную роль в рассуждении.
В заключение, добавим, что в советской философии, превозносившей Маркса и Гегеля, появилось целое направление под названием «диалектическая логика», которая якобы допускала наличие противоречий и даже оценивала их положительно. Такая точка зрения строилась на том, что противоречия – это источник движения и развития, а потому это хорошо, если мы сталкиваемся с ними. Ещё и сегодня можно встретить людей, которые придерживаются подобного мнения. Однако нужно понимать, что речь здесь не идёт о противоречии в логическом смысле (как форме высказывания, которое при любой интерпретации принимает значение «ложь»). Скорее, под противоречием тут следует мыслить несовместимость, плохую сочетаемость ситуаций, феноменов, характеров и т.д. Так во Франции конца XVIII века желание буржуазии участвовать в политической жизни страны плохо сочеталось с формой правления абсолютной монархии, что в итоге привело к буржуазной революции. Можно сказать, что между ними возникло противоречие, но это не имеет никакого отношения к логике.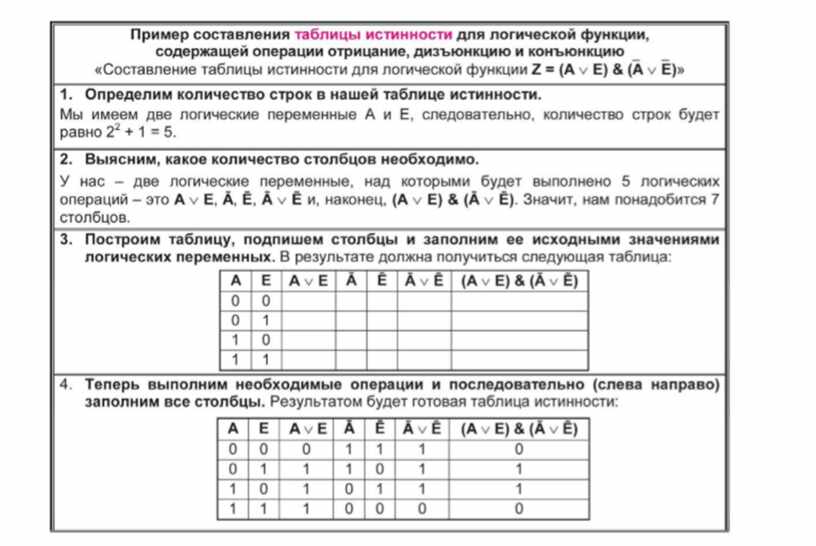
3
Закон исключённого третьего
Закон исключённого третьего имеет следующую форму: А или неверно, что А.
Построим таблицу истинности:
|
А |
или |
неверно, что А |
|
и |
и |
л |
|
л |
и |
и |
Если А принимает значение «истина» и «ложь», то «неверно, что А» соответственно будет принимать значения «ложь» и «истина». Их дизъюнкция всегда будет истинной.
Закон исключённого третьего очень похож на закон противоречия, потому что он точно также утверждает, что высказывание и его отрицание не могут быть одновременно истинными. Истинно либо одно, либо другое, и третьего не дано.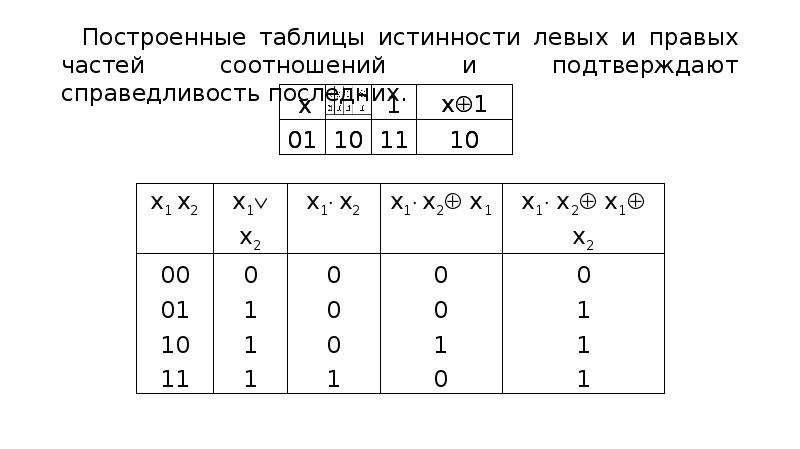 Истинно или высказывание «Глинка был композитором», или его отрицание «Глинка не был композитором», но они не могут быть истинными одновременно. Опять же здесь также стоит следить за тем, чтобы высказывания относились к одному и тому же предмету, говорили о нём в одном и том же отношении и в одно и то же время.
Истинно или высказывание «Глинка был композитором», или его отрицание «Глинка не был композитором», но они не могут быть истинными одновременно. Опять же здесь также стоит следить за тем, чтобы высказывания относились к одному и тому же предмету, говорили о нём в одном и том же отношении и в одно и то же время.
Нужно отметить, что законом исключённого третьего часто пользуются в качестве уловки, пытаясь представить какую-либо сложную ситуацию в виде простой оппозиции. К примеру: «Ты с нами или ты против нас», «Женщины бывают либо умными, либо красивыми», «Они либо патриоты, либо предатели». Особенно часто этим приёмом любят пользоваться политики, пытаясь представить, будто их оппоненты защищают какую-то радикальную позицию, которой те на самом деле не придерживаются. Отчасти эта склонность сводить всё многообразие фактов и позиций к двум противоположностям обусловлена чисто психологическими механизмами работы человеческого мышления. Всё дело в том, что наше мышление работает по так называемому принципу когнитивной экономии: вместо того, чтобы тратить время и энергию на анализ всей сложности ситуации, мы предпочитаем представить её в виде грубой полярной схемы. Поэтому если ваш собеседник или демагог из телевизора говорит вам, что «третьего не дано», подумайте, так ли это: не заключается ли между двумя членами оппозиции целый спектр разнообразных возможностей.
Поэтому если ваш собеседник или демагог из телевизора говорит вам, что «третьего не дано», подумайте, так ли это: не заключается ли между двумя членами оппозиции целый спектр разнообразных возможностей.
Кроме того, с законом исключённого третьего нужно быть аккуратными ещё и потому, что значения высказываний во многих случаях определяются относительно конкретного контекста. Помните Ивана и его детей из прошлого урока? Вполне можно было бы сказать в соответствии с законом исключённого третьего: «Дети Ивана либо лысы, либо нет, третьего не дано». Но ни одна из этих альтернатив не может нас удовлетворить, так как у Ивана нет детей. Таким образом, прежде чем применять закон исключённого третьего, сверьтесь с контекстом высказывания.
Законы тождества, противоречия и исключённого третьего фундаментальны и выполняются в любых логических системах. Без соблюдения этих законов невозможно делать правильные умозаключения. Иногда к ним присоединяют ещё так называемый закон достаточного основания. Этот закон гласит, что любое утверждение должно быть корректно обосновано. Хотя это очень важный принцип, на котором должны базироваться любые рассуждения, законом в собственно логическом смысле он не является, так как не представим в виде логической формы, которая при любой трактовке принимала бы значение «истина». Скорее, это общее требование, вытекающее из самой идеи логичного рассуждения, целью которого как раз и является обоснование тезиса путём правильных умозаключений. О том, как правильно делать умозаключения, мы начнём рассказывать в следующем уроке.
Этот закон гласит, что любое утверждение должно быть корректно обосновано. Хотя это очень важный принцип, на котором должны базироваться любые рассуждения, законом в собственно логическом смысле он не является, так как не представим в виде логической формы, которая при любой трактовке принимала бы значение «истина». Скорее, это общее требование, вытекающее из самой идеи логичного рассуждения, целью которого как раз и является обоснование тезиса путём правильных умозаключений. О том, как правильно делать умозаключения, мы начнём рассказывать в следующем уроке.
Проверьте свои знания
Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.
таблиц истинности и анализ аргументов: примеры
Таблицы истинности
Поскольку сложные логические утверждения могут быть сложными для размышления, мы можем создать таблицу истинности , чтобы отслеживать, какие значения истинности для простых утверждений делают сложное утверждение истинным, а какое ложным
Таблица истинности
Таблица, показывающая, каково результирующее значение истинности сложного утверждения для всех возможных значений истинности для простых утверждений.
Пример 1
Предположим, вы выбираете новый диван, и ваша вторая половинка говорит: «Купите что-нибудь секционное или с шезлонгом.”
Это сложное утверждение, состоящее из двух более простых условий: «является секционным» и «имеет шезлонг». Для простоты воспользуемся S для обозначения «является секционным» и C для обозначения «имеет шезлонг». Условие S выполняется, если кушетка секционная.
Таблица истинности для этого будет выглядеть так:
| S | С | S или C |
|---|---|---|
| т | т | т |
| т | F | т |
| F | т | т |
| F | F | F |
В таблице T означает истину, а F — ложь.В первой строке, если S истинно и C также истинно, то комплексное утверждение « S или C » истинно. Это будет секция, у которой тоже есть шезлонг, что соответствует нашему желанию.
Помните также, что или в логике не исключают; если диван имеет обе функции, он соответствует условию.
Для дальнейшего сокращения наших обозначений мы собираемся ввести некоторые символы, которые обычно используются для и , или , а также , а не .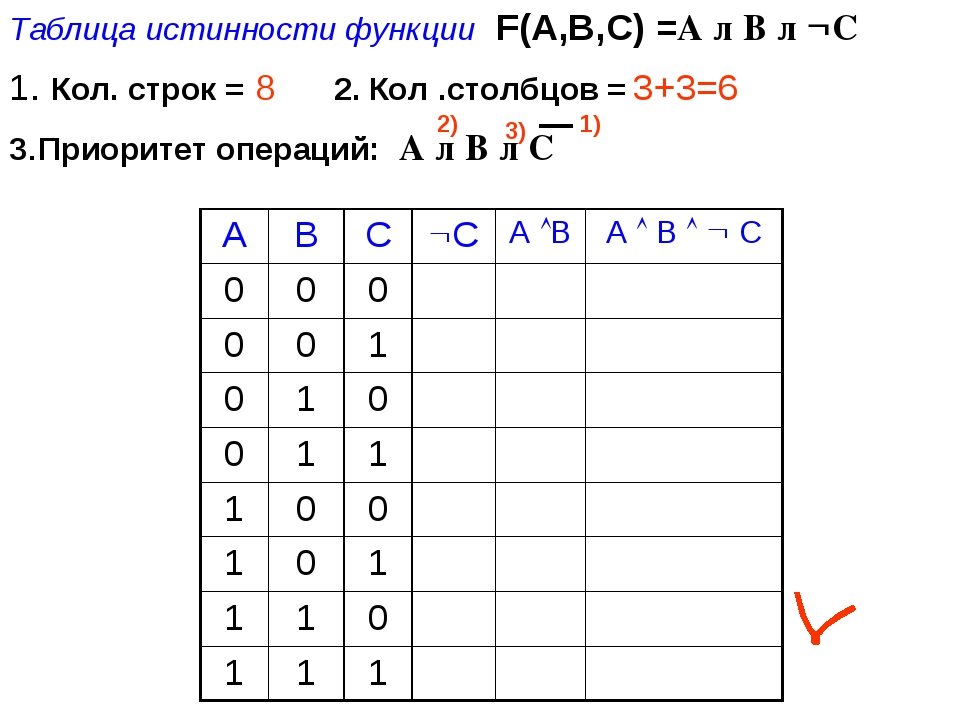
Символы
Символ ⋀ используется для и : A и B обозначен как A ⋀ B .
Символ ⋁ используется для или : A или B обозначается A ⋁ B
Символ ~ используется для , а не : не A обозначается ~ A
Вы можете запомнить первые два символа, связав их с формами объединения и пересечения. A ⋀ B — это элементы, которые существуют в обоих наборах, в A ⋂ B.Аналогично, A ⋁ B будут элементами, которые существуют в любом наборе, в A ⋃ B.
В предыдущем примере таблица истинности на самом деле просто суммировала то, что мы уже знаем о работе операторов или . Таблицы истинности для базовых операторов и , или и , а не показаны ниже.
Основные таблицы истинности
| А | B | A ⋀ B |
|---|---|---|
| т | т | т |
| т | F | F |
| F | т | F |
| F | F | F |
| А | B | A ⋁ B |
|---|---|---|
| т | т | т |
| т | F | т |
| F | т | т |
| F | F | F |
Таблицы истинности действительно становятся полезными при анализе более сложных логических операторов.
Пример 2
Создайте таблицу истинности для утверждения A ⋀ ~ ( B ⋁ C )
Это помогает работать изнутри при создании таблиц истинности и создавать таблицы для промежуточных операций. Начнем с перечисления всех возможных комбинаций значений истинности для A , B и C . Обратите внимание, что первый столбец содержит 4 Ts, за которыми следуют 4 F, второй столбец содержит 2 Ts, 2 F, затем повторяется, а последний столбец чередуется.Этот шаблон обеспечивает учет всех комбинаций. Наряду с этими начальными значениями мы перечислим истинные значения для самого внутреннего выражения: B ⋁ C .
| А | В | С | B ⋁ C |
| т | т | т | т |
| т | т | F | т |
| т | F | т | т |
| т | F | F | F |
| F | т | т | т |
| F | т | F | т |
| F | F | т | т |
| F | F | F | F |
Далее мы можем найти отрицание B ⋁ C , отработав только что созданный столбец B ⋁ C .
| А | В | С | B ⋁ C | ~ ( B ⋁ C ) |
| т | т | т | т | F |
| т | т | F | т | F |
| т | F | т | т | F |
| т | F | F | F | т |
| F | т | т | т | F |
| F | т | F | т | F |
| F | F | т | т | F |
| F | F | F | F | т |
Наконец, мы находим значения A и ~ ( B ⋁ C )
| А | В | С | B ⋁ C | ~ ( B ⋁ C ) | A ⋀ ~ ( B ⋁ C ) |
| т | т | т | т | F | F |
| т | т | F | т | F | F |
| т | F | т | т | F | F |
| т | F | F | F | т | т |
| F | т | т | т | F | F |
| F | т | F | т | F | F |
| F | F | т | т | F | F |
| F | F | F | F | т | F |
Оказывается, это сложное выражение истинно только в одном случае: если A истинно, B ложно, а C ложно.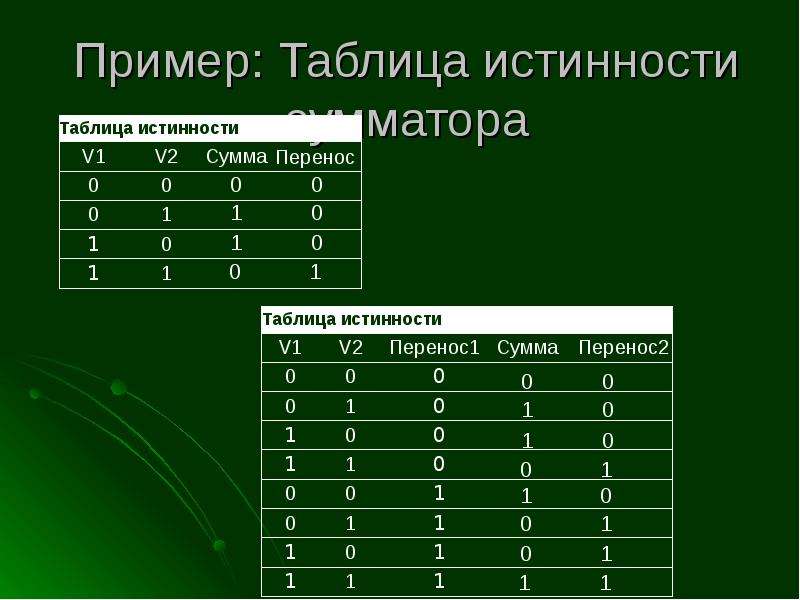
Когда мы обсуждали условия ранее, мы обсуждали тип, при котором мы предпринимаем действие, основанное на значении условия. Теперь мы поговорим о более общей версии условного выражения, которое иногда называют импликацией .
Последствия
Последствия — это логические условные предложения, в которых говорится, что утверждение p , называемое антецедентом, подразумевает следствие q .
Последствия обычно записываются как p → q
Последствия аналогичны условным операторам, которые мы рассматривали ранее; p → q обычно записывается как «если p, то q» или «p, следовательно, q.«Разница между импликациями и условными предложениями заключается в том, что условные выражения, которые мы обсуждали ранее, предполагают действие — если условие истинно, то в результате мы предпринимаем какое-то действие. Последствия — это логическое утверждение, которое предполагает, что следствие должно логически следовать, если антецедент верен.
Пример 3
Английское утверждение «Если идет дождь, значит, в небе облака» является логическим следствием. Это веский аргумент, потому что если предшествующее утверждение «идет дождь» верно, то следствие «в небе облака» также должно быть верным.
Обратите внимание, что это утверждение ничего не говорит нам о том, чего ожидать, если не будет дождя. Если антецедент ложен, то импликация становится неактуальной.
Пример 4
Друг говорит вам, что «если вы загрузите эту фотографию в Facebook, вы потеряете работу». Есть четыре возможных исхода:
- Вы загружаете картинку и сохраняете свою работу
- Вы загружаете фотографию и теряете работу
- Вы не загружаете картинку и сохраняете свою работу
- Вы не загружаете картинку и теряете работу
Есть только один возможный случай, когда ваш друг лгал — первый вариант, когда вы загружаете изображение и сохраняете свою работу.В последних двух случаях ваш друг ничего не сказал о том, что произойдет, если вы не загрузите изображение, поэтому вы не можете сделать вывод, что его утверждение недействительно, даже если вы не загрузили изображение и все равно потеряли свое работа.
В традиционной логике импликация считается действительной (истинной) до тех пор, пока нет случаев, в которых антецедент истинен, а следствие ложно. Важно помнить, что символическая логика не может охватить все тонкости английского языка.
Истинные значения для последствий
| p | q | p → q |
| т | т | т |
| т | F | F |
| F | т | т |
| F | F | т |
Пример 5
Постройте таблицу истинности для утверждения ( m ⋀ ~ p ) → r
Начнем с построения таблицы истинности для антецедента.
| м | п. | ~ п. | м ⋀ ~ p |
| т | т | F | F |
| т | F | т | т |
| F | т | F | F |
| F | F | т | F |
Теперь мы можем построить таблицу истинности для импликации
| м | п.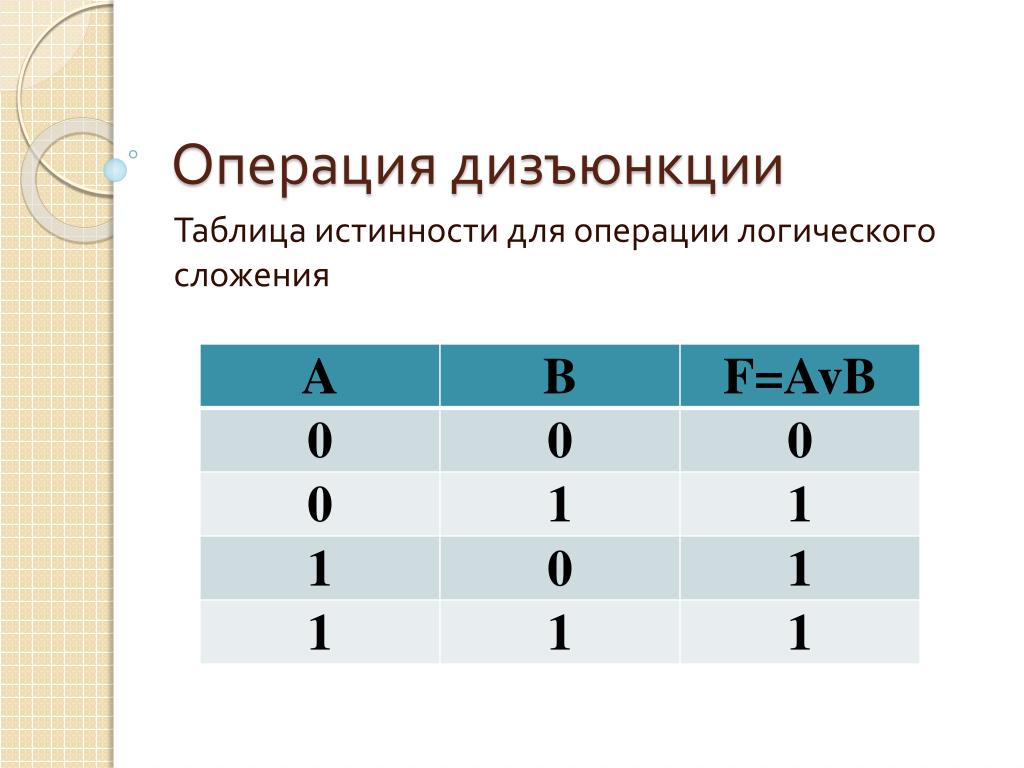 | ~ п. | м ⋀ ~ p | р | ( м ⋀ ~ p ) → r |
| т | т | F | F | т | т |
| т | F | т | т | т | т |
| F | т | F | F | т | т |
| F | F | т | F | т | т |
| т | т | F | F | F | т |
| т | F | т | т | F | F |
| F | т | F | F | F | т |
| F | F | т | F | F | т |
В этом случае, когда m истинно, p ложно и r ложно, тогда антецедент m ⋀ ~ p будет истинным, но последствие ложным, в результате недействительное следствие; любой другой случай дает верное значение.
Для любого импликации есть три связанных утверждения: обратное, обратное и противоположное.
Заявления по теме
Исходное значение: «если p , то q »: p → q
Обратное: «если q , то p »: q → p
Обратное: «если не p , то не q »: ~ p → ~ q
Контрапозитив: «если не q , то не p »: ~ q → ~ p
Пример 6
Снова рассмотрим действительный вывод: «Если идет дождь, то в небе облака.”
Обратное выражение: «Если на небе облака, значит, идет дождь». Это, конечно, не всегда так.
Обратное будет: «Если не идет дождь, то на небе нет облаков». Точно так же это не всегда так.
Контрапозитив будет: «Если на небе нет облаков, значит, не идет дождь». Это утверждение верно и эквивалентно исходному выводу.
Посмотрев на таблицы истинности, мы можем увидеть, что исходное условное и противоположное логически эквивалентны, а обратное и обратное логически эквивалентны.
| Последствия | Конверс | обратный | Контрапозитив | ||
|---|---|---|---|---|---|
| p | q | p → q | q → p | ~ p → ~ q | ~ q → ~ p |
| т | т | т | т | т | т |
| т | F | F | т | т | F |
| F | т | т | F | F | т |
| F | F | т | т | т | т |
Эквивалентность
Условное утверждение и его контрпозитив логически эквивалентны.
Обратное и обратное утверждения логически эквивалентны.
Аргументы
Логический аргумент — это утверждение, что набор предпосылок поддерживает заключение. Есть два основных типа аргументов: индуктивные и дедуктивные.
Есть два основных типа аргументов: индуктивные и дедуктивные.
Типы аргументов
Индуктивный аргумент использует набор конкретных примеров в качестве предпосылок и использует их, чтобы предложить общий вывод.
Дедуктивный аргумент использует набор общих утверждений в качестве предпосылок и использует их, чтобы предложить конкретную ситуацию в качестве заключения.
Пример 7
Аргумент «когда я пошел в магазин на прошлой неделе, я забыл свой кошелек, а когда я пошел сегодня, я забыл свой кошелек. Я всегда забываю свой кошелек, когда иду в магазин », — это индуктивный аргумент.
Помещения:
Я забыл свой кошелек на прошлой неделе
Я забыл свой кошелек сегодня
Вывод:
Я всегда забываю свой кошелек
Обратите внимание, что предпосылки — это конкретные ситуации, а заключение — это общее утверждение.В данном случае это довольно слабый аргумент, поскольку он основан всего на двух примерах.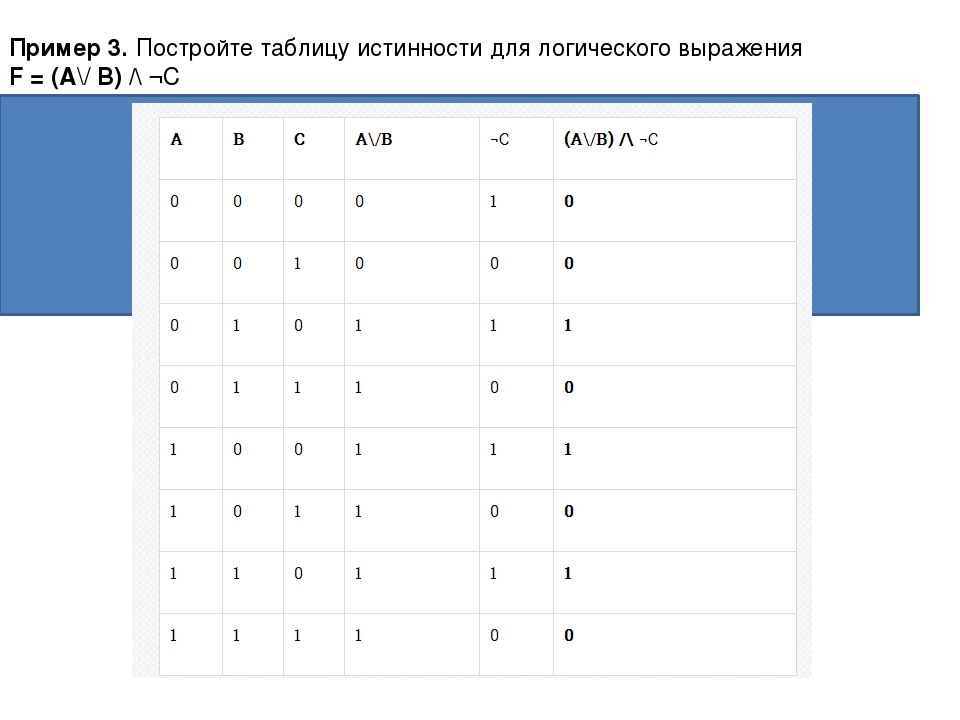
Пример 8
Аргумент «каждый день в течение последнего года над моим домом в 14:00 пролетает самолет. Самолет будет пролетать над моим домом каждый день в 2 часа дня », — это более сильный индуктивный аргумент, поскольку он основан на большем количестве доказательств.
Оценка индуктивных аргументов
Индуктивный аргумент никогда не может доказать истинность вывода, но он может предоставить либо слабые, либо убедительные доказательства того, что это может быть правдой.
Многие научные теории, такие как теория большого взрыва, никогда не могут быть доказаны. Напротив, это индуктивные аргументы, подкрепленные множеством свидетельств. Обычно в науке идея считается гипотезой до тех пор, пока она не будет хорошо проверена, после чего она становится теорией. Все общеизвестные научные теории, такие как теория гравитации Ньютона, выдержали годы испытаний и доказательств, хотя иногда их нужно корректировать на основе новых данных.Что касается гравитации, это произошло, когда Эйнштейн предложил общую теорию относительности.
Дедуктивный аргумент является более достоверным или нет, что упрощает их оценку.
Оценка дедуктивных аргументов
Дедуктивный аргумент считается действительным, если все посылки верны, и вывод логически следует из этих посылок. Другими словами, посылки верны, и вывод обязательно следует из этих посылок.
Пример 9
Аргумент «Все кошки — млекопитающие, а тигр — это кошка, значит, тигр — это млекопитающее» — действенный дедуктивный аргумент.
Помещения:
Все кошки — млекопитающие
Тигр — это кошка
Вывод:
Тигр — млекопитающее
Оба предположения верны. Чтобы увидеть, что посылки должны логически вести к заключению, можно использовать диаграмму Венна. Исходя из первой предпосылки, мы можем заключить, что набор кошек — это подмножество множества млекопитающих. Из второй посылки нам говорят, что тигр находится внутри множества кошек. Из этого мы можем видеть на диаграмме Венна, что тигр также находится внутри множества млекопитающих, поэтому вывод верен.
Анализ аргументов с помощью диаграмм Венна
Анализ аргумента с помощью диаграммы Венна
- Нарисуйте диаграмму Венна на основе посылок аргумента
- Если помещения недостаточно, чтобы определить, что определяет расположение элемента, укажите это.
- Аргумент действителен, если ясно, что заключение должно быть верным
Пример 10
Предпосылка: все пожарные знают CPR
Предпосылка: Джилл знает CPR
Заключение: Джилл — пожарный
Исходя из первой предпосылки, мы знаем, что все пожарные входят в группу тех, кто знает СЛР.Из второй посылки мы знаем, что Джилл является членом этого большего набора, но у нас недостаточно информации, чтобы знать, является ли она также членом меньшего подмножества, то есть пожарных.
Поскольку вывод не обязательно следует из предпосылок, это неверный аргумент, независимо от того, действительно ли Джилл является пожарным.
Важно отметить, что то, действительно ли Джилл является пожарным, не имеет значения для оценки обоснованности аргумента; нас интересует только то, достаточно ли предпосылок, чтобы доказать вывод.
В дополнение к этим предпосылкам категориального стиля в форме «все ___», «некоторые ____» и «нет ____» также часто можно увидеть посылки, которые имеют значение.
Пример 11
Предпосылка: Если вы живете в Сиэтле, вы живете в Вашингтоне.
Предпосылка: Маркус не живет в Сиэтле
Заключение: Маркус не живет в Вашингтоне
Из первой предпосылки мы знаем, что множество людей, живущих в Сиэтле, находится внутри множества тех, кто живет в Вашингтоне.Из второй посылки мы знаем, что Маркус не находится в множестве Сиэтла, но у нас недостаточно информации, чтобы знать, живет ли Маркус в Вашингтоне или нет. Это недопустимый аргумент.
Пример 12
Рассмотрим аргумент «Вы женатый мужчина, значит, у вас должна быть жена».
Это неверный аргумент, поскольку есть, по крайней мере, в некоторых частях мира, мужчины, состоящие в браке с другими мужчинами, поэтому посылка не является недостаточной, чтобы сделать вывод.
Некоторые аргументы лучше анализировать с помощью таблиц истинности.
Пример 13
Рассмотрим аргумент:
Помещение: Если вы купили хлеб, то вы пошли в магазин
Помещение: вы купили хлеб
Вывод: вы пошли в магазин
Хотя мы надеемся, что этот пример является вполне очевидным аргументом, мы можем проанализировать его с помощью таблицы истинности, представив каждую из посылок символически. Затем мы можем посмотреть на импликацию, что все предпосылки вместе подразумевают заключение. Если таблица истинности является тавтологией (всегда верно), то аргумент действителен.
Мы получим, что B означает «вы купили хлеб», а S — «вы пошли в магазин». Тогда аргумент принимает вид:
Помещение: B → S
Помещение: B
Заключение: S
Чтобы проверить достоверность, мы смотрим, подразумевает ли комбинация обеих предпосылок вывод; правда ли, что [( B → S ) ⋀ B ] → S ?
| B | S | B → S | ( B → S ) ⋀ B | [( B → S ) ⋀ B ] → S |
| т | т | т | т | т |
| т | F | F | F | т |
| F | т | т | F | т |
| F | F | т | F | т |
Поскольку таблица истинности для [( B → S ) ⋀ B ] → S всегда истинна, это допустимый аргумент.
Анализ аргументов с использованием таблиц истинности
Чтобы проанализировать аргумент с помощью таблицы истинности:
- Изобразите каждое из помещений символически
- Создайте условное утверждение, соединив все посылки с антецедентом и образуя его, и используя заключение как следствие.
- Создайте таблицу истинности для этого утверждения. Если это всегда правда, то аргумент действителен.
Пример 14
Предпосылка: если я пойду в торговый центр, то куплю новые джинсы
Предпосылка: если я куплю новые джинсы, я куплю к ним рубашку
Вывод: если я приду в торговый центр, я куплю Футболка.
Пусть M = иду в торговый центр, J = покупаю джинсы, а S = покупаю рубашку.
Предпосылки и заключение можно изложить как:
Помещение: M → J
Помещение: J → S
Заключение: M → S
Мы можем построить таблицу истинности для [( M → J ) ⋀ ( J → S )] → ( M → S )
| M | Дж | S | M → Дж | Дж → Ю | ( M → J ) ⋀ ( J → S ) | M → S | [( M → J ) ⋀ ( J → S )] → ( M → S ) |
| т | т | т | т | т | т | т | т |
| т | т | F | т | F | F | F | т |
| т | F | т | F | т | F | т | т |
| т | F | F | F | т | F | F | т |
| F | т | т | т | т | т | т | т |
| F | т | F | т | F | F | т | т |
| F | F | т | т | т | т | т | т |
| F | F | F | т | т | т | т | т |
Из таблицы истинности мы видим, что это действительный аргумент.
таблиц истинности, тавтологий и логических эквивалентностей
таблиц истинности, тавтологий и логических эквивалентностейМатематики обычно используют двузначное число . логика : Каждый оператор либо Истина , либо Неверно . Это называется . Закон Исключенного Среднего .
Утверждение в логике предложений строится из простых утверждений с использованием логические связки,,, и. Правда или ложь утверждения, построенного с помощью этих связок, зависит от истины или ложность его составляющих.
Например, составной оператор строится с использованием логических связок, и. Правда или ложь зависит от правды или ложность P, Q и R.
Таблица истинности показывает, как правда или ложь составного утверждения зависит от истинности или ложности простого утверждения, из которых он построен. Итак, мы начнем с рассмотрения таблицы истинности для пяти логических связок.
Вот таблица для отрицания:
Эта таблица проста для понимания.Если P равно истинно , его отрицание это ложь . Если P ложно , то истинно .
должно быть истинно , когда и P, и Q равны истина и ложь иначе:
равно истинно , если либо P равно истинно , либо Q равно правда (или оба — помните, что мы используем «или» в инклюзивном смысле). Только ложно , если и P, и Q равны ложь .
Вот таблица для логического вывода:
Чтобы понять, почему эта таблица такая, как она есть, рассмотрим следующие пример:
«Если вы получите пятерку, я дам вам доллар».
Утверждение будет истинным , если я сдержу свое обещание и ложь , если я этого не сделаю.
Предположим, что истинно , что вы получили A, а истинно что я даю вам доллар.Поскольку я сдержал свое обещание, подразумевается правда . Это соответствует первой строке в таблице.
Предположим, что истинно , что вы получили A, но это ложно что я даю вам доллар. Поскольку я не сдержал своего обещания , подразумевается ложь . Это соответствует второму строка в таблице.
Что, если вы получите пятерку неверно? Независимо от того, даю ли я вам доллар, я не нарушил свое обещание.Таким образом, значение не может быть false, поэтому (поскольку это двузначная логика) должно быть истинным. Этот объясняет последние две строки таблицы.
означает, что P и Q равны эквивалент . Таким образом, двойное значение истинно , если P и Q оба истинны или если P и Q оба ложны ; в противном случае двойная импликация ложна.
Вы должны помнить — или уметь составлять — таблицы истинности для логических связок.Вы будете использовать эти таблицы для построения таблицы для более сложных предложений. Проще продемонстрировать что делать, чем описывать словами, чтобы вы увидели порядок действий отработано в примерах.
Замечание. (а) Когда вы конструируете истину таблице, вы должны рассмотреть все возможные присвоения True (T) и Ложь (F) для операторов компонентов. Например, предположим, что операторы компонентов — это P, Q и R. Каждый из этих операторов может быть либо правда, либо ложь, значит, есть возможности.
Когда вы перечисляете возможности, вы должны присваивать значения истинности к операторам компонентов систематическим образом, чтобы избежать дублирования или упущение. Самый простой подход — использовать лексикографическая упорядоченность . Таким образом, для составного оператора с три компонента P, Q и R, я бы перечислил возможности этого способ:
(б) Существуют разные способы составления таблиц истинности. Вы можете для например, запишите значения истинности «под» логическим связки составного высказывания, постепенно наращивая столбец для «первичной» связки.
Я напишу подробности, построив столбцы для каждого «кусок» составного высказывания и постепенно наращивая к составному оператору. Любой стиль хорош, пока ты показываешь достаточно работы, чтобы оправдать ваши результаты.
Пример. Постройте таблицу истинности для формула.
Сначала я перечисляю все альтернативы для P и Q.
Затем в третьем столбце я перечисляю значения, основанные на значениях P.Я использую таблицу истинности для отрицание: когда P истинно ложно, а когда P ложно, правда.
В четвертом столбце я перечисляю значения для. Убедитесь сами, что это только ложь («F»), если P истинно («T») и Q ложно («F»).
В пятом столбце приведены значения для моего составного выражения. Это «и» (третий столбец) и (четвертый столбец). «И» верно, только если обе части «и» верны; в противном случае это ложь. Итак, я смотрю на третья и четвертая колонки; если оба верны («T»), я ставлю T в пятом столбце, иначе я поставил F.
Тавтология — это формула, которая «всегда истина «— то есть верно для каждого присвоения истины ценности к его простым компонентам. Вы можете думать о тавтологии как о правило логики .
Противоположность тавтологии — противоречие , формула, которая «всегда ложна». В другими словами, противоречие ложно для каждого присвоения истины ценности к его простым компонентам.
Пример. Показать, что это тавтология.
Я составляю таблицу истинности и показываю, что формула всегда верна.
Последний столбец содержит только буквы T. Следовательно, формула представляет собой тавтология.
Пример. Создайте таблицу истинности для.
Вы можете видеть, что построение таблиц истинности для утверждений с большим количеством связок или множества простых утверждений довольно утомительно и подвержен ошибкам.Хотя могут быть некоторые применения этого (например, для цифровых схем), в какой-то момент лучше всего было бы написать программа для построения таблиц истинности (и это, безусловно, было сделано).
Дело здесь в том, чтобы понять, как истинное значение сложного утверждение зависит от истинности его простых утверждений и его логические связки. В большинстве работ математики обычно не используйте операторы, которые очень сложны с логической точки зрения Посмотреть.
Пример. (a) Предположим, что P ложно и истинно. Скажите, является ли Q истинным, ложным или его истинным значение не может быть определено.
(b) Предположим, что это неверно. Расскажи истинно ли Q, ложно или его истинностное значение не может быть определено.
(a) Поскольку истинно, либо P истинно, либо истинно. Поскольку P ложно, должно быть верно. Следовательно, Q должно быть ложным.
(b) Утверждение «если-то» неверно, когда часть «если» истина, а часть «тогда» — ложь.Поскольку ложно, верно. Утверждение «и» верно только когда обе части верны. В частности, должно быть истинным, поэтому Q ложно.
Пример. Предположим
» » правда.
«» ложно.
«У Кэлвина Баттерболла фиолетовые носки» — правда.
Определите истинность утверждения
Для простоты пусть
P = «».
Q = «».
R = «У Кэлвина Баттерболла фиолетовые носки».
Я хочу определить истинное значение. Поскольку мне были даны конкретные значения истинности для P, Q, и R, я установил таблицу истинности с единственной строкой, используя данную значения для P, Q и R:
Следовательно, утверждение истинно .
Пример. Определите истинное значение утверждение
Утверждение «» ложно. Ты не можешь сказать есть ли в заявлении «Икабод Ксеркс шоколад» кексы «верно или неверно, но это не имеет значения.Если «если» часть утверждения «если-то» ложна, тогда утверждение «если-то» верно. (Проверить правду таблица, если вы не уверены в этом!) данное утверждение должно быть верным.
Два оператора X и Y логически равны эквивалент , если это тавтология. Другой способ сказать это: Для каждого присвоения значений истинности простому элементу операторы , составляющие X и Y, операторы X и Y имеют идентичные значения истинности.
С практической точки зрения вы можете заменить выражение в доказательство любым логически эквивалентным утверждением.
Чтобы проверить, являются ли X и Y логически эквивалентными, вы можете настроить таблица истинности, чтобы проверить, является ли тавтология — это есть ли «все ли Т в его столбце». Однако проще создать таблицу, содержащую X и Y, а затем проверьте, совпадают ли столбцы для X и для Y.
Пример. Покажите, что и логически эквивалентны.
Поскольку столбцы для и идентичны, два оператора логически эквивалент.Эта тавтология называется условной . Разъединение . Вы можете использовать эту эквивалентность для замены условно дизъюнкцией.
Существует бесконечное количество тавтологий и логических эквивалентностей; Я перечислил несколько ниже; более обширный список приведен в конце эта секция.
Когда тавтология имеет форму двусмысленного выражения, два утверждения которые составляют двояковыпуклую, логически эквивалентны. Следовательно, вы может заменить одну сторону на другую без изменения логического имея в виду.
Вам часто нужно будет отрицать математическое выражение . К посмотрим, как это сделать, мы начнем с того, что покажем, как отрицать символическое заявления.
Пример. Запишите отрицание следующие утверждения, упрощающие так, чтобы только простые утверждения отрицается.
(а)
(б)
(а) Я отвергаю данное утверждение, а затем упрощаю, используя логические эквивалентности. Я привел названия логических эквивалентов на правильно, чтобы вы могли видеть, какие из них я использовал.
(б)
Я показал это и логически эквивалентен в предыдущем примере.
В следующих примерах мы будем отрицать утверждения, написанные словами. Это более типично для того, что вам нужно делать по математике. В идея состоит в том, чтобы преобразовать слово-утверждение в символическое утверждение, тогда используйте логические эквивалентности, как мы это делали в последнем примере.
Пример. Используйте закон ДеМоргана, чтобы написать отрицание следующего утверждения, упрощая так, чтобы отрицаются только простые утверждения:
«Кальвина нет дома, или Бонзо в кино.»
Пусть C будет утверждением «Кальвин дома» и пусть B будет заявление «Бонзо в движении». Данное заявление . Я должен опровергнуть это утверждение, затем упростите:
Результат: «Кальвин дома, а Бонзо нет в доме». фильмы ».
Пример. Используйте закон ДеМоргана, чтобы написать отрицание следующего утверждения, упрощая так, чтобы отрицаются только простые утверждения:
«Если Фиби покупает пиццу, то Кэлвин покупает попкорн.»
Пусть P будет утверждением «Фиби покупает пиццу» и пусть C будет заявление «Кэлвин покупает попкорн». Данное заявление . Чтобы упростить отрицание, я буду использовать тавтологию условного дизъюнкции , которая говорит
То есть я могу заменить на (или наоборот).
Итак, вот отрицание и упрощение:
Результат: «Фиби покупает пиццу, а Кэлвин не покупает. Попкорн».
Далее мы применим нашу работу с таблицами истинности и отрицательными утверждениями к задачи, связанные с построением обратного, обратного и противоположность утверждению «если-то».
Пример. Заменить следующую инструкцию на его противоположность:
«Если x и y рациональны, то рационально».
В силу контрапозитивной эквивалентности это утверждение совпадает с утверждением «Если не рационально, значит, это не так. что и x, и y рациональны «.
Этот ответ верен в его нынешнем виде, но мы можем выразить его в немного лучший способ, который удаляет некоторые явные отрицания. Большинству людей легче понять положительное утверждение, чем отрицательное заявление.
По определению действительное число — это иррациональное , если это не рационально. Так что я мог бы заменить часть «если» в противоположно выражению «иррационально».
«Тогда» часть контрапозитива — это отрицание «и» заявление.Вы могли бы повторить это так: «Это не случай, когда и x рационально, и y рационально «. (Слово «оба» гарантирует, что отрицание применимо ко всему «И», а не только «х рационально».)
По закону ДеМоргана это эквивалентно: «x нерационально или y не рационально «. В качестве альтернативы я мог бы сказать:» x есть иррационально или y иррационально ».
Объединив все вместе, я мог бы выразить контрапозитив как: «Если иррационально, то либо x иррационально или y иррационально «.
(Как обычно, я добавил слово «либо», чтобы было ясно, что часть «затем» — это целое выражение «или».)
Пример. Покажите, что обратное и обратное обратное условному выражению логически эквивалентны.
Позвольте быть условным. Обратное. Обратное.
Я мог бы показать, что обратное и обратное эквивалентны построение таблицы истинности для. Вместо этого я воспользуюсь некоторыми известными тавтологиями.
Начнем с:
Помните, что я могу заменить выражение логическим эквивалент.Например, на последнем шаге я заменил Q, потому что два оператора эквивалентны Двойное отрицание.
Пример. Предположим, что x — действительное число. Рассмотреть возможность заявление
«Если, то.»
Постройте обратное, обратное и противоположное. Определите истинность или ложность четырех утверждений — исходное утверждение, обратное, обратное и противоположное — используя свои знания алгебры.
Обратное — «Если, то».
Обратное — «Если, то».
Контрапозитив — «Если, то».
Исходное утверждение неверно:, но. Поскольку исходное утверждение эквивалентно контрапозитивный, контрапозитивный тоже должен быть ложным.
Верно и обратное. Обратное логически эквивалентно обратное, значит, верно и обратное.
\новая страница
\ centerline {\ bigssbold Список тавтологий}
Контактная информация
Домашняя страница Брюса Икенаги
Авторские права 2019 Брюс Икенага
Таблица истинности: определение, правила и примеры — видео и стенограмма урока
Входные значения
Давайте возьмем утверждение: «На улице идет дождь.«Это утверждение, которое мы можем представить с помощью переменной p , истинно или ложно.
p = На улице дождь
Если идет дождь, то p истинно. Если не идет дождь, то p ложно.
отрицание утверждения, называемого , а не p , является утверждением, которое противоречит p и имеет противоположное значение истинности.
не p = на улице нет дождя
Если на улице дождь, то not p неверно.Если на улице нет дождя, то , а не p , верно.
Вот как обе эти возможности представлены в таблице истинности, в которой T представляет истину, а F представляет ложь:
Конъюнкция
Конъюнкция — это составное выражение, представляющее слово «и». Например, у нас есть следующие два утверждения:
p = На улице идет дождь
q = Футбольный матч отменен
Соединение p и q : «На улице дождь, и футбольный матч отменен.’Это утверждение будет верным только в том случае, если верны и p , и q ; то есть, если на улице идет дождь и футбольный матч отменен. Если либо p , либо q ложно, то соединение ложно.
Вот таблица истинности, показывающая возможности конъюнкции:
Дизъюнкция
Дизъюнкция — это составное выражение, представляющее слово ‘или.«Чтобы дизъюнкция была истинной, одно или оба исходных утверждения должны быть истинными. Разъединение приведенных выше утверждений p или q : «На улице идет дождь или футбольный матч отменен». Это утверждение верно, если истинны p или q или оба утверждения.
Вот как выглядит таблица истинности:
Следствие
Импликация — это условное выражение «если-то», например: «Если на улице идет дождь, то футбольный матч отменяется.Поначалу импликации могут показаться сложными, поскольку они ложны только тогда, когда антецедент (часть «если») истинен, а следствие (часть «тогда») ложно.
Итак, подтекст: «Если на улице идет дождь, футбольный матч отменяется». будет ложным, только если p истинно, а q ложно. То есть на улице идет дождь, но футбольный матч не отменяют. Смысл ложен, потому что обещание импликации было нарушено. Однако, если дождь не идет ( p ложно), то обещание импликации не может быть нарушено, поскольку первая часть (часть «если») никогда не происходила, поэтому импликация верна.Подразумевается, что не говорится, что произойдет, если на улице не будет дождя!
Вот как выглядит таблица истинности импликации:
Построение таблиц истинности
Теперь, когда вы ознакомились с некоторыми из основных таблиц истинности, вы можете начать создавать свои собственные для оценки более сложных составных утверждений. Полезно получить несколько советов по составлению таблиц организованным образом, чтобы не упустить никаких возможностей.
Шаг 1: Подсчитайте, сколько операторов у вас есть, и сделайте столбец для каждого оператора.
Шаг 2: Введите различные возможные значения истинности для каждого столбца. Если есть только один оператор, то в первом столбце будет только два случая (TF). Если есть два оператора, то есть четыре различных возможных случая: первый столбец будет (TTFF), а второй будет чередоваться (TFTF). Если есть три утверждения, то есть восемь различных возможных случаев: первый столбец будет (TTTTFFFF), второй будет (TTFFTTFF), а третий будет чередоваться (TFTFTFTF).
Шаг 3: Добавьте столбец для каждого отрицательного утверждения и введите значения истинности.
Шаг 4: Добавьте столбцы для любых союзов, дизъюнкций или импликаций, заключенных в круглые скобки или любых группирующих символов.
Шаг 5: Добавьте последний столбец для полного составного оператора.
Противопозитивный пример
Используя два предыдущих утверждения, давайте построим таблицу истинности для составного утверждения: «Если футбольный матч не отменен, значит, на улице не будет дождя.Это противоположность первоначальному подтексту.
Отзыв:
p = На улице идет дождь
q = Футбольный матч отменен
Мы можем записать контрпозитив как не q , затем не p .
Шаг 1. У нас есть два оператора ( p и q ), поэтому нам нужны два столбца.
Шаг 2: Поскольку есть два утверждения, у нас будет четыре разных случая. Первый столбец будет (TTFF), а второй столбец будет (TFTF).
Шаг 3: Добавьте два столбца: один для , а не для p , и один для , а не для .
Шаг 4: Добавьте последний столбец для , не q , затем , а не p .
Резюме урока
Мы можем использовать таблицу истинности как организованный способ увидеть все возможности при оценке того, является ли составное утверждение истинным или ложным. Буква или переменная обычно представляют утверждения. Чтобы выяснить, является ли утверждение истинным или ложным, мы используем правила логического рассуждения, такие как отрицание , конъюнкция , дизъюнкция и импликация .Эти правила также можно использовать для создания столбцов в таблице истинности, которая обычно включает два столбца case для каждого оператора и отдельные столбцы для каждого отрицательного оператора и полного составного оператора.
Введение в таблицы, утверждения и связки истинности
Таблица истинности — одна из тех вещей в математике, которую гораздо легче понять, если посмотреть, как она выглядит и как работает, чем изучать ее через определение. В любом случае, мы попытаемся определить его, чтобы иметь базовый уровень или базовое понимание того, что это такое.
Таблица определения истины
В математической логике таблица истинности — это диаграмма строк и столбцов, показывающая значение истинности (либо «T» для истины, либо «F» для ложного) каждой возможной комбинации данных утверждений (обычно представленных заглавными буквами P , Q и R) как управляемые логическими связками.
Два компонента таблицы истины
I. Заявление
Определение: Утверждение — это предложение или математическое выражение, которое либо определенно истинно, либо определенно ложно, но не то и другое вместе.Обычно обозначается прописной буквой или переменной. Распространенными являются P, Q, R и S.
II. Логическое соединение
Определение: Логическая связка — это слово, обычно записываемое как символ, который несет определенную логическую инструкцию о том, как работать с оператором или составным оператором. Логические связки также могут использоваться для объединения или объединения двух или более операторов для формирования нового оператора.
Примеры заявлений
- Определенно верные утверждения.
- Определенно ложные утверждения.
ОТКРЫТОЕ ПРЕДЛОЖЕНИЕ
Открытое предложение — это предложение, которое может быть истинным или ложным в зависимости от значения переменной (переменных). Такое предложение НЕ является утверждением, потому что оно должно быть определенно истинным или определенно ложным.
Примеры:
- Число \ color {red} k четное.
Обратите внимание, предложение истинно, если k = 4, или ложно, если k = 7. Поскольку истинность предложения может быть истинной или ложной в зависимости от значения переменной k, то это открытое предложение, а, следовательно, не утверждение.2 = 0. Помните, что 0 не является ни положительным, ни отрицательным. Таким образом, это предложение НЕ является утверждением, а представляет собой простой случай открытого предложения.
Общие логические соединители
В этой части урока моя цель — кратко познакомить вас с пятью распространенными логическими связками, которые также известны как логические операторы. Вы также будете знать символ, используемый для каждого оператора, и его значение.
Примечание. \ large {P} и \ large {Q} — это инструкции.
1) Отрицание
- Символ: ~ или \ neg читается как НЕ
- Пример: ~ P или \ neg P переводится как «не P» или «неверно, что P»
2) Соединение
- Символ: \ клин читается как И
- Пример: P \ клин Q переводится как «P и Q»
3) Дизъюнкция или инклюзивное ИЛИ
- Символ: \ vee читается как OR
- Пример: P \ vee Q переводится как «P или Q»
4) Следствие или условное
- Символ: \ Rightarrow читается как IMPLIES
- Пример: P \ Rightarrow Q означает утверждение «P подразумевает Q»
5) Двойное следствие или Biconditional
- Символ: \ Leftrightarrow читается как ЕСЛИ И ТОЛЬКО ЕСЛИ
- Пример: P \ Leftrightarrow Q означает выражение «P тогда и только тогда, когда Q»
Таблицы истинности для отрицания, соединения и разъединения
Я собираюсь охватить только три основных логических оператора, а именно: отрицание, соединение и дизъюнкцию.Эта часть урока даст вам предварительный обзор того, как может выглядеть таблица истинности.
У меня есть отдельный урок, в котором я подробно обсуждаю, как построить таблицы истинности логических связок, упомянутых здесь, и остальных из них.
А пока давайте сосредоточим наше внимание на приведенных ниже таблицах истинности:
1. Таблица отрицания истинности
Правило для логического оператора отрицания
Значение истинности отрицаемого утверждения прямо противоположно значению истинности исходного утверждения.
2. Таблица истинности соединения
Правило соединения или логического оператора «И»
Составной оператор P и Q, записанный как P \ wedge Q, является ИСТИННЫМ, если оба утверждения P и Q истинны. В противном случае утверждение P \ wedge Q ЛОЖНО.
3. Таблица истинности дизъюнкции
Правило дизъюнкции или логического оператора «ИЛИ»
Составной оператор P или Q, записанный как P \ vee Q, является ИСТИННЫМ, если только одно из утверждений P и Q истинно.Кроме того, поскольку это «включающее ИЛИ», утверждение P \ vee Q также истинно, если и P, и Q истинны. Следовательно, это ЛОЖЬ, только если и P, и Q ложны.
Возможно, вас заинтересует:
Таблицы истинности пяти (5) общих логических связок или операторов
Обратное, обратное и противоположное условному утверждению
Теория логики — Таблицы истинности. Часть III — Введение в… | Хесус Нахера
Теперь, когда мы ознакомились с принципами теории логики, а также с основными обозначениями, пришло время изучить концепцию эквивалентности в логике.В частности, что делает два составных помещения равными?
Две составные посылки X и Y являются логически эквивалентными , если для каждого присвоения значений истинности примитивным посылкам, составляющим X и Y, утверждения X и Y имеют идентичные значения истинности.
Это определение сложно проглотить, но нам важно изучить приложение этого определения. Чтобы добиться этого, мы рассмотрим несколько усложняющихся примеров.Но сначала давайте сделаем небольшой обход, чтобы узнать немного больше о нашем Экскалибур для этого путешествия — одном из самых простых, но мощных инструментов для логиков для доказательства логической эквивалентности: таблиц истинности .
Таблица истинности — это визуальный инструмент в форме диаграммы со строками и столбцами, который показывает истинность или ложность составной предпосылки. Это способ организации информации, чтобы перечислить всех возможных сценариев из предоставленных помещений. Начнем с самого простого примера, таблицы истинности, изображающей манипуляцию с одной предпосылкой: отрицание (~) примитивной предпосылки (P)
Первоначально опубликовано на https: // www.setzeus.com/Таблицы истинности всегда читаются слева направо с примитивной предпосылкой в первом столбце. В приведенном выше примере наша примитивная посылка ( P ) находится в первом столбце; в то время как результирующая посылка ( ~ P ), пост-отрицание , составляет второй столбец.
Здесь легко переоценить ситуацию — не забывайте, что посылка — это просто утверждение, которое либо истинно, , либо ложно. Поскольку в этом примере имеется только одна посылка , нам нужно отслеживать только два результата; в результате получаются две строки, когда P истинно или когда ложно.Первая строка описывает, читая слева направо, что если P истинно, то отрицание P ложно; вторая строка показывает, что если P уже ложно, то отрицание P истинно.
Давайте перейдем к более сложному примеру таблиц истинности в дикой природе, вставив связку, которую мы уже видели: импликация (->). Чтобы сделать это немного более удобоваримым, давайте назначим нашим утверждениям P&Q некоторый контекст, прежде чем строить нашу таблицу истинности:
P: Танос щелкнул пальцами
Q: 50% всех живых существ исчезло
Прежде чем смотреть ниже, продумайте эту структуру с учетом вышеперечисленных деталей.Во-первых, поскольку у нас есть две примитивные посылки (P, Q), мы знаем, что нам понадобится как минимум двух столбцов; кроме того, мы должны подготовиться к результирующей посылке с импликационной связкой (P -> Q), для которой потребуется еще один столбец. Всего трех столбцов .
А как насчет строк? Поскольку у нас есть две предпосылки, каждая из которых может быть истинной или ложной, для учета всех возможных сценариев нам потребуется всего , четыре строк (стр.S — из этого наблюдения можно вывести изящное следствие: таблица истинности, которая учитывает N посылок, требует N² строк) . Давайте теперь нарисуем эту таблицу и убедимся, что она понятна:
Первоначально опубликовано на https://www.setzeus.com/Просмотрите таблицу истинности выше строка за строкой. Первая строка подтверждает, что Танос щелкнул пальцами (P), и 50% всех живых существ исчезли (Q). Поскольку обе посылки верны, то верна и результирующая посылка (импликация или условная):
Первоначально опубликовано на https: // www.setzeus.com/Вторая строка также понятна. На этот раз P по-прежнему верно, однако Q теперь false. Интерпретация здесь такова: «Танос щелкнул пальцами, но 50% всех живых существ не , а исчезли». Поскольку мы собираемся доказать обоснованность импликации, имеет смысл, что предыдущее утверждение делает общую предпосылку однозначно ложной:
Первоначально опубликовано на https://www.setzeus.com/Последние две строки немного более нелогичный.Здесь есть ярлык: нам нужно только посмотреть на первый столбец, чтобы убедиться, что значение истинно. В обеих строках 3 и 4 исходная посылка (P) — ложь — , и это все, что нам нужно знать, независимо от значения посылки Q, чтобы определить импликацию как истинную.
Первоначально опубликовано на https://www.setzeus.com/Почему ложное антецедент всегда приводит к истинному подтексту? Поскольку во вселенной нашего логического утверждения, поскольку предшествующее не произошло, невозможно исключить все возможных сценариев, которые могли вызвать Q.Например, в строке 3 говорится, что «Танос не щелкнул пальцами, но 50% всего живого в любом случае исчезло». Что ж, насколько нам известно, это вымирание могло быть вызвано метеоритом, стихийным бедствием, вторжением инопланетян или множеством других действий — в году любой из этих сценариев, независимо от того, какой из них, значение остается верным, потому что мы все еще не можем докажи, что происходит, когда он щелкает пальцами.
Таблицы истинности — это удобные и удобные логические схемы, которые используются не только в математике, но и в информатике, электротехнике и философии.Обозначения могут отличаться в зависимости от отрасли, в которой вы работаете, но основные концепции остаются неизменными. Это универсальный междисциплинарный инструмент, но мы лишь прикоснулись к их полезности.
Теперь, когда есть таблицы истинности, пора перейти к доказательству эквивалентности между несколькими составными помещениями. В следующей статье этой серии мы используем наши знания о сложном соединении, чтобы доказать, что две различные составные предпосылки, такие как импликация и контрположительный, равны.
первоначально опубликовано на
https://www.setzeus.com/
источников
Логика: теория формального вывода
Основы математики
LESSON # 22
LESSON # 22УРОК № 22
.Таблицы истинности предложений
Задание по чтению: 6.3 (стр.325-331)
Щелкните здесь, чтобы пропустить следующее обсуждение и сразу переходите к заданиям.
Мы можем построить истину таблицы для выписок который покажет все возможные комбинации значений истинности для составные части (буквы). Количество строк (рядов) * в правде таблица зависит от количества различных компонентов в заявление (т. е. сколько существует разных букв).
От вас не потребуется более 16 строк истины. таблица, так что просто помните, что:
| 2 | разные буквы требуется | 4 | строк |
| 3 | разные буквы требуется | 8 | строк |
| 4 | разные буквы требуется | 16 | строк |
См. Текст для получения подробных инструкций по настройке таблица истинности.
ШАГИ:
1. Запишите ваше сложное предложение, обозначенное символами, в одном line с правильным количеством строк под ней.
2. Создайте столбец для каждой буквы и оператора в предложение. Пока не обращайте внимания на круглые скобки, но не затемните их, потому что вам нужно будет прочитать их позже.
3. Начиная с крайней левой буквы , введите столбец ниже со значениями истинности.
4. Двигаясь вправо, создавая новый столбец для каждого новое письмо и игнорирование операторов. ПРИМЕЧАНИЕ: повторений та же буква получает ту же конфигурацию T и F
При настройке таблицы вы делаете первый столбец * (независимо от того, является ли таблица 4, 8 или 16 строк) всегда наполовину верно (1-ая половина) и наполовину ложно. Следующий столбец вы ставите вдвое меньше последовательных Т, чем в первом столбце прежде чем переключиться на F.
В каждом столбце будет вдвое меньше последовательные T и F, чем в предыдущем столбце. Ваш последний столбец всегда будет чередовать 1T и 1F, 1T и 1F.
Так, например, в восьмом ряду стол вы сначала начнете с четырех последовательных Т (поскольку четыре из восьми), то в следующем столбце вы начнете с двух последовательных Т (потому что два — это из четырех), и в вашем последнем столбце будет только один T (потому что один из двух).Ваш последний столбец должен всегда чередуются одна буква Т и одна буква F.
5. После первоначальной настройки таблицы истинности это просто вопрос соблюдения правил для связок (функций истинности). Запоминание «песнопений» из Урока №20 будет здесь очень кстати. Здесь вы снова будете «распаковать» изнутри круглых скобок наружу.
Начиная с самого сокровенного круглые скобки (или одна из них, если их больше одной), двигайтесь вниз по столбцу, сразу глядя на столбцы рядом с ним для истинностных значений простых предложения.
Возможно, вы захотите слегка зачеркните «использованные» столбцы, когда закончите с их.
Когда один столбец завершено, вы будете использовать его и следующий неиспользуемый столбец для заполнения пустого столбца следующего более основного оператора, затем ход это вых.
Когда вы заполнили последний столбец выделите это как-нибудь. Это главный оператор — это это то, что вы будете «читать».
Чтение таблиц истинности
После того, как таблица истинности заполнена, мы можем интерпретировать таблицу и узнайте что-нибудь о нашем заявлении.
Сначала вы научитесь классифицировать отдельные операторы . Вы делаете это, глядя на столбец под основным соединительным элементом.
Во-вторых, , вы научитесь сравнивать два утверждения. Набор вверх по таблице истинности с утверждениями рядом, используя двойная линия, чтобы разделить их.Заполните таблицу и сравните основные связующие столбцы каждого утверждения. ПРИМЕЧАНИЕ: То же буква получает ту же конфигурацию столбца в ОБЕИХ заявления.
| Заявление. . . | при отображении основного соединительного столбца: |
| Эквивалент | то же в каждой строке |
| Противоречивое | наоборот в каждом ряду |
| Ни то, ни другое | то же на некоторых и напротив на некоторых (на не менее одного каждого) |
| Согласованный | По крайней мере одна строка, которая является T в обеих таблицах истинности |
| Несоответствие | В обеих таблицах нет строки с буквой T. |
Logic Coach Assignment: I 1-10, II 1-10
Задание: (по 10 баллов)
ПРИМЕЧАНИЕ : Всегда проверяйте, скопировали ли вы проблему правильно!
A. Используйте таблицы истинности, чтобы определить, символизированные высказывания тавтологи, противоречивый или контингент.
1.(А Б) против С
2. F (G ~ H)
3. P (R P)
4. (R S) (R ~ S)
5. (N P) v (P N)
B. Используйте таблицы истинности, чтобы определить, соответствуют ли следующие пары утверждений логически эквивалентны, противоречивы или ни то, ни другое. Также укажите являются ли они последовательными или непоследовательными.
1.~ (P Q) ~ P v ~ Q
2. P Q Q P
3. P (Q v R) (P Q) v (P R)
4. А ~ В А В
5. ~ (S v T) ~ (S T)
Главная | Содержание | Следующее задание | Вопросы
8.3 Таблицы истинности для анализа аргументов
Таблица истинности аргументов
Мы почти закончили с таблицами истинности.Следующее, для чего мы можем использовать их в логике, — это определить, является ли аргумент в логике высказываний действительным или недействительным.
Ключ состоит в том, чтобы знать, что значит сказать, что аргумент действителен, и знать, как отобразить это в таблице истинности.
Это означает, что , если все посылки верны, невозможно, чтобы заключение было ложным . Это не означает, что все предпосылки верны, но что , если они верны, потребуют истинного заключения.
К этому можно также плодотворно подойти со стороны недействительности. «Недействительный» означает, что даже если все посылки верны, они не требуют, чтобы заключение было верным.
Итак, если вы нашли строку в таблице истинности для аргумента, по которому заключение было F, но все посылки были T, аргумент будет недействительным. И если вы найдете линию, на которой заключение было T, и все посылки также были T, но затем на другой строке, вывод был F, а посылки были T, аргумент также был бы неверным.То есть не должно быть без строки , на которой были бы все помещения T и вывод F, чтобы таблица показывала, что он действителен.
Подход с использованием таблицы истинности означает, что если аргумент недействителен, он действителен. Итак, вы должны проверить аргумент на недействительность, и для этого вы должны четко понимать, что искать.
Что, по вашему мнению, вы должны сказать о аргументе, имеющем противоречивые посылки?
Давайте посмотрим на несколько примеров.
Во-первых, обратите внимание, что я ввел косые черты.Это указывает на то, что у нас есть аргумент. Для отделения помещений друг от друга используется одинарная косая черта. Перед заключением ставится двойная косая черта, которая всегда будет отображаться как самое правое утверждение.
| (п. | > | г) | / ~ с | // ~ д |
| т | т | Т | Факс | f |
| т | Факс | F | Факс | т |
| F | т | Т | т | f |
| F | т | F | т | т |
Это правильно заполнено.Значения для помещений выделены жирным шрифтом , , а значения заключения — строчными. Есть четыре варианта, то есть четыре строки для чтения. В первой строке не обе посылки верны, поэтому вывод F еще не означает, что он недействителен. Во второй строке обе посылки — F, поэтому эта строка нам ничего не говорит. В третьей строке обе посылки обозначены буквой T, а вывод — буквой F, что означает, что он недействителен, потому что это случай, когда истинный вывод не генерируется, несмотря на то, что все предпосылки истинны.Это все, что нам нужно знать, мы можем перестать это читать. Но давайте все равно зачитаем четвертую строчку, потому что она поучительна. В четвертой строке обе посылки — буква Т, как и заключение. Что мы об этом думаем?
Ничего. Это ничего не значит, поскольку третья строка показывает, что этот аргумент не гарантирует T выводов из T предпосылок, но допускает возможность F выводов. Это делает форму ненадежной, не на сто процентов надежной, недействительной.
Надеюсь, вы узнали эту форму; он известен по фразе, описывающей то, что делают его помещения.(Отрицая антецедент.)
[youtube] [/ youtube]
У этого есть имя, которое вы также должны знать:
| (п. | > | г) | / q | // п. |
| т | Т | Т | Т | Т |
| т | F | F | F | Т |
| F | Т | Т | Т | F |
| F | Т | F | F | F |
Недействительность здесь также показана в третьей строке, где обе посылки — T, а заключение — F.Первая строка, в которой и посылки, и заключение являются T, не указывает ничего, что могло бы противодействовать тому, что показывает третья строка, а именно, что эта форма допускает возможность T посылок и F вывода.
Это Подтверждение Следующего .
Вот еще что нужно учитывать:
| ~ | (G | ∙ | М) | / М | v | ~ G | // ~ G |
| Факс | Т | Т | Т | Т | т | F | F |
| т | Т | F | F | F | Факс | F | F |
| т | F | F | Т | Т | т | Т | Т |
| т | F | F | F | F | т | Т | Т |
В помещении сказано: «Не одновременно G и M.Либо M, либо G — ложь ». Вывод: «Не Г.».
Это может быть
Неверно, что и Гарфилд, и Мармадьюк — собаки. Либо Мармадьюк собака, либо не Гарфилд. Следовательно, Гарфилд не один.
Что показывает таблица? Это показывает, что всякий раз, когда вывод — F, по крайней мере, одна посылка тоже F. В первой и второй строках вывод — F. Но в первой строке первая посылка — это F (смотрите под знаком ~), а во второй строке вторая посылка — F (смотрите под v).Это показывает, что он не недействителен, а значит, действителен.
В следующих двух строках показаны все посылки T и заключение T. Но даже если мы не будем внимательно смотреть на них, мы можем сказать, что оно верное, потому что единственный шанс на то, что он недействителен, — это когда вывод F, и мы уже видел все возможности этого.
8 Таблицы истинности аргументов
Вот несколько упражнений, над которыми вы можете практиковаться:
1. P ≡ ~ N // N v P
2.K ≡ ~ L / ~ (L ∙ ~ K) // K> L
3. Z // E> (Z> E)
4. C ≡ D / E v ~ D // E> C
5. A> (B v C) / ~ C v B // A> B
6. J> (K> L) / K> (J> L) // (J v K)> L
7. Если Сартр экзистенциалист, то Витгенштейн написал Трактат, следовательно, если Витгенштейн написал Трактат, Сартр экзистенциалист.
8. Херли — президент, так что либо он президент, либо Аккерманн — декан.
9.Если «время летит» — это метафора, это не совсем так. Если это не совсем так, тогда время не летит, поэтому если «время летит» является метафорой, то время не летит.
10. Если аргумент, исходящий от дизайна, слаб, это слабая аналогия. Чтобы быть слабой аналогией, оно должно проводить неоправданное сравнение, поэтому аргумент от дизайна дает неоправданное сравнение.
11. Зима холодная, а лето жаркое, поэтому либо лето жаркое, либо луна сделана из зеленого сыра.
12.Рассел был либо реалистом, либо эмпириком. Если первое, то он не был идеалистом, значит, он не был эмпириком.
13. Если он любит ее, он женится на ней. Поэтому, если он не любит ее, он не женится на ней.
14. Если люди смогут поселиться на Луне, они смогут поселиться на Марсе. Если они смогут поселиться на Марсе, они смогут поселиться на Юпитере. Итак, если Луна может быть заселена, то и Юпитер может.
15. Этот аргумент недействителен тогда и только тогда, когда он может иметь истинные посылки и ложный вывод.Следовательно, он недействителен, поскольку имеет ложное заключение.
16. Тот факт, что животные менее умны, чем мы, не означает, что мы можем пренебрегать их благополучием. Если мы пренебрегаем их благополучием, то мы бесчеловечны и ничем не лучше самих животных. Таким образом, если мы пренебрегаем их благополучием, будет ошибкой считать, что они менее умны, чем мы.
17. Если Швеция находится в Северной Африке, то либо египтяне голубоглазые, либо шведы смуглые и красивые. Швеция находится не в Северной Африке, поэтому египтяне не голубоглазые.
18.




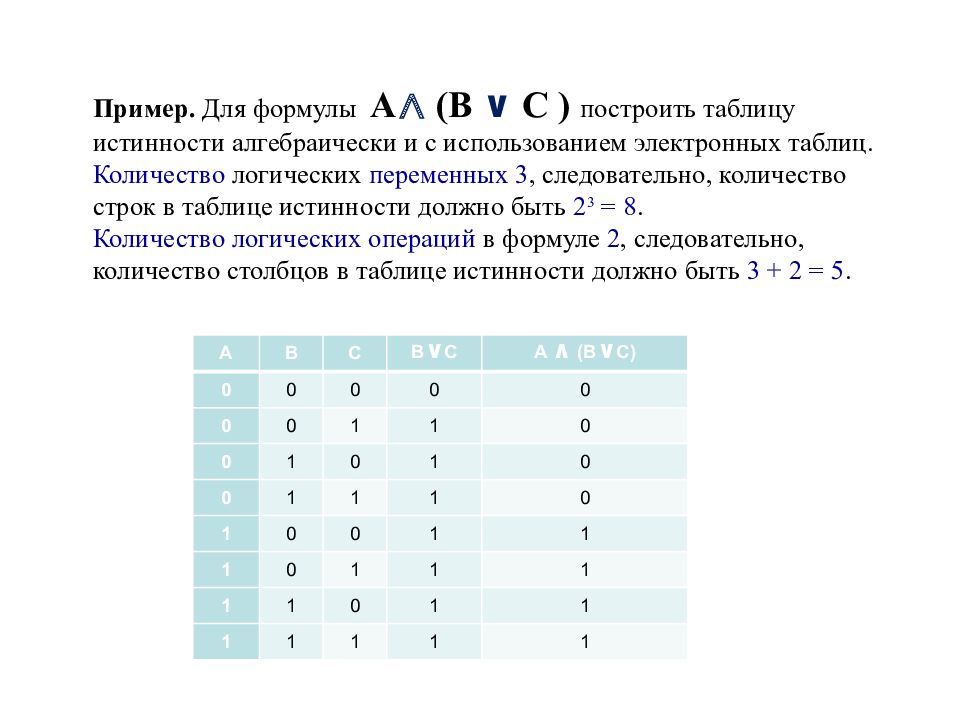 3;
3; Связывает 2 и более выражения союзом ИЛИ. Обозначается знаками ∨, +, |, or. Выражение истинно, если правдива одна часть или сразу обе. Пример: А∨В = «звезды состоят из газа или плазмы». На рисунке изображается объединением множеств;
Связывает 2 и более выражения союзом ИЛИ. Обозначается знаками ∨, +, |, or. Выражение истинно, если правдива одна часть или сразу обе. Пример: А∨В = «звезды состоят из газа или плазмы». На рисунке изображается объединением множеств;  Обозначается ~, ↔️, читается «А эквивалентно В». Выражение истинно, когда обе части одинаковы. Например: А~В = «число делится на 5 тогда, когда его последняя цифра 0 или 5». Эквивалентность противоположна строго-разделительной дизъюнкции.
Обозначается ~, ↔️, читается «А эквивалентно В». Выражение истинно, когда обе части одинаковы. Например: А~В = «число делится на 5 тогда, когда его последняя цифра 0 или 5». Эквивалентность противоположна строго-разделительной дизъюнкции.