Таблицы истинности — Логика
Таблицы истинности
|
4 последовательностью.
Построение таблиц истинности для логических выражений
Похожие презентации:
Построение таблиц истинности для логических выражений
Основы логики.
Таблица истинности. Равносильные логические выражения
Построение таблиц истинности сложных высказываний
Логика высказываний. Таблицы истинности
Алгебра высказываний. Определение высказывания. Таблица истинности для высказываний. Логические тождества. (Лекция 2)
Построение таблиц истинности
Составление таблиц истинности для сложных высказываний
Алгебра логики и таблицы истинности. (лекция 4)
Логика высказываний
Построение таблиц
истинности для логических
выражений
Таблица истинности – таблица, показывающая, какие значения
принимает составное высказывание при всех сочетаниях (наборах)
значений выходящих в него простых переменных
A
B
AvB
¬A
¬B
¬A v ¬B
(A v B) & (¬A v ¬B)
0
0
0
1
1
1
0
0
1
1
1
0
1
1
1
0
1
0
1
1
1
1
1
1
0
0
0
0
Вычисление
истинности
сложных
высказываний
Применение
таблиц
истинности
Определение
тавтологий
Установление
эквивалентности
высказываний
Алгоритм построения таблицы истинности
Подсчитать n – число переменных в логическом выражении2. Подсчитать общее количество логических операций в выражении
3. Установить последовательность выполнения логических операций с учетом скобок
и приоритетов
4. Определить число столбцов в таблице: число переменных + число операций
5. Заполнить шапку таблицы, включив в нее переменные и операции в соответствии с
последовательностью, установленной в пункте 3
6. Определить число строк в таблице по формуле m = 2n + 1
7. Выписать наборы входных переменных
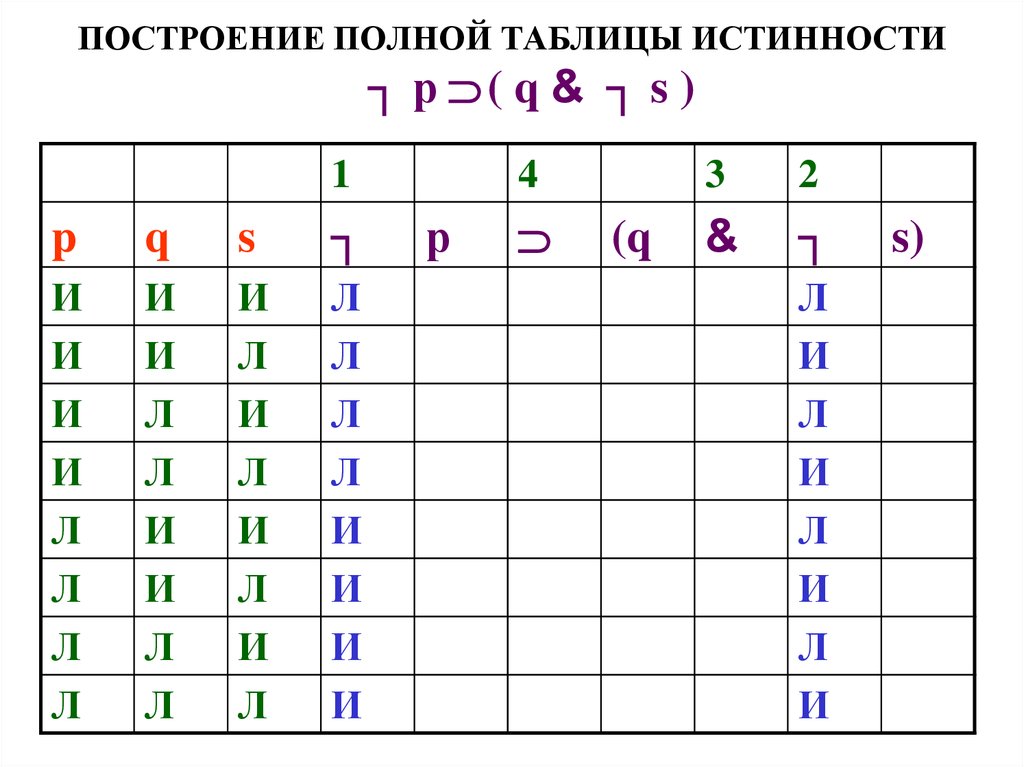
Построить таблицу истинности, для выражения A & (B v ¬B & ¬C)
1.
2.
3.
Считаем число переменных: A B C — 3
Считаем логические операции: &v¬&¬ — 5
Устанавливаем последовательность
действий:
1)
2)
3)
4)
5)
4.
5.
¬B
¬C
¬B & ¬C
B v (¬B & ¬C)
A & (B v ¬B & ¬C)
Находим количество столбцов: 3 + 5 = 8
(пункт 1 + пункт 2)
Находим количество строк: 23 + 1 = 9
A
B
C
¬B
¬C
¬B & ¬C
B v (¬B & ¬C)
A & (B v ¬B & ¬C)
0
0
0
1
1
1
1
0
0
0
1
1
0
0
0
0
1
0
0
1
0
1
0
0
1
1
0
0
0
1
0
1
0
0
1
1
1
1
1
1
0
1
1
0
0
0
0
1
1
0
0
1
0
1
1
1
1
1
0
0
0
1
1
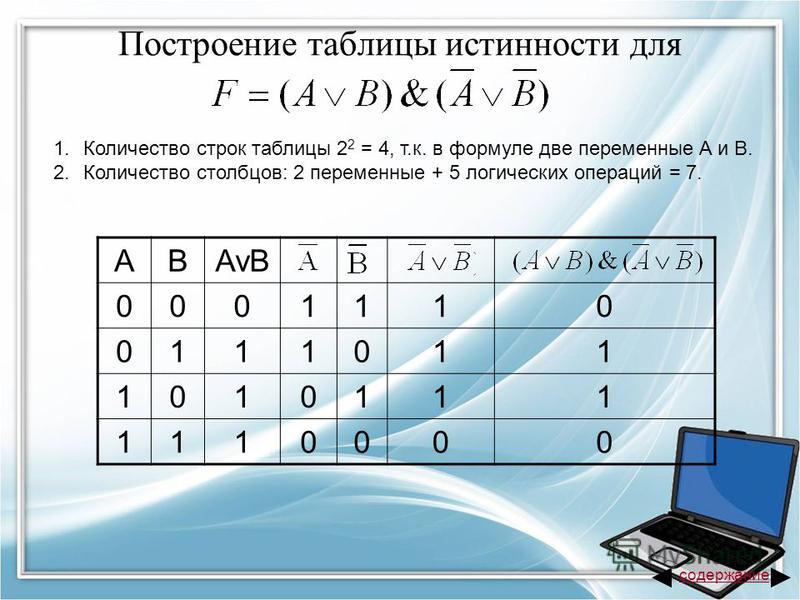
Требуется определить истинность логического выражения
N(A,B) = (A v B) & (¬A v ¬B)
1.
2.
3.
Считаем число переменных: A B — 2
Считаем логические операции: v&¬v¬
-5
Устанавливаем последовательность
действий:
1)
2)
3)
4)
5)
4.
5.
AvB
¬A
¬B
(A v B) & (¬A v ¬B)
Находим количество столбцов: 2 + 5 =
7 (пункт 1 + пункт 2)
Находим количество строк: 22 + 1 = 5
A
B
AvB
¬A
¬B
¬A v ¬B
(A v B) & (¬A v ¬B)
0
0
0
1
1
1
0
0
1
1
1
0
1
1
1
0
1
0
1
1
1
1
1
1
0
0
0
0
Логическое выражение принимает значение ИСТИНА при наборах N(0,1) = 1 и N(1,0) = 1
Задания:
Постройте таблицу истинности для:
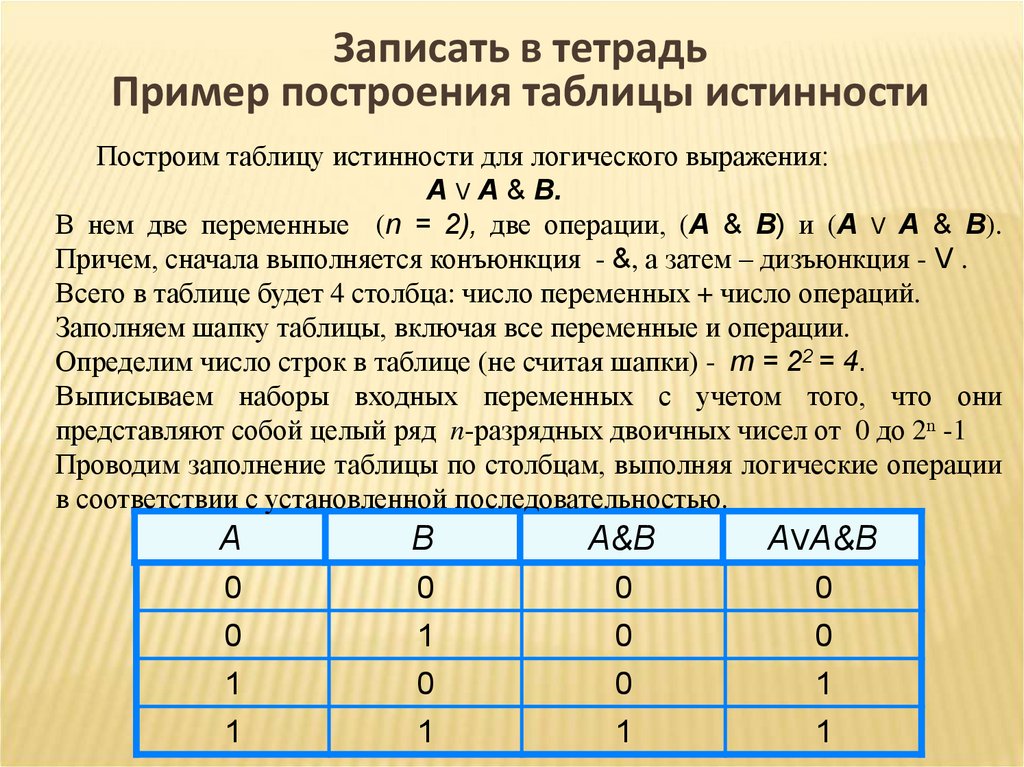
1. A v A & B
2. A & (A v B)
3. ¬ (A & B v C)
English Русский Правила
3 хитрости для построения таблиц истинности — BPI
Публикации в блогах DMN
Прочитать сообщение в блоге
Читать сообщение в блоге
Таблицы истинности датируются 1902 годом логиком Чарльзом Сандерсом Пирсом, который использовал их как метод отображения алгебраической логики.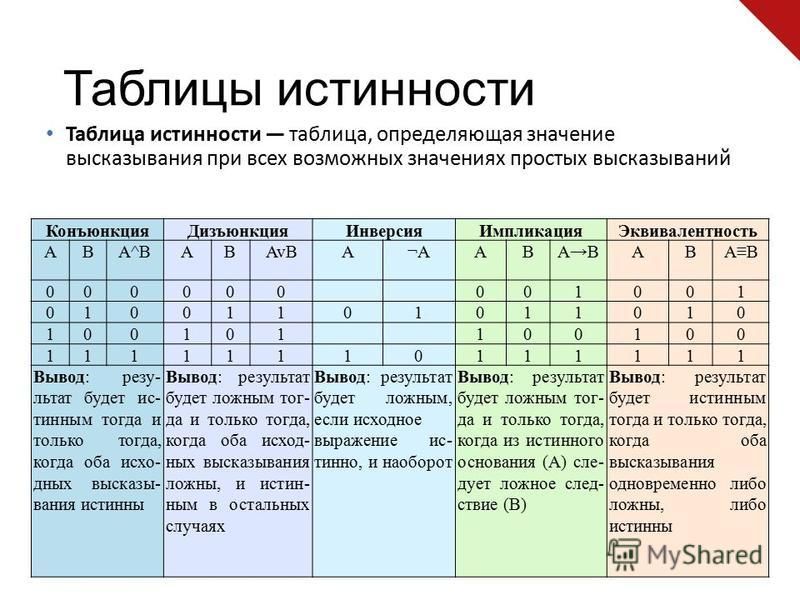
Таблицы истинности развивались с годами. Поскольку все больше людей полагаются на них для представления логических результатов, они стали более полезными в других областях и теперь играют важную роль в бизнес-процессах и автоматизации.
Что такое таблица истинности?
Таблица истинности — это правило, представленное в виде таблицы. Однако в этих таблицах есть нечто большее, чем просто это основное определение. Это способ представления информации и логического потока того, что входные данные делают дальше.
Таблицы истинности встроены в Excel подобно таблицам со строками и столбцами. В верхней части таблицы, в заголовках столбцов, указаны условия, на которых основано правило, выраженные в структуре существительное/глагол.
Например, если вы должны создать таблицу истинности, которая извлекает тип автомобиля из списка производителей автомобилей, у вас может быть столбец с заголовком «Тип автомобиля в списке». «CarType» будет существительным, а «Contains» будет глаголом.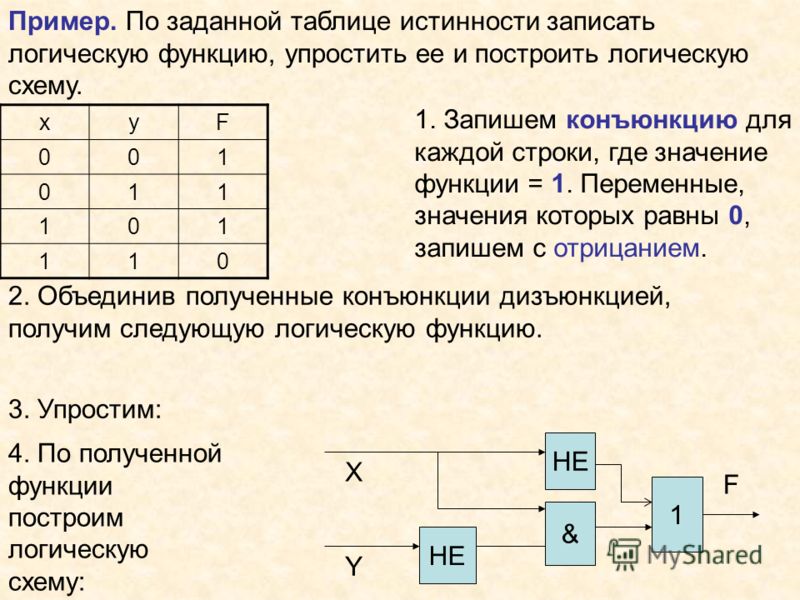
Строки ниже будут обозначать различные типы автомобилей. Важно отметить, что таблица истинности позволяет сравнивать все возможные комбинации из нескольких входных данных; он не ограничивается вводом из одного столбца.
Это помогает предприятиям, позволяя таблице истинности замкнуть цикл с выводом. Последний столбец в таблице истинности выражает результат после сбора данных с входа или входов. Выходными данными могут быть другие данные или инструкции о том, какое действие следует предпринять, вызвав поток. Точно так же, как они могут обрабатывать несколько входных данных, таблицы истинности могут возвращать более одного результата.
Основные приемы построения таблиц истинности
Зависимость традиционных таблиц истинности от математики может затруднить их использование в бизнес-перспективе. Однако, когда вы смотрите на таблицы истинности как на способ определения логических результатов, становится легче увидеть, как они применяются для автоматизации бизнеса и процессов.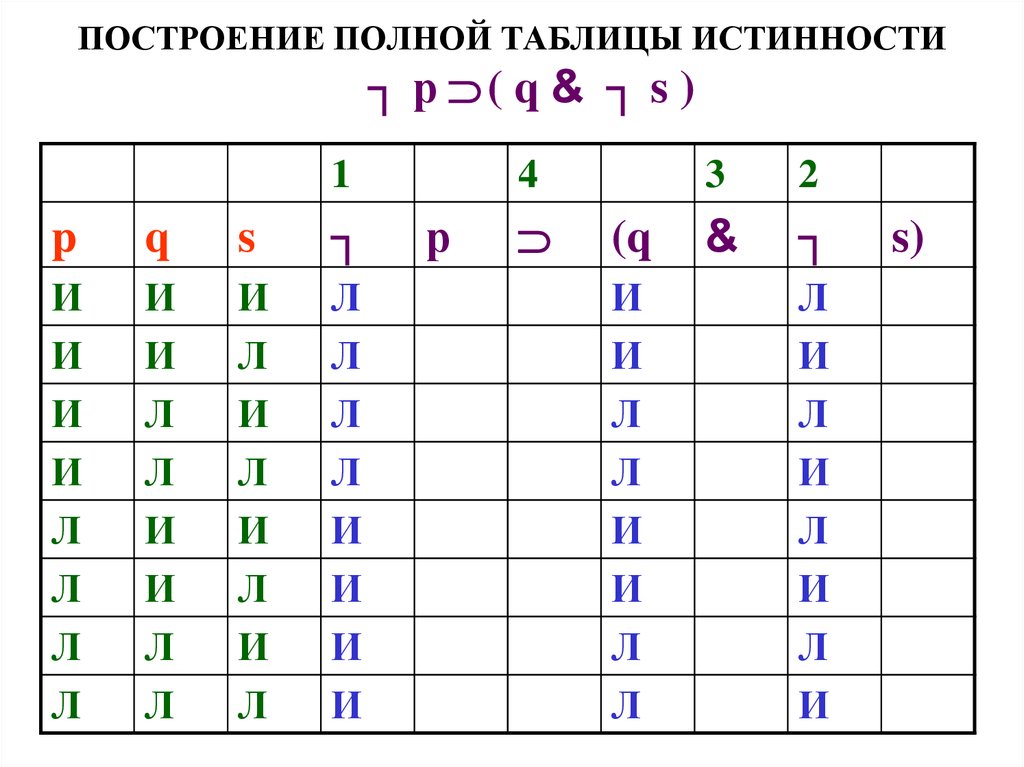
1. Понимание различных типов вывода
Первый прием при построении таблиц истинности заключается в понимании различных типов вывода:
- Правило возврата данных (одиночное) возвращает в поток одну переменную.
- Правило возврата данных (несколько) возвращает несколько переменных в поток.
- Составной тип для случаев, когда у вас есть несколько выходных данных в таблице истинности, если вы хотите получить доступ к каждому выходному сигналу по отдельности, а не как к объекту.
- Правило действия передает значение и выполняет поток.
Понимание различных типов правил позволит вам лучше понять концепцию того, что вы можете делать с таблицами истинности и правилами, которые вы создаете с их помощью.
2.
Понять, как таблицы истинности автоматизируют потоки
Это чрезвычайно полезно, когда вам нужно проанализировать данные из разных источников и принять решение на основе оценки этих данных. На основе оценки входных данных таблица истинности может выводить решение «да» или «нет», указывать ориентировочную стоимость или запрашивать дополнительную информацию. Это может быть полезно, если вы пытаетесь автоматизировать поток самообслуживания для своих конечных пользователей. Таблицы истинности также дают вам возможность отправлять информацию на утверждение или автоматизировать ввод данных на основе оценки ввода. Например, если вход красный, данные могут быть отправлены в один отдел или человеку для утверждения. Если ввод синий, данные переместятся к другому отделу или человеку.
3. Можно использовать внешние таблицы истинности
Не все таблицы истинности требуют ручного ввода данных. Фактически, внешние данные таблицы истинности — это распространенный метод заполнения столбцов таблицы истинности.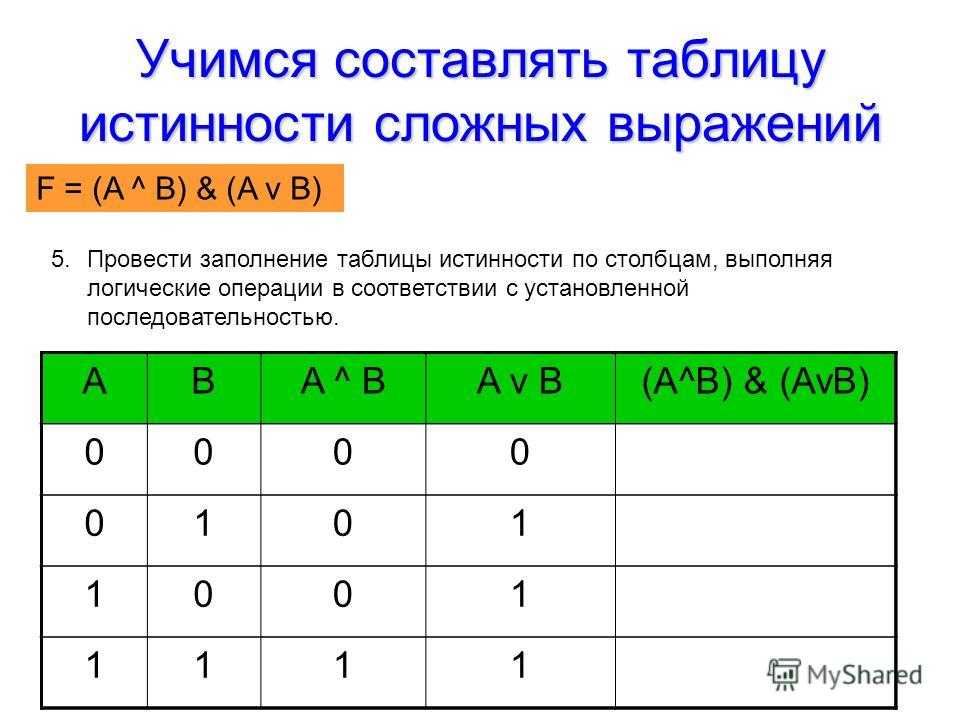
Электронные таблицы Excel, файлы CSV, базы данных и даже данные из веб-службы или очереди сообщений могут заполнять входные данные таблиц истинности, что позволяет таблице истинности собирать информацию из внешних источников, чтобы избежать дублирования ввода данных. Это не только экономит время, но и сохраняет единый источник достоверности, поскольку данные из внешней таблицы истинности необходимо редактировать в источнике, а не в самой таблице истинности. Зарегистрируйтесь, чтобы посмотреть наш недавний вебинар по внешним таблицам истинности здесь.
Как программное обеспечение Decisions помогает вам с таблицами истинности
Когда дело доходит до таблиц истинности, вам нужно решение, которое максимально упрощает не только их построение, но и превращает выходные данные в автоматизированные потоки.
Вот где Решения имеют значение.
Когда дело доходит до построения таблиц истинности, мастер, предоставляемый программным обеспечением, позволяет легко установить ваши утверждения вверху, чтобы создать ваши условия существительного/глагола вместе со столбцами, которые определяют, что происходит с выходными данными.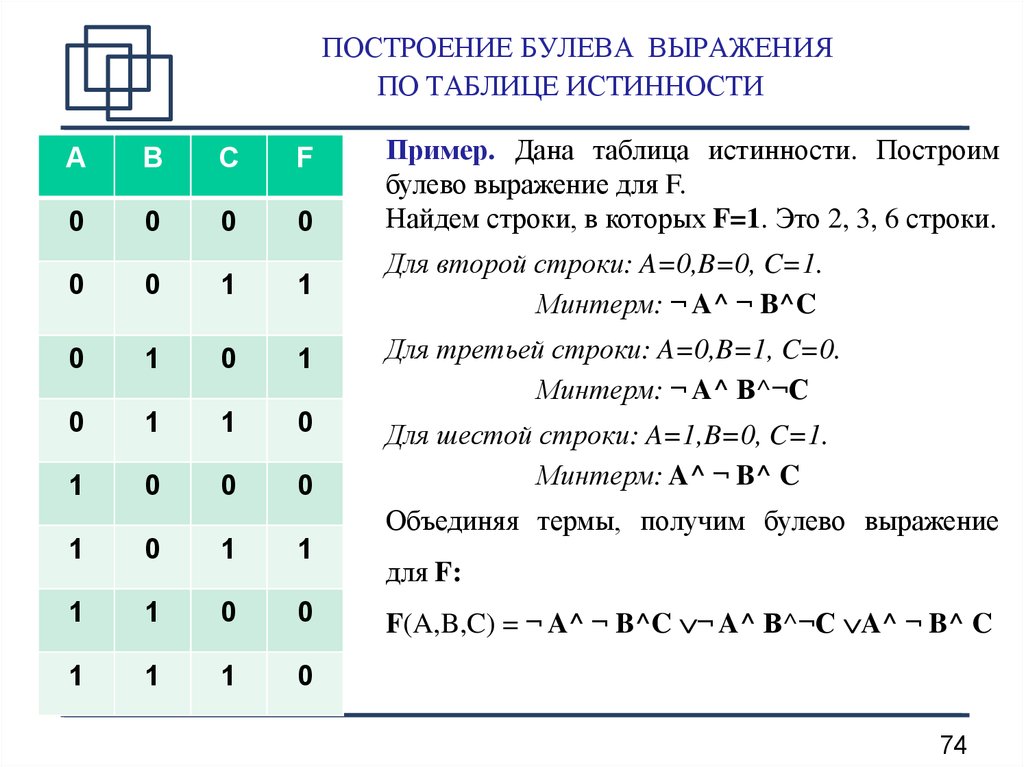
Автоматизацию легко встроить в ваши таблицы истинности с помощью того же простого в использовании мастера. Скажите программному обеспечению, что вы хотите сделать с выводом, и оно поможет вам создать этот автоматизированный поток.
Поддержка внешних таблиц истинности дополняет преимущества использования решений для создания таблиц истинности, которые помогают вашему бизнесу двигаться более эффективно и результативно. Если вы хотите обсудить свой конкретный вариант использования, мы будем рады услышать об этом. Пожалуйста, свяжитесь с нами по адресу [email protected].
Пост «3 хитрости построения таблиц истинности» впервые появился в блоге Decisions.
13.3: Таблицы истинности и анализ аргументов — примеры
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 51653
Таблицы истинности
Поскольку сложные логические утверждения могут быть сложными для понимания, мы можем создать таблицу истинности , чтобы отслеживать, какие значения истинности для простых утверждений делают сложное утверждение истинным и ложным
Таблица истинности
Таблица, показывающая результирующее значение истинности сложного утверждения для всех возможных значений истинности простых утверждений.
Пример 1
Предположим, вы выбираете новый диван, и ваша вторая половинка говорит: «Купите секционный или что-нибудь с шезлонгом».
Это сложное утверждение состоит из двух более простых условий: «является секционным» и «имеет фаэтон». Для простоты давайте использовать S для обозначения «является секционным», а C для обозначения «имеет шезлонг». Условие S верно, если кушетка секционная.
A truth table for this would look like this:
| S | C | S or C |
|---|---|---|
| T | T | T |
| Т | Ф | Т |
| Ф | Т | Т |
| F | F | F |
В таблице T используется для истинного, а F для ложного. В первой строке, если S истинно и C также истинно, то комплексное утверждение « S или C » истинно.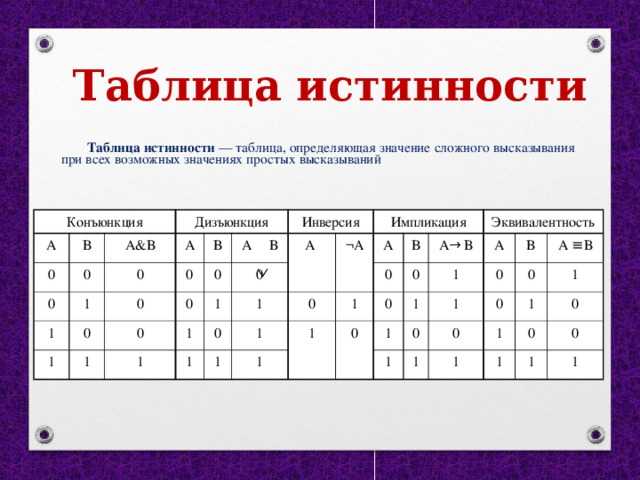
Это будет секционная, в которой также есть шезлонг, что соответствует нашему желанию.
Помните также, что или в логике не являются исключительными; если кушетка имеет обе функции, она соответствует условию.
Чтобы еще больше сократить наши обозначения, мы собираемся ввести некоторые символы, которые обычно используются для и , или и вместо .
Символы
Символ ⋀ используется для и : A и B обозначаются как A ⋀ B .
Символ ⋁ используется для или : A или B обозначается A ⋁ B
Символ ~ используется для не : не A обозначается ~ A
Первые два символа можно запомнить, связав их с фигурами объединения и пересечения. A ⋀ B будут элементами, которые существуют в обоих наборах, в A ⋂ B. Аналогично, A ⋁ B будут элементами, которые существуют в любом наборе, в A ⋃ B.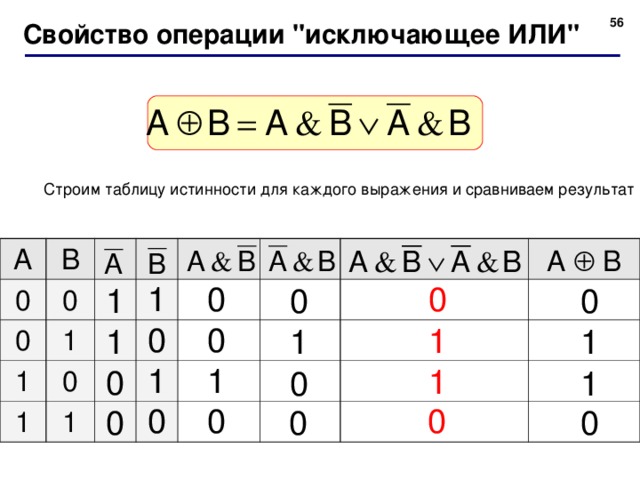
В В предыдущем примере таблица истинности на самом деле просто обобщала то, что мы уже знаем о том, как работают операторы или . Таблицы истинности для основных 9Операторы 0062 и , или и , а не показаны ниже.
Basic Truth Tables
| A | B | A ⋀ B |
|---|---|---|
| T | T | T |
| T | F | F |
| Ф | Т | Ф |
| Ф | Ф | Ф |
| A | B | A ⋁ B |
|---|---|---|
| T | T | T |
| T | F | T |
| F | T | T |
| F | F | F |
| A | ~A |
|---|---|
| T | F |
| F | T |
Таблицы истинности становятся действительно полезными при анализе более сложных логических выражений.
Пример 2
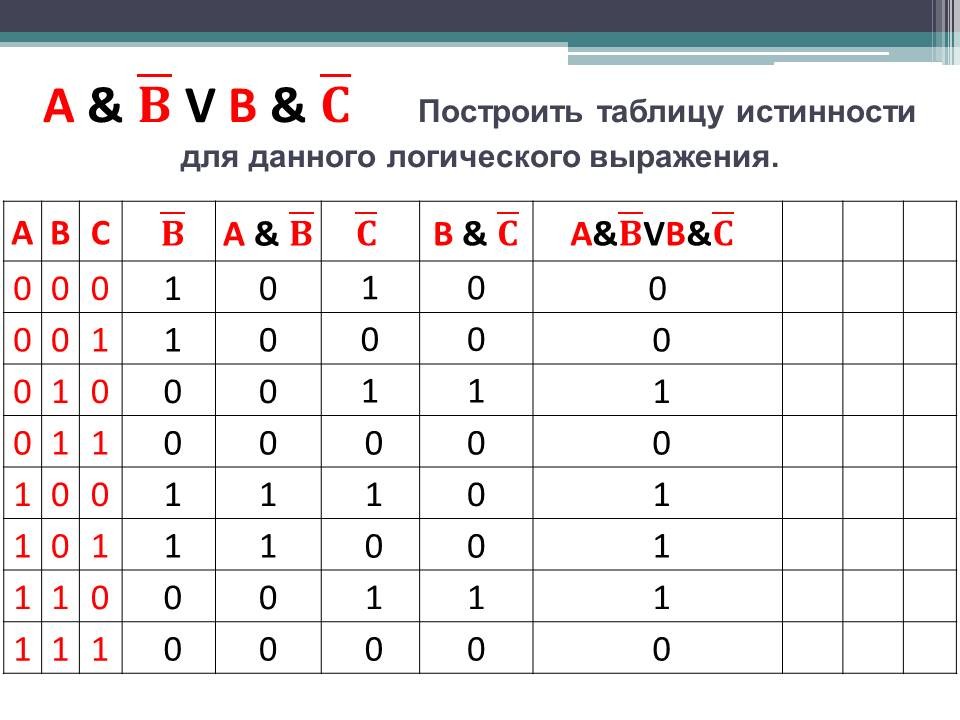
Создание таблицы истинности для утверждения A ⋀ ~( B ⋁ C )
Это помогает работать изнутри наружу при создании таблиц истинности и создавать таблицы для промежуточных операций. Начнем с перечисления всех возможных комбинаций значений истинности для 9.0062 А , В и С . Обратите внимание, что первый столбец содержит 4 T, за которыми следуют 4 F, второй столбец содержит 2 T, 2 F, затем повторяется, а последний столбец чередуется. Этот шаблон гарантирует рассмотрение всех комбинаций. Наряду с этими начальными значениями мы перечислим значения истинности для самого внутреннего выражения, B ⋁ C .
| А | Б | С | B ⋁ C |
| T | T | T | T |
| T | T | F | T |
| T | F | T | T |
| T | F | F | F |
| F | T | T | T |
| F | T | F | T |
| F | F | T | T |
| F | F | F | F |
Next we can find the negation of B ⋁ C , working off столбец B ⋁ C , который мы только что создали.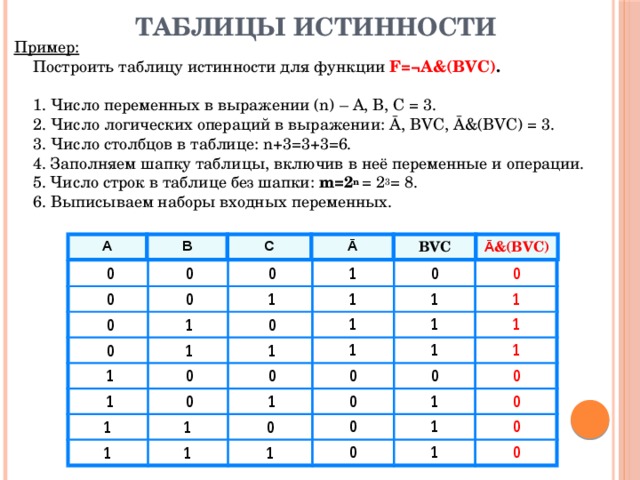
| A | B | C | B ⋁ C | B ⋁ C | B .0062 B ⋁ C ) |
| T | T | T | T | F | |
| T | T | F | T | F | |
| T | F | T | T | F | |
| T | F | F | F | T | |
| F | T | T | T | F | |
| F | T | F | T | F | |
| F | F | T | T | F | |
| F | F | F | F | T |
Finally, we find the values of A and ~( B ⋁ C )
| A | B | C | B ⋁ C | ~( B ⋁ C ) | A ⋀ ~( B ⋁ C ) |
| T | T | T | T | F | F |
| T | T | F | T | F | F |
| T | F | T | T | F | F |
| T | F | F | F | T | T |
| F | T | T | T | F | F |
| F | T | F | T | F | F |
| F | F | T | T | F | F |
| F | F | F | F | T | F |
Оказывается, это сложное выражение верно только в одном случае: если A истинно, B ложно и C ложно.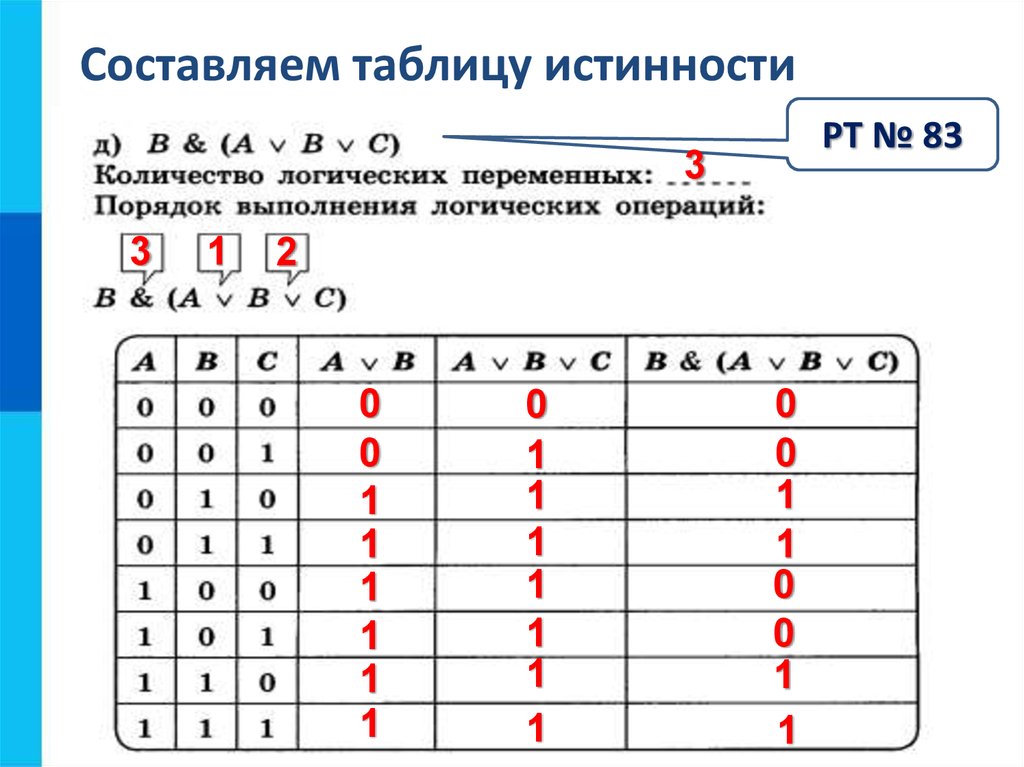
Когда мы обсуждали условия ранее, мы обсуждали тип, при котором мы предпринимаем действие на основе значения условия. Сейчас мы поговорим о более общей версии условного предложения, иногда называемой импликацией .
Импликации
Импликации — это логические условные предложения, утверждающие, что высказывание p , называемое антецедентом, подразумевает следствие q .
Импликации обычно записываются как p → q
Импликации аналогичны условным операторам, которые мы рассматривали ранее; p → q обычно записывается как «если p, то q» или «p, следовательно, q». Разница между импликациями и условными предложениями заключается в том, что условные предложения, которые мы обсуждали ранее, предполагают действие — если условие истинно, то в результате мы предпринимаем какое-то действие. Импликации — это логическое утверждение, предполагающее, что следствие должно логически следовать, если антецедент истинен.
Пример 3
Английское высказывание «Если идет дождь, то облака — это небо» является логическим следствием. Это правильный аргумент, потому что если антецедент «идет дождь» истинен, то следствие «на небе облака» также должно быть истинным.
Обратите внимание, что это утверждение ничего не говорит нам о том, чего ожидать, если не идет дождь. Если антецедент ложен, то импликация становится нерелевантной.
Пример 4
Друг говорит вам, что «если вы загрузите это изображение на Facebook, вы потеряете работу». Возможны четыре исхода:
- Вы загружаете изображение и сохраняете свою работу
- Вы загрузили картинку и потеряли работу
- Вы не загружаете картинку и сохраняете свою работу
- Вы не загрузите картинку и потеряете работу
Есть только один возможный случай, когда ваш друг солгал — первый вариант, когда вы загружаете картинку и сохраняете свою работу. В последних двух случаях ваш друг ничего не сказал о том, что произойдет, если вы не загрузите изображение, поэтому вы не можете заключить, что его заявление недействительно, даже если вы не загрузили изображение и все равно потеряли работа.
В традиционной логике импликация считается достоверной (истинной), если нет случаев, в которых антецедент истинен, а следствие ложно. Важно помнить, что символическая логика не может охватить все тонкости английского языка.
Значения истинности для следствий
| р | q | р → q |
| T | 0147 T | T |
| T | F | F |
| F | T | T |
| F | F | T |
Example 5
Construct a таблица истинности утверждения ( m ⋀ ~ p ) → r
Начнем с построения таблицы истинности для антецедента.
| м | p | ~ p | m ⋀ ~ p |
| T | T | F | F |
| T | F | T | T |
| F | T | F | F |
| F | F | T | F |
Now we can build the truth table for the implication
| m | p | ~ p | m ⋀ ~ p | r | ( m ⋀ ~ p ) → r |
| T | T | F | F | T | T |
| T | F | T | T | T | T |
| F | T | F | F | T | T |
| F | F | T | F | T | T |
| T | T | F | F | F | T |
| T | F | T | T | F | F |
| F | T | F | F | F | T |
| F | F | T | F | F | T |
In this case, when m is true, p is false, и r ложно, то антецедент m ⋀ ~ p будет истинным, но следствие ложным, что приведет к недопустимому импликации; каждый другой случай дает правильное следствие.
Для любого следствия есть три связанных утверждения: обратное, обратное и контрапозитивное.
Связанные операторы
Первоначальное значение: «Если р , то Q »: P → Q
.
Обратный: «Если не р , то не Q »: ~ P → ~ Q
. Контрапозитный «если нет Q , то не P »: ~ Q Q . → ~ р
Пример 6
Рассмотрим еще раз верный вывод: «Если идет дождь, значит, в небе облака».
Обратное: «Если на небе облака, значит, идет дождь». Это, конечно, не всегда верно.
Обратное: «Если не идет дождь, то на небе нет облаков». Точно так же это не всегда верно.
Противоположным было бы: «Если на небе нет облаков, значит, не идет дождь». Это утверждение верно и эквивалентно исходному выводу.
Глядя на таблицы истинности, мы видим, что исходное условное и контрапозитивное логически эквивалентны, а обратное и обратное логически эквивалентны.
| Implication | Converse | Inverse | Contrapositive | ||
|---|---|---|---|---|---|
| p | q | p → q | q → p | ~ p → ~ q | ~ q → ~ p |
| T | T | T | T | T | T |
| T | F | F | T | T | F |
| F | T | T | F | F | T |
| F | F | T | T | T | T |
Эквивалентность
Условное утверждение и его противоположность логически эквивалентны.
Обратное и обратное утверждение логически эквивалентны.
Аргументы
Логический аргумент — это утверждение о том, что набор предпосылок поддерживает вывод. Существует два основных типа аргументов: индуктивные и дедуктивные аргументы.
Типы аргументов
Ан индуктивный 9Аргумент 0030 использует набор конкретных примеров в качестве посылок и использует их, чтобы предложить общий вывод.
дедуктивный аргумент использует набор общих утверждений в качестве предпосылок и использует их, чтобы предложить конкретную ситуацию в качестве вывода.
Пример 7
Аргумент «когда я пошел в магазин на прошлой неделе, я забыл свой кошелек, и когда я пошел сегодня, я забыл свой кошелек. Я всегда забываю свою сумочку, когда иду в магазин» — это индуктивный аргумент.
Посылки:
Я забыл свой кошелек на прошлой неделе
Я забыл свой кошелек сегодня
Вывод:
Я всегда забываю свой кошелек
Обратите внимание, что посылки — это конкретные ситуации, а вывод — это общее утверждение.
. В данном случае это достаточно слабый аргумент, так как он основан всего на двух случаях.
Пример 8
Аргумент «каждый день в течение последнего года в 14:00 над моим домом пролетает самолет. Каждый день в 14:00 над моим домом будет летать самолет» — более сильный индуктивный аргумент, поскольку он основан на большем наборе доказательств.
Оценка индуктивных аргументов
Индуктивный аргумент никогда не может доказать истинность вывода, но он может предоставить как слабое, так и сильное доказательство того, что оно может быть верным.
Многие научные теории, такие как теория большого взрыва, никогда не могут быть доказаны. Вместо этого они представляют собой индуктивные аргументы, подкрепленные широким спектром доказательств. Обычно в науке идея считается гипотезой до тех пор, пока она не будет тщательно проверена, после чего она становится теорией. Все общеизвестные научные теории, такие как теория гравитации Ньютона, выдержали годы испытаний и доказательств, хотя иногда их необходимо корректировать на основе новых данных.
Для гравитации это произошло, когда Эйнштейн предложил общую теорию относительности.
Дедуктивный аргумент является более верным или нет, что облегчает его оценку.
Оценка дедуктивных аргументов
Дедуктивный аргумент считается верным, если все посылки верны и вывод логически следует из этих посылок. Другими словами, посылки истинны, и заключение обязательно следует из этих посылок.
Пример 9
Аргумент «Все кошки — млекопитающие, а тигр — кошка, значит, тигр — млекопитающее» является действительным дедуктивным аргументом.
Посылки:
Все кошки млекопитающие
Тигр есть кошка
Вывод:
Тигр есть млекопитающее
Обе посылки верны. Чтобы увидеть, что посылки должны логически вести к заключению, можно использовать диаграмму Венна. Из первой посылки мы можем заключить, что множество кошек является подмножеством множества млекопитающих. Из второй посылки нам говорят, что тигр находится в множестве кошек. Отсюда на диаграмме Венна видно, что тигр также находится внутри множества млекопитающих, так что вывод верен.
Анализ аргументов с помощью диаграмм Венна
[1]Чтобы проанализировать аргумент с помощью диаграммы Венна
- Нарисуйте диаграмму Венна на основе посылок аргумента
- Если помещения недостаточно для определения того, что определяет расположение элемента, укажите это.
- Аргумент действителен, если ясно, что вывод должен быть верным
Пример 10
Предпосылка: Все пожарные знают CPR
Предпосылка: Джилл знает СЛР
Вывод: Джилл — пожарный
Из первой посылки мы знаем, что все пожарные входят в группу тех, кто знает СЛР. Из второй посылки мы знаем, что Джилл является членом этого большего множества, но у нас недостаточно информации, чтобы узнать, является ли она также членом меньшего подмножества, то есть пожарных.
Поскольку вывод не обязательно следует из предпосылок, это неверный аргумент, независимо от того, действительно ли Джилл является пожарным.
Важно отметить, что действительно ли Джилл пожарный или нет, не имеет значения для оценки обоснованности аргумента; нас интересует только то, достаточно ли посылок для доказательства вывода.
В дополнение к этим категориальным посылкам стиля в форме «все ___», «некоторые ____» и «нет ____», также часто встречаются посылки, являющиеся импликациями.
Пример 11
Помещение: Если вы живете в Сиэтле, вы живете в Вашингтоне.
Посылка: Маркус не живет в Сиэтле
Вывод: Маркус не живет в Вашингтоне
Из первой посылки мы знаем, что множество людей, живущих в Сиэтле, находится внутри множества людей, живущих в Вашингтоне. Из второй посылки мы знаем, что Маркус не входит в набор Сиэтла, но у нас недостаточно информации, чтобы узнать, живет ли Маркус в Вашингтоне или нет. Это неверный аргумент.
Пример 12
Рассмотрим аргумент «Вы женатый человек, поэтому у вас должна быть жена».
Это неверный аргумент, так как есть, по крайней мере, в некоторых частях мира, мужчины, которые женаты на других мужчинах, так что предпосылка не является недостаточной, чтобы подразумевать заключение.
Некоторые аргументы лучше анализировать с помощью таблиц истинности.
Пример 13
Рассмотрим аргумент:
Посылка: Если вы купили хлеб, то вы пошли в магазин. аргумент, мы можем проанализировать его, используя таблицу истинности, представив каждую из посылок символически. Затем мы можем рассмотреть импликацию о том, что посылки вместе подразумевают вывод. Если таблица истинности является тавтологией (всегда истинной), то аргумент действителен.
Мы получим B, означающее «вы купили хлеб», а S — «вы пошли в магазин». Тогда аргумент принимает вид:
Посылка: B → S
Посылка: B
Вывод: S
Чтобы проверить, подразумевает ли вывод обе посылки, следует ли проверить их комбинацию; правда ли, что [( B → S ) ⋀ B ] → S ?
| B | S | B → S | ( B → S ) ⋀ B → S ) ⋀ B → S ). S | |
| T | T | T | T | T |
| T | F | F | F | T |
| F | T | T | F | T |
| F | F | T | F | T |
Since the truth table for [( B → S ) ⋀ B ] → S всегда верно, это действительный аргумент.
Анализ аргументов с использованием таблиц истинности
Чтобы проанализировать аргумент с помощью таблицы истинности:
- Символическое представление каждой посылки
- Создайте условный оператор, соединив все посылки с помощью и, чтобы сформировать антецедент, и используя заключение в качестве следствия.
- Создайте таблицу истинности для этого утверждения. Если это всегда истинно, то аргумент действителен.
Пример 14
Предпосылка: Если я пойду в торговый центр, то я куплю новые джинсы
Предпосылка: Если я куплю новые джинсы, я куплю к ним рубашку
Вывод: Если я пойду в торговый центр , я куплю рубашку.
Let M = Я иду в торговый центр, J = Я покупаю джинсы и S = Я покупаю рубашку.
Посылки и заключение можно сформулировать так:
Предметка: M → J
Предметка: J → S
Заключение: M → S
Мы можем создать таблицу правды ( M
. ⋀ ( J → S )] → ( M → S )
| M | J | S | M → J | J → S | ( M → J ) ⋀ ( J → S ) | M → ) | M → S | M → S | M → S | M → ) | м S ) ⋀ ( J → S )] → ( M → S ) |
| T | T | T | T | T | T | T | T | ||||
| Т | Т | Ф | T | F | F | F | T | ||||
| T | F | T | F | T | F | T | T | ||||
| T | F | F | F | T | F | F | T | ||||
| F | T | T | T | T | T | T | T | ||||
| F | T | F | T | F | F | T | T | ||||
| F | F | T | T | T | T | T | T | ||||
| F | F | F | T | T | T | T | T |
From the truth table, we can see this is a valid argument.
- Технически это круги Эйлера или диаграммы Эйлера, а не диаграммы Венна, но для простоты мы будем продолжать называть их диаграммами Венна. ↵
Контент с лицензией CC, совместно используемый ранее
- Logic. Автор : Дэвид Липпман. Расположен по адресу : http://www.opentextbookstore.com/mathinsociety/. Проект : Математика в обществе. Лицензия : CC BY-SA: Attribution-ShareAlike
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Метки
