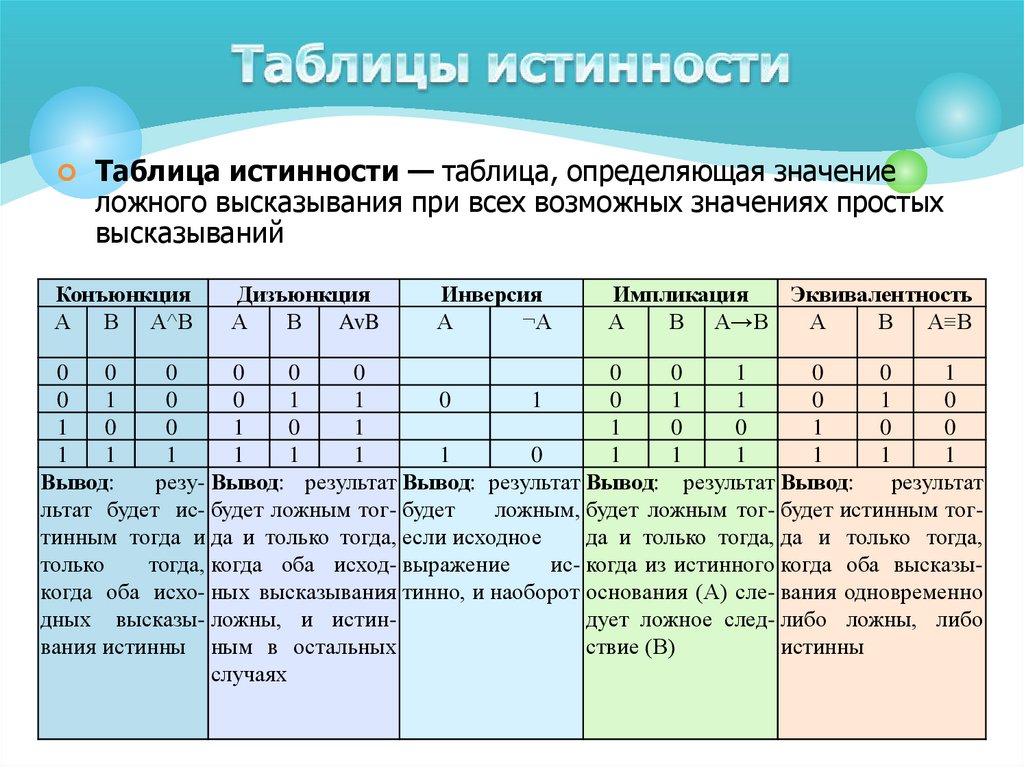
Логические операции и таблицы истинности
Похожие презентации:
Основы логики. Таблица истинности. Равносильные логические выражения
Логические операции
Базовые логические операции и функции. Таблицы истинности. Контактные схемы
Основы программирования на языке Python. Логическая операция
Алгебра логики и таблицы истинности. (лекция 4)
Логические операции
Логические операции
Логические операции компьютеров
Элементарные логические операции
Элементы математической логики
1. Логические операции и таблицы истинности
Учитель информатикиПоборцева Елена Валентиновна
2. КОНЪЮНКЦИЯ
F = A & B.
Логическое умножение
КОНЪЮНКЦИЯ — это
новое сложное выражение
будет истинным только
тогда, когда истинны оба
исходных простых
выражения.
Конъюнкция определяет
соединение двух
логических выражений с
помощью союза И.
A
B
F
1
1
1
1
0
0
0
1
0
0
0
0
3.
 Примеры:
Примеры:10
10
10
10
делится на
не делится
делится на
не делится
2 и 5 больше 3
на 2 и 5 больше 3
2 и 5 не больше 3
на 2 и 5 не больше 3
► F=A&B
Задание: Определить, чему будет равно значение F
для каждого выражения.
4. ДИЗЪЮНКЦИЯ
F=A+BЛогическое сложение –
ДИЗЪЮНКЦИЯ — это
новое сложное выражение
будет истинным тогда и
только тогда,
когда истинно хотя бы
одно из исходных (простых)
выражений.
► Дизъюнкция определяет
соединение двух
логических выражений с
помощью союза ИЛИ
A
B
F
1
1
1
1
0
1
0
1
1
0
0
0
5. Примеры:
► 10делится на
► 10 не делится
► 10 делится на
► 10 не делится
2 или 5 больше 3
на 2 или 5 больше 3
2 или 5 не больше 3
на 2 или 5 не больше 3
F=AVB
Задание: Определить, чему будет равно значение F для
каждого выражения.
6. ИНВЕРСИЯ
Логическое отрицание :
ИНВЕРСИЯ — если исходное
выражение истинно, то
результат отрицания будет
ложным, и наоборот, если
исходное выражение ложно,
то результат отрицания будет
истинным/
Данная операция означает,
что к исходному логическому
выражению добавляется
частица НЕ или слова
НЕВЕРНО, ЧТО
A
_
F=A
1
0
0
1
► Пример:
► Луна
— спутник Земли (А).
► Луна — не спутник Земли (не A)
_
F= A
8. Логическое следование (импликация)
Логическое следование (Импликация) образуется
соединением двух высказываний в одно с помощью союза
«если… то…».
Импликация записывается как посылка следствие; (остриё
всегда указывает на следствие).
F = A B, составное высказывание, образованное с помощью
операции: логическое следование (импликация)
Суждение, выражаемое импликацией, выражается также
следующими способами:
1. Посылка является условием, достаточным для выполнения следствия;
2. Следствие является условием, необходимым для истинности посылки.
9. «Житейский» смысл импликации.
«Житейский» смыслимпликации.
Для более лёгкого понимания смысла импликации и
запоминания ее таблицы истинности может
пригодиться житейская модель:
А — начальник. Он может приказать «работай» (1) или
сказать «делай что хочешь» (0).
В — подчиненный. Он может работать (1) или
бездельничать (0).
В таком случае импликация — не что иное, как
послушание подчиненного начальнику.
По таблице истинности легко проверить, что
послушания нет только тогда, когда начальник
приказывает работать, а подчиненный бездельничает.
10. ИМПЛИКАЦИЯ
Логическое
следование: ИМПЛИКАЦИЯ связывает два простых логических
выражения, из которых первое
является условием (А), а второе
(В)– следствием из этого условия.
Результатом ИМПЛИКАЦИИ
является ЛОЖЬ только тогда,
когда условие А истинно, а
следствие В ложно.
Обозначается A B
символом «следовательно» и
выражается словами ЕСЛИ … ,
ТО …
A
B
F
1
1
1
1
0
0
0
1
1
0
0
1
11. Примеры:
Если данный четырёхугольник квадрат, то около него
можно описать окружность
Если данный четырёхугольник не квадрат, то около
него можно описать окружность
Если данный четырёхугольник квадрат, то около него
нельзя описать окружность
Если данный четырёхугольник не квадрат, то около
него нельзя описать окружность
A B
Задание: Определить, чему будет равно значение F для каждого
выражения.
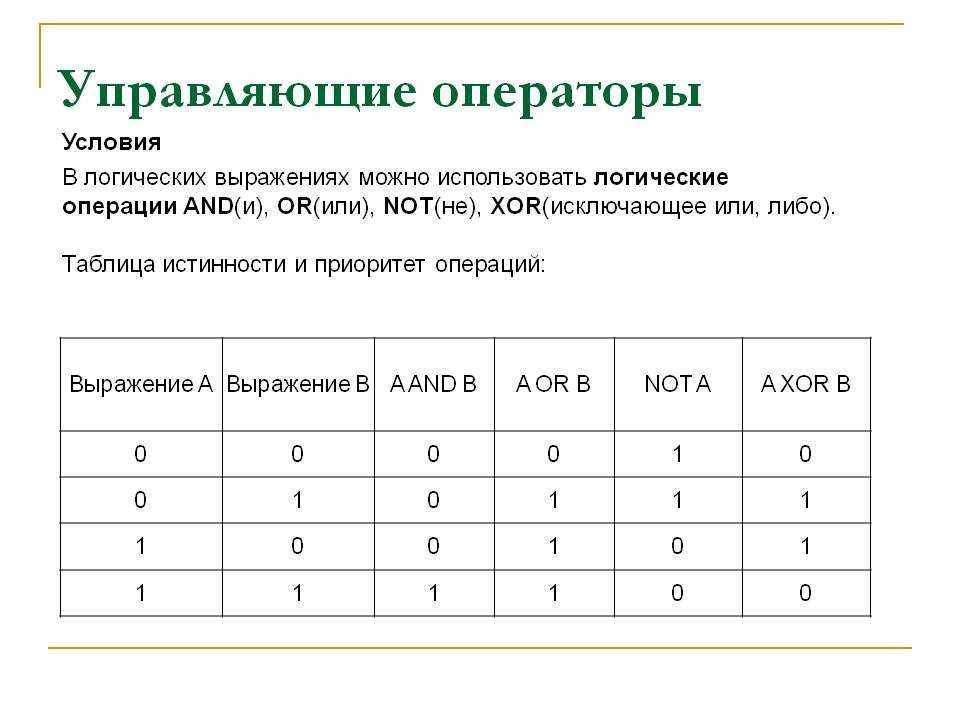
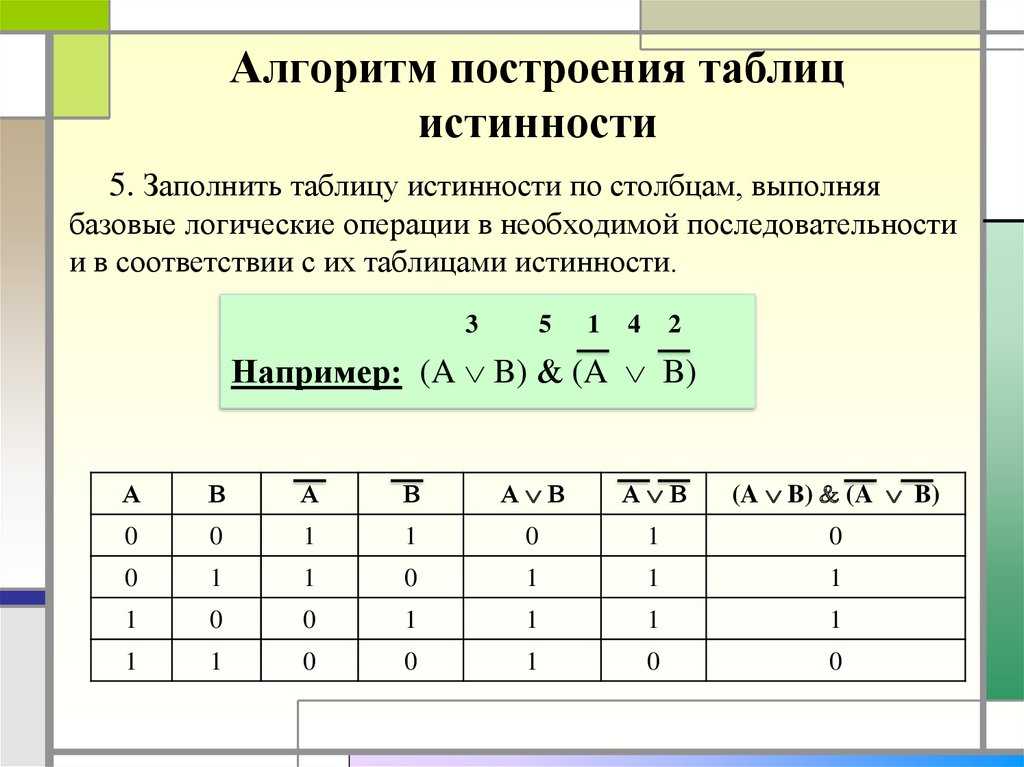
12. Порядок выполнения логических операций
► 1.инверсия
► 2. конъюнкция
► 3. дизъюнкция
► 4. импликация
Для изменения указанного порядка
выполнения операций используются
скобки.
13. Пример задания 1:
Символом F обозначено
одно из указанных ниже
логических выражений от
трех аргументов: X, Y, Z.
Дан фрагмент таблицы
истинности выражения F:
►Какое
1) ¬X ¬Y ¬Z
X
Y
Z
F
1
0
0
1
0
0
0
1
1
1
1
0
выражение соответствует F?
2) X Y Z
3) X Y Z
4) ¬X ¬Y ¬Z
14. Решение :
нужно для каждой строчки подставить заданные
значения X, Y и Z во все функции, заданные в
ответах, и сравнить результаты с соответствующими
значениями F для этих данных
если для какой-нибудь комбинации X, Y и Z результат
не совпадает с соответствующим значением F,
оставшиеся строчки можно не рассматривать,
поскольку для правильного ответа все три результата
должны совпасть со значениями функции F
первое выражение, равно 1 только при X=Y=Z=0 , поэтому это
неверный ответ (первая строка таблицы не подходит)
второе выражение, равно 1 только при X=Y=Z=1, поэтому это
неверный ответ (первая и вторая строки таблицы не подходят)
третье выражение, равно нулю при X=Y=Z=0, поэтому это
неверный ответ (вторая строка таблицы не подходит)
наконец, четвертое выражение, равно нулю только тогда, когда
X=Y=Z=1, а в остальных случаях равно 1, что совпадает с
приведенной частью таблицы истинности
X
Y
Z
F
таким образом, правильный ответ – 4
1) ¬X ¬Y ¬Z
2) X Y Z
3) X Y Z
1
0
0
1
0
0
0
1
1
1
1
0
4) ¬X ¬Y ¬Z
16.
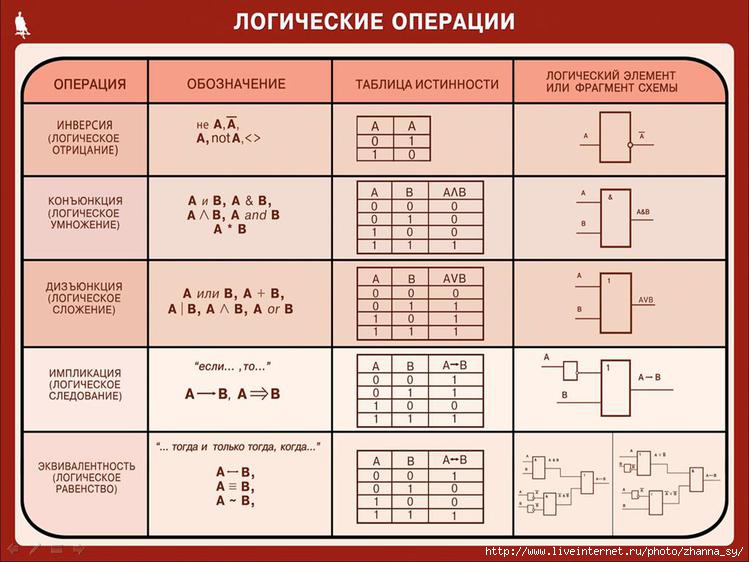 Пример задания 2:
Пример задания 2:Символом F обозначено
одно из указанных ниже
логических выражений от
трех аргументов: X, Y, Z.
Дан фрагмент таблицы
истинности выражения F:
X
Y
Z
F
1
0
0
1
0
0
0
0
1
1
1
0
Какое выражение соответствует F?
1) ¬X ¬Y ¬Z
2) X Y Z
3) X ¬Y ¬Z
4) X ¬Y ¬Z
17. Решение :
В столбце F есть единственная единица
для комбинации X=1, Y=Z=0,
простейшая функция, истинная (только)
для этого случая, имеет вид , она есть
среди приведенных ответов (ответ 3)
таким образом, правильный ответ – 3.
18. Пример задания 3:
Дан фрагмент таблицы
истинности выражения F
(см. таблицу справа).
Какое выражение
соответствует F?
1) (X ¬Y)→ Z
2) (X Y)→ ¬Z
X
Y
Z
F
0
0
0
0
0
1
1
1
1
0
0
1
3) X (¬Y → Z)
4) X Y ¬Z
19. Ответ к заданию 3:
► Найдиправильный ответ:
► 1, 2, 3, 4
English Русский Правила
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
6.
 7. Таблицы истинности — документация по анализу данных
7. Таблицы истинности — документация по анализу данных Таблицы истинности помогают нам понять, как работают логические операторы, показывая все
возможных возвращаемых значений. Давайте посмотрим на таблицу истинности для и , которая
предполагает, что у нас есть два логических выражения, A и B .
6.7.1. Таблица истинности для
и Пример
A | Б | А |
|---|---|---|
| | |
| | |
| | |
| | |
Рассмотрим первую строку таблицы.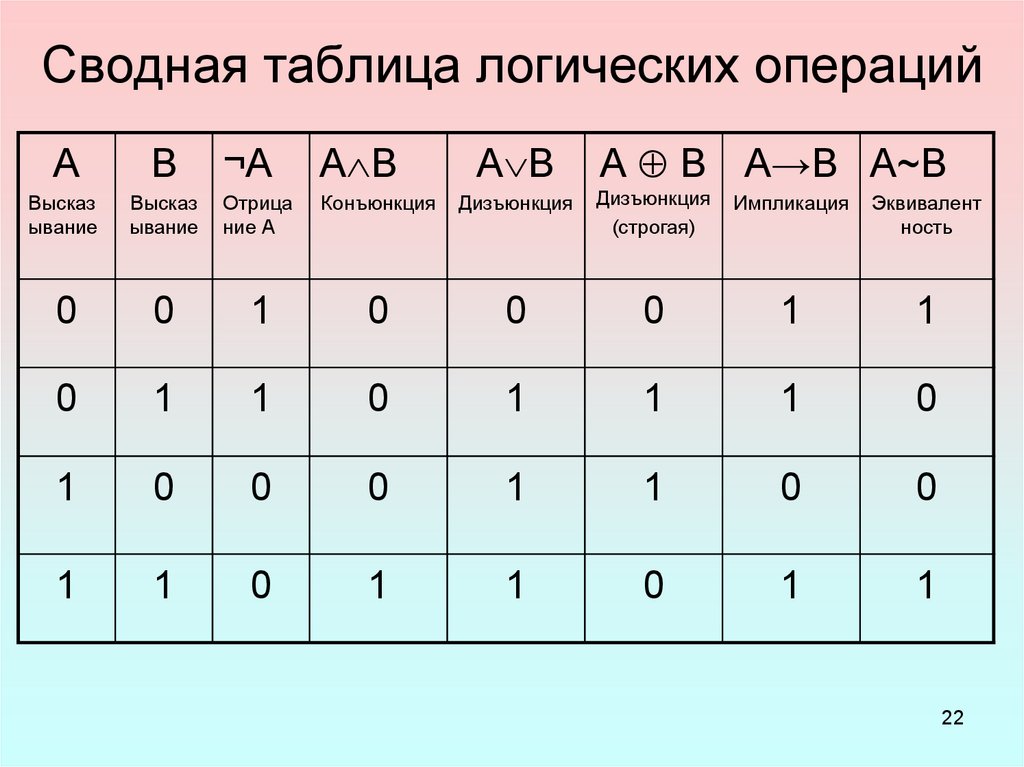 В этой строке говорится, что если A верно
и В истинно, то
В этой строке говорится, что если A верно
и В истинно, то А и В истинно. Две средние строки показывают, что если
либо A, либо B ложны, тогда A и B ложны. Наконец, если и А, и В
false, то A и B ложны.
6.7.2. Таблица истинности для
или Пример
A | Б | А |
|---|---|---|
| | |
| | |
| | |
| | |
Подобно таблице и , если A или B оба верны, то A или B верны.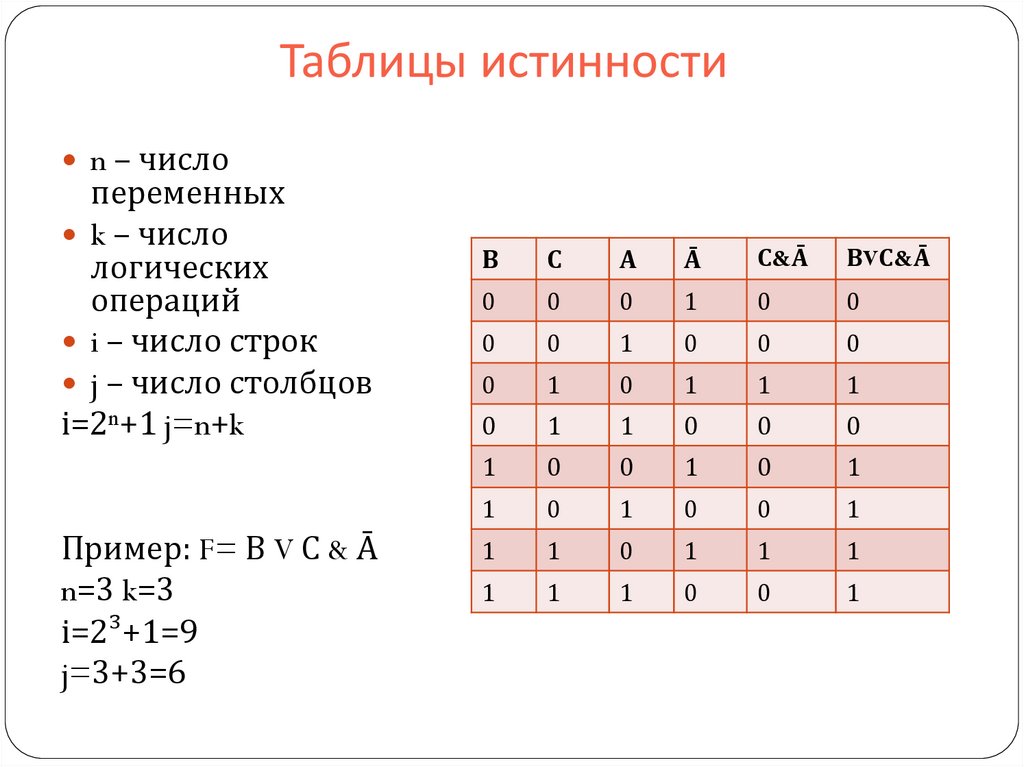 Однако две средние строки показывают, что если либо A, либо B ложны, то
Однако две средние строки показывают, что если либо A, либо B ложны, то A или B по-прежнему остается верным.
Это сильно отличается от таблиц и .
Последняя строка показывает, что если оба варианта ложны, то и все утверждение ложно.
6.7.3. Порядок операций
У нас сейчас много операторов в нашем наборе инструментов, поэтому важно понимать как они относятся друг к другу. Какие операторы выполняются первыми?
Python всегда выполняет операции в определенном порядке:
Сначала выполняются все математические вычисления.
Затем он оценивает все сравнения как
TrueилиFalse.Далее применяются все операторы
, а не.Наконец, он оценивает
ииилиопераций.
Пример
Выражение x * 5 >= 10 и y - 6 <= 20 будет выполнено в следующем порядке:
x * 5вычисляется, затемг - 6.
Сравнение
>=оценивается какTrueилиFalse.Сравнение
<=оценивается какTrueилиFalse.Операторы
иоцениваются последними.
Допустим, x = 2 и y = 46 . Здесь мы шаг за шагом через каждый этап оценки:
Действие | Результат |
|---|---|
Подставьте значения в выражение | |
| |
Сравнение | |
Сравнение | |
Оператор | |
6.
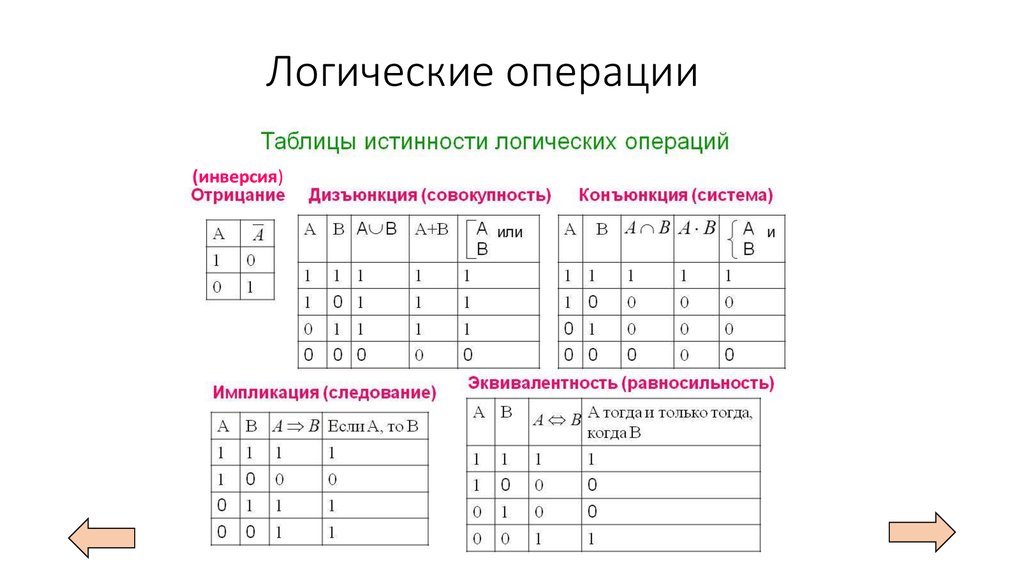 7.3.1. Таблица заказов оператора
7.3.1. Таблица заказов оператораВ следующей таблице операторы перечислены в порядке важности, начиная с (применяется первым) до низшего (применяется последним).
Уровень | Категория | Операторы |
|---|---|---|
(Самый высокий) | Скобки | |
Экспонента | | |
Умножение и деление | | |
Сложение и вычитание | | |
Сравнение | | |
Логический | | |
Логический | | |
(самый низкий) | Логический | |
Совет
Скобки не всегда необходимы, но они имеют БОЛЬШОЕ значение, когда
кто-то другой читает ваш код. Лучше всего использовать круглые скобки, чтобы
код легче читать:
Лучше всего использовать круглые скобки, чтобы
код легче читать:
x * 5 >= 10 и y - 6 <= 20
vs. Проверьте свое понимание
Вопрос
Предположим, у нас есть 3 логических выражения (A, B и C). Какие комбинации
значения (A/B/C) заставят выражение A или B и C оценить как Правда ?
Правда / Правда / Правда
Ложь/Правда/Правда
Верно / Ложно / Верно
Верно / Верно / Ложно
Ложь / Ложь / Верность
Ложь/Правда/Ложь
Верно / Ложно / Ложно
Ложь / Ложь / Ложь
Логика, простые и составные утверждения, логические операции и таблицы истинности, условные утверждения и доказательства Экзаменационные уроки
СОДЕРЖАНИЕ
- Значение простых и составных утверждений.
— Логические операции и таблицы истинности.
- Условные заявления и косвенные доказательства.
ПРОСТЫЕ И СЛОЖНЫЕ ПРЕДЛОЖЕНИЯ
Предлог – это утверждение или предложение, которое либо истинно, либо ложно, но не то и другое одновременно. Мы будем использовать заглавные буквы английского алфавита, такие как A, B, C, D, P, Q, R, S, …, для обозначения простых утверждений или предлогов. Простое высказывание или предложение — это высказывание, не содержащее связок. Другими словами, предложение считается простым, если оно не может быть разбито на подпредложения. С другой стороны, сложное предложение состоит из двух или более предложений, соединенных связками. Этими связками являются и, или, если… то, тогда и только тогда, когда. Их также называют логическими операторами. В таблице ниже показаны логические операторы и их символы. 9
- The statement ∼P is known as отрицание P.
 Q означает P и Q.
Q означает P и Q. - Утверждение PV Q называется дизъюнкцией P и Q. Таким образом, PV Q означает либо P, либо Q, либо оба P и Q. Обратите внимание, что используется включающее или.
- Утверждение P ⇒ Q называется условным оператором P и Q. Условный оператор также известен как импликация P ⇒ Q означает, что если P, то Q или P подразумевает Q.
- Утверждение P ⇔ Q называется биусловным оператором P Q, где символ ⇔ означает тогда и только тогда, когда (или если и только если для краткости). Таким образом, P ⇔ Q означает P ⇔ Q и Q ⇔ P.
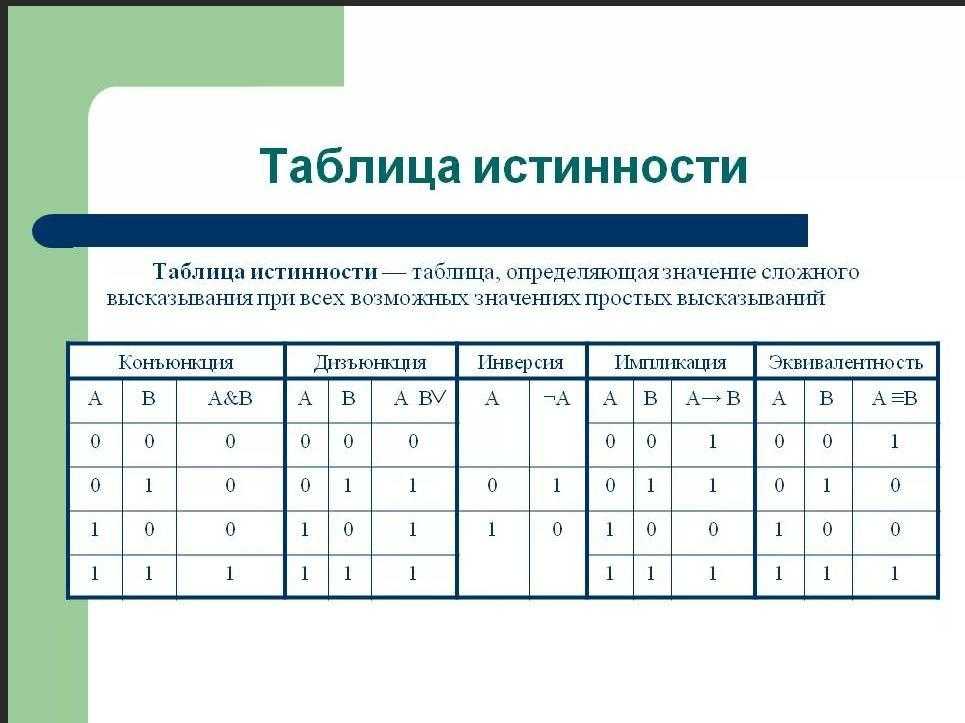
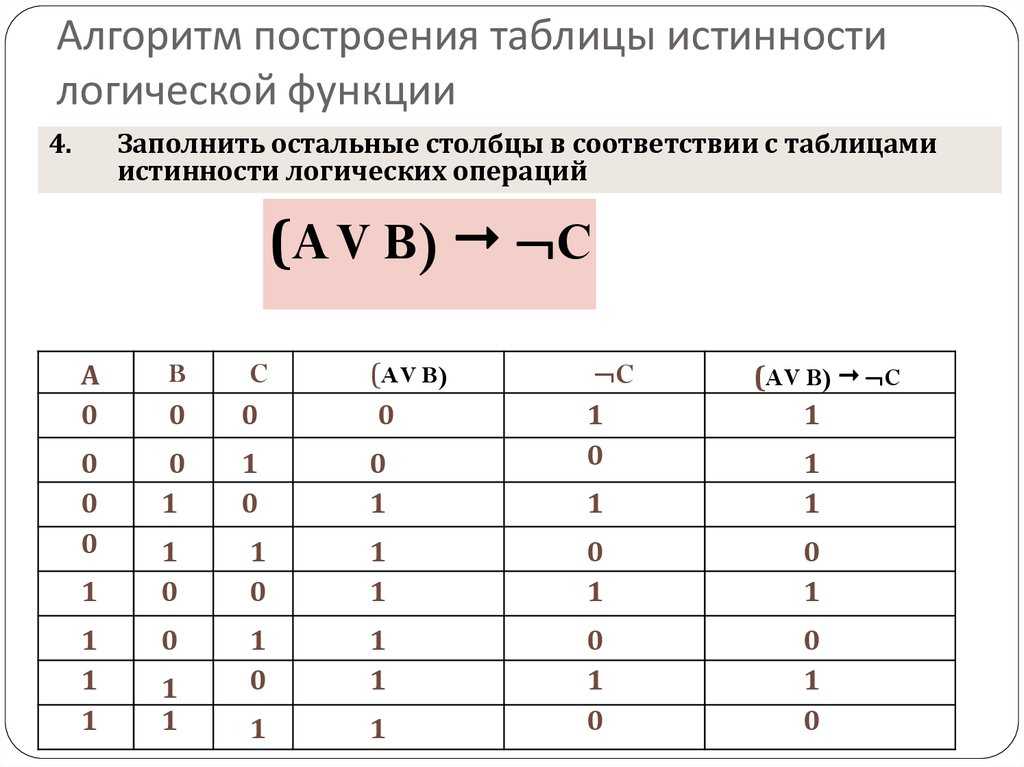
Таблицы истинности
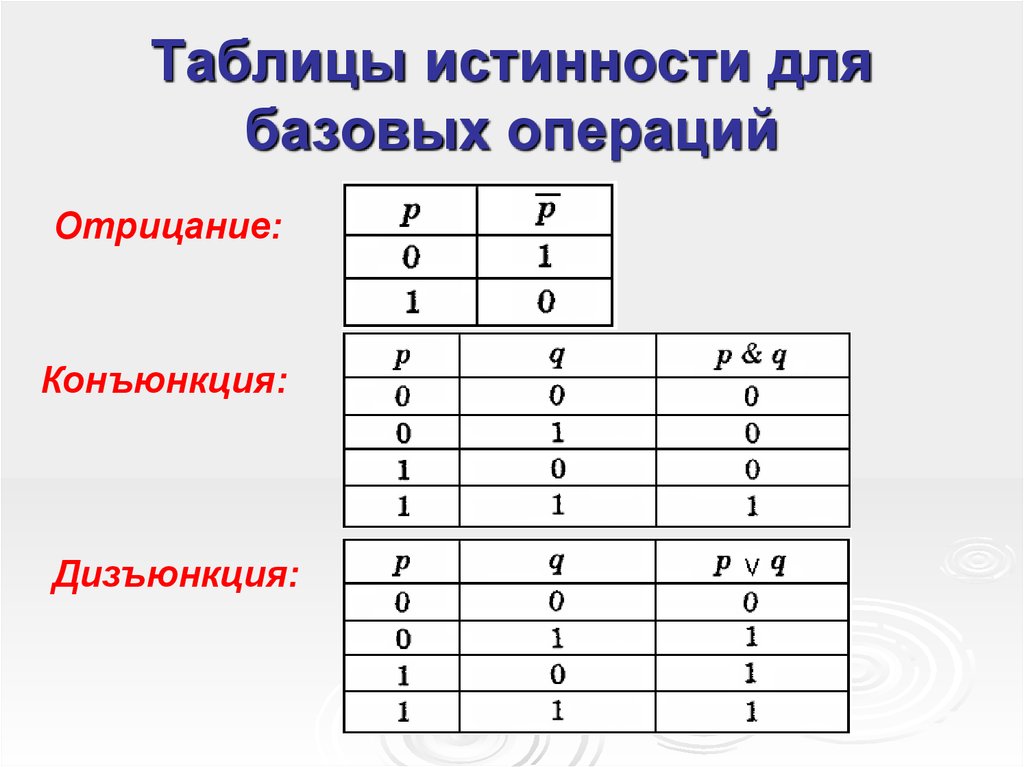
Истинность или ложность предложения есть его истинностное значение, т.е. Истинное предложение имеет значение истинности T, а ложное предложение имеет значение истинности F. Таблицы истинности для логических операторов приведены ниже.
Рисунок 2
| P | ~ P |
| T | F |
| F | T |
| F | T |
| FLAIN |




 Результатом ЭКВИВАЛЕНТНОСТИ является новое логическое выражение,
которое будет истинным тогда и только тогда, когда оба исходных
выражения одновременно истинны или ложны. Обозначается символом
«эквивалентности»
Результатом ЭКВИВАЛЕНТНОСТИ является новое логическое выражение,
которое будет истинным тогда и только тогда, когда оба исходных
выражения одновременно истинны или ложны. Обозначается символом
«эквивалентности»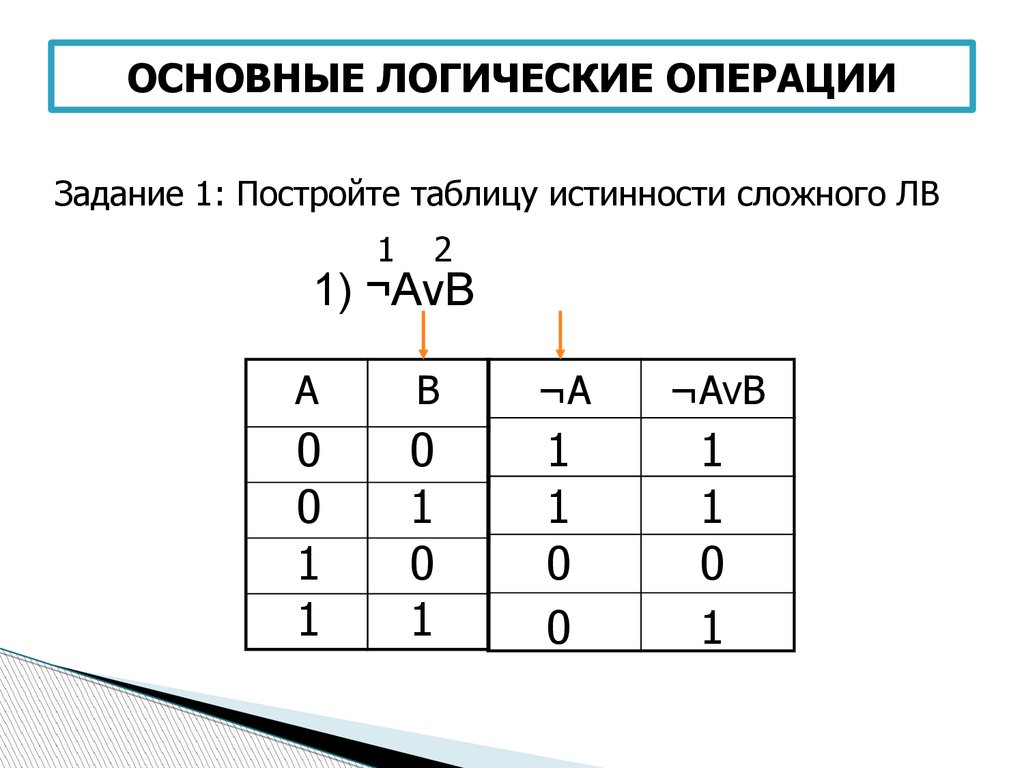
 Q означает P и Q.
Q означает P и Q.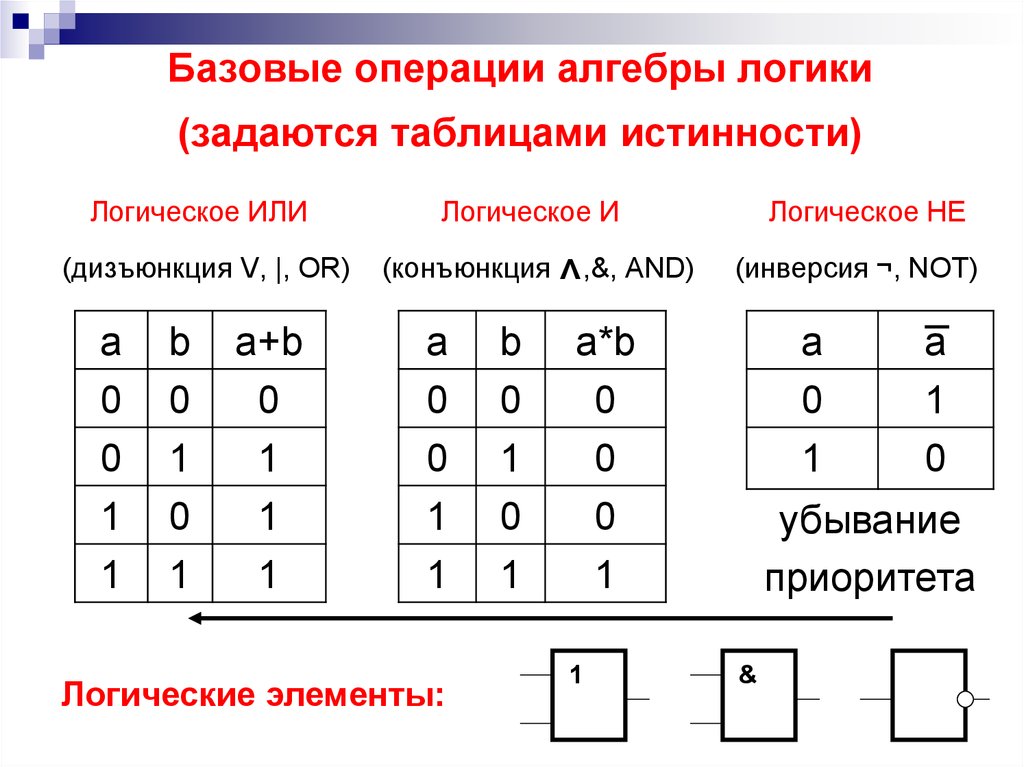 и если P ложно, то ~P истинно.
и если P ложно, то ~P истинно.