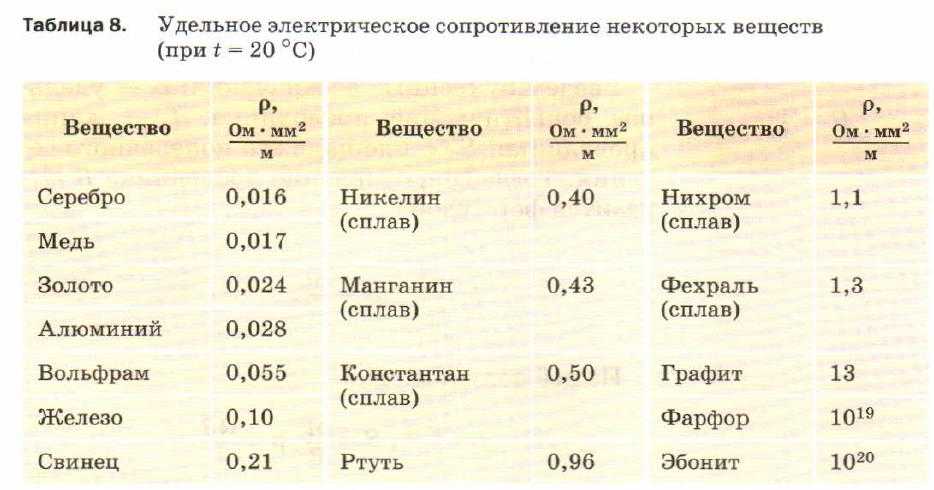
Удельное сопротивление меди
Что надо знать про электрические процессы
Если говорить простым языком, то под сопротивлением принято понимать свойство среды, по которой протекает электрический ток, снижающее его величину.
Так работают провода и изоляторы высоковольтной линии электропередач, показанные на верхней картинке, да и любое вещество.
Изоляторы обладают очень высокими диэлектрическими свойствами, изолируют высоковольтное напряжение, присутствующее на токоведущих шинах от контура земли. Это их основное назначение.
Провода же должны максимально эффективно передавать транслируемые по ним мощности. Их создают так, чтобы они обладали минимальным электрическим сопротивлением, работали с наименьшими потерями энергии на нагрев.
В этом случае передача электричества от источника напряжения к потребителю на любое расстояние будет проходить эффективно.
Приведу для примера картинку из предыдущей моей статьи.
Ее, как и верхнюю, можно представить таким обобщенным видом.
На внешнем участке цепи токоведущие жилы отделены друг от друга воздушной средой и слоем изоляции с высокими диэлектрическими свойствами.
Хорошей проводимостью обладают токоведущие жилы. Подключенный к ним электрический прибор функционирует оптимально.
Как работает резистор
Ток в металлах проходит под действием приложенного напряжения за счет направленного движения электронов. При этом они соударяются, встречаются с положительно и отрицательно заряженными ионами.
Такие столкновения повышают температуру среды, уменьшают силу тока. За направление электрического тока в электротехнике принято движение заряженных частиц от плюса к минусу. Электроны же движутся от катода к аноду.
Аналогичные процессы протекают в любой другой токопроводящей среде, включая газы или жидкости.
Какие существуют виды сопротивлений
В домашних электрических приборах используется большое разнообразие резисторов с постоянной или регулируемой величиной.
Они ограничивают величину тока всех бытовых устройств, а в наиболее сложных модулях их количество может достигать тысячи или более. Резисторы работают практически во всех схемах.
Резисторы работают практически во всех схемах.
При использовании в цепях переменного тока они обладают активным сопротивлением, а конденсаторы и дроссели — реактивным.
Причем, на конденсаторах создается емкостное сопротивление, а у дросселей — индуктивное.
Реактивная составляющая на конденсаторах и дросселях сильно зависит от частоты электромагнитного колебания.
2 Шутки электриков о токах через конденсатор и дроссель
Их я привожу потому, что они позволяют запомнить характер прохождения тока через реактивные элементы.
Шутка №1 о емкости
В домашней сети и внутри многих приборов работают переменный и постоянный токи. Они по-разному ведут себя, если встречают на своем пути конденсатор.
Поскольку он состоит из двух токопроводящих пластин, разделенных слоем диэлектрика, то его обозначают на схемах двумя жирными черточками, расположенными параллельно. К их серединам подключены провода, нарисованные перпендикулярными линиями.
Переменный ток имеет форму гармоничной синусоиды, состоящей из двух симметричных половинок.
Такая гармоника движется от начала координат, встречает на своем пути обкладки, переваливается через них и, скатившись, начинает обгонять приложенное напряжение.
Постоянный ток таким свойством не обладает. Его тупой конец просто упирается в обкладку и останавливается. Пройти через конденсатор он не может. Это для него непреодолимое препятствие.
Шутка №2 о дросселе
Индуктивность выполнена витками изолированного провода. Любой ток проходит по нему. Но синусоида своими волнами путается в витках катушки, начинает отставать от напряжения.
Постоянка же спокойно перемещается внутри провода дросселя без ощущения какого-либо значительного противодействия. Поэтому постоянное напряжение может своим током спалить дроссель, созданный для работы на переменке.
Что же это за зверь: сверхпроводимость
Сто лет назад выявлена способность определенных металлов полностью терять свое сопротивление электрическому току при сверхнизких температурах. Выглядит этот процесс следующим образом.
Со сверхпроводниками домашний мастер не работает
Но на верхнюю часть приведенного графика рекомендую обратить внимание: нагрев металла повышает его электрическое сопротивление
При электротехнических расчетах, требующих получения точного результата, необходимо учитывать температурный коэффициент, взятый из справочников.
Удельное электрическое сопротивление
Сопротивление в омах проводника длиной 1 м, сечением 1 мм² называется удельным сопротивлением
и обозначается греческой буквойρ (ро).
В таблице 1 даны удельные сопротивления некоторых проводников.
Таблица 1
Удельные сопротивления различных проводников
Из таблицы видно, что железная проволока длиной 1 м и сечением 1 мм² обладает сопротивлением 0,13 Ом. Чтобы получить 1 Ом сопротивления нужно взять 7,7 м такой проволоки. Наименьшим удельным сопротивлением обладает серебро. 1 Ом сопротивления можно получить, если взять 62,5 м серебряной проволоки сечением 1 мм². Серебро – лучший проводник, но стоимость серебра исключает возможность его массового применения. После серебра в таблице идет медь: 1 м медной проволоки сечением 1 мм² обладает сопротивлением 0,0175 Ом. Чтобы получить сопротивление в 1 Ом, нужно взять 57 м такой проволоки.
Серебро – лучший проводник, но стоимость серебра исключает возможность его массового применения. После серебра в таблице идет медь: 1 м медной проволоки сечением 1 мм² обладает сопротивлением 0,0175 Ом. Чтобы получить сопротивление в 1 Ом, нужно взять 57 м такой проволоки.
Химически чистая, полученная путем рафинирования, медь нашла себе повсеместное применение в электротехнике для изготовления проводов, кабелей, обмоток электрических машин и аппаратов. Широко применяют также в качестве проводников алюминий и железо.
Сопротивление проводника можно определить по формуле:
где r
– сопротивление проводника в омах;ρ – удельное сопротивление проводника;l – длина проводника в м;S – сечение проводника в мм².
Пример 1.
Определить сопротивление 200 м железной проволоки сечением 5 мм².
Пример 2.
Вычислить сопротивление 2 км алюминиевой проволоки сечением 2,5 мм².
Из формулы сопротивления легко можно определить длину, удельное сопротивление и сечение проводника.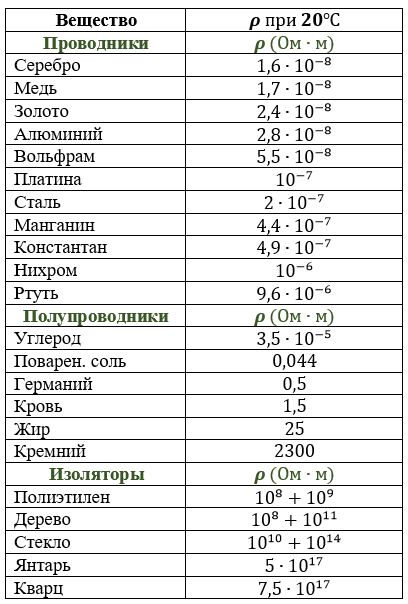
Пример 3.
Для радиоприемника необходимо намотать сопротивление в 30 Ом из никелиновой проволоки сечением 0,21 мм². Определить необходимую длину проволоки.
Пример 4.
Определить сечение 20 м нихромовой проволоки, если сопротивление ее равно 25 Ом.
Пример 5.
Проволока сечением 0,5 мм² и длиной 40 м имеет сопротивление 16 Ом. Определить материал проволоки.
Материал проводника характеризует его удельное сопротивление.
По таблице удельных сопротивлений находим, что таким сопротивлением обладает свинец.
Выше было указано, что сопротивление проводников зависит от температуры. Проделаем следующий опыт. Намотаем в виде спирали несколько метров тонкой металлической проволоки и включим эту спираль в цепь аккумулятора. Для измерения тока в цепь включаем амперметр. При нагревании спирали в пламени горелки можно заметить, что показания амперметра будут уменьшаться. Это показывает, что с нагревом сопротивление металлической проволоки увеличивается.
У некоторых металлов при нагревании на 100° сопротивление увеличивается на 40 – 50 %. Имеются сплавы, которые незначительно меняют свое сопротивление с нагревом. Некоторые специальные сплавы практически не меняют сопротивления при изменении температуры. Сопротивление металлических проводников при повышении температуры увеличивается, сопротивление электролитов (жидких проводников), угля и некоторых твердых веществ, наоборот, уменьшается.
Способность металлов менять свое сопротивление с изменением температуры используется для устройства термометров сопротивления. Такой термометр представляет собой платиновую проволоку, намотанную на слюдяной каркас. Помещая термометр, например, в печь и измеряя сопротивление платиновой проволоки до и после нагрева, можно определить температуру в печи.
Изменение сопротивления проводника при его нагревании, приходящееся на 1 Ом первоначального сопротивления и на 1° температуры, называется температурным коэффициентом сопротивления
и обозначается буквой α.
Если при температуре t
0 сопротивление проводника равноr 0 , а при температуреt равноr t , то температурный коэффициент сопротивления
Примечание.
Расчет по этой формуле можно производить лишь в определенном интервале температур (примерно до 200°C).
Приводим значения температурного коэффициента сопротивления α для некоторых металлов (таблица 2).
Таблица 2
Значения температурного коэффициента для некоторых металлов
Из формулы температурного коэффициента сопротивления определим r t
r t
=r 0 .
Пример 6.
Определить сопротивление железной проволоки, нагретой до 200°C, если сопротивление ее при 0°C было 100 Ом.
r t
=r 0 = 100 (1 + 0,0066 × 200) = 232 Ом.
Пример 7.
Термометр сопротивления, изготовленный из платиновой проволоки, в помещении с температурой 15°C имел сопротивление 20 Ом. Термометр поместили в печь и через некоторое время было измерено его сопротивление. Оно оказалось равным 29,6 Ом. Определить температуру в печи.
Оно оказалось равным 29,6 Ом. Определить температуру в печи.
Зависимость от температуры
Удельное электрическое сопротивление зависит от температуры. Но все группы веществ проявляют себя по-разному при ее изменении. Это необходимо учитывать при расчете проводов, которые будут работать в определенных условиях. К примеру, на улице, где значения температуры зависят от времени года, необходимые материалы с меньшей подверженностью изменениям в диапазоне от -30 до +30 градусов Цельсия. Если же планируется применение в технике, которая будет работать в одних и тех же условиях, то здесь также нужно оптимизировать проводку под конкретные параметры. Материал всегда подбирается с учетом эксплуатации.
В номинальной таблице удельное электрическое сопротивление берется при температуре 0 градусов Цельсия. Повышение показателей данного параметра при нагреве материала обусловлено тем, что интенсивность передвижения атомов в веществе начинает возрастать. Носители электрических зарядов хаотично рассеиваются во всех направлениях, что приводит к созданию препятствий при передвижении частиц.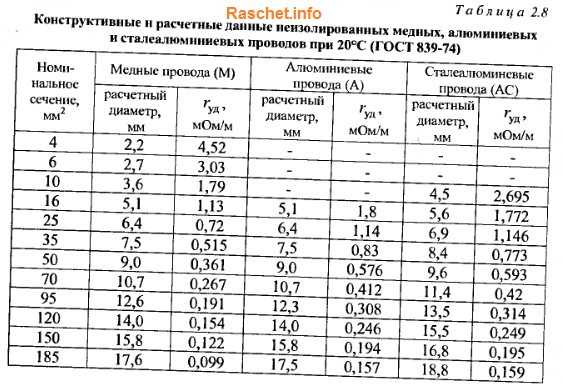
При уменьшении температуры условия прохождения тока становятся лучше. При достижении определенной температуры, которая для каждого металла будет отличаться, появляется сверхпроводимость, при которой рассматриваемая характеристика почти достигает нуля.
Отличия в параметрах порой достигают очень больших значений. Те материалы, которые обладают высокими показателями, могут использовать в качестве изоляторов. Они помогают защищать проводку от замыкания и ненамеренного контакта с человеком. Некоторые вещества вообще не применимы для электротехники, если у них высокое значение этого параметра. Этому могут мешать другие свойства. Например, удельная электрическая проводимость воды не будет иметь большого значения для данный сферы.
| Материалы с высоким удельным сопротивлением | ρ (Ом·м) |
| Бакелит | 1016 |
| Бензол | 1015…1016 |
| Бумага | 1015 |
| Вода дистиллированная | 104 |
| Вода морская | 0.3 |
| Дерево сухое | 1012 |
| Земля влажная | 102 |
| Кварцевое стекло | 1016 |
| Керосин | 1011 |
| Мрамор | 108 |
| Парафин | 1015 |
| Парафиновое масло | 1014 |
| Плексиглас | 1013 |
| Полистирол | 1016 |
| Полихлорвинил | 1013 |
| Полиэтилен | 1012 |
| Силиконовое масло | 1013 |
| Слюда | 1014 |
| Стекло | 1011 |
| Трансформаторное масло | 1010 |
| Фарфор | 1014 |
| Шифер | 1014 |
| Эбонит | 1016 |
| Янтарь | 1018 |
Более активно в электротехнике применяются вещества с низкими показателями. Зачастую это металлы, которые служат проводниками. В них также наблюдается много различий. Чтобы узнать удельное электрическое сопротивление меди или других материалов, стоит посмотреть в справочную таблицу.
Зачастую это металлы, которые служат проводниками. В них также наблюдается много различий. Чтобы узнать удельное электрическое сопротивление меди или других материалов, стоит посмотреть в справочную таблицу.
| Материалы с низким удельным сопротивлением | ρ (Ом·м) |
| Алюминий | 2.7·10-8 |
| Вольфрам | 5.5·10-8 |
| Графит | 8.0·10-6 |
| Железо | 1.0·10-7 |
| Золото | 2.2·10-8 |
| Иридий | 4.74·10-8 |
| Константан | 5.0·10-7 |
| Литая сталь | 1.3·10-7 |
| Магний | 4.4·10-8 |
| Манганин | 4.3·10-7 |
| Медь | 1.72·10-8 |
| Молибден | 5.4·10-8 |
| Нейзильбер | 3.3·10-7 |
| Никель | 8.7·10-8 |
| Нихром | 1.12·10-6 |
| Олово | 1.2·10-7 |
| Платина | 1. 07·10-7 07·10-7 |
| Ртуть | 9.6·10-7 |
| Свинец | 2.08·10-7 |
| Серебро | 1.6·10-8 |
| Серый чугун | 1.0·10-6 |
| Угольные щетки | 4.0·10-5 |
| Цинк | 5.9·10-8 |
| Никелин | 0,4·10-6 |
Что такое сопротивление медного провода
В металлах ток образуется при появлении электрического поля. Оно «заставляет» двигаться электроны упорядоченно, в одном направлении. Электроны дальних орбит атома, слабо удерживаемые ядром, формируют ток.
При прохождении отрицательных частиц сквозь кристаллическую решетку молекул меди, они сталкиваются с атомами и другими электронами. Возникает препятствие или сопротивление направленному движению частиц.
Для оценки противодействия току была введена величина «электрическое сопротивление» или «электрический импеданс». Обозначается она буквой «R» или «r». Вычисляется сопротивление по формуле Георга Ома: R=, где U — разность потенциалов или напряжение, действующее на участке цепи, I — сила тока.
Важно! Чем выше значение импеданса металла, тем меньший ток проходит по нему, и именно медные проводники так широко распространены в электротехнике, благодаря этому свойству. Исходя из формулы Ома, на величину тока влияет приложенное напряжение при постоянном R. Но резистентность медных проводов меняется, в зависимости от их физических характеристик и условий эксплуатации
Но резистентность медных проводов меняется, в зависимости от их физических характеристик и условий эксплуатации
Исходя из формулы Ома, на величину тока влияет приложенное напряжение при постоянном R. Но резистентность медных проводов меняется, в зависимости от их физических характеристик и условий эксплуатации.
Удельное сопротивление» src=»https://www.youtube.com/embed/9ByGynkMIPY?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>Железо как проводник в электротехнике
Железо — самый распространенный в природе и технике металл (после водорода, который металлом тоже является). Он и самый дешевый, и имеет прекрасные прочностные характеристики, поэтому применяется повсюду как основа прочности различных конструкций.
В электротехнике в качестве проводника железо используется в виде стальных гибких проводов там, где нужна физическая прочность и гибкость, а нужное сопротивление может быть достигнуто за счет соответствующего сечения.
Имея таблицу удельных сопротивлений различных металлов и сплавов, можно посчитать сечения проводов, выполненных из разных проводников.
В качестве примера попробуем найти электрически эквивалентное сечение проводников из разных материалов: проволоки медной, вольфрамовой, никелиновой и железной.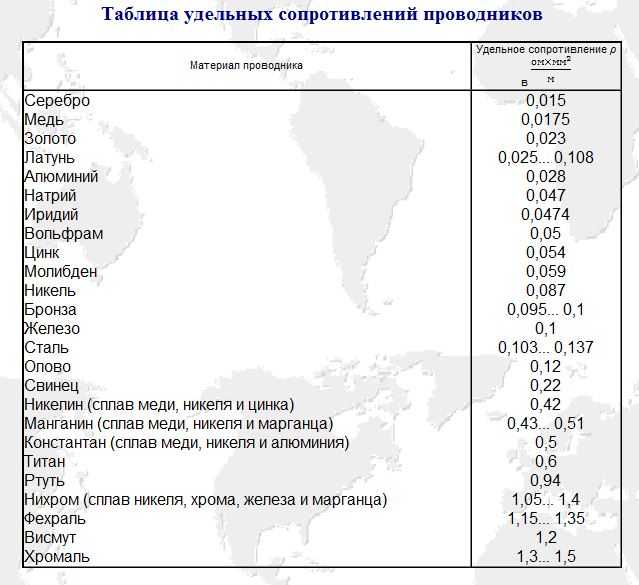 За исходную возьмем проволоку алюминиевую сечением 2,5 мм.
За исходную возьмем проволоку алюминиевую сечением 2,5 мм.
Нам нужно, чтобы на длине в 1 м сопротивление провода из всех этих металлов равнялось сопротивлению исходной. Сопротивление алюминия на 1 м длины и 2,5 мм сечения будет равно
Где R – сопротивление, ρ – удельное сопротивление металла из таблицы, S – площадь сечения, L – длина.
Подставив исходные значения, получим сопротивление метрового куска провода алюминия в омах.
После этого разрешим формулу относительно S
Будем подставлять значения из таблицы и получать площади сечений для разных металлов.
Так как удельное сопротивление в таблице измерено на проводе длиной в 1 м, в микроомах на 1 мм 2 сечения, то у нас и получилось оно в микроомах. Чтобы получить его в омах, нужно умножить значение на 10 -6 . Но число ом с 6 нулями после запятой нам получать совсем не обязательно, так как конечный результат все равно находим в мм 2 .
Как видим, сопротивление железа достаточно большое, проволока получается толстая.
Но существуют материалы, у которых оно еще больше, например, никелин или константан.
Про закон Ома многие слышали, но не все знают, что это такое. Изучение начинается со школьного курса физики. Более подробно проходят на физфаке и электродинамике. Рядовому обывателю эти знания маловероятно пригодятся, но они необходимы для общего развития, а кому-то для будущей профессии. С другой стороны, элементарные знания об электричестве, его устройстве, особенностей в домашних условиях помогут предостеречь себя от беды. Недаром закон Ома называют основным законом электричества. Домашнему мастеру нужно обладать знаниями в области электричества, чтобы не допустить перенапряжения, что может повлечь увеличению нагрузки и возникновению пожара.
Характеристики сплавов
Зависеть электропроводность металлов может не только от количества имеющихся в них примесей, но и от других показателей. К примеру с повышением температуры нагрева способность меди пропускать сквозь себя ток снижается.
Однако больше всего влияют, конечно же, используемые добавки и их количество на электропроводность меди. Таблица ниже представляет читателю исчерпывающую информацию относительно способности пропускать ток наиболее распространенных сплавов этого металла. Электропроводность медных сплавов
| Сплав | Состояние (О — отожженная, Т-твердотянутая) | Электропроводность (%) |
| Чистая медь | О | 101 |
| Т | 98 | |
| Оловянная бронза (0.75 %) | О | 55-60 |
| Т | 50-55 | |
| Кадмиевая бронза (0.9 %) | О | 95 |
| Т | 83-90 | |
| Алюминиевая бронза (2,5 % А1, 2 % Sn) | О | 15-18 |
| Т | 15-18 | |
| Фосфористая бронза (7 % Sn, 0,1 % Ρ) | О | 10-15 |
| Т | 10-15 |
Электропроводность латуни и меди сравнима.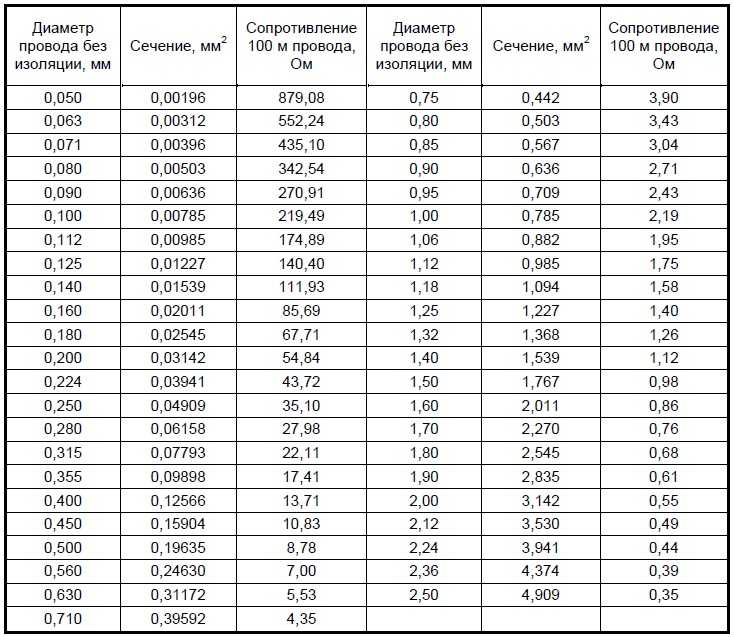 Однако у первого металла этот показатель, конечно же, немного ниже. Но при этом он и выше, чем у бронз. В качестве проводника латунь используется довольно-таки широко. Ток она пропускает хуже меди, но при этом и стоит дешевле. Чаще всего из латуни делают контакты, зажимы и различные детали для радиоаппаратуры.
Однако у первого металла этот показатель, конечно же, немного ниже. Но при этом он и выше, чем у бронз. В качестве проводника латунь используется довольно-таки широко. Ток она пропускает хуже меди, но при этом и стоит дешевле. Чаще всего из латуни делают контакты, зажимы и различные детали для радиоаппаратуры.
Удельное электрическое сопротивление некоторых веществ
Общее сопротивление
Выше показано, что рассматриваемый параметр будет зависеть от свойств определенного вещества. Для корректных вычислений следует учитывать различные характеристики полупроводника и металла, других материалов, сплавов, химических соединений в твердом и жидком состоянии.
Металлические монокристаллы
Для примера в следующем перечне приведены тензорные значения (p1=p2 в 10-8 Ом на метр) для некоторых материалов:
- цинк – 5,9;
- висмут – 109;
- олово – 9,89;
- кадмий – 6,78.
Металлы и сплавы, применяемые в электротехнике
В следующем списке представлены разные проводники, которые применяют для создания электротехнических устройств и силовых агрегатов, линий связи, передачи электроэнергии.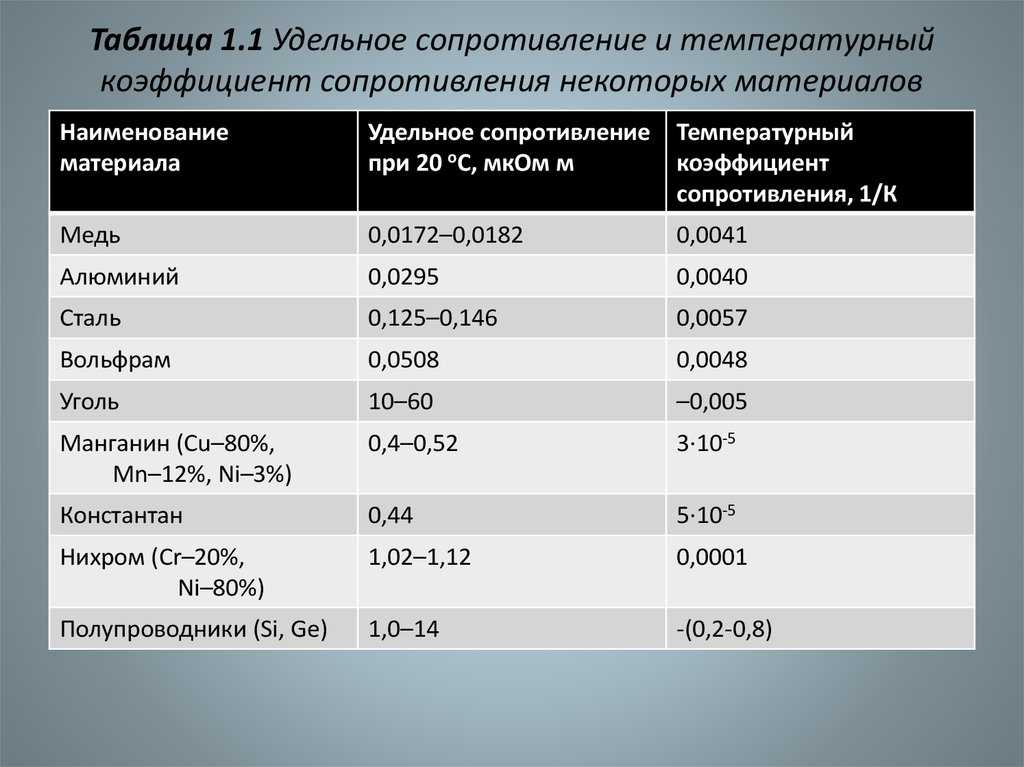 Для удобства практических расчетов удельное электрическое сопротивление приведено в Ом*мм кв./м при поддержании постоянной температуры в процессе измерений на уровне +20°C:
Для удобства практических расчетов удельное электрическое сопротивление приведено в Ом*мм кв./м при поддержании постоянной температуры в процессе измерений на уровне +20°C:
- платина – 0,107:
- никель – 0,087;
- нихром – от 1,05 до 1,4;
- медь – от 0,017 до 0,018;
- сталь – от 0,1 до 0,137;
- золото – 0,023;
- железо – 0,098;
- алюминий – от 0,026 до 0,03.
Приведенные числа демонстрируют, что в сплавах проводимость существенно зависит от состава и количественного распределения составляющих. Определенное значение для металлических проводников имеет чистота материала.
Качественная электротехническая медь отличается минимальным содержанием примесей и небольшим удельным сопротивлением
К сведению. Для создания экономичных линий электропередач нужны соответствующие начальные инвестиции. Однако чистые материалы обеспечивают уменьшение потерь, что уменьшает эксплуатационные затраты.
Другие вещества
При той же контрольной температуре +20°C измеряются удельные сопротивления иных материалов и веществ (значения приведены в Ом*мм кв. /м):
/м):
- резина – от 1016 до 1018;
- углеводородные соединения в сжиженном состоянии – 0,8*1010;
- воздух (при разном уровне относительной влажности) – от 1021 до 1032;
- древесина – от 1015 до 1016.
Тонкие плёнки
При уменьшении слоя толщиной можно пренебречь. Для расчета удельного электрического сопротивления формулу преобразуют следующим образом:
Rs = (R*W)/L,
где:
- Rs – значение сопротивления для прямоугольного участка;
- R – результат измерений;
- W (L) – ширина (длина) контрольного образца.
Выбор сечения кабелей
Для крупных расчетов можно использовать специализированный калькулятор на справочном сайте либо соответствующее программное обеспечение. Следующий алгоритм применяют для последовательного вычисления рабочих параметров по формулам:
- при передаче в подключенную нагрузку мощности P = 1 600 Вт в линии с напряжением U = 220 V постоянный ток (I) определяют следующим образом: I = P/U ≈ 7,27А;
- сопротивление медного проводника (в обе стороны) длиной 800 м и сечением 2,5 мм кв.
 : R = (2*I*p)/S = (2*800*0,0175)/2,5 = 11,2 Ом;
: R = (2*I*p)/S = (2*800*0,0175)/2,5 = 11,2 Ом; - потери по напряжению в этой трассе: ΔU = (2*L*I)/((1/p)*S) = (2*800*7,27)/((1/0,0175)*2,5) = 11 520/ 142,86 = 80,63 V.
Удельное сопротивление
При необходимости последнее выражение несложно математически преобразовать для выбора площади поперечного сечения проводника по суммарному значению подключаемой нагрузки:
S = (2*I*L)/((1/p)*ΔU.
В рассмотренном примере потери напряжения составляют более 36%. Этот результат свидетельствует о необходимости корректировки расчета сопротивления проводника. По действующим нормативам допустимо уменьшение контрольного параметра не более, чем на 5 %. Увеличив диаметр провода, можно получить необходимый результат. При сечении 19 мм кв. напряжение уменьшится до 209,41 V (4,81%).
С учетом увеличенного сопротивления алюминиевого провода предполагаются пропорциональные изменения потерь. Выполнив аналогичный расчет, можно получить рекомендованное сечение 31 мм кв. Использование такого проводника в аналогичных условиях снизит напряжение до 209,2 V, что позволит обеспечить соответствие нормативам – 4,92%.
К сведению. Для проверки расчетных данных можно использовать мультиметр. Измерения выполняют в соответствующем диапазоне с учетом амплитуды сигнала, переменного (постоянного) тока.
При подключении источника питания переменного тока алгоритм вычислений усложняется. Для таких исходных условий пользуются формулой:
ΔU = ((Pа * Rа + Pр * Rи) *L)/ U,
где:
- Pа (Pр) – активная (реактивная) мощность;
- Rа (Rи) – относительное активное (индуктивное) сопротивление линии в Ом на километр.
Для определенных материалов проводников исходные данные берут из справочника. По аналогии с упомянутыми нормативами уменьшение напряжения не должно быть в общем случае более 5%. Дополнительные ограничения применяют с учетом особенностей электрических сетей и подключаемых потребителей (от 1% до 12%). Действующие правила уточняют по тексту последней редакции ПУЭ.
Приведенные итоги расчетов убедительно подтверждают преимущества меньшего удельного сопротивления медного провода. При использовании алюминиевого аналога значительно увеличивается количество материала для передачи электроэнергии с нормативными потерями. Для комплексного анализа следует учитывать лучшие показатели меди по прочности, гибкости.
При использовании алюминиевого аналога значительно увеличивается количество материала для передачи электроэнергии с нормативными потерями. Для комплексного анализа следует учитывать лучшие показатели меди по прочности, гибкости.
Алюминий отличается меньшей стоимостью, легкостью. Но при работе с этим материалом следует исключить вибрационные воздействия и перемещения в процессе эксплуатации. Особо тщательно проектируют изгибы, чтобы сохранить целостность проводника. Электрический контакт нарушается образованием окислов на поверхности изделий, изготовленных из этого металла.
К сведению. В определенных ситуациях многое будет значить свободное место для прокладки трассы. По экономии пространства преимущественными параметрами обладает медь.
Выбор сечения проводника по допустимому нагреву
По мере увеличения силы тока повышается температура проводящего металла. На определенном уровне повреждается слой защитной изоляции, созданный из полимеров. Это провоцирует короткие замыкания и образование пламени. Опасные ситуации предотвращают корректным расчетом площади поперечного сечения. Определенное значение имеет способ прокладки (совместный/ раздельный).
Опасные ситуации предотвращают корректным расчетом площади поперечного сечения. Определенное значение имеет способ прокладки (совместный/ раздельный).
Выбор сечения по потерям напряжения
Как показано в расчетах, при большой длине трасы нужно учитывать снижение напряжения и соответствующие энергетические потери. В крупных проектах рассматривают всю цепь тока с распределительными устройствами и подключаемыми нагрузками.
Для точного определения подходящей кабельной продукции рассматривают особенности процесса эксплуатации. Делают необходимый запас, чтобы предотвратить аварийные ситуации при подключении новых потребителей и бросках напряжения в сети питания.
Удельное сопротивление — что это? Отвечаем на вопрос.
Когда говорят, что медь является более тяжелым металлом, чем алюминий, то сравнивают их плотности. Аналогичным образом, когда говорят, что медь является лучшим проводником, чем алюминий, сравнивают их удельное сопротивление (ρ), значение которых не зависит от размера или формы конкретного образца — только от самого материала.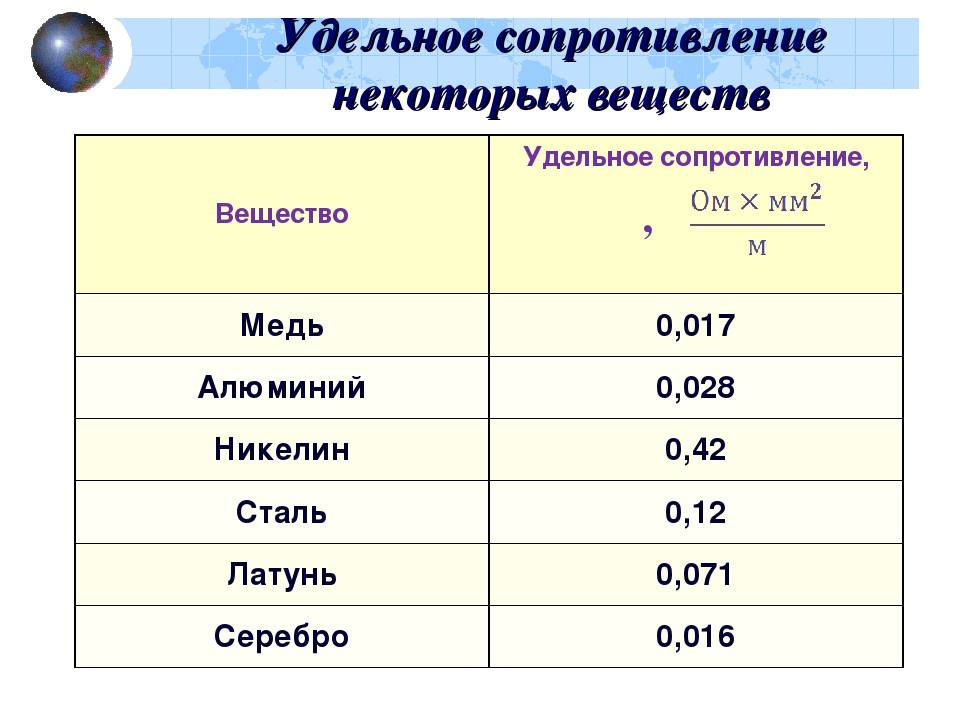
Теоретическое обоснование
Резистентность является мерой сопротивления электрической проводимости для заданного размера материала. Ее противоположность — электрическая проводимость. Металлы — хорошие электрические проводники (высокая проводимость и низкое значение ρ), в то время как неметаллы в основном являются плохими проводниками (низкая проводимость и высокое значение ρ).
Более знакомое термическое электрическое сопротивление измеряет, насколько трудно материалу проводить электричество. Это зависит от размера детали: сопротивление выше для более длинного или более узкого участка материала. Чтобы устранить эффект размера от сопротивления, используется удельное сопротивление провода — это материальное свойство, которое не зависит от размера. Для большинства материалов сопротивление увеличивается с температурой. Исключением являются полупроводники (например, кремний), в которых оно уменьшается с температурой.
Легкость, с которой материал проводит тепло, измеряется теплопроводностью. В качестве первой оценки хорошие электрические проводники также являются хорошими тепловыми проводниками. Сопротивление обозначается символом r, а его единица измерения — омметр. Сопротивление чистой меди составляет 1,7 × 10 -8 Ом. Это очень небольшое число — 0,000 000 017 Ом говорит о том, что кубический метр меди практически не оказывает сопротивление. Чем меньше удельное сопротивление (омметр или Ωm), тем лучше материал используется в электропроводке. Сопротивление — это обратная сторона проводимости.
В качестве первой оценки хорошие электрические проводники также являются хорошими тепловыми проводниками. Сопротивление обозначается символом r, а его единица измерения — омметр. Сопротивление чистой меди составляет 1,7 × 10 -8 Ом. Это очень небольшое число — 0,000 000 017 Ом говорит о том, что кубический метр меди практически не оказывает сопротивление. Чем меньше удельное сопротивление (омметр или Ωm), тем лучше материал используется в электропроводке. Сопротивление — это обратная сторона проводимости.
Классификация материалов
Величина сопротивления материала часто используется для классификации в качестве проводника, полупроводника или изолятора. Твердые элементы классифицируются как изоляторы, полупроводники или проводники по их «статическому сопротивлению» в периодической таблице элементов. Удельное сопротивление в изоляторе, полупроводнике или проводящем материале является основным свойством, которое учитывается для применения в электротехнике.
В таблице показаны некоторые данные ρ, σ и температурных коэффициентов. -3
-3
Серебро
1,59 × 10 -8
6,30 × 10 7
3,8
Медь
1,68 × 10 -8
5,96 × 10 7
3,9
Золото
2,44 × 10 -8
4,10 × 10 7
3,4
Алюминий
2,82 × 10 -8
3,5 × 10 7
3,9
Вольфрам
5,60 × 10 -8
1,79 × 10 7
4.5
Цинк
5,90 × 10 -8
1,69 × 10 7
3,7
Никель
6,99 × 10 -8
1,43 × 10 7
6
Литий
9,28 × 10 -8
1. 08 × 10 7
08 × 10 7
6
Железо
1,0 × 10 -7
1,00 × 10 7
5
Платиновый
1,06 × 10 -7
9,43 × 10 6
3,9
Свинец
2,2 × 10 -7
4,55 × 10 6
3,9
Константан
4,9 × 10 -7
2.04 × 10 6
0,008
Меркурий
9,8 × 10 -7
1,02 × 10 6
0.9
Нихром
1.10 × 10 -6
9,09 × 10 5
0,4
Углерод (аморфный)
5 × 10 -4 до 8 × 10 -4
1,25-2 × 10 3
-0,5
Расчет удельного сопротивления
Для любой заданной температуры мы можем вычислить электрическое сопротивление объекта в омах, используя следующую формулу.
В этой формуле:
- R — сопротивление объекта, в омах;
- ρ – сопротивление (удельное) материала, из которого изготовлен объект;
- L — длина объекта в метрах;
- A—площадь поперечного сечения объекта, в квадратных метрах.
Удельное сопротивление равно определенному количеству омметров. Несмотря на то, что единица ρ в системе СИ, как правило, омметр, иногда применяют размерность ом на сантиметр.
Сопротивление материала определяется по величине электрического поля по нему, что дает определенную плотность тока.
ρ = E/ J, где:
- ρ — в омметр;
- E — величина электрического поля в вольтах на метр;
- J — величина плотности тока в амперах на квадратный метр.
Как определить удельное сопротивление? Многие резисторы и проводники имеют равномерное поперечное сечение с равномерным потоком электрического тока. Поэтому существует более конкретное, но более широко используемое уравнение.
ρ = R*А/ J, где:
- R — сопротивление однородного образца материала, измеренного в омах;
- l — длина части материала, измеренная в метрах, м;
- A — площадь поперечного сечения образца, измеренная в квадратных метрах, м2.

Основы резистивности материалов
Электросопротивление материала также известно как удельное электрическое сопротивление. Это показатель того, насколько сильно материал противостоит потоку электрического тока. Определить его можно через деление сопротивления на единицу длины и на единицу площади поперечного сечения, для конкретного материала при заданной температуре.
Это означает, что низкое ρ указывает на материал, который легко позволяет перемещать электроны. И наоборот, материал с высоким ρ будет иметь высокое сопротивление и препятствовать потоку электронов. Элементы, такие как медь и алюминий, известны своим низким уровнем ρ. Серебро и, в частности, золото имеют очень низкое значение ρ, но по очевидным причинам их использование ограничено.
Область резистивности
Материалы помещаются в разные категории в зависимости от их показателя ρ. Краткое изложение приведено в таблице ниже.
Уровень проводимости полупроводников зависит от уровня легирования. -8
-8
Полупроводники
Переменная
Сверхпроводники
0
Температурный коэффициент сопротивления
В большинстве случаев сопротивление увеличивается с температурой. В результате возникает необходимость в понимании температурной зависимости сопротивления. Причина температурного коэффициента сопротивления в проводнике может быть обоснована интуитивно. Сопротивление материала имеет зависимость от ряда явлений. Одним из них является число столкновений, которые происходят между носителями заряда и атомами в материале. Удельное сопротивление проводника с ростом температуры будет расти, так как увеличивается число столкновений.
Это может быть не всегда, и вызвано тем, что с повышением температуры высвобождаются дополнительные носители заряда, что приведет к снижению удельного сопротивления материалов. Данный эффект часто наблюдается в полупроводниковых материалах.
При рассмотрении температурной зависимости сопротивления обычно считается, что температурный коэффициент сопротивления следует линейному закону.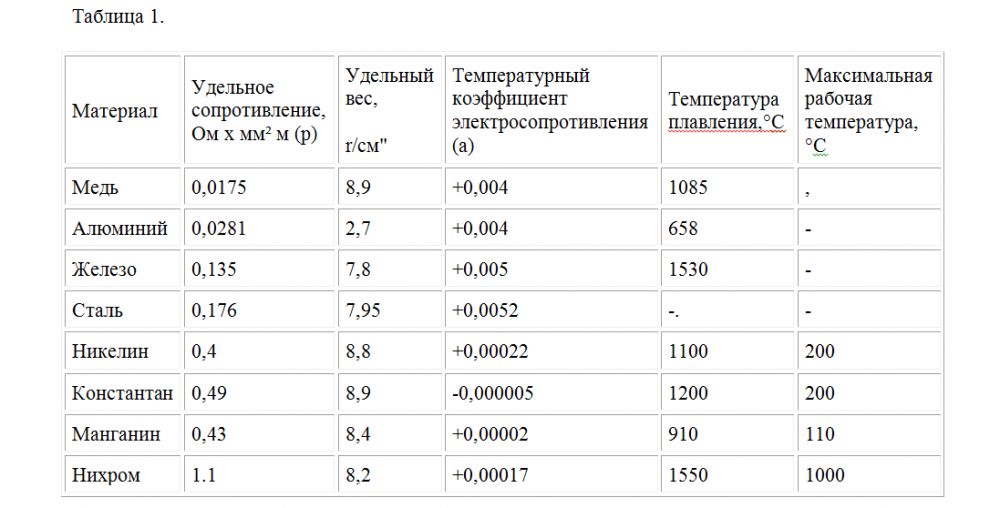 Это касается температуры в помещении и для металлов и многих других материалов. Однако было обнаружено, что эффекты сопротивления, возникающие в результате числа столкновений, не всегда постоянны, особенно при очень низких температурах (явление сверхпроводимости).
Это касается температуры в помещении и для металлов и многих других материалов. Однако было обнаружено, что эффекты сопротивления, возникающие в результате числа столкновений, не всегда постоянны, особенно при очень низких температурах (явление сверхпроводимости).
График температуры сопротивления
Сопротивление проводника при любой заданной температуре можно рассчитать по значению температуры и ее температурному коэффициенту сопротивления.
R= Rref*(1+ α (T- Tref)), где:
- R — сопротивление;
- Rref — сопротивление при эталонной температуре;
- α- температурный коэффициент сопротивления материала;
- Tref -эталонная температура, для которой указан температурный коэффициент.
Температурный коэффициент сопротивления, обычно стандартизованный относительно температуры 20 °C. Соответственно, уравнение, обычно используемое в практическом смысле:
R= R20*(1+ α20 (T- T20)), где:
- R20 = сопротивление при 20 °C;
- α20 — температурный коэффициент сопротивления при 20 °C;
- T20- температура равная 20 °C.

Сопротивление материалов при комнатной температуре
Таблица сопротивлений, приведенная ниже, содержит многие из веществ, широко используемых в электротехнике, включая медь, алюминий, золото и серебро. Эти свойства особенно важны потому, что определяют, может ли вещество использоваться при изготовлении широкого спектра электрических и электронных компонентов от проводов до более сложных устройств, таких как резисторы, потенциометры и многие другие.
| Таблица резистивности различных материалов при температуре наружного воздуха 20 ° C | |
| Материалы | Сопротивление ОМ при температуре 20 ° C |
| Алюминий | 2,8 x 10 -8 |
| Сурьма | 3,9 × 10 -7 |
| Висмут | 1,3 х 10 -6 |
| Латунь | ~ 0,6 — 0,9 × 10 -7 |
| Кадмий | 6 x 10 -8 |
| Кобальт | 5,6 × 10 -8 |
| Медь | 1,7 × 10 -8 |
| Золото | 2,4 х 10 -8 |
| Углерод (графит) | 1 x 10 -5 |
| Германий | 4. 6 x 10 -1 6 x 10 -1 |
| Железо | 1.0 x 10 -7 |
| Свинец | 1,9 × 10 -7 |
| Нихром | 1,1 × 10 -6 |
| Никель | 7 x 10 -8 |
| Палладий | 1.0 x 10 -7 |
| Платиновый | 0,98 × 10 -7 |
| Кварцевый | 7 x 10 17 |
| Кремний | 6,4 × 10 2 |
| Серебряный | 1,6 × 10 -8 |
| Тантал | 1,3 х 10 -7 |
| Вольфрам | 4,9 х 10 -8 |
| Цинк | 5,5 x 10 -8 |
Сравнение проводимости меди и алюминия
Проводники состоят из материалов, которые проводят электрический ток. Немагнитные металлы обычно считаются идеальными проводниками электричества. В проводной и кабельной промышленности используются различные металлические проводники, но наиболее распространенными являются медь и алюминий. Проводники имеют разные свойства, такие как проводимость, прочность на растяжение, вес и воздействие на окружающую среду.
Проводники имеют разные свойства, такие как проводимость, прочность на растяжение, вес и воздействие на окружающую среду.
Удельное сопротивление проводника из меди гораздо чаще используется в производстве кабелей, чем алюминия. Почти все электронные кабели изготовлены из меди, как и другие устройства и оборудование, которые используют высокую проводимость меди. Медные проводники также широко используются в системах распределения и производства электроэнергии, автомобилестроения. Для экономии веса и затрат электропередающие предприятия используют алюминий в воздушных линиях электропередач.
Алюминий используется в отраслях, где важна его легковесность, таких как самолетостроение, в будущем ожидается увеличение применения его в автомобилестроении. Для более мощных кабелей применяют алюминиевую проволоку с медным покрытием, чтобы использовать удельное сопротивление меди, получая значительную экономию веса конструкции от легковесного алюминия.
Медные проводники
Медь — один из древнейших известных материалов. Ее пластичность и электропроводность были использованы ранними экспериментаторами с электричеством, такими, как Бен Франклин и Майкл Фарадей. Низкое ρ материалов меди привело к тому, что она были принята в качестве основных проводников, используемым в изобретениях, таких как телеграф, телефон и электродвигатель. Медь является наиболее распространенным проводящим металлом. В 1913 году был принят международный стандарт по прокаливанию меди (МАКО) для сравнения проводимости других металлов с медью.
Ее пластичность и электропроводность были использованы ранними экспериментаторами с электричеством, такими, как Бен Франклин и Майкл Фарадей. Низкое ρ материалов меди привело к тому, что она были принята в качестве основных проводников, используемым в изобретениях, таких как телеграф, телефон и электродвигатель. Медь является наиболее распространенным проводящим металлом. В 1913 году был принят международный стандарт по прокаливанию меди (МАКО) для сравнения проводимости других металлов с медью.
Согласно этому стандарту, коммерчески чистая отожженная медь обладает проводимостью 100% IACS. Удельное сопротивление материалов сравнивают с эталоном. Коммерчески чистая медь, производимая сегодня, может иметь более высокие значения проводимости IACS, поскольку технология обработки со временем значительно шагнула вперед. В дополнение к превосходной проводимости меди, металл обладает высокой прочностью на растяжение, теплопроводностью и тепловым расширением. Отожженная медная проволока, используемая для электрических целей, соответствует всем требованиям стандарта.
Алюминиевые проводники
Несмотря на то, что медь имеет долгую историю в качестве материала для производства электроэнергии, алюминий обладает определенными преимуществами, которые делают его привлекательным для конкретного применения, а его удельное сопротивление тока позволяет расширить область его использования многократно. Алюминий имеет 61% проводимости меди и только 30% веса меди. Это означает, что провод из алюминия весит в два раза меньше, чем провод из меди, с таким же электрическим сопротивлением.
Алюминий, как правило, дешевле по сравнению с медной жилой. Алюминиевые проводники состоят из различных сплавов, имеют минимальное содержание алюминия 99,5%. В 1960-х и 1970-х годах из-за высокой цены на медь, этот класс алюминия стал широко использоваться для бытовой электропроводки.
Из-за низкого качества изготовления при соединениях и физических различий между алюминием и медью устройства и провода, изготовленные на базе их соединений, в местах контактов медь-алюминий стали пожароопасными.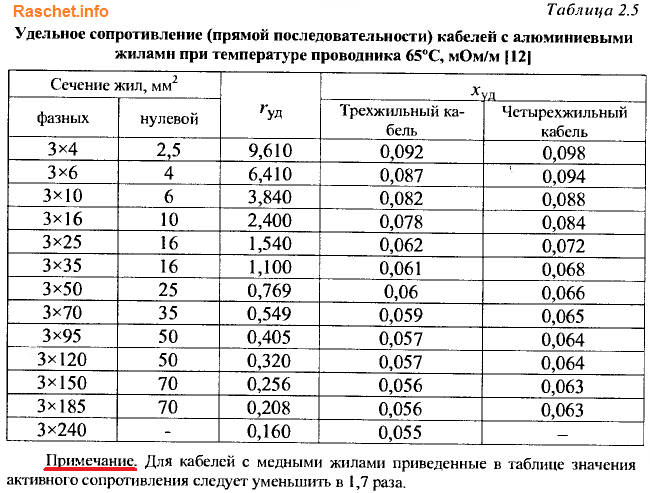 Для противодействия негативному процессу были разработаны алюминиевые сплавы, обладающие свойствами ползучести и удлинения, более похожими на медь. Эти сплавы применяются для изготовления многожильных алюминиевых проводов, удельное сопротивление тока которых приемлемо для массового использования, отвечающих требованиям безопасности для электрических сетей.
Для противодействия негативному процессу были разработаны алюминиевые сплавы, обладающие свойствами ползучести и удлинения, более похожими на медь. Эти сплавы применяются для изготовления многожильных алюминиевых проводов, удельное сопротивление тока которых приемлемо для массового использования, отвечающих требованиям безопасности для электрических сетей.
Если алюминий используется в местах, где ранее использовалась медь, чтобы сохранить равные показатели сети, приходится использовать алюминиевый провод в два раза превышающий размер медного провода.
Применение электропроводности материалов
Многие из материалов, найденных в таблице удельного сопротивления, широко используются в электронике. Алюминий и особенно медь используются из-за их низкого уровня сопротивления. Большинство проводов и кабелей, используемых в наши дни для соединений в электросетях, изготавливаются из меди, поскольку она обеспечивает низкий уровень ρ, и имеют доступную цену. Хорошая проводимость золота, несмотря на цену, также используется в некоторых особо точных приборах.
Часто покрытие золотом встречается на высококачественных низковольтных соединениях, где стоит задача обеспечить наименьшее контактное сопротивление. Серебро не так широко используется в промышленной электротехнике, так как оно быстро окисляется, и это приводит к большому контактному сопротивлению. В некоторых случаях оксид может выступать в качестве выпрямителя. Сопротивление тантала используют в конденсаторах, никель и палладий — в концевых соединениях для многих компонентов поверхностного монтажа. Кварц находит свое основное применение в качестве пьезоэлектрического резонансного элемента. Кристаллы кварца используются в качестве частотных элементах во многих генераторах, где его высокое значение позволяет создавать надежные частотные контуры.
Удельное сопротивление алюминия 0.028 что оно означает. Удельное сопротивление и другие свойства меди
На опыте установлено, что сопротивление R металлического проводника прямо пропорционально его длине L и обратно пропорционально площади его поперечного сечения А :
R = ρL/А (26.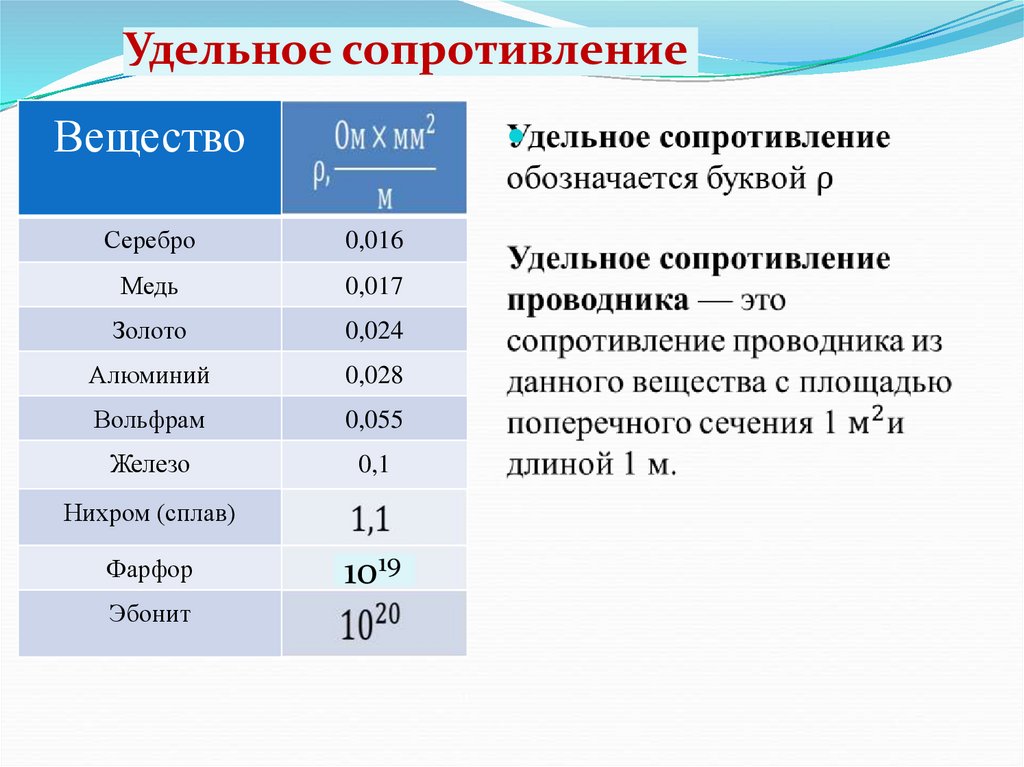 4)
4)
где коэффициент ρ называется удельным сопротивлением и служит характеристикой вещества, из которого изготовлен проводник. Это соответствует здравому смыслу: сопротивление толстого провода должно быть меньше, чем тонкого, поскольку в толстом проводе электроны могут перемещаться по большей площади. И можно ожидать роста сопротивления с увеличением длины проводника, так как увеличивается количество препятствий на пути потока электронов.
Типичные значения ρ для разных материалов приведены в первом столбце табл. 26.2. (Реальные значения зависят от чистоты вещества, термической обработки, температуры и других факторов.)
| Таблица 26.2. Удельное сопротивление и температурный коэффициент сопротивления (ТКС) (при 20 °С) | ||
| Вещество | ρ ,Ом·м | ТКС α ,°C -1 |
| Проводники | ||
| Серебро | 1,59·10 -8 | 0,0061 |
| Медь | 1,68·10 -8 | 0,0068 |
| Алюминий | 2,65·10 -8 | 0,00429 |
| Вольфрам | 5,6·10 -8 | 0,0045 |
| Железо | 9,71·10 -8 | 0,00651 |
| Платина | 10,6·10 -8 | 0,003927 |
| Ртуть | 98·10 -8 | 0,0009 |
| Нихром (сплав Ni, Fe, Сг) | 100·10 -8 | 0,0004 |
| Полупроводники 1) | ||
| Углерод (графит) | (3-60)·10 -5 | -0,0005 |
| Германий | (1-500)·10 -5 | -0,05 |
| Кремний | 0,1 — 60 | -0,07 |
| Диэлектрики | ||
| Стекло | 10 9 — 10 12 | |
| Резина твердая | 10 13 — 10 15 | |
1) Реальные значения сильно зависят от наличия даже малого количества примесей. | ||
Самым низким удельным сопротивлением обладает серебро, которое оказывается, таким образом, наилучшим проводником; однако оно дорого. Немногим уступает серебру медь; ясно, почему провода чаще всего изготовляют из меди.
Удельное сопротивление алюминия выше, чем у меди, однако он имеет гораздо меньшую плотность, и в некоторых случаях ему отдают предпочтение (например, в линиях электропередач), поскольку сопротивление проводов из алюминия той же массы оказывается меньше, чем у медных. Часто пользуются величиной, обратной удельному сопротивлению:
σ = 1/ρ (26.5)
σ называемой удельной проводимостью. Удельная проводимость измеряется в единицах (Ом·м) -1 .
Удельное сопротивление вещества зависит от температуры. Как правило, сопротивление металлов возрастает с температурой. Этому не следует удивляться: с повышением температуры атомы движутся быстрее, их расположение становится менее упорядоченным, и можно ожидать, что они будут сильнее мешать движению потока электронов.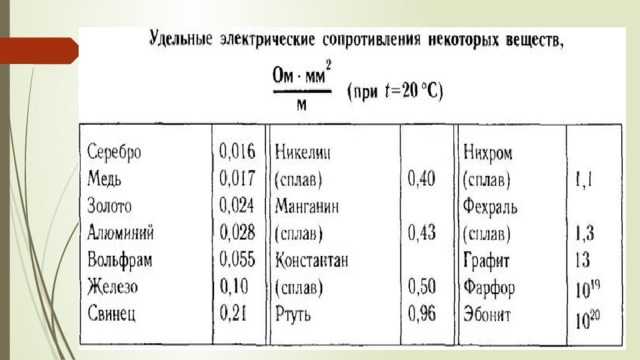 В узких диапазонах изменения температуры удельное сопротивление металла увеличивается с температурой практически линейно:
В узких диапазонах изменения температуры удельное сопротивление металла увеличивается с температурой практически линейно:
где ρ T — удельное сопротивление при температуре Т , ρ 0 — удельное сопротивление при стандартной температуре Т 0 , а α — температурный коэффициент сопротивления (ТКС). Значения а приведены в табл. 26.2. Заметим, что у полупроводников ТКС может быть отрицательным. Это очевидно, поскольку с ростом температуры увеличивается число свободных электронов и они улучшают проводящие свойства вещества. Таким образом, сопротивление полупроводника с повышением температуры может уменьшаться (хотя и не всегда).
Значения а зависят от температуры, поэтому следует обращать внимание на диапазон температур, в пределах которого справедливо данное значение (например, по справочнику физических величин). Если диапазон изменения температуры окажется широким, то линейность будет нарушаться, и вместо (26.6) надо использовать выражение, содержащее члены, которые зависят от второй и третьей степеней температуры:
ρ T = ρ 0 (1+αТ + + βТ 2 + γТ 3),
где коэффициенты β и γ обычно очень малы (мы положили Т 0 = 0°С), но при больших Т вклад этих членов становится существенным.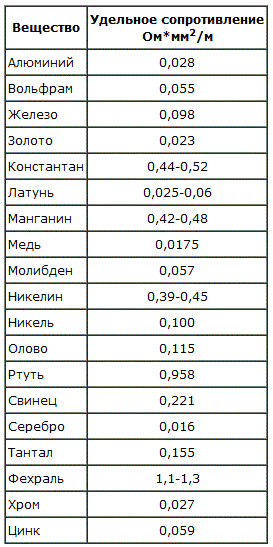
При очень низких температурах удельное сопротивление некоторых металлов, а также сплавов и соединений падает в пределах точности современных измерений до нуля. Это свойство называют сверхпроводимостью; впервые его наблюдал нидерландский физик Гейке Камер-линг-Оннес (1853-1926) в 1911 г. при охлаждении ртути ниже 4,2 К. При этой температуре электрическое сопротивление ртути внезапно падало до нуля.
Сверхпроводники переходят в сверхпроводящее состояние ниже температуры перехода, составляющей обычно несколько градусов Кельвина (чуть выше абсолютного нуля). Наблюдался электрический ток в сверхпроводящем кольце, который практически не ослабевал в отсутствие напряжения в течение нескольких лет.
В последние годы сверхпроводимость интенсивно исследуется с целью выяснить ее механизм и найти материалы, обладающие сверхпроводимостью при более высоких температурах, чтобы уменьшить стоимость и неудобства, обусловленные необходимостью охлаждения до очень низких температур. Первую успешную теорию сверхпроводимости создали Бардин, Купер и Шриффер в 1957 г.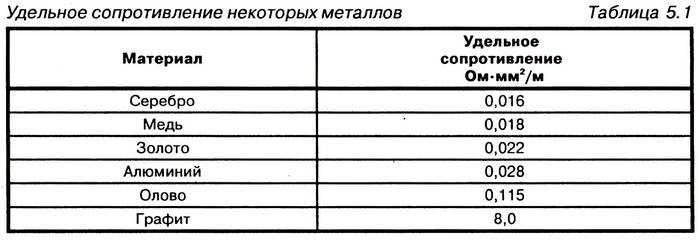 Сверхпроводники уже используются в больших магнитах, где магнитное поле создается электрическим током (см. гл. 28), что значительно снижает расход электроэнергии. Разумеется, для поддержания сверхпроводника при низкой температуре тоже затрачивается энергия.
Сверхпроводники уже используются в больших магнитах, где магнитное поле создается электрическим током (см. гл. 28), что значительно снижает расход электроэнергии. Разумеется, для поддержания сверхпроводника при низкой температуре тоже затрачивается энергия.
Замечания и предложения принимаются по адресу [email protected]
Одним из самых востребованных металлов в отраслях промышленности является медь. Наиболее широкое распространение она получила в электрике и электронике. Чаще всего ее применяют при изготовлении обмоток для электродвигателей и трансформаторов. Основная причина использования именно этого материала заключается в том, что медь обладает самым низким из существующих в настоящий момент материалов удельным электрическим сопротивлением. Пока не появится новый материал с более низкой величиной этого показателя, можно с уверенностью говорить о том, что замены у меди не будет.
Говоря про медь, необходимо сказать, что еще на заре электрической эры она стала использоваться в производстве электротехники. Применять ее стали во многом по причине уникальных свойств, которыми обладает этот сплав. Сам по себе он представляет материал, отличающийся высокими свойствами в плане пластичности и обладающий хорошей ковкостью.
Применять ее стали во многом по причине уникальных свойств, которыми обладает этот сплав. Сам по себе он представляет материал, отличающийся высокими свойствами в плане пластичности и обладающий хорошей ковкостью.
Наряду с теплопроводностью меди, одним из самых главных ее достоинств является высокая электропроводность. Именно благодаря этому свойству медь и получила широкое распространение в энергетических установках , в которых она выступает в качестве универсального проводника. Наиболее ценным материалом является электролитическая медь, обладающая высокой степенью чистоты -99,95%. Благодаря этому материалу появляется возможность для производства кабелей.
Плюсы использования электролитической меди
Применение электролитической меди позволяет добиться следующего:
- Обеспечить высокую электропроводность;
- Добиться отличной способности к уложению;
- Обеспечить высокую степень пластичности.
Сферы применения
Кабельная продукция, изготавливаемая из электролитической меди, получила широкое распространение в различных отраслях. Чаще всего она применяется в следующих сферах:
Чаще всего она применяется в следующих сферах:
- электроиндустрия;
- электроприборы;
- автомобилестроение;
- производство компьютерной техники.
Чему равно удельное сопротивление?
Чтобы понимать, что собой представляет медь и его характеристики, необходимо разобраться с основным параметром этого металла — удельным сопротивлением. Его следует знать и использовать при выполнении расчетов.
Под удельным сопротивлением принято понимать физическую величину, которая характеризуется как способность металла проводить электрический ток.
Знать эту величину необходимо еще и для того, чтобы правильно произвести расчет электрического сопротивления проводника. При расчетах также ориентируются на его геометрические размеры. При проведении расчетов используют следующую формулу:
Это формула многим хорошо знакома. Пользуясь ею, можно легко рассчитать сопротивление медного кабеля, ориентируясь только на характеристики электрической сети. Она позволяет вычислить мощность, которая неэффективно расходуется на нагрев сердечника кабеля. Кроме этого, подобная формула позволяет выполнить расчеты сопротивления любого кабеля. При этом не имеет значения, какой материал использовался для изготовления кабеля — медь, алюминий или какой-то другой сплав.
Она позволяет вычислить мощность, которая неэффективно расходуется на нагрев сердечника кабеля. Кроме этого, подобная формула позволяет выполнить расчеты сопротивления любого кабеля. При этом не имеет значения, какой материал использовался для изготовления кабеля — медь, алюминий или какой-то другой сплав.
Такой параметр, как удельное электрическое сопротивление измеряется в Ом*мм2/м. Этот показатель для медной проводки, проложенной в квартире, составляет 0,0175 Ом*мм2/м. Если попробовать поискать альтернативу меди — материал, который можно было бы использовать вместо нее, то единственным подходящим можно считать только серебро , у которого удельное сопротивление составляет 0,016 Ом*мм2/м. Однако необходимо обращать внимание при выборе материала не только на удельное сопротивление, но еще и на обратную проводимость. Эта величина измеряется в Сименсах (См).
Сименс = 1/ Ом.
У меди любого веса этот параметр состав равен 58 100 000 См/м. Что касается серебра, то величина обратной проводимости у нее равна 62 500 000 См/м.
В нашем мире высоких технологий, когда в каждом доме имеется большое количество электротехнических устройств и установок, значение такого материала, как медь просто неоценимо. Этот материал используют для изготовления проводки , без которой не обходится ни одно помещение. Если бы меди не существовало, тогда человеку пришлось использовать провода из других доступных материалов, например, из алюминия. Однако в этом случае пришлось бы столкнуться с одной проблемой. Все дело в том, что у этого материала удельная проводимость гораздо меньше, чем у медных проводников.
Удельное сопротивление
Использование материалов с низкой электро- и теплопроводностью любого веса ведет к большим потерям электроэнергии. А это влияет на потерю мощности у используемого оборудования. Большинство специалистов в качестве основного материала для изготовления проводов с изоляцией называют медь. Она является главным материалом, из которого изготавливаются отдельные элементы оборудования, работающего от электрического тока.
- Платы, устанавливаемые в компьютерах, оснащаются протравленными медными дорожками.
- Медь также используется для изготовления самых разных элементов, применяемых в электронных устройствах.
- В трансформаторах и электродвигателях она представлена обмоткой, которая изготавливается из этого материала.
Можно не сомневаться, что расширение сфер применения этого материала будет происходить с дальнейшим развитием технического прогресса. Хотя, кроме меди, существуют и другие материалы, но все же конструктора при создании оборудования и различных установок используют медь. Главная причина востребованности этого материала заключается в хорошей электрической и теплопроводности этого металла, которую он обеспечивает в условиях комнатной температуры.
Температурный коэффициент сопротивления
Свойством уменьшения проводимости с повышением температуры обладают все металлы с любой теплопроводностью. При понижении температуры проводимость возрастает. Особенно интересным специалисты называют свойство уменьшения сопротивления с понижением температуры. Ведь в этом случае, когда в комнате температура снижается до определенной величины, у проводника может исчезнуть электрическое сопротивление и он перейдет в класс сверхпроводников.
Особенно интересным специалисты называют свойство уменьшения сопротивления с понижением температуры. Ведь в этом случае, когда в комнате температура снижается до определенной величины, у проводника может исчезнуть электрическое сопротивление и он перейдет в класс сверхпроводников.
Для того чтобы определить показатель сопротивления конкретного проводника определенного веса в условиях комнатной температуры, существует коэффициент критического сопротивления. Он представляет собой величину, которая показывает изменение сопротивления участка цепи при изменении температуры на один Кельвин. Для выполнения расчета электрического сопротивления медного проводника в определенном временном промежутке используют следующую формулу:
ΔR = α*R*ΔT, где α — температурный коэффициент электрического сопротивления.
Заключение
Медь — материал, который широко применяют в электронике. Его используют не только в обмотке и схемах, но и в качестве металла для изготовления кабельной продукции. Чтобы техника и оборудование работали эффективно, необходимо правильно рассчитать удельное сопротивление проводки , прокладываемой в квартире. Для этого существует определенная формула. Зная её, можно произвести расчет, который позволяет узнать оптимальную величину сечения кабеля. В этом случае можно избежать потери мощности оборудования и обеспечить эффективность его использования.
Чтобы техника и оборудование работали эффективно, необходимо правильно рассчитать удельное сопротивление проводки , прокладываемой в квартире. Для этого существует определенная формула. Зная её, можно произвести расчет, который позволяет узнать оптимальную величину сечения кабеля. В этом случае можно избежать потери мощности оборудования и обеспечить эффективность его использования.
Часто в электротехнической литературе встречается понятие «удельное меди». И невольно задаешься вопросом, а что же это такое?
Понятие «сопротивление» для любого проводника непрерывно связано с пониманием процесса протекания по нему электрического тока. Так как речь в статье пойдет о сопротивлении меди, то и рассматривать нам следует ее свойства и свойства металлов.
Когда речь идет о металлах, то невольно вспоминаешь, что все они имеют определенное строение — кристаллическую решетку. Атомы находятся в узлах такой решетки и совершают относительно них Расстояния и местоположение этих узлов зависит от сил взаимодействия атомов друг с другом (отталкивания и притяжения), и различны для разных металлов.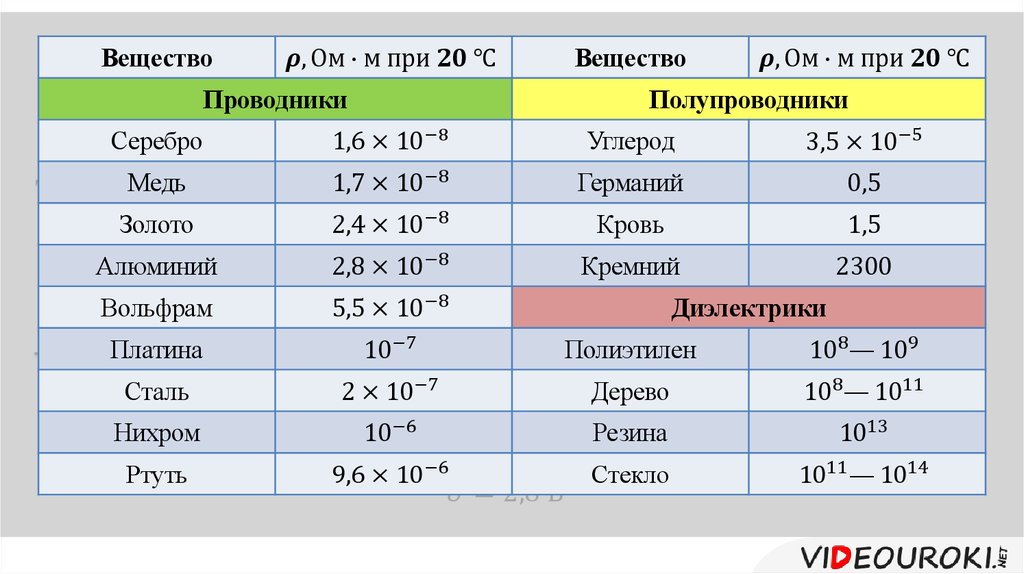 А вокруг атомов по своим орбитам вращаются электроны. Их удерживает на орбите тоже равновесие сил. Только это к атому и центробежная. Представили себе картинку? Можно назвать ее, в некотором плане, статической.
А вокруг атомов по своим орбитам вращаются электроны. Их удерживает на орбите тоже равновесие сил. Только это к атому и центробежная. Представили себе картинку? Можно назвать ее, в некотором плане, статической.
А теперь добавим динамики. На кусок меди начинает действовать электрическое поле. Что же происходит внутри проводника? Электроны, сорванные силой электрического поля со своих орбит, устремляются к его положительному полюсу. Вот Вам и направленное движение электронов, а вернее, электрический ток. Но на пути своего движения они натыкаются на атомы в узлах кристаллической решетки и электроны, еще продолжающие вращаться вокруг своих атомов. При этом они теряют свою энергию и изменяют направление движения. Теперь становится немного понятнее смысл фразы «сопротивление проводника»? Это атомы решетки и вращающиеся вокруг них электроны оказывают сопротивление направленному движению электронов, сорванных электрическим полем со своих орбит. Но понятие сопротивление проводника можно назвать общей характеристикой. Более индивидуально характеризует каждый проводник удельное сопротивление. Меди в том числе. Эта характеристика индивидуальна для каждого металла, поскольку напрямую зависит только от формы и размеров кристаллической решетки и, в некоторой мере, от температуры. При повышении температуры проводника атомы совершают более интенсивное колебание в узлах решетки. А электроны вращаются вокруг узлов с большей скоростью и на орбитах большего радиуса. И, естественно, что свободные электроны при движении встречают и большее сопротивление. Такова физика процесса.
Более индивидуально характеризует каждый проводник удельное сопротивление. Меди в том числе. Эта характеристика индивидуальна для каждого металла, поскольку напрямую зависит только от формы и размеров кристаллической решетки и, в некоторой мере, от температуры. При повышении температуры проводника атомы совершают более интенсивное колебание в узлах решетки. А электроны вращаются вокруг узлов с большей скоростью и на орбитах большего радиуса. И, естественно, что свободные электроны при движении встречают и большее сопротивление. Такова физика процесса.
Для нужд электротехнической сферы налажено широкое производство таких металлов, как алюминий и медь, удельное сопротивление которых достаточно мало. Из этих металлов изготавливают кабели и различного типа провода, которые широко используются в строительстве, для производства бытовых приборов, изготовления шин, обмоток трансформаторов и других электротехнических изделий.
Для каждого проводника существует понятие удельного сопротивления. Эта величина состоит из Омов, умножаемых на квадратный миллиметр, далее, делимое на один метр. Иными словами, это сопротивление проводника, длина которого составляет 1 метр, а сечение — 1 мм2. То же самое представляет собой и удельное сопротивление меди — уникального металла, получившего широкое распространение в электротехнике и энергетике.
Эта величина состоит из Омов, умножаемых на квадратный миллиметр, далее, делимое на один метр. Иными словами, это сопротивление проводника, длина которого составляет 1 метр, а сечение — 1 мм2. То же самое представляет собой и удельное сопротивление меди — уникального металла, получившего широкое распространение в электротехнике и энергетике.
Свойства меди
Благодаря своим свойствам этот металл одним из первых начал применяться в области электричества. Прежде всего, медь является ковким и пластичным материалом с отличными свойствами электропроводимости. До сих пор в энергетике нет равноценной замены этому проводнику.
Особенно ценятся свойства специальной электролитической меди, обладающей высокой чистотой. Этот материал позволил выпускать провода с минимальной толщиной в 10 микрон.
Кроме высокой электропроводности, медь очень хорошо поддается лужению и другим видам обработки.
Медь и ее удельное сопротивление
Любой проводник оказывает сопротивление, если через него пропустить электрический ток. Значение зависит от длины проводника и его сечения, а также от действия определенных температур. Поэтому, удельное сопротивление проводников зависит не только от самого материала, но и от его определенной длины и площади поперечного сечения. Чем легче материал пропускает через себя заряд, тем ниже его сопротивление. Для меди, показатель удельного сопротивления составляет 0,0171 Ом х 1 мм2/1 м и лишь немного уступает серебру. Однако, использование серебра в промышленных масштабах экономически невыгодно, поэтому, медь является лучшим проводником, используемым в энергетике.
Значение зависит от длины проводника и его сечения, а также от действия определенных температур. Поэтому, удельное сопротивление проводников зависит не только от самого материала, но и от его определенной длины и площади поперечного сечения. Чем легче материал пропускает через себя заряд, тем ниже его сопротивление. Для меди, показатель удельного сопротивления составляет 0,0171 Ом х 1 мм2/1 м и лишь немного уступает серебру. Однако, использование серебра в промышленных масштабах экономически невыгодно, поэтому, медь является лучшим проводником, используемым в энергетике.
Удельное сопротивление меди связано и с ее высокой проводимостью. Эти величины прямо противоположны между собой. Свойства меди, как проводника, зависят и от температурного коэффициента сопротивления. Особенно, это касается сопротивление, на которое оказывает влияние температура проводника.
Таким образом, благодаря своим свойствам, медь получила широкое распространение не только в качестве проводника .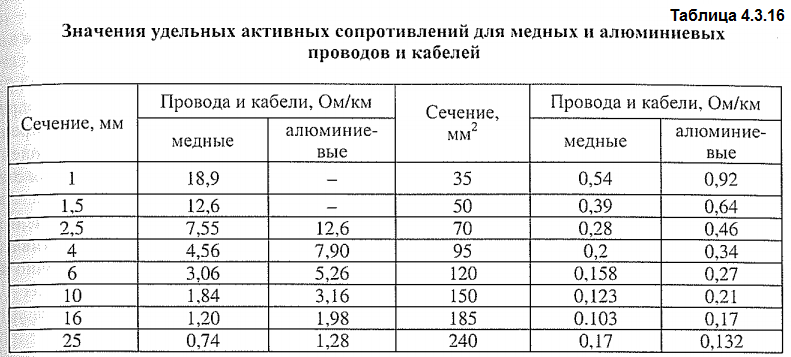 Этот металл используется в большинстве приборов, устройств и агрегатов, функционирование которых связано с электрическим током.
Этот металл используется в большинстве приборов, устройств и агрегатов, функционирование которых связано с электрическим током.
Тепло- и электропроводность алюминия. [коэффициент Зеебека; от 80 до 400/sup 0/K] (Технический отчет)
Тепло- и электропроводность алюминия. [коэффициент Зеебека; от 80 до 400/суп 0/K] (Технический отчет) | ОСТИ.GOVперейти к основному содержанию
- Полная запись
- Другое связанное исследование
- Авторов:
- Кук, Дж.
 Г.; Мур, JP; Мацумура, Т .; Ван дер Меер, член парламента
Г.; Мур, JP; Мацумура, Т .; Ван дер Меер, член парламента
- Дата публикации:
- Исследовательская организация:
- Национальная лаборатория Ок-Ридж, Теннесси (США)
- Идентификатор ОСТИ:
- 5066461
- Номер(а) отчета:
- ОРНЛ-5079
- Номер контракта с Министерством энергетики:
- W-7405-ENG-26
- Тип ресурса:
- Технический отчет
- Страна публикации:
- США
- Язык:
- Английский
- Тема:
- 36 МАТЕРИАЛОВЕДЕНИЕ; АЛЮМИНИЙ; ТЕРМОЭЛЕКТРИЧЕСКИЕ СВОЙСТВА; АЛЮМИНИЕВЫЕ ОСНОВНЫЕ СПЛАВЫ; ЭЛЕКТРИЧЕСКАЯ ПРОВОДИМОСТЬ; ЭФФЕКТ Зеебека; ТЕМПЕРАТУРНАЯ ЗАВИСИМОСТЬ; ТЕПЛОПРОВОДНОСТЬ; СПЛАВЫ; АЛЮМИНИЕВЫЕ СПЛАВЫ; ЭЛЕКТРИЧЕСКИЕ СВОЙСТВА; ЭЛЕМЕНТЫ; МЕТАЛЛЫ; ФИЗИЧЕСКИЕ СВОЙСТВА; ТЕРМОДИНАМИЧЕСКИЕ СВОЙСТВА; 360104* – Металлы и сплавы – Физические свойства
Форматы цитирования
- MLA
- АПА
- Чикаго
- БибТекс
Кук, Дж.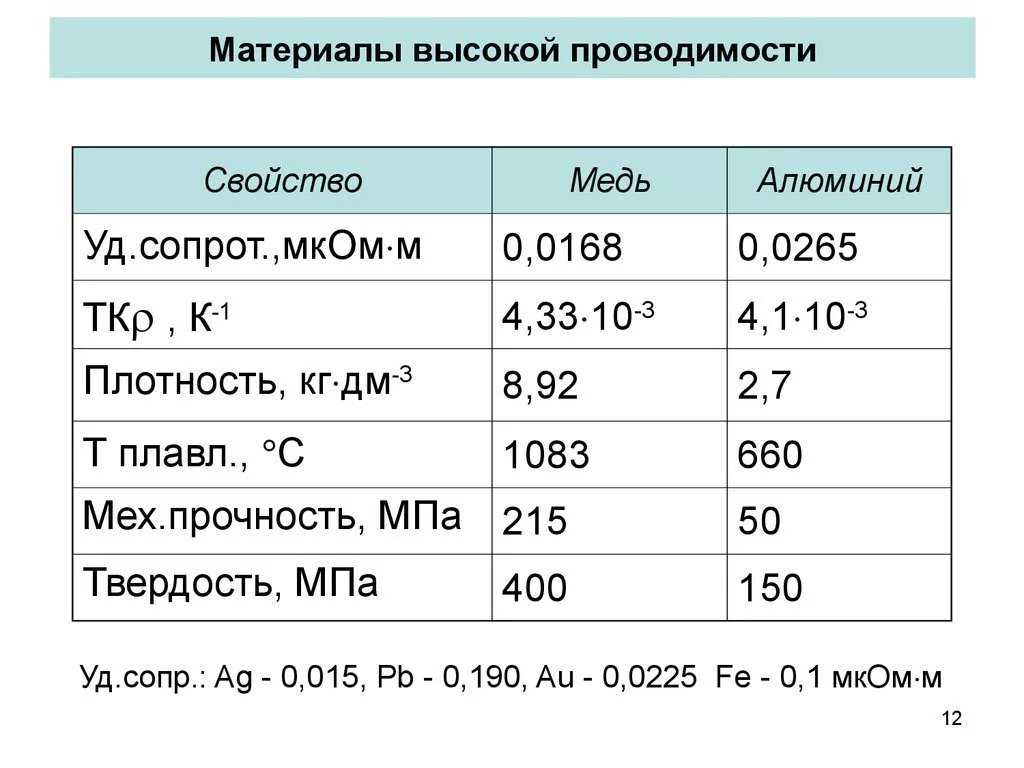 Г., Мур, Дж. П., Мацумура, Т., и Ван дер Меер, член парламента . Тепловая и электрическая проводимость алюминия. [коэффициент Зеебека; от 80 до 400/суп 0/K] . США: Н. П., 1975.
Веб. дои: 10.2172/5066461.
Г., Мур, Дж. П., Мацумура, Т., и Ван дер Меер, член парламента . Тепловая и электрическая проводимость алюминия. [коэффициент Зеебека; от 80 до 400/суп 0/K] . США: Н. П., 1975.
Веб. дои: 10.2172/5066461.
Копировать в буфер обмена
Кук, Дж. Г., Мур, Дж. П., Мацумура, Т., и Ван дер Меер, член парламента Тепло- и электропроводность алюминия. [коэффициент Зеебека; от 80 до 400/суп 0/K] . Соединенные Штаты. https://doi.org/10.2172/5066461
Копировать в буфер обмена
Кук, Дж. Г., Мур, Дж. П., Мацумура, Т., и Ван дер Меер, член парламента, 1975.
«Тепло- и электропроводность алюминия. [Коэффициент Зеебека; от 80 до 400 / суп 0 / K]». Соединенные Штаты. https://doi.org/10.2172/5066461. https://www.osti.gov/servlets/purl/5066461.
Копировать в буфер обмена
@статья{osti_5066461,
title = {Тепло- и электропроводность алюминия. [коэффициент Зеебека; от 80 до 400/суп 0/K]}, 90 109
автор = {Кук, Дж. Г. и Мур, Дж. П., Мацумура, Т. и Ван дер Меер, М. П.},
[коэффициент Зеебека; от 80 до 400/суп 0/K]}, 90 109
автор = {Кук, Дж. Г. и Мур, Дж. П., Мацумура, Т. и Ван дер Меер, М. П.},
abstractNote = {},
дои = {10.2172/5066461},
URL-адрес = {https://www.osti.gov/biblio/5066461},
журнал = {},
номер = ,
объем = ,
место = {США},
год = {1975},
месяц = {9}
}
Копировать в буфер обмена
Посмотреть технический отчет (0,88 МБ)
https://doi.org/10.2172/5066461
Экспорт метаданных
Сохранить в моей библиотеке
Вы должны войти в систему или создать учетную запись, чтобы сохранять документы в своей библиотеке.
Аналогичных записей в сборниках OSTI.GOV:
- Аналогичные записи
Сопротивление и реактивное сопротивление на км медных и алюминиевых кабелей ~ Изучение электротехники
Сопротивление и реактивное сопротивление на км медных и алюминиевых кабелей
Для расчета падения напряжения в кабеле в таблице ниже приведены значения реактивного сопротивления и сопротивления для медных и алюминиевых кабелей:
Значения для медных кабелей
| Размер кабеля, S (мм2) | Одножильный кабель | Двухжильные/трехжильные кабели | ||
| R(Ом/км) при 80°C | X (Ом/км) при 80°C | R(Ом/км) при 80°C | X(Ом/км) при 80°C | |
| 1,5 | 14,8 | 0,168 | 15,1 | 0,118 |
| 2,5 | 8,91 | 0,156 | 9,08 | 0,109 |
| 4 | 5,57 | 0,143 | 5,68 | 0,101 |
| 6 | 3,71 | 0,135 | 3,78 | 0,0955 |
| 10 | 2,24 | 0,119 | 2,27 | 0,0861 |
| 16 | 1,41 | 0,112 | 1,43 | 0,0817 |
| 25 | 0,889 | 0,106 | 0,907 | 0,0813 |
| 35 | 0,641 | 0,101 | 0,654 | 0,0783 |
| 50 | 0,473 | 0,101 | 0,483 | 0,0779 |
| 70 | 0,328 | 0,0965 | 0,334 | 0,0751 |
| 95 | 0,326 | 0,0975 | 0,241 | 0,0762 |
| 120 | 0,188 | 0,0939 | 0,191 | 0,074 |
| 150 | 0,153 | 0,0928 | 0,157 | 0,0745 |
| 185 | 0,123 | 0,0908 | 0,125 | 0,0742 |
| 240 | 0,0943 | 0,0902 | 0,0966 | 0,0752 |
| 300 | 0,0761 | 0,0895 | 0,078 | 0,075 |
Значения для
Алюминиевые кабели
| Размер кабеля, S (мм2) | Одножильный кабель | Двухжильные/трехжильные кабели | ||
| R(Ом/км) при 80°C | X (Ом/км) при 80°C | R(Ом/км) при 80°C | X(Ом/км) при 80°C | |
| 1,5 | 24. 384 384 | 0,168 | 24.878 | 0,118 |
| 2,5 | 14.680 | 0,156 | 14.960 | 0,109 |
| 4 | 9.177 | 0,143 | 9.358 | 0,101 |
| 6 | 6.112 | 0,135 | 6.228 | 0,0955 |
| 10 | 3,691 | 0,119 | 3.740 | 0,0861 |
| 16 | 2,323 | 0,112 | 2,356 | 0,0817 |
| 25 | 1,465 | 0,106 | 1,494 | 0,0813 |
| 35 | 1,056 | 0,101 | 1,077 | 0,0783 |
| 50 | 0,779 | 0,101 | 0,796 | 0,0779 |
| 70 | 0,540 | 0,0965 | 0,550 | 0,0751 |
| 95 | 0,389 | 0,0975 | 0,397 | 0,0762 |
| 120 | 0,310 | 0,0939 | 0,315 | 0,074 |
| 150 | 0,252 | 0,0928 | 0,259 | 0,0745 |
| 185 | 0,203 | 0,0908 | 0,206 | 0,0742 |
| 240 | 0,155 | 0,0902 | 0,159 | 0,0752 |
| 300 | 0,125 | 0,0895 | 0,129 | 0,075 |
Новое сообщение Старый пост Главная
Таблица электропроводности для алюминия — arXiv Vanity
CE Старретт
Лос-Аламосская национальная лаборатория, P. O. Box 1663, Лос-Аламос, NM 87545, США Р. Перрио
Лос-Аламосская национальная лаборатория, P.O. Box 1663, Лос-Аламос, NM 87545, США Н. Р. Шаффер
Лос-Аламосская национальная лаборатория, P.O. Box 1663, Лос-Аламос, NM 87545, США Т. Нельсон
Лос-Аламосская национальная лаборатория, P.O. Box 1663, Лос-Аламос, NM 87545, США Л. А. Коллинз
Лос-Аламосская национальная лаборатория, P.O. Box 1663, Лос-Аламос, NM 87545, США К. Тикнор
Лос-Аламосская национальная лаборатория, P.O. Box 1663, Лос-Аламос, NM 87545, США
O. Box 1663, Лос-Аламос, NM 87545, США Р. Перрио
Лос-Аламосская национальная лаборатория, P.O. Box 1663, Лос-Аламос, NM 87545, США Н. Р. Шаффер
Лос-Аламосская национальная лаборатория, P.O. Box 1663, Лос-Аламос, NM 87545, США Т. Нельсон
Лос-Аламосская национальная лаборатория, P.O. Box 1663, Лос-Аламос, NM 87545, США Л. А. Коллинз
Лос-Аламосская национальная лаборатория, P.O. Box 1663, Лос-Аламос, NM 87545, США К. Тикнор
Лос-Аламосская национальная лаборатория, P.O. Box 1663, Лос-Аламос, NM 87545, США
18 июня 2022 г.
Abstract
Описана новая таблица типа Сезам для электропроводности алюминия. Таблица
основан на расчетах теории функционала плотности и колеблется от 10−3 до 1 раз
плотность твердого тела (2,7 г/см3) и от 10–2 до 103 эВ по температуре. Таблица сравнивается
другим моделированиям и экспериментам и в целом находится в хорошем согласии. Высокая температура,
классический предел проводимости восстанавливается для самых высоких температур и самых низких плотностей. Таблица подвергается критическому анализу и обсуждаются направления улучшений.
Таблица подвергается критическому анализу и обсуждаются направления улучшений.
электропроводность
упак.:
я введение
Электропроводность в плотных материалах является важным физическим параметром для различных приложений. Например, это необходимо для моделирования экспериментов по синтезу магнитных лайнеров gomez14 и импульсная мощность эксперименты stygar15 , или динамо-эффект в ядрах планет stacey01 .
В режиме низкой плотности и высокой температуры классические методы с использованием кулоновских логарифмов точны коэн50 ; lee84 ; braginsky58 и быстро оценить. Однако в плотном режиме эти подходы разрушаются из-за таких эффектов, как корреляция ионов, частичная ионизация, ортогональность ядра и валентности, вырождение, и эффекты многократного рассеяния starrett18a .
Альтернативный подход заключается в использовании точных моделей, которые слишком дороги и сложны для непосредственного использования в
приложения, чтобы сделать таблицы данных. Например, Rinker rinker88 сделал Sesame lyon92 таблицы данных на основе
подход среднего атома в сочетании с приближением Займана ziman60 . Этот метод разумен
в вырожденном режиме (высокая плотность, низкая температура), но неточна в других местах. Desjarlais desjarlais01 также сделал столы Sesame, адаптировав модель Lee-More lee84 на основе Coulomb Log, чтобы лучше соответствовать
доступные экспериментальные данные среди других улучшений. Другой подход заключается в использовании химической модели kuhlbrodt05 9.0641 , который может быть
быстр для оценки, но не включает некоторые важные физические аспекты, такие как ионная структура (обзор см. в ссылке redmer97 ).
Например, Rinker rinker88 сделал Sesame lyon92 таблицы данных на основе
подход среднего атома в сочетании с приближением Займана ziman60 . Этот метод разумен
в вырожденном режиме (высокая плотность, низкая температура), но неточна в других местах. Desjarlais desjarlais01 также сделал столы Sesame, адаптировав модель Lee-More lee84 на основе Coulomb Log, чтобы лучше соответствовать
доступные экспериментальные данные среди других улучшений. Другой подход заключается в использовании химической модели kuhlbrodt05 9.0641 , который может быть
быстр для оценки, но не включает некоторые важные физические аспекты, такие как ионная структура (обзор см. в ссылке redmer97 ).
Мы используем подход, основанный на высокоточной теории функционала плотности (DFT) для моделирования
вся интересующая плоскость плотность-температура, где материал является жидкостью. Мы ориентируемся на алюминий,
поскольку это широко используемый проводник, но этот подход можно применить и к другим материалам. Мы используем два метода:
точная, но дорогая теория функционала плотности молекулярная динамика (DFT-MD) в сочетании с приближением Кубо-Гринвуда desjarlais02 , который
практичен для вырожденных систем, и
более приблизительный потенциал средней силы приближается к starrett17 , что является точным для умеренных
к слабо вырожденной плазме и является относительно недорогим.
Мы используем два метода:
точная, но дорогая теория функционала плотности молекулярная динамика (DFT-MD) в сочетании с приближением Кубо-Гринвуда desjarlais02 , который
практичен для вырожденных систем, и
более приблизительный потенциал средней силы приближается к starrett17 , что является точным для умеренных
к слабо вырожденной плазме и является относительно недорогим.
Также можно использовать метод Кубо-Гринвуда со средней моделью атома старретт12а ; жабра19 ; фоссурье14 ; овечкин16 ; стерн07 ; johnson , но мы решили не использовать этот подход, поскольку он остается чтобы доказать, что это обеспечивает правильное предельное поведение при высокой температуре и требует больших вычислительных затрат. Напротив, Подход с потенциалом средней силы, основанный на приближении времени релаксации, действительно восстанавливает классический лимит starrett18 и быстро оценить.
II Построение стола
Таблица колеблется от 10-3 до 1-кратной плотности твердого тела, принятой здесь за 2,7 г/см3, и от 10-2 до
103 эВ по температуре. Начнем с расчета электропроводности для всего диапазона таблицы
используя потенциал модели средней силы ссылки starrett17 . В этой модели используется BGK bhatnager54 приближение (также известное как приближение времени релаксации). Время релаксации электронов равно
рассчитано с использованием квантово-механического выражения для креста переноса импульса
раздел
Начнем с расчета электропроводности для всего диапазона таблицы
используя потенциал модели средней силы ссылки starrett17 . В этой модели используется BGK bhatnager54 приближение (также известное как приближение времени релаксации). Время релаксации электронов равно
рассчитано с использованием квантово-механического выражения для креста переноса импульса
раздел
| σtr(ϵ)=4πℏ2p2∞∑l=0(l+1)(sin(ηl+1−ηl))2 | (1) |
где p — импульс электрона, ηl — фазовые сдвиги, зависящие от энергии, а сумма
по угловому моменту квантовое число l сходится. Фазовые сдвиги оцениваются путем решения
Уравнение Шредингера для потенциала рассеяния. Этот потенциал, потенциал средней силы VMF(r),
вычисляется с использованием конечной температуры DFT на основе среднего атом-два компонента
плазменная модель (AA-TCP), разработанная в ссылках старретт13 ; старретт14 . Потенциал среднего
сила восстанавливает потенциал Дебая-Хюккеля при высокой температуре и низкой плотности. Он принимает во внимание
учитывают основные состояния, ортогональность ядра и валентности, ионную структуру (через парное распределение
функция) и частичная ионизация.
Он принимает во внимание
учитывают основные состояния, ортогональность ядра и валентности, ионную структуру (через парное распределение
функция) и частичная ионизация.
Такой подход к проводимости становится неточным в системах, где плотность состояний
рассеяние электронов сильно отличается от поведения свободных электронов. Например, в расширенном
металлический режим с температурами ∼ 1 эВ и плотностью ∼ 1/10 твердого тела (т.е. теплого
плотной материи), где электронные состояния изменяются по мере уменьшения плотности, эта модель будет
неточным (см. старретт17 ).
В целом, однако, эта модель является достаточно точной и недорогой в вычислительном отношении, что позволяет построить
из широких таблиц. Поскольку это модель, основанная на ДПФ, мы должны выбрать потенциал обмена и корреляции.
Мы использовали параметризацию LDA, зависящую от температуры, для ссылки ksdt .
Для электрон-электронного вклада в электропроводность использовалась формула
указан в ссылке reinholz15 .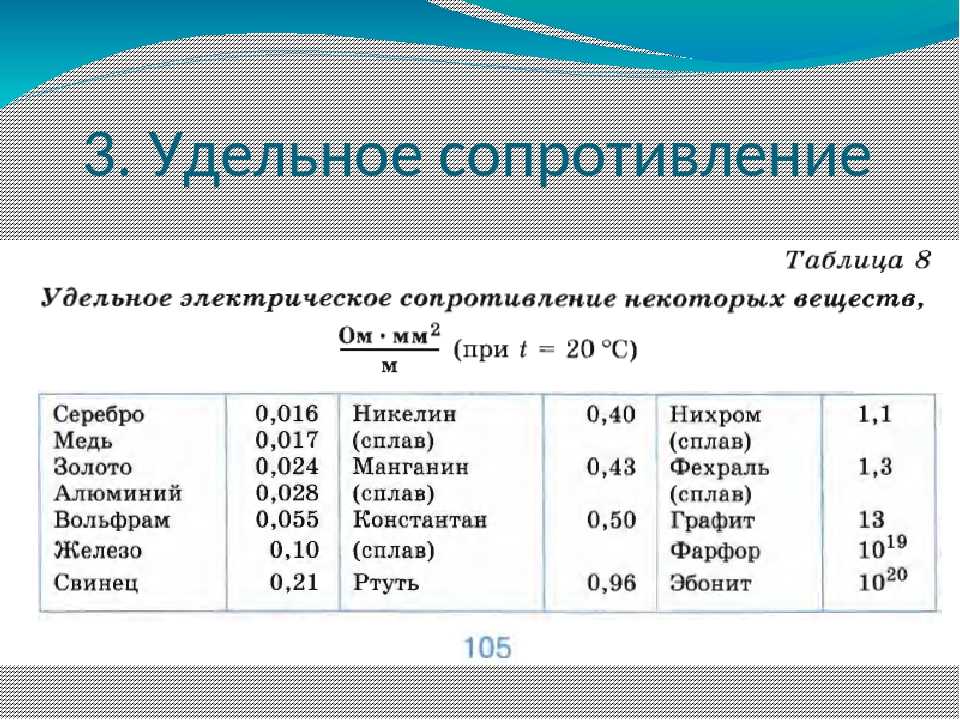
 При самых низких температурах
функция распределения пар показывает значительную дальнодействующую структуру.
При самых низких температурах
функция распределения пар показывает значительную дальнодействующую структуру.В качестве более точного подхода в режиме теплой плотной материи мы используем квантовую молекулярную динамику (КМД) в приближении Борна-Оппенгеймера, которое отделяет ионные компоненты от электронных. Ионы движутся в соответствии с классическими уравнениями движения, управляемыми силами, обусловленными ионами и электронами. Электроны подвергаются квантово-механической обработке, основанной на теории функционала плотности, зависящей от температуры (TD-DFT) мартин04 . Мы следуем реализации Кона-Шэма (KS) и находим электронные орбитали над набором атомов в периодически воспроизводимой ячейке; эти орбитали, в свою очередь, определяют электропроводность посредством приближения Кубо-Гринвуда (КГ) greenwood58 .
Мы выполнили расчеты DFT-MD с помощью пакета моделирования Vienna ab-initio.
(VASP kresse93 ; kresse94 ; kresse96 ; kresse96a ), используя приближение обобщенного градиента в Perdew,
Берк, формулировка Эрнцергофа для функционала обменной корреляции (XC) (GGA-PBE) пбэ ; pbe2 и трехэлектронная (3e) плоскость ГВ, дополненная
волновой (PAW) псевдопотенциал (PP) blochl94; kresse99 с энергией отсечки плоских волн 750 эВ. Все ДПФ-МД
моделирование проводилось при постоянной температуре с использованием термостата Ноуза-Гувера с временным шагом 1-2 фс в одной k-точке (гамма), содержащей все орбитали
или полосы с заполнением Ферми-Дирака более 1 × 10–4.
Все ДПФ-МД
моделирование проводилось при постоянной температуре с использованием термостата Ноуза-Гувера с временным шагом 1-2 фс в одной k-точке (гамма), содержащей все орбитали
или полосы с заполнением Ферми-Дирака более 1 × 10–4.
Образцы, содержащие 64 атома с плотностью ρ, сначала были уравновешены при температуре
T не менее 2 пс. Из этой траектории мы извлекли от пяти до десяти снимков, разделенных временным интервалом примерно 2 τ, чтобы определить
частотно-зависимая электропроводность (переменный ток) с помощью КГ-анализа для температур от 0,25 до 10 эВ. Снимки, разделенные характеристическим или e-кратным временем τ для скорости
автокорреляционную функцию коэффициента самодиффузии принято считать некоррелированной (τ≈ 20-140
ps в зависимости от плотности и температуры).
Для оптического анализа мы использовали сетку Gamma-point или 2x2x2 Monkhorst-Pack (MP) с четырьмя неприводимыми k-точками с числом полос, в два-три раза превышающим выбор MD (набор I).
Мы также проверили сходимость, используя
сетка МП 4x4x4 с 32 k-точками, PAW GW 11e и выборки из 128 и 250 атомов (набор II). Находим для температур выше 0,5 эВ каноническую
выбор из 64 атомов, функционала GGA-PBE XC, GW 3e PAW и 4 k-точек дает результаты, сходящиеся в пределах нескольких процентов от результатов набора II для проводимостей на постоянном токе.
Для температур ниже 0,5 эВ мы используем набор II, хотя набор I дает значения проводимости в пределах 10%.
Находим для температур выше 0,5 эВ каноническую
выбор из 64 атомов, функционала GGA-PBE XC, GW 3e PAW и 4 k-точек дает результаты, сходящиеся в пределах нескольких процентов от результатов набора II для проводимостей на постоянном токе.
Для температур ниже 0,5 эВ мы используем набор II, хотя набор I дает значения проводимости в пределах 10%.
Мы используем этот метод в качестве эталона и корректируем таблицу в соответствии с этими расчетами. Фигура 1 показаны точки, рассчитанные по этим моделям. Большая часть плоскости температура-плотность покрывается потенциалом модели средней силы. В режиме теплого плотного вещества ДПФ-МД результаты используются для руководства режимами интерполяции и экстраполяции, когда модель VMF является менее точным. На рис. 2 показано сравнение новой таблицы (Sesame 23715) к нашим вычислениям DFT-MD. По построению согласие очень хорошее.
На рисунке 3 мы рассматриваем изохору 2,7 г/см3, которая отображает новую таблицу (Сезам 23715),
наши расчеты DFT-MD, расчеты DFT-MD Witte et al. witte18 с использованием двух разных
обменно-корреляционные потенциалы (PBE perdew96 и HSE hse ).
Наши результаты PBE согласуются с результатами Witte et al. witte18 во всем диапазоне температур. Мы также находим необходимость использовать более крупные выборки k-точек и атомов для
получить сходящиеся результаты ниже примерно 0,5 эВ. Это требование могло возникнуть из нескольких условий, например, из-за появления химических процессов, требующих более тонких представлений о природе.
среда и реакции или близость к расплаву (≈ 1000К). Моделирование плавления особенно
трудно выполнить с помощью таких методов, как DFT; также внешнее ограничение, накладываемое периодическими граничными условиями
на малой ячейке может привести к искусственным эффектам, таким как представление неупорядоченной (жидкой) системы под этими
условия становятся нетривиальными. Например, на рис. 4 мы показываем с помощью функции радиального распределения
при ρ=2,7 г/см3 – усиление структурных особенностей в виде пиков ближайших соседей с понижением температуры.
witte18 с использованием двух разных
обменно-корреляционные потенциалы (PBE perdew96 и HSE hse ).
Наши результаты PBE согласуются с результатами Witte et al. witte18 во всем диапазоне температур. Мы также находим необходимость использовать более крупные выборки k-точек и атомов для
получить сходящиеся результаты ниже примерно 0,5 эВ. Это требование могло возникнуть из нескольких условий, например, из-за появления химических процессов, требующих более тонких представлений о природе.
среда и реакции или близость к расплаву (≈ 1000К). Моделирование плавления особенно
трудно выполнить с помощью таких методов, как DFT; также внешнее ограничение, накладываемое периодическими граничными условиями
на малой ячейке может привести к искусственным эффектам, таким как представление неупорядоченной (жидкой) системы под этими
условия становятся нетривиальными. Например, на рис. 4 мы показываем с помощью функции радиального распределения
при ρ=2,7 г/см3 – усиление структурных особенностей в виде пиков ближайших соседей с понижением температуры.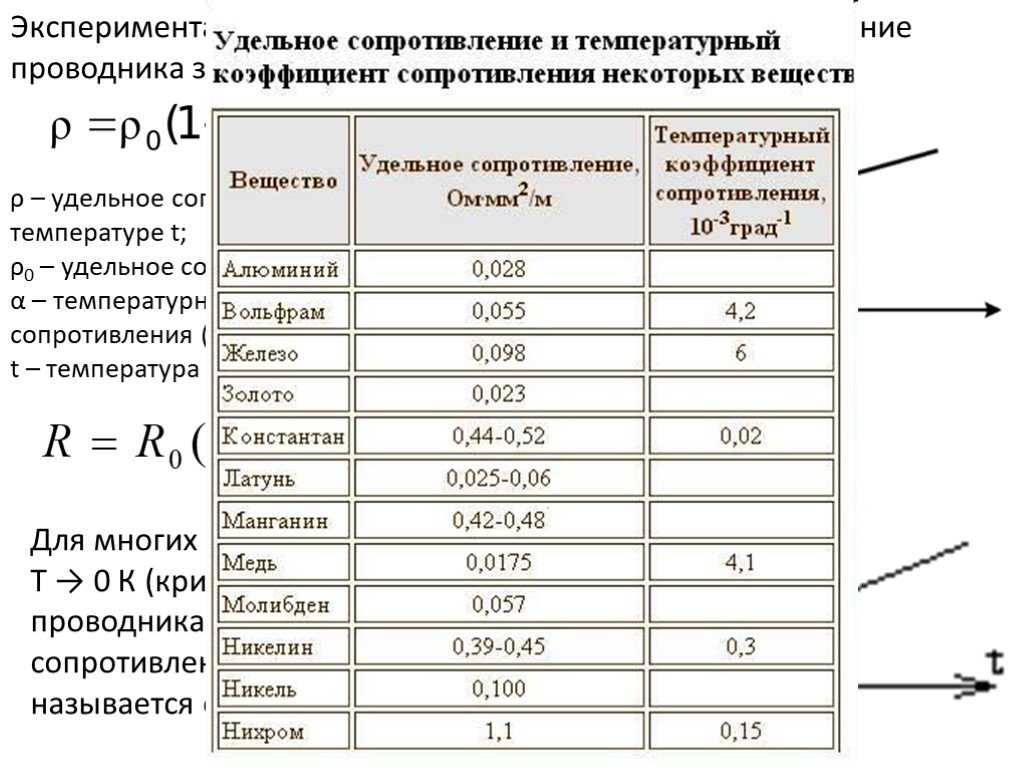
Потенциал среднего результаты силы (VMF) также находятся в разумном согласии с DFT-MD (рис. 3), и согласие улучшается при повышении температуры. Новая таблица (по дизайну) соответствует DFT-MD с использованием PBE в более низкие температуры и результаты VMF при высоких температурах. Также показано более старый Sesame 29371 основан на модели lee84; desjarlais01 . Некоторые важные наблюдаются различия между таблицами (> 50 %), которые могут быть важны в приложениях (например, синарс11 ).
Рисунок 5: (В цвете онлайн) Изотермы (10 кК ≈ 0,86 эВ, 30 кК ≈ 2,59 эВ) для расширенный алюминий по сравнению с экспериментами DeSilva et al desilva98 , эксперимент Clérouin et al. clerouin08 и DFT-MD Desjarlais desjarlais02 . Рисунок 6: (В цвете онлайн) Сравнение с экспериментами Gathers Gathers83 . Эти данные были недавно подтверждены другим экспериментом leitner17 . Также показаны результаты DFT-MD. Витте и др. витте18 . Линия, соединяющая точки Сезам 23715, служит только как
руководство к глазу.
Рис. 7: (В цвете онлайн) Асимптотическое поведение новой таблицы. Пунктирные линии имеют
наклон T3/2 (что правильно в классическом пределе), и подгоняются, чтобы соответствовать
таблица при 1000 эВ. При самой низкой плотности и самых высоких температурах стол восстанавливает этот наклон.
Витте и др. витте18 . Линия, соединяющая точки Сезам 23715, служит только как
руководство к глазу.
Рис. 7: (В цвете онлайн) Асимптотическое поведение новой таблицы. Пунктирные линии имеют
наклон T3/2 (что правильно в классическом пределе), и подгоняются, чтобы соответствовать
таблица при 1000 эВ. При самой низкой плотности и самых высоких температурах стол восстанавливает этот наклон. На рисунке 5 мы сравниваем новую таблицу с экспериментами DeSilva et al. desilva98 и Clèrouin et al. clerouin08 . Эти эксперименты проверяют сложный режим расширенного металла.
при относительно низкой температуре и проверить наш режим интерполяции (рис. 1), где
мы использовали интерполяцию Akima akima70 .
согласие разумно, учитывая, что существует значительное расхождение между экспериментами
самих себя и с помощью DFT-MD ссылки desjarlais02 . Результаты модели VMF
(не показаны, но идентичны новой таблице для плотности < 0,27 г/см3) чувствительны к
выбор обменно-корреляционного потенциала в этом режиме.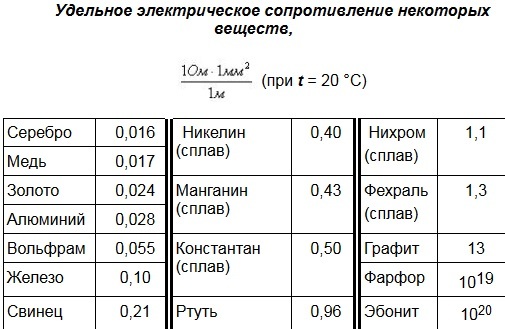 Здесь мы использовали зависимость LDA от температуры. ксдт . В ссылке starrett17 мы использовали параметризацию нулевой температуры pz ,
и обнаружил лучшее согласие с DFT-MD (в котором также использовалась параметризация с нулевой температурой).
Причиной такой чувствительности является низкая ионизация системы, а значит и малое количество
проводящие электроны. Небольшое абсолютное изменение этого числа, вызванное изменением обмена и корреляции
потенциал является значительным относительным изменением, отсюда и влияние на проводимость. Мы выбрали
использовать более физически полный температурно-зависимый обменно-корреляционный потенциал ксдт .
На рисунке также показан старый стол Sesame 29371. Это хорошо согласуется с данными DeSilva et al.
по построению, но отличается от DFT-MD при более высоких плотностях.
Здесь мы использовали зависимость LDA от температуры. ксдт . В ссылке starrett17 мы использовали параметризацию нулевой температуры pz ,
и обнаружил лучшее согласие с DFT-MD (в котором также использовалась параметризация с нулевой температурой).
Причиной такой чувствительности является низкая ионизация системы, а значит и малое количество
проводящие электроны. Небольшое абсолютное изменение этого числа, вызванное изменением обмена и корреляции
потенциал является значительным относительным изменением, отсюда и влияние на проводимость. Мы выбрали
использовать более физически полный температурно-зависимый обменно-корреляционный потенциал ксдт .
На рисунке также показан старый стол Sesame 29371. Это хорошо согласуется с данными DeSilva et al.
по построению, но отличается от DFT-MD при более высоких плотностях.
Новая таблица сравнивается с экспериментами в жидкостном режиме на рис. 6. Эти
данные были недавно подтверждены в ссылке leitner17 . Также показаны
Результаты DFT-MD из ссылки witte18 . Новая таблица хорошо согласуется с PBE
расчеты, как и ожидалось, поскольку он был построен в соответствии с нашими собственными расчетами PBE
в этом режиме (но не в этих точных точках). Таблица и результаты PBE
завышать данные. расчеты HSE тех же авторов witte18 продемонстрировать
чувствительность к обменному и корреляционному потенциалу в этом режиме.
Также показаны
Результаты DFT-MD из ссылки witte18 . Новая таблица хорошо согласуется с PBE
расчеты, как и ожидалось, поскольку он был построен в соответствии с нашими собственными расчетами PBE
в этом режиме (но не в этих точных точках). Таблица и результаты PBE
завышать данные. расчеты HSE тех же авторов witte18 продемонстрировать
чувствительность к обменному и корреляционному потенциалу в этом режиме.
При высоких температурах и низких плотностях проводимость должна хорошо описываться
Модель Spitzer cohen50 , где проводимость увеличивается пропорционально
до Т32 по изохоре. На рисунке 7 показаны изохоры из таблицы. В
самая низкая плотность (в 10-3 раза плотнее твердого тела), модель явно достигает этого классического
результат. Это поведение не навязывается, а является следствием модели BGK.
в сочетании с переходом квантового сечения (уравнение (1)) к своему классическому пределу. Из
На рисунке по мере увеличения плотности это классическое поведение достигается при все большей
высокая температура, а для двух самых высоких плотностей классическое поведение не достигается
на 1000 эВ.
В твердотельном режиме (рис. 1) мы использовали ту же модель, что и указанная в ссылке lee84 .
Регулируемый параметр в этой модели настраивается в соответствии с данными, приведенными в ссылке desai84 .
линия плавления настроена так, чтобы соответствовать эксперименту по ссылке leitner17 . Обратите внимание, что никакого специального рассмотрения
отдается области солидус-ликвидус, или области сосуществования жидкость-пар. Эталонная модель lee84 просто используется ниже Tmelt, а выше Tmelt используется модель на основе DFT. На рисунке
8 мы показываем сравнение новой таблицы с экспериментами ссылки leitner17; брандт07 .
Чтобы избежать артефактов интерполяции, мы показали две изохоры, которые должны ограничивать данные (которые учитывают
на тепловое расширение). Напомним, что
Твердая модель была настроена, чтобы соответствовать данным Desai при плавке desai84 , и данные Desai согласуются с
данные Брандта brandt07 . В новой таблице указаны данные для T > 500 K, но ниже этого
небольшое несоответствие. Ошибка, вероятно, связана с относительно грубой твердотельной моделью, которую мы использовали.
Обратите внимание, что Лейтнер и др. комментируют в своей статье leitner17 , что их данные в твердой фазе должны быть
расценивается как оценка. Данные по жидкой фазе считаются точными (рис. 6).
Эталонная модель lee84 просто используется ниже Tmelt, а выше Tmelt используется модель на основе DFT. На рисунке
8 мы показываем сравнение новой таблицы с экспериментами ссылки leitner17; брандт07 .
Чтобы избежать артефактов интерполяции, мы показали две изохоры, которые должны ограничивать данные (которые учитывают
на тепловое расширение). Напомним, что
Твердая модель была настроена, чтобы соответствовать данным Desai при плавке desai84 , и данные Desai согласуются с
данные Брандта brandt07 . В новой таблице указаны данные для T > 500 K, но ниже этого
небольшое несоответствие. Ошибка, вероятно, связана с относительно грубой твердотельной моделью, которую мы использовали.
Обратите внимание, что Лейтнер и др. комментируют в своей статье leitner17 , что их данные в твердой фазе должны быть
расценивается как оценка. Данные по жидкой фазе считаются точными (рис. 6).
III Обсуждение
Новая таблица восстанавливает известный предел при высокой температуре и достаточно хорошо согласуется с ограниченным
имеются экспериментальные данные. Хотя он интерполирует (используя интерполяцию Akima akima70 ) через
низкотемпературном расширенном металлическом режиме, эта интерполяция основывалась на расчетах DFT-MD и в результате
разумно в этом режиме. Таблица основана на вычислениях ДПФ, которые не имеют настраиваемых параметров.
Однако выбор обменного и корреляционного потенциалов явно важен в низкотемпературных условиях.
режим (при высоких температурах результаты нечувствительны к этому выбору). Кажется вероятным, что наш ДПФ-МД
результаты можно было бы сделать более точными, используя функционал HSE, хотя это требует гораздо больше вычислительных ресурсов.
дорого, и мы уже раздвигаем границы того, что практично для производства столов.
Хотя он интерполирует (используя интерполяцию Akima akima70 ) через
низкотемпературном расширенном металлическом режиме, эта интерполяция основывалась на расчетах DFT-MD и в результате
разумно в этом режиме. Таблица основана на вычислениях ДПФ, которые не имеют настраиваемых параметров.
Однако выбор обменного и корреляционного потенциалов явно важен в низкотемпературных условиях.
режим (при высоких температурах результаты нечувствительны к этому выбору). Кажется вероятным, что наш ДПФ-МД
результаты можно было бы сделать более точными, используя функционал HSE, хотя это требует гораздо больше вычислительных ресурсов.
дорого, и мы уже раздвигаем границы того, что практично для производства столов.
Простую модель, которую мы использовали для твердой фазы, можно улучшить, но такие усилия
будет оправдано только при более низких температурах (т. е. ниже 10–2 эВ ≈ 116 К) или
нужна более высокая точность. Далее, мы не уделяли особого внимания области солидус-ликвидус, или
к региону сосуществования. Это можно было бы улучшить, но на практике это сложно из-за конечного размера.
ограничения подхода DFT.
Это можно было бы улучшить, но на практике это сложно из-за конечного размера.
ограничения подхода DFT.
IV Выводы
Представлена новая таблица типа «Сезам» для электропроводности алюминия. Таблица построены на основе вычислений на основе теории функционала плотности. Сравнения с экспериментами в твердом, жидком и плазменные режимы показывают хорошее совпадение. Восстанавливается высокотемпературный классический предел. Проспекты для улучшение обсуждалось. Таблица должна быть полезна для пользователей в сообществе плотной плазмы.
Благодарности
Лос-Аламосская национальная лаборатория находится в ведении Triad National Security, LLC для Национального управления ядерной безопасности Министерства энергетики США (контракт № 89233218NCA000001). Мы хотели бы отметить полезные беседы с доктором Suxing Hu.
Приложение A Результаты DFT-MD
Результаты для электропроводности нашего моделирования Kubo-Greenwood, DFT-MD приведены в таблице 1.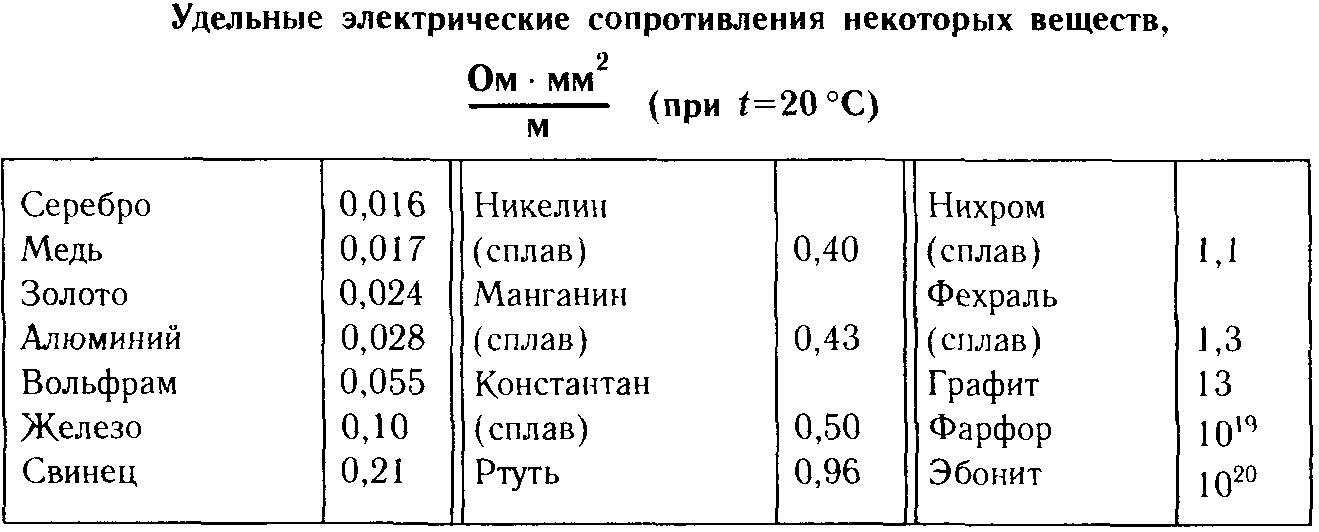
Ссылки
- [1] Мэтью Р. Гомес, Стивен А. Слуц, Адам Б. Сефков, Дэниел Б. Синарс, Келли Д. Хан, Стефани Б. Хансен, Эрик С. Хардинг, Патрик Ф. Кнапп, Пол Ф. Шмит, Кристофер А. Дженнингс и соавт. Экспериментальная демонстрация условий, связанных с термоядерным синтезом, в намагниченный лайнер инерционный термоядерный. Письма с физическим обзором, 113(15):155003, 2014 г.
- [2] В.А.Стигар, Т.Дж. Трепет, Дж. Э. Бейли, Н.Л. Беннетт, Э. У. Бреден, Э. М. Кэмпбелл,
Р.Э. Кларк, Р.А. Купер, М.Е. Кунео, Дж.Б. Эннис и др.
 Концептуальные проекты двух импульсных ускорителей петаваттного класса
для экспериментов по физике высокой плотности энергии.
Физический обзор, специальные темы — ускорители и лучи,
18(11):110401, 2015.
Концептуальные проекты двух импульсных ускорителей петаваттного класса
для экспериментов по физике высокой плотности энергии.
Физический обзор, специальные темы — ускорители и лучи,
18(11):110401, 2015. - [3] Фрэнк Д. Стейси и Орсон Л. Андерсон. Электро- и теплопроводность сплава fe–ni–si при основные условия. Физика Земли и планетарных недр, 124(3):153 – 162, 2001.
- [4] Роберт С. Коэн, Лайман Спитцер и Пол МакР. Рутли. Электропроводность ионизированного газа. физ. Rev., 80:230–238, октябрь 1950 г.
- [5] Йим Т. Ли и Р. М. Мор. Модель электронной проводимости плотной плазмы. Физика жидкостей, 27(5):1273–1286, 19.84.
- [6] С. И. Брагинский. Явления переноса в полностью ионизованной двухтемпературной плазме. сов. физ. ЖЭТФ, 6(33):358–369, 1958.
- [7] К. Э. Старретт. Кулоновский логарифм проводимости плотной плазмы. Физика плазмы, 25(9):092707, 2018.
- [8] Джордж А. Ринкер.
Систематические расчеты коэффициентов переноса плазмы для
периодическая таблица.
 физ. Rev. A, 37:1284–1297, 1988.
физ. Rev. A, 37:1284–1297, 1988. - [9] Стэнфорд П. Лайон. Кунжут: уравнение Лос-Аламосской национальной лаборатории государственная база данных. Отчет Лос-Аламосской национальной лаборатории LA-UR-92-3407, 1992.
- [10] Джон М Зиман. Электроны и фононы: теория явлений переноса в твердые вещества. Издательство Оксфордского университета, 1960.
- [11] член парламента Дежарле. Практические улучшения подветренной проводимости вблизи переход металл-изолятор. Вклад в физику плазмы, 41 (2-3): 267–270, 2001.
- [12] С. Кульбродт, Б. Холст и Р. Редмер. COMPTRA04 – пакет программ для расчета состава и транспортные коэффициенты в плотной плазме. Вклад в физику плазмы, 45 (2): 73–88, 2005 г.
- [13] Рональд Редмер. Физические свойства плотной низкотемпературной плазмы. Отчеты по физике, 282 (2): 35–157, 1997.
- [14] М. П. Дежарле, Дж. Д. Кресс и Л. А. Коллинз.
Электропроводность теплой плотной алюминиевой плазмы и жидкостей.
физ. Ред.
 E, 66:025401, август 2002 г.
E, 66:025401, август 2002 г. - [15] CE Старретт. Потенциал средней силы электропроводности плотной плазмы. Физика высокой плотности энергии, 25:8 – 14, 2017.
- [16] К. Э. Старретт, Дж. Клеруэн, В. Рекуль, Дж. Д. Кресс, Л. А. Коллинз и Д. Э. Хэнсон. Средние транспортные свойства атомов для чистых и смешанных частиц в режимы горячего и теплого плотного вещества. Физика плазмы (1994-настоящее время), 19(10):102709, 2012.
- [17] Н. М. Гилл и К. Э. Старретт. Потенциал рассеяния средней силы для расчета оптических свойств плотная плазма. Физика высокой плотности энергии, 31:24 – 30, 2019.
- [18] Г. Фоссюрье, К. Бланкар, П. Комбис и Л. Видо. Электрическая и теплопроводность в плотной плазме. Физика плазмы (1994-настоящее время), 21(9):092706, 2014.
- [19] А.А. Овечкин, П.А. Лобода и А.Л. Фальков.
Транспортные и диэлектрические свойства плотного ионизированного вещества из
модель среднего атома.
Физика высокой плотности энергии, 20:38 – 54, 2016.

- [20] П.А. Стерн, С.Б. Хансен, Б.Г. Уилсон и В. А. Айзекс. Уравнение состояния, вероятности заполнения и проводимости в код среднего атома чистилища. Физика высокой плотности энергии, 3 (1–2): 278–282, 2007. Радиационные свойства горячей плотной материи.
- [21] W.R. Johnson, C. Guet и G.F. Берч. Оптические свойства плазмы на основе модели среднего атома. Журнал количественной спектроскопии и переноса излучения, 99 (1–3): 327–340, 2006 г. Радиационные свойства горячей плотной материи.
- [22] К. Э. Старретт. Высокотемпературная электронная структура с Метод функции Грина Корринги-Кона-Ростокера. физ. Ред. E, 97:053205, май 2018 г.
- [23] П. Л. Бхатнагар, Э. П. Гросс и М. Крук. Модель столкновительных процессов в газах. я. Малая амплитуда процессы в заряженных и нейтральных однокомпонентных системах. физ. Rev., 94:511–525, май 1954 г.
- [24] К. Э. Старретт и Д. Саумон.
Электронные и ионные структуры теплой и горячей плотной материи.
 физ. Ред. E, 87:013104, январь 2013 г.
физ. Ред. E, 87:013104, январь 2013 г. - [25] CE Starrett и D. Saumon. Простой метод определения ионной структуры теплых плотных иметь значение. Физика высокой плотности энергии, 10:35 – 42, 2014.
- [26] Валентин В. Карасиев, Трэвис Шостром, Джеймс Дафти и С. Б. Трики. Точный однородный электронный газообмен-корреляционная свободная энергия для локальных расчетов спиновой плотности. физ. Rev. Lett., 112:076403, февраль 2014 г.
- [27] Х. Рейнхольц, Г. Рёпке, С. Росмей и Р. Редмер. Электропроводность теплого плотного вещества, в том числе электрон-электронного столкновения. Физический обзор E, 91(4):043105, 2015.
- [28] Хироси Акима. Новый метод интерполяции и плавной аппроксимации кривой на основе локальных процедуры. Журнал ACM (JACM), 17(4):589–602, 1970.
- [29] Джон П. Пердью, Кирон Берк и Матиас Эрнзерхоф. Аппроксимация обобщенного градиента стала проще. Письма с физическим обзором, 77(18):3865, 1996.
- [30] Б. Б.
 Л. Витте, П. Сперлинг, М. Френч, В. Рекуль, С. Х. Гленцер и
Р. Редмер.
Наблюдения нелинейного затухания плазмонов в плотной плазме.
Физика плазмы, 25(5):056901, 2018.
Л. Витте, П. Сперлинг, М. Френч, В. Рекуль, С. Х. Гленцер и
Р. Редмер.
Наблюдения нелинейного затухания плазмонов в плотной плазме.
Физика плазмы, 25(5):056901, 2018. - [31] Р. Л. Мартин. Электронная структура. Издательство Кембриджского университета, 2004.
- [32] Д.А. Гринвуд. Уравнение Больцмана в теории электропроводности в металлы. Труды Физического общества, 71 (4): 585, 1958.
- [33] Георг Крессе и Юрген Хафнер. Молекулярная динамика Ab initio для жидких металлов. Physical Review B, 47(1):558, 1993.
- [34] Георг Крессе и Юрген Хафнер. Ab initio молекулярно-динамическое моделирование переход жидкий металл–аморфный полупроводник в германии. Физическое обозрение B, 49(20):14251, 1994.
- [35] Георг Крессе и Юрген Фуртмюллер. Эффективность расчетов полной энергии ab-initio для металлов и полупроводники с использованием базиса плоских волн. Вычислительное материаловедение, 6(1):15–50, 1996.
- [36]
Георг Крессе и Юрген Фуртмюллер.
 Эффективные итерационные схемы для неэмпирических расчетов полной энергии
с использованием базиса плоских волн.
Физический обзор В, 54(16):11169, 1996.
Эффективные итерационные схемы для неэмпирических расчетов полной энергии
с использованием базиса плоских волн.
Физический обзор В, 54(16):11169, 1996. - [37] Джон П. Пердью, Кирон Берк и Матиас Эрнзерхоф. Обобщенная градиентная аппроксимация стала простой [физ. обр. лет. 77, 3865 (1996)]. физ. Rev. Lett., 78:1396–1396, февраль 1997 г.
- [38] Питер Э. Блёхль. Проекторный метод присоединенных волн. Физический обзор В, 50(24):17953, 1994.
- [39] Георг Кресс и Д Жубер. От ультрамягких псевдопотенциалов к проектору дополненной волны метод. Physical Review B, 59(3):1758, 1999.
- [40] Джон П. Пердью, Кирон Берк и Матиас Эрнзерхоф. Аппроксимация обобщенного градиента стала проще. физ. Rev. Lett., 77:3865–3868, октябрь 1996 г.
- [41] Йохен Хейд, Густаво Э. Скусерия и Матиас Эрнзерхоф. Гибридные функционалы на основе экранированного кулоновского потенциала. Журнал химической физики, 118(18):8207–8215, 2003.
- [42] Д. Б. Синарс, С.
 А. Слуц, М. К. Херрманн, Р. Д. Макбрайд, М. Э. Кунео, К. А.
Дженнингс, Дж. П. Читтенден, А. Л. Великович, К. Дж. Петерсон, Р. А. Веси,
К. Наклех, Э. М. Вайсман, Б. Э. Блю, К. Киллебрю, Д. Шроен,
К. Томлинсон, А. Д. Иденс, М. Р. Лопес, И. К. Смит, Дж. Шорс, В. Бигман,
Г. Р. Беннетт, Б. В. Атертон, М. Сэвидж, В. А. Стигар, Г. Т. Лейфест и
Дж. Л. Портер.
Измерения роста магнито-релеевско-тейлоровской неустойчивости во время
имплозия изначально сплошных металлических гильз.
Физика плазмы, 18(5):056301, 2011.
А. Слуц, М. К. Херрманн, Р. Д. Макбрайд, М. Э. Кунео, К. А.
Дженнингс, Дж. П. Читтенден, А. Л. Великович, К. Дж. Петерсон, Р. А. Веси,
К. Наклех, Э. М. Вайсман, Б. Э. Блю, К. Киллебрю, Д. Шроен,
К. Томлинсон, А. Д. Иденс, М. Р. Лопес, И. К. Смит, Дж. Шорс, В. Бигман,
Г. Р. Беннетт, Б. В. Атертон, М. Сэвидж, В. А. Стигар, Г. Т. Лейфест и
Дж. Л. Портер.
Измерения роста магнито-релеевско-тейлоровской неустойчивости во время
имплозия изначально сплошных металлических гильз.
Физика плазмы, 18(5):056301, 2011. - [43] А. В. ДеСильва и Дж. Д. Кацурос. Электропроводность плотной плазмы меди и алюминия. физ. Rev. E, 57:5945–5951, май 1998 г.
- [44] Жан Клеруэн, Пьер Нуаре, Виктор Н. Коробенко и Анатолий Д. Рахель. Прямые измерения и моделирование ab initio для расширенной жидкости алюминий в области перехода металл-неметалл. Physical Review B, 78(22):224203, 2008.
- [45] Г.Р. Собирается.
Теплофизические свойства жидких меди и алюминия.
Международный журнал теплофизики, 4(3):209–226, 1983.

- [46] Матиас Лейтнер, Томас Лейтнер, Александр Шмон, Кирманж Азиз и Гернот Поттлахер. Теплофизические свойства жидкого алюминия. Metallurgical and Materials Transactions A, 48(6):3036–3045, 2017.
- [47] Дж. П. Пердью и Алекс Зунгер. Поправка на самодействие к приближениям функционала плотности для многоэлектронные системы. физ. Rev. B, 23:5048–5079, май 1981 г.
- [48] Р. Брандт и Г. Нойер. Удельное электрическое сопротивление и теплопроводность чистого алюминия и алюминиевых сплавов до и выше температуры плавления. Международный журнал теплофизики, 28(5):1429–1446, окт. 2007.
- [49] П. Д. Десаи, Х. М. Джеймс и К. Ю. Хо. Удельное электрическое сопротивление алюминия и марганца. Журнал физических и химических справочных данных, 13(4):1131–1172, 1984.
- [50] К. Ю. Хо, М. В. Акерман, К. Ю. Ву, Т. Н. Хэвилл, Р. Х. Богард, Р. А. Матула,
С. Г. О и Х. М. Джеймс.
Удельное электрическое сопротивление десяти выбранных систем бинарных сплавов.



 : R = (2*I*p)/S = (2*800*0,0175)/2,5 = 11,2 Ом;
: R = (2*I*p)/S = (2*800*0,0175)/2,5 = 11,2 Ом;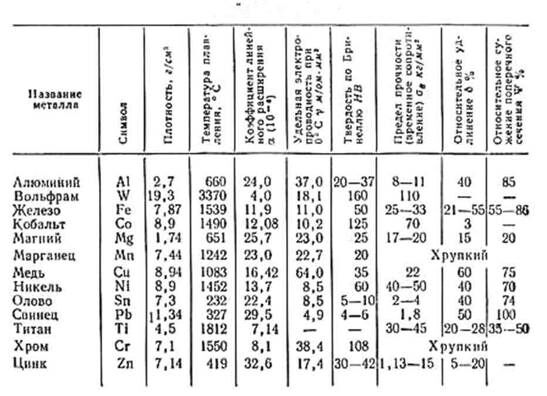

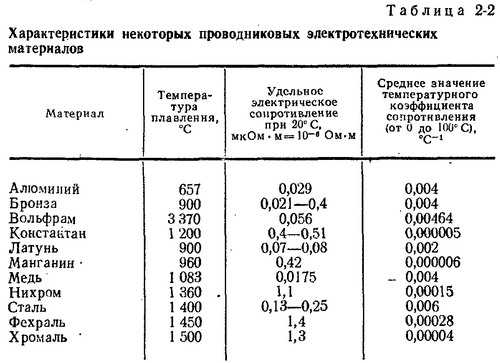 Г.; Мур, JP; Мацумура, Т .; Ван дер Меер, член парламента
Г.; Мур, JP; Мацумура, Т .; Ван дер Меер, член парламента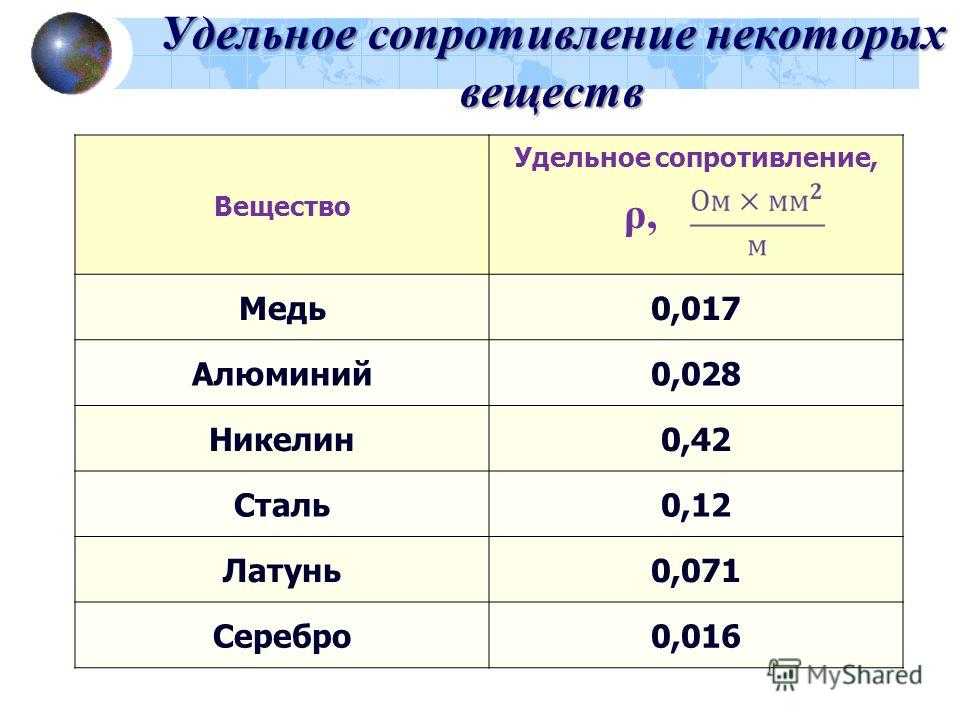 Концептуальные проекты двух импульсных ускорителей петаваттного класса
для экспериментов по физике высокой плотности энергии.
Физический обзор, специальные темы — ускорители и лучи,
18(11):110401, 2015.
Концептуальные проекты двух импульсных ускорителей петаваттного класса
для экспериментов по физике высокой плотности энергии.
Физический обзор, специальные темы — ускорители и лучи,
18(11):110401, 2015.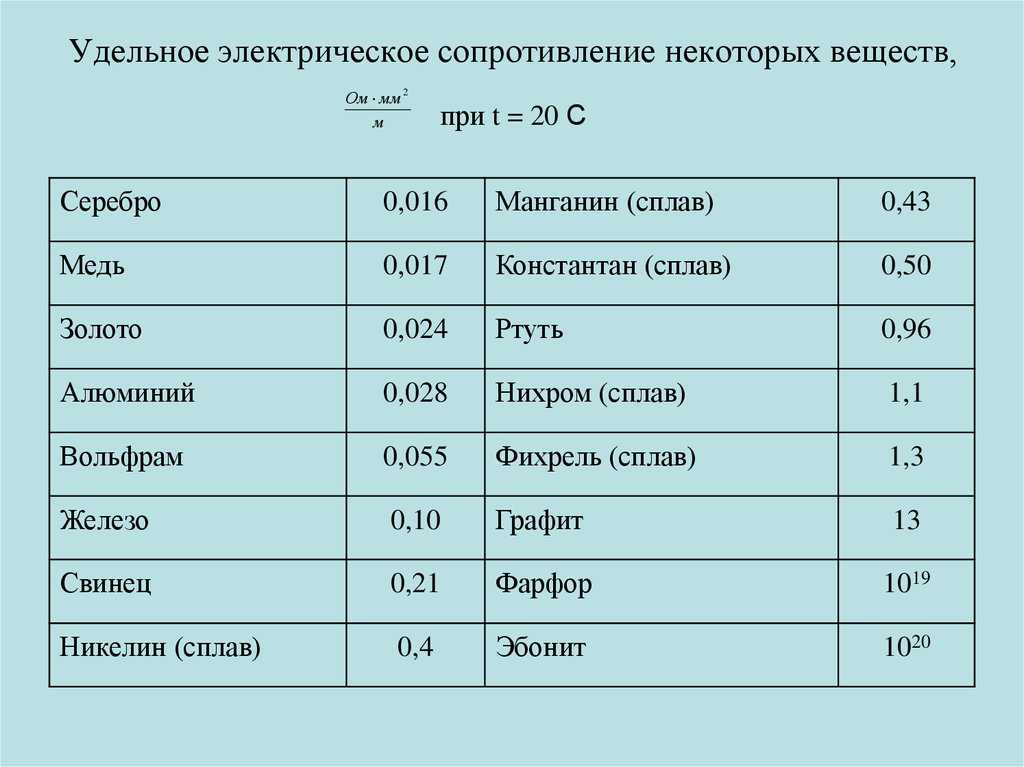 физ. Rev. A, 37:1284–1297, 1988.
физ. Rev. A, 37:1284–1297, 1988. E, 66:025401, август 2002 г.
E, 66:025401, август 2002 г.
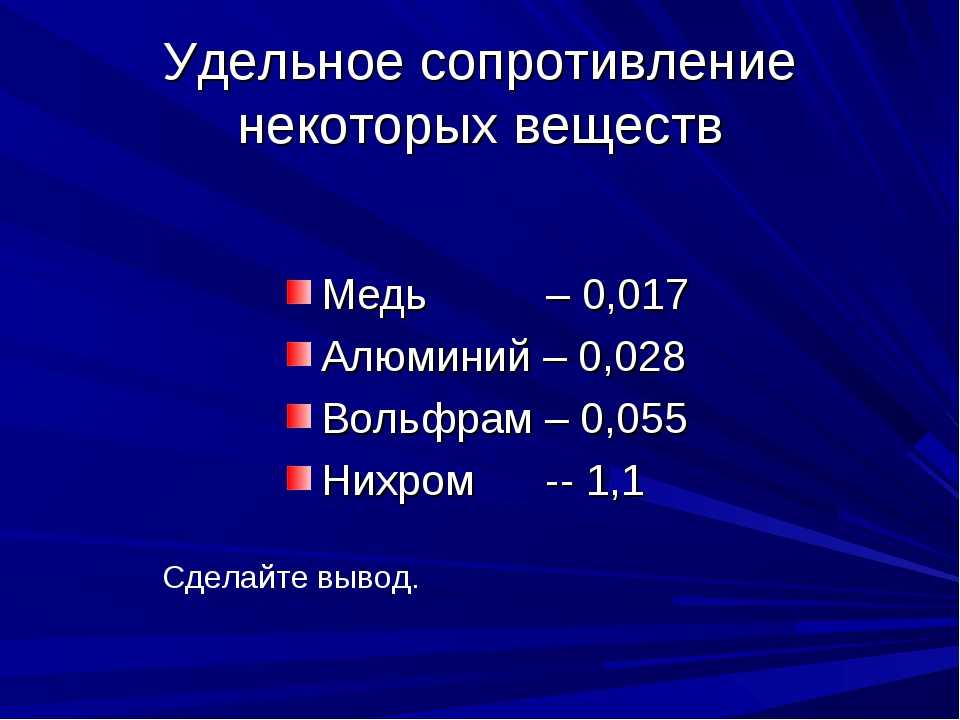 физ. Ред. E, 87:013104, январь 2013 г.
физ. Ред. E, 87:013104, январь 2013 г.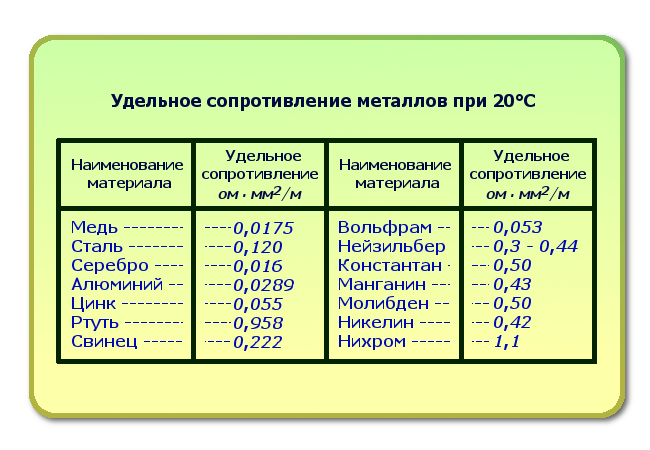 Л. Витте, П. Сперлинг, М. Френч, В. Рекуль, С. Х. Гленцер и
Р. Редмер.
Наблюдения нелинейного затухания плазмонов в плотной плазме.
Физика плазмы, 25(5):056901, 2018.
Л. Витте, П. Сперлинг, М. Френч, В. Рекуль, С. Х. Гленцер и
Р. Редмер.
Наблюдения нелинейного затухания плазмонов в плотной плазме.
Физика плазмы, 25(5):056901, 2018.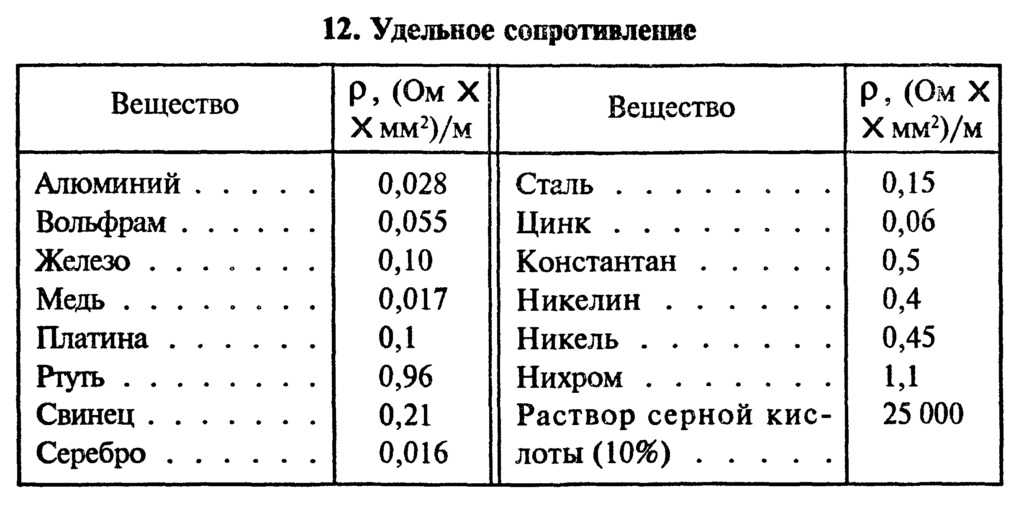 Эффективные итерационные схемы для неэмпирических расчетов полной энергии
с использованием базиса плоских волн.
Физический обзор В, 54(16):11169, 1996.
Эффективные итерационные схемы для неэмпирических расчетов полной энергии
с использованием базиса плоских волн.
Физический обзор В, 54(16):11169, 1996. А. Слуц, М. К. Херрманн, Р. Д. Макбрайд, М. Э. Кунео, К. А.
Дженнингс, Дж. П. Читтенден, А. Л. Великович, К. Дж. Петерсон, Р. А. Веси,
К. Наклех, Э. М. Вайсман, Б. Э. Блю, К. Киллебрю, Д. Шроен,
К. Томлинсон, А. Д. Иденс, М. Р. Лопес, И. К. Смит, Дж. Шорс, В. Бигман,
Г. Р. Беннетт, Б. В. Атертон, М. Сэвидж, В. А. Стигар, Г. Т. Лейфест и
Дж. Л. Портер.
Измерения роста магнито-релеевско-тейлоровской неустойчивости во время
имплозия изначально сплошных металлических гильз.
Физика плазмы, 18(5):056301, 2011.
А. Слуц, М. К. Херрманн, Р. Д. Макбрайд, М. Э. Кунео, К. А.
Дженнингс, Дж. П. Читтенден, А. Л. Великович, К. Дж. Петерсон, Р. А. Веси,
К. Наклех, Э. М. Вайсман, Б. Э. Блю, К. Киллебрю, Д. Шроен,
К. Томлинсон, А. Д. Иденс, М. Р. Лопес, И. К. Смит, Дж. Шорс, В. Бигман,
Г. Р. Беннетт, Б. В. Атертон, М. Сэвидж, В. А. Стигар, Г. Т. Лейфест и
Дж. Л. Портер.
Измерения роста магнито-релеевско-тейлоровской неустойчивости во время
имплозия изначально сплошных металлических гильз.
Физика плазмы, 18(5):056301, 2011.