Напряжение на источнике тока формула
При протекании тока по однородному участку цепи электрическое поле совершает работу. Эту работу называют работой электрического тока. Это соотношение выражает закон сохранения энергии для однородного участка цепи. Закон преобразования работы тока в тепло был экспериментально установлен независимо друг от друга Дж.
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- Формула расчёта напряжения через силу тока и сопротивление
- Источник тока.
- Основные электротехнические формулы.
Мощность. Сопротивление. Ток. Напряжение. Закон Ома.
Определение напряжений на источниках тока. Формула напряжение на источнике тока - ТОК, НАПРЯЖЕНИЕ, СОПРОТИВЛЕНИЕ
- Закон Ома для «чайников»: понятие, формула, объяснение
- Глава 21. Электрический ток. Законы Ома и Джоуля-Ленца
- Закон Ома для полной цепи
- Закон Ома для полной цепи
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: ФИЗИКА закон Ома для полной цепи и ЭДС
Формула расчёта напряжения через силу тока и сопротивление
Для решения задач ЕГЭ на постоянный ток надо знать определения тока, напряжения, сопротивления, закон Ома для участка цепи и замкнутой цепи, закон Джоуля-Ленца, а также уметь находить эквивалентные сопротивления простейших электрически цепей. Рассмотрим эти вопросы. Электрическим током называют упорядоченное движение заряженных частиц. Силой тока в некотором сечении проводника называется отношение заряда , протекшего через это сечение за интервал времени , к этому интервалу времени.
Рассмотрим эти вопросы. Электрическим током называют упорядоченное движение заряженных частиц. Силой тока в некотором сечении проводника называется отношение заряда , протекшего через это сечение за интервал времени , к этому интервалу времени.
Чтобы в проводнике тек электрический ток, в проводнике должно быть электрическое поле, или, другими словами, потенциалы различных точек проводника должны быть разными.
Но при движении электрических зарядов по проводнику потенциалы различных точек проводника будут выравниваться см. Поэтому для протекания тока в течение длительного времени на каких-то участках цепи необходимо обеспечить движение зарядов в направлении противоположном полю.
Такое движение может быть обеспечено только силами неэлектрической природы, которые в этом контексте принято называть сторонними. Эти превращения обеспечивают перемещение заряда противоположно направлению поля, поддерживая движение зарядов по замкнутому пути. Сила тока в однородном участке проводника пропорциональна напряженности электрического поля внутри проводника.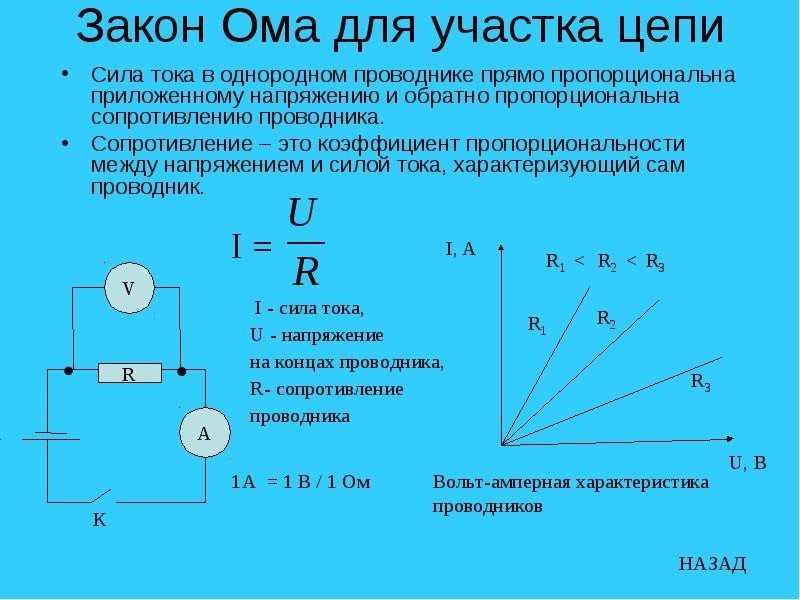
Коэффициент пропорциональности , который принято записывать в знаменатель формулы В результате формула Формула Если проводник является однородным и имеет цилиндрическую форму провод , то его сопротивление пропорционально длине и обратно пропорционально площади сечения.
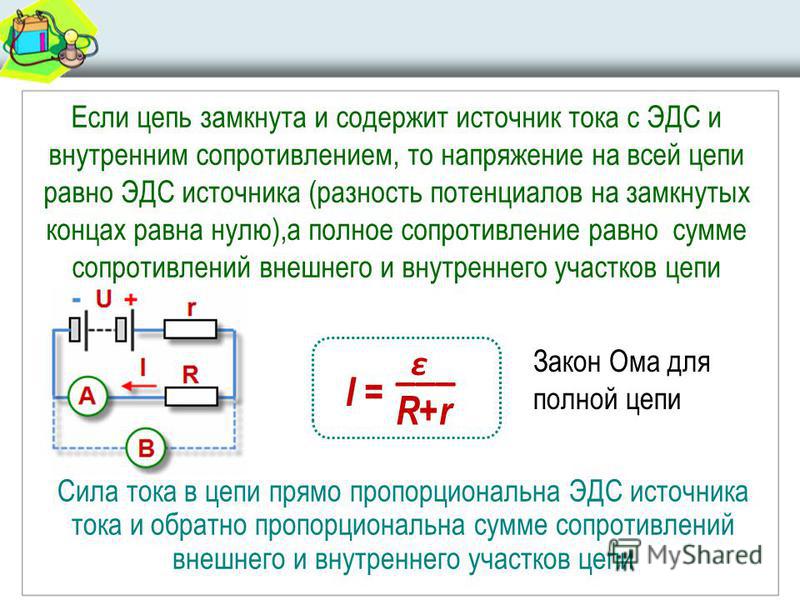
Если участок цепи представляет собой несколько последовательно соединенных однородных проводников с сопротивлениями см. Если участок цепи представляет собой несколько однородных проводников с сопротивлениями , соединенных параллельно см. Рассмотрим теперь закон Ома для замкнутой электрической цепи. Пусть имеется замкнутая электрическая цепь, состоящая из источника сторонних сил с внутренним сопротивлением и внешнего сопротивления.
Пусть при прохождении заряда через источник сторонние силы совершают работу. Электродвижущей силой источника часто используется аббревиатура ЭДС называется отношение работы сторонних сил к заряду.
При прохождении электрического тока через участок цепи электрическое поле совершает работу часто эту работу называют работой тока, хотя термин этот не очень точный. Очевидно, вся эта работа превращается в тепло. Поэтому если через участок цепи прошел заряд , где — сила тока в цепи, — время, то количество выделившейся теплоты равно.
Формулы Из формулы Поэтому отношение. Формулу Структура металла кратко обсуждалась в гл. Они и осуществляют проводимость металла задача Согласно определению Если за 1 мин через сечение проводника протекает заряд 60 Кл задача Применяя далее к этому проводнику закон Ома для участка цепи, получаем В ответ 2. По закону Ома для участка цепи имеем для силы тока через участок цепи после изменения его сопротивления и электрического напряжения на нем задача Согласно закону Ома для участка цепи сопротивление — это коэффициент пропорциональности между напряжением на этом участке и силой тока в нем.
Поэтому в задаче Из-за линейной зависимости тока от напряжения вычисления можно было выполнить и по другим точкам графика, ответ был бы таким же. Как следует из формулы Поэтому из закона Ома для участка цепи В задаче Проще всего применить закон Ома к случаю.
Как следует из формулы Поэтому из закона Ома для участка цепи В задаче Проще всего применить закон Ома к случаю.
Из графика находим силу тока. Имеем Вт ответ 3. Часто школьники не могут ответить на такой вопрос: из формулы для мощности тока следует, что мощность линейно растет с ростом сопротивления, а из формулы — убывает с ростом сопротивления. А как же в действительности мощность зависит от сопротивления?
Давайте разберемся в этом вопросе на примере задачи А на самом деле эти величины от сопротивления зависят, причем эти зависимости могут быть разными для разных источников тока. Внутреннее сопротивление бытовых электрических сетей очень мало. В этом случае из законов Ома для замкнутой цепи и участка цепи Поэтому из формулы заключаем, что мощность, которая выделяется на таком элементе обратно пропорциональна его сопротивлению ответ 3.
Отметим, что из проведенного рассуждения следует, что выделяемая мощность будет очень большой опасная в быту ситуация! Если бы внутреннее сопротивление источника было бы много больше внешнего сопротивления, ток в цепи определялся бы, главным образом, внутренним сопротивлением источника, а от внешнего сопротивления зависел бы слабо.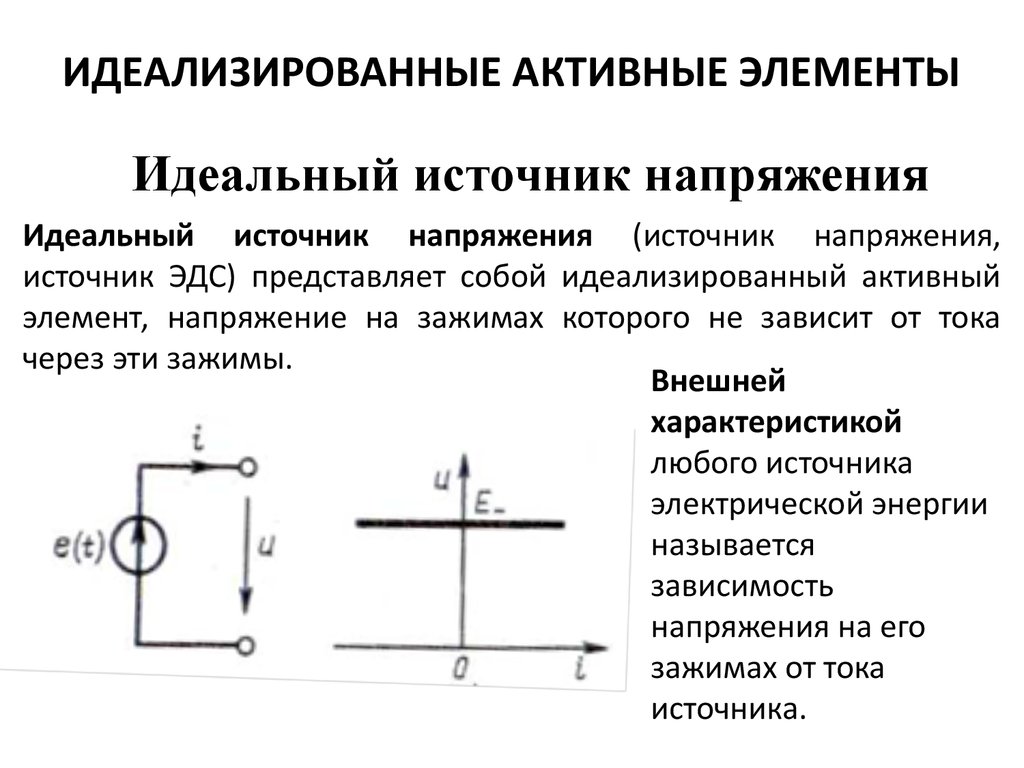
В этом случае мощность тока была бы прямо пропорциональна сопротивлению участка цепи. Как обсуждалось в решении предыдущей задачи, сопротивление элемента, работающего в бытовой электросети равно , где — номинальная мощность данного элемента, — напряжение в сети.
Поэтому отношение сопротивлений ламп мощностью Вт и Вт, рассчитанных на работу в одной и той же бытовой электрической сети задача Поскольку резисторы в задаче Поэтому из закона Ома для участка цепи заключаем, что. При параллельном соединении ламп задача Поэтому из закона Ома для участка цепи следует, что. Рассматриваемый в задаче По правилам сложения сопротивлений находим эквивалентное сопротивление второго участка.
При разомкнутом ключе сопротивление участка цепи, данного в задаче Если ключ замкнут, то цепь сводится к одному резистору так как параллельно двум резисторам включается проводник с пренебрежимо малым сопротивлением.
Поэтому в этом случае сопротивление цепи равно. Таким образом, сопротивление второй цепи составляет две трети от сопротивления первой ответ 1.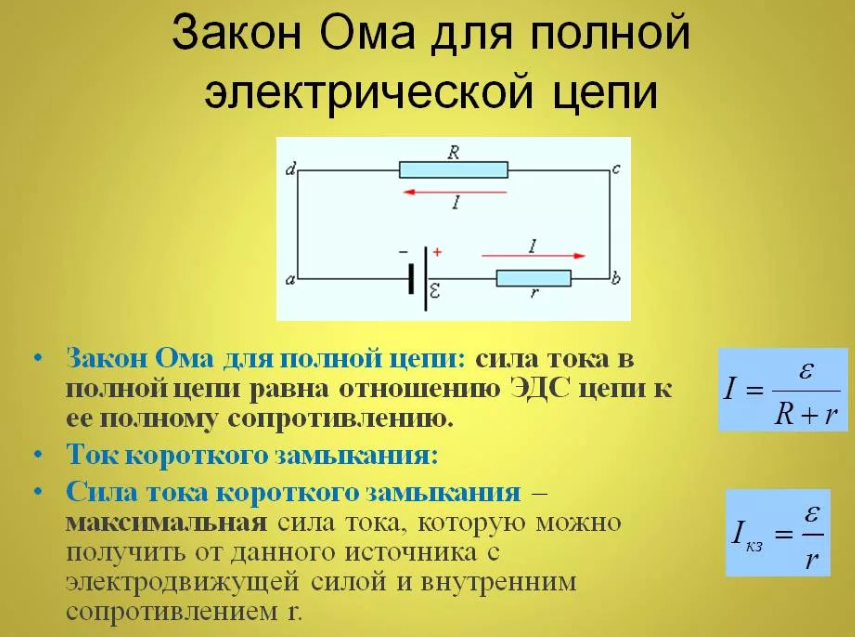
Если две лампы накаливания включены последовательно задача Отсюда следует, что отношение реально выделяемых в лампах мощностей и обратно отношению номинальных мощностей этих ламп:. Работа, совершаемая электрическим полем в проводнике при протекании по нему электрического тока, превращается в энергию тока, которая затем превращается в тепловую энергию.
Поэтому работу поля можно найти из закона Джоуля-Ленца. Для работы поля за время получаем. Из этой формулы находим сопротивление проводника в задаче Поскольку при последовательном соединении резисторов ток через каждый из них одинаков, из закона Джоуля-Ленца Сравним мощности тока на этих сопротивлениях. Учитывая, что при параллельном соединении элементов электрическое напряжение на каждом элементе одинаковое, а при последовательном — складываются значения сопротивлений, получим из законов Ома для верхнего и нижнего участков цепи и закона Джоуля-Ленца.
Поскольку то в представленной схеме наибольшая мощность будет выделяться на сопротивлении ответ 2. Глава Электрический ток. Законы Ома и Джоуля-Ленца Для решения задач ЕГЭ на постоянный ток надо знать определения тока, напряжения, сопротивления, закон Ома для участка цепи и замкнутой цепи, закон Джоуля-Ленца, а также уметь находить эквивалентные сопротивления простейших электрически цепей.
Силой тока в некотором сечении проводника называется отношение заряда , протекшего через это сечение за интервал времени , к этому интервалу времени А поскольку напряженность поля внутри проводника связана с разностью потенциалов его концов или электрическим напряжением на проводнике , то Если проводник является однородным и имеет цилиндрическую форму провод , то его сопротивление пропорционально длине и обратно пропорционально площади сечения Электродвижущей силой источника часто используется аббревиатура ЭДС называется отношение работы сторонних сил к заряду Поэтому если через участок цепи прошел заряд , где — сила тока в цепи, — время, то количество выделившейся теплоты равно Поэтому отношение Рассмотрим теперь задачи.
Согласно формуле Имеем где — ЭДС источника, — сопротивлении е внешней цепи, — сопротивление источника ответ 1. Поэтому где — внутреннее сопротивление источника ответ 3. Поэтому из закона Ома для участка цепи заключаем, что ответ 2. Поэтому из закона Ома для участка цепи следует, что ответ 1. По правилам сложения сопротивлений находим эквивалентное сопротивление второго участка а затем и эквивалентное сопротивление всей цепи ответ 3. Отсюда следует, что отношение реально выделяемых в лампах мощностей и обратно отношению номинальных мощностей этих ламп: ответ 2.
Учитывая, что при параллельном соединении элементов электрическое напряжение на каждом элементе одинаковое, а при последовательном — складываются значения сопротивлений, получим из законов Ома для верхнего и нижнего участков цепи и закона Джоуля-Ленца где — электрическое напряжение, приложенное ко всей цепи.
Источник тока.
Электрический ток I — это упорядоченное движение заряженных частиц. Первая мысль, которая приходит в голову из школьного курса физики — движение электронов.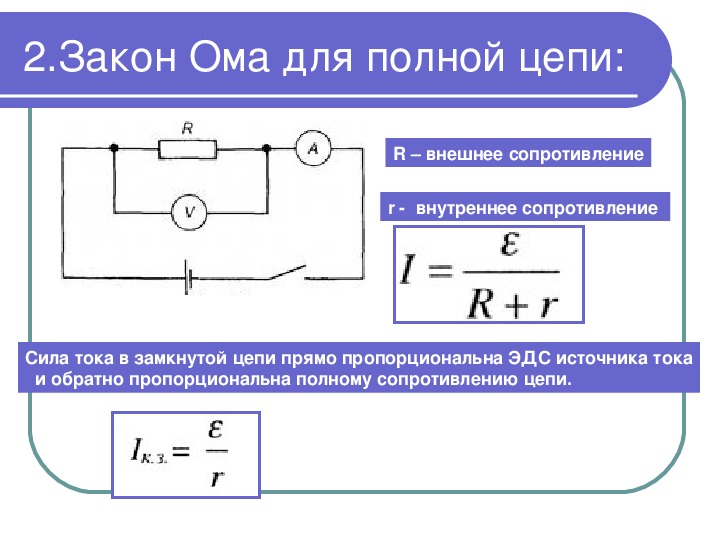 Однако электрический заряд могут переносить не только они, а, например, еще ионы, определяющие возникновение электрического тока в жидкостях и газах. Хочу предостеречь также от сравнения тока с протеканием воды по шлангу.
Однако электрический заряд могут переносить не только они, а, например, еще ионы, определяющие возникновение электрического тока в жидкостях и газах. Хочу предостеречь также от сравнения тока с протеканием воды по шлангу.
Определение напряжений на источниках тока. Общая стандартная форма записи системы уравнений по МКТ для резистивных цепей с источниками.
Основные электротехнические формулы. Мощность. Сопротивление. Ток. Напряжение. Закон Ома.
Так давайте же узнаем вспомним , что это за закон, и смело пойдем гулять. Как понять закон Ома? Нужно просто разобраться в том, что есть что в его определении. И начать следует с определения силы тока, напряжения и сопротивления. Пусть в каком-то проводнике течет ток. То есть, происходит направленное движение заряженных частиц — допустим, это электроны. В таком случае через некоторую поверхность за определенный промежуток времени пройдет конкретный электрический заряд, равный сумме всех зарядов протекших электронов. Отношение заряда к времени и называется силой тока. Чем больший заряд проходит через проводник за определенное время, тем больше сила тока.
Чем больший заряд проходит через проводник за определенное время, тем больше сила тока.
Определение напряжений на источниках тока. Формула напряжение на источнике тока
Давайте попробуем разобраться, что же все таки называют источником тока и как он обозначается в различных схемах. Здесь изображен источник тока в составе генератора тока , собранного с использованием биполярных транзисторов. Источником или генератором тока обычно называют двухполюсник, создающий ток, который не зависит от присоединенного к нему сопротивлению нагрузки. И часто такое название дают любому источнику электрического напряжения розетке, генератору, батарее и т.
На нашем сайте собрано более бесплатных онлайн калькуляторов по математике, геометрии и физике.
ТОК, НАПРЯЖЕНИЕ, СОПРОТИВЛЕНИЕ
Общая стандартная форма записи системы уравнений по МКТ для резистивных цепей с источниками постоянного действия. Записывают уравнения и в матричном виде. R11 —собственное контурное сопротивление первого контура, равное сумме сопротивлений элементов входящих в 1 контур, R22 —контурное сопротивление второго и т. Далее аналогично. Целесообразно применять для сложных схем с несколькими однотипными источниками, у которых частота одна и та же. Если есть L- и C-элементы и частоты источников одинаковые, то применяется в комплексной форме.
Далее аналогично. Целесообразно применять для сложных схем с несколькими однотипными источниками, у которых частота одна и та же. Если есть L- и C-элементы и частоты источников одинаковые, то применяется в комплексной форме.
Закон Ома для «чайников»: понятие, формула, объяснение
При проектировании схем различных устройств радиолюбителю необходимо производить точные расчеты c помощью измерительных приборов и формул. В электротехнике используются формулы для вычислений величин электричества формулы напряжения, сопротивления, силы тока и так далее. Электрическим током является процесс движения заряженных частиц свободных электронов , имеющий вектор направленности. Частицы перемещаются под действием напряженности электрического поля, имеющей векторное направление. Это поле совершает работу по перемещению этих частиц. Влияют на работу электрического поля сила тока, напряжение и сопротивление.
U=I*R где U — напряжение I — сила тока R — сопротивление. вычисления внутреннего напряжения,если r-сопротивление источника тока.
Глава 21. Электрический ток. Законы Ома и Джоуля-Ленца
Характеристикой тока в цепи служит величина, называемая силой тока I. Единица измерения силы тока — 1 ампер 1 А. Определение единицы силы тока основано на магнитном действии тока, в частности на взаимодействии параллельных проводников, по которым идёт электрический ток. Такие проводники притягиваются, если ток по ним идёт в одном направлении, и отталкиваются, если направление тока в них противоположное.
Закон Ома для полной цепи
Электротехника связывает природу электричества со строением вещества и объясняет его движением свободных заряженных частиц под воздействием энергетического поля. Для того чтобы электрический ток протекал по цепи и совершал работу, необходимо иметь источник энергии, совершающий преобразование в электричество:. Все они обладают различными характеристиками. Чтобы классифицировать и описать их параметры принято условное теоретическое разделение на источники:.
При прохождении тока в проводнике выделяется некоторое количество теплоты. Согласно закону сохранения энергии при этом в электрическую цепь должна поступать энергия.
Согласно закону сохранения энергии при этом в электрическую цепь должна поступать энергия.
Закон Ома для полной цепи
Используются также термины генератор тока и идеальный источник тока. Источник тока используется в качестве простейшей модели некоторых реальных источников электрической энергии или как часть более сложных моделей реальных источников, содержащих другие электрические элементы. Следует заметить, что электрические характеристики реальных источников могут быть близки к свойствам источника тока или его противоположности — источника напряжения. В электротехнике источником тока называют любой источник электрической энергии. Сила тока , текущего через идеальный источник тока, всегда одинакова по определению:.
До сих пор при изучении электрического тока мы рассматривали направленное движение свободных зарядов во внешней цепи , то есть в проводниках, подсоединённых к клеммам источника тока. Как мы знаем, положительный заряд :. Теперь нашему положительному заряду нужно замкнуть свою траекторию и вернуться на положительную клемму.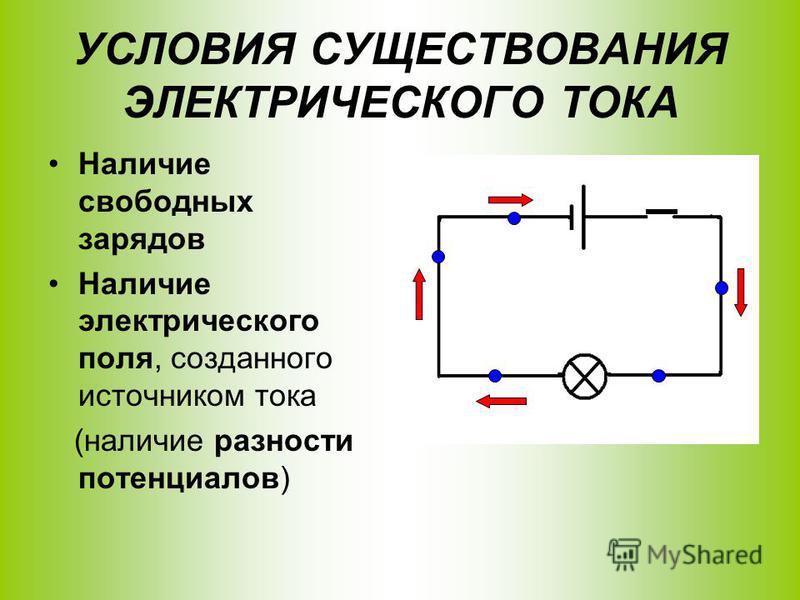
|
Стр 1 из 10Следующая ⇒ В теории электрических цепей используют понятия идеальные источники электрической энергии: источник напряжения и источник тока. Им приписывают следующие свойства: Источник напряжения представляет собой активный элемент с двумя зажимами, напряжение на котором не зависит от тока, проходящего через источник
Рис.2. Идеальный источник напряжения и его вольтамперная характеристика(BAX).
Предполагается, что внутри идеального источника напряжения пассивные сопротивление, индуктивность и емкость отсутствуют и, следовательно, прохождение тока не вызывает падения напряжения. Упорядоченное перемещение положительных зарядов в источнике напряжения от меньшего потенциала к большему возможно за счет работа сторонних сил, которые присущи источнику. Величина работы, производимой данными сторонними силами по перемещению единицы положительного заряда от отрицательного полюса источника напряжения к положительному по полюсу, называется электродвижущей силой (э. На рис.2(а) указано направление напряжения на зажимах идеального источника, которое всегда равно э.д.с. источника по величине и противоположно ей по направлению. Идеальный источник напряжения называют еще источником бесконечноймощности. Это — теоретическое понятие. Величина тока в пассивной цепи зависит от параметров этой цепи и e(t). Если зажимы идеального источника напряжения замкнуть накоротко, то ток цепи должен быть теоретически равен бесконечности. В действительности при замыкании зажимов источника ток имеет конечное значение, так как реальный источник обладает внутренним сопротивлением. Обычно внутренние параметры источника конечной мощности незначительны по сравнению с параметрами внешней цепи и в не которых случаях (по условию задачи) могут вообще не учитываться. Внутреннее сопротивление источника э.д.с.(r0) на схемах замещения изображается последовательно соединенным с самим источником.
Рис.3. Источник напряжения конечной мощности.
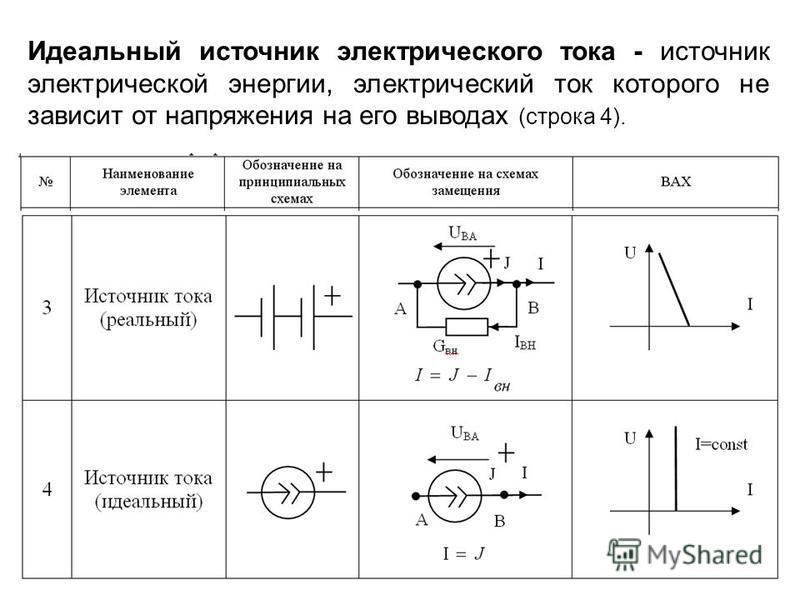
Источник тока представляет собой активный элемент, ток которого не зависит от напряжения на его зажимах.
Рис.4. Идеальный источник тока и его вольтамперная характеристика.
Предполагается, что внутренне сопротивление идеального источника тока равно бесконечности, и поэтому параметры внешней цепи, от которых зависит напряжение на зажимах источника тока, не влияют на ток источника. При увеличении напряжения внешней цепи, присоединенной к источнику тока, напряжение на его зажимах, и следовательно, мощность возрастают. Поэтому идеальный источник тока теоретически так же рассматривается как источник бесконечной мощности. Источник тока конечной мощности изображен на рис.5. g0 – внутренняя проводимость источника. Она характеризует внутренние параметры источника и ограничивает мощность, отдаваемую в цепь. Рис.5. Источник тока конечной мощности.
Часто при решении задач методом эквивалентных преобразований возникает необходимость заменить реальный источник напряжения эквивалентным источником тока или наоборот. Преобразование осуществляется по схеме и формулам рис.6.
(1)
Рис.6. Преобразования источников конечной мощности. Сопротивление. Сопротивлением называется идеализированный элемент цепи в котором происходит необратимый процесс преобразования электрической энергии в тепловую. Кроме того, данный термин применяется для количественной оценки величины, равной отношению напряжения на данном элементе к току, проходящему через него: [Ом] (2) Формула 2 выражает закон Ома. Сопротивление всегда положительно. Величина обратная сопротивлению носит название проводимости: [См] (3)
Рис.7. Графическое изображение сопротивления с выбранными положительными направлениями тока и напряжения.
Мгновенная мощность, поступающая в сопротивление равна: Pr = Ui = i2r = U2q (4) Параметр r в общем случае зависит от тока i (например, вследствие нагревания проводника током). Вольтамперная характеристика (зависимость напряжения на сопротивлении от тока) носит нелинейный характер.
Рис.8. BAX сопротивления: а – нелинейная; б – линейная.
Если сопротивление не зависит от тока, то имеет место прямая пропорциональность, выражающая закон Ома. В этом случае сопротивление называется линейным. Индуктивность. Индуктивностью называется идеализированный элемент электрической цепи, приближающейся по свойствам к индуктивной катушке, в котором накапливается энергия магнитного поля. При этом термин «индуктивность» и его обозначение L применяется как для обозначения самого элемента цепи, так и для количественной оценки отношения потокосцепления самоиндукции к току в данном элементе: [Гн] (5) Индуктивность всегда положительна, так как потокосцепления и ток имеют одинаковые знаки. В общем случае индуктивность зависит от тока и является нелинейной. Если зависимостьy(i) линейная, то индуктивность – величина постоянная.
Рис.9. Зависимость потокосцепления от тока: а — нелинейная, б – линейная.
Рис.10. Графическое изображение индуктивности. (6) eL — электродвижущая сила самоиндукции, которая по закону Ленца противодействует изменению потокосцепления, что учитывается знаком « — ». Если индуктивность L величина постоянная (не зависит от тока), то = (7) Напряжение на индуктивности определяется: (8) Ток на индуктивности: (9) Формулы (8) и (9) выражают закон Ома дифференциальной и интегральной форме для индуктивности. Мгновенная мощность, поступающая в индуктивность равна: (10) Мощность индуктивности связана с процессом нарастания или убывания энергии магнитного поля. Емкость.
Емкостью называется идеализированный элемент электрической цепи приближенно заменяющий конденсатор, в котором накапливается энергия электрического поля. При этом данный термин применяется как для обозначения самого элемента, так и для количественной оценки отношения заряда к напряжению на этом элементе: [Ф] (11) Емкость всегда положительна, так как заряд и напряжение имеют одинаковый знак. В общем случае зависимость заряда от напряжения носит нелинейный характер и, следовательно, параметр С зависит от напряжения. Если зависимость заряда от напряжения линейная, емкость C – величина постоянная.
Рис.11. Зависимость электрического заряда от напряжения, а – нелинейная, б – линейная.
Ток емкости равен производной электрического заряда по времени: (12) Формула (12) выражает закон Ома для емкости. Напряжение на емкости: (13) Условное графическое изображение емкости указано на рис.11. Там же даны положительные направления тока и напряжения.
Рис.12. Условное обозначение емкости.
Мгновенная мощность, поступающая в емкость, равна: (14) Мощность емкости связана с процессом накопления или убыли электрического заряда в емкости. Когда заряд положительный и возрастает ток положительный и в емкость поступает электрическая энергия из внешней цепи. Когда заряд положителен, но убывает, т.е. ток отрицателен, энергия, ранее накопленная в электрическом поле емкости, возвращается во внешнюю цепь. Контрольные вопросы:
1. Изложите основные задачи электротехники. 2. Элементы электрической цепи, их классификация. 3. Определение электрического тока, падения напряжения. 4. 5. Изложите основные сведения об источниках тока и источниках напряжения, их взаимном преобразовании. 6. Чем отличается идеальный источник энергии от источника энергии конечной мощности. 7. Дать краткую характеристику следующим элементам и терминам, их определяющим: сопротивление, емкость, индуктивность.
Законы электрических цепей Цель лекции № 2. Ознакомившись с лекцией № 2 по электротехнике студент должен уметь: 1. В смешанном соединении электрических элементов определять участки с последовательным и параллельным их соединением. 2. Определять потенциал любой точки электрической цепи относительно базиса. 3. Применять обобщенный закон Ома для активного участка ветви. 4. Определять необходимое количество узловых и контурных уравнений и составлять систему уравнений по законам Кирхгофа. 5. Записывать выражение баланса мощностей для сложной электрической цепи.
12345678910Следующая ⇒ Читайте также: |
Источники тока и напряжения — Студопедия
Поделись
Под источником понимают элемент, питающий цепь электромагнитной энергией. Эта энергия потребляется пассивными элементами цепи — запасается в индуктивностях и емкостях и расходуется в активном сопротивлении. Примерами реальных источников электромагнитной энергии могут служить генераторы постоянных, синусоидальных и импульсных сигналов разнообразной формы, сигналы, получаемые от различных датчиков, антенн радиоприемных устройств, источники питания, сигналы, поступающие с выходов электронных устройств и т.д.
Для анализа цепей удобно вводить идеализированные источники двух видов: источник напряжения и источник тока, которые учитывают главные свойства реальных источников. При соответствующем дополнении идеализированных источников пассивными элементами можно передать все свойства реальных источников по отношению к их внешним выводам.
При соответствующем дополнении идеализированных источников пассивными элементами можно передать все свойства реальных источников по отношению к их внешним выводам.
Источник напряжения. Подисточником напряжения понимают такой элемент с двумя выводами (полюсами), напряжение между которыми задано в виде некоторой функции времени независимо от тока, отдаваемого во внешнюю цепь. Зависимость напряжения от тока идеального источника напряжения показана на рис. 1.3. Такой идеализированный источник способен отдавать неограниченную мощность. Наиболее часто применяемые условные графические изображения источника напряжения показаны на том же рисунке, где принятая положительная полярность напряжения источника указывается либо стрелкой внутри кружочка, либо знаками “+”, “-”.
Реальные источники сигнала имеют внутренние сопротивления. К источнику напряжения внутреннее сопротивление подключается последовательно. На рис. 1.4 показаны вольтамперная характеристика и схема реального источника напряжения. Для реального источника выходное напряжение будет равно
Для реального источника выходное напряжение будет равно
Uн = U0 – URвн = U0 – Iн Rвн.
Из формулы видно, что выходное напряжение реального источника тока зависит от тока нагрузки Iн. Чем больше ток нагрузки, тем больше падает напряжение на внутреннем сопротивлении источника, и меньшая часть напряжения U0 поступает на нагрузку (на выход). С другой стороны, чем больше внутреннее сопротивление Rвн при неизменном токе нагрузки, тем больше падает на нем напряжения, что ведет к уменьшению напряжения на выходе источника. Применительно к электронным схемам внутреннее сопротивление источника часто называют выходным сопротивлением.
В случае идеального источника напряжения, его внутреннее сопротивление равно 0 и напряжение на нагрузке не зависит от тока нагрузки. При этом ток нагрузки может возрастать до бесконечности, если сопротивление нагрузки будет стремиться к 0. В действительности невозможно построить идеальный источник напряжения во всем диапазоне изменения выходного тока. Однако, во многих случаях, для ограниченного диапазона изменения выходного тока некоторые источники можно рассматривать как идеальные.
В действительности невозможно построить идеальный источник напряжения во всем диапазоне изменения выходного тока. Однако, во многих случаях, для ограниченного диапазона изменения выходного тока некоторые источники можно рассматривать как идеальные.
Например, источник питания в диапазоне рабочих токов имеет очень малое внутреннее сопротивление, которым можно пренебречь, по сравнению с сопротивлением нагрузки. Или другой пример, выходное сопротивление операционного усилителя, охваченного отрицательной обратной связью, может достигать нескольких сотых долей Ома. Таким внутренним сопротивлением можно пренебречь и рассматривать выход операционного усилителя как идеальный источник напряжения в диапазоне допустимых выходных токов.
Источник тока. Под идеальным источником тока понимают такой элемент цепи, через выводы которого протекает ток с заданным законом изменения во времени независимо от напряжения между выводами. Вольтамперная характеристика и условные графические изображения идеального источника тока показана на рис. 1.5. Независимость тока от напряжения означает, что внутренняя проводимость источника, куда может ответвляться ток, равна 0, а внутреннее сопротивление равно бесконечности. Вольтамперная характеристика и
1.5. Независимость тока от напряжения означает, что внутренняя проводимость источника, куда может ответвляться ток, равна 0, а внутреннее сопротивление равно бесконечности. Вольтамперная характеристика и
схема реального источника тока показана на рис. 6. При увеличении напряжения на нагрузке за счет увеличения сопротивления нагрузки увеличивается внутренний ток источника тока. При этом меньшая часть тока I0 поступает в нагрузку. Выходной ток Iн будет равен
Iн = I0 – Iвн = I0 – Uн / Rвн.
Из формулы видно, что чем больше внутреннее сопротивление источника тока, тем меньше внутренний ток Iвн и большая часть тока I0 отдается в нагрузку. В пределе при Rвн = ∞ весь ток I0 отдается в нагрузку, и ток нагрузки не будет зависеть от напряжения на нагрузке. В этом случае имеем дело с идеальным источником тока. Итак, в идеальном источнике тока внутреннее сопротивление равно бесконечности. В идеальном источнике тока при бесконечной величине сопротивления нагрузки (обрыв цепи нагрузки) на его зажимах будет напряжение бесконечной величины.
В идеальном источнике тока при бесконечной величине сопротивления нагрузки (обрыв цепи нагрузки) на его зажимах будет напряжение бесконечной величины.
Это конечно идеализация – нельзя построить источник тока, у которого величина внутреннего сопротивления рана бесконечности. Однако на практике используются источники тока, построенные на транзисторах, с внутренним сопротивлением, достигающим величин многих мегом и более, работающие в ограниченном диапазоне выходных напряжений. Такие источники тока широко используются в схемах дифференциальных и операционных усилителей, при построении цифро-аналоговых преобразователей, при передаче сигналов по токовой петле и др.
Реальные источники напряжения и тока эквивалентны. Это означает, что относительно своих зажимов схемы ведут себя одинаковым образом, т.е. при анализе схемы один и тот же источник можно рассматривать как реальный источник напряжения или реальный источник тока. Условия эквивалентности можно получить из выражения для напряжения реального источника напряжения
Uн = U0 – Iн Rвн.
Разделим правую и левую части уравнения на Rвн, получим
Uн /Rвн = U0 /Rвн – Iн .
Введем обозначения U0 /Rвн = I0 = const; U0 /Rвн = Iвн и запишем уравнение в следующем виде
Iвн = I0 — Iн или I0 = Iвн + Iн.
Причем на сопротивлениях Rвн и Rн падает одно и то же напряжение Uн, т.е. они соединены параллельно
I0 = Uн /Rвн + Uн /Rн .
Отсюда приходим к схеме реального источника тока, показанного на рис.1.6.
Раз схемы реальных источников напряжения и тока эквивалентны, то возникает вопрос, когда использовать при анализе схемы тот или иной источник? Ответ простой. Используйте тот тип источника, при котором проще анализировать работу схемы. На практике часто поступают следующим образом. Если внутреннее сопротивление источника намного меньше сопротивления нагрузки, то такой источник целесообразно рассматривать как источник напряжения. И в первом приближении величиной внутреннего сопротивления можно пренебречь. Если внутреннее сопротивление намного больше сопротивления нагрузки, то такой источник рассматривают как источник тока. И при первоначальном анализе считают его идеальным. При более детальном анализе схемы учитывают не идеальность источника тока.
Если внутреннее сопротивление источника намного меньше сопротивления нагрузки, то такой источник целесообразно рассматривать как источник напряжения. И в первом приближении величиной внутреннего сопротивления можно пренебречь. Если внутреннее сопротивление намного больше сопротивления нагрузки, то такой источник рассматривают как источник тока. И при первоначальном анализе считают его идеальным. При более детальном анализе схемы учитывают не идеальность источника тока.
Является ли источник тока источником напряжения?
Спросил
Изменено 29 дней назад
Просмотрено 15 тысяч раз
41
Новинка! Сохраняйте вопросы или ответы и организуйте свой любимый контент.
Узнать больше.
\$\начало группы\$
Я путаюсь между источниками тока и напряжения; Я получаю определение из учебника, но я не могу понять разницу в реальном мире. Для меня источники тока и напряжения кажутся одинаковыми. Я понимаю, что идеальных источников не бывает. Что является примером практического источника тока? Чтобы производить ток, нам нужно напряжение, так разве источник тока не является также и источником напряжения? Поскольку батарея является источником напряжения и производит ток при подключении к цепи, не является ли она также источником тока?
Для меня источники тока и напряжения кажутся одинаковыми. Я понимаю, что идеальных источников не бывает. Что является примером практического источника тока? Чтобы производить ток, нам нужно напряжение, так разве источник тока не является также и источником напряжения? Поскольку батарея является источником напряжения и производит ток при подключении к цепи, не является ли она также источником тока?
Пожалуйста, помогите мне понять пример из реальной жизни и использование источника тока и чем он отличается от источника напряжения.
- напряжение
- ток
- источник
\$\конечная группа\$
4
\$\начало группы\$
Источник напряжения обеспечивает, насколько это возможно близко к идеалу, постоянное (или лишь слегка изменяющееся) напряжение при любом требуемом токе (в реальных источниках питания до предела тока, который он может обеспечить)
Источник тока обеспечивает, насколько это возможно, постоянный (или лишь слегка изменяющийся) ток при любом требуемом напряжении (в реальных источниках до предела напряжения, которое он может обеспечить).
Если вы закорачиваете источник напряжения, вы получаете очень большие токи (и обычно перегорает предохранитель/отключает выключатель и т. д.)
Если вы закорачиваете источник тока, вы получаете номинальный ток при очень низком напряжении, и ничего интересно бывает.
Если вы разомкнете цепь источника напряжения, он останется там при номинальном напряжении и не сделает ничего интересного.
Если вы разомкнете цепь источника тока, он выстрелит до максимального напряжения. Если бы это был идеальный источник тока , он разогнал бы себя до достаточного количества киловольт, чтобы образовать дугу и получить номинальный ток, протекающий в плазме. По этой причине нам не нужны идеальные источники тока в большинстве ситуаций.
\$\конечная группа\$
12
\$\начало группы\$
Идеальный источник напряжения должен поддерживать определенное напряжение независимо от потребляемого от него тока.
Идеальный источник тока должен поддерживать определенный ток независимо от напряжения на нем.
Ни одна из этих вещей на самом деле не существует. Оба являются упрощениями, которые мы используем при анализе схем. Даже если бы мы могли построить их, мы, вероятно, не захотели бы. Устройство с бесконечным напряжением холостого хода или бесконечным током короткого замыкания было бы чрезвычайно опасным.
Реальный источник напряжения поддерживает напряжение, близкое к заданному значению, в определенном диапазоне токов.
Реальный источник тока поддерживает ток, близкий к заданному значению, в определенном диапазоне напряжений.
Некоторые источники могут работать в обоих режимах. Хорошим примером является типичный лабораторный источник питания, при малых токах он будет поддерживать заданное напряжение, но как только ток достигнет заданного порога, напряжение уменьшится, чтобы поддерживать постоянный ток.
Идеальный источник тока, включенный параллельно с резистором, эквивалентен идеальному источнику напряжения, включенному последовательно с резистором. Величина резистора одинакова в обоих случаях и известна как «выходное сопротивление». Характеристика напряжения и тока такой цепи будет представлять собой прямую линию между напряжением холостого хода и током короткого замыкания. В более общем смысле мы можем рассматривать выходной импеданс равным dv/di.
Величина резистора одинакова в обоих случаях и известна как «выходное сопротивление». Характеристика напряжения и тока такой цепи будет представлять собой прямую линию между напряжением холостого хода и током короткого замыкания. В более общем смысле мы можем рассматривать выходной импеданс равным dv/di.
Таким образом, вы можете решить, каков приемлемый импеданс источника, чтобы изменение тока было достаточно малым в диапазоне выходного напряжения, а затем преобразовать цепь из источника тока с параллельным резистором в источник напряжения с последовательным резистором.
На практике это работает не так хорошо. Для получения высокого выходного импеданса этим методом требуется источник высокого напряжения, который неэффективен и может создать угрозу безопасности. Таким образом, типичный источник тока будет включать некоторую форму обратной связи для регулировки напряжения в зависимости от нагрузки. Для такого источника график зависимости напряжения от тока, как правило, не будет прямой линией, и, следовательно, выходное сопротивление будет варьироваться в зависимости от напряжения на источнике.
Обычно для этого используется какая-либо схема транзистора или операционного усилителя. Существует множество вариаций в зависимости от характеристик, которыми должен обладать источник.
\$\конечная группа\$
\$\начало группы\$
Для идеальных источников тока и напряжения это так.
Ток, проходящий через источник тока, фиксируется источником тока на постоянном уровне. Напряжение на источнике тока может принимать любое значение.
Напряжение, измеренное от одной клеммы до другой источника напряжения, фиксируется на постоянном уровне источником напряжения. Ток через источник напряжения может принимать любое значение.
Имеет ли это смысл?
\$\конечная группа\$
2
\$\начало группы\$
Насколько я понимаю, реальный источник тока регулирует выходное напряжение, чтобы обеспечить протекание заданного тока через цепь, в то время как источник напряжения создает определенное напряжение вплоть до номинального тока. Но я думаю, что технически оба являются источниками напряжения (потенциала), один из которых представляет собой переменное напряжение, а другой — фиксированное напряжение.
Но я думаю, что технически оба являются источниками напряжения (потенциала), один из которых представляет собой переменное напряжение, а другой — фиксированное напряжение.
Что касается источника тока, много лет назад у меня был ментальный блок, пока инструктор не сделал простое утверждение, что «возможность источника тока считается бесконечной в уравнениях, но в реальной жизни она всегда ограничена возможностями источника». .
\$\конечная группа\$
5
\$\начало группы\$
Что является примером практического источника тока ?
При дуговой сварке необходимо использовать источник питания постоянного тока (CC) или постоянного напряжения (CV) в зависимости от используемого процесса. Некоторые из наиболее распространенных сварочных процессов используют источники питания постоянного тока (например, SMAW, GTAW).
Когда оператор SMAW («палочная» сварка) выполняет сварку, источник постоянного тока покажет относительно небольшое изменение силы тока по сравнению с большим изменением напряжения .
Используя некоторые примеры рабочих параметров для источника питания CC, мы установили машину на 300 А, и мы проверяем напряжение и силу тока на источнике питания, в то время как оператор изменяет длину дуги, удерживая электрод ближе или дальше от работы. :
- Короткая дуга: 30 В — 308 А
- Идеальная дуга: 32 В — 300 А
- Длинная дуга: 34 В — 290 А
Здесь мы видим относительно небольшое изменение силы тока на на 18А при относительно большом изменении напряжения на 4В.
Чтобы производить ток, нам нужно напряжение, так разве источник тока не является также и источником напряжения?
№ Источник тока и источник напряжения — это теоретические определения, которые существуют для анализа электрических цепей.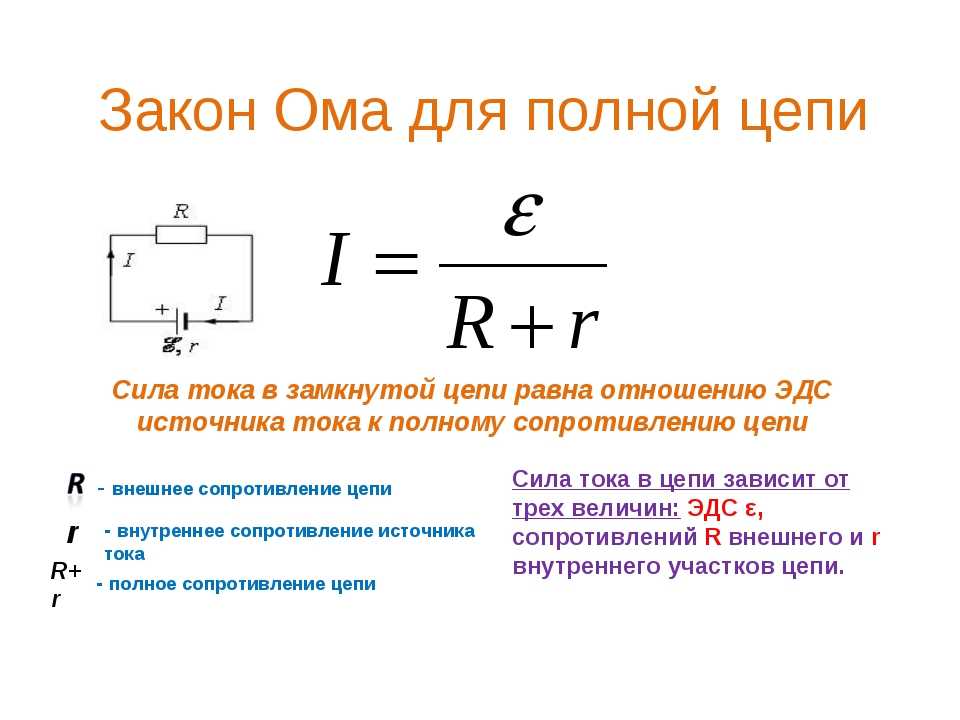 Если вы посмотрите на определения, они не могут быть оба верны.
Если вы посмотрите на определения, они не могут быть оба верны.
Суть в том, что источник тока обеспечивает достаточно стабильный (т.е. постоянный ) ток, а источник напряжения обеспечивает предсказуемое напряжение (например, 12-вольтовые батареи, 120-вольтовые настенные розетки).
\$\конечная группа\$
1
\$\начало группы\$
Вы правы, полагая, что в реальном мире не существует идеального источника напряжения или идеального источника тока.
Вместо этого есть только источники, дающие как напряжение, так и ток. Разница между ними какой из параметров находится под контролем источника а какой под управлением нагрузки .
Для простых резистивных нагрузок у вас есть закон Ома, который прекрасно его иллюстрирует.
У вас есть три параметра — напряжение, ток и сопротивление. Закон Ома связывает все три вместе в очень простую формулу — \$I=\frac{V}{R}\$
Закон Ома связывает все три вместе в очень простую формулу — \$I=\frac{V}{R}\$
Когда у вас есть два из этих значений, вы можете вычислить третье.
С источником (постоянного) напряжения у вас есть фиксированное значение \$V\$ и известное значение \$R\$ (сопротивление нагрузки), поэтому ток \$I\$ является переменным и может быть рассчитан.
И наоборот, для (постоянного) источника тока у вас есть фиксированное значение \$I\$ и известное значение \$R\$, поэтому напряжение \$V\$ является переменным и может быть рассчитано.
Итого:
- В источнике напряжения напряжение фиксировано, а ток изменяется в зависимости от нагрузки
- В источнике тока ток фиксирован, а напряжение изменяется в зависимости от нагрузки
\$\конечная группа\$
\$\начало группы\$
Просто добавить немного математики V= RI (закон Ома) Теперь то, что делает источник напряжения, математически говорит о том, что V является постоянным, поэтому он делает (RI) постоянным, это будет означать
- .
 Для увеличения сопротивления (НАГРУЗКА) потребляется меньше тока.
Для увеличения сопротивления (НАГРУЗКА) потребляется меньше тока. - Однако рассеиваемая мощность одинакова. Подразумевается, что ток в цепи может быть ниже, если требуемая мощность одинакова.
Обратное происходит для источника тока, где даже низкое напряжение удовлетворяет требуемому барьеру мощности. Математически это фундаментальное различие между обоими источниками.
\$\конечная группа\$
\$\начало группы\$
Вы спрашивали о практическом применении токовых петель. Вот несколько. Некоторые из них являются историческими, а некоторые используются до сих пор.
Ранние телетайпы, такие как Model 15, использовали токовые петли 60 мА между машинами. Более поздние модели, такие как Model 33, использовали контуры на 20 мА. Преимущество в обоих случаях состоит в том, что вы можете прокладывать линии на несколько миль между машинами без каких-либо повторителей, поскольку постоянный ток компенсирует любые потери из-за сопротивления линий. Конечно, падение напряжения на этих расстояниях увеличивалось по мере увеличения расстояния, и некоторые линии работали при напряжении питания до 125 В.
Конечно, падение напряжения на этих расстояниях увеличивалось по мере увеличения расстояния, и некоторые линии работали при напряжении питания до 125 В.
Другим преимуществом является то, что вы можете добавлять дополнительные машины последовательно с другими в любом месте контура, а источник питания автоматически компенсирует это, повышая напряжение, управляющее контуром.
Эти петли телетайпа использовали отсутствие тока для «пробела» и наличие тока в линии для «отметки». Поскольку условие интервала (отсутствие данных) было условием по умолчанию, это в большинстве случаев снижало энергопотребление в цепях питания.
Телетайпы модели 33 широко использовались в качестве компьютерных терминалов для мини-компьютеров в 1970–1980-х годах, поэтому большинство из них имели интерфейс 20 мА. Даже исходная последовательная карта для IBM PC имела интерфейс с токовой петлей.
MIDI — еще один пример интерфейса токовой петли. Он использует 5 мА.
Другой тип токовой петли использовался и до сих пор используется в некоторых местах для измерительных приборов. Это называется токовой петлей 4-20 мА (также использовалось 10-50 мА). В отличие от постоянного тока в петлях, описанных выше для отправки цифровых данных, петли 4-20 мА используются для передачи показаний прибора, таких как давление, температура, уровень, расход, pH или другие переменные процесса. Обычно 4 мА представляют собой показание 0, а 20 мА представляют собой показание полной шкалы. Таким образом, если бы полная шкала прибора равнялась 160, то увеличение тока на каждые 100 мкА означало бы увеличение показания на единицу.
Это называется токовой петлей 4-20 мА (также использовалось 10-50 мА). В отличие от постоянного тока в петлях, описанных выше для отправки цифровых данных, петли 4-20 мА используются для передачи показаний прибора, таких как давление, температура, уровень, расход, pH или другие переменные процесса. Обычно 4 мА представляют собой показание 0, а 20 мА представляют собой показание полной шкалы. Таким образом, если бы полная шкала прибора равнялась 160, то увеличение тока на каждые 100 мкА означало бы увеличение показания на единицу.
Устройство, известное как Передатчик, используется для преобразования показаний в переменный ток. Современные достаточно сложны.
Как и цифровые шлейфы 20 мА и 60 мА, преимущество токовых шлейфов 4-20 мА заключается в том, что их можно прокладывать по телефонной паре, например, на больших расстояниях.
Причина, по которой они начали с 4 мА вместо 0 мА, заключается в том, что последний использовался для индикации неисправности (разомкнутый контур).
\$\конечная группа\$
\$\начало группы\$
Нет, источник тока не является источником напряжения.
Я не собираюсь связываться с этой терминологией «идеального источника», она просто слишком все усложняет.
Источник тока «просто» подает ЗАДАННЫЙ ток. Неважно, является ли ток постоянным, постоянным, переменным, модулированным, идеальным, идеальным или каким-либо еще. Напряжение на выходе неизвестно (может быть, известно какому-нибудь электротехнику, разбирающемуся в устройстве, которое он подключает к этому источнику).
Напряжение будет совпадать с током, но это не делает его источником напряжения.
Давайте немного конкретизируем и скажем, что это источник тока 1 Ампер, независимо от типа тока. Вы знаете, что сила тока равна 1 А. Вот и все.
Вот почему вы называете это источником тока. Потому что он «обеспечивает» определенный ток.
Аналогия: Допустим, вы раздаете яблоки. У них есть вес? Конечно! Вы «массовый источник»? Нет. Если вы отдадите 10 яблок, вы знаете о массе? Обычно нет. Вы можете пересчитать яблоки, и они имеют определенный вес, но обычно людей это не слишком волнует. У них есть цвета? Конечно! Они как-то пахнут? Конечно!
У них есть вес? Конечно! Вы «массовый источник»? Нет. Если вы отдадите 10 яблок, вы знаете о массе? Обычно нет. Вы можете пересчитать яблоки, и они имеют определенный вес, но обычно людей это не слишком волнует. У них есть цвета? Конечно! Они как-то пахнут? Конечно!
В данном случае вы источник яблок, а не источник массы, не источник цвета, не источник запаха. Все что идет с яблоком, но это вторично и НЕОПРЕДЕЛЕННО.
То же самое относится к источнику тока. Ток указан, все остальное вызывает удивление (более-менее).
\$\конечная группа\$
\$\начало группы\$
Попробуйте поразмышлять над этой идеей — медленно и спокойно.
Ток реальный. Это физическая реальность [электроны каким-то образом движутся]. Это измеримо. Он переменный [более или менее движущиеся электроны]. Это можно увидеть с помощью ряда инструментов [электронный микроскоп]. Итак, шаг 1 — смириться с существованием механической формы электрического тока — она существует.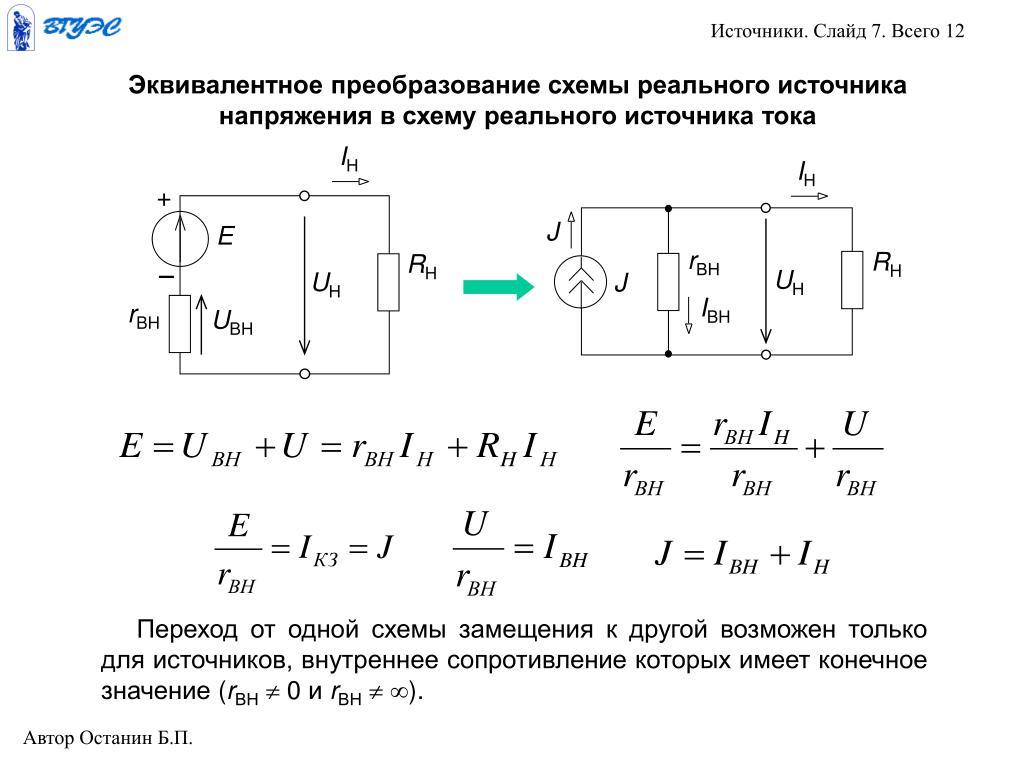 Напряжение не соответствует действительности. В нем нет никаких механических составляющих.
Так что для всех вас, кто ошибочно полагает, что ОБА ток и напряжение реальны, существуют и зависят друг от друга, чтобы иметь какое-то дальнейшее значение — вы ошибаетесь.
Термин «напряжение» нужно было описать еще в те дни, чтобы ОБЪЯСНИТЬ электричество простым способом, а не оставлять предмет запутанным и необъяснимым. Ключевым моментом, который нужно понять здесь, является значение СУЩЕСТВУЮЩЕГО!. Ток существует. Это механический компонент [у него есть масса], состоящий из нескольких строительных блоков [электронов; частицы; атомной структуры плюс взаимодействие между составляющими в соответствии с законами физики]. Напряжение НЕ существует, потому что оно не имеет массы. Мы сами создаем значение напряжения, вставляя специально разработанный и маркированный измерительный прибор в замкнутую цепь, которая позволяет продолжить или начать циркуляцию тока. В зависимости от физических параметров [на электронном уровне] схемы будет зависеть то, что мы видим на нашем скромном устройстве для измерения напряжения.
Напряжение не соответствует действительности. В нем нет никаких механических составляющих.
Так что для всех вас, кто ошибочно полагает, что ОБА ток и напряжение реальны, существуют и зависят друг от друга, чтобы иметь какое-то дальнейшее значение — вы ошибаетесь.
Термин «напряжение» нужно было описать еще в те дни, чтобы ОБЪЯСНИТЬ электричество простым способом, а не оставлять предмет запутанным и необъяснимым. Ключевым моментом, который нужно понять здесь, является значение СУЩЕСТВУЮЩЕГО!. Ток существует. Это механический компонент [у него есть масса], состоящий из нескольких строительных блоков [электронов; частицы; атомной структуры плюс взаимодействие между составляющими в соответствии с законами физики]. Напряжение НЕ существует, потому что оно не имеет массы. Мы сами создаем значение напряжения, вставляя специально разработанный и маркированный измерительный прибор в замкнутую цепь, которая позволяет продолжить или начать циркуляцию тока. В зависимости от физических параметров [на электронном уровне] схемы будет зависеть то, что мы видим на нашем скромном устройстве для измерения напряжения. Интересно, что нам НИКОГДА не нужно определять напряжение как отдельный параметр, если мы хотим придерживаться только реальности двух составляющих схемы, которые на самом деле СУЩЕСТВУЮТ, и точно определяют поток электронов [сопротивление цепи и ток]. Пробует когда-нибудь — скоро становится совсем несложно посчитать.
Интересно, что нам НИКОГДА не нужно определять напряжение как отдельный параметр, если мы хотим придерживаться только реальности двух составляющих схемы, которые на самом деле СУЩЕСТВУЮТ, и точно определяют поток электронов [сопротивление цепи и ток]. Пробует когда-нибудь — скоро становится совсем несложно посчитать.
\$\конечная группа\$
2
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Если цепь имеет только источник тока и не имеет источника напряжения, откуда берется напряжение для питания цепи?
Спросил
Изменено 3 года, 11 месяцев назад
Просмотрено 11 тысяч раз
13
Новинка! Сохраняйте вопросы или ответы и организуйте свой любимый контент.
Узнать больше.
\$\начало группы\$
Например, эта схема. Источник тока — это что-то, что изменяет напряжение на нем, чтобы соответствовать определенному току.
Но где взять источник напряжения для этого или хотя бы иметь напряжение на Vx. Как эта схема работает даже без источника напряжения?
Я посмотрел здесь: Является ли источник тока также источником напряжения?
Пытался понять разницу между источником тока и источником напряжения, но ничего не помогло ответить на этот вопрос.
Может ли в этом случае источник тока действовать как источник напряжения?
Спасибо
- схема-анализ
- схема
\$\конечная группа\$
9
\$\начало группы\$
Идеальный источник тока будет производить любое напряжение, необходимое для подачи заданного тока.
Идеальный источник напряжения будет подавать любой ток, который требуется остальной части цепи, когда он подает заданное напряжение.
Реальные источники тока и напряжения будут иметь ограничения по напряжению (для источника тока) или току (для источника напряжения), которые они могут обеспечить.
\$\конечная группа\$
4
\$\начало группы\$
Это идеализированные элементы. В действительности не существует ни источников напряжения, ни источников тока.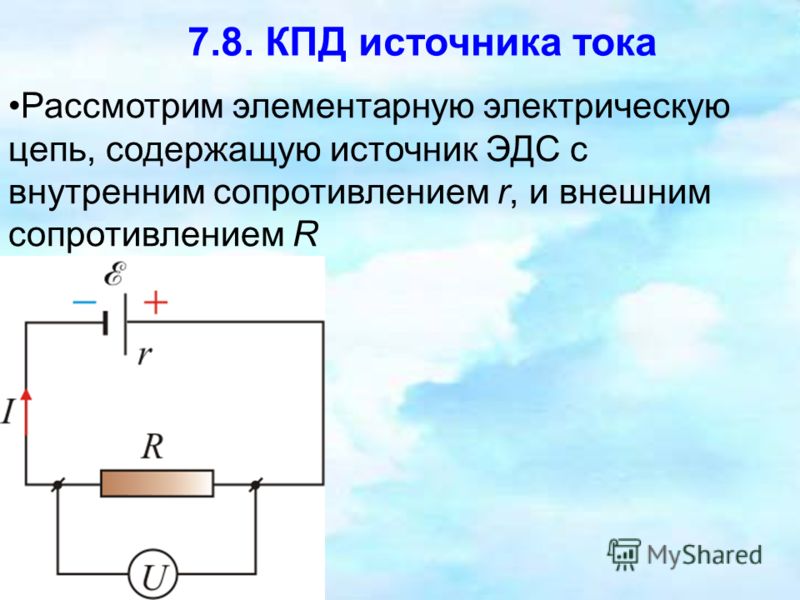 В реальности есть генераторы, гальванические элементы и т. д.
В реальности есть генераторы, гальванические элементы и т. д.
Вы можете смоделировать гальванический элемент как
Конечно, вы всегда можете добавить в свою модель дополнительные элементы, но эти два варианта являются минимальными. Если вы отбрасываете внутреннее сопротивление, подключенное правильно, вы больше не говорите о вещах реального мира, а говорите о своем моделировании.
Вот для чего эти уроки и практика. Научитесь разбираться в моделировании. Таким образом, вы можете создавать и понимать модели для элементов реального мира.
Я думаю, теперь вы легко поймете, что делать с R2, и во что впоследствии можно преобразовать текущий источник и R1.
\$\конечная группа\$
13
\$\начало группы\$
Источник тока должен иметь источник напряжения. Но поскольку источник тока предназначен для подачи фиксированного количества тока, мы можем игнорировать его внутреннюю работу и просто сосредоточиться на его назначении: быть источником тока.
Если подумать, мы часто относимся к источникам как к идеальным, и это прекрасно работает. Если бы мы не могли этого сделать, источник напряжения в цепи должен был бы включать в себя все компоненты, которые позволяют ему выводить это конкретное напряжение. И если бы он был подключен к стене, он должен был бы включать цепь, которая проходила бы через трансформаторы и много миль проводов к источнику электричества…
\$\конечная группа\$
\$\начало группы\$
Источник постоянного тока (CC) имеет собственный источник постоянного тока или его необходимо обеспечить.
Вы можете купить регулятор DC-DC CC или блок питания CC с питанием от переменного тока.
Блок питания CC с питанием от переменного тока будет иметь вход питания AC-DC и выход регулятора DC-DC CC.
Вот очень простой DC-DC понижающий (понижающий) стабилизатор CC, управляющий некоторыми светодиодами.
Ток протекает через резистор R комплект . Микросхема измеряет напряжение на резисторе R , установленном на , для контроля протекания тока.
Микросхема измеряет напряжение на резисторе R , установленном на , для контроля протекания тока.
Если тока недостаточно, внутренний ШИМ-сигнал увеличит рабочий цикл входа SW (переключение), увеличивая ток, проходящий через SW. Наоборот.
Когда рабочий цикл достигает своего максимума (максимальный номинальный ток), источник CC фактически становится источником напряжения.
Это связано с нагрузкой. Когда CC достигает максимального напряжения или тока, он становится источником напряжения.
Пример: если прямое напряжение этих светодиодов больше, чем входное напряжение, достигается максимальное напряжение.
Если нагрузка представляет собой резистивную нагрузку, которая может потреблять больший ток, чем может обеспечить источник CC, достигается максимальный ток.
\$\конечная группа\$
\$\начало группы\$
«Текущий источник» — это просто название (слегка вводящее в заблуждение).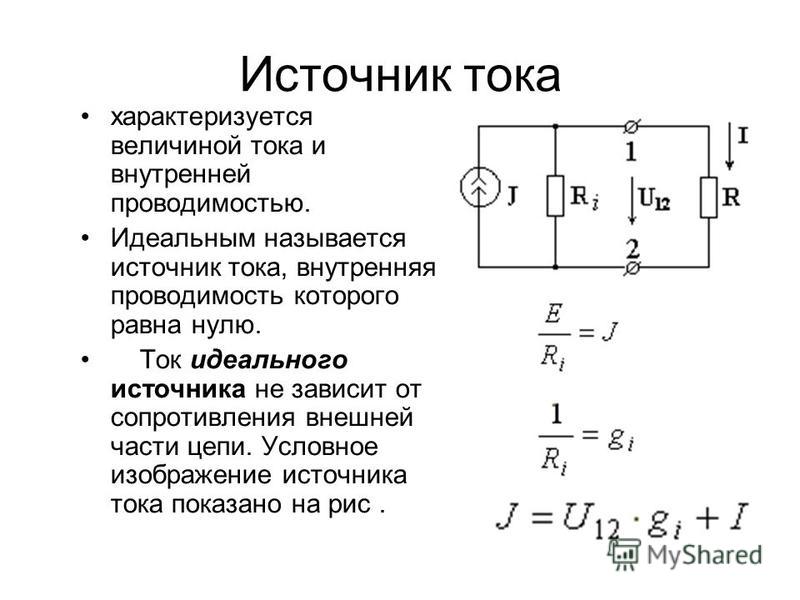 По правде говоря, обычный закон Ома работает как обычно, то есть есть какое-то напряжение, какое-то сопротивление и, следовательно, какой-то ток. Это , а не , как будто есть какая-то магия, которая каким-то образом создает ток из воздуха.
По правде говоря, обычный закон Ома работает как обычно, то есть есть какое-то напряжение, какое-то сопротивление и, следовательно, какой-то ток. Это , а не , как будто есть какая-то магия, которая каким-то образом создает ток из воздуха.
Вы можете себе представить, что реальный источник тока (в отличие от идеального варианта, где мы не заботимся о его внутренностях) имеет обычный источник напряжения (110/220 В переменного тока), преобразует его в некоторое внутреннее постоянное напряжение, а затем какое-то изящное регулирование, которое изменяет напряжение постоянного тока, которое оно подает на свою клиентскую схему, так что оно увеличивается/уменьшается, если фактический ток слишком низок или слишком высок. При изменении напряжения меняется и ток, в зависимости от нагрузки. Таким образом, реальный источник тока по-прежнему является просто источником напряжения, хотя и с быстро меняющимся/адаптирующимся напряжением, и реализация, очевидно, намного сложнее, чем стандартный источник напряжения.
На странице Википедии, посвященной текущим источникам, перечислено довольно много различных реализаций, использующих транзисторы, операционные усилители или другие активные компоненты.
\$\конечная группа\$
0
\$\начало группы\$
Дело, которое вы разоблачаете, представляет собой идеализированный элемент. Таким образом, это модель, которую вы используете для расчетов с другими моделями.
Может ли в этом случае источник тока действовать как источник напряжения?
Если вы посмотрите на регулятор, основанный на преобразователе постоянного тока в токовом режиме, вы убедитесь, что он на самом деле имеет два контура управления:
- «Внутренний» контур регулирует выходной ток в соответствии с запросом внешнего контура.
- Внешний контур, в свою очередь, «запрашивает» ток, необходимый для того, чтобы выходной сигнал соответствовал желаемому напряжению.

Таким образом, весь регулятор можно рассматривать как управляемый источник тока, обеспечивающий необходимый ток, чтобы выходное напряжение было желаемым.
\$\конечная группа\$
\$\начало группы\$
Думайте об источнике тока как об источнике энергии, который каким-то образом выдает почти постоянный ток. На практике он обычно состоит из электронных компонентов, которые измеряют ток и пытаются его стабилизировать, но, грубо говоря, вы можете сделать его с батареей на миллион вольт последовательно с резистором в один мегаом. Это даст довольно близко к одному усилителю, независимо от того, что вы к нему подключаете!
Чтобы измерить источник тока, вы должны замкнуть клеммы (почти) амперметром. Внутреннее напряжение не указано, и попытка его измерения при разомкнутой цепи может быть опасной.
И наоборот, для измерения источника напряжения вы должны использовать высокоомный измеритель, который (почти) не потребляет ток. Ток, который он может выдавать, не указан, и попытка измерить его с помощью короткого замыкания может быть опасной.
Ток, который он может выдавать, не указан, и попытка измерить его с помощью короткого замыкания может быть опасной.
\$\конечная группа\$
\$\начало группы\$
Ток — это поток заряда. Мы знаем, что в металлическом проводнике электроны беспорядочно движутся во всех направлениях. Вам нужна полная цепь и разность потенциалов, чтобы заставить их двигаться (в среднем) к положительному выводу ячейки.
Нет разности потенциалов = нет тока
\$\конечная группа\$
1
\$\начало группы\$
Не эксперт, как другие, но просто хотел добавить, когда вы видите источник тока на изображении схемы, вы не можете предположить, что напряжение на нем равно нулю. В нем есть какое-то напряжение, которое, вероятно, было вам неизвестно в начале задачи, но которое вы можете найти с помощью законов Кирхгофа.
Другая мысль заключается в том, что источник тока — это не простое устройство вроде батареи, поэтому за этой картинкой скрывается довольно сложный элемент, производящий ток. И, как сказал Питер в своем ответе, он будет регулировать напряжение на нем в зависимости от сопротивления остальной части цепи, чтобы производить ток, который он «рекламирует» для производства. Таким образом, источник тока в 1 ампер будет иметь более высокое напряжение на нем при сопротивлении 200 Ом в остальной части цепи, чем при сопротивлении 100 Ом. (А что касается того, как он получает это напряжение, вы можете просто представить себе, что источник тока — это сложное устройство, а не простое, как батарея, которое может регулировать свое собственное напряжение по мере необходимости, чтобы получить правильный ток для данной цепи, с которой он сталкивается. )
\$\конечная группа\$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Я не понимаю источник тока, источник напряжения, бесконечное сопротивление, нулевое сопротивление и т. д.
Печальная правда
… все онлайн-руководства и ответы повторяют одно и то же.
Да, это грустная правда — одни и те же формальные объяснения повторяются тысячи раз… но эти столь важные понятия электричества и электроники остаются непонятыми… и мы начинаем искать собственное объяснение. Что я могу сделать, так это предложить вам самые простые из возможных интуитивных объяснений этих понятий, чтобы обогатить ваше представление о них.
Роль сопротивления
Если что-то обладает бесконечным сопротивлением, ничего не произойдет, потому что все заблокировано?
Я понимаю ваше удивление… но это не просто «бесконечное сопротивление» или «разомкнутая цепь»; это более сложное «дифференциальное бесконечное сопротивление». Не блокирует ток; он блокирует только текущие изменения.
Не блокирует ток; он блокирует только текущие изменения.
Дифференциальное сопротивление — это сложное понятие электроники… но, к счастью, понятия электроники можно объяснить более простыми понятиями электричества. Таким образом, мы можем объяснить, что такое странное дифференциальное сопротивление, с помощью более простого обычного (он же омического, постоянного, статического, линейного…) сопротивления.
Практически все типы источников (как напряжения, так и тока) реализованы одной и той же конфигурацией двух последовательно соединенных элементов – «идеального» источника напряжения и резистора (существующего или преднамеренно введенного сопротивления). Тип сопротивления определяет тип источника. Мне удалось выделить три типа сопротивлений, ведущих к шести типам источников; посмотрим какие они.
Источники напряжения
1. «Идеальный» источник напряжения с нулевым сопротивлением. Поскольку напряжение является основной величиной, определяющей ток, основным элементом всех типов источников является источник напряжения. Если бы последовательно не было сопротивления, не было бы падения напряжения (потери), и это был бы «идеальный» источник постоянного напряжения.
Если бы последовательно не было сопротивления, не было бы падения напряжения (потери), и это был бы «идеальный» источник постоянного напряжения.
2. Источник реального напряжения с постоянным низким сопротивлением. Практически всегда имеется (нежелательное) последовательное сопротивление и падение напряжения на нем при подключении нагрузки. Проблема не столько в самом падении напряжения, сколько в его вариациях при изменении тока нагрузки. Такое расположение будет действовать как неидеальный источник напряжения.
3. Источник постоянного напряжения с нулевым дифференциальным сопротивлением. Мы можем сделать приведенный выше несовершенный источник напряжения почти «идеальным» с помощью простого приема — «динамического сопротивления». Для этого замените постоянный резистор переменным резистором (реостатом) и начните изменять его сопротивление в направлении, противоположном изменению тока.
Фокус прост — по закону Ома V = I.R, при увеличении тока сопротивление уменьшается (и v. v.)… а произведение (падение напряжения) не меняется… как будто сопротивления нет ( это ноль). Например, так действуют диоды с прямым смещением. «Сопротивление» между коллектором и эмиттером транзистора в эмиттерном повторителе является еще одним примером нулевого дифференциального сопротивления.
v.)… а произведение (падение напряжения) не меняется… как будто сопротивления нет ( это ноль). Например, так действуют диоды с прямым смещением. «Сопротивление» между коллектором и эмиттером транзистора в эмиттерном повторителе является еще одним примером нулевого дифференциального сопротивления.
Итак, «нулевое выходное сопротивление» источника постоянного напряжения — это «противоположно изменяющееся» (динамическое) сопротивление… оно же «нулевое дифференциальное сопротивление». Он обладает свойством «стабилизирующего напряжение дифференциального сопротивления» с вертикальной кривой IV.
Интересно, что если сильно усилить этот прием, то получится источник напряжения с S-образным отрицательным сопротивлением (пример — неоновая лампа).
Источники тока
1. Реальный источник тока с постоянным низким сопротивлением. Приведенный выше реальный источник напряжения может действовать как простой источник тока, поскольку последовательно включенный резистор ограничивает ток.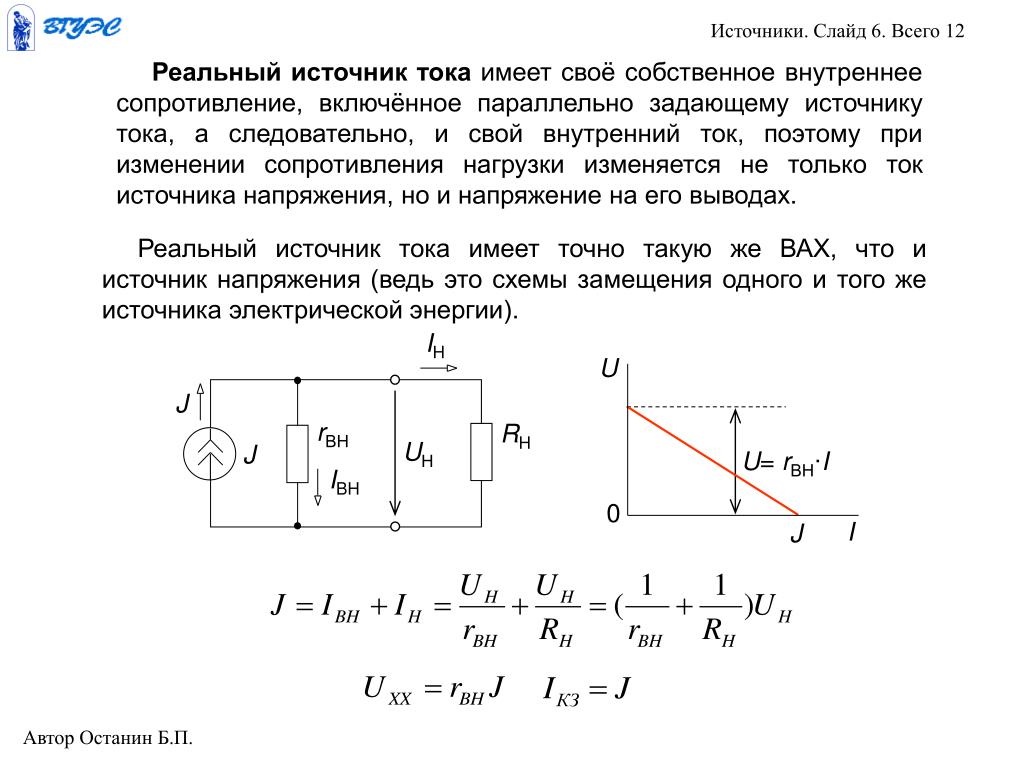 Только это несовершенный источник тока, так как ток сильно зависит от нагрузки и будет срабатывать при изменении сопротивления нагрузки (напряжения).
Только это несовершенный источник тока, так как ток сильно зависит от нагрузки и будет срабатывать при изменении сопротивления нагрузки (напряжения).
2. Реальный источник тока с постоянным высоким сопротивлением. Если мы увеличим сопротивление (а также напряжение), ток будет меньше зависеть от нагрузки, и такое расположение будет действовать как относительно хороший источник тока. Он станет совершенным, если мы увеличим и напряжение, и сопротивление до бесконечности (согласно известному определению идеального источника напряжения в электричестве)… но потери будут огромными. В электронике нужно более умное решение…
3. Источник постоянного тока с бесконечным дифференциальным сопротивлением. Мы можем преобразовать приведенный выше несовершенный источник напряжения в почти «идеальный» источник тока с помощью того же трюка с динамическим сопротивлением. Только переменное сопротивление мы теперь меняем в ту же сторону, что и изменения напряжения.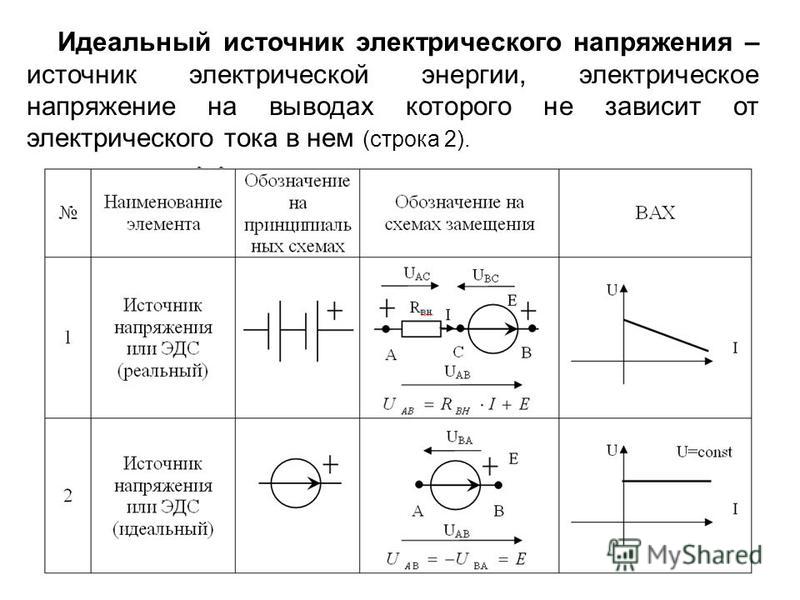


 Мощность. Сопротивление. Ток. Напряжение. Закон Ома.
Мощность. Сопротивление. Ток. Напряжение. Закон Ома. д.с.) источника и обозначается e(t).
д.с.) источника и обозначается e(t).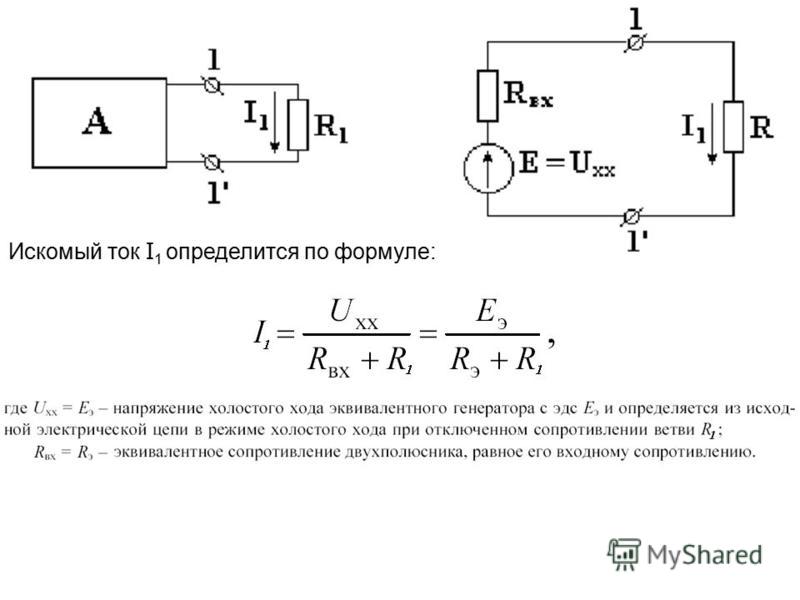




 Что понимают под положительными направлениями тока и напряжения.
Что понимают под положительными направлениями тока и напряжения.
 Для увеличения сопротивления (НАГРУЗКА) потребляется меньше тока.
Для увеличения сопротивления (НАГРУЗКА) потребляется меньше тока.