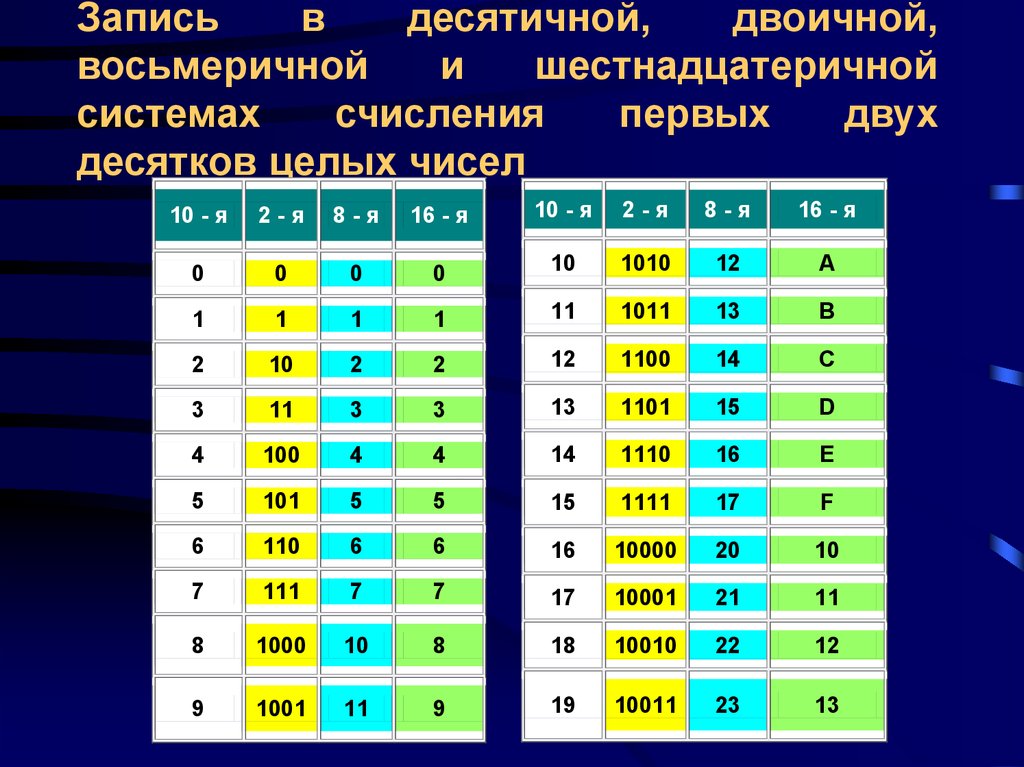
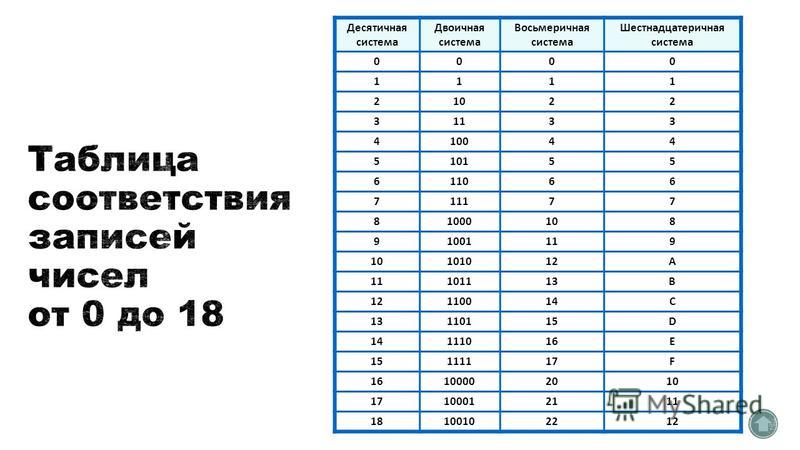
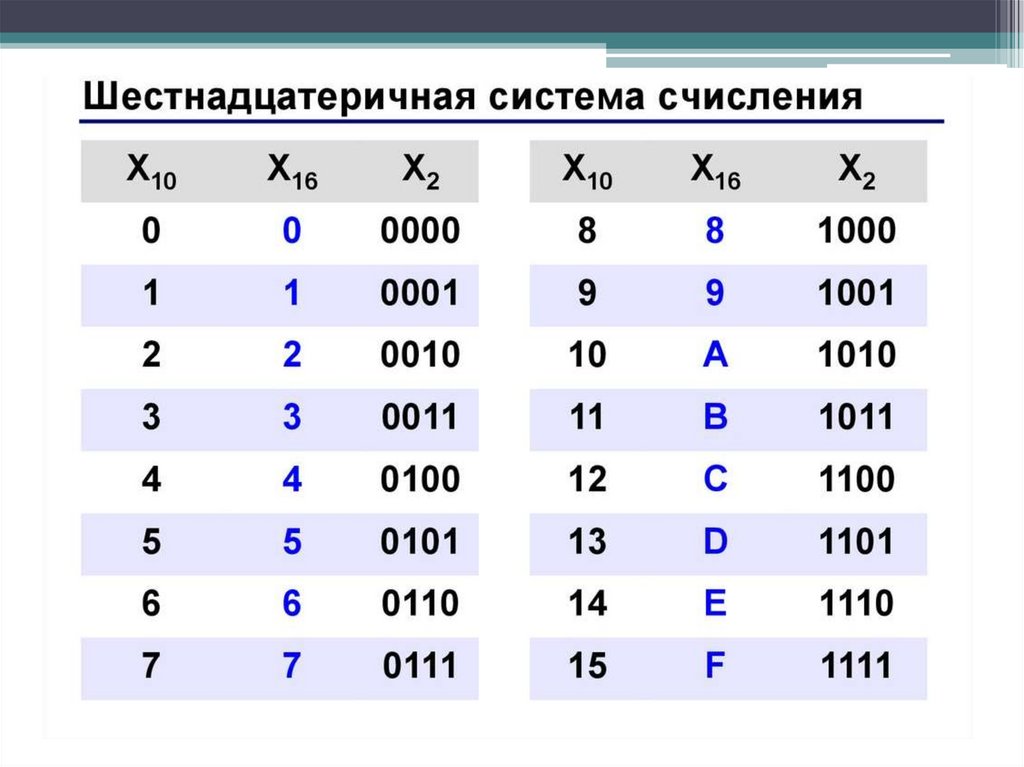
Шестеричная система счисления
Содержание:
Что такое шестеричная система счисления
Как перевести целое десятичное число в шестеричную систему счисления
Как перевести десятичную дробь в шестеричную систему счисления
Как перевести число из шестеричной системы счисления в десятичную
Как перевести дробное шестеричное число в десятичное
Таблица значений десятичных чисел от 0 до 100 в шестеричной системе счисления
Шестеричная система счисления, является позиционной системой счисления, то есть имеется зависимость от позиции цифры в записи числа. Для записи числа в шестеричной системе счисления используется шесть цифр 0, 1, 2, 3, 4 и 5. Для определения в какой системе счисления записано число, внизу, справа от числа ставят цифру, которая называется основанием системы счисления. Например, 33536 или 2156
Если вам необходимо перевести число любой системы счисления в другую систему счисления, воспользуйтесь
калькулятором систем счисления с подробным решением онлайн.
Как перевести целое десятичное число в шестеричную систему счисления
Для того, чтобы перевести целое десятичное число в шестеричную систему счисления нужно десятичное число делить на 6 до тех пор, пока неполное частное не будет равно нулю. В результате будет получено число из остатков деления записанное справа налево.
Например, переведем число 11510 в шестеричную систему счисления:
115 : 6 = 19 остаток: 1
19 : 6 = 3 остаток: 1
3 : 6 = 0 остаток: 3
11510 = 3116
Как перевести десятичную дробь в шестеричную систему счисления
Для того чтобы перевести десятичную дробь в шестеричную систему счисления необходимо сначала перевести целую часть десятичной дроби в шестеричную систему счисления,
а затем дробную часть, последовательно умножать на 6, до тех пор, пока в дробной части произведения не получиться ноль (результатом произведения будет целое число)
или не будет достигнуто необходимое количество знаков после запятой.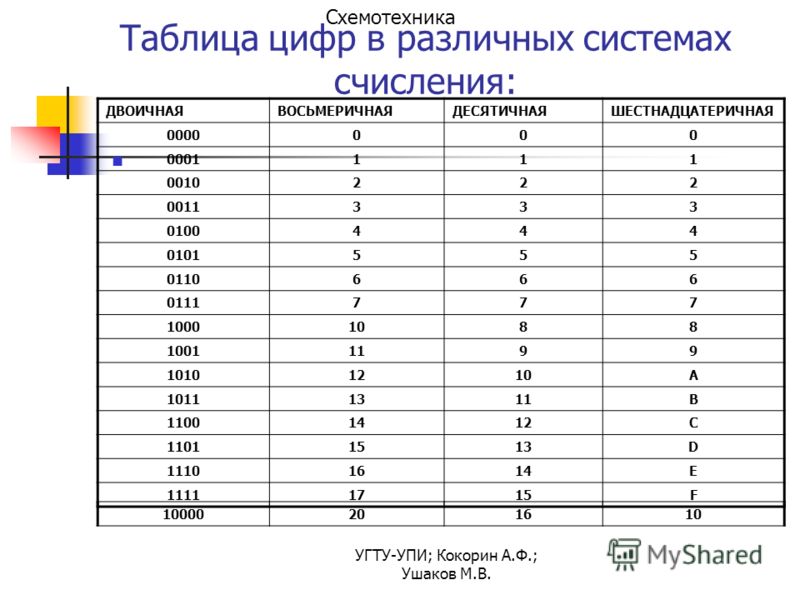
Если в результате умножения целая часть не равна нулю, тогда необходимо заменить значение целой части на ноль.
В результате будет получено число из целых частей произведений, записанное слева направо.
Например, переведем десятичное число 95.3610 в шестеричную систему счисления:
Переведем целую часть
95 : 6 = 15 остаток: 5
15 : 6 = 2 остаток: 3
2 : 6 = 0 остаток: 2
9510 = 2356
Переведем дробную часть
0.36 · 6 = 2.16
0.16 · 6 = 0.96
0.96 · 6 = 5.76
0.76 · 6 = 4.56
0.56 · 6 = 3.36
0.36 · 6 = 2.16
0.16 · 6 = 0.96
0.96 · 6 = 5.76
0.76 · 6 = 4.56
0.56 · 6 = 3.36
0.3610 = 0.20543205436
95.3610 = 235.20543205436
Шестеричные дроби, как и десятичные могут быть как конечными, так и бесконечными. Не всегда конечная десятичная дробь может быть представлена конечной шестеричной.
В данном примере получается бесконечная периодическая шестеричная дробь, поэтому умножение на 6 можно производить бесконечное число раз и все равно дробная часть частного не будет равна нулю.
В данном случае десятичная дробь 95.36 не может быть точно представлена в шестеричной системе счисления.
К примеру, дробь 2.510 может быть представлена в двоичной системе счисления в виде конечной 2.5
Как перевести число из шестеричной системы счисления в десятичную
Для того, чтобы перевести число из шестеричной системы счисления в десятичную систему счисления, необходимо записать позиции каждой цифры в числе с права на лево начиная с нуля.
Каждая позиция цифры будет степенью числа 6, так как система счисления 6-ичная. Необходимо последовательно умножить каждое число на 6 в
степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.
| Позиция в числе | 4 | 3 | 2 | 1 | 0 |
| Число | 5 | 0 | 4 | 2 | 1 |
504216 = 5 ⋅ 64 + 0 ⋅ 63 + 4 ⋅ 62 + 2 ⋅ 61 + 1 ⋅ 60 = 663710
Как перевести дробное шестеричное число в десятичное
Для того, чтобы перевести дробное шестеричное число в десятичное, необходимо записать дробное шестеричное число, убрав точку и затем сверху расставить индексы.
Индексы в дробной части числа начинаются от -1 и продолжаются на уменьшение вправо, индексы в целой части начинаются с 0 и ставятся с права на лево по возрастанию.
Каждая позиция цифры (индекс) будет степенью числа 6, так как система счисления 6-ичная. Необходимо последовательно умножить каждое число на
6 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.
Например, переведем дробное шестеричное число 13.536 в десятичное:
| Позиция в числе | 1 | 0 | -1 | -2 |
| Число | 1 | 3 | 5 | 3 |
13.536 = 1 ⋅ 61 + 3 ⋅ 60 + 5 ⋅ 6-1 + 3 ⋅ 6-2 = 9.916666666666666666666666666910
Таблица значений десятичных чисел от 0 до 100 в шестеричной системе счисления
| Значение числа в десятичной системе счисления | Значение числа в шестеричной системе счисления |
| 010 | 06 |
| 110 | 16 |
| 2 | 26 |
| 310 | 36 |
| 410 | 46 |
| 510 | 56 |
| 610 | 106 |
| 710 | 116 |
| 810 | 126 |
| 910 | 136 |
| 1010 | 146 |
| 1110 | 156 |
| 1210 | 206 |
| 1310 | 216 |
| 1410 | 226 |
| 1510 | 236 |
| 1610 | 246 |
| 1710 | 256 |
| 1810 | 306 |
| 1910 | |
| 2010 | 326 |
| 2110 | 336 |
| 2210 | 346 |
| 2310 | 356 |
| 2410 | 406 |
| 416 | |
| 2610 | 426 |
| 2710 | 436 |
| 2810 | 446 |
| 2910 | 456 |
| 3010 | 506 |
| 3110 | 516 |
| 3210 | 526 |
| 3310 | 536 |
| 3410 | 546 |
| 3510 | 556 |
| 3610 | 1006 |
| 3710 | 1016 |
| 3810 | 1026 |
| 3910 | 1036 |
| 4010 | 1046 |
| 4110 | 1056 |
| 4210 | 1106 |
| 4310 | 1116 |
| 4410 | 1126 |
| 4510 | 1136 |
| 4610 | 1146 |
| 4710 | 1156 |
| 4810 | 1206 |
| 4910 | 1216 |
| 5010 | 1226 |
| Значение числа в десятичной системе счисления | Значение числа в шестеричной системе счисления |
| 5110 | 1236 |
| 5210 | 1246 |
| 5310 | 1256 |
| 5410 | 1306 |
| 5510 | 1316 |
| 5610 | 1326 |
| 5710 | 1336 |
| 5810 | 1346 |
| 5910 | 1356 |
| 6010 | 1406 |
| 6110 | 1416 |
| 6210 | 1426 |
| 6310 | 1436 |
| 6410 | 1446 |
| 6510 | 1456 |
| 6610 | 1506 |
| 6710 | 1516 |
| 6810 | 1526 |
| 6910 | 1536 |
| 7010 | 1546 |
| 7110 | 1556 |
| 7210 | 2006 |
| 7310 | 2016 |
| 7410 | 2026 |
| 7510 | 2036 |
| 7610 | 2046 |
| 7710 | 2056 |
| 7810 | 2106 |
| 7910 | 2116 |
| 8010 | 2126 |
| 8110 | 2136 |
| 8210 | 2146 |
| 8310 | 2156 |
| 8410 | 2206 |
| 8510 | 2216 |
| 8610 | 2226 |
| 8710 | 2236 |
| 8810 | 2246 |
| 8910 | 2256 |
| 9010 | 2306 |
| 9110 | 2316 |
| 9210 | 2326 |
| 9310 | 2336 |
| 9410 | 2346 |
| 9510 | 2356 |
| 9610 | 2406 |
| 9710 | 2416 |
| 9810 | 2426 |
| 9910 | 2436 |
| 10010 | 2446 |
Шестнадцатеричная система счисления простыми словами.
ПримерыАвтор Савельев Николай На чтение 4 мин Просмотров 8.8к. Опубликовано Обновлено
Шестнадцатеричная система (англ. — Hexadecimal system ) — это базовая система счисления с снованием 16. Она, наряду с десятичной и двоичной, является одной из наиболее часто встречающихся систем счисления в мире электроники и программирования. Важно понимать, как она работает, потому что во многих случаях имеет смысл представлять число в ней, а не в двоичной или десятичной.
Шестнадцатеричная система счисления — позиционная система счисления по основанию 16.
Википедия
Существует 16 возможных цифр, которые используют для представления чисел. 10 числовых значений, которые вы привыкли видеть в десятичных числах: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9; эти значения по-прежнему представляют то же значение, что и в десятичной системе.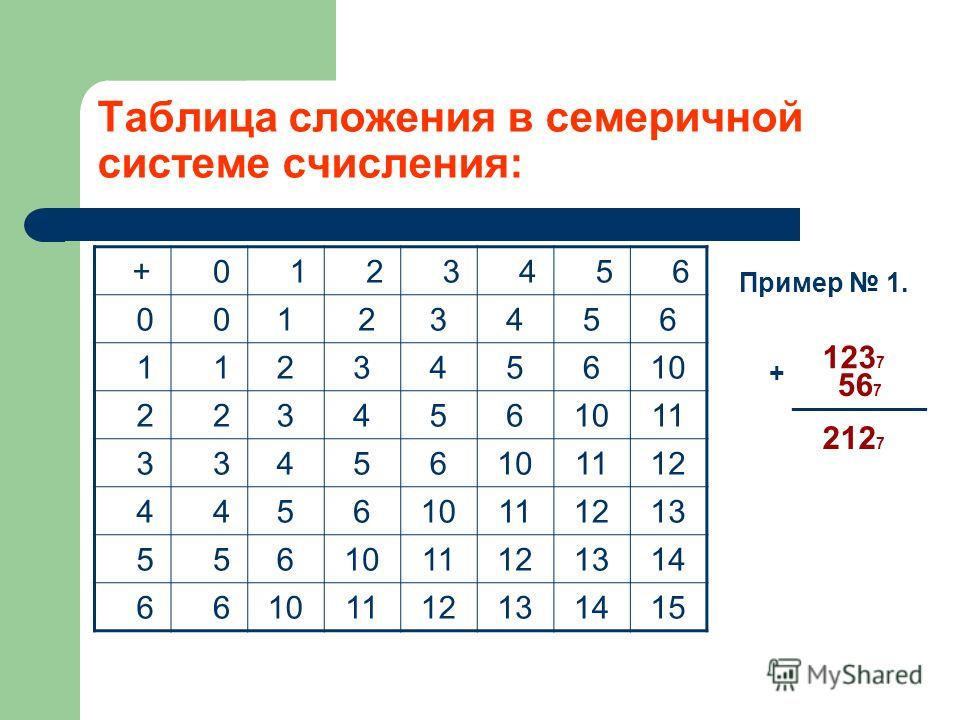
Остальные шесть цифр представлены как A, B, C, D, E и F, которые соответствуют числам 10, 11, 12, 13, 14 и 15.
Возможно, Вы столкнетесь с представлением чисел от 10 до 15 в верхнем и нижнем регистрах. Оба варианта считаются верными. Например, A3F — это то же число, что и a3f.
Эта таблица показывает какой шестнадцатеричной цифре эквивалентно значение в десятичном и двоичном формате.
| Десятичный (основание 10) | Двоичный (основание 2) | Шестнадцатеричный (основание 16) |
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | А |
| 11 | 1011 | B |
| 12 | 1100 | С |
| 13 | 1101 | D |
| 14 | 1110 | Е |
| 15 | 1111 | F |
Содержание
- Перевод из шестнадцатеричной системы и в нее
- Преобразование из десятичной в шестнадцатеричную систему и обратно
- Преобразование из двоичной в шестнадцатеричную систему и обратно
- Использование шестнадцатеричной системы
- Цвета
Перевод из шестнадцатеричной системы и в нее
Преобразование из десятичной в шестнадцатеричную систему и обратно
Чтобы перевести десятичное число в шестнадцатеричное, нужно следовать простому алгоритму преобразования:
- Делим десятичное число на 16.
- Записываем остаток и переводим его в шестнадцатеричный формат.
- Делим результат прошлого действия снова на 16.
- Повторяем, пока в результате мы не получим 0.
- Переписываем записанные остатки в обратном порядке.
- Пример:
Переведем десятеричное число 1515 в шестнадцатеричную систему
| Деление | Частное | Остаток | Порядок записи (от последнего к первому) |
| 1515/16 | 94 | 11 = B | 3 |
| 94/16 | 5 | 14 = E | 2 |
| 5/16 | 0 | 5 = 5 | 1 |
Ответ: 5EB
Читайте также: Проверяю стратегию Мартингейла на Python и показываю, почему она не работает
Чтобы перевести шестнадцатеричное число в десятичное, нужно каждую цифру с конца этого числа умножить на 16 в степени, соответствующей разряду этой цифры.
Преобразование из двоичной в шестнадцатеричную систему и обратно
Чтобы перевести двоичное число в шестнадцатеричное, нужно разделить его на группы по 4 цифры и заменить каждую группу на эквивалент из таблицы
- Пример:
Переведем двоичное число 1010000011111 в шестнадцатеричную систему
Для этого разбиваем число на группу по 4 цифры: 0001 0100 0001 1111
0001 = 1; 0100 = 4; 0001 = 1; 1111 = F
Ответ: 141F
Чтобы сделать обратное преобразование, нужно просто каждую цифру шестнадцатеричного числа заменить на эквивалент по таблице
- Пример:
Переведем шестнадцатеричное число 141F в двоичную систему
1= 0001; 4 = 0100; 1 = 0001; F = 1111
Ответ: 1010000011111
Использование шестнадцатеричной системы
По большей части, шестнадцатеричные коды используются во многих областях вычислительной техники для сокращения двоичного кода до более понятной формы.
Шестнадцатеричный код переводится в двоичный для использования на компьютере. Вот некоторые примеры использования шестнадцатеричного кода:
- Ссылки на цвета в HTML и CSS
- Язык ассемблера
- Сообщения об ошибках
Цвета
Hex система счисления может использоваться для представления цветов на сайтах и в программах редактирования изображений в формате #RRGGBB (# = показатель того, что число было записано в шестнадцатеричном формате, RR = красный, GG = зеленый, BB = синий). Этот система использует две шестнадцатеричных цифры для каждого цвета, например, #AA3300.
Как одна шестнадцатеричная цифра представляет 4 бита, так две шестнадцатеричные цифры вместе составляют 8 бит (1 байт). Значения для каждого цвета находятся в диапазоне от 00 до FF. В двоичной системе, 00 — это 00000000, а FF — это 11111111. Это дает 256 возможных значений для каждого из трех цветов (256 красных х 256 зеленых х 256 синих), а в сумме это больше 16 миллион цветов.
- #FF0000 будет самым чистым красным цветом — Максимум красного, 0 зеленого и 0 синего.
- Черный это #000000 — ни красного, ни зеленого, ни синего.
- Белый — это #FFFFFF — при смешении всех цветов.
Таблица преобразования десятичной-шестнадцатеричной-двоичной системы
Таблица преобразования десятичной-шестнадцатеричной-двоичной системы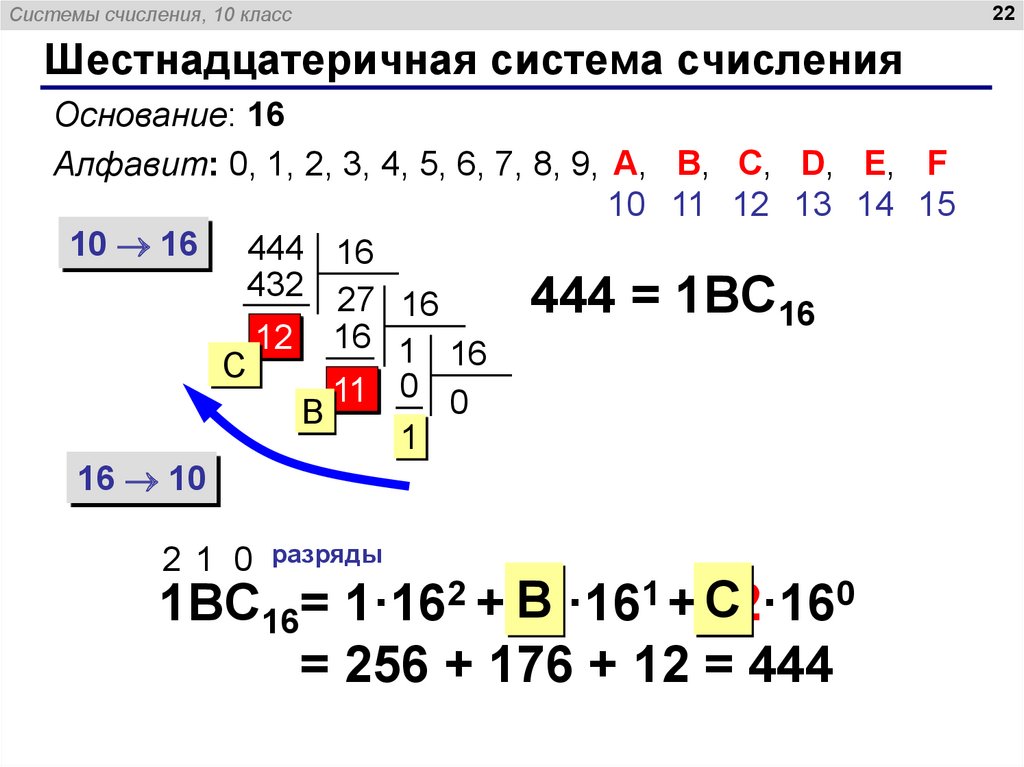
«>
см
э. : Это документ afdl в базе знаний.
Последнее изменение: 2017-11-29 15:56:21 .
Что такое шестнадцатеричная система счисления? Таблица, Преобразование, Примеры
Шестнадцатеричная система счисления — это тип системы счисления, базовое значение которого равно 16. Иногда оно также произносится как «шестнадцатеричный» . Шестнадцатеричные числа представлены всего 16 символами. Эти символы или значения 0, 1, 2, 3, 4, 5, 6, 7, 8, 9., A, B, C, D, E и F. Каждая цифра представляет десятичное значение. Например, D равно основанию 10 13.
Шестнадцатеричные системы счисления могут быть преобразованы в другие системы счисления, такие как двоичная система счисления (основание 2), восьмеричная система счисления (основание 8) и десятичная система счисления (основание 10). Концепция системы счисления широко объясняется в программе 9 класса.
Список из 16 шестнадцатеричных цифр с их эквивалентным десятичным, восьмеричным и двоичным представлением приведен здесь в виде таблицы, которая поможет в преобразовании системы счисления.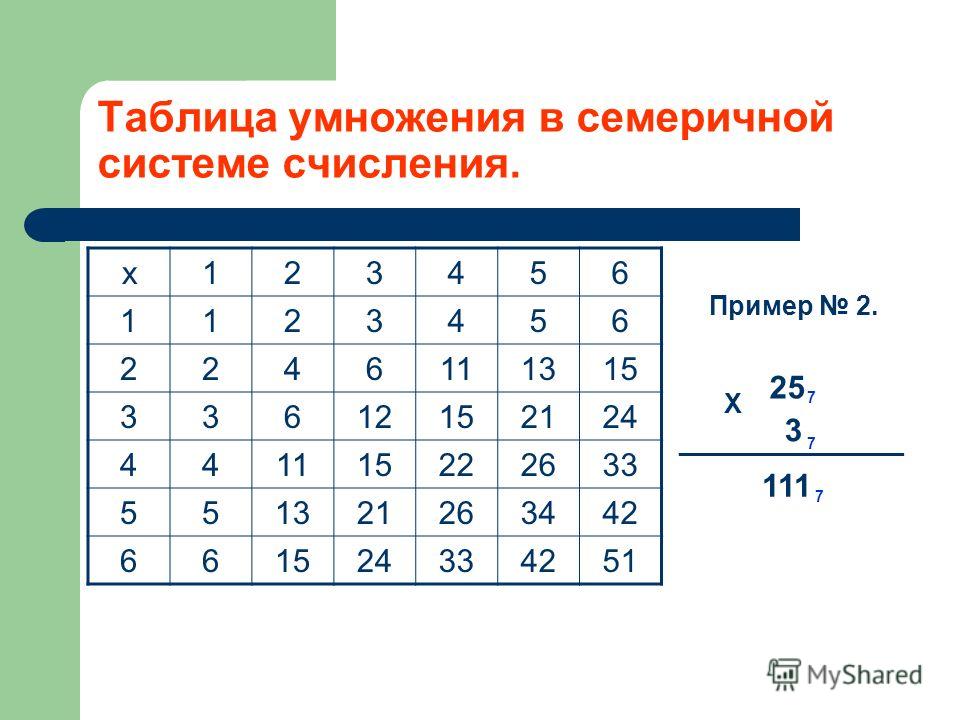
Этот список также можно использовать в качестве переводчика или конвертера.
Таблица шестнадцатеричной системы счисления
Ниже приведена таблица шестнадцатеричных систем счисления с эквивалентными значениями двоичной и десятичной систем счисления.
| Десятичные числа | 4-битный двоичный номер | Шестнадцатеричный номер |
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | А |
| 11 | 1011 | Б |
| 12 | 1100 | С |
| 13 | 1101 | Д |
| 14 | 1110 | Е |
| 15 | 1111 | Ф |
Ниже ссылка на скачивание таблицы.
Учащиеся могут загрузить PDF-файл и учиться в автономном режиме.
Скачать PDF – Шестнадцатеричная система счисления
Преобразование шестнадцатеричной системы счисления
Как мы знаем, в шестнадцатеричной системе счисления 16 цифр, представленных от 0 до 9 так же, как десятичные, но после этого она начинается с алфавитного представления предшествующих чисел, таких как A, B, C, D и E. Пусть мы видим преобразование ‘hex’ в другие системы счисления.
Преобразование шестнадцатеричных чисел в десятичные
Здесь вы увидите представление шестнадцатеричного числа в десятичной форме.
Шестнадцатеричный | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | А | Б | С | Д | Е | Ф |
| Десятичный | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
Преобразование десятичного числа в шестнадцатеричное
Вы научились преобразовывать шестнадцатеричные числа в десятичные числа.
Теперь давайте выясним, как мы можем преобразовать десятичное число в шестнадцатеричную систему счисления. Выполните следующие шаги:
- Сначала разделите число на 16
- Возьмите частное и снова разделите на 16
- Остаток даст шестнадцатеричное значение
- Повторяет шаги до тех пор, пока частное не станет равным 0
Пример: Преобразовать (242) 10 в шестнадцатеричное число.
Решение : Разделите 242 на 16 и повторяйте шаги, пока в частном не останется 0.
Следовательно, (242) 10 = (F2) 16
Преобразование шестнадцатеричных чисел в восьмеричные
Здесь вы увидите представление шестнадцатеричного числа в восьмеричной форме.
Шестнадцатеричный | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | А | Б | С | Д | Э | Ф |
| Восьмеричный | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
Преобразование восьмеричных чисел в шестнадцатеричные
Чтобы преобразовать восьмеричное число в шестнадцатеричное, мы должны сначала преобразовать восьмеричное число в десятичное, а затем десятичное в шестнадцатеричное.
Давайте разберемся с этим на примере;
Пример: Преобразовать (121) 8 в шестнадцатеричное число.
Решение: Сначала преобразуйте 121 в десятичное число.
⇒ 1 × 8 2 + 2 × 8 1 + 1 × 8 0
⇒ 1 × 64 + 2 × 8 + 1 × 1
⇒ 64 + 16 + 1
(121) 8 = 81 10
Теперь преобразуем 81 10 в шестнадцатеричное число.
Следовательно, 81 10 = 51 16
Преобразование шестнадцатеричных чисел в двоичные
Здесь вы увидите представление шестнадцатеричного числа в двоичной форме. Мы можем использовать только 4 цифры для представления каждого шестнадцатеричного числа, где каждая группа имеет отличное значение от 0000 (для 0) до 1111 (для F = 15 = 8 + 4 + 2 + 1).
Шестнадцатеричный | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | А | Б | С | Д | Е | Ф |
| Двоичный | 0 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
Преобразование двоичного кода в шестнадцатеричный
Преобразование двоичного кода в шестнадцатеричный — простой способ.
Вам просто нужно поместить значения двоичного числа в соответствующее шестнадцатеричное число.
Пример: Преобразовать (11100011) 2 в шестнадцатеричное число.
Решение: Из таблицы мы можем написать 11100011 как E3.
Следовательно, (11100011) 2 = (E3) 16
Факты о шестнадцатеричной системе счисления
- Из многих типов методов представления чисел шестнадцатеричная система счисления имеет значение основания 16.
- Таким образом, шестнадцатеричные числа имеют 16 символов или цифровых значений, то есть 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
- A, B, C, D, E, F представляют собой однобитовые представления 10, 11, 12, 13, 14 и 15 соответственно.
- Добавление 9Префикс 2104 o или префикс h указывает на шестнадцатеричный формат.
- Степень 16 — это вес позиции каждой цифры.
Решенные примеры в шестнадцатеричной системе счисления
Пример 1: Что такое 5C6 (шестнадцатеричный)?
Решение: Шаг 1: «5» — это позиция «16 x 16», что означает 5 x 16 x 16
Шаг 2: «C» (12) находится в позиции «16», что означает 12 x 16.
Шаг 3: «6» в позиции «1», значит 6.
Ответ: 5C6 = 5 х 16 х 16 + 12 х 16 + 6 = (1478) в десятичном виде.
Пример 2: Что такое 3C5 (шестнадцатеричный)?
Решение: Шаг 1: «3» — это позиция «16 x 16», так что это означает 3 x 16 x 16
Шаг 2: «C» (12) находится в позиции «16», что означает 12 x 16.
Шаг 3: «5» находится в позиции «1», что означает 5.
Ответ: 3C5 = 3 x 16 x 16 + 12 x 16 + 5 = (965) в десятичном виде.
Пример 3: Что такое 7B5 (шестнадцатеричный)?
Решение: Шаг 1: «7» — это позиция «16 x 16», так что это означает 7 x 16 x 16
Шаг 2: «B» (11) находится в позиции «11», что означает 11 x 16.
Шаг 3: 5 дюймов в позиции «1», что означает 5.
Ответ: 7B5 = 7 х 16 х 16 + 11 х 16 + 5 = (1973) в десятичном виде.
Пример 4: Что такое 2E8 (шестнадцатеричный)?
Решение: Шаг 1: «2» — это позиция «16 x 16», так что это означает 2 x 16 x 16
Шаг 2: буква «Е» (14) находится в позиции «16», что означает 14 x 16.
Шаг 3: «2» стоит в позиции «1», что означает 2.
Ответ: 2E8 = 2 x 16 x 16 + 14 x 16 + 8 = (744) в десятичном виде.
Пример 5: Что такое 4F8 (шестнадцатеричный)?
Решение: Шаг 1: «4» — это позиция «16 x 16», что означает 4 x 16 x 16
Шаг 2: «F» (15) находится в позиции «16», что означает 15 x 16.
Шаг 3: «8» стоит в позиции «1», что означает 8.
Ответ: 4F8 = 4 x 16 x 16 + 15 x 16 + 8 = (1272) в десятичной системе.
Практические вопросы
- Что такое 5D 16 в десятичном виде?
- Преобразование десятичного числа 21 в шестнадцатеричное число.
- Что такое 0110111 2 в шестнадцатеричном формате?
Связанные статьи
- Преобразование системы счисления
- Двоичная система счисления
- Восьмеричная система счисления
- Шестнадцатеричный калькулятор
- Система счисления для класса
- Важные вопросы Класс 9 Математика Глава 1 Система счисления
Продолжайте посещать BYJU’S и подписывайтесь на наш канал YouTube, чтобы изучать систему счисления и другие математические темы в веселой и увлекательной форме.
