Таблицы истинности

Таблицы истинности

---

Приоритет логических операций:

1) инверсия 2) конъюнкция 3) дизъюнкция 4) импликация и эквивалентность

Как составить таблицу истинности?

Согласно определению, таблица истинности логической формулы выражает соответствие между всевозможными наборами значений переменных и значениями формулы.

Для формулы, которая содержит две переменные, таких наборов значений переменных всего четыре: (0, 0), (0, 1), (1, 0), (1, 1). Если формула содержит три переменные, то возможных наборов значений переменных восемь (0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1). Количество наборов для формулы с четырьмя переменными равно шестнадцати и т.д. Удобной формой записи при нахождении значений формулы является таблица, содержащая кроме значений переменных и значений формулы также и значения промежуточных формул.

Примеры.

1. Составим таблицу истинности для формулы , которая содержит две переменные x и y. В первых двух столбцах таблицы запишем четыре возможных пары значений этих переменных, в последующих столбцах — значения промежуточных формул и в последнем столбце — значение формулы. В результате получим таблицу:

Из таблицы видно, что при всех наборах значений переменных x и y формула принимает значение 1, то есть является тождественно истинной.

2. Таблица истинности для формулы

Из таблицы видно, что при всех наборах значений переменных x и y формула принимает значение 0, то есть является тождественно ложной.

3. Таблица истинности для формулы :

Из таблицы видно, что формулав некоторых случаях принимает значение 1, а в некоторых — 0, то есть является выполнимой.

Пример1:

Вася спросил у мамы: «Можно пойти в кино или на футбол?» Мама ответила отрицательно. Как поступить мальчику?

Проверим правильность этого закона с помощью таблицы истинности.

Пример2:

В классе оказалось разбито стекло. Учитель объясняет директору: это сделал Коля или Саша. Но Саша этого на делал, т.к. в это время сдавал мне зачет. Следовательно, это сделал Коля

Решение: Формализуем данное сложное высказывание.

К — это сделал Коля

С — это сделал Саша

Кол-во простых высказываний n = 2.

1) Определить количество строк и столбцов в таблице истинности.

Т.к. каждое из простых высказываний может принимать всего два значения (0 или 1), то количество разных комбинаций значений n высказываний — 2 n . Количество строк в таблице = 2 n + строка на заголовок. Количество столбцов в таблице равно сумме количества простых высказываний (n) и количества разных логических операций, входящих в сложное высказывание.

В нашем примере: количество строк — 2*2 + 1 = 5 , столбцов — 2 + 4 = 6

2) Начертить таблицу и заполнить заголовок

Первая строка — номера столбцов. Вторая строка промежуточные формулы и соответствующие им условные записи операций над значениями .

3) Заполнить первые n столбцов.

В нашем примере сначала заполняем 1-й и 2-й столбцы.

4) Заполнить остальные столбцы.

В соответствии с таблицами истинности соответствующих логических операций, причем при заполнении каждого столбца операции выполняются над значениями одного или двух столбцов, расположенных левее заполняемого. Итак, вычисляем значения 3-го столбца по значениям 2-го, потом значения 4-го — по значениям 1-го и 2-го…

Вывод: получили в последнем столбце все единицы. Значит, значение сложного высказывания истинно при любых значениях простых высказываний К и С. Следовательно, учитель рассуждал логически правильно.

---

§3.2. Алгебра логики | Урок 63 часть 3

Планирование уроков на учебный год (по учебнику Н.Д. Угриновича, профильный уровень)

Главная | Информатика и информационно-коммуникационные технологии | Планирование уроков и материалы к урокам | 10 классы | Планирование уроков на учебный год (по учебнику Н.Д. Угриновича, профильный уровень) | §3.2. Алгебра логики

Содержание урока

3.2.1. Логическое умножение, сложение и отрицание

Алгебра логики

Логические переменные

Логическое умножение (конъюнкция)

Логическое сложение (дизъюнкция)

Логическое отрицание (инверсия)

Практическое задание «Таблицы истинности»

Контрольные вопросы. Задания. Компьютерный практикум

3.2.2. Логические выражения

3.2.3. Логические функции

3.2.4. Логические законы и правила преобразования логических выражений

3.2.5. Решение логических задач

Логическое умножение (конъюнкция)

Объединение двух (или нескольких) высказываний в одно с помощью союза «и» называется операцией логического умножения или конъюнкцией.

Составное высказывание, образованное в результате операции логического умножения (конъюнкции), истинно тогда и только тогда, когда истинны все входящие в него простые высказывания.

Из приведенных ниже четырех составных высказываний, образованных с помощью операции логического умножения, истинно только четвертое, так как в первых трех составных высказываниях хотя бы одно из простых высказываний ложно:

1) «2 х 2 = 5 и 3 х 3 =	10»;
2) «2 х 2 = 5 и 3 х 3 =	9»;
3) «2 х 2 = 4 и 3 х 3 =	10»;
4) «2 х 2 = 4 и 3 х 3 =	9». 

Перейдем теперь от записи высказываний на естественном языке к их записи на формальном языке алгебры логики. Операцию логического умножения (конъюнкцию) принято обозначать значком «&» (амперсенд). Операция логического умножения, аргументами которой являются логические переменные А и В, записывается следующей формулой:

А & В. (3.1)

Значение логической операции логического умножения задается с помощью таблицы истинности

. Таблица истинности показывает, какие значения дает логическая операция при всех возможных наборах ее аргументов (табл. 3.1). Результатом операции логического умножения является «истина» (1) тогда и только тогда, когда оба аргумента принимают значения «истина» (1).

Таблица 3.1. Таблица истинности конъюнкции (логического умножения)

По таблице истинности легко определить истинность составного высказывания, образованного с помощью операции логического умножения.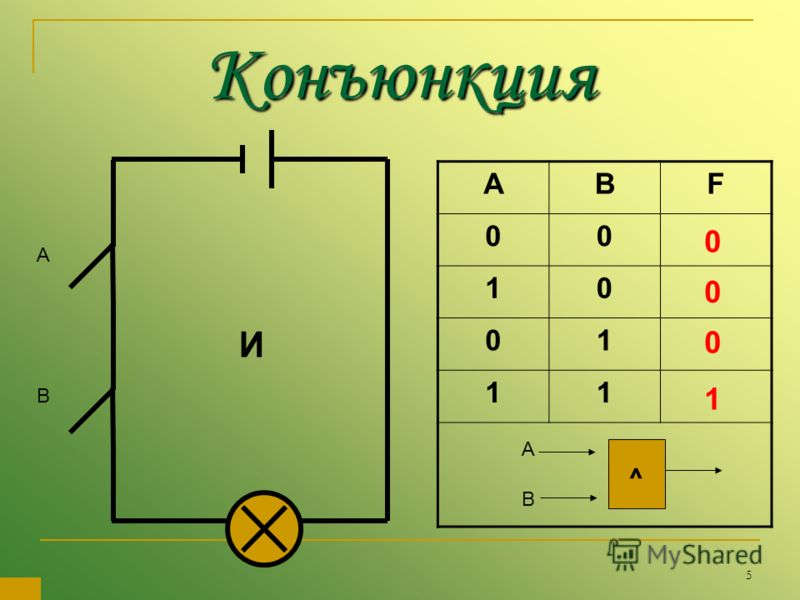

Рассмотрим, например, составное высказывание «2 х 2 = 4 и 3 х 3 = 10». Первое простое высказывание истинно (А = 1), а второе высказывание ложно (В = 0), с использованием таблицы истинности логического умножения определяем, что данное составное высказывание ложно.

Следующая страница Логическое сложение (дизъюнкция)

Cкачать материалы урока

Сравнение конъюнкций и дизъюнкций в таблице истинности

Изучая логику в курсе конечной математики, вы, вероятно, будете работать с таблицами истинности. Таблица истинности — это визуальное представление всех возможных комбинаций значений истинности для данного составного утверждения.

Два типа связок, которые вы часто видите в составных операторах, — это союзы и дизъюнкции, представленные символами ∧ и ∨ соответственно.

Важно знать разницу между этими двумя связками.

Идентификация соединения

Союз p ∧ q, помещает слово и между двумя утверждениями, образуя составное утверждение.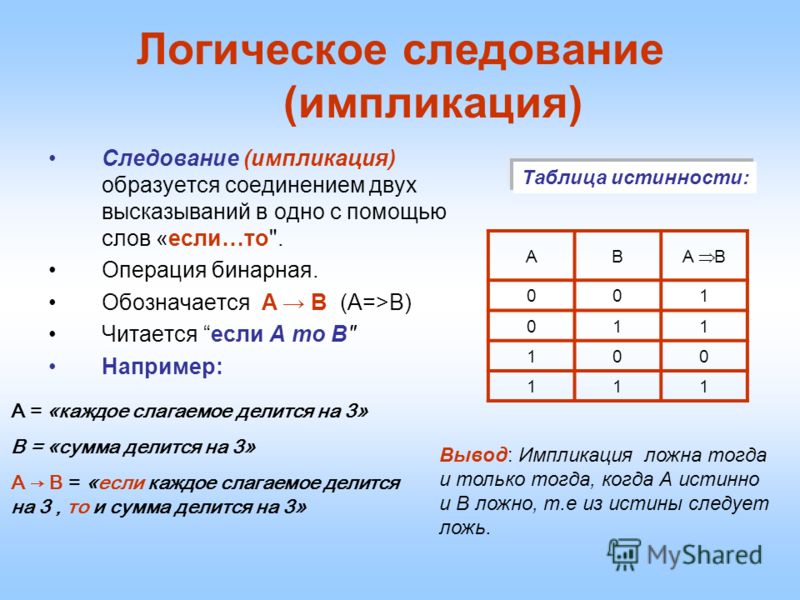

Рассмотрим следующие утверждения:

(1) Чикаго — город в штате Иллинойс.

(2) Красный — цвет американского флага.

(3) 7 + 3 = 11.

(4) Сан-Франциско — город во Флориде.

Утверждения (1) и (2) верны, а утверждения (3) и (4) ложны.

Затем вы строите таблицу истинности для соединения 9 q неверно. Используя утверждения (4) и (2), союз звучит так: «Сан-Франциско — это город во Флориде, а красный цвет — это цвет американского флага».

И, наконец, когда оба утверждения ложны, их соединение ложно. Используя утверждения (3) и (4), союз звучит так: «7 + 3 = 11, а Сан-Франциско — город во Флориде».

По сути, здесь вы видите, что для того, чтобы конъюнкция была истинной, оба утверждения компонента должны быть истинными.

Выявление дизъюнкции

В дизъюнкции p ∨ q используется слово or для создания составного утверждения.

Таблица истинности для дизъюнкции показана здесь:

Чтобы дизъюнкция была истинной, только одно из составляющих утверждений должно быть истинным.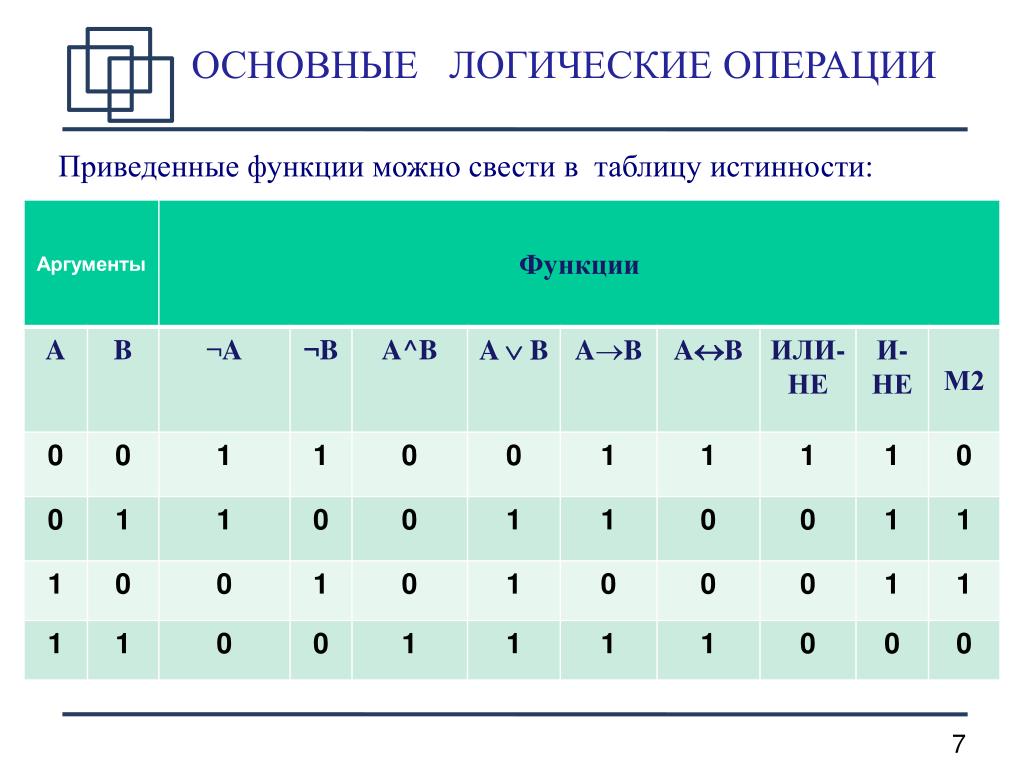

Рассмотрим следующие составные операторы, представляющие четыре строки.

Оба варианта верны; составное утверждение истинно.

TF: «На Гавайях идет дождь, или у всех коров семь ног». Первое утверждение истинно, поэтому составное утверждение истинно.

Второе утверждение истинно, поэтому составное утверждение истинно.

FF: «У всех коров семь ног, или свиньи могут летать». Оба утверждения ложны, поэтому составное утверждение ложно.

Об этой статье

Эта статья взята из книги:

• Конечная математика для чайников,

Об авторе книги:

Мэри Джейн Стерлинг — автор Алгебра I для чайников, Алгебра. и многие другие Для чайников книги. Она преподавала в Университете Брэдли в Пеории, штат Иллинойс, более 30 лет, преподавая алгебру, бизнес-расчеты, геометрию и конечную математику.

Эту статью можно найти в категории:

• Расчет и анализ,

3.2: Таблицы истинности — союз (и), дизъюнкция (или), отрицание (не)

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

52961

• Дэвид Липпман
• Колледж Пирса через OpenTextBookStore

Поскольку о сложных утверждениях может быть сложно думать, мы можем создать таблицу истинности , чтобы отслеживать, какие значения истинности для простых утверждений делают сложное утверждение истинным, а какое ложным.

Таблица истинности

Таблица, показывающая результирующее значение истинности сложного утверждения для всех возможных значений истинности для простых утверждений.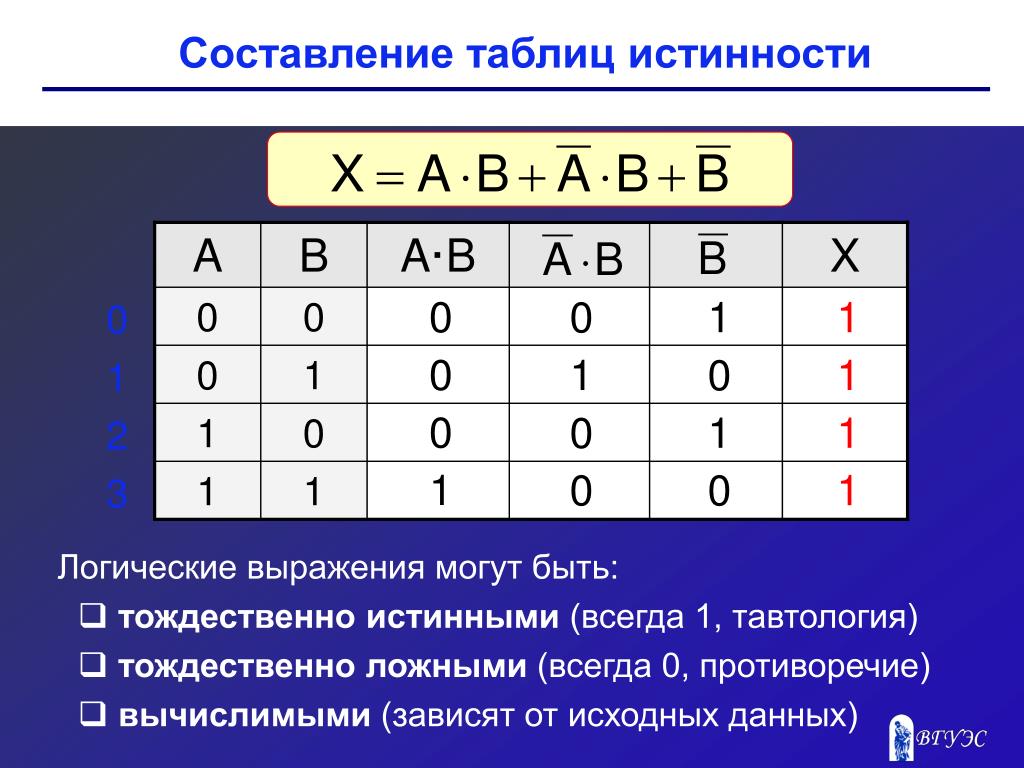

Пример 1

Предположим, вы выбираете новый диван, и ваша вторая половинка говорит: «Купите секционный или что-нибудь с шезлонгом».

Это сложное утверждение, состоящее из двух более простых условий: «является секционным» и «имеет фаэтон». Для простоты давайте использовать p для обозначения «является секционным», а q для обозначения «имеет шезлонг».

Таблица истинности для этой ситуации будет выглядеть так:

\(\begin{array}{|c|c|c|}
\hline p & q & p \text { or } q \\
\hline \mathrm{T} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{F} & \mathrm{F} \\ \hline
\end{массив}\)

В таблице , T используется для true, а F для false. В первой строке, если p истинно и q также истинно, то сложное утверждение «p или q » верно. Это будет секционная, в которой также есть шезлонг, что соответствует нашему желанию.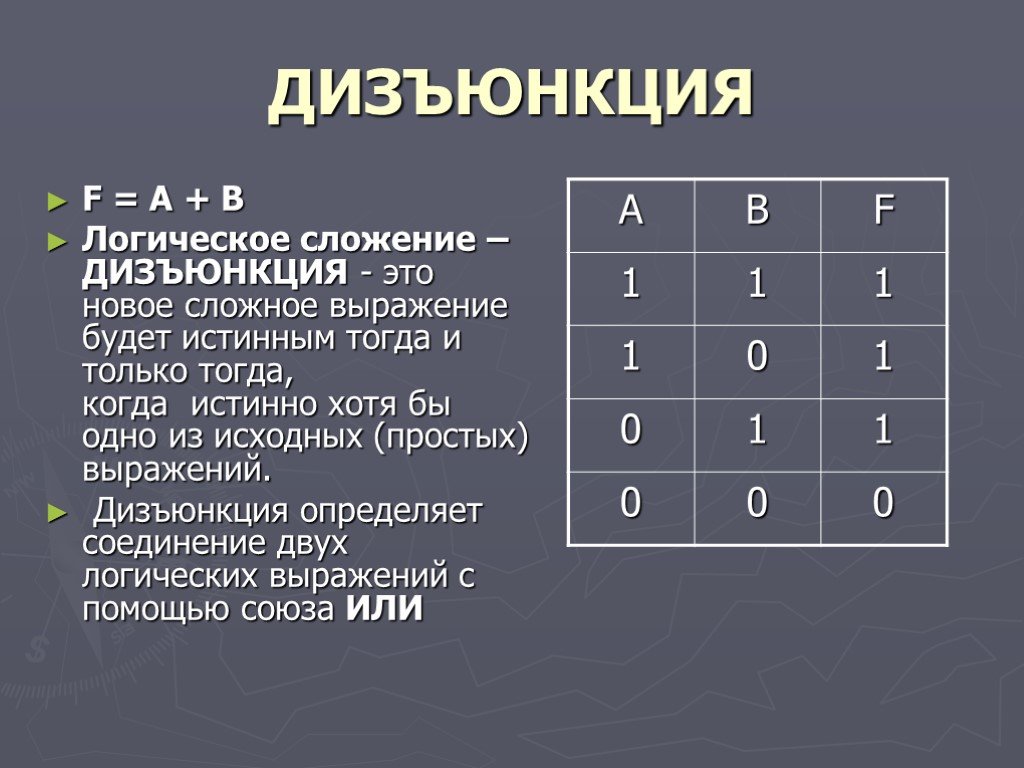 (Помните, что или в логике не являются исключающими; если диван имеет обе функции, он соответствует условию.)

В предыдущем примере с кушеткой таблица истинности просто суммировала то, что мы уже знаем о том, как работают операторы или . Ниже показаны таблицы истинности для основных утверждений и , или и , а не .

Базовые таблицы истинности

Отрицание — Выражает «не», что означает противоположное истинностное значение.

\(\begin{array}{|c|c|}
\hline p & \sim p \\
\hline \mathrm{T} & \mathrm{F} \\
\hline \mathrm{F} & \mathrm{T} \\
\hline
\end{array}\)

Союз — Выражает «и», что означает, что и p, и q должны быть истинными.

\(\begin{array}{|c|c|c|}
\hline p & q & p \wedge q \\
\hline \mathrm{T} & \mathrm{T} & \mathrm{T }\
\hline \mathrm{T} & \mathrm{F} & \mathrm{F} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{F} \\
\hline \mathrm{ F} & \mathrm{F} & \mathrm{F} \\
\hline
\end{массив}\)

Дизъюнкция — Выражает «или», что означает, что либо p, либо q могут быть истинными, либо оба.

\(\begin{array}{|c|c|c|}
\hline p & q & p \vee q \\
\hline \mathrm{T} & \mathrm{T} & \mathrm{T } \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{F} & \mathrm{F} \\
\hline
\end {массив}\)

Таблицы истинности становятся действительно полезными, когда мы анализируем более сложные утверждения.

Пример 2

Создайте таблицу истинности для утверждения \(p \vee \sim q\)

Решение

Когда мы создаем таблицу истинности, нам нужно перечислить все возможные комбинации значений истинности для \(p \) и \(q\). Обратите внимание, что первый столбец содержит 2 T, за которыми следуют \(2 ~\mathrm{Fs}\), а второй столбец чередует \(\mathrm{T}, \mathrm{F}, \mathrm{T}\), F , Этот шаблон гарантирует, что будут учтены все 4 комбинации.

\(\begin{array}{|c|c|}
\hline p & q \\
\hline \mathrm{T} & \mathrm{T} \\
\hline \mathrm{T} & \ mathrm{F} \\
\hline \mathrm{F} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{F} \\
\hline
\end{массив}\)

После создания столбцов с этими начальными значениями мы создаем третий столбец для выражения \(\sim q\). Теперь мы временно проигнорируем столбец для \(p\) и запишем истинные значения для \(\sim q\)

\(\begin{array}{|c|c|c|}
\hline p & q & \sim q \\
\hline \mathrm{T} & \mathrm{T} & \mathrm{F} \\
\hline \mathrm{T} & \mathrm{F} & \ mathrm{T} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{F} \\
\hline \mathrm{F} & \mathrm{F} & \mathrm{T} \\
\hline
\end{array}\)

Далее мы можем найти истинные значения \(p \vee \sim q,\), используя первый и третий столбцы.

\(\begin{array}{|c|c|c|c|}
\hline p & q & \sim q & p \vee \sim q \\
\hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{T} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \ mathrm{T} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\
\hline \mathrm{F} & \mathrm{F} & \ mathrm{T} & \mathrm{T} \\
\hline
\end{array}\)

Таблица истинности показывает, что \(p \vee \sim q\) верно в трех случаях и ложно в одном случае . Если вам интересно, в чем смысл этого, предположим, что это последний день бейсбольного сезона, и две команды, которые не играют друг с другом, соревнуются за финальное место в плей-офф.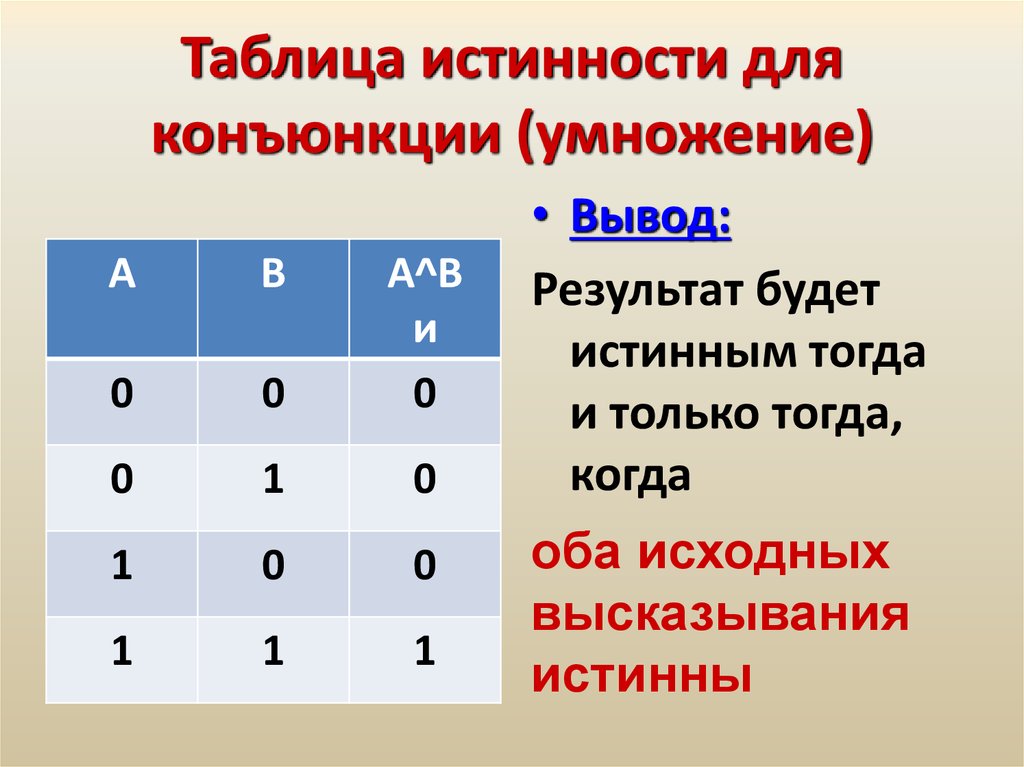 Анахайм выйдет в плей-офф, если выиграет свою игру или , если Бостон не выиграет свою игру. (Анахайм владеет тай-брейком; если обе команды выигрывают или если обе команды проигрывают, то Анахайм получает место в плей-офф.) Если \(p=\) Анахайм выигрывает свою игру и \(q=\) Бостон выигрывает свою игру, тогда \(p \vee\) \(\sim q\) представляет ситуацию «Анахайм выигрывает свою игру или Бостон не выигрывает свою игру». Таблица истинности показывает нам различные сценарии, связанные с выходом Анахайма в плей-офф. В первом ряду Анахайм выигрывает свою игру, а Бостон выигрывает свою игру, так что это правда, что Анахайм выходит в плей-офф. Во втором ряду выигрывает Анахайм, а не Бостон, так что это правда, что Анахайм выходит в плей-офф. В третьем ряду Анахайм не выигрывает свою игру, а Бостон выигрывает свою игру, так что это 9.0250 false что Анахайм выходит в плей-офф. В четвертом ряду Анахайм не побеждает, а Бостон не побеждает, так что это правда, что Анахайм выходит в плей-офф.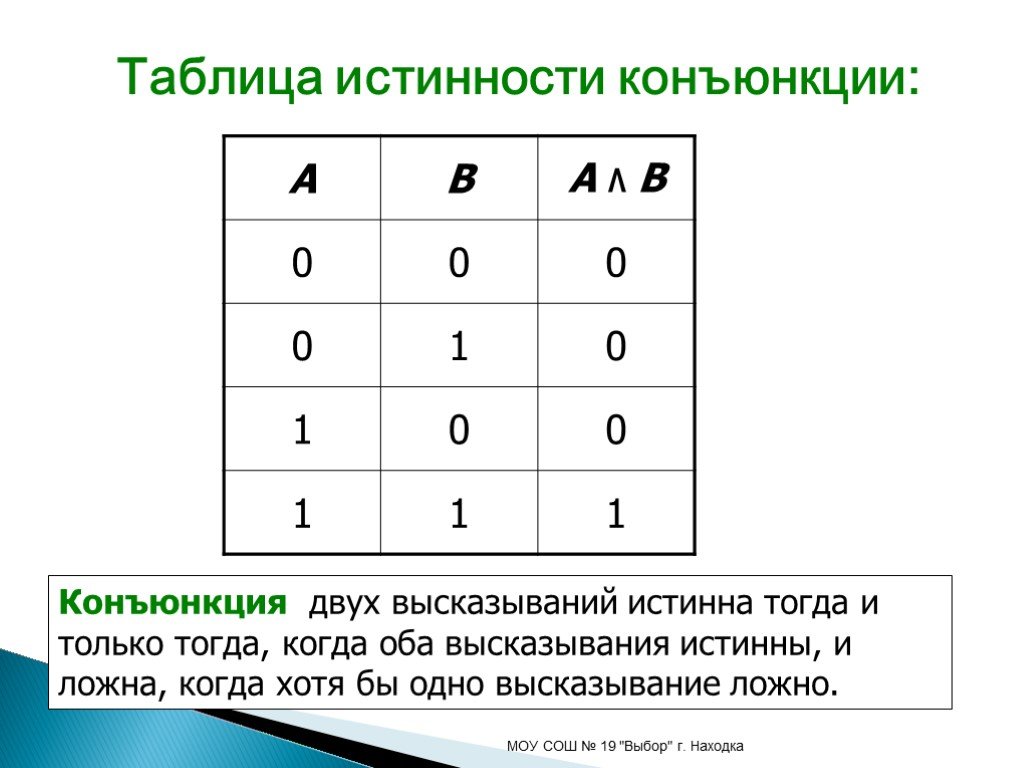

Попробуйте сейчас 1

Создайте таблицу истинности для этого утверждения: \(\sim p \wedge q\)

Ответ

\(\begin{array}{|c|c|c|c|}
\hline p & q & \sim p & \sim p \wedge q \\
\hline \mathrm{T} & \mathrm{ T} и \mathrm{F} & \mathrm{F} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \ mathrm{T} \\
\hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F} \\
\hline
\end{массив}\)

Пример 3

Создайте таблицу истинности для утверждения \(p \wedge \sim(q \vee r)\)

Решение

Это помогает работать изнутри наружу при создании таблицы истинности, и создавать столбцы в таблице для промежуточных операций. Начнем с перечисления всех возможных комбинаций значений истинности для \(p, q,\) и \(r .\). Обратите внимание, что первый столбец содержит 4 T, за которыми следуют \(4 \mathrm{Fs}\), второй столбец содержит \(2 \mathrm{Ts}, 2 \mathrm{Fs}\), затем повторяется, и последний столбец чередуется \(\mathrm{T}, \mathrm{F}, \mathrm{T}, \mathrm{ F} \ldots\) Этот шаблон гарантирует, что будут учтены все 8 комбинаций.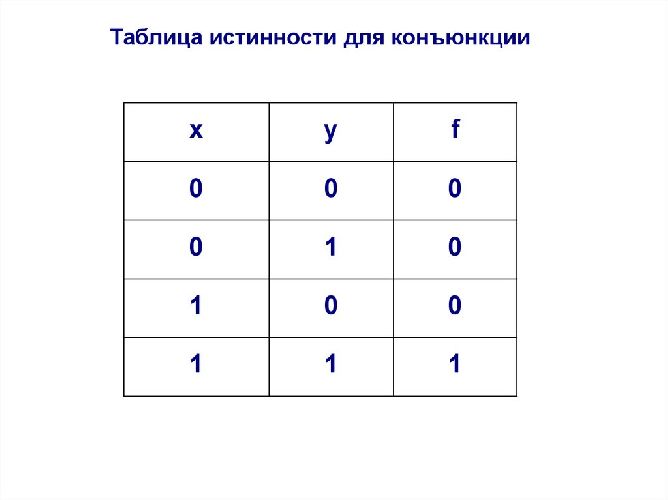 После создания столбцов с этими начальными значениями мы создаем четвертый столбец для самого внутреннего выражения, \(q \vee r .\). Теперь мы временно проигнорируем столбец для \(p\) и сосредоточимся на \(q\) и \ (r\), записывая значения истинности для \(q \vee r\)

\(\begin{array}{|c|c|c|}
\hline p & q & r \\
\hline \mathrm{T} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{T} & \mathrm{T} & \mathrm{F} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{T} \\
\hline \mathrm{ T} & \mathrm{F} & \mathrm{F} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{ T} & \mathrm{F} \\
\hline \mathrm{F} & \mathrm{F} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{F} & \mathrm{ Ф}\
\hline
\end{массив}\)

\(\begin{array}{|c|c|c|c|}
\hline p & q & r & q \vee r \\
\hline \ mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{T} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \ mathrm{T} \\
\hline \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{F} \\
\hline
\end{массив}\)

Далее мы можем найдите отрицание \(q \vee r\), работая с столбцом \(q \vee r\), который мы только что создали. (Игнорируйте первые три столбца и просто инвертируйте значения в столбце \(q \vee r\).)

\(\begin{array}{|c|c|c|c|c|}
\hline p & q & r & q \vee r & \sim(q \vee r) \\
\hline \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\
\hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{F} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{ F} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{F} \\
\hline \mathrm{F} & \mathrm{F} & \ mathrm{T} & \mathrm{T} & \mathrm{F} \\
\hline \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\
\hline
\end{array}\)

Наконец, мы находим значения \(p\) и \(\sim(q \vee r)\). (Второй, третий и четвертый столбцы игнорируйте.)

\(\begin{array}{|c|c|c|c|c|c|}
\hline p & q & r & q \vee r & \sim (q \vee r) & p \wedge \sim (q \vee r \text { ) } \\
\hline \text { T } & \text { T } & \text { T } & \text { T } & \text { F } & \text { F } \\
\hline \text { T } & \ текст { T } & \text { F } & \text { T } & \text { F } & \text { F } \\
\hline \text { T } & \text { F } & \text { T } & \text { T } & \text { F } & \text { F } \\
\hline \text { T } & \text { F } & \text { F } & \text { F } & \text { T } & \text { T } \\
\hline \text { F } & \text { T } & \text { T } & \text { T } & \text { F } & \text { F } \\
\hline \text { F } & \text { T } & \text { F } & \text { T } & \text { F } & \text { F } \\
\hline \text { F } & \ текст { F } & \text { T } & \text { T } & \text { F } & \text { F } \\
\hline \text { F } & \text { F } & \text { F } & \text { F } & \text { T } & \text { F } \\
\hline
\end{array}\)

Оказывается, это сложное выражение верно только в одном случае: когда \( p\) истинно, \(q\) ложно, а \(r\) ложно.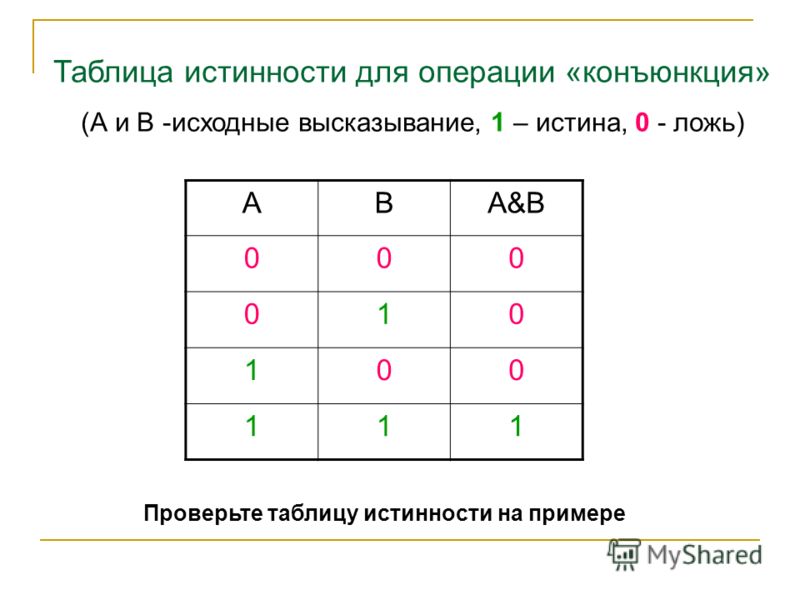 Чтобы проиллюстрировать эту ситуацию, предположим, что Анахайм выйдет в плей-офф, если: (1) Анахайм выиграет и (2) ни Бостон, ни Кливленд не выиграют. TFF — единственный сценарий, при котором «Анахайм» выйдет в плей-офф.

Попробуйте сейчас 2

Создайте таблицу истинности для этого утверждения: \((\sim p \wedge q) \vee \sim q\)

Ответ

\(\begin{array}{|c|c|c|c|c|c|}
\hline p & q & \sim p & \sim p \wedge q & \sim q & (\sim p \ клин q) \vee \sim q \\
\hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{F} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{T} \\
\hline \mathrm{F} & \ mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\
\hline
\end{массив}\)

Вы, наверное, заметили, что разные таблицы истинности имеют разное количество строк в зависимости от того, сколько у нас переменных (или простых выражений).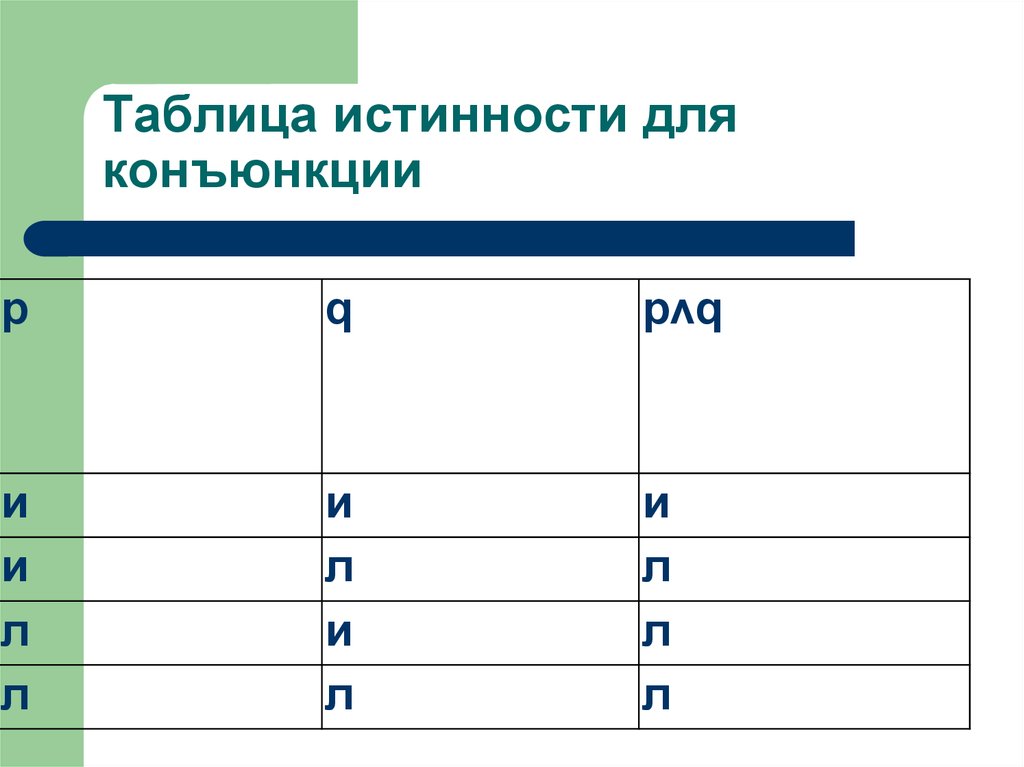 Когда есть только одно простое утверждение (например, наша таблица истинности для отрицания), у нас есть две строки, одна для истинности, а другая для ложности. Когда у нас есть два простых утверждения, \(p\) и \(q\), в таблице истинности есть четыре строки. В примере 3 у нас было три простых утверждения \(p\), \(q\) и \(r\) с восемью строками в таблице истинности. Таким образом, для каждого нового простого оператора количество строк удваивается. Этот шаблон продолжается, поэтому мы можем обобщить его следующим образом. 9к\) строк.

Логически эквивалентны

Два утверждения являются логически эквивалентными , если они имеют одинаковые простые утверждения и при вычислении их таблиц истинности конечные столбцы в таблицах идентичны.

Законы Де Моргана

Отрицание конъюнкции логически эквивалентно дизъюнкции отрицания утверждений, составляющих конъюнкцию. Чтобы отрицать оператор «и», отрицайте каждую часть и замените «и» на «или».

\(\sim(p \wedge q)\) логически эквивалентно \(\sim p \vee \sim q\)

Отрицание дизъюнкции логически эквивалентно конъюнкции отрицания утверждений, составляющих дизъюнкция.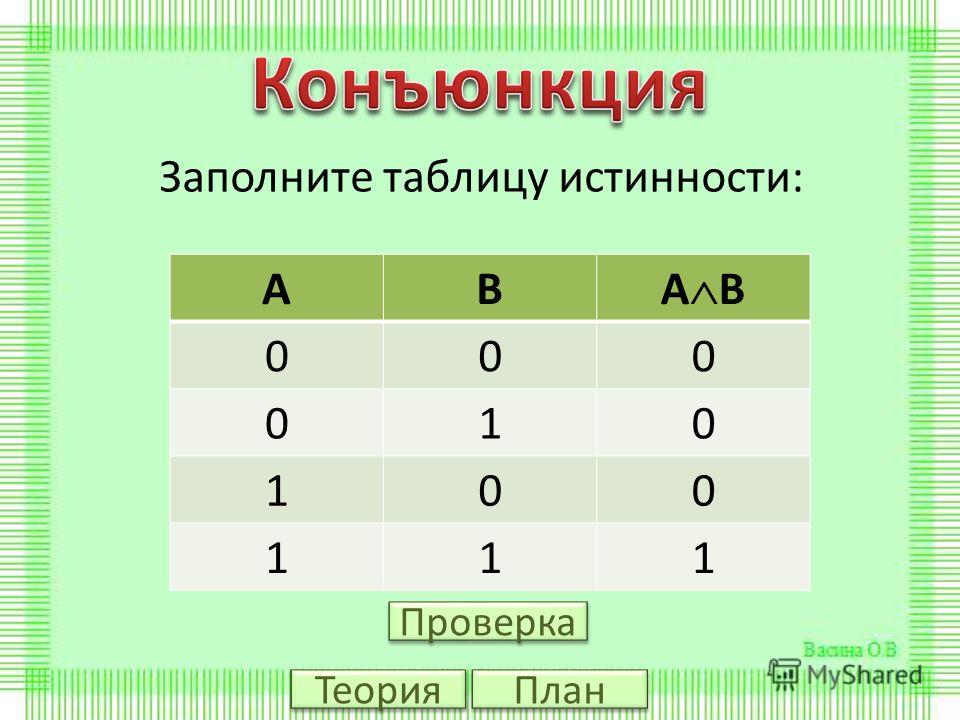 Чтобы отрицать оператор «или», отрицайте каждую часть и замените «или» на «и».

\(\sim(p \vee q)\) логически эквивалентно \(\sim p \wedge \sim q\)

Пример 4

На День святого Валентина вы не получили любимые цветы или конфеты: Какое из следующих утверждений логически эквивалентно?

1. Вы не подарили им цветы или конфеты.
2. Вы не получили им цветы и не получили им конфеты.
3. Ты подарил им цветы или конфеты.

Решение

1. Это утверждение недостаточно далеко; это оставляет открытой возможность того, что вы получили одну из двух вещей.
2. Это утверждение эквивалентно исходному; \(\sim (f \vee c)\) эквивалентно \(\sim f \wedge \sim c\)
3. В этом утверждении говорится, что вы что-то им принесли, но мы знаем, что это не так.

Попробуйте сейчас 3

Чтобы стать президентом США, человек должен родиться в США, быть не моложе 35 лет и прожить в США не менее 14 лет.