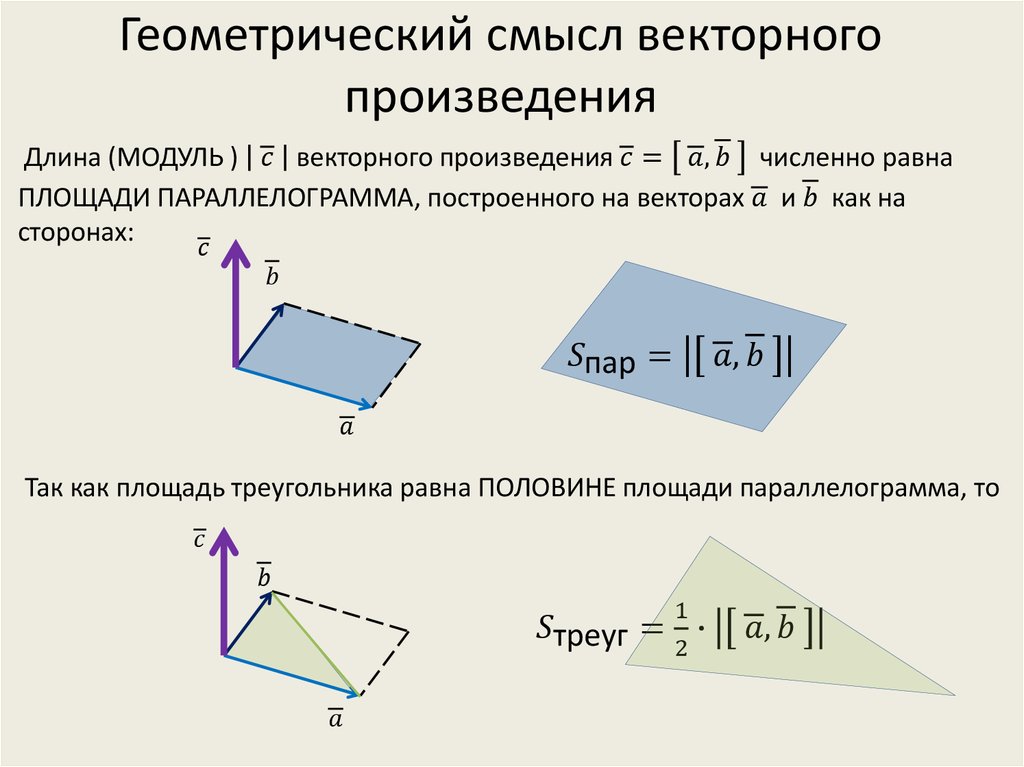
3).вектор направлен в ту сторону, от которого поворот от к на наименьший угол осуществляется против часовой стрелки.
Рис. 1
Алгебраические свойства векторного произведения
Давайте рассмотрим свойства векторного произведения.
Если – произвольные векторы, а – произвольные число, тогда:
- x = x . (Векторное произведение антикоммутативно).
- x = x = x .(Векторное произведение обладает сочетательным свойством относительно скалярного множителя).
- x = x + x .
- x = ||, , . (Два ненулевых вектора коллинеарны только тогда, когда их векторное произведение равно нулевому вектору).
Таблица векторного умножения ортов
x = , x = ;
x = , x = ;
x = , x = .
x = x = x = .
Рис. 2
Векторное произведение одноимённых ортов равняется . При самом коротком повороте от одного орта к другому против часовой стрелки получаем третий орт, а по часовой стрелке – третий орт со знаком .
Формулы векторного произведения в координатной форме
Формулы векторного произведения в координатной форме получаем с учётом таблицы векторного произведения ортов:
x = x = x x x =
x – x + x x =
Примеры нахождения векторного произведения
Чтобы закрепить материал, рассмотрим на примерах, как найти векторное произведение векторов.
Пример 1
Найти векторное произведение векторов = и = . Построить в системе координат векторы и = x .
Обратите внимание, что определитель (1) удобнее вычислять, если применить теорему про разложение за элементами первой строки:
= x = = – + =
Теперь построим векторы по их координатам.
Рис. 3
Из рисунка видно, что положение найденного вектора отвечает определению векторного произведения x .
Пример 2
Найти площадь треугольника , если .
Решение:
Сначала находим векторы:
и и их векторное произведение:
x = = .
Длина полученного вектора по определению численно равняется площади параллелограмма, построенного на данных векторах и поэтому:
пар = x = = .
А площадь треугольника составляет половину найденной площади, то есть:
тр. = пар = x x ,
Средняя оценка 0 / 5. Количество оценок: 0
Поставьте вашу оценку
Сожалеем, что вы поставили низкую оценку!
Позвольте нам стать лучше!
Расскажите, как нам стать лучше?
6907
Закажите помощь с работой
Не отобразилась форма расчета стоимости? Переходи по ссылке
Не отобразилась форма расчета стоимости? Переходи по ссылке
|
Заглавная страница
Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. a={a;0;0} b={b*cos φ;b*sin φ;0}
Найдем векторное произведение . . Единичный вектор перпендикулярный плоскости параллелограмма. С конца этого вектора видим вращение а к b по углу φ против часовой стрелки. Модуль векторного произведения – площадь параллелограмма, построенного на векторах а и b. Физический смысл векторного произведения: Пусть О – точка вращения твердого тела А – точка, где к телу приложена сила F. Тогда момент этой силы можно рассчитать по формуле: M=OA x F ОА – плечо силы |M|=|OA|*sinφ*|F|.
Основные свойства векторного произведения 1. — антикоммутативность. Следует из определения векторного произведения, т.к. переставляя множители местами, переставляем строки в определителе. 2. — дистрибутивность Вывод: 3. , где λ R.
Смешанное произведение. Основные свойства и геометрический смысл В 3-х мерном пространстве смешанное произведение 3-х векторов: (1) Разложим определитель по 1-й строке:
Иногда это свойство принимают в качестве определения. , где V – объем параллелепипеда. Покажем это:
h – высота параллелепипеда. Определение ориентации в пространстве: если , то векторы образуют правую тройку, при этом говорят, что они имеют положительную ориентацию. если , то векторы образуют левую тройку, при этом говорят, что они имеют отрицательную ориентацию. Рассмотрим ориентацию стандартного базиса: Стандартный базис имеет положительную ориентацию. Если вектора линейно зависимы, то они называются компланарными. Условие компланарности векторов: Если в смешанном произведении 2 вектора переставить местами(рядом стоящие), то знак изменится. При циклической перестановке знак не меняется: Выбирая 3 последовательных множителя они образуют циклическую перестановку.
Параметрическое и каноническое уравнение прямой в пространстве Пусть l – прямая. x={x; y; z} l A, B S – направляющий вектор прямой. Тогда АХ и АВ коллинеарны. АХ=λS – параметрическое уравнение прямой, λ – параметр. или Это параметрическое уравнение прямой в координатной плоскости. Исключая параметр λ получаем каноническое уравнение прямой: Вторая формула здесь – уравнение прямой (АВ).
⇐ Предыдущая1234 Читайте также: Коммуникативные барьеры и пути их преодоления Рынок недвижимости. Сущность недвижимости Решение задач с использованием генеалогического метода История происхождения и развития детской игры |
|
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 239; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
b
Тогда формулу (1) надо доказать. Теперь нетрудно показать геометрический смысл смешанного произведения.
Векторный продукт Определение и значение
- Основные определения
- Викторина
- Примеры
- Британский
- Научный
Показывает уровень оценки в зависимости от сложности слова.
Сохрани это слово!
Показывает уровень оценки в зависимости от сложности слова.
существительное
перекрестное произведение.
ВИКТОРИНА
ВЫ ПРОЙДЕТЕ ЭТИ ГРАММАТИЧЕСКИЕ ВОПРОСЫ ИЛИ НАТЯНУТСЯ?
Плавно переходите к этим распространенным грамматическим ошибкам, которые ставят многих людей в тупик.
Удачи!
Вопрос 1 из 7
Заполните пропуск: Я не могу понять, что _____ подарил мне этот подарок.
Происхождение векторного произведения
Впервые записано в 1875–1880 гг. Веда
Dictionary.com Полный текст На основе Random House Unabridged Dictionary, © Random House, Inc., 2022
Как использовать векторный продукт в предложении
Вместе команды работают 24 часа в сутки над продуктом, который обещает гораздо более высокий риск, чем приносит прибыль.
Гонка за вакциной против лихорадки Эбола|Эбби Хагладж|7 января 2015 г.|DAILY BEAST
Миллиардер-филантроп пробует продукт машины, которая перерабатывает человеческие нечистоты в питьевую воду и электричество.
Билл Гейтс пьет воду из канализации|Джек Холмс, The Daily Beast Video|7 января 2015 г.|DAILY BEAST
Биткойн начал 2013 год с бешеной цены в 770 долларов за единицу, и компании направо и налево переходили на эфирный продукт.
Вы ошибались насчет Майли и Биткойн: несбывшиеся прогнозы на 2014 год|Нина Строхлич|31 декабря 2014 г.|DAILY BEAST руки, прежде чем мы это узнаем.
Самые безумные лекарства от похмелья в истории|Джастин Джонс|30 декабря 2014 г.|DAILY BEAST
Получившийся продукт включал четыре варианта с одной бочкой, а также готовые фотографии МакКидда, наслаждающегося стаканом The Macallan.
Ресторан, фляга и фотография, достойные виски Macallan||16 декабря 2014|DAILY BEAST
30 г.
Руководство по клинической диагностике|Джеймс Кэмпбелл Тодд
Затем произведение умножается на количество кубических сантиметров, выделяемых за сутки, и делится на 1000.
Руководство по клинической диагностике|Джеймс Кэмпбелл Тодд средний продукт дневной работы во всем этом регионе.
Взгляд на Европу|Гораций Грили
Я подозреваю, судя по очевидной заботе о нем, что его продукция в значительной степени зависит от продуктов питания.
Взгляд на Европу|Гораций Грили
Виргинский лист все еще продолжает цвести, и сегодня он является важным сельскохозяйственным продуктом штата.
Табак; Его история, разновидности, культура, производство и торговля|E. Р. Биллингс.
Определения Британского словаря для векторного произведения
векторного произведения
сущ. . Его ось перпендикулярна плоскости данных векторов. Записывается: A × B или A ∧ BТакже называется перекрестным произведением. Сравните скалярное произведение 9.0015
Английский словарь Коллинза — полное и полное цифровое издание 2012 г. © William Collins Sons & Co. Ltd., 1979, 1986 © HarperCollins Publishers 1998, 2000, 2003, 2005, 2006, 2007, 2009, 2012
Научные определения векторного произведения
векторного произведения
величина а, величина b и синус угла между а и b. Его направление перпендикулярно плоскости, проходящей через а и b, и ориентировано так, что правое вращение вокруг него переводит а в b на угол, не превышающий 180°.
Обозначение для c равно c = a X b. Также называется перекрестным произведением. См. Также правило правой руки.
Научный словарь American Heritage® Авторские права © 2011. Опубликовано издательством Houghton Mifflin Harcourt Publishing Company. Все права защищены.
Произведение векторов: определение, формула и соотношение
Что такое умножение \(4\) на \(5\), это \(20\), легко. Умножать числа довольно легко, и каждый может это сделать, но что, если вас попросили умножить два вектора, \(\vec{a}=2\hat{i} + 3\hat{j}\) и \(\vec {b}=\шляпа{i} — 3\шляпа{k}\), ну не все так просто. Векторы — это очень отдельная сущность, классические правила числового умножения здесь малопригодны. Чтобы получить произведение двух или более векторов, нам нужно понять концепцию Векторный продукт .
Определение векторного продукта
Обычное умножение двух чисел на этом этапе хорошо определено. Но умножить два вектора не так просто. Произведение двух векторов можно выполнить двумя разными способами; либо по скалярному произведению, либо по векторному произведению.
Скалярное произведение двух векторов дает скалярную величину, как следует из названия. В то время как векторное произведение двух векторов дает вектор, поэтому оно и называется векторным произведением.
Векторное произведение двух векторов дает вектор, который находится в направлении, перпендикулярном плоскости, образованной двумя векторами. Величина результирующего вектора является произведением величин двух исходных векторов и синуса угла между их направлениями.
Предположим, есть два вектора, которые образуют xy панель между собой. Векторное произведение этих векторов будет перпендикулярно плоскости xy, то есть оси z.
Векторный производный продукт
Пусть есть два вектора, \(\vec{A}\) и \(\vec{B}\), и \(\theta\) — угол между ними.
Векторное произведение между ними обозначается \(\vec{A}\times\vec{B}\) (‘\(\times\)’ не следует путать со знаком умножения, здесь оно обозначает векторное произведение ) из-за символа креста векторное произведение также известно как перекрестное произведение .
Теперь, когда векторы и угол между ними установлены, давайте еще раз посмотрим на определение, но в математической манере:
Векторное произведение двух ненулевых векторов \(\vec{A}\) и \(\vec{B}\) равно \(\vec{A}\times\vec{B}=AB\ space sin\theta\space\hat{n}\), где \(A\) и \(B\) — величины векторов, а \(\theta\) — острый угол между двумя векторами. И \(\шляпа{n}\) представляет собой единичный вектор в направлении, перпендикулярном плоскости, образованной двумя векторами.
Важно указать, что ни один из векторов не является нулевым вектором, т.е. нулевым вектором. В этом случае векторное произведение не имеет геометрического значения. В результате векторного произведения получается вектор, имеющий величину \(AB\space sin\theta\) и указывающий в направлении, которое перпендикулярно плоскости, образованной двумя векторами, то есть перпендикулярно обоим векторам одновременно.
Чтобы продемонстрировать, как это выглядит, рассмотрите приведенную ниже диаграмму:
Два вектора A и B образуют другой вектор как их векторное произведение, StudySmarter Originals
Предположим, что векторы ориентированы таким образом, что они лежат в плоскости xy, т.
е. z-компонента векторов равна 0. Если мы возьмем векторное произведение, его можно представить как поворот винта в направлении \(\vec{A}\) к \(\vec{B}\), что равно направление против часовой стрелки. Направление, в котором будет двигаться винт, — вертикально вверх, т. Е. Положительная ось z. Вертикальная стрелка — это в точности вектор, образованный их векторным произведением. На приведенной выше диаграмме \(\vec{A}\) и \(\vec{B}\) имеют одну и ту же начальную точку, но это не обязательно. На самом деле это могут быть любые два вектора, здесь они показаны только для наглядного представления концепции.
Обозначим полученный вектор как \(\vec{C}\), тогда по определению:
$$\vec{C}=AB\space sin\theta\space\hat{n}$$
, а величина определяется простым взятием абсолютного значения с обеих сторон,
$$|\vec{C}|=AB\space sin\theta$$
Величина единичного вектора становится \(1\ ), и все, что у нас осталось, это \(AB\space sin\theta\). Помните, что \(|\vec{C}|=C\), это просто вопрос удобства, какое обозначение предпочитается (то же самое касается \(\vec{A}\) и \(\vec{B} \) или любой другой вектор).
Чтобы визуализировать направление, в котором будет указывать результирующий вектор, очень полезно правило правого винта. Просто поверните пальцы в направлении вектора вращения и наблюдайте за направлением большого пальца. Поверните пальцы от \(\vec{A}\) к \(\vec{B}\), и направление большого пальца задает направление результирующего вектора.
Компонентная форма векторного произведения
До сих пор вы знали, что векторное произведение означает геометрически. Теперь мы рассмотрим его алгебраическую форму более подробно. Чтобы обобщить векторное произведение:
Пусть A вектор такой, что \(\vec{A}=a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k}\), где \ (a_{1},a_{2} \space и \space a_{3}\) являются вещественными константами, такими, что они не являются одновременно \(0\) (иначе это был бы нулевой вектор) и \(\ vec{B}=b_{1}\шляпа{i}+b_{2}\шляпа{j}+b_{3}\шляпа{k}\) , где \(b_{1},b_{2} \ space и \space b_{3}\) являются вещественными константами и снова не являются одновременно \(0\).
{o}=\vec{0}$$ 9{o}=0\), а величина всех единичных векторов равна \(1\). Точно так же \(\hat{j}\times\hat{j}=\vec{0}\) и \(\hat{k}\times\hat{k}=\vec{0}\), где \( \vec{0}\) представляет нулевой вектор. Вычисление других отношений, например,
$$\шляпа{i}\times\шляпа{j}=sin\left(\frac{\pi}{2}\right)\шляпа{k}=\шляпа{ k}$$
Поскольку угол между единичным вектором вдоль оси x и единичным вектором вдоль оси y равен \(\frac{\pi}{2}\) радианам, что дает синусоидальное значение \ (1\). Точно так же мы можем вычислить другие сущности, а именно:
$$\шляпа{j}\times\шляпа{i}=-\шляпа{k}, \пробел \шляпа{i}\times\шляпа{k}=-\шляпа{j}, \пробел \шляпа {k}\times\hat{i}=\hat{j}, \space \hat{j}\times\hat{k}=\hat{i} \space and \space \hat{k}\times\ hat{j}=-\hat{i}$$
Теперь, используя приведенные выше объекты для единичных векторов, мы можем вычислить \(\vec{A} \times \vec{B}\) следующим образом:
$ $\vec{A}\times\vec{B}=(a_{1}\шляпа{i}+a_{2}\шляпа{j}+a_{3}\шляпа{k})\times(b_{ 1}\шляпа{i}+b_{2}\шляпа{j}+b_{3}\шляпа{k})$$
$$\vec{A}\times\vec{B}=(a_{ 2}b_{3}-b_{2}a_{3})\шляпа{i}-(a_{1}b_{3}-a_{3}b_{1})\шляпа{j}+(a_{ 1}b_{2}-a_{2}b_{1})\шляпа{k}$$
Взаимные произведения, которые привели к нулевому вектору, исключаются, и все, что у нас остается, это приведенное выше уравнение.
Приведенное выше уравнение иногда может быть немного утомительным для запоминания и не очень удобным для записи. В результате приведенное выше уравнение часто представляется определителем \(3\) на \(3\), который равен:
$$\vec{A}\times\vec{B}=\begin{vmatrix} \шляпа{i} & \шляпа{j} & \шляпа{k} \\ a_{1} & a_{2} & a_{3} \\b_{1} & b_{2} & b_{3} \ end{vmatrix}$$
, что в конечном итоге соответствует уравнению, полученному ранее. Но определитель относительно легко запомнить. Для словесного выражения элементов определителя первая строка состоит из единичных векторов, вторая и третья строки — из скалярных компонент векторов. Давайте рассмотрим пример, чтобы получить представление о вычислении таких определителей, в конечном счете, векторного произведения.
Тройное произведение векторов
Произведение векторов не ограничивается двумя векторами, но также может быть расширено до трех различных векторов. Пусть есть три ненулевых вектора \(\vec{A}, \space \vec{B} \space и \space \vec{C}\) и мы хотим вычислить векторное тройное произведение между ними: \(\ vec{A} \times (\vec{B} \times \vec{C})\), где порядок векторного произведения очень важен, так как \(\vec{A} \times (\vec{B} \times \vec{C}) \neq (\vec{A} \times \vec{B}) \times \vec{C}\) т.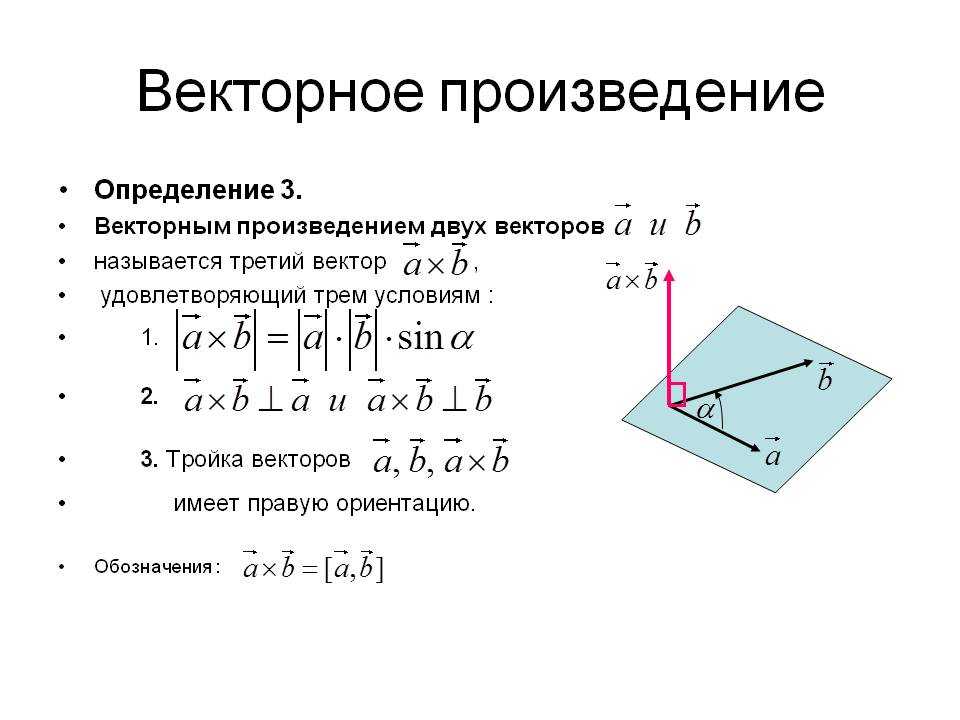
е. векторное тройное произведение не является ассоциативным. По сути, существует два способа вычисления векторного тройного произведения: во-первых, вычисление векторного произведения \(\vec{A}\) и \(\vec{B}\), а затем выполнение его векторного произведения с \( \vec{С}\). Это включает в себя выполнение двух векторных продуктов, одного за другим.
Другой способ расчета векторного произведения — скалярное произведение:
$$ (\vec{A} \times \vec{B}) \times \vec{C}=(\vec{A} \cdot \ vec{C}) \vec{B}-(\vec{B} \cdot \vec{C}) \vec{A} $$
Как видно, эта формула включает скалярное произведение \(\ vec{A}\) с \(\vec{C}\), а затем \(\vec{B}\) с \(\vec{C}\). На практике оба вышеуказанных способа одинаково удобны.
Для векторов: \(\vec{a}=\hat{i}+\hat{j}+\hat{k}\), \(\vec{b}=2 \hat{i}-\ hat{k}\) и \(\vec{c}=\hat{j}-\hat{k}\), найдите векторное тройное произведение: \((\vec{a} \times \vec{b} ) \times \vec{c}\)
Решение:
Мы будем использовать следующую формулу
$$ (\vec{a} \times \vec{b}) \times \vec{c}=(\vec{a} \cdot \vec {c}) \vec{b}-(\vec{b} \cdot \vec{c}) \vec{a} $$
Шаг 1: Оценка \(\vec{a} \cdot \vec {c}\) :
$$ \begin{aligned} \vec{a} \cdot \vec{c} &=(\hat{i}+\hat{j}+\hat{k}) \cdot (\шляпа{j}-\шляпа{к}) \\ &=0+1-1 \\ \поэтому \vec{a} \cdot \vec{c} &=0 \end{aligned} $$
Шаг 2: Оценка \(\vec{b} \cdot \vec{c}\) :
$$ \begin{выровнено} \vec{b} \cdot \vec{c} &=(2 \шляпа{i}-\шляпа{k}) \cdot(\шляпа{j}-\шляпа{k}) \\ &=0+0+1 \\ &=1 \end{выровнено} $$
Шаг 3: Замена \(\vec{a} \cdot \vec{c}\) и \(\vec{b} \cdot \vec{c}\) в \((\vec {a} \times \vec{b}) \times \vec{c}=(\vec{a} \cdot \vec{c}) \vec{b}-(\vec{b} \cdot \vec{ c}) \vec{a}\):
$$ \begin{aligned} (\vec{a} \times \vec{b}) \times \vec{c} &=0-(1) \vec {a} \\ &=-\шляпа{i}-\шляпа{j}-\шляпа{k} \end{aligned} $$
Следовательно, \((\vec{a} \times \vec{b}) \times \vec{c}=-\hat{i}-\hat{j}-\hat{k}\)
Связь между векторным произведением и скалярным произведением
Хотя векторное произведение и скалярное произведение сильно различаются по геометрическому применению и их значению, мы все же можем связать их определенным образом.
{2}\theta$$ 9{2}\) для векторов \(\vec{p}=2 \hat{i}-\hat{k}\) и \(\vec{q}=\hat{j}+\hat{k} \).
Решение:
Шаг 1:
Сначала оценим \(\vec{p} \cdot \vec{q}\):
$$ \begin{aligned} \vec{p} \cdot \vec{q} &=(2 \шляпа{i}-\шляпа{k}) \cdot(\шляпа{j}+\шляпа{k}) \\ &=0+0-1 \\ \ поэтому \vec{p} \cdot \vec{q} &=1 \end{aligned} $$
Шаг 2:
Вычислить \(\vec{p} \times \vec{q}\) :
$$ \begin{aligned} \vec{p} \times \vec{q} &=\left|\begin{array}{ccc} \hat{i} & \hat{j} & \hat{k } \\ 2 & 0 & -1 \\ 0 & 1 & 1 \end{массив}\right| \\ \поэтому \vec{p} \times \vec{q} &=\hat{i}(0+1)-\hat{j}(2+0)+\hat{k}(2-0) \\ \поэтому \vec{p} \times \vec{q} &=\hat{i}-2 \hat{j}+2 \hat{k} \end{aligned} $$ 9{2}\), мы уже вычислили его в шаге 3 :
$$ \text { RHS }=10 $$
Легко видеть, что
$$ \text{LHS}= \text {RHS} $$
Таким образом, личность подтверждена.
Скалярное произведение векторов
Скалярное произведение векторов, , также известное как Скалярное произведение, — это еще один способ умножения двух векторов помимо векторного произведения.
Альтернативное, но одинаково используемое название для Точечный продукт — 9.0134 Скалярное произведение.
Скалярное произведение двух векторов дает скалярную величину, а не другой вектор. Основная причина существования скалярного произведения заключается в том, чтобы измерить величину вектора вдоль направления другого вектора.
Пусть \(\vec{a}\) и \(\vec{b}\) — два ненулевых вектора, образующих между собой острый угол \(\theta\). Формула для скалярного произведения дается следующим образом:
$$\vec{a} \cdot \vec{b}=ab \space cos\theta$$
9{2}}) \space cos(\pi/6)$$$$\vec{p} \cdot \vec{q}=(5)(10) \space \left( \frac{1}{ 2} \right)$$
$$\vec{p} \cdot \vec{q}=25$$
Следовательно, скалярное произведение двух векторов \(\vec{p}=4\hat{ i}+3\hat{j}\) и \(\vec{p}=6\hat{i}-8\hat{j}\) равно \(25\) единицам.
Примеры векторного произведения
Вычислить векторное произведение векторов \(\vec{C}=2\hat{i}+3\hat{j}-\hat{k}\) и \(\vec{D }=-\шляпа{i}+2\шляпа{k}\).
Решение:
Поместив единичные векторы и компоненты в детерминантную форму, как упоминалось ранее, мы получим
$$\vec{C}\times\vec{D}=\begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & 3 & -1 \\- 1 & 0 & 2 \end{vmatrix}$$
Раскладывая определитель, получаем
$$\vec{C} \times \vec{D}=6\hat{i}-3\hat{j }+3\hat{k}$$
, который является результирующим вектором, полученным векторным произведением \(\vec{C}\) и \(\vec{D}\).
Для двух векторов \(\vec{p}=\hat{i}-2\hat{j}\) и \(\vec{q}=-2\hat{i}+\lambda\hat{j }\) такие, что их векторное произведение равно \(\vec{p} \times \vec{q}=2\hat{k}\). Вычислите значение \(\лямбда\).
Решение:
Используя полученную ранее формулу для вычисления векторного произведения двух векторов, мы имеем
$$\vec{p} \times \vec{q}=\lambda\hat{k}- 4\hat{k}=(\lambda-4)\hat{k}$$
Но также дано, что векторное произведение равно \(\vec{p} \times \vec{q}=2\hat {k}\), поэтому, сравнивая коэффициент единичного вектора, мы получаем
$$\lambda-4=2$$
, что дает \(\lambda=6\).
