admhome’s blog — Техника — Расчет катушек индуктивности
Индуктивность катушки зависит от ее размеров, количества витков и способа намотки. Чем больше эти параметры, тем выше индуктивность. Если катушка наматывается плотно виток к витку, то индуктивность ее будет больше по сравнению с катушкой, намотанной неплотно, с промежутками между витками. Когда требуется изготовить катушку по заданным размерам и нет провода нужного диаметра, то при использовании более толстого провода надо сделать больше витков, а тонкого — уменьшить их количество, чтобы получить необходимую индуктивность. Все приведенные выше рекомендации справедливы при намотке катушек без ферритовых сердечников.
Расчет однослойных цилиндрических катушек производится по формуле
где L — индуктивность катушки, мкГн; D — диаметр катушки, см; l — длина намотки катушки, см; и n — число витков катушки.
Расчет катушки выполняется в следующих случаях:
1 — по заданным геометрическим размерам необходимо определить индуктивность катушки;
В первом случае все исходные данные, входящие в формулу, известны, и расчет не представляет затруднений.
Пример. Определим индуктивность катушки, изображенной на рис.1, где l = 2 см, D = 1,8 см, число витков n = 20. Подставив в формулу все необходимые величины, получим
Рисунок 1
Во втором случае известны диаметр катушки и длина намотки, которая, в свою очередь, зависит от числа витков и диаметра провода. Поэтому расчет рекомендуется проводить по следующей схеме. Исходя из конструкции изготавливаемого прибора, определяют размеры катушки (диаметр и длину намотки), а затем рассчитывают число витков по следующей формуле:
Определив число витков, вычисляют диаметр провода с изоляцией по формуле
где d — диаметр провода, мм; l — длина обмотки, мм; n — число витков.
Пример. Нужно изготовить катушку диаметром 1 см при длине намотки 2 см, имеющую индуктивность 0,8 мкГн.
Намотка рядовая, виток к витку.
Подставив в последнюю формулу заданные величины, получим
Диаметр провода
Если катушку наматывать проводом меньшего диаметра, то нужно полученные расчетным путем 14 витков разместить по всей ее длине (20 мм) с равными промежутками между витками, то есть с большим шагом намотки. Индуктивность данной катушки будет на 1-2% меньше номинальной, что следует учитывать при ее изготовлении. Если для намотки берется провод большего диаметра, чем 1,43 мм, следует сделать новый расчет, увеличив диаметр или длину намотки катушки. Возможно, придется увеличить и то, и другое одновременно, пока не будут получены необходимые габариты катушки, соответствующие заданной индуктивности.
Следует заметить, что по приведенным выше формулам рекомендуется рассчитывать катушки, у которых длина намотки l равна половине диаметра или превышает эту величину. Если же она меньше половины диаметра, то более точные результаты можно получить по формулам
Пересчет катушек индуктивности производится при отсутствии провода нужного диаметра, указанного в описании конструкции, и замене его проводом другого диаметра, а также при изменении диаметра каркаса катушки.
Если отсутствует провод нужного диаметра, можно воспользоваться другим. Изменение диаметра в пределах до 25% в ту или другую сторону вполне допустимо и, как правило, не отражается на качестве работы. Более того, увеличение диаметра провода допустимо во всех случаях, так как при этом уменьшается омическое сопротивление катушки и повышается ее добротность. Уменьшение же диаметра ухудшает добротность и увеличивает плотность тока на единицу сечения провода, которая не может быть больше допустимой величины.
Пересчет количества витков однослойной цилиндрической катушки при замене провода одного диаметра другим производится по формуле
где n — новое количество витков катушки; n1 — число витков катушки, указанное в описании; d — диаметр имеющегося провода; d1 — диаметр провода, указанного в описании.
В качестве примера приведем пересчет числа витков катушки, изображенной на рис.1, для провода диаметром 0,8 мм
(длина намотки l = 18×0,8 — 14,4 мм).
Таким образом, количество витков и длина намотки несколько уменьшились. Для проверки правильности пересчета рекомендуется выполнить новый расчет катушки с измененным диаметром провода:
При пересчете катушки, связанном с изменением ее диаметра, следует пользоваться процентной зависимостью между диаметром и числом витков. Эта зависимость заключается в следующем: при увеличении диаметра катушки на определенное число процентов количество витков уменьшается на столько же процентов, и, наоборот, при уменьшении диаметра на равное число процентов увеличивается количество витков. Для упрощения расчетов за диаметр катушки можно принимать диаметр каркаса.
В качестве примера произведем пересчет числа витков катушки, имеющей 40 витков при длине намотки 2 см и диаметр каркаса 1,5 см, на диаметр, равный 1,8 см. Согласно условиям пересчета диаметр каркаса увеличивается на 3 мм, или на 20%. Следовательно, для сохранения неизменной величины индуктивности этой катушки при намотке на каркас большого диаметра нужно уменьшить число витков на 20%, или на 8 витков.
Новая катушка будет иметь 32 витка. Длина намотки также уменьшится на 20%, или до 1,6 см.
Проверим пересчет и определим допущенную погрешность. Исходная катушка имеет индуктивность:
Индуктивность новой катушки на каркасе с увеличенным диаметром:
Ошибка при пересчете составляет 0,32 мкГн, то есть меньше 2,5%, что вполне допустимо для расчетов в радиолюбительской практике.
Расчёт катушки индуктивности под динамик
Данный расчет является примером для определения данных катушки индуктивности на воздушном сердечнике, нагруженной динамиком. В этом примере выбрана катушка без сердечника во избежание искажений, обусловленных перемагничиванием сердечника.
На рисунке показана оптимальная катушка индуктивности в смысле отношения индуктивности катушки и ее активному сопротивлению. Конструкция получается, когда внутренний диаметр цилиндрического слоя обмотки вдвое больше его высоты, а внешний диаметр в четыре раза больше высоты и в два раза больше внутреннего диаметра.
высота 1 см; внутренний диаметр 2 см; внешний диаметр 4 см.
Пример расчета
Современные программы по расчету пассивных фильтров для акустики, дают значение катушек индуктивности в мГн, здесь нужно перевести в мкГн, т.е. умножить на 1000.
Определим данные катушки с индуктивностью 1,25 мГн (или 1250 мкГн) разделительного фильтра, нагруженного динамиком сопротивлением 4 Ом. Активное сопротивление рассчитываемой катушки должно составлять 5% сопротивления динамика. Это соотношение можно считать вполне приемлемым. Активное сопротивление катушки: R = 0,05 х 4 = 0,2 Ом.
- откуда: L/R = 1250 / 0,2 = 6250 мкГн/Ом;
- далее имеем: h = √ ((L/R) / 8,6) = √ (6250 / 8,6) = 26,96 мм;
- длинна жилы: l = 187,3 х √ (L х h) = 187,3 х √ (1250 х 26,96) = 34383 мм = 34,3 м;
- количество витков: ω = 19,88 √(L / h)
- диаметр жилы: d =0,84h / √ω = 0,84 х 26,96 / √ 135,36 = 1,95 мм;
- масса намотки: m = (h3 х 10-3) / 21,4 = (26,963 х 10-3) / 21,4 = (19595,65 х 0,001) / 21,4= 0,9 кг.
Полученные значения должны быть округлены (в первую очередь диаметр жилы) до ближайшего стандартизированного. Окончательные значения индуктивности подгоняют путем отматывания нескольких витков обмотки, намотанной с некоторым превышением числа витков сравнительно с рассчитанным.
Итак имеем данные, которые понадобятся для расчета будущей катушки:
- высота намотки h = 26,96 мм;
- значит внутренний диаметр a = 53,92 мм;
- соответственно внешний: b = 107,84 мм;
- длинна жилы: 34,3 м;
- количество витков: 135;
- диаметр жилы, соответствует стандартизированному: 1,95 мм (по меди).
Статья специально подготовлена для сайта ldsound.info
ПЭТВ-1
ПЭТВ-1 — это обмоточный круглый медный провод с эмалевой изоляцией на основе полиэфиров. Предназначен для …
YAMAHA NS-430
В 1974 году компания Yamaha начала выпуск 2-х полосной акустической системы с фазоинвертором.
YAMAHA NS-410
2-х полосная акустическая система от компании Yamaha. Изготавливались в 1973 году. С 1974 года выпускалась …
75 АС-015 «Союз»
3-х полосная АС изготавливалась на Брянском электромеханическом завода в конце 80-х — начале 90-х годов …
— RF Cafe
HPE изобретает первый мемристорный лазер
«Исследователи из Hewlett Packard Labs, где был создан первый практический мемристор, изобрели новую вариацию на устройство — а мемристорный лазер…»
Катушки индуктивности являются одним из четырех основных типов пассивных электронных компонентов;
остальные три — резистор,
конденсатор, и
мемристор. Катушки индуктивности представляют собой намотанные витки проволоки, прямые
отрезки провода, печатные элементы на печатных платах и на интегральных схемах (ИС)
субстраты. Формованные корпуса с радиальным и осевым выводом и пайкой для поверхностного монтажа
колодки распространены, как и катушки из проволоки, намотанной на магнитные и воздушные сердечники.
с летающими поводками. Основной единицей индуктивности является Генри (Гн).
Эти значения индуктора встречаются чаще всего (у CoilCraft большой выбор).
| 1,0 | 10 | 100 | 1000 |
| 1.1 | 11 | 110 | 1100 |
| 1,2 | 12 | 120 | 1200 |
| 1,3 | 13 | 130 | 1300 |
| 1,5 | 15 | 150 | 1500 |
| 1,6 | 16 | 160 | 1600 |
| 1,8 | 18 | 180 | 1800 |
| 2,0 | 20 | 200 | 2000 |
| 2,2 | 22 | 220 | 2200 |
| 2,4 | 24 | 240 | 2400 |
| 2,7 | 27 | 270 | 2700 |
| 3,0 | 30 | 300 | 3000 |
| 3,3 | 33 | 330 | 3300 |
| 3,6 | 36 | 360 | 3600 |
| 3,9 | 39 | 390 | 3900 |
4. 3 | 43 | 430 | 4300 |
| 4,7 | 47 | 470 | 4700 |
| 5.1 | 51 | 510 | 5100 |
| 5,6 | 56 | 560 | 5600 |
| 6.2 | 62 | 620 | 6200 |
| 6,8 | 68 | 680 | 6800 |
| 7,5 | 75 | 750 | 7500 |
| 8.2 | 82 | 820 | 8200 |
| 8,7 | 87 | 870 | 8700 |
| 9.1 | 91 | 910 | 9100 |
* Нимрод продолжает связываться со мной, чтобы сказать, что настоящего мемристора не существует.
Связанные страницы в RF Cafe
— Катушки индуктивности и Расчет индуктивности
— Преобразование индуктивности
— Стандартные значения индуктивности
— Поставщики индукторов
Справочник по симулятору: Inductor (поиск в таблице)
В этом разделе:
Запись списка соединений
Uxxxx n1 n2 имя_модели [IC=initial_condition] [USEIC=use_ic]
| n1 | узел 1 |
| н2 | узел 2 |
| начальное_условие | Исходное состояние в амперах.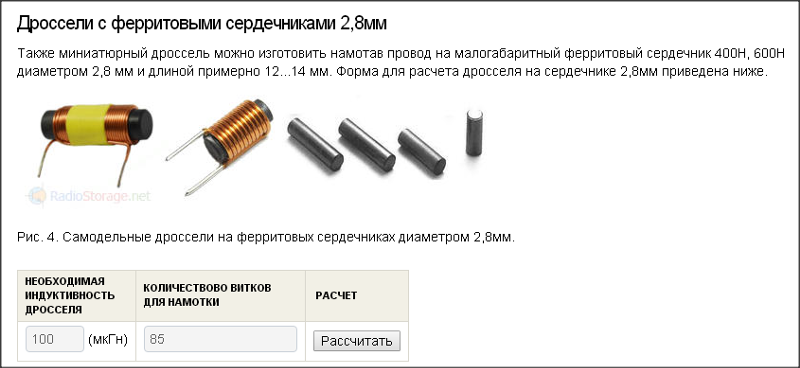 Активен, только если USEIC не равен нулю |
| use_ic 903:00 | Если не ноль, включить начальное условие. Это установит ток в индукторе на значение initial_condition во время анализа рабочей точки постоянного тока. |
Синтаксис модели
.MODEL имя_модели Параметры TABLE_INDUCTOR
| Имя | Описание | Единицы | По умолчанию |
| л | Индуктивность | 1м | Х |
| ТАБЛИЦА | Таблица насыщенности | н/д | |
| ITABLE | Текущая таблица | А | н/д |
| ТАБЛИЦА_SIZE | Количество элементов в таблицах | 2 | |
| RСЕРИЯ | Серия сопротивления | ???МАТЕМАТИКА???\Омега???МАТИКА??? | 0,0 |
| РШАНТ | Шунтовое сопротивление | ???МАТЕМАТИКА???\Омега???МАТИКА??? | 0,0 (устанавливается в INF) |
| LМИН | Минимальная индуктивность | Х | 0,0 |
| ГЛАДКИЙ | Параметр сглаживания (0-3) | 0 |
Пример модели
.
MODEL TABLE_IND table_inductor L=1 USEIC=0 IC=0
+ RSERIES=0 RSHUNT=0 SMOOTH=2 TABLE_SIZE=7
+ ITABLE=[0, 8,3333, 16,666, 25, 33,3333, 41,666, 50]
+ LTABLE=[3.36e-07, 3.36e-07, 3.34e-07, 3.27e-07, 3.09е-07, 1.86е-07, 4.21е-08] В приведенном выше примере индуктивность 3,36e-07H при 0A снижается до 4,21e-08 при 50A.
Граничная индуктивность
Индуктивность для этого устройства определяется справочной таблицей в определенном диапазоне. Однако необходимо также определить поведение при токах, превышающих значения, указанные в таблице. Мы называем индуктивность «граничной индуктивностью». Отсюда следует характеристика формы: 9{2})+LМИН/л \]
Где ???МАТИКА???А???МАТИКА??? и ???МАТИКА???С???МАТИКА??? выбираются таким образом, чтобы абсолютная индуктивность и ???МАТИКА???\frac{dL}{di}???МАТИКА??? соответствует табличной функции в конечной точке.
Функция сглаживания
Параметр SMOOTH может быть установлен на целое число от 1 до 4, чтобы выбрать функцию сглаживания.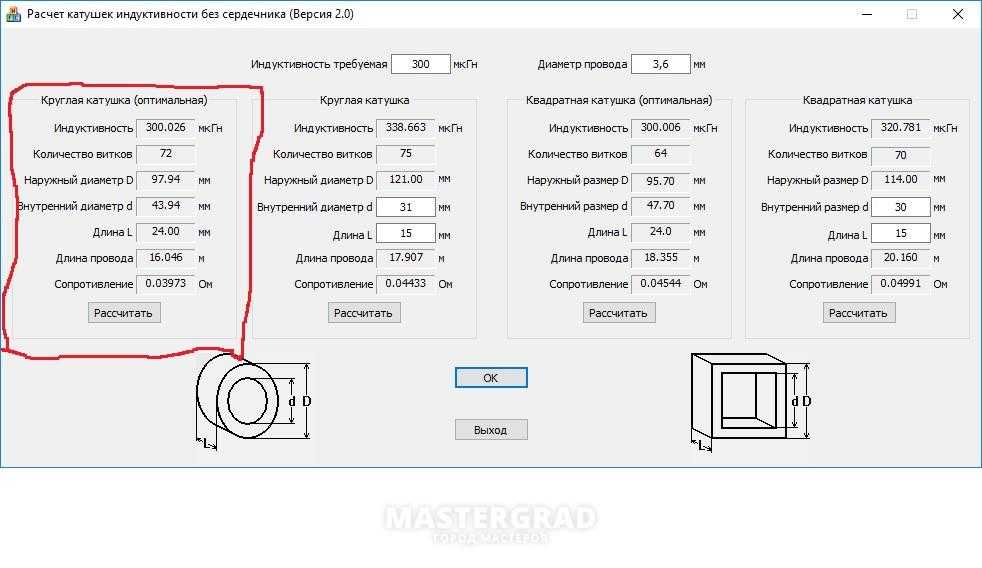
В следующей таблице описаны доступные альтернативные стратегии:
| ГЛАДКОЕ значение | Функция |
| 0 | Функция сглаживания не выбрана. Индуктор соответствует PWL (кусочно-линейной) характеристике |
| 1 | Местный куб. Подбирает кубический полином между каждой парой точек таким образом, чтобы градиент в каждой точке был средним значением наклона по обе стороны от точки. Это непрерывно в первой производной, но не непрерывно во второй производной |
| 2 | Кубический сплайн с граничными условиями: ниже: ???MATH???\frac{dL}{di}=0???MATH??? верхний: ???MATH???\frac{d^{2}L}{di^{2}} = 0???MATH??? |
| 3 | Кубический сплайн с граничными условиями: ниже: ???MATH???\frac{dL}{di}=0???MATH??? верхний: ???MATH???\frac{dL}{di}= \text{slope_of_final_segment}???MATH??? |
SMOOTH=2 и SMOOTH=3 выбирают функцию кубического сплайна.
